Optimizing Periodic Intervals in Multi-Stage Waveguide Stub Bandstop Filters for Microwave Leakage Suppression
Abstract
1. Introduction
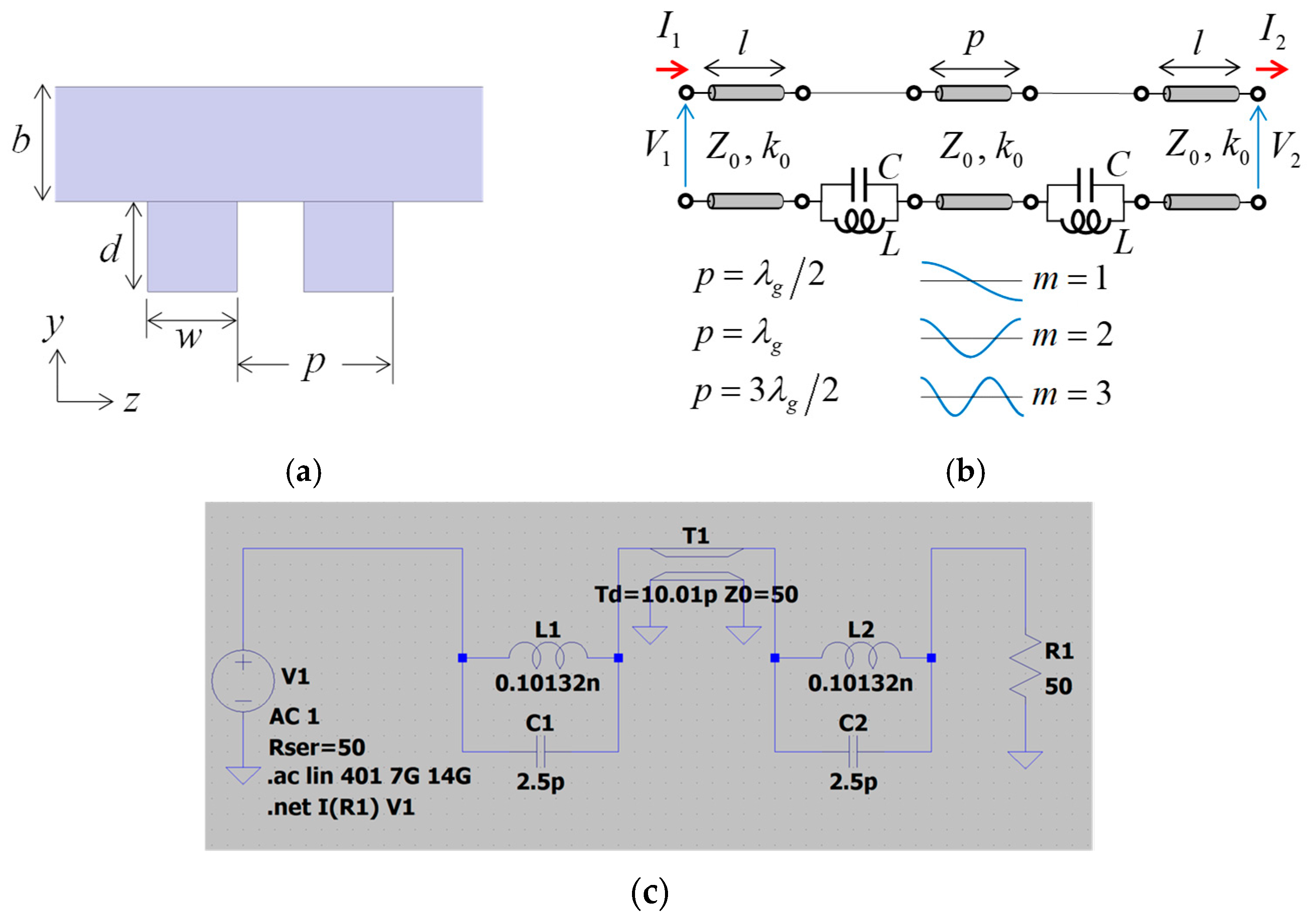
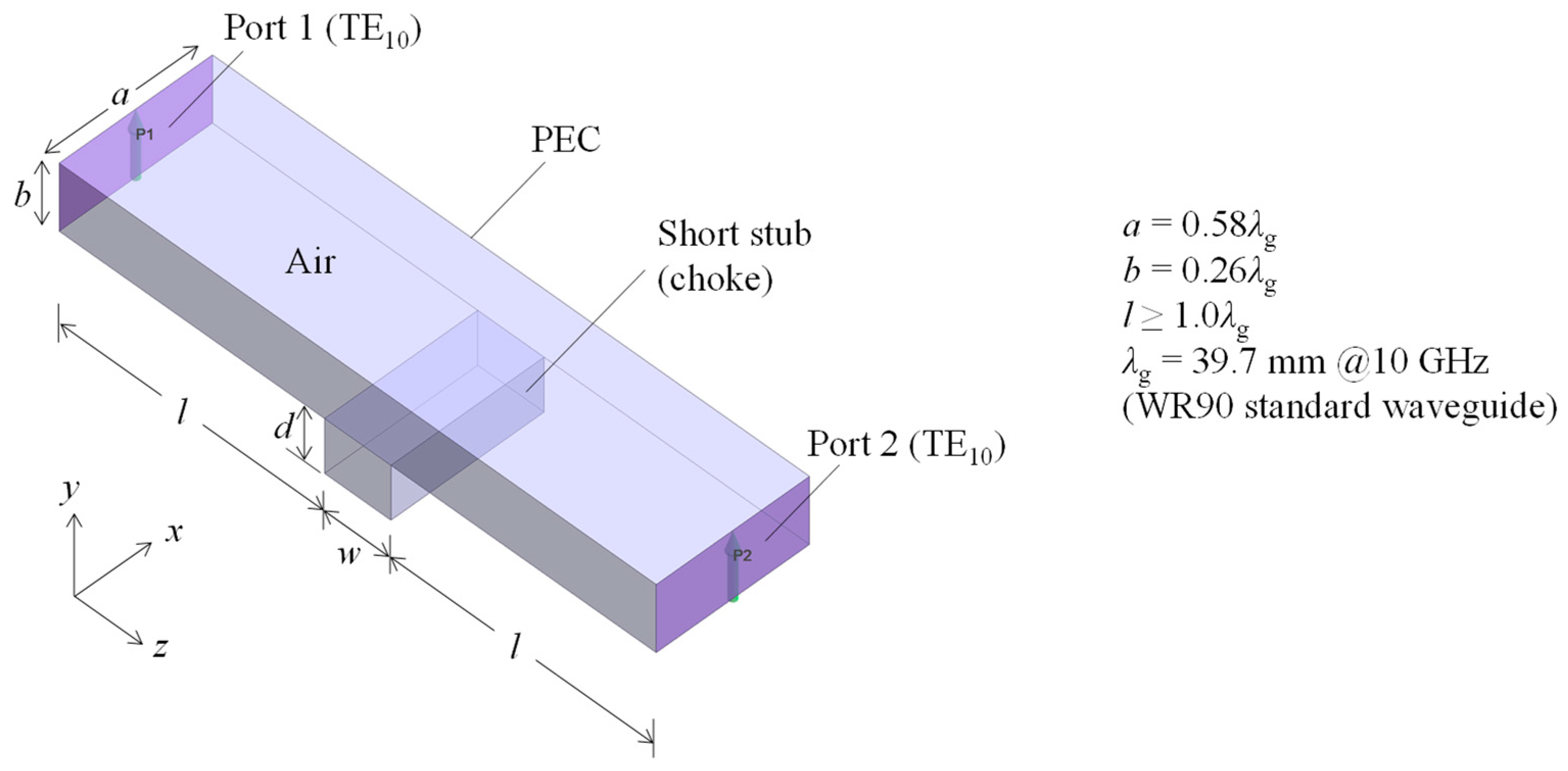
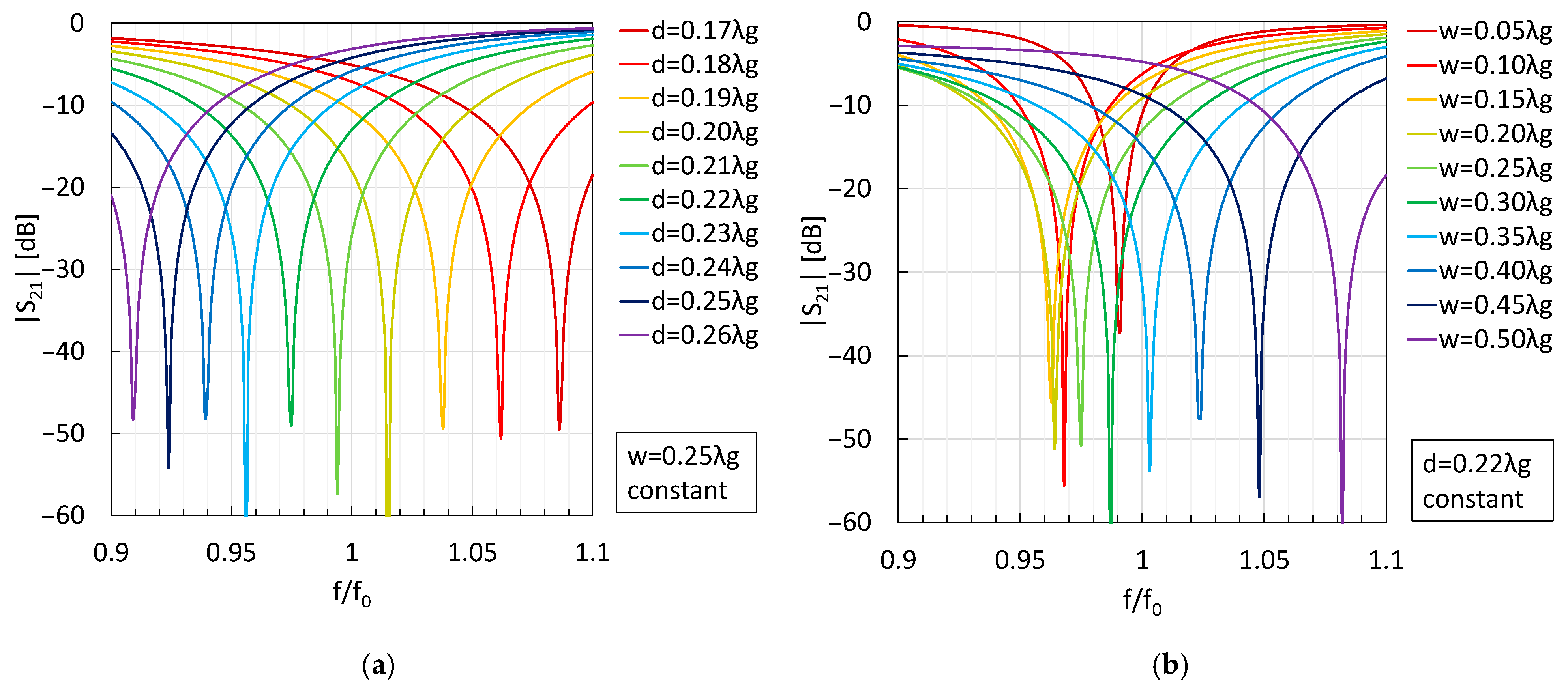
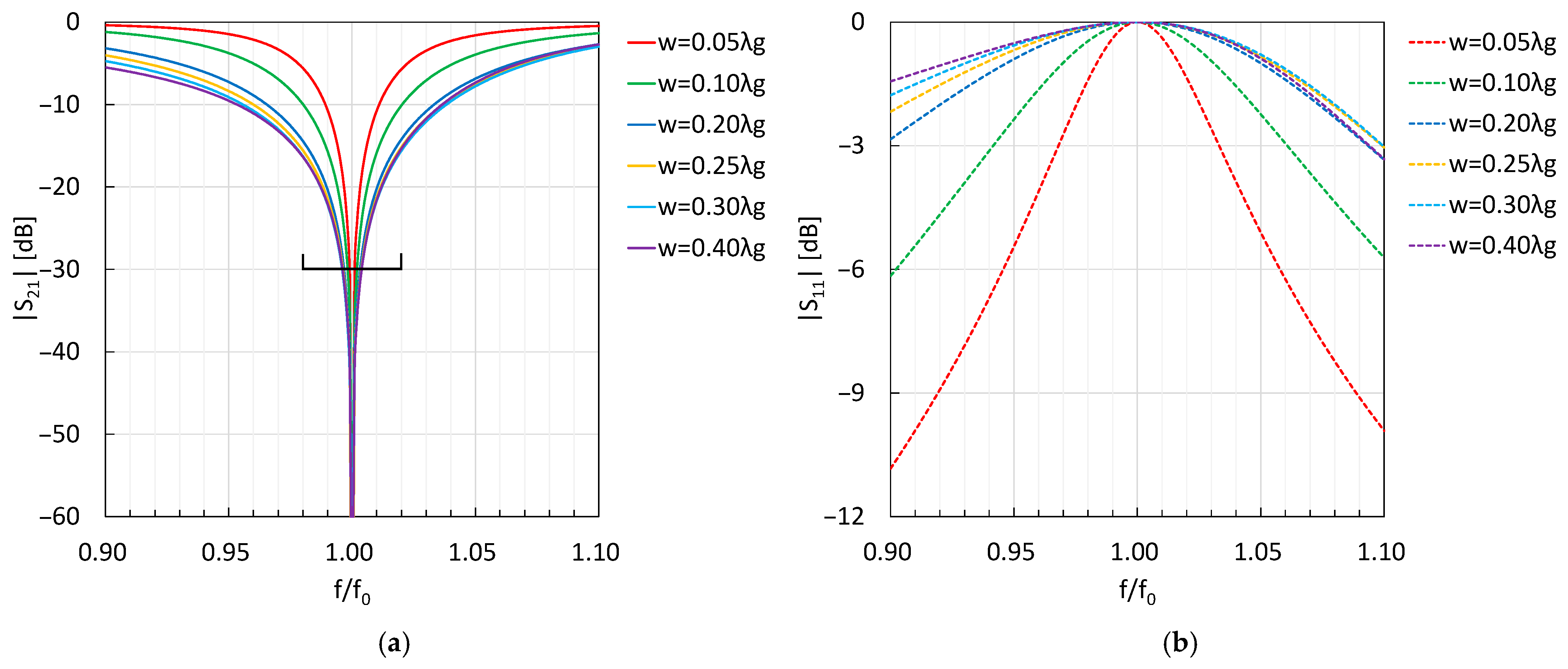
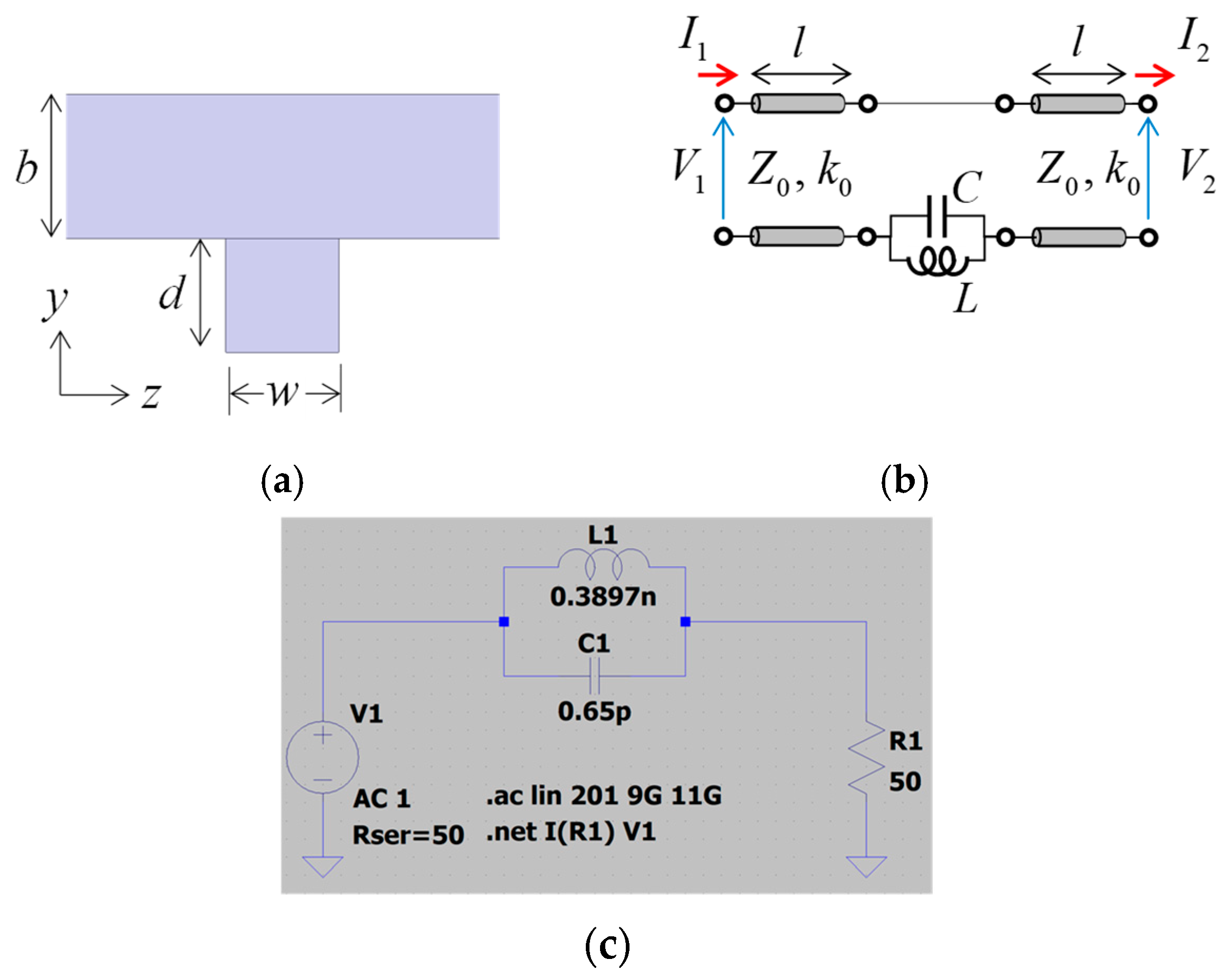
2. Characteristics of a Single Stub
2.1. Electromagnetic Field Simulation
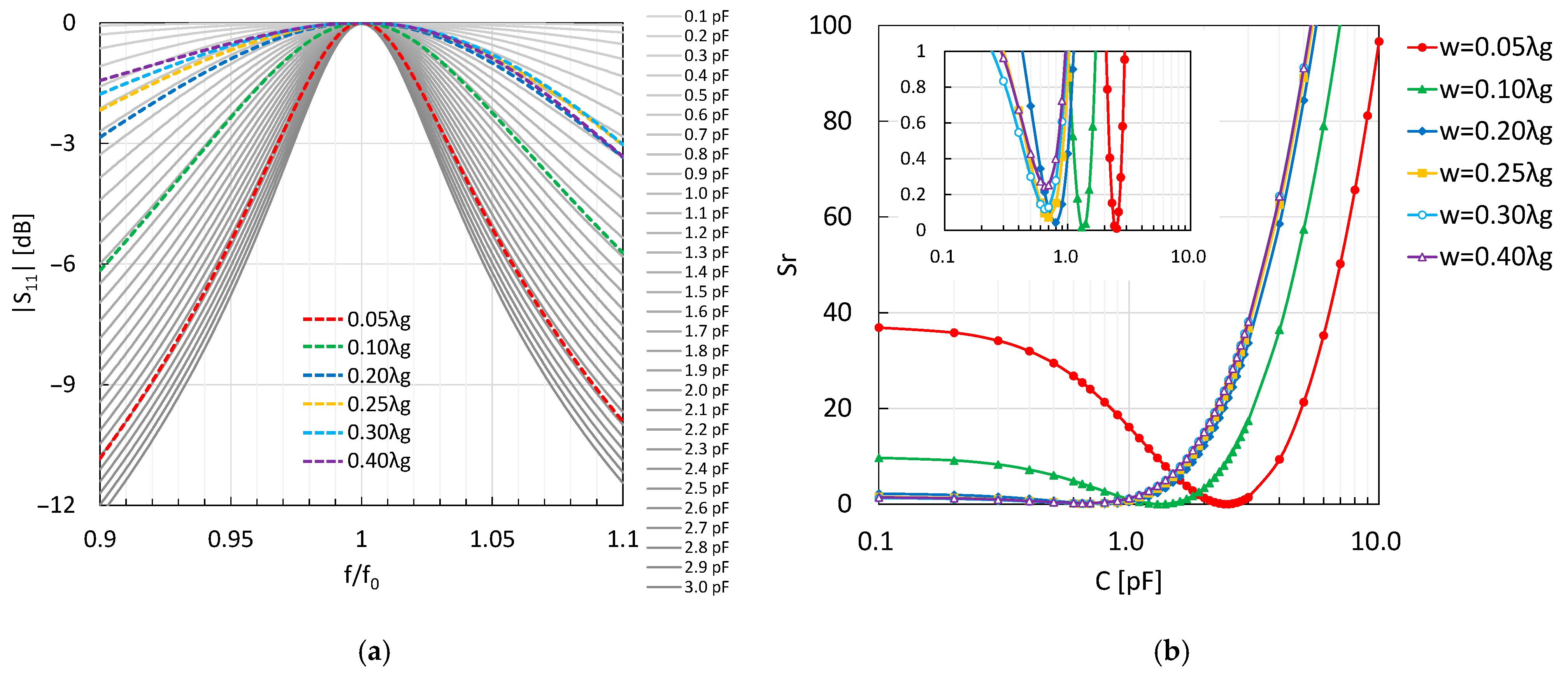
2.2. Extraction of Equivalent Circuit Element Values
3. Characteristics of Two-Stage Cascaded Stub
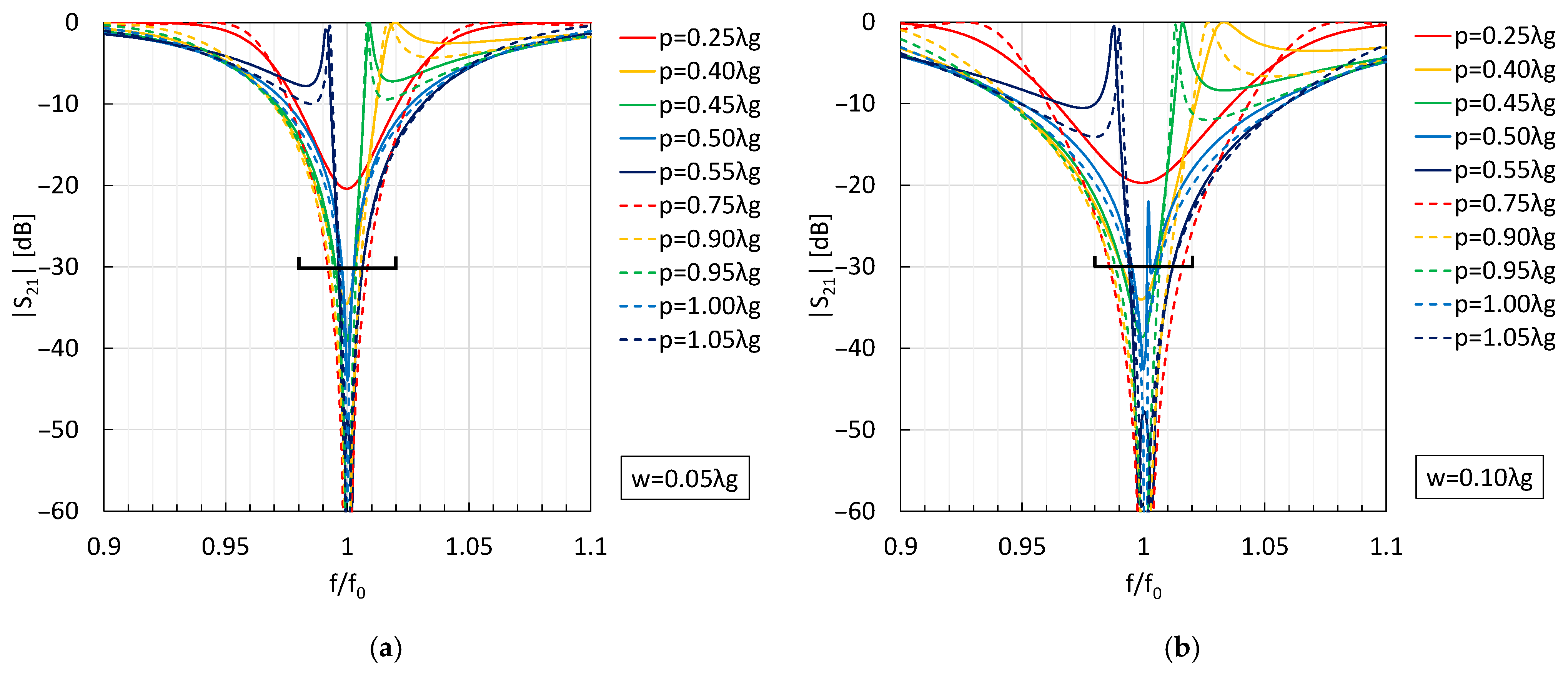
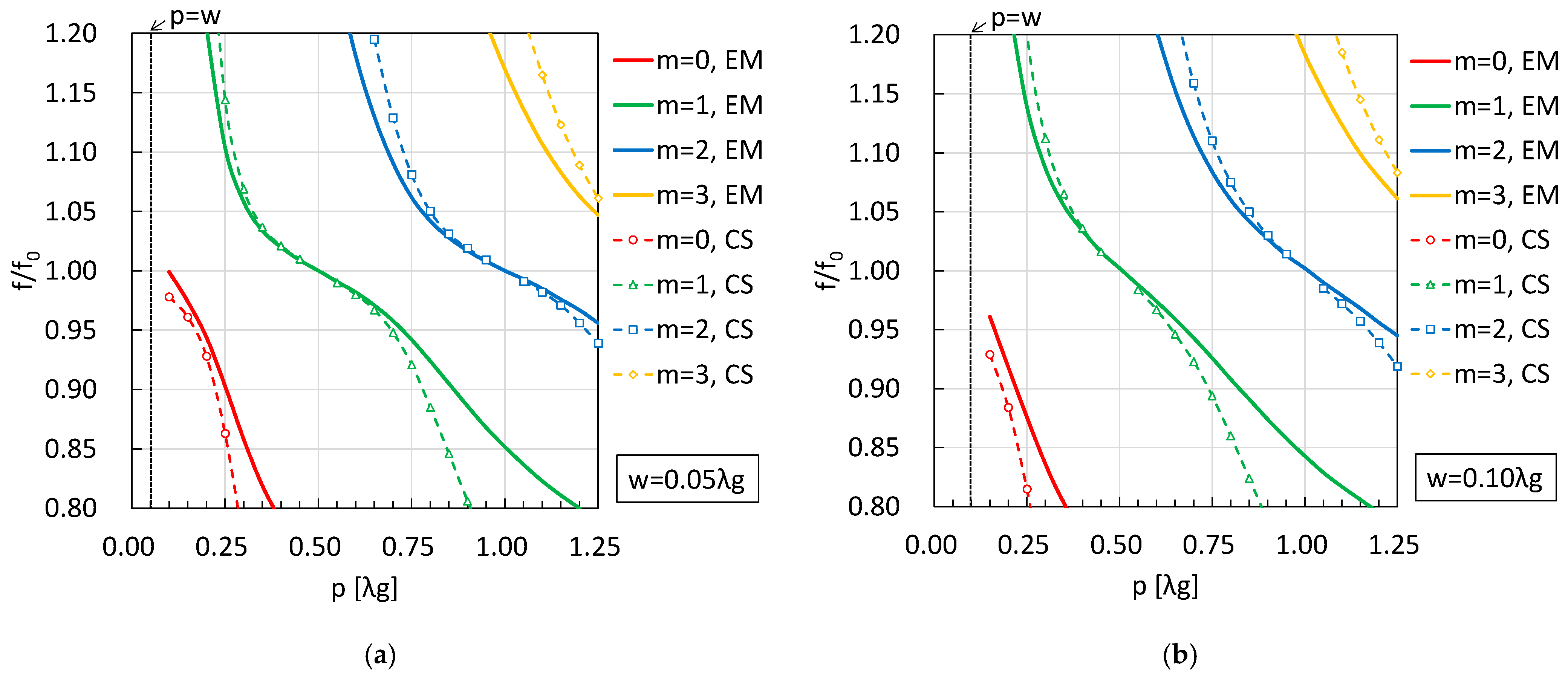
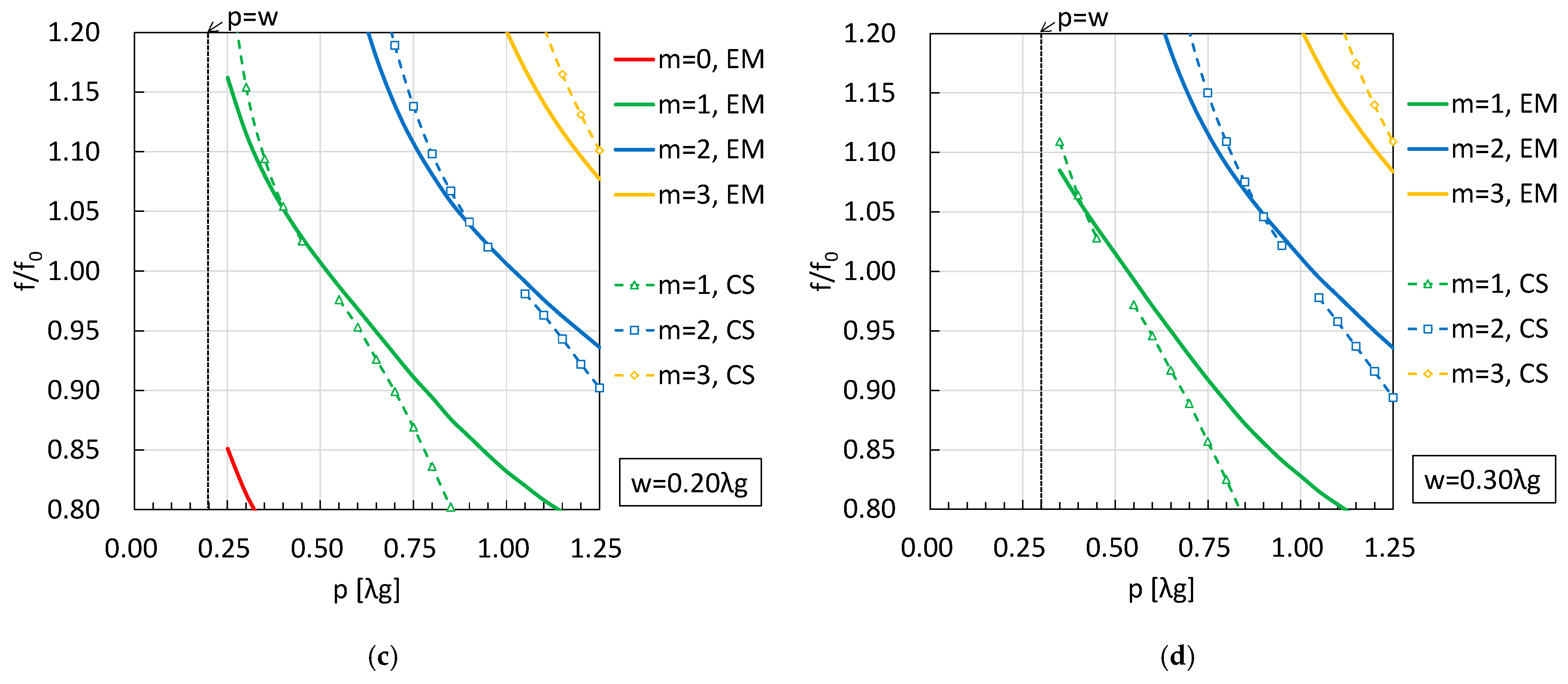
3.1. Cascade Characteristics
3.2. Spurious Generation Mechanism
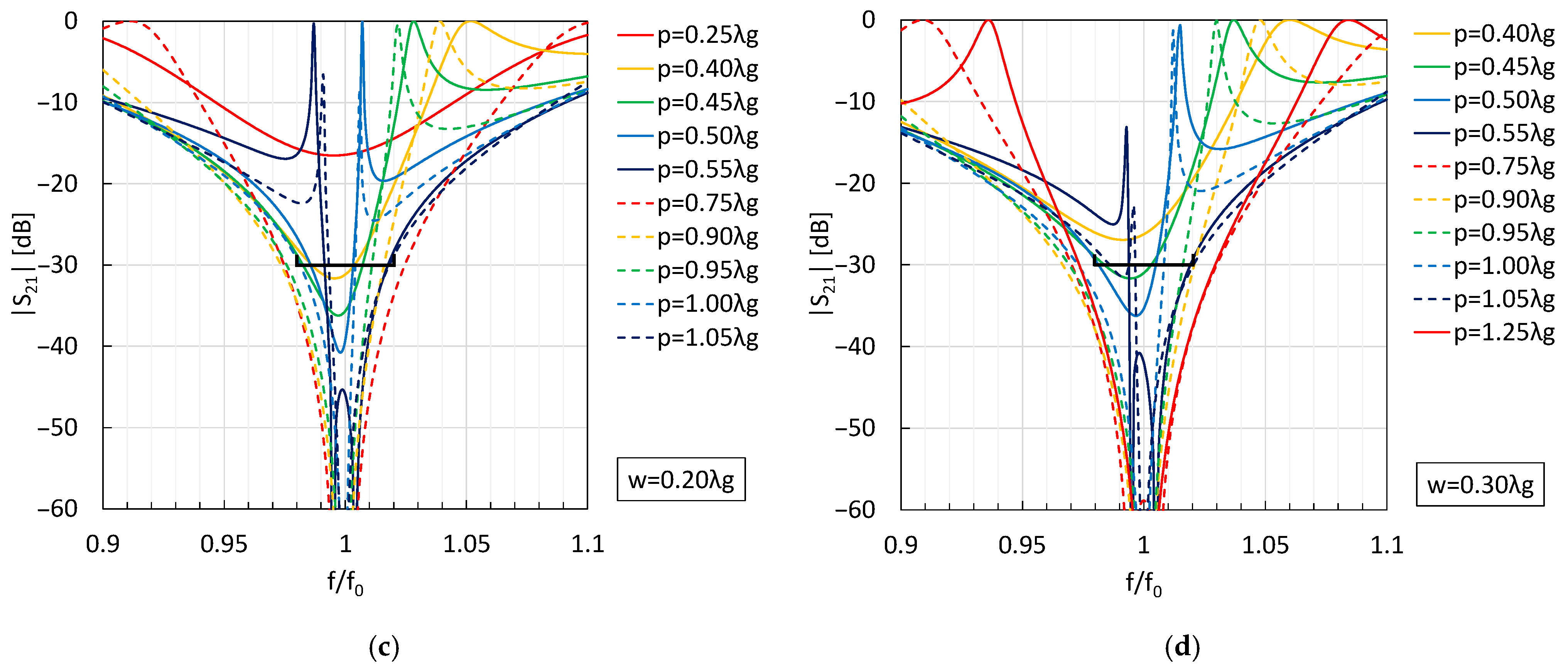
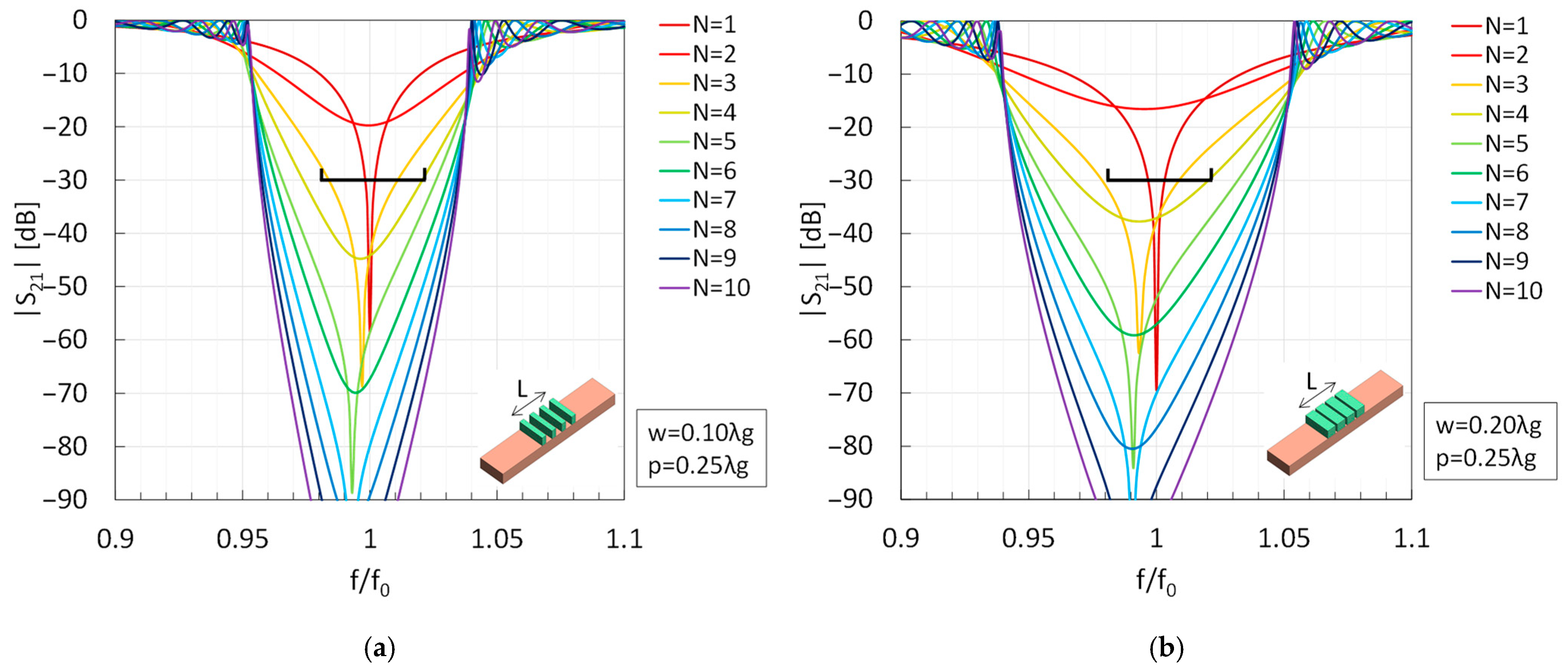
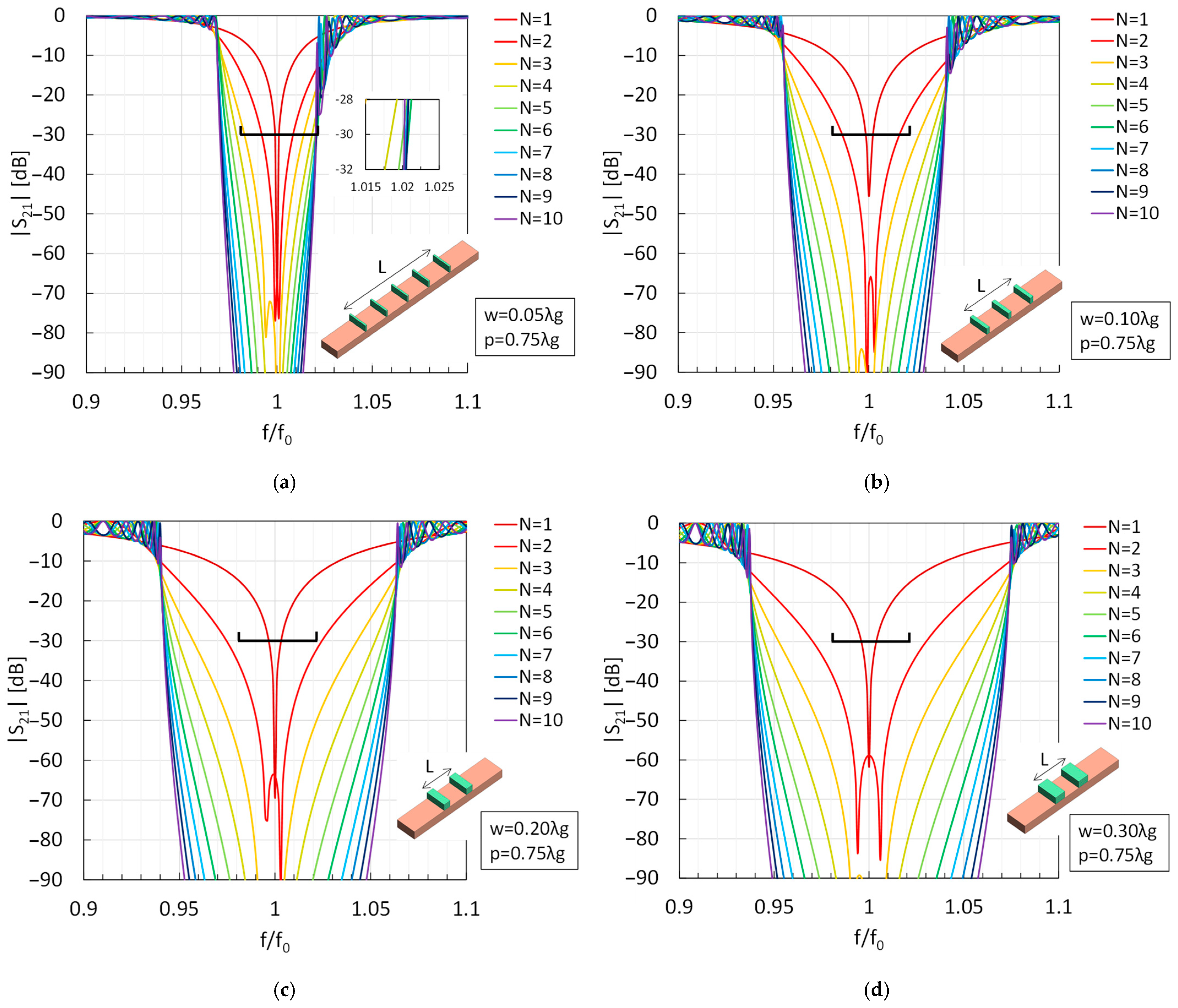
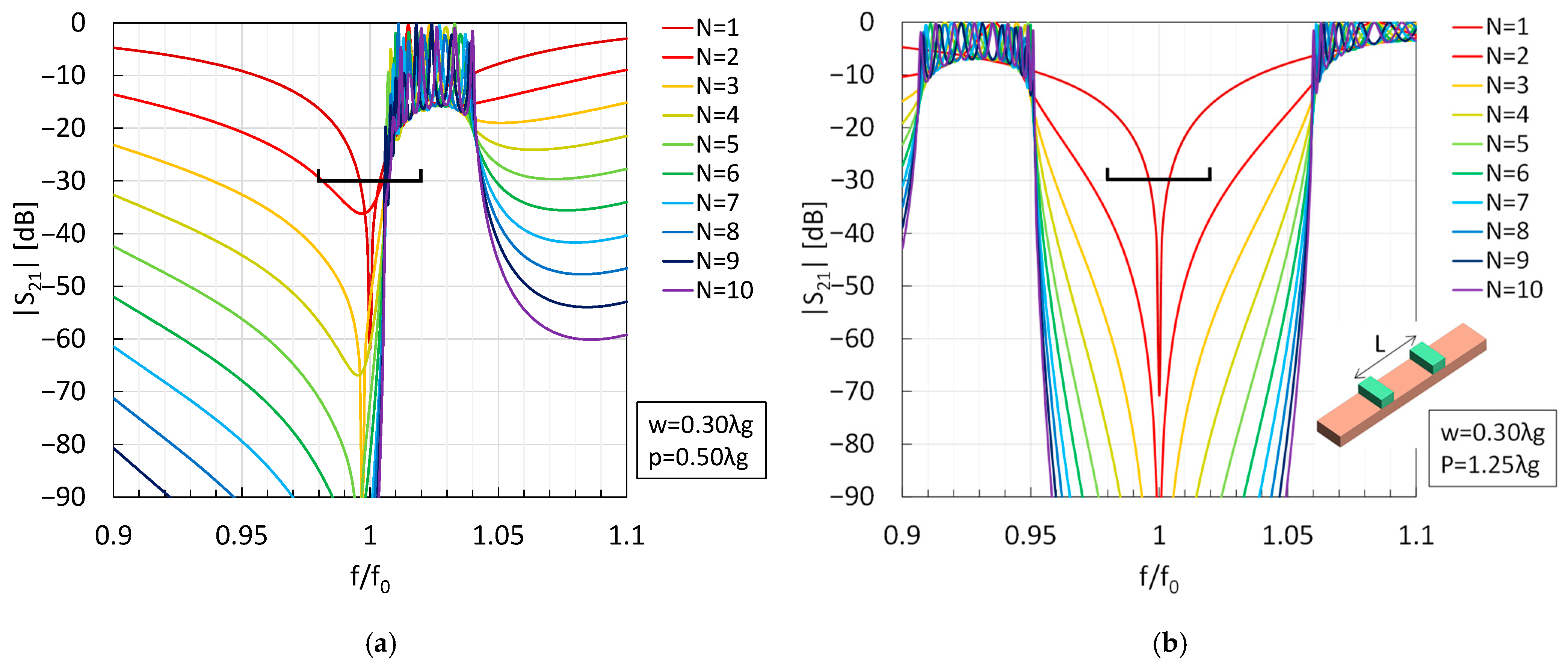
4. Multi-Stage Cascaded Stubs
Multi-Stage Characteristics
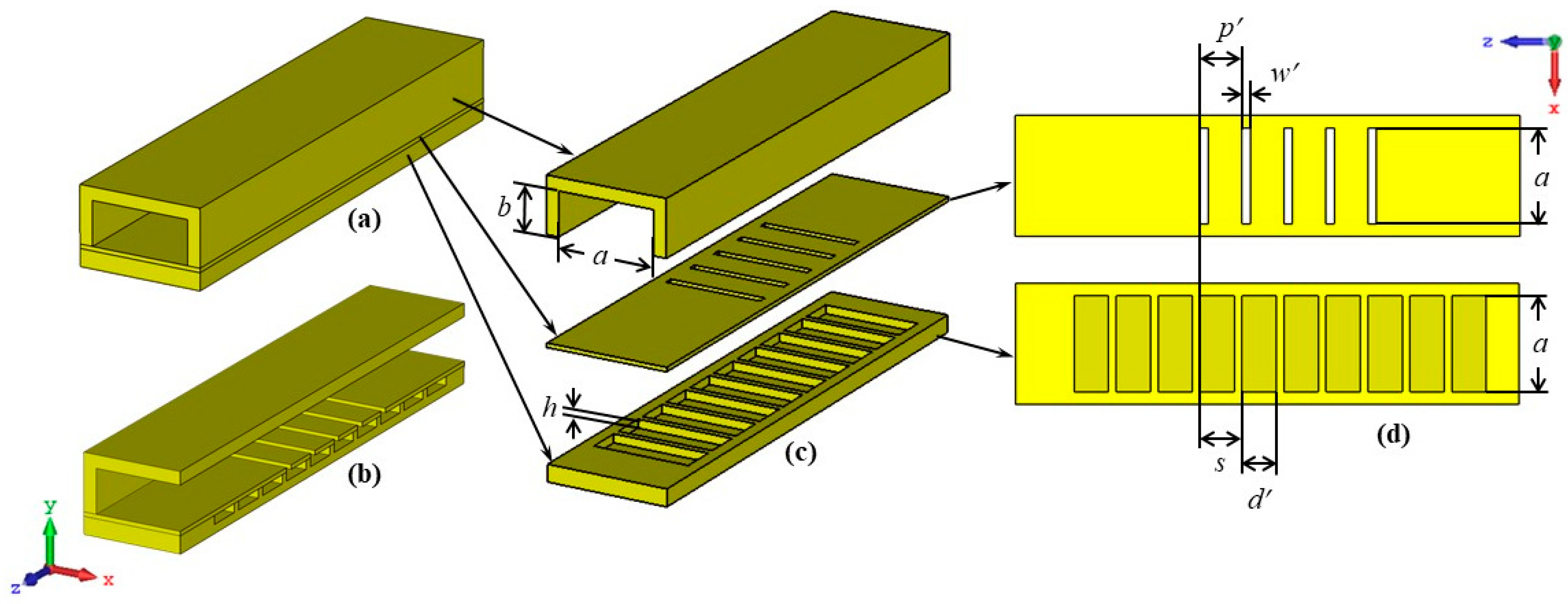
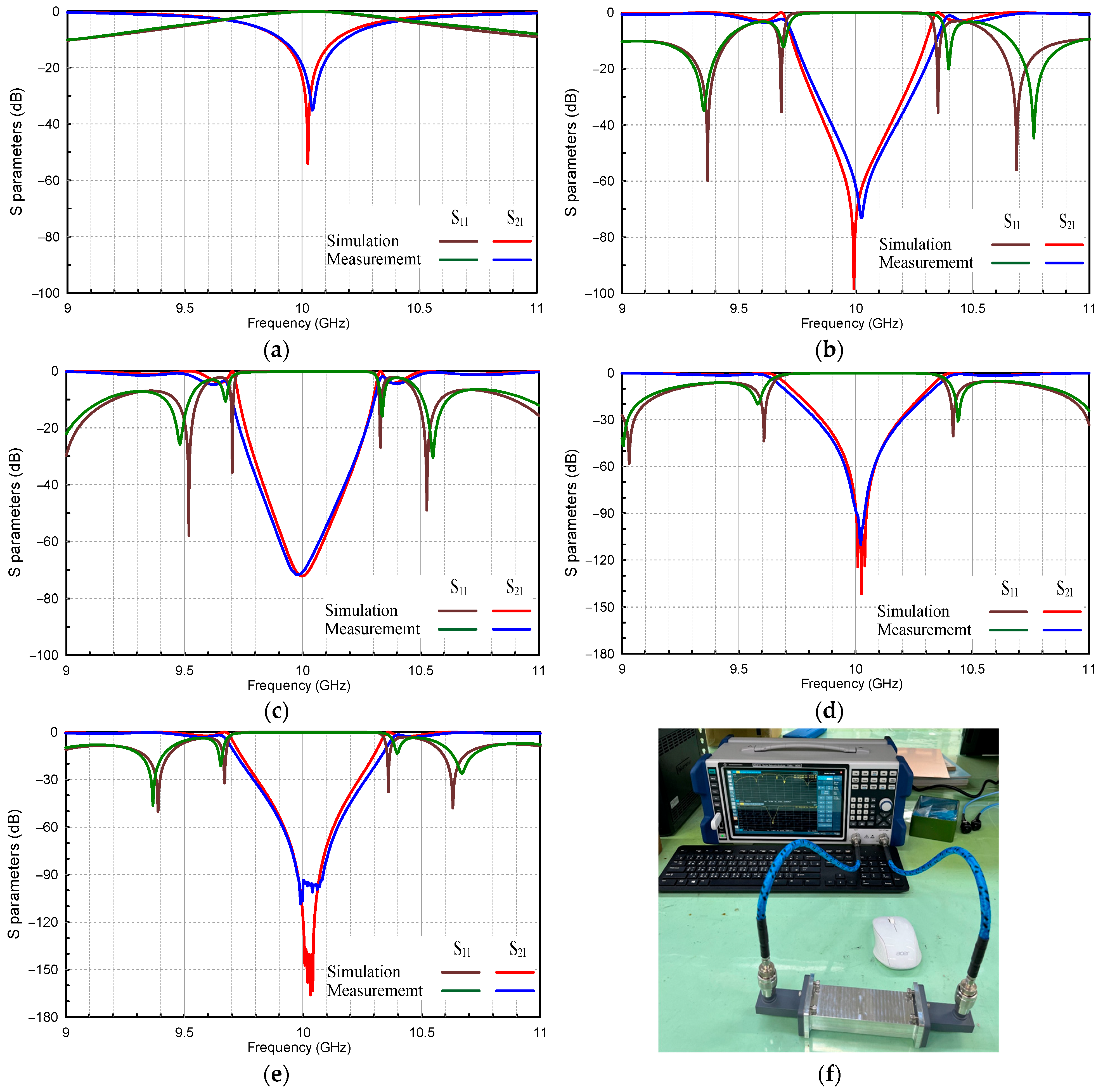
5. Experimental Validation and Measurement Results
6. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Iwabuchi, K.; Fukai, I.; Kashiwa, T. Consumer Applications of Microwaves: Microwave Ovens and Accessories. In Handbook of Microwave Technology; Ishii, T.K., Ed.; Academic Press: San Diego, CA, USA, 1995; Volume 2, pp. 249–275. [Google Scholar]
- Kim, E.; Kim, B.; Nam, S. Analysis of electromagnetic wave transmission through a choke using FE-BIM with arbitrary incident angle/polarization. IEEE Trans. Electromagn. Compat. 1997, 39, 11. [Google Scholar] [CrossRef]
- Pyne, B.; Naruse, R.; Saito, H.; Hirokawa, J.; Ravindra, V.; Akbar, P.R. Robust Contactless Noncircular Choke Flange for Wideband Waveguide Applications. IEEE Trans. Microw. Theory Tech. 2019, 67, 861–867. [Google Scholar] [CrossRef]
- Yagitani, S.; Katsuda, K.; Nojima, M.; Yoshimura, Y.; Sugiura, H. Imaging Radio-Frequency Power Distributions by an EBG Absorber. IEICE Trans. Commun. 2011, E94-B, 2306–2315. [Google Scholar] [CrossRef]
- Li, Y.; Jin, Y.; Raza, H.; Wang, Y.; Chen, Q.; Zou, X.; Ren, Z.; Guo, J.; Zheng, G.; Cheng, J. Dual driving strategy from micro-polarization to macroscopic conductance: Tailoring optimized low-frequency and wide-band microwave absorption in high-entropy oxides. J. Mater. Sci. Technol. 2025, 235, 110–121. [Google Scholar] [CrossRef]
- Matthaei, G.L.; Young, L.; Jones, E.M.T. Microwave Filters, Impedance-Matching Networks, and Coupling Structures; Artech House: Norwood, MA, USA, 1980; pp. 725–773. [Google Scholar]
- Cameron, R.J.; Kudsia, C.M.; Mansour, R.R. Microwave Filters for Communication Systems: Fundamentals, Design, and Applications; Wiley: Hoboken, NJ, USA, 2018; pp. 335–338. [Google Scholar]
- Levy, R. Compact waveguide bandstop filters for wide stopbands. In Proceedings of the 2009 IEEE MTT-S International Microwave Symposium Digest, Boston, MA, USA, 7–12 June 2009. [Google Scholar]
- Zou, H.; Wu, J.; Zhu, M. Ultra-wide Stopband Waveguide Low-pass Filter Design Based on Asymmetric Inductance Unit Structure. In Proceedings of the 2021 IEEE 3rd International Conference on Circuits and Systems (ICCS), Chengdu, China, 29–31 October 2021. [Google Scholar]
- Lin, J.-Y.; Wong, S.-W.; Qian, L.; Wang, Y.; Yang, Y.; Liu, Q.-H. Single and Multiple-Band Bandpass Filters Using Bandstop Resonator Sections. IEEE J. Microw. 2024, 4, 293–302. [Google Scholar] [CrossRef]
- Sullca, J.F.V.; Cogollos, S.; Boria, V.E.; Guglielmi, M.; Bastioli, S.; Snyder, R.V. Dual-Reject-Band Filters With Resonant Apertures in Rectangular Waveguide. IEEE Trans. Microw. Theory Tech. 2025, 73, 606–619. [Google Scholar] [CrossRef]
- D’Auria, M.; Otter, W.J.; Hazell, J.; Gillatt, B.T.W.; Long-Collins, C.; Ridler, N.M. 3-D Printed Metal-Pipe Rectangular Waveguides. IEEE Trans. Compon. Packag. Manuf. Technol. 2015, 5, 1339–1349. [Google Scholar] [CrossRef]
- Massoni, E.; Guareschi, M.; Bozzi, M.; Perregrini, L.; Tamburini, U.A.; Alaimo, G. 3D printing and metalization methodology for high dielectric resonator waveguide microwave filters. In Proceedings of the IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Pavia, Italy, 20–22 September 2017. [Google Scholar]
- Yoneda, S.; Shiraki, Y.; Sasaki, Y.; Miyazaki, C. A Gasket-Free Electromagnetic Shielding Structure for 2.4-GHz and 5-GHz Bands Using Cascaded Dual-Behavior SIW Resonators. IEEE Trans. Electromagn. Compat. 2020, 62, 377–385. [Google Scholar] [CrossRef]
- Xu, F.; Wu, K. Guided-wave and leakage characteristics of substrate integrated waveguide. IEEE Trans. Microw. Theory Tech. 2005, 53, 66–73. [Google Scholar] [CrossRef]
- VanKoughnett, A.L.; Dunn, J.G. Doubly Corrugated Chokes For Microwave Heating Systems. J. Microw. Power 1973, 8, 101–110. [Google Scholar] [CrossRef]
- Iwabuchi, K.; Kubota, T.; Sugaya, Y.; Kashiwa, T.; Itiro, F. Effect of Conductor Losses in New-Structure Filters for Suppressing Microwave Leakage. IEICE Trans. Jpn. Part I Electron. 1992, 75, 179–187. [Google Scholar] [CrossRef]
- Soto, P.; Boria, V.E.; Catala-Civera, J.M.; Chouaib, N.; Guglielmi, M.; Gimeno, B. Analysis, Design, and Experimental Verification of Microwave Filters for Safety Issues in Open-Ended Waveguide Systems. IEEE Trans. Microw. Theory Tech. 2000, 48, 2133–2140. [Google Scholar] [CrossRef]
- Kildal, P.-S.; Alfonso, E.; Nogueira, A.; Iglesias, E. Local Metamaterial-Based Waveguides in Gaps Between Parallel Metal Plates. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 84–87. [Google Scholar] [CrossRef]
- Kirino, H.; Ogawa, K. A 76 GHz Multi-Layered Phased Array Antenna Using a Non-Metal Contact Metamaterial Waveguide. IEEE Trans. Antennas Propag. 2012, 60, 840–853. [Google Scholar] [CrossRef]
- Brazález, A.A.; Rajo-Iglesias, E.; Vázquez-Roy, J.L.; Vosoogh, A.; Kildal, P.-S. Design and Validation of Microstrip Gap Waveguides and Their Transitions to Rectangular Waveguide, for Millimeter-Wave Applications. IEEE Trans. Microw. Theory Tech. 2015, 63, 4035–4050. [Google Scholar] [CrossRef]
- Kirino, H.; Honda, K.; Li, K.; Ogawa, K. A Waffle-Iron Ridge Guide with Combined Fast- and Slow-Wave Modes for Array Antenna Applications. IEICE Trans. Commun. 2018, 101, 349–356. [Google Scholar] [CrossRef]
- Rezaee, M.; Zaman, A.U. Groove Gap Waveguide Filter Based on Horizontally Polarized Resonators for V-Band Applications. IEEE Trans. Microw. Theory Tech. 2020, 68, 2601–2609. [Google Scholar] [CrossRef]
- Sievenpiper, D.; Zhang, L.; Broas, R.F.J.; Alexopolous, N.G.; Yablonovitch, E. High-impedance electromagnetic surfaces with a forbidden frequency band. IEEE Trans. Microw. Theory Tech. 1999, 47, 2059–2074. [Google Scholar] [CrossRef]
- Abhari, R.; Eleftheriades, G.V. Metallo-dielectric electromagnetic bandgap structures for suppression and isolation of the parallel-plate noise in high-speed circuits. IEEE Trans. Microw. Theory Tech. 2003, 51, 1629–1639. [Google Scholar] [CrossRef]
- Mishrikey, M. Analysis and Design of Metamaterials. Ph.D. Thesis, Swiss Federal Institute of Technology, Zurich, Switzerland, 2010. [Google Scholar]
- Kawakami, Y.; Hori, T.; Fujimoto, M.; Yamaguchi, R.; Cho, K. Low-Profile Design of Metasurface Considering FSS Filtering Characteristics. IEICE Trans. Commun. 2012, 95, 477–483. [Google Scholar] [CrossRef]
- Siegel, P.H. Microwaves Are Everywhere: Ovens: From Magnetrons to Metamaterials. IEEE J. Microw. 2021, 1, 523–531. [Google Scholar] [CrossRef]
- Kusama, Y. The Secret of Microwave Oven Doors to Prevent Radio Wave Leakage. In RF World No.51; CQ Publishing: Tokyo, Japan, 2020; pp. 88–96. [Google Scholar]
- Kusuma, Y. Simulations related to reducing leakage waves through gaps. In Interference Countermeasures and Future Prospects for Cooperation/Fusion of Wireless Power Transmission and 5G Communication; Hashimoto, O., Ed.; CMC Publishing: Tokyo, Japan, 2023; pp. 134–141. [Google Scholar]
- Murayama, K.; Kusama, Y. Experimental Study on Miniaturization of Waveguide E-Plane Stubs by Inserting Capacitive Windows. IEICE Trans. Jpn. Electron. 2024, 107, 17–24. [Google Scholar]
- Murata Software Femtet. Available online: https://www.muratasoftware.com/ (accessed on 30 November 2024).
- Ghanevati, M. Fundamentals of RF and Microwave Circuit Design: Practical Analysis and Design Tools, 2nd ed.; RFPTA: River Forest, IL, USA, 2019; pp. 45–47. [Google Scholar]
- S-Parameters with LTspice. Available online: https://wireless-square.com/2016/11/01/s-parameters-with-ltspice/ (accessed on 30 November 2024).
- Marcuvitz, N. Waveguide Handbook; Peter Peregrinus: London, UK, 1986; pp. 336–350. [Google Scholar]
- Harvey, A.F. Microwave Engineering; Academic Press: New York, NY, USA, 1963; pp. 435–495. [Google Scholar]
- Collin, R.E. Foundations for Microwave Engineering, 2nd ed.; McGraw-Hill: New York, NY, USA, 1992; pp. 550–585. [Google Scholar]
- Pozar, D.M. Microwave Engineering, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 381–388. [Google Scholar]
- Vale, C.A.W.; Meyer, P.; Palmer, K.D. A design procedure for bandstop filters in waveguides supporting multiple propagating modes. IEEE Trans. Microw. Theory Tech. 2000, 48, 2496–2503. [Google Scholar] [CrossRef]
- Lech, R.; Mazur, J. Propagation in rectangular waveguides periodically loaded with cylindrical posts. IEEE Microw. Wirel. Compon. Lett. 2004, 14, 177–179. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, B.; Chen, Q.; Wu, K. Simulation-Assisted Formulas for Propagation Constant in Periodic Structures. IEEE Antennas Wirel. Propag. Lett. 2025, 24, 3659–3663. [Google Scholar] [CrossRef]

| w [λg] | d [λg] | b [λg] | w/b | fL/f0 | fH/f0 | BW | FBW [%] |
|---|---|---|---|---|---|---|---|
| 0.05 | 0.2158 | 0.26 | 0.19 | 0.999 | 1.001 | 0.02 | 0.2 |
| 0.10 | 0.2045 | 0.26 | 0.39 | 0.999 | 1.002 | 0.03 | 0.3 |
| 0.20 | 0.2030 | 0.26 | 0.78 | 0.997 | 1.003 | 0.06 | 0.6 |
| 0.25 | 0.2071 | 0.26 | 0.97 | 0.997 | 1.003 | 0.06 | 0.6 |
| 0.30 | 0.2134 | 0.26 | 1.17 | 0.996 | 1.003 | 0.07 | 0.7 |
| 0.40 | 0.2319 | 0.26 | 1.56 | 0.997 | 1.003 | 0.06 | 0.6 |
| w [λg] | d [λg] | C [pF] | L [nH] | XC [Ω] | XL [Ω] | xC [Ω] | xL [Ω] |
|---|---|---|---|---|---|---|---|
| 0.05 | 0.2158 | 2.50 | 0.1013 | −6.366 | 6.366 | −0.127 | 0.127 |
| 0.10 | 0.2045 | 1.30 | 0.1949 | −12.24 | 12.24 | −0.245 | 0.245 |
| 0.20 | 0.2030 | 0.80 | 0.3166 | −19.89 | 19.89 | −0.398 | 0.398 |
| 0.25 | 0.2071 | 0.70 | 0.3619 | −22.74 | 22.74 | −0.455 | 0.455 |
| 0.30 | 0.2134 | 0.65 | 0.3897 | −24.49 | 24.49 | −0.490 | 0.490 |
| 0.40 | 0.2319 | 0.65 | 0.3897 | −24.49 | 24.49 | −0.490 | 0.490 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kusama, Y.; Chen, H.-H.; Hsu, Y.-W.; Murayama, K.; Johnston, R.W. Optimizing Periodic Intervals in Multi-Stage Waveguide Stub Bandstop Filters for Microwave Leakage Suppression. Electronics 2025, 14, 4660. https://doi.org/10.3390/electronics14234660
Kusama Y, Chen H-H, Hsu Y-W, Murayama K, Johnston RW. Optimizing Periodic Intervals in Multi-Stage Waveguide Stub Bandstop Filters for Microwave Leakage Suppression. Electronics. 2025; 14(23):4660. https://doi.org/10.3390/electronics14234660
Chicago/Turabian StyleKusama, Yusuke, Hao-Hui Chen, Yao-Wen Hsu, Kyohei Murayama, and Robert Weston Johnston. 2025. "Optimizing Periodic Intervals in Multi-Stage Waveguide Stub Bandstop Filters for Microwave Leakage Suppression" Electronics 14, no. 23: 4660. https://doi.org/10.3390/electronics14234660
APA StyleKusama, Y., Chen, H.-H., Hsu, Y.-W., Murayama, K., & Johnston, R. W. (2025). Optimizing Periodic Intervals in Multi-Stage Waveguide Stub Bandstop Filters for Microwave Leakage Suppression. Electronics, 14(23), 4660. https://doi.org/10.3390/electronics14234660





