Influence of Multi-Source Electromagnetic Coupling on NVH in Automotive PMSMs
Abstract
1. Introduction
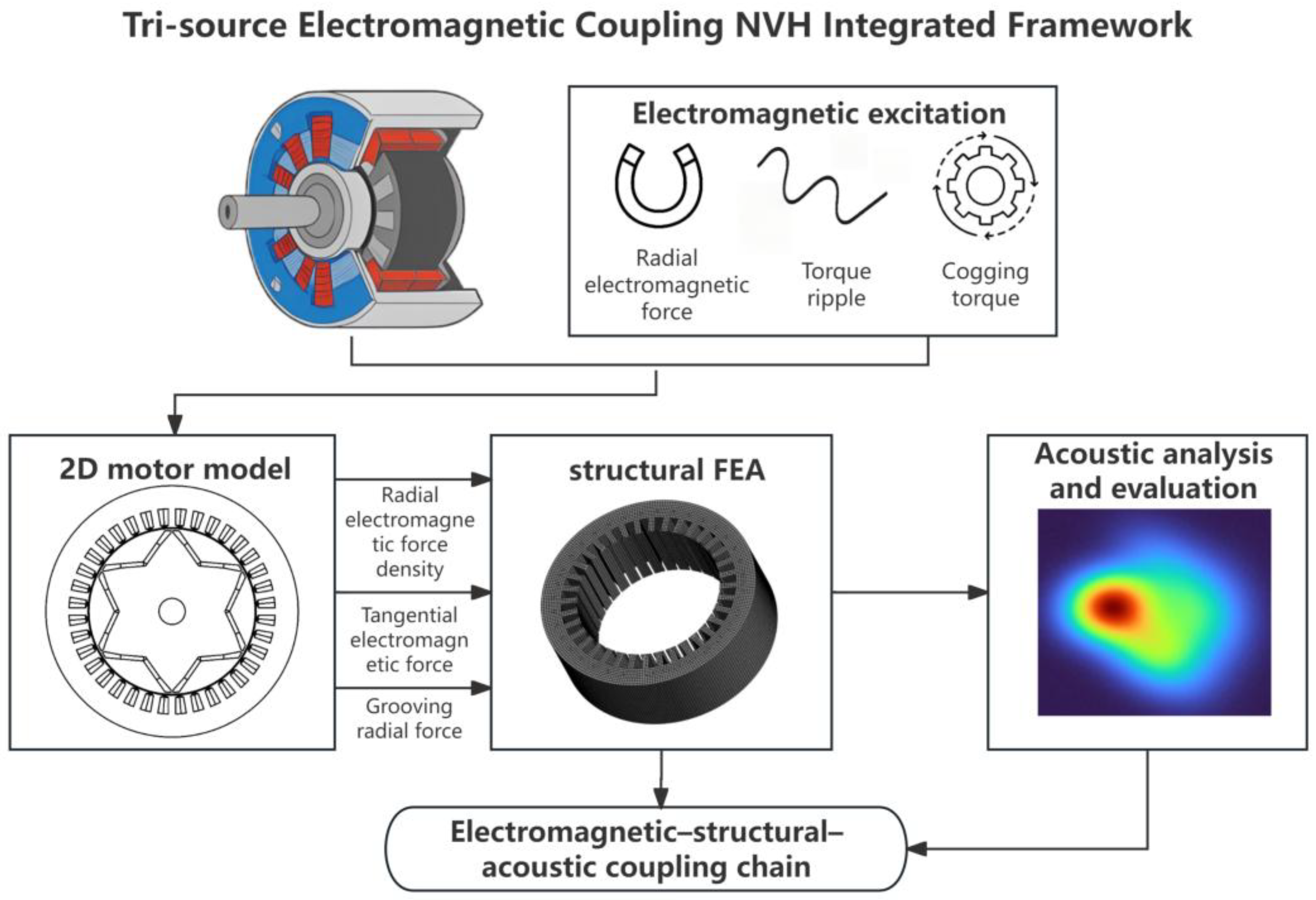
- A Tri-ECNVH integrated three-source coupling framework is proposed, in which radial electromagnetic force harmonics, torque ripple (tangential force), and cogging torque are uniformly mapped into the order domain and synthesized at the complex-amplitude level on a same-order basis.
- An integrated computational chain combining electromagnetic FEA, structural vibro-acoustic coupling, and BEM acoustic analysis is established for a 6-pole 36-slot PMSM; using A-weighted SPL as a unified metric, it enables quantitative assessment of the coupled contributions of the three excitation sources on a consistent scale.
2. Motor Electromagnetic Noise Analysis
2.1. Motor Parameters
2.2. Two-Dimensional Finite Element Model of the PMSM
3. Electromagnetic Noise Analysis of Three Excitation Sources
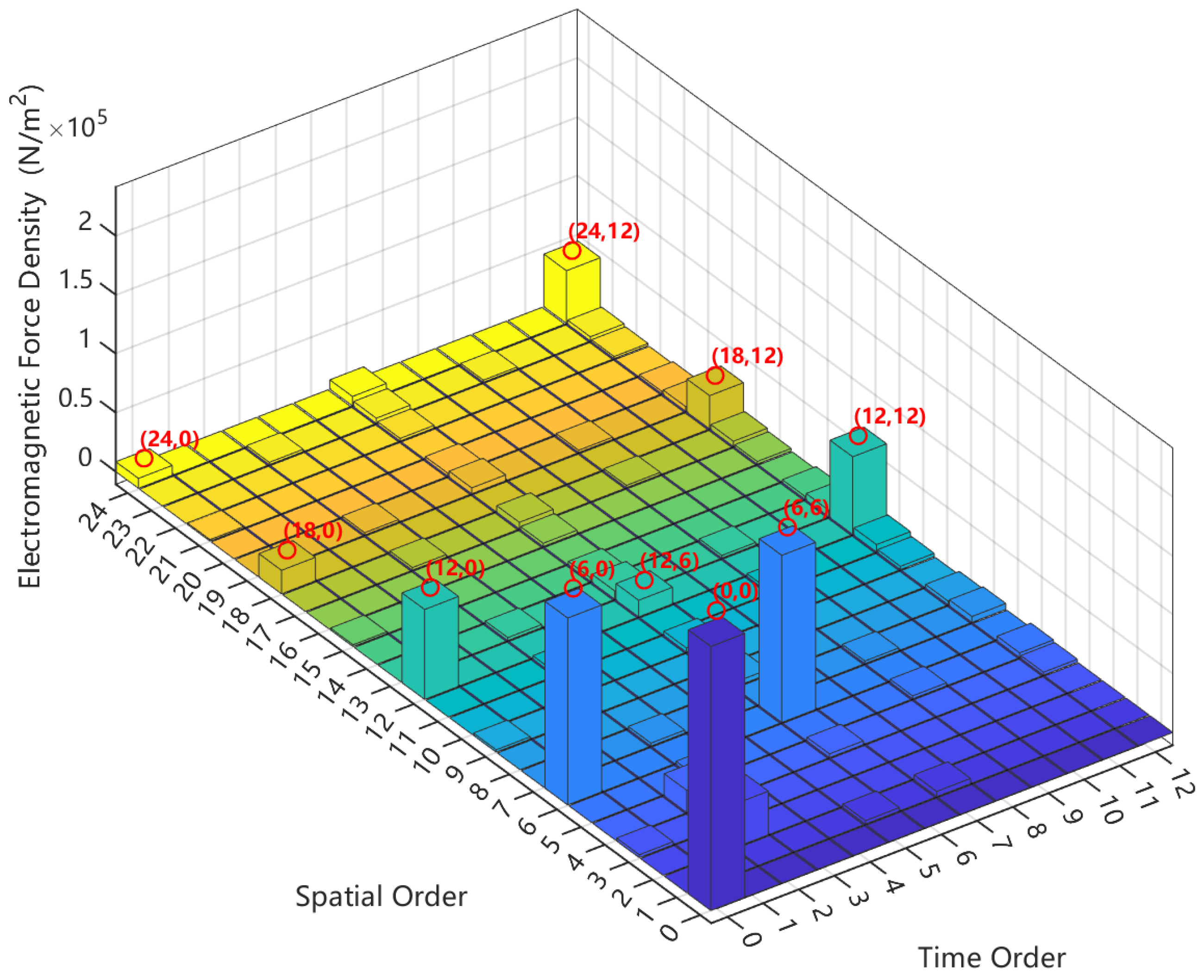
3.1. Electromagnetic Force Analysis
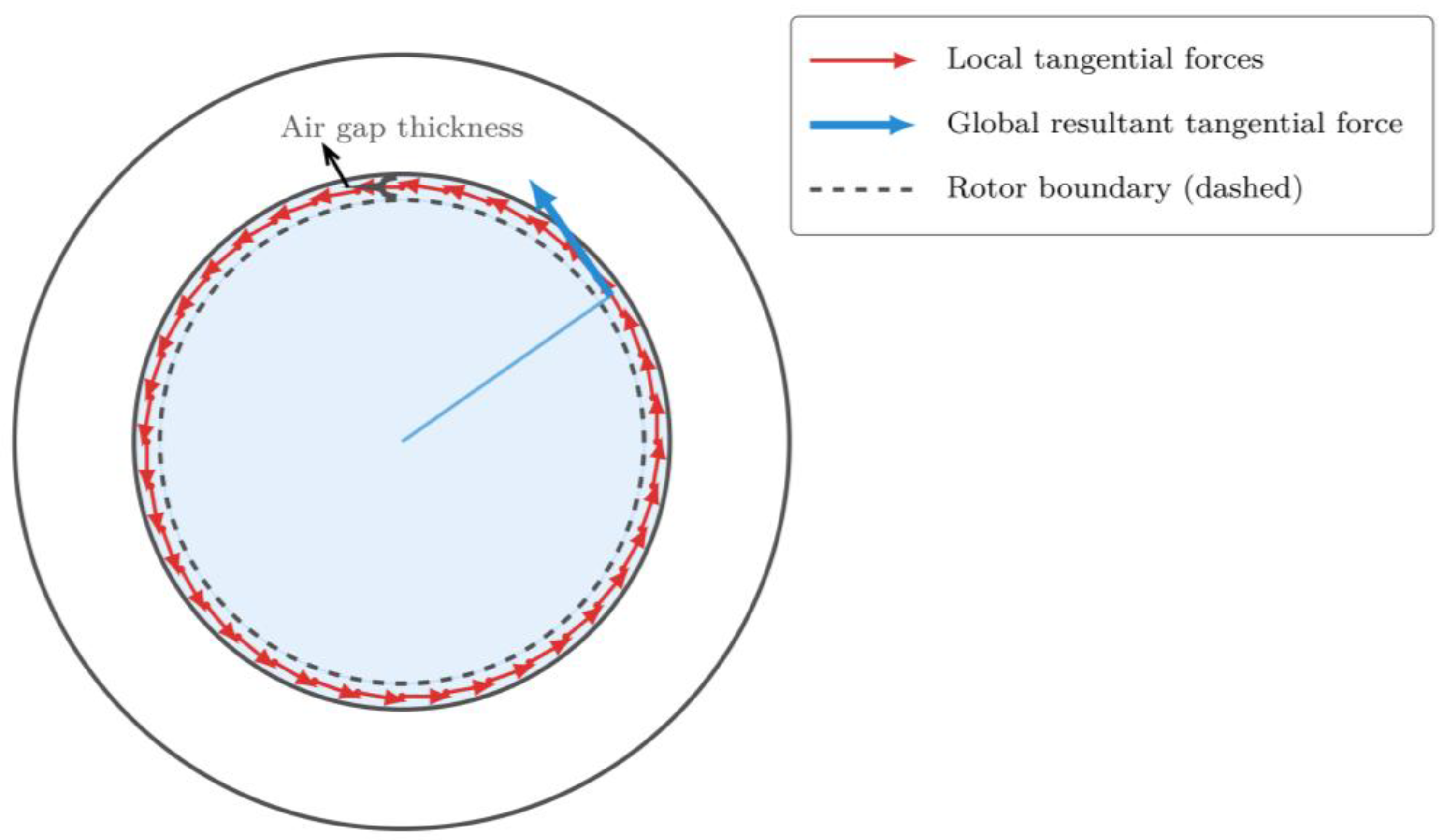
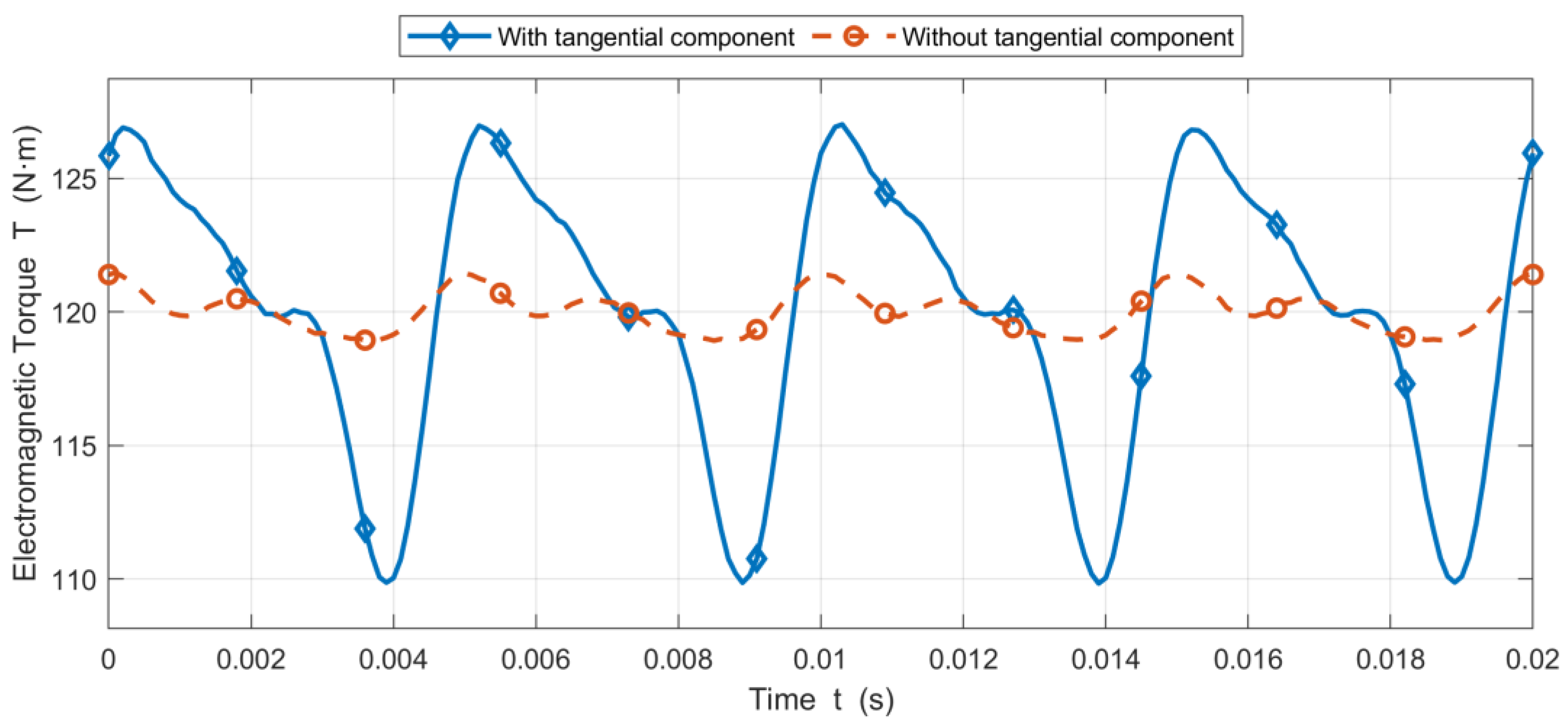
3.2. Torque Ripple Analysis
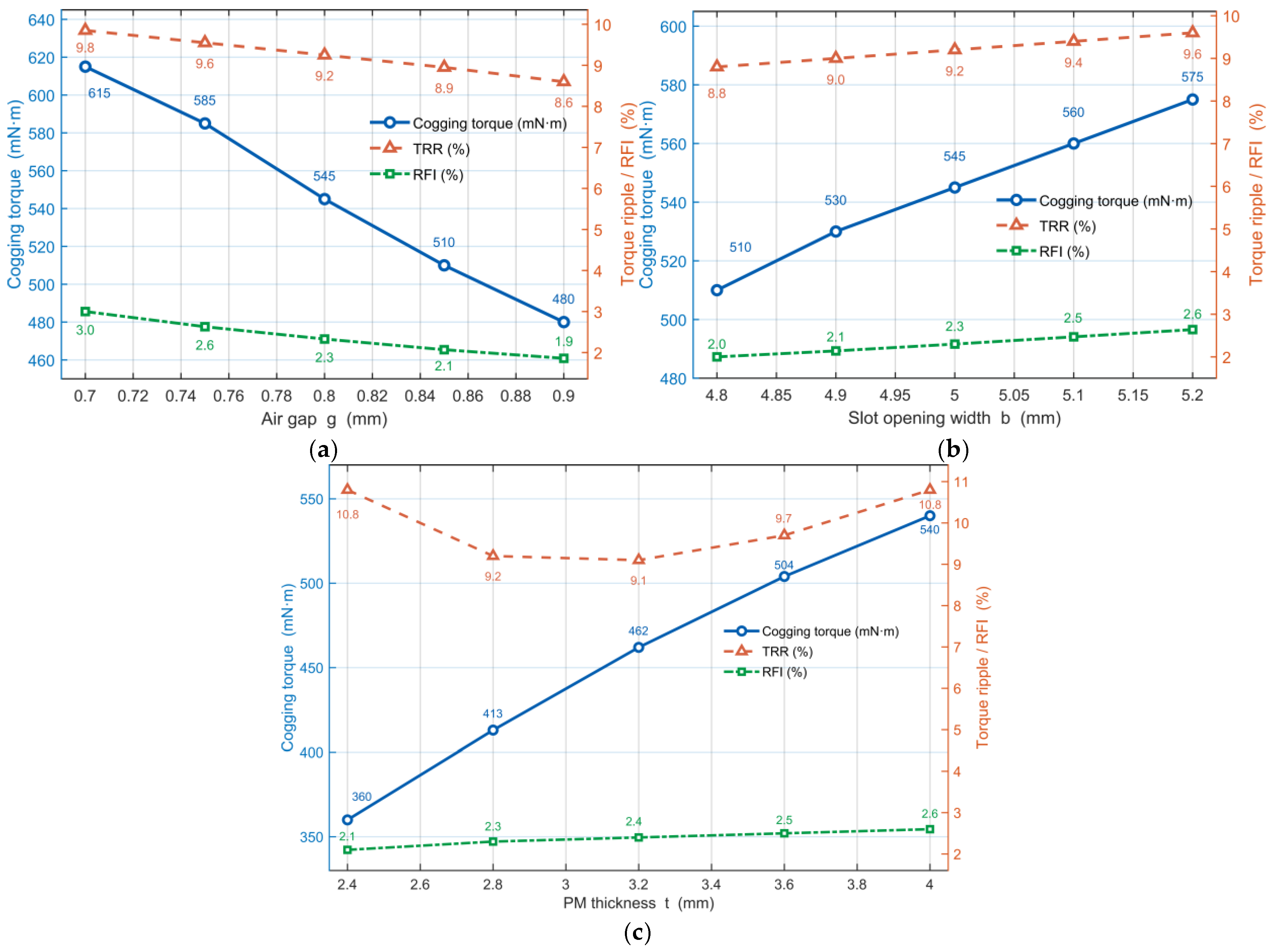
3.3. Cogging Torque Analysis
4. Structural Analysis and Vibro-Acoustic Prediction
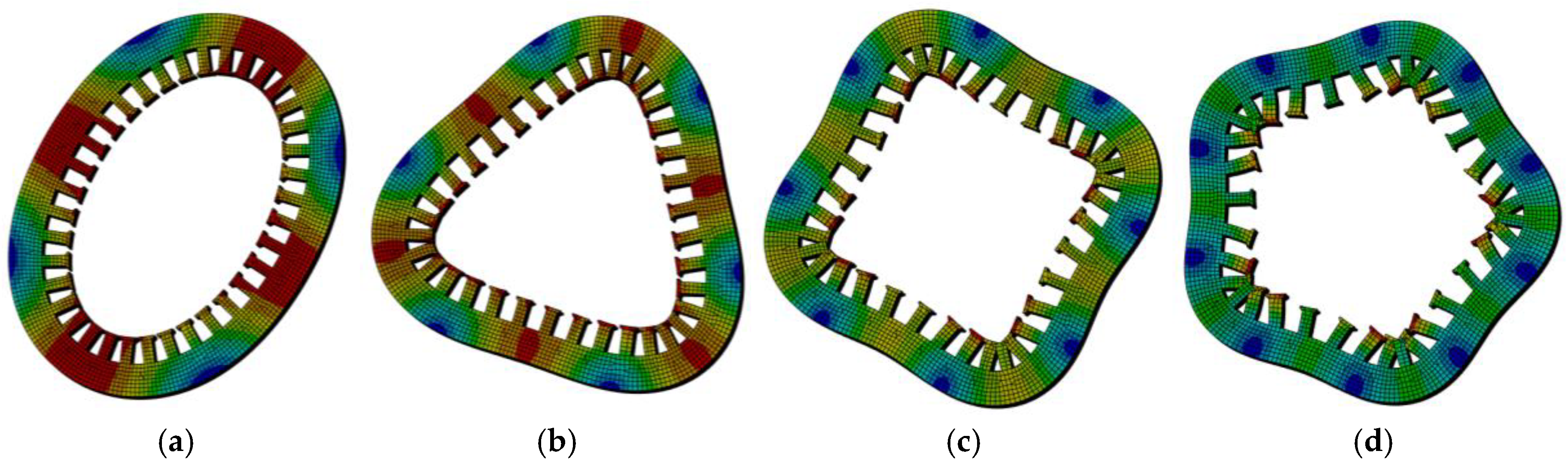
4.1. Structural Analytical Model and Order Alignment Verification
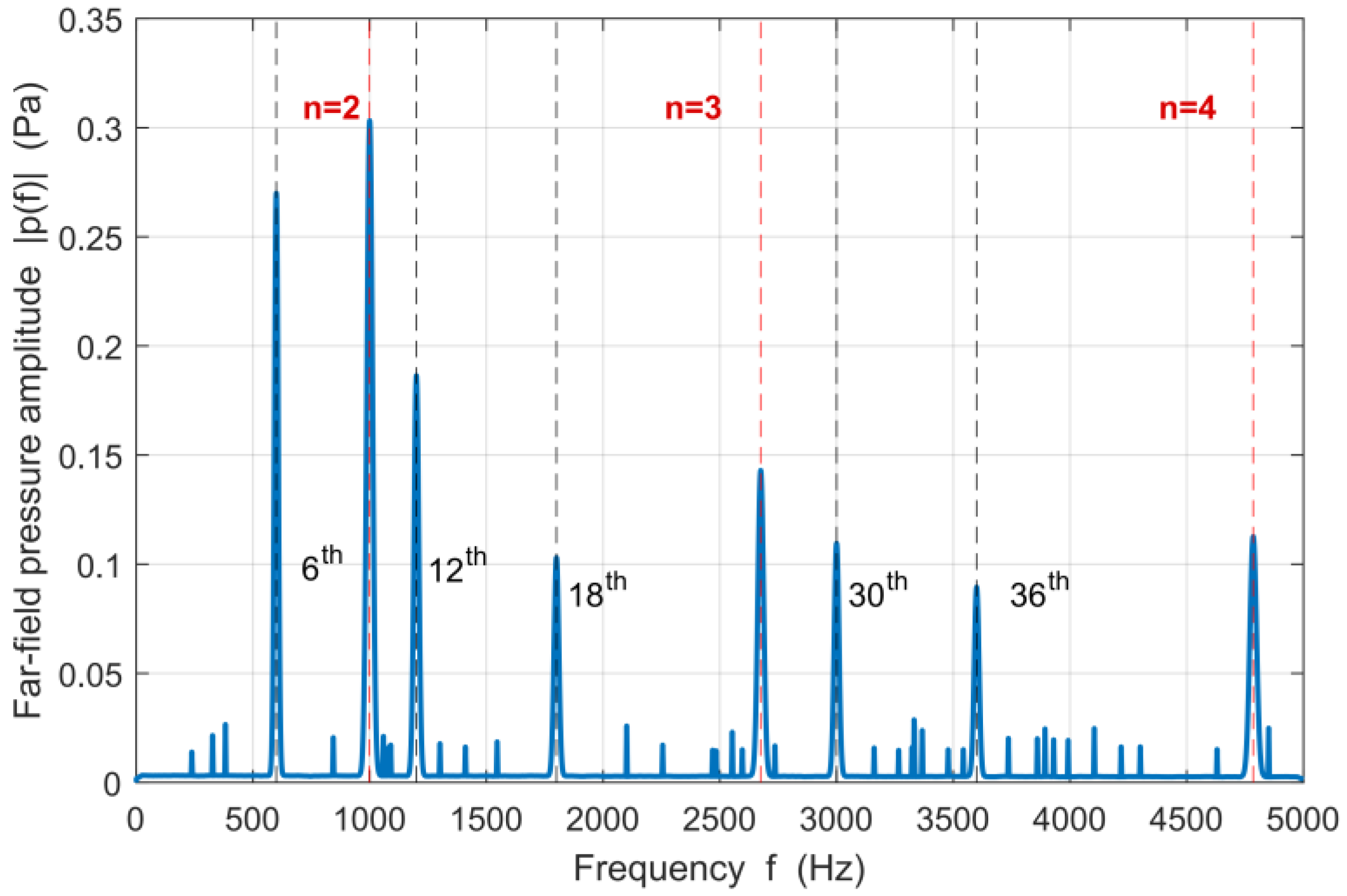
4.2. BEM Modeling and A-Weighted SPL Prediction
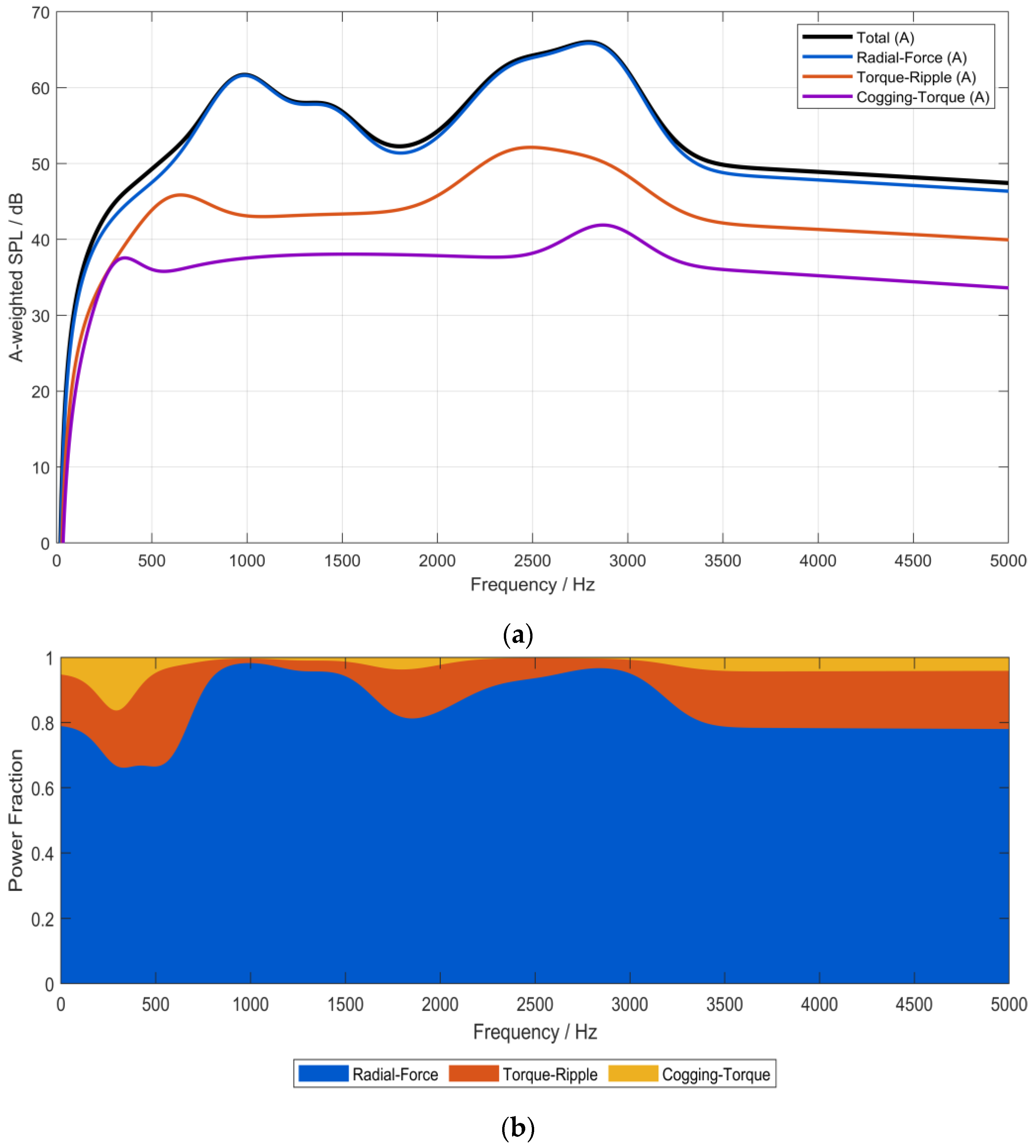
4.3. Coupling Mechanism of Three Electromagnetic Excitations and NVH Correlation
5. Conclusions
- (1)
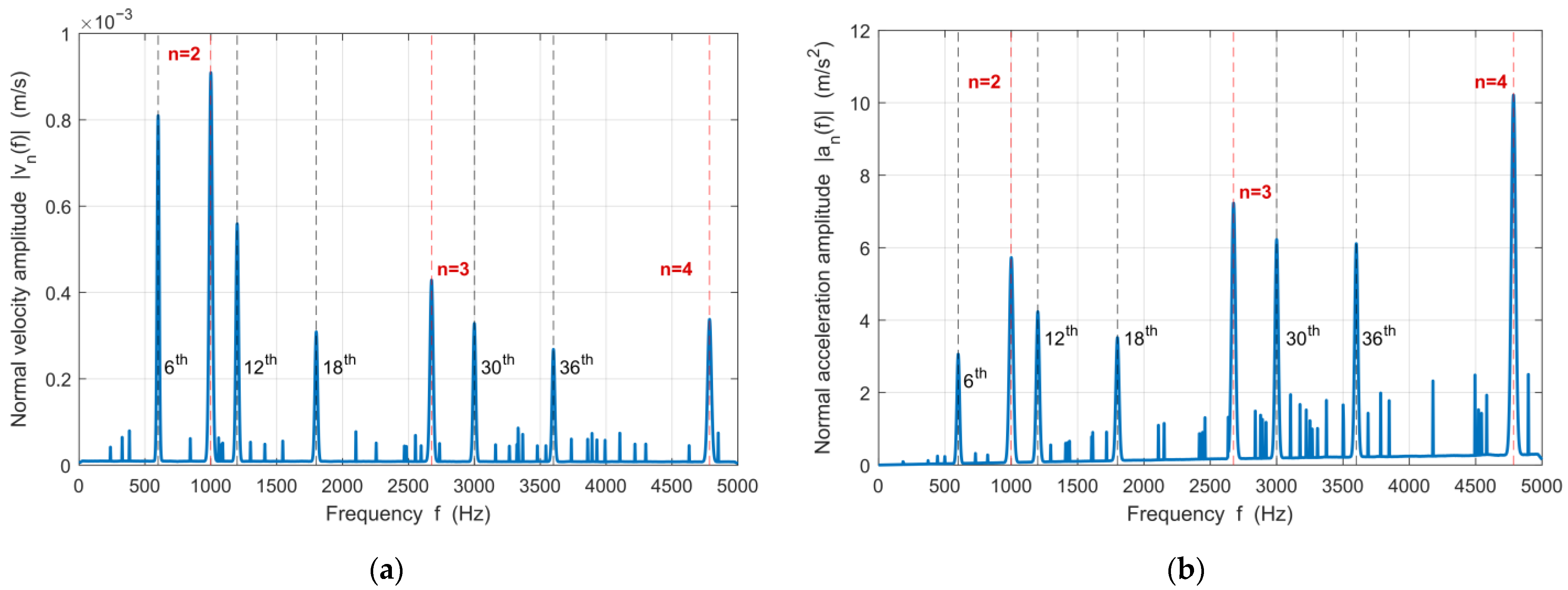
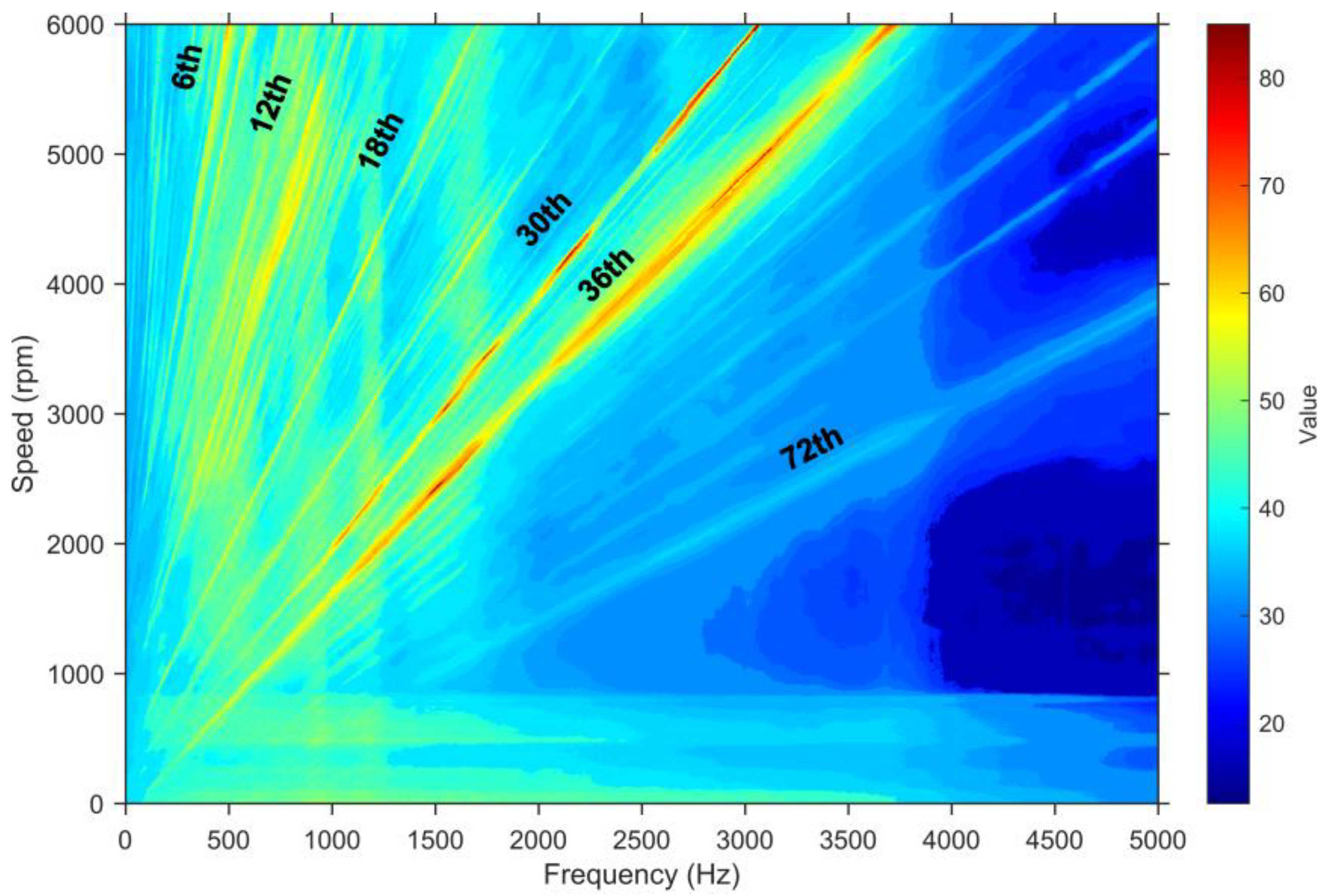
- By mapping the three excitations into the order domain and applying phase-consistent loading, pronounced same-order coupling is observed at the 6th, 12th, 18th, 30th, and 36th spatial orders, with the 36th order remaining highly sensitive over 4000–5500 rpm. Radial electromagnetic force dominates the 6th, 12th, and 18th orders, torque ripple mainly contributes near the 30th order, and cogging torque, driven by slotting modulation, governs the 36th-order band.
- (2)
- A ring-type structural analytical model and a vibro-acoustic FE/BEM chain demonstrate that these dominant electromagnetic orders efficiently excite low-order stator modes and are converted into radiated sound. Using the stator outer-surface normal velocity as a unified Neumann boundary and far-field A-weighted SPL as the response index establishes a consistent link from source excitation to acoustic output.
- (3)
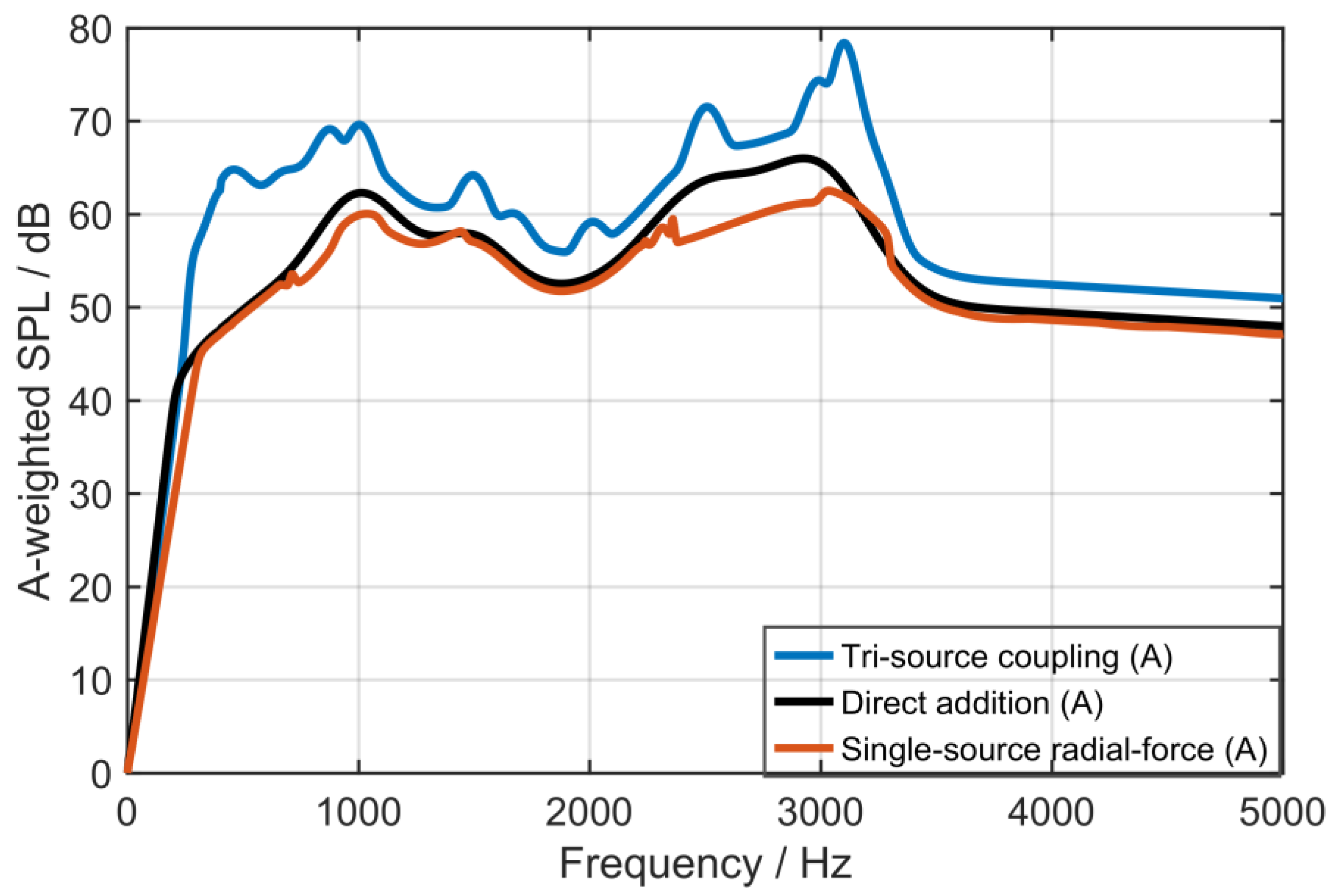
- Within the proposed three-source NVH framework for the 6-pole 36-slot PMSM, the A-weighted Campbell analysis shows that acoustic energy is concentrated in the 30th–36th orders. Under identical conditions, three-source complex-domain coupling yields markedly higher peaks and broader in-band A-weighted SPL around these orders than both traditional power-domain summation and a single-source radial-force chain. This confirms three-source synergy as a principal cause of noise deterioration in the sensitive band of the studied motor and provides a quantitative basis for subsequent co-optimization of motor structure and current-control strategies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PMSM | Permanent-Magnet Synchronous Motor |
| FSCW-PMSMs | Fractional Slot Concentrated Winding Permanent Magnet Synchronous Motors |
| Tri-ECNVH | Tri-source Electromagnetic Coupling NVH Integrated Framework |
| SPL | Sound Pressure Level |
| RFI | Radial Force Index |
| SSRF | Single-Source Radial-Force |
| IPMSM | Interior Permanent Magnet Synchronous Motor |
| TRR | Torque Ripple Ratio |
| LCM | Least Common Multiple |
| GCD | Greatest Common Divisor |
References
- Yang, Y.; He, Q.; Fu, C.; Liao, S.; Tan, P. Efficiency improvement of permanent magnet synchronous motor for electric vehicles. Energy 2020, 213, 118859. [Google Scholar] [CrossRef]
- An, Q.; Lu, Y.; Zhao, M. Review of key technologies of the high-speed permanent magnet motor drive. Energies 2024, 17, 5252. [Google Scholar] [CrossRef]
- Gobbi, M.; Sattar, A.; Palazzetti, R.; Mastinu, G. Traction motors for electric vehicles: Maximization of mechanical efficiency—A review. Appl. Energy 2024, 357, 122496. [Google Scholar] [CrossRef]
- Abdel-Aziz, A.; Elgenedy, M.; Williams, B.W. Review of switched reluctance motor converters and torque ripple minimisation techniques for electric vehicle applications. Energies 2024, 17, 3263. [Google Scholar] [CrossRef]
- Masri, J.; Amer, M.; Salman, S.; Ismail, M.; Elsisi, M. A survey of modern vehicle noise, vibration, and harshness: A state-of-the-art. Ain Shams Eng. J. 2024, 15, 102957. [Google Scholar] [CrossRef]
- Król, E.; Maciążek, M. Identification and analysis of noise sources of permanent magnet synchronous traction motor with interior permanent magnet. Energies 2023, 16, 6018. [Google Scholar] [CrossRef]
- Cao, J.; Cheng, X.; Shang, J.; He, Y. Analysis of the effect of vibration on vehicle LIDAR system. Opt. Eng. 2020, 59, 114101. [Google Scholar] [CrossRef]
- Hots, J.; Oberfeld, D.; Verhey, J.L. Spatial weights in loudness judgements. Acta Acust. 2024, 8, 36. [Google Scholar] [CrossRef]
- Gonzalez, P.; Buigues, G.; Mazon, A.J. Noise in electric motors: A comprehensive review. Energies 2023, 16, 5311. [Google Scholar] [CrossRef]
- Bassani, M.; Pinardi, D.; Toscani, A.; Manconi, E.; Concari, C. Active vibration control via current injection in electric motors. Electronics 2024, 13, 3442. [Google Scholar] [CrossRef]
- Dai, Y.; Lee, H.-J. Torque ripple and electromagnetic vibration suppression of fractional slot distributed winding ISG motors by rotor notching and skewing. Energies 2024, 17, 4964. [Google Scholar] [CrossRef]
- Lee, S.-H.; Song, S.-W.; Yang, I.-J.; Lee, J.; Kim, W.-H. Optimal rotor design for reducing electromagnetic vibration in traction motors based on numerical analysis. Energies 2024, 17, 6206. [Google Scholar] [CrossRef]
- Yi, P.; Zheng, W.; Li, X. Overview of torque ripple minimization methods for permanent magnet synchronous motors based on harmonic injection. Chin. J. Electr. Eng. 2024, 10, 16–29. [Google Scholar] [CrossRef]
- Lee, S.; Yun, G.; Lukman, G.F.; Lee, C. Trade-off between torque ripple and vibration in an IPMSM by examining the temporal and spatial harmonics of flux density. AIP Adv. 2024, 14, 035201. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Bai, C.; Zhang, S. A novel approach to ripple cancellation for low-speed direct-drive servo in aerospace applications. Aerospace 2024, 11, 834. [Google Scholar] [CrossRef]
- Ma, C.; Wang, Y.; Chen, H.; Hong, J.; Wang, Y. Analysis of electromagnetic vibration in permanent magnet motors based on random PWM technology. Machines 2025, 13, 259. [Google Scholar] [CrossRef]
- Dai, M.; Zhang, Z.W.; Dorjoy, M.M.H.; Zeng, L. Analysis and optimization of vibration and noise of high-speed magnetic suspension motor. J. Low Freq. Noise Vib. Act. Control. 2022, 41, 625–636. [Google Scholar] [CrossRef]
- Soresini, F.; Barri, D.; Ballo, F.; Gobbi, M. Numerical Modeling of PMSM Noise Reduction by Harmonic Current Injection. IEEE Access 2025, 13, 60245–60257. [Google Scholar] [CrossRef]
- Lenz, R.; Deutschmann-Olek, A.; Kugi, A.; Kemmetmüller, W. Optimal fault-tolerant control with radial force compensation for multiple open-circuit faults in multiphase PMSMs—A comparison of n-phase and multiple three-phase systems. Control. Eng. Pract. 2024, 147, 105924. [Google Scholar] [CrossRef]
- Rafaq, M.S.; Midgley, W.; Steffen, T. A review of the state of the art of torque ripple minimization techniques for permanent magnet synchronous motors. IEEE Trans. Ind. Inform. 2024, 20, 1019–1031. [Google Scholar] [CrossRef]
- Li, H.; Liang, J.; Zhang, J. Analysis and comparison of performance of permanent magnet servo motors after stator shifting combination. J. Eng. 2020, 2020, 282–291. [Google Scholar] [CrossRef]
- Ciceo, S.; Chauvicourt, F.; Gyselinck, J.; Martis, C. PMSM current shaping for minimum Joule losses while reducing torque ripple and vibrations. IEEE Access 2021, 9, 114705–114714. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Torkaman, H.; Javadi, H. Simultaneous improvement of cogging torque and torque density in axial flux-switching permanent magnet motor. IET Electr. Power Appl. 2024, 18, 312–324. [Google Scholar] [CrossRef]
- Andreou, P.; Hajjaj, A.Z.; Mohammadpour, M.; Theodossiades, S. Analytical multiphysics methodology to predict vibroacoustics in PMSMs combining tangential electromagnetic excitation and tooth modulation effects. IEEE Trans. Transp. Electrif. 2023, 10, 5997–6009. [Google Scholar] [CrossRef]
- Hong, J.; Gui, L.; Cao, J. Analysis and experimental verification of the tangential force effect on electromagnetic vibration of PM motor. IEEE Trans. Energy Convers. 2023, 38, 1893–1902. [Google Scholar] [CrossRef]
- Kim, J.-H.; Won, Y.-J.; Lim, M.-S. Analysis and reduction of radial vibration of FSCW PMSM considering the phase of radial, tangential forces and tooth modulation effect. IEEE Trans. Transp. Electrif. 2024, 11, 2976–2987. [Google Scholar] [CrossRef]
- Król, E.; Maciążek, M.; Wolnik, T. Review of vibroacoustic analysis methods of electric vehicles motors. Energies 2023, 16, 2041. [Google Scholar] [CrossRef]
- Ballo, F.; Gobbi, M.; Mastinu, G.; Palazzetti, R. Noise and vibration of permanent magnet synchronous electric motors: A simplified analytical model. IEEE Trans. Transp. Electrif. 2022, 9, 2486–2496. [Google Scholar] [CrossRef]
- Soresini, F.; Barri, D.; Ballo, F.; Gobbi, M.; Mastinu, G. Noise and vibration modeling of permanent magnet synchronous motors: A review. IEEE Trans. Transp. Electrif. 2024, 10, 8728–8745. [Google Scholar] [CrossRef]
- Hou, P.; Ge, B.; Tao, D.; Wang, Y.; Pan, B. Coupling analysis of electromagnetic vibration and noise of FeCo-based permanent-magnet synchronous motor. Energies 2022, 15, 3888. [Google Scholar] [CrossRef]
- Gómez, I.; García, G.; McCloskey, A.; Almandoz, G. Analytical Model to Calculate Radial Forces in Permanent-Magnet Synchronous Machines. Appl. Sci. 2021, 11, 10865. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y. Electromagnetic Torque Analysis and Structure Optimization of Interior Permanent Magnet Synchronous Machine with Air-Gap Eccentricity. Energies 2023, 16, 1665. [Google Scholar] [CrossRef]
- Jeong, K.-I.; Heidari, R.; Kang, D.-H.; Ahn, T.-J.; Park, G.S.; Ahn, J.-W.; Lukman, G.F. Magnetic Screen Effects on Torque Ripple and Efficiency of Dual Air-Gap Surface Permanent Magnet Synchronous Motor. Energies 2023, 16, 6969. [Google Scholar] [CrossRef]
- Pyrhönen, J.; Jokinen, T.; Hrabovcová, V. Design of Rotating Electrical Machines, 2nd ed.; John Wiley & Sons: Chichester, UK, 2013. [Google Scholar]
- Kim, Y.-S.; Lee, H.-K.; Yang, J.-W.; Jung, W.-S.; Choi, Y.-T.; Jang, J.-H.; Kim, Y.-J.; Shin, K.-H.; Choi, J.-Y. Electromagnetic Noise and Vibration Analyses in PMSMs: Considering Stator Tooth Modulation and Magnetic Force. Electronics 2025, 14, 2882. [Google Scholar] [CrossRef]
- Jędryczka, C.; Danielczyk, D.; Szeląg, W. Torque Ripple Minimization of the Permanent Magnet Synchronous Machine by Modulation of the Phase Currents. Sensors 2020, 20, 2406. [Google Scholar] [CrossRef] [PubMed]
- Liang, W.; Wang, J.; Luk, P.C.K.; Fei, W. Analytical Study of Stator Tooth Modulation on Electromagnetic Radial Force in Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2020, 68, 11731–11739. [Google Scholar] [CrossRef]
- Sunil Kumar, S. Cogging Torque and Torque Ripple Analysis of Permanent Magnet Synchronous Machines. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2019. [Google Scholar]
- Xu, Z.; Shi, D.; Gu, D.; Liu, Z.; Chen, G.; Hu, C.; Sun, X.; Sun, P.; Zhu, B. Innovative Approach to Mitigating Vibration and Noise in an External Rotor Permanent Magnet Synchronous Motor. J. Vib. Control. 2024. [Google Scholar] [CrossRef]
- Zhao, G.; Sun, L.; Niu, N.; Wang, X.; Xing, Z. Analysis of Vibration Characteristics of Stators of Electrical Machines under Actual Boundary. Mech. Syst. Signal Process. 2023, 185, 109778. [Google Scholar] [CrossRef]
- Song, G. Research on Estimation and Control Methods of Natural Frequency of Irregular Building Structure Vibration. J. Vibroeng. 2024, 26, 629–642. [Google Scholar] [CrossRef]
- Sarrazin, M.; Fodorean, D.; Gillijns, S.; Peeters, B.; Van der Auweraer, H.; Martis, C. Multiphysical Analysis of a Three-Phase PWM-Supplied PMSM for Light Vehicle Applications. In Proceedings of the ISMA 2014—International Conference on Noise and Vibration Engineering & USD 2014—International Conference on Uncertainty in Structural Dynamics, Leuven, Belgium, 15–17 September 2014; pp. 1401–1414, ISBN 978-9-0738-0291-9. [Google Scholar]
- Horváth, K.; Zelei, A. Simulating Noise, Vibration, and Harshness Advances in Electric Vehicle Powertrains: Strategies and Challenges. World Electr. Veh. J. 2024, 15, 367. [Google Scholar] [CrossRef]
- Xie, X.; Zuo, Q.; Chen, H.; Lian, H.; Natarajan, S.; Zhao, W.; Chen, X.; Bordas, S.P.-A. A Non-Intrusive Model Order Reduction Boundary Element Method for Frequency Sweeps of 2D Acoustics. J. Sound Vib. 2023, 544, 117396. [Google Scholar] [CrossRef]
- Sathyan, S.; Aydin, U.; Belahcen, A. Acoustic Noise Computation of Electrical Motors Using the Boundary Element Method. Energies 2020, 13, 245. [Google Scholar] [CrossRef]
- IEC 61672-1:2013; Electroacoustics—Sound Level Meters—Part 1: Specifications. International Electrotechnical Commission (IEC): Geneva, Switzerland, 2013.
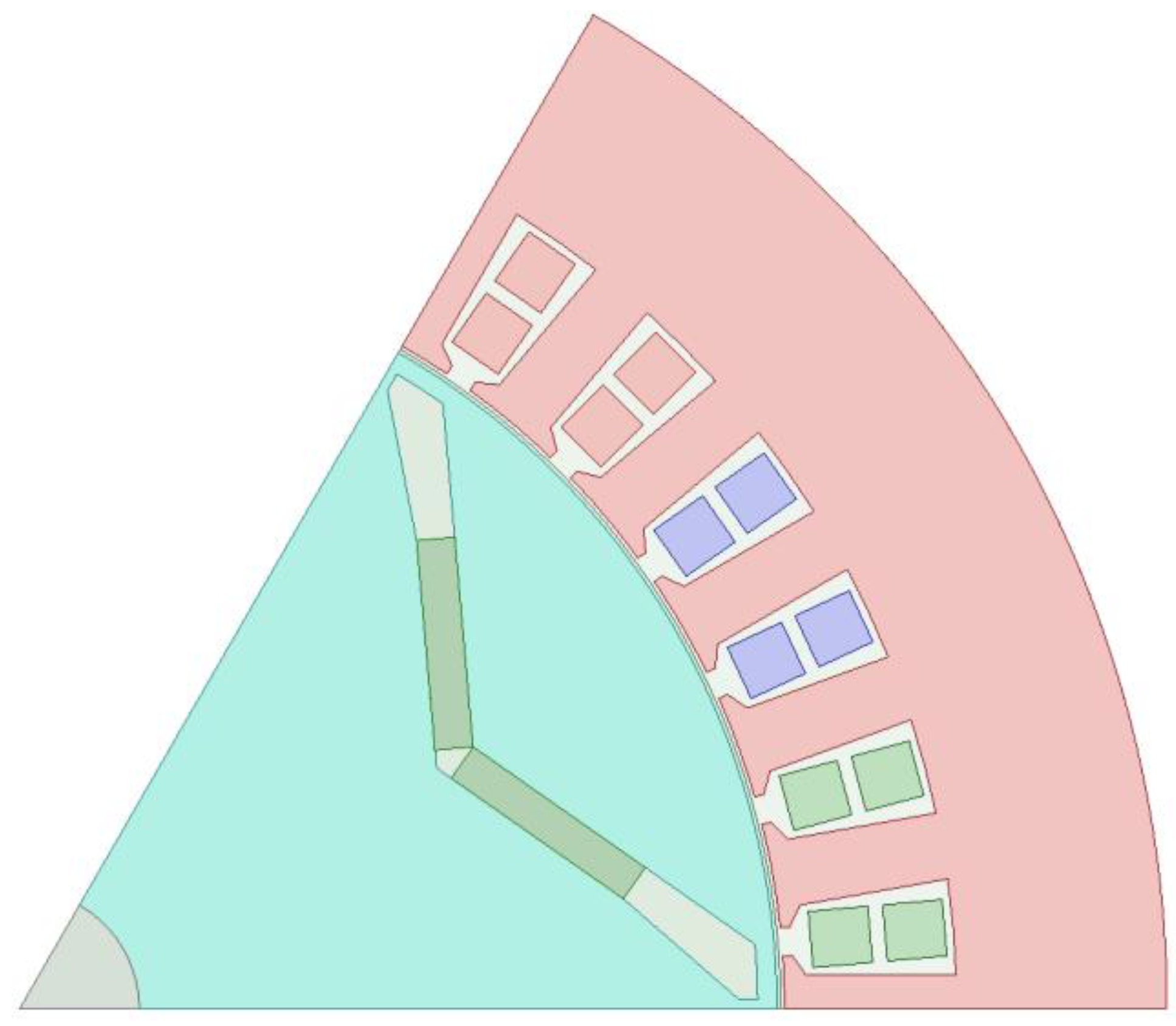
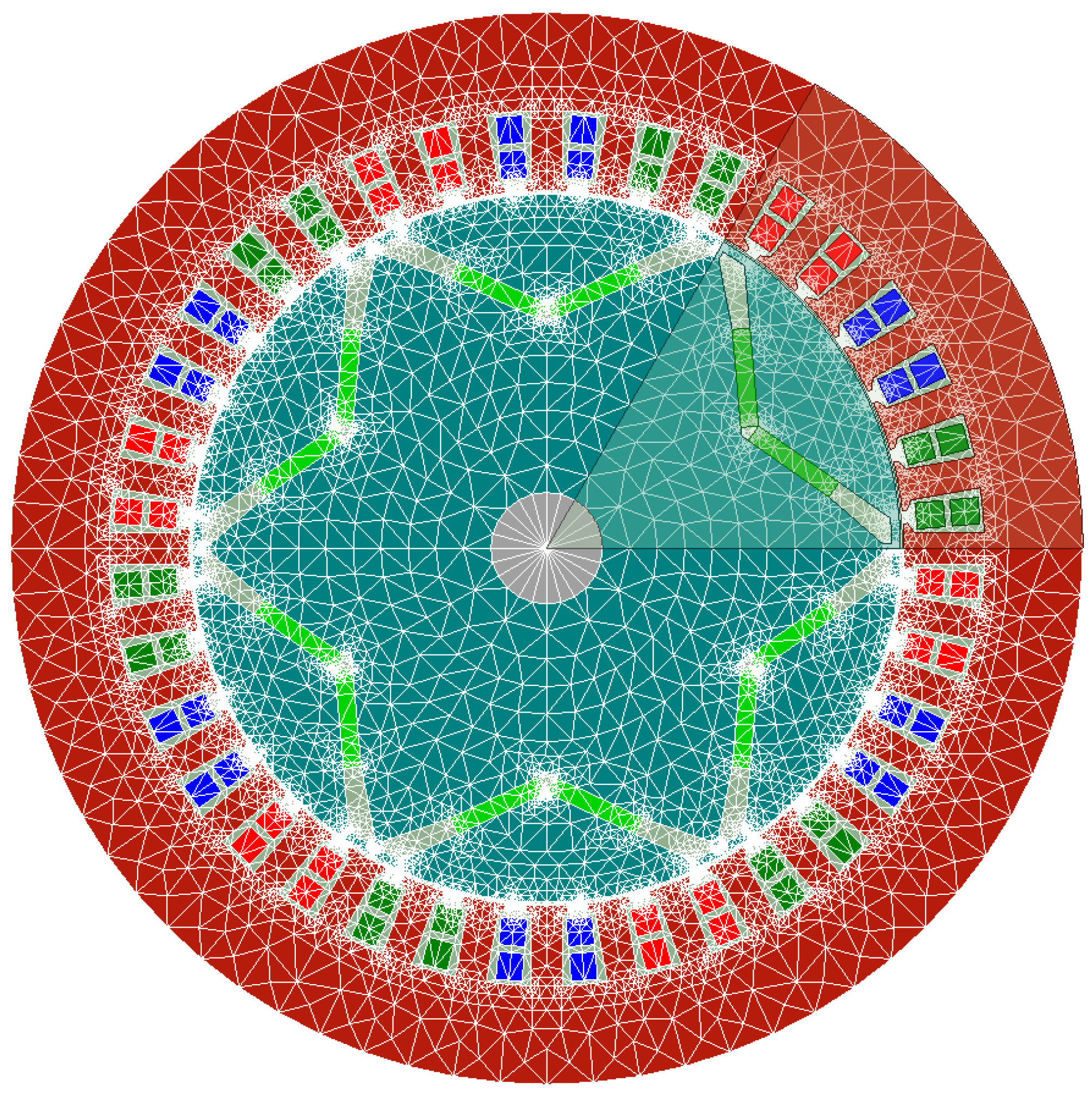
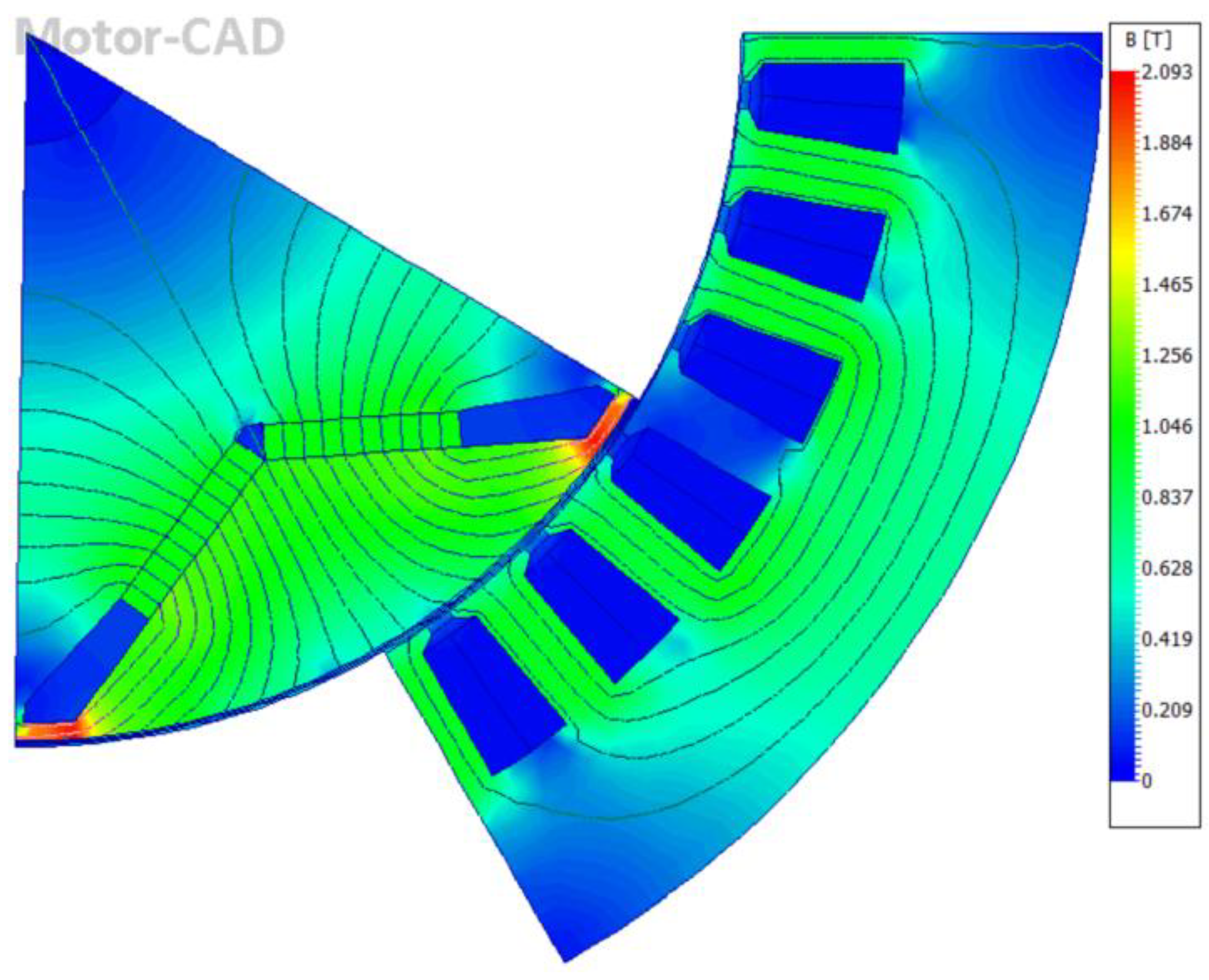
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Stator slots | 36 | Peak power | 220 kW |
| Rotor poles | 6 | Rated speed | 6000 rpm |
| Motor length | 200 mm | Stator outer diameter | 240 mm |
| Permanent magnet width | 1.75 mm | Stator inner diameter | 160 mm |
| Rated torque | 250 N·m | Air-gap length | 0.8 mm |
| Magnet thickness | 3.2 mm | Core length | 180 mm |
| Rated power | 150 kW | Slot opening width | 5 mm |
| Type | Spatial Order | Temporal Order |
|---|---|---|
| Stator | ||
| Permanent magnet | ||
| Interaction term |
| Harmonic Orders of Rotor Permanent-Magnet Field | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | ||
| Harmonic Orders of Armature Reaction Field | 3 | 6/4 | 12/8 | 24/26 | 30/20 | 30/20 | 36/24 | 42/28 |
| 0/0 | 6/4 | 18/12 | 24/16 | 24/16 | 30/20 | 36/24 | ||
| 15 | 18/12 | 24/16 | 30/20 | 36/24 | 42/48 | 48/32 | 54/36 | |
| 12/8 | 6/4 | 0/0 | 6/4 | 12/8 | 18/12 | 24/12 | ||
| 21 | 24/16 | 30/20 | 36/24 | 42/28 | 48/32 | 54/36 | 60/40 | |
| 18/12 | 12/8 | 6/4 | 0/0 | 6/4 | 12/8 | 18/12 | ||
| 33 | 36/24 | 42/28 | 48/32 | 54/36 | 60/40 | 66/44 | 72/48 | |
| 30/20 | 24/16 | 18/12 | 12/8 | 6/4 | 0/0 | 6/4 | ||
| 39 | 42/28 | 48/32 | 54/36 | 60/40 | 66/44 | 72/48 | 78/52 | |
| 36/24 | 30/20 | 24/16 | 18/12 | 12/8 | 6/4 | 0/0 | ||
| Symbol | Parameter | Value |
|---|---|---|
| Stator Radius | 100 | |
| Equivalent Thickness | 15 | |
| Yoke Height | 15 | |
| Elastic Modulus | 200 | |
| Poisson’s Ratio | 0.29 | |
| Density | 7700 |
| Result | n = 2 | n = 3 | n = 4 | n = 5 | |
|---|---|---|---|---|---|
| Model | |||||
| Analytical Frequency (Hz) | 978.5 | 2662.3 | 4991.8 | 7986.8 | |
| Finite Element (Hz) | 998.4 | 2675.1 | 4784.8 | 7042.3 | |
| Relative Error (%) | +1.02% | +0.5% | −4.1% | −11.8% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, T.; Wang, J.; Zhang, W.; Liao, W. Influence of Multi-Source Electromagnetic Coupling on NVH in Automotive PMSMs. Electronics 2025, 14, 4652. https://doi.org/10.3390/electronics14234652
Du T, Wang J, Zhang W, Liao W. Influence of Multi-Source Electromagnetic Coupling on NVH in Automotive PMSMs. Electronics. 2025; 14(23):4652. https://doi.org/10.3390/electronics14234652
Chicago/Turabian StyleDu, Tingwei, Jinbo Wang, Weihai Zhang, and Wei Liao. 2025. "Influence of Multi-Source Electromagnetic Coupling on NVH in Automotive PMSMs" Electronics 14, no. 23: 4652. https://doi.org/10.3390/electronics14234652
APA StyleDu, T., Wang, J., Zhang, W., & Liao, W. (2025). Influence of Multi-Source Electromagnetic Coupling on NVH in Automotive PMSMs. Electronics, 14(23), 4652. https://doi.org/10.3390/electronics14234652






