Bifurcation and Firing Behavior Analysis of the Tabu Learning Neuron with FPGA Implementation
Abstract
1. Introduction
2. Model Formulation and Analysis
2.1. Formulation of the Tabu Learning Single-Neuron Model
2.2. Semi-Analytical Model
- (1)
- When , the period-1 motion is stable.
- (2)
- When , the period-1 motion is unstable.
- (3)
- When and , the period-1 motion reaches the bifurcation boundary.
- (1)
- If and , the period-1 motion undergoes a saddle-node bifurcation.
- (2)
- If and , the period-1 motion undergoes a period-doubling bifurcation.
3. Dynamic Analysis
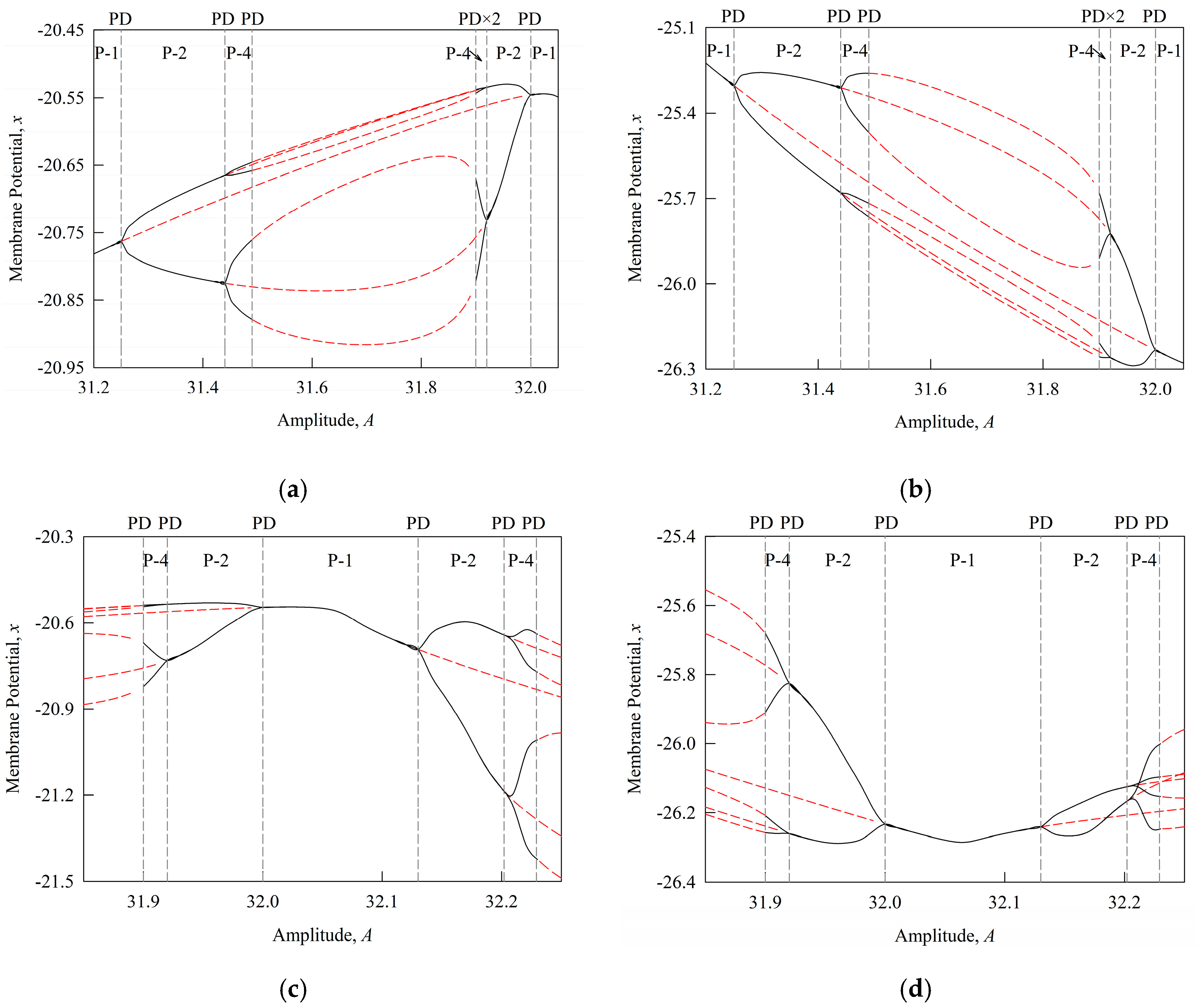
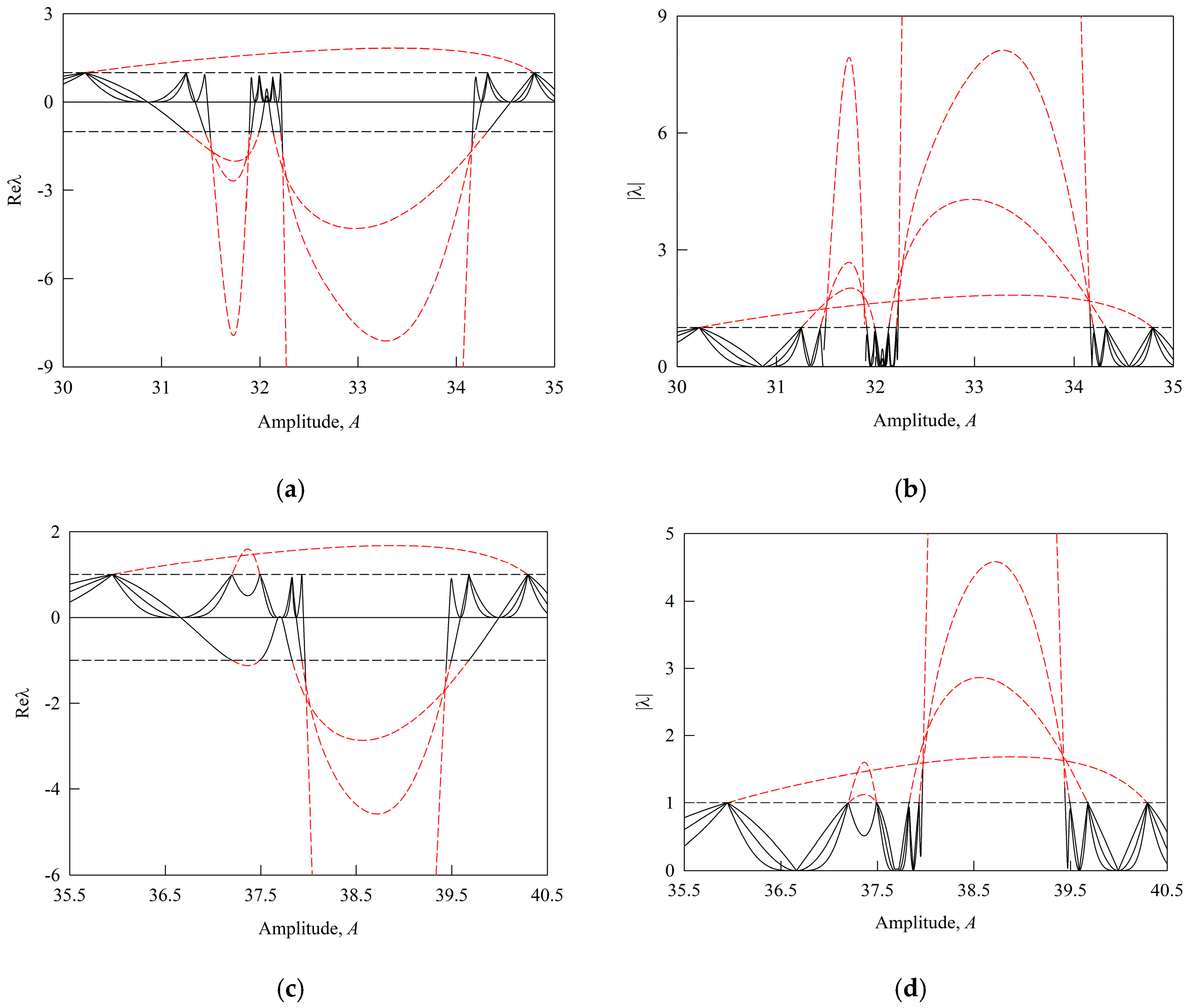
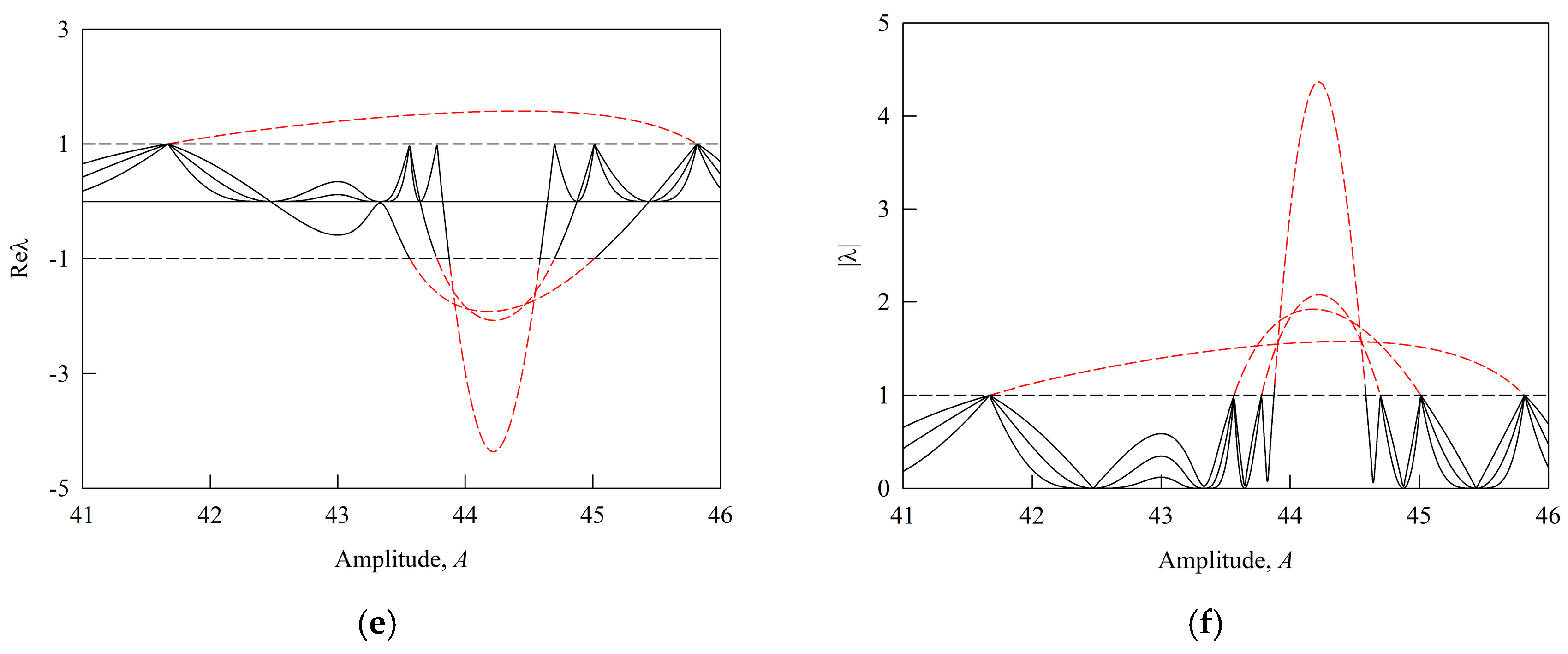
3.1. Bifurcation Evolution
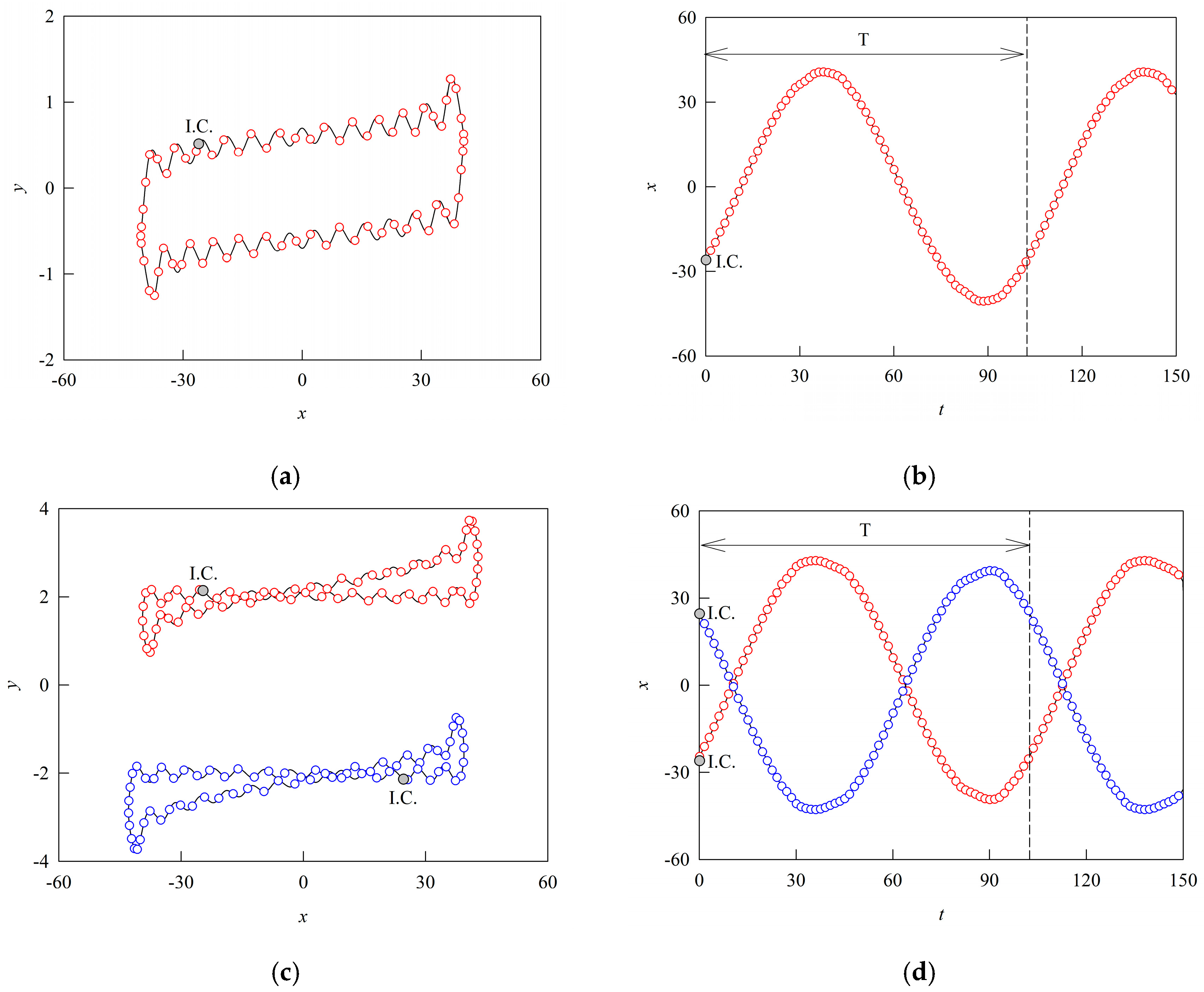
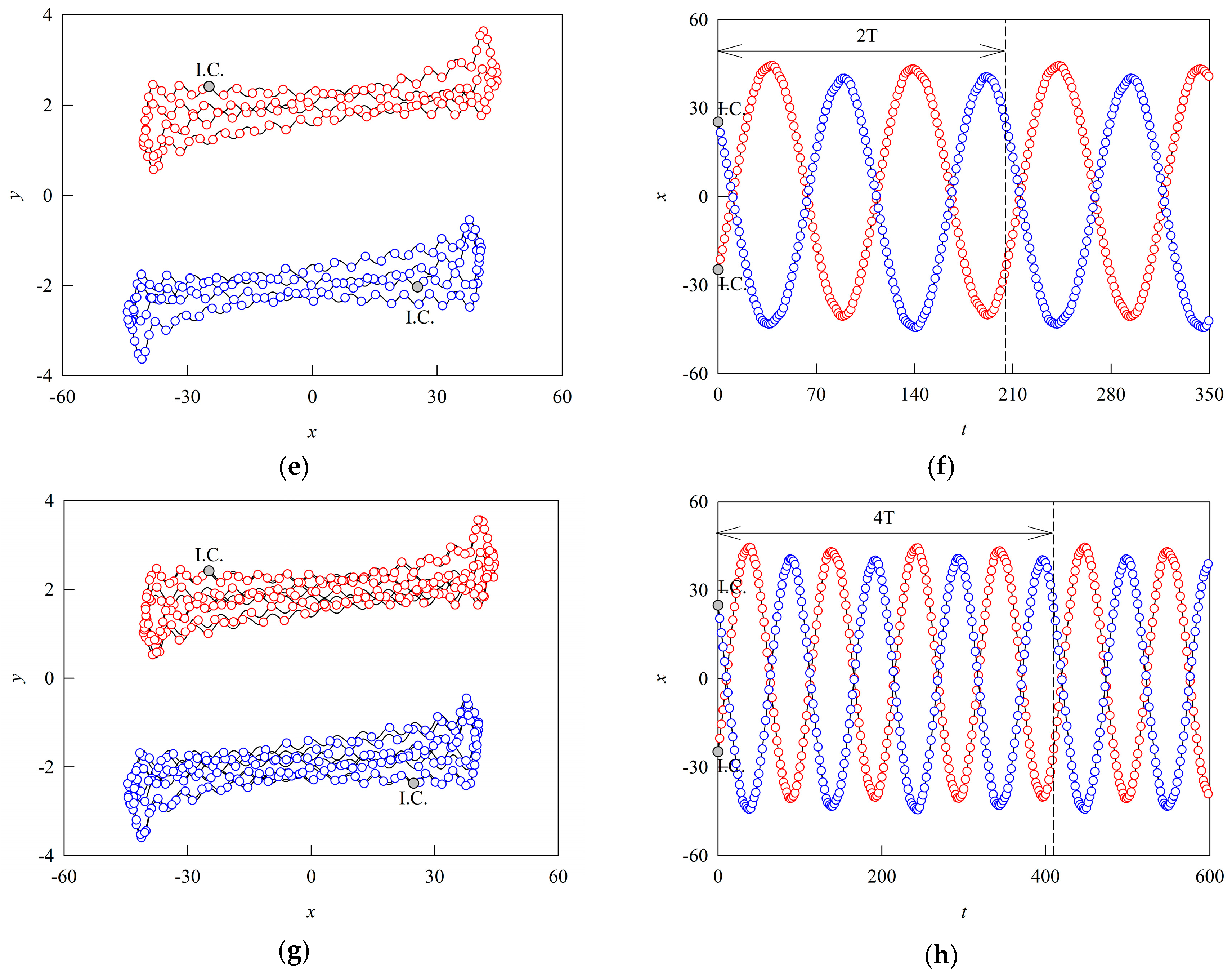
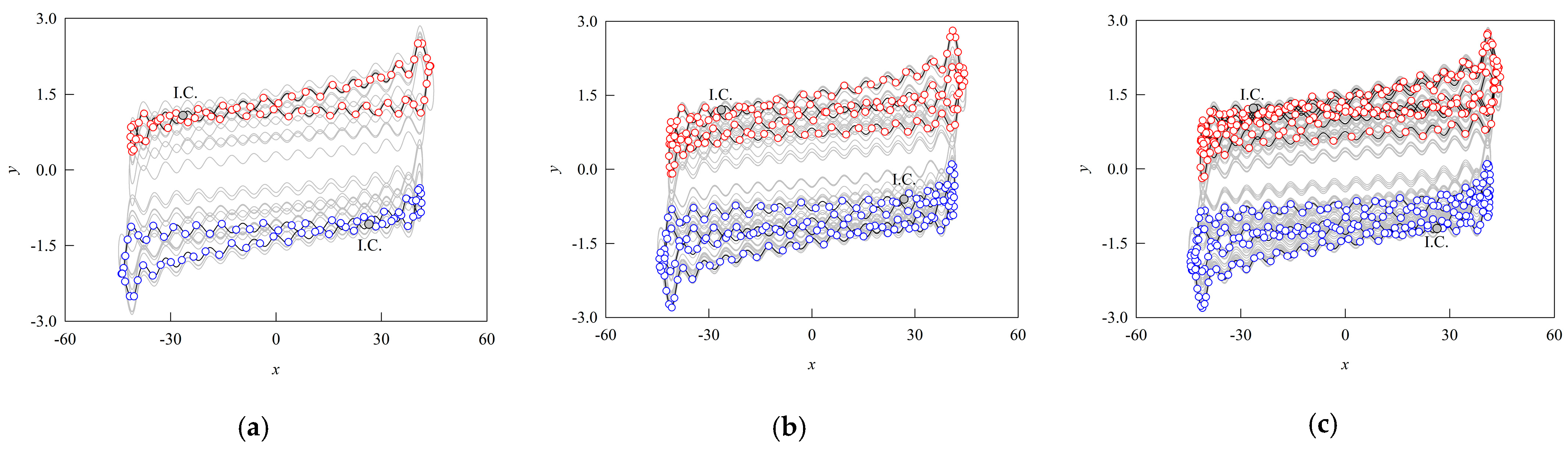
3.2. Firing Behaviors
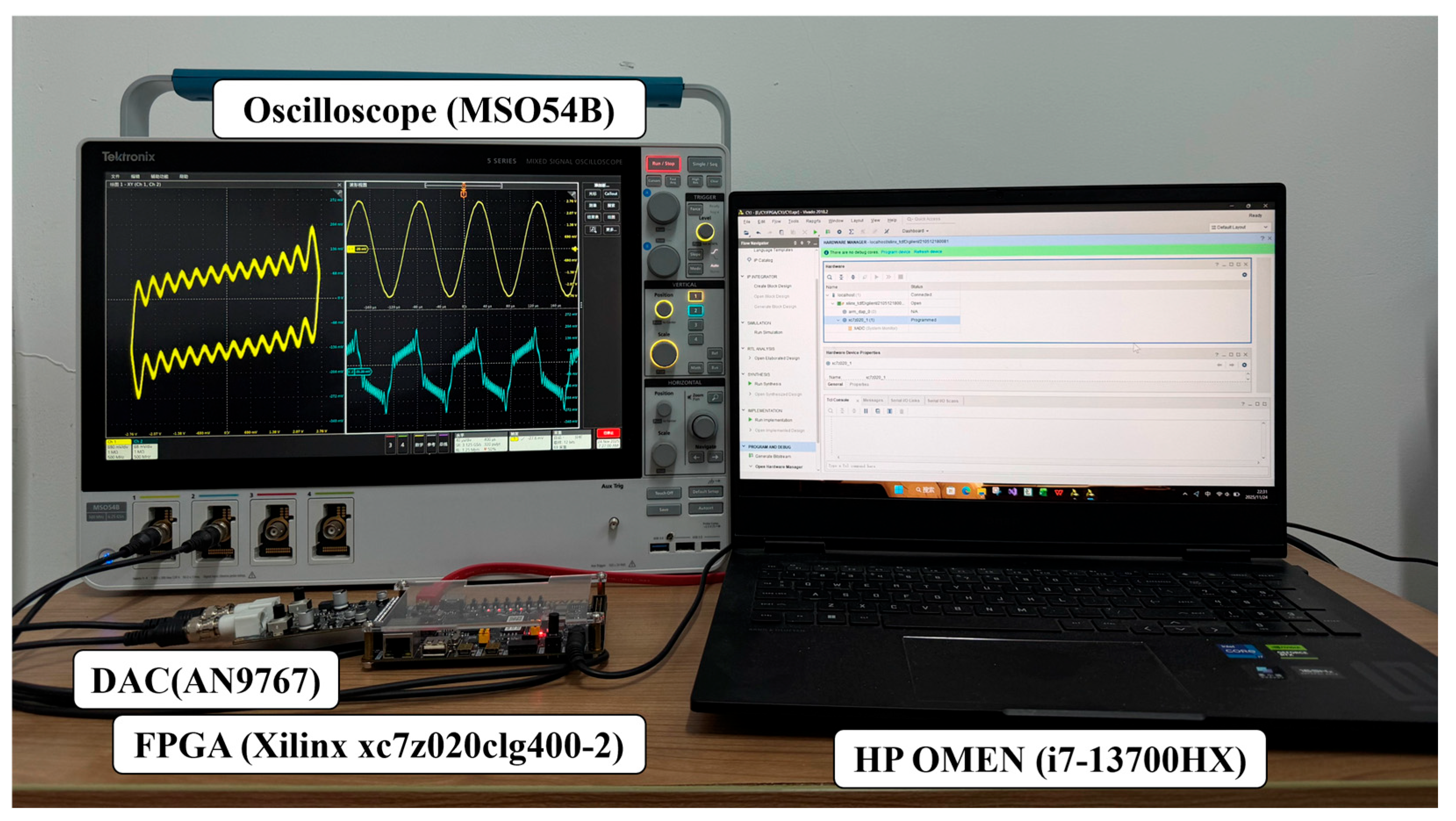
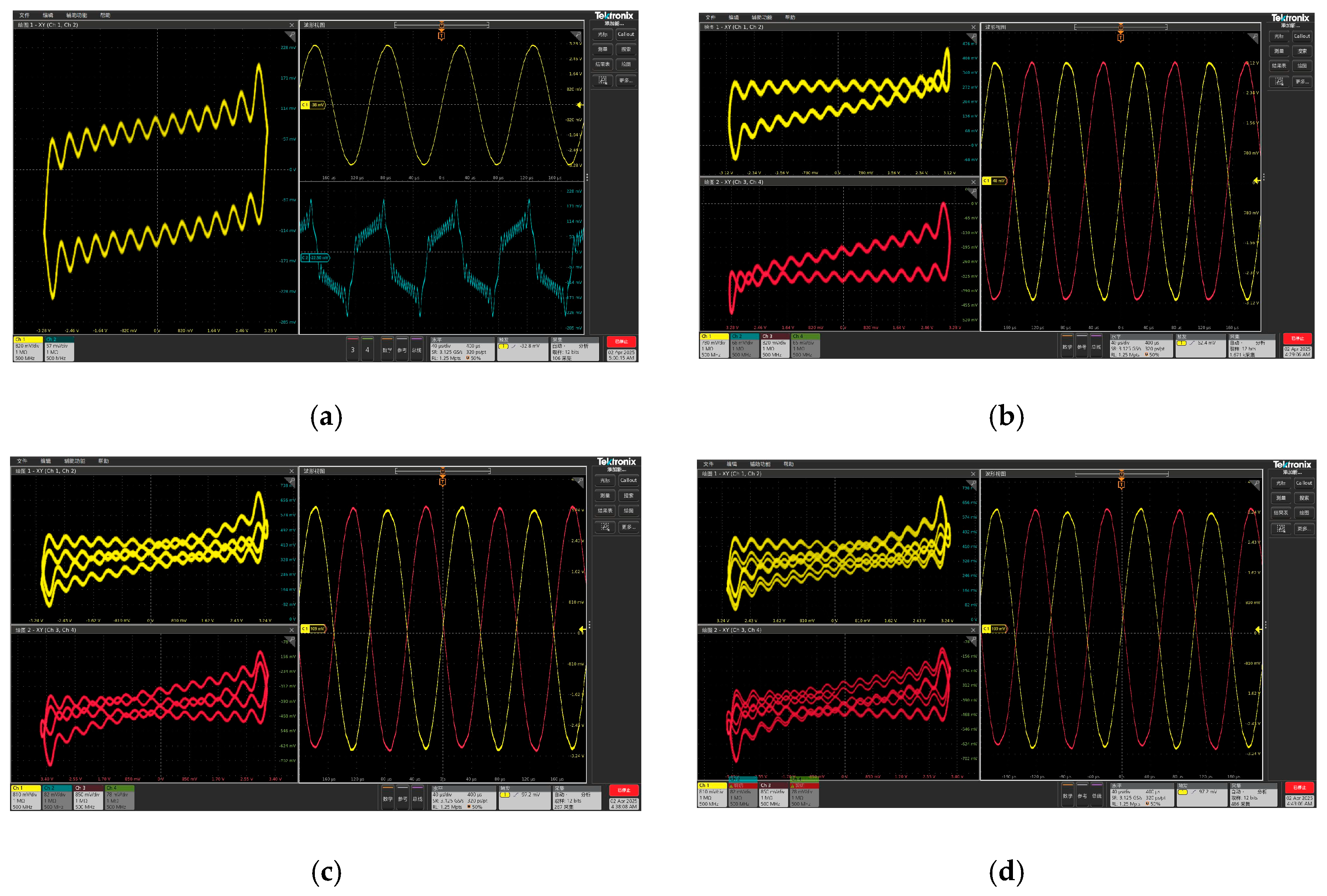
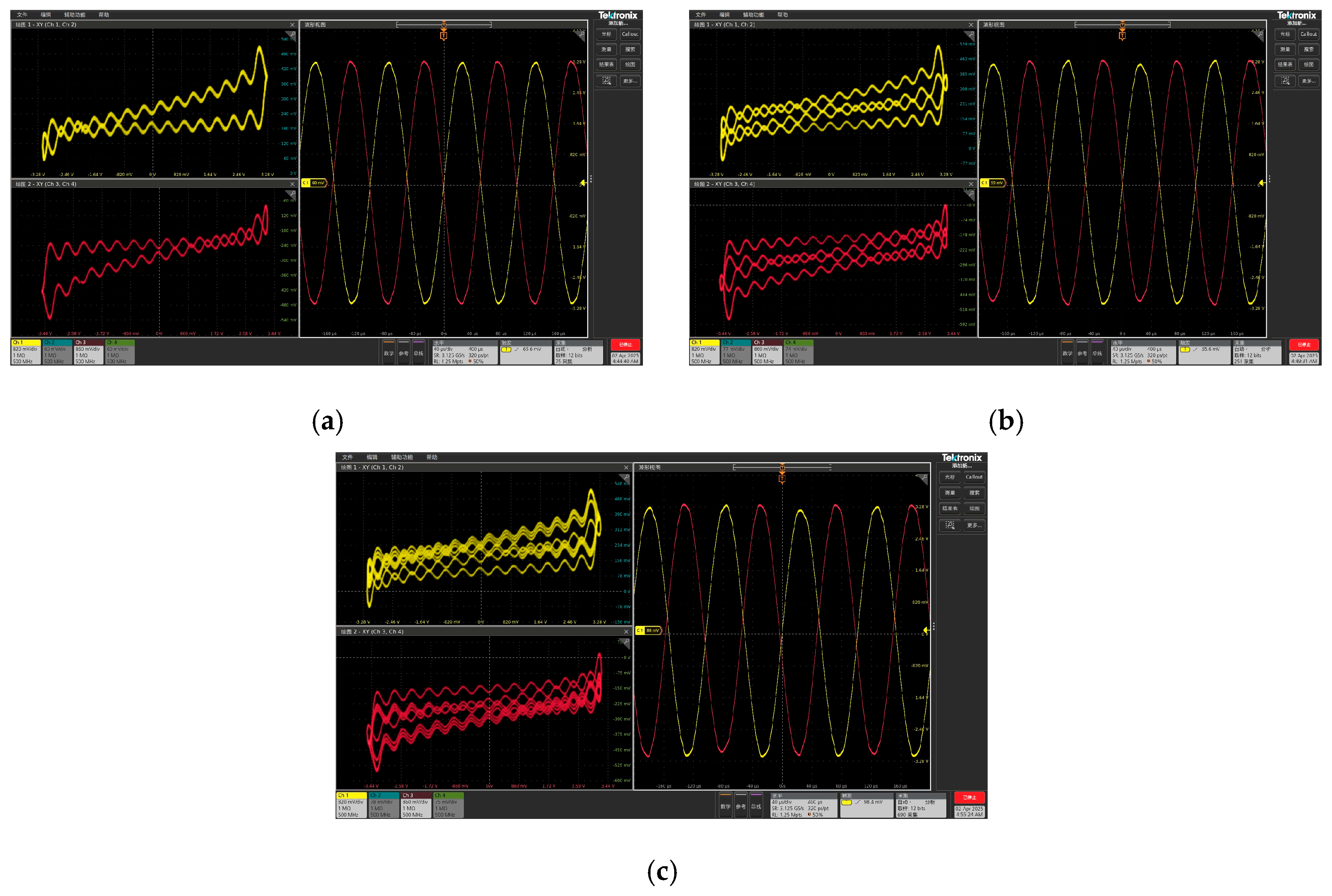
4. Hardware Implementation of the Digital Circuit
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiao, Y.; Liu, Y.; Zhang, B.; Chen, P.; Zhu, H.; He, E.; Zhao, J.; Huo, W.; Jin, X.; Zhang, X.; et al. Bio-Plausible Reconfigurable Spiking Neuron for Neuromorphic Computing. Sci. Adv. 2025, 11, eadr6733. [Google Scholar] [CrossRef]
- Zhang, M.; Luo, X.; Wu, J.; Belatreche, A.; Cai, S.; Yang, Y.; Li, H. Toward Building Human-like Sequential Memory Using Brain-Inspired Spiking Neural Models. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 10143–10155. [Google Scholar] [CrossRef]
- Erkan, E.; Erkan, Y. Effect of Autaptic Synapse on Signal Transmission Performance of Dressed Hodgkin–Huxley Neuron. Chaos Solitons Fract. 2024, 188, 115579. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, P.; Gao, Z.; Wen, D. Artificial Tactile Sensing Neuron with Tactile Sensing Ability Based on a Chitosan Memristor. Adv. Sci. 2024, 11, 2308610. [Google Scholar] [CrossRef]
- Xu, Y.; Qin, H. Dynamical Response in an Electromechanical Arm Driven by Temperature-Dependent Neural Circuit. Chin. J. Phys. 2024, 92, 1384–1394. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. Movement of Sodium and Potassium Ions during Nervous Activity. Cold Spring Harb. Symp. Quant. Biol. 1952, 17, 43–52. [Google Scholar] [CrossRef] [PubMed]
- FitzHugh, R. Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophys. J. 1961, 1, 445–466. [Google Scholar] [CrossRef] [PubMed]
- Morris, C.; Lecar, H. Voltage Oscillations in the Barnacle Giant Muscle Fiber. Biophys. J. 1981, 35, 193–213. [Google Scholar] [CrossRef]
- Beyer, D.A.; Ogier, R.G. Tabu Learning: A Neural Network Search Method for Solving Nonconvex Optimization Problems. In Proceedings of the 1991 IEEE International Joint Conference on Neural Networks, Singapore, 18–21 November 1991; IEEE: Singapore, 1991; Volume 2, pp. 953–961. [Google Scholar]
- Miino, Y. Mode Concept to Construct Diffeomorphisms Representing Smooth/Non-Smooth Dynamical Systems. Nonlinear Theory Appl. 2024, 15, 284–298. [Google Scholar] [CrossRef]
- Xu, Q.; Huang, L.; Wang, N.; Bao, H.; Wu, H.; Chen, M. Initial-Offset-Boosted Coexisting Hyperchaos in a 2D Memristive Chialvo Neuron Map and Its Application in Image Encryption. Nonlinear Dyn. 2023, 111, 20447–20463. [Google Scholar] [CrossRef]
- Cao, H.; Wang, Y.; Banerjee, S.; Cao, Y.; Mou, J. A Discrete Chialvo–Rulkov Neuron Network Coupled with a Novel Memristor Model: Design, Dynamical Analysis, DSP Implementation and Its Application. Chaos Solitons Fract. 2024, 179, 114466. [Google Scholar] [CrossRef]
- Ding, D.; Jin, F.; Zhang, H.; Yang, Z.; Chen, S.; Zhu, H.; Xu, X.; Liu, X. Fractional-Order Heterogeneous Neuron Network Based on Coupled Locally-Active Memristors and Its Application in Image Encryption and Hiding. Chaos Solitons Fract. 2024, 187, 115397. [Google Scholar] [CrossRef]
- Bao, B.; Hu, J.; Bao, H.; Xu, Q.; Chen, M. Memristor-Coupled Dual-Neuron Mapping Model: Initials-Induced Coexisting Firing Patterns and Synchronization Activities. Cogn. Neurodyn. 2024, 18, 539–555. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Wang, K.; Chen, M.; Parastesh, F.; Wang, N. Bursting and Spiking Activities in a Wilson Neuron Circuit with Memristive Sodium and Potassium Ion Channels. Chaos Solitons Fract. 2024, 181, 114654. [Google Scholar] [CrossRef]
- An, X.; Xiong, L.; Shi, Q.; Qiao, S.; Zhang, L. Dynamics Explore of an Improved HR Neuron Model under Electromagnetic Radiation and Its Applications. Nonlinear Dyn. 2023, 111, 9509–9535. [Google Scholar] [CrossRef]
- Shi, Q.; Qu, S.; An, X.; Wei, Z.; Zhang, C. Three-Dimensional m-HR Neuron Model and Its Application in Medical Image Encryption. Chaos Solitons Fract. 2024, 189, 115701. [Google Scholar] [CrossRef]
- Bao, H.; Ding, R.; Chen, B.; Xu, Q.; Bao, B. Two-Dimensional Non-Autonomous Neuron Model with Parameter-Controlled Multi-Scroll Chaotic Attractors. Chaos Solitons Fract. 2023, 169, 113228. [Google Scholar] [CrossRef]
- Lopez-Jimenez, L.M.; Tlelo-Cuautle, E.; Cisneros-Sinencio, L.F.; Diaz-Sanchez, A. Experimental Evaluation of Memristor-Enhanced Analog Oscillators: Relaxation and Wien-Bridge Cases. Dynamics 2025, 5, 4. [Google Scholar] [CrossRef]
- Shi, F.; Xu, X.; Chen, J.; Banerjee, S.; Mou, J. A Novel Memristive Autapse Neuron with ReLU Function: Chaos Dynamics, Attractor Control and Application in Image Encryption. Nonlinear Dyn. 2025, 113, 26753–26772. [Google Scholar] [CrossRef]
- Min, F.; Zhu, J.; Cheng, Y.; Xu, Y. Dynamical Analysis of a Tabu Learning Neuron through the Discrete Implicit Mapping Method. Chaos Solitons Fract. 2024, 181, 114716. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, K.; Shan, Y.; Wu, H.; Chen, M.; Wang, N. Dynamical Effects of Memristive Electromagnetic Induction on a 2D Wilson Neuron Model. Cogn. Neurodyn. 2024, 18, 645–657. [Google Scholar] [CrossRef]
- Huang, Z.; Li, Z.; Wang, Q.; Tan, W.; Wu, X. A Novel Extreme Multistability System Coupled by HR Neuron and Unidirectional Cyclic HNN and Its Application in Medical Image Encryption. Chaos Solitons Fract. 2025, 199, 116674. [Google Scholar] [CrossRef]
- Boya, B.F.B.A.; Tabekoueng, Z.N.; Babenko, L.K.; Kengne, J. Bidirectional Coupling of Two Single Memristive Hopfield Inertial Neurons. Eur. Phys. J. 2025, 140, 406. [Google Scholar] [CrossRef]
- Mosaheb, K.A.; Suerig, B.; Farooq, M.; Hundert, J.; Manzoor, K. Hypokalemic Periodic Paralysis after Steroids Initiation. Am. J. Respir. Crit. Care Med. 2025, 211, A5701. [Google Scholar] [CrossRef]
- Chu, J.; Zhang, W.; Liu, Y.; Gong, B.; Ji, W.; Yin, T.; Gao, C.; Liangwen, D.; Hao, M.; Chen, C.; et al. Biomaterials-Based Anti-Inflammatory Treatment Strategies for Alzheimer’s Disease. Neural Regener. 2024, 19, 100–115. [Google Scholar] [CrossRef]
- Mahmood, A.; Mehroz Khan, M.; Imran, M.; Alhajlah, O.; Dhahri, H.; Karamat, T. End-to-End Deep Learning Method for Detection of Invasive Parkinson’s Disease. Diagnostics 2023, 13, 1088. [Google Scholar] [CrossRef] [PubMed]
- Luo, A.C.J. Periodic Flows to Chaos Based on Discrete Implicit Mappings of Continuous Nonlinear Systems. Int. J. Bifurc. Chaos 2015, 25, 1550044. [Google Scholar] [CrossRef]
- Guo, C.; Luo, A.C.J. Periodic Motions on Bifurcation Trees in an Inverted Pendulum with a Periodically Moving Base. Int. J. Dyn. Control 2021, 9, 410–423. [Google Scholar] [CrossRef]
- Luo, A.C.J.; Xing, S. Bifurcation Trees of Period-3 Motions to Chaos in a Time-Delayed Duffing Oscillator. Nonlinear Dyn. 2017, 88, 2831–2862. [Google Scholar] [CrossRef]
- Min, F.; Xue, L. Routes toward Chaos in a Memristor-Based Shinriki Circuit. Chaos 2023, 33, 023122. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Sun, Y.; Yang, G. Memristive Multi-Wing Chaotic Hopfield Neural Network for LiDAR Data Security. Nonlinear Dyn. 2025, 113, 17161–17176. [Google Scholar] [CrossRef]
- Jee Kim, M.; Lee, H.-M.; Jeong, Y.; Kwak, J.Y. Emerging Neuromorphic Devices-Compatible SNN Hardware with Adaptive STDP and Validation Using Novel CMOS Neuron-Synapse Circuits. IEEE Access 2025, 13, 173739–173751. [Google Scholar] [CrossRef]
- Kimura, N.; Duran, C.; Byambadorj, Z.; Nakane, R.; Iizuka, T. Hardware-Friendly Implementation of Physical Reservoir Computing with CMOS-Based Time-Domain Analog Spiking Neurons. Neuromorph. Comput. Eng. 2025, 5, 24015. [Google Scholar] [CrossRef]
- Nanfak, A.; Nkapkop, J.D.D.; Zourmba, K.; Ngono, J.M.; Moreno-López, M.F.; Tlelo-Cuautle, E.; Borda, M.-E.; Effa, J.Y. Dynamic Analysis and FPGA Implementation of a 2D Fractional Sine-Cosine Map for Image Encryption Using Bit-Level Permutation and Genetic Algorithm. Math. Comput. Simul. 2026, 240, 105–136. [Google Scholar] [CrossRef]
| Category | Representative Works | Main Advantages | Limitations Relative to This Work |
|---|---|---|---|
| Classical neuron models with numerical analysis | HH, FHN, ML, HR, and related neuron models with numerical studies of firing/bifurcations [9,10,11,12,13] | Rich spiking/bursting and nonlinear dynamics | Unstable periodic orbits in chaos not explicitly located |
| Tabu Learning neuron models with numerical analysis | Single-neuron and field-driven Tabu Learning neuron models analyzed via phase portraits and bifurcation diagrams [20,21] | Diverse firing patterns and coexistence in Tabu Learning neuron | Use conventional numerical integration; unstable periodic motions not systematically captured |
| Discrete implicit mapping analyses | Discrete implicit mapping and related semi-analytical methods for nonlinear oscillators and chaotic systems [29,30,31] | Accurately locate stable/unstable periodic orbits and bifurcations | Mainly treat generic nonlinear systems, not neuron models; no FPGA neuron implementation or firing-behavior validation |
| FPGA-based neuron implementations | FPGA implementations of spiking neurons and neuromorphic circuits [32] | Provide real-time/high-throughput neuromorphic hardware | Typically use standard numerical schemes; unstable periodic motion structures rarely analyzed on hardware |
| This work | Improved Tabu Learning neuron with discrete implicit mapping and FPGA realization | Semi-analytical framework + FPGA circuit that reproduces stable and unstable periodic motions | Currently focuses on a single neuron; extension to multi-neuron/network-level FPGA implementations left for future work |
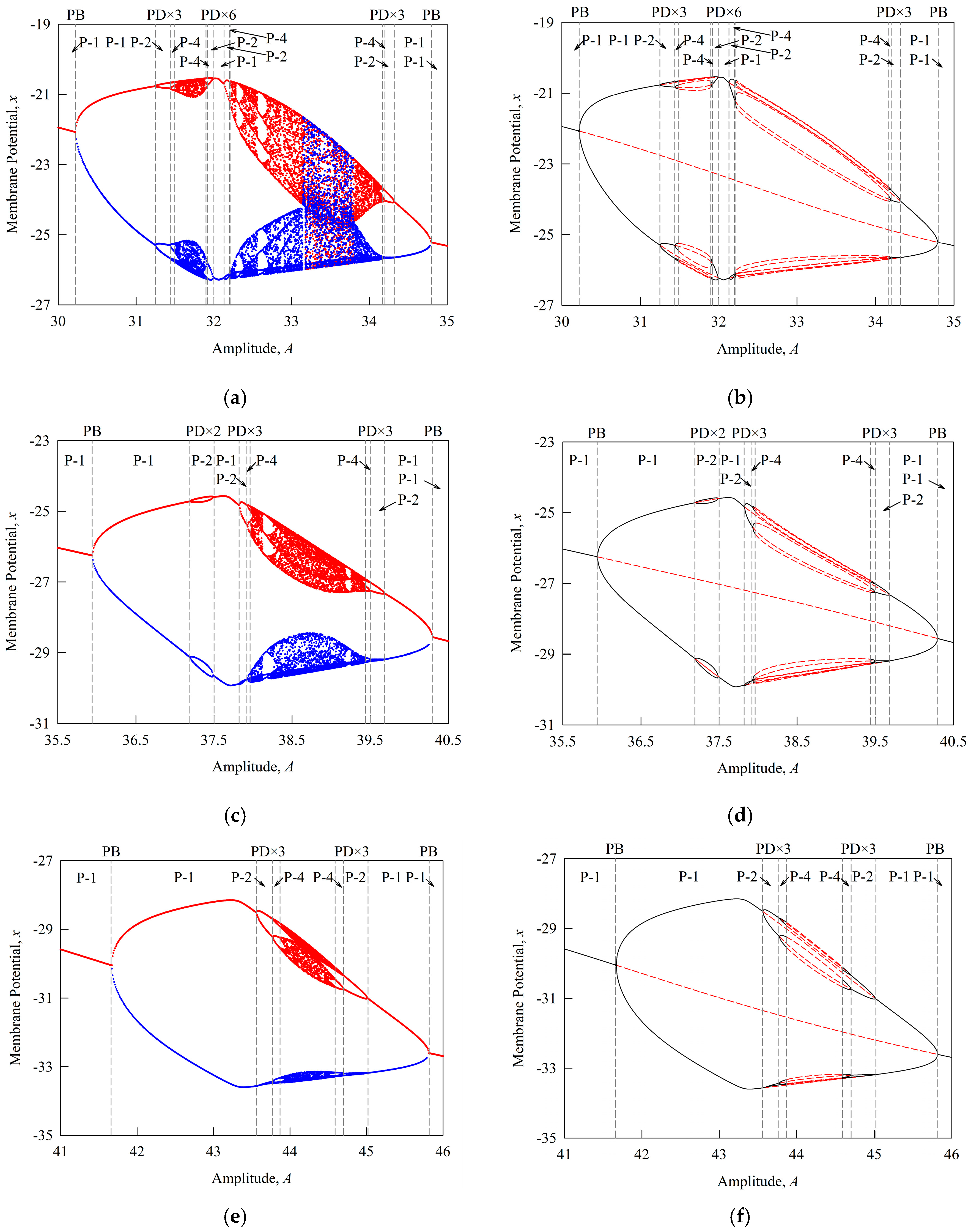
| Period-m | Left Bifurcation | Right Bifurcation | Stability | |
|---|---|---|---|---|
| Common P-1 | (30.00, 30.22) | - | PB | S |
| (30.22, 34.80) | PB | PB | U | |
| (34.80, 35.00) | PB | - | S | |
| Coexisting P-1 | (30.22, 31.25) | PB | PD | S |
| (31.25, 32.00) | PD | PD | U | |
| (32.00, 32.13) | PD | PD | S | |
| (32.13, 34.32) | PD | PD | U | |
| (34.32, 34.80) | PD | PB | S | |
| Coexisting P-2 | (31.25, 31.44) | PD | PD | S |
| (31.44, 31.92) | PD | PD | U | |
| (31.92, 32.00) | PD | PD | S | |
| (32.13, 32.20) | PD | PD | S | |
| (32.20, 34.20) | PD | PD | U | |
| (34.20, 34.32) | PD | PD | S | |
| Coexisting P-4 | (31.44, 31.49) | PD | PD | S |
| (31.49, 31.90) | PD | PD | U | |
| (31.90, 31.92) | PD | PD | S | |
| (32.20, 32.22) | PD | PD | S | |
| (32.22, 34.17) | PD | PD | U | |
| (34.17, 34.20) | PD | PD | S |
| Period-m | Left Bifurcation | Right Bifurcation | Stability | |
|---|---|---|---|---|
| Common P-1 | (35.50, 35.94) | - | PB | S |
| (35.94, 40.30) | PB | PB | U | |
| (40.30, 40.50) | PB | - | S | |
| Coexisting P-1 | (35.94, 37.19) | PB | PD | S |
| (37.19, 37.50) | PD | PD | U | |
| (37.50, 37.82) | PD | PD | S | |
| (37.82, 39.68) | PD | PD | U | |
| (39.68, 40.30) | PD | PB | S | |
| Coexisting P-2 | (37.19, 37.50) | PD | PD | S |
| (37.82, 37.92) | PD | PD | S | |
| (37.92, 39.50) | PD | PD | U | |
| (39.50, 39.68) | PD | PD | S | |
| Coexisting P-4 | (37.92, 37.96) | PB | PD | S |
| (37.96, 39.44) | PD | PD | U | |
| (39.44, 39.50) | PD | PD | S |
| Period-m | Left Bifurcation | Right Bifurcation | Stability | |
|---|---|---|---|---|
| Common P-1 | (41.00, 41.60) | - | PB | S |
| (41.60, 45.82) | PB | PB | U | |
| (45.82, 46.00) | PB | - | S | |
| Coexisting P-1 | (41.60, 43.56) | PB | PD | S |
| (43.56, 45.02) | PD | PD | U | |
| (45.02, 45.82) | PD | PB | S | |
| Coexisting P-2 | (43.56, 43.77) | PD | PD | S |
| (43.77, 44.70) | PD | PD | U | |
| (44.70, 45.02) | PD | PD | S | |
| Coexisting P-4 | (43.77, 43.87) | PD | PD | S |
| (43.87, 44.59) | PD | PD | U | |
| (44.59, 44.70) | PD | PD | S |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Chen, Y.; Min, F. Bifurcation and Firing Behavior Analysis of the Tabu Learning Neuron with FPGA Implementation. Electronics 2025, 14, 4639. https://doi.org/10.3390/electronics14234639
Sun H, Chen Y, Min F. Bifurcation and Firing Behavior Analysis of the Tabu Learning Neuron with FPGA Implementation. Electronics. 2025; 14(23):4639. https://doi.org/10.3390/electronics14234639
Chicago/Turabian StyleSun, Hongyan, Yujie Chen, and Fuhong Min. 2025. "Bifurcation and Firing Behavior Analysis of the Tabu Learning Neuron with FPGA Implementation" Electronics 14, no. 23: 4639. https://doi.org/10.3390/electronics14234639
APA StyleSun, H., Chen, Y., & Min, F. (2025). Bifurcation and Firing Behavior Analysis of the Tabu Learning Neuron with FPGA Implementation. Electronics, 14(23), 4639. https://doi.org/10.3390/electronics14234639






