Frequency-Domain Modeling and Multi-Agent Game-Theory-Based Low-Carbon Optimal Scheduling Strategy for Integrated Energy Systems
Abstract
1. Introduction
2. Frequency-Domain Modeling of Heating and Gas Networks
2.1. Dynamic Frequency-Domain Modeling of Heating Pipelines
2.2. Mixing Equation of Heating Node Temperature
2.3. Frequency-Domain Model of Temperature Continuity Equation
2.4. Dynamic Frequency-Domain Modeling of Gas Supply Pipelines
3. IES Device Modeling
3.1. P2G
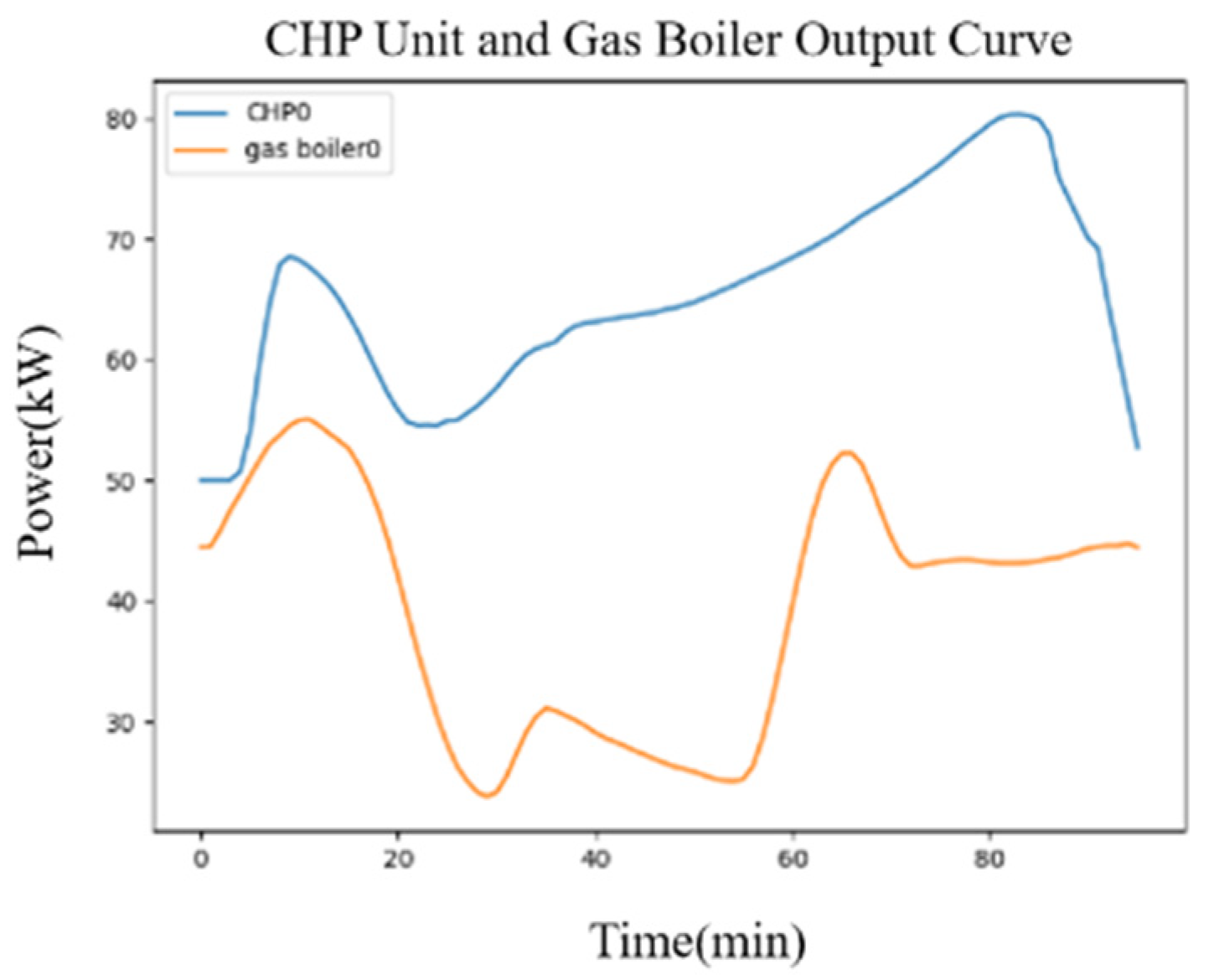
3.2. CHP Unit
3.3. Boiler
4. Multi-Agent Game Model
4.1. Multi-Agent Alliance Rules
- (1)
- Renewable energy providers: Upon entering the cooperative alliance, they gain bidirectional transaction entitlements. Specifically, they can either sell electrical energy to the power grid at benchmark electricity rates or provide power to carbon capture facilities and P2G systems via direct procurement contracts. The electricity contract price for such direct transactions follows the formula . This move breaks through the single-electricity-sales model and achieves energy cascade utilization.
- (2)
- Carbon capture power plants: After participating in the alliance, a dual-channel energy supply system is formed; in addition to conventional power grid purchases, green-electricity-driven carbon capture equipment within the alliance can be purchased based on real-time electricity price optimization strategies. The captured CO2 is sold as a commodity to the CCS system, building a value chain of “electricity input, carbon asset output”.
- (3)
- Gas–thermal power plants: Their membership in the alliance grants them the following flexible energy procurement rights: when meeting the dynamic energy consumption needs of P2G equipment, they can independently choose to purchase electricity from the grid or through agreements within the alliance, and maximize the synergistic benefits of heat and electricity through their monopoly position in the heating network.
- Identify All Possible Coalitions: For participants (set ), enumerate all non-empty subsets (from single-agent to full coalitions).
- Calculate Coalition Payoffs: For each coalition , solve its internal optimization problem (e.g., energy interaction and collaborative scheduling) to obtain total payoff . For singleton sets, is the individual payoff.
- Compute Marginal Contributions: For agent , calculate its marginal contribution to each coalition as (where is without ).
- Calculate Shapley Values: The Shapley value for agent is the weighted average of its marginal contributions across all coalitions containing , with weights reflecting coalition probabilities as follows:where (coalition size) and is the weight factor.
- e.
- Payoff Distribution: Allocate total coalition payoffs based on ensuring fairness.
- (1)
- Renewable energy output constraints are as follows:where denotes the total generation from renewable energy sources at time , represents wind power generation, signifies photovoltaic power generation at time , stands for the generation from conventional renewable energy sources at time , is the renewable energy power allocated to power-to-gas (P2G) at time , refers to the renewable energy power dedicated to energy storage at time , indicates the maximum available photovoltaic power capacity at time , and is the forecasted photovoltaic power generation at time .
- (2)
- System operation constraints are as follows:where denotes the power output of the captive power plant at time , represents the power from the thermal power unit allocated for gas production at time , is the renewable energy power utilized for gas production at time , is the power purchased from the external power grid at time , and refers to renewable energy power used for other applications at time .
- (3)
- Power balance constraints are as follows:where is the output of conventional generation units at time , denotes the power generated by the combined heat and power (CHP) unit at time , represents the discharge power of the energy storage system at time , signifies the charging power of the energy storage system at time , is the power input to the power-to-gas (P2G) system at time , refers to the heat supplied by the boiler at time , denotes the heat supplied by the CHP unit at time , is the heat release power of the thermal energy storage at time , represents the heat absorption power of the thermal energy storage at time , and is the heat load at time .
4.2. Multi-Agent Alliance Constraint Conditions
5. Case Analysis
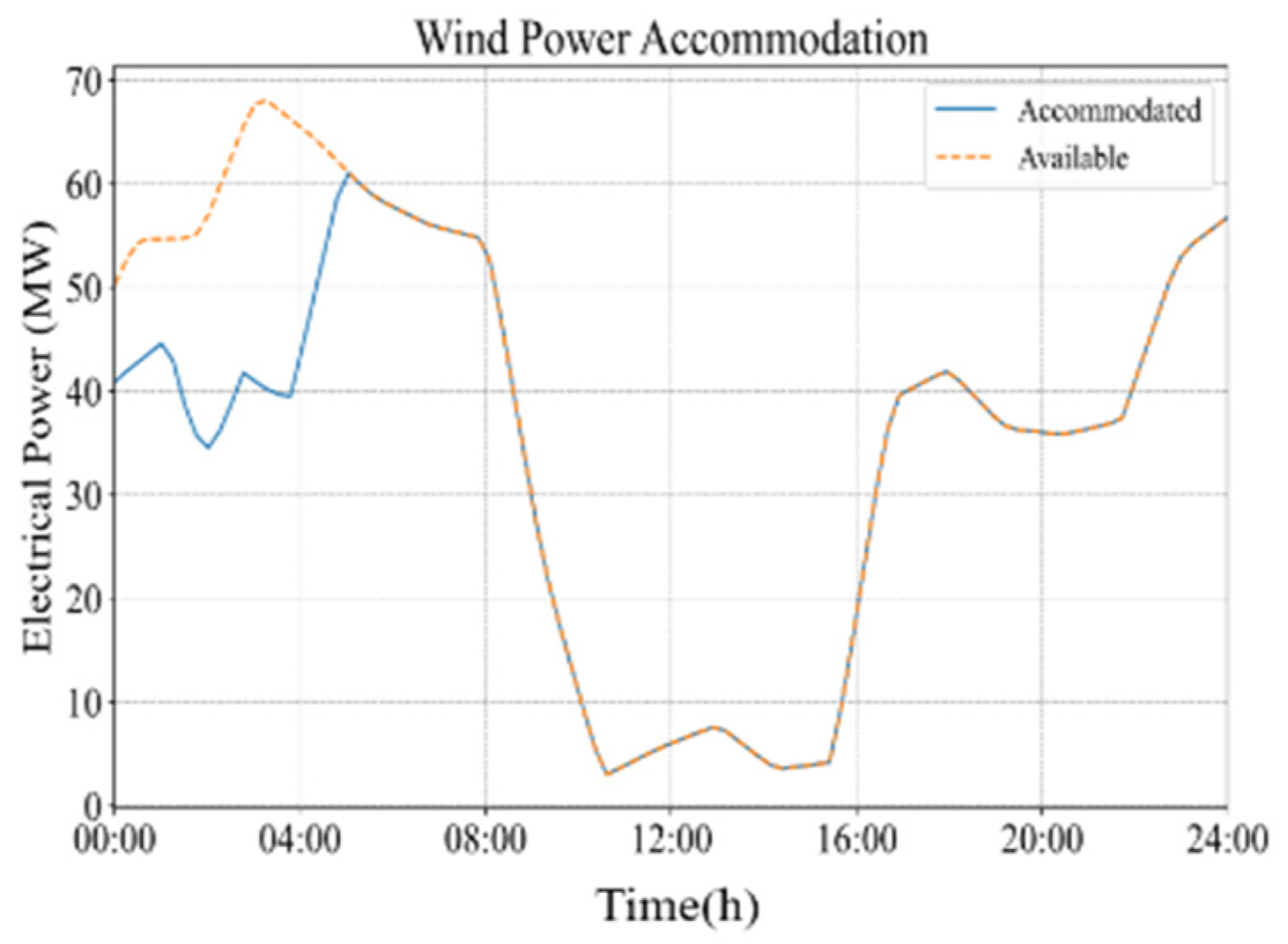
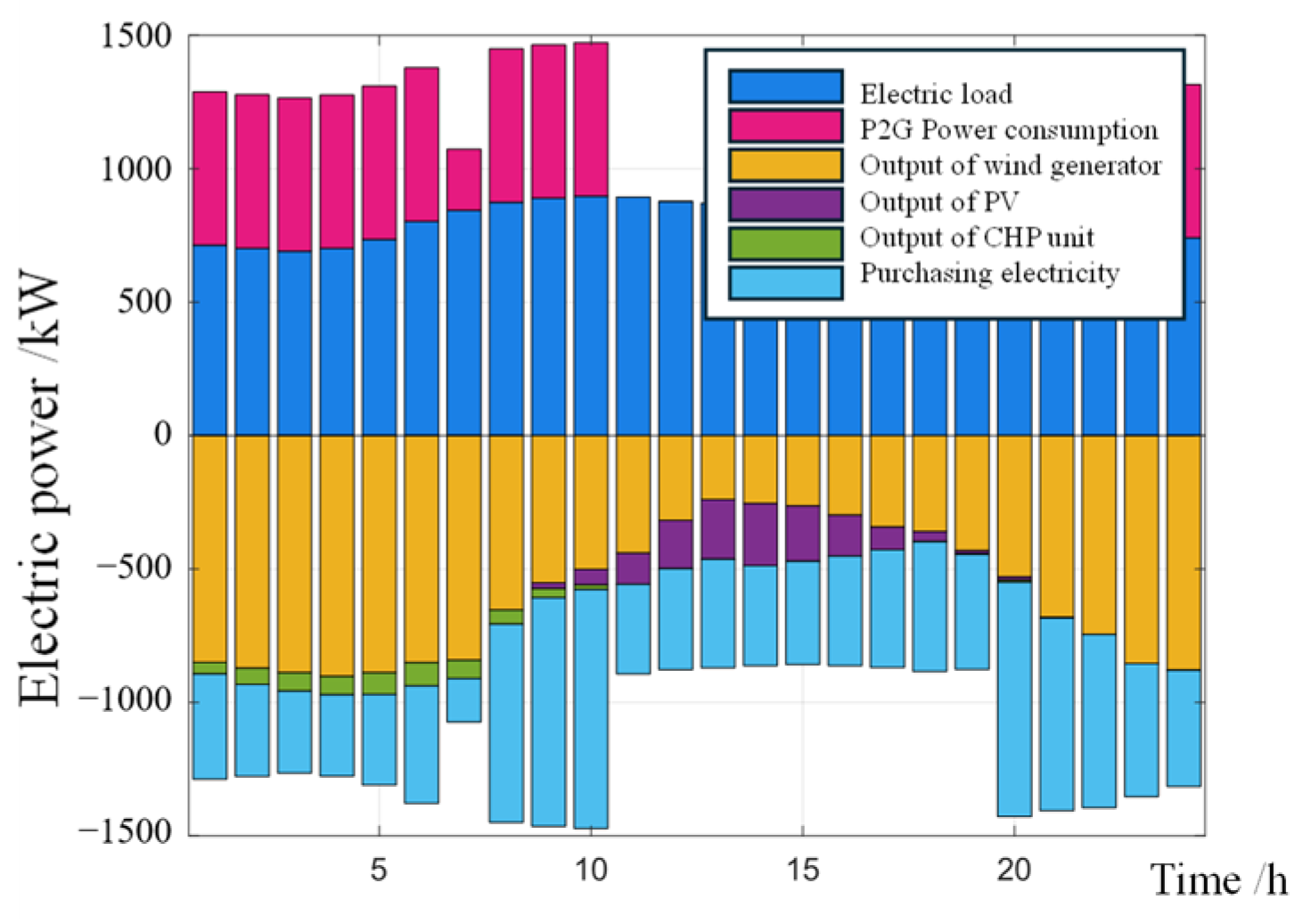
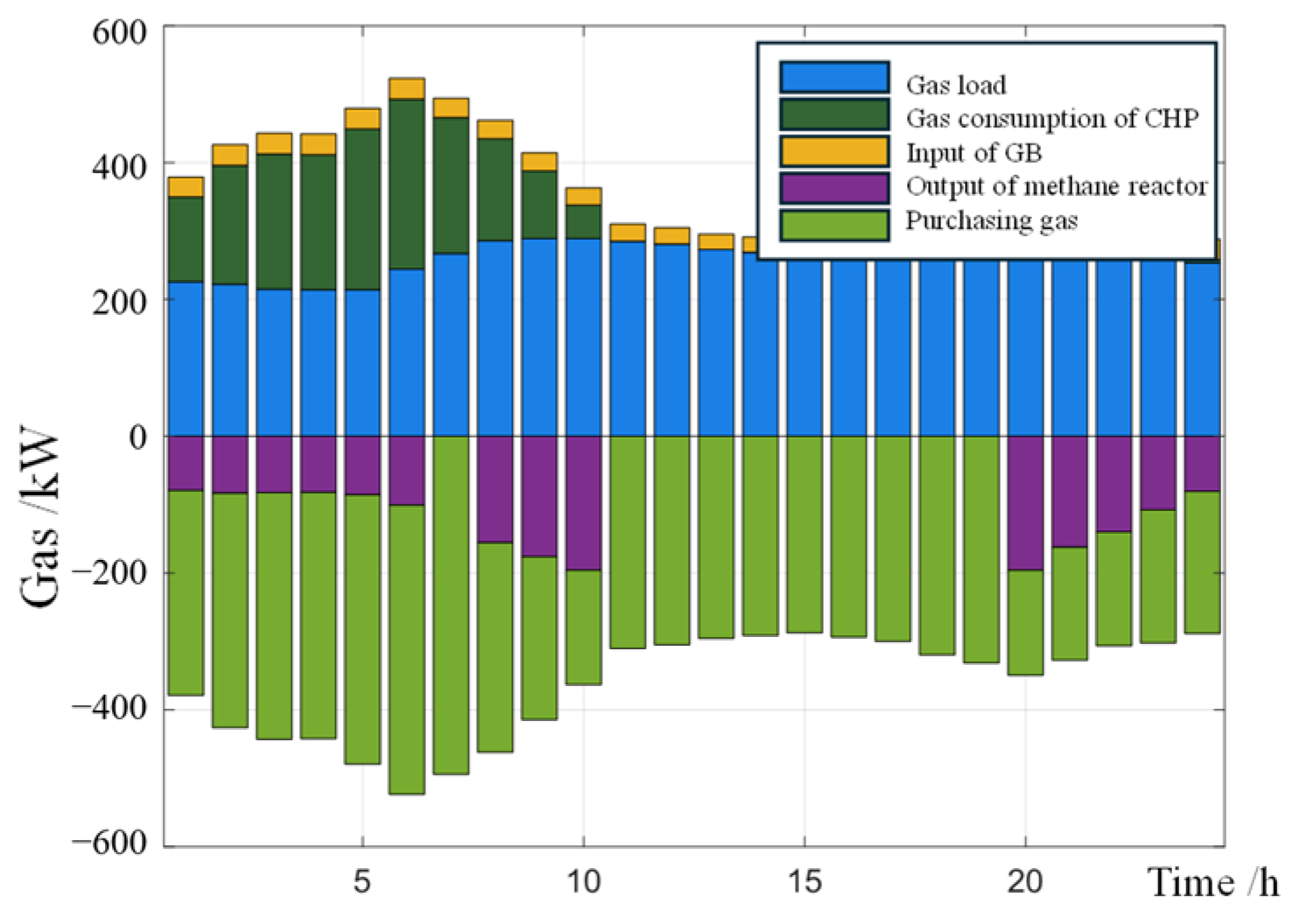
5.1. Scheduling Results
5.2. Carbon Reduction Results
- (1)
- Scenario Design for Sensitivity Analysis
- (2)
- Results of Sensitivity Analysis
5.3. Error Quantification of Frequency-Domain Model Under Out-of-Range Perturbation Scenarios
5.3.1. Scenario Design
5.3.2. Error Quantification Results
5.4. Numerical Comparison with Benchmark Methods
5.5. Frequency Component Truncation Validation
6. Conclusions
6.1. Core Research Innovations
6.2. Research Limitations
6.3. Outlook for Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- U.S. Energy Information Administration. Annual Energy Outlook 2020 with Projections to 2050; U.S. Energy Information Administration: Washington, DC, USA, 2024; pp. 19–35.
- Zheng, L.; Zhou, X.; Zheng, L.; Yang, L. Day-ahead optimal dispatch of an integrated energy system considering multiple uncertainty. Power Syst. Technol. 2020, 44, 2466–2473. [Google Scholar]
- Wang, Y.; Su, J.; Xue, Y.; Chang, X.; Li, Z.; Sun, H. Toward on rolling optimal dispatch strategy considering alert mechanism for antarctic electricity-hydrogen-heat integrated energy system. IEEE Trans. Sustain. Energy 2024, 15, 2457–2471. [Google Scholar] [CrossRef]
- Dong, L. Day-Ahead Optimal Operation Research on Hybrid CCHP System. Ph.D. Thesis, Shandong University, Jinan, China, 2019. [Google Scholar]
- Deng, B.; Fang, J.; Hui, Q.; Zhang, T.; Chen, Z.; Teng, Y.; Xi, X. Optimal scheduling for combined district heating and power systems using subsidy strategies. CSEE J. Power Energy Syst. 2019, 5, 399–408. [Google Scholar] [CrossRef]
- Wang, K.; Xue, Y.; Zhou, Y.; Li, Z.; Chang, X.; Sun, H. Distributed coordinated reconfiguration with soft open points for resilience-oriented restoration in integrated electric and heating systems. Appl. Energy 2024, 365, 123207. [Google Scholar] [CrossRef]
- Lin, C.; Wu, W.; Zhang, B.; Sun, Y. Decentralized solution for combined heat and power dispatch through benders decomposition. IEEE Trans. Sustain. Energy 2017, 8, 1361–1372. [Google Scholar] [CrossRef]
- Zou, Y.; Yang, L.; Li, J.; Xiao, L.; Ye, H.; Lin, Z. Robust optimal dispatch of micro-energy grid with multi-energy complementation of cooling heating power and natural gas. Autom. Electr. Power Syst. 2019, 43, 65–72. [Google Scholar]
- Fang, J.; Zeng, Q.; Ai, X.; Chen, Z.; Wen, J. Dynamic optimal energy flow in the integrated natural gas and electrical power systems. IEEE Trans. Sustain. Energy 2018, 9, 188–198. [Google Scholar] [CrossRef]
- Gan, W.; Yan, M.; Yao, W.; Guo, J.; Ai, X.; Fang, J.; Wen, J. Decentralized computation method for robust operation of multi-area joint regional-district integrated energy systems with uncertain wind power. Appl. Energy 2021, 298, 117280. [Google Scholar] [CrossRef]
- Tang, J.; Liu, J.; Sun, T.; Kang, H.; Hao, X. Multi-time-scale optimal scheduling of integrated energy system considering demand response. IEEE Access 2023, 11, 135891–135904. [Google Scholar] [CrossRef]
- Yang, M.; Cui, Y.; Huang, D.; Su, X.; Wu, G. Multi-time-scale coordinated optimal scheduling of integrated energy system considering frequency out-of-limit interval. Int. J. Electr. Power Energy Syst. 2022, 141, 108268. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, R.; Wang, L.; Zeng, S.; Li, Y. Optimal operation of regional integrated energy system considering demand response. Appl. Therm. Eng. 2021, 191, 116860. [Google Scholar] [CrossRef]
- CJ/T 447-2014; Automatic Shut-Off Valve for Pipeline Gas. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2014.
- GB/T 19963.1-2021; Technical Specifications for the Connection of Wind Farms to the Electricity System Part 1: Onshore Wind Farms. China Standards Press: Beijing, China, 2021.
- Ye, Y.F.; Li, D.F. Joint replenishment model with fuzzy demand and cost allocation approach based on egalitarian Shapley value. Syst. Eng. Theory Pract. 2024, 44, 1229–1245. [Google Scholar]
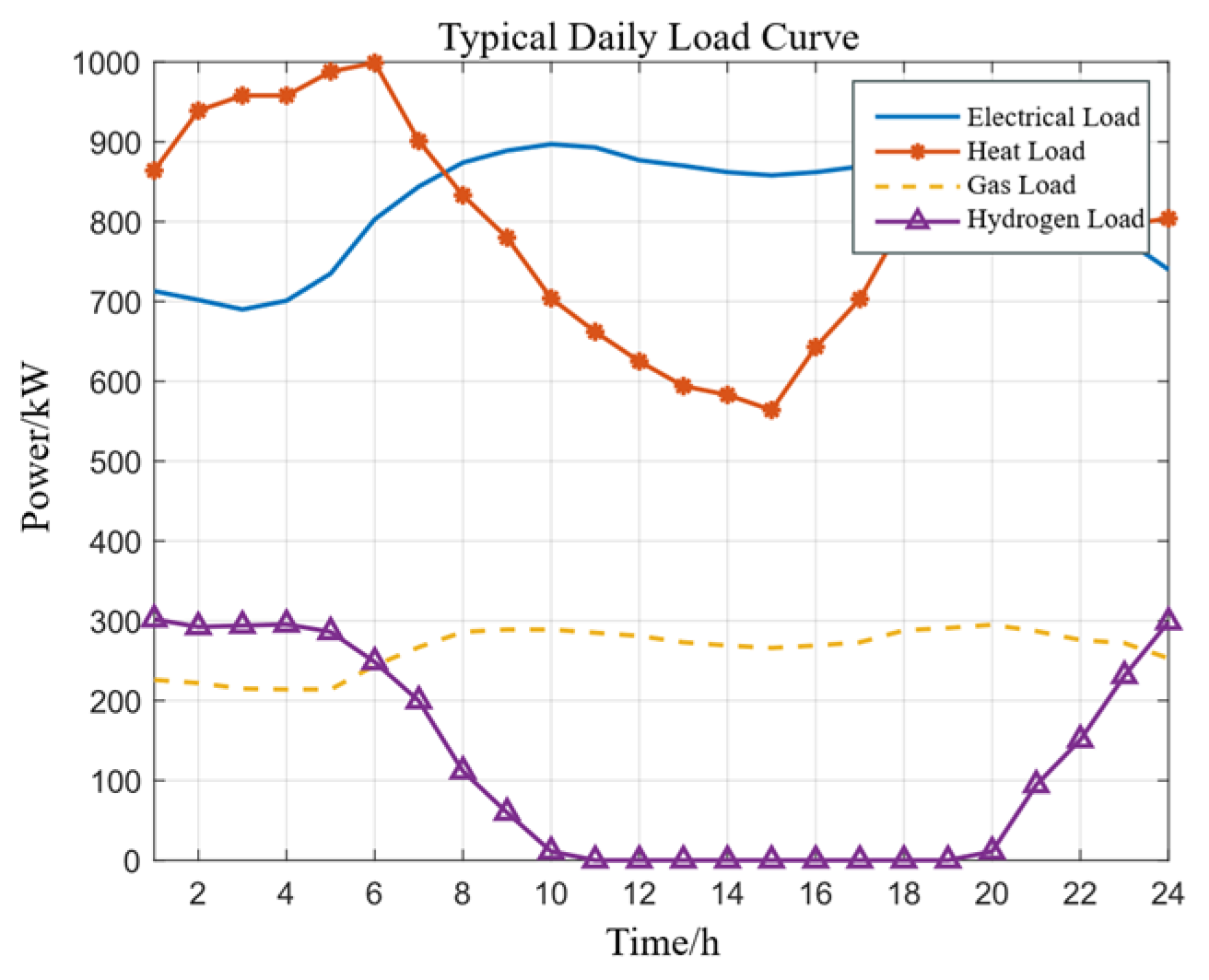
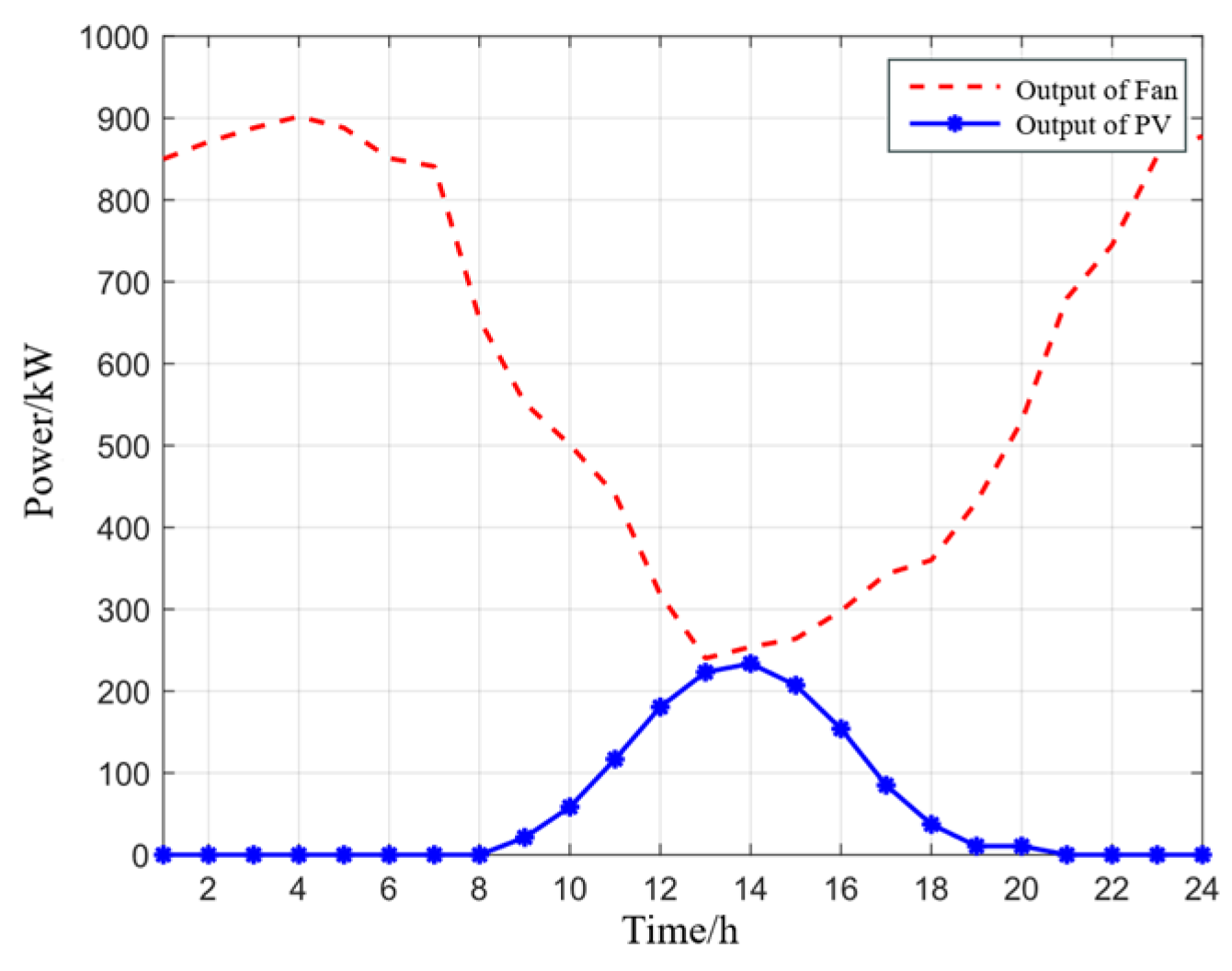
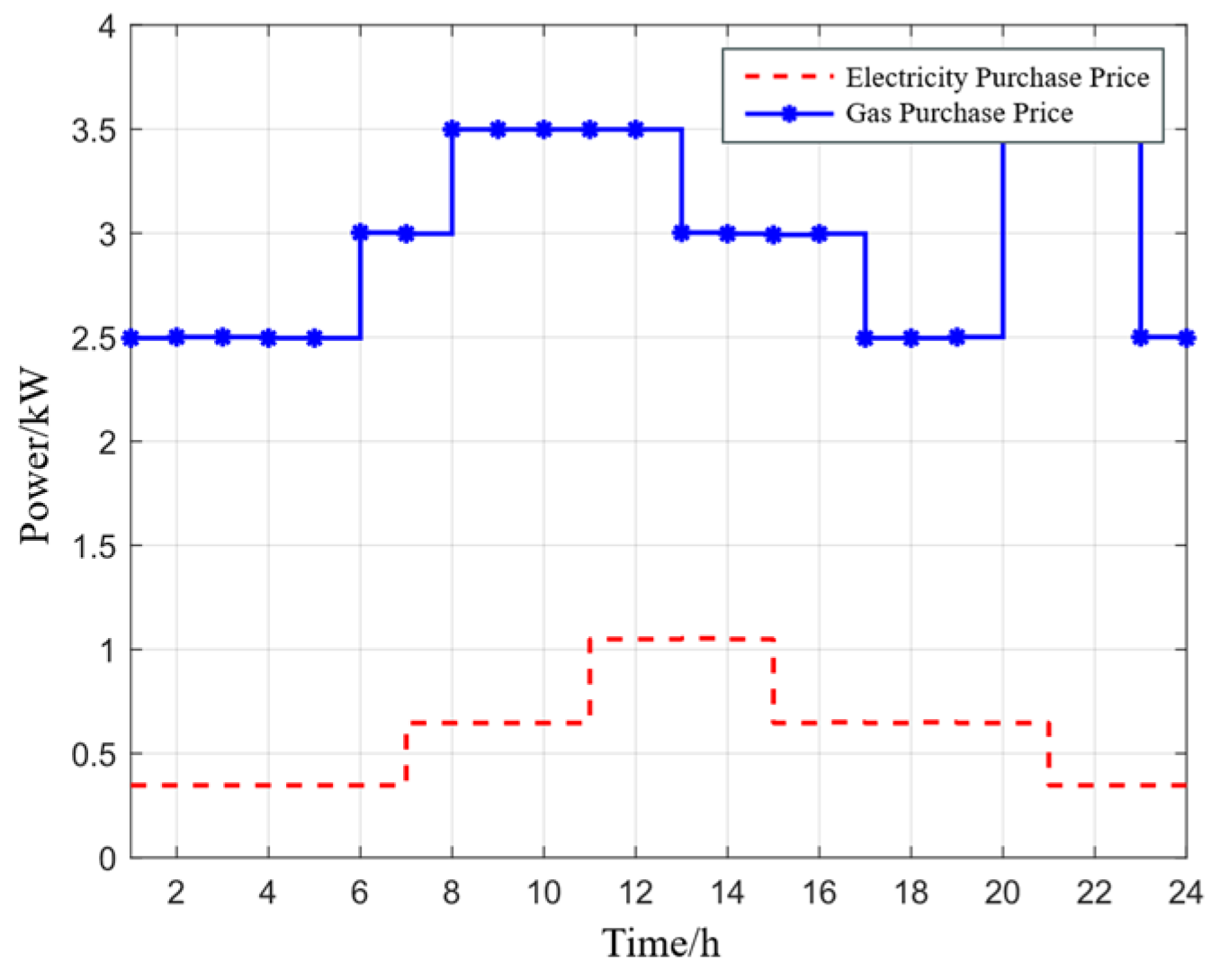
| Parameter Name | Value |
|---|---|
| FeasibilityTol | 1 × 10−6 |
| OptimalityTol | 1 × 10−4 |
| MIPGap | 1 × 10−3 |
| TimeLimit | 3600 s |
| Threads | 8 |
| Presolve | 2 (Aggressive) |
| Cuts | 3 (Moderate) |
| Equipment Type | Key Coefficient | Value | Uncertainty Range |
|---|---|---|---|
| CHP Unit | Power Generation Efficiency | ±0.02 (≈±5%) | |
| Heat Supply Efficiency | ±0.024 (≈±5%) | ||
| Gas Consumption Coefficient | ±0.2 MJ/m3 | ||
| Gas Boiler | Thermal Efficiency | ±0.018 (≈±2%) | |
| Gas Consumption Coefficient | ±0.2 MJ/m3 |
| Confidence Level | Net Operating Cost |
|---|---|
| 100% improved | 705.25 |
| 90% improved | 710.30 |
| 80% improved | 715.25 |
| 70% improved | 710.30 |
| Scenario Type | Load Fluctuation Amplitude | Renewable Energy (Wind/PV) Fluctuation Amplitude |
|---|---|---|
| Baseline | 10% (≤12%) | 15% (≤18%) |
| Out-of-range 1 | 15% (>12%) | 25% (>18%) |
| Out-of-range 2 | 20% (>12%) | 30% (>18%) |
| Out-of-range 3 | 25% (>12%) | 35% (>18%) |
| Scenario Type | Heating Network Outlet Temperature Error (Average/Maximum) | Gas Network Node Pressure Error (Average/Maximum) | System Carbon Emissions Error (Average/Maximum) |
|---|---|---|---|
| Baseline | 1.2%/2.8% | 0.9%/2.1% | 0.7%/1.5% |
| Out-of-range 1 | 3.5%/5.7% | 2.8%/4.3% | 2.2%/3.8% |
| Out-of-range 2 | 6.8%/9.2% | 5.3%/7.9% | 4.5%/6.3% |
| Out-of-range 3 | 12.3%/15.8% | 9.7%/13.5% | 8.2%/11.4% |
| Comparison Indicators | Traditional Steady-State Modeling Method | Time-Domain Dynamic Modeling Method | Proposed Method |
|---|---|---|---|
| Computational Time (s) | 42.3 | 187.6 | 3.87 |
| Heating Network Outlet Temperature Error (%) | 8.5 | 2.1 | 1.2 |
| Gas Network Node Pressure Error (%) | 7.9 | 1.8 | 0.9 |
| Total Operating Cost (USD) | 126,840 | 119,720 | 110,630 |
| Wind Power Accommodation Rate (%) | 82.3 | 85.4 | 90.9 |
| Carbon Emission Reduction Rate (%) | 12.5 | 17.3 | 30.0 |
| K Value | Pressure MAE (%) | Pressure MRE (%) | Mass Flow MAE (%) | Mass Flow MRE (%) | Computational Time (s) |
|---|---|---|---|---|---|
| 5 | 1.28 | 2.35 | 1.41 | 2.57 | 1.86 |
| 8 | 0.63 | 1.21 | 0.75 | 1.38 | 2.54 |
| 10 | 0.41 | 0.93 | 0.52 | 1.07 | 3.12 |
| 12 | 0.35 | 0.78 | 0.42 | 0.91 | 3.87 |
| 15 | 0.32 | 0.69 | 0.39 | 0.80 | 5.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.; Liu, X.; Wang, Z.; Lv, Y.; Zhang, Z.; Zhang, S. Frequency-Domain Modeling and Multi-Agent Game-Theory-Based Low-Carbon Optimal Scheduling Strategy for Integrated Energy Systems. Electronics 2025, 14, 4635. https://doi.org/10.3390/electronics14234635
Chang Y, Liu X, Wang Z, Lv Y, Zhang Z, Zhang S. Frequency-Domain Modeling and Multi-Agent Game-Theory-Based Low-Carbon Optimal Scheduling Strategy for Integrated Energy Systems. Electronics. 2025; 14(23):4635. https://doi.org/10.3390/electronics14234635
Chicago/Turabian StyleChang, Yingxian, Xin Liu, Zhiqiang Wang, Yifan Lv, Ziyang Zhang, and Song Zhang. 2025. "Frequency-Domain Modeling and Multi-Agent Game-Theory-Based Low-Carbon Optimal Scheduling Strategy for Integrated Energy Systems" Electronics 14, no. 23: 4635. https://doi.org/10.3390/electronics14234635
APA StyleChang, Y., Liu, X., Wang, Z., Lv, Y., Zhang, Z., & Zhang, S. (2025). Frequency-Domain Modeling and Multi-Agent Game-Theory-Based Low-Carbon Optimal Scheduling Strategy for Integrated Energy Systems. Electronics, 14(23), 4635. https://doi.org/10.3390/electronics14234635





