Self-Tuning Current Control via ANN for Enhanced Harmonic Mitigation in Hybrid PV–Battery Storage Systems Utilizing the 3L-HANPC Inverter
Abstract
1. Introduction
- Self-Tuning Current Control Solution: This study presents the design of an ANN-based current controller for a 3L-HANPC inverter. By adopting this approach, the inherent limitations associated with the design and parameterization of traditional PI controllers, including the subsequent need for time-consuming manual tuning in energy management systems, are effectively eliminated, resulting in a robust self-tuning control solution.
- Multi-Criteria Design Methodology: A multi-criteria selection methodology was employed for determining the optimal architecture of the MLP-based ANN controller. This methodology incorporates both conventional training error metrics and practical indicators, such as THD performance and training duration, ensuring the chosen network structure satisfies implementation-oriented constraints for high-efficiency PV-BSS applications.
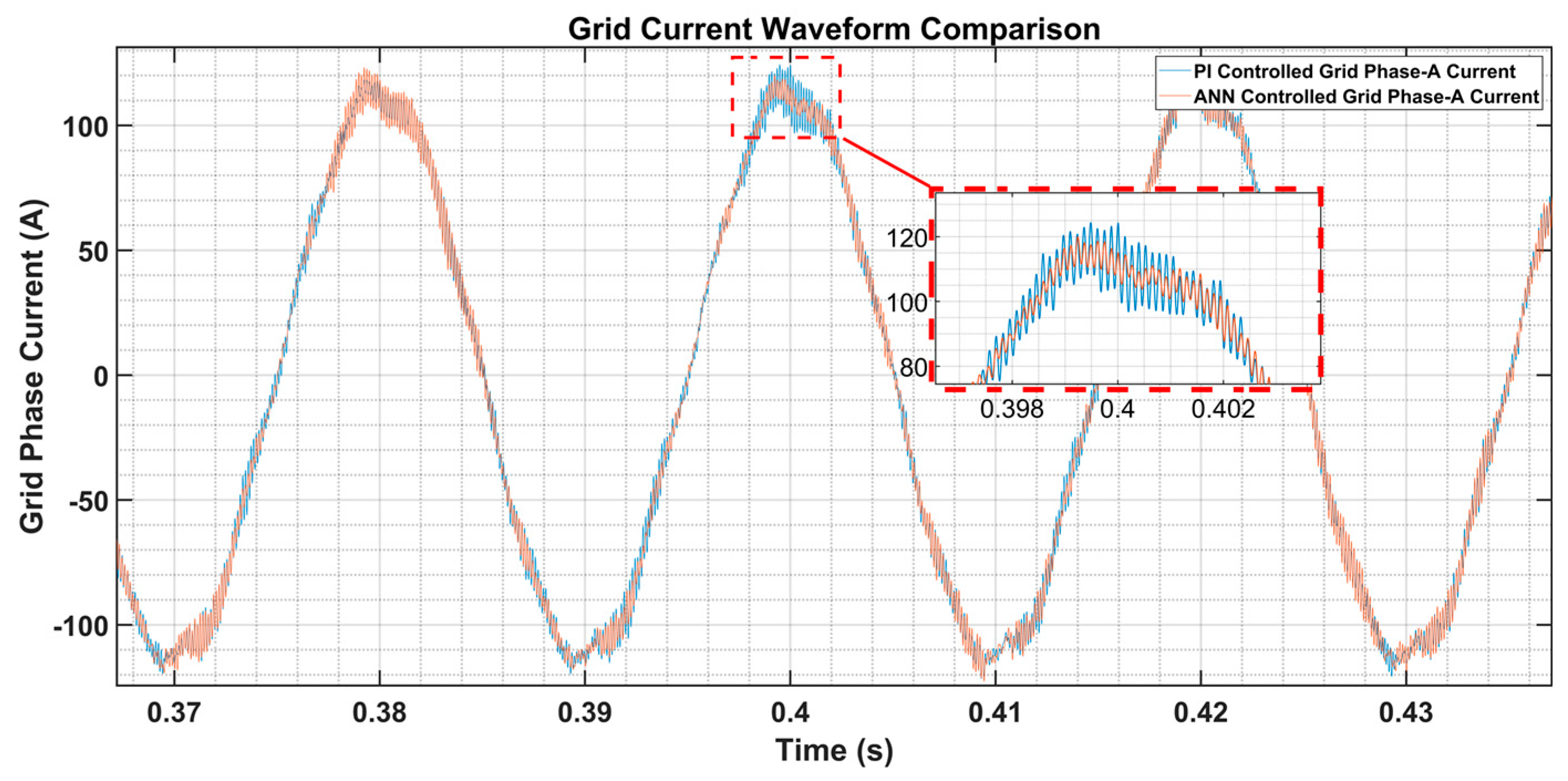
- Enhanced Performance Validation: Simulation studies conclusively demonstrate that the THD of the 3L-HANPC inverter output current is significantly reduced (Enhanced Harmonic Mitigation) when utilizing the ANN-based current controller, compared to conventional PI methods. Notably, the proposed controller yields superior or comparable THD performance across a wide range of power factor and active/reactive loading scenarios. Furthermore, the ANN-based controller exhibits improved dynamic transition performance, ensuring faster and more stable responses under varying operating conditions.
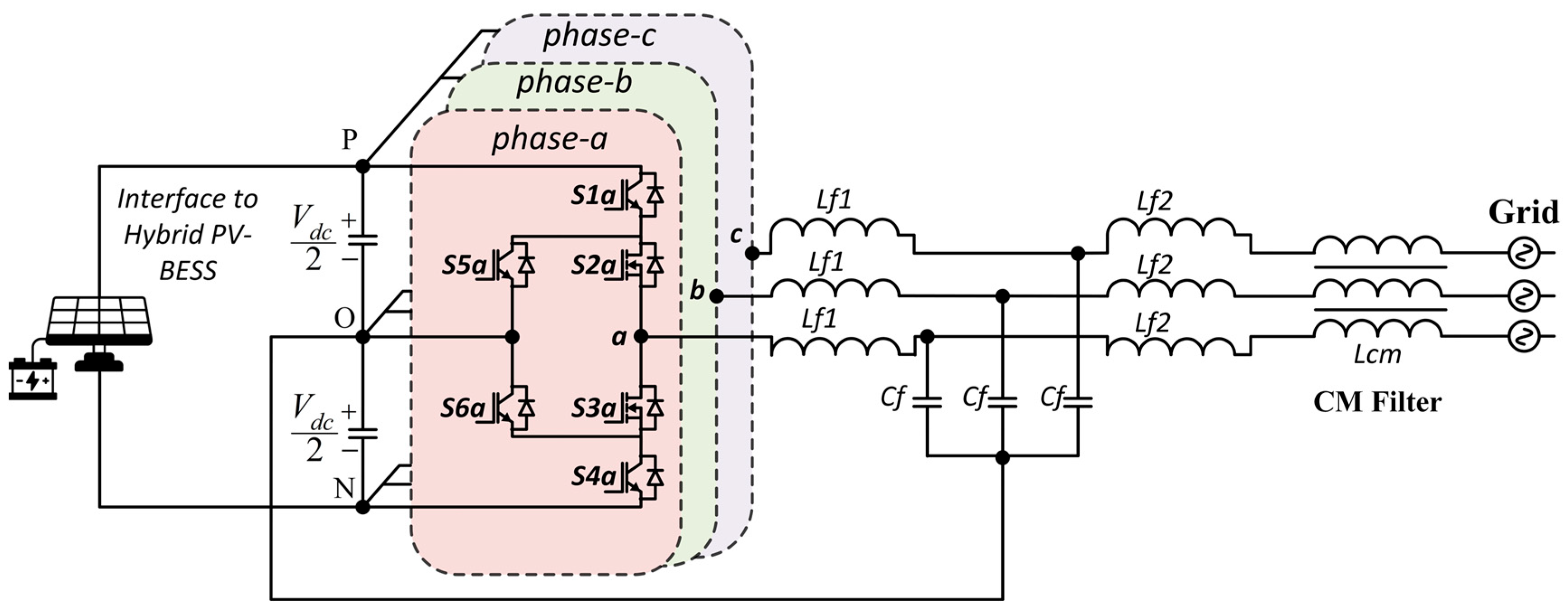
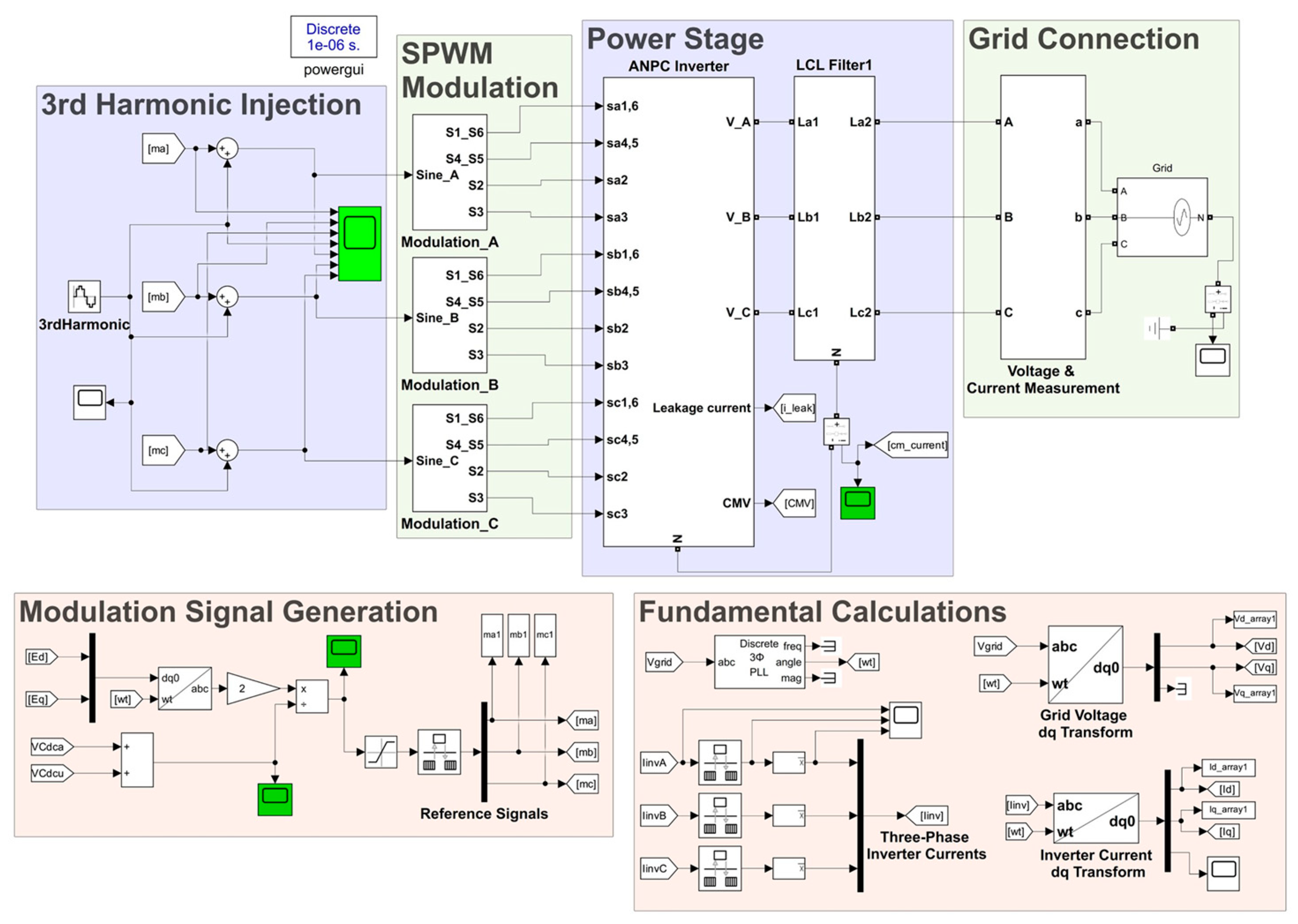
2. 3L-HANPC Inverter
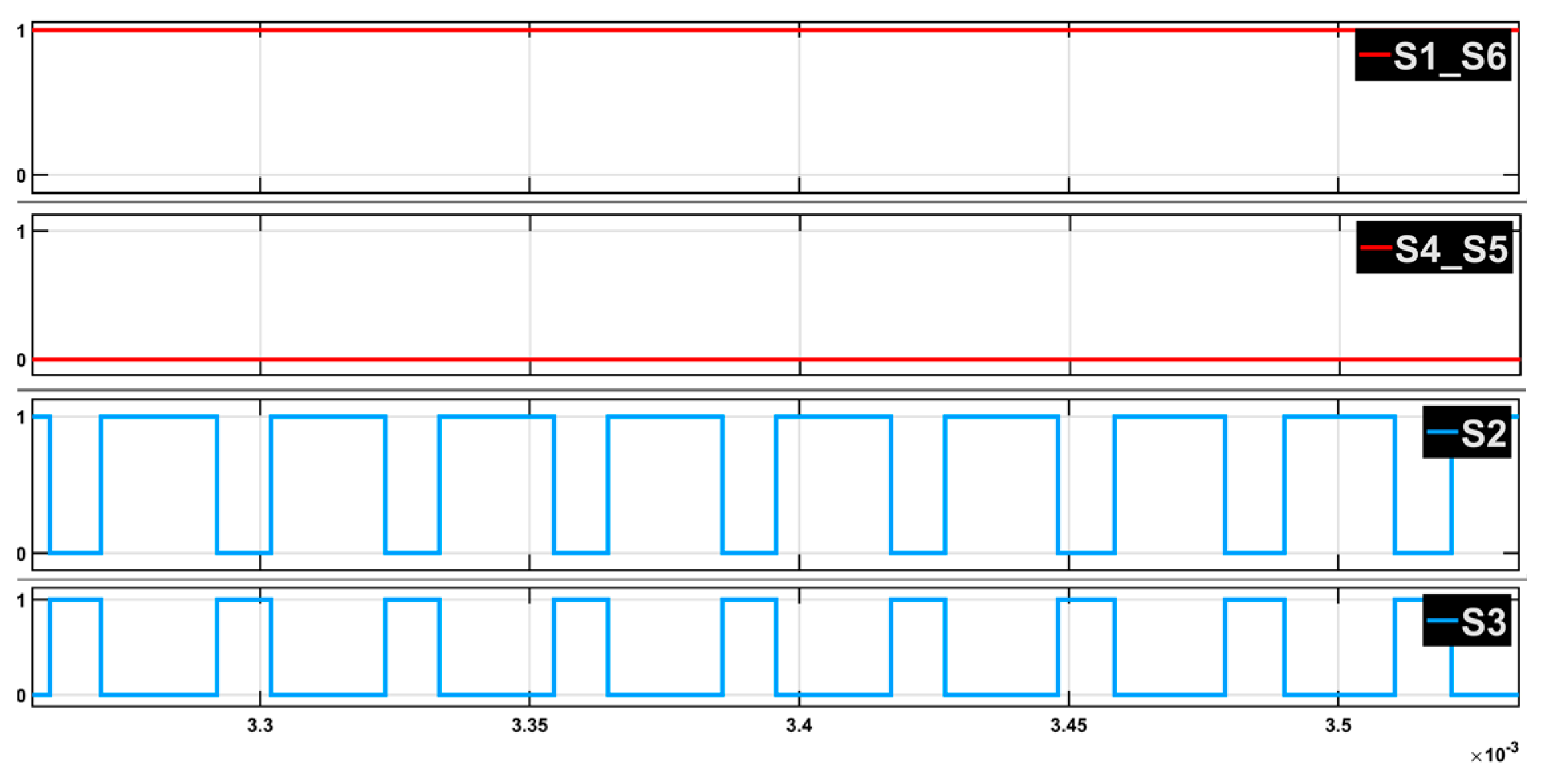
2.1. Topology and Switching States
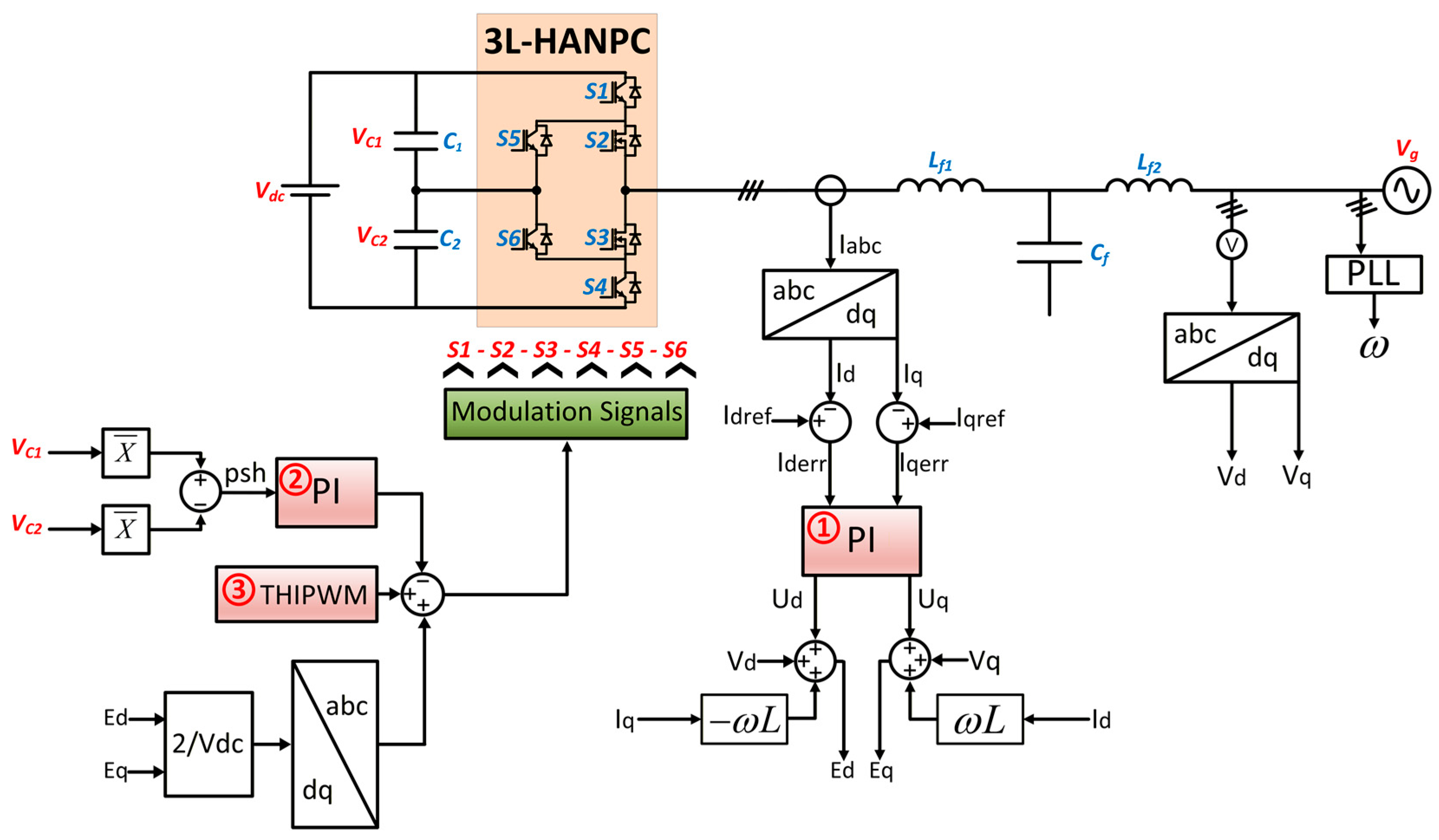
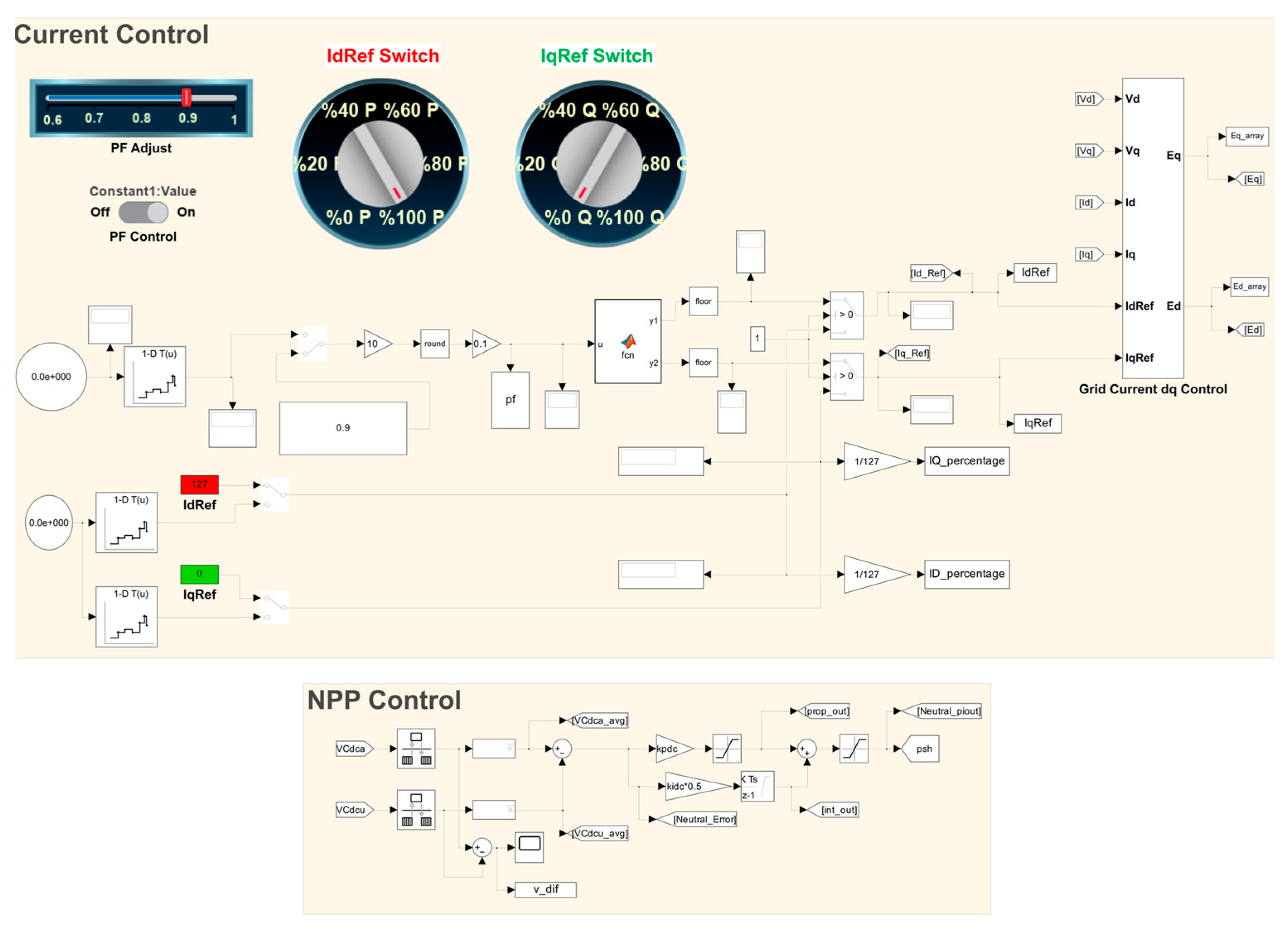
2.2. Modulation and Conventional Control Strategy
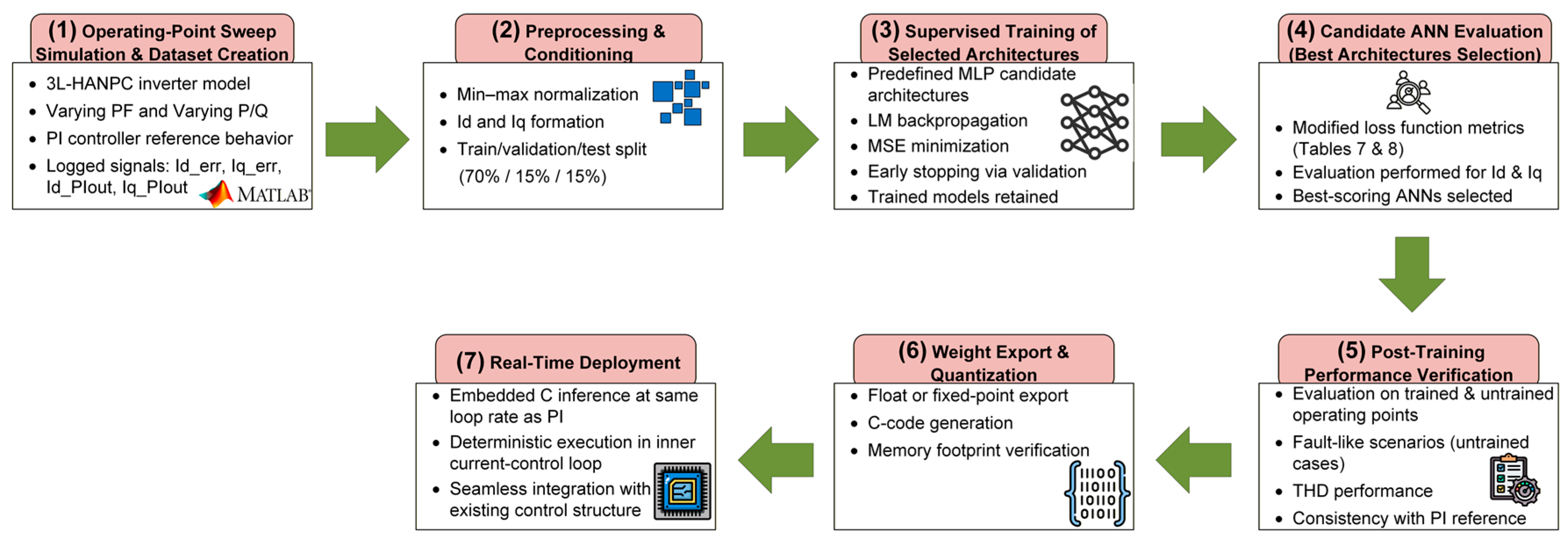
3. Proposed ANN-Based Control of 3L-HANPC Inverter
3.1. ANN Architecture
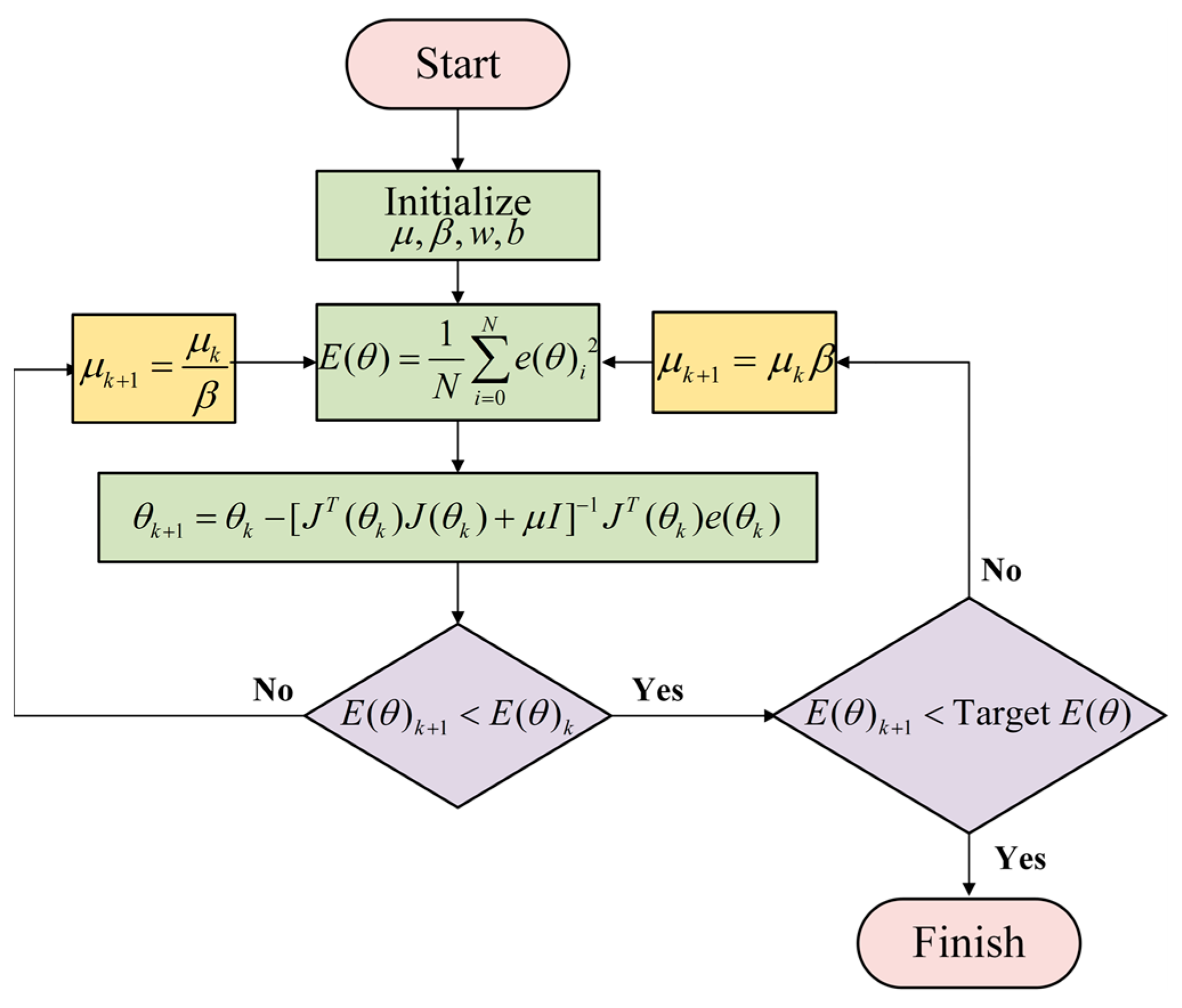
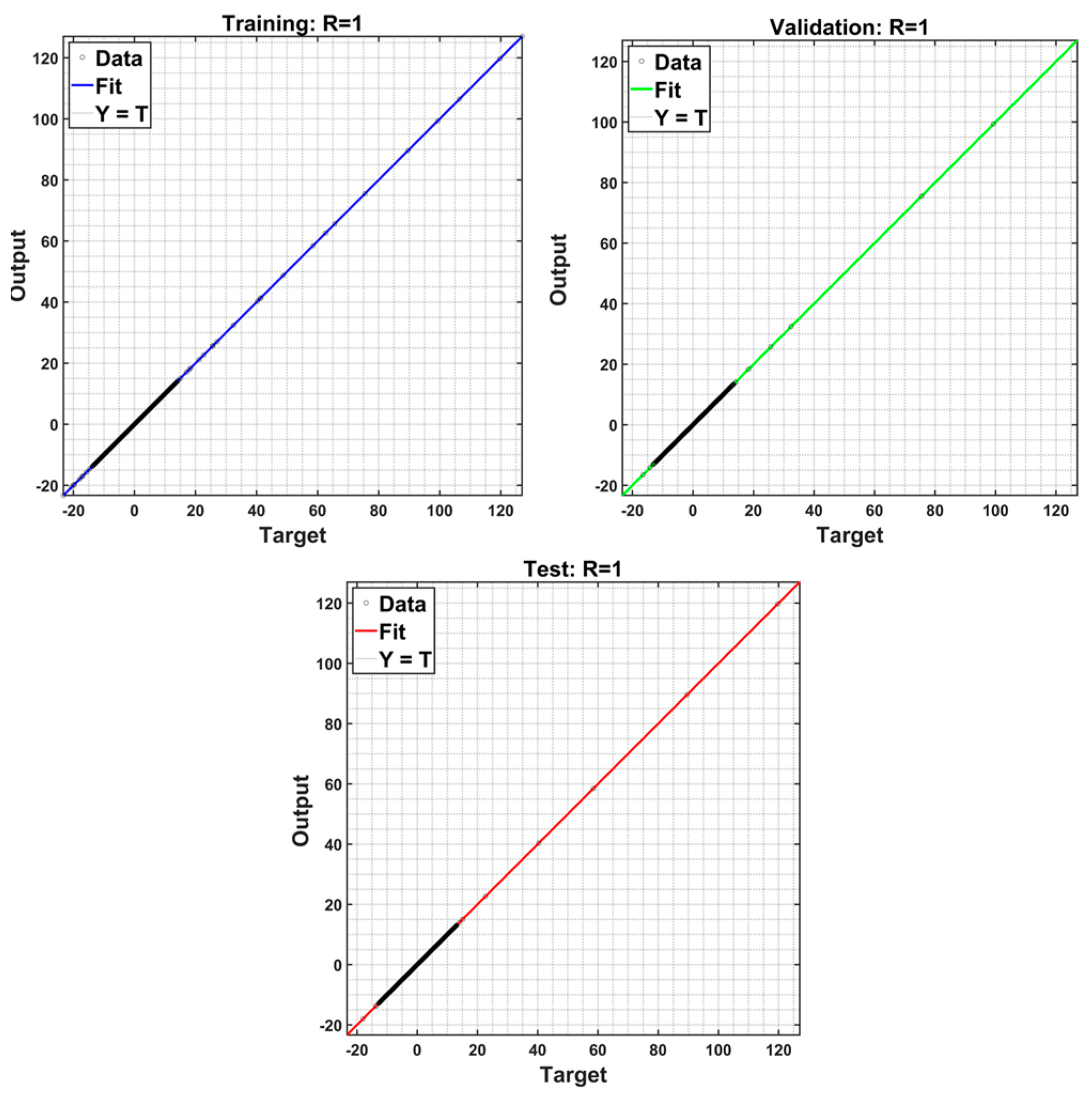
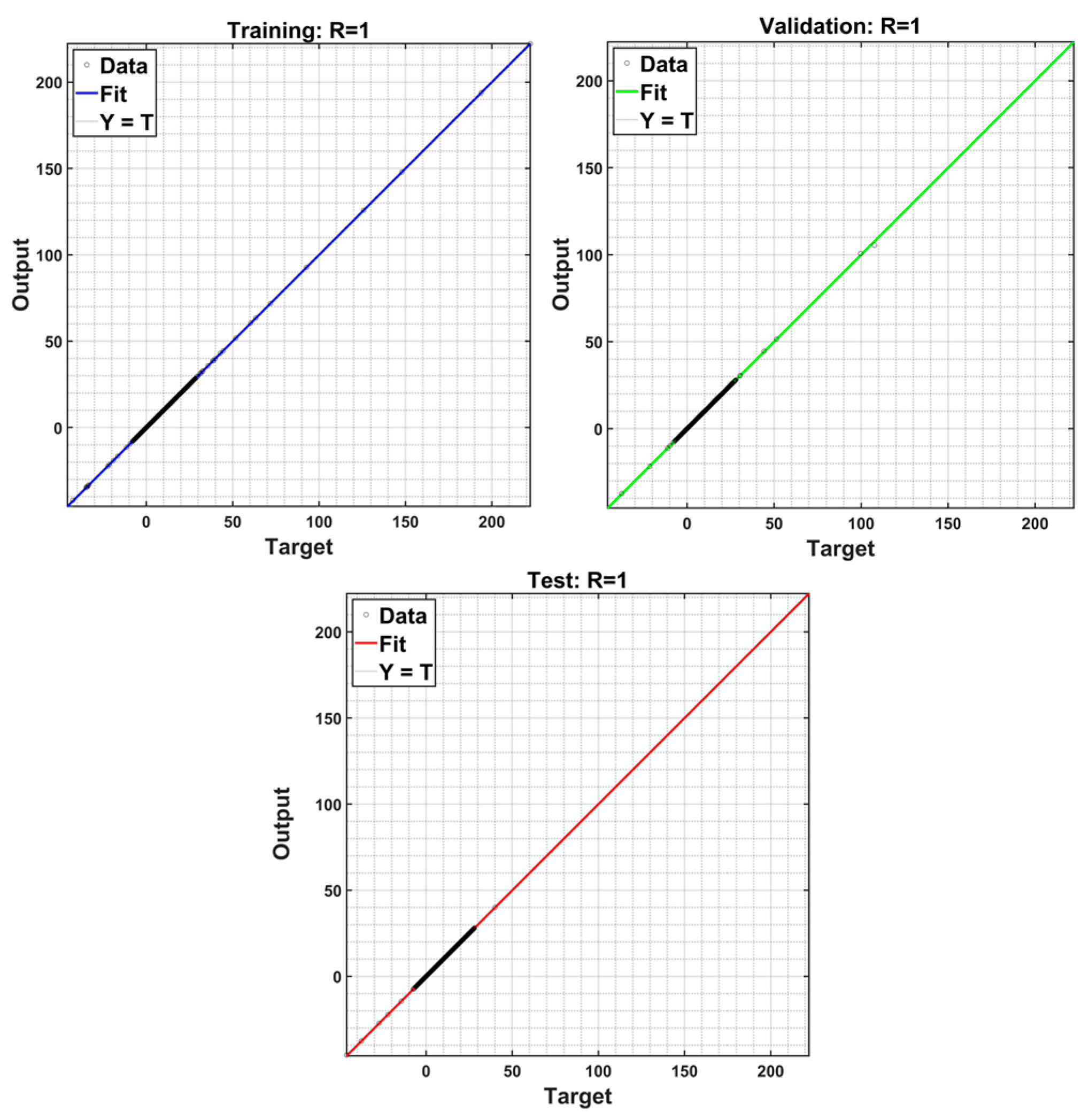
3.2. Network Training Methodology
- (1)
- VarPF: Five different power factor levels are considered, namely 0.6, 0.7, 0.8, 0.9, and 1.0.
- (2)
- VarP: Five active power levels corresponding to 100%, 80%, 60%, 40%, and 20% of the rated output power are employed. In this region, the inverter supplies active power to the grid.
- (3)
- VarQ: Five reactive power levels corresponding to 100%, 80%, 60%, 40%, and 20% of the rated output power are employed. In this region, the inverter supplies reactive power to the grid.
3.3. Evaluation Criteria for Network Selection
- Full-load THD Performance: The model’s ability to generalize to full-load conditions is a critical measure of its practical effectiveness. In the context of energy saving management, achieving low THD directly translates to reduced harmonic losses, which is a key performance metric for high-efficiency PV-BSS applications. We consider the THD performance in both active and reactive power regions to ensure robust and reliable operation under varying load conditions.
- Training Time: The computational efficiency of the training process is a significant factor in network selection, particularly for large-scale or real-time applications. A reduced training time is vital for ensuring the practical feasibility and deployment speed of this self-tuning control solution. A model with excellent performance but an excessively long training time may not be a viable solution.
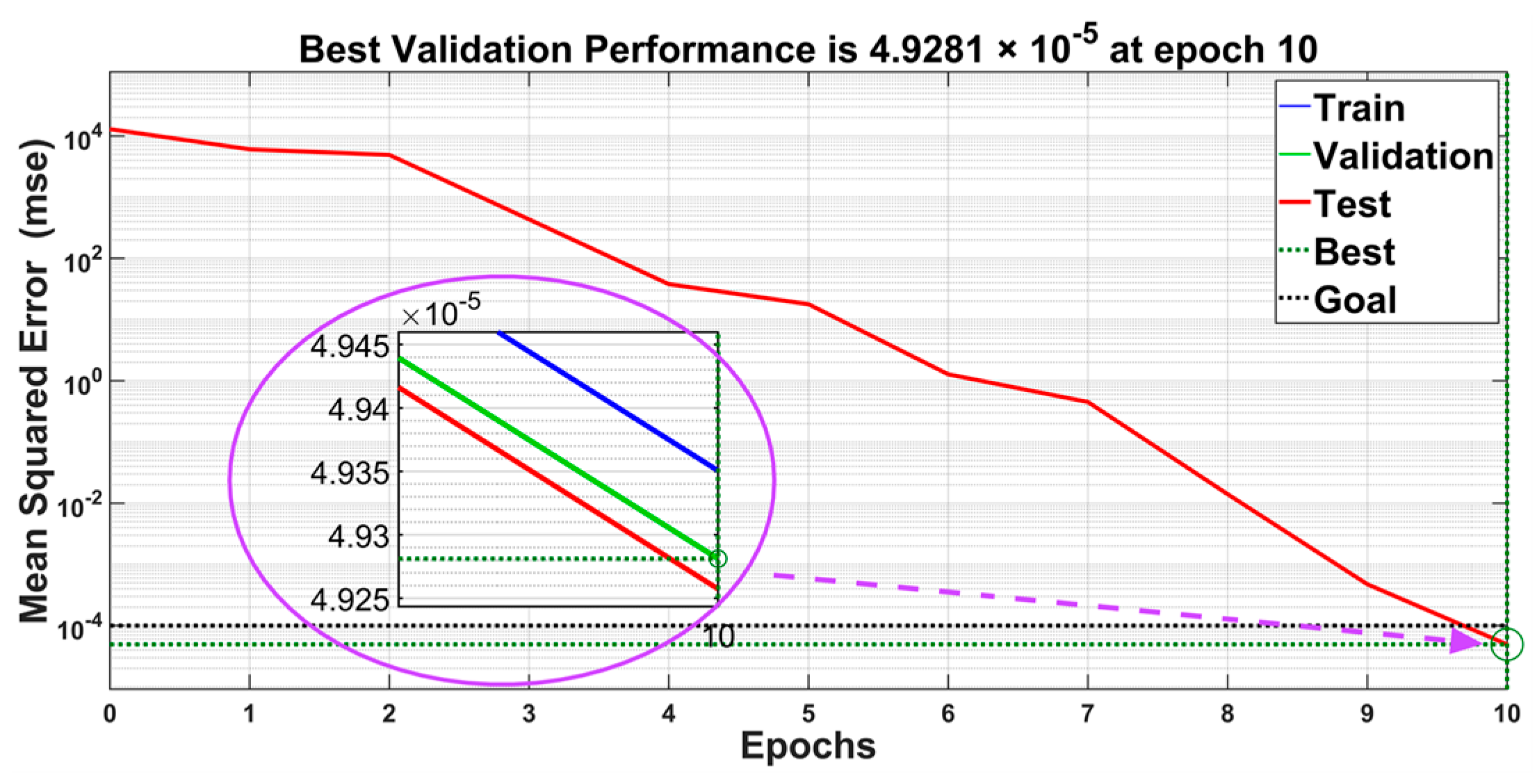
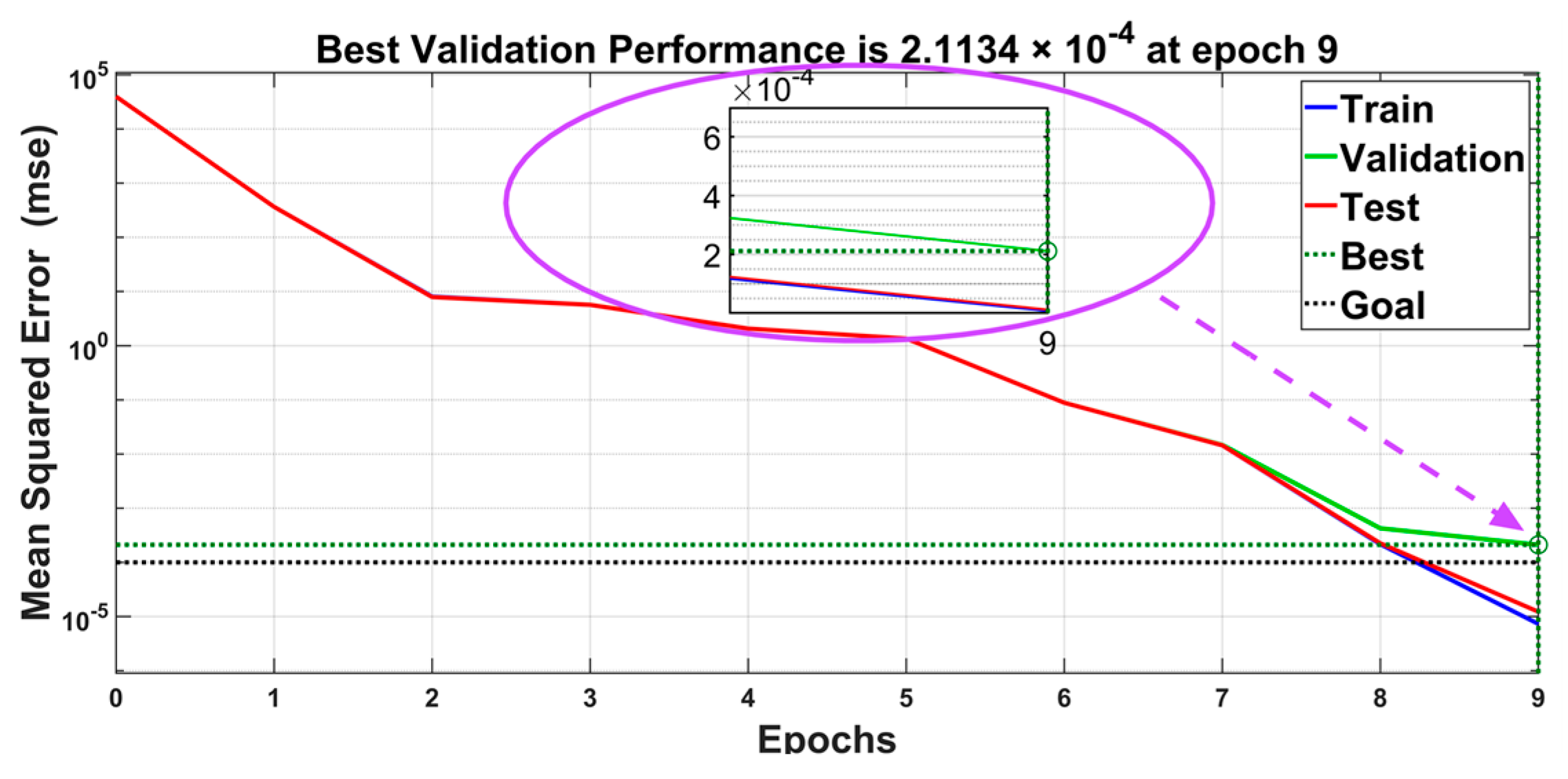
3.4. Performance Assessment
4. Simulation Studies
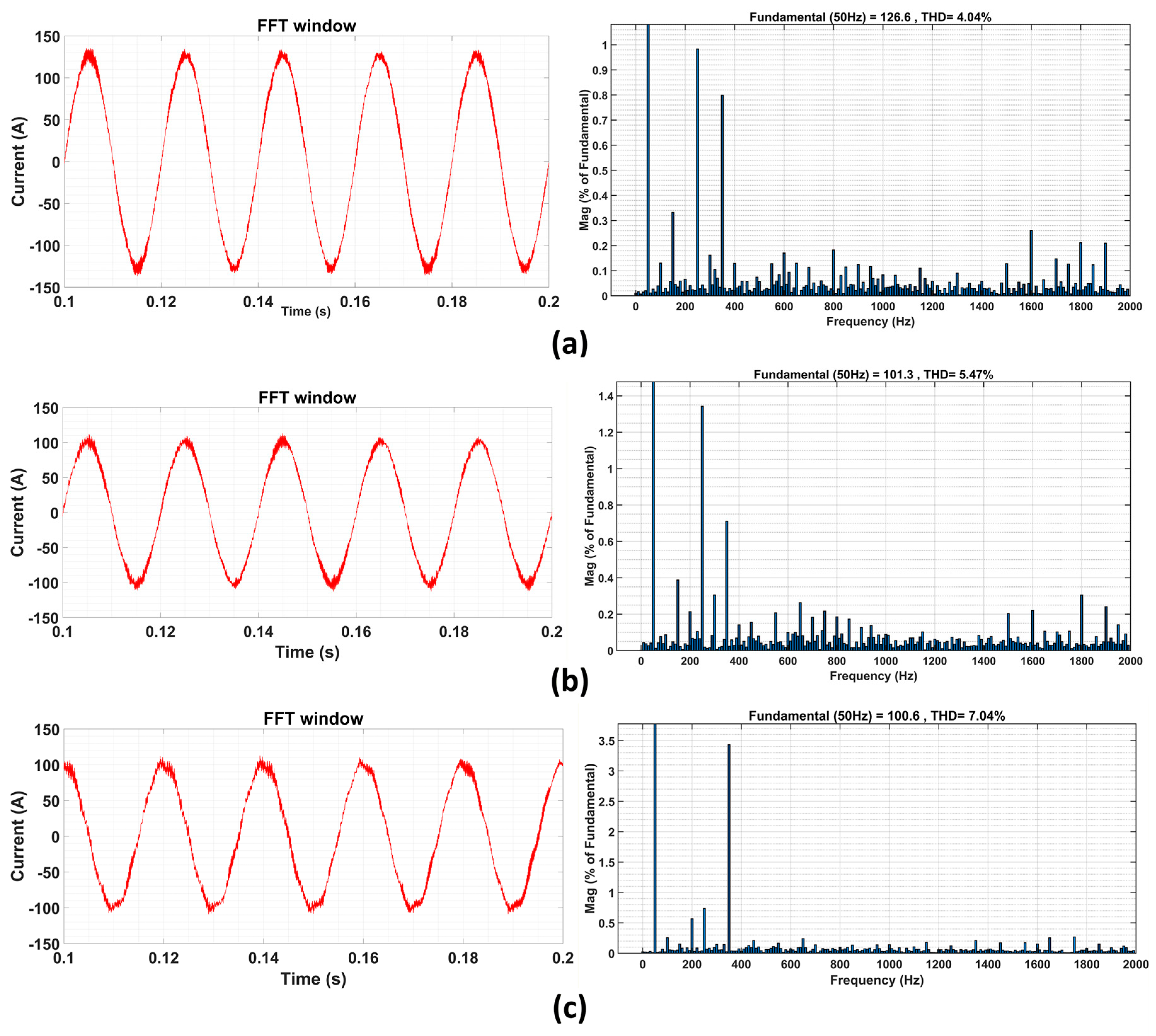
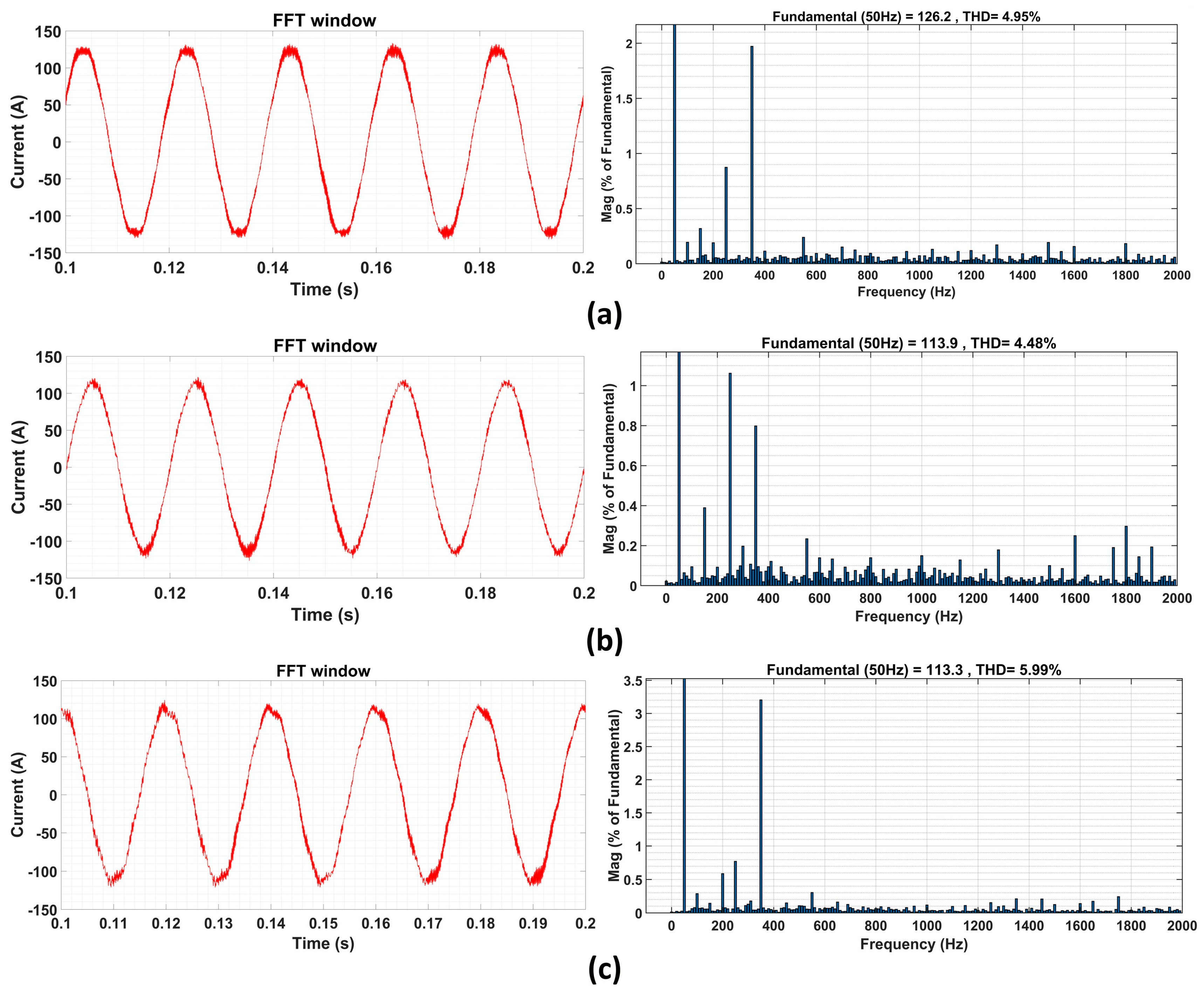
4.1. Steady-State Performance and THD Analysis
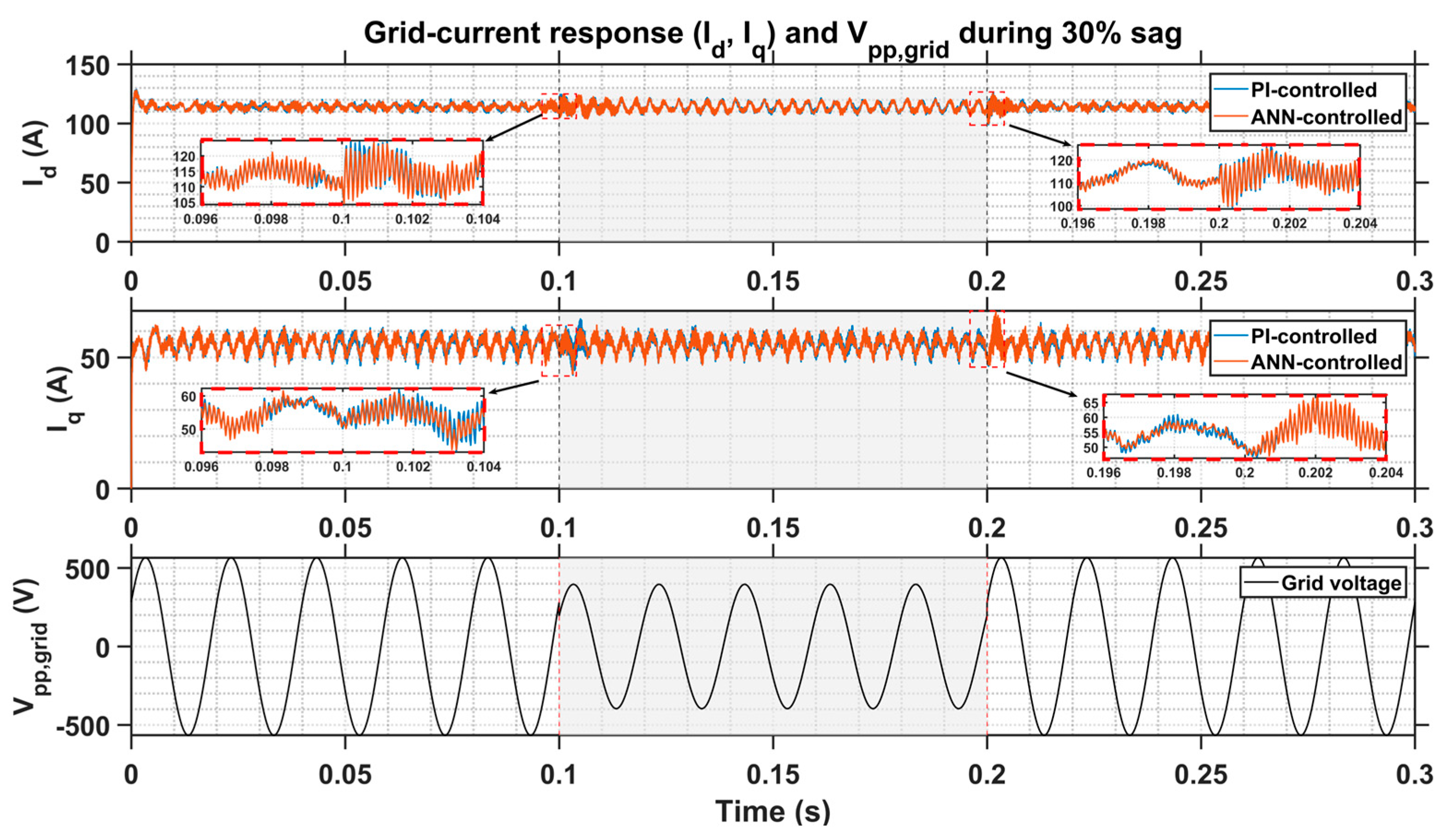
4.2. Dynamic Performance Analysis
4.3. Computational Burden and Real-Time Implementation Analysis
4.3.1. Memory Footprint Analysis
4.3.2. Latency and Computational Feasibility
- Calculation of (Core Operations)
- Total Multiplications ():
- Total Additions ():
- Calculation of (Total FLOPs)
4.3.3. Justification Against Simpler Techniques
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Snapshot 2024—IEA-PVPS. Available online: https://iea-pvps.org/snapshot-reports/snapshot-2024/ (accessed on 9 April 2025).
- Renewables 2024—Analysis—IEA. Available online: https://www.iea.org/reports/renewables-2024 (accessed on 9 April 2025).
- Čorba, Z.; Popadić, B.; Katić, V.; Dumnić, B.; Milićević, D. Future of High Power PV Plants-1500V Inverters. In Proceedings of the 2017 International Symposium on Power Electronics, Novi Sad, Serbia, 19–21 October 2017. [Google Scholar] [CrossRef]
- Serban, E.; Ordonez, M.; Pondiche, C. DC-Bus Voltage Range Extension in 1500 v Photovoltaic Inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 901–917. [Google Scholar] [CrossRef]
- IEC 62109-1:2010|IEC. Available online: https://webstore.iec.ch/en/publication/6470 (accessed on 19 November 2025).
- IEC 62109-2:2011|IEC. Available online: https://webstore.iec.ch/en/publication/6471 (accessed on 19 November 2025).
- Rodriguez, J.; Bernet, S.; Steimer, P.K.; Lizama, I.E. A Survey on Neutral-Point-Clamped Inverters. IEEE Trans. Ind. Electron. 2010, 57, 2219–2230. [Google Scholar] [CrossRef]
- Jin, F.; Qie, T.; Liu, Y.; Zhang, Z.; Watts, J.; Iu, H.H.C.; Fernando, T.; Zhang, X. A Novel Adaptive Model Predictive Current Control for Three-Level Neural-Point-Clamped Inverter with RL Load. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 13, 2234–2245. [Google Scholar] [CrossRef]
- Zakzewski, D.; Resalayyan, R.; Khaligh, A. Hybrid Neutral Point Clamped Converter: Review and Comparison to Traditional Topologies. IEEE Trans. Transp. Electrif. 2023, 10, 6087–6099. [Google Scholar] [CrossRef]
- Yu, T.; Wan, W.; Duan, S. A Modulation Method to Eliminate Leakage Current and Balance Neutral-Point Voltage for Three-Level Inverters in Photovoltaic Systems. IEEE Trans. Ind. Electron. 2023, 70, 1635–1645. [Google Scholar] [CrossRef]
- Jung, J.H.; Ku, H.K.; Im, W.S.; Kim, J.M. A Carrier-Based PWM Control Strategy for Three-Level NPC Inverter Based on Bootstrap Gate Drive Circuit. IEEE Trans. Power Electron. 2020, 35, 2843–2860. [Google Scholar] [CrossRef]
- Nabae, A.; Takahashi, I.; Akagi, H. A New Neutral-Point-Clamped PWM Inverter. IEEE Trans. Ind. Appl. 1981, IA-17, 518–523. [Google Scholar] [CrossRef]
- Wu, B.; Narimani, M. High-Power Converters and AC Drives, 2nd ed.; IEEE Press: Piscataway, NJ, USA, 2017. [Google Scholar]
- Zhao, T.; Zhang, X.; Mao, W.; Wang, F.; Xu, J.; Gu, Y. A Modified Hybrid Modulation Strategy for Suppressing DC Voltage Fluctuation of Cascaded H-Bridge Photovoltaic Inverter. IEEE Trans. Ind. Electron. 2018, 65, 3932–3941. [Google Scholar] [CrossRef]
- Jiao, Y.; Lee, F.C. New Modulation Scheme for Three-Level Active Neutral-Point-Clamped Converter with Loss and Stress Reduction. IEEE Trans. Ind. Electron. 2015, 62, 5468–5479. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, T.; Gafford, J.; Essakiappan, S.; Manjrekar, M. Design of a 1500V Si IGBT/SiC MOSFET Hybrid Switch-Based Three-Level Active NPC Inverter. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition, ECCE 2021—Proceedings, Vancouver, BC, Canada, 10–14 October 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 168–173. [Google Scholar] [CrossRef]
- Zhao, S.; Feng, Z.; Sun, Z.; Zhang, X.; Zhao, Z.; Zhao, T.; Cao, Q. A Efficiency Optimization and Loss Balancing Method for Hybrid Three-Level Active Neutral Point Clamped Inverter. Electr. Eng. 2025, 107, 7575–7586. [Google Scholar] [CrossRef]
- Zhang, L.; Lou, X.; Li, C.; Wu, F.; Gu, Y.; Chen, G.; Xu, D. Evaluation of Different Si/SiC Hybrid Three-Level Active NPC Inverters for High Power Density. IEEE Trans. Power Electron. 2020, 35, 8224–8236. [Google Scholar] [CrossRef]
- Feng, Z.; Zhang, X.; Wang, J.; Yu, S. A High-Efficiency Three-Level ANPC Inverter Based on Hybrid SiC and Si Devices. Energies 2020, 13, 1159. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhai, Z.; Mao, M.; Wang, S.; Sun, S.; Mei, D.; Hu, Q. Control and Intelligent Optimization of a Photovoltaic (PV) Inverter System: A Review. Energies 2024, 17, 1571. [Google Scholar] [CrossRef]
- Boscaino, V.; Ditta, V.; Marsala, G.; Panzavecchia, N.; Tinè, G.; Cosentino, V.; Cataliotti, A.; Di Cara, D. Grid-Connected Photovoltaic Inverters: Grid Codes, Topologies and Control Techniques. Renew. Sustain. Energy Rev. 2024, 189, 113903. [Google Scholar] [CrossRef]
- Nie, K.; Gao, F.; Xu, T.; Cao, Y. A Full-ANN Control Scheme of Single-Phase Grid-Connected Inverter. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference, IPEMC 2024 ECCE Asia, Chengdu, China, 17–20 May 2024; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2024; pp. 173–177. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Ker, P.J.; Begum, R.A.; Agelidis, V.G.; Blaabjerg, F. Power Electronics Contribution to Renewable Energy Conversion Addressing Emission Reduction: Applications, Issues, and Recommendations. Appl. Energy 2019, 251, 113404. [Google Scholar] [CrossRef]
- Qashqai, P.; Babaie, M.; Zgheib, R.; Al-Haddad, K. A Model-Free Switching and Control Method for Three-Level Neutral Point Clamped Converter Using Deep Reinforcement Learning. IEEE Access 2023, 11, 105394–105409. [Google Scholar] [CrossRef]
- Zhao, S.; Blaabjerg, F.; Wang, H. An Overview of Artificial Intelligence Applications for Power Electronics. IEEE Trans. Power Electron. 2021, 36, 4633–4658. [Google Scholar] [CrossRef]
- Babaie, M.; Sharifzadeh, M.; Mehrasa, M.; Chouinard, G.; Al-Haddad, K. Supervised Learning Model Predictive Control Trained by ABC Algorithm for Common-Mode Voltage Suppression in NPC Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3446–3456. [Google Scholar] [CrossRef]
- Babaie, M.; Al-Haddad, K. ANN Based Model-Free Sliding Mode Control for Grid-Connected Compact Multilevel Converters: An Experimental Validation. In Proceedings of the IEEE International Symposium on Industrial Electronics, Kyoto, Japan, 20–23 June 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, S.; Hussaini, H.; Yang, T.; Dragicevic, T.; Bozhko, S.; Wheeler, P.; Vazquez, S. Inverse Application of Artificial Intelligence for the Control of Power Converters. IEEE Trans. Power Electron. 2023, 38, 1535–1548. [Google Scholar] [CrossRef]
- Sun, Y.; Li, S.; Lin, B.; Fu, X.; Ramezani, M.; Jaithwa, I. Artificial Neural Network for Control and Grid Integration of Residential Solar Photovoltaic Systems. IEEE Trans. Sustain. Energy 2017, 8, 1484–1495. [Google Scholar] [CrossRef]
- Zhu, Y.; Fei, J. Adaptive Global Fast Terminal Sliding Mode Control of Grid-Connected Photovoltaic System Using Fuzzy Neural Network Approach. IEEE Access 2017, 5, 9476–9484. [Google Scholar] [CrossRef]
- Fei, J.; Chu, Y. Double Hidden Layer Output Feedback Neural Adaptive Global Sliding Mode Control of Active Power Filter. IEEE Trans. Power Electron. 2020, 35, 3069–3084. [Google Scholar] [CrossRef]
- Fu, X.; Li, S. Control of Single-Phase Grid-Connected Converters with LCL Filters Using Recurrent Neural Network and Conventional Control Methods. IEEE Trans. Power Electron. 2015, 31, 5354–5364. [Google Scholar] [CrossRef]
- Zaid, S.A.; Mohamed, I.S.; Bakeer, A.; Liu, L.; Albalawi, H.; Tawfiq, M.E.; Kassem, A.M. From MPC-Based to End-to-End (E2E) Learning-Based Control Policy for Grid-Tied 3L-NPC Transformerless Inverter. IEEE Access 2022, 10, 57309–57326. [Google Scholar] [CrossRef]
- Babaie, M.; Sebaaly, F.; Sharifzadeh, M.; Kanaan, H.Y.; Al-Haddad, K. Design of an Artificial Neural Network Control Based on Levenberg-Marquart Algorithm for Grid-Connected Packed U-Cell Inverter. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, VIC, Australia, 8 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1202–1207. [Google Scholar] [CrossRef]
- Babaie, M.; Sharifzadeh, M.; Al-Haddad, K. Three-Phase Grid-Connected NPC Inverter Based on a Robust Artificial Neural Network Controller. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Yarikkaya, S.; Vardar, K. Neural Network Based Predictive Current Controllers for Three Phase Inverter. IEEE Access 2023, 11, 27155–27167. [Google Scholar] [CrossRef]
- Khan, D.; Qais, M.; Hu, P. A Reinforcement Learning-Based Control System for Higher Resonance Frequency Conditions of Grid-Integrated LCL-Filtered BESS. J. Energy Storage 2024, 93, 112373. [Google Scholar] [CrossRef]
- Yuan, X.; Laird, I.; Walder, S. Opportunities, Challenges, and Potential Solutions in the Application of Fast-Switching SiC Power Devices and Converters. IEEE Trans. Power Electron. 2021, 36, 3925–3945. [Google Scholar] [CrossRef]
- Chen, J.; Deng, J.; Ming, L.; Xin, Z.; Yin, W.; Wang, P. A Variable Switching Frequency Control for ZVS Three-Phase Three-Level T-Type Inverter Using Hybrid Discontinuous PWM. IEEE Trans. Power Electron. 2023, 38, 13456–13466. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, Z.; Shen, L.; Yao, G.; Wang, G.; Yang, S. Control of the Neutral Point Voltage Balance in the Hybrid Three-Level Active Neutral-Point Clamped Inverter. IEEE Trans. Power Electron. 2025, 40, 6685–6699. [Google Scholar] [CrossRef]
- Xia, T.; Feng, X.; Li, C.; Han, R.; Wang, C.; Zhang, M.; Yang, H.; Li, W.; Zhao, R.; He, X. A Hybrid Three-Level Hybrid Switch (Hybrid2) Active Neutral-Point-Clamped Converter with Optimal Switching Strategy. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 3046–3058. [Google Scholar] [CrossRef]
- Hakami, S.S.; Halabi, L.M.; Lee, K.B. Dual-Carrier-Based PWM Method for DC-Link Capacitor Lifetime Extension in Three-Level Hybrid ANPC Inverters. IEEE Trans. Ind. Electron. 2023, 70, 3303–3314. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Zhang, L. Hybrid ANPC Grid-Tied Inverter Design with Passivity-Based Sliding Mode Control Strategy. Energies 2024, 17, 3655. [Google Scholar] [CrossRef]
- Mu, X.; Chen, H.; Wang, X.; Wu, W.; Wang, H.; Yuan, L.; Chung, H.S.-H.; Blaabjerg, F. A Review of Hybrid Three-Level ANPC Inverters: Topologies, Comparison, Challenges and Improvements in Applications. Energies 2025, 18, 2613. [Google Scholar] [CrossRef]
- Najjar, M.; Kouchaki, A.; Nielsen, J.; Dan Lazar, R.; Nymand, M. Design Procedure and Efficiency Analysis of a 99.3% Efficient 10 KW Three-Phase Three-Level Hybrid GaN/Si Active Neutral Point Clamped Converter. IEEE Trans. Power Electron. 2022, 37, 6698–6710. [Google Scholar] [CrossRef]
- Escobar, G.; Lopez-Sarabia, J.L.; Valdez-Fernandez, A.A.; Silva-Vera, E.D.; Valdez-Resendiz, J.E.; Mayo-Maldonado, J.C. Differential and Common-Mode Model-Based Controller for a Grid-Tied Three-Phase NPC Converter. IEEE Access 2025, 13, 68481–68491. [Google Scholar] [CrossRef]
- Wang, Q.-G.; Lee, T.-H.; Fung, H.-W.; Bi, Q.; Zhang, Y. PID Tuning for Improved Performance. IEEE Trans. Control. Syst. Technol. 1999, 7, 457–465. [Google Scholar] [CrossRef]
- Gutiérrez-Escalona, J.; Roncero-Clemente, C.; Husev, O.; Matiushkin, O.; Blaabjerg, F. Artificial Intelligence in the Hierarchical Control of AC, DC, and Hybrid AC/DC Microgrids: A Review. IEEE Access 2024, 12, 157227–157246. [Google Scholar] [CrossRef]
- Yuksel, A.; Sefa, I.; Altin, N. DC-Link Voltage Stabilization and Capacitor Size Reduction in Active Neutral-Point-Clamped Inverters Using an Advanced Control Method. Energies 2025, 18, 3143. [Google Scholar] [CrossRef]
- Foti, S.; Nevoloso, C.; Khan, H.H.; Di Tommaso, A.O.; Testa, A.; Miceli, R. A Simple Carrier-Based Neutral Point Voltage Control Strategy for NPC Three-Level Inverters. IEEE Open J. Power Electron. 2025, 6, 416–431. [Google Scholar] [CrossRef]
- Umbría, F.; Gordillo, F.; Gómez-Estern, F.; Salas, F.; Portillo, R.C.; Vázquez, S. Voltage Balancing in Three-Level Neutral-Point-Clamped Converters via Luenberger Observer. Control. Eng. Pr. 2014, 25, 36–44. [Google Scholar] [CrossRef]
- Chen, H.C.; Tsai, M.J.; Wang, Y.B.; Cheng, P.T. A Modulation Technique for Neutral Point Voltage Control of the Three-Level Neutral-Point-Clamped Converter. IEEE Trans. Ind. Appl. 2018, 54, 2517–2524. [Google Scholar] [CrossRef]
- Pou, J.; Pindado, R.; Boroyevich, D.; Rodríguez, P. Evaluation of the Low-Frequency Neutral-Point Voltage Oscillations in the Three-Level Inverter. IEEE Trans. Ind. Electron. 2005, 52, 1582–1588. [Google Scholar] [CrossRef]
- Hu, H.; Zhao, M.; Lu, M.; Chung, C. A Novel Combined Injection Method for Neutral Point Voltage Control of Three-Level NPC Inverter Under Carrier-Based VSVPWM. IEEE Trans. Ind. Electron. 2025, 1–11. [Google Scholar] [CrossRef]
- Ben Mahmoud, Z.; Khedher, A. A Comprehensive Review on Space Vector Based-PWM Techniques for Common Mode Voltage Mitigation in Photovoltaic Multi-Level Inverters. Energies 2024, 17, 916. [Google Scholar] [CrossRef]
- Leon, J.I.; Kouro, S.; Franquelo, L.G.; Rodriguez, J.; Wu, B. The Essential Role and the Continuous Evolution of Modulation Techniques for Voltage-Source Inverters in the Past, Present, and Future Power Electronics. IEEE Trans. Ind. Electron. 2016, 63, 2688–2701. [Google Scholar] [CrossRef]
- Mahato, B.; Majumdar, S.; Chandra Jana, K. Carrier-Based PWM Techniques for Multi-Level Inverters: A Comprehensive Performance Study. Gazi Univ. J. Sci. Part A Eng. Innov. 2018, 5, 101–111. Available online: https://dergipark.org.tr/en/pub/gujsa/issue/39415/434367 (accessed on 19 November 2025).
- Franquelo, L.G.; Rodriguez, J.; Leon, J.I.; Kouro, S.; Portillo, R.; Prats, M.A.M. The Age of Multilevel Converters Arrives. IEEE Ind. Electron. Mag. 2008, 2, 28–39. [Google Scholar] [CrossRef]
- Alemdar, O.S.; Oner, M.U.; Altun, O.; Keysan, O. Ripple Minimization in Asymmetric Interleaved DC-DC Converters Using Neural Networks. IEEE Trans. Power Electron. 2024, 39, 3411–3421. [Google Scholar] [CrossRef]
- Ibrahim, A.A.; Zilio, A.; Younis, T.; Biadene, D.; Caldognetto, T.; Mattavelli, P. Artificial Neural Networks Approach for Reduced RMS Currents in Triple Active Bridge Converters. In Proceedings of the IECON Proceedings (Industrial Electronics Conference), Brussels, Belgium, 17–20 October 2022; IEEE Industrial Electronics Society: Washington, DC, USA, 2022. [Google Scholar] [CrossRef]
- Bose, B.K. Neural Network Applications in Power Electronics and Motor Drives—An Introduction and Perspective. IEEE Trans. Ind. Electron. 2007, 54, 14–33. [Google Scholar] [CrossRef]
- Teoh, E.J.; Tan, K.C.; Xiang, C. Estimating the Number of Hidden Neurons in a Feedforward Network Using the Singular Value Decomposition. IEEE Trans. Neural Netw. 2006, 17, 1623–1629. [Google Scholar] [CrossRef]
- Ramadhan, M.M.L.; Jati, G.; Jatmiko, W. Building Damage Assessment Using Feature Concatenated Siamese Neural Network. IEEE Access 2024, 12, 19100–19116. [Google Scholar] [CrossRef]
- Du, K.L.; Leung, C.S.; Mow, W.H.; Swamy, M.N.S. Perceptron: Learning, Generalization, Model Selection, Fault Tolerance, and Role in the Deep Learning Era. Mathematics 2022, 10, 4730. [Google Scholar] [CrossRef]
- Huang, S.-C.; Huang, Y.-F. Bounds on Number of Hidden Neurons of Multilayer Perceptrons in Classification and Recognition. In Proceedings of the 1990 IEEE International Symposium on Circuits and Systems (ISCAS), New Orleans, LA, USA, 1–3 May 1990; IEEE: Piscataway, NJ, USA, 1990. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; De Jesús, B. Neural Network Design, 2nd ed.; eBook. 2014; Available online: https://hagan.okstate.edu/NNDesign.pdf (accessed on 19 November 2025).
- Rice, J.A. Mathematical Statistics and Data Analysis, 3rd ed.; Brooks/Cole, Cengage Learning: Belmont, CA, USA, 2007. [Google Scholar]
- Seber, G.A.F.; Lee, A.J. Linear Regression Analysis, 2nd ed.; Wiley Series: Hoboken, NJ, USA, 2003. [Google Scholar]
- Manor, E.; Ben-David, A.; Greenberg, S. CORDIC Hardware Acceleration Using DMA-Based ISA Extension. J. Low Power Electron. Appl. 2022, 12, 4. [Google Scholar] [CrossRef]
- Khan, D.; Qais, M.H.; Hasanien, H.; Alghuwainem, S.; Sami, I.; Hu, P. Enhanced Stability of Grid-Connected Inverter Using Adaptive Filtering Damping of Capacitive Current Feedback of LCL Filter. Ain Shams Eng. J. 2025, 16, 103465. [Google Scholar] [CrossRef]
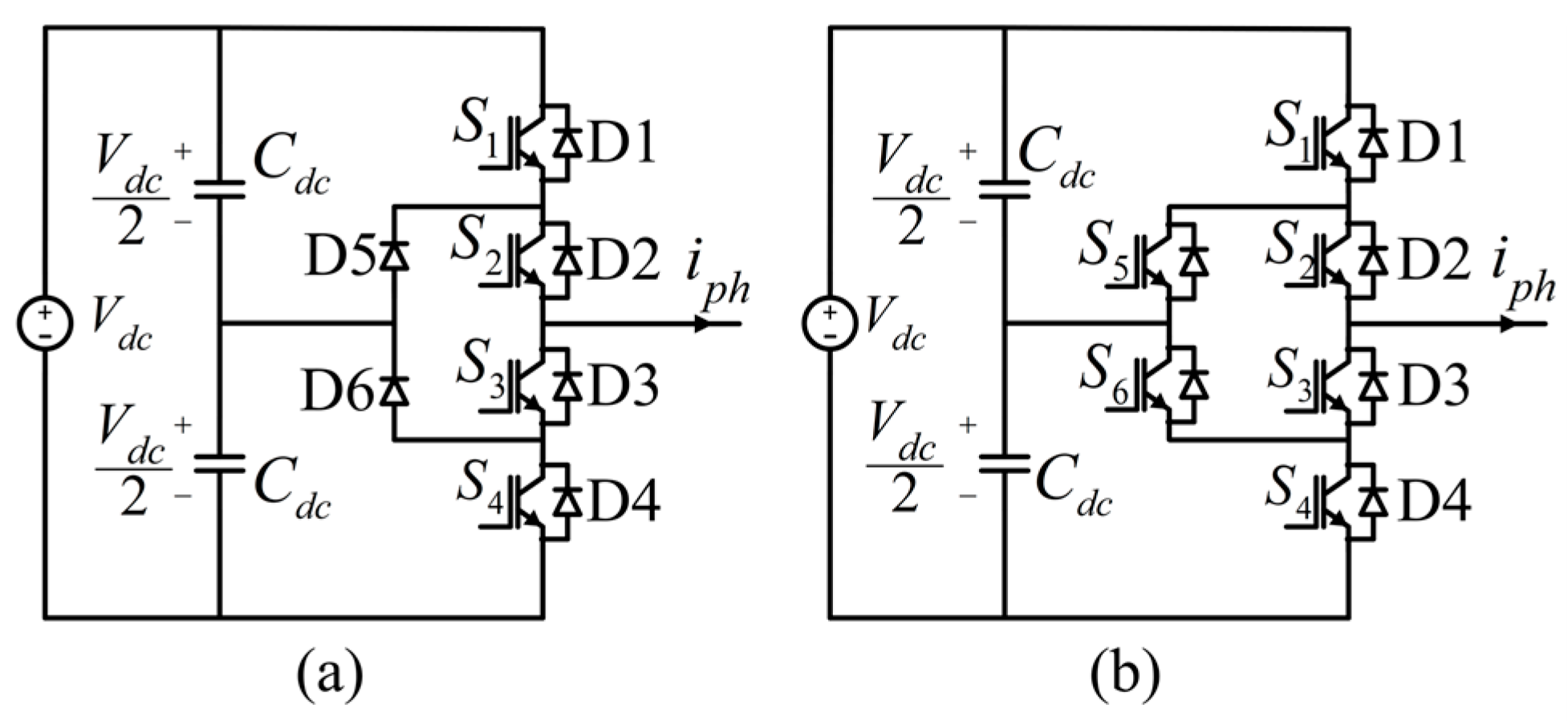
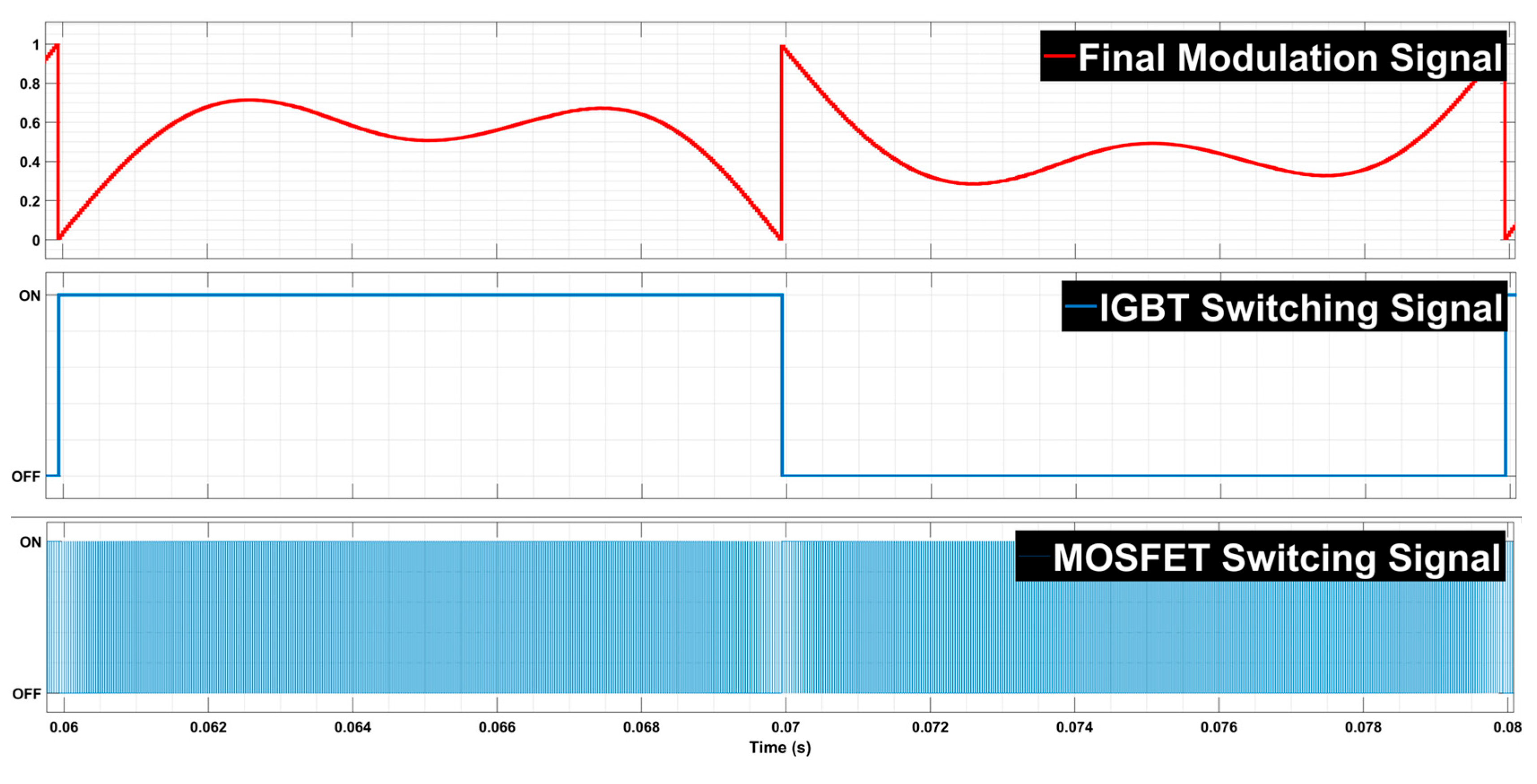
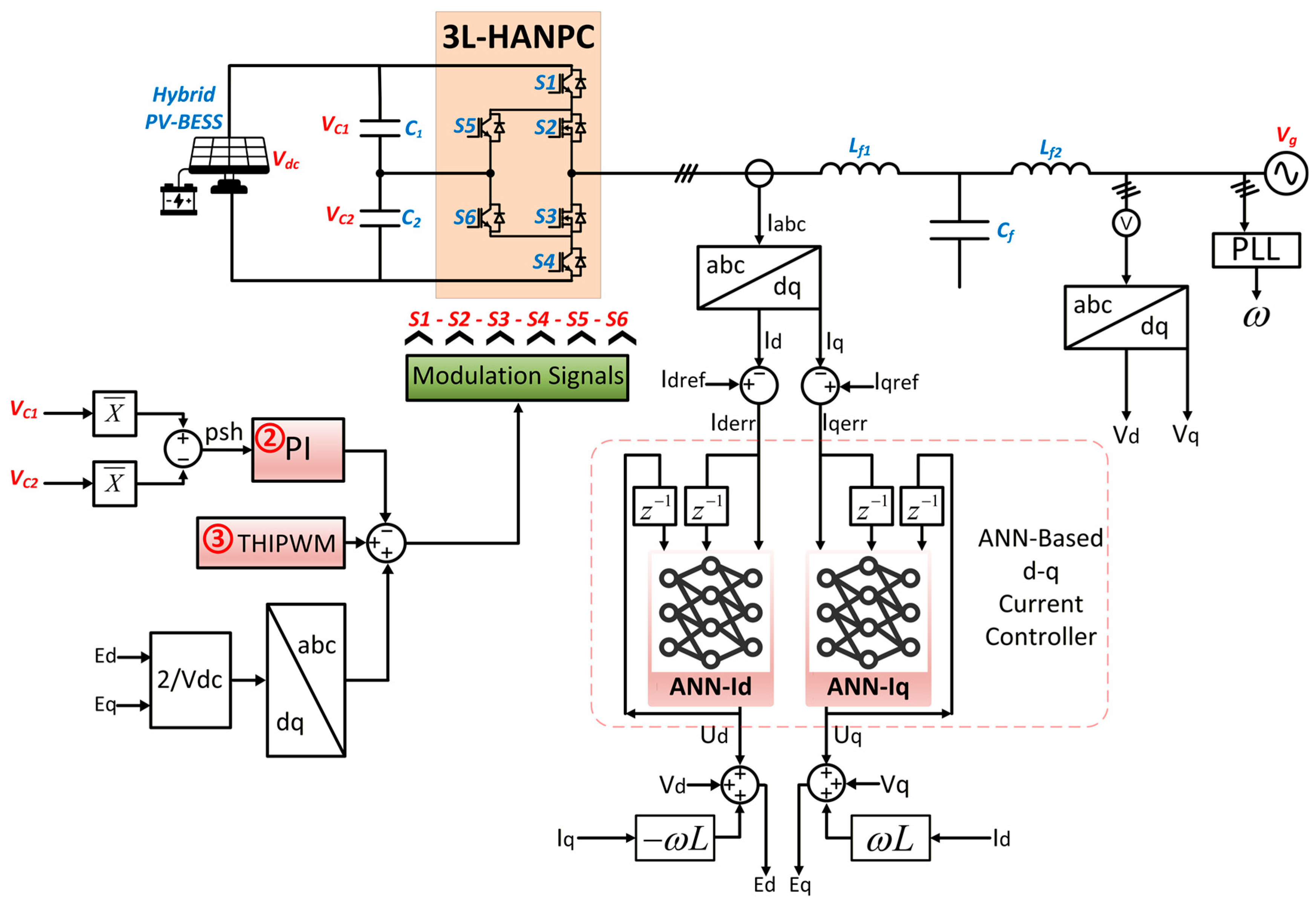
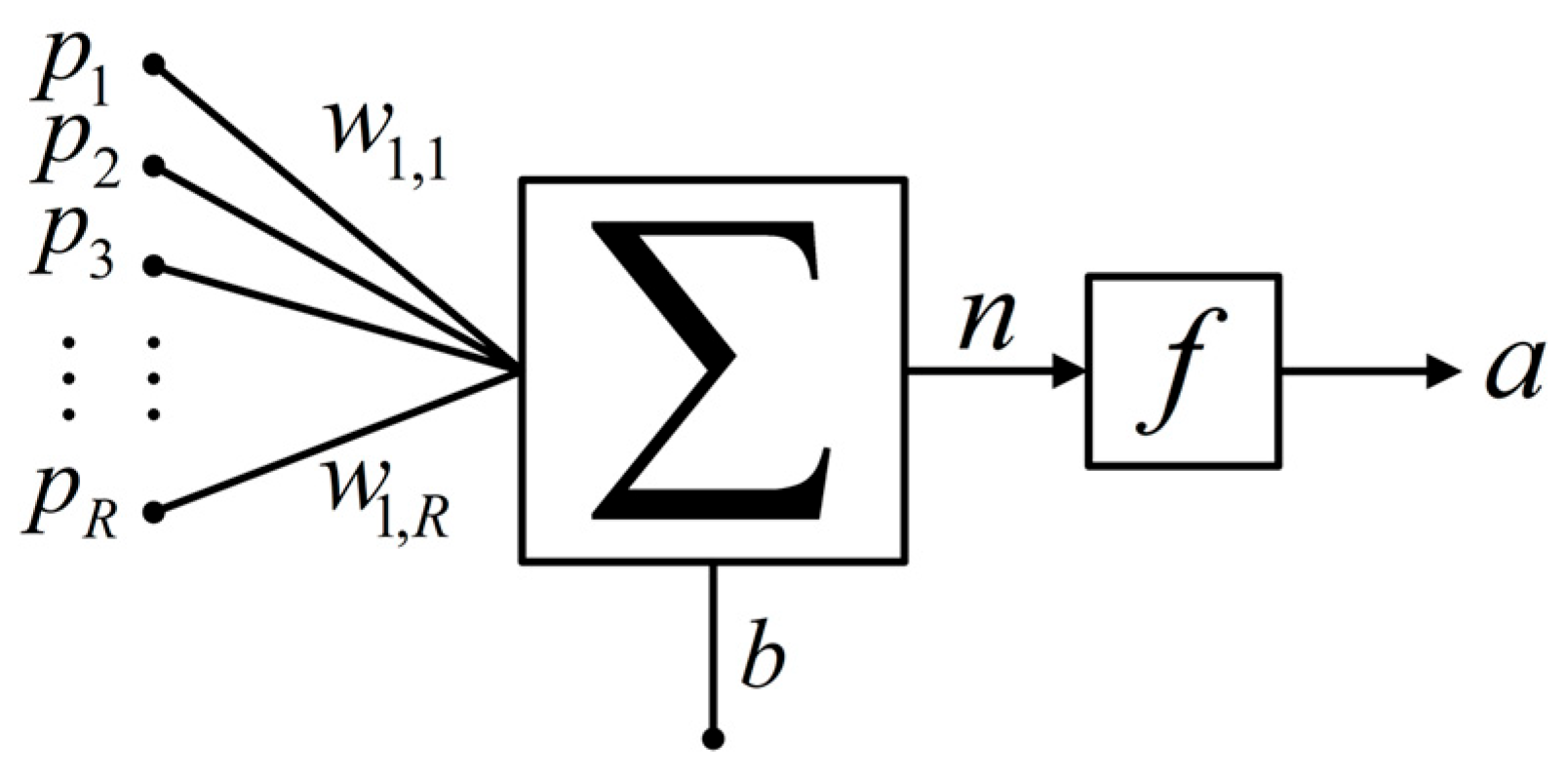
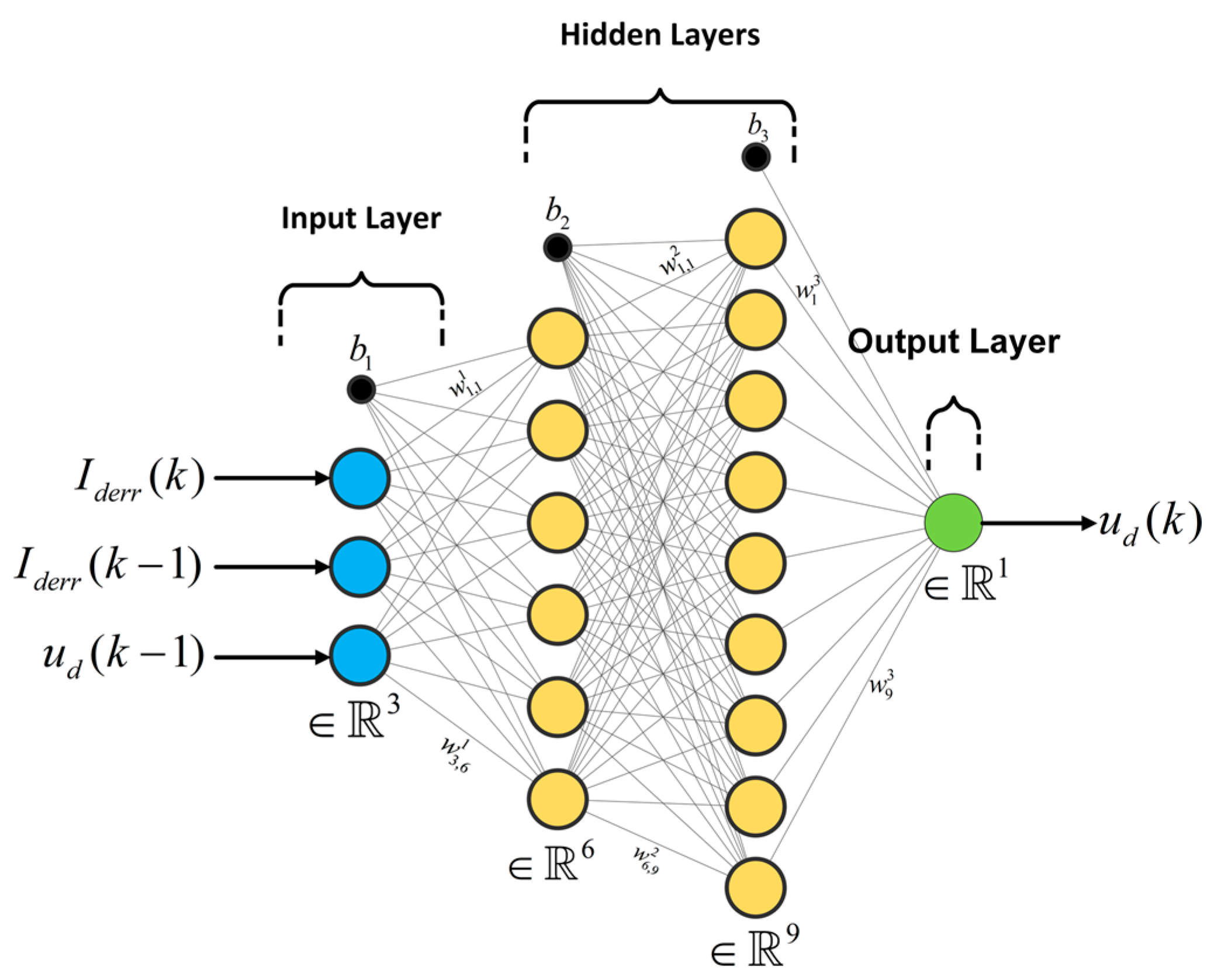
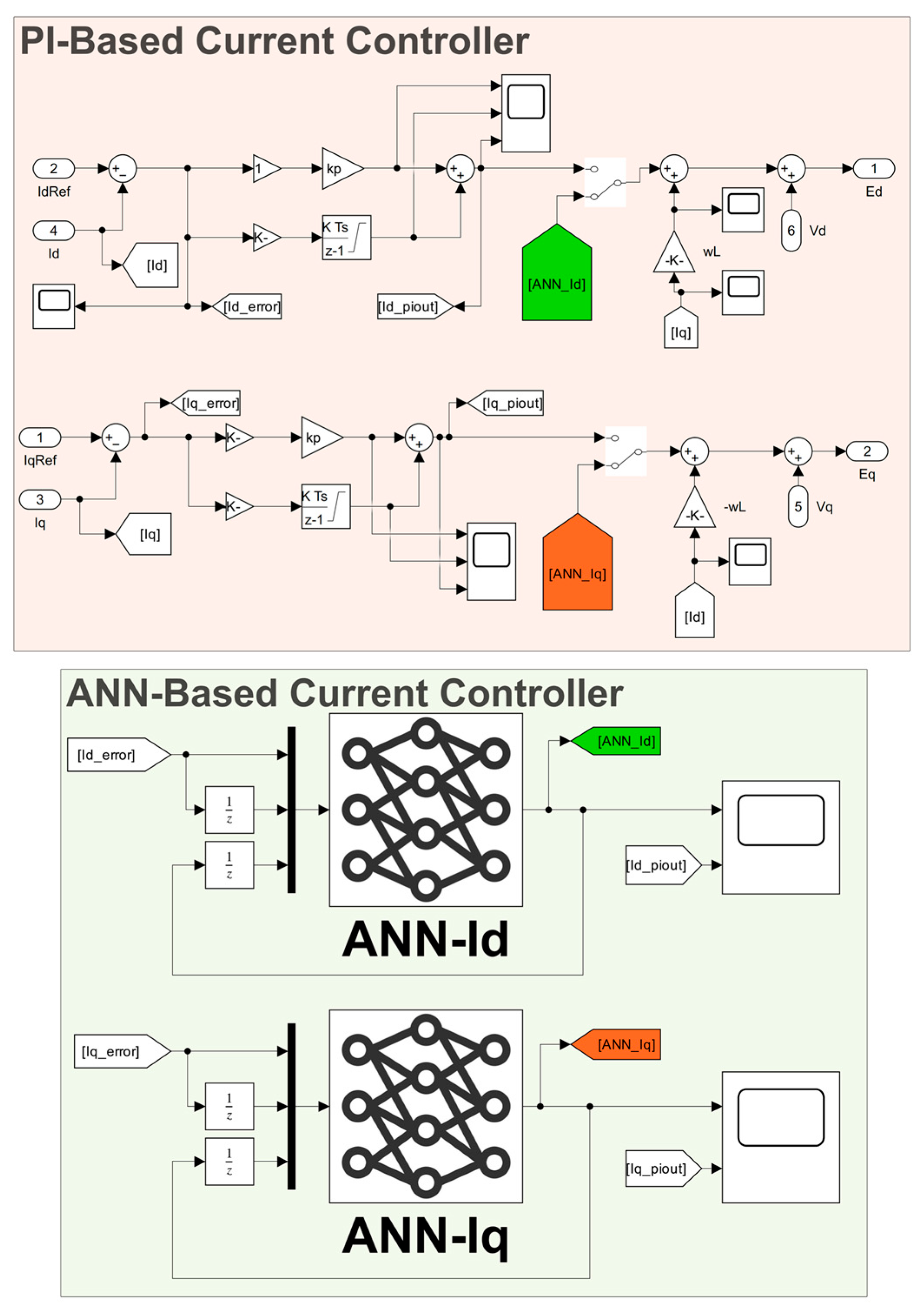
| States | S1 | S2 | S3 | S4 | S5 | S6 | VxO |
|---|---|---|---|---|---|---|---|
| P | 1 | 1 | 0 | 0 | 0 | 1 | +Vdc/2 |
| OU1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| OU2 | 0 | 1 | 0 | 1 | 1 | 0 | |
| OL1 | 0 | 0 | 1 | 0 | 0 | 1 | |
| OL2 | 1 | 0 | 1 | 0 | 0 | 1 | |
| N | 0 | 0 | 1 | 1 | 1 | 0 | −Vdc/2 |
| Candidate Number | Formation | Candidate Number | Formation |
|---|---|---|---|
| 1 | [3] | 11 | [3 × 12] |
| 2 | [6] | 12 | [6 × 3] |
| 3 | [9] | 13 | [6 × 9] |
| 4 | [12] | 14 | [6 × 12] |
| 5 | [3 × 3] | 15 | [9 × 3] |
| 6 | [6 × 6] | 16 | [9 × 6] |
| 7 | [9 × 9] | 17 | [9 × 12] |
| 8 | [12 × 12] | 18 | [12 × 3] |
| 9 | [3 × 6] | 19 | [12 × 6] |
| 10 | [3 × 9] | 20 | [12 × 6] |
| Parameter | Value |
|---|---|
| DC Link Voltage— | 900 V |
| Grid Voltage (rms, line-to-line) | 400 V |
| Rated Output Power | 62.5 kW |
| Grid Frequency | 50 Hz |
| Controller Sampling Time | 31.25 µs |
| Simulation Model Sampling Time | 1 µs |
| Solver Type | Fixed Step |
| DC-Link Capacitors ( and ) | 0.3 mF |
| Inverter Side Inductance () | 160 µH |
| Grid Side Inductance () | 40 µH |
| Switching Frequency () | 32 kHz |
| Id Controller Kp | 1 |
| Id Controller Ki | 1000 |
| Iq Controller Kp | 1.75 |
| Iq Controller Ki | 1000 |
| Name of OR | # of OP | Power Factor (pf) | IdRef Value (A) | IqRef Value (A) | Recording Time Range (s) |
|---|---|---|---|---|---|
| VarPF | 1 | 1 | 127 | 0 | 0–0.4 |
| 2 | 0.9 | 114 | 55 | 0.4–0.8 | |
| 3 | 0.8 | 102 | 76 | 0.8–1.2 | |
| 4 | 0.7 | 89 | 91 | 1.2–1.6 | |
| 5 | 0.6 | 76 | 102 | 1.6–2.0 | |
| VarP | 6 | 1 | 127 | 0 | 0–0.4 |
| 7 | 1 | 101.6 | 0 | 0.4–0.8 | |
| 8 | 1 | 76.2 | 0 | 0.8–1.2 | |
| 9 | 1 | 50.8 | 0 | 1.2–1.6 | |
| 10 | 1 | 25.4 | 0 | 1.6–2.0 | |
| VarQ | 11 | 0 | 0 | 127 | 0–0.4 |
| 12 | 0 | 0 | 101.6 | 0.4–0.8 | |
| 13 | 0 | 0 | 76.2 | 0.8–1.2 | |
| 14 | 0 | 0 | 50.8 | 1.2–1.6 | |
| 15 | 0 | 0 | 25.4 | 1.6–2.0 |
| Parameter | Value |
|---|---|
| Maximum Iterations (Epoch) | 5000 |
| MSE Goal (Test Error) | 1 × 10−4 |
| Minimum Gradient | 1 × 10−3 |
| 1 × 10−3 | |
| 10 | |
| Time Constraint | No |
| Maximum Validation Failures | 6 |
| Number of Parallel Workers (local machine) | 8 |
| Name of OR | # of OP | Grid Current THD (%) | Explanations |
|---|---|---|---|
| VarPF | 1 | 4.25 | pf = 1 |
| 2 | 5.25 | pf = 0.9 | |
| 3 | 5.52 | pf = 0.8 | |
| 4 | 5.56 | pf = 0.7 | |
| 5 | 5.42 | pf = 0.6 | |
| VarP | 6 | 4.25 | 100% rated power |
| 7 | 5.63 | 80% rated power | |
| 8 | 7.17 | 60% rated power | |
| 9 | 11.70 | 40% rated power | |
| 10 | 22.07 | 20% rated power | |
| VarQ | 11 | 5.60 | 100% rated power |
| 12 | 7.34 | 80% rated power | |
| 13 | 10.26 | 60% rated power | |
| 14 | 14.70 | 40% rated power | |
| 15 | 23.68 | 20% rated power |
| Network Number | Network Type | MSE (Test Dataset) | Full Active Power Grid Current THD (%) | Full Reactive Power Grid Current THD (%) | Training Time (s) | Modified Loss () |
|---|---|---|---|---|---|---|
| 1 | [3] | 2.07 × 10−4 | 3.78 | 5.68 | 5.25 | 1.28 |
| 2 | [6] | 1.52 × 10−4 | 3.92 | 5.49 | 2.74 | 1.01 |
| 3 | [9] | 6.98 × 10−5 | 3.81 | 5.53 | 2.78 | 6.41 × 10−1 |
| 4 | [12] | 4.85 × 10−4 | 4 | 5.6 | 2.83 | 2.48 |
| 5 | [3 × 3] | 1.28 × 10−4 | 4.02 | 5.49 | 8.37 | 9.82 × 10−1 |
| 6 | [6 × 6] | 1.65 × 10−4 | 4.12 | 5.6 | 4.5 | 1.10 |
| 7 | [9 × 9] | 5.62 × 10−5 | 4.13 | 5.94 | 12.04 | 7.34 × 10−1 |
| 8 | [12 × 12] | 6.11 × 10−5 | 4.15 | 5.71 | 3.95 | 6.37 × 10−1 |
| 9 | [3 × 6] | 7.29 × 10−5 | 3.97 | 5.52 | 8.43 | 7.39 × 10−1 |
| 10 | [3 × 9] | 1.17 × 10−4 | 3.86 | 5.62 | 5.17 | 8.87 × 10−1 |
| 11 | [3 × 12] | 9.40 × 10−5 | 3.97 | 5.3 | 5.9 | 7.91 × 10−1 |
| 12 | [6 × 3] | 7.07 × 10−5 | 4.15 | 5.38 | 12.31 | 7.87 × 10−1 |
| 13 | [6 × 9] | 4.92 × 10−5 | 4 | 5.32 | 3.02 | 5.55 × 10−1 |
| 14 | [6 × 12] | 6.62 × 10−5 | 3.89 | 5.58 | 3.13 | 6.34 × 10−1 |
| 15 | [9 × 3] | 2.43 × 10−4 | 3.77 | 5.65 | 15.245 | 1.58 |
| 16 | [9 × 6] | 1.56 × 10−4 | 3.85 | 5.74 | 7.02 | 1.09 |
| 17 | [9 × 12] | 1.56 × 10−4 | 4 | 5.2 | 3.57 | 1.03 |
| 18 | [12 × 3] | 1.50 × 10−4 | 3.96 | 5.38 | 16.02 | 1.18 |
| 19 | [12 × 6] | 1.23 × 10−4 | 3.75 | 5.53 | 17.57 | 1.08 |
| 20 | [12 × 9] | 1.00 × 10−4 | 3.92 | 5.48 | 3.4 | 7.86 × 10−1 |
| Network Number | Network Type | MSE (Test Dataset) | Full Active Power Grid Current THD (%) | Full Reactive Power Grid Current THD (%) | Training Time (s) | Modified Loss () |
|---|---|---|---|---|---|---|
| 1 | [3] | 2.29 × 10−4 | 3.78 | 5.68 | 2.79 | 1.23 |
| 2 | [6] | 7.44 × 10−5 | 3.92 | 5.49 | 6.05 | 6.99 × 10−1 |
| 3 | [9] | 3.59 × 10−5 | 3.81 | 5.53 | 16.04 | 7.38 × 10−1 |
| 4 | [12] | 2.78 × 10−4 | 4 | 5.6 | 2.91 | 1.43 |
| 5 | [3 × 3] | 1.45 × 10−5 | 4.02 | 5.49 | 12.21 | 5.89 × 10−1 |
| 6 | [6 × 6] | 1.35 × 10−4 | 4.12 | 5.6 | 3.75 | 8.99 × 10−1 |
| 7 | [9 × 9] | 1.22 × 10−5 | 4.13 | 5.94 | 2.76 | 4.17 × 10−1 |
| 8 | [12 × 12] | 6.05 × 10−5 | 4.15 | 5.71 | 3.42 | 6.10 × 10−1 |
| 9 | [3 × 6] | 6.88 × 10−5 | 3.97 | 5.52 | 3.01 | 6.23 × 10−1 |
| 10 | [3 × 9] | 2.36 × 10−5 | 3.86 | 5.62 | 3.69 | 4.60 × 10-1 |
| 11 | [3 × 12] | 1.29 × 10−4 | 3.97 | 5.3 | 4.17 | 8.71 × 10−1 |
| 12 | [6 × 3] | 6.80 × 10−4 | 4.15 | 5.38 | 9.48 | 3.10 |
| 13 | [6 × 9] | 3.44 × 10−5 | 4 | 5.32 | 3.1 | 4.87 × 10−1 |
| 14 | [6 × 12] | 1.93 × 10−5 | 3.89 | 5.58 | 2.9 | 4.28 × 10−1 |
| 15 | [9 × 3] | 1.10 × 10−4 | 3.77 | 5.65 | 4.09 | 7.98 × 10−1 |
| 16 | [9 × 6] | 5.90 × 10−4 | 3.85 | 5.74 | 8.08 | 2.73 |
| 17 | [9 × 12] | 1.76 × 10−4 | 4 | 5.2 | 6.66 | 1.10 |
| 18 | [12 × 3] | 2.16 × 10−4 | 3.96 | 5.38 | 4.27 | 1.21 |
| 19 | [12 × 6] | 9.12 × 10−5 | 3.75 | 5.53 | 2.9 | 6.99 × 10−1 |
| 20 | [12 × 9] | 1.37 × 10−4 | 3.92 | 5.48 | 2.95 | 8.81 × 10−1 |
| Name of OR | # of OP | PI Control THD (%) | ANN Control THD (%) | Explanations |
|---|---|---|---|---|
| VarPF | 1 | 4.25 | 4.04 | pf = 1 |
| 2 | 5.25 | 5.17 | pf = 0.9 | |
| 3 | 5.52 | 5.44 | pf = 0.8 | |
| 4 | 5.56 | 5.42 | pf = 0.7 | |
| 5 | 5.42 | 5.52 | pf = 0.6 | |
| VarP | 6 | 4.25 | 4.04 | 100% rated power |
| 7 | 5.63 | 5.47 | 80% rated power | |
| 8 | 7.17 | 7.38 | 60% rated power | |
| 9 | 11.70 | 12.25 | 40% rated power | |
| 10 | 22.07 | 20.69 | 20% rated power | |
| VarQ | 11 | 5.60 | 5.47 | 100% rated power |
| 12 | 7.34 | 7.04 | 80% rated power | |
| 13 | 10.26 | 10.26 | 60% rated power | |
| 14 | 14.70 | 15.18 | 40% rated power | |
| 15 | 23.68 | 25.78 | 20% rated power |
| Name of OR | PI Control THD (%) | ANN Control THD (%) | Explanations |
|---|---|---|---|
| VarPF | 4.86 | 4.81 | pf = 0.93 |
| 5.35 | 4.95 | pf = 0.88 | |
| 5.19 | 5.51 | pf = 0.85 | |
| 5.74 | 5.60 | pf = 0.75 | |
| 5.54 | 5.37 | pf = 0.65 | |
| VarP | 4.92 | 4.48 | 90% rated power |
| 6.17 | 6.28 | 75% rated power | |
| 6.41 | 6.16 | 73% rated power | |
| 9.09 | 8.73 | 50% rated power | |
| 15.91 | 15.08 | 30% rated power | |
| VarQ | 6.06 | 5.99 | 90% rated power |
| 8.85 | 8.89 | 70% rated power | |
| 9.23 | 8.99 | 65% rated power | |
| 11.24 | 10.60 | 55% rated power | |
| 20.76 | 19.46 | 25% rated power |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Başkaya, A.; Tamyurek, B. Self-Tuning Current Control via ANN for Enhanced Harmonic Mitigation in Hybrid PV–Battery Storage Systems Utilizing the 3L-HANPC Inverter. Electronics 2025, 14, 4617. https://doi.org/10.3390/electronics14234617
Başkaya A, Tamyurek B. Self-Tuning Current Control via ANN for Enhanced Harmonic Mitigation in Hybrid PV–Battery Storage Systems Utilizing the 3L-HANPC Inverter. Electronics. 2025; 14(23):4617. https://doi.org/10.3390/electronics14234617
Chicago/Turabian StyleBaşkaya, Aydın, and Bunyamin Tamyurek. 2025. "Self-Tuning Current Control via ANN for Enhanced Harmonic Mitigation in Hybrid PV–Battery Storage Systems Utilizing the 3L-HANPC Inverter" Electronics 14, no. 23: 4617. https://doi.org/10.3390/electronics14234617
APA StyleBaşkaya, A., & Tamyurek, B. (2025). Self-Tuning Current Control via ANN for Enhanced Harmonic Mitigation in Hybrid PV–Battery Storage Systems Utilizing the 3L-HANPC Inverter. Electronics, 14(23), 4617. https://doi.org/10.3390/electronics14234617






