Abstract
A three-node cooperative communication system with one-way transmission and a decode-and-forward relaying scheme is considered. The outage probability of the system is analyzed under the assumption that both the source and relay are energy harvesting nodes, and signal space diversity is employed to enhance transmission reliability. Exact closed-form and asymptotic expressions for the outage probability are derived. An optimization problem is also formulated to minimize the outage probability with respect to the transmission powers of the source and relay. Our analysis shows that the outage probability is a convex function of the transmit powers, with a unique global minimum. Monte Carlo simulations are conducted to validate the exact closed-from expression of the outage probability and the optimal transmit powers. In contrast to traditional battery-powered systems, the results show that increasing the transmit power in energy harvesting cooperative communication systems may result in a higher outage probability. The results also show that, at high SNRs, the optimal transmit power of a node is the power that balances its energy harvesting and depletion rates, leading to the best energy utilization.
1. Introduction
Combining cooperative communication with energy harvesting technology in communication systems presents a promising solution to enhance both performance and sustainability [1]. Cooperative communication improves network reliability, coverage, and spectral efficiency by enabling nodes to assist each other through relaying, especially in fading-prone environments [2]. When integrated with energy harvesting—where nodes harvest energy from ambient sources such as solar, RF, or thermal energy—this cooperation becomes sustainable even in energy-constrained scenarios like wireless sensor networks or remote area deployments [3]. The synergy between these technologies supports the development of self-sustaining networks that are not only energy-efficient but also robust against link failures and intermittent connectivity [4]. This integration is particularly valuable for next-generation wireless systems, including the Internet of Things (IoT) and 6G networks, where energy autonomy and high reliability are critical [5].
Cooperative communication systems can be broadly categorized into those using a single relay and those employing multiple relays, each with distinct characteristics and trade-offs. In single-relay systems, a single intermediate node assists the source in forwarding information to the destination. These systems are attractive due to their lower complexity, simpler channel estimation, and reduced energy and signaling overhead, making them suitable for resource-constrained environments like the IoT or wireless sensor networks [6]. In contrast, systems with multiple relays offer higher spatial diversity and improved reliability, as they can select the best relay (relay selection) or use multiple relays simultaneously to combat fading and enhance throughput [7]. However, multi-relay systems typically involve greater coordination, increased processing complexity, and higher power consumption due to the need for synchronization and relay selection protocols [8]. The choice between single and multiple relays depends on the specific performance requirements, energy constraints, and deployment scenario of the network.
This paper considers a single-relay cooperative communication system—commonly referred to as a three-node cooperative system—comprising a source, a relay, and a destination. Such systems have been extensively studied in the literature under both conventional battery-powered configurations [9,10,11,12] and architectures incorporating energy harvesting technologies [13,14,15,16,17,18,19,20,21,22,23,24,25]. Closely related to our work, the study in [13] integrates rate-splitting multiple access with simultaneous wireless information and power transfer, where the source transmits both common and private message components, and the relay—equipped with a power-splitting receiver—harvests energy from the received signal to assist in forwarding data to the destination. The system in [14] incorporates beamforming and time-switching strategies between energy collection and cooperation, highlighting the performance benefits of multi-antenna configurations. The work in [15] introduces a cooperative rate-splitting strategy tailored for the three-node setup, jointly optimizing precoding and resource allocation to enhance system performance and demonstrating superiority over traditional cooperative NOMA schemes. Similarly, [16] investigates a Gaussian relay channel in which both the source and relay harvest energy, proposing power allocation algorithms aimed at maximizing throughput under energy constraints for both delay-sensitive and delay-tolerant traffic while also introducing the concept of energy diversity. In [17], a two-way system is considered where both nodes act as sources and destinations, employing a decode-and-forward (DF) relay equipped with a nonlinear energy harvesting unit. This system utilizes power splitting for energy harvesting, successive interference cancellation for decoding, and digital network coding for re-encoding, with performance evaluated in terms of outage probability and throughput over Rayleigh fading channels. Similarly, the system in [18] adopts a two-way cooperative system with a hybrid signal space diversity–amplify–forward relaying scheme, assuming that only the relay performs energy harvesting; the authors analyze the resulting outage probability and throughput performance. Outage analysis remains a central theme in [19,20,21], which investigate cooperative systems employing free-space optical links and signal space diversity (SSD). Furthermore, the work in [22] studies channel capacity under adaptive modulation in systems where all nodes are capable of energy harvesting, while [23] focuses on bit error rate performance. The study in [24] evaluates the packet delivery ratio in scenarios where both the source and relay harvest energy, assuming the presence of a direct source-to-destination link. Lastly, the authors in [26] investigate energy harvesting cognitive radio networks (CRNs) by introducing two cooperation modes, namely, energy cooperation and joint cooperation, between primary users (PUs) and secondary users (SUs). They formulate and solve throughput maximization problems under various network scenarios, demonstrating how optimal time allocation and cooperation strategies can significantly enhance the total achievable throughput.
Similar to the studies in [18,19,20,21], this paper analyzes the system performance in terms of the outage probability by deriving both exact closed-form and asymptotic expressions. Our analysis focuses on a DF relaying scheme, assuming the presence of a direct source-to-destination link, as considered in [24]; energy harvesting capabilities at both the source and the relay, consistent with the models in [22,24]; and the use of SSD, as in [19,20]. The SSD technique is adopted in this work to further improve the outage performance of the system by introducing diversity at the modulation level rather than relying solely on multiple antennas or time/frequency diversity [27]. Specifically, the SSD technique involves rotating the signal constellation and interleaving components of the transmitted symbols across different channel uses or paths. This approach ensures that no single fading event can completely erase the transmitted information, as different parts of the symbol are affected by independent fading instances, thereby leading to a reduced outage probability.
Building on this model, we formulate an optimization problem aimed at minimizing the outage probability with respect to the transmit powers of the source and relay. In energy harvesting cooperative communication systems, increasing the transmit power improves the reliability of the communication links by reducing their individual outage probabilities. However, it simultaneously increases the risk that a node may not have sufficient harvested energy to support transmission within a given time block. While the former effect enhances system performance, the latter may degrade it. Therefore, the overall outage probability must be carefully optimized by jointly considering the transmit powers of both the source and the relay. Our analysis reveals that the outage probability of the system is convex with respect to the transmit powers, attaining a unique global minimum. Monte Carlo simulations are conducted to validate the analytical expressions for the outage probability and optimal transmit powers. Unlike conventional battery-powered systems, the results show that increasing the transmit power in energy harvesting cooperative communication systems can actually lead to a higher outage probability. In addition, at high SNR levels, the optimal transmit power for a node is the one that balances energy harvesting with energy consumption, ensuring the most efficient use of available energy.
To the best of our knowledge, the outage performance of a three-node cooperative communication system employing a DF relaying scheme, where both the source and relay are energy harvesting and SSD is applied, has not yet been studied. Applying SSD in a DF relay scenario with energy harvesting nodes complicates the derivation of outage probability because both the source and relay are energy harvesting, and it introduces complexity in power allocation and performance analysis due to energy availability being time-varying and stochastic, which is the main novelty of this work. In addition, this paper presents novel closed-form and asymptotic expressions for outage probability, providing deep analytical insights into system performance under practical constraints. The main contributions of this work are as follows:
- Deriving the exact closed-form and asymptotic expressions for the outage probability of a three-node cooperative communication system employing a DF relaying scheme with SSD, where both the source and relay are energy harvesting.
- Formulating an optimization problem to minimize the outage probability subject to the transmit power of the source and the transmit power of the relay.
- Deriving expressions for the optimal transmit powers based on the asymptotic outage probability expression.
- Verifying the derived outage probability expressions and the optimal transmit powers using Monte Carlo simulations.
The rest of this paper is organized as follows: Section 2 presents the system model. Section 3 and Section 4 derive the exact closed-form and asymptotic expressions for the outage probability, respectively. Section 5 formulates the optimization problem and determines the optimal solution. Section 6 discusses the results, and Section 7 concludes the paper.
2. System Model
As illustrated in Figure 1, we consider a three-node cooperative communication system comprising a source (S), a relay (R), and a destination (D). Following the models in [22,24], the source communicates with the destination either directly or via the relay node. Both the source and the relay are equipped with omnidirectional antennas and operate as energy harvesting nodes, each supported by a rechargeable battery with an infinite storage capacity, as assumed in [20,24,28].
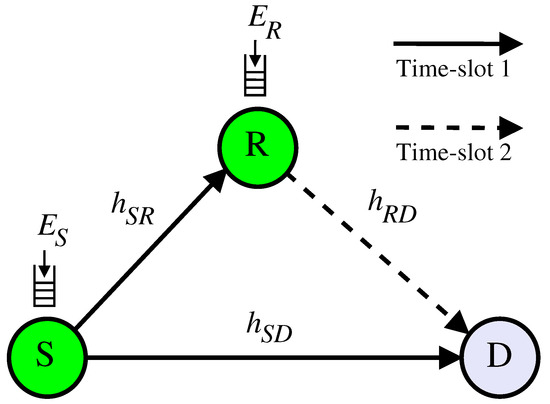
Figure 1.
System model, consisting of an energy harvesting source, energy harvesting relay, and destination.
We assume that the system operates in a one-way, half-duplex mode using a time-division multiple access (TDMA) protocol, where time is divided into blocks, and each block consists of two equal time slots. In the first time slot, the source broadcasts its transmission to both the relay and the destination. In the second time slot, the relay—if it successfully decodes the source’s message from the first time slot—forwards the decoded message to the destination. If the relay fails to decode the source transmission, it remains silent in the second time slot, which results in no transmission occurring during that slot. At the destination, in each time block, it receives symbols either from the source alone or from both the source and relay. These received symbols are then used to estimate the transmitted symbol. Section 2 A provides further details on how the destination utilizes the source’s transmission alone or jointly with the relay’s transmission to decode the original message from the source.
Unlike in [24], the source is assumed to have data to transmit to the destination in every time block, while the relay does not have its own data to transmit, as its sole role is to forward the source’s transmission to the destination during the second time slot of each block. Furthermore, we assume that the wireless channels between nodes experience independent, non-identically distributed (i.n.i.d.) slow Rayleigh fading and that channel state information (CSI) is available only at the receiving nodes, namely, the relay and the destination.
2.1. Signal Model
As mentioned in Section 1, both the source and relay employ the SSD technique, where, in time slot 1, the source selects two original symbols, rotates them, and then interleaves them to generate two SSD-based symbols. The source then transmits one of these rotated and interleaved symbols to both the relay and the destination. In time slot 2, the relay forwards the symbol that it received in time slot 1 to the destination, but only if it successfully decodes it. If the relay fails to decode the symbol, it remains silent. Upon receiving the symbol from either the source or both the source and the relay, the destination de-interleaves the received symbols and applies maximum likelihood detection to estimate the transmitted symbol.
To derive the outage probability for the individual links and for the overall cooperative channel under the SSD scheme, let represent the channel between the source and destination, represent the channel between the source and relay, and represent the channel between the relay and destination. It is assumed that these channels are modeled as zero-mean additive white Gaussian noise (AWGN) with variance . The coefficients for these channels are denoted by , , and , respectively, while the variances are denoted by , , and , respectively. The geometric gain for each channel is modeled as a function of distance and path loss exponent . Specifically, the geometric gain for the channel is given by , the geometric gain for the channel is given by , and the geometric gain for the channel is given by , where is the distance, is the distance, and is the distance. In addition, and represent the transmission powers of the source and the relay, respectively.
Using the geometric gains, the instantaneous SNR at D from S is , the instantaneous SNR at R from S is , and the instantaneous SNR at D from R is . Consequently, the average SNR at the destination from the source is , the average SNR at the relay from the source is , and the average SNR at the destination from the relay is . Given that the channels experience independent, non-identically distributed (i.n.i.d.) slow Rayleigh fading, the outage probability of channel , where , in a given time block can be expressed as
where , and is the minimum required transmission rate.
As for the outage probability of the cooperation link, let be the average mutual information for the cooperation link at D, which can be given by
Given that the SSD technique is employed—where the destination combines the signals received over both the and links to decode the transmitted signal—and given that the and links experience independent fading, the outage probability of the cooperative link at the destination in a given time block can be calculated as
where , and is the joint PDF of and . Thus,
which can be simplified to
Using Taylor series to approximate the exponential, (5) can be written as
Rearranging (6) yields
Solving the integral, we obtain
2.2. Energy Harvesting Model
We model the energy harvesting process of node i, , as a discrete random variable [20,24,28]. In the nth time block, node i harvests an amount of energy k with probability ; that is, with probability , where is the amount of energy harvested per time block, and is the maximum amount of energy that can be harvested. Similar to [20,24,28], the energy collected in a time block is stored in the battery for future use. Thus, in time block n, the source harvests amount of energy and transmits data in the first time slot only if it has sufficient energy, i.e., if its energy battery level . Therefore, the battery energy level of the source of the next time block can be expressed as
where is the indicator function. As for the relay, in time block n, it harvests amount of energy and transmits data in the second time slot only if the source transmits, it has sufficient energy, and it decodes successfully from the source in the first time slot. Specifically, these conditions are as follows: the source’s battery level satisfies , the relay’s battery level satisfies , and the instantaneous SNR at the relay from the source is at least , i.e., . As a result, the relay’s battery level at the beginning of the next time block will be
where is the indicator function.
From (9), it can be seen that the battery energy level of the source depends solely on its current battery state and the amount of energy harvested in the current block . Similarly, the relay’s battery level in (10) is determined only by its current battery state , the current battery level of the source , the amount of energy harvested in the current block , and the instantaneous outage status of the channel, i.e., . Given this structure, both and can be modeled as a Markov Chain. Consequently, following the approach in [28] and similar to [19,20], the probability that a node (either the source or the relay) has sufficient energy is the ratio of its energy harvesting rate to its energy depletion rate. Therefore, the probability that the source has sufficient energy in a given time block can be expressed as
where is the energy harvesting rate of the source, and is its energy depletion rate. However, the probability that the relay has sufficient energy in a given time block can be expressed as
where is the energy harvesting rate of the relay, and is its energy depletion rate. The probability , which represents the probability that the channel is not in outage. Using (11), (12) can be rewritten as
3. Outage Probability
In battery-powered communication systems, the outage probability quantifies the likelihood that communication links fail to maintain reliable transmission due to unfavorable channel conditions such as fading, interference, or noise. In contrast, in energy harvesting communication systems, the outage probability accounts for both the likelihood of unreliable transmission due to poor channel conditions and the possibility that a node may run out of energy. Therefore, in energy harvesting systems, the outage probability reflects a combined effect of channel impairments and energy availability, offering a more comprehensive measure of system reliability.
Accordingly, this section derives the exact closed-form expression for the outage probability of the proposed system, accounting for both channel fading and the stochastic nature of energy availability. The system is considered to be in outage if any of the following mutually exclusive events occur: (1) the source has sufficient energy, the link is in outage, and the link is in outage; (2) the source has sufficient energy, the link is not in outage, the relay has sufficient energy, and the cooperative link at D is in outage; (3) the source has sufficient energy, the link is not in outage, the link is in outage, and the relay does not have sufficient energy; or (4) the source does not have sufficient energy. Based on these events, the total outage probability of the system can be mathematically expressed as
where the probability is given by
If (15) is substituted into (14) and the bracket in the first term of (14) is expanded, the expression yields four terms, each corresponding to the probability of one of the four aforementioned mutually exclusive events. Using (11), (13), and (15), the outage probability in (14) can be rewritten as shown in (16), i.e., the exact-closed form expression. As mentioned earlier, and as evident from (16), the outage probability of the system is determined by both the reliability of all communication channels—individual and cooperative channels—and the energy availability at the source and relay nodes—an essential characteristic of any energy harvesting communication system.
4. Asymptotic Outage Probability
The exact outage probability derived from (16) is mathematically complex, making it difficult to extract analytical insights and to obtain optimal solutions. To overcome this complexity, the expression can be approximated by analyzing the asymptotic outage probability, which captures the system’s dominant behavior at high SNRs and enables a more tractable performance evaluation. Accordingly, this section focuses on deriving the asymptotic expression for the outage probability. This simplified form will later be employed to optimize the transmit power at both the source and the relay.
The asymptotic expression is derived under the assumption of a high SNR. Under this assumption, the probability that the channel is not in outage, denoted by , is approximated as 1; the outage probability of channel , where , is approximated as
and the outage probability of the cooperation link at D is approximated as
5. Transmission Power Optimization
As discussed in Section 1, in energy harvesting cooperative communication systems, increasing the transmit power reduces the outage probability of individual channel links. However, it also raises the risk that a node may not have sufficient energy to transmit during a given block. While the former effect improves system reliability, the latter can degrade performance by increasing the overall outage probability. This interplay between the transmit power and the link outage probability results in a convex outage probability function, which has a unique global minimum. To study this effect, we plotted the outage probability versus the relay transmit power for various values of the source transmit power . Figure 2 illustrates the outage probability as a function of for three different values of : 1, 3, and 5. As evident from the figure, the outage probability demonstrates a convex behavior with a distinct global minimum for each . This observation highlights the importance of jointly optimizing the transmit powers and to minimize the system’s outage probability.
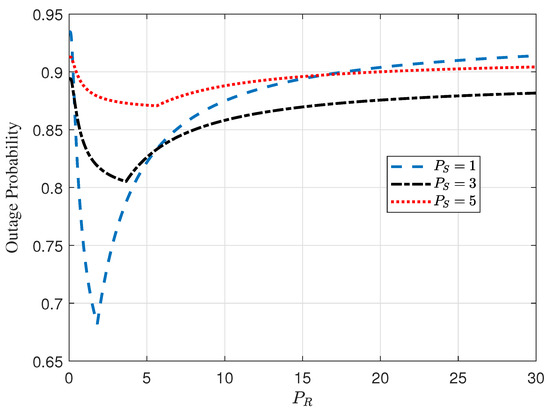
Figure 2.
Outage probability as a function of relay transmit power for three different source transmit powers: , , and .
Mathematically, the optimization problem can be formulated as follows:
As mentioned earlier, the exact closed-form expression of the outage probability is analytically intractable, making it challenging to obtain the optimal solution for the optimization problem in (20). To facilitate a more tractable analysis, the asymptotic outage probability expression given in (19) is employed in (20) to determine the optimal solution, which is the optimal transmit power of the source and the optimal transmit power of the relay .
The asymptotic outage probability is derived under the assumption of a high SNR. In this regime—and as will be verified in Section 6—the outage probability is minimized when the energy harvesting rate of each node matches its energy depletion rate. When these two rates are equal, the probability that a node has sufficient energy in each block will be 1. This implies that the node will never run out of energy during operation. Furthermore, it ensures that the total harvested energy over the system’s operational period is fully utilized, thereby achieving the best energy utilization. Based on this, for the source node, the energy harvesting rate per time block is , while its energy depletion rate is equal to its transmit power . The optimal transmit power of the source is therefore the value that balances the harvesting and depletion rates, yielding
For the relay node, the energy harvesting rate per time block is , while its energy depletion rate is given by . Equating these two rates, the optimal transmit power of the relay can be given by
6. Results
This section evaluates the outage probability and determines the optimal transmit power for the proposed system, using a 4-QAM modulation with SSD and the following system parameters: , (urban environment), , , , and . The energy harvesting rates and and the transmit powers and are set based on the scenario. The derived exact closed-form expression and the asymptotic expression of the outage probability, along with the optimal transmit powers at both the source and the relay, are validated through Monte Carlo simulations. The outage probability and the optimal transmit powers are plotted as functions of the average signal-to-noise ratio per bit ().
Figure 3 illustrates both the analytical and simulated outage probabilities for the scenario in which the system operates using the aforementioned parameters, with the energy harvesting rates set to . In this setup, the outage probability is evaluated—analytically and via simulation—for three different sets of transmit powers: , and , and and . As can be observed in the figure, the theoretical outage probability closely matches the simulated outage probability, confirming the accuracy of the derived exact closed-form expression. Moreover, the figure shows that, for a given set of transmit powers, the outage probability decreases as the SNR increases, which is consistent with the expected behavior—the typical waterfall behavior of outage probability versus the SNR. However, unlike conventional battery-powered systems, the figure also reveals that increasing the transmit power can lead to a higher outage probability. This counterintuitive result highlights a fundamental characteristic of energy harvesting cooperative communication systems: a higher transmit power increases the likelihood that a node will exhaust its available energy within a time block, thereby raising the overall system outage probability. Consequently, it is essential to balance transmit power with energy availability to ensure reliable system performance. This trade-off motivates the core objective of this work, which is minimizing the outage probability with respect to the transmit powers at both the source and the relay.
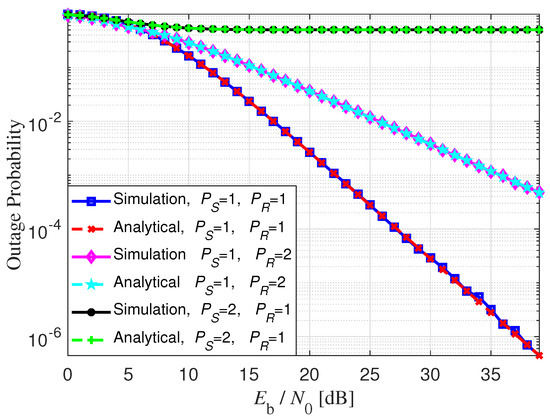
Figure 3.
Outage probability when and for various sets of transmit powers.
Figure 4a presents the analytical, simulated, and asymptotic outage probabilities for the scenario where the energy harvesting rates are set to and , with the transmit powers set to . As observed in the figure, the asymptotic outage probability converges to both the analytical and simulated results as the SNR increases, and it closely aligns with them in the high-SNR regime, validating the accuracy of the derived asymptotic expression for the outage probability. Furthermore, Figure 4b shows the optimal transmit powers for both the source and the relay under the same scenario. It is evident from the figure that the analytically obtained optimal transmit powers closely match their simulated counterparts. This consistency confirms the validity of the derived expressions for the source and relay optimal transmit powers given in (21) and (23), respectively. This consistency also supports the claim made in Section 5 that, in the high-SNR regime, the optimal transmit power for a node is the value that balances its energy harvesting rate with its energy depletion rate.
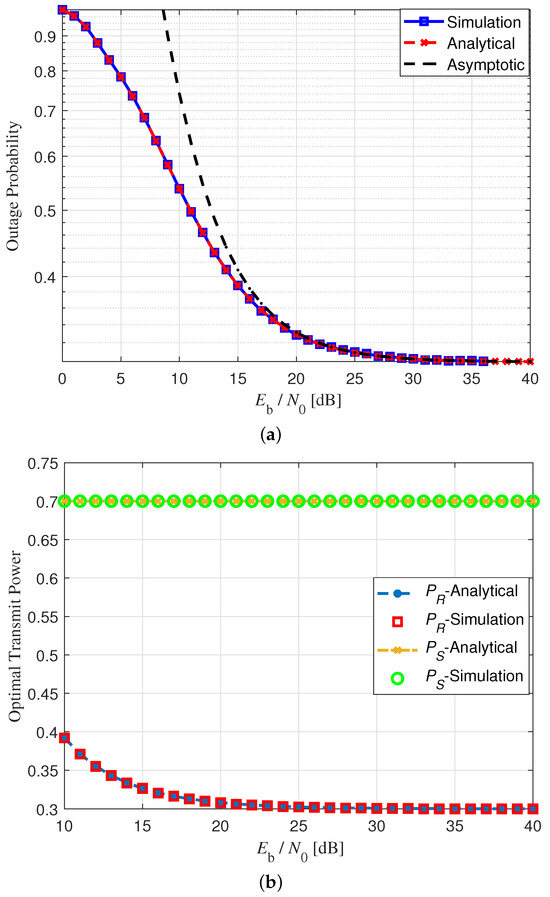
Figure 4.
Outage probability and optimal transmit powers when and .
Figure 5a,b present the results for the same scenario described in the previous paragraph but with the energy harvesting rates set to and . As observed in the figures, the asymptotic outage probability closely matches both the analytical and simulated results at a high SNR, further validating the accuracy of the asymptotic expression. Moreover, it is evident that the analytically derived optimal transmit powers are in close agreement with those obtained via simulation, reinforcing the findings from the earlier scenario and supporting the validity of the power optimization approach.
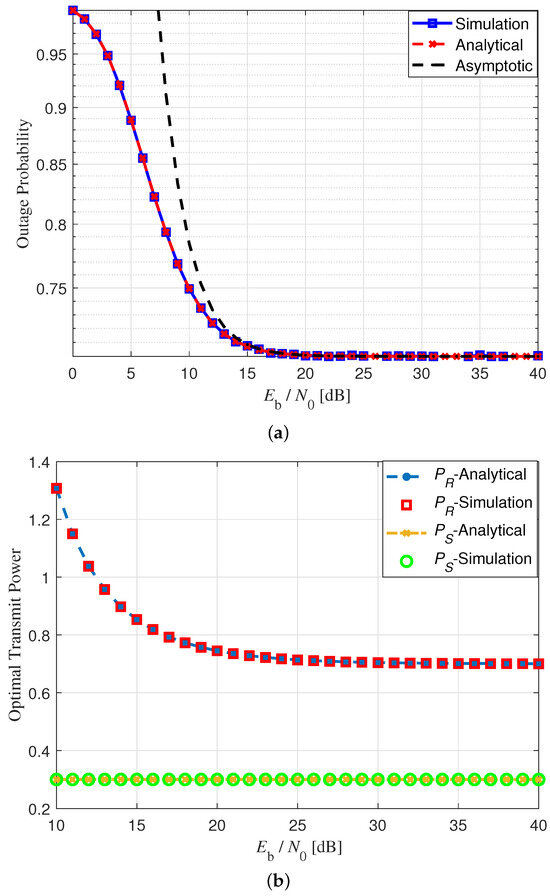
Figure 5.
Outage probability and optimal transmit powers when and .
Note that the outage probabilities in Figure 4a and Figure 5a saturate at in the high-SNR regime. This behavior is expected. For the parameter settings in Figure 4a, the outage probability is dominated by the third condition in (15), while in Figure 5a, the outage probability is dominated by the fourth condition in the same equation. In both cases, as the SNR increases, the outage probabilities of all communication links tend toward zero. Consequently, the overall outage probability converges to the probability that the source does not have sufficient energy to transmit, which is 1 −. Given that in both scenarios, this saturation level simplifies to .
7. Conclusions
This work considers a three-node cooperative communication network in which both the source and the relay are powered by energy harvesting. The system employs signal space diversity at both the source and relay, along with a decode-and-forward relaying scheme. Exact closed-form and asymptotic expressions for the outage probability are derived and validated through Monte Carlo simulations. In addition, an optimization problem is formulated to minimize the outage probability with respect to the transmit power of both the source and the relay. Our analysis shows that the optimization problem is a convex function of the transmit powers, with a unique global minimum. In contrast to traditional battery-powered systems, the results indicate that increasing the transmit power in energy harvesting cooperative communication systems can lead to a higher outage probability, as a higher transmit power may increase the likelihood that a node may not have sufficient energy for transmission. The results also show that, at high SNRs, the optimal transmit power of a node is the value that balances its energy harvesting and depletion rates. Lastly, as a future research direction, this work could be extended to a multiple-relay scenario, where relay selection or cooperative strategies among multiple energy harvesting relays may further improve system performance.
Author Contributions
Conceptualization, A.A. and M.A.K.; Methodology, A.A. and M.A.K.; Validation, A.A.; Formal analysis, A.A.; Writing—original draft, A.A.; Writing—review & editing, M.A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors gratefully acknowledge the T. J. Smull College of Engineering at Ohio Northern University for its generous support to complete this research.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
References
- Tan, Y.K.; Panda, S.K. Review of Energy Harvesting Technologies for Sustainable WSN. In Sustainable Wireless Sensor Networks; Seah, W., Tan, Y.K., Eds.; IntechOpen: Rijeka, Croatia, 2010; Chapter 2. [Google Scholar] [CrossRef]
- Sudevalayam, S.; Kulkarni, P. Energy Harvesting Sensor Nodes: Survey and Implications. IEEE Commun. Surv. Tutor. 2011, 13, 443–461. [Google Scholar] [CrossRef]
- Chen, H.; Li, Y.; Luiz Rebelatto, J.; Uchoa-Filho, B.F.; Vucetic, B. Harvest-Then-Cooperate: Wireless-Powered Cooperative Communications. IEEE Trans. Signal Process. 2015, 63, 1700–1711. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying Protocols for Wireless Energy Harvesting and Information Processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Di Renzo, M.; Ntontin, K.; Song, J.; Danufane, F.H.; Qian, X.; Lazarakis, F.; De Rosny, J.; Phan-Huy, D.T.; Simeone, O.; Zhang, R.; et al. Reconfigurable Intelligent Surfaces vs. Relaying: Differences, Similarities, and Performance Comparison. IEEE Open J. Commun. Soc. 2020, 1, 798–807. [Google Scholar] [CrossRef]
- Sendonaris, A.; Erkip, E.; Aazhang, B. User cooperation diversity. Part I. System description. IEEE Trans. Commun. 2003, 51, 1927–1938. [Google Scholar] [CrossRef]
- Laneman, J.; Tse, D.; Wornell, G. Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Trans. Inf. Theory 2004, 50, 3062–3080. [Google Scholar] [CrossRef]
- Ikki, S.; Ahmed, M.H. Performance Analysis of Cooperative Diversity Wireless Networks over Nakagami-m Fading Channel. IEEE Commun. Lett. 2007, 11, 334–336. [Google Scholar] [CrossRef]
- Srikamu, C.; Meera, S.; Jayabharathy, R. Analysis of Bit-Error-Rate for D2D AF Cooperative System Using Various Modulation Techniques. In Proceedings of the 2021 Sixth International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai, India, 25–27 March 2021; pp. 204–208. [Google Scholar] [CrossRef]
- Liu, X.; Yu, Y.; Li, F.; Durrani, T.S. Throughput Maximization for RIS-UAV Relaying Communications. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19569–19574. [Google Scholar] [CrossRef]
- Tayakout, H.; Boutellaa, E.; Bouchibane, F.Z. On the Robustness of Digital Modulation Recognition for Cooperative Relaying Networks under Imperfect CSI. In Proceedings of the 2022 7th International Conference on Image and Signal Processing and their Applications (ISPA), Mostaganem, Algeria, 8–9 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Guo, X.; Bao, J.; Xu, X.; Liu, C.; Jiang, B. Optimized Incremental Selection Hybrid Decode-Amplify-Forward Relaying Cooperation for Average Transmission Power Reduction. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Online, 20–22 October 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Yan, J.Q.; Hou, J. Performance Analysis of Cooperative RSMA-SWIPT Communication System. In Proceedings of the 2025 International Conference on Computing, Networking and Communications (ICNC), Honolulu, HI, USA, 17–20 February 2025; pp. 854–858. [Google Scholar] [CrossRef]
- Liang, H.; Zhong, C.; Suraweera, H.A.; Zheng, G.; Zhang, Z. Optimization and Analysis of Wireless Powered Multi-Antenna Cooperative Systems. IEEE Trans. Wirel. Commun. 2017, 16, 3267–3281. [Google Scholar] [CrossRef]
- Zhang, J.; Clerckx, B.; Ge, J.; Mao, Y. Cooperative Rate Splitting for MISO Broadcast Channel With User Relaying, and Performance Benefits Over Cooperative NOMA. IEEE Signal Process. Lett. 2019, 26, 1678–1682. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, R.; Cui, S. Throughput Maximization for the Gaussian Relay Channel with Energy Harvesting Constraints. IEEE J. Sel. Areas Commun. 2013, 31, 1469–1479. [Google Scholar] [CrossRef]
- Dao, T.T.T.; Son, P.N. Two-Way SWIPT Relaying Networks with Nonlinear Power Splitting, Digital Network Coding and Selection Combining. Wirel. Pers. Commun. 2023, 133, 2445–2465. [Google Scholar] [CrossRef]
- Gurjar, D.S.; Singh, U.; Upadhyay, P.K. Energy harvesting in hybrid two-way relaying with direct link under Nakagami-m fading. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Khan, M.A.; Ammar, A. Modulation Diversity in a Two-Way Cooperative System with an Energy Harvesting Relay. In Proceedings of the 2021 IEEE International Black Sea Conference on Communications and Networking (BlackSeaCom), Bucharest, Romania, 24–28 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Ammar, A.; Khan, M.A. Signal Space Diversity in a DF Cooperative System with an Energy Harvesting Relay. In Proceedings of the 2021 IEEE International Mediterranean Conference on Communications and Networking (MeditCom), Athens, Greece, 7–10 September 2021; pp. 425–430. [Google Scholar] [CrossRef]
- Abou-Rjeily, C.; Kaddoum, G. Free Space Optical Cooperative Communications via an Energy Harvesting Harvest-Store-Use Relay. IEEE Trans. Wirel. Commun. 2020, 19, 6564–6577. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Throughput and ergodic capacity of wireless energy harvesting based DF relaying network. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; pp. 4066–4071. [Google Scholar] [CrossRef]
- Babaei, M.; Aygölü, F.; Basar, E. BER Analysis of Dual-Hop Relaying With Energy Harvesting in Nakagami- m Fading Channel. IEEE Trans. Wirel. Commun. 2018, 17, 4352–4361. [Google Scholar] [CrossRef]
- Ammar, A.; Reynolds, D. Energy Harvesting Networks: Energy Versus Data Cooperation. IEEE Commun. Lett. 2018, 22, 2128–2131. [Google Scholar] [CrossRef]
- Clementi, G.; Cottone, F.; Di Michele, A.; Gammaitoni, L.; Mattarelli, M.; Perna, G.; Lopez-Suarez, M.; Baglio, S.; Trigona, C.; Neri, I. Review on Innovative Piezoelectric Materials for Mechanical Energy Harvesting. Energies 2022, 15, 6227. [Google Scholar] [CrossRef]
- Zheng, K.; Liu, X.; Zhu, Y.; Chi, K.; Liu, K. Total Throughput Maximization of Cooperative Cognitive Radio Networks With Energy Harvesting. IEEE Trans. Wirel. Commun. 2020, 19, 533–546. [Google Scholar] [CrossRef]
- Boutros, J.; Viterbo, E. Signal space diversity: A power- and bandwidth-efficient diversity technique for the Rayleigh fading channel. IEEE Trans. Inf. Theory 1998, 44, 1453–1467. [Google Scholar] [CrossRef]
- Yu, P.; Lee, J.; Quek, T.Q.S.; Hong, Y.W.P. Energy Harvesting Personal Cells-Traffic Offloading and Network Throughput. In Proceedings of the IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 2184–2189. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).