Advances in Electrolyzer Emulators: A Comprehensive Review
Abstract
1. Introduction
2. Basic Operation and Comparison of EL Types
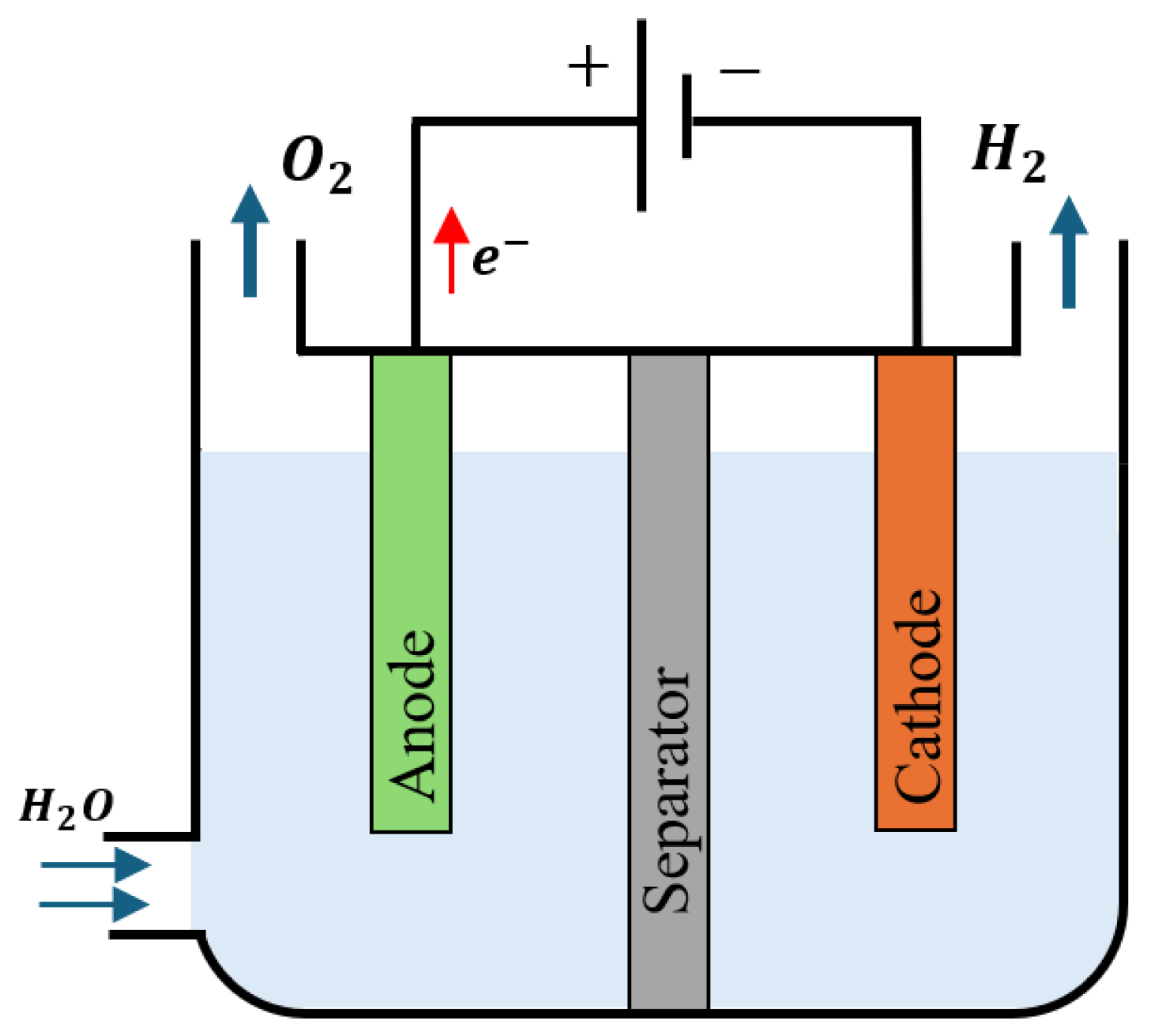
2.1. Basic Operation of Water Electrolysis
2.2. Reaction Equations
2.3. Comparison of EL Types
| PEM | AWE | SOEC | AEM | |
|---|---|---|---|---|
| Operation temperature, °C | 50–80 | 70–90 | 700–850 | 60–80 |
| Cell pressure, bar | <50 | <30 | 1 | <35 |
| Typical current density range, A·cm−2 | 1–6 | 0.2–0.8 | 0.3–1.0 | 0.2–2.0 |
| Voltage range, V | 1.4–2.3 | 1.4–3 | 1.0–1.5 | 1.4–2.0 |
| System efficiency range, % | 46–60 | 51–60 | 76–81 | <75 |
| System specific energy consumption range, kWh·Nm−3 | 4.53–6.1 | 4.0–5.47 | 3.7–3.9 | 4.2–5.5 |
| Stack efficiency range (based on LHV *), % | 60–68 | 63–71 | ∼100 | 60–83 |
| Stack specific energy consumption range, kWh·Nm−3 | 4.3–5.8 | 3.8–5.2 | 3 | 3.95–5.2 |
| Max * stack power, MW | 6.5 | 5 | <0.01 | 2 |
| Max * hydrogen production, Nm3·h−1 | 1110 | 1050 | <10 | 462 |
| Lifetime range, kh | 30–40 | 60–80 | 8–20 | <2 |
| Degradation rate, % per year | 0.5–2.5 | 0.25–1.5 | 3–50 | – |
| Capital cost, €/kW | 1400–2100 | 500–800 | >2000 | 200 |
| Environmental impact | Moderate | Lowest | Highest | Potentially low |
| Renewable energy compatibility | Excellent | Low | Low | Potentially high |
| Technology maturity | Commercialized | Mature | R&D | Emerging |
| Application | Mobility, Large-scale | Industrial Large-scale | Industrial High temperature | Industrial, Mobility potential |
| ELs | Advantages | Disadvantages |
|---|---|---|
| PEM | - High current density - Fast system response - Greater hydrogen production rate - High dynamic operation - Excellent operational flexibility (0–100%) - Rapid cold and hot start (<10 s) | - High cost of noble materials (iridium and platinium) - Moderate degradation rate (0.5–2.5%/year) - Limited lifetime (30,000 h–40,000 h) - Operates in acidic environment |
| AWE | - Most mature and well-established technology - Non-noble electrocatalysts - Longer lifetime >60,000 h - Low degradation rate (0.25–1.5%/year) - Low capital cost | - Low current density (0.25–0.8 A/cm2) - Corrosive electrolyte - Slow start-up time (1–2 h) - Lower load flexibility for RES |
| SOEC | - Very high efficiency - High temperatures - RES integration with heat | - Still in research phase - High degradation rate (3–50%/year) - Low flexibility (−100/+100) - Very high capital cost - Slow start-up time |
| AEM | - Low cost - Excellent operational flexibility (0–100 %) - Fast cold start (5–10 min) | - Emerging technology - Durability remains uncertain - Stability up to 10,000 h |
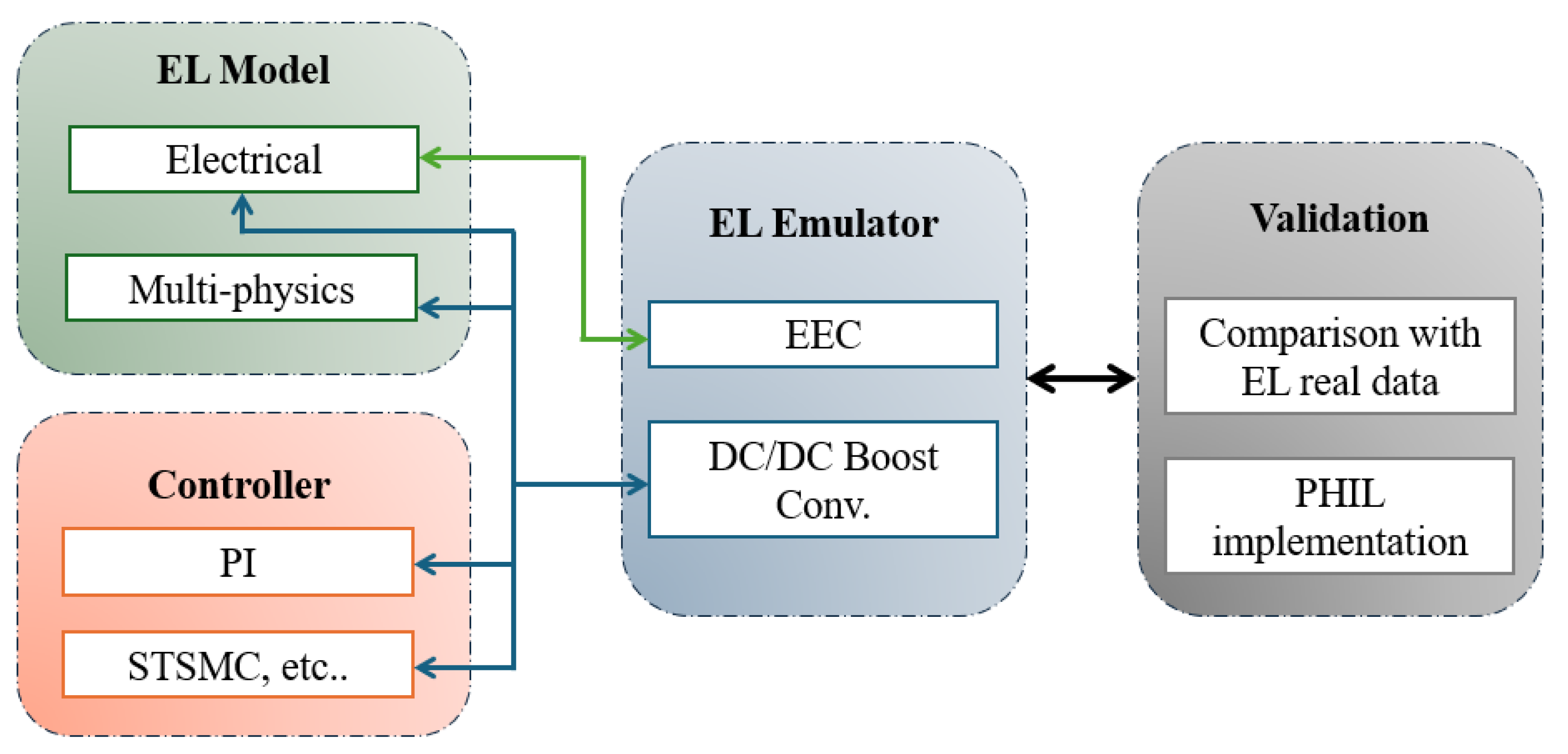
3. Emulator Fundamentals
3.1. Proposed Emulators in the Literature
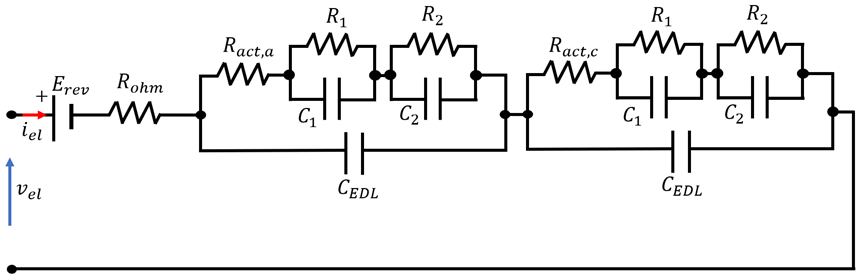
3.1.1. EEC-Based Emulator
3.1.2. DC-DC Boost Converter-Based Emulators
3.2. Model Verification Based PHIL Concept
3.3. Comparison of Existing EL Emulator
4. Mathematical Model of ELs
4.1. EL Voltage According to the Current Density
4.1.1. Reversible Voltage
4.1.2. Activation Overpotential
4.1.3. Ohmic Overpotential
4.1.4. Concentration Overpotential
4.2. Efficiency
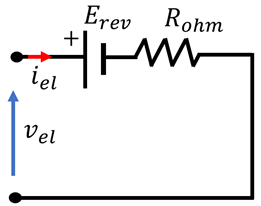
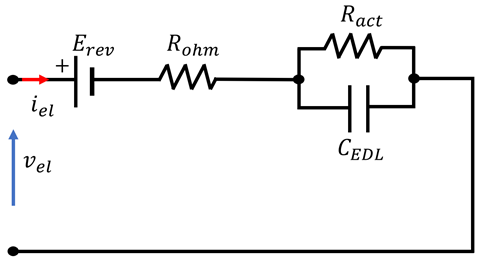
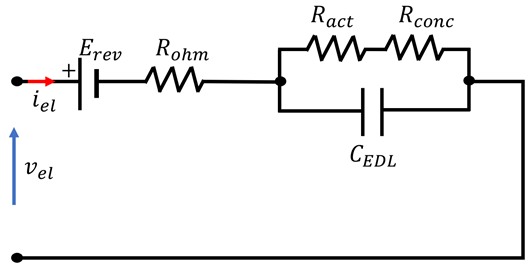
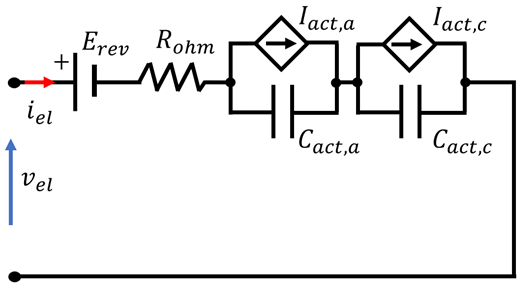
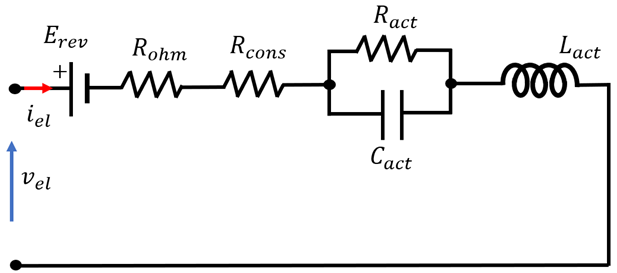
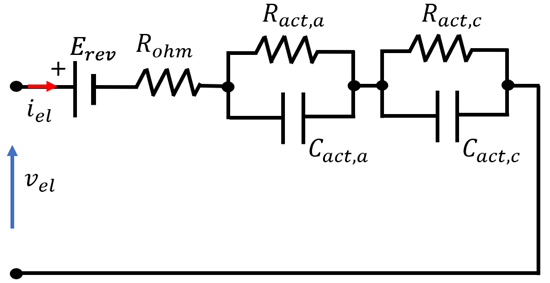
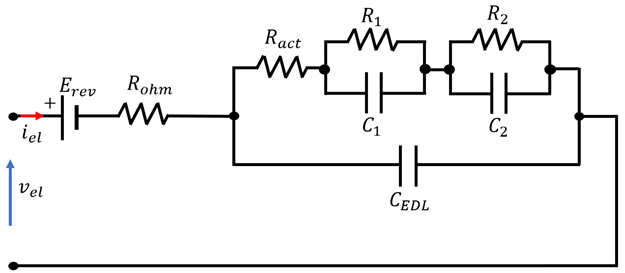
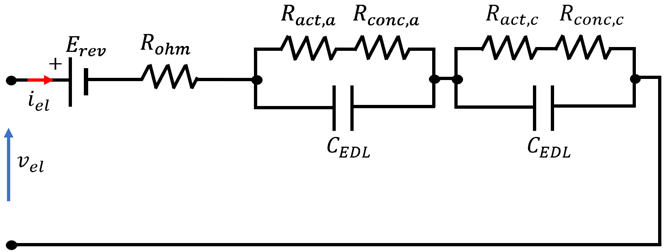
4.3. Overview of EEC Representation of EL
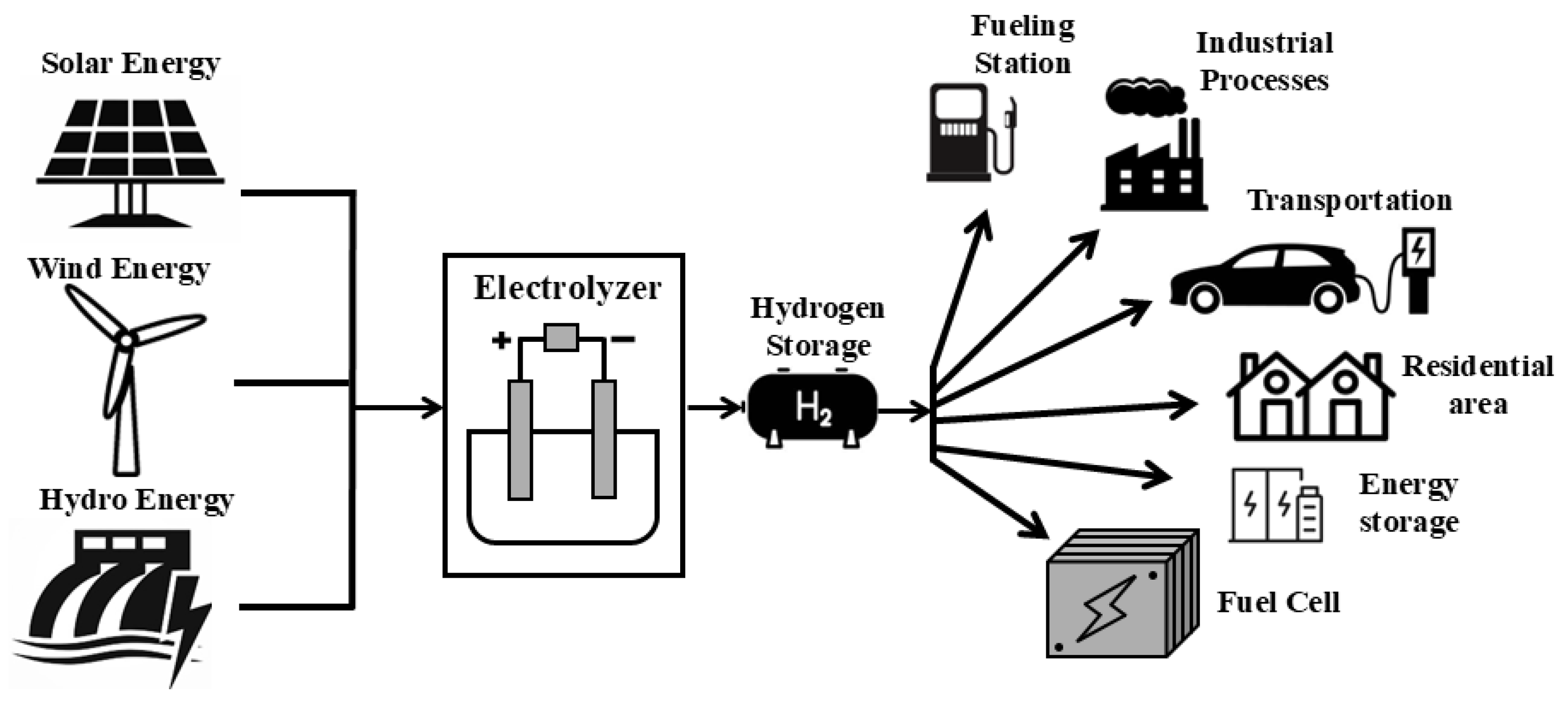
5. Integration of EL in a Power-Grid-Based Renewable Energy System
6. Discussions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ELs | Electrolyzers | RES | Renewable energy source |
| GHG | Greenhouse gas | CO2 | Carbon dioxide |
| PEMEL | Proton exchange membrane electrolyzer | AWE | Alkaline water electrolyzers |
| AEM | Anion exchange membrane | SOEC | Solid oxide electrolysis cells |
| EEC | Equivalent electrical circuit | PHIL | Power-hardware-in-loop |
| EIS | Electrochemical impedance spectroscopy | RSOEC | Reversible solid oxide electrolysis cells |
| BoP | Balance-of-plant | PRO | Partial reinforcement optimizer |
| GE | General Electric | MEA | Membrane electrode assembly |
| DC | Direct current | SPE | Solid polymer electrolyte |
| OER | Oxygen evolution reaction | HER | Hydrogen evolution reaction |
| EDL | Electric double layer | PI | Proportional-integral |
| ST-SMC | Supertwisting sliding-mode control | cRIO | CompactRIO |
| FPGA | Field-programmable gate array | COG | Causal ordering graphs |
| MPPT | Maximum power point tracking | PV | Photovoltaic |
References
- Xu, X.; Zhou, Q.; Yu, D. The future of hydrogen energy: Bio-hydrogen production technology. Int. J. Hydrogen Energy 2022, 47, 33677–33698. [Google Scholar] [CrossRef]
- Rasul, M.G.; Hazrat, M.A.; Sattar, M.A.; Jahirul, M.I.; Shearer, M.J. The future of hydrogen: Challenges on production, storage and applications. Energy Convers. Manag. 2022, 272, 116326. [Google Scholar] [CrossRef]
- Trattner, A.; Klell, M.; Radner, F. Sustainable hydrogen society—Vision, findings and development of a hydrogen economy using the example of Austria. Int. J. Hydrogen Energy 2022, 47, 2059–2079. [Google Scholar] [CrossRef]
- Zainal, B.S.; Ker, P.J.; Mohamed, H.; Ong, H.C.; Fattah, I.M.R.; Rahman, S.M.A.; Nghiem, L.D.; Mahlia, T.M.I. Recent advancement and assessment of green hydrogen production technologies. Renew. Sustain. Energy Rev. 2024, 189, 113941. [Google Scholar] [CrossRef]
- Dincer, I.; Acar, C. Innovation in hydrogen production. Int. J. Hydrogen Energy 2017, 42, 14843–14864. [Google Scholar] [CrossRef]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The Role of Renewable Energy in the Global Energy Transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Rizwan, M.; Alstad, V.; Jäschke, J. Design considerations for industrial water electrolyzer plants. Int. J. Hydrogen Energy 2021, 46, 37120–37136. [Google Scholar] [CrossRef]
- Rao, X.; Zhang, S.; Zhang, J. Carbon Semi-Tubes for Electrochemical Energy Catalysis. Electrochem. Energy Rev. 2025, 8, 7. [Google Scholar] [CrossRef]
- Makhsoos, A.; Kandidayeni, M.; Boulon, L.; Pollet, B.G. A comparative analysis of single and modular proton exchange membrane water electrolyzers for green hydrogen production—A case study in Trois-Rivières. Energy 2023, 282, 128911. [Google Scholar] [CrossRef]
- Falcão, D.S.; Pinto, A.M.F.R. A Review on PEM Electrolyzer Modelling: Guidelines for Beginners. J. Clean. Prod. 2020, 261, 121184. [Google Scholar] [CrossRef]
- Mohammadi, A.; Mehrpooya, M. A Comprehensive Review on Coupling Different Types of Electrolyzer to Renewable Energy Sources. Energy 2018, 158, 632–655. [Google Scholar] [CrossRef]
- Akyüz, E.S.; Telli, E.; Farsak, M. Hydrogen generation electrolyzers: Paving the way for sustainable energy. Int. J. Hydrogen Energy 2024, 81, 1338–1362. [Google Scholar] [CrossRef]
- Shiva Kumar, S.; Himabindu, V. Hydrogen Production by PEM Water Electrolysis—A Review. Mater. Sci. Energy Technol. 2019, 2, 442–454. [Google Scholar] [CrossRef]
- Hayati, M.M.; Majidi Gharehnaz, H.; Biabani, H.; Aminlou, A.; Abapour, M. An Overview of Energy and Exergy Analysis for Green Hydrogen Power Systems. In Green Hydrogen Production, Storage and Utilization; Springer: Cham, Switzerland, 2024; pp. 1–24. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Chen, Z.; Liao, Z.; Xu, C.; Du, X. Energy and exergy analysis of a proton exchange membrane water electrolysis system without additional internal cooling. Renew. Energy 2021, 180, 1333–1343. [Google Scholar] [CrossRef]
- Gracia, L.; Casero, P.; Bourasseau, C.; Chabert, A. Use of Hydrogen in Off-Grid Locations, a Techno-Economic Assessment. Energies 2018, 11, 3141. [Google Scholar] [CrossRef]
- Maoulida, F.; Guilbert, D.; Camara, M.-B.; Dakyo, B. Dynamic electrical degradation of PEM electrolyzers under renewable energy intermittency: Mechanisms, diagnostics, and mitigation strategies—A comprehensive review. Renew. Sustain. Energy Rev. 2026, 225, 116170. [Google Scholar] [CrossRef]
- Ayers, K.E.; Marina, O.A. State of the art in low-temperature and high-temperature electrolysis. MRS Bull. 2024, 49, 1226–1234. [Google Scholar] [CrossRef]
- Yodwong, B. Contribution to the Development of a High-Power Low-Voltage DC-DC Converter for Proton Exchange Membrane Electrolyzer Applications. Ph.D. Thesis, Université de Lorraine, Nancy, France, King Mongkut’s University of Technology North Bangkok, Bangkok, Thailand, 2022. Available online: https://hal.univ-lorraine.fr/tel-03794828 (accessed on 20 November 2024).
- Yodwong, B.; Guilbert, D.; Hinaje, M.; Phattanasak, M.; Kaewmanee, W.; Vitale, G. Proton Exchange Membrane Electrolyzer Emulator for Power Electronics Testing Applications. Processes 2021, 9, 498. [Google Scholar] [CrossRef]
- Guilbert, D.; Vitale, G. Dynamic Emulation of a PEM Electrolyzer by Time Constant Based Exponential Model. Energies 2019, 12, 750. [Google Scholar] [CrossRef]
- El-Shafie, M. Hydrogen production by water electrolysis technologies: A review. Results Eng. 2023, 20, 101426. [Google Scholar] [CrossRef]
- Hernández-Gómez, Á.; Langarica-Cordoba, D.; Martinez-Rodriguez, P.R.; Guilbert, D.; Ramirez, V.; Saldivar, B. PEM Fuel Cell Emulators: A Review. Electronics 2023, 12, 2812. [Google Scholar] [CrossRef]
- Machac, D.; Reichert, P.; Albert, C. Emulation of dynamic simulators with application to hydrology. J. Comput. Phys. 2016, 313, 352–366. [Google Scholar] [CrossRef]
- Khalid Ratib, M.; Muttaqi, K.M.; Islam, M.R.; Sutanto, D.; Agalgaonkar, A.P. Electrical Circuit Modeling of Proton Exchange Membrane Electrolyzer: The State-of-the-Art, Current Challenges, and Recommendations. Int. J. Hydrogen Energy 2024, 49, 625–645. [Google Scholar] [CrossRef]
- Hernández-Gómez, Á.; Ramirez, V.; Guilbert, D. Investigation of PEM electrolyzer modeling: Electrical domain, efficiency, and specific energy consumption. Int. J. Hydrogen Energy 2020, 45, 14625–14639. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, Y.; Zhang, J.; Benigni, A. Real-Time Simulation of an Electrolyzer with a Diode Rectifier and a Three-Phase Interleaved Buck Converter. In Proceedings of the 2022 IEEE 13th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Kiel, Germany, 27–30 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Tijani, A.S.; Abdol Rahim, A.H. Numerical Modeling the Effect of Operating Variables on Faraday Efficiency in PEM Electrolyzer. Procedia Technol. 2016, 26, 419–427. [Google Scholar] [CrossRef]
- Ganjehsarabi, H. Performance assessment of solar-powered high pressure proton exchange membrane electrolyzer: A case study for Erzincan. Int. J. Hydrogen Energy 2019, 44, 9701–9707. [Google Scholar] [CrossRef]
- Koundi, M.; El Fadil, H. Mathematical modeling of PEM electrolyzer and design of a voltage controller by the SMPWM approach. In Proceedings of the 2019 International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Istanbul, Turkey, 26–27 August 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Gusain, D.; Cvetković, M.; Bentvelsen, R.; Palensky, P. Technical Assessment of Large Scale PEM Electrolyzers as Flexibility Service Providers. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 1074–1078. [Google Scholar] [CrossRef]
- Stansberry, J.M.; Brouwer, J. Experimental Dynamic Dispatch of a 60 kW Proton Exchange Membrane Electrolyzer in Power-to-Gas Application. Int. J. Hydrogen Energy 2020, 45, 9305–9316. [Google Scholar] [CrossRef]
- Virji, M.; Randolf, G.; Ewan, M.; Rocheleau, R. Analyses of Hydrogen Energy System as a Grid Management Tool for the Hawaiian Isles. Int. J. Hydrogen Energy 2020, 45, 8052–8066. [Google Scholar] [CrossRef]
- Correa, G.; Marocco, P.; Muñoz, P.; Falagüerra, T.; Ferrero, D.; Santarelli, M. Pressurized PEM Water Electrolysis: Dynamic Modelling Focusing on the Cathode Side. Int. J. Hydrogen Energy 2022, 47, 4315–4327. [Google Scholar] [CrossRef]
- Hancke, R.; Holm, T.; Ulleberg, Ø. The Case for High-Pressure PEM Water Electrolysis. Energy Convers. Manag. 2022, 261, 115642. [Google Scholar] [CrossRef]
- Crespi, E.; Guandalini, G.; Mastropasqua, L.; Campanari, S.; Brouwer, J. Experimental and Theoretical Evaluation of a 60 kW PEM Electrolysis System for Flexible Dynamic Operation. Energy Convers. Manag. 2023, 277, 116622. [Google Scholar] [CrossRef]
- Dong, Y.; Ma, S.; Han, Z.; Bai, J.; Wang, Q. Research on the Adaptability of Proton Exchange Membrane Electrolysis in Green Hydrogen–Electric Coupling System Under Multi-Operating Conditions. Energy Rep. 2023, 9, 4789–4798. [Google Scholar] [CrossRef]
- Hemauer, J.; Rehfeldt, S.; Klein, H.; Peschel, A. Performance and Cost Modelling Taking into Account the Uncertainties and Sensitivities of Current and Next-Generation PEM Water Electrolysis Technology. Int. J. Hydrogen Energy 2023, 48, 25619–25634. [Google Scholar] [CrossRef]
- Koo, T.; Ko, R.; Ha, D.; Han, J. Development of Model-Based PEM Water Electrolysis HILS (Hardware-in-the-Loop Simulation) System for State Evaluation and Fault Detection. Energies 2023, 16, 3379. [Google Scholar] [CrossRef]
- Samani, A.E.; De Kooning, J.D.M.; Urbina Blanco, C.A.; Vandevelde, L. Flexible Operation Strategy for Formic Acid Synthesis Providing Frequency Containment Reserve in Smart Grids. Int. J. Electr. Power Energy Syst. 2022, 139, 107969. [Google Scholar] [CrossRef]
- Dozein, M.G.; De Corato, A.M.; Mancarella, P. Virtual Inertia Response and Frequency Control Ancillary Services from Hydrogen Electrolyzers. IEEE Trans. Power Syst. 2023, 38, 2447–2459. [Google Scholar] [CrossRef]
- Hernández-Gómez, Á.; Ramirez, V.; Guilbert, D.; Saldivar, B. Development of an Adaptive Static-Dynamic Electrical Model Based on Input Electrical Energy for PEM Water Electrolysis. Int. J. Hydrogen Energy 2020, 45, 18817–18830. [Google Scholar] [CrossRef]
- Samani, A.; D’Amicis, A.; Kooning, J.; Bozalakov, D.; Silva, P.; Vandevelde, L. Grid Balancing with a Large-Scale Electrolyser Providing Primary Reserve. IET Renew. Power Gener. 2020, 14, 3070–3078. [Google Scholar] [CrossRef]
- Tuinema, B.; Adabi, E.; Ayivor, P.; Suárez, V.; Liu, L.; Perilla, A.; Ahmad, Z.; Torres, J.; Meijden, M.; Palensky, P. Modelling of Large-Size Electrolysers for Real-Time Simulation and Study of the Possibility of Frequency Support by Electrolysers. IET Gener. Transm. Distrib. 2020, 14, 1985–1992. [Google Scholar] [CrossRef]
- Hernández-Gómez, Á.; Ramirez, V.; Guilbert, D.; Saldivar, B. Cell Voltage Static-Dynamic Modeling of a PEM Electrolyzer Based on Adaptive Parameters: Development and Experimental Validation. Renew. Energy 2021, 163, 1508–1522. [Google Scholar] [CrossRef]
- Nguyen, B.L.H.; Panwar, M.; Hovsapian, R.; Nagasawa, K.; Vu, T.V. Power Converter Topologies for Electrolyzer Applications to Enable Electric Grid Services. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; IEEE: Toronto, ON, Canada, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Raj, J.; Rajasree, S.R. A Microgrid with Hybrid Solar—Fuel Cell System With CHP Application. In Proceedings of the 2022 IEEE 2nd International Conference on Sustainable Energy and Future Electric Transportation (SeFeT), Hyderabad, India, 4–6 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Koundi, M.; El Fadil, H.; EL Idrissi, Z.; Lassioui, A.; Intidam, A.; Bouanou, T.; Nady, S.; Rachid, A. Investigation of Hydrogen Production System-Based PEM EL: PEM EL Modeling, DC/DC Power Converter, and Controller Design Approaches. Clean Technol. 2023, 5, 531–568. [Google Scholar] [CrossRef]
- Wilberforce, T.; Olabi, A.G.; Imran, M.; Sayed, E.T.; Abdelkareem, M.A. System modelling and performance assessment of green hydrogen production by integrating proton exchange membrane electrolyser with wind turbine. Int. J. Hydrogen Energy 2023, 48, 12089–12111. [Google Scholar] [CrossRef]
- Arsad, A.Z.; Hannan, M.A.; Al-Shetwi, A.Q.; Begum, R.A.; Hossain, M.J.; Ker, P.J.; Mahlia, T.M.I. Hydrogen electrolyser technologies and their modelling for sustainable energy production: A comprehensive review and suggestions. Int. J. Hydrogen Energy 2023, 48, 27841–27871. [Google Scholar] [CrossRef]
- Sorrenti, I.; Zheng, Y.; Singlitico, A.; You, S. Low-carbon and cost-efficient hydrogen optimisation through a grid-connected electrolyser: The case of GreenLab Skive. Renew. Sustain. Energy Rev. 2023, 171, 113033. [Google Scholar] [CrossRef]
- Yousri, D.; AlKuwaiti, R.H.; Farag, H.E.Z.; Zeineldin, H.; El-Saadany, E. Advanced Modeling of PEM Electrolyzers for Microgrid Systems: Incorporating Electrochemical and Thermal Models. Int. J. Hydrogen Energy 2024, 83, 755–773. [Google Scholar] [CrossRef]
- Yodwong, B.; Guilbert, D.; Kaewmanee, W.; Phattanasak, M. Energy efficiency based control strategy of a three-level interleaved DC-DC buck converter supplying a proton exchange membrane electrolyzer. Electronics 2019, 8, 933. [Google Scholar] [CrossRef]
- Guilbert, D.; Sorbera, D.; Vitale, G. A stacked interleaved DC-DC buck converter for proton exchange membrane electrolyzer applications: Design and experimental validation. Int. J. Hydrogen Energy 2020, 45, 64–79. [Google Scholar] [CrossRef]
- Zorica, S.; Vukšić, M.; Betti, T. Design considerations of the multi-resonant converter as a constant current source for electrolyser utilisation. Int. J. Electr. Power Energy Syst. 2019, 111, 237–247. [Google Scholar] [CrossRef]
- Koundi, M.; El Fadil, H.; El Idrissi, Z.; Lassioui, A.; Bouanou, T.; Nady, S.; Rachid, A.; Hilmani, A. Electrical modelling, design, and implementation of a hardware PEM electrolyzer emulator for smart grid testing. Int. J. Emerg. Electr. Power Syst. 2025, 26, 85–105. [Google Scholar] [CrossRef]
- Zhou, T.; Francois, B. Modeling and Control Design of Hydrogen Production Process for an Active Hydrogen/Wind Hybrid Power System. Int. J. Hydrogen Energy 2009, 34, 21–30. [Google Scholar] [CrossRef]
- Ruuskanen, V.; Koponen, J.; Sillanpää, T.; Huoman, K.; Kosonen, A.; Niemelä, M.; Ahola, J. Design and Implementation of a Power-Hardware-in-Loop Simulator for Water Electrolysis Emulation. Renew. Energy 2018, 119, 106–115. [Google Scholar] [CrossRef]
- Ruuskanen, V.; Koponen, J.; Huoman, K.; Kosonen, A.; Niemelä, M.; Ahola, J. PEM Water Electrolyzer Model for a Power-Hardware-in-Loop Simulator. Int. J. Hydrogen Energy 2017, 42, 10775–10784. [Google Scholar] [CrossRef]
- Jessen, K.; Soltani, M.; Hajizadeh, A.; Schaltz, E.; Jensen, S.H.; Török, L. Real-time emulation of reversible solid oxide electrolyzer’s electrical behavior for rapid-prototyping of power electronics. IEEE Access 2024, 12, 89394–89404. [Google Scholar] [CrossRef]
- Bintz, S.; Fischer, M.; Roth-Stielow, J. Load emulation for electrolysis rectifiers. In Proceedings of the 2019 IEEE 13th International Conference on Power Electronics and Drive Systems (PEDS), Toulouse, France, 9–12 July 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Olivier, P.; Bourasseau, C.; Bouamama, B. Low-temperature electrolysis system modelling: A review. Renew. Sustain. Energy Rev. 2017, 78, 280–300. [Google Scholar] [CrossRef]
- Zhang, K.; Liang, X.; Wang, L.; Sun, K.; Wang, Y.; Xie, Z.; Wu, Q.; Bai, X.; Hamdy, M.S.; Chen, H.; et al. Status and perspectives of key materials for PEM electrolyzer. Nano Res. Energy 2022, 1, 9120032. [Google Scholar] [CrossRef]
- Järvinen, L.; Puranen, P.; Kosonen, A.; Ruuskanen, V.; Ahola, J.; Kauranen, P.; Hehemann, M. Automized parametrization of PEM and alkaline water electrolyzer polarisation curves. Int. J. Hydrogen Energy 2022, 47, 31985–32003. [Google Scholar] [CrossRef]
- Abdol Rahim, A.H.; Tijani, A.S.; Kamarudin, S.K.; Hanapi, S. An overview of polymer electrolyte membrane electrolyzer for hydrogen production: Modeling and mass transport. J. Power Sources 2016, 309, 56–65. [Google Scholar] [CrossRef]
- Yodwong, B.; Guilbert, D.; Phattanasak, M.; Kaewmanee, W.; Hinaje, M.; Vitale, G. Proton Exchange Membrane Electrolyzer Modeling for Power Electronics Control: A Short Review. C 2020, 6, 29. [Google Scholar] [CrossRef]
- García-Vite, P.M.; Reyes-García, B.L.; Valdez-Hernández, C.L.; Martínez-Salazar, A.L. Microcontroller-based emulation of a PEM fuel cell. Int. J. Hydrogen Energy 2020, 45, 13767–13776. [Google Scholar] [CrossRef]
- Priya, M.S.; Saravanan, S.; Vijaya Chandrakala, K.R.M.; Subramaniam, U.; Selvam, S. Techno-Economic Viability of Fuel Cell Emulator Toward Sustainable Energy Systems: A Survey. IEEE Access 2025, 13, 126649–126683. [Google Scholar] [CrossRef]
- Ma, Z.; Witteman, L.; Wrubel, J.A.; Bender, G. A Comprehensive Modeling Method for Proton Exchange Membrane Electrolyzer Development. Int. J. Hydrogen Energy 2021, 46, 17627–17643. [Google Scholar] [CrossRef]
- Wang, J.; Wen, J.; Wang, J.; Yang, B.; Jiang, L. Water electrolyzer operation scheduling for green hydrogen production: A review. Renew. Sustain. Energy Rev. 2024, 203, 114779. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, R.; Shao, Z.; Zhang, C. The economic analysis for hydrogen production cost towards electrolyzer technologies: Current and future competitiveness. Int. J. Hydrogen Energy 2023, 48, 13767–13779. [Google Scholar] [CrossRef]
- Khan, M.A.; Zhao, H.; Zou, W.; Chen, Z.; Cao, W.; Fang, J.; Xu, J.; Zhang, L. Recent progresses in electrocatalysts for water electrolysis. Electrochem. Energy Rev. 2018, 1, 483–530. [Google Scholar] [CrossRef]
- Carmo, M.; Fritz, D.L.; Mergel, J.; Stolten, D. A comprehensive review on PEM water electrolysis. Int. J. Hydrogen Energy 2013, 38, 4901–4934. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, L.; Zhang, J.; Wang, J.; Hu, Y.; Jiang, H.; Li, C. Anion exchange membrane water electrolyzer: Electrode design, lab-scaled testing system and performance evaluation. EnergyChem 2022, 4, 100087. [Google Scholar] [CrossRef]
- Shiva Kumar, S.; Lim, H. An overview of water electrolysis technologies for green hydrogen production. Energy Rep. 2022, 8, 13793–13813. [Google Scholar] [CrossRef]
- Rashid, M.M.; Al Mesfer, M.K.; Naseem, H.; Danish, M. Hydrogen production by water electrolysis: A review of alkaline water electrolysis, PEM water electrolysis and high temperature water electrolysis. Int. J. Eng. Adv. Technol. 2015, 4, 80–93. [Google Scholar]
- IRENA. Green Hydrogen Cost Reduction: Scaling Up Electrolysers to Meet the 1.5 ∘C Climate Goal; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2020; Available online: https://www.irena.org/publications/2020/Dec/Green-hydrogen-cost-reduction (accessed on 20 November 2024).
- Benghanem, M.; Mellit, A.; Almohamadi, H.; Haddad, S.; Chettibi, N.; Alanazi, A.M.; Dasalla, D.; Alzahrani, A. Hydrogen Production Methods Based on Solar and Wind Energy: A Review. Energies 2023, 16, 757. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, B. Recent advances in electrochemical hydrogen production from water assisted by alternative oxidation reactions. ChemElectroChem 2019, 6, 3214–3226. [Google Scholar] [CrossRef]
- López-Fernández, E.; Gómez Sacedón, C.; Gil-Rostra, J.; Yubero, F.; González-Elipe, A.R.; de Lucas-Consuegra, A. Recent Advances in Alkaline Exchange Membrane Water Electrolysis and Electrode Manufacturing. Molecules 2021, 26, 6326. [Google Scholar] [CrossRef]
- Yue, M.; Lambert, H.; Pahon, E.; Roche, R.; Jemei, S.; Hissel, D. Hydrogen energy systems: A critical review of technologies, applications, trends and challenges. Renew. Sustain. Energy Rev. 2021, 146, 111180. [Google Scholar] [CrossRef]
- Colli, A.N.; Girault, H.H.; Battistel, A. Non-Precious Electrodes for Practical Alkaline Water Electrolysis. Materials 2019, 12, 1336. [Google Scholar] [CrossRef]
- Hua, D.; Huang, J.; Fabbri, E.; Rafique, M.; Song, B. Development of anion exchange membrane water electrolysis and the associated challenges: A review. ChemElectroChem 2023, 10, e202200999. [Google Scholar] [CrossRef]
- Lima, A.; Torrubia, J.; Valero, A.; Valero, A. Non-Renewable and Renewable Exergy Costs of Water Electrolysis in Hydrogen Production. Energies 2025, 18, 1398. [Google Scholar] [CrossRef]
- Ngando Ebba, J.D.; Camara, M.B.; Doumbia, M.L.; Dakyo, B.; Song-Manguelle, J. Large-scale hydrogen production systems using marine renewable energies: State-of-the-art. Energies 2024, 17, 130. [Google Scholar] [CrossRef]
- Yodwong, B.; Guilbert, D.; Phattanasak, M.; Kaewmanee, W.; Hinaje, M.; Vitale, G. AC-DC converters for electrolyzer applications: State of the art and future challenges. Electronics 2020, 9, 912. [Google Scholar] [CrossRef]
- Şahin, M.E. An overview of different water electrolyzer types for hydrogen production. Energies 2024, 17, 4944. [Google Scholar] [CrossRef]
- Wei, X.; Sharma, S.; Waeber, A.; Margni, M.; Maréchal, F.; Van Herle, J. Comparative life cycle analysis of electrolyzer technologies for hydrogen production:Manufacturing and operations. Joule 2024, 8, 3347–3372. [Google Scholar] [CrossRef]
- Tofighi-Milani, M.; Fattaheian-Dehkordi, S.; Lehtonen, M. Electrolysers: A Review on Trends, Electrical Modeling, and Their Dynamic Responses. IEEE Access 2025, 13, 39870–39885. [Google Scholar] [CrossRef]
- Hossain, M.B.; Islam, M.R.; Muttaqi, K.; Sutanto, D.; Agalgaonkar, A. Dynamic electrical equivalent circuit modeling of the grid-scale proton exchange membrane electrolyzer for ancillary services. In Proceedings of the 2022 IEEE Industry Applications Society Annual Meeting (IAS), Detroit, MI, USA, 9–14 October 2022. [Google Scholar] [CrossRef]
- Koubaa, A.; Krichen, L.; Ouali, A. Design of Fuel Cell and Electrolyzer Emulators for Photovoltaic Applications. In Proceedings of the International Aegean Conference on Electrical Machines and Power Electronics and Electromotion, Joint Conference, Istanbul, Turkey, 8–10 September 2011; pp. 687–692. [Google Scholar] [CrossRef]
- Toure, I.; Camara, M.B.; Dakyo, B. Literature review based control strategies of electrolyzers systems. In Proceedings of the 2024 IEEE International Conference on Smart Grid (icSmartGrid), Setubal, Portugal, 27–29 May 2024; pp. 155–161. [Google Scholar] [CrossRef]
- Toure, I.; Payman, A.; Camara, M.-B.; Dakyo, B. Energy management in a renewable-based microgrid using a model predictive control method for electrical energy storage devices. Electronics 2024, 13, 4651. [Google Scholar] [CrossRef]
- Ruuskanen, V.; Koponen, J.; Kosonen, A.; Niemelä, M.; Ahola, J.; Tiainen, R. Hardware-in-loop emulator for water electrolysers. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 4133–4138. [Google Scholar] [CrossRef]
- João, M.A.; Araújo, R.E. Towards a digital model for emulation of an electrolyzer in real-time: An initial study. In Proceedings of the 2025 9th International Young Engineers Forum on Electrical and Computer Engineering (YEF-ECE), Caparica/Lisbon, Portugal, 4 July 2025; pp. 224–228. [Google Scholar] [CrossRef]
- Saidi, S.; Brahim, T.; Rejeb, O.; Jemni, A. Electrochemical and Thermodynamic Modeling of PEM Electrolyzer Performance: A Comparative Study with and Without Diffusion Overpotential. Int. J. Hydrogen Energy 2025, 50, 13243–13257. [Google Scholar] [CrossRef]
- Xu, B.; Ouyang, T.; Wang, Y.; Yang, Y.; Li, J.; Jiang, L.; Qin, C.; Ye, D.; Chen, R.; Zhu, X.; et al. Progresses on Two Phase Modeling of Proton Exchange Membrane Water Electrolyzer. Energy Rev. 2024, 3, 100073. [Google Scholar] [CrossRef]
- Vedrtnam, A.; Kalauni, K.; Pahwa, R. Water Electrolysis Technologies and Their Modeling Approaches: A Comprehensive Review. Eng 2025, 6, 81. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, Y.; Zhang, J.; Li, Y. Parametric Sensitivity of a PEM Electrolyzer Mathematical Model. Energies 2024, 18, 2217. [Google Scholar] [CrossRef]
- Yang, D.; Wang, H.; Li, Y.; Liu, M.; Han, J.; Huang, N. Simulation Research on the Performance of PEMEC with Single Channel Flow Field Established by Orthogonally Sinusoidal Function with Different Amplitudes and Angular Frequencies. Int. J. Energy Res. 2024, 2024, 5683908. [Google Scholar] [CrossRef]
- Tawalbeh, M.; Shomope, I.; Al Othman, A.; Alshraideh, H. Prediction of Hydrogen Production in PEM Water Electrolysis via Neural Networks. Int. J. Thermofluids 2024, 24, 100849. [Google Scholar] [CrossRef]
- Caparrós Mancera, J.J.; Segura Manzano, F.; Andújar, J.M.; Vivas, F.J.; Calderón, A.J. An Optimized Balance of Plant for a Medium-Size PEM Electrolyzer: Design, Control and Physical Implementation. Electronics 2020, 9, 871. [Google Scholar] [CrossRef]
- Huang, C.; Rueda Torres, J.L.; Zong, Y.; You, S.; Jin, X. A review of alkaline electrolyzer technology modeling and applications for decision-making optimization in energy systems. Renew. Sustain. Energy Rev. 2025, 224, 116005. [Google Scholar] [CrossRef]
- Bzovsky, I.; Kudriavtsev, S. Modeling of a PEM Electrolyzer Operating at Part Load Conditions for Dynamic Simulation in DWSIM. Period. Polytech. Chem. Eng. 2024, 68, 655–664. [Google Scholar] [CrossRef]
- Colbertaldo, P.; GómezAláez, S.L.; Campanari, S. Simulation of a Continuous Laboratory Scale PEM Electrolyzer During Water Electrolysis (CFD Modelling). Int. J. Hydrogen Energy 2025, 50, 203–217. [Google Scholar] [CrossRef]
- Situmbeko, D. Simulation of PEM Electrolyzer Power Management with Renewable Energy Integration. Energies 2024, 18, 208. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, G.; Li, T.; Yang, L. Dynamic Performance Prediction of PEM Electrolyzers Combining a Neural Network and Lumped-Parameter Model. J. Renew. Sustain. Energy 2025, 17, 239–254. [Google Scholar] [CrossRef]
- Asiaban, S.; Bozalakov, D.; Vandevelde, L. Development of a Dynamic Mathematical Model of PEM Electrolyser for Integration into Large Scale Power Systems. Energy Convers. Manag. X 2024, 23, 100610. [Google Scholar] [CrossRef]
- Reimann, A.; Kohlenbach, P.; Röntzsch, L. Development of a Novel Quasi 2D PEM Electrolyzer Model in Modelica. In Proceedings of the 15th International Modelica Conference, Aachen, Germany, 9–11 October 2023. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Y.; Bin, S.; Chen, Z.; Zhang, F.; Gong, S.; Xia, Y.; Duan, X. Effects of Key Design and Operating Parameters on the Performance of PEM Water Electrolysis for Hydrogen Production. Renew. Sustain. Energy Rev. 2025, 235, 121290. [Google Scholar] [CrossRef]
- Hüner, B. Mathematical Modeling of an Integrated Photovoltaic Assisted PEM Water Electrolyzer System for Hydrogen Production. Int. J. Hydrogen Energy 2024, 49, 594–608. [Google Scholar] [CrossRef]
- Aouali, F.Z.; Becherif, M.; Ramadan, H.S.; Emziane, M.; Khellaf, A.; Mohammedi, K. Analytical Modelling and Experimental Validation of Proton Exchange Membrane Electrolyser for Hydrogen Production. Int. J. Hydrogen Energy 2017, 42, 1366–1374. [Google Scholar] [CrossRef]
- Folgado, F.J.; González, I.; Calderón, A.J. PEM Electrolyzer Digital Replica Based on Internal Resistance Determination Applied to Hydrogen Energy Storage. J. Energy Storage 2024, 75, 109694. [Google Scholar] [CrossRef]
- Marefatjouikilevaee, H.; Auger, F.; Olivier, J.-C. Static and Dynamic Electrical Models of Proton Exchange Membrane Electrolysers: A Comprehensive Review. Energies 2023, 16, 6503. [Google Scholar] [CrossRef]
- Chang Domínguez, D.; Dam, A.P.; Richter, T.; Sundmacher, K.; Alia, S.M. Application of a Temporal Multiscale Method for Efficient Simulation of Degradation in PEM Water Electrolysis under Dynamic Operation. arXiv 2024, arXiv:2410.06863. [Google Scholar] [CrossRef]
- Schofield, L.; Paren, B.; Macdonald, R.; Shao Horn, Y.; Mallapragada, D. Dynamic Optimization of Proton Exchange Membrane Water Electrolyzers Considering Usage Based Degradation. arXiv 2024, arXiv:2405.06766. [Google Scholar] [CrossRef]
- Aouali, F.Z.; Becherif, M.; Tabanjat, A.; Emziane, M.; Mohammedi, K.; Krehi, S.; Khellaf, A. Modelling and experimental analysis of a PEM electrolyser powered by a solar photovoltaic panel. Energy Procedia 2014, 62, 714–722. [Google Scholar] [CrossRef]
- Agbli, K.S.; Péra, M.C.; Hissel, D.; Rallières, O.; Turpin, C.; Doumbia, I. Multiphysics simulation of a PEM electrolyser: Energetic Macroscopic Representation approach. Int. J. Hydrogen Energy 2011, 36, 1382–1398. [Google Scholar] [CrossRef]
- García-Valverde, R.; Espinosa, N.; Urbina, A. Simple PEM water electrolyser model and experimental validation. Int. J. Hydrogen Energy 2012, 37, 1927–1938. [Google Scholar] [CrossRef]
- Folgado, F.J.; González, I.; Calderón, A.J. Simulation platform for the assessment of PEM electrolyzer models oriented to implement digital Replicas. Energy Convers. Manag. 2022, 267, 115917. [Google Scholar] [CrossRef]
- Yigit, T.; Selamet, O.F. Mathematical modeling and dynamic Simulink simulation of high-pressure PEM electrolyzer system. Int. J. Hydrogen Energy 2016, 41, 13901–13914. [Google Scholar] [CrossRef]
- Benmehel, A.; Chabab, S.; Do Nascimento Rocha, A.L.; Chepy, M.; Kousksou, T. PEM water electrolyzer modeling: Issues and reflections. Energy Convers. Manag. X 2024, 24, 100738. [Google Scholar] [CrossRef]
- Pfennig, M.; Schiffer, B.; Clees, T. Thermodynamical and Electrochemical Model of a PEM Electrolyzer Plant in the Megawatt Range with a Literature Analysis of the Fitting Parameters. Int. J. Hydrogen Energy 2025, 104, 567–583. [Google Scholar] [CrossRef]
- Espinosa-López, M.; Darras, C.; Poggi, P.; Glises, R.; Baucour, P.; Rakotondrainibe, A.; Besse, S.; Serre-Combe, P. Modelling and Experimental Validation of a 46 kW PEM High Pressure Water Electrolyzer. Renewable Energy 2018, 119, 160–173. [Google Scholar] [CrossRef]
- Görgün, H. Dynamic modelling of a proton exchange membrane (PEM) electrolyzer. Int. J. Hydrogen Energy 2006, 31, 29–38. [Google Scholar] [CrossRef]
- Vinuelas Ferrando, J. Modelling and Simulation of Hydrogen Electrolyzers for Power System Applications. Ph.D. Dissertation, KTH, School of Electrical Engineering and Computer Science, Stockholm, Sweden, 2023. Available online: https://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-344444 (accessed on 8 September 2025).
- Ruiz Diaz, D.F.; Wang, Y. Component-level modeling of solid oxide water electrolysis cell for clean hydrogen production. J. Clean. Prod. 2024, 443, 140940. [Google Scholar] [CrossRef]
- Gambou, F.; Guilbert, D.; Zasadzinski, M.; Rafaralahy, H. A Comprehensive Survey of Alkaline Electrolyzer Modeling: Electrical Domain and Specific Electrolyte Conductivity. Energies 2022, 15, 3452. [Google Scholar] [CrossRef]
- Ursúa, A.; Sanchis, P. Static–dynamic modelling of the electrical behaviour of a commercial advanced alkaline water electrolyser. Int. J. Hydrogen Energy 2012, 37, 18598–18614. [Google Scholar] [CrossRef]
- Hossain, M.A.; Islam, M.R.; Hossain, M.A.; Hossain, M.J. Control strategy review for hydrogen–renewable energy power system. J. Energy Storage 2023, 72, 108170. [Google Scholar] [CrossRef]
- Ghazavi, M. System Dynamics of Low-Carbon Grids: Fundamentals, Challenges, and Mitigation Solutions. Ph.D. Thesis, University of Melbourne, Melbourne, Australia, 2022. [Google Scholar]
- Agredano-Torres, M.; Zhang, M.; Söder, L.; Xu, Q. Decentralized Dynamic Power Sharing Control for Frequency Regulation Using Hybrid Hydrogen Electrolyzer Systems. IEEE Trans. Sustain. Energy 2024, 15, 1847–1858. [Google Scholar] [CrossRef]
- Guilbert, D.; Vitale, G. Variable Parameters Model of a PEM Electrolyzer Based Model Reference Adaptive System Approach. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; IEEE: Madrid, Spain, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Ngando Ebba, J.D.; Camara, M.B.; Doumbia, M.L.; Dakyo, B.; Song-Manguelle, J. Industrial-scale renewable hydrogen production system: A comprehensive review of power electronics converters and electrical energy storage. Electronics 2025, 14, 3471. [Google Scholar] [CrossRef]
- Ruuskanen, V.; Koponen, J.; Kosonen, A.; Hehemann, M.; Keller, R.; Niemelä, M.; Ahola, J. Power quality estimation of water electrolyzers based on current and voltage measurements. J. Power Sources 2020, 450, 227603. [Google Scholar] [CrossRef]
- Ursúa, A.; Sanchis, P.; Marroyo, L. Electric Conditioning and Efficiency of Hydrogen Production Systems and Their Integration with Renewable Energies. In Renewable Hydrogen Technologies: Production, Purification, Storage, Applications and Safety; Elsevier: Amsterdam, The Netherlands, 2013; pp. 333–360. [Google Scholar] [CrossRef]
- Ursúa, A.; Marroyo, L.; Gubía, E.; Gandía, L.M.; Diéguez, P.M.; Sanchis, P. Influence of the power supply on the energy efficiency of an alkaline water electrolyser. Int. J. Hydrogen Energy 2009, 34, 3221–3233. [Google Scholar] [CrossRef]
- Parache, F.; Schneider, H.; Turpin, C.; Richet, N.; Debellemanière, O.; Bru, É.; Thieu, A.T.; Bertail, C.; Marot, C. Impact of power converter current ripple on the degradation of PEM electrolyzer performances. Membranes 2022, 12, 109. [Google Scholar] [CrossRef]
- Yuan, T.; Li, H.; Wang, J.; Jia, D. Research on the influence of ripple voltage on the performance of a proton exchange membrane electrolyzer. Energies 2023, 16, 6912. [Google Scholar] [CrossRef]
- Buitendach, H.P.C.; Gouws, R.; Martinson, C.A.; Minnaar, C.; Bessarabov, D. Effect of a ripple current on the efficiency of a PEM electrolyser. Results Eng. 2021, 10, 100216. [Google Scholar] [CrossRef]
- Guilbert, D.; Collura, S.M.; Scipioni, A. DC/DC converter topologies for electrolyzers: State-of-the-art and remaining key issues. Int. J. Hydrogen Energy 2017, 42, 23966–23985. [Google Scholar] [CrossRef]
- Şahin, M.E.; Okumuş, H.İ.; Aydemir, M.T. Implementation of an electrolysis system with DC/DC synchronous buck converter. Int. J. Hydrogen Energy 2014, 39, 6802–6812. [Google Scholar] [CrossRef]
- Aguirre, O.A.; Ocampo-Martinez, C.; Camacho, O. Control strategies for alkaline water electrolyzers: A survey. Int. J. Hydrogen Energy 2024, 86, 1195–1213. [Google Scholar] [CrossRef]
- Cozzolino, R.; Bella, G. A review of electrolyzer-based systems providing grid ancillary services: Current status, market, challenges and future directions. Front. Energy Res. 2024, 12, 1358333. [Google Scholar] [CrossRef]
- Jain, R.; Nagasawa, K.; Veda, S.; Sprik, S. Grid ancillary services using electrolyzer-based power-to-gas systems with increasing renewable penetration. E-Prime Electr. Eng. Electron. Energy 2023, 6, 100308. [Google Scholar] [CrossRef]
- Alshehri, F.; García Suárez, V.; Rueda Torres, J.L.; Perilla, A.; van der Meijden, M.A.M.M. Modelling and evaluation of PEM hydrogen technologies for frequency ancillary services in future multi-energy sustainable power systems. Heliyon 2019, 5, e01396. [Google Scholar] [CrossRef]
- Mohanpurkar, M.; Luo, Y.; Terlip, D.; Dias, F.; Harrison, K.; Eichman, J.; Hovsapian, R.; Kurtz, J. Electrolyzers Enhancing Flexibility in Electric Grids. Energies 2017, 10, 1836. [Google Scholar] [CrossRef]
- Suárez, V.G.; Rueda, J.L.; Tuinema, B.; Perilla Guerra, A.; van der Meijden, M. Integration of Power-to-Gas Conversion into Dutch Electrical Ancillary Services Markets. In Proceedings of the 12th Conference on Energy Economics and Technology, Dresden, Germany, 27 April 2018; pp. 1–7. Available online: https://tu-dresden.de/bu/wirtschaft/ee2/tagungen/enerday (accessed on 20 November 2024).
- Bartels, J.; Varela, C.; Wassermann, T.; Medjroubi, W.; Zondervan, E. Integration of water electrolysis facilities in power grids: A case study in northern Germany. Energy Convers. Manag. X 2022, 14, 100209. [Google Scholar] [CrossRef]
- Toghyani, S.; Fakhradini, S.; Afshari, E.; Baniasadi, E.; Abdollahzadeh Jamalabadi, M.Y.; Safdari Shadloo, M. Optimization of operating parameters of a polymer exchange membrane electrolyzer. Int. J. Hydrogen Energy 2019, 44, 6403–6414. [Google Scholar] [CrossRef]
- Han, B.; Steen, S.M.; Mo, J.; Zhang, F.-Y. Electrochemical performance modeling of a proton exchange membrane electrolyzer cell for hydrogen energy. Int. J. Hydrogen Energy 2015, 40, 7006–7016. [Google Scholar] [CrossRef]
- Henao, C.; Agbossou, K.; Hammoudi, M.; Dubé, Y.; Cardenas, A. Simulation tool based on a physics model and an electrical analogy for an alkaline electrolyser. J. Power Sources 2014, 250, 58–67. [Google Scholar] [CrossRef]
- Kim, H.; Park, M.; Lee, K.S. One-dimensional dynamic modeling of a high-pressure water electrolysis system for hydrogen production. Int. J. Hydrogen Energy 2013, 38, 2596–2609. [Google Scholar] [CrossRef]
- Zhang, H.; Su, S.; Lin, G.; Chen, J. Efficiency calculation and configuration design of a PEM electrolyzer system for hydrogen production. Int. J. Electrochem. Sci. 2012, 7, 4143–4157. [Google Scholar] [CrossRef]
- Hammoudi, M.; Henao, C.; Agbossou, K.; Dubé, Y.; Doumbia, M.L. New multi-physics approach for modelling and design of alkaline electrolyzers. Int. J. Hydrogen Energy 2012, 37, 13895–13913. [Google Scholar] [CrossRef]
- Marangio, F.; Santarelli, M.; Calì, M. Theoretical model and experimental analysis of a high pressure PEM water electrolyser for hydrogen production. Int. J. Hydrogen Energy 2009, 34, 1143–1158. [Google Scholar] [CrossRef]
- Lee, B.; Park, K.; Kim, H.-M. Dynamic simulation of PEM water electrolysis and comparison with experiments. Int. J. Electrochem. Sci. 2013, 8, 235–248. [Google Scholar] [CrossRef]
- Diéguez, P.M.; Ursúa, A.; Sanchis, P.; Sopena, C.; Guelbenzu, E.; Gandía, L.M. Thermal performance of a commercial alkaline water electrolyzer: Experimental study and mathematical modeling. Int. J. Hydrogen Energy 2008, 33, 7338–7354. [Google Scholar] [CrossRef]
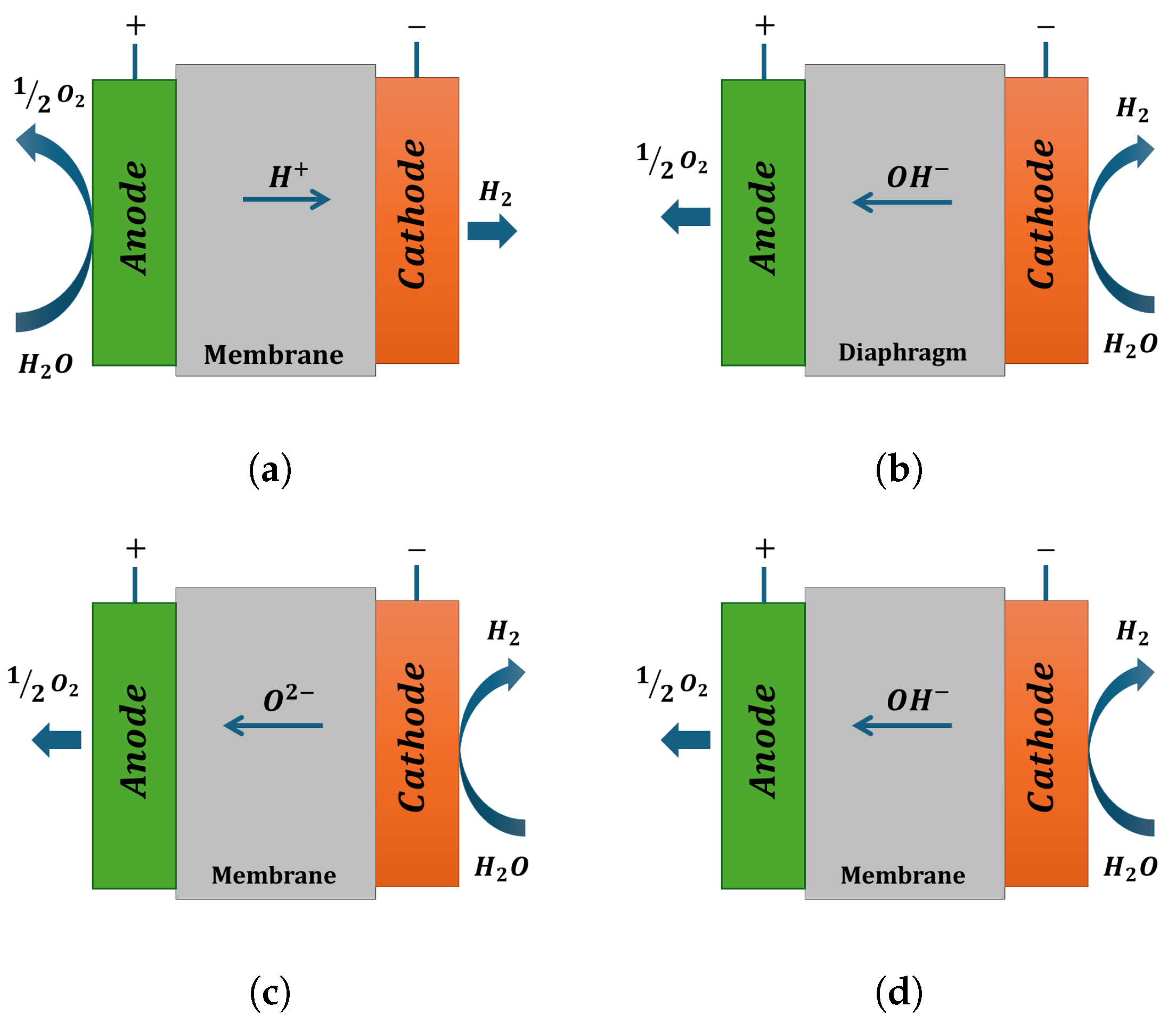
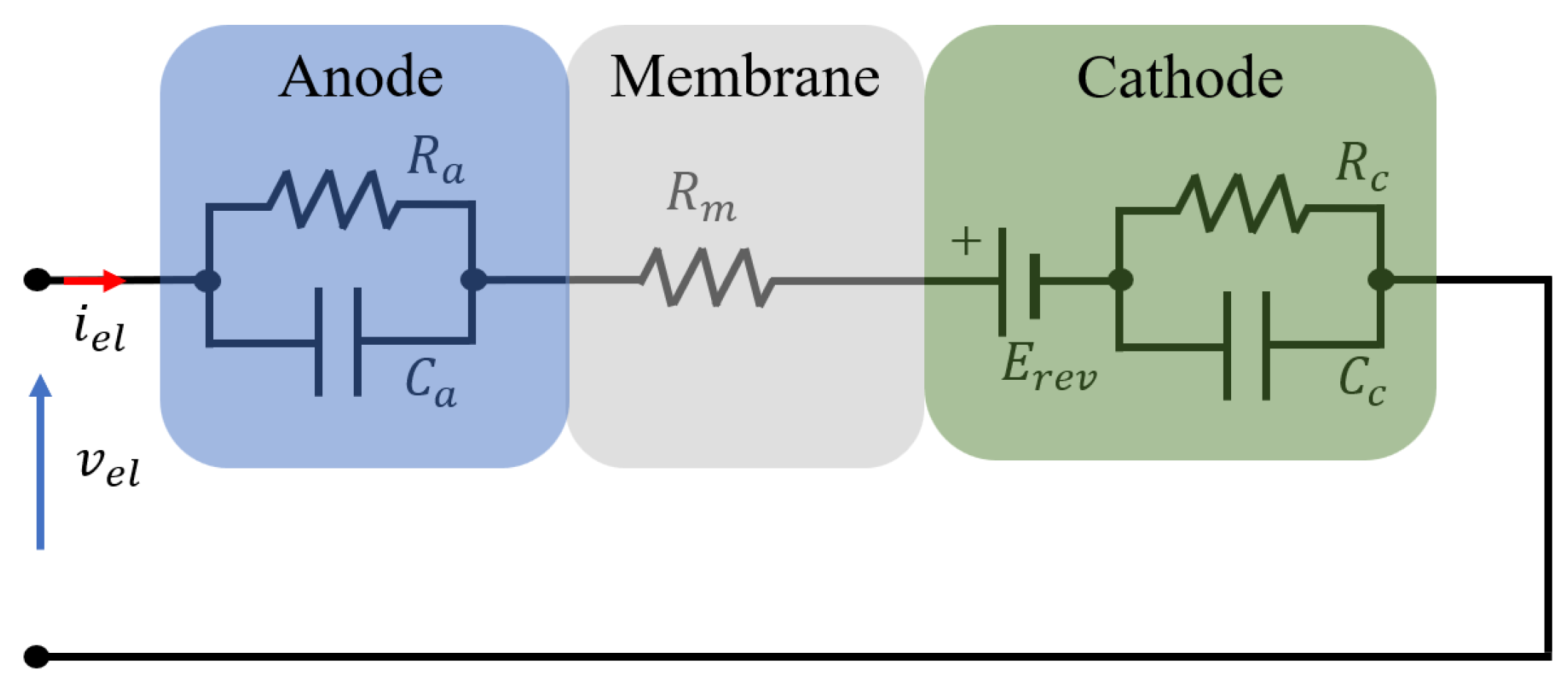
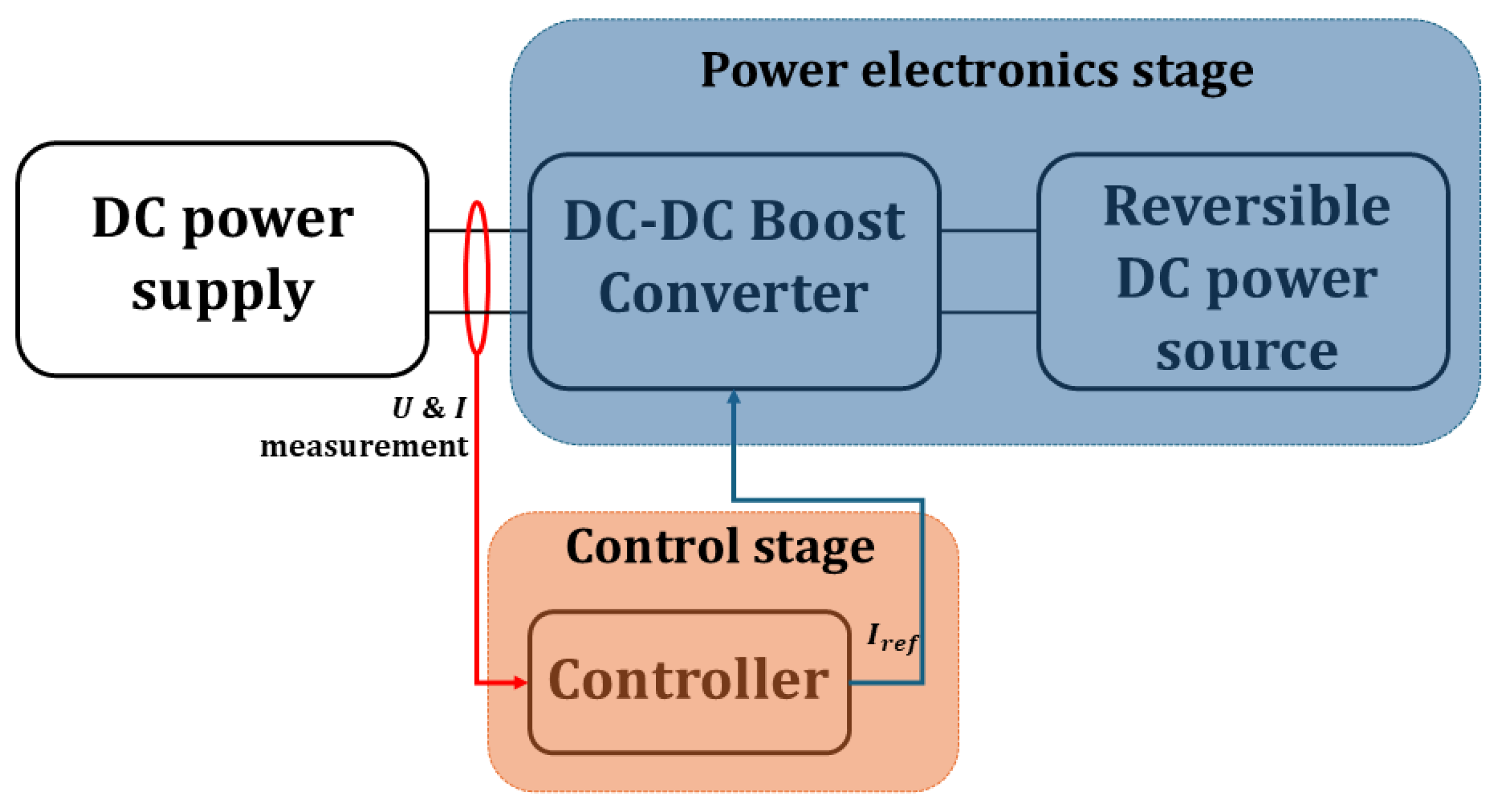

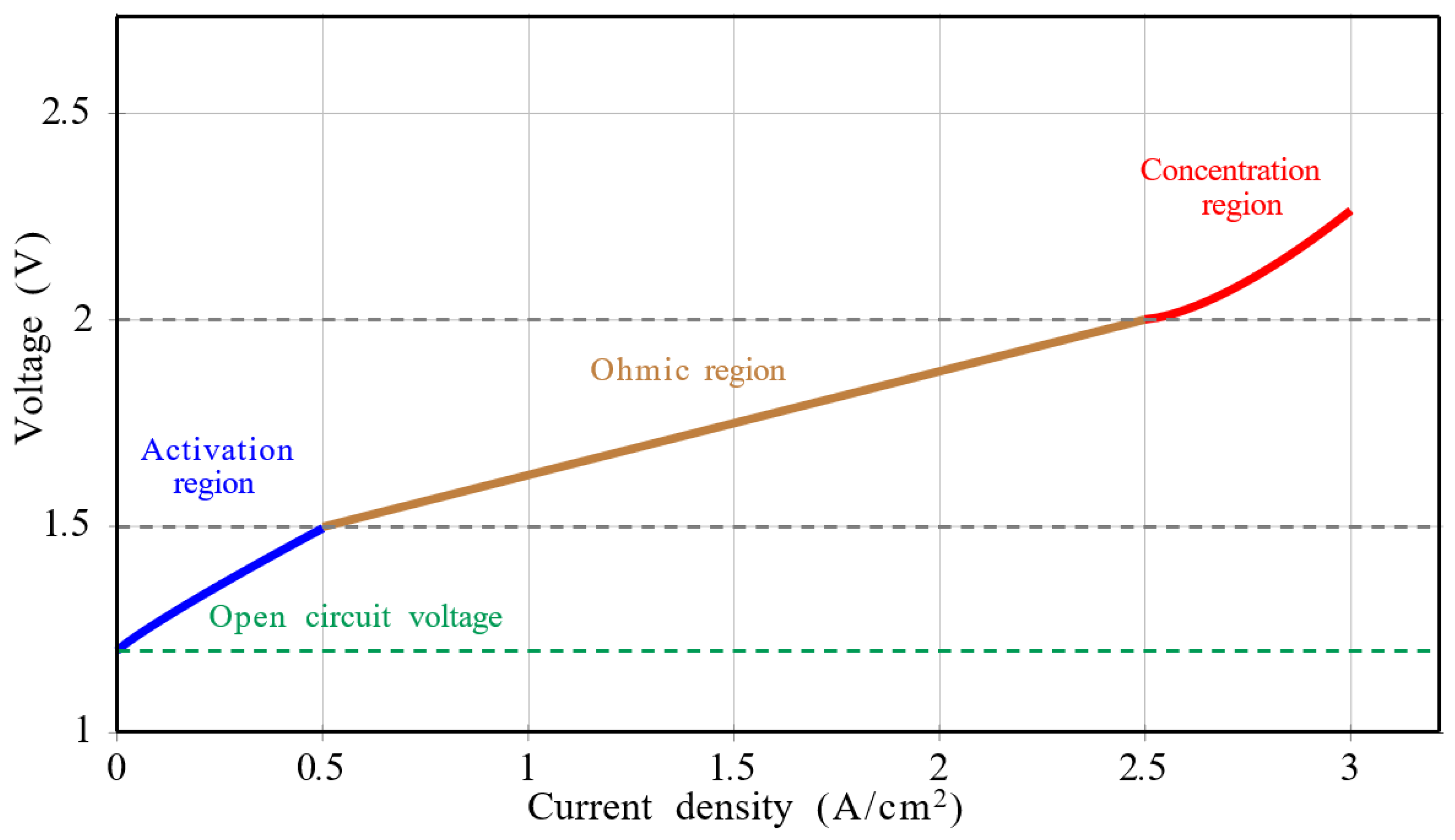
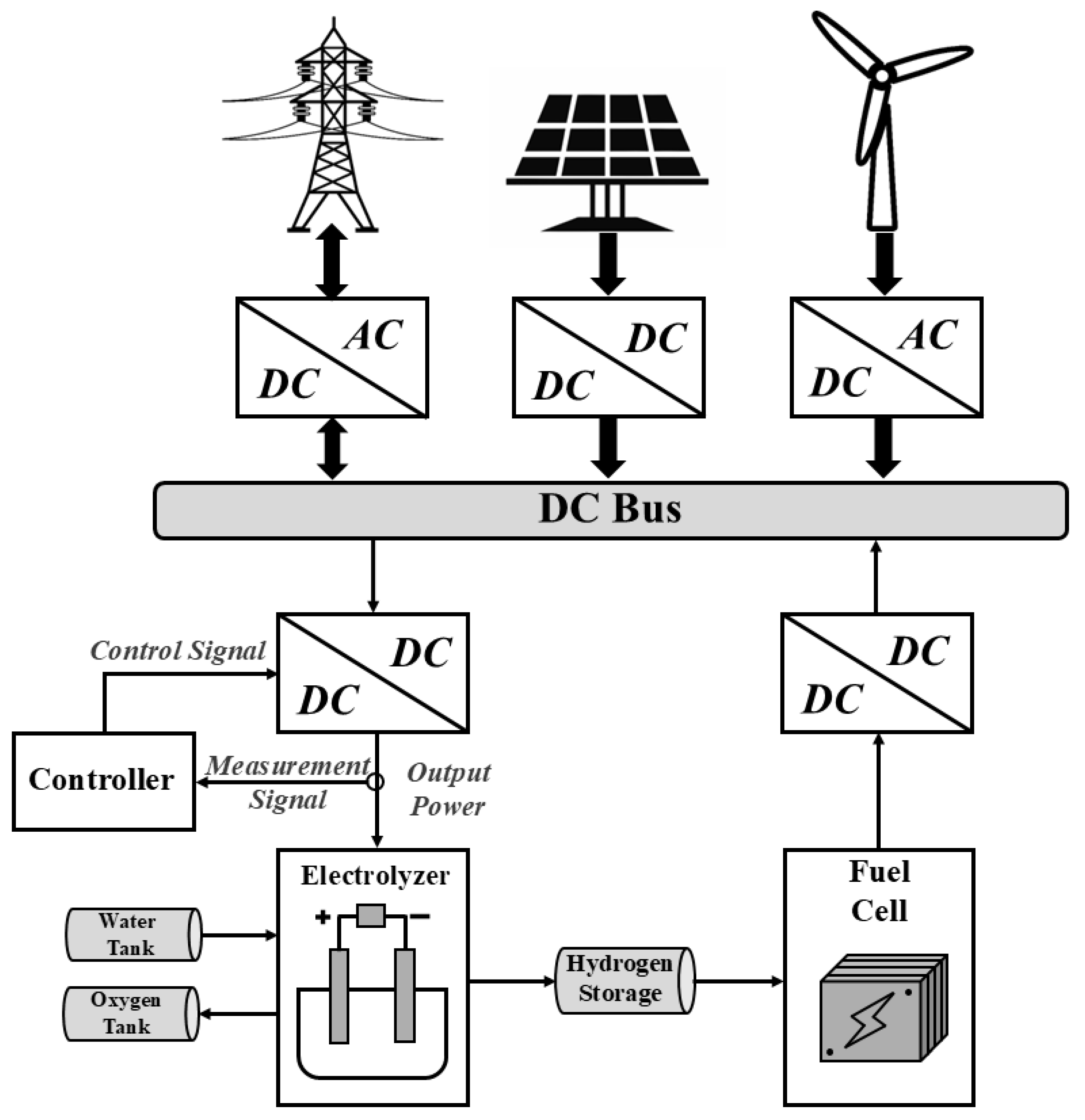
| Anode Reaction | Cathode Reaction | |
|---|---|---|
| PEM | ||
| AWE | ||
| SOEC | ||
| AEM |
| Classical Used Controller | Advantages | Limitations |
|---|---|---|
| PI | - Simple and well-known, easy to design and implement - Reliable for current regulation - Reduces steady-state error and ensures accurate tracking | - Limited robustness to system uncertainties - Performance may degrade under nonlinear dynamics or parameter variations - Poor tuning may cause oscillations or steady-state error - Slower dynamic response than advanced controllers |
| ST-SMC | - High robustness against uncertainties and disturbances - Ensures overall stability - Provides precise current tracking through the inductor | - Control discontinuity may induce chattering - Requires careful design of sliding surface and control law - Increased complexity compared to linear controllers |
| Study No. | Ref. | EEC | Boost Conv. | PHIL | Exp.* | Grid Int.* | Software | Accuracy Metric |
|---|---|---|---|---|---|---|---|---|
| PEM Studies | ||||||||
| 1 | [20] | ✓ | ✗ | ✗ | ✓ | ✗ | MATLAB/Simulink | Max error 8.75% (transient), ≤10% (steady-state) |
| 2 | [21] | ✓ | ✗ | ✗ | ✓ | ✗ | MATLAB/Simulink | Max error |
| 3 | [56] | ✓ | ✓ | ✓ | ✓ | ✓ | MATLAB/Simulink, dSPACE | Dynamic error < 4% & >15% in static models |
| 4 | [58,59,94] | ✗ | ✓ | ✓ | ✓ | ✓ | LabVIEW, CompactRIO | <5% deviation in V–I curves |
| 5 | [95] | ✓ | ✗ | ✗ | ✗ | ✗ | MATLAB/Simulink | Voltage error ≈ 0.1 V, Current error ≈ 1–2 A |
| AWE Studies | ||||||||
| 1 | [57] | ✗ | ✓ | ✓ | ✓ | ✓ | MATLAB/Simulink, DSP | Good tracking of power and hydrogen flow references |
| 2 | [61] | ✓ | ✗ | ✓ | ✓ | ✗ | PLECS | Close track of V–I behavior |
| RSOEC Studies | ||||||||
| 1 | [60] | ✓ | ✗ | ✗ | ✓ | ✗ | MATLAB/Simulink, dSPACE | <5% deviation in static V–I curves |
| Not specified | ||||||||
| – | [91] | ✗ | ✓ | ✗ | ✗ | ✓ | – | – |
| Study No. | Ref | Application | Advantages | Limitation |
|---|---|---|---|---|
| PEM Studies | ||||
| 1 | [20] | - Testing new DC-DC converters and controls. - Modeling dynamic behavior with supercapacitors. | - Uses low-cost, common components and a linear circuit to reproduce the physical model. - Avoids parasitic switching interference. | - Voltage errors during current decrease. - Trade-off needed to reduce transient errors. |
| 2 | [21] | - Emulation of PEMEL dynamic behavior. - Testing power electronics converters. - Tests EL design and performance. | - Validated with experimental data. - Incorporation of double-layer capacitance effects. - Efficient analysis of losses, efficiency, and hydrogen production. | - Limited to a small current range. - Assumes constant parameters. |
| 3 | [56] | - Performance evaluation in smart grids. - Develops a DC-DC boost converter-based hardware emulator that replicates PEMEL dynamic behavior. | - New EEC developed using the PSO algorithm. - Cost-effective testing. - Seamless integration with smart grid emulators. | - Parameter accuracy might not reflect EL characteristics. - Model comparison needed for further validation. - No smart grid testing to assess performance yet. |
| 4 | [58] | - Emulates industrial-scale EL in smart grid setups. - Analyzes EL power supply electronics. | - Higher power capability than previous systems. - Enables testing under real industrial load conditions. - Robust and cost-effective using commercial converters. | - Inability to fully exploit available PV power. - Hydrogen production is lower due to limited current changes in the stack. |
| 5 | [95] | - Development of digital real-time models focuses on error analysis from discretization methods. | - Provides systematic comparison of discretization methods. | - Only static model and no experimental validation. |
| AWE Studies | ||||
| 1 | [57] | - Hydrogen production process. - Integration with wind energy systems. - Real-time control testing. | - Characterizes relations among physical quantities. - Regulates power and hydrogen flow. | - Constant temperature assumption. - Pressure control fails with fast power changes. - Limited power slope reduces flexibility. |
| 2 | [61] | - Testing of rectifiers for electrolysis in the context of RES. - Scalable platform to test control strategies and rectifier designs. | - Enables testing under various grid/rectifier conditions. - High dynamic performance. | - Oscillations occur when the current drops to zero. - Experimental validation only at a small scale (5 kW). |
| RSOEC Studies | ||||
| 1 | [60] | - Rapid prototyping of power electronic converters for cyclic operation. | - Low-cost, accessible, simple, suitable for rapid prototyping. | - Component tolerances cause minor deviations. |
| Not specified | ||||
| - | [91] | - Design of emulators for fuel cells and EL used for PV application. | - Show hydrogen and oxygen production/consumption. | - Simulation results may not fully reflect real-world behavior. |
| EL Simulations | EL Emulators | |
|---|---|---|
| Cell/Stack Level | ||
| Electrical model | [52,112,119,123,125,150,151,152,153,154,155] | [20,21,57,58,59,60,61,91,94,95] |
| Thermal model | [52,112,117,119,123,150,153,155] | – |
| Fluidics model | [118,156] | [57] |
| Mass transfer model | [123,153,157] | – |
| System level | ||
| BoP considerations | [39,118,154,158] | [57] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Assal, H.; Camara, M.-B.; Guilbert, D. Advances in Electrolyzer Emulators: A Comprehensive Review. Electronics 2025, 14, 4576. https://doi.org/10.3390/electronics14234576
El Assal H, Camara M-B, Guilbert D. Advances in Electrolyzer Emulators: A Comprehensive Review. Electronics. 2025; 14(23):4576. https://doi.org/10.3390/electronics14234576
Chicago/Turabian StyleEl Assal, Hoda, Mamadou-Baïlo Camara, and Damien Guilbert. 2025. "Advances in Electrolyzer Emulators: A Comprehensive Review" Electronics 14, no. 23: 4576. https://doi.org/10.3390/electronics14234576
APA StyleEl Assal, H., Camara, M.-B., & Guilbert, D. (2025). Advances in Electrolyzer Emulators: A Comprehensive Review. Electronics, 14(23), 4576. https://doi.org/10.3390/electronics14234576