Comprehensively Improve Fireworks Algorithm and Its Application in Photovoltaic MPPT Control

Abstract

Maximum power point tracking (MPPT) control is a key technology for increasing the power generation of photovoltaic arrays under varying light and temperature conditions. Traditional perturb and observe methods and incremental conductance methods can achieve good tracking performance for single-peak characteristics. However, under complex conditions such as partial shading or dust accumulation, the power-voltage curve of a photovoltaic array exhibits multi-peak characteristics. In such cases, traditional methods may get trapped in local optima, preventing the photovoltaic array from operating at the maximum power point. Swarm intelligence algorithms perform well when solving multi-extremum functions and can be used for MPPT control of photovoltaic arrays in complex environments. Therefore, this paper focuses on the fireworks algorithm (FWA). To improve the computational speed and global optimization capability of the FWA, the characteristics of each stage of the algorithm are analyzed, a comprehensive improved fireworks algorithm (CIFWA) is proposed, and it is applied to the MPPT control of photovoltaic systems. The improved algorithm introduces an adaptive resource allocation and selection strategy with community inheritance features and applies tent chaos mapping to the algorithm’s explosion behavior. Multiple sets of test functions are used to compare the performance metrics of the optimization algorithm, demonstrating improvements in computational speed and global search capability of CIFWA. Finally, a control strategy for the MPPT of photovoltaic arrays based on CIFWA is presented, and a simulation experimental platform is built to analyze and verify the control performance.

1. Introduction

Maximum power point tracking is one of the key technologies to determine the power generation efficiency of photovoltaic systems, and the P-U curves of photovoltaic cells often show multimodal characteristics due to the influence of the external environment and the performance of photovoltaic modules [1,2]. MPPT control methods based on sampling data, such as the perturbation observation method and conductivity increment method, often fail due to falling into the local optimal value [3]. The swarm intelligence algorithm provides a new idea for solving the extreme value problem of nonlinear functions and has been widely used in photovoltaic MPPT control [4,5,6]. However, swarm intelligence algorithms generally have inherent drawbacks such as parameter sensitivity, difficulty in balancing convergence and diversity, and inconsistent mechanisms for multi-objective extension. No single algorithm can consistently outperform others in all problems, but optimizing an algorithm for specific engineering applications can achieve relatively good performance [7]. Therefore, discussing the optimization and application of the FWA in response to the needs and characteristics of photovoltaic array MPPT control has practical engineering value.

The fireworks algorithm is a new swarm intelligence algorithm that simulates the process of fireworks explosion [8,9], which mainly uses the randomness and divergence of the spark position during the fireworks explosion to achieve the purpose of area search. Explosive search behavior is a unique feature of FWA, which has strong exploration ability and high optimization accuracy, but it also has problems such as being easy to fall into local optimization and low efficiency. At present, the methods of improving the fireworks algorithm are mainly divided into three aspects. The first is the adaptive adjustment of the algorithm parameters, such as in [10], an enhanced fireworks algorithm with adaptive parameters is proposed, which is applied to the intelligent energy management system of plug-in hybrid electric vehicles. In [11], a fireworks algorithm with dynamically variable parameters was proposed, and the optimization efficiency of the algorithm was improved. The second is to adjust the inheritance strategy of the algorithm, such as in [12], the inheritance mechanism of each generation of fireworks is adjusted to enable the exchange of information between different generations of fireworks. In [13], a gyroscope fireworks algorithm was proposed, which adopted the frameworks of multi-stage and multi-search strategies to enhance the local search ability of the algorithm. In [14], a fireworks algorithm based on elite selection and optimal particle guidance strategy is proposed, which is conducive to transmitting more optimal information to the next generation of particles. The third is to combine the fireworks algorithm with other intelligent algorithms, such as in [15], the fireworks algorithm is combined with the gray wolf algorithm to enhance the global search ability of the algorithm. In [16], the fireworks algorithm and ant colony algorithm are combined and applied to the vehicle driving path planning problem, and good results are obtained. To summarize, how to comprehensively improve the optimization speed and ergodability is still the main problem faced by the fireworks algorithm.

Based on the research of existing fireworks algorithms, this paper proposes a comprehensive and improved fireworks algorithm. In the process of algorithm resource allocation, the strategy of adaptive radius and adaptive spark number is adopted to optimize the resource allocation of the algorithm. Introducing the tent chaos map into the algorithm’s explosive behavior is applied to individuals that still do not produce better solutions after multiple updates, avoiding local optima and improving the algorithm’s global search capability. In the process of algorithmic offspring selection, a community inheritance strategy is introduced. Based on the optimization status of the community, the explosion radius and the number of sparks are adjusted, making resource allocation more aligned with the actual situation of individuals, which can reduce the waste of computational resources and improve the algorithm’s computation speed. The calculation results of standard test functions demonstrate the performance improvement of CIFWA. Applying CIFWA to photovoltaic maximum power point tracking control, simulations and experiments show that CIFWA can find the global optimum faster and more accurately than traditional intelligent algorithms, effectively improving photovoltaic power generation efficiency.

This paper proposes detailed optimization strategies to improve the computational speed and global search capability of the fireworks algorithm. At the same time, to enhance the power generation efficiency of photovoltaic systems, the optimized algorithm is applied to the maximum power point tracking control of photovoltaics, followed by simulation and experimental validation.

The overall structure of this paper is as follows: the first part is the introduction, which presents the problem to be addressed and the current state of research; the second part introduces and validates the proposed algorithm; the third part covers the application and validation of the algorithm in maximum power point tracking control for photovoltaics; the fourth part discusses the shortcomings of this paper and provides an outlook; the fifth part is the conclusion.

2. Optimization Algorithm and Validation

2.1. Original Fireworks Algorithm

The FWA is mainly composed of three parts [17]: resource allocation, explosive behavior, and selection strategy.

Suppose the form of the optimization problem to be solved is shown in Equation (1):

$$\min f(\mathit{x})\in R,\mathit{x}\in \Omega$$

(1)

where x is the unknown to be solved, R is the constraint, and Ω is the feasible domain of the solution.

The algorithm first initializes a certain number of fireworks randomly within the feasible domain of the solution and calculates the fitness of each firework. The resource allocation operator determines the explosion radius and number of sparks of fireworks one by one. The radius of the explosion is calculated by Equation (2), and the number of sparks is calculated by Equation (3):

$$r_i=A\times {\displaystyle \frac{f(x_i)-f_{\min }+\epsilon }{{\displaystyle \sum _{n=1}^N(f(x_n)-f_{\min })+\epsilon }}}$$

(2)

$$S_i=B\times {\displaystyle \frac{f_{\max }-f(x_i)+\epsilon }{{\displaystyle \sum _{n=1}^N(f_{\max }-f(x_n))+\epsilon }}}$$

(3)

where x_i is the position of the ith firework, r_i is the explosion radius, S_i is the number of sparks, N is the number of fireworks, A is the control parameter used to adjust the explosion radius, B is the control parameter used to adjust the number of explosion sparks, f_min is the minimum value of the current population fitness, and f_max is the maximum value of the current population fitness. ε is the mechanical minimum amount and is used to avoid division by zero operation.

The expression for the detonation behavior is shown below:

$$x_{jk}=x_{ik}+r_i·rand(-1,1)$$

(4)

where k is the dimension, x_j is a new firework obtained through an explosion, and rand(−1,1) is a random number between −1 and 1.

In order to increase the diversity of the population, the Gaussian mutation operator is introduced into the calculation of the location of some sparks; that is, the Gaussian mutation spark is generated. The expression is as follows:

$$x_{jk}=x_{ik}·norm(1,1)$$

(5)

where norm(1,1) is a Gaussian random number with both a mean and a standard deviation of 1.

Amounts beyond the feasible domain are mapped to the new location as follows:

$$x_{jk}=a+\left|x_{ik}\right|\mathrm{mod}(b-a)$$

(6)

where mod(·) is modular.

In the selection strategy, the individuals with the best fitness in the population will be kept as the next generation of fireworks, and the selection of the remaining N-1 fireworks will be selected among all individuals using roulette. The expression is

$$p(x_i)={\displaystyle \frac{{\displaystyle \sum _{x_j\in D}‖x_i-x_j‖}}{{\displaystyle \sum _{x_j\in D}{x}_j}}}$$

(7)

where p(x_i) is the probability that the candidate x_i will be selected, and D is the set of candidates.

2.2. Comprehensive Improved Fireworks Algorithm

In this section, the characteristics of the three parts of the FWA are analyzed and the corresponding improvement methods are given.

In the resource allocation process, fireworks with good fitness will produce more sparks in a smaller radius, and fireworks with poor fitness will produce fewer sparks in a larger radius. When the change trend of the function to be found in the optimal region is fast, the adaptability of fireworks close to the best advantage may also be poor, so it is easy to miss the best advantage. On the other hand, fireworks that fall into the local optimal have better adaptability, and the algorithm is easy to fall into the local optimum. In this paper, an adaptive resource allocation strategy is proposed in which the explosion radius is calculated by Equation (8) and the number of sparks is calculated by Equation (9):

$$r_i=r/4^{m_i}$$

(8)

$$S_i=S+rand(m_{i}S/M)$$

(9)

where m_i is the adaptive coefficient of the ith firework, and its initial value is 0. S is the initial number of sparks of fireworks; M is a constant; and rand(·) is a rounding function based on the principle of rounding.

The calculation rule of m_i is as follows:

If the ith firework is the optimal firework, its explosion produces better offspring, then m_i is subtracted by 1; otherwise, self-add 1 when m_i is less than 0 so that m_i is equal to 0. The m_i of the optimal fireworks is not limited by the upper limit M, but there is an upper limit on the number of sparks, and if the number of sparks exceeds the upper limit, the upper limit is taken.

If the ith firework is not the optimal firework, its explosion produces better offspring, then the m_i does not change; otherwise, self-add 1.When the m_i exceeds the upper limit M, it can be considered to fall into the local optimum, and the tent chaos map is activated to make it jump out of the local optimal region, and the m_i is set to zero.

The results of the tent chaotic map are evenly distributed, which is used to change the position of the fireworks caught in the local optimum. Firstly, the value of the arbitrary dimension of the local optimal fireworks is transformed into the chaotic space according to Equation (10), then iterated according to Equation (11), and finally, the position of the fireworks is obtained by Equation (12):

$$C_k^1=(x_{ik}-a)/(b-a)$$

(10)

$$C_k^{l+1}=\left\{\begin{array}{c}2\times C_k^l\\ 2\times (1-C_k^l)\end{array}\begin{array}{c},0\le C_k^l\le 0.5\\ ,0.5<C_k^l\le 1\end{array}\right.$$

(11)

$$x_{ik}=a+C_k^{l+1}\times (b-a)$$

(12)

where l is the number of iterations, and C is the number of chaos.

In the explosion behavior, it can be seen from the characteristics of Gaussian distribution that the probability of Gaussian sparks near the original fireworks position is large, so its ergodic performance is poor. In order to save algorithm resources, the improved algorithm only produces ordinary sparks.

In the selection strategy, only the optimal individual can continuously converge, which leads to a low optimization speed of the algorithm. In order to improve the search efficiency, this paper applies the community inheritance strategy to the FWA selection strategy. The spark generated by a firework and the firework itself are used as a community, and the individuals with the best fitness in the community are selected as the next generation of fireworks. In this way, each community has a good convergence performance and is simple to calculate.

The CIFWA optimization process is carried out in the following steps:

(1)

Initialize the algorithm parameters, randomly generate the initial fireworks in the feasible domain, and calculate their fitness.

(2)

The explosion radius and number of sparks of fireworks are determined according to Equations (8) and (9), and the number of sparks of the optimal fireworks exceeds the upper limit.

(3)

Performing an explosive act produces a normal spark, and the spark fitness is calculated. Determine whether the maximum number of iterations is reached, and if so, the optimal individual is the output, and the algorithm is terminated; otherwise, go to the next step.

(4)

The optimal individuals in the community are selected as the offspring of fireworks, and the adaptive coefficient is updated.

(5)

For fireworks whose adaptive coefficient exceeds the upper limit and is not globally optimal, the chaotic map is used to change its position, and its adaptive coefficient is set to zero.

(6)

Update the fireworks position and adaptive coefficient and continue with steps (2)~(6).

2.3. Validation of the CIFWA

To verify the effectiveness of the proposed optimization strategy, this section conducts comparative experiments among PSO, FWA, and the proposed CIFWA on four representative benchmark functions (Sphere, Rastrigin, Ackley, and Griewank) [18]. The comprehensive performance is evaluated in terms of convergence accuracy, stability, convergence speed and success rate. Statistical results are summarized in

Table 1. Test results of each algorithm on different benchmark functions.

Function	Algorithm	Best Value	Average Value	Standard Deviation (Std)	Convergence Generation	Running Time (s)	Success Rate (%)
Sphere	PSO	1.2 × 10−4	3.5 × 10−3	2.1 × 10−3	850	0.72	85
	FWA	3.8 × 10−5	1.2 × 10−3	1.1 × 10−3	720	0.91	90
	CIFWA	1.1 × 10−6	2.3 × 10−4	2.5 × 10−4	420	0.83	100
Rastrigin	PSO	2.15	6.78	3.12	1200	0.78	60
	FWA	1.34	4.21	2.05	980	0.95	70
	CIFWA	0.18	1.05	0.47	580	0.89	98
Ackley	PSO	1.89 × 10−2	4.32 × 10−2	1.56 × 10−2	1350	0.81	55
	FWA	1.12 × 10−2	2.87 × 10−2	1.02 × 10−2	1100	0.98	68
	CIFWA	1.5 × 10−3	6.1 × 10−3	2.3 × 10−3	640	0.92	96
Griewank	PSO	1.34 × 10−2	3.76 × 10−2	1.89 × 10−2	1400	0.80	58
	FWA	8.7 × 10−3	2.43 × 10−2	1.21 × 10−2	1150	0.97	72
	CIFWA	9.8 × 10−4	5.7 × 10−3	2.1 × 10−3	660	0.90	97

, where the bold entries indicate the best value for each metric.

As shown in Table 1, CIFWA outperforms the other two algorithms in key metrics such as convergence accuracy, stability, convergence speed, and success rate. Its best and average values are one to two orders of magnitude higher than those of PSO and FWA, the standard deviation is reduced to 14–25% of the comparators, the required number of generations is decreased by 46–52%, and the global success rate remains between 96% and 100%. However, the runtime required by CIFWA is longer compared to PSO, which reflects the fact that no algorithm can be superior in all aspects. CIFWA performs more complex computations than PSO, sacrificing computational speed in exchange for accuracy. In the MPPT control of photovoltaics, since the rate of environmental change is much slower than the algorithm’s running time, control accuracy is more important relative to the control speed. The proposed optimization method is more practical in actual photovoltaic power generation control engineering.

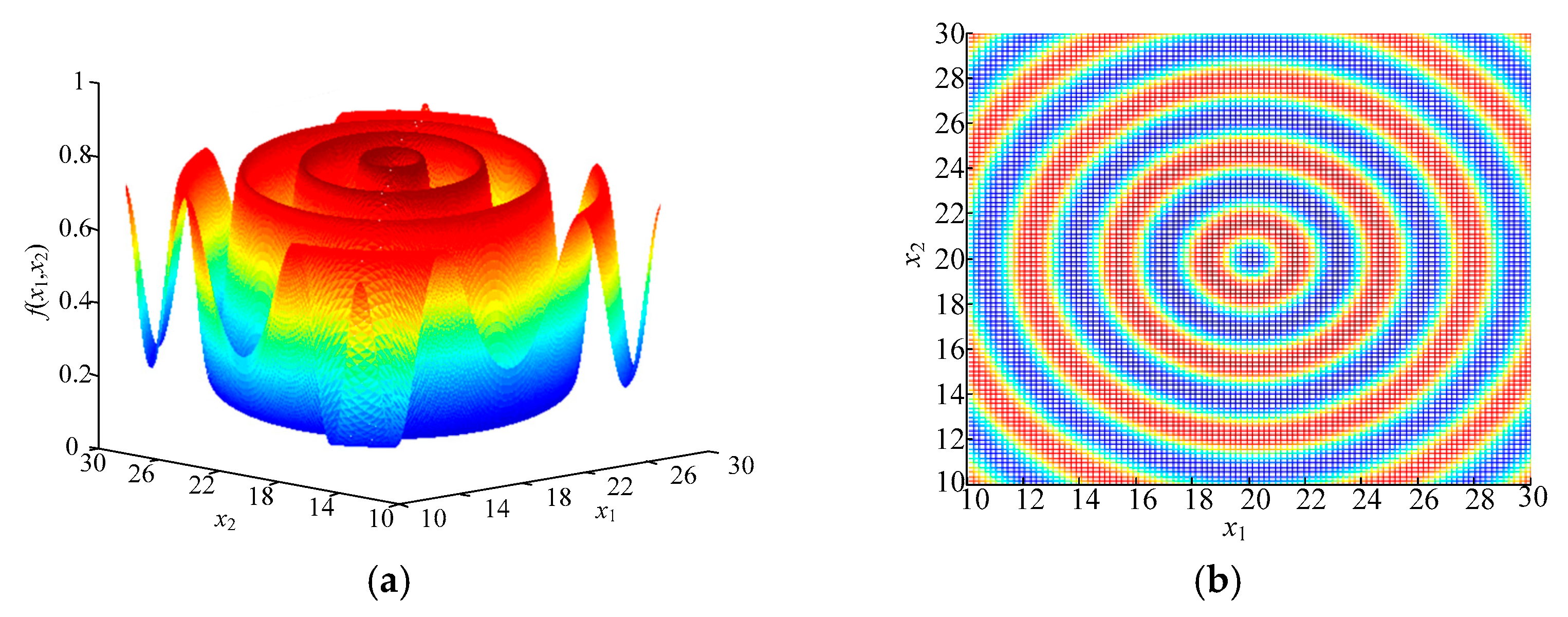
To intuitively demonstrate the improvement in global search capability brought by the proposed modifications, the Schaffer function is employed to test the algorithms before and after optimization, and the entire execution trace is visualized on the coordinate plane. Record the coordinates of each individual during the algorithm’s search process and mark them all on the coordinate axis. This way, the areas explored by the algorithm during the search process can be clearly displayed.

The Schaffer function is a two-dimensional complex function with an infinite number of minima, and the function has strong oscillation, which makes it difficult to find the global optimal value, which is suitable for testing the global search performance of the algorithm [19,20]. The expression is

$$f(x_1,x_2)=0.5+{\displaystyle \frac{{(\sin \sqrt{x_1^2+x_2^2})}^2-0.5}{{(1+0.001(x_1^2+x_2^2))}^2}}$$

(13)

In the test, the position offset is 20, the search range is 10 to 30, and the function achieves a minimum value of 0 at the point (20, 20). A three-dimensional plot and a top view of the function are shown in Figure 1.

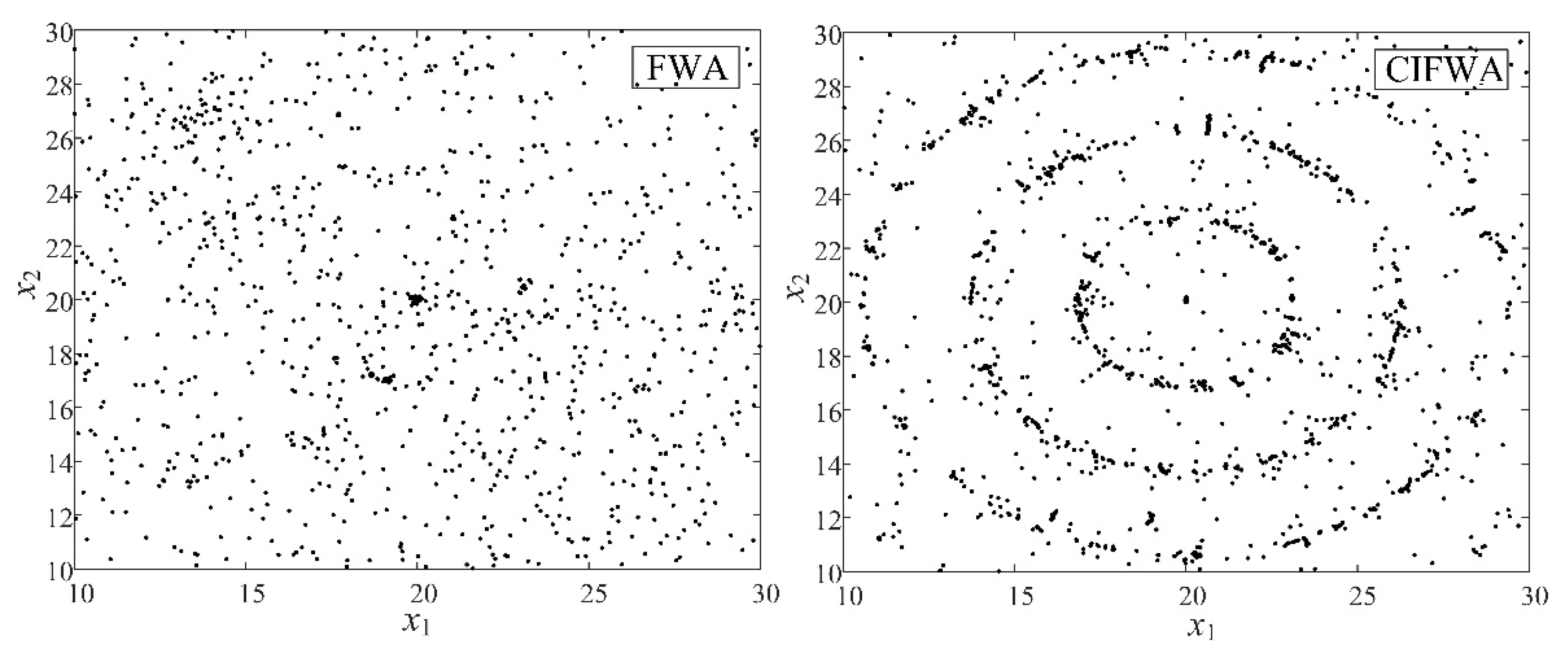
Set the number of fireworks in the algorithm to 10, set A = 25, B = 40 in FWA, set the upper limit of sparks to 20, and set the lower limit to two. In CIFWA, r = 5, S = 2, and M = 3 are set, and the maximum number of sparks for the optimal fireworks is eight. Figure 2 shows the distribution of fireworks of each generation with 100 iterations of the four algorithms.

As can be seen from the above figure, the progeny selection strategy of FWA makes the distribution of fireworks positions scattered, but only the optimal fireworks have convergence ability, and the other fireworks belong to random searches and contribute little to the algorithm. All fireworks in CIFWA have good convergence ability, the community inheritance strategy can judge whether the fireworks fall into the local optimal in time, and the tent chaotic map makes the fireworks jump out of the local optimal and has good distribution characteristics, so CIFWA can reach the extreme points of the function with high efficiency.

3. Application of CIFWA in Photovoltaic MPPT

3.1. MPPT Control Strategy Based on CIFWA

When the PV array is in the condition of local shading, its P-U curve shows multimodal characteristics. The PV MPPT control system is actually faced with the problem of multi-pole nonlinear function optimization, so CIFWA can be used to realize the multi-peak maximum power point tracking of PV arrays. The position of the fireworks is defined as the output voltage, and the fitness value is the output power value of the photovoltaic array.

The algorithm sets up two starting modes: natural start and power mutation start. Through the analysis of the light intensity from 6:00 to 18:00 a day, it is found that the change in light intensity within 2 min does not exceed 40 W/m², and the corresponding power change is 0.01 W. Therefore, the algorithm is set to automatically restart every 2 min. When the PV array is suddenly obscured by clouds or other complex conditions, the mutation of its output power is generally greater than 0.1 W, so the condition for the algorithm to mutate and restart is that the power mutation is greater than 0.1 W.

3.2. Simulation Analysis

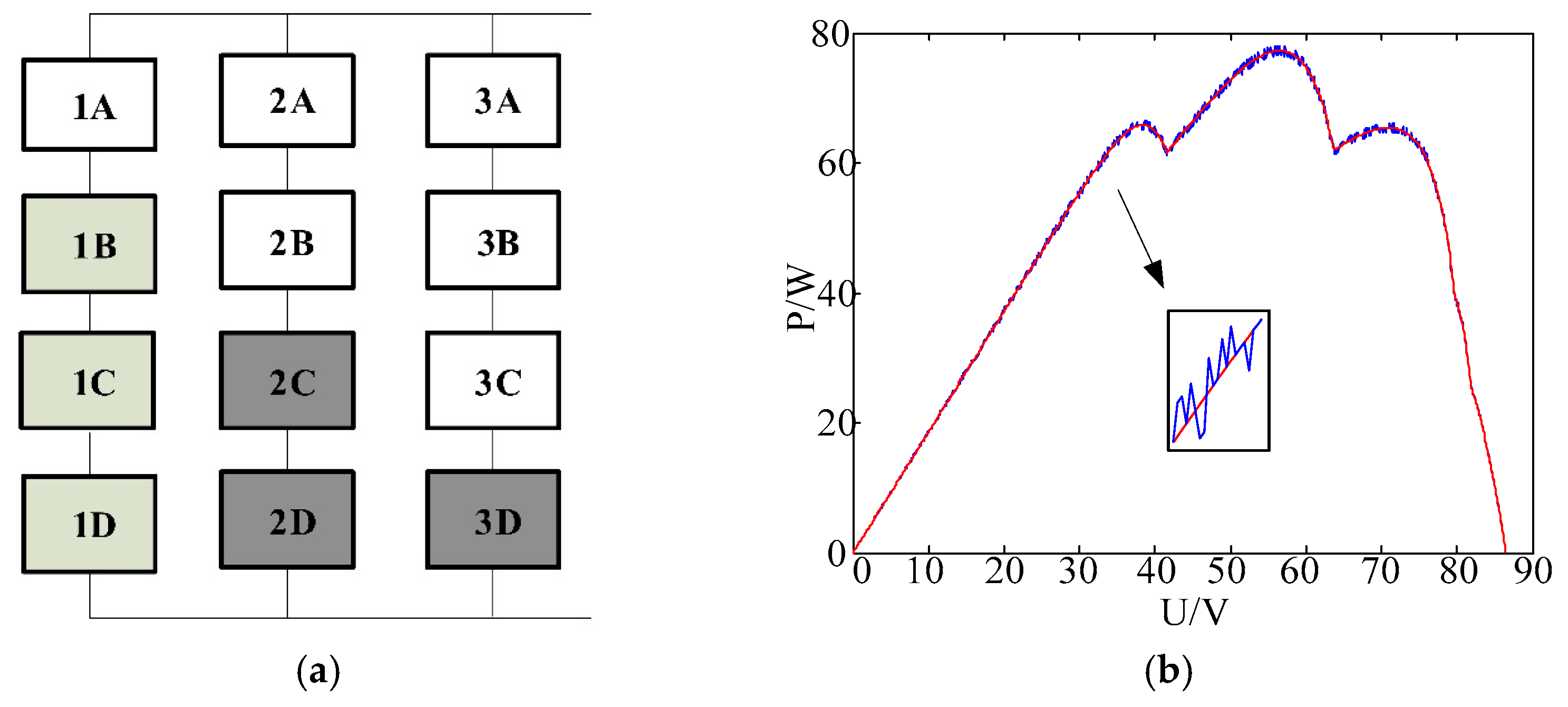
In the simulation, 12 photovoltaic cells of the same type were connected in series and parallel to form a 3 × 4 photovoltaic array panel, as shown in Figure 3a. The standard parameters of the battery are U_oc = 21.6 V, I_sc = 0.62 A, maximum power point voltage U_mpp = 17.5 V, maximum power point current I_mpp = 0.57 A, and maximum output power P_m = 10 W ± 3%. Among them, the light intensity of 1B, 1C, and 1D is 400 W/m²; 2C, 2D, and 3D light intensity: 200 W/m²; and the rest of the components are based on a reference light intensity of 1000 W/m². The reference temperature is 25 °C, and the measurement noise and range points are taken as ±1% and ±3% of the sampling current, respectively. The recursive least squares method is used to perform real-time filtering preprocessing of the P-U characteristic curve under local shading, as shown in Figure 3b.

The control algorithm is a commonly used particle swarm optimization (PSO) algorithm. The total number of PSO populations is four, the inertia weight factor is 0.5, the acceleration factor is two, the number of CIFWA fireworks is two, r = 20, S = 2, M = 3, the upper limit of the number of sparks of the optimal fireworks is six, and the number of algorithm iterations is 20.

Table 2. Comparison of algorithm optimization results.

Algorithm	Avg/W	Variance
PSO	77.2933	0.0446
CIFWA	77.3658	1.5463 × 10−4

shows the average and variance of the maximum power obtained by each of the two algorithms after 50 runs each.

Table 2 shows that the CIFWA-controlled PV system can generate 3.132 kW·h more electricity per 12 h than the PSO-controlled PV system.

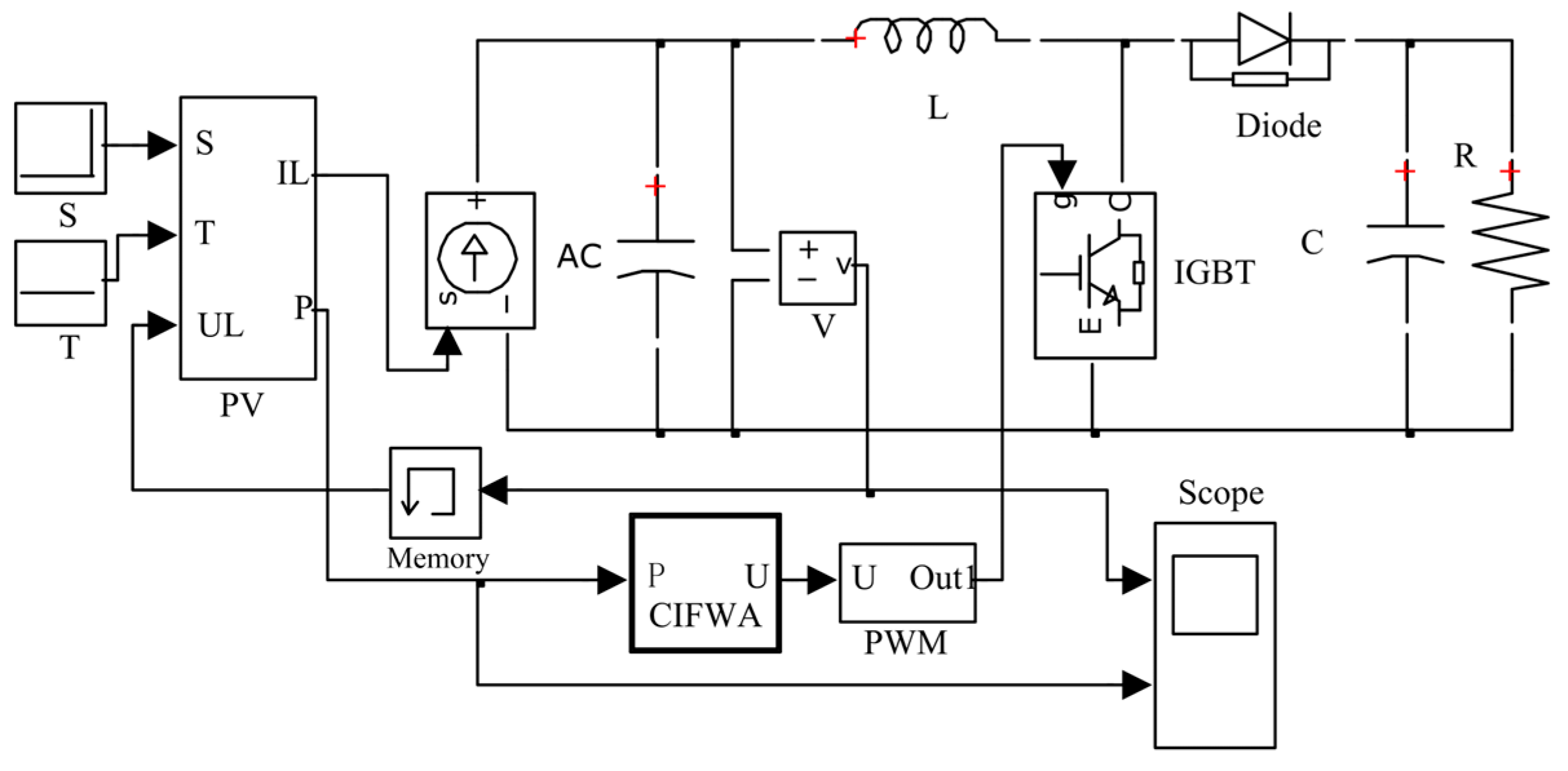
In order to test the dynamic performance of the algorithm in the case of system mutation, a dynamic simulation platform was built based on MATLAB/SIMULINK(R2016b), and its module structure is shown in Figure 4.

The simulation parameters are set as follows: the boost inductor L is 5 mH, the input filter capacitor C₁ is 100 μF, the capacitor C₂ is 1000 μF, and the resistance R is 200 Ω. The illumination intensity of the 2C, 2D, and 3D modules is set to change from 300 W/m² to 600 W/m² at 0.2 s to simulate shadow fading, and the auto-start performance of the algorithm in the case of sudden environmental changes is verified. The output power of the system under PSO and CIFWA control is shown in Figure 5.

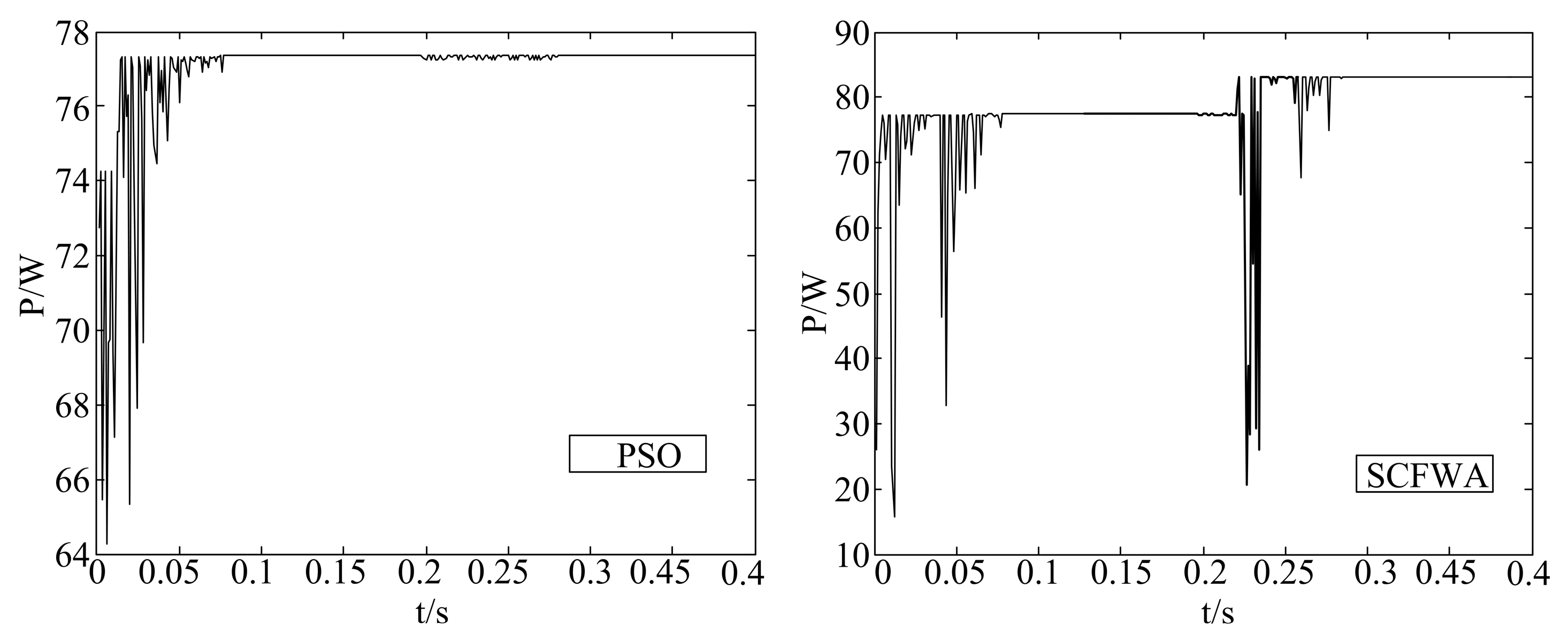
As can be seen from the above figure, both algorithms can self-start when the environment changes suddenly, but only CIFWA can control the system to work at the new maximum power point. The reason is that the PSO algorithm is a tracking search, and there is a phenomenon of the aggregation of individuals, and the more concentrated the individual location, the worse the search ability of the algorithm. The search performance of CIFWA is not affected by the initial position of the individual, so it is more suitable for the PV MPPT control system than the traditional swarm intelligence algorithm that uses tracking search behavior.

3.3. Experimental Analysis

In this paper, a low-power experimental platform for the MPPT control system based on the K60 microcontroller is built, as shown in Figure 6. The main control chip is an MK60DN-512VLL10 microcontroller, and the boost circuit structure is shown in Figure 4. Among L = 4 mH, C₂ = 470 μF, f = 30 kHz, the load is a high-power potentiometer.

In order to simulate the complex environment, some of the photovoltaic modules were gradually covered from 13:00 to simulate the situation of cloud blocking of the photovoltaic array. The algorithm uses the same parameters as in the simulation, except that the population position is set to be initialized at the time of PSO self-starting.

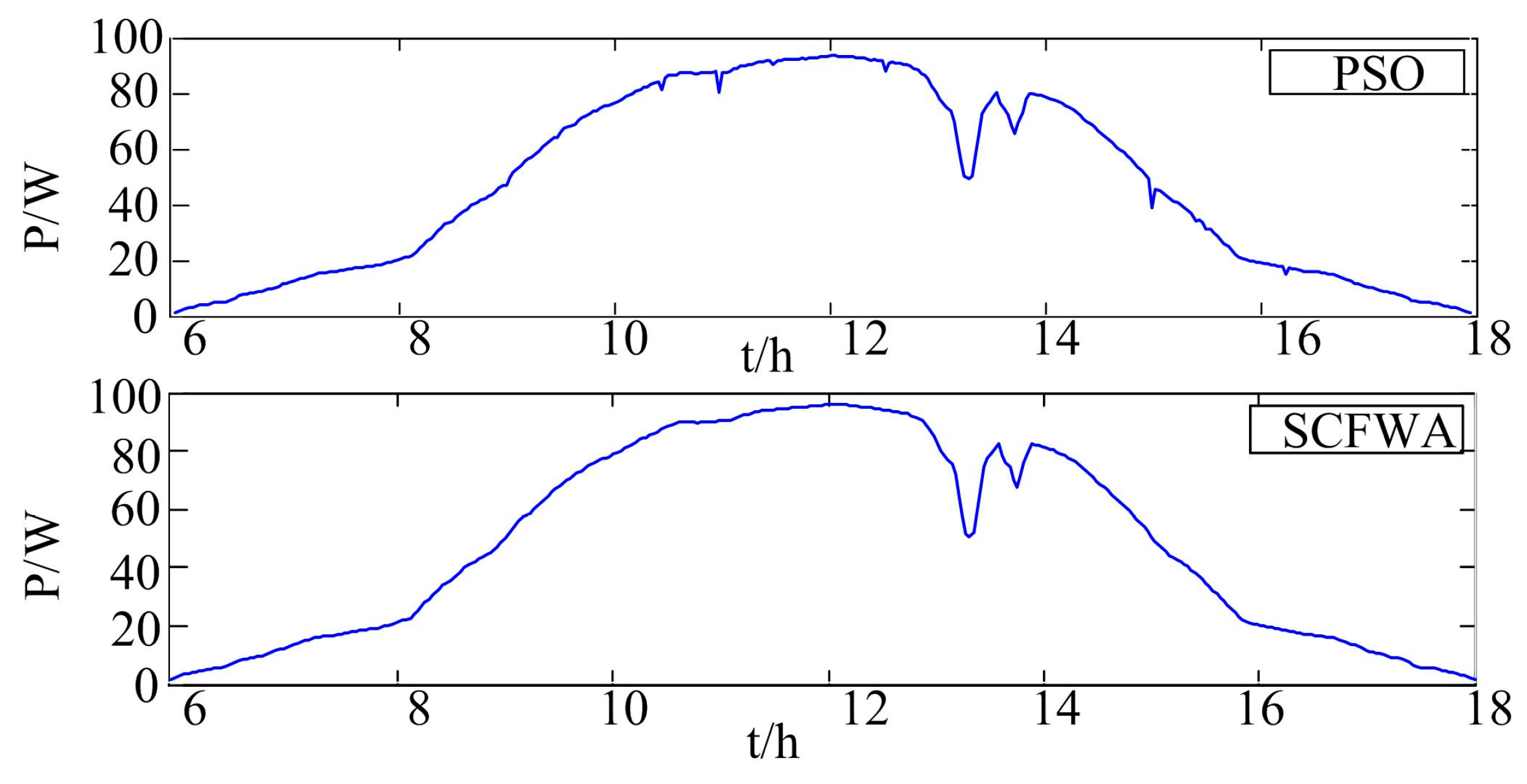
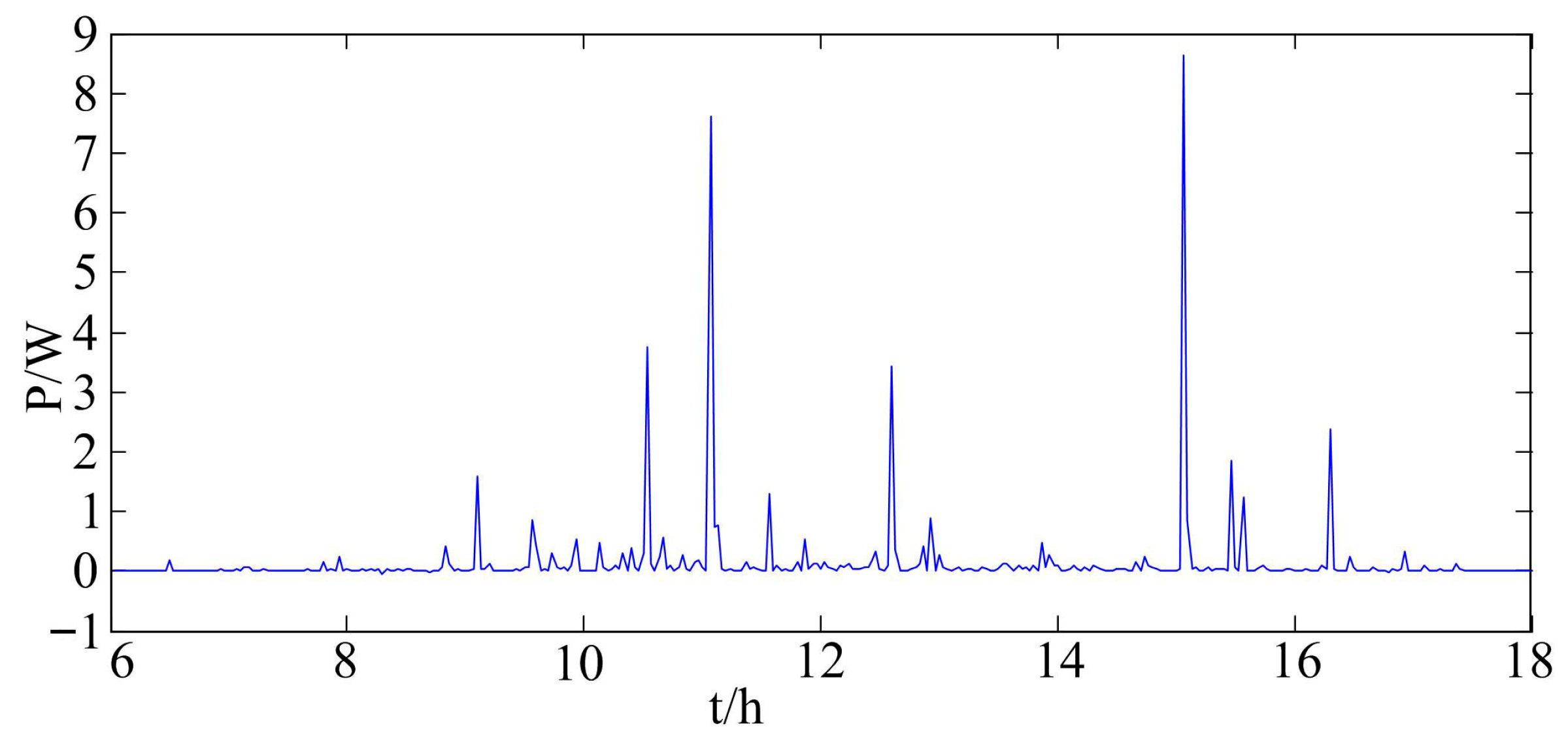
Figure 7 shows the maximum power obtained by PSO and CIFWA control from 6:00 to 18:00 in a PV array from 6:00 to 18:00 in a day. Figure 8 shows the power increment of CIFWA compared to PSO.

As can be seen from the results in the above figure, CIFWA can more accurately control the photovoltaic system to work at the maximum power point in practical application, indicating that CIFWA can improve the power generation efficiency of the photovoltaic system.

4. Discussion

This paper has made preliminary progress in improving the fireworks algorithm and its application in photovoltaic MPPT control. Both simulation and experimental results reflect that the proposed method enhances global search capabilities and can increase power generation in photovoltaic MPPT control.

However, the actual effectiveness of this algorithm still requires verification with more practical usage data. For example, when the photovoltaic power-voltage characteristics exhibit more complex nonlinear multi-peak behavior, can the algorithm still be effective? It is also necessary to consider whether additional range constraints should be added as inputs to the algorithm to prevent rapid power drops when attempting parameters beyond the local range. Moreover, an analysis of the scalability and applicability of the control algorithm in higher power applications is needed. Further research is also required to compare it with other new algorithms.

Future work will focus on these issues, systematically supplement more experimental data, refine the algorithm mechanism and performance evaluation, and further explore adaptability under different photovoltaic conditions in order to better advance the practical application of the results presented in this paper.

5. Conclusions

This paper proposes the CIFWA by optimizing various search components of the original FWA and applies it to the photovoltaic MPPT control system. Multiple function tests indicate that the combination of the adaptive resource allocation strategy, population inheritance strategy, and tent chaotic mapping strategy can improve the FWA’s convergence speed and global search capability. In the application phase, a CIFWA-based photovoltaic MPPT control strategy was formulated, and its effectiveness was demonstrated through simulations and experiments. Compared with traditional intelligent control algorithms, the CIFWA can more effectively improve the accuracy of maximum power tracking in photovoltaic systems under complex environments, thereby increasing power generation.