DeepRoute: A Fast FPGA Routing Algorithm Using Graph Embedding for Node Filtering

Abstract

In this paper, we present DeepRoute, an improved FPGA routing algorithm that introduces graph embedding into FPGA routing to accelerate this most time-consuming stage of the FPGA design flow. By adapting the random walk method with simple yet effective modifications, high-quality graph embeddings are generated. These embeddings enable the filtering of unpromising nodes, significantly reducing the router’s search space. To further enhance DeepRoute’s performance, two engineering enhancements are implemented, timing criticality constraints and detailed search regions. Experimental results show that DeepRoute achieves routing speedups of 51.31% over Verilog-to-Routing 8 (VTR8), rising to 54.25% for larger circuits, while maintaining timing performance and acceptable wirelength changes.

1. Introduction

Field-Programmable Gate Arrays (FPGAs), with their high flexibility and parallel processing capabilities [1,2,3,4], have become pivotal components across a wide range of modern applications, including data centers, artificial intelligence, industrial control systems, neural network accelerators, and the Internet of Things [5,6,7,8,9]. However, as FPGA designs continue to grow in scale and complexity to meet increasingly demanding computational needs [10], the runtime of corresponding Computer-Aided Design (CAD) tools has risen significantly [11,12,13]. This prolonged design cycle poses substantial challenges for FPGA users, such as extended development time and reduced productivity. Within the CAD flow, the routing process is identified as a time-consuming stage, accounting for the majority of the total tool runtime [12,14]. Therefore, accelerating the routing process is critically important for improving the overall efficiency of FPGA design.

The primary objective of the routing stage in FPGA CAD is to establish electrical connections between designated pins by efficiently utilizing available routing resources, while simultaneously addressing two critical constraints: mitigating routing congestion to ensure legal solution and optimizing key performance metrics, like timing performance. Formally, the FPGA Routing Problem is defined on a directed routing resource graph (RRG) $G=(V,E)$, where V denotes the set of programmable connection points and E represents the available routing edges. Let the set of nets be $\mathcal{N}=\{1,2,\dots ,N\}$, where each net $i\in \mathcal{N}$ is defined as $ne{t}_i=(s_i,T_i)$, with $s_i\in V$ being the source node and $T_i\subset V$ the set of one or more sink nodes. The routing task is to find, for each $ne{t}_i$, a subgraph $A_i=(V_i,E_i)$ of G, where $V_i\subseteq V$ and $E_i\subseteq E$, such that there exists a connected path from $s_i$ to every $t\in T_i$, subject to the capacity constraint ${\sum }_i{x}_e\left(i\right)\le c_e$, where $x_e\left(i\right)\in \{0,1\}$ indicates whether edge e is used by net i, and $c_e$ denotes the capacity of edge e. Under these constraints, the optimization objective is typically to minimize the weighted sum of total delay and congestion cost, thereby achieving globally optimal circuit performance in terms of timing and resource utilization. The most widely-used pathfinder algorithm [15], which operates on a negotiated congestion framework, employs an A*-based search method. This method iteratively explores all potential child nodes from the current wavefront and progressively expands the search frontier. While effective in finding viable paths, this exhaustive approach results in a substantial expansion of the search space, which in turn leads to significantly longer routing runtime, particularly for large-scale designs. Furthermore, the algorithm’s net-based routing strategy, which processes interconnections sequentially, along with the inherent need for excessive repetitive operations across multiple iterations to resolve resource conflicts, collectively contribute to the overall slow execution of the routing process.

Many researches have been dedicated to accelerating the FPGA routing process. For instance, CRoute [16] introduces a connection-based routing algorithm that enhances the traditional cost function to more accurately evaluate path quality and guide the search, thereby improving routing efficiency. RORA [17] and Air [18] focus on minimizing redundant computations within the routing algorithm; they introduce a series of enhancements, including heuristic strategies and iterative optimization mechanisms, to reduce repetitive operations across negotiation cycles. In a different approach, Baig and Farooq [19] attempt to leverage reinforcement learning to accelerate routing, utilizing learned historical routing decisions to intelligently guide the path search and reduce computational overhead.

However, a fundamental limitation persists in these methods: they do not adequately address the root cause of routing latency, the exponentially large search space. By largely adhering to global expansion strategies that explore a vast number of nodes, these approaches fail to curtail the core number of nodes visited by the router, thus fundamentally capping further speed improvements. FCRoute [20] represents a notable exception by employing a soft pruning mechanism to actively limit the number of nodes explored during the search. Nevertheless, its strategy, which narrowly focuses on a small set of nodes closest to the target, is often overly restrictive. This severely limited search scope increases the probability of routing failures and necessitates frequent backtracking, which in turn forms a critical bottleneck that hinders more significant runtime optimization.

In recent years, an increasing number of machine learning methods have been applied to CAD tools and have achieved impressive results [21,22,23]. We believe that machine learning approaches also hold great potential for addressing the FPGA routing problem. We can leverage graph embedding techniques to preprocess this RRG for performance improvement. These techniques [24,25,26,27] are designed to learn the intricate topological relationships within a graph and encode its structural information into low-dimensional node representations. By capturing the connectivity patterns and functional roles of nodes, these embeddings can potentially guide the router toward more efficient path exploration and significantly reduce its search space. Established methods like DeepWalk [28] exemplify this approach; it operates by first sampling the graph through numerous random walk sequences to capture node co-occurrences and then employs a Skip-gram model to train high-quality, latent node embeddings that preserve structural similarities. A Skip-gram model is a neural network–based embedding model originally proposed in natural language processing, which learns vector representations by predicting the surrounding context of each node. The model consists of an input layer representing the current node, a hidden layer encoding its latent features, and an output layer predicting neighboring nodes within a defined window.

However, the direct application of such conventional random walk-based methods is fundamentally ill-suited for the highly constrained and heterogeneous nature of the RRG. The RRG is characterized by a diversity of node types, such as Source, Sink, Opin, and Ipin, each endowed with distinct and rigid connectivity properties. For instance, a Source node possesses no incoming edges, a Sink node has no outgoing edges, an Opin can only be driven by a Source, and an Ipin can only drive a Sink. These specific rules and directional constraints mean that a conventional random walk, which traverses edges without regard for these functional roles, would frequently generate sequences that are electrically and logically invalid within the RRG context. Consequently, the conventional random walk algorithm underpinning DeepWalk cannot be directly applied without violating the fundamental routing constraints. This incompatibility necessitates the design of a specialized, topology-aware random walk algorithm that respects the unique characteristics and node-type rules of the RRG to generate useful and high-quality embeddings.

In this paper, we propose DeepRoute, an innovative graph embedding guided routing framework that effectively reduces FPGA routing runtime while maintaining comparable timing performance and acceptable wirelength overhead. The key insight of our work is to leverage graph embedding technology to intelligently filter the routing search space, thereby addressing the fundamental bottleneck in FPGA routing process. To the best of our knowledge, this represents the first successful integration of graph embedding technology into the FPGA routing process to efficiently filter candidate nodes. The key contributions of our work are as follows:

• To address the unique structural properties and constraints inherent in RRG, we have fundamentally modified the conventional random walk algorithm. Our approach incorporates domain-specific constraints directly into the random walk process, including a novel reverse walk mechanism explicitly invoked for Sink nodes. These adaptations enable the generation of a higher-quality RRG walk set that respects the graph’s directional semantics and node-type relationships, ultimately producing more meaningful embedding vectors that capture the true routing connectivity.
• We introduce the improved connection routing process with a node filtering strategy that combines graph embedding results with congestion. Our filtering strategy leverages the learned node representations to identify and eliminate unpromising routing directions early in the search process. This approach enables the router to proactively filter the majority of useless nodes while prioritizing exploration toward more promising regions, substantially reducing the search space complexity and minimizing backtracking operations, which collectively contribute to significant routing acceleration.
• We conducted extensive experiments using the VTR flagship architecture and benchmark suites [29]. Our results demonstrate that DeepRoute achieves a remarkable 51.31% improvement in routing speed compared to the baseline VTR8 router [29], while maintaining identical critical path delay and limiting total wirelength degradation to within 10%. Furthermore, when compared to FCRoute [20], our method achieves an additional ~10% speedup, with this performance advantage becoming more pronounced on larger circuits where we observe approximately 13% improvement, demonstrating superior scalability.

2. DeepRoute

In this section, we introduce DeepRoute, an improved routing algorithm based on graph embedding results to filter nodes explored by the router. The advantage of DeepRoute is that it can reduce the number of backtracks while filtering nodes, thus significantly speeding up routing.

2.1. How Does Graph Embedding Help Accelerate Routing

The primary bottleneck in FPGA routing runtime stems from the enormous number of nodes explored by the router during the pathfinding process. Consequently, the fundamental challenge becomes how to effectively reduce this exploration space while simultaneously ensuring routing solutions remain congestion-free and meet timing requirements. Graph embedding technology emerges as a powerful solution to this problem, providing a fast and structurally-aware methodology for intelligent search space reduction.

Graph embedding operates as a preprocessing step on the RRG, learning to represent topological relationships through dense vector representations. In this context, a net is defined as consisting of a single starting point, referred to as the Source node, and multiple endpoints called Sink nodes. In FPGA routing, the overall task is to establish connection paths for all nets, each connecting its Source node to all corresponding Sink nodes, across the programmable interconnect resources, while simultaneously resolving routing congestion and preserving optimal circuit performance. This embedding process effectively quantifies node similarity within the graph structure, where higher similarity scores indicate stronger connectivity patterns, more potential connecting paths, or shorter topological distances between nodes (the precise definition of the similarity metric and its computation will be detailed in Section 2.4). During the routing process, we leverage these learned similarity metrics to implement an intelligent node filtering strategy: from the set of candidate child nodes, we selectively retain only those that exhibit greater similarity to the target Sink node, while filtering out those less similar to it. This approach dramatically reduces the number of nodes explored during routing, thereby accelerating the process. More importantly, by preserving nodes that maintain high connectivity to the Sink, this method inherently preserves many viable routing paths, which naturally helps mitigate congestion issues that arise from exploring unpromising directions.

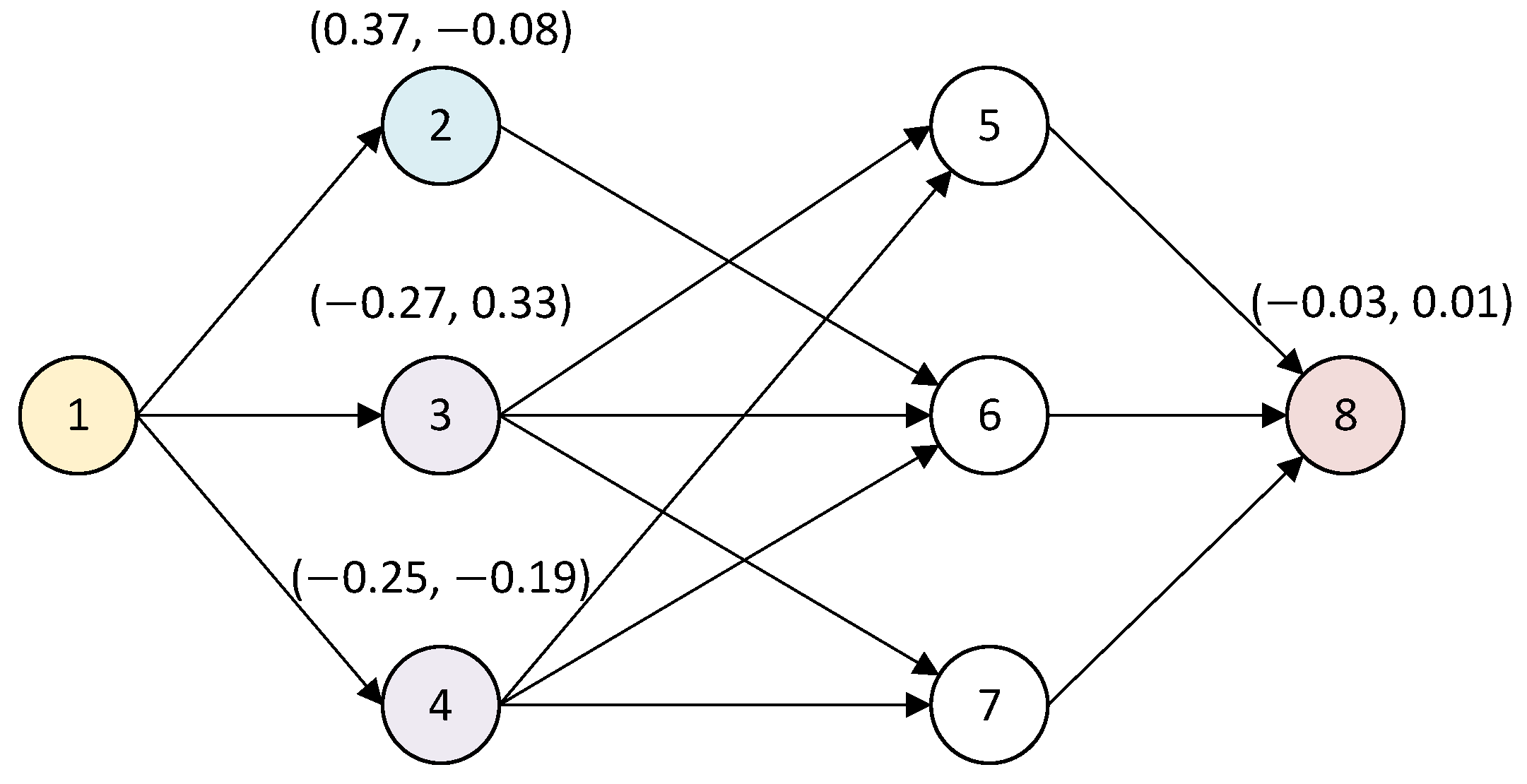
Figure 1 provides a concrete illustration of this node filtering mechanism using graph embedding results. In this scenario, the objective is to find a path from Source node 1 to Sink node 8. Prior to pathfinding, we perform graph embedding operations on the RRG. Specifically, the embedding process is based on a random-walk approach, where multiple random walks are conducted on the graph to generate a series of sampled node sequences. These samples are then used to train a neural network to learn dense vector representations for the nodes. The detailed procedure of this graph embedding method is described in Section 2.3. As an example, the obtained vector representations for relevant nodes are as follows: node 2 (0.37, −0.08), node 3 (−0.27, 0.33), node 4 (−0.25, −0.19), and the target node 8 (−0.03, 0.01). For this example, we assume an embedding dimension $d=2$ and utilize the DeepWalk [28] algorithm to generate these representations. When the router expands from the current Source node 1, which has three child nodes (2, 3, and 4), we compute the similarity between each child node of Source node 1 and the target Sink node 8, yielding cosine similarity of −0.99, 0.85, and 0.56, respectively. The calculation for cosine similarity is shown in Formula (2). Based on these metrics, node 2 (with strongly negative similarity) is filtered out from further exploration. This strategic filtering eliminates one-third of the candidate nodes while remarkably preserving six-sevenths of the potential paths to the target. This selective filtering significantly increases the probability of finding congestion-free paths by directing the search toward more promising regions of the RRG.

We systematically integrate this conceptual approach into the practical routing framework. Building upon established routing mechanism of Versatile Place and Route (VPR), we incorporate our node filtering procedure immediately before all child nodes of the current node are added to the priority queue (heap), where all nodes are thoroughly explored. The filtering decision synthesizes two critical factors: the embedding-based similarity between each candidate node and the Sink, combined with real-time congestion awareness. When this filtering strategy is further coordinated with VPR’s timing-driven routing infrastructure, we achieve a comprehensive solution that effectively addresses congestion concerns while simultaneously achieving substantial reductions in routing runtime.

2.2. Overview of DeepRoute

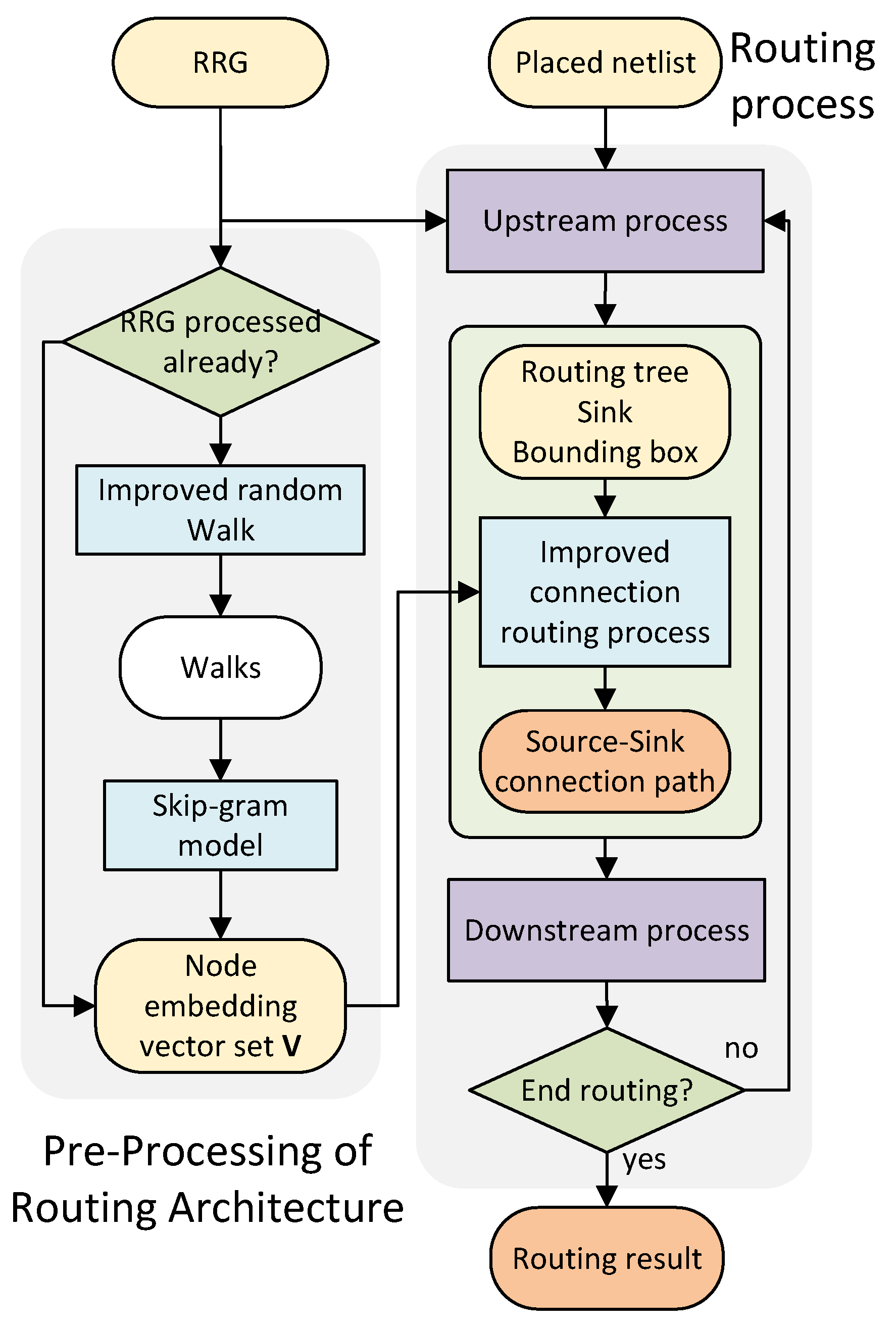
As illustrated in Figure 2, the proposed DeepRoute framework comprises two distinct stages designed to optimize the FPGA routing process. The first stage, which needs to run only once for each RRG, operates as preprocessing of routing architecture, where we perform a modified random walk algorithm on the RRG that is specifically tailored to FPGA routing constraints. This sampling process generates meaningful walk sequences that capture the RRG’s connectivity patterns, which are subsequently used to train a Skip-gram model that produces low-dimensional node embeddings, effectively encoding the topological relationships and functional characteristics of routing resources.

The second stage is the improved connection routing process, which integrates seamlessly into the standard CAD flow. This process leverages the precomputed graph embeddings to intelligently guide the routing process. During the connection establishment between each Source and Sink pair, this enhanced algorithm incorporates a sophisticated node filtering mechanism that utilizes the embedding similarities to filter unpromising search directions while preserving viable paths, thereby significantly accelerating the routing convergence without compromising solution quality.

Since DeepRoute introduces both preprocessing of routing architecture and an enhanced connection-based routing strategy with node filtering capabilities, it requires the definition of several new parameters to configure its operation effectively.

Table 1. Input parameters of DeepRoute.

Parameter	Meaning of the Parameter
$WL$	Length of the walk during random walk process
$WN$	Number of walks per node during random walk process
$VS$	Size of the embedded vector
$RP$	Proportion of nodes being explored

summarizes these parameters, which primarily control the graph embedding generation and node filtering behavior, ensuring flexibility and adaptability across different FPGA architectures and design requirements.

2.3. Preprocessing of Routing Architecture

Prior to the initiation of the standard CAD flow, the FPGA routing architecture undergoes a comprehensive preprocessing stage that generates high-quality embedding vectors to guide the subsequent node filtering process during routing. This preprocessing phase utilizes three key parameters: $WL$ (Walk Length) and $WN$ (Walk Number), and $VS$ (Vector Size). Specifically, $WL$ defines the number of nodes included in each random walk sequence starting from a given node, thereby determining the exploration depth of each walk. $WN$ represents the number of random walks initiated from each node, controlling how many independent traversal samples are collected to ensure sufficient coverage of the RRG. $VS$ denotes the dimensionality of the embedding vectors produced by the Skip-gram model, reflecting the representational capacity of the learned embeddings. These parameters collectively control a modified random walk procedure to generate comprehensive and representative walk sequences. As illustrated in Figure 2, our DeepWalk-based methodology follows a systematic two-step approach: first generating representative walk sequences that comprehensively cover the RRG topology through modified random walks, then training a Skip-gram model on these sequences to obtain the final graph embeddings that capture nuanced topological relationships. Importantly, for any given FPGA routing architecture, this complete preprocessing procedure, including both the constrained random walk generation and Skip-gram model training, needs to be executed only once for each RRG, and remains valid independent of changes in the design benchmarks, providing significant computational efficiency across multiple routing tasks.

Algorithm 1 generates structurally-constrained walk sequences over the directed RRG by incorporating domain-specific connectivity rules to ensure topological validity. The algorithm accepts as input the RRG, a node type mapping function T, the walk length parameter $WL$, and the walk number parameter $WN$, returning a comprehensive list of walk sequences $Walks$. The initialization occurs in Line 1 where $Walks$ is created as an empty list. Line 2 begins an outer loop iterating over each node s in the RRG to ensure complete graph coverage. For each starting node s, Line 3 initiates an inner loop to generate exactly $WN$ independent walks. Line 4 initializes a new walk sequence W with s and designates s as the current node c.

Algorithm 1 Modified Random Walk Algorithm

Abbreviations: S:Source, O:Opin, T:Sink, I:Ipin Require: $RRG$, Node type mapping T, Walk length $WL$, Number of walks per node $WN$ Ensure: List of walk sequences $Walks$ Temp: Walk W, Candidates set C, Current node c 1: $Walks\leftarrow \varnothing$ 2: for each node s in $RRG$ do 3:     for $w=1$ to $WN$ do 4:         $W\leftarrow \left[s\right]$, $c\leftarrow s$ 5:         if $T\left(s\right)\in \{\mathbf{I},\mathbf{T}\}$ then 6:            for $i=1$ to $WL-1$ do 7:                $r\leftarrow WL-\left|W\right|$ 8:                if $r>2$ then 9:                    $C\leftarrow \{n\in \mathrm{pred}(c)\mid T(n)\notin \{\mathbf{O},\mathbf{S}\left\}\right\}$ 10:                else if $r=2$ then 11:                    $C\leftarrow \{n\in \mathrm{pred}(c)\mid T(n)=\mathbf{O}\}$ 12:                else 13:                    $C\leftarrow \{n\in \mathrm{pred}(c)\mid T(n)=\mathbf{S}\}$ 14:                end if 15:                if $C=\varnothing$ then break 16:                end if 17:                $n\leftarrow \mathrm{RandomSelect}\left(C\right)$ 18:                Insert n at head of W 19:                $c\leftarrow n$ 20:            end for 21:         else 22:            for $i=1$ to $WL-1$ do 23:                $r\leftarrow WL-\left|W\right|$ 24:                if $r>2$ then 25:                    $C\leftarrow \{n\in \mathrm{succ}(c)\mid T(n)\notin \{\mathbf{I},\mathbf{T}\left\}\right\}$ 26:                else if $r=2$ then 27:                    $C\leftarrow \{n\in \mathrm{succ}(c)\mid T(n)=\mathbf{I}\}$ 28:                else 29:                    $C\leftarrow \{n\in \mathrm{succ}(c)\mid T(n)=\mathbf{T}\}$ 30:                end if 31:                if $C=\varnothing$ then break 32:                end if 33:                $n\leftarrow \mathrm{RandomSelect}\left(C\right)$ 34:                Append n to W 35:                $c\leftarrow n$ 36:            end for 37:         end if 38:         Append W to $Walks$ 39:     end for 40: end for 41: return $Walks$

The algorithm then diverges based on node type in Line 5: if s is classified as Sink or Ipin, it executes a reverse search (Lines 6–20); otherwise, it performs a forward search (Lines 22–36). In the reverse search path, Line 7 calculates remaining steps r as $WL$ minus current walk length. Lines 8–14 impose type-based constraints on candidate predecessor nodes according to r: when $r>2$, nodes of type Opin and Source are excluded; when $r=2$, only Opin-type nodes are permitted; when $r=1$, exclusively Source-type nodes are allowed. Line 15 terminates the walk if no valid candidates exist. Line 17 randomly selects a predecessor node n from qualified candidates, Line 18 inserts n at the head of W in reverse order, and Line 19 updates the current node c to n. Similarly, in the forward search branch (Lines 22–36), Lines 24–30 enforce type restrictions on successor nodes: for $r>2$, Ipin and Sink are excluded; for $r=2$, only Ipin is allowed; for $r=1$, exclusively Sink is permitted. Line 31 breaks the loop upon empty candidate sets, Line 33 randomly chooses a successor n, Line 34 appends n to W, and Line 35 updates c to n. After each complete walk generation, Line 38 appends W to $Walks$, with the final collection returned in Line 41.

Algorithm 1 introduces two significant methodological improvements that substantially enhance the quality and representational power of random walks over the RRG. First, the algorithm implements a novel reverse walk strategy specifically activated when the starting node is identified as type Sink or Ipin. This addresses a fundamental limitation of conventional random walk approaches: due to the intrinsic connectivity constraints where Sink nodes possess no outgoing edges and Ipin nodes exclusively drive Sink nodes, traditional methods typically generate severely truncated sequences (often limited to length-1 or length-2 walks) that fail to capture adequate contextual information for these critical node types. By strategically reversing the traversal direction to explore parent nodes rather than child nodes, the algorithm ensures substantially broader topological coverage and richer contextual embedding for Sink and Ipin nodes, thereby producing more meaningful representation learning for these structurally constrained nodes.

Second, the algorithm incorporates rigorously defined type constraints throughout the walk generation process to prevent premature termination and ensure structurally complete paths. In conventional random walk methodologies, encountering a Sink node immediately terminates the walk sequence, resulting in truncated paths that poorly reflect actual routing scenarios. To overcome this limitation, our algorithm implements progressive type restrictions during forward walks: during initial and intermediate steps ($r>2$), nodes of types Ipin and Sink are systematically excluded from candidate selection; only when the remaining steps r equal 2 are Ipin-type nodes permitted, and exclusively when $r=1$ are Sink-type nodes allowed as valid successors. A symmetrically constrained approach is applied during reverse walks, with corresponding restrictions on Opin and Source nodes based on remaining steps. This sophisticated constraint mechanism guarantees that each generated walk reaches the predetermined length $WL$ while capturing complete logical paths from Source to Sink, thereby more accurately modeling the actual signal propagation pathways in FPGA routing and producing random walk sequences that effectively simulate comprehensive routing paths for subsequent embedding training.

The Skip-gram model serves as the core computational component for transforming the structurally-enhanced walk sequences into meaningful graph embeddings that capture the topological properties of the Routing Resource Graph. This model accepts the comprehensive set of constrained random walks, denoted as $Walks$, as its training corpus and produces as output the dense vector representations V for all nodes in the graph, with each vector $v_i\in V$ encoding the structural role and connectivity patterns of its corresponding node. The embedding procedure rigorously follows the DeepWalk methodology [28], employing a neural network architecture that learns to predict contextual nodes within a defined window size for each node occurrence in the walk sequences. Through this self-supervised training paradigm, the model develops high-quality embeddings where nodes with similar topological positions and connectivity characteristics reside in proximate regions of the vector space. Once obtained through this offline training process, these semantically-rich embeddings are subsequently utilized during the improved routing process to quantitatively assess node similarities and strategically guide the node filtering mechanism, thereby enabling more intelligent and efficient path exploration while maintaining routing solution quality.

The graph embedding results generated during the preprocessing of the routing architecture are stored in a text file, where each line represents the embedding vector of the corresponding node. During the routing stage, these embedding vectors are efficiently loaded into memory as an array for fast access.

2.4. Improved Connection Routing Process

This section details the improved connection routing process, which introduces a key parameter, $RP$ (Retain Proportion), to govern the precise proportion of nodes retained during the filtering process.

The foundational principle of DeepRoute’s accelerated routing flow is the systematic filtration of child nodes at the pathfinding stage, thereby deliberately excluding non-critical nodes from the expansive A* search process. This selective filtering directly reduces the combinatorial exploration space the router must evaluate, resulting in significant computational acceleration. However, the design of this filtering mechanism must carefully address a critical trade-off: to achieve substantial speedup, the process must aggressively remove a high proportion of irrelevant child nodes. Conversely, excessively stringent filtering can prematurely and severely constrain the search space, potentially eliminating viable paths and causing routing failures. Such failures subsequently trigger computationally expensive backtracking processes, which can paradoxically increase the total routing time. To navigate this balance, our method integrates the graph embeddings generated during the preprocessing of the routing architecture directly into the node filtering mechanism. This integration provides a data-driven, topological understanding of node importance and connectivity, enabling a more intelligent discrimination between critical and non-critical nodes and consequently achieving a superior balance between aggressive acceleration and routing success.

The principal innovation of this refined methodology is its strategic integration of node embedding outcomes directly into the node filtering mechanism. By synergistically combining these learned embeddings with real-time assessments of routing congestion, the process achieves a more intelligent and nuanced selection. This enables the systematic filtration of nodes that contribute the least to the overall solution, as well as those that are persistently identified as overutilized congestion points, thereby optimizing resource allocation and improving overall routing efficiency.

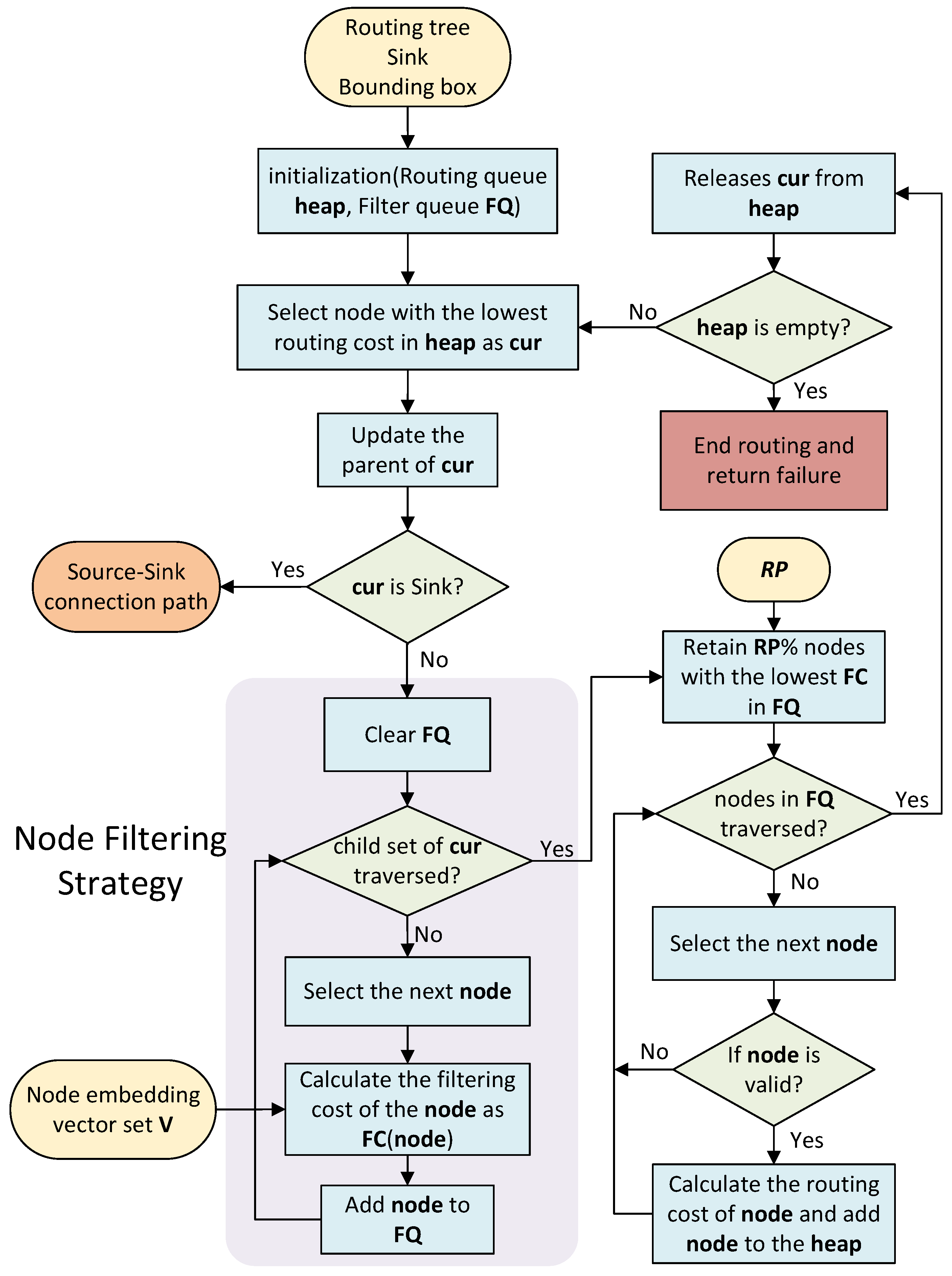
Figure 3 illustrates the workflow of the improved connection routing strategy. The process is initiated by DeepRoute through the initialization of a routing heap alongside a specialized filter queue ($FQ$), which collectively manage the filtering of nodes. The algorithm operates iteratively, each time extracting the node with the minimum cost from the heap, designated as the current node ($cur$). It then updates this node’s parent reference and checks if $cur$ corresponds to the target Sink node. If this condition is met and the constructed path is legally valid, the path is successfully returned. Should $cur$ not be the Sink, a comprehensive filtering procedure is activated. This involves first clearing the $FQ$, then evaluating every child node of $cur$ using a dedicated $FC$ value metric. All child nodes are subsequently inserted into the $FQ$, sorted in ascending order of their $FC$ values to prioritize nodes deemed more promising. The $FC$ value itself is a composite metric derived from the following formula:

$$FC\left(node\right)={\displaystyle \frac{(occ\left(node\right)+1)\times (p_{fac}+1)\times h\left(node\right)}{CS\left(vec\right(node),vec(Sink\left)\right)+1}}$$

(1)

$$CS(vec\left(node\right),vec\left(Sink\right))={\displaystyle \frac{{\sum }_{i=1}^{VS}(A_i\times B_i)}{\sqrt{{\sum }_{i=1}^{VS}{\left(A_i\right)}^2}\times \sqrt{{\sum }_{i=1}^{VS}{\left(B_i\right)}^2}}}$$

(2)

$FC\left(node\right)$ means the cost of a neighbor node of the current node. In this formulation, $occ\left(node\right)$ quantifies the frequency of the node’s prior usage, $p_{fac}$ is a dynamic penalty factor reflecting immediate congestion conditions, and $h\left(node\right)$ encodes the node’s historical congestion level. All these data is generated and recorded throughout the routing process, and can be directly accessed as needed. A pivotal component is the cosine similarity term, $CS\left(\mathrm{vec}\right(node),\mathrm{vec}(Sink\left)\right)$, which measures the directional alignment in the embedded space between the $node$ and the target Sink; here, $A_i$ and $B_i$ represent the respective elements of the $node$ and Sink embedding vectors. The design of the $FC$ value is explicitly intended to balance two critical, and often competing, objectives: mitigating localized node congestion and promoting globally efficient connectivity toward the Sink. It integrates the present usage pressure via $\left(occ\right(node)+1)$, incorporates the accumulated congestion history through $h\left(node\right)$, and uses $(p_{fac}+1)$ to ensure congestion penalties are effectively propagated and compounded across successive routing iterations.

A key contribution of DeepRoute is its strategic use of graph embedding similarity as a primary heuristic, moving beyond a reliance on mere physical Manhattan distance. Unlike approaches such as FCRoute [20], which inherently favor geometrically proximate nodes, this methodology leverages the richer, structural connectivity information inherent in the routing architecture’s graph embedding. Nodes exhibiting higher embedding similarity to the Sink are more likely to reside within robustly connected logical substructures, thereby increasing the probability of discovering a valid path. This strategic focus significantly reduces the likelihood of encountering routing failure and the subsequent need to invoke computationally intensive backtracking.

Following the computation of $FC$ values for all child nodes of $cur$, a selective subset comprising the nodes with the smallest $FC$ values is retained for further expansion. The size of this subset is precisely controlled by the retention parameter $RP$. These prioritized nodes within the $FQ$ subsequently undergo standard routing exploration procedures, which include the calculation of the A* cost and rigorous validation checks such as bounding box constraints check before being inserted into the main routing heap, shown as $heap$ in Figure 3. The node with the lowest cost in the $heap$ is selected as the $cur$ which is then permanently removed from the $heap$. This iterative cycle continues until either a viable path to the Sink is successfully constructed or the routing heap is exhausted, the latter condition signifying a pathfinding failure for the current connection. Subsequently, the router will attempt alternative strategies, such as expanding the bounding box, to search for a legal path connecting the Source and Sink node pairs. If no viable path can be found through these methods, the routing attempt will be considered a failure.

2.5. Timing Criticality Constraints and Detailed Search Regions

To ensure the quality of the routing results while simultaneously minimizing redundant computational effort, our methodology incorporates two supplemental techniques: timing criticality constraints and detailed search regions.

Timing criticality constraints serve as a safeguard for preserving the integrity of the most performance-sensitive paths. We establish a criticality threshold of 0.95, meaning any connection with a criticality value exceeding this value is exempted from the node filtering process. Instead, it undergoes a comprehensive, unfiltered A* search. This exemption is justified by the outsized impact that these highly critical connections exert on overall critical path delay. Furthermore, the population of connections meeting this stringent threshold is inherently small, ensuring that the computational overhead of performing exhaustive searches on them is marginal and does not materially compromise the overarching goal of accelerated routing. Specifically, statistical analysis of the $arm\_core$ benchmark circuit, which contains 14,247 nets, with an average fan-out of 4.3 and a maximum fan-out of 3919, shows that nets with criticality values between 0.9 and 1.0 account for only about 0.4% of all nets. Within this narrow range, most nets have a criticality below 0.95, and those exceeding 0.95 represent an even smaller fraction, but they are almost all located on the most timing-critical paths. Therefore, setting the threshold at 0.95 is a deliberate trade-off: on one hand, it conservatively protects the very small subset of nets that have a significant impact on overall timing convergence; on the other hand, it avoids prematurely excluding less timing-critical connections that can safely participate in filtering-based acceleration. This threshold design achieves a sound balance between maintaining timing stability and improving routing acceleration efficiency, ensuring that the filtering algorithm remains timing-sensitive while fully leveraging its performance advantages.

The detailed search regions is a mechanism designed to curtail repetitive work, particularly the significant cost of backtracking from a late-stage pathfinding failure. As the routing wavefront advances and nears the vicinity of the target Sink node, the imperative shifts from exploratory speed to guaranteed pathfinding success. This is because a substantial portion of the computational investment has already been committed to reaching this advanced state; a failure here would invalidate that prior work and trigger extensive recomputation. To pre-empt this, the algorithm suspends node filtering when the wavefront enters a defined proximity to the Sink. We configure this detailed search regions with a value of 2, which dictates that a full A* search is executed whenever the distance from the wavefront to the Sink node is equal to or less than 2. In our preliminary experiments, we observed that setting the size of the detailed search region to 1 resulted in a higher number of routing failures, while increasing it to 2 significantly reduced such failures. Therefore, the value of 2 was selected to achieve a practical balance between routing reliability and computational efficiency. This ensures an exhaustive and reliable exploration of the final path segment, thereby securing a successful connection and effectively eliminating costly backtracking loops.

3. Experiments

3.1. Experimental Setup

The experiments are conducted on an Intel Core i7 CPU with 128 GB of memory running Ubuntu 20.04. All VTR benchmarks are placed and routed using the VTR flagship architecture [29]. The architecture is embedded prior to the CAD flow to enable the improved routing process to utilize graph embeddings during routing. In our evaluation, “delay” denotes the critical path delay, “TWL” the total wirelength, and “RT” the routing time. Note that RT accounts only for net routing time [20].

Detailed information regarding the benchmark circuits and the corresponding FPGA architectures is summarized in

Table 2. Benchmark information.

Blif	LUT	IO	CLB	Memory
arm_core	9487	312	847	25
bgm	25,830	289	2696	0
blob_merge	3361	136	494	0
diffeq1	297	258	31	0
diffeq2	200	162	22	0
LU32PEEng	69,383	216	7412	168
LU64PEEng	135,086	216	14,287	340
LU8PEEng	19,512	216	2126	45
mcml	82,003	392	6438	159
mkDelayWorker32B	436	1059	464	44
mkPktMerge	176	467	30	15
mkSMAdapter4B	1128	398	175	5
or1200	2364	747	246	2
raygentop	1064	541	120	1
sha	1215	74	132	0
spree	682	77	61	3
stereovision0	6858	366	710	0
stereovision1	6358	260	680	0
stereovision2	8443	331	1498	0
stereovision3	120	13	15	0

and

Table 3. Architecture information.

Benchmark	FPGA Size	CLB	IO	Memory
arm_core	36 × 36	850	1088	25
bgm	62 × 62	2700	1920	80
blob_merge	28 × 28	494	832	16
diffeq1	16 × 16	140	448	4
diffeq2	16 × 16	140	448	4
LU32PEEng	102 × 102	7500	3200	208
LU64PEEng	141 × 141	14,456	4448	414
LU8PEEng	56 × 56	2160	1728	63
mcml	95 × 95	6510	2976	180
mkDelayWorker32B	50 × 50	1728	1536	48
mkPktMerge	28 × 28	494	832	16
mkSMAdapter4B	20 × 20	234	576	9
or1200	26 × 26	432	768	12
raygentop	19 × 19	221	544	4
sha	16 × 16	140	448	4
spree	14 × 14	108	384	4
stereovision0	33 × 33	713	992	20
stereovision1	40 × 40	1064	1216	30
stereovision2	80 × 80	4524	2496	130
stereovision3	7 × 7	20	160	0

. Table 2 lists the specific resource usage for each circuit.

Additionally, as the VPR toolchain is employed to adapt the FPGA grid size to fit different circuit scales, the architecture specifications vary per benchmark. Table 3 provides the architecture information, including the total number of available resources and the specific FPGA dimensions used for each evaluated case.

For comparison with [20], we use the Base results reported therein. The engineering enhancement proposed in [20] targeted the classic lookahead method, which has since been superseded by the map lookahead in the VPR8 [29]. Thus, its relevance is diminished. Our evaluation focuses primarily on routing speed improvement achieved by reducing the number of nodes explored during routing.

3.2. Selection of Input Parameters

Based on extensive experimental validation, we have identified a set of parameters that optimally balance the trade-off between routing acceleration and acceptable performance degradation, the specifics of which are detailed in

Table 4. Parameter selection.

Parameters	WL	WN	VS	RP
Value	15	10	5	0.65

. It is important to note that these parameters can be further calibrated by users to align with the particular characteristics of their target FPGA architecture and application requirements, thereby enhancing the model’s overall effectiveness. Our configuration guidelines are as follows.

The walk length ($WL$) parameter should be configured to exceed the average net length observed in the target circuit. This ensures that the random walks capture a sufficiently extensive topological context, which is crucial for generating high-quality node embeddings and subsequently improving the pathfinding success rate. We choose $WL=15$, which enables the random walks to capture meaningful topological context beyond the average net length, without introducing redundant information or incurring unnecessary computational overhead. For the walk number ($WN$), our experiments indicate that a value between 10 and 15 generally yields robust performance; however, for designs with exceptionally large or complex routing resource graphs, a higher value may be necessary to achieve adequate sampling coverage and enhance the representational quality of the embeddings. In our implementation, we set $WN=10$. This configuration offers stable and sufficiently diverse random-walk sampling, ensuring consistent embedding quality while preserving high routing efficiency.

A smaller vector size ($VS$) for the embeddings contributes noticeably to routing acceleration. As the node filtering process is a preliminary and frequently executed step, employing higher-dimensional vectors introduces significant and often unnecessary computational overhead during the critical cosine similarity calculations. This overhead can paradoxically reduce the very routing speed that the acceleration flow aims to improve.

The parameter $RP$ constitutes the most influential configuration within the accelerated routing framework, as it directly governs the aggressiveness of the node filtering strategy. Specifically, a smaller $RP$ value leads to a more restrictive filtering process, with a greater proportion of nodes being filtered out from the search space. The selection of this single parameter carries significant implications for the final solution quality, critically impacting the critical path delay, the total wirelength, and the overall routing runtime. To empirically determine a balanced value for $RP$, we conducted a series of preliminary experiments.

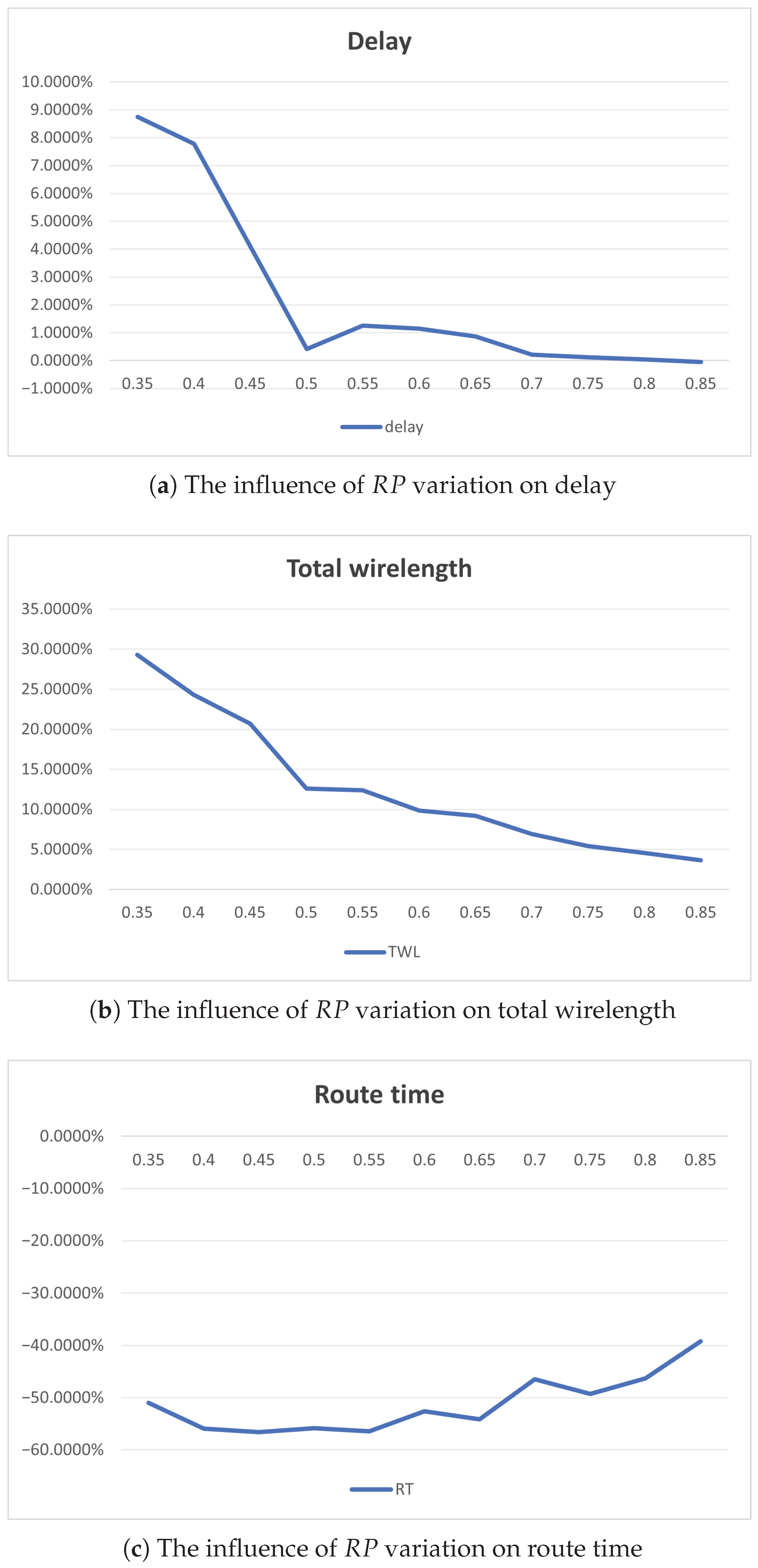
The results of this analysis are presented in Figure 4, which plots the $RP$ values on the x-axis against the relative performance changes in DeepRoute compared to the VTR8 [29] baseline on the y-axis. We conducted an $RP$ sweep from 0.35 to 0.85 with a step size of 0.05. The results show that when $RP<0.65$, the aggressive filtering leads to unacceptable degradation, the total wirelength increases by more than 10% and the delay degradation exceeds 1%. From $RP=0.65$ onward, however, the deterioration in both metrics becomes modest, with delay degradation below 1% and wirelength increase within 10%.

A noticeable local minimum of critical-path delay appears at $RP=0.5$. This effect may result from the interaction between the node-filtering mechanism and resource allocation. When $RP=0.5$, certain timing-critical nodes that were previously over-constrained can be released and reused, leading to improved delay performance. As $RP$ increases, more non-critical nodes are explored, which may introduce congestion and slightly increase delay, whereas overly small $RP$ values may over-restrict the search space and degrade routing quality.

To quantitatively evaluate the trade-off between routing quality and speed, we defined a composite metric as the product of total wirelength, delay, and route time, where smaller values indicate better overall performance. It should be noted that this metric serves as an approximate indicator of the overall trade-off rather than a direct measure of routing quality itself. This metric achieves its minimum at $RP=0.55$, followed by $RP=0.5$ and $RP=0.65$. However, although $RP=0.55$ and $RP=0.5$ achieve lower composite values, they do so at the expense of routing quality, as both exhibit excessive degradation in timing and wirelength compared to higher $RP$ setting. Therefore, we select $RP=0.65$ as the optimal configuration, which offers the best balance between routing quality and acceleration.

We also posit that more extensive experimentation across a wider set of benchmarks could yield a further refined value. It is also crucial to note that the ideal $RP$ value is not universal and is likely to vary across different FPGA architectures, being highly contingent upon specific factors such as the density and distribution of routing resources and the characteristic complexity of routing patterns. Thus, we strongly recommend that users conduct preliminary experiments using one or two representative circuits to determine the appropriate value for the $RP$ parameter for their FPGA.

3.3. Comparison Between Traditional and Modified Random Walk Algorithms

In a comprehensive evaluation conducted on a RRG comprising 65,442 nodes and 527,241 edges, we compared the performance of the traditional random walk algorithm [28] against our modified methodology, using parameters $WL=15$ and $WN=10$. The traditional algorithm demonstrated a critical shortcoming, producing walks with an average length of merely 3.67, which fell drastically short of the target $WL$. This early termination was primarily attributable to the fact that 99.97% of the paths prematurely halted upon encountering Sink nodes. A further analysis revealed that although Sink nodes constitute only 6% of the total graph, they accounted for 27.18% of all nodes visited by these walks, leading to insufficient graph coverage and consequently poor-quality node embeddings.

In stark contrast, our modified algorithm successfully achieved an average walk length of 14.54. Furthermore, it generated complete paths from a Source to a Sink node in 14.13% of all walks. This capability allows the method to more accurately simulate genuine routing behavior, thereby providing substantially richer contextual information for model training and preserving the inherent topology of the RRG more faithfully.

It is noteworthy that the average path length remains slightly below the target $WL$, a phenomenon influenced by the graph’s structural properties, as the presence of part of Ipin nodes, which lack outgoing edges, and part of Opin nodes, which lack incoming edges. Ultimately, the Source-to-Sink sampling strategy offers a more realistic emulation of the actual routing process. The features learned through this method are consequently more aligned with the underlying FPGA architecture and its routing demands, which directly translates into higher prediction accuracy and superior optimization performance during the routing phase.

3.4. Experimental Results and Data Analysis

As shown in

Table 5. Runtime and quality of routing results compared with VTR8.

Benchmark	VTR8			DeepRoute
	Delay (ns)	TWL	RT (s)	Delay (ns)	TWL	RT(s)
LU64PEEng	73.273	3,026,894	136.741	73.277	3,223,255	60.764
mcml	46.562	946,495	39.601	46.616	1,004,039	17.450
LU32PEEng	71.966	1,319,937	65.688	72.066	1,420,951	21.474
stereovision2	14.170	386,588	9.440	14.137	410,668	4.584
bgm	20.042	363,490	6.657	20.050	392,107	4.285
LU8PEEng	73.702	308,466	9.528	73.731	331,720	4.029
stereovision0	4.009	55,432	0.918	4.009	62,994	0.488
stereovision1	5.288	117,489	3.020	5.289	125,439	1.579
arm_core	23.611	162,467	6.282	23.616	175,396	2.347
blob_merge	15.351	61,643	0.902	15.354	66,817	0.558
or1200	9.179	41,546	0.897	9.164	44,994	0.431
mkDelayWorker32B	7.259	24,023	0.951	7.453	26,345	0.394
raygentop	4.725	21,288	0.578	4.893	22,654	0.376
mkSMAdapter4B	6.257	16,833	0.345	6.257	18,780	0.163
sha	11.149	12,230	0.251	11.146	12,984	0.141
mkPktMerge	4.254	13,760	0.533	4.404	16,907	0.145
spree	11.292	11,778	0.398	11.291	13,459	0.208
diffeq1	17.309	8573	0.286	17.265	9319	0.165
diffeq2	13.364	7109	0.327	12.972	7318	0.271
stereovision3	2.028	302	0.025	2.025	349	0.011
GEOMEAN	13.018	57,177.749	1.748	13.059	62,421.602	0.851
				0.31%	9.17%	−51.31%
GEOMEAN (>10 K)	23.929	382,055.665	11.567	23.933	411,785.866	5.292
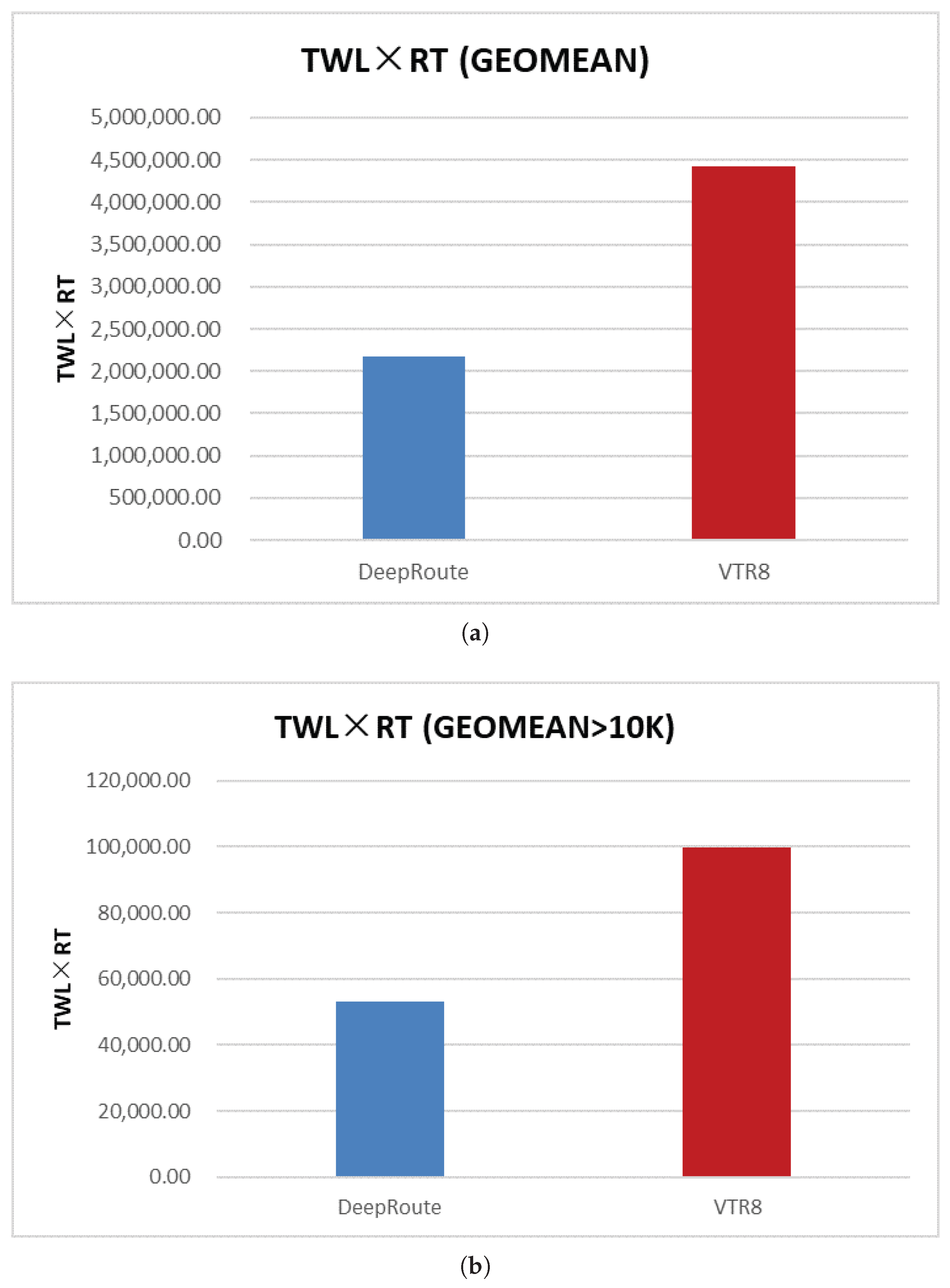
				0.02%	7.78%	−54.25%

, experimental results are reported for different circuit subsets: GEOMEAN (which includes all benchmark circuits) and GEOMEAN (>10 K) (comprising specifically those circuits exceeding 10,000 netlist primitives). DeepRoute achieves a significant reduction in routing runtime, delivering a 51.31% speedup compared to the VTR8 baseline on the standard VTR benchmark set. This acceleration is even more pronounced for larger-scale circuits, where a 54.25% reduction in runtime is observed for the subset exceeding 10K primitives. This performance improvement, however, is accompanied by a trade-off in resource utilization, manifesting as a 9.10% increase in total wirelength across all circuits. Notably, this wirelength overhead decreases to 7.78% for the larger circuit subset, indicating a more favorable scalability profile. To provide a unified assessment of routing efficiency and quality, we introduce the wirelength–runtime product (TWL × RT) as a composite performance indicator that jointly reflects resource usage and computational cost. Figure 5 visualizes the TWL × RT for both GEOMEAN and GEOMEAN (>10 K) cases. The results show that DeepRoute maintains a substantially smaller TWL×RT value than VTR8, highlighting its superior trade-off performance, particularly in large-scale FPGA designs.

It is worth noting that the recently released VTR9 [30] introduces the run-flat routing algorithm, which unifies intra- and inter-cluster routing to enhance coordination between the two levels of interconnection. In contrast, the proposed DeepRoute framework focuses on global inter-cluster routing and improves routing efficiency through graph embedding based node filtering. Since run-flat and DeepRoute emphasize different aspects of the routing process, they can be regarded as complementary approaches. The DeepRoute method could also be extended to VTR9 to further enhance inter-cluster routing performance.

Further comparative analysis against FCRoute [20], as detailed in

Table 6. Comparison of routing result with FCRoute [20] (Baseline: VTR8 [29]).

	FCRoute [20]			DeepRoute
	RT Change	Delay Change	TWL Change	RT Change	Delay Change	TWL Change
GEOMEAN [20]	−41.53%	−0.17%	0.16%	−51.55%	0.58%	9.43%
GEOMEAN (>10 K)	−41.09%	−0.11%	0.48%	−54.25%	0.02%	7.78%

(where the GEOMEAN [20] column represents results for circuits available in the cited work), highlights the competitive advantage of our approach. DeepRoute achieves approximately 10% greater acceleration overall (51.31% vs. 41.53%), with the margin widening to 13% for larger circuits (54.25% vs. 41.09%). While the observed wirelength increase remains a noticeable cost, it is consistently maintained below 10% and demonstrates a decreasing trend in larger benchmarks. This represents a practical and often acceptable engineering trade-off given the substantial gains in routing speed.

The observed wirelength degradation may be attributed to several factors. Primarily, it could stem from limitations of DeepWalk, which employs a relatively simple Skip-gram model to train the embedding vector representations of nodes. Consequently, this model may struggle to effectively learn the paths sampled during the random walk process, resulting in suboptimal quality of the generated embeddings. Concurrently, the node filtering strategy itself might indirectly contribute to wirelength growth by encouraging non-timing-critical connections to utilize longer paths to alleviate congestion for critical nets. Moreover, the current graph embedding process does not fully account for the heterogeneous nature of the RRG. Each node in the RRG has unique attributes, such as capacity, type, and length, yet the current graph embedding primarily captures the topological structure. As a result, the learned node embedding may not accurately reflect the true routing characteristics, potentially leading to a suboptimally filtered result and an increased wirelength. Additionally, certain parameters in the current framework remain static. For instance, during the random-walk phase, all nodes share identical walk lengths and walk number, even though some nodes play more critical roles in the RRG structure. Similarly, the $RP$ parameter used in the filtering process is fixed across all nodes, despite the fact that RRG nodes differ in type and number of child nodes. Such uniform parameterization may limit the optimization potential and contribute to wirelength growth.

To mitigate these issues, future research could explore two complementary directions. First, the graph embedding process can be enhanced by incorporating node specific attributes into the embedding space, leading to better node representations. Second, the node filtering process can be improved by adopting a dynamic $RP$ adjustment strategy that adapts parameter values based on node type, number of child nodes, etc. These refinements are expected to yield embeddings and filtering results that better align with the characteristics of FPGA routing architectures, thereby reducing overall wirelength while maintaining routing efficiency.

Despite the increase in wirelength, DeepRoute provides substantial improvements in routing speed that significantly enhance the efficiency of the CAD workflow and accelerate research and development iteration cycles. These results compellingly demonstrate the practical value and potential of graph embedding-based acceleration strategies in modern FPGA routing.

3.5. Experiment on Modified FPGA Architecture

In this part, we describe an additional experiment designed to evaluate whether the proposed DeepRoute algorithm maintains its performance across different routing architectures. Unlike the baseline VTR Flagship architecture used in the previous experiments, which features CLBs with ten fracturable 6-LUTs, length-4 routing segments, and flexibility of $F_{c,in}=0.15$, we selected a modified architecture to test generalization. The modified architecture is configured with eight fracturable 6-LUTs per CLB. It employs shorter routing wire segments of length-2. The flexibility parameters are also adjusted to $F_{c,in}=0.20$.

The corresponding scaled FPGA architecture specifications for each circuit are detailed in

Table 7. Architecture information on the modified FPGA architecture.

Blif	FPGA Size	CLB	IO	Memory
arm_core	39 × 39	1036	1184	30
bgm	23 × 23	336	672	9
blob_merge	32 × 32	660	960	20
diffeq1	16 × 16	140	448	4
diffeq2	16 × 16	140	448	4
LU32PEEng	92 × 92	6030	2880	180
LU64PEEng	132 × 132	12,610	4160	357
LU8PEEng	50 × 50	1728	1536	48
mcml	92 × 92	6030	2880	180
mkDelayWorker32B	50 × 50	1728	1536	48
mkPktMerge	28 × 28	494	832	16
mkSMAdapter4B	20 × 20	234	576	9
or1200	27 × 27	475	800	12
raygentop	19 × 19	221	544	4
sha	18 × 18	192	512	4
spree	14 × 14	108	384	4
stereovision0	37 × 37	910	1120	25
stereovision1	40 × 40	1064	1216	30
stereovision2	80 × 80	4524	2496	130
stereovision3	6 × 6	12	128	0

. Based on these specifications, we performed routing experiments on the set of benchmarks listed in

Table 8. Benchmark information on the modified FPGA architecture.

Circuit Name	LUT Used	IO Used	CLB Used	Memory Used
arm_core	9816	312	989	24
bgm	2832	289	303	0
blob_merge	6190	136	648	0
diffeq1	478	258	43	0
diffeq2	286	162	28	0
LU32PEEng	46,971	216	4951	168
LU64PEEng	90,170	216	9384	340
LU8PEEng	14,088	216	1485	45
mcml	73,837	392	5631	159
mkDelayWorker32B	407	1059	476	47
mkPktMerge	172	467	28	15
mkSMAdapter4B	1120	398	159	5
or1200	2691	779	265	2
raygentop	1288	540	123	1
sha	1647	74	177	0
spree	735	77	64	3
stereovision0	9645	366	862	0
stereovision1	9008	258	852	0
stereovision2	23,273	331	2119	0
stereovision3	88	12	8	0

. We reran the routing experiments on this new architecture using the parameters listed in Table 4, and obtained the results shown in

Table 9. Routing results on the modified FPGA architecture (geomean).

Method	Route Time (s)	Delay (ns)	TWL
VTR8	3.13	15.84	45,093
DeepRoute	1.61	16.08	49,045
Change (%)	−48.56%	+1.51%	+8.76%

. As illustrated in the table, DeepRoute continues to achieve strong performance compared to VTR8 on the new architecture. The routing time is reduced by 48.56%, while the total wirelength increases by 8.76%, and the delay increases by 1.51%. These results demonstrate that DeepRoute provides robust acceleration across different FPGA routing architectures.

Regarding the critical path delay, we observe a slightly higher increase (1.51%) compared to the baseline experiments (0.3%). This difference is likely attributed to the architectural shift from length-4 to length-2 wire segments. In an L2 architecture, long-distance connections require traversing a higher number of programmable switches (more hops). Consequently, the impact introduced by the filtering process of DeepRoute may accumulate to be more noticeable than in an architecture dominated by longer segments. Despite this, the results demonstrate that DeepRoute provides robust acceleration across different FPGA routing architectures.

These results are consistent with the result obtained using the original VTR Flagship architecture, demonstrating that DeepRoute achieves robust acceleration for different FPGA routing architecture.

4. Conclusions

This article introduces DeepRoute, an FPGA routing algorithm that incorporates graph embedding to guide node filtering during routing. The proposed methodology introduces multiple optimizations. These include a structurally constrained random walk algorithm as well as an embedding-guided node filtering strategy controlled by the $RP$ parameter. In addition, timing-critical constraints are applied to preserve delay-sensitive paths, while a detailed search region mechanism minimizes redundant backtracking and enhances routing stability. Experimental results demonstrate that DeepRoute reduces routing runtime by 51.31% compared to VTR8, with further improvement to 54.25% on larger circuits, outperforming existing approaches. Beyond these quantitative improvements, DeepRoute demonstrates strong practical potential for integration into FPGA CAD toolchains. Its embedding guided node filtering mechanism can serve as a lightweight, modular component within existing routing engines, reducing routing search complexity and accelerating the overall routing process. Such integration could facilitate faster design closure.

In the future, we plan to investigate reinforcement learning based adaptive routing strategies, enabling dynamic decision making informed by real-time routing feedback. Moreover, parallelization techniques will be explored to further reduce runtime and enhance scalability for industrial scale FPGA designs. Moreover, we aim to incorporate more dynamic parameter planning to achieve adaptive optimization within the existing framework, particularly for the type-constraint random walk, detailed search region control, and node filtering processes. By enabling these modules to adjust their parameters dynamically, the framework is expected to achieve higher robustness, better timing closure, and improved overall routing efficiency.