Enhanced RRT* Algorithm for Efficient Path Planning in Robotics and Autonomous Driving

Abstract

Planning algorithms are essential for reducing computational complexity in robotics and autonomous driving. While the Rapidly exploring Random Tree Star (RRT*) algorithm offers probabilistic completeness and asymptotic optimality, its practical efficiency is hampered by slow convergence, high initial path cost, and excessive invalid sampling due to uninformed tree expansion. To address these limitations, this study introduces the A-RRT* algorithm. The key improvements include: utilizing an A* path to define an adaptive sampling region for faster initial solution quality and convergence; incorporating a goal bias strategy to guide random node generation; and implementing a steering angle criterion during parent node reselection within a multi-iteration replanning framework to refine the path to global optimality. Simulation confirm that the proposed A-RRT* algorithm effectively enhances planning efficiency and path quality compared to the comparison algorithms. Specifically, it reduces the initial solution time by up to 55%, lowers the initial path cost by 4.5–12.5%, and achieves final path cost that is 1.6–9.8% shorter.

1. Introduction

Autonomous mobile robots (ARM) are assuming an increasingly critical role across a diverse spectrum of applications such as industrial automation, healthcare, agriculture, service industries, and security [1,2,3,4,5]. For mobile robots to efficiently accomplish their tasks, ARM require path planning algorithms that enable navigation from start to goal while dynamically avoiding static and dynamic obstacles [6,7].

In recent years, Sampling-based path planning methods have advanced the field, offering flexible and highly effective solutions for complex problems [8,9]. Optimal Rapidly Exploring Random Trees (RRT*) [10], an important milestone in sampling-based path planning methods, has demonstrated excellent performance characteristics in mobile robotics applications [11]. However, Refs. [12,13,14,15], the convergence speed of the RRT* algorithm is limited by its uniform random sampling mechanism applied to the entire configuration space [16]. Fast convergence of path planning algorithms is one of the indispensable requirements in real mobile robot applications [17].

To address the limitations of the RRT* algorithm, many researchers have proposed various optimization strategies to enhance its performance. Urmson and Simmons [18] introduced a search tree construction method with a goal bias strategy. This method adjusts the probability density function of sampling points during random tree expansion by means of heuristic bootstrapping, which effectively improves the quality of the eventual path. To further improve the convergence efficiency of the RRT algorithm, researchers have successively developed a series of novel algorithms [19,20]. Committed to the use of triangular inequalities to improve ChooseParent and Rewire, covering a wider range of potential parent nodes selection, accelerating the convergence speed. Yi et al. [21] introduced a hybrid expansion mechanism combining target bias and random sampling. This approach aims to optimize the convergence rate without compromising the global exploration capability in the solution space.

Aiming at the lack of direction in the growth process of the RRT algorithm, Yuan et al. [22] introduced the BG-RRT algorithm, which promotes the efficient expansion of the tree structure to the target region by incorporating heuristic guidance as a means of improving the convergence speed and path quality of the algorithm. Yu et al. [23] proposed a method to accelerate the convergence speed by centralized sampling in the region where a feasible path exists with a high probability, convergence speed. This method optimizes the search process and enables the algorithm to find high-quality paths more quickly. Cui et al. [24] developed the Quick RRT* algorithm to solve the problem of long search times in traditional RRT* algorithms. Fan et al. [25], on the other hand, proposed a goal-biased two-way APF-RRT* algorithm. This algorithm not only obtains higher-quality sampling points and shortens the convergence time, but also effectively solves the problem of dense obstacles around the starting point or target point, and improves the efficiency and reliability of path planning. While reinforcement learning (RL) methods have shown promise in dynamic path planning, they often require extensive training and lack guarantees in unseen environments [26]. In contrast, sampling-based methods like A-RRT* combine heuristic guidance with probabilistic completeness, offering a more computationally efficient and reliable alternative for real-time applications.

Zammit [27] conducted a comparative analysis of the performance of the A* and RRT algorithms in the context of UAV path planning, pointing out the applicability of the two in different application scenarios. The study shows that the A* algorithm usually outperforms RRT in terms of path length optimization and computational efficiency, especially when the complexity of the scenario is increased. To tackle the limitations of RRT in disverse environments, Ben and Kwame [28] proposed the ORRT-A* algorithm. This algorithm combines the shortest path search capability of A* with the stochastic exploration property of RRT, and introduces techniques such as goal bias and spline interpolation to achieve path smoothing, which improves the path quality and utility. In addition, Reza Mashayekhi et al. [29] introduced the Informed RRT*-Connect algorithm, which aims to address the inefficiency of the traditional RRT* algorithm when searching the entire configuration space. By restricting the search space to an elliptical region, this method markedly increased the algorithm’s convergence speed. However, this elliptical region growth strategy may have limited improvement when facing highly complex maps.

Referring to the empirical methods of other scholars, in this paper, a heuristic sampling A-RRT* algorithm based on path extension is proposed. The algorithm further improves the quality of the initial solution as well as increases the rate of convergence to the optimal solution. The algorithm restricts the sampling interval based on the RRT* algorithm, and a guiding region is quickly formulated by the A* algorithm, after which it is ensured that all the sample points of the RRT* algorithm come from within this region, which can effectively improve the efficiency of path generation. At the same time, the judgment of steering angle when re-selecting the sampling root node is introduced, and the path length optimization selection is added to gain the optimal path through iteration.

2. Background

2.1. Problem Definition

In this paper, mathematical symbols are used to describe the path planning problem of mobile robots. Let X denotes the configuration space of the planning problem, $X_{obs}$ is the obstacle region, $X_{search}=X\setminus X_{obs}$ is the free space, $x_{start}\in X_{search}$ is the start point. $x_{goal}\in X_{search}$ is the goal point. Let the continuous function $\sigma :[0,1]\to X$ of bounded variables be a path. If $\forall \tau \in [0,1]$, $\sigma \left(\tau \right)\in X_{search}$, the continuous parameter $\tau$ traces the path from the initial to the final configuration. the path $\sigma$ is collision-free.

Definition 1.

Feasible path planning is to find a path σ such that σ is collision-free, $\sigma \left(0\right)=x_{start}$ and $\sigma \left(1\right)=x_{goal}$ for a given motion planning problem. If no feasible path is found under the prescribed conditions, report a failure.

Definition 2.

Optimal path planning is to find a feasible path ${\sigma }^{*}$ that minimizes the cost $c\left({\sigma }^{*}\right)$ such that $c\left({\sigma }^{*}\right)=\mathit{min}\{c\left(\sigma \right):\sigma \mathit{is}\mathit{feasible}\}$ for a given motion planning problem, where $c\left({\sigma }^{*}\right)$ is the full length of the path σ. If no exists, report a failure.

The definition of symbols in this paper is shown in

Table 1. Definition of symbols.

Symbol	Description
A-RRT*	The proposed enhanced RRT* algorithm in this work.
RRT*	Rapidly exploring Random Tree Star algorithm.
A*	A* search algorithm.
X	Configuration space.
$X_{obs}$	Obstacle region within the configuration space.
$X_{search}$	Free space ($X\setminus X_{obs}$).
$x_{start}$	Starting point.
$x_{goal}$	Goal point.
$\sigma$	A path.
$c\left(\sigma \right)$	Cost (typically length) of path $\sigma$.
$q_{rand}$	Randomly sampled point.
$q_{nearest}$	Nearest node in the tree to $q_{rand}$.
$q_{new}$	New node added to the tree.
L	Expansion step size.
r	Radius of the A*-guided sampling region.
m	Goal bias probability threshold.
C	Total cost of a path segment (Equation (3)).
$D_i$	Euclidean length of the i-th path segment.
${\theta }_i$	Steering angle at the i-th node.
$P_{A^{*}}^i$	i-th key node on the A* path.

.

2.2. Randomness of Growth

The random sampling based RRT algorithm constructs a connected graph by iteratively adding nodes that represent locations within the configuration space. Whenever the algorithm selects a new randomized position, it tries to connect this position to the closest existing tree node and ensures that the newly formed path does not intersect with obstacles in the configuration space. Over time, such a process can effectively cover the entire configuration space and discover efficient paths to reach the destination.

The non-directionality of tree growth and the stochasticity inherent in sample collection processes significantly affect the efficacy of path planning algorithms. These properties may lead to an increase in the complexity of the search space, which in turn affects the efficiency of finding paths and the quality of solutions.

The non-directional nature of the tree structure often leads to uniform expansion in all directions. When combined with random sampling, this approach increases the likelihood of encountering obstacles or suboptimal paths during exploration. To maintain algorithmic effectiveness and robustness, more sophisticated path-planning strategies may be required for optimization.

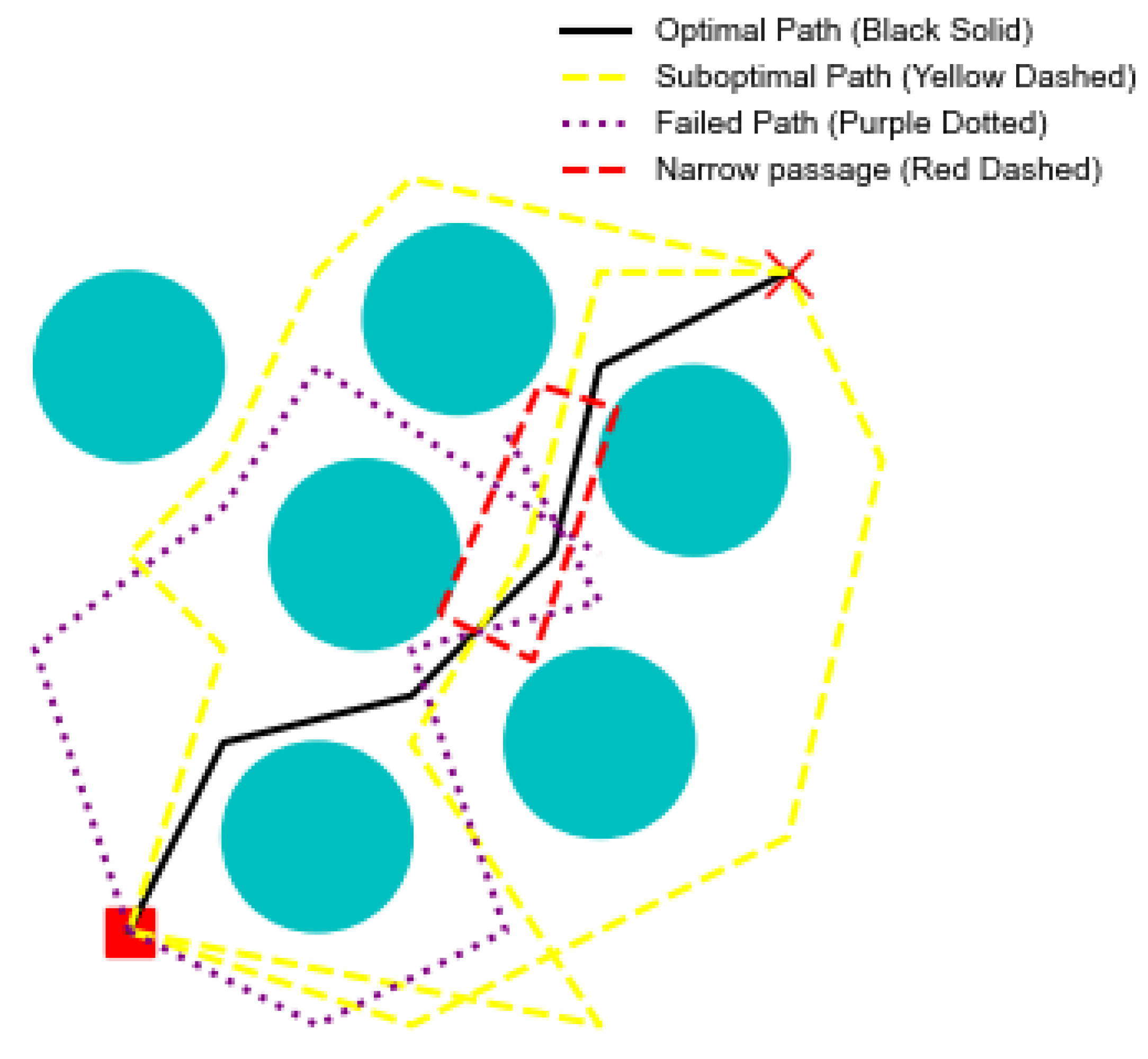
Although uniform random sampling in RRT* enables exploration of the global space, it can also generate invalid configurations. As shown in Figure 1, although the yellow paths successfully circumvent obstacles, their trajectories are suboptimal. In the narrow passage environment marked by the red dashed line, the tree expansion direction tends to be biased toward obstacles, leading to local optima. The purple paths illustrate cases where the algorithm may become trapped in suboptimal solutions upon encountering obstacles. These paths avoid collisions but fail to converge on the globally optimal trajectory. The figure demonstrates that sampling points near the black path would efficiently circumvent obstacles while significantly reducing path length. This suggests that under specific conditions, the method can effectively avoid obstacles and identify an optimal route to the target.

2.3. Valid and Invalid Extensions

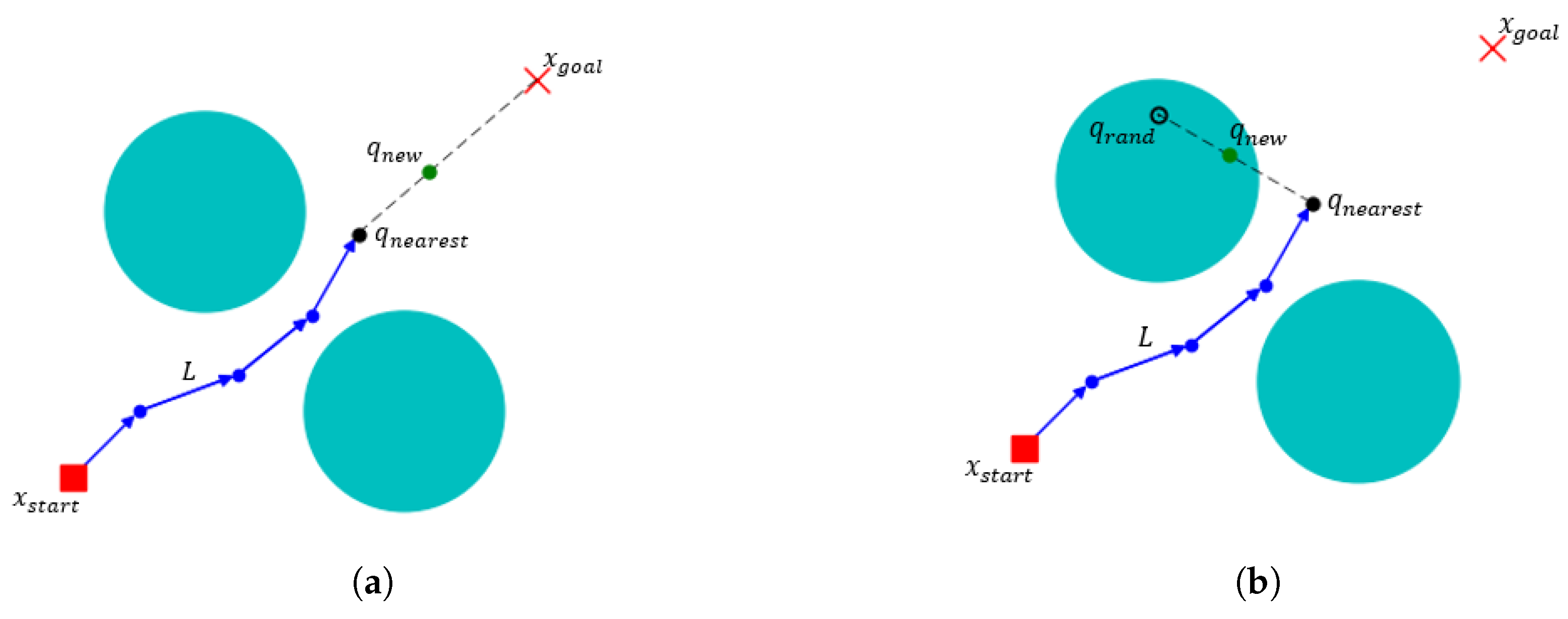
Figure 2 illustrates the RRT* tree expansion process. The blue points represent existing sampling points in the RRT* tree, with a predefined expansion step size L between connected points. The red square points denote the starting configuration $x_{start}$, The goal configuration is marked by the red X points $x_{goal}$. while the black circles indicate randomly sampled points $q_{rand}$. The green point marks the newly extended node $q_{new}$, which is generated by extending from the nearest node $q_{nearest}$ in the existing RRT* tree toward $q_{rand}$ at a distance L.

As shown in Figure 2a, a valid expansion occurs when the connection between $q_{rand}$ and its nearest node $q_{nearest}$ lies entirely within the feasible configuration space, maintaining both path connectivity and collision-free properties. Conversely, Figure 2b demonstrates an invalid expansion case where the connecting segment between $q_{rand}$ and $q_{nearest}$ intersects an obstacle region, rendering the extension infeasible due to collision constraints.

2.4. Problem Taxonomy and Evaluation Baseline

In

Table 2. Problem Taxonomy.

Category	Description
Environment Complexity	Simple, Medium, Complex
Planning Objective	Shortest path, Minimum time
Evaluation Metrics	Initial path cost, Final path cost, Convergence time, Stability (Std)

, classify the path planning problems according to these dimensions.

Select the following algorithms as baseline comparisons.

• BG-RRT*: RRT* variant with goal bias.
• Informed-RRT*: RRT* improved with elliptical sampling.
• A-RRT* (Proposed): Combines A* guidance region and goal bias strategy.

3. A-RRT* Path Planning Algorithm

3.1. Design of Sampling of A* Steering Area

This paper, a new method combining A* heuristic search and RRT* is proposed. A* is used to optimize the growth direction of RRT* so that it tends to find the target. Moreover, it can skillfully deal with the situation of encountering obstacles, and convert the node path generated by A* into sampling band to guide the extensions process of RRT*. The following are the specific implementation steps and methods:

3.1.1. Path Discretization

The discretization process: The path generated by A * is discretized into a series of key nodes $\{(x_{A^{*}}^1,y_{A^{*}}^1),(x_{A^{*}}^2,y_{A^{*}}^2),\dots ,(x_{A^{*}}^n,y_{A^{*}}^n)\}$ from the starting point to the end point.

Node spacing: According to the complexity of the path and the characteristics of the configuration space, the appropriate node spacing can be selected to guarantee the smoothness and continuity of the path.

3.1.2. Definition of Sampling Region

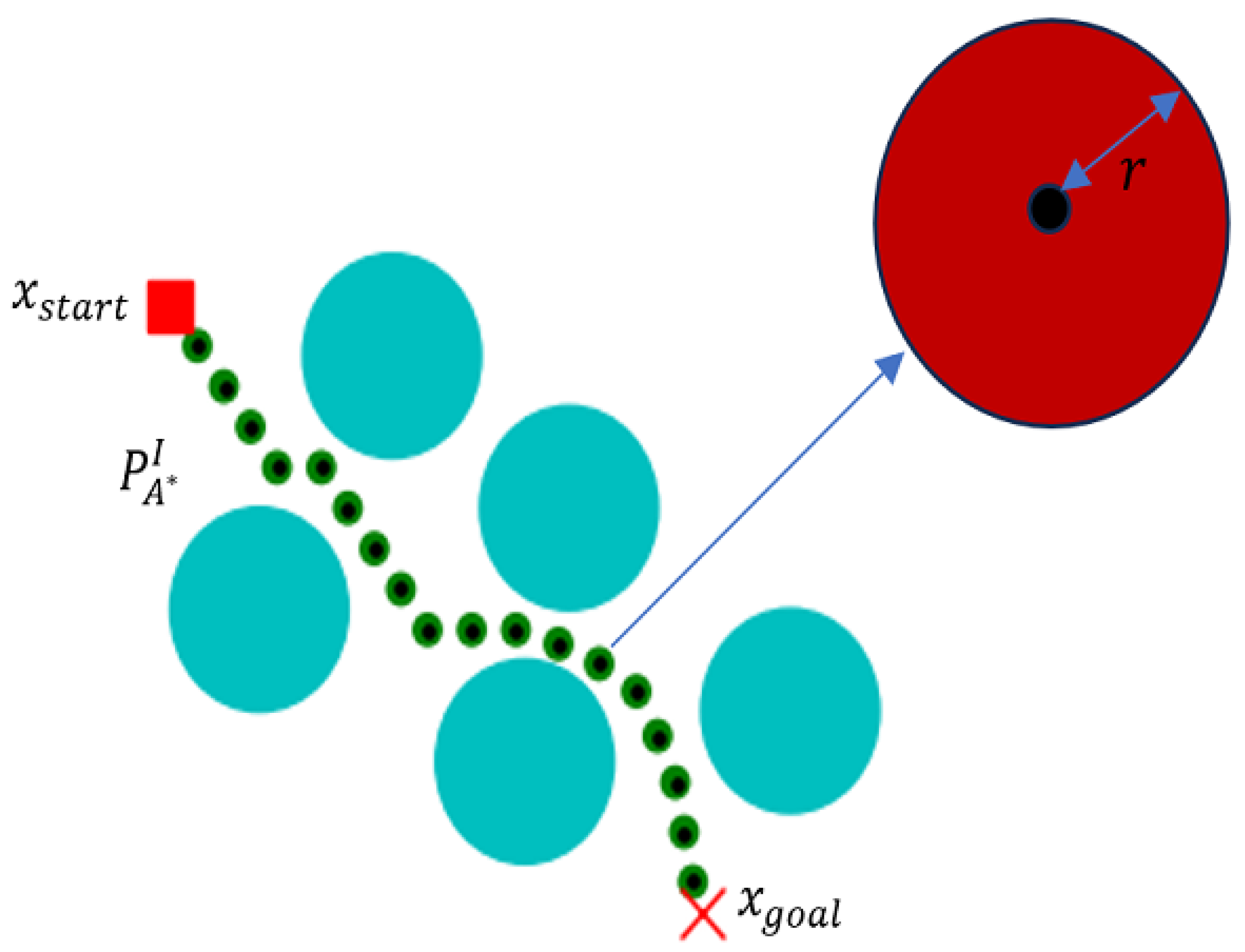
Definition of sampling band: As shown in Figure 3, for any key node $P_{A^{*}}^I=\left(x_{A*}^i,y_{A*}^i\right)$ where $P_{A^{*}}^I$ is the point on the optimal path from the start position to the target position determined by the A* algorithm, on the basis of which we define a circular sampling region centered on the node, where we ensure the consistent exploration in all directions and consider the computational efficiency and implementation simplicity. Here to ensure consistent exploration in all directions, and considering the computational efficiency and simplicity of implementation, a circular region with a diameter of $2r$ is usually chosen to provide a uniform exploration space. The radius of this sampling region is determined by the parameter r, which is denoted as:

$$\sqrt{{\left(x-x_{A^{*}}^i\right)}^2+{\left(y-y_{A^{*}}^i\right)}^2}\le r$$

(1)

Combining the strengths of the A* algorithm and the RRT* algorithm, an improved sampling strategy is used to guide the selection of new nodes. Under this framework, newly generated nodes in the RRT* algorithm are not entirely stochastic during the iterative process, but is influenced by the optimal paths computed by the A* algorithm. Specifically, a circular range is defined around each critical node $P_{A^{*}}^I$ to guide the generation of new nodes. Let r be a predefined distance threshold representing the exploration range around $P_{A^{*}}^I$, then this circular area can be mathematically described as the set of all points that satisfy the above inequality, as shown in Equation (1).

By limiting the generation of new nodes to a circular region around the key nodes, this method can effectively avoid invalid search expansion. For example, the algorithm no longer blindly extends to obstacles or explored areas, but transforms random exploration of RRT* into targeted search. This strategy significantly boosts the speed of path planning and the quality of the final solution. This method combines heuristic search and random exploration, which aims to balance the relationship between exploration and priority selection, and provides an efficient solution strategy for path planning in complex context.

3.2. Goal Bias Strategy

In this paper, a sampling strategy with target bias is adopted when constructing a random tree. This means that when selecting a new sampling point, not only the possibility of random selection is considered, but also the target point is selected with a certain probability. This approach facilitates a more targeted search process, thereby expediting the algorithm’s convergence towards the target district.

$$\begin{array}{cc}\hfill q_{\mathrm{rand}}& =\left\{\begin{array}{cc}\mathrm{rand},\hfill & \mathrm{if}\mathrm{rand}\left(\right)>m\hfill \\ \mathrm{goal},\hfill & \mathrm{else}\hfill \end{array}\right.\hfill \end{array}$$

(2)

Equation (2) indicates that when adding new nodes, the algorithm first generates a random number $rand$ uniformly distributed in [0,1]. This random number is compared with the predefined goal bias probability $m\in [0,1]$. If $rand>m$, random sample is drawn from uniform distribution over the configuration space; otherwise, the goal configuration is selected as the sample to bias the tree growth toward the target.

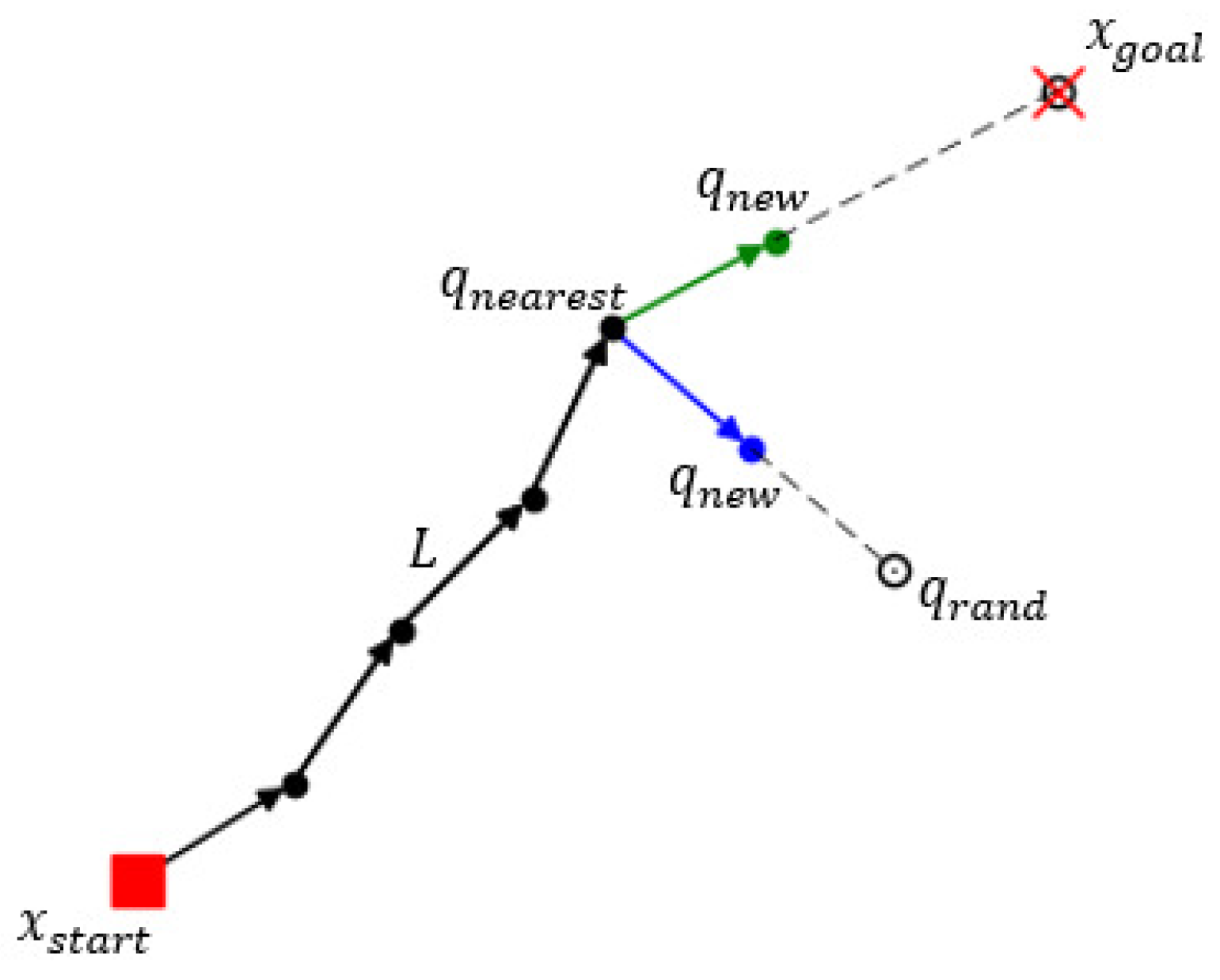
Figure 4 depicts the process of generating new nodes using the goal bias strategy. $x_{start}$ and $x_{goal}$ denote the starting point and destination of the path, $q_{rand}$ is a random sampling point in space, and $q_{nearest}$ is the search tree closest to the node close to $q_{rand}$. In expanding the search tree, the destination point $x_{goal}$ is used as a random sampling point to generate a new node $q_{new}$ with a certain probability, which guides the direction of the tree growth.

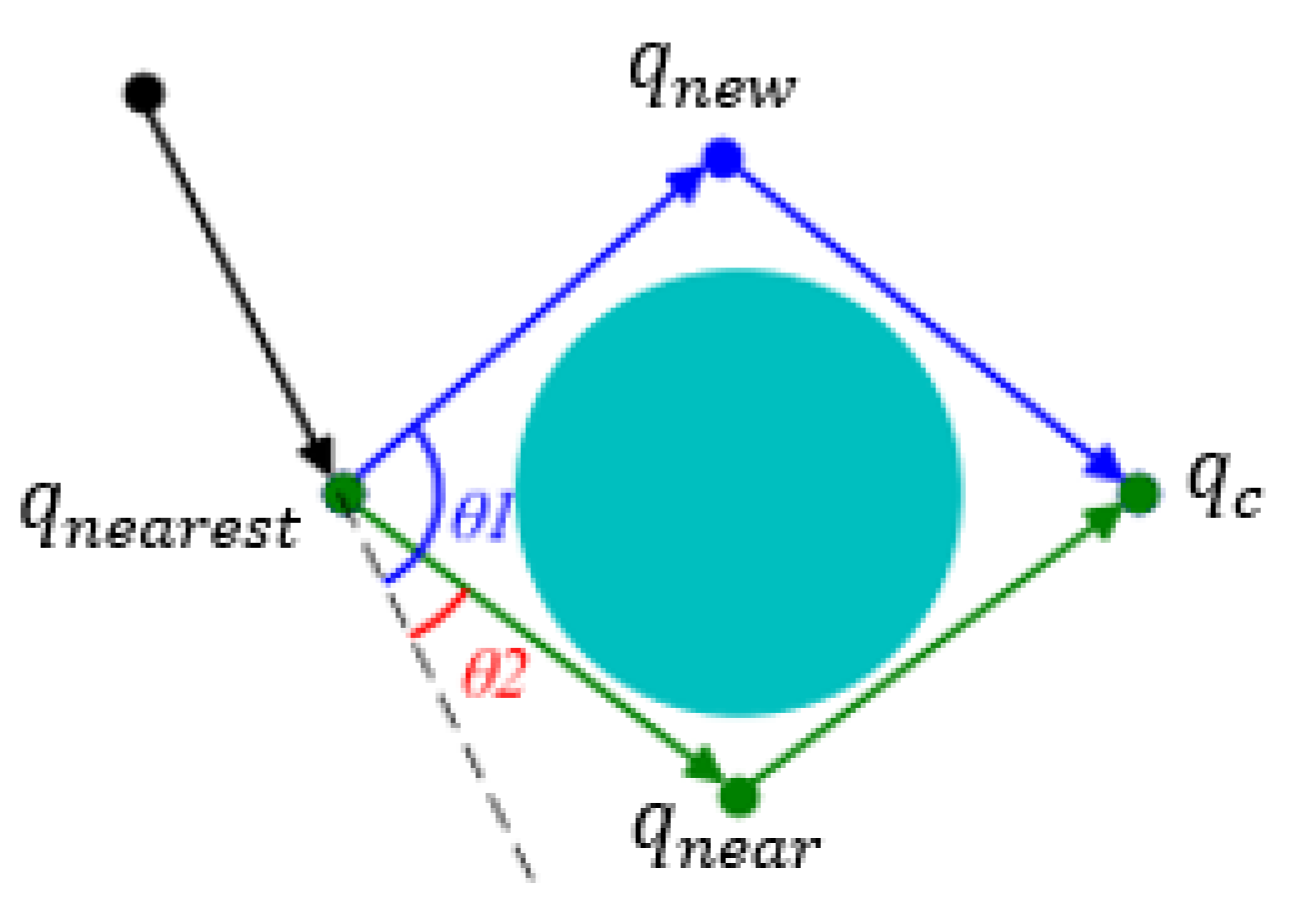
3.3. Reprogramming Algorithm

The Rewire proposed in this paper searches for potential path segments around $q_{new}$. This operation maintains the asymptotic optimality of the path when adding $q_{new}$ to the path-planning tree. The $q_{near}$ path segment is determined by calculating the Euclidean distance and ensuring that there is no obstacle between $q_{near}$ and $q_c$. A locally optimal path segment is obtained, while corner values of $q_{new}$ and $q_{near}$ are included in the evaluation criteria. Finally, the cost function presented in Equation (3) produces the eventual path segment, $q_{near}$ via the steering angle in both left and right directions.in Equation (3), C is the total cost of the path segment, $D_i$ is the Euclidean length of the i-th path segment, R is a constant scaling factor, representing an effective turning radius, ${\theta }_i$ is the steering angle at the i-th node, n is the total number of segments in the local path. To facilitate the global path planning, a reevaluation process is integrated with the algorithm.

$$C=\sum _{i=1}^n{D}_i+R\sum _{i=1}^n\left|{\theta }_i\right|$$

(3)

Figure 5 shows the parent re-planning method in A-RRT*, where the parent node of $q_{new}$ is $q_{nearest}$. The signed angle between the vector from $q_{nearest}$ to $q_{near}$ and the vector from $q_{nearest}$ to $q_{new}$ is computed. Let $\overrightarrow{u}$(from $q_{near}$ to $q_{nearest}$) and $\overrightarrow{v}$(from $q_{new}$ to $q_{nearest}$). The angle $\phi$ between them is calculated through Equation (4). Then the path costs of $q_{near}$ and $q_{new}$ are compared through Equation (5). Finally, the rewiring process described by

Table 3. Rewire($P_1,P_2$).

Rewire(${\mathit{P}}_1,{\mathit{P}}_2$)
IF Condition_free($p_1$, $p_2$) THEN
$P_{{\mathrm{parent}}_2}\leftarrow p_2[i=1]$
IF Cost($p_2$) > Cost($p_1$) and ${\theta }_1(p_1,p_2)<{\theta }_2(p_2,P_{{\mathrm{parent}}_2})$ THEN
IF (Check_confusion($p_{\mathrm{nergrest}}$, $p_2$)) THEN
$P_{\mathrm{parent}}\leftarrow p_2$
Cost ← Cost($p_2$)
End if
End if

is used to decide whether to re-plan the parent node of $q_{near}$ and $q_{new}$ to achieve the local optimal path.

$$\phi =arctan(\overrightarrow{u}\times \overrightarrow{v},\overrightarrow{u}·\overrightarrow{v})$$

(4)

$$d=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$$

(5)

Global path re-planning is a crucial process that involves comprehensive path planning, collision detection, and path length evaluation. Multiple candidate paths are generated and compared to select the optimal one. The comparison between current and previous path lengths is illustrated in Figure 6. The cost function is defined as follows:

$$C\left(n\right)=\sum _{i=1}^{N-1}\parallel p_{i+1}-p_i\parallel$$

(6)

in Equation (6), where $p_i$ denotes the i-th node in the path, N is the total number of nodes, and $C\left(n\right)$ represents the total path length for the n-th planning iteration. To obtain a shorter path, multiple searches are performed, and the path with the minimal $C\left(n\right)$ is selected.

Determine whether the path reaches the path-optimal solution, and converge to the optimal solution rapidly when several global path re-planning is performed. In the tree structure $T=(V,E)$, V denotes the set of all state nodes generated during the planning process, while E represents the feasible path segments connecting these nodes. Let $A_n$ be the set of all collision-free paths in the tree, where $a_n$ and $a_n^{\prime }$ denote two distinct paths in $A_n$. Under the assumption that the path planning algorithm satisfies the probabilistic completeness and the Lipschitz continuity condition, as the number of iterations n approaches infinity, the difference between the lengths of any two paths that are sufficiently close in the configuration space will converge to zero. in Equation (7), $L\left(\alpha \right)$ denotes the length of path $\alpha$. This property ensures that the path planning algorithm stably approaches the globally optimal solution even under multiple instances of global planning.

$$P\left(\underset{n\to \infty }{lim}|{\alpha }_n-{\alpha }_n^{\prime }|=0\right)=1$$

(7)

3.4. Selection of Parameter r

The choice of the parameter r has a significant effect on the performance of the algorithm. To describe more specifically the effect of parameter r on the algorithmic ground, the exploration efficiency, path quality and convergence speed are discussed here.

3.4.1. Exploring Efficiency

Exploration efficiency can be defined as the probability of finding a new node within a given time. The measurement method is to consider the probability that the sample falls in the effective region. Assuming that the area of the configuration space is S, and the circular area with each node as the center and a radius of d is $S_r$, then:

$$P_{\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{l}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}\approx {\displaystyle \frac{\sum S_r}{s}}$$

(8)

In Equation (8), $\sum S_r$ is the sum of all circular areas, and the actual value will be smaller than this estimate, taking into account the possibility of overlap. As r increases, $P_{\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{l}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}$ increases because each sample point covers a larger area, but as r increases further, the growth of $P_{\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{l}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}$ slows down due to the increased overlap between the spheres.

3.4.2. Path Quality

For path quality, it can be evaluated by comparing the generated path length L with the shortest path length $L^{*}$. Assuming that the random samples are evenly distributed in the entire configuration space, the probability of discovering a better path can be expressed as:

$$P_{\mathrm{improvement}}=1-e^{-\lambda r^2}$$

(9)

In Equation (9), where $\lambda$ is a constant related to the complexity of the environment, and $r^2$ indicates that the Area of Circle increases quadratically with r. When r is small, the improvement probability is low, because the sample is concentrated near the existing path; as r increases, the probability of improvement increases, but similarly, when r becomes too large, the distance between sample points is too far, making it difficult to form an effective connection, thereby reducing the probability of improvement.

3.4.3. Rate of Convergence

The rate of convergence is the rate at which the algorithm reaches a certain level of performance. Suppose that the proportion of path length reduction after each iteration is a constant factor $\mu$, Then the change of path length with time t can be approximated as exponential decay:

$$L\left(t\right)=L_0{e}^{-\mu t}$$

(10)

In Equation (10), $L_0$ is the initial path length. The choice of r will affect the size of $\mu$, and usually a smaller r will lead to a larger $\mu$, which means faster initial convergence, but may eventually converge to the suboptimal solution; the larger r may lead to smaller $\mu$, and the initial convergence is slower, but it helps to find a better solution.

In summary, the choice of r is a trade-off issue. Smaller r is beneficial to quickly optimize the known path, but may limit the global search ability. A larger r increases the chance of finding a better path, but also increases the computational cost. Therefore, in practice, the setting of r should be adjusted according to the characteristics of specific problems.

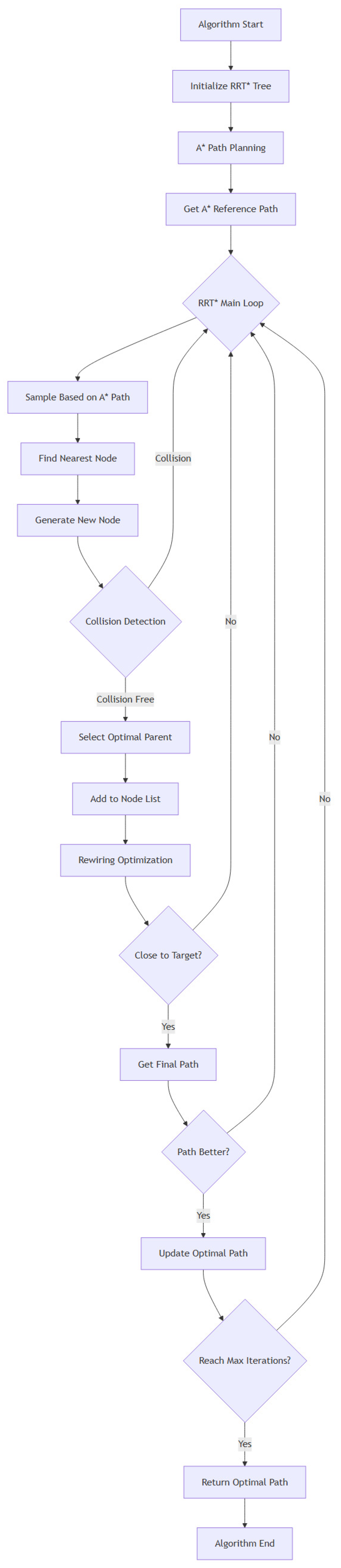
3.5. The Algorithm of A-RRT*

In this paper, a new hybrid algorithm is proposed to simultaneously optimize two key performance indicators, path length and time spent. The algorithm flowchart is shown in Figure 7. The algorithm capitalizes on the merits of A*, RRT* and target offset strategy to achieve more efficient path planning.

Specifically, firstly, a feasible path is obtained in advance by using the efficient path search ability of A * in a known environment, and it is used as a guide domain to guide the sampling process of RRT*. This not only avoids the invalid sampling that RRT* may produce, but also significantly improves the quality of its initial solution. Secondly, by introducing the target bias strategy, that is, setting the target point as the sampling point with a certain probability, the number of iterations required to achieve the target is effectively reduced, thereby shortening the overall calculation time. Finally, in the Rewire stage of RRT*, the node selection mechanism is improved to further optimize the path cost.

In summary, by combining the dominance of three different methods, the proposed hybrid algorithm not only ensures the path quality, but also significantly enhances the search efficiency, which provides a new idea and solution for addressing the path planning issues.

4. Simulation Results

In this section, A-RRT* is com-pared with two existing algorithms (Informed-RRT* and BG-RRT*). The experimental results indicate that using A* as the guiding domain of RRT* sampling and adding the target bias strategy, while re-planning the rewire, the speed and quality of calculating the initial solution are improved, and the path cost is reduced. As the sampling algorithm is non-deterministic, each algorithm runs 30 times, and each algorithm iterates 200 times. In

Table 4. Parameters.

Parameter	Value	Description
Step Size	1	Maximum expansion step per iteration.
Goal Bias	0.1	Probability of sampling the goal directly.
Max Iterations	200	Maximum number of iterations per run.
Number of Runs	30	Independent runs for statistical significance.

, all algorithms adopt the following parameter settings.

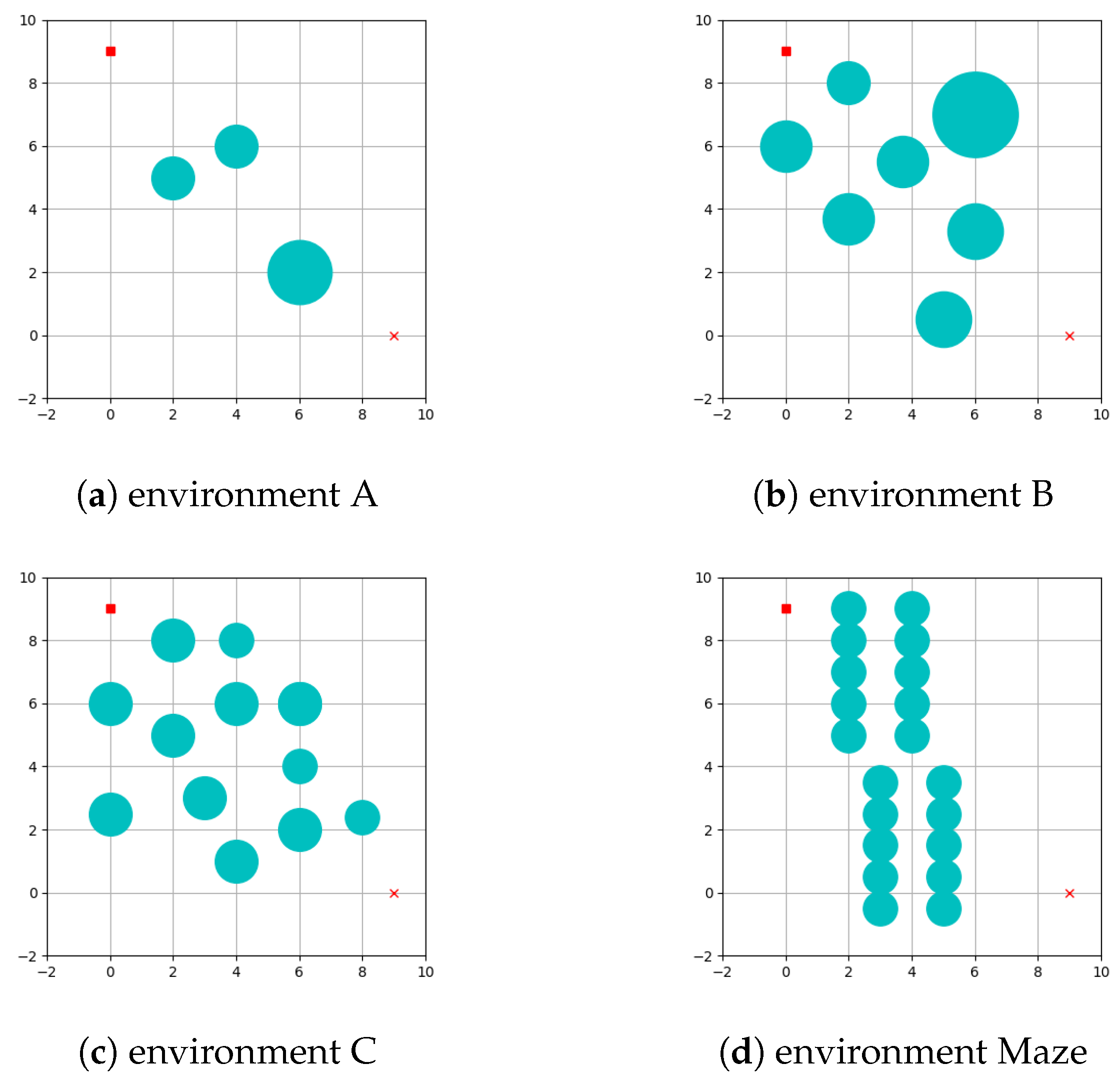
The map range used in the test is set to 12 × 12 m in $2D$ space. The three experimental environments are shown in Figure 8 In the environment, the beginning point is expressed by a red square, the coordinates are set to (0,9), the goal point is represented by a red X mark, the coordinates are set to (9,0), the cyan circle represents the obstacle, The yellow dotted line indicates the explored path, while the black line represents the final optimized trajectory. Algorithm performance is compared under identical sampling conditions to guarantee comparability. In

Table 5. Evaluation protocol.

Index	Description
$T_{\mathrm{init}}$	Time to find the first feasible path (seconds)
$C_{\mathrm{init}}$	Cost of the initial path
$C_{\mathrm{final}}$	Cost of the final optimized path
$St{d}^C$	Standard deviation of path costs across runs

, the evaluation of the algorithm adopts the following evaluation protocol. The simulation is implemented on Intel (R) Core (TM) i5-10200H CPU with 16 G RAM. The simulation platform is Python 3.11.2.

4.1. Environment A

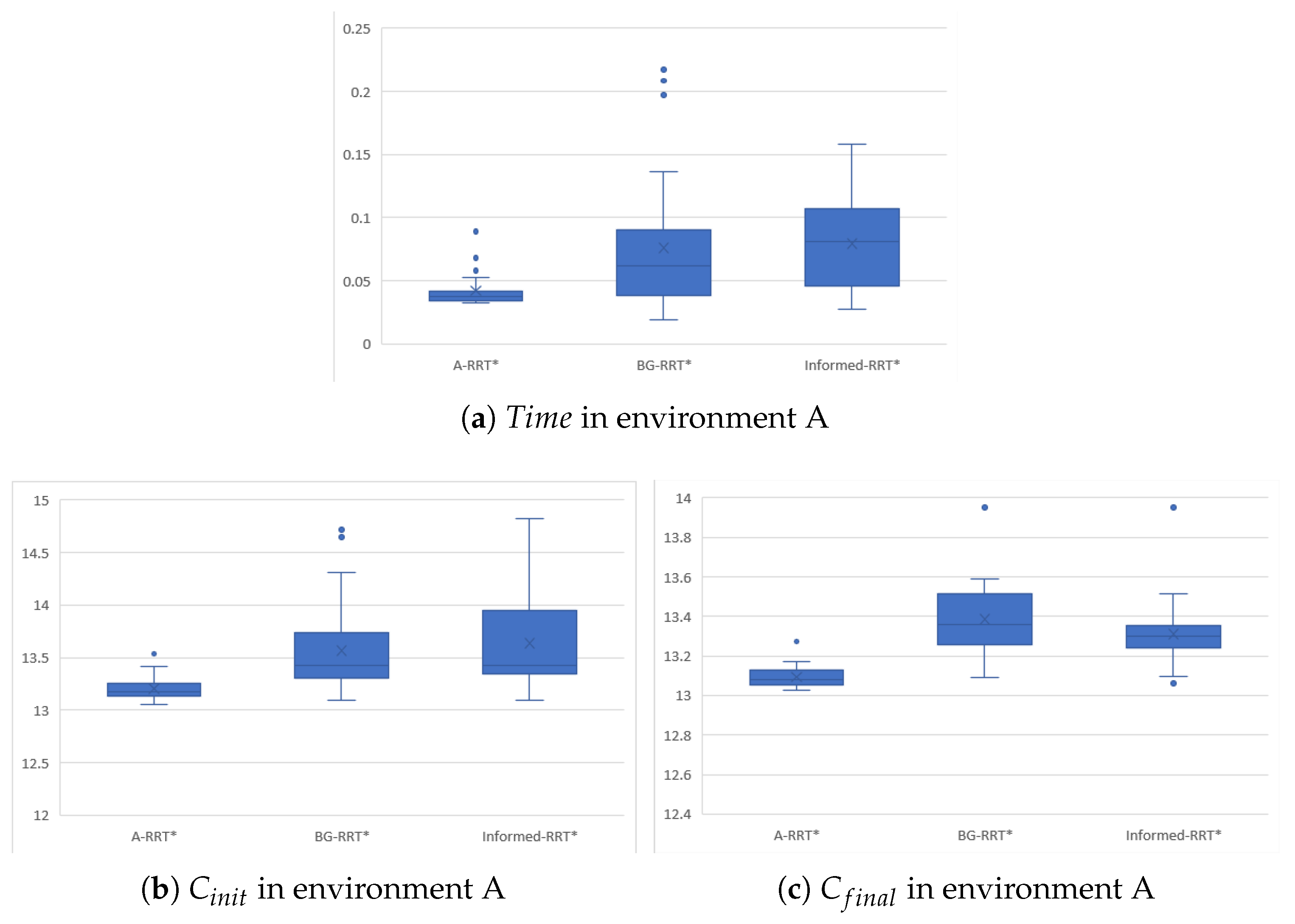
The box diagram in Figure 9 shows the performance indicators of the three algorithms in Environment A, including the time of the initial path and the initial path cost and the cost of the final path of each algorithm in 30 runs.

Table 6. Data analysis in A.

Algorithm	${\mathit{T}}_{\mathbf{init}}$	${\mathit{C}}_{\mathbf{init}}$	${\mathbf{Std}}_{\mathbf{init}}^{\mathit{C}}$	${\mathit{C}}_{\mathbf{final}}$	${\mathbf{Std}}_{\mathbf{final}}^{\mathit{C}}$
BG-RRT*	0.076068	13.56709	0.42038	13.38514	0.183638
Informed-RRT*	0.079424	13.63548	0.441831	13.31148	0.157337
A-RRT*	0.042189	13.20602	0.111687	13.09393	0.052028

clearly records the results of 30 runs, A-RRT*, BG-RRT* and In-formed-RRT* are evaluated from the aspects of the time required to generate the initial path ($T_{init}$), The cost of the initial path ($C_{init}$) and final path ($C_{final}$), and their corresponding standard deviations ($St{d}_{init}^C$, $St{d}_{final}^C$). From the results, the initial solution time of A-RRT* is only 55% and 53% of BG-RRT* and Informed-RRT*, indicating that the algorithm has higher efficiency in generating initial solutions. Compared with the comparison algorithm, the initial path cost generated by A-RRT* is lower, which is 2.8% and 4.5% lower than BG-RRT* and In-formed-RRT*, respectively, which verifies that the algorithm can obtain a near-optimal path solution in the initial stage. After path optimization, A-RRT* still maintains the optimal performance, and the final path cost is further decreased by 2.2% and 1.6% compared with BG-RRT* and Informed-RRT*, which proves its ability to continuously approach the theoretical optimal solution. A-RRT* is significantly better than the comparison algorithm in the standard deviation of path cost, showing higher stability and robustness. The experimental results show that by optimizing the sampling strategy and convergence mechanism, A-RRT* improves the convergence speed while ensuring the quality of the initial solution, reduces the path cost and achieves a balance between efficiency and quality.

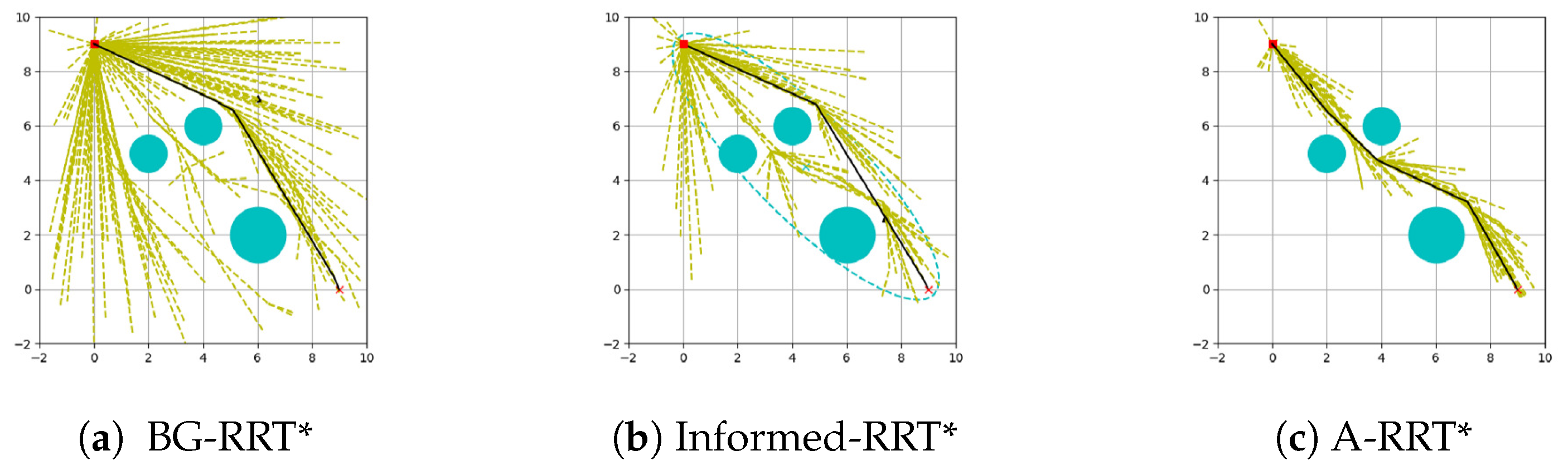
The results of the three algorithms in Environment A are displayed in Figure 10. It can be seen from the figure that all algorithms generate a large number of path samples in the initial stage, showing high flexibility of path exploration. However, BG-RRT* and In-formed-RRT* increase many unnecessary samples, which reduces the convergence speed of the algorithm. The path sample distribution of A-RRT* is more concentrated, the probability of finding a high-quality initial solution is greater, and the path cost is reduced.

4.2. Environment B

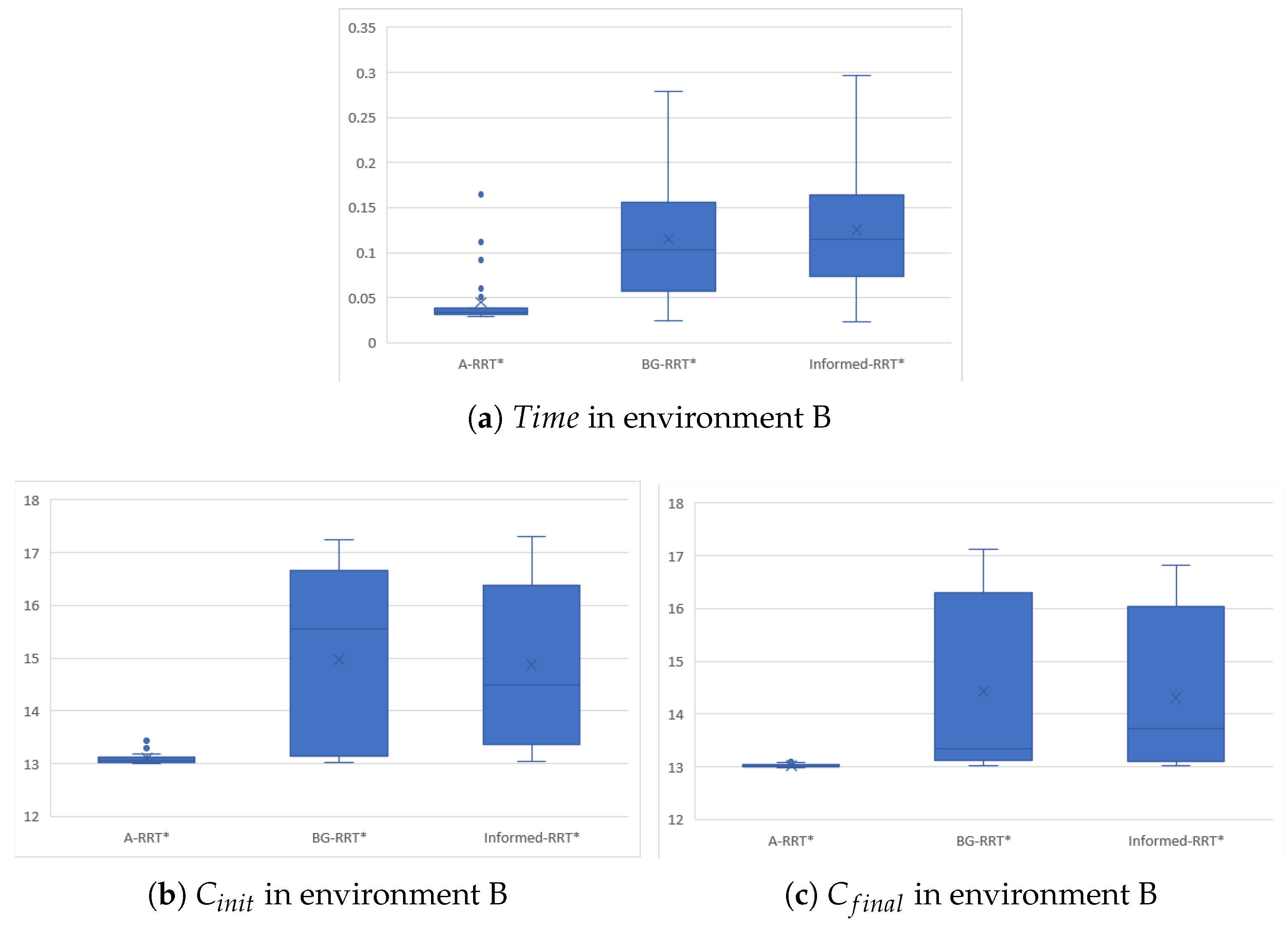
From the results shown in Figure 11 and

Table 7. Data analysis in B.

Algorithm	${\mathit{T}}_{\mathbf{init}}$	${\mathit{C}}_{\mathbf{init}}$	${\mathbf{Std}}_{\mathbf{init}}^{\mathit{C}}$	${\mathit{C}}_{\mathbf{final}}$	${\mathbf{Std}}_{\mathbf{final}}^{\mathit{C}}$
BG-RRT*	0.1153	14.9739	1.74341	14.4359	1.57279
Informed-RRT*	0.12532	14.8642	1.51864	14.316	1.3725
A-RRT*	0.04506	13.1042	0.11544	13.0265	0.0331

, it can be seen that in environment B, A-RRT* is significantly better than BG-RRT* and In-formed-RRT* in terms of path planning efficiency, path quality and stability. In terms of computational efficiency, the initialization time of A-RRT* is only 39% of BG-RRT* and 36% of Informed-RRT*, showing faster convergence ability. In terms of path quality, the initial path cost generated by A-RRT* is 12.5% and 11.8% lower than that of BG-RRT* and Informed-RRT*, respectively. After optimization, the final path cost remains the lowest, which is about 9.0% and 9.8% lower than that of the comparison algorithm. In addition, the path cost of A-RRT* is only reduced by 0.59% in the optimization process, indicating that the initial solution is close to the optimal solution and the optimization space is limited, which reflects the robustness of the algorithm. At the same time, the variance of the final path cost is significantly lower than that of the comparison algorithm, which verifies the ad-vantage of A-RRT * in stability.

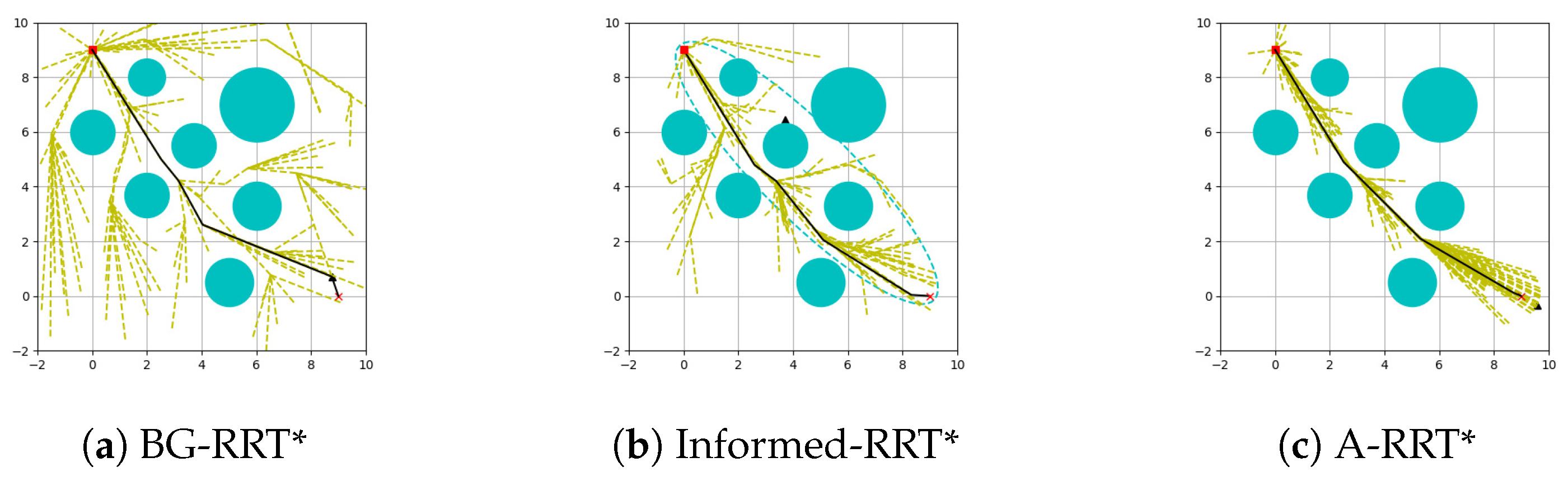
The results of the three algorithms in Environment B are shown in Figure 12. It can be seen from the graph that as environmental diversity is increasing, BG-RRT* and Informed-RRT* generate some unnecessary inflection points in path search, which will in-crease the cost of the path and reduce the smoothness of the path. In contrast, the proposed algorithm generates better random points by using the target offset strategy, directs the random tree to generate better random points, and maintains good path quality in complex environments.

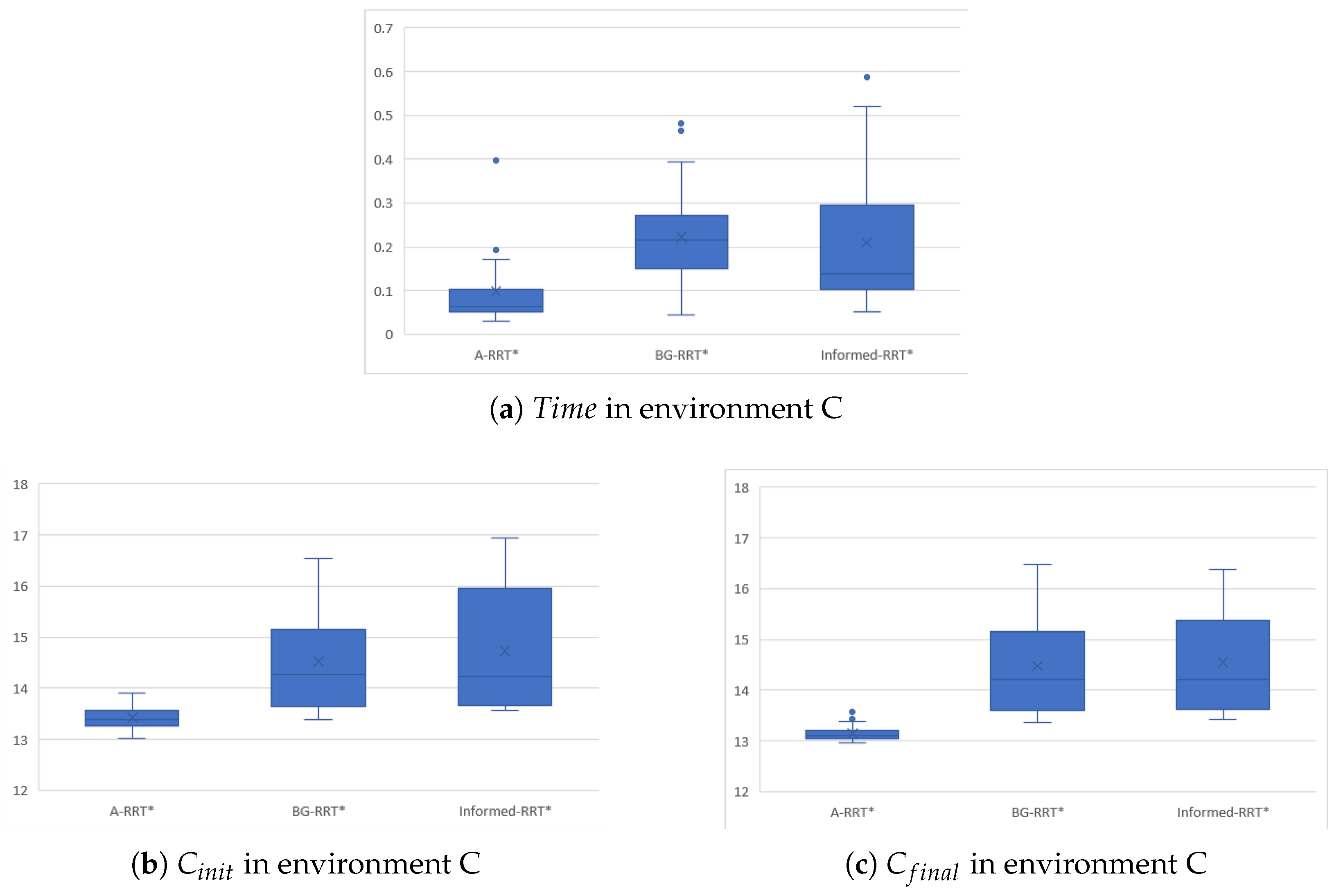
4.3. Environment C

Based on the data analysis of Figure 13 box diagram and

Table 8. Data analysis in C.

Algorithm	${\mathit{T}}_{\mathbf{init}}$	${\mathit{C}}_{\mathbf{init}}$	${\mathbf{Std}}_{\mathbf{init}}^{\mathit{C}}$	${\mathit{C}}_{\mathbf{final}}$	${\mathbf{Std}}_{\mathbf{final}}^{\mathit{C}}$
BG-RRT*	0.221863	14.52206	0.991276	14.4792	0.998229
Informed-RRT*	0.209613	14.73196	1.142608	14.55518	0.981758
A-RRT*	0.098873	13.42153	0.229114	13.14838	0.153822

, in Environment C, A-RRT* algorithm is significantly better than the comparison algorithm in terms of planning efficiency, path quality and robustness. In terms of planning efficiency, the initial planning time of A-RRT* is only 44.5% of BG-RRT* and 47.2% of In-formed-RRT*, which reflects its efficient sampling strategy and path search mechanism. In terms of path quality, the initial path cost is 7.6% and 8.9% lower than that of BG-RRT* and In-formed-RRT*, respectively, and the final path cost is further reduced by 9.2% and 9.7% after optimization. In terms of robustness, the initial path cost standard deviation and the final path cost standard deviation are significantly better than the other two algorithms, indicating that the algorithm has more stable optimization performance.

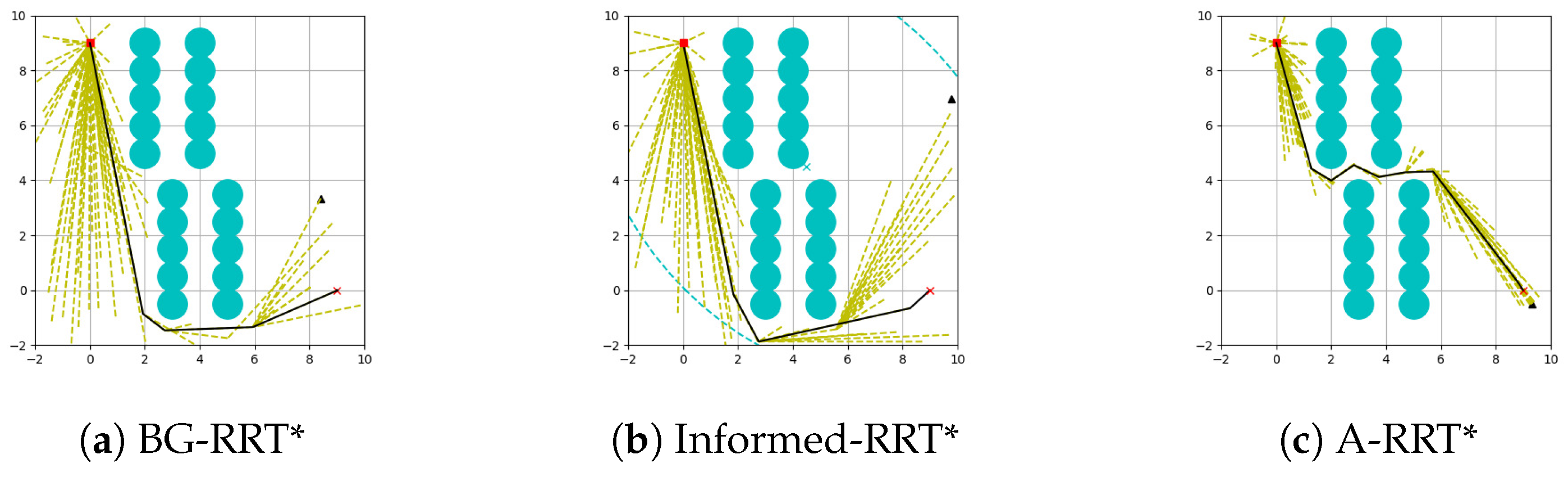
The results of the three algorithms in environment C are shown in Figure 14. It can be seen from the figure that the environment C has a higher density of obstacle distribution, which puts forward more stringent requirements for the path planning algorithm. The analysis shows that although the BG-RRT* and Informed-RRT* algorithms achieve direction guidance through the target bias strategy, there is still significant randomness in the exploration process, resulting in unnecessary path inflection points and increasing path costs. In contrast, A-RRT* achieves dual optimization through the A* guidance domain guidance mechanism: on the one hand, the exploration range is significantly reduced through dynamic sampling space constraints, and on the other hand, the probability of the algorithm converging to the optimal solution is improved by combining the goal-oriented strategy.

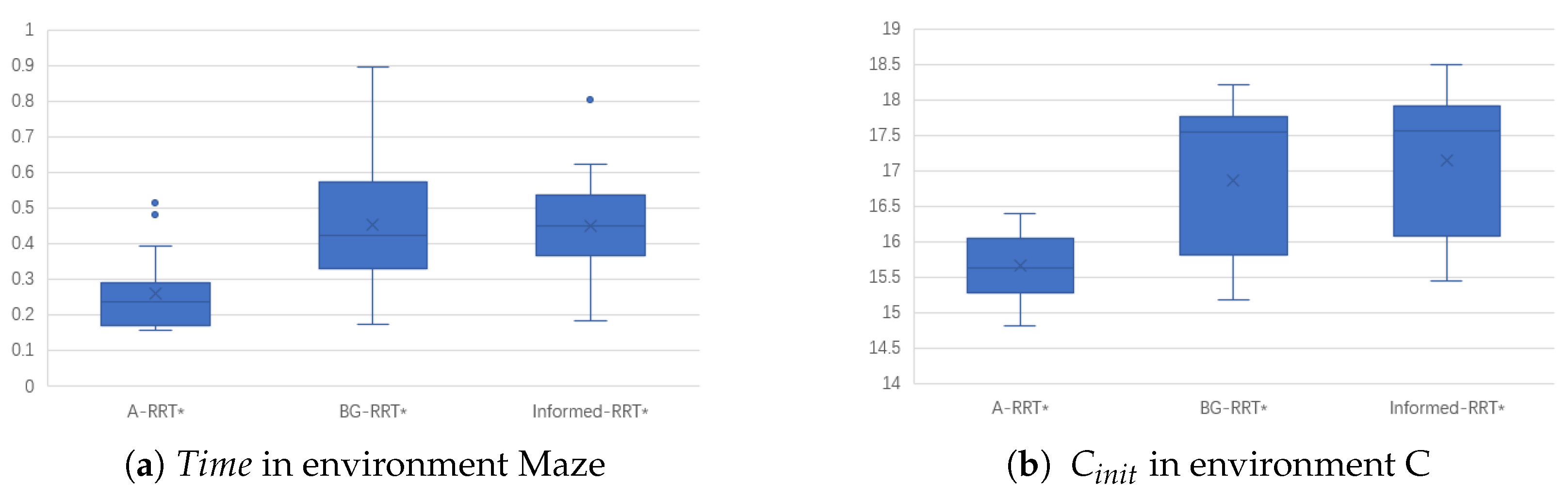
4.4. Environment Maze

Figure 15 and

Table 9. Data analysis in Maze.

Algorithm	${\mathit{T}}_{\mathbf{init}}$	${\mathit{C}}_{\mathbf{init}}$	${\mathbf{Std}}_{\mathbf{init}}^{\mathit{C}}$
BG-RRT*	0.45218	16.86853	1.043297
Informed-RRT*	0.448932	17.15274	0.97485
A-RRT*	0.264186	15.66468	0.436304

clearly present the experimental data of three algorithms in a maze environment. In terms of initial solution time, the proposed A-RRT* algorithm requires only 0.264 s, reducing the time by 41.6% and 41.1% compared to BG-RRT* and Informed-RRT*, respectively. Regarding path quality, the initial path generated by A-RRT* has a cost of 15.665, outperforming the comparison algorithms. More importantly, its standard deviation of path cost is only 0.436, significantly lower than BG-RRT* and Informed-RRT*, reducing performance fluctuation by approximately 55%. This demonstrates A-RRT*’s exceptional stability and robustness. This stems primarily from restricting random sampling to high-quality guidance regions, minimizing algorithmic susceptibility to random interference. Consequently, it consistently produces paths of comparable quality across multiple runs, drastically reducing sampling and computation in ineffective regions, thereby achieving a significant acceleration in convergence speed.

The results of the three algorithms in the maze environment are shown in Figure 16. From the experimental results, it is evident that the random nodes of the proposed A-RRT* algorithm are significantly concentrated within the guiding region defined by the A* path, demonstrating an efficient directional exploration pattern that avoids ineffective wandering between obstacles. As a result, the final path is more direct and smooth. In contrast, the sampling point distributions of BG-RRT* and Informed-RRT* are more scattered and random, generating numerous redundant path branches and unnecessary inflection points, which lead to more convoluted and lengthy final paths. This clearly validates the effectiveness of the A*-guided sampling mechanism, which fundamentally enhances the efficiency and quality of path planning by focusing random exploration on high-potential regions.

4.5. Sampling Radius r Parameter Analysis

The sampling radius r is the most critical parameter in the A-RRT* algorithm, as it directly influences the width of the sampling region, thereby determining the exploration-exploitation balance of the algorithm. A systematic analysis will be conducted to examine the impact of different r values on the algorithm’s performance.

To accurately evaluate the impact of the parameter r, a comparative experiment was conducted in Environment B by varying only the value of r while keeping other parameters fixed (target bias probability $m=0.1$, step size $L=1.0$, maximum iterations = 200). For each value of r, the experiment was independently run 30 times, and the average values of the performance metrics were calculated.

From

Table 10. Performance Comparison of Different Sampling Radii r (Environment B).

r	${\mathit{T}}_{\mathbf{init}}$	${\mathit{C}}_{\mathbf{init}}$	${\mathit{C}}_{\mathbf{final}}$
0.10	0.043873	13.11025	13.03765
0.20	0.035934	13.12522	13.02266
0.25	0.028924	13.11827	13.03251
0.30	0.032941	13.23498	13.0203
0.40	0.024152	13.15435	13.02314

, the following observations can be made:

Initial Solution Time ($T_{init}$): The optimal value of 0.241524 s is achieved at $r=0.4$. As r decreases from 0.4 to 0.1, the initial solution time generally increases. This is because smaller sampling radii result in more concentrated sampling around the A* path, requiring more time to find feasible paths that navigate around obstacles. The longest initial solution time occurs at $r=0.1$ (0.043873), indicating that overly restricted sampling can significantly impact planning efficiency.

Initial Path Cost ($C_{init}$): The best initial path cost of 13.11025 is obtained at $r=0.1$. As r increases, the initial path cost generally shows an increasing trend, with the highest value of 13.23498 at $r=0.3$. This demonstrates that smaller sampling radii help obtain better initial solutions by focusing sampling in promising regions near the A* path.

Final Path Cost ($C_{final}$): The optimal final path cost of 13.02030 is achieved at $r=0.3$, closely followed by $r=0.2$ (13.02266). The performance difference among different r values in terms of final path cost is relatively small (within 0.017), indicating that the rewiring and optimization processes in RRT* can effectively improve path quality regardless of the initial sampling strategy.

The experimental results demonstrate that A-RRT* algorithm exhibits good robustness to parameter r variations, with all tested values producing satisfactory final path quality. The choice of r represents a trade-off between initial solution speed and initial path quality, while the final optimized path quality remains consistently high across different parameter settings.

5. Conclusions and Prospect

Aiming at the issues of poor efficiency and high initial path cost caused by random sampling in the traditional RRT* algorithm, this paper proposes an improved algorithm, A-RRT*. This algorithm integrates the advantages of A* heuristic search and concentrates sampling activities in high-potential path areas to minimize path costs. At the same time, it is combined with the goal-oriented strategy to further constrain the range of random sampling, and through the optimization of the rewiring mechanism, it effectively reduces the path cost and promotes the algorithm to approach the optimal solution speed.

However, this study also acknowledges the limitations of the proposed algorithm, which point to directions for future research. Firstly, the algorithm’s performance hinges on the quality of the initial A* path; in cluttered environments with multiple homotopies, or in weighted/anisotropic cost fields, a single A* path may bias sampling away from globally superior paths. Secondly, key parameters such as the sampling band radius r and the goal bias threshold m are currently selected empirically, lacking online adaptation criteria and a systematic sensitivity evaluation, which may affect the algorithm’s robustness in unknown environments.

To overcome these challenges, future work will focus on two main aspects: (1) Developing a multi-path guidance mechanism that utilizes shortest paths or a set of paths considering different homotopy classes to define the sampling region, thereby reducing reliance on a single initial path and enhancing the algorithm’s ability to discover the global optimum. (2) Designing an adaptive parameter adjustment strategy that dynamically optimizes the values of parameters r and m based on environmental complexity and real-time feedback from the search process. This aims to achieve an optimal balance between exploration and exploitation across various scenarios without manual intervention, further improving the algorithm’s robustness and applicability. (3) In highly constrained environments, such as narrow corridors, the performance remains limited due to the fixed sampling area defined by parameter r. Replace the corridor constraint form with kinematic constraints during the sampling process.

Despite the promising results, the current study is limited to four specific simulation environments. To further validate the robustness and generalizability of the proposed A-RRT* algorithm, future work will involve more comprehensive testing in a wider variety of scenarios. Mainly includes narrow corridor environments and environments with various obstacle types and densities.