A 4–5 GHz Sub-Sampling PLL with TDC-Free Digital Coarse Loop

Abstract

This paper proposes a sub-sampling phase-locked loop (SSPLL) that combines a time-to-digital converter (TDC)-free digital coarse loop with a high-gain analog SSPD fine loop. The coarse loop follows a counter-assisted, frequency-domain DPLL framework with an auxiliary FLL, enabling wide capture range and fast initial acquisition. Precise fractional-N operation without a TDC is achieved by reusing the fine loop delta–sigma modulator (DSM) and digital-to-time converter (DTC) in the coarse loop: the DSM maps the frequency control word (FCW) fraction to a variable integer sequence for integer-domain fractional synthesis, while the DTC aligns reference clock to the nearest oscillator edge to cancel DSM-induced quantization error. An LMS-based DTC gain calibration is enabled in the coarse loop, and its calibrated gain is handed off to the fine loop, stabilizing loop switching despite the narrow locking range of the SSPD. Constraining arithmetic to the integer path eliminates a need of TDC and simplifies hardware, improving area efficiency while preserving accurate frequency/phase alignment. Simulations in 28 nm CMOS over 4–5 GHz with a 104 MHz reference demonstrate 177-fs RMS jitter, −245.6 dB FoM, 0.146-mm² active area, and 8.94 mW power, validating wide capture, low in-band phase noise, and robust coarse-to-fine handover.

1. Introduction

The proliferation of next-generation communication technologies—vehicle-to-everything (V2X), massive machine-type communications (mMTC), ultra-reliable and low-latency communications (URLLC), and network slicing—is being realized through the deployment of 5G New Radio (5G NR) [1,2,3,4]. 5G NR exploits both sub-6 GHz and millimeter-wave (mmWave) bands and meeting the stringent error vector magnitude (EVM) requirements specified by 3GPP necessitates high-performance clocks with low phase noise (PN) and low reference spurs [5]. Looking ahead to 6G, integrated sensing and communications (ISAC) scenarios will demand even higher data rates and local oscillators (LOs) that satisfy more stringent specifications [6].

As an alternative to meeting these requirements, the sub-sampling phase-locked loop (SSPLL) has attracted significant attention. An SSPLL is an analog PLL that directly samples the high-speed voltage-controlled oscillator (VCO) output with a low-rate reference clock. Compared with a conventional phase-frequency-detector/charge-pump (PFD–CP) PLL, its phase detector (PD) exhibits higher gain, allowing a reduction in CP current and thus lower current-source thermal noise; furthermore, the absence of a feedback divider eliminates divider-induced thermal noise and power consumption. Because the CP-originated output noise of a PLL scales inversely with the square of the loop gain, the in-band phase noise (PN) of a divider-less SSPLL is suppressed more strongly than that of a conventional PLL [7]. On the other hand, the sub-sampling PD (SSPD) is highly sensitive to phase error, has a narrow capture range, is vulnerable to disturbances, and does not provide frequency information; therefore, the SSPD alone cannot acquire lock at the desired frequency. Practical systems thus accompany it with a coarse loop that assists stable SSPD operation and lock acquisition. Prior works have adopted a dead-zone PFD–CP PLL as the coarse loop [5,7]. However, a PFD–CP PLL requires an analog loop filter, incurring area overhead, and loop handover demands precise loop gain matching, increasing design complexity. Moreover, stable fractional-N operation requires a delta–sigma modulator (DSM), a digital-to-time converter (DTC), and DTC gain calibration; executing such calibration during analog PLL operation calls for additional circuitry. More recently, to reduce area and power while maintaining stable fractional-N behavior, digital coarse loops have been reported [8]; nevertheless, they still rely on a time-to-digital converter (TDC), which complicates design and necessitates extra calibration to set a conversion range aligned with the VCO period.

This paper proposes a SSPLL with a TDC-free digital coarse loop built on a counter-assisted digital PLL (DPLL). In the coarse loop, a DSM and a DTC jointly replace fractional error sensing of the TDC, while the counter-assisted frequency-domain framework forms an auxiliary frequency-locked loop (FLL) to provide a wide capture range and precise fractional-N synthesis. The fine loop employs a high-gain SSPD to suppress in-band PN, and the DTC gain calibrated in the coarse loop is handed off to the fine loop to stabilize loop handover. The proposed 4–5 GHz PLL achieves an active area of 0.146 mm², 177 fs RMS jitter, and a figure of merit (FoM) of −245.6 dB under a 104 MHz reference. The remainder of this paper is organized as follows: Section 2 shows the system architecture, Section 3 explains the DSM-based frequency control word (FCW) modulation, Section 4 describes the DTC gain calibration, Section 5 presents simulation results, and Section 6 concludes the work.

2. System Architecture

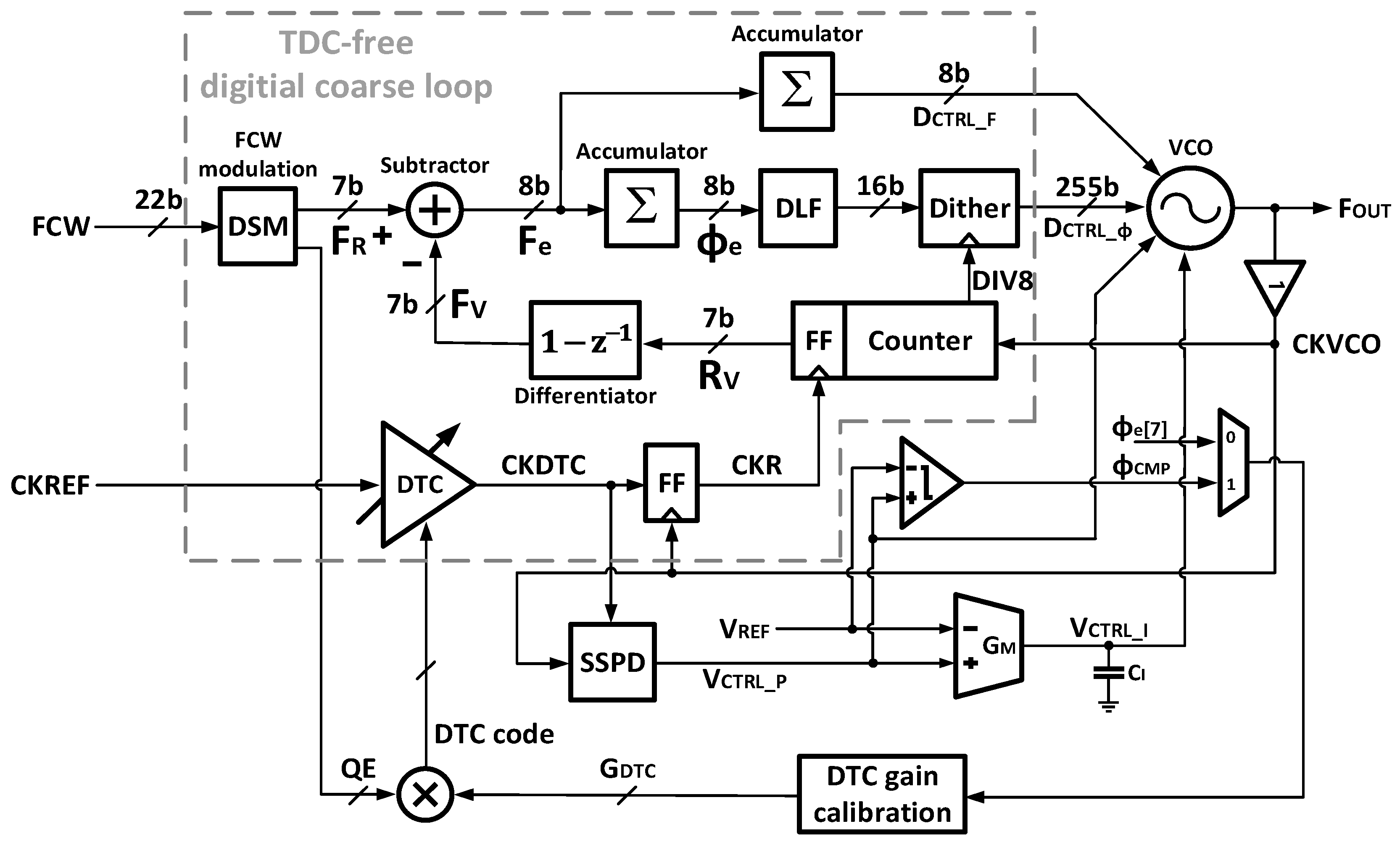
Figure 1 shows the overall block diagram of the proposed sub-sampling PLL. The proposed PLL adopts a dual-loop architecture comprising a digital coarse loop and an analog fine loop. The coarse loop employs a counter-assisted DPLL that, unlike conventional divider-based DPLLs, dispenses with the divider and uses a transition counter to count the number of VCO clock (CKVCO) rising edges within one period of the reference clock (CKREF). This provides a digital estimate of phase, which is compared with the integrated FCW to produce a digital phase error code [9]. Compared with divider-based DPLLs, this approach avoids shaped quantization noise and being digital-intensive, benefits from the speed and scaling of advanced CMOS nodes. In this work, a differentiator is inserted in the feedback path of the counter-assisted DPLL to convert the VCO phase code R_V into a frequency code F_V; comparing F_V with the reference FCW yields a frequency-error code F_e. An additional integrator inside the coarse loop forms an auxiliary FLL path, enabling fast frequency convergence during initial acquisition. Once the frequency is quickly settled, the same counter-assisted framework transitions to phase locking: the frequency error F_e is routed through an integrator and a digital loop filter (DLF) along the PLL path to complete lock.

The fine loop adopts an analog SSPLL structure. It comprises a VCO isolation buffer, an SSPD that converts the phase difference between CKDTC and CKVCO into a proportional-path voltage V_{CTRL_P}, a voltage-to-current converter (GM) with an integrating capacitor C_I, a comparator, and the DTC, DSM, and VCO shared with the coarse loop. In conventional sampling PLLs, a differential-phase topology is often used to suppress common-mode noise and improve sampling accuracy. However, if the time-to-voltage slope of the two paths is not perfectly symmetric, fixed spurs arise. Moreover, to suppress sampler-induced feedthrough and Binary frequency-shift keying (BFSK)-like effects, a VCO buffer is required; yet inserting the buffer tends to make the voltage slopes excessively large, necessitating a ramp generator. Implementing two ramp generators for the differential-phase symmetrically is technically challenging due to rising/falling edge timing differences and circuit imbalance. For these reasons, the proposed design adopts a single-phase topology, which avoids symmetry issues and allows the lock point to be selected simply by setting the reference voltage, easing the DC biasing of the comparator and GM.

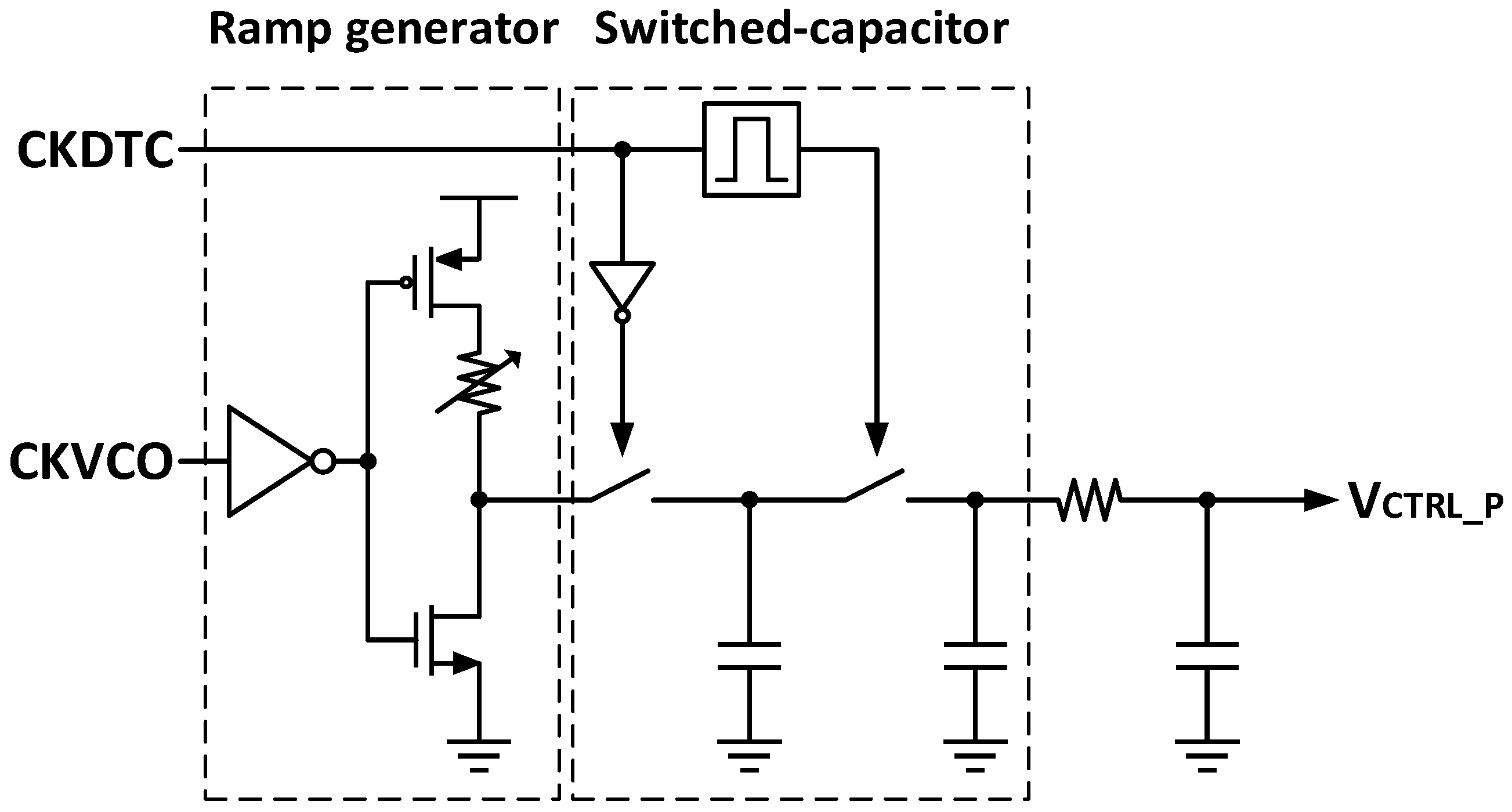
Figure 2 shows the circuit of the designed SSPD. In the fine loop, the SSPD is the key block that detects phase error by converting the time difference between CKDTC and CKVCO into voltage. A higher SSPD gain K_SSPD (output voltage per input phase) lowers the in-band PN of the PLL, improving jitter performance. The gain is set by the voltage slope of the ramp generator K_SLOPE as

$$K_{SSPD}={\displaystyle \frac{\Delta v}{\Delta \varphi }}={\displaystyle \frac{K_{SLOPE}}{2\pi f_{ref}}}.$$

(1)

The in-band PN contribution of the PD/CP can be expressed as an equivalent noise power spectral density (PSD). Using the transconductance $g_m$ of the GM cell, Boltzmann constant $k$, and absolute temperature $T$, it is given by

$${PSD}_{PD+CP}={\displaystyle \frac{16}{3}}\cdot {\displaystyle \frac{kT}{K_{SSPD}^2\hspace{0.17em}{g}_m}}.$$

(2)

Substituting the design values $g_m=1.5 \mu S$ and $K_{SLOPE}=10 GV/s$ (with $T=300 K$ and $f_{ref}=104 MHz$) yields $K_{SSPD}\approx 144/\left(2\pi \right)$, i.e., a very high SSPD gain. Consequently, the in-band noise floor due to the SSPD is calculated to be about −160 dBc/Hz or lower, indicating that the SSPD noise does not limit the PN performance of the fine loop and enables low-PN operation.

However, an SSPD with such high gain is extremely sensitive to input phase error and therefore exhibits a narrow locking range. To hand over control between the coarse and fine loops without instability, the coarse loop must achieve a phase lock as precise as possible. In a conventional counter-assisted DPLL, a TDC is typically employed to reach this precision, but the required high resolution and linearity, together with a conversion range matched to the VCO period, increases circuit complexity and design burden. Moreover, when a DTC is used—as in this SSPLL—an inaccurate DTC gain prevents effective cancelation of DSM-induced quantization error (QE), so the input phase error of the SSPD cannot be kept near zero; with a very narrow locking range, such gain mismatch can even cause the fine loop to fail to converge. To solve the problems simultaneously, the fine loop reuses the DSM and DTC of fine loop and converts the reference path into an integer sequence by DSM-based FCW modulation, achieving precise phase locking without a TDC. In addition, an LMS-based DTC gain calibration is enabled in the coarse stage so that the gain reaches its target and is handed off directly to the fine loop, enabling stable loop switching despite the high SSPD gain. A further benefit is that the VCO phase information accumulated by the counter is processed entirely in the integer domain, allowing the subtractor and integrator to be realized with integer bits only, which simplifies hardware and reduces active area.

3. DSM-Based FCW Modulation

As noted in the previous section, the SSPD in fine loop has a constrained locking range due to its high PD gain. To enable a stable handover from the coarse loop to the fine loop, the fractional-N error should be pre-canceled in the integer domain of the coarse loop. Accordingly, this section proposes (i) converting the FCW into a variable integer sequence via a DSM and (ii) aligning integer-domain grids of the two paths by DTC-based retiming.

In a conventional counter-assisted DPLL, a retimed clock CKR is generated by sampling CKREF with CKVCO so that the number of VCO rising edges within one CKREF period can be counted reliably. Directly sampling the transition counter, which runs in the VCO domain at CKREF timing, would otherwise risk metastability and timing violations due to clock asynchrony; if a CKREF rising edge occurs near a CKVCO rising edge, the counter output can be latched mid-transition and produce an erroneous code [10]. Beyond this practical necessity, the retiming can be interpreted as a quantization of the VCO path: because CKR aligns each CKREF event to the next VCO rising edge, the measured F_V at every CKR cycle is confined to an integer-domain grid. Hence, in the absence of a TDC, F_V appears as an integer-only, periodically varying sequence at steady state. By contrast, the reference frequency code F_R is fixed as same as the FCW that is composed of integer part FCW_int and fractional part FCW_frac; therefore, each quantization of F_V inevitably produces a fractional error code, leading to a mismatch between F_V and F_R in steady state that becomes a dominant source of residual phase error.

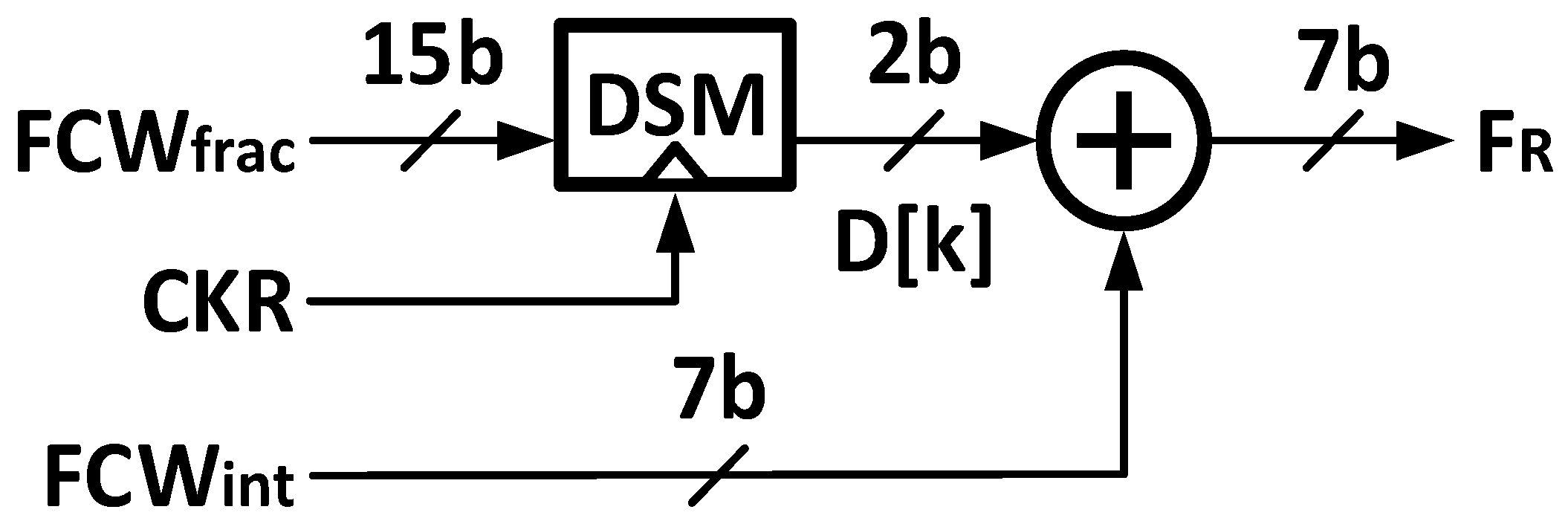
Figure 3 illustrates a block diagram of the proposed DSM-based integer FCW modulation. The DSM modulates FCW_frac into an integer sequence D[k] at each rising edge of CKR indexed by k. The reference frequency code F_R is then redefined as

$$F_R\left[k\right]={FCW}_{int}+D\left[k\right].$$

(3)

The sequence D[k] is constructed as its long-term average equals FCW_frac; hence, the time average of F_R[k] equals the original FCW. Because F_R[k] is quantized by the DSM so that is integer-only rather than a fixed constant, comparing it with F_V causes no fractional mismatch error.

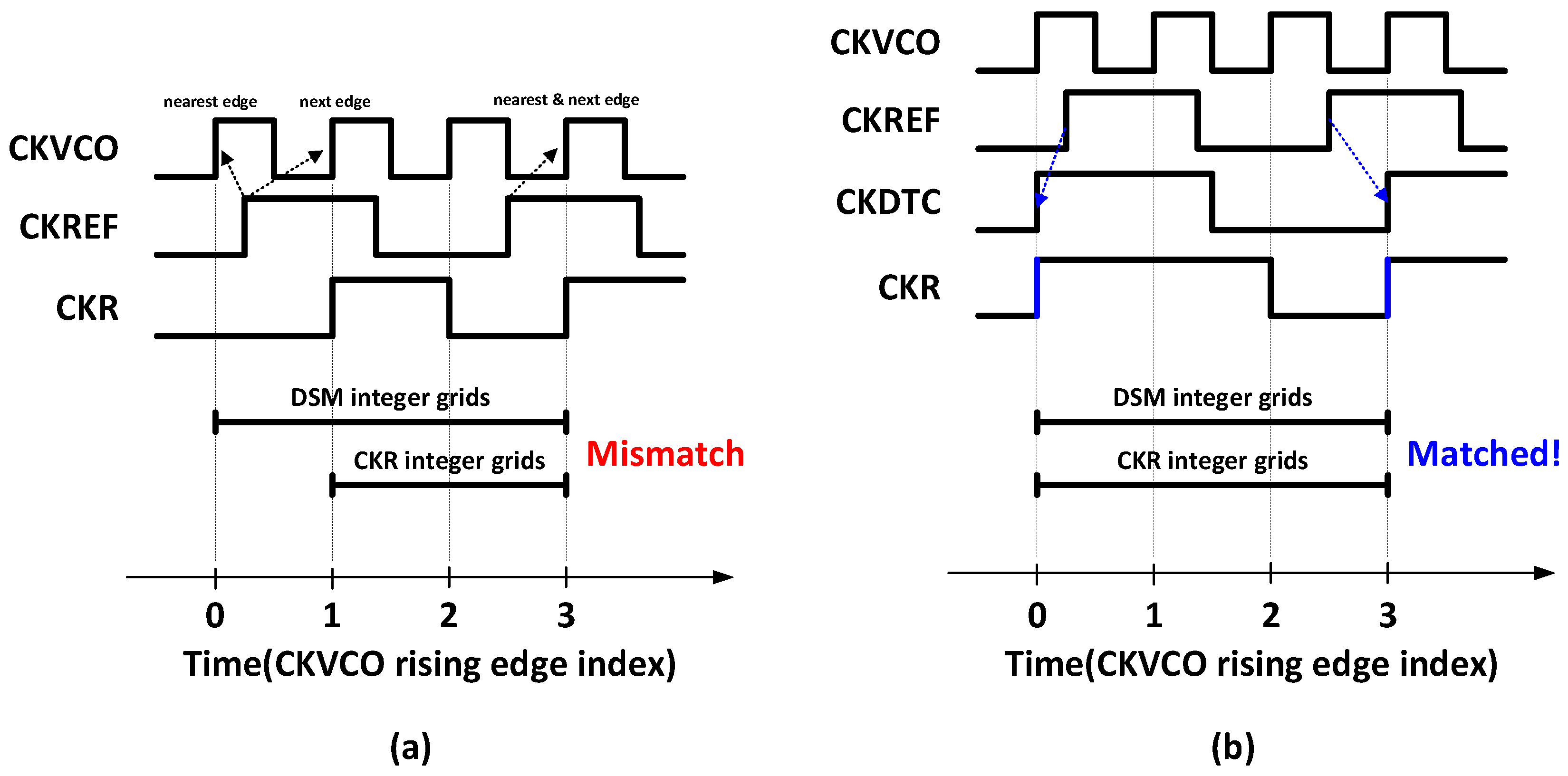
Both F_R and F_V are expressed as integers by the DSM-based FCW modulation; however, their quantization mechanisms are different. Specifically, F_R is quantized by DSM, whereas F_V is quantized by CKR retiming. Figure 4a conceptually depicts the timing of this integer-domain operation when CKR is generated by retiming CKREF. In this case, the DSM performs quantization with respect to the VCO rising edge nearest to each CKREF rising edge, so F_R assumes values set by the DSM integer-grid. By contrast, CKR retiming aligns each CKREF event to the next VCO rising edge, so F_V follows the CKR integer-grid offset. As a result, a mismatch between F_V and F_R reappears.

To fix this mismatch, the quantization of F_V must occur on the same VCO rising edge used by the DSM. Therefore, CKR is now generated by retiming CKDTC with CKVCO instead of retiming CKREF. Because DTC removes the DSM-computed quantization error (QE), CKDTC is aligned to the VCO rising edge nearest each CKREF event. When CKR is derived from CKDTC, CKR is aligned to the same CKVCO edge designated by the DSM, and the quantization of F_V is performed on those identical edges. Figure 4b conceptually illustrates this integer-domain timing: unlike Figure 4a, CKR retiming uses CKDTC, so F_V assumes the same integer-grid offset as F_R. Finally, F_R and F_V are quantized under same integer-grids, and the error F_e = F_R − F_V converges to zero at steady state, enabling precise phase alignment in the coarse stage without a TDC.

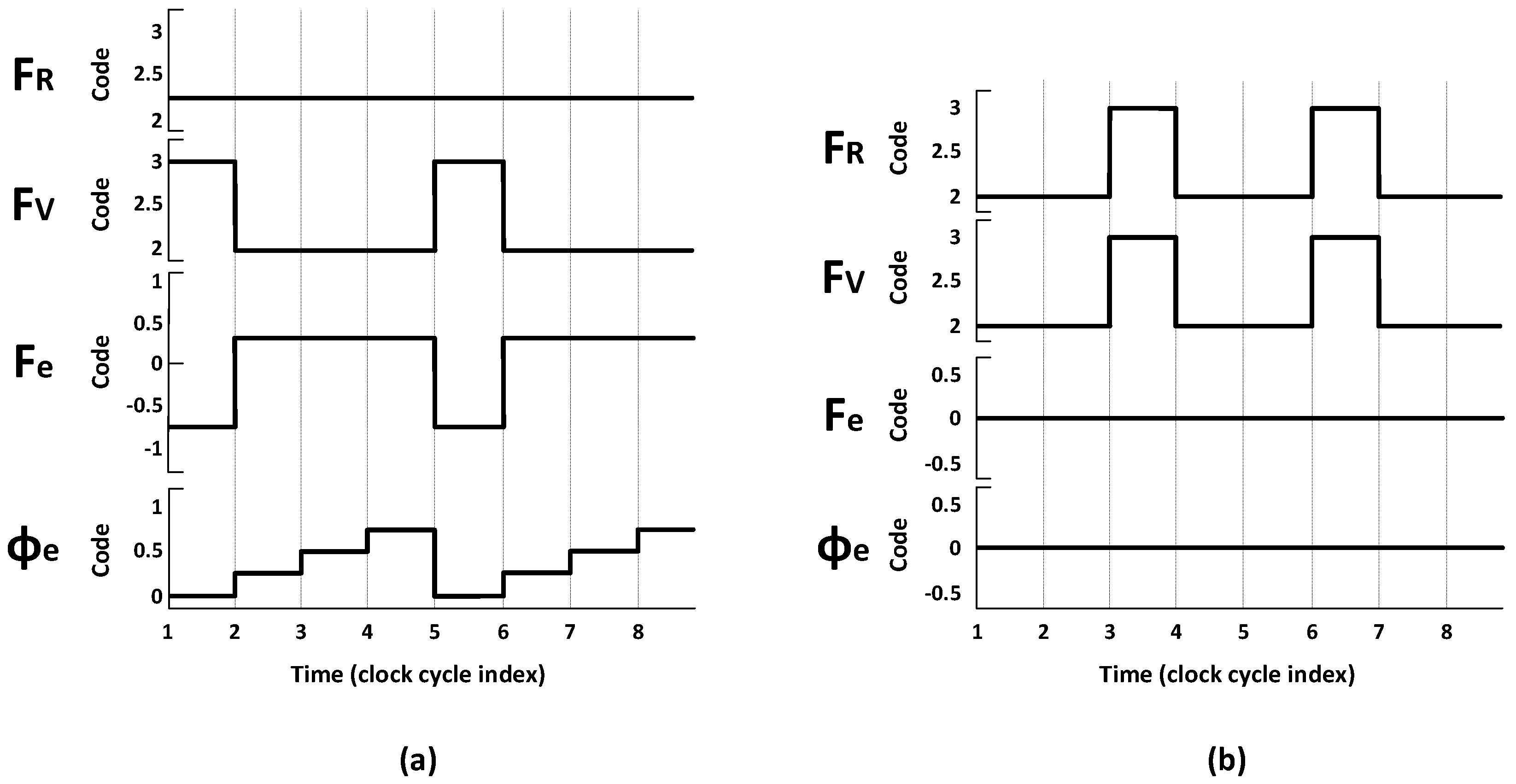
Figure 5 illustrates coarse-loop error detection for FCW = 2.25, comparing cases (a) without and (b) with DSM-based integer FCW modulation. In Figure 5a, F_R is fixed at 2.25 containing both integer and fractional parts, whereas F_V is a periodically varying integer sequence due to CKR retiming; thus, the error F_e = F_R − F_V does not converge to zero and the phase error Φ_e exhibits stair-like values. In contrast to Figure 5a, in Figure 5b, the DSM modulates the FCW into an integer sequence F_R[k]; with DTC-based retiming, F_V is aligned to the same integer-domain grid, so F_e and Φ_e are held at zero in steady state.

In summary, the proposed method (i) quantizes the FCW by using a DSM to modulate its fractional part into a time-varying integer sequence, (ii) unifies the integer-domain grids of the two paths by shifting the reference edge with a DTC, and (iii) achieves precise phase lock without a TDC via the steady-state convergence of F_e to zero. Because any DTC gain deviation maps directly to grid misalignment, a background gain calibration loop is essential; its implementation is detailed in the next section.

4. DTC Gain Calibration

Building on the integer FCW modulation and DTC retiming of the previous section, the coarse loop achieves zero F_e at steady state. To preserve this alignment across the operating range and hand over control to the high-gain fine loop without instability, it is essential to rapidly converge and maintain the DTC gain G_DTC during the coarse stage and continuously carry its value into the fine loop. This section explains the role of DTC gain calibration in the proposed architecture, specifies the stage-wise requirements for the coarse loop and fine loop, and presents a calibration loop that meets these requirements. DTC generates the time delay corresponding to the DSM-computed quantization error (QE), aligning CKDTC to the CKVCO edge designated by the DSM. If G_DTC is erroneous, the QE compensation becomes under- or over-scaled, leaving integer-grid misalignment and preventing F_e from remaining at zero. In the fine loop, any G_DTC error likewise hinders removal of fractional-N error and can induce unstable behavior at the SSPD output due to its narrow locking range. Therefore, (i) in the coarse stage, G_DTC must be driven quickly to its target to satisfy loop-switching conditions, and (ii) in the fine stage, calibration must proceed with a narrow bandwidth to minimize residual error and spurs.

The optimal value of G_DTC is defined as follows: the actual time delay corresponding to the QE is

$$t_{QE}=T_{VCO}\times QE.$$

(4)

To compensate for QE, a DTC with single-LSB time resolution $\Delta t_{DTC}$ produces a delay

$$t_{DTC}=\Delta t_{DTC}\times DTC code.$$

(5)

Introducing the scale factor DTC gain G_DTC,

$$DTC code=G_{DTC}\times QE,$$

(6)

so that

$$t_{DTC}=\Delta t_{DTC}\times G_{DTC}\times QE.$$

(7)

The alignment condition requires that

$$t_{QE}=t_{DTC},$$

(8)

which yields the proportionality constant that maps the digital code to physical time delay:

$$G_{DTC}={\displaystyle \frac{T_{VCO}}{\Delta t_{DTC}}} .$$

(9)

When this relation holds, DTC generates the correct time delay proportional to QE, aligns CKDTC to the nearest rising edge of CKVCO, and thereby cancels the quantization error in the time domain.

Due to this process, supply voltage, and temperature (PVT) variations, the DTC unit delay $\Delta t_{DTC}$ deviates from its design value and drifts over time; hence, background DTC gain calibration is essential for robust operation. An LMS-based scheme is adopted that incrementally updates the current G_DTC from the correlation between the signs of the DSM QE and the loop error, and the calibration is divided into coarse and fine stages to achieve, respectively, fast convergence and high precision. The update of coarse stage is

$$G_{n+1}=G_n+{\alpha }_c\times \hspace{0.17em}sgn\left(Q{E}_n\right)\hspace{0.17em}\times sgn\left({\varphi }_{e,n}\right),$$

(10)

where ${\alpha }_c$sets the calibration bandwidth, $sgn(\cdot )$ denotes the sign function, and Φ_e,n is the digital phase error at iteration n. To drive G_DTC rapidly toward its target, a relatively large ${\alpha }_c$ is chosen; however, if ${\alpha }_c$ is too large and the coarse stage calibration bandwidth exceeds the bandwidth of the coarse loop, the calibration loop can become unstable and the residual gain error may produce a fractional error outside the locking range of the SSPD. Thus, ${\alpha }_c$ is selected considering the bandwidth of the coarse loop and the SSPD lock range. After G_DTC has converged to its optimum value and Φ_e,n remains within a preset threshold for ≥63 digital clock cycles, the system declares convergence of the coarse loop and performs handover to the fine loop. The update of the fine stage is

$$G_{n+1}=G_n+{\alpha }_f\times sgn\left(Q{E}_n\right)\times sgn\left({\varphi }_{cmp,n}\right),$$

(11)

where Φ_cmp,n is the phase polarity signal of the fine loop derived by the comparator and small ${\alpha }_f$ narrows the fine stage calibration bandwidth to refine G_DTC. A too small ${\alpha }_f$ prolongs the removal of residual error, so it is chosen with lock time in mind. With this fine stage calibration, the G_DTC handed off from the coarse stage is tightly trimmed, reducing fractional error in the fine loop and minimizing spur and jitter sensitivity to gain drift.

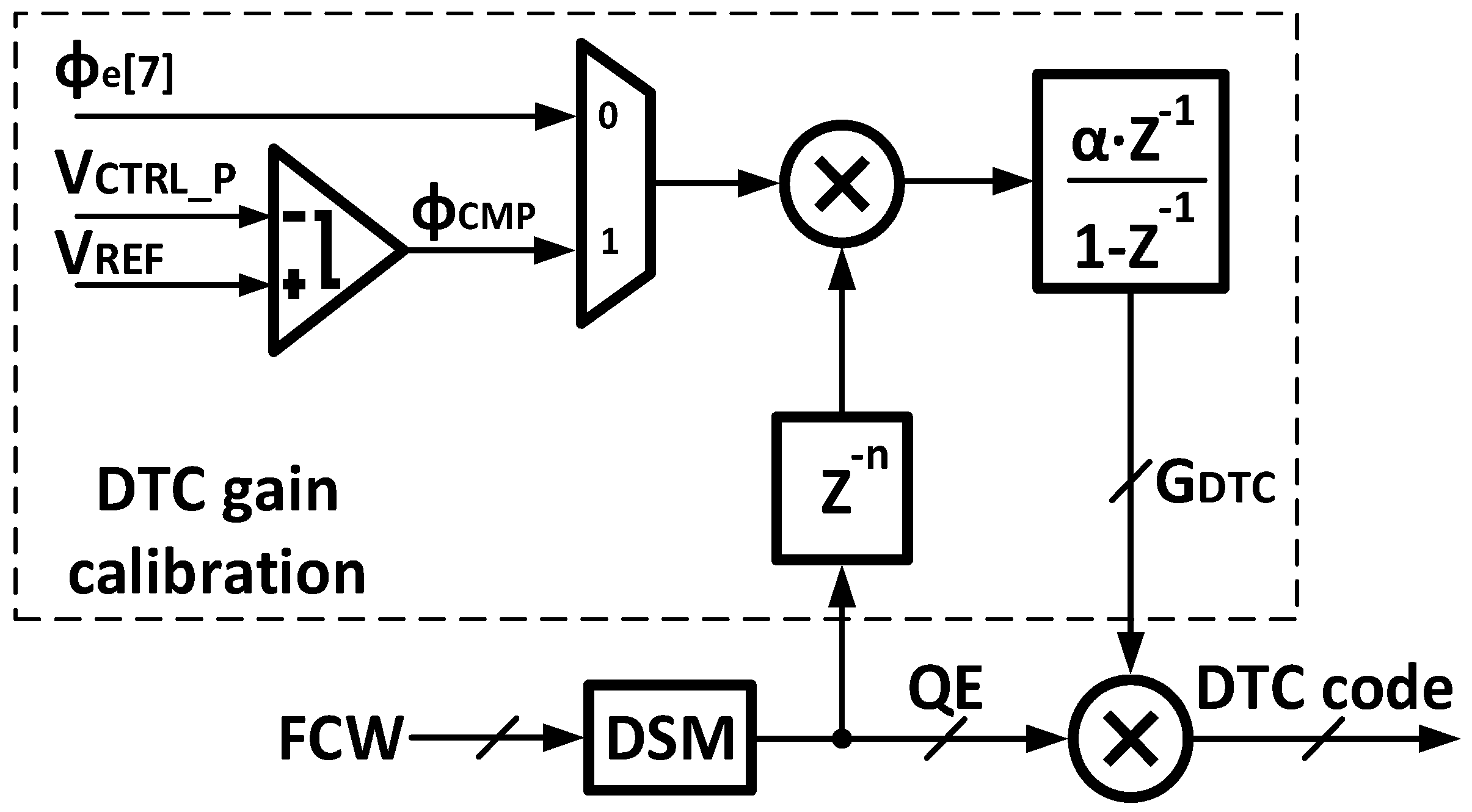
Figure 6 depicts the block diagram of the DTC gain calibration. The loop implements an LMS-based correlation algorithm and operates in two stages. In the coarse stage, the input is the digital phase error of the coarse loop Φ_e. In the fine stage, the input is the comparator output Φ_cmp, which represents the polarity of the phase error of fine loop. A MUX selects between these two signals according to the active stage, and the adaptation step sizes ${\alpha }_c$ and ${\alpha }_f$ are programmed for the coarse and fine stages, respectively.

In summary, this hierarchical LMS calibration drives G_DTC rapidly to its optimum, removing the DSM-induced QE, improving accuracy of phase detection in both loops, and ensuring robust coarse-to-fine loop switching.

5. Simulation Results

Section 5 presents the implementation and simulation results of the proposed PLL. The circuit was implemented in a 28 nm CMOS process (Samsung 28 nm LPP CMOS) using the Cadence Virtuoso environment. Post-layout parasitics were extracted with Synopsys StarRC and included in the simulations. Mixed-signal behavior was verified using the Cadence AMS flow with Specter for the analog parts and Verilog models for the digital logic. Figures 8 and 9 present post-layout transient simulation results including the extracted parasitics. For the system-level verification and calibration analysis in Figures 10 and 11, the transistor-level analog circuits were replaced by behavioral models while keeping the digital logic unchanged; these simulations were also carried out in the Cadence AMS environment. All waveform data used to generate Figures 8–11 were exported from the simulator and post-processed in MATLAB to produce the plotted results. Figure 7 shows the layout of the PLL implemented in a 28 nm CMOS process. The PLL operates over 4–5 GHz with an active area of 0.146 mm². At a 104 MHz reference, the fine loop consumes 8.94 mW.

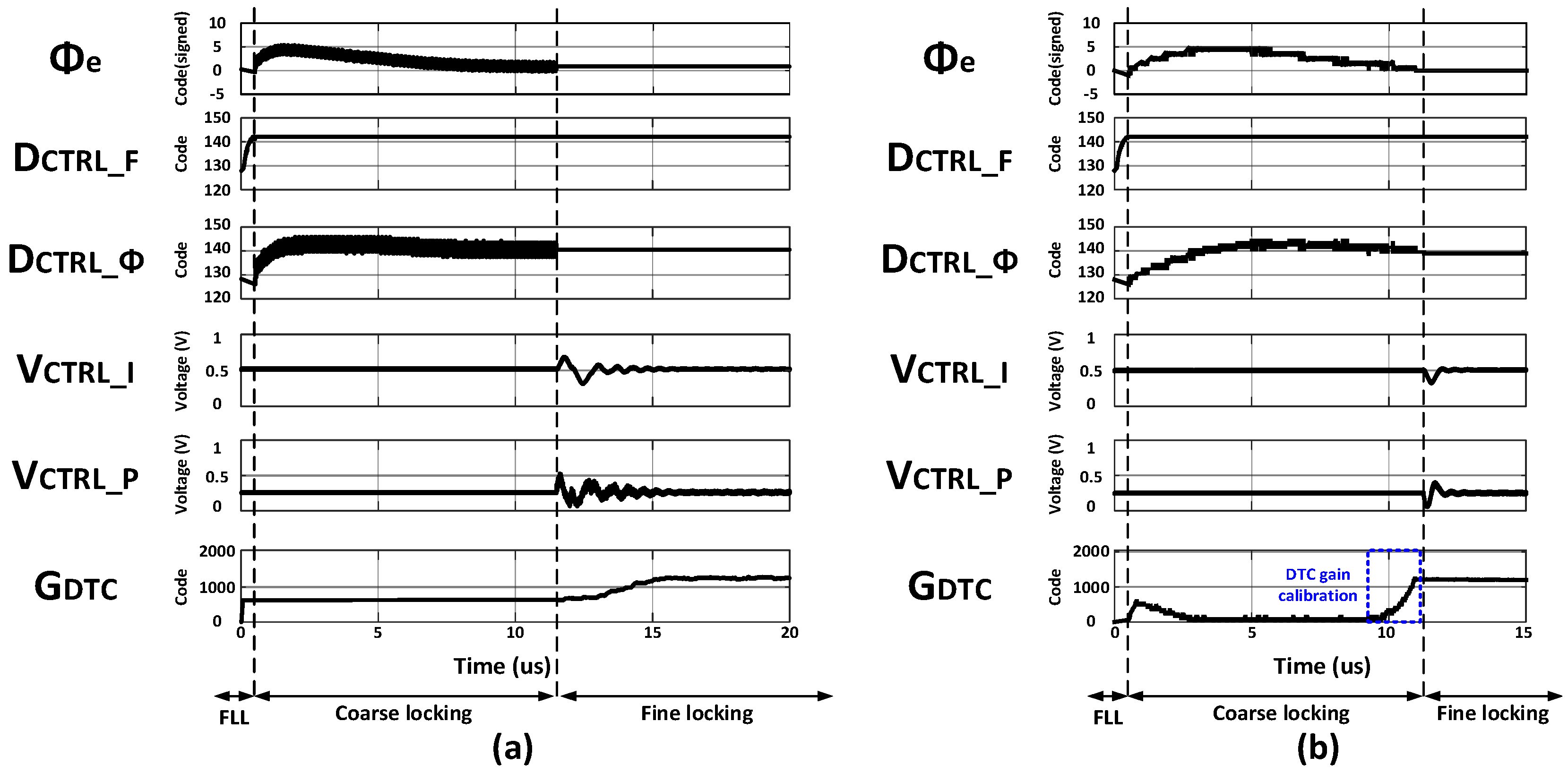
Figure 8 presents post-layout transient simulation results that visualize phase locking and calibration of the overall PLL. Figure 8a shows the case without DSM-based FCW modulation. Here, the reference path code F_R remains fixed to the FCW (containing both integer and fractional parts), whereas the variable path code F_V is quantized by reference retiming. Consequently, the error F_e = F_R − F_V does not converge to zero, and the accumulated phase error Φ_e exhibits a staircase profile at steady state. The coarse-loop control code D_{CTRL_Φ} therefore fails to settle precisely, and fine phase locking is not achieved. In addition, because no DTC gain calibration runs in the coarse loop, G_DTC cannot reach its optimum; the resulting input error can exceed locking range of the SSPD. After handover to the fine loop, V_{CTRL_I} and V_{CTRL_P} do not settle promptly, requiring extra time for both phase alignment and DTC gain correction; the overall lock time is thus prolonged. Figure 8b shows the case with DSM-based FCW modulation. Unlike Figure 8a, the coarse loop quantizes F_R via DSM and aligns it to the same integer-domain convention as F_V; as a result, F_e and Φ_e are held at zero in steady state. In parallel, G_DTC converges near its target already within the coarse loop and is handed off to the fine loop, keeping the SSPD input phase error small. Following handover, V_{CTRL_I} and V_{CTRL_P} settle within 1 µs, yielding a noticeably shorter lock time. In summary, DSM-based FCW modulation enables precise coarse-loop phase alignment and effective DTC gain calibration at the coarse stage, which together improve the stability of loop switching and reduce acquisition time.

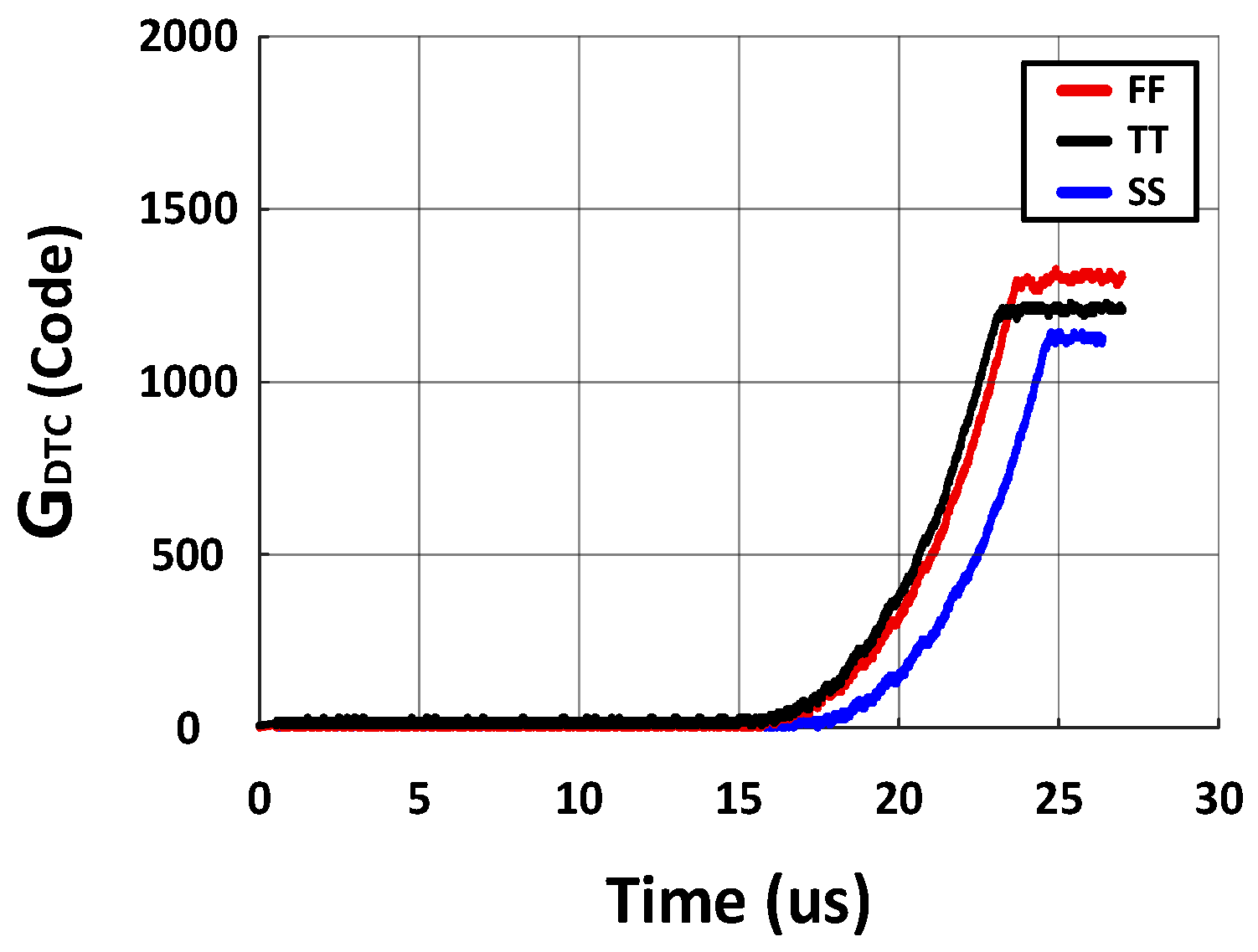
Figure 9 presents the post-layout transient results of the coarse-loop DTC gain calibration across CMOS process corners (SS, TT, FF). The ideal DTC gain, given by Equation (9), is $G_{DTC}={\displaystyle \frac{T_{VCO}}{\Delta t_{DTC}}}$. With the VCO target frequency fixed at 4.5 GHz, the minimum delay of DTC ($\Delta t_{DTC}$) varies with the process corner; hence, G_DTC differs across SS/TT/FF—higher for smaller $\Delta t_{DTC}$ and lower for larger $\Delta t_{DTC}$. Figure 9 shows that the implemented PLL successfully calibrates the gain across all three corners.

The models used in the simulations for Figure 10 and Figure 11 were designed to operate in a manner closely matching the actual circuits based on design parameters. In particular, the time resolution corresponding to one least significant bit (LSB) of the DTC code, denoted as $\Delta t_{DTC}$, was set to the design value of 750 fs/LSB, and the DTC nonlinearity was incorporated into the model.

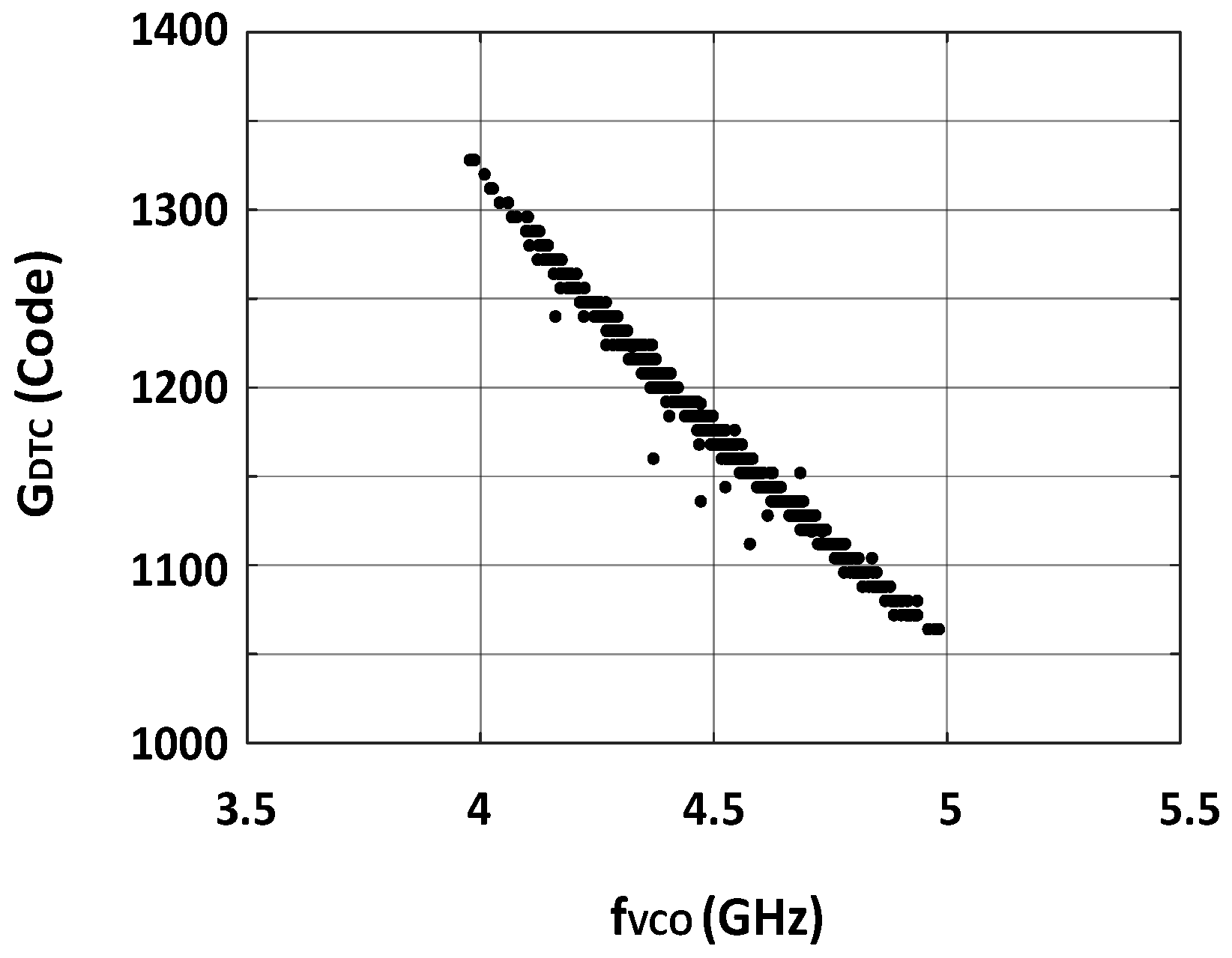
Figure 10 presents the DTC gain calibration results obtained from modeling simulations in the coarse loop. As shown in Figure 10, the converged G_DTC values are distributed almost linearly with respect to the VCO operating frequency, indicating that the condition of Equation (9) was satisfied and the DTC gain was accurately calibrated across the entire PLL operating range through coarse loop gain calibration alone.

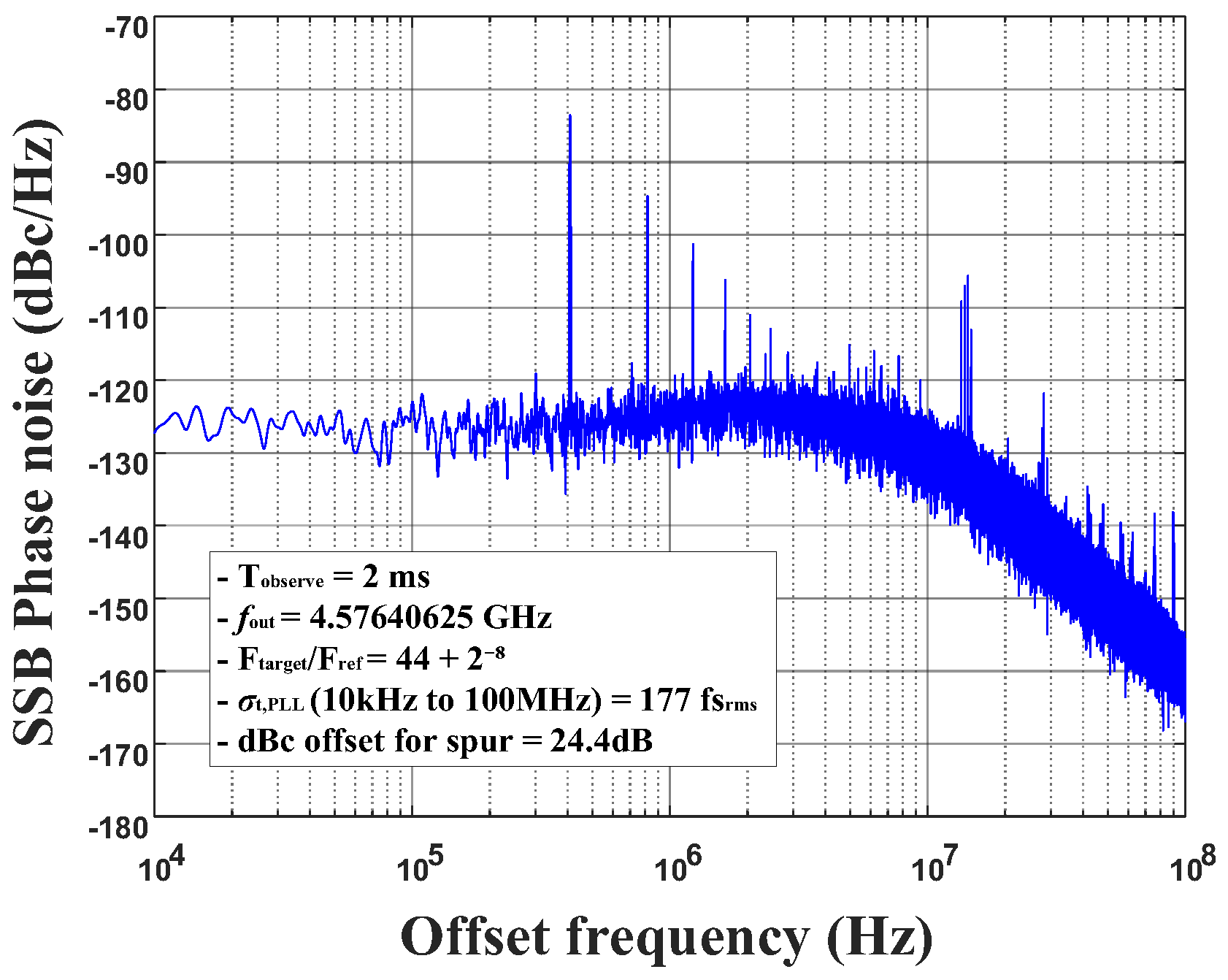
Figure 11 shows the simulated PN spectrum of the proposed PLL using modeling. At the output frequency of 4.57640625 GHz ($FCW=44+2^{-8}$), the integrated RMS jitter over the 10 kHz–100 MHz offset range was evaluated to be 177 fs,_RMS. This result demonstrates that the proposed fine loop achieves high performance with low jitter as designed.

Table 1. Performance comparisons with previous LC-VCO analog PLLs.

Research		This Work	JSSC’19 [5]	ISSCC’19 [11]	JSSC’18 [12]	JSSC’16 [13]
Technology (nm)		28	28	28	65	28
Architecture	Fine loop	Sub-Sampling PLL	Sampling PLL	PFD-CP PLL	ILCM PLL	Sub-Sampling PLL
	Coarse loop	Counter-assisted DPLL	PFD-CP PLL	NA	Bang-Bang DPLL	NA
fREF (MHz)		104	52X2	40X4	115	40
fOUT (GHz)		4–5	6.33	5.83	6.75–8.25	10.1–12.4
RMS jitter (fs)		177 (10 k to 100 M)	75 (10 k to 10 M)	110 (10 k to 10 M)	177 (10 k to 30 M)	197 (10 k to 40 M)
Power (mW)		8.94	18.9	22.8	13.4	5.6
FoMPN * (dB)		−245.6	−249.7	−245.6	−243.8	−247.6
FoMArea * (dB)		−254	−253.2	−248.9	−249.5	−253.6
Core area (mm2)		0.146	0.45	0.47	0.27	0.25
Supply voltage (V)		1	1.1	NA	0.9	NA

* FoM_PN = 10 · log (σ(s)² + P(mW)), FoM_Area = FoM_PN + 10 · log (Area(mm²)).

compares the performance of the proposed PLL with that of recently reported LC-VCO-based analog PLLs. The proposed PLL achieved a FoM regarding PN (FoM_PN) of –245.6 dB and an area-normalized FoM (FoM_Area) of –254 dB, confirming that the area efficiency of this work is competitive among state-of-the-art analog PLLs.

6. Conclusions

This work presented a 4–5 GHz SSPLL that integrates a TDC-free digital coarse loop with a high-gain SSPD fine loop. The counter-assisted frequency-domain structure of the coarse loop, augmented by an FLL path, provides rapid initial frequency acquisition. By reusing DSM and DTC in the coarse loop—DSM for integer-domain FCW modulation and DTC for time-domain alignment on the same quantization grid—the phase error of the coarse loop is driven to zero in steady state, enabling precise fractional-N synthesis without a TDC. A hierarchical LMS-based DTC gain calibration operates in the coarse and fine loop, and the calibrated G_DTC is handed off to the fine loop, yielding fast gain convergence and stable loop switching even with narrow locking range of the SSPD. Simulations of a 28 nm CMOS implementation confirm 0.146 mm² active area, 8.94 mW power, and 177 fs RMS jitter, indicating high performance per area and reliable operation across the target band. Future directions include nonlinearity compensation of the DTC to further reduce fractional spurs and long-term robustness studies under on-chip temperature/voltage variations and aging, as well as silicon validation of the proposed architecture.