Multi-Functional Impedance Measurement by Means of Fractional-Order Harmonic Injection

Abstract

As power electronic converters increase in scale, impedance measurement has become critical for assessing system stability, detecting islanding, and performing other critical analyses. This paper derives the impedance from the voltage and current responses measured after controlled perturbations, employing d-q frame impedance matrices. A static var generator (SVG) with redundant capacity is employed as the perturbation source, and a fractional-order repetitive control (FORC) strategy is introduced to inject the multi-frequency signal efficiently, eliminating the need for additional hardware. By optimizing the perturbation design and suppressing the dynamic error of the phase-locked loop, the method achieves both convergence and accuracy. Comprehensive simulations and experiments validate the approach.

1. Introduction

With the growing penetration of renewable energy sources, power electronic devices like photovoltaic inverters and energy storage converters have been widely integrated into the power grid [1]. As a core parameter reflecting converter characteristics, the impedance model serves as the theoretical basis for system analysis, with typical applications including stability analysis, islanding detection, and fault location [2]. Methods for obtaining the impedance model include analytical impedance modeling and actual impedance measurement [3,4]. The former requires detailed converter parameters, which limits its practical application. Thus, direct impedance measurement at the port has emerged as a key approach in research.

Impedance measurement methods can be broadly categorized into passive measurement and active perturbation injection methods [5]. Passive methods are hampered by limited accuracy and the inability to conduct targeted measurements. As a result, existing impedance measurement methods mainly rely on active perturbation injection, which involves injecting excitation signals into the system and analyzing the corresponding response data to compute the impedance [6]. This approach offers higher accuracy and flexibility, making it the preferred choice for applications requiring detailed impedance characterization.

To measure the impedance at each frequency, the active method injects small-signal perturbations into the system. In [7,8], impedance was measured precisely using single-sine perturbation, which offers the optimal signal-to-noise ratio (SNR) but requires a relatively long measurement time. To achieve rapid impedance measurement, wideband perturbation signals are adopted. Refs. [9,10], respectively, proposed impedance identification methods based on segmented chirp and Gaussian pulse, which can achieve rapid measurement. However, the parameters need to be carefully determined, such as the number of segments in [9] and the pulse width in [10]. Liu et al. modified the pseudo-random binary sequence (PRBS) and ternary sequence into the driving signal to avoid affecting the operation of the converter [11], but the spectral energy was uncontrollable and prone to noise interference. Berg et al. eliminated the cross-coupling of DQ domain perturbations through orthogonal sequence injection and frequency-domain interpolation [12]. Li et al. improved the accuracy by quantifying the frequency coupling error based on generalized SNR and extracting with error bar overlap [13], but it relies on the maximum estimation of noise, and the actual noise statistical characteristics are difficult to obtain. Multi-sine signal injection combines the advantages of high measurement efficiency and controllable spectral characteristics [14]. Ref. [15] proposed a multistage multi-sine design method, but it involves complex calculations and requires multiple sets of measurements, resulting in an increase in time consumption.

Apart from the considerations of accuracy and time, these perturbation signals are generated by specially designed devices. Refs. [9,16] proposed series voltage or parallel current perturbation devices. These devices, however, entail high costs and complex control, which increases the hardware expense and complexity. Some novel impedance measurement methods in [17,18] inject disturbances internally within the controller, a strategy that may help reduce the cost but overlooks the black-box nature of converters.

In conclusion, existing impedance matrix measurement schemes are hindered by two critical limitations that impede their engineering application. First, they predominantly rely on dedicated perturbation equipment, which not only incurs high hardware costs but also necessitates complex modifications to system wiring. Second, the injected perturbation signals in these schemes face difficulty in simultaneously balancing three key objectives: spectrum controllability, logarithmic uniform distribution of frequency points, and avoidance of frequency coupling.

To address the issues, considering that static var generators (SVGs) have been widely deployed in modern power systems, this paper proposes a multi-functional impedance measurement method based on fractional harmonic injection. The main contributions are as follows.

(1)

Hardware cost reduction via SVG reuse: This method utilizes the redundant capacity of SVGs to implement disturbance current injection, eliminating the need for system wiring modifications and reducing hardware costs.

(2)

Flexible frequency control via fractional-order repetitive control (FORC): A multi-sine perturbation signal control scheme based on FORC is proposed, which enables flexible configuration of disturbance signal frequencies.

(3)

Multi-objective perturbation signal design: A perturbation signal design scheme is introduced.

The frequency of the disturbance signals avoids background harmonics to prevent interference and meets the requirement of logarithmic scale uniformity in Bode diagram analysis.

2. FORC

To enable the simultaneous injection of disturbance signals at multiple frequencies, repetitive control (RC) is employed in this paper. RC, based on the internal model principle, significantly enhances the system’s tracking accuracy for periodic signals. The structure of traditional RC is depicted in Figure 1a, where, the input is the tracking error. Here, $Q\left(z\right)$ functions as a low-pass filter, and its expression is given by

$$Q\left(z\right)=a_{1}z+a_0+a_1{z}^{-1}$$

(1)

$$2a_1+a_0=1$$

(2)

Additionally, $G_f\left(z\right)$ is a phase-lead filter, employed to enhance system stability. In this control scheme, $z^{-N}$ denotes an N-step delay, where $N=f_s/f_b$. Here, $f_s$ represents the sampling frequency, and $f_b$ is the fundamental frequency of the perturbation signal. The RC introduces poles near the fundamental frequency and its integer multiples. As a result, the magnitude response of the RC exhibits peaks at these frequencies, thereby enabling precise tracking of multi-frequency sinusoidal signals.

However, this control limits the range of perturbation frequencies that can be selected, as N must be an integer. Under this constraint, the selection of frequency points can rarely satisfy the requirements for Bode plots. The FORC method provides a solution for implementing fractional-order delays, thereby allowing the frequencies of perturbation signals over a broader range. The implementation of FORC is shown in Figure 1b. This method approximates the equivalent fractional-order delay using the Lagrange interpolation method. When N is a non-integer, $z^{-N}$ can be expressed as $z^{-N_i-F}$, where $N_i$ represents the integer part of N, and F denotes the fractional part. The $N_i$-order delay is directly implemented, whereas the F-order delay is equivalently represented using a Lagrange interpolation polynomial, as follows:

$$z^{-F}\approx \sum _{k=0}^n{A}_k{z}^{-k}$$

(3)

where $k=0,1,\dots ,n$, and n is the order of the polynomial. $A_k$ represents the coefficients of the polynomial, which are given as

$$A_k=\prod _{i=0,i\ne k}^n{\displaystyle \frac{F-i}{k-i}},k,i=0,1,\dots ,n$$

(4)

Consider an example where the system sampling frequency is 10 kHz and the fundamental frequency of the reference signal is 220 Hz. In this scenario, the value of $N_i$ can be determined to be 45, while $F=5/11$. For the control configuration, $n=3$ is selected to approximate the fractional-order delay. Additionally, the low-pass filter $Q\left(z\right)$ is set to $0.1z+0.8+0.1z^{-1}$, and $G_f\left(z\right)=z^2$ is employed for phase compensation. The Bode plot of FORC is depicted in Figure 2. As observed, substantial gains are present at 220 Hz and its integer multiples, while the phase remains at $0^{\circ }$ at these frequencies. This result verifies the controller’s accurate tracking capability without introducing additional phase shift.

3. Multi-Functional Control for Impedance Measurement

The renewable energy system contains a variety of converters, each serving different functions. For instance, there are renewable energy converters for power transfer from renewable sources, as well as devices that enhance the system’s power quality, such as SVGs and active power filters. To measure the output impedance of converters, this paper proposes using the SVG with redundant capacity as the perturbation current injection device. This approach significantly reduces the investment required for impedance measurement equipment. Based on this setup, the key issue in impedance measurement lies in how to accurately inject the perturbation signal into the system while satisfying the requirements for spectral controllability, logarithmic uniform distribution of frequency points, and avoiding frequency coupling. This section therefore presents the control strategy and design process for the perturbation signal to address this key challenge.

3.1. Multi-Functional Controller

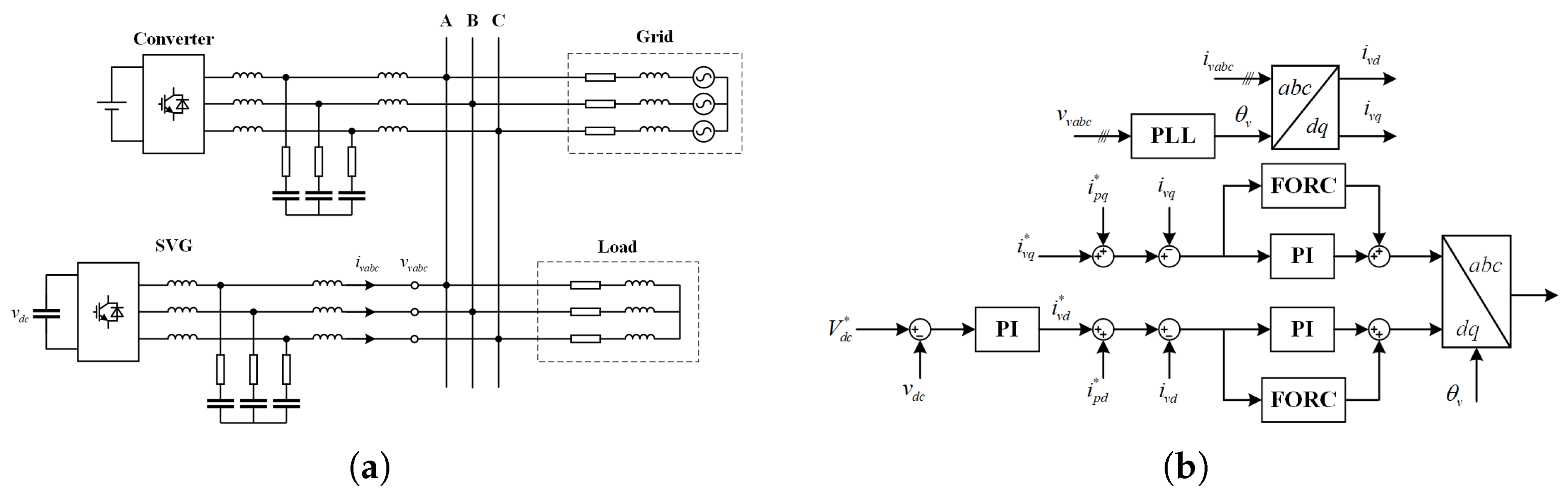
Figure 3a shows a simplified renewable energy system, where a renewable energy converter is connected to the point of common coupling (PCC), with its control structure is presented later.The load $Z_L=R_L+\mathrm{j}{\mathrm{X}}_{\mathrm{L}}$ represents a three-phase inductive load. An SVG is employed to compensate for the system’s reactive power and is connected to an LCL filter. Moreover, the SVG also serves to inject perturbation currents into the system. To fulfill these dual roles, the control strategy of the SVG needs to be optimized, as detailed in Figure 3b.

In this paper, perturbation signals with multiple frequencies are injected simultaneously. To achieve precise control of multi-frequency sinusoidal signals, the perturbation controller must have appropriate control characteristics. For this purpose, FORC is employed as the perturbation controller.

In the figure, $V_{dc}$ denotes the DC-side capacitor voltage, while $v_{vabc}$ and $i_{vabc}$ represent the voltage and current at the output port of the SVG, respectively. The controller comprises a voltage loop and a current loop. The voltage loop regulates the DC-side voltage via Proportional–Integral (PI) control, with $V_{dc}^{*}$ serving as the reference voltage value. The current loop is designed to control reactive power and the perturbation current. Here, $i_d^{*}$ and $i_q^{*}$ represent the reference values of the d-axis and q-axis currents, respectively. These reference values are derived by summing the DC reference values $i_{vd}^{*}$ and $i_{vq}^{*}$ with the perturbation signal reference values $i_{pd}^{*}$ and $i_{pq}^{*}$. Specifically, $i_{vq}^{*}$ determines the output reactive power. $i_{vd}$ and $i_{vq}$ denote the d-axis and q-axis currents, respectively. ${\theta }_v$ represents the synchronous phase obtained from the phase-locked loop (PLL). The control structure of the current loop combines a PI controller and a perturbation controller, used to regulate the DC reference signal and the perturbation signal, respectively.

Based on this control strategy, the sensitivity of the dominant poles to various parameters is analyzed in Figure 4. Sensitivity is defined as the per-unit value of the variation in the modulus of the dominant pole divided by the per-unit value of the variation in the parameter. Figure 4 analyzes the degree of influence of each control parameter in the SVG controller and the grid inductance $L_g$ on the dominant poles. The control parameters include the proportional gain $k_{pv}$ and integral gain $k_{iv}$ of the voltage control loop, the proportional gain $k_{pc}$ and integral gain $k_{ic}$ of the current control loop, the proportional gain $k_{pp}$ and integral gain $k_{ip}$ of the PLL, and the proportional gain $k_r$ of FORC. As shown in the figure, the primary factors influencing the dominant poles are $k_{pp}$ and $L_g$, while $k_r$ has a relatively minor impact. This indicates that FORC exhibits favorable robustness in terms of parameter adjustment, and variations in its parameters do not significantly affect the stability of the system.

3.2. Impedance Measurement Method

The output impedance or admittance of the power converters is a crucial parameter for identifying the state of the system. The three-phase converter shown in Figure 5 is widely utilized in distributed energy systems. $v_{abc}$ is the three-phase voltage at the PCC, and $i_{abc}$ refers to the output current. The converter adopts a current control strategy and utilizes a PLL to maintain phase synchronization between the output current and the PCC voltage. The controller is implemented in the dq domain, where PI controllers are used to track the reference signal, and pulse width modulation (PWM) is used to generate control signals.

Given the inherent nonlinearity of the converter shown in Figure 5, impedance measurement should be performed around a stable operating point of the converter. Therefore, when implementing impedance measurement techniques, a small-amplitude perturbation signal is typically injected into the system while it is operating in a stable state. The output impedance of the converter is then determined by measuring the corresponding voltage and current responses to this perturbation signal.

As depicted in Figure 6, there are two types of perturbation signals. One is the current perturbation signal injected in parallel, and the other is the voltage perturbation signal injected in series. Thus, the output impedance of the converter at the frequency ${\omega }_p$ can be computed in accordance with the voltage $\Delta v_p\left(j{\omega }_p\right)$ and current $\Delta i_p\left(j{\omega }_p\right)$. In this paper, the parallel injection method is employed. Firstly, the parallel injection method is more straightforward to implement in engineering applications, as it avoids changing the system’s connection configuration. Secondly, this perturbation injection approach can be integrated into the existing equipment in the system.

Owing to the inherent structural asymmetry of the three-phase converter, its impedance model is characterized by a matrix. This paper employs the impedance model in the d-q frame as an implementation case for impedance measurement. As described in [19], the d-q frame of the three-phase converter system is distinguished into two sets: the system d-q frame that tracks the phase angle of the grid voltage and the controller d-q frame that follows the phase of the PLL. The impedance model is constructed on the system d-q frame. Consequently, to accurately measure the impedance model of the converter, it is essential to capture the voltage and current responses on the system d-q frame. An illustration of measuring the converter’s output impedance using parallel current disturbances is depicted in Figure 7. Variables marked with the superscript ’s’ denote the system d-q frame variables. To ensure that these variables remain aligned with the system d-q frame, the disturbance current source in Figure 7 is synchronized with the grid voltage via an improved PLL. During impedance measurement, orthogonal current disturbances are injected. The disturbances on the d-q frame, as indicated by $i_{pd}$ and $i_{pq}$ in the figure, can be represented by the following expressions:

$$\begin{array}{cc}\hfill i_{pd}& =I_P\cos \left({\omega }_{ip}t\right)\cos \left({\varphi }_{ip}\right)\hfill \\ \hfill i_{pq}& =I_P\cos \left({\omega }_{ip}t\right)\sin \left({\varphi }_{ip}\right)\hfill \end{array}$$

(5)

where $I_P$, ${\omega }_{ip}$, and ${\varphi }_{ip}$ represent the amplitude, frequency, and phase angle of the perturbation signal, respectively. Through coordinate transformation, the system will be subjected to injection with three-phase perturbation currents. In Figure 7, two phases are required to perform impedance measurement. One is the phase for disturbance signal injection, denoted as ${\theta }_p$. In this paper, the SVG is used to inject the disturbance signal. Therefore, this phase is obtained via the PLL in the SVG controller, i.e., phase ${\theta }_v$ in Figure 3b. The other phase is used for impedance calculation: it converts the three-phase voltage and current data into the data in the system dq frame. This phase is derived from the improved PLL described in this paper.

The impedance can be calculated by measuring the components of voltage and current at the disturbance frequency. The impedance is represented by four elements. To determine the impedance at a given frequency, at least two independent perturbations must be injected into the system. Denoting the measurement results of the first and second injections with subscripts 1 and 2, respectively, the impedance at frequency ${\omega }_{ip}$ can then be calculated as follows:

$$\begin{array}{cccc}\hfill {\mathbf{Z}}_{dq}\left({\omega }_{ip}\right)=& \left[\begin{array}{cc}{Z}_{dd}\left({\omega }_{ip}\right)\hfill & Z_{dq}\left({\omega }_{ip}\right)\hfill \\ Z_{qd}\left({\omega }_{ip}\right)\hfill & Z_{qq}\left({\omega }_{ip}\right)\hfill \end{array}\right]=\hfill & \hfill -\left[\begin{array}{cc}{v}_{od1}^s\left({\omega }_{ip}\right)\hfill & v_{od2}^s\left({\omega }_{ip}\right)\hfill \\ v_{oq1}^s\left({\omega }_{ip}\right)\hfill & v_{oq2}^s\left({\omega }_{ip}\right)\hfill \end{array}\right]·& {\left[\begin{array}{cc}{i}_{od1}^s\left({\omega }_{ip}\right)\hfill & i_{od2}^s\left({\omega }_{ip}\right)\hfill \\ i_{oq1}^s\left({\omega }_{ip}\right)\hfill & i_{oq2}^s\left({\omega }_{ip}\right)\hfill \end{array}\right]}^{-1}\hfill \end{array}$$

(6)

3.3. Design for Disturbance Signal

The input of the FORC is the difference between the reference value of the perturbation signal and its actual measured value. The design of this reference value is crucial in determining the efficiency and accuracy of impedance measurements. The reference value of the perturbation signal with multiple frequencies is expressed as

$$\begin{array}{cc}\hfill i_{pdref}& =\sum _{k=1}^K\left[I_{pk}\cos \left(2\pi f_{pk}t\right)\cos {\phi }_{pk}\right]\hfill \\ \hfill i_{pqref}& =\sum _{k=1}^K\left[I_{pk}\cos \left(2\pi f_{pk}t\right)\sin {\phi }_{pk}\right]\hfill \end{array}$$

(7)

$f_{pk}$, $I_{pk}$, and ${\phi }_{pk}$ represent the frequency, amplitude, and phase angle of the k-th component of the multi-sine signal, respectively. These three parameters need to be designed to improve the accuracy of impedance measurements and to minimize the impact of the perturbation signal on the system.

When selecting the frequency of the perturbation signal, the frequency coupling characteristics of the system should be considered to avoid. Specifically, the coupling phenomena appear as follows: injecting a perturbation current signal with a frequency of $f_{pk}$ into the d-q frame results in the generation of current signals with frequencies $f_0+f_{pk}$ and $f_0-f_{pk}$ in the three-phase stationary coordinate system, where $f_0$ is the grid frequency. These two frequencies are known as sideband frequencies. Therefore, in choosing the frequency of the perturbation signal, the following three conditions should be considered and balanced: (1) Avoid interference from background harmonics and between different perturbation signals. Specifically, the sideband frequencies of each perturbation signal should not be equal to the harmonic frequencies of the system. In addition, the sideband frequencies should not be equal to each other. (2) The perturbation frequencies should maintain a certain integer multiple relationship to leverage the advantages of FORC and enhance measurement efficiency. (3) The perturbation frequencies should be distributed as uniformly as possible on a logarithmic scale to align with spectral characteristics. After selecting the perturbation frequencies, the indicator U can be used to quantify the degree of uniformity of the frequencies on a logarithmic scale, and its calculation process is given in (8) and (9). Here, n is the total number of selected frequency points. Values of U closer to 1 indicate more uniform distribution on a logarithmic scale. When designing the frequencies, it is advisable to ensure that $U>0.98$.

$$U={\displaystyle \frac{1}{1+\frac{1}{n-2}{\sum }_{i=1}^{n-1}{\left(d_i-\frac{1}{n-1}{\sum }_{i=1}^{n-1}{d}_i\right)}^2}}$$

(8)

$$d_i=\lg f_{i+1}-\lg f_{i}i=1,2,\cdots ,n-1$$

(9)

To fulfill the aforementioned conditions, this paper employs the following method to set the perturbation frequencies: The frequency range is divided into several logarithmically spaced intervals, and the number of measurement frequencies per zone are specified. Next, several base frequencies are chosen in each interval, and subsequent frequencies are generated by integer multiples of these base frequencies. The selected fundamental frequencies and the subsequent frequencies generated must meet the first condition. Lastly, appropriate frequencies are chosen from the generated frequencies to ensure that U is sufficiently large. As an example, consider a measurement frequency range from 10 Hz to 1000 Hz, which is divided into three logarithmically spaced intervals. The frequency intervals are [10 Hz, 46.4 Hz], [46.4 Hz, 215.4 Hz], and [215.4 Hz, 1000 Hz]. In each zone, seven measurement frequency points are set. For the first zone, the fundamental frequencies of the perturbation signal can be selected as 5.2 Hz and 12.9 Hz. The selected frequencies for the first zone are [10.4, 12.9, 15.6, 20.8, 25.8, 31.2, 38.7] Hz. For the second and third frequency zones, the frequencies within these two zones should be multiples of the frequencies in the first zone, with the multiple coefficients being 5.01 and 25.1, respectively.

For perturbation signals at the same frequency, two independent perturbations should be injected to determine the converter’s output impedance. This is accomplished by changing the phase of the perturbation signal. Specifically, in this paper, the phases of the two perturbations are set to 0 and $\pi /2$, respectively.

The design of the perturbation signal amplitude should take into account two factors. First, it should satisfy the small-signal assumption, meaning the amplitude should be sufficiently small to ensure the system remains linear around the steady-state operating point. Second, the amplitude needs to be large enough to overcome internal system harmonic distortions and noise, ensuring that the response signal can be accurately extracted. In the frequency design of the perturbation signal discussed earlier, the perturbation signal is designed to avoid background harmonic interference. This enables the use of smaller perturbation amplitude. Based on these considerations, the amplitude of the perturbation signal is determined based on the following principles: The amplitude of a single-frequency perturbation signal should be less than 5% of the steady-state operating point, and the combined amplitude of multiple perturbation signals should be less than 10% of the steady-state operating point. Within these constraints, the perturbation amplitude is maximized to ensure reliable and accurate system response measurements.

In the context of the aforementioned design, multiple reference values for perturbation signals are generated. It should be noted that each reference value of the perturbation signal contains multiple sinusoidal frequency components. These frequencies are all multiples of a specific fundamental frequency within a given frequency range.

Based on the control strategy and measurement method, the impedance measurement process is illustrated in Figure 8. Initially, the reference value of the perturbation signal is designed. Subsequently, the control parameters of the FORC are updated based on this reference value. Specifically, the order of the delay link and the coefficients of the Lagrange interpolation formula are determined according to the fundamental frequency of the reference value, as given in (4). Next, two independent disturbance currents are injected into the system. The three-phase voltage and current data at the test port are then collected and transformed into the d-q coordinate system. Finally, the components of the voltage and current signals in the d-q coordinate system at the disturbance frequencies are extracted, and the impedance at these frequencies is calculated. By iterating through the perturbation signals across all frequencies and repeating the aforementioned steps, the wideband impedance of the system under test can be obtained.

3.4. Improved PLL

To obtain the impedance model of the three-phase converter, it is necessary to perform a coordinate transformation to shift the response signals from the abc frame to the system d-q frame, not the controller d-q frame. This requires the use of a phase angle, which is typically estimated using a PLL or other mathematical algorithms. However, since disturbance signals are injected, dynamic synchronization effects caused by the phase angle estimation method may be introduced. Essentially, the d-q frame components calculated through this phase angle are those of the controller d-q frame. This leads to inaccurate impedance model measurements below the PLL bandwidth. To mitigate the impact of phase angle dynamics on impedance measurement, an improved PLL is adopted to compensate for the dynamic effects of the PLL.

The structure of the PLL is depicted in Figure 9, and the output is the phase angle of the controller d-q frame, denoted by ${\theta }_c$. To track grid fluctuations, the bandwidth of the PLL needs to be sufficiently high. This, however, may result in a difference between the angles of the two d-q frames [19], denoted as $\Delta \theta$, due to the injected disturbance. It can be shown that the relationship between the angles of the two frames is as follows:

$${\theta }_s={\theta }_c-\Delta \theta$$

(10)

where ${\theta }_s$ represents the phase angle in the system d-q frame.

To accurately determine the system d-q frame components, it is essential to accurately determine the phase difference $\Delta \theta$. $\Delta \theta$ is derived as shown in Figure 9. Specifically, the PLL frequency small-signal component is extracted using a high-pass filter (HPF) and then integrated to obtain $\Delta \theta$. The expression for the high-pass filter is given by

$$G_{HPF}\left(s\right)={\displaystyle \frac{s^2}{s^2+2\xi {\omega }_{n}s+{\omega }_n^2}}$$

(11)

Here, $\xi$ is the damping factor, typically set to 0.707, and ${\omega }_n$ is the cut-off frequency of the HPF. Its value should be less than the minimum frequency of the disturbance signal to accurately extract the angle difference.

Using this improved PLL, the system d-q frame components can be derived through two methods. One is to transform coordinates with ${\theta }_s$ to directly compute the system d-q frame components. The other is to use ${\theta }_c$ for an initial coordinate transformation to obtain the controller d-q frame components, which are then converted to the system d-q frame components using the following equation:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{v}_d^s\\ v_q^s\end{array}\right]=& {\left[\begin{array}{cc}\cos \left(\Delta \theta \right)\hfill & \sin \left(\Delta \theta \right)\hfill \\ -\sin \left(\Delta \theta \right)\hfill & \cos \left(\Delta \theta \right)\hfill \end{array}\right]}^{-1}\left[\begin{array}{c}{v}_d^c\\ v_q^c\end{array}\right]\hfill \end{array}$$

(12)

where $v_d^s$ and $v_q^s$ represent the voltage of the system d-q frame, and $v_d^c$ and $v_q^c$ represent the voltage of the controller d-q frame. The dq axis current can be calculated by the same method.

4. Validation Results

In this section, the impedance measurement method based on fractional harmonic injection proposed in this paper was verified through simulations and experiments.

4.1. Simulation Results

To verify the effectiveness of the impedance measurement method, simulation tests were conducted in MATLAB/Simulink with the assistance of PLECS. The simulation model is depicted in Figure 3a. Switching delay and background noise are ignored. The grid-connected converter operates at 10 kW, and the parallel load is $Z_L=7.744+j5.812$$\Omega$. The SVG is employed to compensate for reactive power and inject perturbation signals.

First, the SVG’s capability in controlling perturbation signals is verified. In this test, the reference frequencies of the perturbation signals are set to 10.4 Hz, 15.6 Hz, 20.8 Hz, and 31.2 Hz, while the amplitudes of the d-axis and q-axis perturbation signals are set as 1 A and 0.5 A, respectively. As shown in Figure 10a, the waveforms of the voltage and output current of the SVG are shown. The current waveforms lag the voltage waveforms by ${90}^{\circ }$, indicating that the SVG delivers a purely reactive power of 9 kvar. In addition to the fundamental frequency component, the voltage and current signals also contain small-signal disturbances at multiple frequencies. The frequency spectra of the d-axis and q-axis current signals are presented in Figure 10b. It can be observed that the frequencies and amplitudes of these small-signal perturbations closely match the reference values.

The equivalent impedance of each port can be calculated based on the voltage and current response signals at each port in the system. For the system illustrated in Figure 3a, the impedances of the load and the converter are measured. Figure 11a presents the impedance measurement results of the load, where the red curve denotes the theoretical impedance model and the blue dots represent the measured results. The results show good agreement.

Figure 11b illustrates the impedance measurement results of the converter. The theoretical expression for the converter impedance is detailed in [20]. The diagonal-axis impedance measurements are accurate, and the dd-axis impedance demonstrates the current source characteristics of the converter. In the figure, $Z_{dq}$ and $Z_{qd}$ exhibit some deviations at low frequencies. This phenomenon arises because the converter exhibits characteristics of high impedance in the low-frequency region. On the one hand, the grid-side impedance is relatively low. Therefore, due to the shunting of the low impedance, the perturbation current output by the SVG flows toward the grid side, while the disturbance current on the converter side is relatively small. On the other hand, since the converter adopts unity power factor control, the coupling between the d-axis and q-axis is weak. Compared with the diagonal-axis impedances, the values of $Z_{dq}$ and $Z_{qd}$ are smaller, which results in a smaller voltage response signal excited by the disturbance signal. During sampling and calculation, these small signals are easily affected, ultimately leading to errors in the off-diagonal-axis impedances within the low-frequency range. In fact, for the frequency range characterized by high impedance, voltage disturbance signals are more suitable because voltage disturbances tend to distribute on the high-impedance side. However, injecting voltage disturbances requires modifying the system connection mode, since the disturbance source needs to be connected in series within the system. Thus, only the current disturbance injection method is adopted in this study.

Figure 12 presents the results of impedance measurement conducted using a PRBS voltage perturbation signal. PRBS signals provide higher measurement efficiency, however, their spectral energy is uncontrollable, making them susceptible to coupling characteristics. In terms of the load impedance, this measurement method exhibits a higher error in the high-frequency range of the off-diagonal axis impedance. For the converter impedance, the measured results demonstrate a closer alignment with the model in the low-frequency range. This is because the PRBS method injects disturbances through a voltage source connected in series within the system, which inevitably alters the connection structure of the system. However, similar to the load impedance measurement, significant errors are observed in the high-frequency range; notably, such errors also manifest in the high-frequency segment of the dd-axis phase characteristics. On the other hand, it is important to note that the measured frequency points illustrated in the figure are non-uniformly distributed on a logarithmic scale.

To further validate the impedance measurement method, a $CIGR\acute{E}$ 18-node simulation system, as illustrated in Figure 13a, was constructed. In this system, node 1 is connected to the grid and equipped with an SVG for reactive power compensation. Nodes 11, 16, and 18 are connected to constant power loads of 30 kVA, 5 kVA, and 5 kVA, respectively, all with a power factor of 0.95. Additionally, node 18 is linked to a passive load with an impedance of $23+j7.54$$\Omega$. Nodes 15 and 17 are configured with converters rated at 35 kVA and 20 kVA, respectively, both operating at a unity power factor.

By utilizing the SVG to inject perturbation signals, the impedance at node 1 was measured, with the results presented in Figure 13b. The measured results are in good agreement with the theoretical model, thus verifying the accuracy of the impedance measurement method proposed in this paper.

4.2. HiL Results

To provide further verification of the impedance measurement scheme, experimental validations were conducted using the hardware-in-the-loop (HiL) setup shown in Figure 14a. The renewable energy converter and SVG are built in the RT Box, and the structure is shown in Figure 3a. The PWM carrier frequency is 10 kHz, with a switching delay of 1 µs.

In the HiL tests, two operating conditions were considered. Under the first condition, the grid-connected converter outputs 5kW of active power. Under the second condition, 10 kW of active power is output. The voltage and current waveforms at the sampling point are added with Gaussian-distributed white noise, where the noise amplitude is approximately 1% of the steady-state operating value, considering the influence of background noise. The impedance measurement results under both conditions are shown in Figure 14b. As the output power increases, the amplitude of the qq-axis impedance shows an obvious decreasing trend, which enhances the effect of negative damping. Additionally, the results from both conditions are consistent in their overall trends and numerical values, verifying the effectiveness of the impedance measurement method.

4.3. Experimental Results

To further verify the impedance measurement method, experimental validations were conducted using a laboratory setup. The experimental setup is as depicted in Figure 15. It comprises two Danfoss VLT AutomationDrive FC 302 converters: one serving as the distributed converter, and the other as the SVG. The DC sides of the two converters are connected to DC power supplies and capacitors, while the AC sides are connected to the actual power grid. The control algorithms were implemented on a real-time control system based on the digital signal processor (DSP), model TMS320C28346. The sampling frequency and PWM carrier frequency are both 10 kHz, with a switching delay of 1 µs. Compared with the inherent control of the SVG, when implementing impedance measurement, the DSP only needs to additionally implement FORC, the improved PLL, and the coordinate transformation. Thus, relative to the standard control of the SVG, the impedance measurement adds minimal computational burden, and processing with a DSP is sufficient. In addition, in this paper, the order of the Lagrange interpolation polynomial is 3. If it is necessary to further reduce the computational burden, this order can be lowered, but this will reduce the control accuracy of the disturbance signal.

Figure 16 presents the experimental results, where Figure 16a shows the phase A voltage at the PCC and the output current of the converter. Disturbance harmonics introduced by the disturbance current output from the SVG exist in the voltage and current waveforms, and these harmonic components can be clearly observed in the current waveform.

The upper computer collects voltage and current data in the system d-q frame and then uses MATLAB R2021a (9.10.0.1602886) programs to calculate the impedance matrix. Figure 16b displays the impedance measurement results. It demonstrates general agreement between the impedance obtained via the impedance measurement method and the theoretical model. Compared to simulation, HiL and experimental verification results show some errors in the high-frequency range. This is because various delays exist in the system under test, such as calculation delay, sampling delay, switching delay, etc. The theoretical model takes into account the calculation and sampling delays, but switching delays and parasitic resistance in the experimental environment have not been considered. Therefore, the measurement results more accurately reflect the actual converter characteristics.

4.4. Discussions

In impedance measurement, attention should be paid to factors such as measurement efficiency, accuracy, and cost. Existing methods adopt different types of perturbation signals and injection devices. The advantages and limitations of these methods are presented in

Table 1. Comparison with state-of-the-art methods.

Impedance Measurement Method	Advantages	Limitations
Single-sine signal-based technique [7]	High SNR over wide frequency range	Low efficiency
Non-sinusoidal signal-based technique (binary sequence, Gaussian pulse) [10,11,21]	High efficiency	Unable to design each frequency component precisely; complex algorithm
Multi-sine signal-based technique [13,15]	High efficiency	Hardware cost
Internal perturbation signal-based technique [17,18]	Low cost	Neglect the black-box nature
Proposed method (multi-sine current signal)	High efficiency; low cost; signal can be freely designed	Require redundant capacity

. This paper utilizes the redundant capacity of SVG to inject multi-sine signals and implements control through FORC. Compared with existing methods, its main advantages are as follows: (1) Lower cost of the perturbation injection. (2) Flexible frequency design while ensuring measurement efficiency.

Several other aspects require consideration during the measurement process.

Communication Delay. When an impedance measurement command is issued, no synchronization is required between the injection of the disturbance signal and the impedance calculation. Therefore, communication delay will not affect the measurement accuracy. The impact of communication delay is reflected in the asynchrony of multi-channel data. If a communication delay causes deviations in the data acquisition timings of different channels, it will lead to calculation errors. This problem can be mitigated by providing a high-precision clock source for the acquisition module to reduce data asynchrony.

Stability and Nonlinearity Issue. This paper adopts small-signal disturbance injection to measure the converter impedance. Thus, the measured impedance is a linearized small-signal impedance model. During the measurement process, the frequencies of the disturbance signal avoid the fundamental and harmonic frequencies, and the amplitude is limited to ensure that the converter operates in the linear region. This ensures that the system operates within the linear region, preventing the triggering of large-scale nonlinear oscillations or shifts in the system’s operating point. Furthermore, as shown in Figure 4, the FORC parameter has a relatively minor impact on the stability of the dominant poles of the system, thereby demonstrating the robustness of FORC.

Perturbation Signal. To ensure measurement accuracy, perturbation signals should generate sufficient response signals. On the one hand, the type of signal source should be carefully selected. Current perturbation mostly flows through low impedance paths, resulting in low utilization of the signal in high-impedance frequency ranges. In contrast, voltage perturbation signals tend to distribute across high impedance. Based on this, the hybrid current–voltage perturbation method can be used to improve measurement accuracy. However, this method requires adding extra interfaces, switching devices, mode selection programs, and hardware, which departs from this paper’s focus on "no extra hardware costs". On the other hand, the perturbation signal cancellation effect should be avoided, especially in multi-converter parallel systems. The harmonic suppression function of the converter may produce reverse cancellation against the disturbance signal, or the impedance difference between converters may weaken the response signal. To solve this, one solution is to avoid these suppressed frequency bands when designing perturbation signals and to discard low-SNR data during data processing. Another alternative method is to measure the impedance of part of the system in sequence, so that the response of the measured converter will not be canceled by other converters. However, this requires distributed measurement equipment and is not applicable to the method described in this paper.

5. Conclusions

The multi-functional impedance measurement method based on fractional harmonic injection proposed in this paper employs SVG with redundant capacity as the disturbance injection device. It enables efficient injection of multi-frequency disturbance signals, avoiding the need for additional dedicated equipment. This provides significant cost savings and operational convenience in engineering applications. In the design of disturbance signals, frequency coupling characteristics are taken into consideration to ensure no mutual interference between signals and their ability to accurately trigger system responses. Both simulation and experimental results indicate that the measured impedances of loads and converters generally agree with the theoretical models.

It should be noted that this method has some limitations in real-world use. First, this method depends on the redundant capacity. Second, in high-impedance situations, the perturbation current is likely to shunt the low impedance side. It is also susceptible to interference, reducing measurement accuracy. To solve these problems, future work will focus on the SVG capacity allocation algorithm and optimized signal extraction methods to further improve measurement accuracy.