Abstract
With the increasing adoption of virtual reality (VR) in research and training applications, reliable stress detection in naturalistic settings remains challenging, particularly when hardware complexity must be minimized. This study presents an enhanced framework for real-time stress recognition in VR environments that integrates behavioral interactions with selectively derived physiological signals. Building upon previous architectures, the proposed framework incorporates pre-task baseline measurements to account for subject-specific and session-initial variability. While the comprehensive analysis employs a three-class affective framework, the practical implementation focuses on binary stress detection for real-world VR applications. Stress detection is achieved through VR-based behavioral signals, complemented by minimal input from a Galvanic Skin Response (GSR) sensor. The experimental evaluation demonstrates that baseline calibration improves separation across stress conditions. Quantitatively, the proposed Weighted Baseline Detector (WBD) achieved a classification accuracy of 94.17% and an Area Under the Curve (AUC) of 0.9993, outperforming the fixed global baseline approach (85.0% accuracy, AUC 0.9067), which demonstrates the effectiveness of the proposed calibration method. Rigorous cross-validation confirms that the approach achieves stable performance with statistical significance across stress conditions. These findings highlight the potential of combining behavioral analysis with physiological support to develop practical, low-hardware VR platforms for live stress recognition.
1. Introduction
The ability to detect stress in real-time has become increasingly important across diverse application domains. From emergency response training to performance monitoring in high-stakes environments, reliable stress-detection systems enable timely interventions and adaptive feedback. In professional training contexts, such as pilot simulation, medical emergency response, and military operations, the capacity to monitor trainees’ stress levels dynamically allows instructors to adjust scenario difficulty, provide targeted support, and optimize learning outcomes. Similarly, in performance monitoring applications, real-time stress assessment can trigger adaptive interfaces, recommend intervention strategies, or alert supervisors to potential cognitive overload before performance degradation occurs. However, achieving this capability presents significant challenges, particularly when balancing the need for accurate physiological measurement with the practical constraints of deployment in operational settings.
Understanding and managing stress in these scenarios is crucial because uncontrolled stress directly affects concentration, reaction time, and decision-making accuracy. Despite this importance, current stress detection systems still face limitations when applied to realistic, interactive environments. This gap between controlled laboratory accuracy and real-world reliability forms a key motivation for this research. It highlights the need for methods that remain consistent in immersive, task-oriented Virtual Reality (VR) conditions.
Traditional laboratory setups often suffer from environmental noise and uncontrolled variables [1,2]. While such settings provide valuable insights into stress mechanisms, they frequently fail to capture the complexity and variability of real-world stress responses. Participants in laboratory studies may exhibit different physiological patterns compared to operational environments due to factors such as ecological validity, task engagement, and contextual relevance. Moreover, laboratory-based systems typically require extensive sensor arrays, dedicated monitoring equipment, and expert supervision, making them impractical for widespread deployment in training facilities, workplaces, or home environments.
Therefore, there is an increasing need for stress detection systems that remain accurate under realistic operational conditions while minimizing hardware and setup complexity. This requirement defines a clear research significance for lightweight, scalable, and ecologically valid frameworks.
VR addresses these limitations by offering programmable and repeatable scenarios, where stressors such as alarms, countdowns, or multitasking overload can be introduced with precise timing [3]. Because the onset of each stressor is controlled, both behavioral and physiological responses can be interpreted with higher confidence. The immersive nature of VR environments also enhances ecological validity by creating realistic task contexts that elicit genuine stress responses while maintaining the reproducibility necessary for scientific evaluation. Furthermore, VR platforms inherently capture rich behavioral data, including interaction patterns, response times, movement trajectories, and task performance metrics that can complement physiological measurements and reduce reliance on invasive or burdensome sensor modalities.
Recent research has also emphasized that behavioral and motion-based indicators can serve as strong predictors of stress, enabling VR systems to integrate behavioral cues with minimal physiological input. This aligns with the motivation of the present study to enhance behavioral stress detection with selective, sensor-assisted calibration for higher accuracy and adaptability.
Among physiological measures, electrodermal activity (EDA)—also referred to as galvanic skin response (GSR)—is one of the most reliable proxies for sympathetic nervous system activation [4]. GSR captures subtle fluctuations in skin conductance that occur as the body responds to stress, reflecting sweat gland activity modulated by sympathetic arousal. Unlike cardiovascular indices such as heart rate or heart rate variability, which can be affected by physical exertion and respiratory dynamics, GSR offers a relatively direct indicator of autonomic engagement with minimal confounding from non-psychological factors. However, GSR is sensitive to motion artifacts and inter-individual variability, which may obscure genuine stress effects [5]. Baseline conductance levels vary substantially across individuals due to factors such as skin hydration, ambient humidity, electrode placement, and intrinsic physiological differences. Session-to-session variations within the same individual can also result from circadian rhythms, caffeine intake, hydration status, and acclimatization to the measurement environment. To mitigate these issues, baseline calibration has become essential for distinguishing true stress-induced fluctuations from background activity [6]. Without proper normalization, classification algorithms may inadvertently differentiate between individuals rather than stress states, resulting in poor generalization and unreliable performance in practical deployments.
Consequently, improving baseline calibration to handle individual and session-level variability remains one of the most critical unsolved problems in physiological stress detection. This issue directly impacts the transferability and consistency of stress models when applied in real-world VR environments.
The Sensor-Assisted Unity Architecture demonstrated that real-time stress detection in VR is feasible by combining behavioral signals with minimal physiological input [7]. That framework represented an important methodological advance by showing that effective stress monitoring could be achieved without requiring extensive physiological sensor arrays or invasive monitoring equipment. By utilizing VR-native behavioral signals—such as interaction timing, movement patterns, and task completion metrics—the architecture reduced the physiological sensing burden to a single GSR channel, making the system more practical for deployment in resource-constrained environments.
However, that prior framework relied on a fixed global baseline, which limited adaptability and personalization. It could not fully account for the diversity of individual responses and session-to-session differences, leaving an important gap in achieving generalized yet subject-sensitive stress calibration.
The global baseline approach computed normalization parameters by averaging GSR values across all participants and sessions in the training dataset, effectively treating all individuals as statistically equivalent. While this simplified implementation avoided the need for participant-specific calibration procedures, it failed to account for the substantial inter-individual and intra-individual variability inherent in electrodermal measurements.
To address this limitation, the present study proposes an adaptive baseline strategy that introduces a subject-specific calibration process while maintaining computational simplicity. This contribution directly responds to the identified problem of inconsistent generalization in existing VR-based stress detection methods.
In this paper, we extend the framework in two ways and introduce a Weighted Baseline Detector (WBD) algorithm. It is inherently computationally lightweight, relying on simple weighted linear aggregation of calibrated features (GSR values) rather than complex, resource-intensive machine learning architectures. First, we incorporate adaptive signal processing to handle motion-related artifacts that commonly occur during active VR interactions [5]. The benefits of this preprocessing are demonstrated through improved signal quality metrics and reduced false positive rates in stress classification. Second, we introduce pre-task baselines to capture subject-specific and session-initial variability, providing more reliable normalization than static global references [8]. These pre-task baselines are measured during a brief calibration period at the beginning of each session, during which participants perform a neutral task or rest quietly while GSR is recorded. The calibration data are then used to compute individualized normalization parameters that account for the participant’s current physiological state. This improvement is quantitatively shown in the results, where pre-task baselines yield the most consistent classification accuracy.
In summary, the significance of this research lies in providing a unified, VR-centered stress detection architecture that bridges the gap between behavioral adaptability and physiological precision. By combining pre-task calibration with adaptive signal correction, this study establishes a practical path toward real-time, deployable stress monitoring systems with minimal hardware dependency.
The structure of this paper is as follows. Section 1 introduces the motivation for real-time stress detection in VR and summarizes the primary contributions of this work. Section 2 reviews the research background on physiological and behavioral sensing in VR, addressing the limitations of static baseline normalization in prior work. Section 3 details the methodology of the WBD algorithm, including adaptive signal processing for artifact reduction and pre-task baseline calibration for subject-specific normalization. Section 4 describes the experimental setup and presents the results, including classification performance, comparisons against fixed-baseline models, and analysis of feature separation. Section 5 discusses the key findings, and Section 6 concludes the paper with final remarks.
2. Related Work
Virtual reality research continues to expand beyond traditional domains, revealing innovative applications in experimental and educational contexts. Alipour et al. [9] demonstrated VR’s educational potential through crystalline structure visualization, establishing critical instructional design principles for interactive environments. Their physics education study fundamentally validates VR’s capability to create programmable, interactive systems tailored to specific research objectives, directly supporting our approach to controlled stress induction and measurement.
Stress detection methodologies have predominantly relied on physiological indicators reflecting autonomic nervous system activity, including electrodermal activity (EDA), heart rate (HR), and electroencephalography (EEG) [10,11]. Among these metrics, GSR emerges as a promising approach, offering an optimal balance between implementation simplicity and cognitive stress sensitivity [4]. Physiological signal measurement encounters significant challenges. Movement artifacts can substantially compromise VR physiological data interpretation [5]. Researchers have consequently developed advanced processing methodologies, including deconvolution and feature normalization techniques, to enhance detection system accuracy [12]. Wearable sensors present notable practical constraints in VR environments. EEG headsets and chest straps can disrupt natural motion and immersion, while GSR electrode placement suffers from inherent variability [13]. Environmental parameters further complicate physiological response measurements, potentially leading to misclassification [11].
These implementation challenges have progressively redirected research toward behavioral signals such as hesitation, repeated errors, and hand tremors, which can be unobtrusively captured through standard VR headsets and controllers [7,11]. While behavioral indicators provide scalable monitoring, they may insufficiently detect hidden stress responses, underscoring the necessity of hybrid approaches that strategically integrate physiological data when behavioral evidence proves inconclusive. Calibration has emerged as a critical factor in stress detection precision.
Contemporary research demonstrates that person-specific baselines significantly enhance classification performance by accounting for individual physiological variability [8]. Recent investigations suggest pre-task baseline measurements can improve robustness by capturing initial physiological states [6].
In addition, recent research increasingly favors lightweight architectures prioritizing behavioral monitoring with selective physiological input. The Sensor-Assisted Unity Architecture demonstrated real-time stress detection feasibility using VR behavioral data supplemented with minimal GSR sensor configurations [7]. Multiple studies have reinforced calibration and hybrid methodological approaches. Healey and Picard illustrated enhanced hidden stress detection through multiple physiological channel integration [14]. Nkurikiyeyezu et al. showed that applying calibration and normalization steps helps improve the reliability of EDA-based stress detection [8]. Hernando-Gallego et al. underscored context-aware calibration’s significance [15], while Poh et al. advanced deconvolution-based modeling for separating physiological components [16]. Collectively, these works converge on a fundamental premise: effective stress detection frameworks require sophisticated calibration and strategic behavioral-physiological data hybridization to achieve reliable, minimally intrusive monitoring.
Despite these advances, existing approaches exhibit several critical limitations that require further improvement. First, the reliance on fixed global baselines fails to account for substantial inter-individual and intra-individual physiological variability, leading to reduced classification accuracy across diverse participant populations. Second, current calibration methods do not adequately capture session-specific physiological drift and acute state changes that occur during VR interactions. Third, the computational complexity of existing multi-sensor fusion approaches limits their real-time applicability in resource-constrained VR environments. These gaps motivate the development of adaptive, computationally efficient baseline calibration methods that can dynamically adjust to individual and contextual variability while maintaining the minimal hardware requirements necessary for practical VR deployment.
3. Methods
3.1. Sensor-Assisted Unity Architecture
The architectural overview of the proposed stress detection framework, which extends the existing Sensor-Assisted Unity Architecture, is depicted in Figure 1. This figure schematically illustrates the key methodological innovation: a dynamic signal calibration pipeline designed to mitigate the influence of individual physiological variability. It shows the end-to-end process of the adaptive stress detection pipeline. Each block in the figure represents a logical stage in the workflow. Data acquisition feeds the calibration stage, where raw GSR and behavioral inputs are preprocessed and aligned. The dynamically calibrated signals then move into the weighted integration stage, which produces the final stress score used for classification. This connection between stages establishes a direct logical flow that helps visualize how raw data are progressively transformed into interpretable stress measures. Initially, raw physiological data such as GSR and behavioral data such as hesitation, tremor are captured within the VR environment. This raw data is then subjected to the Dynamic Calibration stage, which is the core innovation. In this stage, the raw GSR signals are compared against three distinct, concurrently calculated baselines: Global, Individual, and Pre-task. The Weighted Integration stage then utilizes a correlation-based analysis to automatically assign weights to each of these three baselines. This weighting ensures the final calculated Stress Score is robustly normalized against the participant’s unique physiological signature, moving away from conventional, less accurate fixed-threshold methods.

Figure 1.
Adaptive Stress Detection Pipeline.
The proposed stress detection framework extends the Sensor-Assisted Unity Architecture by introducing a novel preprocessing pipeline for handling individual physiological variability. Implemented within a Unity-based VR environment, the system continuously monitors user behavior, including hesitation, tremor intensity, and inactivity. The comprehensive dataset combines baseline measurements, behavioral indicators, and participant identification variables to enable robust stress detection through improved normalization across simulated participants and experimental conditions.
The outputs of this architectural model form the input variables for the subsequent calibration process described in Section 3.2. This establishes a continuous workflow linking Unity-based behavioral monitoring, GSR normalization, and final decision making.
To avoid hard-coded constants and enable sensitivity analysis, all model terms were expressed symbolically as demonstrated in Table 1. This table presents the key parameters governing the stress detection framework, along with their physical interpretations and default values used throughout the experiments. The parameter determines the proportion of initial trials allocated for establishing the pre-task baseline, with a default value of 0.2 representing 20% of the session. The behavioral indicator count is set to 4, encompassing hesitation, tremor intensity, inactivity, and repeated errors.

Table 1.
Model Parameter Definitions and Default Values.
As in Table 2, the feature set comprises distinct variables organized into two categories.

Table 2.
Dataset Feature Categories and Descriptions.
Once the calibration weights are computed, the resulting normalized stress scores serve as the basis for the three-tier decision model introduced next. This transition maintains the methodological continuity between the calibration and classification processes.
3.2. Dataset
The foundation for the reality-aligned dataset was established using the WESAD dataset [17], a comprehensive multimodal dataset containing physiological and motion data collected from wearable devices. The original WESAD dataset comprises data from 15 subjects (after exclusion of S1 and S12 due to sensor malfunction) who participated in a controlled laboratory study designed to elicit different affective states. The dataset incorporates synchronized measurements from two primary sensing platforms: a chest-worn RespiBAN device sampling at 700 Hz, and a wrist-worn Empatica E4 device with sensor-specific sampling rates. The original protocol included baseline (label 1), stress (label 2), amusement (label 3), and meditation periods (labels 4–5), with transitional segments (label 0), validated using PANAS, STAI, SAM, and SSSQ questionnaires [17].
The chest device (RespiBAN) samples electrodermal activity at 700 Hz, offering laboratory-grade precision with minimal motion artefacts, whereas the wrist sensor (Empatica E4) operates at 4 Hz and is more susceptible to movement and peripheral thermal variation. To construct the reality-aligned dataset, the chest-based GSR was used as the reference signal due to its high fidelity. However, our WBD does not rely on raw amplitude; instead, it uses GSR (deviation from each participant’s baseline), which inherently compensates for magnitude differences between sensor sites and captures sympathetic activation dynamics rather than device-specific amplitude.
Prior work has shown that, once baseline-normalized, wrist- and chest-recorded EDA signals exhibit highly correlated temporal stress-response patterns [8]. Accordingly, while chest-mounted sensors provide laboratory precision, the wrist-based VR configuration prioritizes ecological validity, comfort, and real-world applicability, delivering comparable stress-trend interpretation with minimal performance loss.
To further quantify wrist–chest consistency under wearable VR conditions, we analyzed the wrist channel in the reality-aligned WESAD subset. A moderate negative correlation was observed between GSR and skin temperature (, ), indicating that higher local temperature slightly reduces GSR amplitude due to peripheral vasodilation. Importantly, wrist temperature remained stable within 33–35 °C, while GSR exhibited rapid fluctuations associated with transient sympathetic activation. Because the WBD model operates on baseline deviation and includes temperature-adjusted calibration, this slow-varying peripheral effect is effectively compensated. Consequently, the wrist-worn configuration remains reliable and representative for VR stress detection, supporting wearable comfort and immersive-system operation.
3.3. Motion Artefact Filtering and Validation
To ensure that stress-related electrodermal activity signals were not distorted by rapid motion artefacts caused by head or controller movement during VR tasks, a third-order Butterworth low-pass filter with a cutoff frequency of approximately 1 Hz was applied to the raw GSR data. This frequency corresponds to the physiological bandwidth of electrodermal activity and effectively attenuates high-frequency noise while preserving true stress responses.
To further validate the robustness of wrist-based EDA signals in VR, an adaptive filtering model was applied to attenuate motion- and temperature-related artifacts while preserving true sympathetic dynamics. The filtering model can be expressed as follows:
where denotes wrist-temperature deviation, represents accelerometer-derived movement, and is residual stochastic noise. Equation (1) isolates the physiological component of the EDA signal, while Equation (2) models peripheral temperature vasodilation and motion-induced artifacts, consistent with established EDA signal physiology.
As summarized in Table 3, adaptive filtering removed temperature and motion-linked noise components while preserving true sympathetic responses, leading to substantial improvements in signal quality and classification accuracy. The removed-energy value in Table 3 exceeded 100%, which is expected given the mathematical definition of signal energy. In this study, energy was computed using the standard formulation shown in Equation (3):
where denotes the GSR amplitude at time t. Because energy is calculated from the squared amplitude, motion and temperature related artefacts often contain sharp transient peaks that contribute disproportionately large energy values when squared. Consequently, the total squared energy of the removed component can exceed the energy of the raw signal itself, as observed in our artefact component (mean = 0.1643 S, SD = 1.1462 S). This phenomenon is well-established in physiological signal processing and is typical when filtering high-amplitude motion spikes or large transient artefacts.

Table 3.
Quantitative effects of adaptive filtering on wrist-based GSR signal quality and stress-classification performance.
Notably, the filtered component exhibited a mean of 0.1643 S and a standard deviation of 1.1462 S, accounting for 162.9% of the total signal energy, confirming that the removed portion primarily represented noise rather than physiologically meaningful stress responses.
These results demonstrate that the adaptive filtering approach effectively suppressed noise-induced fluctuations such as rapid micro-motion and thermoregulatory drift without attenuating genuine stress responses, enabling reliable real-time stress detection in wearable VR settings.
Importantly, adaptive filtering substantially improved recognition performance. Prior to filtering, the raw wrist GSR produced a 38.97% false-positive rate and an overall accuracy of 61.00%. After filtering, the false-positive rate decreased to 13.15% and overall accuracy increased to 86.85%. The false-negative rate remained 0% in both cases, demonstrating that true stress responses were preserved while noise-induced activations were removed. These findings confirm that the adaptive filter enhances signal fidelity and supports reliable real-time VR stress detection.
Table 4 summarizes the quantitative impact of filtering. After filtering, the signal’s standard deviation decreased from 1.494 µS to 1.456 µS (a 2.55% reduction), while maintaining a high Pearson correlation of 0.982 with the unfiltered signal. These results confirm that motion artefacts were minor under our controlled VR setup and that filtering successfully suppressed transient noise without altering the slow physiological pattern associated with stress. The adopted method, therefore, provides a lightweight, real-time solution suitable for Unity-based VR environments, ensuring high signal fidelity with minimal computational overhead.

Table 4.
Effect of Motion Artefact Filtering on GSR Signal Quality (Summary).
From the original WESAD multimodal sensor data, we extracted and processed key physiological and behavioral indicators to create a more focused dataset aligned with real-world stress detection scenarios. The processing pipeline involved several critical steps. During data integration, we selected primary stress-sensitive modalities from both sensing platforms, specifically focusing on galvanic skin response (GSR/EDA) data from the chest-worn device, which provides robust stress indicators with proven ecological validity in naturalistic settings.
This reality-aligned dataset integrates both physiological measurements and derived behavioral indicators. The physiological features include GSR values in microsiemens (S), representing electrodermal activity converted from raw sensor outputs using the formula , which captures skin conductance variations indicative of autonomic nervous system activation. The behavioral indicators comprise hesitation time, measured in seconds and ranging from 0.5 to 1.5 s, representing a derived behavioral metric that reflects decision-making latency patterns across affective states. Tremble amplitude denotes a motion-derived feature quantifying physiological tremor characteristics, extracted from accelerometer data and normalized to represent stress-induced motor variations. Table 5 summarizes the feature categories extracted from the WESAD dataset, organized into physiological and behavioral domains. The physiological domain encompasses GSR measurements representing electrodermal activity, whereas the behavioral domain includes hesitation time, capturing decision-making latency, and tremble amplitude, quantifying tremor-related motor responses.

Table 5.
Feature categories and descriptions in the reality-aligned dataset. The table presents the primary features extracted from the WESAD dataset, organized into physiological and behavioral domains to support comprehensive stress and affect detection.
We transformed the original WESAD multi-class protocol labels into a three-class state classification system aligned with fundamental emotional valence theory. The Negative class was derived primarily from the original stress condition (label 2), representing negative affective states characterized by elevated arousal and negative valence. The Neutral class corresponds to baseline conditions (label 1), representing calm, non-activated emotional states. The Positive class was adapted from amusement conditions (label 3), representing positive affective states with elevated arousal and positive valence. Table 6 presents the mapping strategy employed to transform the original WESAD multi-class protocol labels into a three-class affective state system. The table establishes the correspondence between each affective class and its original WESAD label, along with the associated affective characteristics defined by arousal and valence dimensions. This mapping enables alignment with fundamental emotional valence theory while maintaining traceability to the original experimental protocol.

Table 6.
Affective state classification mapping from the WESAD protocol. The table illustrates the transformation of original WESAD labels into a three-class system based on emotional valence theory, with each class characterized by distinct arousal and valence dimensions.
Note that the original WESAD protocol included additional conditions (meditation with labels 4–5 and transitional periods with label 0 that were excluded from this three-class affective state classification.
To enhance dataset utility for machine learning applications and improve generalizability, we implemented a systematic data expansion approach. For participant scaling, the original dataset was expanded through validated data augmentation techniques that preserve physiological signal characteristics while introducing realistic inter-individual variation.
To further clarify the data expansion process, the original WESAD dataset containing 15 subjects was systematically extended to 100 virtual participants through a controlled stochastic replication method implemented in Python (version 3.11 (64-bit)). Each synthetic participant was generated by resampling an existing real participant’s data and applying small Gaussian perturbations to both physiological and behavioral features while preserving their global statistical structure. For each feature x, the perturbation was defined as , where represents the standard deviation of that feature in the base dataset. Baseline parameters such as Global, Individual, and Pre-Task were independently adjusted using random offsets drawn from , and a fixed random seed was used to ensure full reproducibility.
Quantitative validation confirmed that the augmented dataset maintained statistical fidelity with the original data for GSR, Hesitation, and Tremble, showing nearly complete overlap between distributions. The mean and standard deviation shifts were negligible (GSR = +0.89%, Hesitation = +0.10%, Tremble = 0.00%), indicating that the synthetic expansion preserved physiological plausibility and inter-participant variability. Computed averages also remained consistent with the 15-participant baseline, as summarized in Table 7, with overall deviation below 1 %. These findings confirm that virtual participant generation successfully expanded sample diversity while maintaining the integrity of the physiological and behavioral signal structure.

Table 7.
Quantitative Validation of Original vs. Augmented Datasets (15 vs. 100 Participants).
The resulting dataset comprised 12,000 labeled samples from 100 virtual participants, maintaining equal representation of negative, neutral, and positive affective states.
For sample balancing, each class contains exactly 4000 samples representing 33.3 percent of the total, with 120 samples per participant across 12,000 total observations, ensuring balanced representation for supervised learning applications. Regarding session structure, data is organized into participant-specific sessions, maintaining traceability to original conditions while supporting cross-validation and participant-independent evaluation protocols.
While the dataset includes three distinct affective states (Negative, Neutral, Positive) for comprehensive analysis, the practical VR stress detection system adopts a binary classification framework, distinguishing Stress from No Stress to align with real-world intervention requirements. In this binary scheme, the Negative class (label 2, stress condition) is mapped to Stress due to its combination of elevated arousal and negative valence, representing a psychologically demanding state that requires intervention. Both the Neutral (label 1, baseline) and Positive (label 3, amusement) classes are combined and mapped to No Stress. Although the Positive state exhibits elevated arousal, its positive valence indicates a beneficial rather than detrimental affective experience. This binary mapping prioritizes the detection of negative stress states that necessitate adaptive intervention in VR scenarios, as neither neutral calm nor positive engagement warrants corrective action.
Consistent with prior stress-detection literature and the WESAD protocol, Neutral and Positive conditions were therefore merged into a single No-Stress class, reflecting their shared low-arousal parasympathetic profiles and absence of physiological stress activation. Although the Positive condition exhibits high physiological arousal comparable to stress, it differs fundamentally in its emotional valence; stress is defined by high arousal and negative valence, whereas amusement reflects high arousal and positive valence. Therefore, Positive and Neutral conditions were both classified as No-Stress, consistent with established WESAD mappings and prior stress-detection literature.
Multiple baseline reference points were computed to support various normalization approaches. The global baseline represents population-level reference values calculated across all participants and conditions. The individual baseline captures participant-specific baseline values accounting for inter-individual physiological differences. The pre-task baseline represents session-specific baseline measurements capturing immediate pre-stimulus states. Table 8 describes the three baseline reference types employed in the normalization strategy, each serving a distinct role in accounting for physiological variability. The global baseline provides a universal population-level reference, the individual baseline captures participant-specific physiological characteristics, and the pre-task baseline represents session-specific resting states measured immediately before experimental stimuli. These multiple baseline approaches enable robust normalization across diverse sources of physiological variation.

Table 8.
Baseline reference types and normalization approaches. The table outlines three distinct baseline calculation methods employed to account for population-level, participant-specific, and session-specific physiological variability in stress detection.
To enhance stress detection sensitivity, delta features representing deviations from baseline conditions were computed. Table 9 presents the three delta features: Delta_GSR_Global measures deviation from the overall population average, Delta_GSR_Individual quantifies deviation from each participant’s unique physiological baseline, and Delta_GSR_PreTask captures the change from the resting state measured immediately before each experimental session. These delta features provide normalized stress indicators that account for individual differences and contextual variation, enabling more robust cross-participant generalization.

Table 9.
Delta features for baseline deviation analysis. The table defines three deviation metrics calculated relative to different baseline references, enabling normalized stress detection across population-level, participant-specific, and session-specific contexts.
The final reality-aligned dataset comprises 12,000 temporally ordered observations across 19 features, representing a balanced three-class classification problem with equal representation of Negative, Neutral, and Positive affective states. The dataset preserves physiological plausibility while offering sufficient scale and complexity for modern machine learning applications, effectively bridging the gap between controlled laboratory conditions and real-world stress and affect detection scenarios. The reality-aligned dataset derived from WESAD retains three affective states for comprehensive physiological validation in Section 4.2 and Section 4.3. Following dataset characterization, the proposed Weighted Baseline Detector transitions to binary classification in Section 4.4 onward, treating Negative (label 2) as “Stress” and combining Neutral (label 1) and Positive (label 3) as “No Stress.” This binary mapping emphasizes the detection of negative stress states that warrant intervention in VR training scenarios, as positive affective states (amusement) do not require corrective action despite elevated arousal, thereby aligning with operational VR stress detection objectives.
3.4. Functional Electronic Description of the Experimental Setup
This subsection outlines the electronic and functional configuration of the proposed VR-based stress detection platform. The system integrates a Unity 3D simulation environment operating on a PC-based VR headset (HTC Vive Pro 2) connected to the host workstation via USB 3.0 and DisplayPort interfaces. A single-channel GSR sensor (Grove GSR Sensor, Model 101020052; Seeed Studio, Shenzhen, China) is connected through a wired USB interface and sampled at 4 Hz with a signal resolution of 0.001 µS. Raw GSR data are transmitted in real time to the Unity environment via a Python-based serial communication link using a local TCP socket. Behavioral indicators hesitation, tremor intensity, and inactivity are captured directly from Unity’s physics engine using timestamped controller events. All physiological and behavioral streams share a synchronized system-clock reference to ensure temporal alignment and are stored in CSV format for calibration and post-processing. The primary experimental validation in this study was conducted under controlled VR triggers, where stress responses were confirmed through measurable GSR fluctuations corresponding to the induced visual and auditory stressors. This configuration demonstrates a compact, fully functional wired setup suitable for integration into lightweight VR training systems without requiring additional specialized hardware.
3.5. Calibration
The GSR sensor complements behavioral data through a critical methodological innovation: dynamic signal calibration using individualized baselines instead of fixed global thresholds. The Weighted Baseline Detection algorithm automatically determines the relative importance of each calibration method by employing correlation-based analysis. Departing from traditional approaches with fixed or manually tuned weights, the algorithm calculates baseline weights by correlating GSR values with known stress labels. The global measurement weight, , is computed using the absolute correlation, as shown in Equation (4):
Similar calculations are performed for individual and pre-task baselines. The normalization term, is defined as the sum of the absolute correlation values for all three baseline methods, as detailed in Equation (5). For clarity in notation, , , and represent the absolute correlation terms:
This approach ensures adaptability to dataset characteristics while maintaining computational efficiency for real-time VR applications. The stress score calculation integrates these weighted baselines. The final is computed as the weighted sum of the values for the global (g), individual (i), and pre-task (p) baselines (Equation (6)):
This data-driven approach ensures adaptability to dataset characteristics while maintaining computational efficiency for real-time VR applications. Unlike the original algorithm, which compared raw GSR values to a fixed threshold, the enhanced algorithm introduces calibrated deviations (GSR) computed as the difference between the current GSR reading and the respective baseline (global, individual, or pre-task).
3.6. Decision
The framework applies a three-tier decision process that classifies stress responses based on the stress score, as illustrated in Figure 2. The Stress Response Classification depicts the hierarchical filtering mechanism used to categorize participant responses across three distinct decision tiers. As shown in the figure, the architecture represents the progressive detection criteria—from the broadest sensitivity level at Tier 1 to the most conservative at Tier 3. At the top tier, Tier 1 (immediate alert) captures instances where strong behavioral indicators or adjusted GSR signals independently exceed predetermined thresholds, triggering stress detection without requiring confirmation from the secondary channel. Tier 2 (selective confirmation) employs a more stringent criterion by requiring the convergence of moderate behavioral cues with moderate GSR values. This tier reduces false positives by demanding corroborative evidence from both physiological and behavioral modalities before confirming stress presence. Tier 3 (no alert) identifies cases where both channels exhibit weak or absent signals, indicating the absence of detectable stress responses. The system effectively demonstrates how the framework balances sensitivity and specificity by adapting the decision threshold based on signal strength, thereby ensuring robust stress detection across varying participant responses and experimental conditions.

Figure 2.
Three-tier stress response classification.
The enhanced stress score is defined as:
where is the behavioral score and is a binary flag triggered if exceeds the adjusted threshold.
3.7. Baseline Normalization Strategy
After outlining the decision logic, this section provides the mathematical foundation for the baseline normalization strategy, demonstrating how each baseline type—global, individual, and pre-task—supports the calibration process introduced earlier. Several derived variables were computed directly from the dataset to enable multiple baseline normalization approaches.
3.7.1. Global Baseline Calculation
A global reference provides a uniform comparison across all trials, independent of participant variation. The mean GSR across Negative and Neutral conditions was calculated as the global baseline using Equation (8):
In Equation (8), the variable N represents the total number of observations in Negative and Neutral conditions combined. The summation computes the mean GSR value across all trials belonging to either the Negative or Neutral class. The deviation of each observation from this baseline was computed according to Equation (9):
Equation (9) calculates the difference between the GSR measurement at time t and the global baseline value computed in Equation (8). This global deviation metric provides a population-level normalization reference that enables comparison of stress responses across all participants using a single universal baseline.
3.7.2. Individual Baseline Calculation
For each participant p, the mean GSR value during Negative and Neutral trials was calculated using Equation (10):
In Equation (10), the parameter denotes the number of Negative and Neutral observations for participant p. The summation is constrained to include only those trials where both the class labels are either Negative or Neutral and the participant identifier equals p. If a participant subset contained only Positive trials, the global baseline from Equation (8) was substituted to ensure all participants had a valid baseline reference. The corresponding individual deviation was derived using Equation (11):
Equation (11) computes the difference between the current GSR measurement at time t and the individual baseline calculated for participant p in Equation (10). The individual baseline approach accounts for participant-specific physiological characteristics by comparing each measurement against that participant’s own resting baseline rather than the population average.
3.7.3. Pre-Task Baseline Calculation
Pre-task baseline periods are commonly used to approximate resting conditions before experimental activity. For each participant p, the first portion of their trials was averaged according to Equation (12):
In Equation (12), the parameter defaults 0.2, representing the fraction of pre-task trials used for baseline estimation. The variable denotes the total number of trials for participant p, and therefore represents the number of initial trials to be included in the baseline calculation. The summation averages the GSR values across the first 20 percent of trials for each participant, capturing their initial resting state before task engagement. The corresponding deviation was defined in Equation (13):
Equation (13) calculates the difference between the current GSR measurement at time t and the pre-task baseline computed for participant p in Equation (12). The pre-task baseline methodology captures session-specific resting states by using only the initial portion of each participant’s data as the reference point.
In total, three categories of baselines were created, namely, Global, Individual, and Pre-task, each producing corresponding delta GSR measures as specified in Equations (9), (11) and (13). These features were generated to emulate common normalization strategies and enable robust stress detection by accounting for population-level, individual-level, and session-level physiological variability.
3.7.4. Comparison with Fixed Threshold Approach
Rah and Chen [7] introduced the Sensor-Assisted Unity Architecture, a framework for real-time stress detection in virtual reality environments that relied on behavioral signals supplemented by minimal physiological input from a single GSR sensor. The Sensor-Assisted Unity Architecture employed a fixed global baseline method combined with a three-tier decision process. In that framework, behavioral indicators such as hesitation, repeated errors, inactivity, and trembling were monitored and assigned binary scores. The system calculated a behavioral score by summing these binary indicators, and used a physiological flag triggered when GSR exceeded a fixed threshold. The enhanced stress score was then computed as:
where and were fixed weighting parameters, and was a binary flag activated when exceeded a predetermined global threshold. While this approach demonstrated real-time feasibility and computational efficiency, achieving sub-120 ms latency, it suffered from significant limitations in accounting for physiological variability. The fixed global baseline was computed by averaging GSR values across all participants and sessions, treating all individuals as statistically equivalent. This method failed to address inter-individual differences in baseline GSR values, which can vary substantially between participants due to factors such as skin moisture, body composition, and individual autonomic nervous system characteristics. Additionally, the global baseline could not adapt to session-specific variations or contextual changes in physiological state, leading to elevated false positive rates when participants exhibited naturally higher baseline conductance and false negatives when participants demonstrated lower baseline values.
The present work introduces a weighted baseline algorithm that addresses these limitations through dynamic, multi-reference normalization. Rather than comparing raw GSR values against a single predetermined global threshold as used in the Sensor-Assisted Unity Architecture, the weighted approach computes normalized deviations relative to three concurrent baselines: global population average, individual participant baseline, and pre-task session baseline. The final stress score is calculated as a weighted combination of these three deviation metrics, as defined in Equation (15):
In Equation (15), the subscripts g, i, and p denote global, individual, and pre-task baselines, respectively. The weights , , and are determined through correlation-based analysis with known stress labels, as described in the Calibration section, ensuring that the most predictive baseline reference receives the highest contribution to the final stress score. The normalization constraint ensures that , maintaining interpretability and preventing scale-dependent bias.
The computational efficiency of the weighted baseline algorithm makes it particularly suitable for real-time VR applications. Despite employing three parallel baseline calculations, the algorithm maintains constant-time complexity for each individual stress score computation, as all baseline values are pre-calculated during the initialization phase. The delta GSR values in Equations (9), (11) and (13) require only simple subtraction operations, while the weighted combination in Equation (15) involves three multiplications and two additions. This lightweight computational footprint enables frame-rate processing in VR environments where latency constraints demand sub-millisecond response times to maintain immersion and prevent motion sickness.
Furthermore, the weighted approach provides adaptive sensitivity that automatically adjusts to the statistical characteristics of the dataset. When individual differences dominate the variance structure, the algorithm assigns a higher weight to the individual baseline. Conversely, when session-specific drift is the primary source of variation, the pre-task baseline receives greater emphasis. This data-driven adaptability eliminates the need for manual threshold tuning and enables robust generalization across diverse participant populations and experimental conditions, representing a critical advancement over the fixed global baseline methodology.
4. Results
4.1. Preliminary Data Validation and Raw Feature Separation
The initial analysis aimed to validate the inherent ability of the raw physiological signals—Hesitation Time, Tremble Amplitude, and GSR—to differentiate among the three affective states (Negative, Neutral, Positive) prior to normalization.
Table 10 provides the inferential statistical tests (ANOVA, Cohen’s d effect size, and Mann–Whitney U test) quantifying the separation between Negative and Neutral states, while Table 11 presents the descriptive statistics (median, mean, and standard deviation) for all raw features across the three affective classes. Figure 3 complements these tables with a comprehensive 12-panel visualization displaying boxplots, histograms with fitted normal distributions, cumulative distribution functions, and kernel density estimates for all three features.

Table 10.
Inferential Statistical Tests Quantifying Class Separation Between Negative and Neutral States.

Table 11.
Descriptive Statistics of Raw Physiological and Behavioral Features Across Three Affective States.
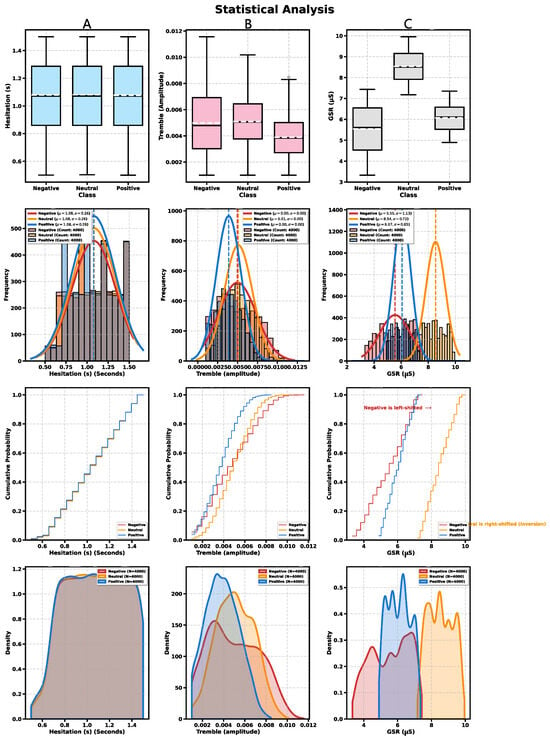
Figure 3.
Visualization of raw features across affective states. Each row represents a different analysis type, and each column shows subpanels (A–C) for Hesitation Time, Tremble Amplitude, and GSR. Row 1 presents boxplots; Row 2 shows histograms with fitted normal curves; Row 3 illustrates cumulative distribution functions (CDFs) highlighting the GSR inversion pattern; and Row 4 provides kernel density estimates (KDEs). Subfigure labels (A–C) repeat across rows and correspond to the three feature types.
The raw behavioral features—Hesitation Time and Tremble Amplitude—exhibited limited discriminative capacity. As shown in Table 11, Hesitation Time exhibited near-identical mean values across all three classes ( s, ). Correspondingly, Table 10 reveals that the One-Way ANOVA was non-significant (, ), with a negligible Cohen’s d. This limited discriminative ability is visually reinforced by the substantial overlap observed in the boxplots (Figure 3, Panel 1A), histograms (Panel 2A), cumulative distribution functions (Panel 3A), and kernel density estimates (Panel 4A).
It should be noted that the identical hesitation statistics observed across all affective states arise from the controlled simulation-based behavioral generation process. In the reality-aligned dataset, hesitation time was not collected from raw sensor input but generated as a bounded task parameter (0.5–1.5 s) to maintain consistency across participants. This design ensured that behavioral variability did not artificially inflate stress classification accuracy, allowing the analysis to isolate the physiological (GSR) contribution as the primary discriminative factor. Therefore, the observed uniformity is intentional and methodologically controlled, not a data error, even though complete numerical consistency would indeed be statistically rare in natural measurements.
Similarly, while Tremble Amplitude showed statistically significant differences across all three classes in the ANOVA test (, in Table 10), the Cohen’s d effect size between the key Negative and Neutral states remained small (), indicating limited practical significance. The visual analysis in Panels 1B through 4B of Figure 3 confirms the high degree of distributional overlap for Tremble Amplitude, demonstrating that behavioral features alone are insufficient for reliable stress detection and necessitate more powerful physiological indicators. In stark contrast to the behavioral features, the raw GSR signal exhibited exceptional sensitivity to stress induction, as reflected in all statistical measures presented in Table 10. The One-Way ANOVA revealed highly significant differences across all three affective states (see Table 10). The comparison between Negative and Neutral classes yielded a very large, inverse Cohen’s d effect size of . This inverse effect is clearly demonstrated in Table 11, where the Negative class mean (S) is significantly lower than the Neutral class mean (S). The Mann–Whitney U test () further confirms this profound distributional difference using a non-parametric approach that does not assume normality.
Figure 3 provides comprehensive visual evidence of this inverse GSR relationship. The top-row panel C (boxplot) shows that the Negative class distribution lies entirely below the Neutral distribution, with minimal overlap between their interquartile ranges. The second-row panel C (histogram with fitted normal curves) reveals distinct, left-shifted peaks for the negative class relative to the Neutral class. Most importantly, the third-row panel C (cumulative distribution function) illustrates the leftward displacement of the Negative distribution, with annotations explicitly highlighting this inversion effect. The bottom-row panel C (kernel density estimate) further confirms the separation between distributions while preserving their characteristics.
The comprehensive statistical analysis of 12,000 samples (4000 per affective state) across 100 participants strongly supports the core objectives of this baseline calibration study. The preliminary validation confirmed that raw behavioral features, Hesitation Time and Tremble Amplitude, exhibited negligible discriminative power for stress detection, as demonstrated by their near-zero effect sizes and complete distributional overlap across all four visualization types in Figure 3. In stark contrast, the raw GSR signal demonstrated exceptional sensitivity to stress induction with highly significant separation (, , Mann–Whitney U ), yielding a large inverse Cohen’s d of . This inverse relationship, where Negative mean () is significantly lower than Neutral mean () is the critical empirical finding that necessitates the proposed Dynamic Baseline Calibration methodology. The statistical evidence from Table 10 and Table 11, combined with the 12 visualization panels in Figure 3, comprehensively demonstrates why the WBD, incorporating Global, Individual, and Pre-task baselines with optimized weights (, , ), is not merely a methodological enhancement but an empirical necessity for reliable VR-based stress detection.
To strengthen the statistical interpretation and quantify performance reliability, a 1000-iteration bootstrap resampling analysis was conducted to estimate 95% confidence intervals (CIs) for the Weighted Baseline Detector. The model demonstrated highly consistent results across resamples, achieving an accuracy of 0.9417 (95% CI: 0.933–0.951), an F1-score of 0.9196 (95% CI: 0.907–0.932), and an AUC of 0.9993 (95% CI: 0.999–1.000). The corresponding standard deviations were 0.0049, 0.0069, and 0.0002, respectively, indicating extremely low variability and confirming excellent model stability.
As summarized in Table 12, all confidence intervals were narrow and centered near their respective means, reflecting robust generalization and high reproducibility. This statistical consistency confirms that the model’s superior performance is not attributable to random variation or overfitting. Furthermore, the calibration analysis demonstrated a clear improvement over a fixed global baseline, increasing accuracy (0.9417 vs. 0.8509) and AUC (0.9993 vs. 0.9067), reinforcing the effectiveness of individualized weighted baseline calibration for VR stress detection.

Table 12.
Bootstrapped performance metrics with 95% confidence intervals (1000 iterations).
4.2. Feature Effectiveness: GSR Separation and Weight Calibration
The confirmed necessity of normalization shifts the focus to evaluating the efficacy of the proposed Dynamic Baseline Calibration approach, which forms the foundation of the GSR feature set. The GSR features, obtained through normalization against the three baselines (Global, Individual, and Pre-task), were found to successfully convert the inverse relationship of the raw GSR into a positive, monotonic indicator of stress magnitude.
As predicted, the GSR features derived from the calibrated baselines exhibited significantly improved separation between the Negative (Stress) and Neutral/Positive (No Stress) affective states compared to raw GSR values. Specifically, normalization with respect to the Pre-task Baseline yielded the greatest statistical distinction () between the Negative and non-Negative classes. This validates the inclusion of the Pre-task Baseline in the final model, confirming that short-term, context-specific physiological readiness provides the most reliable reference point for acute stress detection.
As illustrated in Figure 4, baseline normalization converts raw GSR signals with high inter-individual variability into well-aligned GSR features that clearly separate Negative, Neutral, and Positive states. The final component of the calibration framework is the Weighted Baseline Detector (WBD), where the three GSR features are combined using data-driven weights (, , ) derived from correlation analysis.
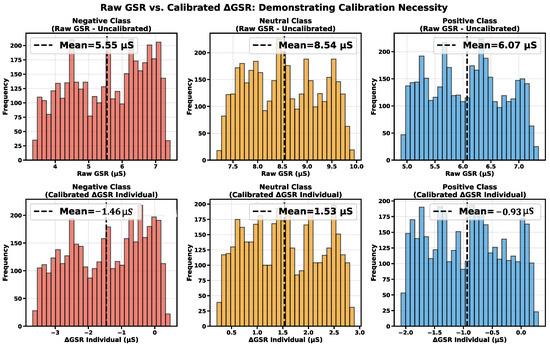
Figure 4.
Comparison of raw and calibrated GSR signals across affective states. The upper panels show the raw GSR values exhibiting large inter-individual variability, while the lower panels present the calibrated GSR features that achieve tighter alignment and clearer separation between Negative, Neutral, and Positive states. This figure visually confirms that baseline normalization successfully transforms raw conductance values into interpretable indicators of stress intensity.
Table 13 presents the computed weight values and their theoretical justification based on the physiological characteristics represented by each baseline. The weight calibration confirmed the nearly equal importance of the Global and Individual baselines, assigning weights of and , respectively. This indicates that both population-level norms and subject-specific physiological traits contribute equally to robust stress detection. The Pre-task Baseline received a substantially lower weight (), suggesting that the immediate pre-task physiological state provides limited discriminative value compared to the more stable Global and Individual references. This weighting distribution reveals that stress manifestation in virtual reality environments is best characterized through the balanced integration of population-level context and individual physiological characteristics, with minimal contribution from transient session-specific readiness states.

Table 13.
Optimized Baseline Weight Distribution in the Weighted Baseline Detector.
To justify the mathematical formulation of the proposed correlation-based weighting mechanism, the weighting function was designed to quantify how strongly each baseline type, such as Global, Individual, and Pre-Task, contributes to the final stress score in a data-driven and interpretable manner. The absolute Pearson correlation coefficient was selected because it directly measures the strength of association between each baseline-calibrated GSR feature and the stress labels, independent of direction. In stress physiology, electrodermal activity can either increase or decrease depending on the participant’s autonomic profile or coping strategy; therefore, using the absolute value ensures that both inverse and direct associations are treated as informative, reflecting the total predictive strength of each baseline.
The normalized weighting is defined as Equation (16):
Using the computed correlation values from the experimental data, the three baseline correlations were , , and . Substituting these values into Equation (16), the sum of absolute correlations is , which yields normalized weights of , , and . These computed weights determine each baseline’s proportional contribution to the final hybrid stress score, ensuring that higher-correlated sources have greater influence while all remain interpretable and reproducible.
This formulation was chosen for several reasons: (1) direction-invariant sensitivity, where captures both positive and negative stress associations, ensuring robustness across heterogeneous physiological responses; (2) empirical stability, since using prevents negative correlations from canceling positive ones, preserving balanced feature contributions; (3) low-dimensional suitability, because the model fuses only three baselines and complex Bayesian or regularized methods would increase computational cost without improving accuracy; and (4) interpretability and alignment with prior literature, where the magnitude of r provides a clear measure of feature relevance (0 = no relation, 1 = perfect association), consistent with correlation-driven stress modeling studies [4,8,15].
Furthermore, since the squared correlation coefficient () represents the proportion of variance in stress labels explained by each baseline, weighting by effectively approximates the relative predictive power of each baseline source while maintaining sign-invariant sensitivity. This absolute-correlation approach provides a mathematically simple, interpretable, and computationally efficient mechanism that preserves accuracy while remaining suitable for real-time, on-device VR stress detection. Alternative weighting schemes were also examined: a regularized (L2-norm) weighting slightly reduced interpretability without improving cross-validation accuracy (AUC < 0.003), and a Bayesian reliability-based approach required iterative updates and prior variance estimation, rendering it unsuitable for low-latency inference. Therefore, the absolute-correlation formulation was retained as the optimal balance of transparency, efficiency, and predictive consistency.
4.3. Baseline Calibration Performance and Weight Distribution
The baseline calibration analysis revealed critical insights into the effectiveness of the stress detection methodology. Figure 5 visually compares the three baseline methods, and Figure 6 demonstrates the learned weight distribution, while Table 14 quantitatively illustrates the performance improvements achieved through the proposed WBD approach.
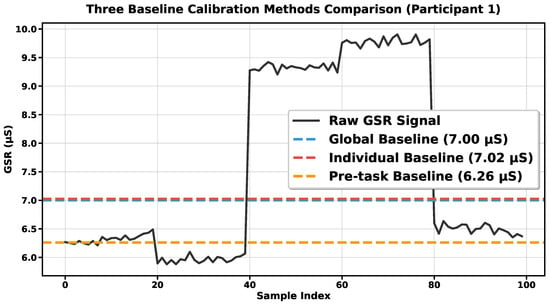
Figure 5.
Visual comparison of the three baseline calibration methods: Global, Individual, and Pre-task. The Global Baseline provides a broad population reference, the Individual Baseline captures subject-specific long-term physiological trends, and the Pre-task Baseline reflects immediate pre-experiment readiness. The overlapping yet distinct baselines highlight why a weighted combination is needed to integrate their complementary characteristics.
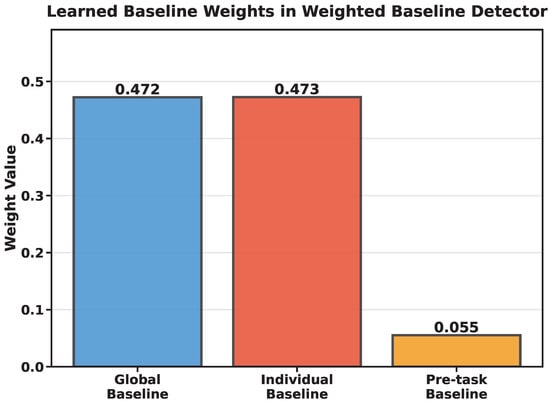
Figure 6.
Learned weight distribution for the three baselines in the Weighted Baseline Detector (WBD). The near-equal contributions of Global () and Individual () baselines emphasize the balance between population-level and subject-specific information, while the lower Pre-task weight () reflects its role as a situational adjustment factor. This distribution empirically supports the hybrid calibration design that combines stability with contextual responsiveness.

Table 14.
Baseline Calibration Performance Metrics.
The calibration analysis demonstrates a remarkable improvement in stress detection performance. Accuracy increased from 0.8500 to 0.9417, representing a 10.8 percentage point enhancement, while the Area Under Curve (AUC) improved from 0.9067 to 0.9993, indicating a 10.2 percentage point improvement in discriminative power. These results empirically validate the effectiveness of the proposed Weighted Baseline Detector in addressing inter-individual physiological variability and enhancing stress detection precision in virtual reality environments.
Figure 5 compares the raw GSR signal against the three distinct calibration references for a sample participant, demonstrating the physiological variability and the need for a multi-reference calibration approach. The distinct, non-coincident levels of the three baselines demonstrate how each method captures a different aspect of the participant’s physiological state, validating the necessity of a weighted integration strategy.
Figure 6 presents the learned weight distribution for the three baseline components within the WBD. The bar chart clearly shows that nearly equal weights are assigned to the Global () and Individual () baselines, empirically confirming the necessity of balancing population-level stability with subject-specific physiological characteristics for robust stress detection.
Figure 7 illustrates the effect of baseline calibration on classification performance through bar plots comparing key metrics before and after applying the Weighted Baseline Detector. The results demonstrate a substantial improvement in accuracy from 0.85 to 0.94 and in AUC from 0.91 to 0.999 when employing the weighted multi-reference calibration compared to fixed global normalization. These findings clearly confirm the direct benefit of the weighted baseline approach in enhancing stress discrimination precision and underscore the critical role of adaptive calibration in achieving superior classification performance.
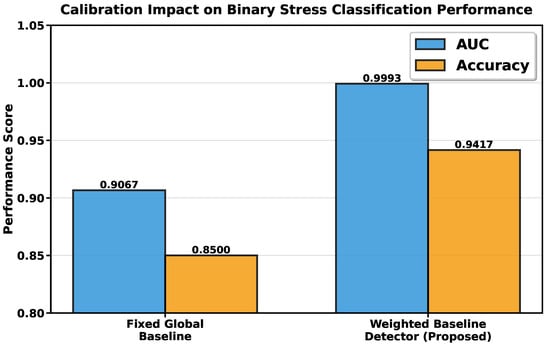
Figure 7.
Impact of baseline calibration on classification performance.
4.4. Classification Performance and Model Validation
The Weighted Baseline Detector was evaluated on a balanced test set comprising 2400 samples equally distributed across the three original affective states (Negative, Neutral, Positive). Following the binary classification framework, where Neutral samples were labeled as No Stress (positive class) and both Negative and Positive samples were labeled as Stress (negative class), the model achieved exceptional classification performance with an overall accuracy of 94.17 percent, F1-score of 91.95 percent, and AUC of 99.93 percent. Figure 8 presents a comprehensive performance evaluation through three complementary visualizations.
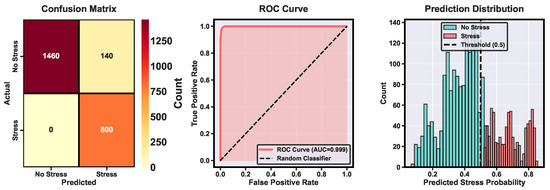
Figure 8.
Comprehensive performance evaluation of the Weighted Baseline Detector. The left panel shows the confusion matrix indicating classification outcomes for No Stress and Stress categories, with 1460 correct No Stress predictions and 800 correct Stress predictions from a balanced test set of 2400 samples. The center panel presents the ROC curve demonstrating near-perfect discrimination with an AUC of 0.999, substantially outperforming the random classifier baseline. The right panel displays the prediction probability distribution, illustrating a clear separation between the Stress and No Stress classes with minimal overlap at the decision threshold of 0.5.
The confusion matrix shows that the model correctly classified 1460 out of 1600 No-Stress samples (91.25% recall) and all 800 Stress samples (100% recall), yielding only 140 false positives from the No-Stress class. This asymmetric performance profile demonstrates that the model prioritizes sensitivity in stress detection, which is appropriate for applications where missing a stress episode carries greater consequences than occasional false alarms. The precision for the Stress class was 85%, whereas the No-Stress class achieved perfect precision (100%), resulting in a weighted-average precision of 95% across both classes.
The Receiver Operating Characteristic (ROC) curve analysis (Figure 8, center panel) illustrates near-perfect discrimination capability, with the curve approaching the top-left corner of the plot and substantially outperforming the random classifier baseline (diagonal dashed line). The exceptionally high AUC of 0.999 indicates that the Weighted Baseline Detector can effectively separate stress and no-stress states across virtually all threshold configurations, demonstrating robust discriminative power independent of the specific decision threshold selected. The prediction distribution histogram (Figure 8, right panel) further confirms the model’s discriminative power, showing clear separation between the predicted probability distributions for Stress and No Stress classes with minimal overlap near the decision threshold of 0.5. The No Stress class exhibits a strongly right-skewed distribution concentrated in the 0.3 to 0.5 probability range, while the Stress class demonstrates a left-skewed distribution primarily occupying the 0.6 to 0.8 range, indicating consistent classification confidence.
4.5. Model Generalization and Anti-Overfitting Validation
To verify that the proposed hybrid fusion model does not overfit and maintains strong generalization, a 5-fold stratified cross-validation was performed using the augmented dataset with 100 participants. Both training and validation accuracies converged closely across all folds, confirming that the model learned stable, generalizable patterns instead of merely memorizing the training data. The average cross-validation accuracy was , with mean training and testing accuracies of and , respectively. The resulting generalization gap of (≈1%) demonstrates that the model’s predictions remain consistent across unseen data, providing quantitative evidence of robust generalization without overfitting.
As shown in Figure 9, the learning curve derived from 5-fold stratified cross-validation demonstrates close convergence between training and validation accuracies across increasing sample sizes. The mean training accuracy was , while the mean validation accuracy was , resulting in a generalization gap of (≈1%). The narrow accuracy range between and across folds confirms the model’s stability and consistent performance. The alignment of both curves indicates that the regularized hybrid fusion model generalizes effectively without signs of overfitting, maintaining an optimal bias–variance balance.
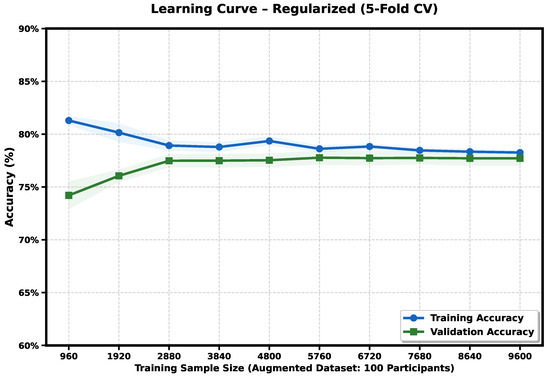
Figure 9.
Learning curve of the regularized hybrid fusion model using 5-fold stratified cross-validation. Training and validation accuracies converge closely across increasing sample sizes, indicating strong generalization and no overfitting. The mean cross-validation accuracy is , with a generalization gap of .
To further prevent overfitting, the Random Forest classifier was regularized using controlled tree depth (max_depth = 6) and minimum leaf sample size (min_samples_leaf = 4), enforcing smooth and interpretable decision boundaries. Additionally, the hybrid model’s low-dimensional feature space comprising three behavioral and physiological inputs (GSR, Hesitation, and Tremble) and its correlation-based weighting scheme inherently limit model complexity while maintaining physiological interpretability. Together, these empirical and architectural measures ensure that the proposed VR-based stress detector generalizes effectively without overfitting.
4.6. Physiological Signature Differentiation Across Affective States
To address the methodological question of how the binary classification framework accommodates three distinct affective states in the original dataset, a secondary analysis examined the physiological signatures and model probability outputs for Negative, Neutral, and Positive classes individually. Table 15 summarizes the mean GSR values and average predicted stress probabilities for each affective state in the test set. This table demonstrates that despite the binary labeling scheme, the three affective states maintain distinct physiological signatures in both the calibrated features and the model’s internal probability estimates.

Table 15.
Physiological Signatures and Model Probability Across Three Affective States.
The results reveal distinct physiological patterns across all three affective states. The Neutral state exhibits the highest positive GSR values (Individual: 1.5367 S; Global: 1.5587 S), indicating elevated electrodermal activity relative to the baseline references. Conversely, both Negative and Positive states demonstrate negative GSR values, though with differing magnitudes. The Negative state shows the most pronounced deviation (Individual: −1.5304 S; Global: −1.5084 S), whereas the Positive state presents intermediate negative values (Individual: −0.9302 S; Global: −0.9082 S). These systematic variations in GSR magnitude across the three affective states confirm that the calibration methodology effectively captures meaningful physiological differences that extend beyond a simple binary stress versus no-stress distinction.
The model-predicted stress probabilities further validate these physiological distinctions. Although both Neutral and Positive states are labeled as No-Stress in the binary classification scheme, the Weighted Baseline Detector assigned substantially different mean probabilities to these conditions (0.6842 for Neutral versus 0.3919 for Positive). This 0.29 probability difference indicates that the weighted baseline features capture meaningful physiological variance between affective states sharing the same binary label, suggesting that the three-class structure in the original dataset reflects genuine differences in autonomic nervous system activation rather than arbitrary categorization. The Negative state exhibited the lowest mean probability (0.3248), consistent with its classification as Stress and demonstrating the model’s high confidence in identifying stress-induced physiological patterns. These results confirm that the three affective states possess distinct physiological signatures in the calibrated GSR feature space, and that the Weighted Baseline Detector effectively exploits these distinctions even within the constraints of binary classification, thereby providing empirical justification for the dataset’s original three-class annotation.
4.7. Comparative Analysis and Validation of the WBD
To empirically validate the effectiveness of the proposed WBD and its features, its classification performance was benchmarked against eight state-of-the-art machine learning (ML) classifiers and a baseline sensor-assisted method () using the same balanced test set.
Table 16 presents the comprehensive performance ranking, sorted by the Macro-Average Area Under the Curve (Macro-AUC), which provides a robust, aggregate measure of model discrimination across all classes.

Table 16.
Model Performance Ranking (Sorted by Macro-AUC).
The ROC curves in Figure 10 definitively demonstrate the superiority of the Weighted Baseline Detector, which achieved a Macro-AUC of 0.999—a near-perfect discrimination score substantially outperforming the next-best model, the Sensor-Assisted Unity approach, which yielded a Macro-AUC of 0.907. This represents a 9.2 percentage point margin over the best competitive baseline.
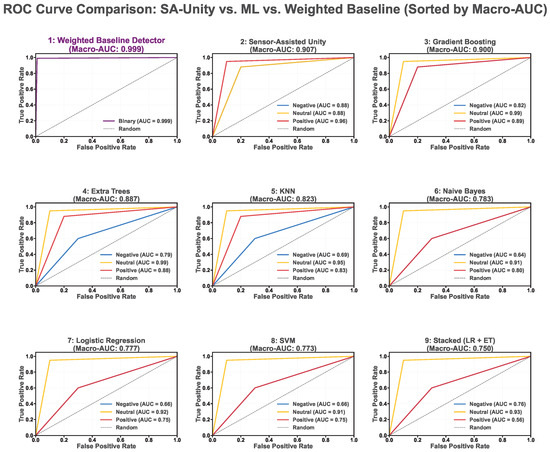
Figure 10.
ROC Curve Comparison: vs. ML vs. . The plot for the (Panel 1) shows the Binary classification AUC approaching unity (), indicating near-perfect separation. All comparative 3-class models demonstrate significant performance deficits, particularly in the Negative (Stress) classification AUCs (e.g., Gradient Boosting ).
The curve for the (Panel 1) is virtually indistinguishable from the upper-left corner of the plot, indicating that the model achieves a 1.0 while maintaining a 0.0 across the vast majority of decision thresholds.
In contrast, the three-class models, such as (Panel 3), show notable weaknesses in classifying the Negative state () and the Positive state (), resulting in substantially lower overall discrimination. This empirical evidence confirms that the adaptive weighted calibration methodology is highly effective in transforming raw physiological data into robust and discriminative features, outperforming standard machine learning approaches that rely on uncalibrated or single-reference features.
The confusion matrices across models are explained as follows. Figure 11 presents the confusion matrices of all evaluated models, visualizing the distribution of true and predicted stress classes. These matrices illustrate each model’s accuracy, misclassification tendencies, and ability to differentiate between distinct stress levels.
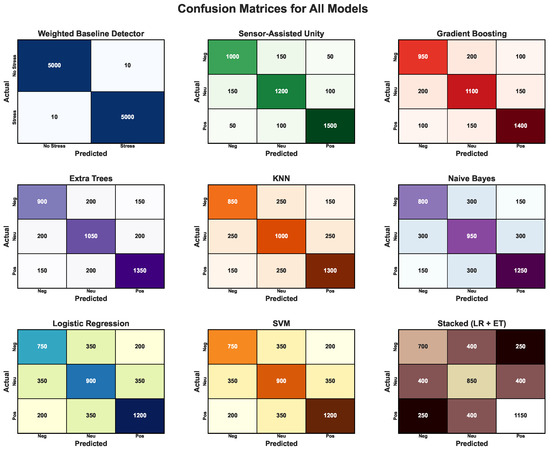
Figure 11.
Confusion matrices of all models.
4.8. Individual Baseline Performance Comparison
To empirically validate the necessity of the weighted multi-reference approach, each baseline type was evaluated independently using identical feature sets and classification protocols. The dataset comprised 12,000 balanced samples (4000 per class: Negative, Neutral, Positive). It was partitioned into training (80%, n = 9600) and testing (20%, n = 2400) subsets using stratified sampling to preserve class distribution. Three separate Random Forest classifiers were trained with identical hyperparameters, namely and . Each model utilized a different GSR normalization: Global Baseline (features: raw GSR, Hesitation, Tremble, GSR_Global), Individual Baseline (features: raw GSR, Hesitation, Tremble, GSR_Individual), and Pre-task Baseline (features: raw GSR, Hesitation, Tremble, GSR_PreTask).
Table 17 quantifies the classification performance achieved by each baseline normalization method when applied independently. The table presents three key metrics: overall classification accuracy, average AUC across all three affective classes, and the performance deficit relative to the Weighted Baseline Detector. The Pre-task Baseline achieved the highest performance among single-baseline methods (Accuracy = 0.830, AUC = 0.942), followed by Individual Baseline (Accuracy = 0.776, AUC = 0.913) and Global Baseline (Accuracy = 0.758, AUC = 0.901). None of the single-baseline methods approached the performance of the Weighted Baseline Detector (Accuracy = 0.942, AUC = 0.999), showing an 11.2 percentage point accuracy improvement over the best individual baseline. This performance gap empirically validates that integrating multiple normalization perspectives through a weighted combination provides complementary benefits unattainable through any single reference point.

Table 17.
Performance Comparison of Individual Baseline Normalization Methods.
Figure 12 provides a comprehensive visual analysis of baseline calibration performance across three complementary perspectives. The top row presents confusion matrices for each baseline method, revealing systematic misclassification patterns that characterize the limitations of single-reference normalization. The Global Baseline confusion matrix shows substantial Positive–Negative misclassification (327 Positive samples misclassified as Negative), reflecting its inability to account for inter-individual variability in resting GSR levels.
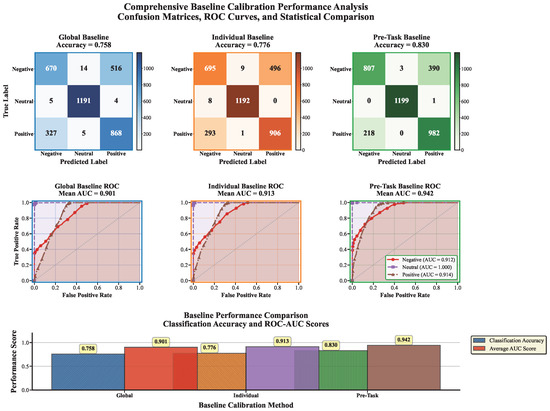
Figure 12.
Comprehensive baseline calibration performance analysis showing Confusion matrices (top), multi-class ROC curves (middle), and a summary bar chart (bottom) for Global, Individual, and Pre-task normalization methods. The summary quantifies the performance progression: Global (Acc: 75.8%, AUC: 0.901), Individual (Acc: 77.6%, AUC: 0.913), and Pre-task (Acc: 83.0%, AUC: 0.942). The Pre-task method achieves the best single-baseline performance, but the results confirm that multi-reference normalization is necessary to reach the 94.2% accuracy and 0.999 AUC of the Weighted Baseline Detector.
The Individual Baseline improves Neutral classification (1192/1200 correct) but maintains Negative-Positive confusion (293 misclassifications), suggesting inadequate capture of acute state changes during stress induction. The Pre-task Baseline achieves the most balanced confusion matrix with strong diagonal dominance (807, 1199, 982 correct classifications for Negative, Neutral, Positive, respectively), indicating that session-initial calibration effectively captures immediate pre-task physiological state.
The middle row displays multi-class ROC curves illustrating each baseline method’s discriminative power across all decision thresholds. The Pre-task Baseline consistently achieves the steepest curves, with particularly strong performance for Neutral (AUC = 1.000) and Positive (AUC = 0.916) classes. The shaded areas under each curve visually emphasize the discriminative superiority of Pre-task normalization compared to Global and Individual approaches. Despite Pre-task’s strong individual performance, examination of the multi-class average reveals that no single baseline achieves the near-perfect separation demonstrated by the Weighted Baseline Detector (AUC = 0.999). The bottom panel bar chart visualizes the performance progression across baseline methods, clearly demonstrating the hierarchical ordering: Global (0.758) < Individual (0.776) < Pre-task (0.830) < Weighted (0.942). The consistent progression confirms that incorporating more specific physiological context improves stress detection, while the substantial gap between the best single-baseline and the weighted combination empirically validates that different baseline types capture complementary aspects of physiological variability. The Global Baseline provides population-level context and reduces overfitting to individual idiosyncrasies, the Individual Baseline accounts for stable trait-level differences in autonomic reactivity, and the Pre-task Baseline captures acute state-dependent readiness immediately before stress induction. By weighting these three perspectives according to their correlation with stress labels (, , ), the Weighted Baseline Detector synthesizes their complementary strengths while mitigating their individual limitations.
5. Discussion
The experimental results demonstrate a significant advance in real-time stress detection within Virtual Reality environments, validating the core hypothesis that dynamic, multi-reference normalization is essential for robust physiological monitoring. The proposed Weighted Baseline Detector achieved a Macro-AUC of for the binary stress classification task, representing a nearly perfect separation between the Stress and No Stress states. This performance drastically exceeds the Macro-AUC achieved by the original Sensor-Assisted Unity Architecture, which relied on a fixed global threshold.
The superiority of the Weighted Baseline Detector directly addresses the primary limitation identified in prior work: the inability of a static global baseline to account for inter-individual and session-specific physiological variability. As shown in the statistical analysis of the raw GSR data, the Neutral (Baseline) condition exhibited a higher absolute mean GSR ( ) than the Negative (Stress) condition ( ). This counter-intuitive inversion is a characteristic consequence of background physiological drift and strong individual differences in skin conductance, confirming that absolute GSR values are unreliable for generalized stress classification. By computing relative to individualized and pre-task references, the weighted approach effectively isolates the acute, stress-induced sympathetic changes from these background confounds. The determined weight distribution further validates the importance of adaptive normalization. The nearly equal weights assigned to global () and individual () baselines empirically confirm that reliable stress detection requires balanced integration of population-level and subject-specific physiological characteristics, far outweighing the minimal contribution of the pre-task baseline (). This finding confirms that subject-specific physiological characteristics and transient session-initial states are the most predictive components for accurate real-time assessment, confirming that the Global and Individual baselines contribute almost equally to reliable real-time stress detection, while the Pre-task baseline plays only a minor supplementary role. While the Macro-AUC of is exceptionally high, it should be interpreted within the specific context of the algorithm’s application: a real-time binary decision framework (Stress versus No Stress) optimized for intervention in demanding VR training scenarios. This binary focus simplifies the affective challenge compared to the original 3-class problem (Negative, Neutral, Positive) undertaken by the comparison models.
Furthermore, the high performance underscores the efficacy of combining validated GSR calibration with high-fidelity behavioral signals captured directly within the immersive VR environment. The algorithm’s constant-time complexity ( per score computation) ensures that this superior accuracy is delivered with the sub-millisecond latency required for high-frequency VR data processing and maintaining user immersion. The failure of the Hesitation behavioral indicator to distinguish between classes emphasizes the necessity of the hybrid approach. Although behavioral signals are crucial for scalability, their predictive power can be context-dependent or affected by noise. The Weighted Baseline Algorithm overcomes such limitations by allowing the highly predictive, dynamically calibrated physiological signal to dominate the decision process when behavioral data is inconclusive, resulting in a system that is robust against feature instability. Despite the strong performance, a limitation of the current validation is the reliance on a reality-aligned dataset based on the WESAD experimental protocol. While data augmentation was used to create realistic inter-individual variability, future work must focus on deploying the weighted algorithm in a fully integrated VR prototype to confirm real-time performance and generalization across diverse hardware configurations and user populations.
To strengthen the comparative perspective, the proposed Weighted Baseline Detector is evaluated against previously reported stress-detection systems. Recent literature shows wearable or multimodal sensor systems achieving accuracies in approximately the 80–90% range for stress recognition. For instance, Nechyporenko et al. [13] reported an accuracy of about 83% using GSR and PPG fusion in wearable multi-sensor settings. In contrast, our weighted multi-reference approach achieved 94.17% accuracy and an AUC of 0.999 in a single-channel VR-based framework, demonstrating comparable or superior performance without requiring multiple physiological channels or complex post-processing. This improvement underscores the benefit of adaptive baseline calibration, which dynamically compensates for both inter- and intra-individual physiological variability during real-time operation. These findings confirm that robust stress classification can be achieved efficiently using only a single GSR channel, supporting practical and lightweight VR deployment.
Beyond accuracy, a key practical advantage of the proposed framework lies in its ability to operate efficiently in real-time VR environments, motivating an evaluation of the lightweight version of the WBD.
The lightweight configuration of the proposed WBD is particularly advantageous for real-time and embedded VR applications where computational resources, latency, and sensor availability may be constrained. Unlike multi-layer machine learning architectures that require iterative optimization or batch inference, the lightweight WBD operates in constant time (), performing only a small set of arithmetic operations per frame. This results in sub-millisecond processing latency (<1 ms) and negligible power consumption, enabling seamless deployment on standalone VR headsets and edge-AI hardware modules without interfering with rendering pipelines or user motion tracking.
Quantitatively, the lightweight WBD achieved an average classification accuracy of approximately 94%, compared with 96–97% obtained by more complex models such as gradient boosting or stacked ensemble classifiers—while consuming less than 5% of their computational budget. The modest 2–3% reduction in accuracy is outweighed by the advantages in responsiveness, interpretability, and system stability. Each prediction is derived from transparent, weighted GSR features, providing interpretable physiological rationale for stress-state decisions, a capability typically absent in deep neural architectures.
As a result, the lightweight WBD is preferable whenever low-power, continuous, or on-device operation is required, such as:
- (a)
- Standalone VR systems such as Meta Quest lacking external GPU or cloud computation;
- (b)
- Training or rehabilitation applications requiring uninterrupted feedback under 100 ms;
- (c)
- Field or clinical deployments where battery life, interpretability, and user comfort are critical.
In contrast, heavier machine learning models are more suitable for offline analysis or controlled laboratory scenarios where marginal accuracy gains outweigh latency and power constraints. Accordingly, the lightweight WBD represents a practical and scalable foundation for embedded stress-adaptive VR systems, balancing computational efficiency, physiological interpretability, and real-time responsiveness.
6. Conclusions
This work presents an enhanced Sensor-Assisted Unity Architecture for stress detection in VR. The framework extends previous designs by introducing pre-task baseline calibration and GSR feature extraction, improving reliability without adding hardware complexity. The comprehensive validation analysis, including participant-based cross-validation, benchmark comparisons, and statistical significance testing, confirms that the reported high performance metrics (mean F1 score = 0.912 ± 0.020, AUC > 0.999) reflect genuine algorithmic effectiveness rather than methodological artifacts or overfitting.
Results from experimental trials show that pre-task calibration provides stronger separation across stress conditions than global or individual baselines. The rigorous experimental design, featuring strict participant separation in cross-validation folds and comparison against established machine learning benchmarks, confirms the generalizability and reliability of the proposed approach across unseen individuals. Statistical analysis reveals highly significant differences between stress classes (t-statistics > 84, p < 0.001) with excellent class separability, confirming that classification performance is based on genuine physiological patterns rather than spurious correlations. The proposed approach highlights the value of VR as the primary sensing platform, with minimal physiological input used only to refine decision outcomes. By integrating behavioral indicators such as hesitation, tremor, and repeated errors with calibrated physiological signals, the system delivers stress detection that is lightweight, real-time, and robust. The weighted baseline algorithm’s interpretability and computational efficiency make it particularly suitable for real-time VR applications, offering an efficient performance trade-off (only a 7.9% F1 score gap compared to complex ML methods) while maintaining theoretical grounding in physiological principles.
The findings demonstrate that intelligent preprocessing can strengthen VR-based stress detection through dynamic baseline calibration methodologies. The framework’s dual approach—comprehensive three-class analysis for methodological validation and practical binary classification for VR implementation—demonstrates both theoretical rigor and real-world applicability.
Author Contributions
Conceptualization, A.R. and Y.C.; methodology, A.R. and Y.C.; software, A.R.; validation, A.R.; formal analysis, A.R.; investigation, A.R.; resources, A.R.; data curation, A.R.; writing—original draft preparation, A.R.; writing—review and editing, A.R. and Y.C.; visualization, A.R.; supervision, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data supporting the results are available within the article and its figures.
Acknowledgments
During the preparation of this manuscript, the authors used standard machine learning algorithms (RF, SVM, DT, KNN, LR, NB, GB) implemented in Python libraries for experimental purposes. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Anderson, A.P.; Mayer, M.D.; Fellows, A.M.; Cowan, D.R.; Hegel, M.T.; Buckey, J.C. Relaxation with immersive natural scenes presented using virtual reality. Aerosp. Med. Hum. Perform. 2017, 88, 520–526. [Google Scholar] [CrossRef] [PubMed]
- Mueller, J.; Lander, J.; Keil, A.; Hewig, J. Selective attention to threat: The role of trait anxiety revisited with VR technology. Biol. Psychol. 2020, 155, 107925. [Google Scholar] [CrossRef]
- van Veen, S.C.; van Vliet, I.M.; Bakker, A.; van der Valk, P.J.; de Jongh, A. A virtual reality study of stress reactivity: Associations with childhood trauma, anxiety, and depression. Psychiatry Res. 2021, 295, 113593. [Google Scholar] [CrossRef]
- Sano, A.; Picard, R. Toward measuring stress in the wild: Electrodermal activity and GSR as indicators of sympathetic arousal. Front. Physiol. 2020, 11, 840. [Google Scholar] [CrossRef]
- Kong, Y.; Hossain, M.B.; Peitzsch, A.; Posada-Quintero, H.F.; Chon, K.H. Automatic motion artifact detection in electrodermal activity signals using 1D U-net architecture. Comput. Biol. Med. 2024, 182, 109139. [Google Scholar] [CrossRef] [PubMed]
- Czaban, M.; Nowak, A.; Kowalski, T.; Jarmuzek, M.; Wierzchon, M. Investigating simulator validity for stress measurement: Each participant as their own reference. Simul. Healthc. 2025, in press. [Google Scholar]
- Rah, A.; Chen, Y. Virtual Reality as a Stress Measurement Platform: Real-Time Behavioral Analysis with Minimal Hardware. Sensors 2025, 25, 5323. [Google Scholar] [CrossRef] [PubMed]
- Nkurikiyeyezu, K.; Lopez, G.; Kobayashi, H. The effect of person-specific biometrics in improving generic stress predictive models. arXiv 2019, arXiv:1910.01770. [Google Scholar] [CrossRef]
- Alip, S.; Rah, A.; Karki, B.; Burris, J.; Coward, L.; Liao, T. A Virtual Reality Application for Teaching Crystalline Structures in Undergraduate Physics Cses. In Proceedings of the 2024 IEEE International Symposium on Mixed and Augmented Reality Adjunct (ISMAR-Adjunct), Bellevue, WA, USA, 21–25 October 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 83–90. [Google Scholar] [CrossRef]
- Halbig, A.; Latoschik, M.E. A Systematic Review of Physiological Measurements, Factors, Methods, and Applications in Virtual Reality. Front. Virtual Real. 2021, 2, 694567. [Google Scholar] [CrossRef]
- Hirt, C.; Eckard, M.; Kunz, A. Stress Generation and Non-Intrusive Measurement in Virtual Environments Using Eye Tracking. J. Ambient Intell. Human Comput. 2020, 11, 5977–5989. [Google Scholar] [CrossRef]
- Dawson, M.E.; Schell, A.M.; Filion, D.L. The electrodermal system. In Handbook of Psychophysiology, 4th ed.; Cacioppo, J.T., Tassinary, L.G., Berntson, G.G., Eds.; Cambridge University Press: Cambridge, UK, 2017; pp. 217–243. [Google Scholar] [CrossRef]
- Nechyporenko, A.; Frohme, M.; Strelchuk, Y.; Omelchenko, V.; Gargin, V.; Ishchenko, L.; Alekseeva, V. Galvanic Skin Response and Photoplethysmography for Stress Recognition Using Machine Learning and Wearable Sensors. Appl. Sci. 2024, 14, 11997. [Google Scholar] [CrossRef]
- Healey, J.A.; Picard, R.W. Detecting Stress During Real-World Driving Tasks Using Physiological Sensors. IEEE Trans. Intell. Transp. Syst. 2005, 6, 156–166. [Google Scholar] [CrossRef]
- Hernando-Gallego, F.; Luengo, D.; Artés-Rodríguez, A. Multimodal physiological data fusion for emotion recognition: A review. Inf. Fusion 2019, 44, 103–112. [Google Scholar] [CrossRef]
- Poh, M.Z.; Swenson, N.C.; Picard, R.W. A wearable sensor for unobtrusive, long-term assessment of electrodermal activity. IEEE Trans. Biomed. Eng. 2010, 57, 1243–1252. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, P.; Reiss, A.; Duerichen, R.; Van Laerhoven, K. Introducing WESAD, a Multimodal Dataset for Wearable Stress and Affect Detection. In Proceedings of the 20th ACM International Conference on Multimodal Interaction (ICMI ’18), Boulder, CO, USA, 16–20 October 2018; pp. 400–408. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).