IB-PC: An Information Bottleneck Framework for Point Cloud-Based Building Information Modeling
Abstract
1. Introduction
- We develop an IB-PC formulation that redefines point-cloud representation learning under an information-theoretic trade-off between compression and sufficiency, providing both theoretical insight and practical regularization for architectural point clouds.
- We establish an extended evaluation protocol encompassing not only accuracy but also calibration (ECE, Brier score, NLL), robustness to degradation (noise, occlusion, density variation), efficiency (FLOPs, parameters, latency, memory), and structural fidelity (residuals for planes and cylinders, inlier ratios).
2. Related Work
2.1. Information Bottleneck and Its Variational Formulation
2.2. Extensions and Applications
2.3. Learning-Based and Compression-Based Architectures
3. Problem Formulation
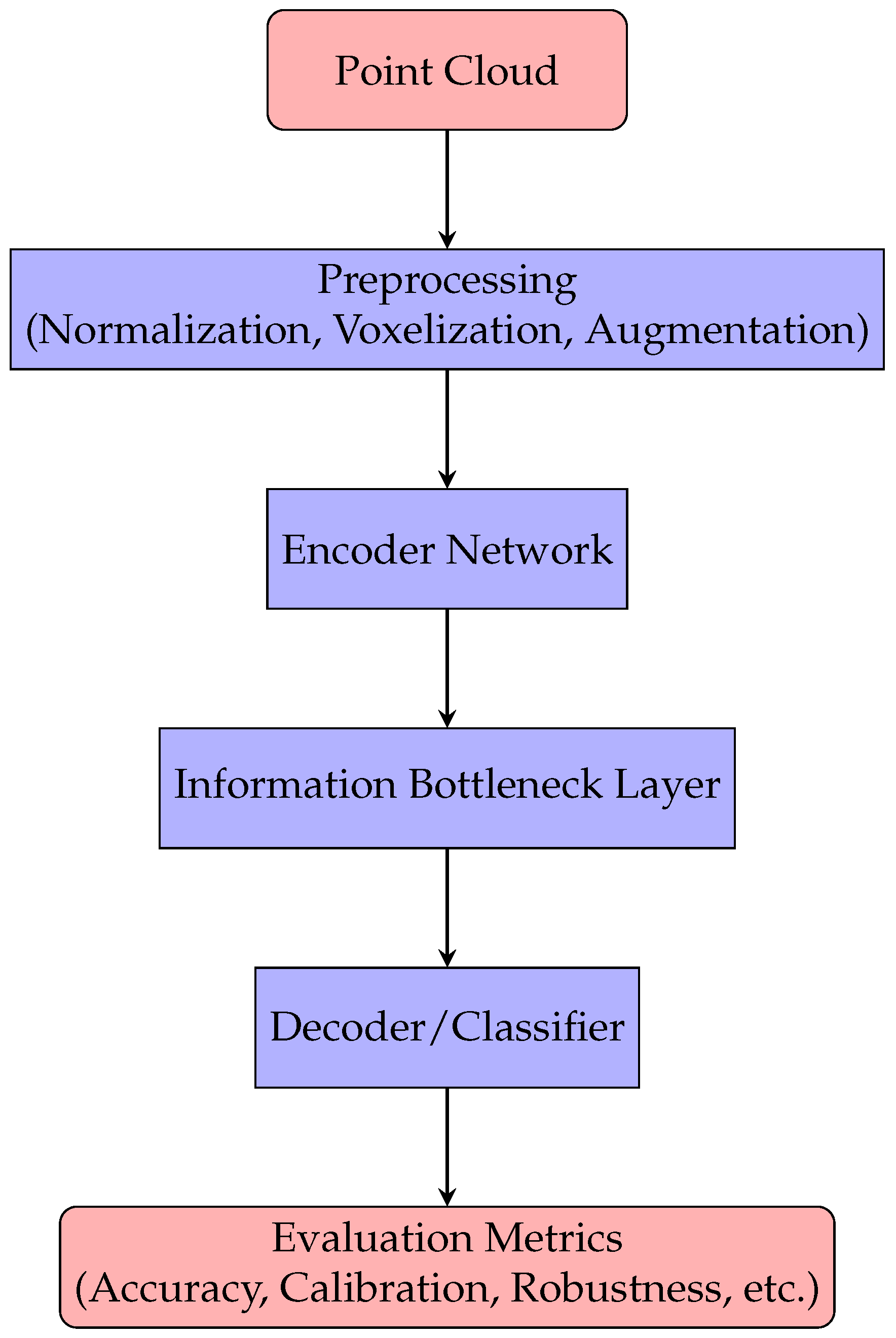
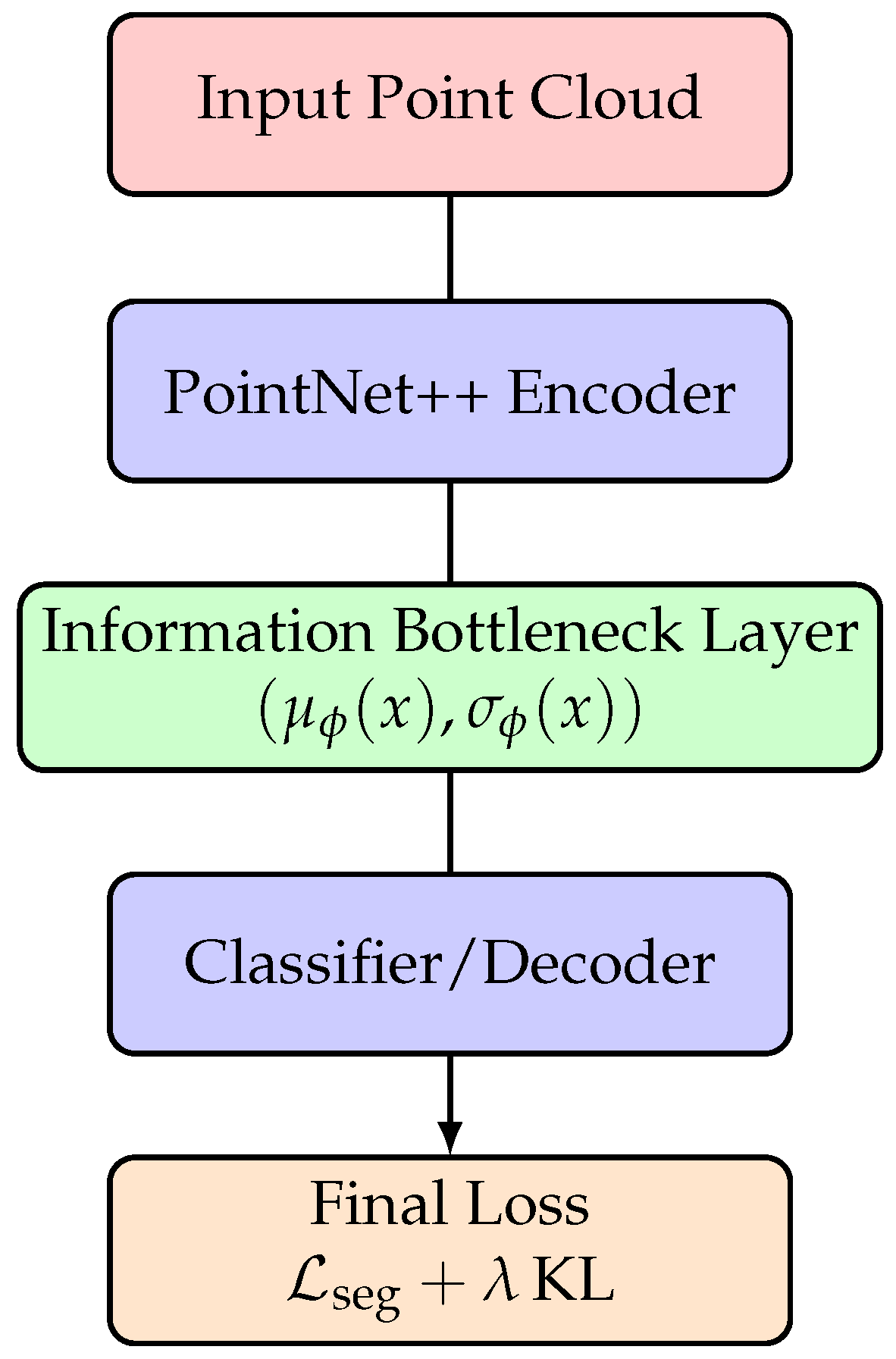
4. Method
4.1. Preprocessing
- Normalization: Each point block is centered by subtracting its centroid and scaled to fit within a unit sphere, removing translation and scale bias.
- Voxelization: The spatial density is regularized by discretizing the 3D space into voxels, with one representative point per voxel. The voxel size (2–8 cm for indoor scenes, 5–20 cm for outdoor scenes) balances fidelity and efficiency.
- Feature Augmentation: In addition to coordinates, RGB color, surface normals (via PCA), and relative height are concatenated to enrich the representation.
- Block Sampling: Overlapping blocks of 4k–8k points are randomly extracted to form training batches, ensuring diversity and memory feasibility.
4.2. Encoder Network
4.3. Information Bottleneck Layer
4.4. Decoder and Classifier
5. Experimental Setting
5.1. Datasets
- TUM RGB-D (Indoor) (https://vision.in.tum.de/data/datasets/rgbd-dataset, accessed on 2 September 2025): Comprising RGB-D sequences of office and residential environments, this dataset highlights structural elements such as walls, floors, ceilings, windows, and furniture. It poses challenges related to occlusion, lighting, and sensor noise, closely reflecting indoor scan-to-BIM scenarios.
- Semantic3D (Outdoor) (http://www.semantic3d.net, accessed on 3 September 2025): A large-scale LiDAR benchmark of urban and architectural environments, including streets, squares, and façades. Each scan contains millions of points labeled into categories such as building, vegetation, ground, and vehicles. It tests scalability, class imbalance handling, and geometric generalization.
5.1.1. Training Protocol
5.1.2. Evaluation Metrics
- Accuracy: The core segmentation quality is evaluated using the Intersection over Union (IoU):We report mean IoU (mIoU), overall accuracy (OA), mean class accuracy (mAcc), macro F1, and Cohen’s .
- Calibration: Reliability of predicted confidence is quantified by the Expected Calibration Error (ECE, 15 bins):complemented by the Negative Log-Likelihood (NLL) and the Brier score.
- Robustness: Sensitivity to input perturbations is measured under point jitter, occlusion, and density variation. The Corruption Error (CE) denotes the relative degradation in mIoU with respect to clean input data.
- Computational Efficiency: We assess floating-point operations (FLOPs), parameter count, inference latency, throughput, GPU memory footprint, and an energy proxy, capturing the scalability of the approach.
- Data Efficiency: Models are trained on subsets containing of the labeled data to evaluate generalization under limited supervision.
- Geometric Consistency: For architectural categories (e.g., walls, floors, façades), we compute plane and cylinder fitting residuals and inlier ratios, forming a Geometric Consistency Score (GCS) that quantifies spatial regularity and alignment with architectural priors.
5.1.3. Baseline Methods
- Learning-based architectures:
- –
- PointNet [22]: The pioneering neural network that directly consumes unordered point sets without voxelization or rasterization. It employs shared multilayer perceptrons (MLPs) and a symmetric max-pooling operation to ensure permutation invariance, providing a unified and efficient framework for 3D object classification, part segmentation, and scene parsing. However, as noted in subsequent studies, its global pooling mechanism neglects local geometric context.
- –
- PointNet++ [23] introduces a hierarchical architecture that recursively applies PointNet to local neighborhoods defined in metric space. This design enables the extraction of fine-grained local features and their aggregation across multiple scales, improving generalization to complex and non-uniformly sampled scenes.
- –
- Point Transformer [34] extends this line of research by introducing self-attention mechanisms into point-cloud learning. Inspired by advances in natural language processing and 2D vision transformers, it models local feature relationships through attention-weighted aggregation, achieving state-of-the-art performance on large-scale benchmarks such as S3DIS and SemanticKITTI. Its ability to adaptively capture long-range dependencies makes it particularly effective for semantic segmentation and object classification in complex 3D environments.
- –
- Point Transformer V3 (PTv3) [35] focuses on scaling efficiency while maintaining accuracy. Instead of introducing new attention mechanisms, PTv3 emphasizes architectural simplicity and scalability through efficient serialized neighbor mapping and large receptive fields. This design achieves significant improvements in speed and memory efficiency, while setting new performance records across more than twenty indoor and outdoor point-cloud benchmarks. Together, these models highlight the evolution from MLP-based encoders to attention-driven architectures, forming a strong foundation for subsequent information-theoretic regularization such as the proposed IB-PC framework.
- Compression-based baselines: To disentangle the contribution of representation compression from architectural learning, we include three non-learning and autoencoding baselines: (i) Random Subsampling (RS), which uniformly reduces point density for efficiency analysis; (ii) PCA Projection, which projects points onto their top-k principal axes to evaluate linear compression performance; and (iii) Autoencoder (AE), a reconstruction-based latent embedding method serving as a learned compression reference. These methods span naive geometric reduction to unsupervised feature learning, providing a meaningful contrast to the IB-regularized framework.
5.2. Experimental Results
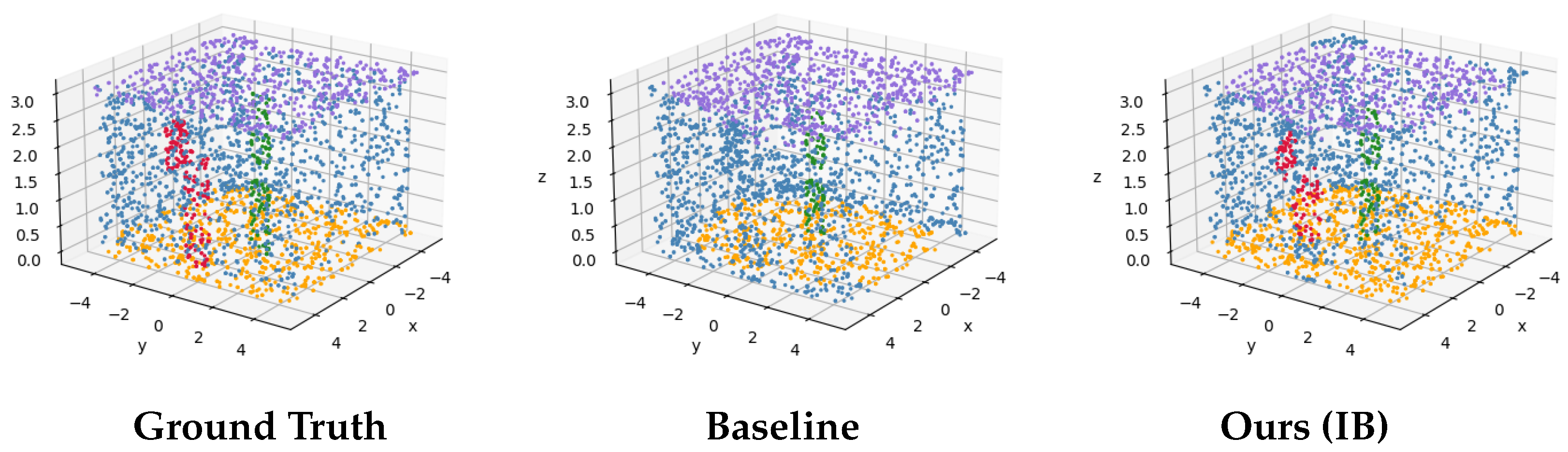
5.2.1. Three-Dimensional Semantic Results in the Indoor Environment
5.2.2. Three-Dimensional Semantic Results in the Outdoor Environment
5.3. Discussion and Analyses
5.3.1. Balancing Accuracy, Efficiency, and Reliability
5.3.2. Robustness and Geometric Consistency
5.3.3. Architectural and Industrial Implications
5.3.4. Limitations and Future Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IB | Information Bottleneck |
| MI | Mutual Information |
| BIM | Building Information Modeling |
| AEC | Architecture, Engineering, and Construction |
Appendix A. Variational Information Bottleneck
Appendix A.1. IB Objective
Appendix A.2. Upper Bound on I(X;Z)
Appendix A.3. Lower Bound on I(Z;Y)
Appendix A.4. VIB Training Objective
Appendix A.5. Gaussian Encoder and Reparameterization
Appendix A.6. Choosing the Bottleneck Strength
References
- Li, Y.; Chen, H.; Yu, P.; Yang, L. A Review of Artificial Intelligence in Enhancing Architectural Design Efficiency. Appl. Sci. 2025, 15, 1476. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014, arXiv:1406.2661. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. arXiv 2020, arXiv:2006.11239. [Google Scholar] [CrossRef]
- Li, C.; Zhang, T.; Du, X.; Zhang, Y.; Xie, H. Generative AI Models for Different Steps in Architectural Design: A Literature Review. arXiv 2024, arXiv:2404.01335. [Google Scholar] [CrossRef]
- Asadi, E.; da Silva, M.G.; Antunes, C.H.; Dias, L. Multi-objective Optimization for Building Retrofit Strategies: A Model and an Application. Energy Build. 2012, 44, 81–87. [Google Scholar] [CrossRef]
- Shan, R.; Jia, X.; Su, X.; Xu, Q.; Ning, H.; Zhang, J. AI-Driven Multi-Objective Optimization and Decision-Making for Urban Building Energy Retrofit: Advances, Challenges, and Systematic Review. Appl. Sci. 2025, 15, 8944. [Google Scholar] [CrossRef]
- Sharma, A.; Kosasih, E.; Zhang, J.; Brintrup, A.; Calinescu, A. Digital Twins: State of the Art Theory and Practice, Challenges, and Open Research Questions. J. Ind. Inf. Integr. 2022, 30, 100383. [Google Scholar] [CrossRef]
- Matarneh, S.; Danso-Amoako, M.; Al-Bizri, S.; Gaterell, M.; Matarneh, R. Building Information Modeling for Facilities Management: A Literature Review and Future Research Directions. J. Build. Eng. 2019, 24, 100755. [Google Scholar] [CrossRef]
- Khattra, S.; Jain, R. Building Information Modeling: A Comprehensive Overview of Concepts and Applications. Adv. Res. 2024, 25, 140–149. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y.; Pan, Y.; Ding, L. Advanced Informatic Technologies for Intelligent Construction: A Review. Eng. Appl. Artif. Intell. 2024, 137 Pt A, 109104. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep Learning for 3D Point Clouds: A Survey. arXiv 2020, arXiv:1912.12033. [Google Scholar] [CrossRef]
- Xu, T.; Tian, B.; Zhu, Y. Tigris: Architecture and Algorithms for 3D Perception in Point Clouds. In Proceedings of the 52nd Annual IEEE/ACM International Symposium on Microarchitecture (MICRO ’52), Columbus, OH, USA, 12–16 October 2019; pp. 629–642. [Google Scholar] [CrossRef]
- Skrzypczak, I.; Oleniacz, G.; Leśniak, A.; Zima, K.; Mrówczyńska, M.; Kazak, J.K. Scan-to-BIM Method in Construction: Assessment of the 3D Buildings Model Accuracy in Terms of Inventory Measurements. Build. Res. Inf. 2022, 50, 859–880. [Google Scholar] [CrossRef]
- He, S.; Qu, X.; Wan, J.; Li, G.; Xie, C.; Wang, J. PRENet: A Plane-Fit Redundancy Encoding Point Cloud Sequence Network for Real-Time 3D Action Recognition. arXiv 2024, arXiv:2405.06929. [Google Scholar]
- Sarker, S.; Sarker, P.; Stone, G.; Gorman, R.; Tavakkoli, A.; Bebis, G.; Sattarvand, J. A Comprehensive Overview of Deep Learning Techniques for 3D Point Cloud Classification and Semantic Segmentation. Mach. Vis. Appl. 2024, 35, 67. [Google Scholar] [CrossRef]
- Tishby, N.; Pereira, F.C.; Bialek, W. The Information Bottleneck Method. In Proceedings of the 37th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 22–24 September 1999; pp. 368–377. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep Learning and the Information Bottleneck Principle. arXiv 2015, arXiv:1503.02406. [Google Scholar] [CrossRef]
- Alemi, A.; Fischer, I.; Dillon, J.; Murphy, K. Deep Variational Information Bottleneck. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Si, S.; Wang, J.; Sun, H.; Wu, J.; Zhang, C.; Qu, X.; Cheng, N.; Chen, L.; Xiao, J. Variational Information Bottleneck for Effective Low-Resource Audio Classification. arXiv 2021, arXiv:2107.04803. [Google Scholar] [CrossRef]
- Sun, H.; Pears, N.; Gu, Y. Information Bottlenecked Variational Autoencoder for Disentangled 3D Facial Expression Modelling. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2022; pp. 2334–2343. [Google Scholar] [CrossRef]
- Cheng, H.; Han, X.; Shi, P.; Zhu, J.; Li, Z. Multi-Trusted Cross-Modal Information Bottleneck for 3D Self-Supervised Representation Learning. Knowl.-Based Syst. 2024, 283, 111217. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. arXiv 2017, arXiv:1612.00593. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. Adv. Neural Inf. Process. Syst. (NeurIPS) 2017, 30, 5105–5114. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Kong, L.; Xu, X.; Cen, J.; Zhang, W.; Pan, L.; Chen, K.; Liu, Z. Calib3D: Calibrating Model Preferences for Reliable 3D Scene Understanding. arXiv 2025, arXiv:2403.17010. [Google Scholar]
- Hagemann, A.; Knorr, M.; Stiller, C. Deep Geometry-Aware Camera Self-Calibration from Video. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 4–6 October 2023; pp. 3415–3425. [Google Scholar] [CrossRef]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A Benchmark for the Evaluation of RGB-D SLAM Systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Algarve, Portugal, 7–12 October 2012. [Google Scholar]
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3D Semantic Parsing of Large-Scale Indoor Spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1534–1543. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Løkse, S.; Jenssen, R.; Principe, J.C. Cauchy-Schwarz Divergence Information Bottleneck for Regression. arXiv 2024, arXiv:2404.17951. [Google Scholar] [CrossRef]
- Goldfeld, Z.; Polyanskiy, Y. The Information Bottleneck Problem and Its Applications in Machine Learning. arXiv 2020, arXiv:2004.14941. [Google Scholar] [CrossRef]
- Zhu, K.; Feng, X.; Du, X.; Gu, Y.; Yu, W.; Wang, H.; Chen, Q.; Chu, Z.; Chen, J.; Qin, B. An Information Bottleneck Perspective for Effective Noise Filtering on Retrieval-Augmented Generation. In Proceedings of the 62nd Annual Meeting of the Association for Computational Linguistics (ACL), Bangkok, Thailand, 11–16 August 2024; pp. 1044–1069. Available online: https://aclanthology.org/2024.acl-long.59/ (accessed on 3 September 2020). [CrossRef]
- Li, F.; Zhang, M.; Wang, Z.; Yang, M. InfoCons: Identifying Interpretable Critical Concepts in Point Clouds via Information Theory. arXiv 2025, arXiv:2505.19820. [Google Scholar] [CrossRef]
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.D.; Schindler, K.; Pollefeys, M. Semantic3D.net: A new Large-scale Point Cloud Classification Benchmark. arXiv 2017, arXiv:1704.03847. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.; Koltun, V. Point Transformer. Adv. Neural Inf. Process. Syst. (NeurIPS) 2021, 34, 16259–16270. [Google Scholar]
- Wu, X.; Jiang, L.; Wang, P.-S.; Liu, Z.; Liu, X.; Qiao, Y.; Ouyang, W.; He, T.; Zhao, H. Point Transformer V3: Simpler, Faster, Stronger. arXiv 2024, arXiv:2312.10035. [Google Scholar] [CrossRef]
- Bank, D.; Koenigstein, N.; Giryes, R. Autoencoders. arXiv 2021, arXiv:2003.05991. [Google Scholar]
- Birdal, T.; Ilic, S. CAD Priors for Accurate and Flexible Instance Reconstruction. arXiv 2017, arXiv:1705.03111. [Google Scholar] [CrossRef]
- Coughlan, J.M.; Yuille, A.L. The Manhattan world assumption: Regularities in scene statistics which enable Bayesian inference. In Proceedings of the 14th International Conference on Neural Information Processing Systems (NIPS’00); MIT Press: Cambridge, MA, USA, 2000; pp. 809–815. [Google Scholar]

| Dataset | Scenes | Classes | Avg. Points/Scene |
|---|---|---|---|
| TUM RGB-D | ∼50 | 10 | 1– |
| Semantic3D | 15 | 8 | – |
| Dimension | Metrics | Objective |
|---|---|---|
| Accuracy | mIoU, OA, mAcc, F1, | Predictive correctness |
| Calibration | ECE, NLL, Brier | Confidence reliability |
| Robustness | CE under noise/occlusion | Stability under perturbations |
| Computational Efficiency | FLOPs, latency, memory | Scalability and cost |
| Data Efficiency | mIoU vs. data fraction | Performance under low data |
| Geometric Consistency | GCS (plane/cylinder residuals) | Alignment with geometry priors |
| Metric | PointNet | PointNet++ | IB (Ours) | IB (PointNet++) |
|---|---|---|---|---|
| mIoU (%) | 65.4 ± 0.3 | 69.1 ± 0.2 | 71.5 ± 0.3 | 73.1 ± 0.2 |
| OA (%) | 78.2 ± 0.4 | 81.5 ± 0.3 | 83.3 ± 0.3 | 84.6 ± 0.2 |
| mAcc (%) | 71.0 ± 0.3 | 74.6 ± 0.3 | 76.2 ± 0.2 | 77.9 ± 0.2 |
| MacroF1 (%) | 68.1 ± 0.4 | 71.6 ± 0.3 | 73.8 ± 0.3 | 75.6 ± 0.3 |
| ECE (%)↓ | 8.2 ± 0.2 | 7.1 ± 0.2 | 5.5 ± 0.1 | 4.9 ± 0.1 |
| Brier↓ | 0.142 ± 0.002 | 0.132 ± 0.002 | 0.119 ± 0.001 | 0.112 ± 0.001 |
| Metric | Point Transformer | Point Transformer v3 | IB (Ours) | IB (PTv3) |
|---|---|---|---|---|
| mIoU (%) | 74.8 ± 0.3 | 76.5 ± 0.2 | 78.3 ± 0.3 | 79.7 ± 0.2 |
| OA (%) | 86.2 ± 0.3 | 87.5 ± 0.2 | 88.6 ± 0.2 | 89.8 ± 0.2 |
| mAcc (%) | 80.5 ± 0.3 | 82.1 ± 0.3 | 83.5 ± 0.2 | 84.7 ± 0.2 |
| MacroF1 (%) | 78.6 ± 0.3 | 80.3 ± 0.3 | 81.7 ± 0.3 | 83.1 ± 0.3 |
| ECE (%)↓ | 6.2 ± 0.2 | 5.6 ± 0.2 | 4.3 ± 0.1 | 3.8 ± 0.1 |
| Brier↓ | 0.118 ± 0.002 | 0.111 ± 0.002 | 0.103 ± 0.001 | 0.098 ± 0.001 |
| Model | Wall | Floor | Ceiling | Column | Window | Door |
|---|---|---|---|---|---|---|
| PointNet++ | 78.3 | 85.6 | 82.1 | 61.4 | 57.9 | 54.2 |
| IB (PointNet++) | 81.7 | 87.5 | 84.3 | 65.9 | 62.8 | 59.6 |
| Model | Walls | Floors | Columns | Facades |
|---|---|---|---|---|
| PointNet++ | 12.5/84.9 | 8.8/90.1 | 17.2/75.1 | 15.5/79.6 |
| IB (PointNet++) | 10.9/87.8 | 7.7/92.3 | 15.2/79.6 | 13.5/83.1 |
| Metric | PointNet | PointNet++ | RS/PCA/AE | IB (Ours) | IB (PointNet++) |
|---|---|---|---|---|---|
| mIoU (%) | 68.2 ± 0.3 | 71.4 ± 0.3 | 69.5 ± 0.4 | 73.8 ± 0.3 | 75.2 ± 0.2 |
| OA (%) | 80.5 ± 0.3 | 83.2 ± 0.3 | 81.1 ± 0.3 | 85.0 ± 0.3 | 86.0 ± 0.2 |
| MacroF1 (%) | 71.3 ± 0.3 | 74.1 ± 0.3 | 72.5 ± 0.3 | 76.9 ± 0.3 | 78.6 ± 0.3 |
| ECE (%)↓ | 7.8 ± 0.2 | 6.9 ± 0.2 | 7.3 ± 0.2 | 5.0 ± 0.1 | 4.4 ± 0.1 |
| NLL↓ | 0.92 ± 0.01 | 0.81 ± 0.01 | 0.88 ± 0.01 | 0.70 ± 0.01 | 0.64 ± 0.01 |
| FLOP Red. | – | – | 28–35% | 30% | 28% |
| Params (M) | 3.6 | 12.2 | 3.6–5.1 | 3.9 | 12.6 |
| Latency (ms) | 18 | 29 | 15–20 | 17 | 27 |
| Metric | Point Transformer | Point Transformer v3 | IB (Ours) | IB (PTv3) |
|---|---|---|---|---|
| mIoU (%) | 77.6 ± 0.3 | 79.1 ± 0.2 | 81.2 ± 0.3 | 82.6 ± 0.2 |
| OA (%) | 88.9 ± 0.3 | 90.3 ± 0.2 | 91.4 ± 0.2 | 92.5 ± 0.2 |
| MacroF1 (%) | 80.2 ± 0.3 | 81.9 ± 0.3 | 83.5 ± 0.3 | 84.9 ± 0.3 |
| ECE (%)↓ | 5.8 ± 0.2 | 5.1 ± 0.2 | 3.9 ± 0.1 | 3.3 ± 0.1 |
| NLL↓ | 0.78 ± 0.01 | 0.72 ± 0.01 | 0.64 ± 0.01 | 0.59 ± 0.01 |
| FLOP Red. | – | – | 27% | 25% |
| Params (M) | 12.8 | 13.5 | 13.1 | 13.8 |
| Latency (ms) | 32 | 35 | 30 | 33 |
| Setting | mIoU (%) | MacroF1 (%) | ECE (%)↓ | Latency (ms) |
|---|---|---|---|---|
| 74.2 | 77.4 | 5.1 | 28 | |
| 75.2 | 78.6 | 4.4 | 27 | |
| 74.8 | 78.1 | 4.6 | 26 | |
| 72.1 | 75.0 | 4.9 | 25 |
| Placement | mIoU (%) | MacroF1 (%) | ECE (%)↓ | FLOPs Red. |
|---|---|---|---|---|
| Early | 73.1 | 76.0 | 5.3 | 33% |
| Mid | 74.0 | 77.0 | 4.8 | 30% |
| Late | 75.2 | 78.6 | 4.4 | 28% |
| Model | AURC ↓ | Cov@1%R ↑ |
|---|---|---|
| PointNet++ | 0.118 | 62.1 |
| IB (PointNet++) | 0.097 | 68.9 |
| Corruption (Severity) | CE PointNet++ | CE IB (PointNet++) |
|---|---|---|
| Jitter ( m) | 5.1 | 3.2 |
| Occlusion (30%) | 8.5 | 6.1 |
| Density Shift (+50% voxel) | 7.2 | 4.6 |
| Model | Throughput | Latency (ms) | Peak Mem (MB) | Energy (J/Sample) |
|---|---|---|---|---|
| PointNet++ | 170 | 29 | 980 | 0.82 |
| IB (PointNet++) | 185 | 27 | 900 | 0.71 |
| Train Fraction | PointNet++ | IB (PointNet++) |
|---|---|---|
| 10% | 58.0 | 62.4 |
| 25% | 64.7 | 68.3 |
| 50% | 68.9 | 72.0 |
| 100% | 71.4 | 75.2 |
| Voxel (cm) | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| PointNet++ | 71.4 | 69.2 | 66.0 | 62.3 |
| IB (PointNet++) | 75.2 | 73.1 | 70.0 | 66.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xie, B.; Xu, T.; Bi, Y.; Luo, Z. IB-PC: An Information Bottleneck Framework for Point Cloud-Based Building Information Modeling. Electronics 2025, 14, 4399. https://doi.org/10.3390/electronics14224399
Zhang Y, Xie B, Xu T, Bi Y, Luo Z. IB-PC: An Information Bottleneck Framework for Point Cloud-Based Building Information Modeling. Electronics. 2025; 14(22):4399. https://doi.org/10.3390/electronics14224399
Chicago/Turabian StyleZhang, Yameng, Bingxue Xie, Ting Xu, Yanqiu Bi, and Zhongbin Luo. 2025. "IB-PC: An Information Bottleneck Framework for Point Cloud-Based Building Information Modeling" Electronics 14, no. 22: 4399. https://doi.org/10.3390/electronics14224399
APA StyleZhang, Y., Xie, B., Xu, T., Bi, Y., & Luo, Z. (2025). IB-PC: An Information Bottleneck Framework for Point Cloud-Based Building Information Modeling. Electronics, 14(22), 4399. https://doi.org/10.3390/electronics14224399







