MultiHeadEEGModelCLS: Contextual Alignment and Spatio-Temporal Attention Model for EEG-Based SSVEP Classification

Abstract

Steady-State Visual Evoked Potentials (SSVEPs) offer a robust basis for brain–computer interface (BCI) systems due to their high signal-to-noise ratio, minimal user training requirements, and suitability for real-time decoding. In this work, we propose MultiHeadEEGModelCLS, a novel Transformer-based architecture that integrates context-aware representation learning into SSVEP decoding. The model employs a dual-stream spatio-temporal encoder to process both the input EEG trial and a contextual signal (e.g., template or reference trial), enhanced by a learnable classification ([CLS]) token. Through self-attention and cross-attention mechanisms, the model aligns trial-level representations with contextual cues. The architecture supports multi-task learning via signal reconstruction and context-informed classification heads. Evaluation on benchmark datasets (Speller and BETA) demonstrates state-of-the-art performance, particularly under limited data and short time window scenarios, achieving higher classification accuracy and information transfer rates (ITR) compared to existing deep learning methods such as the multi-branch CNN (ConvDNN). Our method achieved an ITR of 283 bits/min and 222 bits/min for the Speller and BETA datasets, and a ConvDNN of 238 bits/min and 181 bits/min. These results highlight the effectiveness of contextual modeling in enhancing the robustness and efficiency of SSVEP-based BCIs.

1. Introduction

A Brain–Computer Interface (BCI) is a system designed to translate neural activity into control commands, thereby enabling a non-muscular channel of communication. Such systems hold considerable potential in a range of applications, including assistive technologies for individuals with motor impairments [1], enhancement of communication capabilities in healthy individuals [2], interactive entertainment [2], and neuromarketing research [3]. Neural activity can be captured using various neuroimaging modalities, such as magnetic resonance imaging (MRI) and electroencephalography (EEG). Among these, EEG is particularly favored due to its low cost, portability, and relatively simple setup. EEG-based BCIs exploit distinct neural phenomena, including motor imagery and visually evoked responses. In this context, Steady-State Visual Evoked Potentials (SSVEPs) represent one of the most promising paradigm, as they offer higher Information Transfer Rates (ITRs) and demand minimal training from the user compared to alternative approaches [4,5]. SSVEPs are elicited when a user visually fixates on a periodic visual stimulus, typically flashing at a constant frequency. This stimulus induces a measurable oscillatory response in the occipital and occipito-parietal regions of the brain, commonly referred to as the SSVEP response [6]. These responses are characterized by sinusoidal components at the stimulus frequency and its harmonics. The primary objective of SSVEP-based BCI systems is to identify and discriminate between these frequency-specific components in the EEG signal and to map them onto corresponding control commands using signal processing and machine learning algorithms. Such systems have been successfully applied in various domains, including the development of assistive technologies such as brain-controlled wheelchairs [7] and robotic exoskeletons [8], as well as in communication systems, human-computer interaction [9,10], biometric identification [11], affective computing [12], and immersive entertainment platforms [13]. Despite these advances, the reliable detection and classification of SSVEP signals in realistic, noisy environments remains a significant technical challenge.

The classification of Steady-State Visual Evoked Potential (SSVEP) responses commonly involves the application of Machine Learning (ML) techniques. Traditional linear classifiers, such as Support Vector Machines (SVMs) and Linear Discriminant Analysis (LDA), have been widely employed for SSVEP detection tasks [9,14]. To enhance the discriminative power of feature representations, Multivariate Linear Regression (MLR) has been proposed as an effective approach for SSVEP classification [15]. Building on this, kernel-based variants of MLR have been introduced, incorporating SSVEP-specific kernels within a Sparse Bayesian Learning (SBL) framework to further improve performance [16]. First attemps with Deep Learning utilize Convolutional Neural Networks (CNNs) combined with time-frequency analysis to automatically learn hierarchical representations from raw EEG data for SSVEP classification [17,18,19]. Despite their effectiveness, these DL-based methods typically require long-duration SSVEP trials to adequately train the model, which can adversely affect the Information Transfer Rate (ITR), limiting their applicability in real-time BCI systems.

SSVEP responses exhibit distinct frequency- and spatial-domain characteristics, which have been leveraged in the development of specialized signal processing methods. One of the earliest techniques to exploit these properties is Canonical Correlation Analysis (CCA) [20]. CCA employs sinusoidal reference signals and formulates an optimization problem using multichannel EEG data to derive spatial filters that maximize the correlation between the EEG and the reference signals. Several extensions of CCA have been proposed to enhance its performance by incorporating subject-specific and task-relevant information obtained from calibration data, while also attenuating the influence of spontaneous background EEG activity [21,22,23,24,25,26]. Among spatial filtering approaches, Task-Related Component Analysis (TRCA) has demonstrated superior performance in SSVEP classification tasks [24]. The fundamental principle of TRCA is to construct spatial filters that maximize reproducibility of task-related SSVEP components across trials while minimizing noise. TRCA-based methods are typically followed by a target detection step, wherein the correlation between the spatially filtered test signal and a corresponding filtered template is computed to identify the visual stimulus. All spatial filtering-based approaches, including CCA and TRCA, are ultimately grounded in the solution of a generalized eigenvalue problem [27,28]. However, the various methods differ in the formulation and construction of the matrices involved in this optimization process, which directly impacts their effectiveness and generalizability [28]. Further advancements include Correlated Component Analysis (CORCA) [29], which assumes that task-relevant components are shared across subjects and applies transfer learning techniques to construct covariance matrices accordingly. Additionally, Task Discriminant Component Analysis (TDCA) has been introduced [30], utilizing within-class and between-class covariance matrices based on different SSVEP target categories to enhance discriminability. In summary, traditional SSVEP decoding methods have largely relied on template-based and correlation-driven strategies such as CCA and TRCA. These methods are designed to maximize the correlation between the EEG response and either synthetic sinusoids or empirical templates. While they perform effectively under ideal conditions—such as clean and synchronous recordings—they often struggle with robustness in noisy, asynchronous, or cross-subject contexts. Adaptive extensions of these methods have been developed to improve resilience, yet they remain constrained by their reliance on handcrafted priors and lack the scalability required for deployment in dynamic, real-world BCI environments.

To address the limitations of handcrafted features modern deep learning methods in SSVEP research utilizing transformers architectures and combines the CCNs with filter banks. For instance, Guney et al. [31] introduced a multi-branch CNN with dual-stage training, enhancing spatial and temporal feature extraction. Later models like the Filter Bank CNN (FBCNN) [32] leveraged frequency-specific subbands through parallel convolutional paths, leading to improved performance, especially in user-independent (UI) settings. Lightweight and efficient models, such as FB-EEGNet [33] and FB-tCNN [34], further extended this paradigm by combining sub-band fusion with temporal convolutions, enabling faster inference and better generalization on short time windows (TW). Furthermore [35] has proposed a new deep model with a CNN module in conjunction with a kernel-based selective mechanism, providing very promising results. While in [36] graph neural networks in combination with CNN modules have been proposed.

More recently, Transformer models have gained popularity in EEG processing due to their ability to capture global dependencies via self-attention mechanisms [37,38,39,40,41]. Furthemore, in contradiction to a typical transformer architecture, SSVEPformer [42] has replaced the attention mechanism with a CNN module. In general the attention mechanism has the goal to find long term temporal relationships inside the data. However, in SSVEP signals these relationships can be capture by transforming the data into frequency domain. For this reason in [40,42] the EEG data have been preprocessed by transforming them into the frequency domain. However, these architectures often require substantial large time windows to achieve the required frequency resolution. Furthermore, to address cross-subject variability, transfer learning strategies have been introduced. For example, Xiong et al. [40] proposed a frequency-domain adaptation framework that leverages pretraining and subject-specific fine-tuning to improve generalization with minimal calibration. However, in all these works, little attention have been given with respect to: (1) the loss function and the training objectives, and (2) possible cross-attention scenarios. In our work these aspects have been addressed by proposing a multi-head dual-stream framework.

In this work, we introduce MultiHeadEEGModelCLS, a Transformer-inspired architecture designed for SSVEP decoding. The model employs a dual-input encoder framework that independently processes both the input EEG trial and a contextual signal (e.g., a class template or an averaged reference trial). A learnable [CLS] token is introduced at the start of the context sequence and updated through self-attention mechanisms to encode a holistic representation of the context. This updated context representation, including the [CLS] token, is then used as the key and value inputs in a cross-attention mechanism where the trial representation serves as the query. Through this attention-based interaction, the model dynamically integrates contextual information into the encoding of the input trial. Final outputs are produced through two parallel heads for signal reconstruction and context-aware [CLS]-based classification. We evaluate our method on multiple SSVEP benchmark datasets and show that it consistently outperforms state-of-the-art approaches, particularly under limited-data and cross-subject scenarios.

2. SSVEP Datasets

An SSVEP dataset is a collection of multichannel EEG trials ${\{{\mathbf{X}}_1^{\left(s\right)},{\mathbf{X}}_2^{\left(s\right)},\dots ,{\mathbf{X}}_M^{\left(s\right)}\}}_{s=1}^{N_s}$, where M is the number of trials of a participant, $\left(s\right)$ is the index of the participant, and $N_s$ is the number of participants. Each ${\mathbf{X}}_m^{\left(s\right)},m=1,\dots ,M,s=1,\dots ,N_s$ is a matrix of $N_{ch}\times N_t$, where $N_{ch}$ is the number of channels and $N_t$ the number of samples. Additionally, we assume that the multi-channel EEG signals are centralized since, in practice, the EEG trials are bandpass filtered or detrended.

In this study, we utilized two benchmark SSVEP datasets: the Speller dataset and the BETA dataset. Below, we provide a brief description of each dataset. The Speller dataset [43] contains SSVEP responses from 35 subjects, with 40 distinct stimuli. The stimulation frequencies range from 8 Hz to 15.8 Hz in 0.2 Hz increments, with a phase difference of $0.5\pi$ between adjacent frequencies. EEG signals were recorded using the Synamps2 EEG system with 64 channels, following the extended 10–20 system. In this study, we selected nine channels covering the occipital and parietal-occipital regions (Pz, PO5, PO3, POz, PO4, PO6, O1, Oz, and O2). Each subject completed six blocks, with each block consisting of a 5-s visual stimulus presentation for each of the 40 targets. After extracting EEG trials, the signals were band-pass filtered between 7 and 90 Hz using an infinite impulse response (IIR) filter in a forward and reverse manner to achieve zero phase distortion.

The BETA dataset [44] follows a similar configuration as the Speller dataset but includes a larger sample size of 70 subjects. As in the Speller dataset, we used the same nine occipital and parietal-occipital channels (Pz, PO5, PO3, POz, PO4, PO6, O1, Oz, and O2). Each subject participated in four blocks, where the visual stimulus duration varied: 2 s for subjects S1–S15 and 3 s for subjects S16–S70. Further details on the experimental setup can be found in [44]. The selection of these nine EEG channels was based on well-documented neuroimaging findings indicating that SSVEP signals exhibit peak amplitude and spatial consistency in the occipital and parieto-occipital regions—areas known to be functionally specialized for visual stimulus processing and characterized by high signal-to-noise ratios.

Experimental Settings

Typically, in a SSVEP experiment a number of experimental settings must be defined and reported. More specifically, it is important to report the following settings:

• $N_p$ number of subjects;
• $N_B$ number of blocks;
• $N_f$ number of stimuli frequency;
• $N_{ch}$ number of EEG channels;
• $D_{tr}$ trial duration;

which for the two SSVEP datasets are provided in

Table 1. Experimental Settings for the two SSVEP datasets.

Parameter	Speller	BETA
$N_p$	35	70
$N_B$	6	4
$N_f$	40	40
$N_{ch}$	9	9
$D_{tr}$	5 s	2–3 s

.

3. Multi-Head EEG Model with Contextual CLS Token

Let $\mathbf{X}\in {\mathbb{R}}^{B\times C\times T}$ denote the main EEG input, and ${\mathbf{X}}_{\mathrm{ctx}}\in {\mathbb{R}}^{B\times C\times T}$ be an optional context input (e.g., a reference or template), where B is the batch size, C the number of input channels, and T the number of time points.

3.1. Spatio-Temporal Encoding

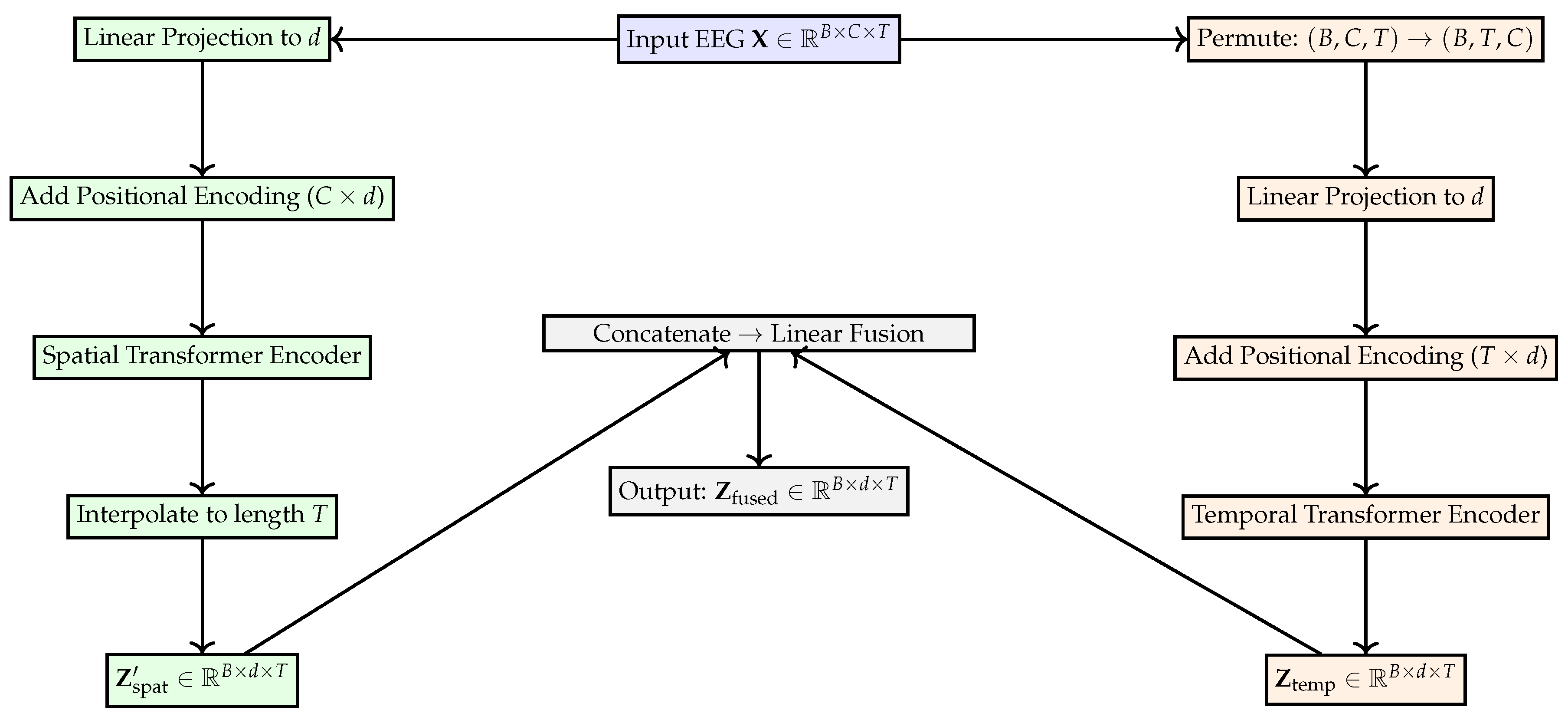
In this section, we introduce the Spatio-Temporal Encoder, a core component of the MultiHeadEEGModelCLS architecture designed to learn meaningful representations from EEG signals. Its purpose is to capture how brain activity evolves over time (temporal dynamics) and how it is distributed across different brain regions (spatial dependencies). To achieve this, the encoder follows a dual-branch design composed of a Temporal Transformer Encoder and a Spatial Transformer Encoder, which process the same EEG input from complementary perspectives before combining their outputs. The Temporal Transformer Encoder focuses on how EEG activity changes over time. Each time point of the EEG signal is treated as a separate “token,” similar to a word in a sentence. Through the self-attention mechanism of the Transformer, the model can directly compare all time points with one another, identifying both short-term and long-term patterns in neural activity. This is particularly important for SSVEP signals, where frequency-locked responses evolve continuously over a given time window. In parallel, the Spatial Transformer Encoder models how information is distributed across the EEG channels placed on the scalp. Here, each electrode is treated as a token representing a specific brain region’s activity. The self-attention mechanism allows the encoder to learn relationships between distant electrodes, effectively capturing coordinated activity across visual and parietal areas that are known to generate SSVEP responses. After processing by these two branches, the model combines their outputs through a fusion step. The spatial features are interpolated to match the temporal resolution, and the two representations are concatenated and linearly projected to create a unified spatio-temporal embedding. This fused representation preserves both “when” and “where” aspects of neural dynamics, providing a rich foundation for subsequent stages such as context alignment and classification. In summary, the Spatio-Temporal Encoder enables MultiHeadEEGModelCLS to model EEG data in a comprehensive way—capturing temporal rhythms and spatial organization simultaneously. By leveraging Transformer-based attention, it overcomes the limitations of traditional convolutional or recurrent networks, which often miss global dependencies across time and channels. This design is key to achieving more accurate and robust decoding of brain responses in SSVEP-based BCI systems. Finally, in Figure 1 we provide a diagram of the encoder and in

Table 2. Spatio-Temporal Encoder Hyperparameters.

Component	Temporal Encoder	Spatial Encoder
Input Dim	C (channels)	T (time points)
Projection Dim	d	d
Positional Embedding	Learnable, length T	Learnable, length C
Transformer Layers	$L_{\mathrm{temp}}$	$L_{\mathrm{spat}}$
Attention Heads	$h_{\mathrm{temp}}$	$h_{\mathrm{spat}}$
Feedforward Dim	$d_{\mathrm{ff}}$	$d_{\mathrm{ff}}$
Output Shape	${\mathbb{R}}^{B\times d\times T}$	${\mathbb{R}}^{B\times d\times C}$

its hyperparameters.

3.1.1. Temporal Transformer Encoder

EEG signals exhibit rich temporal dynamics that reflect neural processing over time. Capturing these temporal dependencies is essential for decoding neural intent, especially in SSVEP paradigms where frequency-locked responses unfold across extended time windows. To model such dependencies effectively, we utilize a Temporal Transformer Encoder that treats each time step as a token and applies self-attention mechanisms across the temporal axis. Unlike convolutional or recurrent approaches that operate with limited receptive fields or sequential bias, the Transformer encoder allows for direct pairwise interactions between all time points, enabling the model to capture both short- and long-range temporal patterns [45]. This design enhances the model’s ability to detect frequency-specific structure, temporal coherence, and event-locked fluctuations in the EEG time series.

The temporal stream is designed to extract temporal context and long-range dependencies across time for each EEG channel. The input tensor is first permuted to shape $(B,T,C)$ so that each time step becomes an individual token composed of C-dimensional spatial information. This sequence is projected into a d-dimensional latent space via a linear transformation:

$${\mathbf{X}}_{\mathrm{temp}}=\mathrm{Linear}\left({\mathbf{X}}^{\top }\right)\in {\mathbb{R}}^{B\times T\times d}.$$

(1)

To encode temporal order, we add learnable positional embeddings:

$${\tilde{\mathbf{X}}}_{\mathrm{temp}}={\mathbf{X}}_{\mathrm{temp}}+{\mathbf{P}}_T,{\mathbf{P}}_T\in {\mathbb{R}}^{T\times d}.$$

(2)

This enriched representation is passed through a stack of L Transformer encoder blocks operating across time. These self-attention layers enable the model to integrate temporal dependencies beyond local context:

$${\mathbf{Z}}_{\mathrm{temp}}={\mathrm{Transformer}}_{\mathrm{temporal}}\left({\tilde{\mathbf{X}}}_{\mathrm{temp}}\right)\in {\mathbb{R}}^{B\times T\times d}.$$

(3)

The output is finally transposed to shape $(B,d,T)$ to align with downstream expectations.

3.1.2. Spatial Transformer Encoder

EEG data are inherently multivariate, with channels positioned across the scalp to capture spatially distributed neural activity. Modeling spatial dependencies among these channels is crucial for decoding patterns such as inter-regional synchronization and source localization effects. The Spatial Transformer Encoder explicitly attends over the channel dimension, allowing each electrode to interact with others via attention-weighted relationships. By treating each channel as a token and applying a spatial self-attention mechanism, the model learns to aggregate information from functionally relevant regions, regardless of their physical proximity. This enables the extraction of distributed spatial representations that are better aligned with the brain’s topographic organization.

In parallel, the spatial branch models inter-channel (topographic) relationships at each time step. Each sample is treated as a sequence of C tokens—one per EEG channel—where each token reflects temporal patterns. A linear projection maps the input to a d-dimensional embedding:

$${\mathbf{X}}_{\mathrm{spat}}=\mathrm{Linear}\left(\mathbf{X}\right)\in {\mathbb{R}}^{B\times C\times d}.$$

(4)

Spatial structure is encoded using a positional embedding matrix:

$${\tilde{\mathbf{X}}}_{\mathrm{spat}}={\mathbf{X}}_{\mathrm{spat}}+{\mathbf{P}}_C,{\mathbf{P}}_C\in {\mathbb{R}}^{C\times d}.$$

(5)

The spatial sequence is processed using Transformer blocks operating across channels, allowing for attention-based fusion of information from topographically distant electrodes:

$${\mathbf{Z}}_{\mathrm{spat}}={\mathrm{Transformer}}_{\mathrm{spatial}}\left({\tilde{\mathbf{X}}}_{\mathrm{spat}}\right)\in {\mathbb{R}}^{B\times C\times d}.$$

(6)

The result is permuted to shape $(B,d,C)$ for fusion.

3.1.3. Fusion of Temporal and Spatial Streams

While temporal and spatial encoders capture complementary aspects of EEG data, their integration is essential for forming unified neural representations. The fusion step combines the temporal dynamics and spatial dependencies into a cohesive embedding that preserves both types of structure. By aligning temporal and spatial outputs along a common axis and fusing them through concatenation and linear projection, the model is able to jointly reason over when and where neural activity occurs. This multi-perspective representation serves as a robust input to downstream modules, supporting tasks such as classification, reconstruction, and context-aware attention.

To combine the temporal and spatial representations, we first ensure alignment along the time axis. If $C\ne T$, the spatial output is interpolated to match the temporal resolution:

$${\mathbf{Z}}_{\mathrm{spat}}^{\prime }=\mathrm{Interpolate}({\mathbf{Z}}_{\mathrm{spat}},\mathrm{size}=T).$$

(7)

Next, the temporal and spatial outputs are concatenated along the feature dimension (i.e., $2d$ channels), forming a unified representation that captures both temporal sequences and spatial configurations:

$${\mathbf{Z}}_{\mathrm{fused}}=\mathrm{Linear}\left([{\mathbf{Z}}_{\mathrm{temp}};{\mathbf{Z}}_{\mathrm{spat}}^{\prime }]\right)\in {\mathbb{R}}^{B\times T\times d}.$$

(8)

This fused embedding is transposed to the canonical format $(B,d,T)$ and passed to downstream components such as cross-attention, classification, and reconstruction heads. The fusion strategy allows the model to benefit from the complementary structure of both domains, ultimately leading to more robust EEG representations.

3.2. CLS Token Integration

To enable global aggregation of context-aware information, we introduce a learnable classification token, denoted by ${\mathbf{c}}_{\mathrm{init}}\in {\mathbb{R}}^{1\times 1\times d}$, where d is the model’s embedding dimension. This token is designed to serve as a dedicated representation for summarizing context-level information across time. It is expanded along the batch dimension to match the number of samples:

$$\begin{array}{cc}\hfill \mathbf{c}& ={\mathbf{c}}_{\mathrm{init}}^{\oplus B}\in {\mathbb{R}}^{B\times 1\times d},\hfill \end{array}$$

(9)

where $\oplus B$ denotes broadcasting across B samples. The CLS token is prepended to the context representation sequence ${\mathbf{S}}^{\top }\in {\mathbb{R}}^{B\times T\times d}$, yielding the augmented sequence:

$$\begin{array}{cc}\hfill {\mathbf{S}}_{\mathrm{cls}}& =[\mathbf{c};{\mathbf{S}}^{\top }]\in {\mathbb{R}}^{B\times (T+1)\times d},\hfill \end{array}$$

(10)

where the semicolon denotes concatenation along the sequence length dimension.

This augmented sequence is processed using a standard multi-head self-attention mechanism. By allowing all tokens—including the learnable CLS token—to attend to each other, the model enables the CLS token to accumulate information from all context tokens in a content-adaptive and order-sensitive manner:

$$\begin{array}{cc}\hfill {\mathbf{S}}^{\prime }& =\mathrm{MultiHeadAttention}({\mathbf{S}}_{\mathrm{cls}},{\mathbf{S}}_{\mathrm{cls}},{\mathbf{S}}_{\mathrm{cls}}).\hfill \end{array}$$

(11)

The updated CLS token, extracted as the first element of the attended sequence, captures a compressed summary of the entire context input:

$$\begin{array}{cc}\hfill {\mathbf{c}}_{\mathrm{updated}}& ={\mathbf{S}}^{\prime }[:,0,:]\in {\mathbb{R}}^{B\times d}.\hfill \end{array}$$

(12)

This updated vector serves as a context-aware latent representation, which is subsequently used as a key/value embedding in the cross-attention mechanism that aligns it with the target EEG trial. Semantically, this CLS token functions as a form of “query-independent” pooling, distilling relational structure from the context into a single embedding that guides downstream decisions such as classification or alignment.

3.3. Cross Attention: Main Input Attends to Context

To explicitly align the main input sequence with the contextual information, we apply a cross-attention mechanism that allows the target EEG trial to selectively focus on relevant parts of the encoded context. Let ${\mathbf{Z}}^{\top }\in {\mathbb{R}}^{B\times T\times d}$ denote the temporally encoded representation of the main input, and let ${\mathbf{S}}^{\prime }\in {\mathbb{R}}^{B\times (T+1)\times d}$ be the context sequence after the CLS-token self-attention refinement. The main sequence attends to this enriched context via:

$${\mathbf{Z}}^{\prime }=\mathrm{MultiHeadAttention}({\mathbf{Z}}^{\top },{\mathbf{S}}^{\prime },{\mathbf{S}}^{\prime })\in {\mathbb{R}}^{B\times T\times d},$$

(13)

where the query is the target trial and both key and value come from the updated context stream. This formulation enables dynamic interaction between the trial and its reference, allowing the model to extract contextually modulated representations that are sensitive to stimulus-specific structure or inter-trial relationships.

In cases where no external context is available—such as during ablation studies or baseline configurations—the model gracefully degrades to a self-attention mechanism by replacing the context with the input itself:

$${\mathbf{Z}}^{\prime }=\mathrm{MultiHeadAttention}({\mathbf{Z}}^{\top },{\mathbf{Z}}^{\top },{\mathbf{Z}}^{\top }).$$

(14)

This fallback ensures architectural consistency while removing explicit conditioning, allowing for direct comparisons between context-aware and self-contained modeling. Overall, this cross-attention mechanism acts as a structured information bridge between the trial and its context, enabling the model to perform relational inference in a fully differentiable and task-adaptive fashion. Finally, the output of cross attention module is processed according to the following equation:

$$\tilde{\mathbf{Z}}=\mathrm{Dropout}{\left(\mathrm{ReLU}\left({\mathbf{Z}}^{\prime }\right)\right)}^{\top }\in {\mathbb{R}}^{B\times d\times T}$$

(15)

before use it to the Output Heads.

3.4. Output Heads

In this section, we present the Multi-Head learning module, illustrated as the final stage in Figure 2. This module receives the context-enhanced trial embedding generated after the cross-attention fusion between the trial and the CLS-integrated context representations. Its purpose is to transform these enriched EEG features into interpretable outputs for model prediction and regularization. The module contains two complementary heads: a classification head and a reconstruction head. The classification head processes the cross-attended trial features through a fully connected layer to produce the final class probabilities corresponding to the visual stimulus frequencies. In parallel, the reconstruction head attempts to rebuild the original EEG representation from the same latent features, encouraging the encoder to preserve physiologically meaningful information. This dual-head configuration ensures that the network learns embeddings that are both task-discriminative and signal-preserving, improving robustness and generalization across SSVEP trials.

3.4.1. Reconstruction Head

The reconstruction head in MultiHeadEEGModelCLS is implemented as a lightweight convolutional decoder that transforms the latent feature representation back to the raw EEG space. Given the encoded representation $\mathbf{Z}\in {\mathbb{R}}^{B\times d\times T}$—after cross-attention and nonlinear activation—the reconstruction module aims to produce an output $\hat{\mathbf{X}}\in {\mathbb{R}}^{B\times C\times T}$, where C is the number of EEG channels and T the number of time samples.

The module consists of two temporal 1D convolutional layers:

• The first layer applies 64 filters of size 3 with padding, followed by Batch Normalization and ReLU activation.
• The second layer maps the intermediate features to the final output dimensionality C using another convolutional layer with the same kernel size.

Formally, the transformation is defined as:

$$\hat{\mathbf{X}}=f_{\mathrm{rec}}\left(\mathbf{Z}\right)={\mathrm{Conv}1\mathrm{D}}_{64\to C}\circ \mathrm{ReLU}\circ \mathrm{BN}\circ {\mathrm{Conv}1\mathrm{D}}_{d\to 64}\left(\mathbf{Z}\right),$$

(16)

where $f_{\mathrm{rec}}$ denotes the reconstruction module. Furthermore, the kernel size, the padding, and the stride were set to 3, 1 and 1, respectively. During training, the reconstructed signal is supervised using the ${\mathcal{l}}_2$ loss:

$${\mathcal{L}}_{\mathrm{rec}}={\displaystyle \frac{1}{B}}\sum _{i=1}^B{∥{\mathbf{X}}_i-{\hat{\mathbf{X}}}_i∥}_2.$$

(17)

This head enforces the preservation of fine-grained spatial-temporal structure in the learned representation and acts as an auxiliary self-supervised objective during pretraining and multitask learning.

3.4.2. CLS-Based Classification Head

The CLS-based classification head is responsible for mapping the learned [CLS] token to a target class probability distribution. Following the attention-based fusion stage, a learnable [CLS] token ${\mathbf{c}}_{\mathrm{updated}}\in {\mathbb{R}}^{B\times d}$—which has attended to the context representation—is extracted from the output of the self-attention module applied on the contextual signal. This token is passed through a fully connected layer (linear classifier) that projects the d-dimensional embedding to the number of output classes K:

$${\hat{\mathbf{y}}}_{\mathrm{cls}}=f_{\mathrm{cls}}\left({\mathbf{c}}_{\mathrm{updated}}\right)=\mathrm{Softmax}(\mathbf{W}{\mathbf{c}}_{\mathrm{updated}}^{\top }+\mathbf{b}),$$

(18)

where $\mathbf{W}\in {\mathbb{R}}^{K\times d}$ and $\mathbf{b}\in {\mathbb{R}}^K$ are learnable parameters.

The classification is supervised using a standard cross-entropy loss:

$${\mathcal{L}}_{\mathrm{cls}}=-{\displaystyle \frac{1}{B}}\sum _{i=1}^B\sum _{k=1}^K{y}_{i,k}log\left({\hat{y}}_{i,k}^{\left(\mathrm{cls}\right)}\right),$$

(19)

where $y_{i,k}$ is the one-hot encoded ground truth label for sample i. This head encourages the [CLS] token to act as a global summary of the contextual representation and enables class discrimination from context-conditioned features.

3.5. Final Output

The MultiHeadEEGModelCLS architecture produces two distinct outputs, each corresponding to a different learning objective:

• Reconstructed EEG signal $\hat{\mathbf{X}}\in {\mathbb{R}}^{B\times C\times T}$: Generated by the reconstruction head, this output aims to approximate the original input EEG $\mathbf{X}$ by minimizing a signal-level reconstruction loss. It supports self-supervised learning and regularizes the encoder to retain fine-grained spatial-temporal structure.
• CLS-based classification ${\hat{\mathbf{y}}}_{\mathrm{cls}}\in {\mathbb{R}}^{B\times K}$: This output is computed from the context-updated [CLS] token and reflects predictions conditioned on contextual alignment. It enables the model to perform trial classification based on inter-trial structure or template similarity.

During training, the total loss combines all two objectives:

$${\mathcal{L}}_{\mathrm{total}}={\lambda }_{\mathrm{rec}}{\mathcal{L}}_{\mathrm{rec}}+{\lambda }_{\mathrm{cls}}{\mathcal{L}}_{\mathrm{cls}},$$

(20)

where each $\lambda$ controls the relative importance of the corresponding task. This multi-objective formulation allows the model to simultaneously learn robust signal reconstructions, discriminative features, and context-aligned representations. Hence, finally, the model returns the reconstructed signals and the predicted labels:

$$(\hat{\mathbf{X}},{\hat{\mathbf{y}}}_{\mathrm{cls}})$$

(21)

3.5.1. Special Case: When Input Equals Context

In the case where the main EEG input $\mathbf{X}\in {\mathbb{R}}^{B\times C\times T}$ is identical to the context input ${\mathbf{X}}_{\mathrm{ctx}}\in {\mathbb{R}}^{B\times H\times T}$, the model operates in a degenerate but meaningful configuration. Since both inputs are passed through the same spatio-temporal encoder, their representations become indistinguishable, i.e., $\mathbf{Z}=f_{\mathrm{enc}}\left(\mathbf{X}\right)=f_{\mathrm{enc}}\left({\mathbf{X}}_{\mathrm{ctx}}\right).$ As a result, the cross-attention mechanism effectively reduces to self-attention, with the [CLS] token attending to the same sequence it is derived from. In this scenario, the [CLS] token serves as a learnable global summary of the input rather than an alignment vector relative to an external context.

This configuration is functionally equivalent to the encoding stage of a Vision Transformer (ViT) or BERT-like architecture, where a special token is appended to a single sequence and trained to capture its semantic content. When used during pretraining, this setup allows the model to jointly optimize for reconstruction and global classification objectives without requiring a distinct reference template. It provides a stable training regime and encourages the model to incorporate salient features within each trial, facilitating subsequent transfer to context-aware tasks.

3.5.2. Context-Aware Representation Learning in EEG

Conventional deep learning approaches for EEG decoding often treat each trial as an independent sample, learning a direct mapping from raw signals to class labels. However, this trial-centric perspective neglects potential relational or structural information across trials. In real-world scenarios—especially in SSVEP-based paradigms—EEG signals are highly variable, noisy, and subject-dependent. As a result, the information content of a single trial may be insufficient for robust classification, particularly under low-data or cross-subject conditions.

Context-aware representation learning aims to mitigate this limitation by incorporating auxiliary signals that provide semantic or statistical reference. Rather than learning in isolation, the model is encouraged to interpret each trial in relation to additional context, such as template responses, averaged class trials, or support sets. This strategy enables the model to align, contrast, or calibrate trial-level features against a stable reference, improving both accuracy and generalization.

In the proposed MultiHeadEEGModelCLS, this paradigm is explicitly realized by introducing a dual-stream input: the primary trial and a contextual signal. A learnable [CLS] token is appended to the context and updated through self-attention, producing a condensed representation that guides the encoding of the primary trial via cross-attention. This mechanism enforces trial-to-context alignment and allows the model to make classification decisions that are sensitive to inter-trial structure. As such, the model embodies the principles of context-aware learning in a fully differentiable, end-to-end architecture.

3.5.3. Summary of Forward Pass in MultiHeadEEGModelCLS

Let $\mathbf{X}\in {\mathbb{R}}^{B\times C\times T}$ denote the input EEG trial and ${\mathbf{X}}_{\mathrm{ctx}}\in {\mathbb{R}}^{B\times C\times T}$ the corresponding contextual EEG signal (e.g., a template or class average). The model’s forward pass proceeds as follows:

• Dual Encoding: Both $\mathbf{X}$ and ${\mathbf{X}}_{\mathrm{ctx}}$ are independently passed through a shared spatio-temporal encoder, yielding $\mathbf{Z},\mathbf{S}\in {\mathbb{R}}^{B\times T\times d}$ after LayerNorm and temporal permutation.
• Contextual CLS Token: A learnable [CLS] token ${\mathbf{c}}_{\mathrm{init}}\in {\mathbb{R}}^{1\times 1\times d}$ is broadcast across the batch and prepended to the contextual representation:

  $${\mathbf{S}}^{\prime }=\left[{\mathbf{c}}_{\mathrm{init}};\mathbf{S}\right]\in {\mathbb{R}}^{B\times (T+1)\times d}$$
• Self-Attention on Context: The context sequence with the [CLS] token undergoes self-attention:

  $${\mathbf{S}}^{″}=\mathrm{SelfAttn}({\mathbf{S}}^{\prime },{\mathbf{S}}^{\prime },{\mathbf{S}}^{\prime })$$

  The updated [CLS] token ${\mathbf{c}}_{\mathrm{updated}}={\mathbf{S}}^{″}[:,0,:]$ acts as a global summary of the context.
• Cross-Attention: The encoded trial $\mathbf{Z}$ attends to the full contextual representation ${\mathbf{S}}^{″}$ (including the [CLS] token):

  $${\mathbf{Z}}^{\prime }=\mathrm{CrossAttn}(\mathbf{Z},{\mathbf{S}}^{″},{\mathbf{S}}^{″})$$
• Post-Attention Processing: The cross-attended representation is passed through ReLU activation and dropout, then transposed to shape ${\mathbb{R}}^{B\times d\times T}$.
• Output Heads:
  • Reconstruction: $\hat{\mathbf{X}}=f_{\mathrm{rec}}\left({\mathbf{Z}}^{\prime }\right)$ reconstructs the raw EEG signal.
  • CLS Classification: ${\hat{\mathbf{y}}}_{\mathrm{cls}}=f_{\mathrm{cls}}\left({\mathbf{c}}_{\mathrm{updated}}\right)$ uses the context-aware [CLS] token for class prediction.
  • The model returns the tuple $(\hat{\mathbf{X}},{\hat{\mathbf{y}}}_{\mathrm{cls}})$
  Finally, a compact diagram describing the proposed model is provided in Figure 2.

3.6. Model’s Training Procedure

The training of the MultiHeadEEGModelCLS model follows a two-stage strategy designed to balance cross-subject generalization with subject-specific adaptation (See Algorithm 1). In the first stage, the model undergoes global pretraining using data pooled from all available subjects, excluding the trials belonging to a specific evaluation block. This allows the model to learn representations that are not biased toward a single subject or temporal segment. The EEG signals are reshaped and standardized, and both the input and context branches of the model are fed with the same EEG trials. This configuration corresponds to a special case where the model is effectively trained in a self-supervised manner, without relying on external context templates. The training objective is a composite loss that combines a cross-entropy term for classification with a reconstruction loss (mean squared error) between the input and its reconstruction. The model is optimized using the Adam algorithm with L2 regularization, and training continues for up to 100 epochs with early stopping based on performance stability.

In the second stage, the pretrained model is fine-tuned separately for each subject to improve adaptation to individual EEG characteristics. A leave-one-block-out strategy is employed, where each block of trials serves as the test set once, and the remaining blocks are used for training. The data are again reshaped and normalized before being passed into the model, with the same EEG segment used for both input and context. This setup ensures consistency with the first stage while allowing the model to specialize on subject-specific dynamics. Fine-tuning is performed using the same composite loss function, and training lasts for 10 epochs per subject. After training, the model predicts class labels using only the output associated with the CLS token, reflecting its context-informed classification decision. Classification accuracy is computed for each subject and test block, and results are logged for downstream comparison. This two-phase process enables the model to capture both population-level structure and individual-specific variability, enhancing its performance in real-world SSVEP decoding scenarios.

Algorithm 1: Two-Stage Training Procedure for MultiHeadEEGModelCLS

4. Experimental Results

The SSVEP signals were processed with a filter-bank approach: each trial was band-pass filtered in three sub-bands—[8, 90] Hz, [16, 90] Hz, and [24, 90] Hz (to capture the fundamental and harmonics). Note that each band was intentionally designed to include specific portions of the harmonic components [31,46]. The three filtered copies of the original nine occipital/parieto-occipital channels were then concatenated along the channel dimension, yielding an effective input of 27 channels (9 × 3). During global pretraining we use mini-batches of 16 trials to stabilize gradient estimates across subjects, while subject-specific fine-tuning uses 8 trials per batch. Optimization is performed with Adam (learning rate $1\times {10}^{-4}$, weight decay $1\times {10}^{-3}$), and the network is trained with a multi-task objective combining classification and reconstruction where ${\lambda }_{\mathrm{cls}}=1$ and ${\lambda }_{\mathrm{rec}}=0.01$. Furthermore, in

Table 3. Values of key Hyperparameters.

Component	Temporal Encoder	Spatial Encoder
Input Dim	$C=27$ (channels)	$T=50$ (time points)
Projection Dim	$d=128$	$d=128$
Positional Embedding	Learnable, length $T=50$	Learnable, length $C=27$
Transformer Layers	$L_{\mathrm{temp}}=4$	$L_{\mathrm{spat}}=4$
Attention Heads	$h_{\mathrm{temp}}=4$	$h_{\mathrm{spat}}=4$
Feedforward Dim	$d_{\mathrm{ff}}=256$	$d_{\mathrm{ff}}=256$
Output Shape	${\mathbb{R}}^{B\times 128\times 50}$	${\mathbb{R}}^{B\times 128\times 27}$

we provide the values of key hyperparameters. This setting was selected based on empirical tuning, aiming to balance convergence stability and generalization performance. Note that hyperparameter T depends on the size of TW, hence, in Table 3 we use TW = 0.2 s. The code is available for reproducibility at https://github.com/vangelis2015/MultiHeadEEG (accessed on 29 September 2025).

For evaluating the performance of the examined algorithms we have used the following metrics:

• Classification Accuracy: Constitutes the most straightforward performance evaluation metric and is defined as the ratio between the number of correctly classified trials to the total number of trials.
• Information Transfer Rate (ITR): While classification accuracy indicates how often a BCI system correctly predicts user intent, it does not account for the number of available options or the time required for classification—both critical factors in system efficiency. To address this, the Information Transfer Rate (ITR) metric is used, quantifying how much information the BCI system transmits over time (in bits per minute), enabling fair comparisons across different SSVEP BCI configurations. More specifically, ITR is used to quantify the rate of information transmitted by the BCI system and is measured (in bits/min) by the following equation [16,42]:

  $$ITR=\left({log}_{2}K+P·{log}_{2}P+(1-P){log}_2\left[{\displaystyle \frac{1-P}{K-1}}\right]\right)·\left({\displaystyle \frac{60}{T}}\right)$$

  (22)

  with K being the number of classes, P the classification accuracy, and T the time (in seconds) required for the classification process to complete.

Finally, with respect to each metric, we utilized the paired t-test to assess the statistical significance of the improvements between the proposed method and ConvDNN.

As a baseline method for comparison purposes we use the convolutional architecture (ConvDNN) proposed in [31], which introduced a lightweight deep neural network for classifying steady-state visual evoked potentials (SSVEP) directly from raw EEG signals. This model employs a sequence of temporal and spatial convolutional layers designed to extract frequency and channel-specific patterns in an end-to-end fashion. The temporal filters are responsible for capturing SSVEP frequency components, while the spatial filters model inter-channel dependencies analogous to common spatial patterns (CSP). The network is finalized with fully connected layers and a softmax classifier, yielding a compact architecture that is particularly well-suited for real-time BCI applications, where achieving a high ITR is essential for efficient and responsive system performance. Despite its simplicity, the model demonstrated competitive performance and improved information transfer rate (ITR), especially when compared with traditional correlation-based methods such as Canonical Correlation Analysis (CCA) and Task-Related Component Analysis (TRCA). However, the architecture processes each EEG trial independently, without explicitly incorporating contextual or cross-trial information. Additionally, the learning objective is focused solely on single-head classification via cross-entropy loss, limiting its flexibility in modeling auxiliary representations.

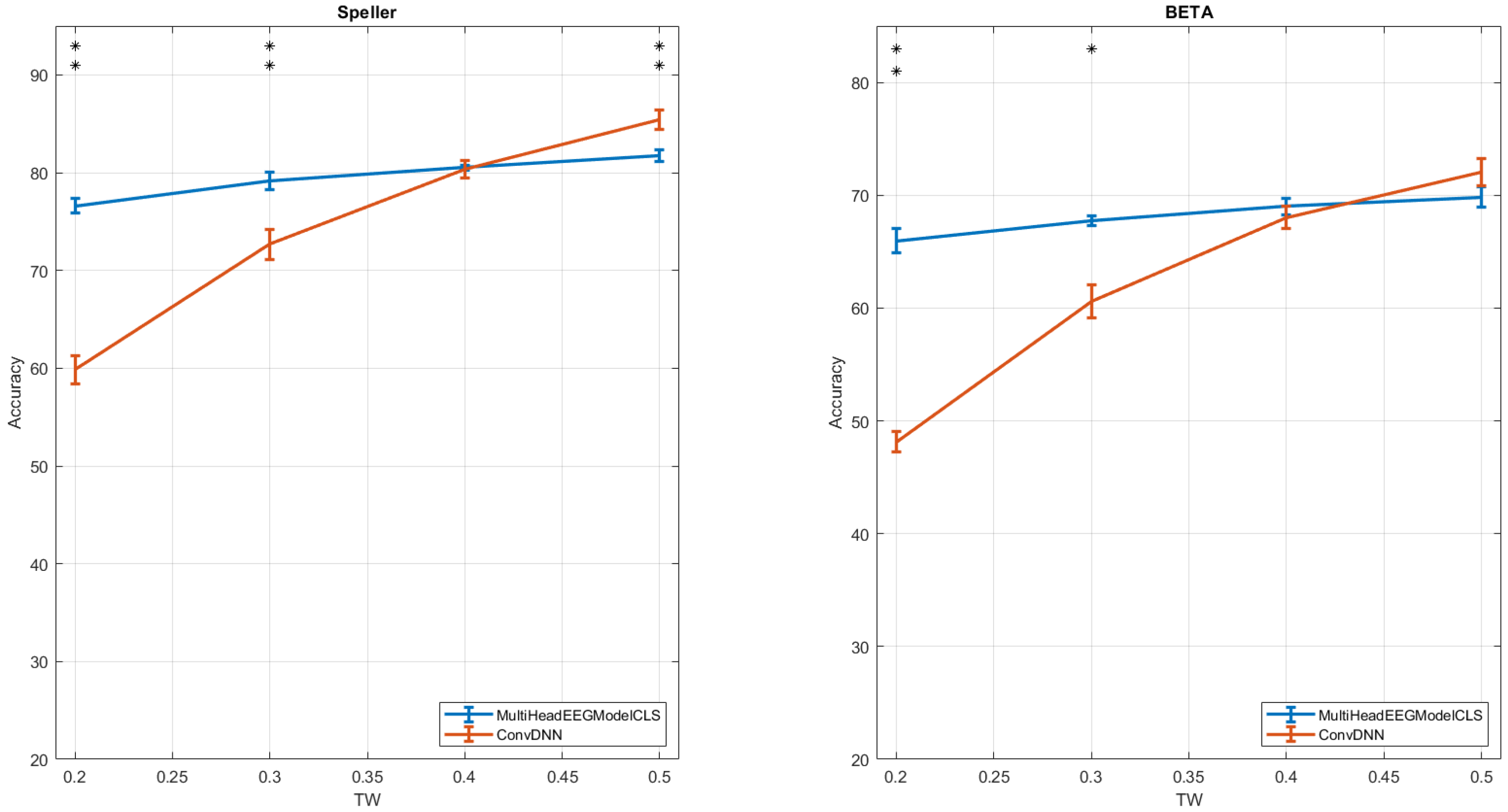
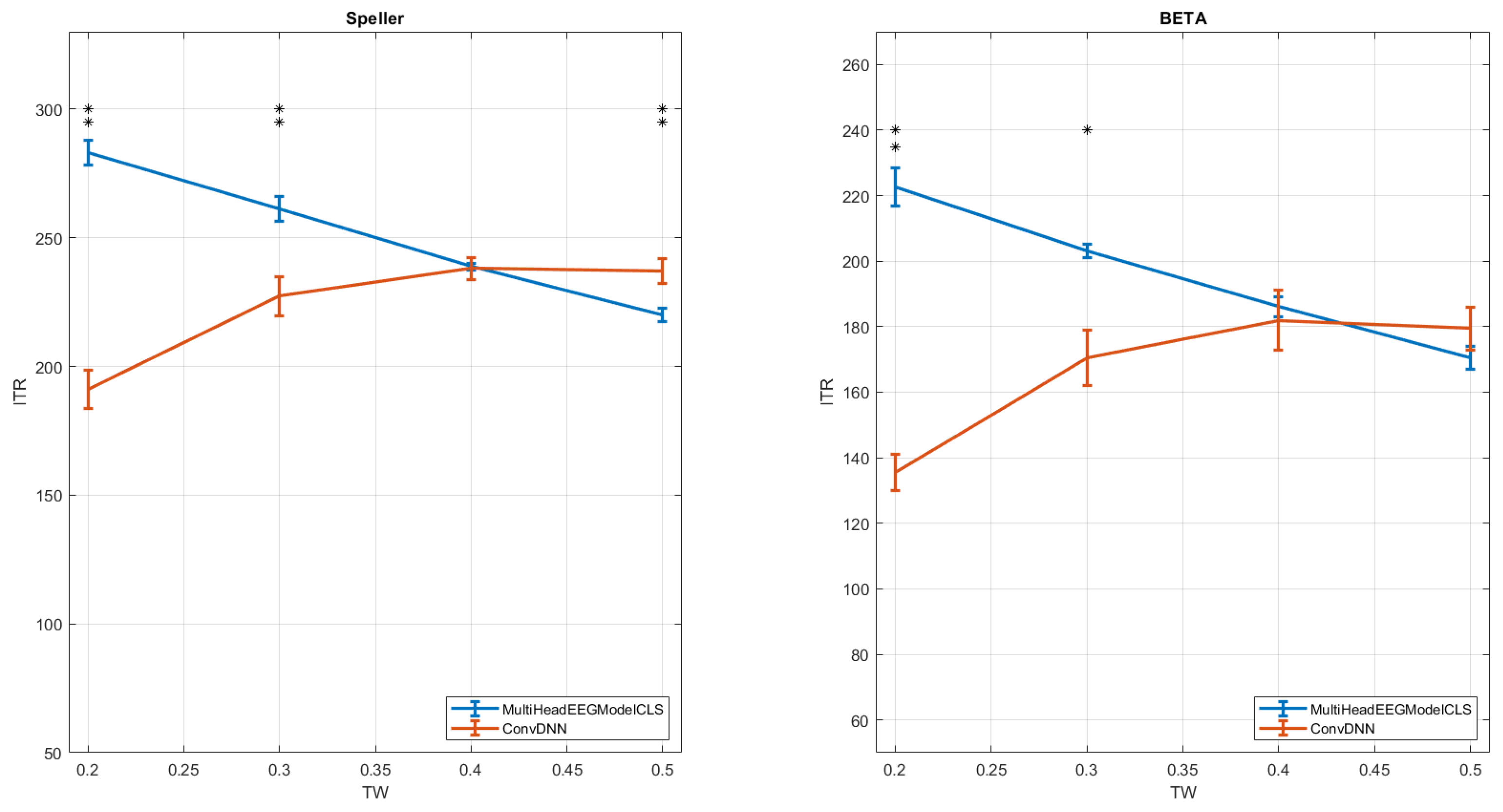
In our experiments, we adopt a standard approach commonly used in the analysis of SSVEP datasets, wherein the performance of each method is evaluated across varying time windows. Specifically, we assess the classification accuracy for time durations ranging from 0.2 s to 0.5 s, with increments of 0.1 s. The corresponding results for all competing methods across the two datasets are presented in Figure 3. As illustrated, the MultiHeadEEGModelCLS method consistently demonstrates superior performance compared to the ConvDNN when we have small TWs. For example when TW = 0.2 s our method has achieved accuracy of 76% and 65% for the Speller and the BETA datasets respectively, while the ConvDNN below 60% for both datasets. Furthermore, a similar trend is observed when considering the Information Transfer Rate (ITR), as shown in Figure 4. Notably, the MultiHeadEEGModelCLS method achieves the highest ITR in the majority of time windows, thereby highlighting its effectiveness under varying temporal constraints. Our method achieved its highest ITR (when TW = 0.2 s) of 283 bits/min and 222 bits/min for the Speller and BETA datasets, while, the ConvDNN achieved its highest ITR (in TW = 0.4 s) of 238 bits/min and 181 bits/min. Finally, the statistical analysis using paired t-test reveals that the observed differences between the two methods are significant in many cases of TWs. More specifically, when the Speller dataset is used, the two methods presents significant differences for TWs of 0.2 s, 0.3 s and 0.5 s, while, in the case of BETA dataset for TWs of 0.2 s and 0.3 s. Note here, the above observations are valid for both metrics, Classification Accuracy and ITR (see Figure 3 and Figure 4).

It is worth emphasizing that the classification accuracy reported for the MultiHeadEEGModelCLS model represents, to the best of our knowledge, the highest performance documented for the specific time windows and SSVEP datasets under consideration, when compared to a broad range of existing methods in the literature. A comparative analysis is presented in

Table 4. Comparative Analysis of the MultiHeadEEGModelCLS with three deep learning algorithm (the ConvDNN, the ConvCA, and the FBCNN-TKS) and one spatial filtering algorithm (the eTRCA). Note that the comparison is performed on both SSVEP datasets with respect to the Accuracy, where we adopt TW of 0.2 s.

Method	Accuracy
Speller dataset
MultiHeadEEGModelCLS	66%
ConvDNN [31]	57%
ConvCA [47]	52%
eTRCA [31]	45%
FBCNN-TKS [35]	60%
BETA dataset
MultiHeadEEGModelCLS	62%
ConvDNN [31]	46%
ConvCA [47]	39%
eTRCA [31]	35%
FBCNN-TKS [35]	55%

. In this table we provide the results of the proposed method and four other well-documented methods from the literature. More specifically, the ConvDNN [31], the ConvCA [47], the extended TRCA (eTRCA) [24,31] and the recently introduced FBCNN-TKS [35]. All these methods represents a wide spectrum of methodological aspects such as spatial filters and deep learning models. From the results shown in this table, it is evident that the proposed method achieves the highest accuracy particularly in scenarios involving short time windows (i.e., less than 0.5 s). This observation carries significant implications for the design and practical deployment of SSVEP-based BCI systems. In general, achieving high accuracy in shorter time windows directly contributes to higher Information Transfer Rate (ITR), which is a critical performance metric in real-world BCI applications. As a result, the provided method presents the highest ITR values for the analyzed SSVEP datasets, reinforcing the effectiveness of the proposed model in delivering fast and reliable communication rates in brain–computer interface systems.

5. Discussion

In this study, we employ the MultiHeadEEGModelCLS model in a self-conditioned setting, where the input EEG trial and the context signal are identical. Although originally designed as a context-aware architecture for SSVEP decoding—capable of jointly encoding a target trial and a distinct reference via dual spatio-temporal Transformer encoders—the model also admits a degenerate but analytically useful configuration in which the same trial is passed to both branches. Under this setup, the learnable [CLS] token aggregates information through self-attention over the input, and the resulting context representation is used in a cross-attention mechanism to refine the encoding of the same trial. This effectively reduces the model to a self-alignment scheme while preserving its full architectural structure. Such a design enables a clear attribution of performance gains to the attention mechanisms themselves, independently of external context or class templates. Moreover, the model retains its multi-head supervision strategy, combining CLS-based classification and input reconstruction, which jointly encourage the learning of both high-level discriminative patterns and low-level structural fidelity. This self-conditioned formulation serves both as a strong standalone method and as a principled baseline for assessing the role of contextual information in end-to-end neural SSVEP decoding.

A key strength of the proposed MultiHeadEEGModelCLS architecture lies in its multi-task learning framework, which simultaneously optimizes for both classification and signal reconstruction. By incorporating a reconstruction head alongside the classification objective, the model is encouraged to retain fine-grained spatial and temporal details of the EEG signal, effectively acting as a form of self-supervised regularization. This dual objective not only enhances feature robustness but also improves generalization under noisy or data-limited conditions. Hence, the model demonstrates superior performance on short-duration EEG trials—achieving high classification accuracy with windows as brief as 0.2 s. This capability is particularly important for real-time BCI applications, where reducing trial duration directly contributes to increased ITR and faster system responsiveness, even in the presence of environmental noise or user variability.

In

Table 5. Summary of Loss Functions Used in Deep Learning Models for SSVEP Classification.

	Loss Function	Mathematical Form (If Stated)	Regularization
Convolutional Correlation Analysis for SSVEP [47]	Cross-Entropy Loss	$\mathcal{L}=-{\sum }_i{y}_{i}log\left({\hat{y}}_i\right)$	-
Filter Bank CNN for SSVEP Classification [32]	Cross-Entropy (implied)	Not explicitly stated	-
Transformer-Based DNN for SSVEP [42]	Cross-Entropy + L2	${\mathcal{L}}_{\mathrm{total}}={\mathcal{L}}_{\mathrm{CE}}+\lambda {\parallel \theta \parallel }_2^2$	L2 with $\lambda =0.001$
FB-CNN for Short-Time Window SSVEP [34]	Cross-Entropy (implied)	Not explicitly stated	-
FB-EEGNet: Fusion Across Bands [33]	Cross-Entropy (standard)	Not explicitly stated	-
Deep Transfer Learning for Frequency Domain SSVEP [40]	SVM Loss (post-CNN)	Not applicable (non-differentiable model)	Uses SVM hinge loss
A DNN for SSVEP BCI [31]	Cross-Entropy (implied)	Not explicitly stated	-

we provide a comparative overview of how various deep learning architectures formulate their training objectives when decoding Steady-State Visual Evoked Potentials (SSVEPs). Most of the surveyed models adopt cross-entropy loss as the primary objective, reflecting the classification nature of the SSVEP decoding task. However, the explicit mathematical formulation of this loss is often omitted in the original literature, indicating a reliance on standard implementations rather than task-specific modifications. Only a few models, such as the convolutional correlation analysis approach, explicitly report the canonical form of cross-entropy, which penalizes the negative log-likelihood of the true class probability. This highlights a general trend in the field: while classification accuracy is prioritized, little attention is paid to loss function design or to transparency in reporting training objectives.

In addition, the table reveals that regularization techniques are sparsely applied or underreported across most methods. Among the exceptions, Transformer-based architectures introduce an L2 penalty on the model weights, reflecting their higher parameterization and need for regularization to prevent overfitting. Interestingly, one approach departs from neural objectives altogether by using an SVM-based loss in a post-hoc fashion after deep feature extraction. This creates a discontinuity between feature learning and classification, contrasting with the fully differentiable end-to-end training adopted by most neural methods. Overall, the matrix illustrates that current practices in loss design for SSVEP decoding remain largely conventional and uniform, suggesting an opportunity for innovation through multi-objective formulations, context-aware loss terms, or contrastive learning frameworks—such as those introduced in the proposed MultiHeadEEGModelCLS.

Also, the proposed MultiHeadEEGModelCLS architecture aligns closely with the principles underpinning foundation models in machine learning [48], particularly through its use of general-purpose Transformer encoders, multi-head supervision, and flexible input conditioning. Similar to foundation models that are pretrained on large, diverse datasets to learn transferable representations, our model employs a two-stage training strategy—global pretraining followed by subject-specific fine-tuning—to capture both shared and individual EEG dynamics. The incorporation of a learnable [CLS] token for context-aware summarization and the use of cross-attention for relational reasoning mirror the mechanisms used in foundational architectures like BERT and Vision Transformers. Furthermore, the model’s ability to perform multiple tasks (e.g., classification and reconstruction) within a unified framework reflects the multi-objective learning paradigm typical of foundation models, suggesting its potential as a generalizable backbone for future EEG-based BCI applications beyond SSVEP decoding.

In the future we intent to extend the proposed framework in several directions to further enhance its representational capacity and neurophysiological relevance. First, we plan to incorporate a dedicated head for contrastive learning between trial and context, allowing the model to explicitly capture similarity structures across EEG trials [49]. In addition, we will explore advanced contextual learning strategies, in which sinusoidal, averaged, or weighted templates serve as contextual references to improve cross-subject generalization and robustness. Spatial adaptability will also be examined by evaluating the model using larger number of EEG channels, combined with channel-selection or attention mechanisms to dynamically focus on the most informative cortical regions [28,50]. Another important direction involves enhancing the model’s robustness and interpretability. We will investigate weighted loss functions to better handle imbalanced datasets or clinical cases, ensuring fairer training across heterogeneous data distributions. To strengthen the understanding of the learned representations, we will conduct comprehensive model-interpretability and neurophysiological relevance analyses, including attention visualization, channel-importance estimation, and temporal activation mapping [51]. Finally, we aim to extend the framework to multimodal classification tasks, such as EEG–fNIRS integration [52] and EEG-based diagnosis of Autism Spectrum Disorder (ASD) through multi-domain EEG analysis [53], thereby broadening the applicability of our approach to both cognitive and clinical neuroscience.

6. Conclusions

In this study, we introduced MultiHeadEEGModelCLS, a novel context-aware architecture for SSVEP decoding that leverages the strengths of Transformer-based representation learning and cross-attention mechanisms. By jointly encoding the target EEG trial and a contextual signal—such as a class template—the model effectively integrates spatio-temporal dependencies and inter-trial structure through a unified end-to-end framework. The incorporation of a learnable [CLS] token allows the model to summarize and align contextual information, thereby improving discriminability and robustness, especially in challenging scenarios such as cross-subject conditions.

Our experimental evaluation on benchmark SSVEP datasets demonstrates that the proposed model outperforms state-of-the-art methods in both classification accuracy and ITR, particularly when short time windows are used. This improvement is critical for the development of fast and efficient BCI systems suitable for real-world applications. Furthermore, the two-stage training strategy—comprising global pretraining and subject-specific fine-tuning—enables the model to generalize across participants while retaining the ability to adapt to individual differences. Overall, the proposed framework highlights the potential of context-aware learning in EEG-based neural decoding and paves the way for future research on integrating relational reasoning, contrastive objectives, and few-shot learning into BCI systems.