An Online Remaining Useful Life Prediction Method for Tantalum Capacitors Based on Temperature Measurements

Abstract

Accurate remaining useful life (RUL) prediction of tantalum capacitors is essential for enhancing the reliability and maintainability of power electronic systems. However, online RUL prediction remains a challenging task due to the difficulty of accessing internal degradation states and the non-stationarity of operating conditions. This paper presents a novel CNN-LSTM-Attention-based deep learning framework for accurate online RUL prediction of tantalum capacitors, leveraging infrared surface temperature measurements and ambient thermal compensation. The proposed framework initiates with the collection of degradation temperature data under controlled accelerated aging experiments, where true degradation indicators are extracted by eliminating ambient temperature interference through dual-sensor compensation. The resulting preprocessed data are used to train a hybrid deep neural network model that integrates convolutional layers for local feature extraction, long short-term memory (LSTM) units for sequential dependency modeling, and a soft attention mechanism to selectively focus on the critical degradation patterns. A channel attention module is further embedded to adaptively optimize the importance of different feature channels. Experimental validation using three groups of aging data demonstrates the effectiveness and superiority of the proposed method over conventional LSTM and CNN-LSTM baselines. The CNN-LSTM-Attention model achieves a substantial improvement in prediction accuracy, with mean absolute percentage error (MAPE) reductions of up to 60.97%, root mean squared error (RMSE) reductions of up to 65.63%, and coefficient of determination (R²) increases of up to 68.67%. The results confirm the ability to deliver precise and robust online RUL predictions for tantalum capacitors under complex operational conditions.

1. Introduction

With the continuous advancement of power electronics and miniaturized embedded systems, the health prognostics and management (PHM) of passive components, especially tantalum capacitors, have become increasingly critical [1,2,3,4,5,6]. Tantalum capacitors are widely used in high-reliability applications such as the oil and gas industry, aerospace, communication base stations, and industrial control due to their high-capacitance density and stable performance [7,8,9,10,11,12]. However, their degradation behavior under thermal and electrical stress directly threatens system reliability [13,14,15,16,17,18]. To address this, condition monitoring (CM) and remaining useful life (RUL) prediction techniques have been increasingly adopted. Among various RUL prediction paradigms, data-driven approaches based on sensor measurements have shown strong potential thanks to their ability to model complex degradation patterns without relying on precise physical failure models [19,20,21,22]. In this context, deep learning methods, especially those capable of capturing temporal and nonlinear characteristics of degradation signals, offer powerful tools for modeling the aging process of tantalum capacitors [23,24,25,26].

Unlike mechanical systems that often exhibit evident vibration-based degradation patterns, the internal deterioration process of tantalum capacitors is typically latent and difficult to observe directly during their operational lifespan. Among the various indicators, temperature, particularly the internal core temperature, has proven to be one of the most sensitive signals for tracking capacitor degradation [27], as it reflects the combined effects of increased leakage current, elevated equivalent series resistance (ESR), and thermal stress accumulation. However, due to structural limitations, direct access to the core temperature is impractical in real-world applications. In contrast, the surface temperature of the capacitor casing can be conveniently monitored using noncontact infrared temperature sensors. These surface measurements, when corrected for environmental effects, serve as reliable proxies for internal degradation trends. Notably, such temperature data inherently possess rich temporal dynamics and exhibit strong correlations with the degradation states of the component. This requires the adoption of advanced modeling approaches that can effectively capture both sequential dependencies and complex feature interactions within the temperature measurement data, providing a solid foundation for accurate and online remaining useful life (RUL) prediction.

In recent years, deep learning has emerged as a promising method for the RUL prediction of capacitors. Delanyo D.K.B. et al. [28] successfully used bidirectional long short-term memory (BiLSTM) to predict the RUL of aluminum electrolytic capacitors. The network can better capture the degradation trend of AEC and improve the prediction accuracy compared with traditional LSTM. Z. Wang et al. [29] used the ARI-MA-Bi-LSTM hybrid model, which combined ARIMA’s ability to extract nonlinear features from linear Bi-LSTM, to achieve AEC prediction from an early stage. F. Wang et al. [30] proposed an ensemble learning method combining Chained-SVR and 1D-CNN for the prognostics of the RUL of aluminum electrolytic capacitors (AECs). The experimental results show that the proposed method not only improves the robustness of the individual models but also achieves the best performance among all the compared methods. Q. Sun et al. [9] proposed a residual lifetime prediction method for electrolytic capacitors based on GRU and PSO-SVR. They achieved better prediction accuracy compared to traditional methods on both NASA and experimental datasets. G. Lou et al. [31] proposed a two-stage online RUL prediction framework based on the bidirectional long short-term memory (BiLSTM) network and the H∞ observer. The results indicate that the BiLSTM network can explain more than 99% of the variation of capacitance, achieving competitive prediction accuracy when compared with offline methods. Z. Yi et al. [32] introduced a novel method for SOH estimation and RUL prediction, based on a hybrid neural network optimized by an improved honey badger algorithm (HBA). The method combines the advantages of a convolutional neural network (CNN) and a bidirectional long short-term memory (BiLSTM) neural network. The results show that the proposed hybrid model effectively extracts features, enriches local details, and enhances global perception capabilities. A.F. Shahraki et al. [33] proposed an RUL prediction method based on the long short-term memory (LSTM) model. This method can reduce computational time and complexity while ensuring high prediction performance. X. Zhao et al. [34] applied the fuzzy theory to the fault diagnosis of a shunt capacitor. At the same time, they proposed a map-based fault diagnosis system. This method not only improves the accuracy of power capacitor fault diagnosis and identification but also provides a new method for the application of power capacitor fault research and development.

Despite the growing application of deep learning techniques in RUL prediction, several critical challenges remain unresolved in the context of tantalum capacitors. First, the degradation behavior of capacitors is often modulated by complex and dynamic environmental conditions, such as fluctuating ambient temperature and electrical loading, which introduce significant noise and obscure the true degradation signals. Second, most existing approaches are trained on offline datasets and lack the capacity for real-time inference, limiting their applicability in scenarios requiring continuous health monitoring and timely maintenance decisions. Third, conventional neural network architectures often fall short in modeling the multiscale temporal dependencies and intricate feature correlations embedded within long-term degradation data. These challenges collectively underscore the need for a unified and adaptive prediction framework that can (i) effectively suppress environmental interference; (ii) support online, real-time prognostics; and (iii) robustly extract and learn subtle yet informative degradation patterns. Overcoming these limitations is essential for achieving accurate and dependable RUL estimation of passive electronic components in high-reliability and safety-critical applications.

To address the aforementioned challenges, this paper presents a novel CNN-LSTM-Attention-based framework for online RUL prediction of tantalum capacitors operating under complex and variable conditions. The key contributions of this work are summarized as follows:

(1) A temperature-based data preprocessing method is proposed, in which a dual-sensor configuration (comprising an infrared temperature sensor and an ambient temperature sensor) is utilized to compensate for environmental interference. This strategy enables the extraction of degradation-relevant thermal signals, thereby improving the quality and reliability of the input features.

(2) A unified hybrid deep learning architecture is developed by integrating convolutional neural networks (CNNs), long short-term memory (LSTM) units, and attention mechanisms. This architecture effectively captures local degradation features, models long-term temporal dependencies, and dynamically emphasizes the most informative patterns within the data. Additionally, a channel attention mechanism is incorporated to adaptively reweight feature channels, enhancing the model’s capacity to extract subtle yet critical degradation cues across spatial dimensions.

(3) Extensive experimental evaluations based on the accelerated aging data of real-world tantalum capacitors demonstrate the proposed method’s superior performance over conventional LSTM and CNN-LSTM baselines. The model achieves significant improvements in prediction accuracy, robustness, and generalization capability. Notably, the proposed approach is particularly well suited for online prognostic scenarios where only non-intrusive surface temperature measurements are available and holds strong potential for extension to other types of capacitors and passive electronic components in broader PHM applications.

The rest of this paper is organized as follows. Section 2 presents the problem formulation and related preliminaries, including the temperature degradation modeling of tantalum capacitors. Section 3 details the proposed online RUL prediction method, including the data preprocessing strategy and the hybrid CNN-LSTM-Attention architecture. Section 4 validates the proposed framework using accelerated degradation experiments on real-world tantalum capacitors and discusses the prediction results. Finally, Section 5 concludes the paper and outlines potential directions for future research.

2. Preliminaries

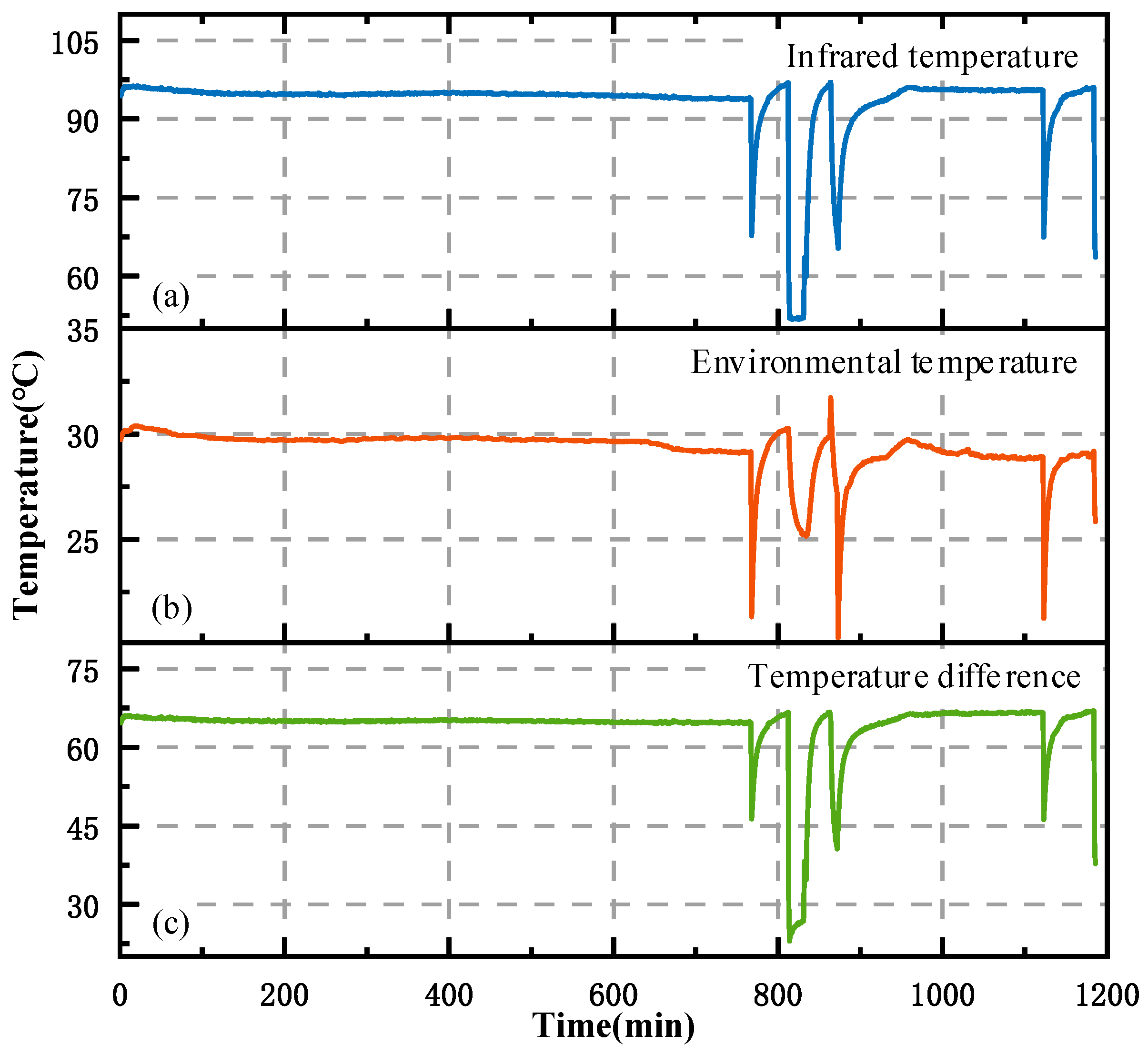
During the degradation process of tantalum capacitors, the core temperature plays a critical role in determining their performance and operational life. However, under complex working conditions, obtaining the core temperature of tantalum capacitors is challenging. In contrast, the operating temperature of the capacitor, which corresponds to the surface casing temperature, can be conveniently measured using noncontact detection methods. The operating temperature of a capacitor is influenced by the ambient temperature, heat dissipation conditions, and electrical operating parameters. Heat dissipation is affected by variables such as the structure of packaging, spatial configuration, and the accumulation of dust. In high-reliability application scenarios, these factors are typically stable under long-term operating conditions. Therefore, this work neglects the impact of heat dissipation conditions. The relationship between the core temperature and the operating temperature is described as follows:

$$T_h(t)=\alpha T(t)=T_e(t)+T_{dc}(t)+T_{ac}(t)$$

(1)

where T_h(t) represents the core temperature of the tantalum capacitor at moment t. α is a constant that only relates to the ambient thermal resistance. T(t) represents the operating temperature of the tantalum capacitor at moment t. T_e(t) is ambient temperature. T_dc(t) denotes the temperature induced by losses due to leakage current. T_ac(t) denotes the temperature induced by losses due to ripple current. From Equation (1), the operating temperature can be derived:

$$T(t)={\displaystyle \frac{1}{\alpha }}(T_e(t)+T_{dc}(t)+T_{ac}(t))$$

(2)

Equation (2) elucidates the relationship between the operating temperature and the core temperature of tantalum capacitors. Specifically, the operating temperature is determined by the heat dissipation arising from two components: leakage current and ripple current. Additionally, the ambient temperature plays a significant role as an indispensable factor influencing the operating temperature. The temperature rise of the operating temperature in tantalum capacitors caused by leakage current follows the relationship described below.

$$\Delta T_{dc}={\displaystyle \frac{U_{dc}\Delta i_c}{HS}}=\beta U_{dc}\Delta i_c$$

(3)

where U_dc represents the DC voltage that remains unchanged during capacitor degradation. i_c is the leakage current. H is the thermal conductivity. S refers to the surface area of the capacitor. 1/HS is simplified as a constant value, β. The temperature rise of the operating temperature in tantalum capacitors caused by ripple current can be described as follows:

$$\Delta T_{ac}=\beta {\displaystyle \frac{3}{2}}{I}_{ic}^{2}ESR$$

(4)

Combining Equation (2), the total temperature variation in the operating temperature of tantalum capacitors caused by performance degradation can be expressed as follows:

$$\Delta T(t)={\displaystyle \frac{1}{\alpha }}(\Delta T_{dc}(t)+\Delta T_{ac}(t)+\Delta T_e(t))={\displaystyle \frac{\beta }{\alpha }}(U_{dc}\Delta i_c+{\displaystyle \frac{3}{2}}{I}_{ic}^{2}ESR)+{\displaystyle \frac{\Delta T_e(t)}{\alpha }}$$

(5)

The core temperature representing the degradation state of the tantalum capacitor can be expressed as follows:

$$\Delta T_h(t)=\beta (U_{dc}\Delta i_c+{\displaystyle \frac{3}{2}}{I}_{ic}^{2}ESR)+\Delta T_e(t)$$

(6)

During the aging process of tantalum capacitors, the degradation of performance significantly accelerates the rise of the operating temperature. Specifically, the degradation of performance parameters and the equivalent series resistance (ESR) lead to a rapid increase in the core temperature of the tantalum capacitor. Therefore, long-term continuous monitoring of the core temperature provides a convenient means to predict the remaining useful life (RUL) of the tantalum capacitor.

3. The Proposed Method

3.1. Overview of Proposed Method

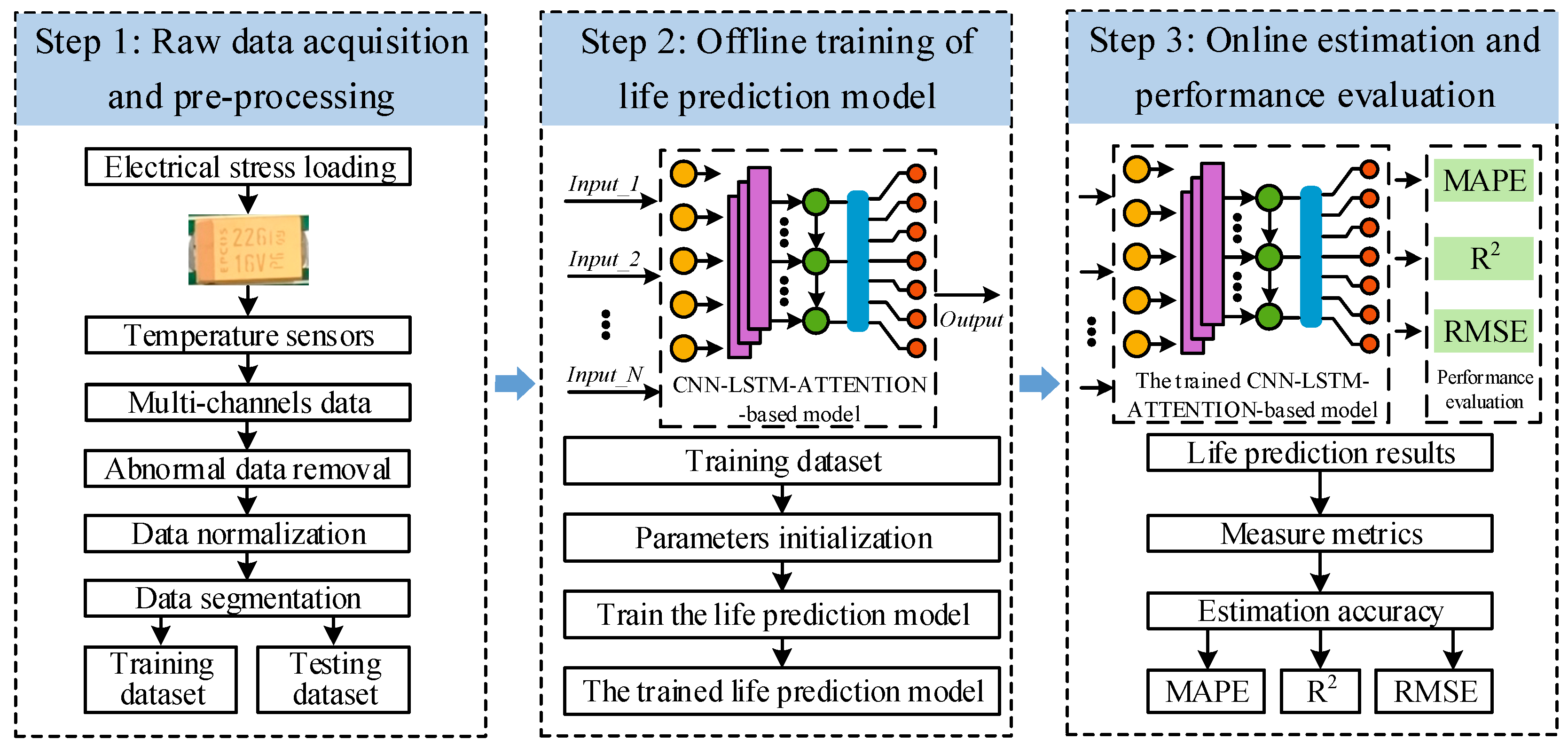
Figure 1 illustrates the framework of the proposed CNN-LSTM-Attention-based method for predicting the RUL of tantalum capacitors, which consists of three main steps.

(1) The first step involves the acquisition and preprocessing of temperature data for the tantalum capacitors. The degradation data used in this study is sourced from accelerated degradation tests. During the data preprocessing phase, the degradation data of the tantalum capacitors are processed to remove interference caused by environmental temperature. Considering the potential impact of environmental temperature changes on the degradation process, this study considers multiple factors, including the operating temperature and temperature rise slope. These factors are integrated to construct the input dataset, which is then used to train the neural network model. Meanwhile, during the initial phase of accelerated testing, considering that the rapid temperature rise of the capacitor does not represent its gradual aging process, the lifetime is calculated after the temperature stabilizes. The acquired lifetime data is preprocessed to generate the dataset for the tantalum capacitor lifetime prediction algorithm.

(2) The second step involves the offline training of the lifetime prediction model. The purpose is to systematically train the deep neural network model using the training dataset. To be specific, the input data and corresponding degradation labels are simultaneously fed into the constructed neural network. The input data is propagated through the multi-layer structure of the model, ultimately yielding the predicted lifetime of the capacitor. The error between the predicted values and the actual lifetime is calculated, and the backpropagation algorithm is employed to optimize the internal parameters of the model. This process continues until the predefined number of training iterations is reached.

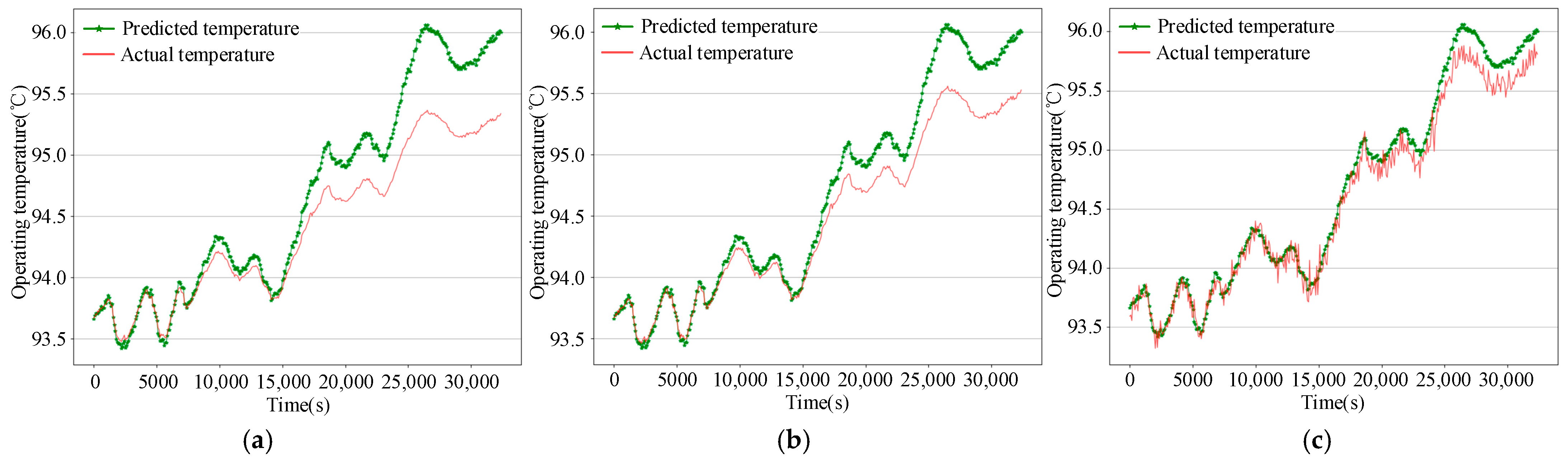
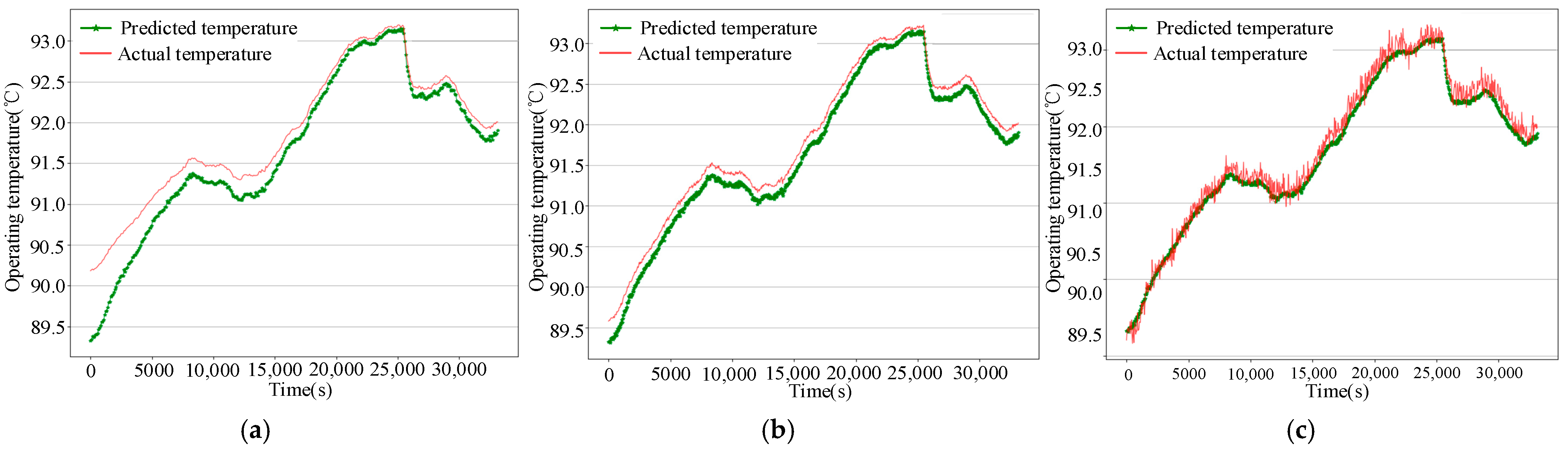
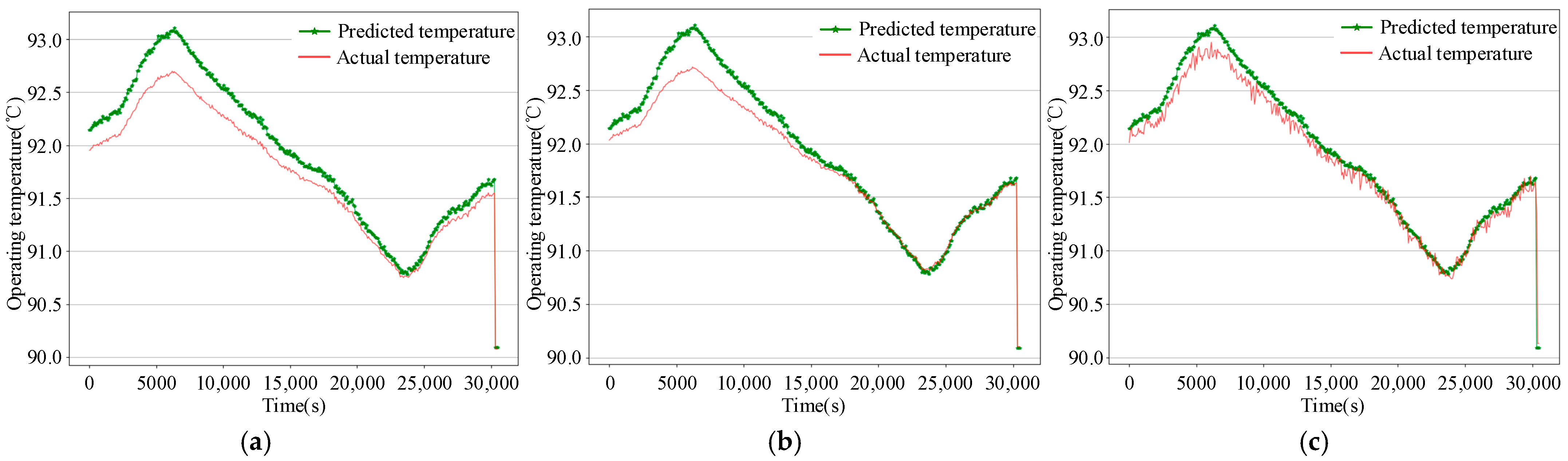
(3) The third step involves online prediction and performance evaluation. The target of online prediction is to estimate the remaining lifetime of the tantalum capacitor in real time. At this stage, predictions are made based on current and historical data. Sample data from the test set is input into the trained neural network model, and the model outputs the predicted remaining lifetime of the capacitor. Various evaluation metrics, such as MAPE and RMSE, are then used to quantitatively assess the accuracy of the model’s predictions, thereby evaluating the overall performance of the model. Additionally, the predicted lifetime values are compared with the actual lifetime values recorded from accelerated tests to validate the effectiveness and accuracy of the model.

3.2. Data Preprocessing Method

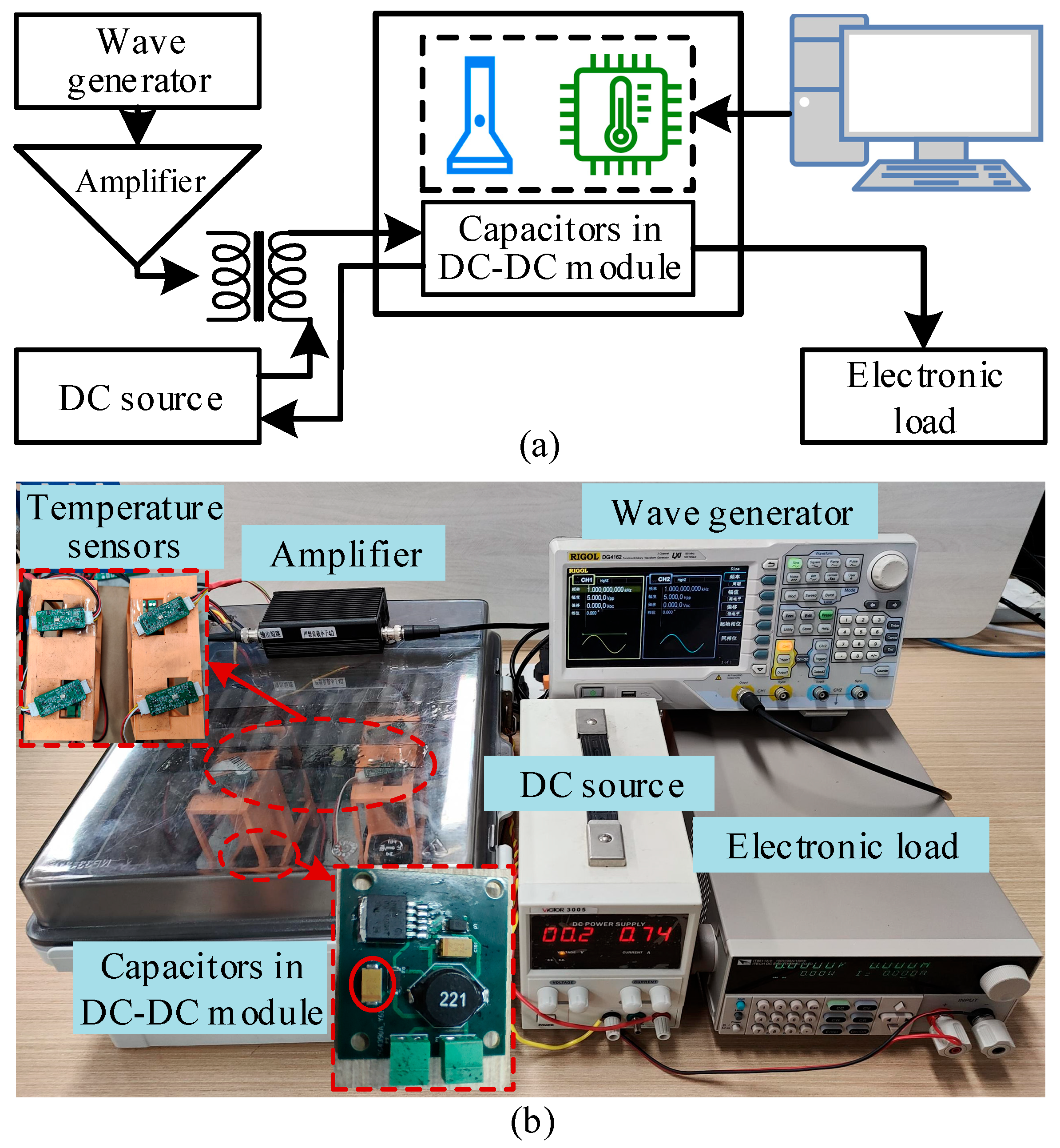
During the accelerated testing process, considering the potential impact of ambient temperature on the degradation temperature data of the tantalum capacitor, data preprocessing measures are implemented with the aim of minimizing the interference from ambient temperature, thereby ensuring the accuracy of the acquired tantalum capacitor degradation temperature data. To be specific, two temperature sensors are adopted in the experimental setup. Herein, y₁(t) represents the tantalum capacitor degradation temperature data measured by an infrared temperature sensor, while y₂(t) indicates the real-time ambient temperature conditions surrounding the tantalum capacitor, monitored by an ambient temperature sensor. y₃(t) represents the true temperature data of the tantalum capacitor, which is calculated using the following formula:

$$y_3(t)=y_1(t)-y_2(t)$$

(7)

By subtracting the ambient temperature data from the measured tantalum capacitor temperature data, the true temperature data of the tantalum capacitor can be obtained, thereby minimizing the potential interference of ambient temperature on the test data and ensuring a high degree of reliability and accuracy in the dataset used for training the CNN-LSTM-Attention model.

3.3. The Proposed CNN-LSTM-Attention-Based Remaining Useful Life Prediction Method

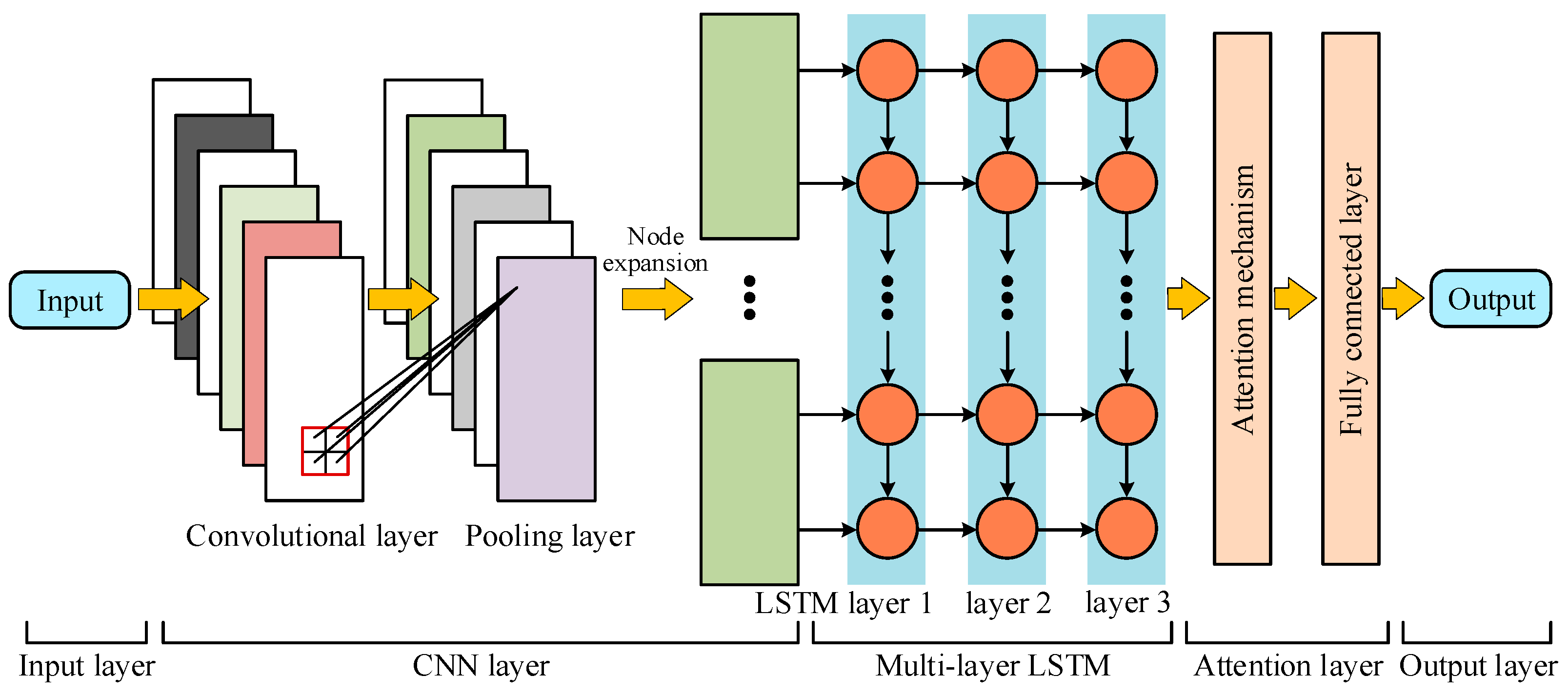
The workflow for predicting the RUL of tantalum capacitors integrates deep learning techniques with the physical degradation mechanisms of the capacitors. It estimates the remaining lifetime by analyzing multi-dimensional degradation data, including operating temperature, electrical parameters, and environmental conditions. Given the strong feature extraction capability of convolutional neural networks (CNNs) and considering the long time series of degradation data for tantalum capacitors, a CNN-LSTM-Attention-based model has been developed for RUL prediction. The structure of the prediction model is illustrated in Figure 2.

To be specific, the CNN is composed of convolutional layers, pooling layers, and fully connected layers. It can automatically learn meaningful features from the input data without the need for manual feature preprocessing. The convolutional layers serve as the foundation and core of the CNN, carrying out the critical task of feature extraction. The convolution operation is expressed as follows:

$$C_{i,j}={\displaystyle {\sum }_{p,q}{I}_{i=p, j=q}·K_{p,q}+b}$$

(8)

where C_i,j represents the value of the output feature map at position (i, j). I is the input data. K is a convolution kernel of size p × q. b is the offset term. As the convolutional kernel slides over the input layer, the equation can be expressed as

$$C_{i^{\prime },j^{\prime }}={\displaystyle {\sum }_{p,q}{I}_{i + m - p, j + n - q}·K_{p,q}+b}$$

(9)

By comparing Equations (8) and (9), it can be observed that i′ = i + m, j′ = j + m, meaning the output values undergo the same spatial displacement as the input. This convolution operation provides the CNN with a degree of translation invariance, enabling it to preserve the spatial information of the input data. To ensure consistency between the spatial dimensions of the input data and the output feature maps, zero-padding is applied when the convolution kernel reaches the edges of the input data. The number of convolutional kernels directly determines the depth (number of channels) of the output feature maps. Additionally, the size of the convolutional kernels is a key factor in defining the receptive field, as kernels of different sizes can extract spatial features at various scales.

The pooling layer is a crucial structure in CNN for reducing the spatial dimensions of data and is typically placed after convolutional layers. By reducing the dimensions of feature maps while maintaining the number of channels, the pooling layer decreases the number of parameters in subsequent layers, enhancing computational efficiency and helping to mitigate overfitting. The most common pooling methods are Average Pooling and Max Pooling. Considering the superior performance of Max Pooling in capturing and extracting prominent features, this study adopts the Max Pooling strategy. The mathematical expression is as follows:

$$output=\max (I)$$

(10)

After being processed by the convolutional and pooling layers, the data needs to be flattened before being input into the fully connected (FC) layer. The function of the FC layer is to further integrate and reduce the dimensionality of the features extracted and fused by the preceding network layers, ultimately producing the prediction results through the forward propagation algorithm. The mathematical representation of the fully connected layer typically involves a linear combination of weight matrices and bias vectors. The expression for the fully connected layer is as follows:

$$z=wa+b$$

(11)

where z represents the output of the current layer, w represents the parameter value of the current layer, a represents the output of the previous layer, and b represents the offset item.

LSTM (long short-term memory) networks are designed to address the vanishing and exploding gradient problems commonly encountered when processing long sequence data. The core architecture consists of a forget gate, an input gate, an output gate, and a memory cell. The forget gate regulates the extent to which previous memory cell content is retained. The input gate determines how much new information is stored in the memory cell. The output gate controls how much of the memory unit content will be used to calculate the current hidden state and output. These gates perform computations based on the current input and the previous hidden state, using a Sigmoid activation function that produces outputs between 0 and 1, representing the proportion of information that passes through. The update mechanisms for the three gates and the memory cell are as follows:

$$\left\{\begin{array}{l}{f}_t=\sigma (W_f·x_t+R_f·h_{t-1}+b_f)\\ i_t=\sigma (W_i·x_t+R_i·h_{t-1}+b_i)\\ o_t=\sigma (W_o·x_t+R_o·h_{t-1}+b_o)\end{array}\right\}$$

(12)

In the equation, $\overline{C_t}$ represents the intermediate memory unit at the current time step, derived by applying the tanh activation function to the current input and the previous hidden state. The outputs of the forget gate and input gate regulate the extent of memory unit updates, enabling the storage and propagation of temporal information within the LSTM network. Finally, the output of the output gate, combined with the tanh-activated value of the current memory unit, determines the output at the current time step. This output is then used to update the hidden state for the next time step. This design allows the LSTM to incorporate the historical information of the entire input sequence into a state update at each time step, enhancing the performance in processing long sequence data.

The application of attention mechanisms in deep learning is inspired by the human visual attention system, which allows for the concentration and shifting of attention during information processing. Attention mechanisms are generally classified into two types: hard attention and soft attention. Considering the advantages of dynamic weight allocation in soft attention, this study adopts the soft attention mechanism. The mathematical expression of the soft attention mechanism can be represented as follows:

$${\widehat{z}}_t={\displaystyle \sum {\alpha }_{t,i}}{a}_i$$

(13)

where ${\widehat{z}}_t$ represents the weighted output of the model in time steps, ${\alpha }_{t,i}$ represents the attention weight for the i-th element of the input data, and $a_i$ denotes the corresponding input feature.

Through this weighting process, the model dynamically adjusts its focus at each time step, prioritizing the processing of input features assigned higher weights. This mechanism not only enhances the flexibility of the model in processing information but also significantly improves its ability to capture and utilize critical data features.

The channel attention mechanism is specifically designed to optimize the importance of channels in the convolutional layers of a model, serving as a key implementation of soft attention. The mechanism is implemented by introducing both a squeeze module and an excitation module. The squeeze module is adopted to reduce the feature map of each channel into a single scalar value, effectively capturing and representing the global information of that channel. The mathematical expression is as follows:

$$z_{c,i,j}={\displaystyle \sum _{h=1}^H{\displaystyle \sum _{w=1}^W{u}_c}}(h,w)$$

(14)

where H represents the height of the convolution layer, and W represents the width of the convolution layer. u_c represents the convolution kernel parameter of the c-th channel.

The excitation module evaluates and determines the relative importance of each channel by applying an activation function. The specific implementation process is as follows:

$$s=F_{ex}(z,W)=\sigma (g(z,W))=\sigma \left(W_2\delta \left(W_{1}z\right)\right)$$

(15)

where δ represents a specific nonlinear threshold function, such as ReLU. σ represents the activation function that processes the global information of each channel, such as a Sigmoid. Through this mechanism, the excitation module assigns a weight to each channel, reflecting its contribution and importance within the entire network. The channel importance adjustment method, based on dynamic learning, provides an effective means for deep learning models to process complex information in a more refined and flexible manner, thereby enhancing the accuracy and efficiency of the model.

4. Experimental Results and Discussion

4.1. Experimental Description

To closely emulate the actual operating conditions of tantalum capacitors, the test specimens in this study are meticulously designed based on the DC/DC modules from the original control board. This approach ensured not only consistency in the constituent components but also an identical structural layout of the DC/DC module. The schematic diagram and the actual photograph of the experimental circuit are presented in Figure 3a,b, respectively. The key parameters of the tantalum capacitors are summarized in

Table 1. Electrical parameters of tantalum capacitor.

Parameter (Unit)	Value
rated voltage (V)	16
rated capacitance ($\mathrm{\mu }\mathrm{F}$)	100
initial ESR ($\mathrm{\Omega }$)	1.8
maximum leakage current ($\mathrm{\mu }\mathrm{A}$)	16
maximum loss factor (%)	10

. The schematic diagram and the actual photograph of the experimental platform are depicted in Figure 4a,b, respectively. The electrical stress is generated by adopting a combination of DC and AC. The DC voltage is supplied via a constant voltage power source, while the AC ripple signal is generated using a signal generator. The AC ripple signal is amplified using a power amplifier and coupled with the DC voltage via a transformer, thereby achieving hybrid electrical stress loading. For safety considerations, the entire DC/DC module under test is placed inside an explosion-proof test chamber. Considering the sufficient volume of the explosion-proof chamber and the limitations of the power amplifier, multiple aging test boards are simultaneously arranged in the explosion-proof chamber, allowing repetitive aging tests to be conducted at the same time. Each test board shared the same voltage input and load, ensuring uniform operating conditions for all capacitors. Temperature-monitoring devices are mounted above the test boards to collect degradation data during the aging process. Each monitoring device consisted of an infrared temperature sensor and an ambient temperature sensor. The collected temperature data are processed by an integrated microcontroller unit (MCU), which transmits the data via an RS485 bus to an RS485-to-Ethernet module. Finally, the data are transmitted to a PC for storage and further analysis. The collected data are subsequently utilized to train and test a deep learning model designed to analyze and predict capacitor degradation.

4.2. Data Preprocessing

Figure 5 illustrates the temperature data of the tantalum capacitor obtained by the temperature sensors and the corresponding preprocessing results. To be specific, Figure 5a depicts the degradation temperature curve of the tantalum capacitor during operation, as measured by the infrared sensor. Figure 5b presents the data simultaneously recorded by the ambient temperature sensor, which reflects the environmental temperature variations surrounding the capacitor and serves as critical reference information for subsequent data preprocessing. Figure 5c shows the results of the preprocessing procedure, where the environmental temperature component is subtracted from the total temperature measured by the infrared sensor to isolate the actual degradation temperature of the tantalum capacitor. This preprocessing step not only enhances the accuracy and reliability of the data but also ensures that subsequent analyses focus specifically on the thermal degradation characteristics of the capacitor itself. The preprocessed degradation temperature data of the tantalum capacitor are then adopted as the training dataset for the CNN-LSTM-Attention model. This facilitates detailed learning and training aimed at developing a prediction model capable of capturing fine-grained variations with high accuracy. This preprocessing step is critical for improving the overall performance of the model and ensuring its reliability in predicting the degradation temperature of tantalum capacitors.

4.3. Experimental Results Analysis and Discussion

Based on the aforementioned experimental system, this section aims to simulate the aging process of tantalum capacitors under actual application conditions to collect and record temperature data during the degradation process. These temperature data are utilized to train the constructed lifetime prediction model, which is subsequently validated using an independent test dataset. The target is to ensure the accuracy and reliability of the model in various application scenarios. To eliminate the influence of random factors on the experimental results, three sets of repeated tests are conducted in this research. The experimental results are shown in Figure 6, corresponding to Groups 1, 2, and 3. In these figures, the green curves represent the actual degradation trends, while the red curves depict the predicted degradation trends generated by the CNN-LSTM-Attention-based model.

To comprehensively evaluate the accuracy and reliability of the developed lifetime prediction model, three evaluation metrics are proposed: root mean squared error (RMSE), mean absolute percentage error (MAPE), and the coefficient of determination (R²). To be specific, RMSE focuses on the absolute magnitude of the differences between the predicted and actual values, making it highly sensitive to error magnitude. A smaller RMSE indicates better predictive performance for the model. The mathematical expression for RMSE is as follows:

$$RMSE=\sqrt{{\displaystyle \frac{{\displaystyle {\sum }_{i=1}^N(y_i-{\widehat{y}}_i)}}{N}}}$$

(16)

where N represents the total number of samples. ${\widehat{y}}_i$ is the predicted value of the tantalum capacitance at the i sample point. y_i is the actual value of the tantalum capacitance at the i sample point. $\overline{y}$ is the average of the actual values.

MAPE focuses on the relative magnitude of errors, representing the absolute difference between the predicted and actual values as a percentage of the actual value. A lower MAPE indicates higher accuracy for the model. The mathematical expression is as follows:

$$MAPE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^N\left|\frac{({\widehat{y}}_i-y_i)}{y_i}\right|}\times 100\%$$

(17)

The R² metric is adopted to evaluate the degree of fitting between the predicted values and the actual values of the model. A value closer to 1 indicates a better fit to the data and stronger predictive performance.

$$R^2=1-{\displaystyle \frac{{{\displaystyle {\sum }_{i=1}^N(y_i-{\widehat{y}}_i)}}^2}{{{\displaystyle {\sum }_{i=1}^N(y_i-\overline{y})}}^2}}$$

(18)

Based on the dataset constructed from the experimental data of Group 1, the CNN-LSTM-Attention model is used for prediction, and the prediction results are shown in Figure 6. In order to assess the prediction accuracy of the models on the test set, evaluation metrics, including RMSE, MAPE, and R², are calculated for the three network models, and the values are shown in

Table 2. Evaluation metrics for the predictions of the three network models in Group 1.

Network Type	MAPE	RMSE	R2
LSTM	0.269	0.350	0.826
CNN-LSTM	0.166	0.207	0.939
CNN-LSTM-Attention	0.105	0.125	0.978

. As analyzed in Table 2, the MAPE of the CNN-LSTM-Attention model decreases by 36.75% and 60.97% compared to the CNN-LSTM and LSTM models, respectively. The RMSEs of the CNN-LSTM-Attention model decreased by 39.61% and 64.29% compared to the CNN-LSTM and LSTM models, respectively. The R2 values of the CNN-LSTM-Attention model increased by 4.15% and 18.40% compared to the CNN-LSTM and LSTM networks, respectively, indicating the high accuracy and reliability in the lifetime prediction of the CNN-LSTM-Attention model.

The lifetime of a tantalum capacitor is considered to reach the endpoint when its performance degrades to a predefined failure threshold. In this work, the moment corresponding to the highest temperature during the stable degradation phase is defined as the end-of-life of the capacitor. When the capacitor reaches the highest temperature during the stable degradation phase, it can be considered to have failed, completing the prediction of the RUL of the capacitor. The RUL prediction results are compared with the actual lifetime values obtained from accelerated degradation experiments, and the error analysis results are presented in

Table 3. RUL prediction error results for Group 1.

Network Type	Predicted RUL (s)	Actual RUL (s)	Prediction Error (s)	MAPE (%)
LSTM	25,307	21,664	3643	16.82
CNN-LSTM	24,381	21,664	2717	12.54
CNN-LSTM-Attention	23,972	21,664	2308	10.65

. By analyzing the life prediction results of the LSTM network, CNN-LSTM network, and CNN-LSTM-Attention network, it can be seen that the prediction relative error of the RUL prediction method based on the CNN-LSTM-Attention network is 10.65%, while the prediction relative errors of the CNN-LSTM and LSTM networks are 12.54% and 16.82%, respectively. The prediction error of the CNN-LSTM-Attention network is reduced by 15.07% and 36.68% compared to the CNN-LSTM and LSTM networks, respectively, revealing the high accuracy and reliability of the experimental results.

Utilizing the dataset from the experimental data of Group 2, predictions are conducted employing the CNN-LSTM-Attention model. The results are depicted in Figure 7. The evaluation metrics, including RMSE, MAPE, and R², are calculated and exhibited in

Table 4. Evaluation metrics for the predictions of the three network models in Group 2.

Network Type	MAPE	RMSE	R2
LSTM	0.230	0.271	0.919
CNN-LSTM	0.148	0.140	0.978
CNN-LSTM-Attention	0.121	0.136	0.980

. It can be seen that the CNN-LSTM-Attention model exhibits a notable decrease in MAPE by 18.24% and 47.39% when compared to the CNN-LSTM and LSTM models, respectively. Similarly, the RMSE for the CNN-LSTM-Attention model is reduced by 2.86% and 49.81% in comparison to the CNN-LSTM and LSTM models. Furthermore, the R2 value for the CNN-LSTM-Attention model increases by 0.20% and 6.64% relative to the CNN-LSTM and LSTM networks, respectively. These results underscore the enhanced accuracy and dependability of the CNN-LSTM-Attention model in predicting lifetimes.

As shown in Figure 7, it can be concluded that the tantalum capacitor corresponding to the degradation moment has already failed, thus completing the prediction of the remaining life (RUL) of the tantalum capacitor. Then, the RUL prediction results are analyzed with the real life of the capacitor obtained from the accelerated degradation test, and the prediction errors of the three types of networks are compared, as shown in

Table 5. RUL prediction error results for Group 2.

Network Type	Predicted RUL (s)	Actual RUL (s)	Prediction Error (s)	MAPE (%)
LSTM	7166	8360	1194	14.28
CNN-LSTM	7540	8360	820	9.81
CNN-LSTM-Attention	7925	8360	435	5.20

. It can be seen that the prediction relative error of the RUL prediction method based on the CNN-LSTM-Attention network is 5.20%, while the prediction relative errors of the CNN-LSTM and LSTM networks are 9.81% and 14.28%, respectively. The prediction error of the CNN-LSTM-Attention network is reduced by 46.99% and 63.59% compared to the CNN-LSTM and LSTM networks, respectively, which indicates the high accuracy and reliability of the experimental results.

Employing the dataset from the experimental data of Group 3, the CNN-LSTM-Attention model is applied for predictive modeling, with the results shown in Figure 8. It can be observed that the degradation trend of this group decreases during the failure phase, which is due to the ambient temperature variation masking the real performance degradation trend. The performance of the CNN-LSTM-Attention model is assessed using key metrics such as RMSE, MAPE, and R2, which are detailed in

Table 6. Evaluation metrics for the predictions of the three network models in Group 3.

Network Type	MAPE	RMSE	R2
LSTM	0.194	0.212	0.903
CNN-LSTM	0.125	0.170	0.938
CNN-LSTM-Attention	0.101	0.128	0.965

. It can be seen from Table 6 that the MAPE of the CNN-LSTM-Attention model decreases by 19.20% and 47.12% compared to the CNN-LSTM and LSTM models, respectively. The RMSE of the CNN-LSTM-Attention model decreased by 24.71% and 65.63% compared to the CNN-LSTM and LSTM models, respectively. The R² of the CNN-LSTM-Attention model increased by 28.79% and 68.67% compared to the CNN-LSTM and LSTM networks, respectively. The above key metrics show the high accuracy and reliability in the lifetime prediction of the CNN-LSTM-Attention model.

The relative errors of prediction for the three types of networks are shown in

Table 7. RUL prediction error results for Group 3.

Network Type	Predicted RUL (s)	Actual RUL (s)	Prediction Error (s)	MAPE (%)
LSTM	16,013	18,248	2235	12.25
CNN-LSTM	17,602	18,248	646	3.54
CNN-LSTM-Attention	17,689	18,248	559	3.06

. It can be seen that the prediction relative error of the RUL prediction method based on the CNN-LSTM-Attention network is 3.06%, while the prediction relative errors of CNN-LSTM and LSTM networks are 3.54% and 12.25%, respectively. The prediction error of the CNN-LSTM-Attention network is reduced by 13.56% and 75.02% compared to the CNN-LSTM and LSTM networks, respectively, indicating the high accuracy and reliability of the predictive model based on CNN-LSTM-Attention.

5. Conclusions

This article has proposed a novel deep learning-based framework for online remaining useful life (RUL) prediction for tantalum capacitors, leveraging CNN-LSTM-Attention mechanisms to enable accurate and reliable prognostics based on temperature measurements. The key innovations of the proposed method are summarized as follows: (1) a hybrid degradation-aware modeling approach was developed by integrating convolutional feature extraction, long-term temporal memory, and soft attention mechanisms to dynamically enhance degradation pattern recognition, and (2) a channel attention mechanism was embedded to adaptively reweight critical feature channels, improving the model’s sensitivity to subtle degradation trends under varying operating conditions. Extensive experiments using real-world accelerated aging data demonstrated the superiority of the proposed approach in terms of prediction accuracy and generalization. Compared with baseline models, the CNN-LSTM-Attention framework achieved significant reductions in MAPE and RMSE, along with notable improvements in R², consistently across multiple test groups. These results validate the robustness and effectiveness of the proposed method for the health prognostics of tantalum capacitors under complex thermal and electrical stresses. Future work will focus on extending this framework to address broader classes of electronic components with different degradation modalities, integrating multi-source sensory information beyond temperature, and exploring lightweight model architectures for deployment in embedded and resource-constrained prognostics scenarios. Moreover, potential applications in the condition-based maintenance of power electronic systems and real-time health monitoring in industrial IoT environments will be investigated to further demonstrate the scalability and adaptability of the proposed approach.