Review of Planar Optical System: Lens Based on Metasurfaces
Abstract
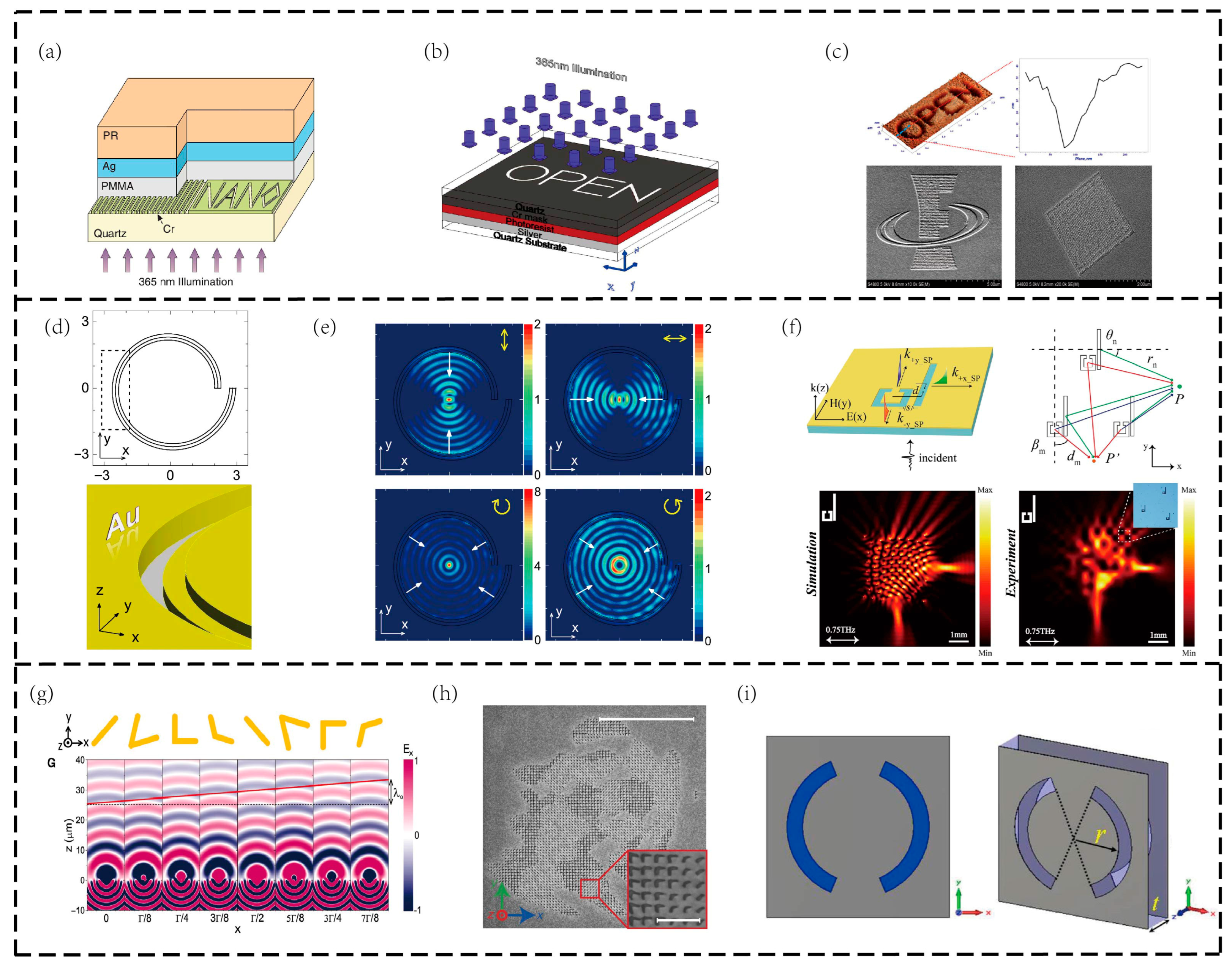
1. Introduction
2. Basic Principles
2.1. Generalized Snell’s Law
2.2. Phase Gradient Method
- The ideal phase gradient method requires the phase to vary continuously with spatial position (e.g., beam deflection needs to satisfy the relation “phase gradient = 2sinθ/”, where θ is the deflection angle and is the wavelength). However, the phase of a metalens is provided by “discrete elements”—each element can only achieve a limited number of discrete phase values (e.g., divided into 8-level or 16-level phases within the range of 0~2), which fails to cover a continuous phase distribution. The discretized phase gradient will generate “step errors”, causing part of the incident light to be unable to propagate in the preset direction. Instead, the light is converted into parasitic diffraction orders (e.g., stray light appearing beside the main beam), which reduces the energy utilization efficiency of the metalens.
- The phase gradient of metalens exhibits a strong wavelength dependence, which is jointly determined by the intrinsic dispersion characteristics of the material and the geometric dispersion of the structure. The chromatic aberration caused by the intrinsic dispersion of the element structure material and the diffraction effect of the structural geometry will seriously affect the imaging quality of the metalens. This wavelength dependence manifests as a significant shift in the focal length with changes in the wavelength, which severely limits the performance of the metalens in broadband applications.
- Most metalenses based on the phase gradient method (such as nanopillar metalenses and V-shaped antenna metalenses) are polarization-sensitive—their phase response to the elements is only effective for a specific polarization state (e.g., p-polarization or s-polarization of linearly polarized light, or left-handed or right-handed circular polarization of circularly polarized light), and they have almost no phase manipulation capability for light of other polarization states.
- The design of the phase gradient method is based on the “normal incidence” assumption—the preset phase gradient can only meet the requirement of “optical path difference matching” when the incident light is perpendicular to the metalens surface. When the incident light is obliquely incident (incident angle θ > 0), the optical path difference of the incident light on the metalens surface changes, resulting in a deviation between the actual phase gradient and the preset value.
- The phase gradient of a metalens is jointly determined by the size, shape, and spacing of subwavelength elements. Typically, the size of these elements is on the order of 100–1000 nm (approaching the lithography limit). The phase gradient method imposes extremely high precision requirements on the fabrication process, and any minor process error will cause the phase gradient to deviate from the designed value.
2.3. Modulation Methods

3. Plasmonic Metalenses
4. Dielectric Metalenses
5. Tunable Metalenses
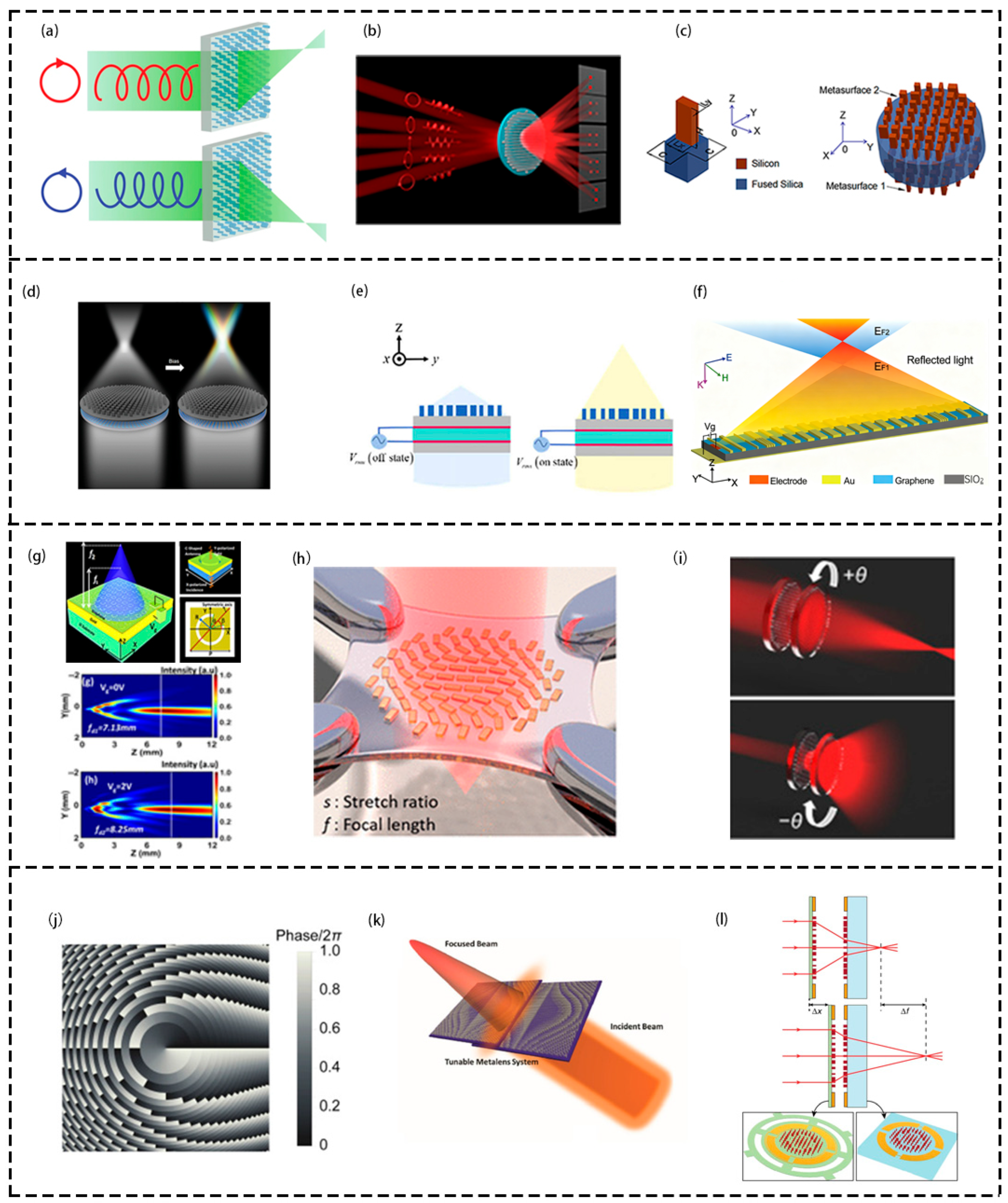
6. Large-Field-of-View Metalenses

7. Achromatic Metalenses
8. Deep Learning in Metalenses
9. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, J.; Dong, T.; Chi, B.; Zhang, Y. Metasurfaces for Terahertz Wavefront Modulation: A Review. J. Infrared Millim. Terahertz Waves 2020, 41, 607–631. [Google Scholar] [CrossRef]
- Kawanishi, T.; Sakamoto, T.; Izutsu, M. High-Speed Control of Lightwave Amplitude, Phase, and Frequency by Use of Electrooptic Effect. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 79–91. [Google Scholar] [CrossRef]
- Born, M. Principles of Optics; Elsevier: Amsterdam, The Netherlands, 1980; pp. 36–111. ISBN 978-1-4831-0320-4. [Google Scholar]
- Jackson, J.D.; Fox, R.F. Classical Electrodynamics, 3rd ed. Am. J. Phys. 1999, 67, 841–842. [Google Scholar] [CrossRef]
- Bürger, J.; Riedl, T.; Lindner, J.K.N. Influence of Lens Aberrations, Specimen Thickness and Tilt on Differential Phase Contrast STEM Images. Ultramicroscopy 2020, 219, 113118. [Google Scholar] [CrossRef]
- Lidwell, M.O. Achromatism of Lenses for Thermal IR. In Proceedings of the SPIE Optical Systems Engineering IV, Cambridge, MA, USA, 23–26 October 1984; Yoder, P.R., Jr., Ed.; SPIE: Bellingham, WA, USA, 1984; Volume 518, pp. 73–80. [Google Scholar]
- Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Planar Photonics with Metasurfaces. Science 2013, 339, 1232009. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Jornet, J.M.; Han, C. Terahertz Band: Next Frontier for Wireless Communications. Phys. Commun. 2014, 12, 16–32. [Google Scholar] [CrossRef]
- Liu, S.; Cui, T.J.; Zhang, L.; Xu, Q.; Wang, Q.; Wan, X.; Gu, J.Q.; Tang, W.X.; Qi, M.Q.; Han, J.G.; et al. Convolution Operations on Coding Metasurface to Reach Flexible and Continuous Controls of Terahertz Beams. Adv. Sci. 2016, 3, 1600156. [Google Scholar] [CrossRef] [PubMed]
- Valentine, J.; Zhang, S.; Zentgraf, T.; Ulin-Avila, E.; Genov, D.A.; Bartal, G.; Zhang, X. Three-Dimensional Optical Metamaterial with a Negative Refractive Index. Nature 2008, 455, 376–379. [Google Scholar] [CrossRef] [PubMed]
- Walia, S.; Shah, C.M.; Gutruf, P.; Nili, H.; Chowdhury, D.R.; Withayachumnankul, W.; Bhaskaran, M.; Sriram, S. Flexible Metasurfaces and Metamaterials: A Review of Materials and Fabrication Processes at Micro- and Nano-Scales. Appl. Phys. Rev. 2015, 2, 11303. [Google Scholar] [CrossRef]
- Watts, C.M.; Liu, X.; Padilla, W.J. Metamaterial Electromagnetic Wave Absorbers. Adv. Mater. 2012, 24, OP98–OP120. [Google Scholar] [CrossRef]
- Wong, Z.J.; Wang, Y.; O’Brien, K.; Rho, J.; Yin, X.; Zhang, S.; Fang, N.; Yen, T.-J.; Zhang, X. Optical and Acoustic Metamaterials: Superlens, Negative Refractive Index and Invisibility Cloak. J. Opt. 2017, 19, 84007. [Google Scholar] [CrossRef]
- Moitra, P.; Yang, Y.; Anderson, Z.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. Realization of an All-Dielectric Zero-Index Optical Metamaterial. Nat. Photonics 2013, 7, 791–795. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Li, G.; Bai, B.; Tan, Q.; Jin, G.; Zentgraf, T.; Zhang, S. Dispersionless Phase Discontinuities for Controlling Light Propagation. Nano Lett. 2012, 12, 5750–5755. [Google Scholar] [CrossRef]
- Aieta, F.; Genevet, P.; Kats, M.A.; Yu, N.; Blanchard, R.; Gaburro, Z.; Capasso, F. Aberration-Free Ultrathin Flat Lenses and Axicons at Telecom Wavelengths Based on Plasmonic Metasurfaces. Nano Lett. 2012, 12, 4932–4936. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Starr, T.; Starr, A.F.; Padilla, W.J. Infrared Spatial and Frequency Selective Metamaterial with Near-Unity Absorbance. Phys. Rev. Lett. 2010, 104, 207403. [Google Scholar] [CrossRef]
- Chen, G.; Li, Y.; Wang, X.; Wen, Z.; Lin, F.; Dai, L.; Chen, L.; He, Y.; Liu, S. Super-Oscillation Far-Field Focusing Lens Based on Ultra-Thin Width-Varied Metallic Slit Array. IEEE Photonics Technol. Lett. 2016, 28, 335–338. [Google Scholar] [CrossRef]
- Li, F.; Tang, T.; Li, J.; Luo, L.; Li, C.; Shen, J.; Yao, J. Chiral Coding Metasurfaces with Integrated Vanadium Dioxide for Thermo-Optic Modulation of Terahertz Waves. J. Alloys Compd. 2020, 826, 154174. [Google Scholar] [CrossRef]
- Lu, X.; Zeng, X.; Lv, H.; Han, Y.; Mou, Z.; Liu, C.; Wang, S.; Teng, S. Polarization Controllable Plasmonic Focusing Based on Nanometer Holes. Nanotechnology 2020, 31, 135201. [Google Scholar] [CrossRef]
- Holloway, C.L.; Kuester, E.F.; Gordon, J.A.; O’Hara, J.; Booth, J.; Smith, D.R. An Overview of the Theory and Applications of Metasurfaces: The Two-Dimensional Equivalents of Metamaterials. IEEE Antennas Propag. Mag. 2012, 54, 10–35. [Google Scholar] [CrossRef]
- Estakhri, N.M.; Alù, A. Recent Progress in Gradient Metasurfaces. J. Opt. Soc. Am. B 2016, 33, A21–A30. [Google Scholar] [CrossRef]
- Lalanne, P.; Chavel, P. Metalenses at Visible Wavelengths: Past, Present, Perspectives. Laser Photonics Rev. 2017, 11, 1600295. [Google Scholar] [CrossRef]
- Grady, N.K.; Heyes, J.E.; Chowdhury, D.R.; Zeng, Y.; Reiten, M.T.; Azad, A.K.; Taylor, A.J.; Dalvit, D.A.R.; Chen, H.-T. Terahertz Metamaterials for Linear Polarization Conversion and Anomalous Refraction. Science 2013, 340, 1304–1307. [Google Scholar] [CrossRef]
- Pfeiffer, C.; Grbic, A. Bianisotropic Metasurfaces for Optimal Polarization Control: Analysis and Synthesis. Phys. Rev. Appl. 2014, 2, 44011. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at Visible Wavelengths: Diffraction-Limited Focusing and Subwavelength Resolution Imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef]
- Arbabi, A.; Arbabi, E.; Kamali, S.M.; Horie, Y.; Han, S.; Faraon, A. Miniature Optical Planar Camera Based on a Wide-Angle Metasurface Doublet Corrected for Monochromatic Aberrations. Nat. Commun. 2016, 7, 13682. [Google Scholar] [CrossRef]
- Pan, M.; Fu, Y.; Zheng, M.; Chen, H.; Zang, Y.; Duan, H.; Li, Q.; Qiu, M.; Hu, Y. Dielectric metalens for miniaturized imaging systems: Progress and challenges. Light Sci. Appl. 2022, 11, 195. [Google Scholar] [CrossRef]
- Arbabi, A.; Horie, Y.; Ball, A.J.; Bagheri, M.; Faraon, A. Subwavelength-Thick Lenses with High Numerical Apertures and Large Efficiency Based on High-Contrast Transmitarrays. Nat. Commun. 2015, 6, 7069. [Google Scholar] [CrossRef]
- Arbabi, E.; Arbabi, A.; Kamali, S.M.; Horie, Y.; Faraon, A. Multiwavelength Polarization-Insensitive Lenses Based on Dielectric Metasurfaces with Meta-Molecules. Optica 2016, 3, 628–633. [Google Scholar] [CrossRef]
- Chen, C.; Song, W.; Chen, J.-W.; Wang, J.-H.; Chen, Y.H.; Xu, B.; Chen, M.-K.; Li, H.; Fang, B.; Chen, J.; et al. Spectral Tomographic Imaging with Aplanatic Metalens. Light Sci. Appl. 2019, 8, 99. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T.; Zhu, A.Y.; Sanjeev, V.; Khorasaninejad, M.; Shi, Z.; Lee, E.; Capasso, F. A Broadband Achromatic Metalens for Focusing and Imaging in the Visible. Nat. Nanotechnol. 2018, 13, 220–226. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Sisler, J.; Bharwani, Z.; Capasso, F. A Broadband Achromatic Polarization-Insensitive Metalens Consisting of Anisotropic Nanostructures. Nat. Commun. 2019, 10, 355. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T.; Zhu, A.Y.; Sisler, J.; Huang, Y.-W.; Yousef, K.M.A.; Lee, E.; Qiu, C.-W.; Capasso, F. Broadband Achromatic Metasurface-Refractive Optics. Nano Lett. 2018, 18, 7801–7808. [Google Scholar] [CrossRef]
- Chen, X.; Huang, L.; Mühlenbernd, H.; Li, G.; Bai, B.; Tan, Q.; Jin, G.; Qiu, C.-W.; Zhang, S.; Zentgraf, T. Dual-Polarity Plasmonic Metalens for Visible Light. Nat. Commun. 2012, 3, 1198. [Google Scholar] [CrossRef]
- Fan, Q.; Wang, Y.; Liu, M.; Xu, T. High-Efficiency, Linear-Polarization-Multiplexing Metalens for Long-Wavelength Infrared Light. Opt. Lett. 2018, 43, 6005–6008. [Google Scholar] [CrossRef]
- Fan, Z.-B.; Shao, Z.-K.; Xie, M.-Y.; Pang, X.-N.; Ruan, W.-S.; Zhao, F.-L.; Chen, Y.-J.; Yu, S.-Y.; Dong, J.-W. Silicon Nitride Metalenses for Close-to-One Numerical Aperture and Wide-Angle Visible Imaging. Phys. Rev. Appl. 2018, 10, 14005. [Google Scholar] [CrossRef]
- Groever, B.; Chen, W.T.; Capasso, F. Meta-Lens Doublet in the Visible Region. Nano Lett. 2017, 17, 4902–4907. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Oh, J.; Capasso, F. Super-Dispersive off-Axis Meta-Lenses for Compact High Resolution Spectroscopy. Nano Lett. 2016, 16, 3732–3737. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Zhu, A.Y.; Oh, J.; Devlin, R.C.; Rousso, D.; Capasso, F. Multispectral Chiral Imaging with a Metalens. Nano Lett. 2016, 16, 4595–4600. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Shi, Z.; Zhu, A.Y.; Chen, W.T.; Sanjeev, V.; Zaidi, A.; Capasso, F. Achromatic Metalens over 60 Nm Bandwidth in the Visible and Metalens with Reverse Chromatic Dispersion. Nano Lett. 2017, 17, 1819–1824. [Google Scholar] [CrossRef] [PubMed]
- Lin, R.J.; Su, V.-C.; Wang, S.; Chen, M.K.; Chung, T.L.; Chen, Y.H.; Kuo, H.Y.; Chen, J.-W.; Chen, J.; Huang, Y.-T.; et al. Achromatic Metalens Array for Full-Colour Light-Field Imaging. Nat. Nanotechnol. 2019, 14, 227–231. [Google Scholar] [CrossRef]
- Paniagua-Domínguez, R.; Yu, Y.F.; Khaidarov, E.; Choi, S.; Leong, V.; Bakker, R.M.; Liang, X.; Fu, Y.H.; Valuckas, V.; Krivitsky, L.A.; et al. A Metalens with a Near-Unity Numerical Aperture. Nano Lett. 2018, 18, 2124–2132. [Google Scholar] [CrossRef]
- Shrestha, S.; Overvig, A.C.; Lu, M.; Stein, A.; Yu, N. Broadband Achromatic Dielectric Metalenses. Light Sci. Appl. 2018, 7, 85. [Google Scholar] [CrossRef] [PubMed]
- Vo, S.; Fattal, D.; Sorin, W.V.; Peng, Z.; Tran, T.; Fiorentino, M.; Beausoleil, R.G. Sub-Wavelength Grating Lenses with a Twist. IEEE Photonics Technol. Lett. 2014, 26, 1375–1378. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.-C.; Lai, Y.-C.; Chen, M.-K.; Kuo, H.Y.; Chen, B.H.; Chen, Y.H.; Huang, T.-T.; Wang, J.-H.; et al. A Broadband Achromatic Metalens in the Visible. Nat. Nanotechnol. 2018, 13, 227–232. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.-C.; Lai, Y.-C.; Hung Chu, C.; Chen, J.-W.; Lu, S.-H.; Chen, J.; Xu, B.; Kuan, C.-H.; et al. Broadband Achromatic Optical Metasurface Devices. Nat. Commun. 2017, 8, 187. [Google Scholar] [CrossRef]
- Ye, M.; Ray, V.; Peng, Y.; Guo, W.; Yi, Y.S. Linear Polarization Distinguishing Metalens in Visible Wavelength. Opt. Lett. 2019, 44, 399–402. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, J.; Zheng, H.; An, S.; Lin, H.; Zheng, B.; Du, Q.; Yin, G.; Michon, J.; Zhang, Y.; et al. Ultra-Thin High-Efficiency Mid-Infrared Transmissive Huygens Meta-Optics. Nat. Commun. 2018, 9, 1481. [Google Scholar] [CrossRef] [PubMed]
- Zhu, A.Y.; Chen, W.-T.; Khorasaninejad, M.; Oh, J.; Zaidi, A.; Mishra, I.; Devlin, R.C.; Capasso, F. Ultra-Compact Visible Chiral Spectrometer with Meta-Lenses. APL Photonics 2017, 2, 36103. [Google Scholar] [CrossRef]
- Zuo, H.; Choi, D.; Gai, X.; Ma, P.; Xu, L.; Neshev, D.N.; Zhang, B.; Luther-Davies, B. High-Efficiency All-Dielectric Metalenses for Mid-Infrared Imaging. Adv. Opt. Mater. 2017, 5, 1700585. [Google Scholar] [CrossRef]
- Lin, D.; Fan, P.; Hasman, E.; Brongersma, M.L. Dielectric Gradient Metasurface Optical Elements. Science 2014, 345, 298–302. [Google Scholar] [CrossRef]
- Zhang, S.; Soibel, A.; Keo, S.A.; Wilson, D.; Rafol, S.B.; Ting, D.Z.; She, A.; Gunapala, S.D.; Capasso, F. Solid-Immersion Metalenses for Infrared Focal Plane Arrays. Appl. Phys. Lett. 2018, 113, 111104. [Google Scholar] [CrossRef]
- Aieta, F.; Kats, M.A.; Genevet, P.; Capasso, F. Multiwavelength Achromatic Metasurfaces by Dispersive Phase Compensation. Science 2015, 347, 1342–1345. [Google Scholar] [CrossRef]
- Devlin, R.C.; Khorasaninejad, M.; Chen, W.T.; Oh, J.; Capasso, F. Broadband High-Efficiency Dielectric Metasurfaces for the Visible Spectrum. Proc. Natl. Acad. Sci. USA 2016, 113, 10473–10478. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Zhang, H.; Chen, S.; Bai, B.; Tan, Q.; Jin, G.; Cheah, K.-W.; Qiu, C.-W.; et al. Three-Dimensional Optical Holography Using a Plasmonic Metasurface. Nat. Commun. 2013, 4, 2808. [Google Scholar] [CrossRef]
- Ni, X.; Kildishev, A.V.; Shalaev, V.M. Metasurface Holograms for Visible Light. Nat. Commun. 2013, 4, 2807. [Google Scholar] [CrossRef]
- Wang, B.; Dong, F.; Li, Q.-T.; Yang, D.; Sun, C.; Chen, J.; Song, Z.; Xu, L.; Chu, W.; Xiao, Y.-F.; et al. Visible-Frequency Dielectric Metasurfaces for Multiwavelength Achromatic and Highly Dispersive Holograms. Nano Lett. 2016, 16, 5235–5240. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface Holograms Reaching 80% Efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Bouchard, F.; De Leon, I.; Schulz, S.A.; Upham, J.; Karimi, E.; Boyd, R.W. Optical Spin-to-Orbital Angular Momentum Conversion in Ultra-Thin Metasurfaces with Arbitrary Topological Charges. Appl. Phys. Lett. 2014, 105, 101905. [Google Scholar] [CrossRef]
- Karimi, E.; Schulz, S.A.; De Leon, I.; Qassim, H.; Upham, J.; Boyd, R.W. Generating Optical Orbital Angular Momentum at Visible Wavelengths Using a Plasmonic Metasurface. Light Sci. Appl. 2014, 3, e167. [Google Scholar] [CrossRef]
- Li, G.; Kang, M.; Chen, S.; Zhang, S.; Pun, E.Y.-B.; Cheah, K.W.; Li, J. Spin-Enabled Plasmonic Metasurfaces for Manipulating Orbital Angular Momentum of Light. Nano Lett. 2013, 13, 4148–4151. [Google Scholar] [CrossRef]
- Spektor, G.; David, A.; Gjonaj, B.; Bartal, G.; Orenstein, M. Metafocusing by a Metaspiral Plasmonic Lens. Nano Lett. 2015, 15, 5739–5743. [Google Scholar] [CrossRef]
- Devlin, R.C.; Ambrosio, A.; Rubin, N.A.; Mueller, J.P.B.; Capasso, F. Arbitrary Spin-to–Orbital Angular Momentum Conversion of Light. Science 2017, 358, 896–901. [Google Scholar] [CrossRef]
- Kang, S.; Qian, Z.; Rajaram, V.; Calisgan, S.D.; Alù, A.; Rinaldi, M. Ultra-Narrowband Metamaterial Absorbers for High Spectral Resolution Infrared Spectroscopy. Adv. Opt. Mater. 2019, 7, 1801236. [Google Scholar] [CrossRef]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared Perfect Absorber and Its Application as Plasmonic Sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
- Liu, X.; Tyler, T.; Starr, T.; Starr, A.F.; Jokerst, N.M.; Padilla, W.J. Taming the Blackbody with Infrared Metamaterials as Selective Thermal Emitters. Phys. Rev. Lett. 2011, 107, 45901. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, S.; Masuda, K.; Takagawa, Y.; Kimata, M. Polarization-Selective Uncooled Infrared Sensor with Asymmetric Two-Dimensional Plasmonic Absorber. Opt. Eng. 2014, 53, 107110. [Google Scholar] [CrossRef]
- Ogawa, S.; Okada, K.; Fukushima, N.; Kimata, M. Wavelength Selective Uncooled Infrared Sensor by Plasmonics. Appl. Phys. Lett. 2012, 100, 21111. [Google Scholar] [CrossRef]
- Ogawa, S.; Takagawa, Y.; Kimata, M. Polarization-Selective Uncooled Infrared Sensor Using a One-Dimensional Plasmonic Grating Absorber. In Proceedings of the SPIE Defense + Security, Baltimore, MD, USA, 4 June 2015; Andresen, B.F., Fulop, G.F., Hanson, C.M., Norton, P.R., Eds.; SPIE: Bellingham, WA, USA, 2015; p. 94511K. [Google Scholar]
- Tan, X.; Zhang, H.; Li, J.; Wan, H.; Guo, Q.; Zhu, H.; Liu, H.; Yi, F. Non-Dispersive Infrared Multi-Gas Sensing via Nanoantenna Integrated Narrowband Detectors. Nat. Commun. 2020, 11, 5245. [Google Scholar] [CrossRef]
- Miller, D.A.B. Why optics needs thickness. Science 2023, 379, 41–54. [Google Scholar] [CrossRef]
- Tseng, M.L.; Semmlinger, M.; Zhang, M.; Arndt, C.; Huang, T.-T.; Yang, J.; Kuo, H.Y.; Su, V.-C.; Chen, M.K.; Chu, C.H.; et al. Vacuum Ultraviolet Nonlinear Metalens. Sci. Adv. 2022, 8, eabn5644. [Google Scholar] [CrossRef]
- Li, K.; Martins, A.; Bohora, S.; Dhakal, A.; Martins, E.R.; Krauss, T.F. Hybrid Metalens for Miniaturised Ultraviolet Fluorescence Detection. Adv. Opt. Mater. 2023, 11, 2300852. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, C.; Zhang, Y.; Song, W.; Min, C.; Yuan, X. Ultraviolet Metalens for Photoacoustic Microscopy with an Elongated Depth of Focus. Opt. Lett. 2023, 48, 3435–3438. [Google Scholar] [CrossRef]
- Cheng, K.; Cui, H.; Li, Q.; Zhao, Y.; Zhou, Y. Simulation of Multiwavelength Achromatic Metalens in the Extreme Ultraviolet. Opt. Commun. 2024, 557, 130345. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Yuan, H.; Wang, Z.; Deng, Y.; Huang, C.; Wu, J.; Yang, J. Ultraviolet Metalens and Metalens Array of Focused Vortex Beams. Chin. Phys. B 2023, 32, 64206. [Google Scholar] [CrossRef]
- Shi, X.; Yang, F.; Hou, E.; Liang, Z. Integrated Deep Ultraviolet Doublet Metalens for Projection Imaging. Appl. Sci. 2024, 14, 1316. [Google Scholar] [CrossRef]
- Avayu, O.; Almeida, E.; Prior, Y.; Ellenbogen, T. Composite Functional Metasurfaces for Multispectral Achromatic Optics. Nat. Commun. 2017, 8, 14992. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhang, F.; Li, Q.; Wu, J.; Wu, L. A High-Efficiency Dual-Wavelength Achromatic Metalens Based on Pancharatnam-Berry Phase Manipulation. Opt. Express 2018, 26, 34919–34927. [Google Scholar] [CrossRef]
- Fan, Z.-B.; Qiu, H.-Y.; Zhang, H.-L.; Pang, X.-N.; Zhou, L.-D.; Liu, L.; Ren, H.; Wang, Q.-H.; Dong, J.-W. A Broadband Achromatic Metalens Array for Integral Imaging in the Visible. Light Sci. Appl. 2019, 8, 67. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Aieta, F.; Kanhaiya, P.; Kats, M.A.; Genevet, P.; Rousso, D.; Capasso, F. Achromatic Metasurface Lens at Telecommunication Wavelengths. Nano Lett. 2015, 15, 5358–5362. [Google Scholar] [CrossRef]
- Yu, C.-Y.; Chen, Y.-C.; Zeng, Q.-C.; Hsu, W.-L.; Wang, C.-M. Optical Performance of Synthetic Aperture Metalens Based on Hybrid Unit-Cells. Mater. Sci. Semicond. Process. 2024, 170, 107982. [Google Scholar] [CrossRef]
- Moon, S.; Kim, J.; Park, C.; Kim, W.; Yang, Y.; Kim, J.; Lee, S.; Choi, M.; Sung, H.; Park, J.; et al. Wafer-Scale Manufacturing of near-Infrared Metalenses. Laser Photonics Rev. 2024, 18, 2300929. [Google Scholar] [CrossRef]
- Li, R.-K.; Wei, J.-Y.; Wang, L.; Ma, Y.-G.; Li, Y.-H. Restoration of Infrared Metalens Images with Deep Learning. Opt. Commun. 2024, 552, 130069. [Google Scholar] [CrossRef]
- He, C.; Sun, T.; Guo, J.; Cao, M.; Xia, J.; Hu, J.; Yan, Y.; Wang, C. Chiral Metalens of Circular Polarization Dichroism with Helical Surface Arrays in Mid-Infrared Region. Adv. Opt. Mater. 2019, 7, 1901129. [Google Scholar] [CrossRef]
- Shalaginov, M.Y.; An, S.; Zhang, Y.; Yang, F.; Su, P.; Liberman, V.; Chou, J.B.; Roberts, C.M.; Kang, M.; Rios, C.; et al. Reconfigurable All-Dielectric Metalens with Diffraction-Limited Performance. Nat. Commun. 2021, 12, 1225. [Google Scholar] [CrossRef] [PubMed]
- Ou, K.; Yu, F.; Li, G.; Wang, W.; Miroshnichenko, A.E.; Huang, L.; Wang, P.; Li, T.; Li, Z.; Chen, X.; et al. Mid-Infrared Polarization-Controlled Broadband Achromatic Metadevice. Sci. Adv. 2020, 6, eabc0711. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Yuan, Q.; Chen, R.; Zou, X.; Zang, W.; Li, T.; Zheng, G.; Wang, S.; Wang, Z.; Zhu, S. Chromatic Dispersion Manipulation Based on Metasurface Devices in the Mid-Infrared Region. Chin. Opt. Lett. 2020, 18, 82401. [Google Scholar] [CrossRef]
- Guo, K.; Li, X.; Ai, H.; Ding, X.; Wang, L.; Wang, W.; Guo, Z. Tunable Oriented Mid-Infrared Wave Based on Metasurface with Phase Change Material of GST. Results Phys. 2022, 34, 105269. [Google Scholar] [CrossRef]
- Ou, K.; Yu, F.; Li, G.; Wang, W.; Chen, J.; Miroshnichenko, A.E.; Huang, L.; Li, T.; Li, Z.; Chen, X.; et al. Broadband Achromatic Metalens in Mid-Wavelength Infrared. Laser Photonics Rev. 2021, 15, 2100020. [Google Scholar] [CrossRef]
- Qin, X.; Sun, W.; Zhou, Z.; Fu, P.; Li, H.; Li, Y. Waveguide Effective Plasmonics with Structure Dispersion. Nanophotonics 2022, 11, 1659–1676. [Google Scholar] [CrossRef]
- Chen, J.; Wang, B.X.; Zhao, C.Y. Near-Field Radiative Heat Transport between Nanoparticles inside a Cavity Configuration. Int. J. Heat Mass Transf. 2022, 196, 123213. [Google Scholar] [CrossRef]
- Yang, F.; Song, B. Strong Suppression of Near-Field Thermal Transport between Twisted Bilayer Graphene near the Magic Angle. Mater. Today Phys. 2022, 24, 100692. [Google Scholar] [CrossRef]
- Yang, Y.; Qin, P.; Zheng, B.; Shen, L.; Wang, H.; Wang, Z.; Li, E.; Singh, R.; Chen, H. Magnetic Hyperbolic Metasurface: Concept, Design, and Applications. Adv. Sci. 2018, 5, 1801495. [Google Scholar] [CrossRef]
- Liu, W.; Hu, B.; Huang, Z.; Guan, H.; Li, H.; Wang, X.; Zhang, Y.; Yin, H.; Xiong, X.; Liu, J.; et al. Graphene-Enabled Electrically Controlled Terahertz Meta-Lens. Photonics Res. 2018, 6, 703–708. [Google Scholar] [CrossRef]
- Abbaszadeh, A.; Ahmadi-Boroujeni, M.; Tehranian, A. A Compact Polarization Insensitive All-Dielectric Metasurface Lens for Gaussian to Tophat Beam Shaping in Sub-Terahertz Regime. Opt. Commun. 2020, 462, 125313. [Google Scholar] [CrossRef]
- Chang, M.; Mu, Y.; Han, J.; Li, G.; Li, Y.; Liu, H.; Li, L.; Cui, T.J. Tailless Information–Energy Metasurface. Adv. Mater. 2024, 36, 2313697. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Chen, X.; Liu, K.; Lang, Y.; Xu, Q.; Singh, R.; Cao, T.; Tian, Z. On-Chip Non-Volatile Reconfigurable THz Varifocal Metalens. Laser Photonics Rev. 2023, 17, 2300482. [Google Scholar] [CrossRef]
- Jiang, Z.; Chao, M.; Liu, Q.; Cheng, B.; Song, G.; Liu, J. High-Efficiency Spin-Selected Multi-Foci Terahertz Metalens. Opt. Lasers Eng. 2024, 174, 107816. [Google Scholar] [CrossRef]
- Iba, A.; Ikeda, M.; Agulto, V.C.; Mag-usara, V.K.; Nakajima, M. A Study of Terahertz-Wave Cylindrical Super-Oscillatory Lens for Industrial Applications. Sensors 2021, 21, 6732. [Google Scholar] [CrossRef]
- Kohlberger, C.; Hüttner, R.; Wagner, C.; Stelzer, A. Metamaterial Lenses for Monostatic and Bistatic 77 GHz Radar Systems. Int. J. Microw. Wirel. Technol. 2023, 15, 1021–1026. [Google Scholar] [CrossRef]
- Zelenchuk, D.; Kirillov, V.; Kärnfelt, C.; Gallée, F.; Munina, I. Metamaterial-Based LTCC Compressed Luneburg Lens Antenna at 60 GHz for Wireless Communications. Electronics 2023, 12, 2354. [Google Scholar] [CrossRef]
- Wang, Z.X.; Wu, J.W.; Yang, H.Q.; Zhou, Q.Y.; Wang, S.R.; Xu, H.; Wu, L.J.; Quan, Y.; Cheng, Q.; Cui, T.J. A Hybrid Architecture for Programmable Meta-System Using a Few Active Elements. Laser Photonics Rev. 2024, 18, 2400062. [Google Scholar] [CrossRef]
- Aguilar-Garib, J.A. Editor’s Message: Microwave Imaging Advances. J. Microw. Power Electromagn. Energy 2021, 55, 1–2. [Google Scholar] [CrossRef]
- Du, Y.; Zhou, J.; He, F.; Zang, P.; Gong, H.; Liu, C.; Yang, P. A Bright Future: Advanced Nanotechnology-Assisted Microwave Therapy. Nano Today 2023, 52, 101963. [Google Scholar] [CrossRef]
- Ji, W.; Cai, T.; Xi, Z.; Urbach, P. Highly Efficient and Broadband Achromatic Transmission Metasurface to Refract and Focus in Microwave Region. Laser Photonics Rev. 2022, 16, 2100333. [Google Scholar] [CrossRef]
- Guo, Y.; Pu, M.; Ma, X.; Li, X.; Shi, R.; Luo, X. Experimental Demonstration of a Continuous Varifocal Metalens with Large Zoom Range and High Imaging Resolution. Appl. Phys. Lett. 2019, 115, 163103. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, W. Modified Metasurface Alvarez Lens Based on the Phase Compensation in a Microwave Band. Opt. Express 2022, 30, 25400–25409. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.C.; Tsai, W.-Y.; Chen, W.T.; Huang, Y.-W.; Chen, T.-Y.; Chen, J.-W.; Liao, C.Y.; Chu, C.H.; Sun, G.; Tsai, D.P. Versatile Polarization Generation with an Aluminum Plasmonic Metasurface. Nano Lett. 2017, 17, 445–452. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Zhang, Y.; Ma, L.; Zeng, X.; Li, X.; Zhan, Z.; Ren, X.; He, C.; Liu, C.; Cheng, C. Nanoscale Optical Lattices of Arbitrary Orders Manipulated by Plasmonic Metasurfaces Combining Geometrical and Dynamic Phases. Nanoscale 2019, 11, 14024–14031. [Google Scholar] [CrossRef]
- Decker, M.; Staude, I.; Falkner, M.; Dominguez, J.; Neshev, D.N.; Brener, I.; Pertsch, T.; Kivshar, Y.S. High-Efficiency Dielectric Huygens’ Surfaces. Adv. Opt. Mater. 2015, 3, 813–820. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Zhu, A.Y.; Roques-Carmes, C.; Chen, W.T.; Oh, J.; Mishra, I.; Devlin, R.C.; Capasso, F. Polarization-Insensitive Metalenses at Visible Wavelengths. Nano Lett. 2016, 16, 7229–7234. [Google Scholar] [CrossRef]
- Kamali, S.M.; Arbabi, A.; Arbabi, E.; Horie, Y.; Faraon, A. Decoupling Optical Function and Geometrical Form Using Conformal Flexible Dielectric Metasurfaces. Nat. Commun. 2016, 7, 11618. [Google Scholar] [CrossRef] [PubMed]
- Bomzon, Z.; Biener, G.; Kleiner, V.; Hasman, E. Space-Variant Pancharatnam–Berry Phase Optical Elements with Computer-Generated Subwavelength Gratings. Opt. Lett. 2002, 27, 1141–1143. [Google Scholar] [CrossRef] [PubMed]
- Ebbesen, T.W.; Lezec, H.J.; Ghaemi, H.F.; Thio, T.; Wolff, P.A. Extraordinary Optical Transmission through Sub-Wavelength Hole Arrays. Nature 1998, 391, 667–669. [Google Scholar] [CrossRef]
- Fang, N.; Lee, H.; Sun, C.; Zhang, X. Sub-Diffraction-Limited Optical Imaging with a Silver Superlens. Science 2005, 308, 534–537. [Google Scholar] [CrossRef]
- Verslegers, L.; Catrysse, P.B.; Yu, Z.; Fan, S. Planar Metallic Nanoscale Slit Lenses for Angle Compensation. Appl. Phys. Lett. 2009, 95, 71112. [Google Scholar] [CrossRef]
- Wang, C.; Gao, P.; Zhao, Z.; Yao, N.; Wang, Y.; Liu, L.; Liu, K.; Luo, X. Deep Sub-Wavelength Imaging Lithography by a Reflective Plasmonic Slab. Opt. Express 2013, 21, 20683–20691. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, C.; Hu, X. A Spiral Plasmonic Lens with Directional Excitation of Surface Plasmons. Sci. Rep. 2016, 6, 32345. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, X.; Xu, Y.; Li, Q.; Li, Y.; Ouyang, C.; Tian, Z.; Gu, J.; Zhang, W.; Zhang, X.; et al. Plasmonic Metalens Based on Coupled Resonators for Focusing of Surface Plasmons. Sci. Rep. 2016, 6, 37861. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-Q.; Chen, W.; Du, X.; Shu, Y.; Wu, L.; Ren, Z.; Yin, H.; Sun, J.; Qi, K.; Che, Y.; et al. An Ultra-Thin High-Efficiency Plasmonic Metalens with Symmetric Split Ring Transmitarray Metasurfaces. Results Phys. 2023, 47, 106366. [Google Scholar] [CrossRef]
- Liang, H.; Lin, Q.; Xie, X.; Sun, Q.; Wang, Y.; Zhou, L.; Liu, L.; Yu, X.; Zhou, J.; Krauss, T.F.; et al. Ultrahigh Numerical Aperture Metalens at Visible Wavelengths. Nano Lett. 2018, 18, 4460–4466. [Google Scholar] [CrossRef]
- Gao, S.; Park, C.; Lee, S.; Choi, D. A Highly Efficient Bifunctional Dielectric Metasurface Enabling Polarization-Tuned Focusing and Deflection for Visible Light. Adv. Opt. Mater. 2019, 7, 1801337. [Google Scholar] [CrossRef]
- Leitis, A.; Heßler, A.; Wahl, S.; Wuttig, M.; Taubner, T.; Tittl, A.; Altug, H. All-Dielectric Programmable Huygens’ Metasurfaces. Adv. Funct. Mater. 2020, 30, 1910259. [Google Scholar] [CrossRef]
- Groever, B.; Rubin, N.A.; Mueller, J.P.B.; Devlin, R.C.; Capasso, F. High-Efficiency Chiral Meta-Lens. Sci. Rep. 2018, 8, 7240. [Google Scholar] [CrossRef] [PubMed]
- Yao, B.; Zang, X.; Zhu, Y.; Yu, D.; Xie, J.; Chen, L.; Han, S.; Zhu, Y.; Zhuang, S. Spin-Decoupled Metalens with Intensity-Tunable Multiple Focal Points. Photonics Res. 2021, 9, 1019–1032. [Google Scholar] [CrossRef]
- Fu, R.; Li, Z.; Zheng, G.; Chen, M.; Yang, Y.; Tao, J.; Wu, L.; Deng, Q. Reconfigurable Step-Zoom Metalens without Optical and Mechanical Compensations. Opt. Express 2019, 27, 12221–12230. [Google Scholar] [CrossRef]
- Shen, Z.; Zhou, S.; Li, X.; Ge, S.; Chen, P.; Hu, W.; Lu, Y. Liquid Crystal Integrated Metalens with Tunable Chromatic Aberration. Adv. Photonics 2020, 2, 36002. [Google Scholar] [CrossRef]
- Fan, C.-Y.; Chuang, T.-J.; Wu, K.-H.; Su, G.-D.J. Electrically Modulated Varifocal Metalens Combined with Twisted Nematic Liquid Crystals. Opt. Express 2020, 28, 10609–10617. [Google Scholar] [CrossRef]
- Zhang, Z.; Qi, X.; Zhang, J.; Guo, C.; Zhu, Z.; Hong, Z. Graphene-enabled electrically tuunability of metalens in the terahertz range. Opt. Express 2020, 28, 28101–28112. [Google Scholar] [CrossRef]
- Ullah, N.; Liu, W.; Wang, G.; Wang, Z.; Khalid, A.U.R.; Hu, B.; Liu, J.; Zhang, Y. Gate-Controlled Terahertz Focusing Based on Graphene-Loaded Metasurface. Opt. Express 2020, 28, 2789–2798. [Google Scholar] [CrossRef]
- Ullah, N.; Hu, B.; Khalid, A.U.R.; Guan, H.; Khan, M.I.; Liu, J. Efficient Tuning of Linearly Polarized Terahertz Focus by Graphene-Integrated Metasurface. J. Phys. D Appl. Phys. 2020, 53, 205103. [Google Scholar] [CrossRef]
- Ee, H.-S.; Agarwal, R. Tunable Metasurface and Flat Optical Zoom Lens on a Stretchable Substrate. Nano Lett. 2016, 16, 2818–2823. [Google Scholar] [CrossRef]
- Wei, S.; Cao, G.; Lin, H.; Yuan, X.; Somekh, M.; Jia, B. A Varifocal Graphene Metalens for Broadband Zoom Imaging Covering the Entire Visible Region. ACS Nano 2021, 15, 4769–4776. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Y.; Feng, X.; Xiao, S.; Wang, Z.; Hu, T.; Hu, M.; Song, J.; Wegener, M.; Zhao, M.; et al. Compact Optical Polarization-Insensitive Zoom Metalens Doublet. Adv. Opt. Mater. 2020, 8, 2000142. [Google Scholar] [CrossRef]
- Yilmaz, N.; Ozdemir, A.; Ozer, A.; Kurt, H. Rotationally Tunable Polarization-Insensitive Single and Multifocal Metasurface. J. Opt. 2019, 21, 45105. [Google Scholar] [CrossRef]
- Cui, Y.; Zheng, G.; Chen, M.; Zhang, Y.; Yang, Y.; Tao, J.; He, T.; Li, Z. Reconfigurable Continuous-Zoom Metalens in Visible Band. Chin. Opt. Lett. 2019, 17, 111603. [Google Scholar] [CrossRef]
- Iwami, K.; Ogawa, C.; Nagase, T.; Ikezawa, S. Demonstration of Focal Length Tuning by Rotational Varifocal Moiré Metalens in an Ir-A Wavelength. Opt. Express 2020, 28, 35602–35614. [Google Scholar] [CrossRef] [PubMed]
- Colburn, S.; Zhan, A.; Majumdar, A. Varifocal Zoom Imaging with Large Area Focal Length Adjustable Metalenses. Optica 2018, 5, 825–831. [Google Scholar] [CrossRef]
- Colburn, S.; Majumdar, A. Simultaneous Achromatic and Varifocal Imaging with Quartic Metasurfaces in the Visible. ACS Photonics 2020, 7, 120–127. [Google Scholar] [CrossRef]
- Arbabi, E.; Arbabi, A.; Kamali, S.M.; Horie, Y.; Faraji-Dana, M.; Faraon, A. MEMS-Tunable Dielectric Metasurface Lens. Nat. Commun. 2018, 9, 812. [Google Scholar] [CrossRef]
- Roy, T.; Zhang, S.; Jung, I.W.; Troccoli, M.; Capasso, F.; Lopez, D. Dynamic Metasurface Lens Based on MEMS Technology. APL Photonics 2018, 3, 21302. [Google Scholar] [CrossRef]
- Han, Z.; Colburn, S.; Majumdar, A.; Böhringer, K.F. MEMS-Actuated Metasurface Alvarez Lens. Microsyst. Nanoeng. 2020, 6, 79. [Google Scholar] [CrossRef] [PubMed]
- Meng, C.; Thrane, P.C.V.; Ding, F.; Gjessing, J.; Thomaschewski, M.; Wu, C.; Dirdal, C.; Bozhevolnyi, S.I. Dynamic Piezoelectric MEMS-Based Optical Metasurfaces. Sci. Adv. 2021, 7, eabg5639. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Ma, X.; Pu, M.; Li, X.; Zhao, Z.; Luo, X. High-Efficiency and Wide-Angle Beam Steering Based on Catenary Optical Fields in Ultrathin Metalens. Adv. Opt. Mater. 2018, 6, 1800592. [Google Scholar] [CrossRef]
- Arbabi, A.; Briggs, R.M.; Horie, Y.; Bagheri, M.; Faraon, A. Efficient Dielectric Metasurface Collimating Lenses for Mid-Infrared Quantum Cascade Lasers. Opt. Express 2015, 23, 33310–33317. [Google Scholar] [CrossRef]
- Aieta, F.; Genevet, P.; Kats, M.; Capasso, F. Aberrations of Flat Lenses and Aplanatic Metasurfaces. Opt. Express 2013, 21, 31530–31539. [Google Scholar] [CrossRef]
- Pu, M.; Li, X.; Guo, Y.; Ma, X.; Luo, X. Nanoapertures with Ordered Rotations: Symmetry Transformation and Wide-Angle Flat Lensing. Opt. Express 2017, 25, 31471–31477. [Google Scholar] [CrossRef]
- Fan, C.-Y.; Lin, C.-P.; Su, G.-D.J. Ultrawide-Angle and High-Efficiency Metalens in Hexagonal Arrangement. Sci. Rep. 2020, 10, 15677. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Pu, M.; Li, X.; Ma, X.; Guo, Y.; Gao, P.; Yu, H.; Gu, M.; Luo, X. Extreme-Angle Silicon Infrared Optics Enabled by Streamlined Surfaces. Adv. Mater. 2021, 33, 2008157. [Google Scholar] [CrossRef]
- Engelberg, J.; Zhou, C.; Mazurski, N.; Bar-David, J.; Kristensen, A.; Levy, U. Near-IR Wide-Field-of-View Huygens Metalens for Outdoor Imaging Applications. Nanophotonics 2020, 9, 361–370. [Google Scholar] [CrossRef]
- Chen, J.; Ye, X.; Gao, S.; Chen, Y.; Zhao, Y.; Huang, C.; Qiu, K.; Zhu, S.; Li, T. Planar Wide-Angle-Imaging Camera Enabled by Metalens Array. Optica 2022, 9, 431–437. [Google Scholar] [CrossRef]
- Lee, G.-Y.; Hong, J.-Y.; Hwang, S.; Moon, S.; Kang, H.; Jeon, S.; Kim, H.; Jeong, J.-H.; Lee, B. Metasurface Eyepiece for Augmented Reality. Nat. Commun. 2018, 9, 4562. [Google Scholar] [CrossRef]
- Wang, P.; Mohammad, N.; Menon, R. Chromatic-Aberration-Corrected Diffractive Lenses for Ultra-Broadband Focusing. Sci. Rep. 2016, 6, 21545. [Google Scholar] [CrossRef]
- Zhao, Z.; Pu, M.; Gao, H.; Jin, J.; Li, X.; Ma, X.; Wang, Y.; Gao, P.; Luo, X. Multispectral Optical Metasurfaces Enabled by Achromatic Phase Transition. Sci. Rep. 2015, 5, 15781. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Liu, C.-H.; Ren, X.; Lauhon, L.J.; Odom, T.W. Plasmonic Lattice Lenses for Multiwavelength Achromatic Focusing. ACS Nano 2016, 10, 10275–10282. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.-L.; Zhang, S.; Wang, G.P. Wide-Angled off-Axis Achromatic Metasurfaces for Visible Light. Opt. Express 2016, 24, 23118–23128. [Google Scholar] [CrossRef]
- Arbabi, E.; Arbabi, A.; Kamali, S.M.; Horie, Y.; Faraon, A. Multiwavelength Metasurfaces through Spatial Multiplexing. Sci. Rep. 2016, 6, 32803. [Google Scholar] [CrossRef] [PubMed]
- Balli, F.; Sultan, M.A.; Ozdemir, A.; Hastings, J.T. An Ultrabroadband 3D Achromatic Metalens. Nanophotonics 2021, 10, 1259–1264. [Google Scholar] [CrossRef]
- Lu, H.; Chen, J.; Yan, K.; Jin, Q.; Xue, Y.; Gao, Z. A Hybrid Feature Selection Algorithm for Gene Expression Data Classification. Neurocomputing 2017, 256, 56–62. [Google Scholar] [CrossRef]
- Zhang, X.-M.; Han, Q.-L.; Wang, Z.; Zhang, B.-L. Neuronal State Estimation for Neural Networks with Two Additive Time-Varying Delay Components. IEEE Trans. Cybern. 2017, 47, 3184–3194. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, K.; Luo, M.; Yin, C.; Lai, X. Extreme Learning Machine and Adaptive Sparse Representation for Image Classification. Neural Netw. 2016, 81, 91–102. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Luo, M. Outlier-Robust Extreme Learning Machine for Regression Problems. Neurocomputing 2015, 151, 1519–1527. [Google Scholar] [CrossRef]
- Hu, L.; Wen, H.; Wu, B.; Pan, F.; Liao, R.-F.; Song, H.; Tang, J.; Wang, X. Cooperative Jamming for Physical Layer Security Enhancement in Internet of Things. IEEE Internet Things J. 2018, 5, 219–228. [Google Scholar] [CrossRef]
- Liu, H.-C.; Quan, M.-Y.; Li, Z.; Wang, Z.-L. A New Integrated MCDM Model for Sustainable Supplier Selection under Interval-Valued Intuitionistic Uncertain Linguistic Environment. Inf. Sci. 2019, 486, 254–270. [Google Scholar] [CrossRef]
- Yan, K.; Ji, Z.; Shen, W. Online Fault Detection Methods for Chillers Combining Extended Kalman Filter and Recursive One-Class SVM. Neurocomputing 2017, 228, 205–212. [Google Scholar] [CrossRef]
- Jiang, S.; Shi, H.; Lin, W.; Liu, H.-C. A Large Group Linguistic Z-DEMATEL Approach for Identifying Key Performance Indicators in Hospital Performance Management. Appl. Soft Comput. 2020, 86, 105900. [Google Scholar] [CrossRef]
- Xiang, R.; Jiang, H.; Ying, Y. Recognition of Clustered Tomatoes Based on Binocular Stereo Vision. Comput. Electron. Agric. 2014, 106, 75–90. [Google Scholar] [CrossRef]
- Zhang, X.-M.; Han, Q.-L.; Ge, X.; Zhang, B.-L. Passivity Analysis of Delayed Neural Networks Based on Lyapunov–Krasovskii Functionals with Delay-Dependent Matrices. IEEE Trans. Cybern. 2020, 50, 946–956. [Google Scholar] [CrossRef]
- Wang, X.; Yan, W.Q. Human Gait Recognition Based on Frame-by-Frame Gait Energy Images and Convolutional Long Short-Term Memory. Int. J. Neural Syst. 2020, 30, 1950027. [Google Scholar] [CrossRef]
- Chang, Y.-W.; Hsu, P.-Y.; Yang, Q.-M. Integration of Online and Offline Channels: A View of O2O Commerce. Internet Res. 2018, 28, 926–945. [Google Scholar] [CrossRef]
- Cao, F.; Ye, H.; Wang, D. A Probabilistic Learning Algorithm for Robust Modeling Using Neural Networks with Random Weights. Inf. Sci. 2015, 313, 62–78. [Google Scholar] [CrossRef]
- Che Sidik, N.A.; Mohd Rosdzimin, A.R. Simulation of Natural Convection Heat Transfer in an Enclosure Using Lattice Boltzmann Method. J. Mek. 2008, 27, 42–50. [Google Scholar]
- Yang, Y.; Xu, X. A Differential Game Model for Closed-Loop Supply Chain Participants under Carbon Emission Permits. Comput. Ind. Eng. 2019, 135, 1077–1090. [Google Scholar] [CrossRef]
- Lu, H.; Yang, L.; Yan, K.; Xue, Y.; Gao, Z. A Cost-Sensitive Rotation Forest Algorithm for Gene Expression Data Classification. Neurocomputing 2017, 228, 270–276. [Google Scholar] [CrossRef]
- Ding, X.-F.; Liu, H.-C.; Shi, H. A Dynamic Approach for Emergency Decision Making Based on Prospect Theory with Interval-Valued Pythagorean Fuzzy Linguistic Variables. Comput. Ind. Eng. 2019, 131, 57–65. [Google Scholar] [CrossRef]
- Li, C.; Li, J.; Li, Y.; He, L.; Fu, X.; Chen, J. Fabric Defect Detection in Textile Manufacturing: A Survey of the State of the Art. Secur. Commun. Netw. 2021, 2021, 9948808. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Leung, J.Y.-T. Worker Assignment and Production Planning with Learning and Forgetting in Manufacturing Cells by Hybrid Bacteria Foraging Algorithm. Comput. Ind. Eng. 2016, 96, 162–179. [Google Scholar] [CrossRef]
- Lu, H.; Du, B.; Liu, J.; Xia, H.; Yeap, W.K. A Kernel Extreme Learning Machine Algorithm Based on Improved Particle Swam Optimization. Memetic Comput. 2017, 9, 121–128. [Google Scholar] [CrossRef]
- Cao, F.; Chen, J.; Ye, H.; Zhao, J.; Zhou, Z. Recovering Low-Rank and Sparse Matrix Based on the Truncated Nuclear Norm. Neural Netw. 2017, 85, 10–20. [Google Scholar] [CrossRef] [PubMed]
- Yao, K.; Liang, J.; Liang, J.; Li, M.; Cao, F. Multi-View Graph Convolutional Networks with Attention Mechanism. Artif. Intell. 2022, 307, 103708. [Google Scholar] [CrossRef]
- Gao, C.; Ye, H.; Cao, F.; Wen, C.; Zhang, Q.; Zhang, F. Multiscale Fused Network with Additive Channel–Spatial Attention for Image Segmentation. Knowl.-Based Syst. 2021, 214, 106754. [Google Scholar] [CrossRef]
- Lu, H.-J.; An, C.-L.; Zheng, E.-H.; Lu, Y. Dissimilarity Based Ensemble of Extreme Learning Machine for Gene Expression Data Classification. Neurocomputing 2014, 128, 22–30. [Google Scholar] [CrossRef]
- Hu, M.; Feng, X.; Ji, Z.; Yan, K.; Zhou, S. A Novel Computational Approach for Discord Search with Local Recurrence Rates in Multivariate Time Series. Inf. Sci. 2019, 477, 220–233. [Google Scholar] [CrossRef]
- Xiong, J.-J.; Zhang, G.-B.; Wang, J.-X.; Yan, T.-H. Improved Sliding Mode Control for Finite-Time Synchronization of Nonidentical Delayed Recurrent Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 2209–2216. [Google Scholar] [CrossRef]
- Liu, H.; Cao, F.; Wen, C.; Zhang, Q. Lightweight Multi-Scale Residual Networks with Attention for Image Super-Resolution. Knowl.-Based Syst. 2020, 203, 106103. [Google Scholar] [CrossRef]
- Li, X.; Zhu, C.; Xu, C.; Zhu, J.; Li, Y.; Wu, S. VR Motion Sickness Recognition by Using EEG Rhythm Energy Ratio Based on Wavelet Packet Transform. Comput. Methods Programs Biomed. 2020, 188, 105266. [Google Scholar] [CrossRef]
- Du, Z.; Ye, H.; Cao, F. A Novel Local–Global Graph Convolutional Method for Point Cloud Semantic Segmentation. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 4798–4812. [Google Scholar] [CrossRef]
- Zhu, W.; Peng, B. Sparse and Low-Rank Regularized Deep Subspace Clustering. Knowl.-Based Syst. 2020, 204, 106199. [Google Scholar] [CrossRef]
- Luo, M.; Zhang, K. Robustness of Full Implication Algorithms Based on Interval-Valued Fuzzy Inference. Int. J. Approx. Reason. 2015, 62, 61–72. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Leung, J.Y.-T. Integrated Bacteria Foraging Algorithm for Cellular Manufacturing in Supply Chain Considering Facility Transfer and Production Planning. Appl. Soft Comput. 2018, 62, 602–618. [Google Scholar] [CrossRef]
- Chang, Y.-W.; Hsu, P.-Y.; Shiau, W.-L.; Tsai, C.-C. Knowledge Sharing Intention in the United States and China: A Cross-Cultural Study. Eur. J. Inf. Syst. 2015, 24, 262–277. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.; Yan, K. Gait Recognition Based on Gabor Wavelets and (2D)~2PCA. Multimed. Tools Appl. 2018, 77, 12545–12561. [Google Scholar] [CrossRef]
- Lu, J.; Zhao, J.; Cao, F. Extended Feed Forward Neural Networks with Random Weights for Face Recognition. Neurocomputing 2014, 136, 96–102. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, S.; He, B.; Sha, Q.; Shen, Y.; Yan, T.; Nian, R.; Lendasse, A. Gaussian Derivative Models and Ensemble Extreme Learning Machine for Texture Image Classification. Neurocomputing 2018, 277, 53–64. [Google Scholar] [CrossRef]
- Cao, F.; Wang, D.; Zhu, H.; Wang, Y. An Iterative Learning Algorithm for Feedforward Neural Networks with Random Weights. Inf. Sci. Int. J. 2016, 328, 546–557. [Google Scholar] [CrossRef]
- Shi, H.; Wang, L.; Li, X.-Y.; Liu, H.-C. A Novel Method for Failure Mode and Effects Analysis Using Fuzzy Evidential Reasoning and Fuzzy Petri Nets. J. Ambient Intell. Hum. Comput. 2020, 11, 2381–2395. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Yang, L.; Mi, H. Unsupervised Learning for Community Detection in Attributed Networks Based on Graph Convolutional Network. Neurocomputing 2021, 456, 147–155. [Google Scholar] [CrossRef]
- Cao, F.; Cai, M.; Tan, Y.; Zhao, J. Image Super-Resolution via Adaptive Regularization and Sparse Representation. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1550–1561. [Google Scholar] [CrossRef]
- Li, J.; Hao, J.; Sun, X.; Feng, Q. Forecasting China’s Sovereign CDS with a Decomposition Reconstruction Strategy. Appl. Soft Comput. 2021, 105, 107291. [Google Scholar] [CrossRef]
- Cao, F.; Guo, W. Deep Hybrid Dilated Residual Networks for Hyperspectral Image Classification. Neurocomputing 2020, 384, 170–181. [Google Scholar] [CrossRef]
- Li, D.; Luo, Z.; Cao, B. Blockchain-Based Federated Learning Methodologies in Smart Environments. Cluster Comput. 2022, 25, 2585–2599. [Google Scholar] [CrossRef]
- Cao, F.; Yao, K.; Liang, J. Deconvolutional Neural Network for Image Super-Resolution. Neural Netw. 2020, 132, 394–404. [Google Scholar] [CrossRef]
- Cao, H.; Cao, F.; Wang, D. Quantum Artificial Neural Networks with Applications. Inf. Sci. 2015, 290, 1–6. [Google Scholar] [CrossRef]
- Wang, J.; Liu, C.; Zhou, M. Improved Bacterial Foraging Algorithm for Cell Formation and Product Scheduling Considering Learning and Forgetting Factors in Cellular Manufacturing Systems. IEEE Syst. J. 2020, 14, 3047–3056. [Google Scholar] [CrossRef]
- Zhao, J.; Hu, H.; Cao, F. Image Super-Resolution via Adaptive Sparse Representation. Knowl.-Based Syst. 2017, 124, 23–33. [Google Scholar] [CrossRef]
- Xiang, R. Image Segmentation for Whole Tomato Plant Recognition at Night. Comput. Electron. Agric. 2018, 154, 434–442. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, L.; Liu, H. Emergency Decision Making with Extended Axiomatic Design Approach under Picture Fuzzy Environment. Expert Syst. 2020, 37, e12482. [Google Scholar] [CrossRef]
- Ding, X.-F.; Liu, H.-C. An Extended Prospect Theory–VIKOR Approach for Emergency Decision Making with 2-Dimension Uncertain Linguistic Information. Soft Comput. 2019, 23, 12139–12150. [Google Scholar] [CrossRef]
- Peng, X.; Xu, D.; Shen, J. A Twin Projection Support Vector Machine for Data Regression. Neurocomputing 2014, 138, 131–141. [Google Scholar] [CrossRef]
- Liu, Z.; Jia, X.; Xu, X. Study of Shrimp Recognition Methods Using Smart Networks. Comput. Electron. Agric. 2019, 165, 104926. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Q.; Yan, K.; Du, Y. Deep Learning Enhanced Solar Energy Forecasting with AI-Driven IoT. Wireless Commun. Mobile Comput. 2021, 2021, 9249387. [Google Scholar] [CrossRef]
- Cao, F.; Guo, W. Cascaded Dual-Scale Crossover Network for Hyperspectral Image Classification. Knowl.-Based Syst. 2020, 189, 105122. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Y.; Wang, B.; Wang, Z. Design and Analysis of Associative Memories Based on External Inputs of Delayed Recurrent Neural Networks. Neurocomputing 2014, 136, 337–344. [Google Scholar] [CrossRef]
- Liang, W.; Zhou, X.; Huang, S.; Hu, C.; Xu, X.; Jin, Q. Modeling of Cross-Disciplinary Collaboration for Potential Field Discovery and Recommendation Based on Scholarly Big Data. Future Gener. Comput. Syst. 2018, 87, 591–600. [Google Scholar] [CrossRef]
- Li, X.-Y.; Xiong, Y.; Duan, C.-Y.; Liu, H.-C. Failure Mode and Effect Analysis Using Interval Type-2 Fuzzy Sets and Fuzzy Petri Nets. J. Intell. Fuzzy Syst. 2019, 37, 693–709. [Google Scholar] [CrossRef]
- Lu, H.; Gao, H.; Ye, M.; Wang, X. A Hybrid Ensemble Algorithm Combining AdaBoost and Genetic Algorithm for Cancer Classification with Gene Expression Data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 18, 863–870. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, F.; Zhao, J.; Chu, J. Segmentation of White Blood Cells Image Using Adaptive Location and Iteration. IEEE J. Biomed. Health Inform. 2017, 21, 1644–1655. [Google Scholar] [CrossRef]
- Chen, Z.; Cao, F. Scattered Data Approximation by Neural Networks Operators. Neurocomputing 2016, 190, 237–242. [Google Scholar] [CrossRef]
- Luo, M.; Zhou, X. Robustness of Reverse Triple I Algorithms Based on Interval-Valued Fuzzy Inference. Int. J. Approx. Reason. 2015, 66, 16–26. [Google Scholar] [CrossRef]
- Cao, F.; Chen, B. New Architecture of Deep Recursive Convolution Networks for Super-Resolution. Knowl.-Based Syst. 2019, 178, 98–110. [Google Scholar] [CrossRef]
- Lu, H.; Xu, Y.; Ye, M.; Yan, K.; Gao, Z.; Jin, Q. Learning Misclassification Costs for Imbalanced Classification on Gene Expression Data. BMC Bioinform. 2019, 20, 681. [Google Scholar] [CrossRef]
- Cao, F.; Hu, H.; Lu, J.; Zhao, J.; Zhou, Z.; Wu, J. Pose and Illumination Variable Face Recognition via Sparse Representation and Illumination Dictionary. Knowl.-Based Syst. 2016, 107, 117–128. [Google Scholar] [CrossRef]
- Gu, P.; Han, Y.; Gao, W.; Xu, G.; Wu, J. Enhancing Session-Based Social Recommendation through Item Graph Embedding and Contextual Friendship Modeling. Neurocomputing 2021, 419, 190–202. [Google Scholar] [CrossRef]
- Cao, F.; Liu, Y.; Wang, D. Efficient Saliency Detection Using Convolutional Neural Networks with Feature Selection. Inf. Sci. 2018, 456, 34–49. [Google Scholar] [CrossRef]
- Hou, L.-X.; Mao, L.-X.; Liu, H.-C.; Zhang, L. Decades on Emergency Decision-Making: A Bibliometric Analysis and Literature Review. Complex Intell. Syst. 2021, 7, 2819–2832. [Google Scholar] [CrossRef]
- Zhao, J.; Lv, Y.; Zhou, Z.; Cao, F. A Novel Deep Learning Algorithm for Incomplete Face Recognition: Low-Rank-Recovery Network. Neural Netw. 2017, 94, 115–124. [Google Scholar] [CrossRef]
- Han, H.; Fang, L.; Lu, W.; Zhai, W.; Li, Y.; Zhao, J. A GCICA Grant-Free Random Access Scheme for M2M Communications in Crowded Massive MIMO Systems. IEEE Internet Things J. 2022, 9, 6032–6046. [Google Scholar] [CrossRef]
- Cao, F.; Liu, H. Single Image Super-Resolution via Multi-Scale Residual Channel Attention Network. Neurocomputing 2019, 358, 424–436. [Google Scholar] [CrossRef]
- Karumanchi, S.; Mancini, S.; Winter, A.; Yang, D. Quantum Channel Capacities with Passive Environment Assistance. IEEE Trans. Inf. Theory 2016, 62, 1733–1747. [Google Scholar] [CrossRef]
- Jiang, X.W.; Yan, T.H.; Zhu, J.J.; He, B.; Li, W.H.; Du, H.P.; Sun, S.S. Densely Connected Deep Extreme Learning Machine Algorithm. Cognit. Comput. 2020, 12, 979–990. [Google Scholar] [CrossRef]
- Chen, J.; Cai, H.; Wang, W. A New Metaheuristic Algorithm: Car Tracking Optimization Algorithm. Soft Comput. 2018, 22, 3857–3878. [Google Scholar] [CrossRef]
- Winter, A.; Yang, D. Potential Capacities of Quantum Channels. IEEE Trans. Inf. Theory 2016, 62, 1415–1424. [Google Scholar] [CrossRef]
- Li, W.; Jiang, S.; Jin, Q. Overlap Community Detection Using Spectral Algorithm Based on Node Convergence Degree. Future Gener. Comput. Syst. 2018, 79, 408–416. [Google Scholar] [CrossRef]
- Lu, H.; Meng, Y.; Yan, K.; Gao, Z. Kernel Principal Component Analysis Combining Rotation Forest Method for Linearly Inseparable Data. Cognit. Syst. Res. 2019, 53, 111–122. [Google Scholar] [CrossRef]
- Mao, L.-X.; Lan, J.; Chen, A.; Shi, H.; Liu, H.-C. New Approach for Quality Function Deployment Based on Linguistic Distribution Assessments and CRITIC Method. Mathematics 2025, 13, 240. [Google Scholar] [CrossRef]
- Zou, H. Clustering Algorithm and Its Application in Data Mining. Wireless Pers. Commun. 2020, 110, 21–30. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J. Cell Formation and Task Scheduling Considering Multi-Functional Resource and Part Movement Using Hybrid Simulated Annealing. Int. J. Comput. Intell. Syst. 2016, 9, 765–777. [Google Scholar] [CrossRef]
- Kong, D.; Zhu, J.; Wu, S.; Duan, C.; Lu, L.; Chen, D. A Novel IRBF-RVM Model for Diagnosis of Atrial Fibrillation. Comput. Methods Programs Biomed. 2019, 177, 183–192. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Wang, Z.; Cao, F.; Wang, D. A Local Learning Algorithm for Random Weights Networks. Knowl.-Based Syst. 2015, 74, 159–166. [Google Scholar] [CrossRef]
- Yang, B.; Xiang, X.; Xu, D.; Wang, X.; Yang, X. 3D Palmprint Recognition Using Shape Index Representation and Fragile Bits. Multimed. Tools Appl. 2017, 76, 15357–15375. [Google Scholar] [CrossRef]
- Wang, H. On Extended Progressive and Iterative Approximation for Least Squares Fitting. Visual Comput. 2022, 38, 591–602. [Google Scholar] [CrossRef]
- Luo, M.; Zhou, X. Interval-Valued Quintuple Implication Principle of Fuzzy Reasoning. Int. J. Approx. Reason. 2017, 84, 23–32. [Google Scholar] [CrossRef]
- Zhao, R.; Luo, M.; Li, S. A Dynamic Distance Measure of Picture Fuzzy Sets and Its Application. Symmetry 2021, 13, 436. [Google Scholar] [CrossRef]
- Han, H.; Zhao, J.; Zhai, W.; Xiong, Z.; Niyato, D.; Di Renzo, M.; Pham, Q.-V.; Lu, W.; Lam, K.-Y. Reconfigurable Intelligent Surface Aided Power Control for Physical-Layer Broadcasting. IEEE Trans. Commun. 2021, 69, 7821–7836. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, Q.; Cui, X.; Guo, H.; Wang, K.; Zhu, D. High-Throughput Corn Ear Screening Method Based on Two-Pathway Convolutional Neural Network. Comput. Electron. Agric. 2020, 175, 105525. [Google Scholar] [CrossRef]
- Xu, X.-G.; Xiong, Y.; Xu, D.-H.; Liu, H.-C. Bipolar Fuzzy Petri Nets for Knowledge Representation and Acquisition Considering Non-Cooperative Behaviors. Int. J. Mach. Learn. Cybern. 2020, 11, 2297–2311. [Google Scholar] [CrossRef]
- Li, Y.; Zuo, Z.; Pan, J. Sensor-Based Fall Detection Using a Combination Model of a Temporal Convolutional Network and a Gated Recurrent Unit. Future Gener. Comput. Syst. 2023, 139, 53–63. [Google Scholar] [CrossRef]
- An, S.; Fowler, C.; Zheng, B.; Shalaginov, M.Y.; Tang, H.; Li, H.; Zhou, L.; Ding, J.; Agarwal, A.M.; Rivero-Baleine, C.; et al. A Deep Learning Approach for Objective-Driven All-Dielectric Metasurface Design. ACS Photonics 2019, 6, 3196–3207. [Google Scholar] [CrossRef]
- An, S.; Zheng, B.; Shalaginov, M.Y.; Tang, H.; Li, H.; Zhou, L.; Ding, J.; Agarwal, A.M.; Rivero-Baleine, C.; Kang, M.; et al. Deep Learning Modeling Approach for Metasurfaces with High Degrees of Freedom. Opt. Express 2020, 28, 31932–31942. [Google Scholar] [CrossRef]
- Liu, S.; Cao, W.; Jiang, S.; He, L.; Lin, F.; He, X. 3D Dirac Semimetal Supported Tunable Multi-Frequency Terahertz Metamaterial Absorbers. Adv. Quantum Technol. 2024, 7, 2300386. [Google Scholar] [CrossRef]
- Shi, J.; Yang, C.; Chen, Y.; Wang, T.; Yu, H.; Cao, J.; Geng, Z.; Wang, Z.; Wen, H.; Tan, H.; et al. Precise Mode Control of Mid-Infrared High-Power Laser Diodes Using on-Chip Advanced Sawtooth Waveguide Designs. High Power Laser Sci. Eng. 2024, 12, e42. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Zhang, G. Nanophononic Metamaterials Induced Proximity Effect in Heat Flux Regulation. Front. Phys. 2024, 19, 23204. [Google Scholar] [CrossRef]
- Hou, T.; Ge, Y.; Xue, S.; Chen, H. Curved Anisotropic Polaritons. Front. Phys. 2024, 19, 32201. [Google Scholar] [CrossRef]
- Seo, J.; Jo, J.; Kim, J.; Kang, J.; Kang, C.; Moon, S.-W.; Lee, E.; Hong, J.; Rho, J.; Chung, H. Deep-Learning-Driven End-to-End Metalens Imaging. Adv. Photonics 2024, 6, 66002. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, Q.; Shen, B.; Tao, Y.; Zhang, X.; Tao, Z.; Xing, L.; Ge, Z.; Li, T.; Bai, B.; et al. Multifunctional Mixed Analog/Digital Signal Processor Based on Integrated Photonics. Opto-Electron. Sci. 2024, 3, 240012. [Google Scholar] [CrossRef]
- Zhang, X.G.; Hu, Q.C.; Li, Q.Y.; Huang, Z.; Xu, L.; Quan, Y.; Zhu, Q.; Wang, B.Y.; Chen, X.X.; Cui, T.J.; et al. Anisotropic Programmable Metasurfaces with Individually Controllable 2-Bit Elements. Photonics Res. 2024, 12, 2660–2666. [Google Scholar] [CrossRef]
- Yu, Z.; Li, M.; Xing, Z.; Gao, H.; Liu, Z.; Pu, S.; Mao, H.; Cai, H.; Ma, Q.; Ren, W.; et al. Genetic Algorithm Assisted Meta-Atom Design for High-Performance Metasurface Optics. Opto-Electron. Sci. 2024, 3, 240016. [Google Scholar] [CrossRef]
- Wang, H.X.; He, Y.L.; Zhu, H.W.; Dong, H.; Wang, S.N. Research Progress and Prospects of Metasurface Polarization Devices. Opto-Electron. Eng. 2024, 51, 119–143. [Google Scholar] [CrossRef]
- Taha, B.A.; Addie, A.J.; Haider, A.J.; Chaudhary, V.; Apsari, R.; Kaushik, A.; Arsad, N. Exploring Trends and Opportunities in Quantum-Enhanced Advanced Photonic Illumination Technologies. Adv. Quantum Technol. 2024, 7, 2300414. [Google Scholar] [CrossRef]
- Zhou, L.; Lou, H.; Deng, Z.; Qin, X.; Pan, J.; Di, Y.; Gu, C.; Luo, D.; Li, W. Compact Mid-Infrared Dual-Comb Spectrometer over 3–4 Μm via Intra-Pulse Difference Frequency Generation in LiNbO3 Waveguides. High Power Laser Sci. Eng. 2024, 12, e23. [Google Scholar] [CrossRef]
- Sakib Rahman, M.S.; Ozcan, A. Physics and Artificial Intelligence: Illuminating the Future of Optics and Photonics. Adv. Photonics 2024, 6, 50500. [Google Scholar] [CrossRef]
- Han, L.; Duan, Q.; Duan, J.; Zhu, S.; Chen, S.; Yin, Y.; Chen, H. Unidirectional Propagation of Water Waves near Ancient Luoyang Bridge. Front. Phys. 2024, 19, 32206. [Google Scholar] [CrossRef]
- Zeng, H.; Cong, X.; Wang, S.; Gong, S.; Huang, L.; Wang, L.; Liang, H.; Lan, F.; Cao, H.; Wang, Z.; et al. Ultrafast Modulable 2DEG Huygens Metasurface. Photonics Res. 2024, 12, 1004–1015. [Google Scholar] [CrossRef]
- Zeng, B.; Li, C.; Fang, B.; Hong, Z.; Jing, X. Flexible Tuning of Multifocal Holographic Imaging Based on Electronically Controlled Metasurfaces. Photonics Res. 2024, 12, 61–69. [Google Scholar] [CrossRef]
- Zhou, J.; Yin, Y.; Tang, J.; Xia, Y.; Yin, J. Information Transmission through Parallel Multi-Task-Based Recognition of High-Resolution Multiplexed Orbital Angular Momentum. Front. Phys. 2024, 19, 52202. [Google Scholar] [CrossRef]
- Zhang, J.C.; Chen, M.K.; Fan, Y.; Chen, Q.; Chen, S.; Yao, J.; Liu, X.; Xiao, S.; Tsai, D.P. Miniature Tunable Airy Beam Optical Meta-Device. Opto-Electron. Adv. 2024, 7, 230171. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Wang, T.; Zhu, Q.; Gu, M. Ultrahigh Performance Passive Radiative Cooling by Hybrid Polar Dielectric Metasurface Thermal Emitters. Opto-Electron. Adv. 2024, 7, 230194. [Google Scholar] [CrossRef]
- Ullah, M.; Mikki, S. Optical Nonreciprocity in a Multimode Cavity Optomechanical System Controlled by Dynamic Casimir Force. Adv. Quantum Technol. 2024, 7, 2400007. [Google Scholar] [CrossRef]
- Refaeli, Z.; Marcus, G.; Shamir, Y. A Simple Method for Pulse Contrast Enhancement via Self-Focusing. High Power Laser Sci. Eng. 2024, 12, e18. [Google Scholar] [CrossRef]
- Hao, Z.; Chen, H.; Yin, Y.; Qiu, C.-W.; Zhu, S.; Chen, H. Efficient Conversion of Acoustic Vortex Using Extremely Anisotropic Metasurface. Front. Phys. 2024, 19, 42202. [Google Scholar] [CrossRef]
- Shen, C.-Y.; Li, J.; Li, Y.; Gan, T.; Bai, L.; Jarrahi, M.; Ozcan, A. Multiplane Quantitative Phase Imaging Using a Wavelength-Multiplexed Diffractive Optical Processor. Adv. Photonics 2024, 6, 56003. [Google Scholar] [CrossRef]
- Berhe, A.M.; As’ham, K.; Al-Ani, I.; Hattori, H.T.; Miroshnichenko, A.E. Strong Coupling and Catenary Field Enhancement in the Hybrid Plasmonic Metamaterial Cavity and TMDC Monolayers. Opto-Electron. Adv. 2024, 7, 230181. [Google Scholar] [CrossRef]
- Zheng, C.; Li, H.; Liu, J.; Wang, M.; Zang, H.; Zhang, Y.; Yao, J. Full-Stokes Metasurface Polarimetry Requiring Only a Single Measurement. Photonics Res. 2024, 12, 514. [Google Scholar] [CrossRef]
- Nan, T.; Zhao, H.; Guo, J.; Wang, X.; Tian, H.; Zhang, Y. Generation of Structured Light Beams with Polarization Variation along Arbitrary Spatial Trajectories Using Tri-Layer Metasurfaces. Opto-Electron. Sci. 2024, 3, 230052. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, D.; Rodrigues, S.P.; Lee, K.-T.; Cai, W. Generative Model for the Inverse Design of Metasurfaces. Nano Lett. 2018, 18, 6570–6576. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, X.; Liu, K.; Zhang, H.; Shi, L.; Song, S.; Tang, D.; Guo, Y. Complex-Amplitude Metasurface Design Assisted by Deep Learning. Ann. Phys. 2022, 534, 2200188. [Google Scholar] [CrossRef]
- Zhang, C.-L.; Hu, K.-X.; Zhang, J.; Cao, J.; Zhang, S.; Wang, H.-F. Topological Phase Transition and Edge States with Tunable Localization in the Cyclic Four-Mode Optical System. Adv. Quantum Technol. 2024, 7, 2400165. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, S.; Tian, Y.; Li, C.; Huang, W.; Liu, Y.; Jin, Y.; Fang, B.; Hong, Z.; Jing, X. Focus Control of Wide-Angle Metalens Based on Digitally Encoded Metasurface. Opto-Electron. Adv. 2024, 7, 240095. [Google Scholar] [CrossRef]
- Zhan, H.; Gu, M.; Tian, Y.; Feng, H.; Zhu, M.; Zhou, H.; Jin, Y.; Tang, Y.; Li, C.; Fang, B.; et al. Review for Wireless Communication Technology Based on Digital Encoding Metasurfaces. Opto-Electron. Adv. 2025, 8, 240315. [Google Scholar] [CrossRef]
- Gong, P.; Du, A.B.; Zhang, F.; Pu, M.B.; Tang, T.J.; Li, L.T.; Luo, X.G. Torsion Pendulum Design for Metasurface-Based Diffraction Light Sail Optical Force Measurement. Opto-Electron. Eng. 2024, 51, 154–163. [Google Scholar] [CrossRef]
- Martín-Hernández, R.; Grünewald, L.; Sánchez-Tejerina, L.; Plaja, L.; Conejero Jarque, E.; Hernández-García, C.; Mai, S. Optical Magnetic Field Enhancement Using Ultrafast Azimuthally Polarized Laser Beams and Tailored Metallic Nanoantennas. Photonics Res. 2024, 12, 1078–1092. [Google Scholar] [CrossRef]
- Jiang, J.; Fang, B.; Li, C.; Hong, Z.; Jing, X. Improvement of Terahertz Beam Modulation Efficiency for Baseless All-Dielectric Coded Gratings. Photonics Res. 2023, 11, 1738–1750. [Google Scholar] [CrossRef]
- Xiang, S.Y.; Song, Z.W.; Zhang, Y.H.; Guo, X.X.; Han, Y.N.; Hao, Y. Progress in the Research of Optical Neural Networks. Opto-Electron. Eng. 2024, 51, 29–52. [Google Scholar] [CrossRef]
- Meng, X.; Qin, C.; Liang, X.; Zhang, G.; Chen, R.; Hu, J.; Yang, Z.; Huo, J.; Xiao, L.; Jia, S. Deep Learning in Two-Dimensional Materials: Characterization, Prediction, and Design. Front. Phys. 2024, 19, 53601. [Google Scholar] [CrossRef]
- Roche, L.J.; Betz, F.; Yang, Y.; Limame, I.; Shih, C.; Burger, S.; Reitzenstein, S. Numerical Investigation of a Coupled Micropillar—Waveguide System for Integrated Quantum Photonic Circuits. Adv. Quantum Technol. 2024, 7, 2400195. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, Y.; Li, C.; Fang, B.; Liu, J.; Hong, Z.; Jing, X. All-Dielectric Double-Layer Honeycomb Tunable Metamaterial Absorber with Integrated Gold Nanoparticles. Photonics Res. 2024, 12, 2344–2353. [Google Scholar] [CrossRef]
- Jiang, Q.; Liu, J.; Li, J.; Jing, X.; Li, X.; Huang, L.; Wang, Y. Multiwavelength Achromatic Metalens in Visible by Inverse Design. Adv. Opt. Mater. 2023, 11, 2300077. [Google Scholar] [CrossRef]
- Ha, Y.; Luo, Y.; Pu, M.; Zhang, F.; He, Q.; Jin, J.; Xu, M.; Guo, Y.; Li, X.; Li, X.; et al. Physics-Data-Driven Intelligent Optimization for Large-Aperture Metalenses. Opto-Electron. Adv. 2023, 6, 230133. [Google Scholar] [CrossRef]
- Jing, X.; Gui, X.; Zhou, P.; Hong, Z. Physical explanation of Fabry-Pérot cavity for broadband bilayer metamaterials polarization converter. J. Light. Technol. 2018, 36, 2322–2327. [Google Scholar] [CrossRef]
- Xia, R.; Jing, X.; Gui, X.; Tian, Y. Broadband terahertz half-wave plate based on anisotropic polarization conversion metamaterials. Opt. Mater. Express 2017, 7, 977–988. [Google Scholar] [CrossRef]
- Zhao, J.; Jing, X.; Wang, W.; Tian, Y.; Zhu, D.; Shi, G. Steady method to retrieve effective electromagnetic parameters of bianisotropic metamaterials at one incident direction in the terahertz region. Opt. Laser Technol. 2017, 95, 56–62. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Li, C.X.; Fang, B.; Ke, L.; Lu, J.; Ma, X.; Hong, Z.; Jing, X. Flexible and Independent Control of Asymmetric Vortex Beams Based on Spin Multiplexing all Dielectric Metasurface. J. Light. Technol. 2023, 41, 1–7. [Google Scholar] [CrossRef]
- Zeng, B.; Li, C.; Cheng, H.; Fang, B.; Lu, J.; Ma, X.; Wang, L.; Hong, Z.; Jing, X. Anisotropic programmable metasurface beam splitter based on diode real-time control. Opt. Lasers Eng. 2023, 169, 107723. [Google Scholar] [CrossRef]
- Qin, G.; Dong, Y.; Zhang, P.; Liu, J.; Li, C.; Huang, W.; Hong, Z.; Shen, C.; Jing, X. Broadband absorber coupled with anti-reflection inverted pyramid type all-dielectric microstructure. Opt. Lasers Eng. 2023, 160, 107288. [Google Scholar] [CrossRef]
- Jing, X.; Tang, X.; Tian, Y.; Kong, Z.; Li, C.; Shen, C.; Hong, Z. Enhancement of Diffraction Efficiency Based on the Addition Principle of Coded Digital Gratings. J. Light. Technol. 2022, 40, 136–142. [Google Scholar] [CrossRef]
- Cheng, H.L.; Fang, B.; Huang, W.K.; Li, R.; Shen, C.; Ke, L.; Jing, X.; Li, C.; Hong, Z. Far-field steering of beams based on dynamic encoding metasurface. Opt. Laser Technol. 2022, 156, 108520. [Google Scholar] [CrossRef]
- Wang, W.; Jing, X.; Zhao, J.; Li, Y.; Tian, Y. Improvement of accuracy of simple methods for design and analysis of a blazed phase grating microstructure. Opt. Appl. 2017, 47, 183–198. [Google Scholar] [CrossRef]
- Jiang, L.; Fang, B.; Yan, Z.; Fan, J.; Qi, C.; Liu, J.; He, Y.; Li, C.; Jing, X.; Gan, H.; et al. Terahertz high and near-zero refractive index metamaterials by double layer metal ring microstructure. Opt. Laser Technol. 2020, 123, 105949. [Google Scholar] [CrossRef]
- Jiang, L.; Fang, B.; Yan, Z.; Li, C.; Fu, J.; Gan, H.; Hong, Z.; Jing, X. Improvement of unidirectional scattering characteristics based on multiple nanospheres array. Microw. Opt. Technol. Lett. 2020, 62, 2405–2414. [Google Scholar] [CrossRef]
- Jing, X.; Xu, Y.; Gan, H.; He, Y.; Hong, Z. High Refractive Index Metamaterials by Using Higher Order Modes Resonances of Hollow Cylindrical Nanostructure in Visible Region. IEEE Access 2019, 7, 144945–144956. [Google Scholar] [CrossRef]
- Luo, Z.Y.; Ding, Y.Q.; Peng, F.L.; Wei, G.; Wang, Y.; Wu, S.T. Ultracompact and high-efficiency liquid-crystal-on-silicon light engines for augmented reality glasses. Opto-Electron. Adv. 2024, 7, 240039. [Google Scholar] [CrossRef]
- Li, S.S.; Fang, Y.N.; Wang, J.F. Control of light–matter interactions in two-dimensional materials with nanoparticle-on-mirror structures. Opto-Electron. Sci. 2024, 3, 240011. [Google Scholar] [CrossRef]
- Liang, M.W.; Lu, D.Z.; Ma, Y.G. Vectorial optical fields manipulation via metasurfaces. Opto-Electron. Eng. 2024, 51, 240068. [Google Scholar] [CrossRef]
- Naglaa, A.; Almokhtar, M.; Khouqeer, G.; Abood, I.; Soliman, S.E. Rainbow Trapping with Engineered Topological Corner States and Cavities in Photonic Crystals. Adv. Quantum Technol. 2024, 7, 2400050. [Google Scholar] [CrossRef]
- Istokskaia, V.; Lefebvre, B.; Versaci, R.; Dreghici, B.D.; Doria, D.; Grepl, F.; Olšovcová, V.; Schillaci, F.; Stanček, S.; Tryus, M.; et al. Real-time bremsstrahlung detector as a monitoring tool for laser–plasma proton acceleration. High Power Laser Sci. Eng. 2024, 12, 05000e57. [Google Scholar] [CrossRef]
- Peters, C.; Forbes, A. Controlling the hidden parity in vectorial light with metasurfaces. Adv. Photonics 2024, 6, 040501. [Google Scholar] [CrossRef]
- Zhang, S.X.; Li, H.; Fan, C.Z.; Zeng, Z.; Xiong, C.; Wu, J.; Yan, Z.; Liu, D.; Sun, Q. Adaptive decentralized AI scheme for signal recognition of distributed sensor systems. Opto-Electron. Adv. 2024, 7, 240119. [Google Scholar] [CrossRef]
- Rane, S.; Prabhu, S.; Chowdhury, D.R. Physics and applications of terahertz metagratings. Opto-Electron. Sci. 2024, 3, 230049. [Google Scholar] [CrossRef]
- Yang, H.; He, H.; Hu, Y.Q.; Duan, H. Metasurface-empowered vector light field regulation, detection and application. Opto-Electron. Eng. 2024, 51, 240168. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, F.; Pu, M.; Guo, Y.; Li, X.; Ma, X. Recent advances of wide-angle metalenses:principle, design, and applications. Nanophotonics 2022, 11, 1–20. [Google Scholar] [CrossRef]
- Li, Z.; Lin, P.; Huang, Y.-W.; Park, J.-S.; Chen, W.T.; Shi, Z.; Qiu, C.-W.; Cheng, J.-X.; Capasso, F. Meta-Optics Achieves RGB-Achromatic Focusing for Virtual Reality. Sci. Adv. 2021, 7, eabe4458. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chen, S.; Liang, H.; Ren, X.; Luo, L.; Ling, Y.; Liu, S.; Su, Y.; Wu, S.-T. Ultracompact Multifunctional Metalens Visor for Augmented Reality Displays. Photonix 2022, 3, 29. [Google Scholar] [CrossRef]
- Li, Y.; Ansari, M.A.; Ahmed, H.; Wang, R.; Wang, G.; Chen, X. Longitudinally Variable 3D Optical Polarization Structures. Sci. Adv. 2023, 9, eadj6675. [Google Scholar] [CrossRef]
- Cattoni, A.; Chen, J.; Decanini, D.; Shi, J.; Haghiri-Gosnet, A.-M. Soft UV Nanoimprint Lithography: A Versatile Tool for Nanostructuration at the 20nm Scale. In Recent Advances in Nanofabrication Techniques and Applications; Cui, B., Ed.; InTech: Berlin, Germany, 2011; ISBN 978-953-307-602-7. [Google Scholar][Green Version]
- Lan, H.; Liu, H. UV-Nanoimprint Lithography: Structure, Materials and Fabrication of Flexible Molds. J. Nanosci. Nanotechnol. 2013, 13, 3145–3172. [Google Scholar] [CrossRef] [PubMed]
- Plachetka, U. Wafer Scale Patterning by Soft UV-Nanoimprint Lithography. Microelectron. Eng. 2004, 73–74, 167–171. [Google Scholar] [CrossRef]
- Traub, M.C.; Longsine, W.; Truskett, V.N. Advances in Nanoimprint Lithography. Annu. Rev. Chem. Biomol. Eng. 2016, 7, 583–604. [Google Scholar] [CrossRef]
- Moharana, A.R.; Außerhuber, H.M.; Mitteramskogler, T.; Haslinger, M.J.; Mühlberger, M.M. Multilayer Nanoimprinting to Create Hierarchical Stamp Masters for Nanoimprinting of Optical Micro- and Nanostructures. Coatings 2020, 10, 301. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, Y.; Choi, C.L.R.; Zhang, P.; Wu, T.; Chan, Y.K. Continuous Roller Nanoimprinting: Next Generation Lithography. Nanoscale 2023, 15, 11403–11421. [Google Scholar] [CrossRef]
- Rodriguez, A.; Echeverría, M.; Ellman, M.; Perez, N.; Verevkin, Y.K.; Peng, C.S.; Berthou, T.; Wang, Z.; Ayerdi, I.; Savall, J.; et al. Laser Interference Lithography for Nanoscale Structuring of Materials: From Laboratory to Industry. Microelectron. Eng. 2009, 86, 937–940. [Google Scholar] [CrossRef]
- Shimizu, Y. Laser Interference Lithography for Fabrication of Planar Scale Gratings for Optical Metrology. Nanomanuf. Metrol. 2021, 4, 3–27. [Google Scholar] [CrossRef]
- Seo, J.-H.; Park, J.H.; Kim, S.-I.; Park, B.J.; Ma, Z.; Choi, J.; Ju, B.-K. Nanopatterning by Laser Interference Lithography: Applications to Optical Devices. J. Nanosci. Nanotechnol. 2014, 14, 1521–1532. [Google Scholar] [CrossRef] [PubMed]
- Thiel, M.; Bertoncini, A.; Hoose, T.; Blaicher, M. Advancement in Two-Photon Grayscale Lithography. In Proceedings of the 3D Printed Optics and Additive Photonic Manufacturing III, Strasbourg, France, 3 April–23 May 2022; SPIE: Bellingham, WA, USA, 2022. [Google Scholar] [CrossRef]
- Skidanov, R.V.; Moiseev, O.Y.; Ganchevskaya, S.V. Additive Process for Fabrication of Phased Optical Diffraction Elements. J. Opt. Technol. 2016, 83, 23–25. [Google Scholar] [CrossRef]



| Mechanism | Wavelength | NA | Eff. | Focal Length | Ref. |
|---|---|---|---|---|---|
| Light-controlled | 532 nm | 0.05 | 70% | 18 mm | [127] |
| Light-controlled | 0.6 Thz | — | 21.8–24.5% | 0, ±1, 4 mm | [128] |
| Light-controlled | 658 nm | 0.21 | 23.1–35.1% | 60 μm | [129] |
| Electric controlled | 0.9–1.4 Thz | 0.13 | 26.1%/33.9% | 12 mm | [130] |
| Electric controlled | 650 nm | 0.2–0.7 | 40%/70% | 10 μm/45 μm | [131] |
| Electric controlled | 10 Thz | — | 61.62% | 161.1–251.5 μm | [132] |
| Electric controlled | 360 μm | 0.21 | — | 7.13–25 mm | [133] |
| Mechanically controlled | 632.8 nm | — | — | 150–250 μm | [145] |
| Mechanically controlled | 900 nm | 0.5 | >60% | ±1.73–±5 mm | [147] |
| FOV | Aberration Correction Strategy | NA | Eff. | Ref. |
|---|---|---|---|---|
| 10° | Spherical Substrate + Equal Optical Path Phase Distribution | 0.5 | — | [149] |
| >60° | Cascaded Dual Metalenses + Phase Cooperative Optimization | 0.55 | 70% | [27] |
| >160° | Symmetry Transformation | — | <10% | [150] |
| 120° | Symmetry Transformation | 0.89 | 80% | [147] |
| 170° | Optimized Phase Profile | 0.25 | 82% | [151] |
| 178° | Suppression of Off-Axis Coma Aberration | 0.49 | Nearly 100% | [152] |
| Material | Wavelength | Focal Length | Eff. | Focal Length Deviation | Ref. |
|---|---|---|---|---|---|
| Si | 1300 nm 1550 nm 1800 nm | 7.5 mm | Nearly 10% | The focal spot approaches the diffraction limit | [54] |
| Au-SiO2-Au | 1200–1680 nm | 100 μm | <12.44% | The focal spot approaches the diffraction limit | [47] |
| GaN | 400–660 nm | 235 μm | 40% | The focal spot approaches the diffraction limit | [46] |
| TiO2 | 460–700 nm | 67 μm | 30% | <9% | [33] |
| Al, Ag, Au | 450 nm 550 nm 650 nm | 1 mm | 5.8–8.7% | <10% | [79] |
| a-Si | 915 nm, 1550 nm | 286 μm | 37%, 30% | <5%, <12% | [160] |
| Si | 3.5–5 μm | 200 μm | 40% | <5% | [88] |
| Resin | 450–1700 nm | 36 μm | 60% | <6% | [161] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, L.; Tian, Y.; Jing, X. Review of Planar Optical System: Lens Based on Metasurfaces. Electronics 2025, 14, 4322. https://doi.org/10.3390/electronics14214322
Zeng L, Tian Y, Jing X. Review of Planar Optical System: Lens Based on Metasurfaces. Electronics. 2025; 14(21):4322. https://doi.org/10.3390/electronics14214322
Chicago/Turabian StyleZeng, Linyu, Ying Tian, and Xufeng Jing. 2025. "Review of Planar Optical System: Lens Based on Metasurfaces" Electronics 14, no. 21: 4322. https://doi.org/10.3390/electronics14214322
APA StyleZeng, L., Tian, Y., & Jing, X. (2025). Review of Planar Optical System: Lens Based on Metasurfaces. Electronics, 14(21), 4322. https://doi.org/10.3390/electronics14214322







