Comparative Analysis of Traditional Statistical Models and Deep Learning Architectures for Photovoltaic Energy Forecasting Using Meteorological Data
Abstract
1. Introduction
2. State of the Art
| Study (Year) | Model(s) Used | Dataset | Prediction Type | Key Results |
|---|---|---|---|---|
| Aravena-Cifuentes et al. (2025) | RNN (LSTM), CNN, MLP, DT, LR, RF | Austria (2015–2017) | Single-step: 1 h Multi-step: 24 h | Single-step: RNN (MSE = 0.0045, MAE = 0.0427) Multi-step: CNN (MSE = 0.1956, MAE = 0.2367) |
| Zoubir et al. (2024) [51] | LightGBM, RF, XGBoost, CatBoost, DT | Residential PV (Morocco) | Hourly | LightGBM (MAE = 0.180, = 0.96) |
| Quan et al. (2024) [23] | Dung beetle-optimized BiLSTM | Industrial PV | Ultra-short-term | Optimized BiLSTM outperformed standard LSTMs/GRUs (MAE = 0.175) |
| Chandel et al. (2023) [22] | LSTM, GRU, hybrid DL | Industrial PV | Multi-horizon | LSTM best for all horizons; GRU better with limited data |
| Hybrid: Wavelet, DCNN, Quantile Regression | 15, 30, 60, and 120 min | MAPE: 0.0382–0.0385 RMSE: 3.8772–14.3381 MAE: 2.0340–8.0759 | ||
| Hybrid: CNN, Variational Mode Decomposition | 60, 360, and 720 min | RMSE-2.0533 MAE-1.5418 MASE-0.1752 | ||
| Hybrid: GRU K-means clustering | 12 step size | MAE: 0.0379–0.0409 RMSE: 0.0683–0.725 | ||
| PM, ARIMAX, MLP, LSTM, ALSTM | 7.5, 15, 30, and 60 min | 60 min MAE: PM 2.12 ARIMAX 1.98 MLP 1.63 LSTM 1.48 ALSTM 1.47 | ||
| Li et al. (2023) [45] | FCM ISD MAOA ESN | Zero-energy buildings | Short-term | MAE: 0.16639 |
| Park et al. (2022) [46] | POST-enCNN | On-site PV (Korea) | Day-ahead | MAE: 2.15 RMSE: 3.83 MAPE(%): 51.7 |
3. Materials and Methods
3.1. Software and Hardware
3.2. Dataset
3.2.1. Time Series Data
- Generation and Consumption
- –
- X_solar_generation_actual: (number): PV energy generation in the country X in MW.
- –
- X_wind_onshore_generation_actual: (number): onshore wind energy generation in country X in MW.
- –
- X_load_entsoe_transparency: (number): total load in country X in MW obtained from ENTSO-E Transparency Platform.
- –
- X_load_entsoe_power_statistics: (number): total load in country X in MW obtained from ENTSO-E Data Portal/Power Statistics.
- Temporal
- –
- utc_timestamp: (datetime): date and time of measurement in UTC format.
- –
- cet_cest_timestamp: (datetime): date and time of measurement in CET-CEST format.
- Other
- –
- interpolated_values: (text): columns where missing values in the original database were estimated by interpolation.
- –
- X_price_day_ahead: (number): daily spot price for country X in Euro per MW/h.
3.2.2. Weather Data
- Meteorological
- –
- X_windspeed_10m (float number): wind speed at 10 m height in country X in .
- –
- X_temperature (float number): temperature in country X in °C.
- –
- X_radiation_direct_horizontal (float number): horizontal direct radiation for country X in .
- –
- X_radiation_diffuse_horizontal (float number): horizontal diffuse radiation for country X in .
- Temporal
- –
- utc_timestamp (datetime): date and time of measurement in UTC format.
3.3. Preprocessing—Austria Case Study
- Time Series Data: This dataset has 108,818 rows and 7 columns, which have information on electricity consumption and solar and wind power generation covering from 31 December 2005 up to 31 May 2018. It is important to note that daily spot price data is not available in this dataset.
- Weather Data: This dataset has 324,361 rows and 5 columns and contains all the weather variables mentioned above. It covers the period from 1 January 1980 to 30 June 2017.
- utc_timestamp → date_time
- AT_solar_generation_current → portal_load
- AT_wind_onshore_generation_current → calculated_load
- AT_load_entsoe_transparency → solar_generation
- AT_load_entsoe_power_statistics → wind_generation
- AT_temperature → temperature
- AT_radiation_direct_horizontal → radiation_direct
- AT_radiation_diffuse_horizontal → radiation_diffuse
3.4. Feature Engineering
3.4.1. Circular Time Features
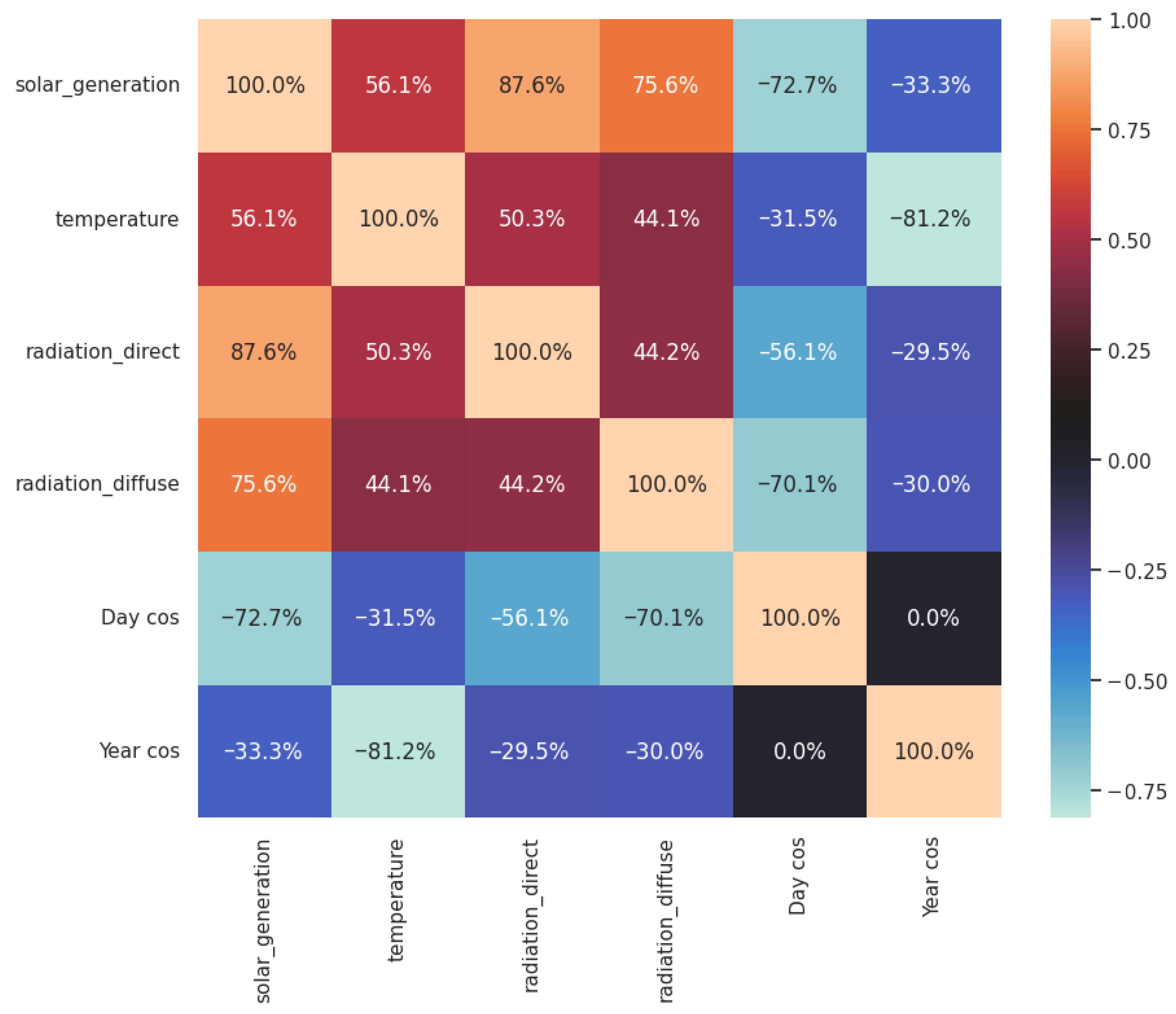
3.4.2. Correlation Analysis
3.5. Model Validation
| Algorithm 1 Time series sliding window generator |
|
3.6. Models
3.6.1. Baseline
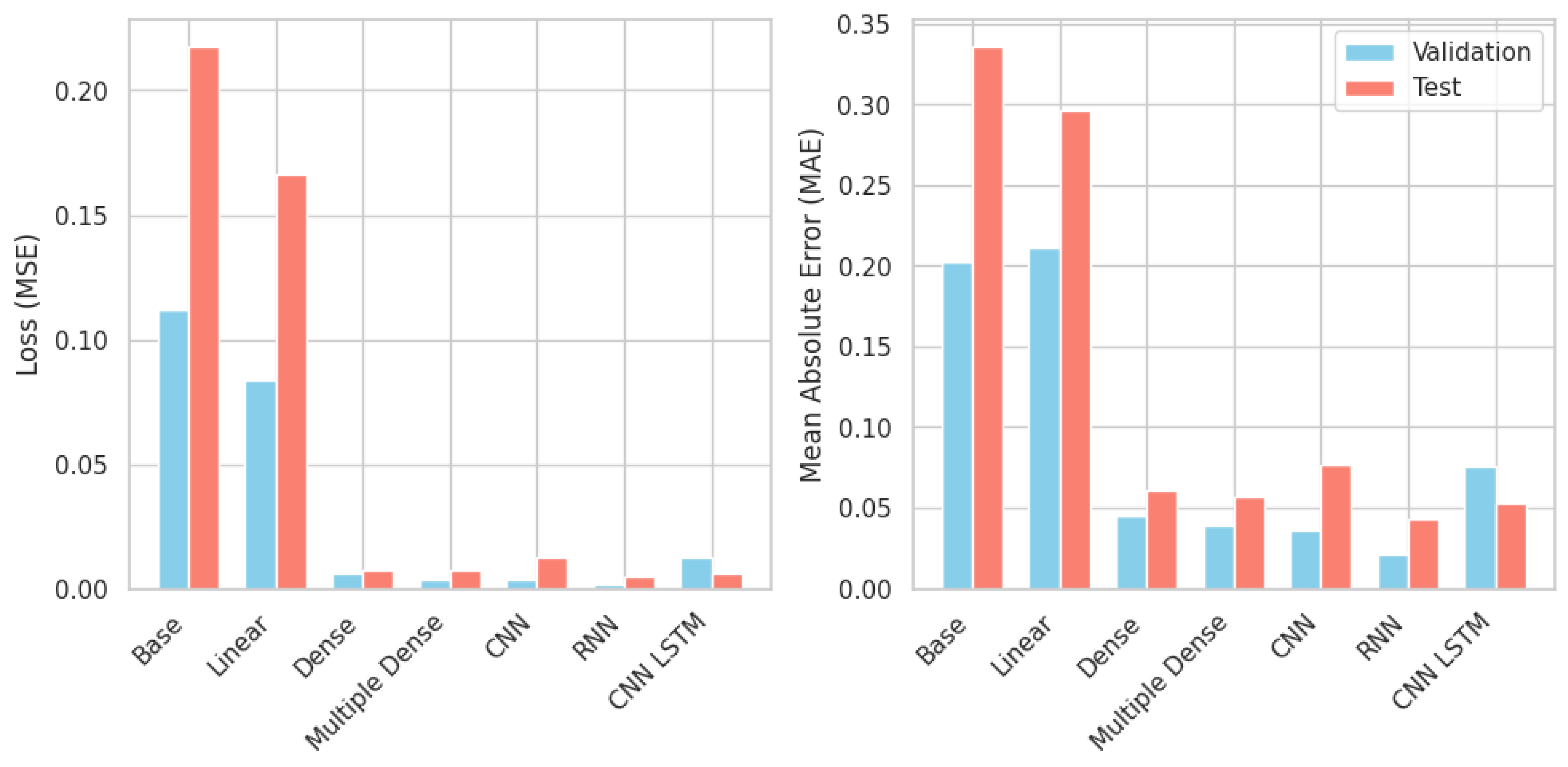
3.6.2. One-Step Neural Models
Linear Perceptron Model
Dense Perceptron Model
Multiple Input Dense Perceptron Model
Convolutional Neural Network
Recurrent Neural Network
3.6.3. Multi-Step Models
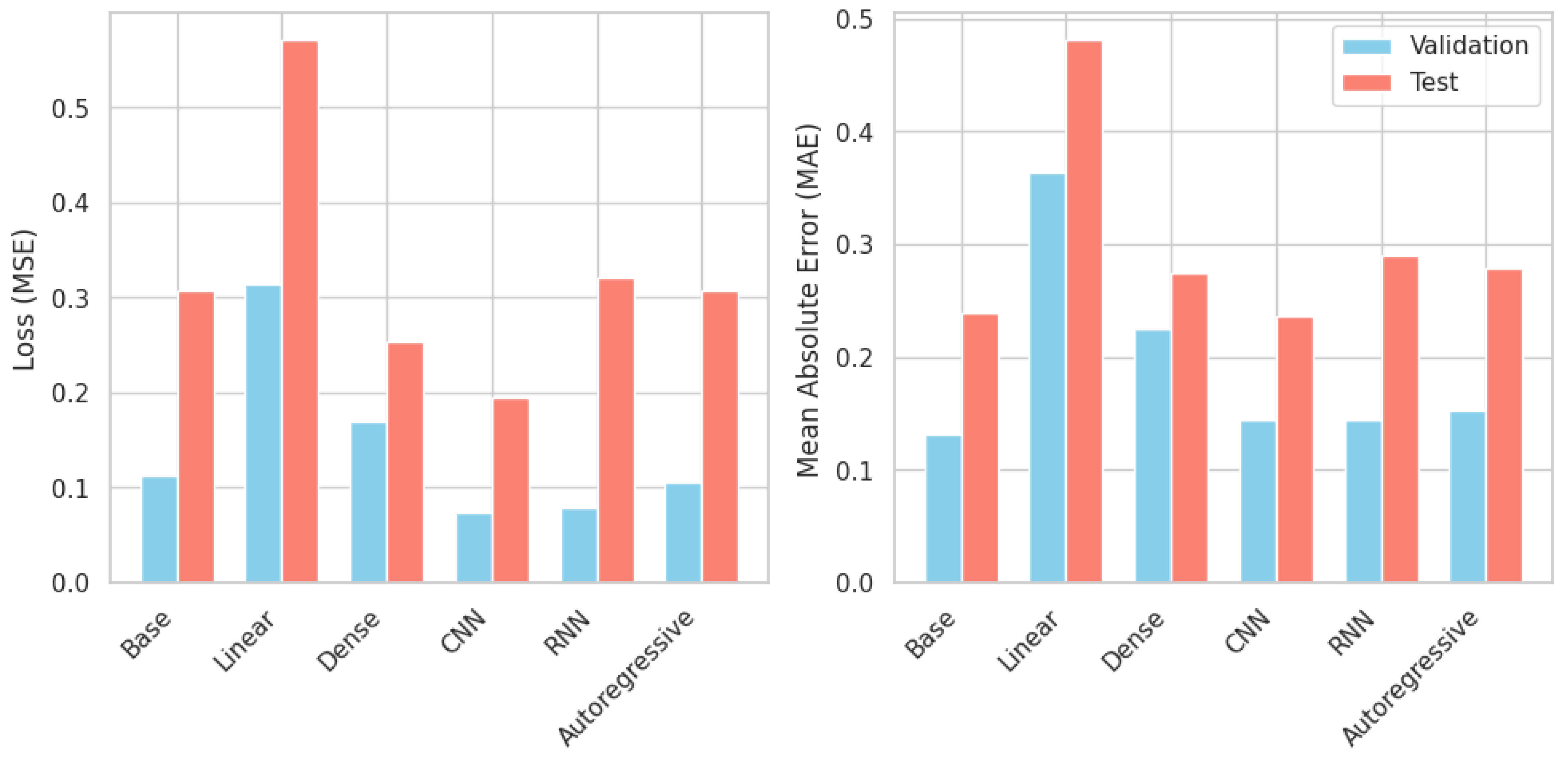
Baseline Model
Linear Perceptron Model
Dense Perceptron Model
Convolutional Neural Network
Recurrent Neural Network
Autoregressive Model
4. Results
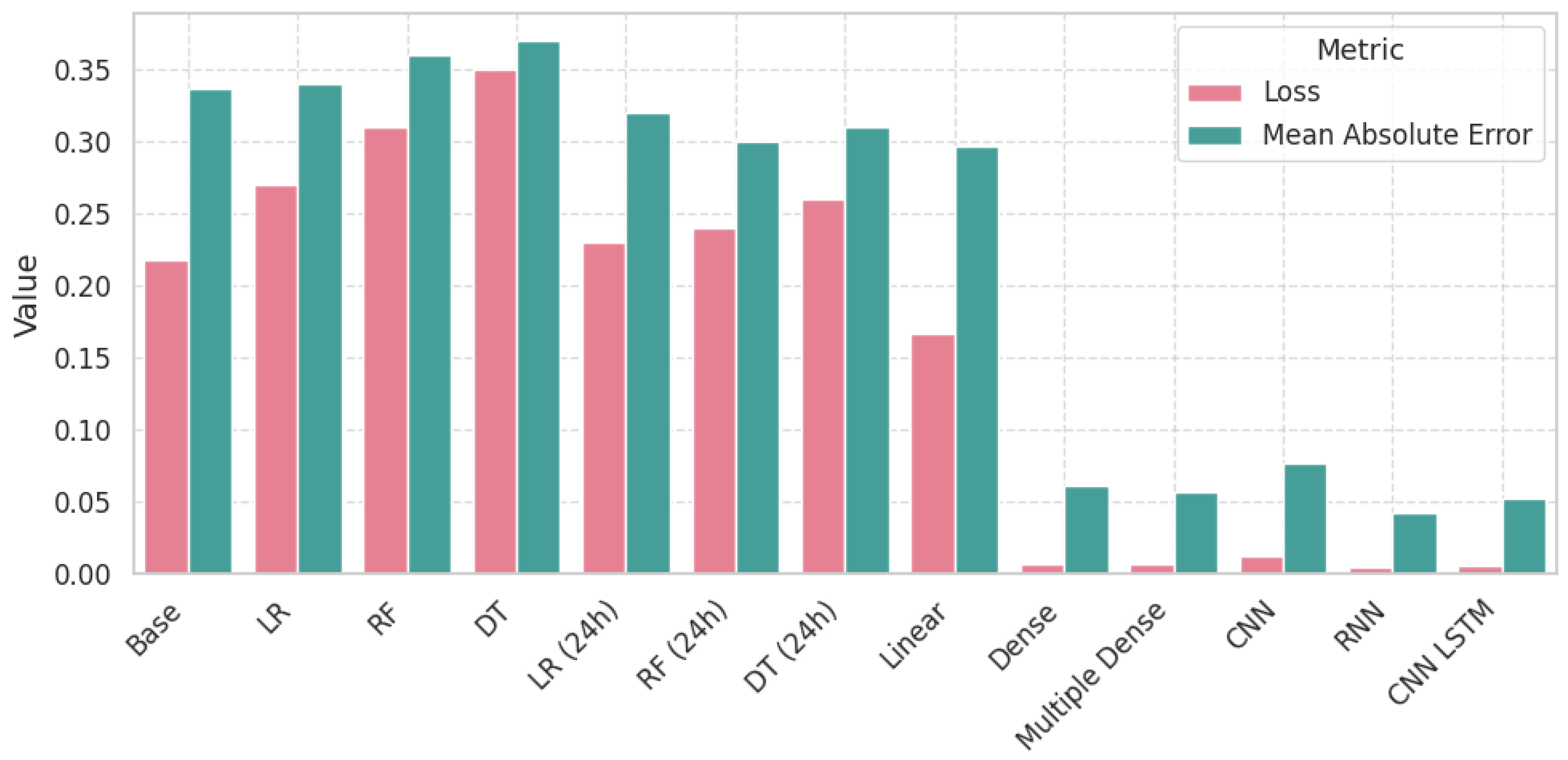
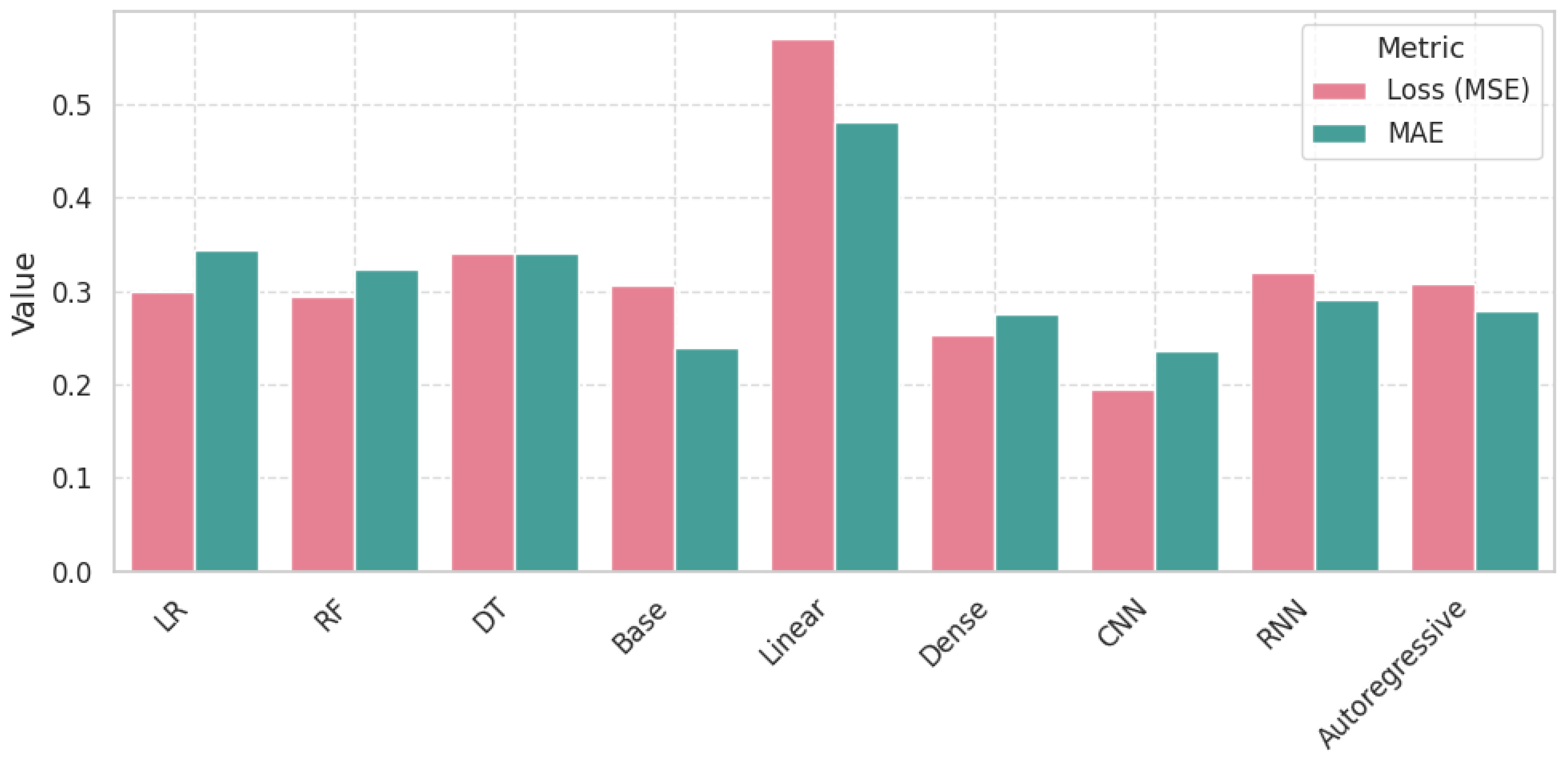
4.1. Results of One-Step Models
4.2. Results of Multi-Step Models
5. Discussion and Conclusions
5.1. Discussion
5.2. Conclusions
5.3. Limitations and Future Work
- Geographical and Temporal Scope:
- Validation was conducted exclusively on Austrian data (2015–2017). Generalizability to regions with distinct climatic patterns (e.g., tropical zones with higher irradiance volatility) remains unverified.
- The dataset excludes extreme weather events (e.g., storms), potentially limiting robustness under anomalous conditions.
- Data Dependency: Model performance relies on high-quality historical data; degradation may occur with noisy or incomplete inputs. Future work will integrate anomaly detection mechanisms to enhance resilience.
- Computational Efficiency: While RNN/CNN architectures achieved high accuracy, their resource demands may hinder deployment in low-infrastructure settings (e.g., edge devices). Simpler models (e.g., Random Forest) could be explored for resource-constrained applications.
- Methodological Refinements: Hyperparameter tuning employed random search, which may yield suboptimal efficiency. Bayesian optimization or evolutionary algorithms will be investigated to accelerate convergence.
Future Directions
- Geographical Transferability: apply transfer learning to adapt models to diverse regions using limited local data.
- Robustness Enhancement: incorporate real-time anomaly detection and data imputation techniques for noisy environments.
- Edge Deployment: develop lightweight model variants (e.g., quantized CNNs) for embedded systems in distributed PV installations.
- Hybrid Physical–AI Modeling: fuse physics-based irradiance models with deep learning to improve extrapolation beyond training conditions.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- U.E.I.A. (EIA). Installed Electricity Capacity. 2022. Available online: https://www.iea.org/reports/renewables-2022 (accessed on 12 July 2024).
- I.R.E.A. (IRENA). Renewable Energy Statistics 2024. 2024. Available online: https://www.irena.org/Publications/2024/Jul/Renewable-energy-statistics-2024 (accessed on 12 July 2024).
- I.R.E.A. (IRENA). Renewable Power Generation Costs in 2022. 2023. Available online: https://www.irena.org/Publications/2023/Aug/Renewable-Power-Generation-Costs-in-2022 (accessed on 12 July 2024).
- Lameirinhas, R.A.M.; Torres, J.P.N.; de Melo Cunha, J.P. A Photovoltaic Technology Review: History, Fundamentals and Applications. Energies 2022, 15, 1823. [Google Scholar] [CrossRef]
- Charpentier, B.; Cristianetti, R.; Denelle, F.; Dolle, N.; Falcone, G.; Griffiths, C.; Jethwa, D.; Primrose, J.; Seiller, B.; Taupy, J.A.; et al. Specifications for the application of the United Nations Framework Classification for Fossil Energy and Mineral Reserves and Resources 2009 to Renewable Energy Resources; UNECE: Geneva, Switzerland, 2016. [Google Scholar]
- Wang, M.; Peng, J.; Luo, Y.; Shen, Z.; Yang, H. Comparison of different simplistic prediction models for forecasting PV power output: Assessment with experimental measurements. Energy 2021, 224, 120162. [Google Scholar] [CrossRef]
- Górriz, J.; Álvarez Illán, I.; Álvarez-Marquina, A.; Arco, J.E.; Atzmueller, M.; Ballarini, F.; Barakova, E.; Bologna, G.; Bonomini, P.; Castellanos-Dominguez, G.; et al. Computational approaches to Explainable Artificial Intelligence: Advances in theory, applications and trends. Inf. Fusion 2023, 100, 101945. [Google Scholar] [CrossRef]
- Li, L.L.; Wen, S.Y.; Tseng, M.L.; Wang, C.S. Renewable energy prediction: A novel short-term prediction model of photovoltaic output power. J. Clean. Prod. 2019, 228, 359–375. [Google Scholar] [CrossRef]
- Villemin, T.; Farges, O.; Parent, G.; Claverie, R. Monte Carlo prediction of the energy performance of a photovoltaic panel using detailed meteorological input data. Int. J. Therm. Sci. 2024, 195, 108672. [Google Scholar] [CrossRef]
- Coelho, S.; Machado, J.; Monteiro, V.; Afonso, J.L. Chapter 11—Power electronics technologies for renewable energy sources. In Recent Advances in Renewable Energy Technologies; Jeguirim, M., Ed.; Academic Press: Cambridge, MA, USA, 2022; pp. 403–455. [Google Scholar] [CrossRef]
- Mousavi Ajarostaghi, S.S.; Mousavi, S.S. Solar energy conversion technologies: Principles and advancements. In Solar Energy Advancements in Agriculture and Food Production Systems; Elsevier: Amsterdam, The Netherlands, 2022; pp. 29–76. [Google Scholar] [CrossRef]
- Ghosh, S.; Yadav, R. Future of photovoltaic technologies: A comprehensive review. Sustain. Energy Technol. Assessments 2021, 47, 101410. [Google Scholar] [CrossRef]
- Peratikou, S.; Charalambides, A.G. Short-term PV energy yield predictions within city neighborhoods for optimum grid management. Energy Build. 2024, 323, 114773. [Google Scholar] [CrossRef]
- Jha, S.K.; Bilalovic, J.; Jha, A.; Patel, N.; Zhang, H. Renewable energy: Present research and future scope of Artificial Intelligence. Renew. Sustain. Energy Rev. 2017, 77, 297–317. [Google Scholar] [CrossRef]
- Afridi, Y.; Ahmad, K.; Hassan, L. Artificial Intelligence Based Prognostic Maintenance of Renewable Energy Systems: A Review of Techniques, Challenges, and Future Research Directions. Int. J. Energy Res. 2021, 46, 21619–21642. [Google Scholar] [CrossRef]
- Yousef, L.A.; Yousef, H.; Rocha-Meneses, L. Artificial Intelligence for Management of Variable Renewable Energy Systems: A Review of Current Status and Future Directions. Energies 2023, 16, 8057. [Google Scholar] [CrossRef]
- Li, Y.; Janik, P.; Schwarz, H. Prediction and aggregation of regional PV and wind generation based on neural computation and real measurements. Sustain. Energy Technol. Assess. 2023, 57, 103314. [Google Scholar] [CrossRef]
- Hu, J.; Lim, B.H.; Tian, X.; Wang, K.; Xu, D.; Zhang, F.; Zhang, Y. A Comprehensive Review of Artificial Intelligence Applications in the Photovoltaic Systems. CAAI Artif. Intell. Res. 2024, 3, 9150031. [Google Scholar] [CrossRef]
- Rezaul Karim, S.; Sarker, D.; Monirul Kabir, M. Analyzing the impact of temperature on PV module surface during electricity generation using machine learning models. Clean. Energy Syst. 2024, 9, 100135. [Google Scholar] [CrossRef]
- Parenti, M.; Fossa, M.; Delucchi, L. A model for energy predictions and diagnostics of large-scale photovoltaic systems based on electric data and thermal imaging of the PV fields. Renew. Sustain. Energy Rev. 2024, 206, 114858. [Google Scholar] [CrossRef]
- Tsai, W.C.; Tu, C.S.; Hong, C.M.; Lin, W.M. A Review of State-of-the-Art and Short-Term Forecasting Models for Solar PV Power Generation. Energies 2023, 16, 5436. [Google Scholar] [CrossRef]
- Chandel, S.S.; Gupta, A.; Chandel, R.; Tajjour, S. Review of deep learning techniques for power generation prediction of industrial solar photovoltaic plants. Sol. Compass 2023, 8, 100061. [Google Scholar] [CrossRef]
- Quan, R.; Qiu, Z.; Wan, H.; Yang, Z.; Li, X. Dung beetle optimization algorithm-based hybrid deep learning model for ultra-short-term PV power prediction. iScience 2024, 27, 111126. [Google Scholar] [CrossRef] [PubMed]
- Boza, P.; Evgeniou, T. Artificial Intelligence to Support the Integration of Variable Renewable Energy Sources to the Power System. Appl. Energy 2021, 290, 116754. [Google Scholar] [CrossRef]
- Raza, M.Q.; Khosravi, A. A Review on Artificial Intelligence Based Load Demand Forecasting Techniques for Smart Grid and Buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Shapi, M.K.M.; Ramli, N.A.; Awalin, L.J. Energy Consumption Prediction by Using Machine Learning for Smart Building: Case Study in Malaysia. Dev. Built Environ. 2021, 5, 100037. [Google Scholar] [CrossRef]
- Ridha, H.M.; Hizam, H.; Mirjalili, S.; Othman, M.L.; Ya’acob, M.E.; Wahab, N.I.B.A.; Ahmadipour, M. A novel prediction of the PV system output current based on integration of optimized hyperparameters of multi-layer neural networks and polynomial regression models. Next Energy 2025, 8, 100256. [Google Scholar] [CrossRef]
- Wahid, F.; Kim, D. A Prediction Approach for Demand Analysis of Energy Consumption Using K-Nearest Neighbor in Residential Buildings. Int. J. Smart Home 2016, 10, 97–108. [Google Scholar] [CrossRef]
- Martínez-Álvarez, F.; Troncoso, A.; Riquelme, J.C.; Aguilar-Ruiz, J.S. Energy Time Series Forecasting Based on Pattern Sequence Similarity. IEEE Trans. Knowl. Data Eng. 2011, 23, 1230–1243. [Google Scholar] [CrossRef]
- Sun, F.; Li, L.; Bian, D.; Ji, H.; Li, N.; Wang, S. Short-term PV power data prediction based on improved FCM with WTEEMD and adaptive weather weights. J. Build. Eng. 2024, 90, 109408. [Google Scholar] [CrossRef]
- Al-Dahidi, S.; Alrbai, M.; Rinchi, B.; Al-Ghussain, L.; Ayadi, O.; Alahmer, A. A tiered NARX model for forecasting day-ahead energy production in distributed solar PV systems. Clean. Eng. Technol. 2024, 23, 100831. [Google Scholar] [CrossRef]
- Massidda, L.; Bettio, F.; Marrocu, M. Probabilistic day-ahead prediction of PV generation. A comparative analysis of forecasting methodologies and of the factors influencing accuracy. Sol. Energy 2024, 271, 112422. [Google Scholar] [CrossRef]
- Dewi, T.; Mardiyati, E.N.; Risma, P.; Oktarina, Y. Hybrid Machine learning models for PV output prediction: Harnessing Random Forest and LSTM-RNN for sustainable energy management in aquaponic system. Energy Convers. Manag. 2025, 330, 119663. [Google Scholar] [CrossRef]
- Tripathi, A.K.; Aruna, M.; Elumalai, P.; Karthik, K.; Khan, S.A.; Asif, M.; Rao, K.S. Advancing solar PV panel power prediction: A comparative machine learning approach in fluctuating environmental conditions. Case Stud. Therm. Eng. 2024, 59, 104459. [Google Scholar] [CrossRef]
- Aler, R.; Huertas-Tato, J.; Valls, J.M.; Galván, I.M. Improving Prediction Intervals Using Measured Solar Power with a Multi-Objective Approach. Energies 2019, 12, 4713. [Google Scholar] [CrossRef]
- Souabi, S.; Chakir, A.; Tabaa, M. Data-driven prediction models of photovoltaic energy for smart grid applications. Energy Rep. 2023, 9, 90–105. [Google Scholar] [CrossRef]
- Peng, Z.; Peng, S.; Fu, L.; Lu, B.; Tang, J.; Wang, K.; Li, W. A novel deep learning ensemble model with data denoising for short-term wind speed forecasting. Energy Convers. Manag. 2020, 207, 112524. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Ghasemi, M.; Dehghan Manshadi, M.; Mosavi, A. Deep Learning for Wave Energy Converter Modeling Using Long Short-Term Memory. Mathematics 2021, 9, 871. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, D.; Li, X.; Peng, Y.; Wu, C.; Pu, H.; Zhou, D.; Cao, Y.; Zhang, J. Significant Wave Height Prediction through Artificial Intelligent Mode Decomposition for Wave Energy Management. Energy AI 2023, 14, 100257. [Google Scholar] [CrossRef]
- Aravena-Cifuentes, A.P.; Nuñez-Gonzalez, J.D.; Elola, A.; Ivanova, M. Development of AI-Based Tools for Power Generation Prediction. Computation 2023, 11, 232. [Google Scholar] [CrossRef]
- Maciel, J.N.; Ledesma, J.J.G.; Junior, O.H.A. Hybrid prediction method of solar irradiance applied to short-term photovoltaic energy generation. Renew. Sustain. Energy Rev. 2024, 192, 114185. [Google Scholar] [CrossRef]
- Roldán-Blay, C.; Abad-Rodríguez, M.F.; Abad-Giner, V.; Serrano-Guerrero, X. Interval-based solar photovoltaic energy predictions: A single-parameter approach with direct radiation focus. Renew. Energy 2024, 230, 120821. [Google Scholar] [CrossRef]
- Singh, K.; Mistry, K.D.; Patel, H.G. Optimizing power loss in mesh distribution systems: Gaussian Regression Learner Machine learning-based solar irradiance prediction and distributed generation enhancement with Mono/Bifacial PV modules using Grey Wolf Optimization. Renew. Energy 2024, 237, 121590. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, X.; Li, C.; Cheng, F.; Tai, Y. CRAformer: A cross-residual attention transformer for solar irradiation multistep forecasting. Energy 2025, 320, 135214. [Google Scholar] [CrossRef]
- Li, N.; Li, L.; Huang, F.; Liu, X.; Wang, S. Photovoltaic power prediction method for zero energy consumption buildings based on multi-feature fuzzy clustering and MAOA-ESN. J. Build. Eng. 2023, 75, 106922. [Google Scholar] [CrossRef]
- Park, J.; Kim, J.; Lee, S.; Choi, J.K. Machine learning based photovoltaic energy prediction scheme by augmentation of on-site IoT data. Future Gener. Comput. Syst. 2022, 134, 1–12. [Google Scholar] [CrossRef]
- Dai, H.; Zhen, Z.; Wang, F.; Lin, Y.; Xu, F.; Duić, N. A short-term PV power forecasting method based on weather type credibility prediction and multi-model dynamic combination. Energy Convers. Manag. 2025, 326, 119501. [Google Scholar] [CrossRef]
- Xu, X.; Guan, L.; Wang, Z.; Yao, R.; Guan, X. A double-layer forecasting model for PV power forecasting based on GRU-Informer-SVR and Blending ensemble learning framework. Appl. Soft Comput. 2025, 172, 112768. [Google Scholar] [CrossRef]
- Li, Y.; Huang, W.; Lou, K.; Zhang, X.; Wan, Q. Short-term PV power prediction based on meteorological similarity days and SSA-BiLSTM. Syst. Soft Comput. 2024, 6, 200084. [Google Scholar] [CrossRef]
- Markovics, D.; Mayer, M.J. Comparison of machine learning methods for photovoltaic power forecasting based on numerical weather prediction. Renew. Sustain. Energy Rev. 2022, 161, 112364. [Google Scholar] [CrossRef]
- Zoubir, Z.; Es-sakali, N.; Er-retby, H.; Mghazli, M.O. Prediction of energy production in a building-integrated photovoltaic system using machine learning algorithms. Procedia Comput. Sci. 2024, 236, 75–82. [Google Scholar] [CrossRef]
- Wiese, F.; Schlecht, I.; Bunke, W.D.; Gerbaulet, C.; Hirth, L.; Jahn, M.; Kunz, F.; Lorenz, C.; Mühlenpfordt, J.; Reimann, J.; et al. Open Power System Data – Frictionless data for electricity system modelling. Appl. Energy 2019, 236, 401–409. [Google Scholar] [CrossRef]
- Muehlenpfordt, J. Data Package Time Series. 2018. Available online: https://data.open-power-system-data.org/time_series/2018-06-30 (accessed on 12 May 2024).
- Pfenninger, S.; Staffell, I. Data Package Weather Data. 2018. Available online: https://data.open-power-system-data.org/weather_data/2018-09-04 (accessed on 12 May 2024).
- Allison, D. How to Encode the Cyclic Properties of Time with Python. 2018. Available online: https://medium.com/@dan.allison/how-to-encode-the-cyclic-properties-of-time-with-python-6f4971d245c0 (accessed on 12 May 2024).
- Kaleko, D. Feature Engineering–Handling Cyclical Features. 2017. Available online: https://blog.davidkaleko.com/feature-engineering-cyclical-features.html (accessed on 12 May 2024).
- Zheng, A.; Casari, A. Feature Engineering for Machine Learning: Principles and Techniques for Data Scientists; O’Reilly Media: Sebastopol, CA, USA, 2018. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: http://tensorflow.org/ (accessed on 12 May 2024).
- Amarasinghe, K.; Marino, D.L.; Manic, M. Deep neural networks for energy load forecasting. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 1483–1488. [Google Scholar] [CrossRef]
- Sadouk, L. CNN approaches for time series classification. Time Ser. Anal.-Data Methods Appl. 2019, 5, 57–78. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aravena-Cifuentes, A.P.; Nuñez-Gonzalez, J.D.; Graña, M.; Altamiranda, J. Comparative Analysis of Traditional Statistical Models and Deep Learning Architectures for Photovoltaic Energy Forecasting Using Meteorological Data. Electronics 2025, 14, 4263. https://doi.org/10.3390/electronics14214263
Aravena-Cifuentes AP, Nuñez-Gonzalez JD, Graña M, Altamiranda J. Comparative Analysis of Traditional Statistical Models and Deep Learning Architectures for Photovoltaic Energy Forecasting Using Meteorological Data. Electronics. 2025; 14(21):4263. https://doi.org/10.3390/electronics14214263
Chicago/Turabian StyleAravena-Cifuentes, Ana Paula, J. David Nuñez-Gonzalez, Manuel Graña, and Junior Altamiranda. 2025. "Comparative Analysis of Traditional Statistical Models and Deep Learning Architectures for Photovoltaic Energy Forecasting Using Meteorological Data" Electronics 14, no. 21: 4263. https://doi.org/10.3390/electronics14214263
APA StyleAravena-Cifuentes, A. P., Nuñez-Gonzalez, J. D., Graña, M., & Altamiranda, J. (2025). Comparative Analysis of Traditional Statistical Models and Deep Learning Architectures for Photovoltaic Energy Forecasting Using Meteorological Data. Electronics, 14(21), 4263. https://doi.org/10.3390/electronics14214263









