Abstract
In strong clutter and maneuvering scenarios, radar track initiation faces the dual challenges of a low initiation rate and high false alarm rate. Although the existing deep learning methods show promise, the commonly adopted “feature flattening” input strategy destroys the intrinsic temporal structure and feature relationships of track data, limiting its discriminative performance. To address this issue, this paper proposes a novel radar track initiation method based on Dual-Attention Temporal Convolutional Network (DA-TCN), reformulating track initiation as a binary classification task for very short multi-channel time series that preserve complete temporal structure. The DA-TCN model employs the TCN as its backbone network to extract local dynamic features and innovatively constructs a dual-attention architecture: a channel attention branch dynamically calibrates the importance of each kinematic feature, while a temporal attention branch integrates Bi-GRU and self-attention mechanisms to capture the dependencies at critical time steps. Ultimately, a learnable gated fusion mechanism adaptively weights the dual-branch information for optimal characterization of track characteristics. Experimental results on maneuvering target datasets demonstrate that the proposed method significantly outperforms multiple baseline models across varying clutter densities: Under the highest clutter density, DA-TCN achieves 95.12% true track initiation rate (+1.6% over best baseline) with 9.65% false alarm rate (3.63% reduction), validating its effectiveness for high-precision and highly robust track initiation in complex environments.
1. Introduction
1.1. The Critical Role and Fundamental Challenges of Radar Track Initiation
In modern multi-target tracking systems, track initiation, as the foundational stage of the tracking process, directly impacts the effectiveness of subsequent track maintenance, data association, and situational awareness. This task aims to rapidly and accurately identify and establish the motion trajectories of true targets from discrete, noisy, and temporally irregular measurements obtained by radar, while effectively suppressing false tracks arising from background clutter, sensor noise, or interference. In high-stakes applications such as military air defense, air traffic control, and autonomous driving, the accuracy of track initiation is of paramount importance [1].
Radar track initiation consistently faces two fundamental and intertwined challenges: measurement origin uncertainty and target model uncertainty [2].
Measurement origin uncertainty stems from the complex electromagnetic environment. While detecting targets, a radar system inevitably receives a large volume of non-target echoes, known as clutter. This clutter can originate from natural sources such as ground terrain, sea waves, and atmospheric turbulence, or from the internal thermal noise of the sensor. In contemporary battlefields or congested urban environments, the number of clutter plots can far exceed that of true target measurements, creating severe low signal-to-clutter ratio conditions. Track initiation algorithms must operate in this environment, where any combination of two or more plots that appear kinematically related could constitute a candidate track. As clutter density increases, the number of candidate tracks grows exponentially [3], which not only imposes a substantial computational burden but also significantly elevates the risk of erroneously confirming a random combination of clutter plots as a true track, leading to a sharp increase in the false alarm rate.
Target model uncertainty arises primarily from the maneuvering behavior of non-cooperative targets. Unlike commercial aircraft that follow predetermined flight paths, military targets or unmanned aerial vehicles (UAVs) frequently execute high-speed, high-g maneuvers—such as serpentine movements, sharp turns, or rapid acceleration/deceleration—to evade detection or achieve tactical objectives. These maneuvers cause the trajectory of the target to deviate from simple kinematic models such as constant velocity or constant-rate turns. If a track initiation algorithm relies on a fixed, overly simplistic motion model to predict and associate plots, a true target measurement is likely to be incorrectly excluded from the association gate during a maneuver, resulting in track fragmentation or initiation failure. Therefore, the algorithm must possess sufficient robustness to accommodate the unknown and abrupt changes in a target’s motion patterns.
These two challenges collectively constitute the core dilemma of the track initiation problem. An algorithm must strike a delicate balance between suppressing a massive number of false combinations and confirming true trajectories with complex dynamic behaviors. In practice, the upper performance limit of the entire multi-target tracking system is largely determined by the track initiation stage. Both the failure to detect a high-threat target and the generation of numerous false tracks that consume the computational resources of subsequent processing stages can lead to the failure of the entire defense or surveillance mission. Consequently, developing a track initiation algorithm that maintains high performance under the dual challenges of dense clutter and high maneuverability is not merely a technical problem but a critical bottleneck in enhancing the capabilities of the entire surveillance and defense system.
1.2. From Traditional to Data-Driven Methods
To address the challenges of track initiation, research methodologies have evolved from traditional algorithms to modern data-driven approaches. Traditional algorithms are primarily categorized into two classes: sequential processing and batch processing.
Sequential processing methods, such as heuristic rule-based methods [4] and their various heuristic improvements [5,6,7], represent the most intuitive class of algorithms. Their core principle involves processing radar data on a scan-by-scan basis. A temporary observation track is established, and a predefined kinematic gate is used to attempt to associate new measurements with the existing observation track. If an association is successful, the track is extended; if successful associations occur over several consecutive scans, the track is confirmed as a true track. In ideal conditions with low clutter and stable target motion, these methods exhibit high efficiency due to their low computational cost and simple implementation. However, their fundamental weakness lies in an over-reliance on prior knowledge and rigid rules. When clutter density increases, multiple candidate plots may fall within the association gate, and the fixed association logic is easily disrupted, leading to a proliferation of false tracks. When a target performs an aggressive maneuver, its kinematic parameters may exceed the predefined thresholds, causing the loss of true tracks [8].
Batch processing methods adopt a different strategy, with the Hough transform [9] and its improved algorithms [10,11] being the most representative. This approach transforms the track initiation problem from the time-domain space to a parameter space. For instance, all points on a linear trajectory will correspond to multiple curves that intersect at a single point in the parameter space. By accumulating votes in this space and identifying peak points, trajectories present in the data can be detected. This method demonstrates strong robustness to noise and minor data loss. However, its inherent high computational complexity and substantial memory overhead make it difficult to meet the stringent real-time requirements of modern radar systems, especially when more complex motion models are considered, which further increases the dimensionality of the parameter space and leads to the “curse of dimensionality.” In recent years, research has also emerged that utilizes relative topological features between targets for track association to mitigate the effects of radar system bias, offering a new direction for batch processing methods [12].
Data-driven methods, propelled by advancements in computational power and the availability of massive datasets, have introduced the deep learning paradigm as a novel solution pathway for track initiation. The core idea is to reframe the problem as a data-driven binary classification task. Specifically, a large number of candidate tracks are first generated through a strategic process. The kinematic features of each candidate track are then extracted and fed into a deep neural network. The objective of the network is to learn a complex, non-linear decision boundary to distinguish whether a sequence of plots originates from a true target following physical laws of motion or is merely a combination affected by clutter. This end-to-end learning approach obviates the need for manually designing complex rules and precise kinematic models, theoretically enabling the network to automatically discover deeper and more robust patterns for differentiating true and false tracks from data.
1.3. Limitations in Existing Deep Learning Models
Although deep learning has brought a paradigm shift to track initiation, many current implementations suffer from a fundamental limitation: the widespread adoption of a “feature flattening” input construction strategy. A candidate track is inherently a structured two-dimensional (2D) entity, with dimensions corresponding to time steps and features. This 2D tensor contains rich structural information: the sequential relationship along the time axis reflects the target’s motion continuity, while the intrinsic correlation between different kinematic quantities along the feature axis reflects physical laws.
However, existing methods typically “flatten” this 2D tensor into a long one-dimensional (1D) vector through a simple concatenation operation before feeding it into the network. For example, a track composed of time steps, each with features, is forcibly converted into a 1D vector of length . While this approach may seem to simplify the input, it comes at a high cost. It completely destroys the inherent temporal dependencies of the data and the structural relationships among the multi-dimensional features, violating a critical principle of deep learning model design: respecting and leveraging the intrinsic inductive bias of the data.
Inductive bias refers to the set of additional assumptions a learning algorithm makes to generalize from finite data to unseen data. For instance, the tremendous success of Convolutional Neural Networks (CNNs) stems from the inductive biases of spatial locality and translation invariance embedded in their architecture [13]. By employing “feature flattening,” researchers are effectively discarding the most valuable temporal structure within the track data. This forces the neural network to expend a significant number of model parameters and a large amount of training data to re-learn the fundamental relationships of time and kinematics from an unstructured long vector—relationships that should have been preserved from the outset. Therefore, to truly unlock the potential of deep learning for the track initiation task, it is imperative to abandon this information-destroying preprocessing method and design network architectures capable of directly processing and understanding structured, temporal track data.
1.4. Contributions and Organization of This Paper
To address the aforementioned “feature flattening” problem, this paper proposes a novel Dual-Attention Temporal Convolutional Network (DA-TCN). Its core design philosophy is to preserve and fully exploit the original 2D structure of track data, redefining the track initiation task as a binary classification problem for very short, multi-channel time series that retain their complete temporal structure. The main contributions of this paper are as follows:
- DA-TCN directly processes a 2D tensor input with the shape of time step × feature dimension, which preserves the temporal correlation and feature semantics of the track data, and avoids the loss of information caused by “feature flattening” fundamentally.
- The model innovatively adopts a two-branch attention mechanism to dynamically learn the most important information dimensions in the trajectory data. The channel attention branch evaluates the importance of different kinematic features, while the temporal attention branch focuses on locating the key time nodes that determine the authenticity of the trajectory.
- A gated fusion mechanism is introduced to dynamically weight the fusion of the outputs of the dual attention branches, so that the network can dynamically adjust its dependence on the dual branches according to the specific characteristics of the candidate trajectories to achieve optimal information fusion.
- Comprehensive evaluations on a simulated dataset containing various complex, high-speed maneuvering patterns validate the proposed method. The results demonstrate that its performance is significantly superior to that of multiple baseline models that rely on feature flattening, proving the method’s effectiveness, robustness, and practical value for track initiation in high-clutter and target-maneuvering scenarios.
The remainder of this paper is organized as follows: Section 2 will provide a comprehensive review of related work, covering foundational deep learning architectures for sequence analysis, various advanced attention mechanisms, and feature fusion strategies, situating our work within the context of existing research. Section 3 will elaborate on the proposed DA-TCN framework, including its system pipeline, input construction method, and core model architecture. Section 4 will describe the experimental setup and evaluation metrics. Section 5 will present a detailed analysis and discussion of the experimental results, including comparative experiments, ablation studies, and visualization. Finally, Section 6 will summarize the entire paper and discuss future research directions.
2. Related Work
2.1. Foundational Deep Learning Architectures for Sequence Analysis
The core of track initiation is to classify a sequence of plots as either true or false, which is essentially a time-series binary classification task. For such tasks, researchers have developed various foundational deep learning architectures, each with its own advantages and application scenarios.
One-Dimensional Convolutional Neural Network (1D-CNN): Similar to the Convolutional Neural Networks (CNNs) used for image processing, 1D-CNNs extract local patterns in a sequence by sliding a convolutional kernel along the time axis [14]. Their advantages lie in strong parallel computing capabilities and high computational efficiency. By stacking multiple convolutional layers and using kernels of different sizes, they can capture features at various time scales. In the context of track initiation, 1D-CNNs can effectively capture local dynamic changes between adjacent plots, such as velocity and acceleration.
Recurrent Neural Network (RNN) and its Variants [15]: RNNs are classic models designed for processing sequential data. Their core lies in passing a hidden state between time steps through recurrent units, which theoretically enables them to capture temporal dependencies of arbitrary length. To address the gradient vanishing/explosion problem in traditional RNNs, the Long Short-Term Memory (LSTM) network and the Gated Recurrent Unit (GRU) were introduced. As a more lightweight variant, the GRU controls the flow of information through update and reset gates, demonstrating performance comparable to LSTM in many tasks with lower computational overhead. GRUs are widely used in track initiation to capture the contextual information of the entire candidate track sequence. To more comprehensively capture the sequence’s context, the Bidirectional Gated Recurrent Unit (Bi-GRU) was proposed. It processes the sequence using two independent GRU networks, one forward and one backward, ensuring that the output at any time point incorporates information from both before and after , thereby achieving a more profound understanding of the current time step.
Transformer: The Transformer model, proposed by Vaswani et al. [16], was initially applied in the field of natural language processing and quickly became the gold standard for sequence modeling. Its core is the Self-Attention mechanism, which discards the recurrent structure of RNNs and the local convolutional operations of CNNs. It directly captures global dependencies by calculating mutual importance scores between all pairs of elements in a sequence. This mechanism allows for efficient parallel computation and excels at processing long sequences. In track initiation tasks, the Transformer model is also used as a powerful baseline, capable of directly processing 2D temporal inputs and examining the intrinsic correlations between plots from a global perspective.
However, for a specialized task like track initiation, which typically involves very short sequences, the choice of these foundational architectures involves a significant trade-off. While the global self-attention mechanism of the Transformer is powerful, it may not be optimal for capturing the high-frequency dynamic changes between adjacent points in very short sequences; its strength lies in modeling long-range dependencies. The sequential processing mechanism of RNNs makes them difficult to fully parallelize. In contrast, the Temporal Convolutional Network (TCN) [17], as a special type of CNN architecture, can achieve both parallel computation and a large receptive field through the combination of causal and dilated convolutions. More importantly, by adjusting the dilation factor, a TCN can flexibly shift its focus.
2.2. Classification of Attention Mechanisms for Feature Optimization
Attention mechanisms, inspired by the human visual system, enable neural networks to focus their limited computational resources on the most informative parts of the input data. In the track initiation task, this means the model needs to learn to pay attention to the feature dimensions or time steps that are most indicative of a track’s authenticity. Based on their scope of action, relevant attention mechanisms can be classified as follows.
Efficient Channel Attention Network (ECA-Net) [18]: Addressing the issue that the dimensionality reduction operation introduced in earlier channel attention models like Squeeze-and-Excitation Networks (SENet) [19] to reduce computational load could harm performance, ECA-Net proposes a local cross-channel interaction strategy without dimensionality reduction. It achieves information exchange between channels through a 1D convolution with an adaptively determined kernel size, which is both efficient and avoids information bottlenecks. This mechanism allows the model to learn effective channel dependencies with extremely low parameter overhead.
Convolutional Block Attention Module (CBAM): CBAM [20] proposes a strategy of applying attention sequentially. It first uses a channel attention module to decide “what to focus on,” which leverages both global average pooling and global max pooling to generate channel weights. The channel-weighted features are then fed into a spatial attention module, which decides “where to focus on” by performing pooling operations across the channel dimension and incorporating a convolutional layer. This serial structure allows the model to refine features sequentially.
Self-Attention: As the core of the Transformer, Self-Attention dynamically generates a context-aware representation for each time step by calculating the association weights between all-time steps within a sequence. In track initiation, this means the model can automatically discover which measurement or motion state at a particular time point is most critical for determining the authenticity of the entire track.
Bidirectional Focal Attention (BiFA): Traditional attention mechanisms, when computing shared semantics, typically assign weights to all segments, even irrelevant ones receive a small weight, which can interfere with the final semantic representation and lead to semantic misalignment. To solve this, BiFA proposes a novel “focal attention” mechanism [21], whose core idea is to completely eliminate irrelevant segments rather than just reducing their weights. The mechanism operates in a three-step process: first, initial attention weights are pre-assigned based on cross-modal relationships; second, truly relevant segments are identified by calculating the relative importance of each segment with respect to all others; finally, attention weights are re-assigned and normalized only for these identified relevant segments, thereby concentrating all attention on the critical information.
The DA-TCN model proposed in this paper draws upon and develops these ideas by designing parallel channel and temporal attention branches, positing that “what to focus on” and “when to focus on” are two decouplable and equally important questions that should be analyzed independently before being intelligently fused.
2.3. Comparative Analysis of Feature Fusion Strategies
Once a model extracts multiple features from different branches or modules, how to effectively fuse them into a unified representation is a critical step that determines the model’s performance. Fusion strategies can range from simple to complex, and from static to dynamic.
Static Fusion Strategies: These are the most straightforward methods, employing fixed fusion rules regardless of the input data.
- Element-wise Summation: Models in the style of the Dual Attention Network for Scene Segmentation (DA-NET) [22] assume that features from different sources are semantically aligned and can be directly added. This method is computationally simple, but if the feature scales or semantic meanings differ significantly, it can lead to information interference.
- Concatenation Fusion: Models like Densely Connected Convolutional Networks (DenseNet) [23] concatenate different feature vectors along their dimensions, preserving all original information and delegating the fusion task to subsequent fully connected layers. This is a robust baseline approach, but the subsequent layers must learn a fixed fusion weighting that is the same for all samples.
Dynamic Fusion Strategies: These strategies can adaptively adjust the fusion method based on the specific content of the input data.
- Attentional Feature Fusion: Represented by the Attentional Feature Fusion (AFF) framework [24], this approach treats the fusion process itself as an attention process to be learned. Specifically, AFF uses a dedicated attention module (such as its proposed Multi-Scale Channel Attention Module, MS-CAM) that takes the features to be fused as input and outputs a set of weights. These weights are then used to perform a weighted sum of the original features. This elevates the fusion process from simple addition or concatenation to an intelligent, content-aware weighted average.
- Gated Fusion: This is a powerful and non-linear dynamic fusion mechanism. Its core is the introduction of a “gating unit,” typically a fully connected layer with a Sigmoid activation function. The output of this unit is a “gate” signal between 0 and 1. This signal controls the information flow from other branches through element-wise multiplication. A value of 1 means the information passes through completely, while a value of 0 means it is completely blocked. This mechanism endows the model with a “switch-like” capability to dynamically and non-linearly decide on the flow of information based on the input.
2.4. Current State of Deep Learning-Based Track Initiation Research
In recent years, the application of deep learning to radar track initiation has been a burgeoning field of research, showing several distinct trends. A mainstream paradigm is to transform the track initiation problem into a data-driven binary classification task, i.e., distinguishing between true and false tracks. Within this framework, researchers have explored various model architectures and processing pipelines.
For example, some studies adopt a two-stage “traditional method + deep learning” strategy, first using heuristic or logic-based methods to generate candidate tracks, and then using a 1D-CNN to perform a secondary discrimination on the kinematic features of these candidates, thereby learning a classification boundary superior to fixed thresholds [25]. Other research focuses on constructing more complex hybrid models to fuse spatio-temporal information. A common approach is to separately extract temporal variation vectors and spatial distribution vectors, and then process them with parallel deep learning modules. For instance, one work uses a GRU to capture temporal features while using a 1D-CNN to extract spatial features [26], or employs parallel GRU networks to process spatio-temporal features separately [27], finally fusing them and weighting them with a self-attention mechanism to enhance the model’s discriminative power.
Furthermore, the problem formulation has also diversified. Some researchers have attempted to reframe track initiation as an object detection task from computer vision, converting radar echo data over a period of time into an image-like 2D representation, and then using mature deep detection networks to directly detect and locate target trajectories within these images [28]. With the success of the Transformer model in sequence processing, it has also been introduced to the track initiation task. A representative method involves first using a Kalman filter to generate a temporary set of tracks containing both true and false tracks from the raw measurement data, and then feeding the kinematic features of these tracks into a Transformer model. The model’s core self-attention mechanism is used to directly capture global dependencies within the sequence, thereby efficiently extracting motion features and completing the classification [29].
Against this research backdrop, the DA-TCN method proposed in this paper has a clear positioning and innovation. It follows the mainstream technical route of using deep learning for classification and adopts an efficient hybrid processing pipeline. However, its core innovation lies in the fact that it does not simply apply off-the-shelf general-purpose models. Instead, it features a specialized architecture designed for the unique characteristics of the track initiation task—namely, processing very short, multi-channel time series that retain their complete 2D structure. By explicitly rejecting “feature flattening” and constructing a decoupled dual-attention and gated fusion architecture capable of adaptive arbitration, DA-TCN aims to overcome the mismatch between model design and the intrinsic properties of the data found in existing methods, providing a more targeted and efficient solution for high-precision track initiation in complex environments.
3. DA-TCN Framework
3.1. System Overview
The DA-TCN based track initiation method proposed in this paper constitutes a complete processing flow as shown in Figure 1. The process takes raw radar measurements as input and outputs confirmed, conflict-free target tracks, which mainly consists of four stages:
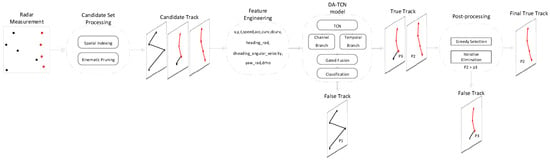
Figure 1.
Overall Framework of the DA-TCN Based Track Initiation Method.
- Candidate trajectory generation: in order to cope with the problem of exploding measurement combinations, a backtracking search strategy combining spatial indexing and kinematic constraint pruning is adopted in this phase. Specifically, discrete radar traces are first grouped by time and a KD-Tree [30] spatial index is constructed for each group to accelerate the neighborhood query. Subsequently, a depth-first recursive backtracking algorithm is used to extend the traces to the subsequent subgroups, starting from the starting time subgroup. In the extension process, the spatial search path is limited by the maximum search speed, and the KD-Tree is utilized to efficiently screen the candidate points and prune them based on the kinematic thresholds such as velocity and acceleration, so as to efficiently generate a collection of candidate trails conforming to the physical laws from a large number of combinations.
- Feature engineering: construct a 2D feature tensor for each candidate track that retains the complete spatial and temporal structure.
- DA-TCN classification and discrimination: Input the feature tensor into DA-TCN, the core model of this paper, to classify and discriminate between true and false tracks.
- Conflict resolution post-processing: since different candidate tracks may share the same radar point track, the high confidence track output from the model is post-processed in this stage. Specifically, a greedy strategy based on confidence ranking is adopted: first, all candidate tracks with confidence exceeding a preset threshold are filtered and ranked from high to low confidence; then, starting from the track with the highest confidence, it is added to the final set, and all conflicting tracks with which it shares the same point track are removed from the final set; the process is iterated until the list is empty, which ensures that each track is unique and outputs the final track without any ambiguities.
3.2. Input Construction and Feature Engineering
The core difference between the methodology of this paper and previous methods is the way in which the inputs to the trajectory data are constructed. In this study, the radar measurements are described using the Cartesian Coordinate System with horizontal coordinates , vertical coordinates , and timestamps . For consecutive scanning cycles, the set of radar measurements can be represented as , where is the set of all measurement points for the scanning cycle. A candidate track is formed by combining one radar measurement point from each consecutive scanning cycle to form a track sequence of length . In this study is set.
For such a candidate track consisting of four points, a feature tensor of shape is constructed by adding features as inputs to the DA-TCN model. The feature set of any candidate trajectory at each time step consists of the following components:
Original Cartesian coordinates and corresponding timestamps:
Speed: describes the magnitude of the instantaneous rate of target motion.
Acceleration: describes the target’s maneuvering state.
Curvature: describes the degree of curvature of the target trajectory.
Rate of change of curvature: describes the rate of change of the degree of curvature of the target trajectory.
Heading Angle: describes the direction of target movement.
Heading Angle Velocity: quantifies the target turning rate.
Yaw angle: measure the turning behavior, where is the heading angle.
Point Spacing: describes the distance between neighboring points.
The above differentials are computed by numerical difference methods, and the angular features are processed continuously to avoid jumping artifacts when −π and π are switched.
Before the feature tensor is fed into the model, a global min-max normalization method is employed to eliminate scale disparities among the different features and to accelerate model convergence. This method involves first iterating through all samples and time steps within the entire training dataset to compute the global minimum and maximum values for each of the 11 feature dimensions. Subsequently, all data are scaled to the interval using the following formula:
where is the original feature value, while and are the corresponding global minimum and maximum values for that feature, respectively. The term is a small positive constant () added to prevent division-by-zero errors in cases where a feature’s value is constant across the dataset. The tensor, normalized through this process, serves as the final input to the model.
3.3. DA-TCN Model Architecture
DA-TCN is the technical core of this paper, and its architecture is shown in Figure 2:
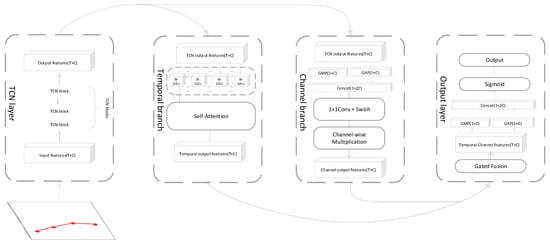
Figure 2.
Architecture of DA-TCN model.
It is designed to efficiently extract and fuse information from the structured feature tensor of . Before describing the overall data flow, the core technical components on which the model relies and their application value in this paper are first introduced:
Temporal Convolutional Networks (TCN): TCN is a convolutional architecture designed for sequential data, with the advantages of high parallel computation capability and gradient stabilization. For the very short sequence of length only 4 in this paper, this study pays more attention to the fine variations between neighboring time steps rather than the long-term dependence. Therefore, the TCN expansion rate used in the model is set to 1 and the convolution kernel size is 2 so that it focuses on capturing the local dynamic information of the highest frequency.
Bi-Directional Gated Recurrent Unit (Bi-GRU): GRU is a highly efficient recurrent neural network capable of capturing temporal dependencies. By processing sequences in both forward and backward directions, Bi-GRU is capable of generating representations for each point in time that contain complete contextual information, which is crucial for accurately understanding the state of the motion at a given moment.
Self-Attention: The Self-Attention mechanism focuses on the parts that are critical for decision making by calculating mutual importance scores between all elements within a sequence. In the track initiation task, it helps the model to localize to the critical time points where drastic maneuvers or measurement anomalies occur.
Dual-Pooling Channel Attention: While traditional channel attention mechanisms (e.g., SE-Net) usually rely only on global average pooling to extract channel statistics, this paper utilizes a dual-pooling channel attention mechanism to dynamically assess the importance of different feature channels. For trajectory data, the model can learn that features such as “acceleration” or “curvature” may be more discriminative than “position” itself under certain circumstances, and adaptively amplify the impact of these key features.
The DA-TCN data flow is as follows: an input feature tensor is first passed through a TCN backbone network consisting of 3 temporal residual blocks stacked together to extract the underlying temporal feature map . This feature map is fed into two attention branches:
- The channel attention branch: this branch generates weight vectors for the feature channels by performing global average pooling and maximum pooling in the time dimension, and splicing the results to perform a nonlinear transformation. Finally, by element-wise multiplication.
- Temporal Attention Branch: This branch first inputs into a Bi-GRU network to capture the complete contextual information of each time point to generate the hidden state sequence . Subsequently, a self-attention mechanism is applied to the sequence to compute the importance weights of each time step and generate the weighted sequence representation .
The outputs of the two branches and are not simply spliced or summed, but are integrated through a gated fusion mechanism. This mechanism aims to solve the problem of fragmentation of feature and timing information in the existing methods, and realize the dynamic and adaptive fusion of the two. Specifically, the output features of the two branches are spliced and fed into a fully connected layer with a Sigmoid activation function to generate a learnable gating signal .
The gating signal computational formula can be expressed as follows:
where and are the learnable parameters of the fully connected layer, represents the splicing operation of the two branch features.
The fused feature is calculated by the following equation:
Finally, the fused feature is globally averaged, maximally pooled, and the result is spliced and fed into a fully connected layer with a Sigmoid activation function, which outputs a scalar value between 0 and 1 indicating the confidence level that the candidate track is a real track.
Given that this task is a binary classification problem to determine the authenticity of a track, the model employs the binary cross-entropy loss function. This function effectively measures the discrepancy between the model’s predicted probabilities and the true labels, imposing a significant penalty on high-confidence incorrect predictions. Its formula is defined as follows:
where is the true label of the sample, and is the confidence score predicted by the model that the track is authentic.
To account for the potential imbalance in the number of true and false tracks within the training data, this study incorporates a Class Weighting mechanism into the training process. Based on the class distribution in the training set, this mechanism assigns a higher weight to the loss contribution of the minority class. This prevents the model from developing a bias towards the majority class and enhances its ability to identify samples from the underrepresented class.
For model optimization, the Adam optimizer is employed to update the parameters, with an initial learning rate set to . The Adam optimizer combines the benefits of momentum and adaptive learning rates, enabling it to dynamically adjust the update step size for different parameters, which facilitates rapid and stable convergence. To further enhance generalization, an Early Stopping strategy is integrated into the training regimen. This strategy terminates the training process prematurely if performance on the validation set ceases to improve, thereby effectively preventing overfitting.
The learnability of the gating signal facilitates a dynamic fusion strategy that adaptively weights the channel and temporal branches, thereby overcoming the fragmented feature and temporal processing inherent in existing methods.
4. Experimental Evaluation
4.1. Simulation Environment and Data Set
To comprehensively evaluate the algorithm’s tracking performance in highly dynamic scenarios, this study constructed a simulation dataset covering a wide range of maneuvering modes. Given the significant challenges in obtaining real-world data for highly dynamic targets with true trajectories, this study employs a physics-based simulation method to generate data samples.
Unlike existing studies that often use uniform linear motion models, this study focuses on generating maneuvering targets to more realistically simulate modern airspace confrontation scenarios, so as to more rigorously evaluate the algorithm’s robustness and generalization capabilities.
The dataset consists of 50,000 positive samples (real trajectories) and 50,000 negative samples (false trajectories), and each trajectory consists of 4 measurement points with consecutive scanning periods set to 5 s and a radar detection range of 100 km.
The generation of true tracks follows the principle of kinematic consistency. A modified coordinated turn model is utilized, which allows for both acceleration and yaw angular velocity of the target. The trajectory generation adheres to a standard second-order kinematic model, where the target’s tangential acceleration and angular velocity are assumed to be constant within a short time window, a common assumption in the field of target tracking. To simulate diverse maneuvering behaviors, five different sets of velocity and acceleration intervals were established. For each true track, its initial velocity, tangential acceleration, and yaw rate were randomly sampled once from their respective intervals and held constant for the 4-time steps of its generation. This ensures that each trajectory is physically realizable, kinematically smooth, and logically self-consistent.
The key kinematic parameters were set with reference to publicly available performance data of real aircraft:
- Velocity Range: [100, 1100] m/s, covering various targets from low-speed UAVs to high-speed reconnaissance aircraft.
- Tangential Acceleration Range: [−0.5, 4.5] m/s2, simulating typical aircraft acceleration and deceleration capabilities.
- Yaw Rate Range: [−2, 2] deg/s, slightly below the standard-rate turn to simulate sustained tactical maneuvers.
Through this method, this study ensures that the generated positive samples are not only physically plausible but also representative of various real-world scenarios, from stable flight to maneuvering.
The generation of false trajectories is designed to simulate “ghost” tracks arising from clutter, noise-induced false alarms, or association errors, with their core characteristic being kinematic inconsistency. To achieve this, a mechanism of resampling at each time step is employed to generate negative samples: for each false track, its acceleration and yaw rate are independently and randomly sampled at each time step. Their parameter ranges were intentionally expanded to increase the challenge:
- Yaw Rate Range: [−20, 20] deg/s, simulating physically impossible, drastic changes in direction;
- Tangential Acceleration Range: [−5, 45] m/s2, simulating velocity pulses that do not conform to the laws of inertia.
This method phenomenologically abstracts the essence of a false track—the violation of kinematic continuity—thereby effectively testing the algorithm’s fundamental ability to discriminate between tracks.
The positive and negative sample generation simulation parameters are shown in Table 1:

Table 1.
Simulation Parameters for Positive and Negative Sample Generation.
In order to simulate the real radar detection environment, clutter and measurement errors are added to the simulation scenario [31]. The clutter points obey the spatial uniform distribution in the monitoring area, while the number of clutter points appearing in each scanning cycle obeys the Poisson distribution, and its mean value parameter is varied from 50 to 250 in the experiment to simulate the environment from sparse to dense clutter. The number of clutter points is generated by an inverse function transformation [32]: first a uniformly distributed random number is generated in the interval and then the smallest non-negative integer is found that satisfies the following inequality:
The measurement error of the radar is modeled by adding zero-mean Gaussian noise to the polar coordinate representation of the true position, where the standard deviation of the ranging error is set to 100 m and the standard deviation of the angular error is set to 0.2 degrees.
Representative samples obtained from the simulation experiments are presented in Figure 3.
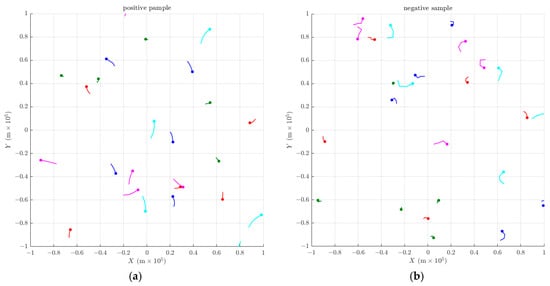
Figure 3.
(a) Representative Examples of Positive Samples; (b) Representative Examples of Negative Samples. The 25 trajectories in each panel are composed of five trajectories from each of the following speed intervals: [100, 300), [300, 500), [500, 700), [700, 900), and [900, 1100] m/s. Distinct colors are used to denote these different speed ranges.
4.2. Baseline Modeling and Evaluation Metrics
In order to validate the superiority of the proposed method, three deep learning-based track initiation methods are selected as the baseline in this study. The common feature of these models is that they all adopt a “feature flattening” strategy to process the input data, which is in direct contrast to the structure preserving method proposed in this study. Additionally, a general Transformer model was included as another point of comparison.
CNN-BASED: This model is a generalized architecture based on a one-dimensional convolutional neural network. It splices the kinematic features of candidate track across multiple time steps into a one-dimensional long vector, which is then input to the model for classification [25].
1DCNN-GRU: This model is a hybrid architecture that distinguishes feature vectors into temporal variation vectors and spatial distribution vectors. Among them, 1DCNN is used to extract spatial distribution features, while GRU is used to process time-varying features, and finally fuses the two for discrimination [26].
GRU-GRU: This model also distinguishes features into temporal and spatial vectors, but both vectors are processed by an independent GRU network to extract their respective deep features and finally fused for classification [27].
Transformer: This model employs a standard Transformer encoder architecture. Similar to the DA-TCN in this study, it directly accepts a 2D temporal input. The input data is first mapped to the feature dimension via a Dense layer and combined with positional encoding. It is then fed into a Transformer encoder containing multi-head self-attention and a feed-forward network, which captures global dependencies within the sequence. Finally, a fully connected layer and a Softmax layer output the classification result [29].
4.3. Evaluation Metrics
This paper adopts the three industry-recognized core metrics that are used to comprehensively evaluate the performance of the track initiation algorithm:
- True Track Initiation Rate : This metric measures the ability of the algorithm to discover real targets, defined as the ratio of the number of real trajectories successfully initiated to the total number of real trajectories in the scene.
- False Track Alarm Rate : This metric measures the ability of the algorithm to suppress clutter and false combinations, and is defined as the ratio of the number of false trajectories incorrectly initiated as real trajectories to the total number of all initiated trajectories.
- Average Start Time : This metric measures the computational efficiency of the algorithm and is defined as the average time required to complete a complete track initiation task.
5. Results and Analysis
This section aims to comprehensively evaluate the track initiation performance of the proposed DA-TCN model in complex environments through a series of simulation experiments and to validate the effectiveness of its core designs (dual-attention mechanism, gated fusion). The experiments include: a performance comparison with baseline models and the Transformer model, an ablation study of the model’s internal components, a comparison with other advanced attention and fusion strategies, a visualization analysis of the attention mechanisms, a hyperparameter sensitivity analysis, and an assessment of computational complexity.
5.1. Comparative Performance in High Clutter Maneuvering Scenarios
To simulate a challenging operational environment, a scenario was designed with 25 maneuvering targets. Clutter points, following a Poisson distribution with mean parameters () of 50, 100, 150, 200, and 250, were added in each scan cycle. For each clutter density, 50 Monte Carlo experiments were conducted, and the averaged results are presented in Table 2, Figure 4, Figure 5 and Figure 6 illustrate the performance comparison between DA-TCN and each baseline model under different clutter densities.

Table 2.
Performance comparison of different models under various clutter densities.
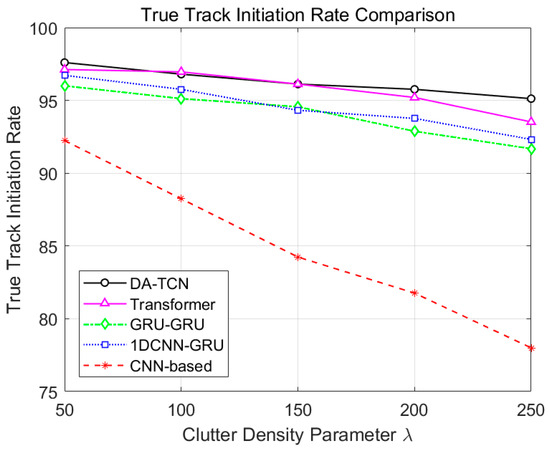
Figure 4.
Comparison of True Track Initiation Rate of different models.
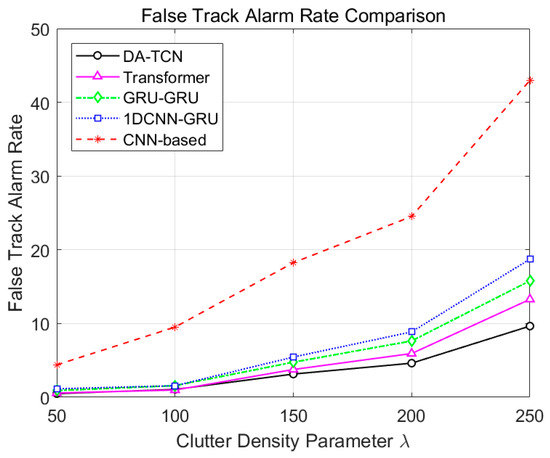
Figure 5.
Comparison of False Track Alarm Rate between models.
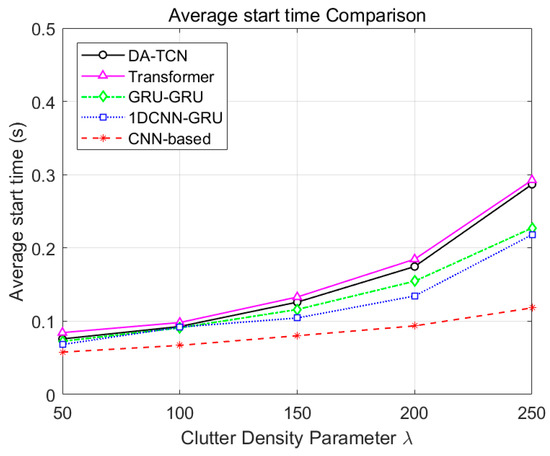
Figure 6.
Comparison of Average Start Time across models.
True Track Initiation Rate : As shown in Figure 4, the performance of all algorithms decreases with the increase of clutter density , but DA-TCN exhibits optimal robustness. In the low clutter environment of , the performance of DA-TCN has slightly outperformed that of not only 1DCNN-GRU and GRU-GRU but also the Transformer model. When the clutter density increases to the harsh environment of , the performance advantage of DA-TCN becomes more and more significant. This indicates that its structure-preserving input and dual-attention mechanism are particularly effective at rejecting the kinematically inconsistent tracks formed by random clutter. The feature-flattening baselines suffer severely, as the loss of structural information makes them unable to distinguish the kinematic consistency of true tracks from dense interference. While the Transformer is powerful, its global attention mechanism can be disrupted by dense clutter, whereas DA-TCN’s focused approach proves more resilient.
False Track Alarm Rate : DA-TCN maintains a low across all clutter densities and grows the most gently at all clutter densities. This is primarily attributed to the complementary strengths of the dual-attention branches. The architecture’s high sensitivity to kinematic and logical inconsistencies in both the channel and temporal dimensions allows it to accurately identify and suppress false tracks formed from random clutter combinations that may appear continuous but are physically implausible.
In terms of the Average Start Time : the time consumed by all algorithms increases with the increase in clutter density, which is due to the increase in the number of candidate tracks. DA-TCN exhibits better performance than the Transformer in this regard, but due to their more refined architectures, both have slightly higher computation times than the other baseline models. However, this increase is moderate and does not show exponential growth, indicating good scalability. Considering the great improvement of DA-TCN in the two key performance metrics of and , especially the strong suppression of false tracks in strong clutter environments, this moderate increase in computational cost is reasonable, and its overall efficiency is still within the real-time requirements of most radar systems.
The results of an experiment in environment is shown in Figure 7:
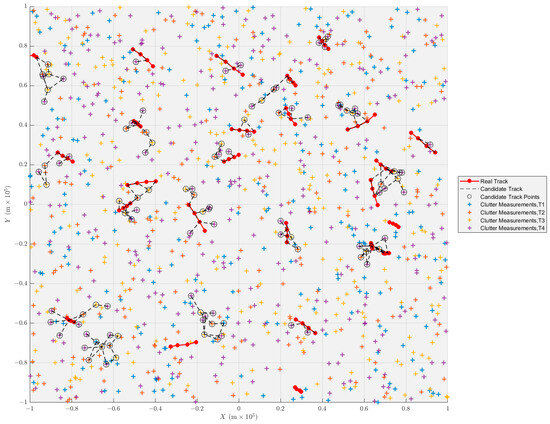
Figure 7.
Experimental results in a particular environment, 25 real tracks were successfully initiated and no false tracks were initiated incorrectly.
5.2. Analysis of Model Component Effectiveness
To precisely quantify the contribution of each innovative component within DA-TCN to the overall performance, a series of ablation experiments were conducted in the most demanding clutter environment (). The results are shown in Table 3.

Table 3.
Ablation study of DA-TCN components.
Based on the results, the contribution of each component is analyzed as follows:
- The underlying TCN backbone network has been able to achieve better performance than the baseline model, confirming the initial advantages of preserving the temporal structure.
- Analysis of the channel attention branch shows that introducing a simple channel attention mechanism (using Global Average Pooling, GAP) to the TCN backbone significantly reduces from 14.0466% to 9.885%, demonstrating the effectiveness of dynamically weighting the 11 kinematic features. However, employing the dual-pooling channel attention module yields a better of 95.04%. This suggests that for discriminating maneuvering targets, relying solely on global average pooling can obscure critical transient peak information. The dual-pooling mechanism more effectively captures abrupt changes in features like “acceleration” or “curvature” within the short sequence, thereby enhancing the identification of true targets.
- In the temporal attention branch, introducing a Bi-GRU as the base reduces to 13.0058%, confirming the necessity of capturing the full sequence context. While TCN excels at extracting local dynamics, the final judgment of a track’s authenticity depends on the overall evolutionary logic of the sequence, which Bi-GRU provides by generating a context-aware representation for each time step. Further integrating a multi-head attention mechanism on top of the Bi-GRU degrades performance, suggesting that this mechanism is overly complex for such short sequences and hinders convergence. In contrast, integrating self-attention achieves a of 10.2506%. This proves that self-attention effectively helps the model pinpoint key nodes where sharp maneuvers or measurement anomalies occur, thus efficiently suppressing tracks that do not conform to kinematic logic.
- Finally, the complete DA-TCN with Gated Fusion achieves the best performance on both metrics simultaneously, especially the simultaneous enhancement on and . This decisively proves the superiority of the gated fusion mechanism: instead of a fixed combination of the two-branch information, it adaptively learns the fusion weights according to the characteristics of the input trajectories, and thus makes more accurate and robust decisions.
5.3. Comparison with Other Attention and Fusion Mechanisms
To comprehensively evaluate the performance of the proposed DA-TCN model, it was compared against a general Transformer-based sequence model and several TCN variants integrated with other novel attention mechanisms. All experiments were conducted in the most severe clutter environment (). The results are summarized in Table 4.

Table 4.
Performance comparison of DA-TCN with other attention and fusion mechanisms.
Analysis of the single-path attention models reveals that the Transformer, as a general-purpose sequence model, performs worse than all TCN-based variants. This suggests that for processing the very short, multi-channel time-series data characteristic of track initiation, the TCN backbone is more advantageous for capturing local dynamic features than global self-attention. Among the TCN variants, TCN-ECA, focusing solely on channel attention, achieves one of the highest scores but has a relatively high . Conversely, TCN-BiFA, using a complex temporal focal attention mechanism, achieves the lowest but at the cost of a significantly lower and the highest computational expense. TCN-CBAM, with its sequential fusion, provides balanced but unremarkable performance. These single-path models expose a fundamental issue: the model is forced to compromise between “what features to focus on” and “what moments to focus on.” This strongly validates the necessity of the parallel dual-branch architecture proposed in this paper, which decouples the channel and temporal attention computations.
This study further compared different branch fusion strategies. The element-wise summation used in the DA-NET style model resulted in a high of 11.21%, indicating that simple information addition can cause feature interference and fail to effectively suppress false tracks. The AFF style, which uses a more complex MS-CAM module to learn the fusion, still yielded a of 10.89% while adding computational overhead. Concatenation fusion is a robust baseline that preserves all information, but it relies on subsequent fully connected layers to learn a fixed fusion weighting, lacking flexibility.
In contrast, the gated fusion mechanism employed by DA-TCN achieves the best overall performance. This mechanism is not a simple static fusion. Instead, it uses a lightweight gating unit to dynamically generate a scalar weight, , based on the features output by the two branches. This data-dependent weighting allows the model to adaptively balance the importance of channel and temporal information according to the unique characteristics of each track. For instance, when a track exhibits chaotic temporal logic, the model can learn to increase the weight of the temporal branch to suppress it as a false track. This intelligent and efficient fusion strategy ultimately achieves the optimal balance between and , validating its superior design.
5.4. Visualization and Interpretability Analysis of Attention Mechanisms
To gain deeper insight into the internal decision-making process of the DA-TCN model and to verify its interpretability, this study conducted a visualization analysis of the model’s temporal attention matrix, channel attention weights, and gated fusion weights. Figure 8 and Figure 9 show representative visualization results for a true track and a false track, respectively, clearly revealing the model’s attention distribution and fusion strategy across different dimensions.
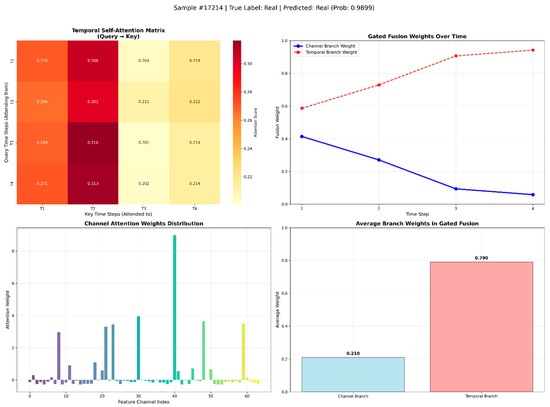
Figure 8.
Representative visualization results for a true track.
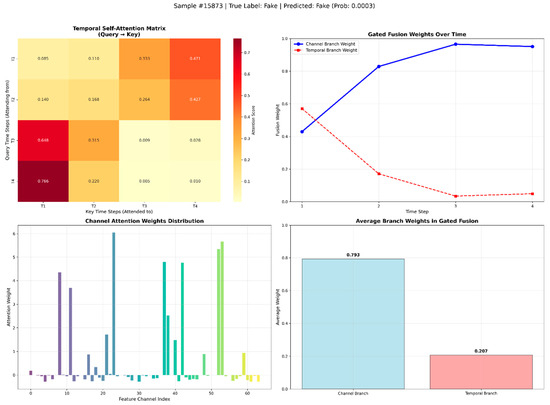
Figure 9.
Representative visualization results for a false track.
The analysis reveals the following:
Temporal Attention Analysis: In Figure 8 (true track), the temporal attention matrix shows a relatively uniform and smooth distribution. The query at each time step tends to focus on T1 and T2, indicating that when confirming the track as a kinematically smooth and logically consistent true track, the model’s attention is not concentrated on a single abrupt point but rather integrates the motion states from the early part of the sequence to confirm its continuity. Conversely, in Figure 9 (false track), the attention distribution is highly concentrated and sharp. This drastic differentiation in attention weights and the anomalous focus on later time steps clearly indicate that the model has detected a rupture in the kinematic logic within the false track’s temporal evolution. This confirms the effectiveness of the temporal attention branch in capturing dependencies at critical time nodes and identifying trajectories that defy kinematic logic.
Channel Attention Analysis: The distribution of channel attention weights reveals the model’s ability to dynamically assess different kinematic features. The significant difference in channel attention distributions between the two samples shows that the model can adaptively adjust its reliance on different feature dimensions based on the track’s characteristics. In Figure 8, the model assigns significant positive weights to features in certain channel ranges. In Figure 9, the model’s focus is entirely different, indicating that it leverages kinematic implausibility to identify the false track. This confirms the critical role of the channel attention branch in dynamically calibrating the importance of multi-dimensional features.
Gated Fusion Analysis: The visualization of the gated fusion mechanism provides the most compelling evidence of DA-TCN’s adaptive decision-making capability. In Figure 8, the gate weight is clearly biased towards the temporal branch, indicating that when judging a kinematically smooth true track, the model places more trust in the “kinematic logic consistency” evidence provided by the temporal branch. In Figure 9, however, the gate weight shifts significantly towards the channel branch. This shows that when the temporal branch detects a logical break and the channel branch simultaneously identifies feature anomalies, the fusion mechanism intelligently chooses to prioritize the channel evidence, leading to a high-confidence rejection of the false track. This process exemplifies the dynamic arbitration capability of the gated fusion mechanism in complex decision scenarios.
In summary, this analysis demonstrates that DA-TCN does not simply combine temporal and channel information. Instead, it constructs a hierarchical, interpretable, and dynamic decision-making framework: the dual-attention branches extract discriminatory evidence from the independent dimensions of motion logic and feature representation, while the gated fusion mechanism adaptively integrates these clues based on the specific patterns of the input sample to achieve more accurate and robust track discrimination.
5.5. Model Configuration and Hyperparameter Sensitivity Analysis
To ensure the reproducibility of the experiments and to clearly define the proposed model, the specific architecture and key hyperparameter settings of the DA-TCN model are summarized in Table 5.

Table 5.
Summary of model architecture and key hyperparameter settings.
To further investigate the impact of key hyperparameters on performance and computational complexity, and to validate the reasonableness of the chosen configuration, a series of hyperparameter sensitivity analyses were conducted on an NVIDIA RTX 4060 platform. The analysis primarily examined the effects of the TCN backbone’s width (with channel counts in subsequent branches adjusted accordingly), depth, and the use of dilated convolutions on model performance, inference time, parameter count, and FLOPs. The results are summarized in Table 6.

Table 6.
Hyperparameter sensitivity analysis of the model.
The analysis reveals the following:
- Impact of Network Width: Reducing the channel width to 32 significantly decreases the parameter count and FLOPs but leads to a noticeable drop in performance, especially a sharp increase in , indicating insufficient model capacity. Increasing the width to 128 dramatically raises the parameter count and FLOPs, yielding a slight improvement in but a minor degradation in , with a sharp rise in inference time. This suggests diminishing returns and unnecessary complexity. Therefore, a width of 64 strikes an effective balance between performance and efficiency.
- Impact of Network Depth: Decreasing the number of TCN blocks to 2 reduces complexity but results in a clear increase in , suggesting that insufficient depth hinders the full extraction of dynamic features. Increasing the depth to 4 adds complexity and provides only marginal gains in while slightly increasing . For a very short sequence of length 4, a deeper network does not yield significant benefits; three TCN blocks are sufficient.
- Impact of Dilated Convolutions: With nearly identical parameter counts and FLOPs, the model using dilated convolutions shows a significant performance degradation. This aligns with the ablation study findings and confirms that for the short-sequence track initiation task, expanding the receptive field is not only unnecessary but can also be detrimental by skipping adjacent time steps, thereby interfering with the capture of local, high-frequency dynamics.
In conclusion, the hyperparameter sensitivity analysis demonstrates that the final model configuration (width = 64, depth = 3, no dilation) achieves the optimal trade-off among true track initiation rate, false track suppression, and computational efficiency, validating the effectiveness and reasonableness of this setup.
5.6. Computational Complexity and Efficiency Analysis
Beyond model performance, computational complexity and operational efficiency are critical metrics for assessing the practicality of a track initiation algorithm. This study conducted a comprehensive evaluation of all compared models on parameter count (Params), floating-point operations (FLOPs), convergence speed (epochs to converge), training time, training speed, average single-sample inference time, and inference throughput. The results are summarized in Table 7.

Table 7.
Summary of computational efficiency metrics for all compared models.
The analysis of the table reveals the following:
- Model Complexity: The parameter counts and FLOPs of DA-TCN are comparable to the DA-Net style model and are moderate compared to models with complex attention or modulation mechanisms like AFF and TCN-BiFA. However, DA-TCN is significantly more complex than lightweight single-path models (TCN-CBAM, TCN-ECA), the Transformer, and the traditional baselines. This is primarily due to its parallel dual-branch architecture and the additional computational load from the Bi-GRU and self-attention mechanisms in the temporal branch.
- Training Efficiency: DA-TCN requires 83 epochs to converge, has the longest total training time, and a lower training speed than most competitors. This indicates that its complex structure and gated fusion mechanism require more iterations for full parameter optimization.
- Inference Efficiency: DA-TCN’s single-sample inference time is 5.33 ms, with a throughput of 187 samples/s, which is similar to the DA-Net style model but significantly slower than more streamlined architectures like the Transformer and lightweight TCN variants. This further reflects the inference overhead introduced by the parallel structure and complex internal modules.
5.7. Section Summary
This section provided a systematic and comprehensive evaluation of the DA-TCN track initiation method through simulation experiments. The results demonstrate that in scenarios with high clutter and maneuvering targets, DA-TCN significantly outperforms traditional baseline models, the general-purpose Transformer architecture, and various TCN variants with other attention and fusion strategies on the key performance indicators of true track initiation rate and false track suppression. Ablation studies and hyperparameter analysis validated the effectiveness of the core components and the reasonableness of the final configuration. Furthermore, attention visualization analysis revealed the model’s internal mechanism for dynamically fusing channel and temporal information, enhancing its interpretability. Although DA-TCN incurs a certain computational overhead, its significant advantages in tracking accuracy and robustness fully demonstrate its effectiveness and practical value for high-precision track initiation in complex environments.
6. Conclusions
In this paper, a novel radar track initiation method based on Dual-Attention Temporal Convolutional Network (DA-TCN) is proposed to address the limitation of “feature flattening” that generally exists in existing deep learning track initiation methods. The core of this method is to decouple and analyze the trajectory information from two dimensions, namely, feature and time series, by preserving the two-dimensional structure of the trajectory data and designing a dual-attention mechanism to dynamically focus on the trajectory information. Ultimately, the dual-branch information is adaptively fused through a learnable gating mechanism, which enables the model to intelligently weigh the information in different dimensions according to the unique characteristics of each candidate trajectory, and thus make more accurate discriminations.
Comprehensive experimental evaluations in simulation environments containing multiple complex maneuvering modes and different densities of clutter show that the proposed DA-TCN method significantly outperforms multiple baseline models relying on feature flattening strategies in terms of both the true track initiation rate and false track suppression ability, especially in the demanding scenarios with high clutter and maneuverability. The ablation experiments further quantify and confirm the critical role of each innovative component in the model, especially the dual-attention and gating fusion mechanisms, in enhancing the overall performance.
Despite the promising performance achieved by the DA-TCN model, it possesses certain inherent limitations regarding its practical application. First, the model is highly dependent on the completeness of the input data. The DA-TCN presented in this study operates on fixed-length, complete plot sequences, meaning it cannot directly handle cases of missing plots, such as those caused by radar detection failures. This contrasts with some traditional methods capable of processing incomplete sequences using statistical approaches or “N/M” rules, thus placing higher demands on preceding data processing and fusion stages. Second, concerning computational complexity and efficiency, DA-TCN’s pursuit of higher discrimination accuracy through a parallel dual-branch architecture, which integrates modules like Bi-GRU and self-attention, inevitably introduces additional computational overhead. Experimental data indicate that, compared to lightweight baseline models and the Transformer, DA-TCN has a significantly higher parameter count and FLOPs, resulting in the longest training time, a relatively high single-sample inference latency, and lower throughput. This trade-off between performance and efficiency may pose challenges for deployment on edge devices with highly constrained computational resources.
In summary, this study provides an efficient, accurate and robust solution to the radar track onset problem in complex environments, validating the importance of respecting and utilizing the intrinsic structure of the data in deep learning model design. Future work will be directed at addressing the aforementioned limitations. The primary objectives will be: first, to enhance the model’s adaptability to incomplete sequences and variable-length inputs to improve its robustness in real-world scenarios; and second, to explore model light weighting techniques—such as knowledge distillation, network pruning, and quantization—to find an optimal balance between performance and efficiency, thereby increasing the method’s practicality and deployment flexibility.
Author Contributions
Conceptualization, H.W.; methodology, H.W.; investigation, H.W.; writing—original draft, H.W. and Y.H.; writing—review and editing, H.W. and Y.H.; data curation, Y.H.; formal analysis, M.L.; validation, M.L.; project administration, W.C.; supervision, W.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are not publicly available due to privacy or ethical restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mayor, M.A.; Carroll, R.L. A Multi-Target Track Initiation Algorithm. In Proceedings of the 1987 American Control Conference, Minneapolis, MN, USA, 10–12 June 1987; pp. 1128–1130. [Google Scholar] [CrossRef]
- Skolnik, M. Radar Handbook, 3rd ed.; McGraw-Hill Education: New York, NY, USA, 2008. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Trunk, G.V.; Wilson, J.D. Track initiation of occasionally unresolved radar targets. IEEE Trans. Aerosp. Electron. Syst. 1981, 17, 122–130. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, W.; Pan, M.; Liu, D. A novel track initiation method based on rule knowledge and deep detection network. In Sixteenth International Conference on Signal Processing Systems (ICSPS 2024); SPIE: Bellingham, WA, USA, 2024; Volume 13559, pp. 1256–1267. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, F.; Chen, X.; Cheng, M.; Hu, Q.; He, S. Track Initiation Method Based on Deep Learning and Logic Method. In Proceedings of the 2023 7th International Conference on Machine Vision and Information Technology (CMVIT), Xiamen, China, 24–26 March 2023; pp. 57–61. [Google Scholar] [CrossRef]
- Konopko, M.; Malanowski, M.; Hardejewicz, J. Multi-Hypothesis Track Initialization with the Use of Multiple Trajectory Models. In Proceedings of the 2021 21st International Radar Symposium (IRS), Berlin, Germany, 21–22 June 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Blackman, S.; Popoli, R. Design and Analysis of Modern Tracking Systems; Artech House: Norwood, MA, USA, 1999. [Google Scholar]
- Smith, M.C. Feature space transform for multitarget detection. In Proceedings of the 1980 19th IEEE Conference on Decision and Control including the Symposium on Adaptive Processes, Albuquerque, NM, USA, 10–12 December 1980; pp. 835–836. [Google Scholar]
- Dong, X.; Hao, C.; Chunsheng, X.; Jiwei, L. A new Hough transform applied in track initiation. In Proceedings of the 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet), Xianning, China, 16–18 April 2011; pp. 30–33. [Google Scholar] [CrossRef]
- Zeng, L.; Xiao, G.; Ding, C.; He, Y. Track initiation based on adaptive gates and fuzzy Hough transform. SIViP 2023, 17, 4057–4065. [Google Scholar] [CrossRef]
- Wei, S.; Zhou, X.; Wang, J.; Pang, R.; Li, X.; Liu, Q. Adaptive Multi-Radar Anti-Bias Track Association Algorithm Based on Reference Topology Features. Remote Sens. 2025, 17, 1876. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Ige, A.O.; Sibiya, M. State-of-the-Art in 1D Convolutional Neural Networks: A Survey. IEEE Access 2024, 12, 144082–144105. [Google Scholar] [CrossRef]
- Mienye, I.D.; Swart, T.G.; Obaido, G. Recurrent Neural Networks: A Comprehensive Review of Architectures, Variants, and Applications. Information 2024, 15, 517. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 11531–11539. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Liu, C.; Mao, Z.; Liu, A.-A.; Zhang, T.; Wang, B.; Zhang, Y. Focus Your Attention: A Bidirectional Focal Attention Network for Image-Text Matching. In Proceedings of the 27th ACM International Conference on Multimedia (MM ’19), Nice, France, 21–25 October 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 3–11. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual Attention Network for Scene Segmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3141–3149. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef]
- Dai, Y.; Gieseke, F.; Oehmcke, S.; Wu, Y.; Barnard, K. Attentional feature fusion. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Online, 5–9 January 2021; pp. 3560–3569. [Google Scholar]
- Xiong, F.; Wang, G.; Bai, Y.; Bian, L. Radar track initiation method based on the convolutional neural network. Electron. Meas. Technol. 2020, 43, 78–83. [Google Scholar] [CrossRef]
- Shen, G.; Xu, X.; Fan, Y. A track initiation algorithm based on temporal-spatial characteristics of radar measurement. J. Terahertz Sci. Electron. Inf. Technol. 2022, 20, 1269–1276. [Google Scholar] [CrossRef]
- Yang, F.; Xia, X.; Gao, T. A Deep Learning-Based Radar Track Initiation Algorithm with Spatiotemporal Feature Fusion. In Proceedings of the 2024 13th International Conference on Control, Automation and Information Sciences (ICCAIS), Ho Chi Minh City, Vietnam, 26–28 November 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, S.; Li, H.; Mu, H. A novel multi-target track initiation method based on convolution neural network. In Proceedings of the 2017 International Workshop on Remote Sensing with Intelligent Processing (RSIP), Shanghai, China, 18–21 May 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Yang, D.; Zhao, G.; Li, D.; Li, S. A track initiation method based on the combination of Kalman filtering and the transformer model. In Proceedings of the IET International Radar Conference (IRC 2023), Chongqing, China, 3–5 December 2023; pp. 980–986. [Google Scholar] [CrossRef]
- Bentley, J.L. Multidimensional Binary Search Trees Used for Associative Searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Skolnik, M.I. Introduction to Radar Systems, 3rd ed.; McGraw-Hill: New York, NY, USA, 2001; pp. 385–435. [Google Scholar]
- Ross, S.M. Simulation, 5th ed.; Academic Press: Boston, MA, USA, 2013; pp. 69–73. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).