LPI Radar Waveform Modulation Recognition Based on Improved EfficientNet
Abstract
1. Introduction
- A deep network architecture based on improved EfficientNet is proposed. By incorporating the SimAM into EfficientNet’s MBConv structure and designing a parallel architecture, we effectively mitigate the impact of noisy features in time–frequency images on payment method recognition.
- During training, the Focal Loss function is used in place of the original cross-entropy loss function to overcome the problem of misclassification caused by similarities across specific modulation. By dynamically allocating higher loss weights to samples that are hard to recognize during training, this strategy forces the model to concentrate more on samples that are hard to recognize, thus increasing recognition accuracy.
- Experiments were carried out using a simulated dataset with 13 types of LPI radar modulation. The results indicate that the suggested approach reaches a classification accuracy of 96.48%.
2. LPI Radar Signal and Processing
2.1. LPI Radar Signal Model
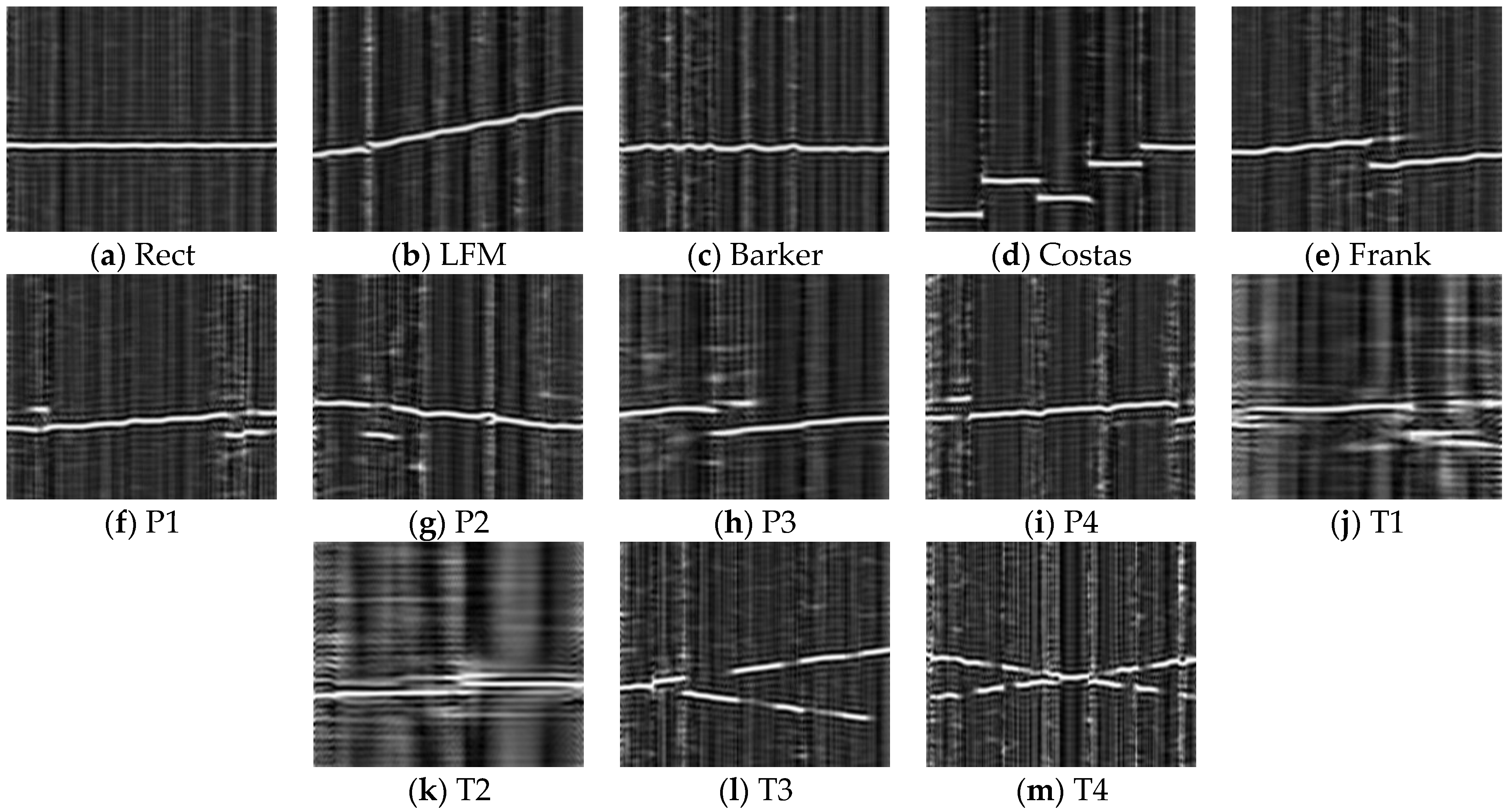
2.2. CWD Method
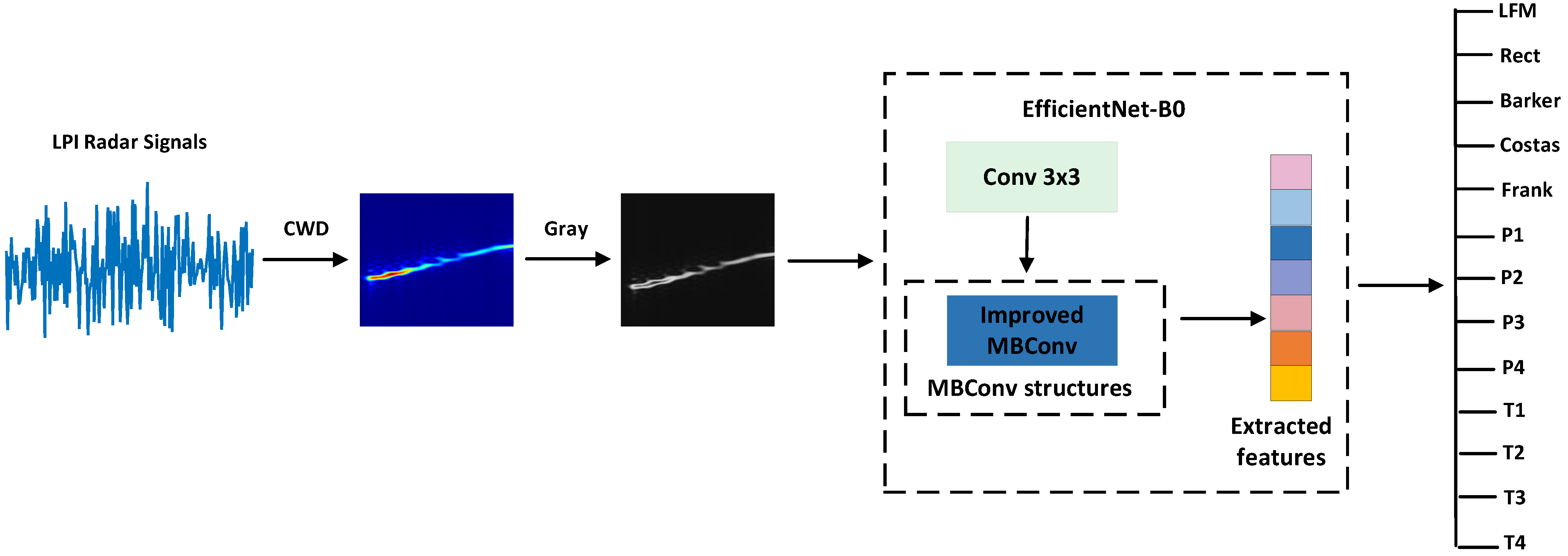
3. The Proposed Method
3.1. EfficientNet-B0 Baseline Network
3.2. SimAM Attention Mechanism
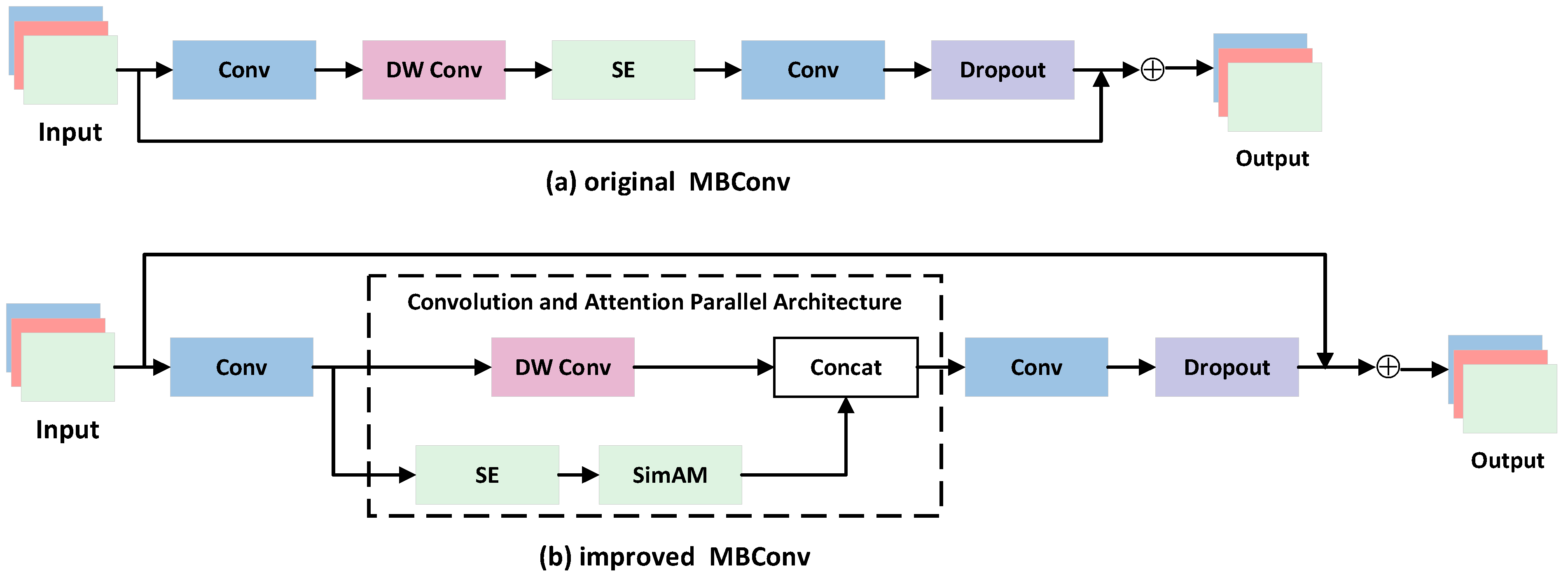
3.3. Improved MBConv Module
3.4. Focal Loss Function
4. Experiments and Discussions
4.1. Experimental Setup
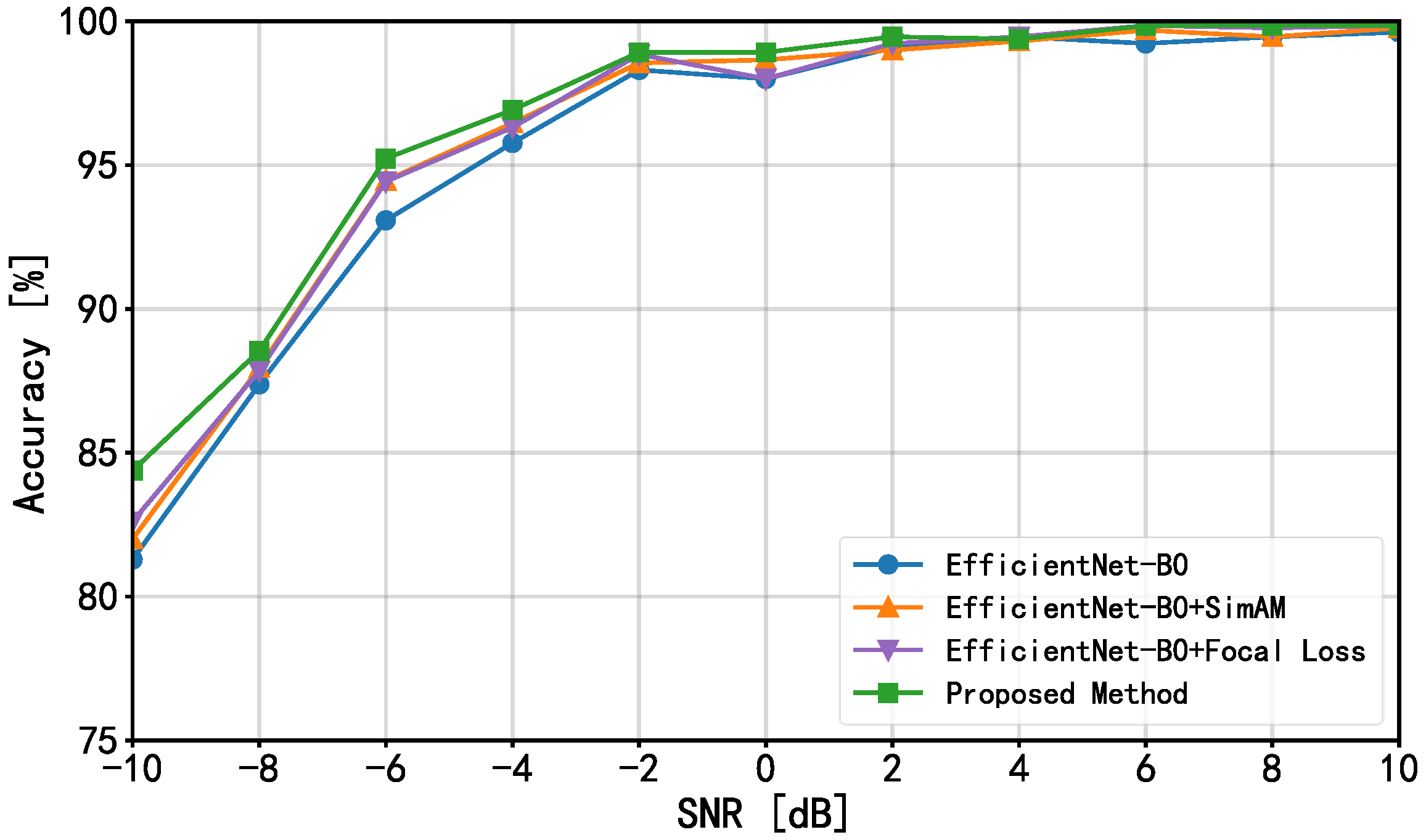
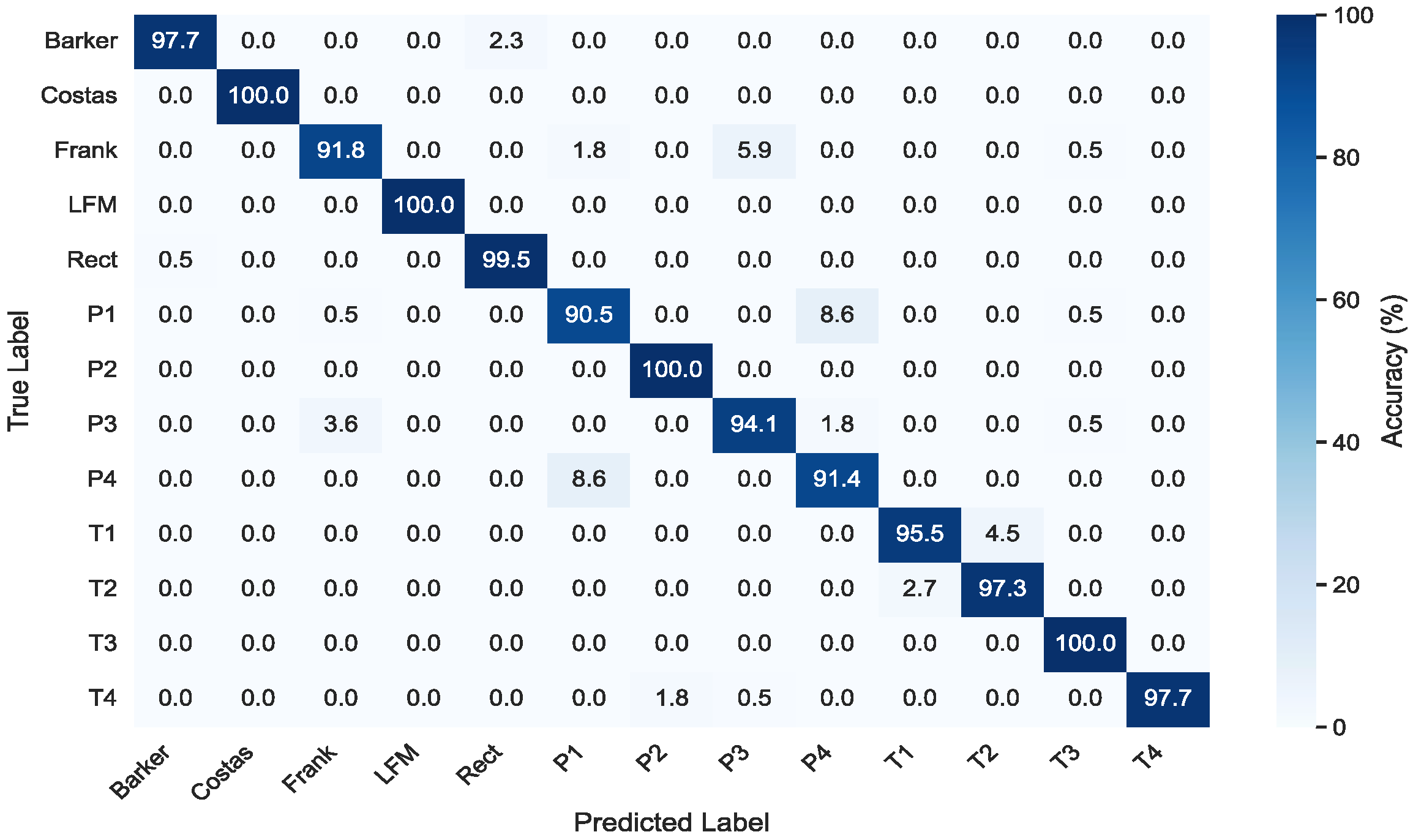
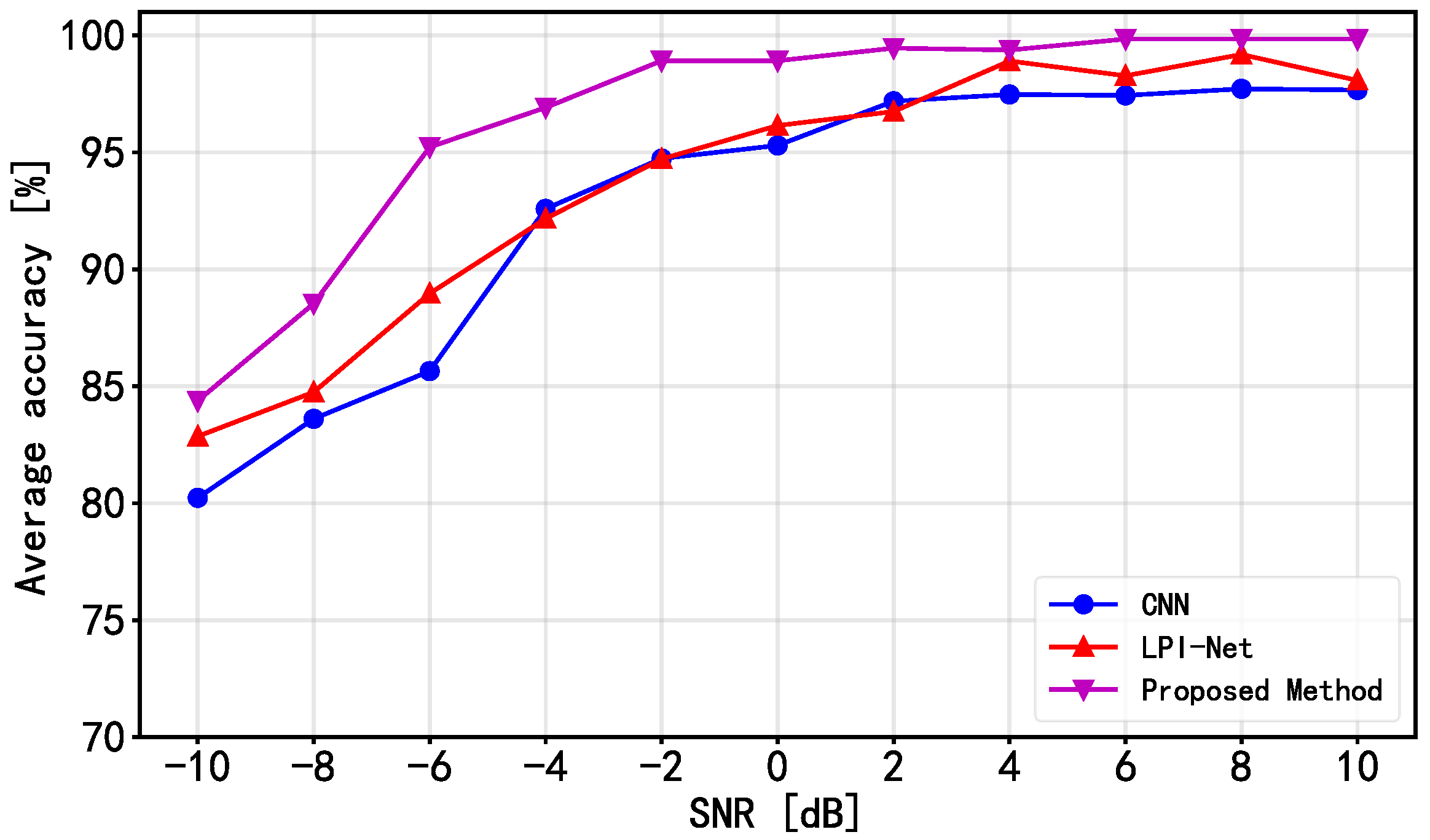
4.2. Experimental Results and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kong, S.H.; Kim, M.; Hoang, L.M.; Kim, E. Automatic LPI Radar Waveform Recognition Using CNN. IEEE Access 2018, 6, 4207–4219. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, L.; Diao, M. LPI Radar Waveform Recognition Based on Time-Frequency Distribution. Sensors 2016, 16, 1682. [Google Scholar] [CrossRef] [PubMed]
- Kishore, T.R.; Rao, K.D. Automatic Intrapulse Modulation Classification of Advanced LPI Radar Waveforms. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 901–914. [Google Scholar] [CrossRef]
- Li, P. Research on radar signal recognition based on automatic machine learning. Neural Comput. Appl. 2020, 32, 1–11. [Google Scholar] [CrossRef]
- Xu, T.; Yuan, S.; Liu, Z.; Guo, F. Radar Emitter Recognition Based on Parameter Set Clustering and Classification. Remote Sens. 2022, 14, 4468. [Google Scholar] [CrossRef]
- Gupta, P.; Jain, P.; Kakde, O. Deep Learning Techniques in Radar Emitter Identification. Def. Sci. J. 2023, 73, 551–563. [Google Scholar] [CrossRef]
- Huynh-The, T.; Doan, V.S.; Hua, C.H.; Pham, Q.V.; Nguyen, T.V.; Kim, D.S. Accurate LPI Radar Waveform Recognition With CWD-TFA for Deep Convolutional Network. IEEE Wirel. Commun. Lett. 2021, 10, 1638–1642. [Google Scholar] [CrossRef]
- Chen, B.; Wang, X.; Zhu, D.; Yan, H.; Xu, G.; Wen, Y. LPI Radar Signals Modulation Recognition in Complex Multipath Environment Based on Improved ResNeSt. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 8887–8900. [Google Scholar] [CrossRef]
- Ni, X.; Wang, H.; Meng, F.; Hu, J.; Tong, C. LPI Radar Waveform Recognition Based on Multi-Resolution Deep Feature Fusion. IEEE Access 2021, 9, 26138–26146. [Google Scholar] [CrossRef]
- Jiang, W.; Li, Y.; Liao, M.; Wang, S. An Improved LPI Radar Waveform Recognition Framework With LDC-Unet and SSR-Loss. IEEE Signal Process. Lett. 2022, 29, 149–153. [Google Scholar] [CrossRef]
- Wei, S.; Qu, Q.; Su, Y.-Y.; Wang, M.; Jun, S.H.I.; Hao, X. Intra-pulse modulation radar signal recognition based on CLDN network. IET Radar Sonar Navig. 2020, 14, 803–810. [Google Scholar] [CrossRef]
- Wu, B.; Yuan, S.; Li, P.; Jing, Z.; Huang, S.; Zhao, Y. Radar Emitter Signal Recognition Based on One-Dimensional Convolutional Neural Network with Attention Mechanism. Sensors 2020, 20, 6350. [Google Scholar] [CrossRef] [PubMed]
- Yakkati, R.R.; Boddu, A.B.; Pardhasaradhi, B.; Yeduri, S.R.; Cenkeramaddi, L.R. Low Probability of Intercept Radar Signal Classification using Multi-Channel 1D-CNN. In Proceedings of the 2024 10th International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, India, 12–14 April 2024; pp. 536–541. [Google Scholar]
- Kim, J.; Cho, S.; Hwang, S.; Lee, W.; Choi, Y. Enhancing LPI Radar Signal Classification Through Patch-Based Noise Reduction. IEEE Signal Process. Lett. 2024, 31, 716–720. [Google Scholar] [CrossRef]
- Luo, L.; Huang, J.; Yang, Y.; Hu, D. Radar Waveform Recognition with ConvNeXt and Focal Loss. IEEE Access 2024, 12, 171993–172003. [Google Scholar] [CrossRef]
- Wang, X.; Xu, G.; Yan, H.; Zhu, D.; Wen, Y.; Luo, Z. LPI Radar Signals Modulation Recognition Based on ACDCA-ResNeXt. IEEE Access 2023, 11, 45168–45180. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference on Machine Learning; Long Beach, CA, USA, 9–15 June 2019, pp. 6105–6114.
- Qin, L.; Wei, L.; Niu, C.; Yintu, B.; Zhoubo, H. Radar Signal Waveform modulation Recognition Based on Split EfficientNet Network under Low Signal-to-Noise Ratio. Chin. J. Electron. 2023, 51, 675–686. [Google Scholar]
- Ahmad, A.A.; Aji, M.M.; Abdulkadir, M.; Adunola, F.O.; Lawan, S. Analysis of Normal Radar Signal Based on Different Time-Frequency Distribution Configurations. Arid. Zone J. Eng. Technol. Environ. 2024, 20, 699–712. [Google Scholar]
- Li, X.; Cai, Z. Deep Learning and Time-Frequency Analysis Based Automatic Low Probability of Intercept Radar Waveform Recognition Method. In Proceedings of the 2023 IEEE 23rd International Conference on Communication Technology (ICCT), Nanjing, China, 20–22 October 2023; pp. 291–296. [Google Scholar]
- Yang, L.; Zhang, R.Y.; Li, L.; Xie, X. Simam: A simple, parameter-free attention module for convolutional neural networks. In Proceedings of the 38th International Conference on Machine Learning, Virtual Event, 18–24 July 2021; pp. 11863–11874. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2999–3007. [Google Scholar]
- Li, X.; Lv, C.; Wang, W.; Li, G.; Yang, L.; Yang, J. Generalized Focal Loss: Towards Efficient Representation Learning for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 3139–3153. [Google Scholar] [CrossRef] [PubMed]


| Stage | Operator | Resolution | Channels | Layers |
|---|---|---|---|---|
| 1 | Conv3 × 3 | 224 × 224 | 32 | 1 |
| 2 | MBConv1, k3 × 3 | 112 × 112 | 16 | 1 |
| 3 | MBConv6, k3 × 3 | 112 × 112 | 24 | 2 |
| 4 | MBConv6, k5 × 5 | 56 × 56 | 40 | 2 |
| 5 | MBConv6, k3 × 3 | 28 × 28 | 80 | 3 |
| 6 | MBConv6, k5 × 5 | 14 × 14 | 112 | 3 |
| 7 | MBConv6, k5 × 5 | 14 × 14 | 192 | 4 |
| 8 | MBConv6, k3 × 3 | 7 × 7 | 320 | 1 |
| 9 | Conv1 × 1, FC | 7 × 7 | 1280 | 1 |
| Modulation Types | Parameters | Value |
|---|---|---|
| Rect | ] | |
| LFM | ] | |
| Bandwidth | ] | |
| Costas | ] | |
| Frequency hop | ||
| Barker | Code length | |
| Cycles per phase code | ||
| ] | ||
| Frank | Number of frequency steps | |
| P1, P2 | ] | |
| Number of frequency steps | ||
| P3, P4 | ] | |
| {36, 39, 64} | ||
| T1, T2 | ] | |
| Number of segments | ||
| T3, T4 | ] | |
| Number of segments | ||
| Bandwidth | ] |
| No | Parameter | Value |
|---|---|---|
| 1 | Batch size | 32 |
| 2 | Iterations | 50 |
| 3 | Optimizer | Adam |
| 4 | Learning rate | 0.001 |
| 5 | in Focal Loss | 0.25 |
| 6 | in Focal Loss | 2 |
| Focal Loss | SimAM | Accuracy (%) |
|---|---|---|
| × | × | 95.54 |
| × | √ | 95.91 |
| √ | × | 96.01 |
| √ | √ | 96.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Y.; Ni, L.; Feng, X.; Li, H.; Zhao, Y. LPI Radar Waveform Modulation Recognition Based on Improved EfficientNet. Electronics 2025, 14, 4214. https://doi.org/10.3390/electronics14214214
Qi Y, Ni L, Feng X, Li H, Zhao Y. LPI Radar Waveform Modulation Recognition Based on Improved EfficientNet. Electronics. 2025; 14(21):4214. https://doi.org/10.3390/electronics14214214
Chicago/Turabian StyleQi, Yuzhi, Lei Ni, Xun Feng, Hongquan Li, and Yujia Zhao. 2025. "LPI Radar Waveform Modulation Recognition Based on Improved EfficientNet" Electronics 14, no. 21: 4214. https://doi.org/10.3390/electronics14214214
APA StyleQi, Y., Ni, L., Feng, X., Li, H., & Zhao, Y. (2025). LPI Radar Waveform Modulation Recognition Based on Improved EfficientNet. Electronics, 14(21), 4214. https://doi.org/10.3390/electronics14214214






