Capacity Enhancement of Optimized Deployment Active RISs-Assisted CF MIMO Networks

Abstract

Cell-free (CF) networks, with their distributed architecture of access points, offer considerable potential for improving spectral efficiency and expanding coverage. However, the need for dense access point deployment leads to high infrastructure cost and energy consumption. This paper incorporates active reconfigurable intelligent surfaces (RISs)—a low-cost and energy-efficient technology—into cell-free multiple-input multiple-output (MIMO) systems to tackle these challenges and enhance network capacity. Unlike existing active RIS schemes, the proposed method optimizes the spatial configuration of the active elements under a fixed panel layout, harnessing element-level spatial freedom to suppress interference and improve system capacity. We establish a joint optimization framework for active element selection and precoding aimed at maximizing the weighted sum-rate (WSR). An adaptive tabu search (ATS) algorithm is applied to optimize the element topology, and a Lagrangian dual reformulation (LDR) method is introduced to handle the precoding optimization. Simulation results indicate that at a transmit power of $0\mathrm{dBm}$, the passive RIS yields only a $62.49\%$ gain over the no-RIS baseline due to multiplicative fading, whereas the conventional active RIS achieves a $217.46\%$ improvement and the proposed optimized deployment-active RIS further increases the gain to $269.43\%$; thus, our scheme delivers the most significant performance enhancement.

1. Introduction

The proliferation of the Internet of Everything (IoE) has continuously exacerbated the demand for spectrum resources, exacerbating challenges such as capacity limitations, signal interference, and spectrum bottlenecks [1]. To address these issues, CF networks were introduced in [2,3,4]. These networks offer a boundary-free cellular service to multiple users through a network of widely distributed base stations (BSs), thereby optimizing signal transmission, enhancing spectral efficiency [5], alleviating interference, extending coverage, and providing more flexible management of network resources.

Despite the various advantages and potential of CF networks, they also present several shortcomings. For instance, to further increase network capacity, CF networks typically necessitate a denser deployment of distributed BSs, resulting in elevated infrastructure expenditures and increased energy usage. Emerging in response to these challenges, RIS [6,7,8] enable dynamic manipulation of the wireless channel characteristics while maintaining high energy efficiency and low implementation costs. Indeed, RIS technology has the potential to address the limitations of CF network architecture in future communications systems. Recently, research has focused on passive RIS-assisted CF MIMO networks under various deployments [9,10]. For instance, in [11], an energy-saving technology called passive-assisted CF network was proposed. The strategic integration of passive RIS elements to supplant a subset of conventional high-power BSs in CF architectures can enhance overall energy efficiency without compromising network performance. Reference [12] examines a cell-free massive MIMO architecture enhanced by passive RIS for 6G aerial communications, formulating a max–min fairness optimization scheme to maximize the reachability of all user equipment (UE). However, the capacity gains of conventional passive RIS-assisted CF MIMO networks are limited due to the multiplicative fading effect. To address this inherent physical constraint, active RIS technology has been proposed [13]. This advanced approach integrates additional power amplifiers to provide both signal amplification and controlled reflection, enabling independent control over both the amplitude and phase of the reflected signal. Unlike conventional passive RIS limited to phase modulation, active RIS supports precise beamforming while also amplifying the signal [14,15]. This significantly enhances the RIS array gain and effectively converts multiplicative fading into additive fading. Consequently, active RIS can be seamlessly integrated with the active beamforming strategies of distributed APs in CF networks, leading to substantial gains in spectral efficiency. As a result, active RIS-assisted CF MIMO networks can achieve more significant performance gains. For instance, ref. [16] applies active RIS to CF networks to suppress the multiplicative fading effect in these networks, and the proposed networks are analyzed by examining their energy efficiency equity. Building on this foundation, an integrated beamforming and resource allocation strategy was designed by employing alternating optimization together with fractional programming techniques. In a related effort, ref. [17] introduced the framework of active RIS-enhanced CF massive MIMO networks and investigated their spectral efficiency performance in Rayleigh fading environments.

In the existing research on active RIS-assisted CF MIMO networks, feedback-induced self-interference [18] between active elements is rarely considered, but it may significantly affect the performance improvement of the network. In addition, the number of active RIS elements predominantly governs the performance boundaries of conventional active RIS architectures [19,20,21,22], but activating more RIS elements brings additional power consumption. Consequently, suppressing self-interference among active elements and improving the capacity of active RIS-assisted communication systems with limited element counts becomes crucial.

Our Contributions

This paper introduces the concept of optimized deployment active RIS-assisted CF massive MIMO networks. This approach is designed to suppress self-interference among active elements and overcome the capacity constraints inherent in conventional active RIS-assisted communication systems. The principal contributions of this work are delineated as follows:

• To address self-interference challenges in cell-free massive MIMO systems, we propose an active-element selection optimization framework for RIS panels with fixed physical positions. By exploiting the spatial sparsity characteristics of active RIS elements, the proposed method acquires element-level spatial degrees of freedom to ensure guaranteed WSR performance. This topology optimization framework demonstrates significant capacity gains under constrained active element budgets (Section 2).
• We formulate a WSR maximization problem and decompose it into two interdependent subproblems: active-element topology design and precoding optimization. The former is solved through an ATS algorithm, while joint BS precoding and RIS beamforming are addressed via LDR. Computational complexity analyses for both methods are provided (Section 3).
• Simulation results confirm that our proposed scheme effectively mitigates active RIS self-interference compared to conventional approaches, delivering substantial capacity gains while maintaining robust performance. The numerical investigations quantitatively characterize how system performance varies with RIS element count, grid arrangement, and self-interference level, offering comprehensive verification of our theoretical findings (Section 4).

The organization of the paper is as follows. Section 2 introduces the system model for optimized active RIS deployment in cell-free networks, along with the formulated WSR maximization problem. To address these challenges, Section 3 proposes a joint topology-precoding optimization framework. Section 4 provides numerical results to validate the proposed scheme’s performance, followed by concluding remarks in Section 5. The main mathematical symbols and notations used throughout this paper are summarized in

Table 1. Summary of symbols.

Symbol	Description
$\mathbb{C}$	Set of complex numbers
$\mathbb{R}$	Set of real numbers
${\left[·\right]}^{-1}$	Inverse operation
${\left[·\right]}^{\ast }$	Conjugate operation
${\left[·\right]}^{\mathrm{T}}$	Transpose operation
${\left[·\right]}^{\mathrm{H}}$	Conjugate transpose operation
${\left[·\right]}^{+}$	Negative truncation
${\left[\mathbf{A}\right]}_i$	i-th element of vector $\mathbf{A}$
${\left[\mathbf{B}\right]}_{i,j}$	Element at i-th row and j-th column of matrix $\mathbf{B}$
$∥·∥$	Euclidean norm of a vector
${∥·∥}_{\mathsf{F}}$	Frobenius norm of a matrix
$\mathbb{E}\left\{·\right\}$	Expectation operator
$\mathrm{diag}\left(·\right)$	Diagonal operation
$\Re \left\{·\right\}$	Real part of the argument
⊗	Kronecker product
$\mathsf{ln}\left(·\right)$	Natural logarithm
$\mathcal{C}\mathcal{N}\left(\alpha ,\Sigma \right)$	Complex multivariate Gaussian distribution with mean $\alpha$ and covariance $\Sigma$
${\mathbf{I}}_L$	$L\times L$ identity matrix
${\mathbf{0}}_L$	$L\times L$ zero matrix
${\mathbf{e}}_l$	Elementary vector with 1 at the l-th position
${\mathbf{1}}_L$	L-length vector with all elements equal to one

.

2. System Model and Problem Formulation

In this section, we introduce the system model for optimized active RIS deployment in CF networks. Subsequently, we discuss transmitters and receivers. Lastly, the WSR maximization problem for optimized deployment active RIS-assisted CF networks is proposed.

2.1. System Architecture

Figure 1 illustrates our investigation into the optimized deployment of an active RIS-assisted CF massive MIMO system. The network architecture includes K UEs, each equipped with multiple antennas, R RISs, and B BSs, where each BS is equipped with M transmitting antennas to communicate with K multi-antenna users. The optimized deployment of active RISs, with N active elements, assists communication. These N active RIS elements are optimally deployed on $N_S$ grid points ($N_S>N$), with adjacent grid points spaced at ${\displaystyle \frac{\lambda }{2}}$, where $\lambda$ denotes the carrier wavelength [23]. The proposed active RIS deployment optimization is realized through selective activation of RIS elements at designated grid points, while deactivating unselected ones via diode-controlled impedance matching to a load [24]. All BSs and RISs are linked to a central processing unit (CPU) that synchronizes their transmissions, enabling simultaneous service to multiple users over common time-frequency resources. Additionally, the system employs multi-carrier transmission, with a total of P available subcarriers. The number of antennas at the b-th BS is denoted by $M_b$, and the number of antennas at the k-th user is denoted by $U_k$. For tractability of the analysis, we assume uniform parameters with $M_b=M$ and $U_k=U$, which does not affect the general applicability of our results.

We define $\mathcal{N}=1,\dots ,N_S$, $\mathcal{B}=1,\dots ,B$, $\mathcal{R}=1,\dots ,R$, $\mathcal{K}=1,\dots ,K$, and $\mathcal{P}=1,\dots ,P$ to optimize the index set for the optimized deployment of active RIS grids, BSs, RISs, users, and subcarriers, respectively.

2.2. Transmitter and Receiver

This article concentrates exclusively on data transmission in the downlink. The formula for the signal emitted by the b-th BS is as follows:

$${\mathbf{x}}_{b,p}=\sum _{k=1}^K{\mathbf{w}}_{b,p,k}{s}_{p,k},$$

(1)

where ${\mathbf{w}}_{b,p,k}\in {\mathbb{C}}^M$ denotes the precoding vector associated with the b-th BS, and $s_{p,k}$ is the symbol transmitted on subcarrier p. The symbol vector is defined as ${\mathbf{s}}_p={\left[s_{p,1},\dots ,s_{p,K}\right]}^{\mathrm{T}}\in {\mathbb{C}}^K$, and the transmitted symbols are assumed to be normalized such that $\mathbb{E}\left[{\mathbf{s}}_p{\mathbf{s}}_p^{\mathrm{H}}\right]={\mathbf{I}}_K,\forall p\in \mathcal{P}$.

Under ideal conditions where self-interference is negligible, the signal reflected by an active RIS is formulated as

$$\mathbf{r}=\underset{\mathrm{Desired}\mathrm{signal}}{\underbrace{\sum _{r=1}^R{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{x}}_{b,p}}}+\underset{\mathrm{Amplified}\mathrm{noise}}{\underbrace{\sum _{r=1}^R{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{v}_{r,p}}}+{\mathbf{e}}_{k,p}.$$

(2)

Simplified to

$$\mathbf{r}=\sum _{r=1}^R{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r\left({\mathbf{x}}_{b,p}+v_{r,p}\right)+{\mathbf{e}}_{k,p}.$$

(3)

The downlink signal on subcarrier p from BS b to user k is mathematically expressed as

$$\begin{array}{cc}\hfill & {\mathbf{y}}_{b,k,p}=\left({\mathbf{H}}_{b,k,p}^{\mathrm{H}}+\sum _{r=1}^R{\mathbf{F}}_{r,k,p}^{\mathrm{H}}{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{G}}_{b,r,p}\right)\sum _{j=1}^K{\mathbf{w}}_{b,p,j}{s}_{p,j}\hfill \\ \hfill & +\sum _{r=1}^R{\mathbf{F}}_{r,k,p}^{\mathrm{H}}{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{v}_{r,p}+{\mathbf{e}}_{k,p},\hfill \end{array}$$

(4)

where ${\mathbf{H}}_{b,k,p}^{\mathrm{H}}\in {\mathbb{C}}^{U\times M}$, ${\mathbf{G}}_{b,r,p}\in {\mathbb{C}}^{N_S\times M}$, and ${\mathbf{F}}_{r,k,p}^{\mathrm{H}}\in {\mathbb{C}}^{U\times N_S}$ denote the frequency-domain channels corresponding to the BS–user, BS–RIS, and RIS–user links on subcarrier p, respectively. The active RIS phase-shift matrix is expressed as ${\mathbf{\Psi }}_r\in {\mathbb{C}}^{N_S\times N_S}=\mathrm{diag}\left({\mathit{\psi }}_r\right)=\mathrm{diag}\left({\mathbf{\Theta }}_r\mathit{\alpha }\right)$, where ${\mathbf{\Theta }}_r=\mathrm{diag}({\theta }_{r,1},\dots ,{\theta }_{r,N_S})\in {\mathbb{C}}^{N_S\times N_S}$, $\forall r\in \mathcal{R}$, and each ${\theta }_{r,n}\in (0,2\pi )$ together with $\mathit{\alpha }\in {\mathbb{C}}^{N_S\times 1}$ specify the phase adjustments and amplification factors of the RIS r elements.The dynamic noise generated by the active RIS r is modeled as $v_{r,p}\sim \mathcal{C}\mathcal{N}(\mathbf{0},{\sigma }_v^2{\mathbf{I}}_{N_S})$. The topology of the r-th active RIS is described by the diagonal matrix ${\mathbf{Z}}_r=\mathrm{diag}\left({\mathbf{z}}_r\right)\in {\mathbb{C}}^{N_S\times N_S}$, where ${\mathbf{z}}_r={[z_{r,1},\dots ,z_{r,N_S}]}^{\mathrm{H}}$, and each $z_{r,n}\in \{0,1\}$ indicates the deployment state, with “1” denoting an active element and “0” corresponding to an inactive one. In addition, ${\mathbf{e}}_{k,p}\triangleq {[e_{k,p,1}^{\mathrm{T}},\dots ,e_{k,p,U}^{\mathrm{T}}]}^{\mathrm{T}}$ represents the additive white Gaussian noise (AWGN) vector at user k on subcarrier p, characterized by zero mean ${\mathbf{0}}_U$ and covariance matrix ${\Xi }_{k,p}={\sigma }^2{\mathbf{I}}_U$.

Referring to ref. [9], Formula (4) is simplified as follows:

$$\begin{array}{cc}\hfill & {\mathbf{y}}_{b,k,p}=\left({\mathbf{H}}_{b,k,p}^{\mathrm{H}}+\sum _{r=1}^R\left({\mathbf{F}}_{r,k,p}^{\mathrm{H}}+v_{r,p}\right){\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{G}}_{b,r,p}\right)\hfill \\ \hfill & \times \sum _{j=1}^K\sqrt{{\mathbf{w}}_{b,p,j}}{\widehat{s}}_{p,j}+{\mathbf{e}}_{k,p},\hfill \end{array}$$

(5)

Building on the system model described earlier and taking into account the transmission power constraints of BSs and RISs, the objective is to maximize the WSR of the proposed optimized deployment of active RIS-assisted CF network. Initially, the received signal ${\mathbf{y}}_{b,k,p}$ is simplified as follows:

$$\begin{array}{cc}\hfill {\mathbf{y}}_{k,p}& \stackrel{\left(a\right)}{=}\sum _{b=1}^B\sum _{j=1}^K\left({\mathbf{H}}_{b,k,p}^{\mathrm{H}}+\sum _{r=1}^R{\widehat{\mathbf{F}}}_{r,k,p}^{\mathrm{H}}{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{G}}_{b,r,p}\right){\widehat{\mathbf{w}}}_{b,p,j}{\widehat{s}}_{p,j}+{\mathbf{e}}_{k,p},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & \stackrel{\left(b\right)}{=}\sum _{b=1}^B\sum _{j=1}^K\left({\mathbf{H}}_{b,k,p}^{\mathrm{H}}+{\widehat{\mathbf{F}}}_{k,p}^{\mathrm{H}}{\mathbf{\Psi }}^{\mathrm{H}}\mathbf{Z}{\mathbf{G}}_{b,p}\right){\widehat{\mathbf{w}}}_{b,p,j}{\widehat{s}}_{p,j}+{\mathbf{e}}_{k,p},\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & \stackrel{\left(c\right)}{=}\sum _{b=1}^B\sum _{j=1}^K{\mathbf{h}}_{b,k,p}^{\mathrm{H}}{\widehat{\mathbf{w}}}_{b,p,j}{\widehat{s}}_{p,j}+{\mathbf{e}}_{k,p},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & \stackrel{\left(d\right)}{=}\sum _{j=1}^K{\mathbf{h}}_{k,p}^{\mathrm{H}}{\widehat{\mathbf{w}}}_{p,j}{\widehat{s}}_{p,j}+{\mathbf{e}}_{k,p},\hfill \end{array}$$

(9)

where (a) holds by defining ${\widehat{\mathbf{F}}}_{r,k,p}^{\mathrm{H}}={\mathbf{F}}_{r,k,p}^{\mathrm{H}}+v_{r,p}$, ${\widehat{\mathbf{w}}}_{b,p,k}=\sqrt{{\mathbf{w}}_{b,p,k}}$; (b) holds by defining $\mathbf{\Psi }=\mathrm{diag}({\mathbf{\Psi }}_1,\dots ,{\mathbf{\Psi }}_R)$, $\mathbf{Z}=\mathrm{diag}({\mathbf{Z}}_1,\dots ,{\mathbf{Z}}_R)$, ${\widehat{\mathbf{F}}}_{k,p}={\left[{\widehat{\mathbf{F}}}_{1,k,p}^{\mathrm{T}},\dots ,{\widehat{\mathbf{F}}}_{R,k,p}^{\mathrm{T}}\right]}^{\mathrm{T}}$, ${\mathbf{G}}_{b,p}={\left[{\mathbf{G}}_{b,1,p}^{\mathrm{T}},\dots ,{\mathbf{G}}_{b,R,p}^{\mathrm{T}}\right]}^{\mathrm{T}}$; (c) holds by defining ${\mathbf{h}}_{b,k,p}^{\mathrm{H}}={\mathbf{H}}_{b,k,p}^{\mathrm{H}}+{\widehat{\mathbf{F}}}_{k,p}^{\mathrm{H}}{\mathbf{\Psi }}^{\mathrm{H}}\mathbf{Z}{\mathbf{G}}_{b,p}$; (d) holds by defining ${\mathbf{h}}_{k,p}={\left[{\mathbf{h}}_{1,k,p}^{\mathrm{T}},\dots ,{\mathbf{h}}_{B,k,p}^{\mathrm{T}}\right]}^{\mathrm{T}}$ and ${\widehat{\mathbf{w}}}_{p,k}={\left[{\widehat{\mathbf{w}}}_{1,p,k}^{\mathrm{T}},\dots ,{\widehat{\mathbf{w}}}_{B,p,k}^{\mathrm{T}}\right]}^{\mathrm{T}}$.

The signal-to-interference-plus-noise ratio (SINR) for user k with respect to the symbol $s_{p,k}$ on subcarrier p is given by

$${\gamma }_{k,p}={\displaystyle \frac{{\widehat{\mathbf{w}}}_{p,k}^{\mathrm{H}}{\mathbf{h}}_{k,p}{\mathbf{h}}_{k,p}^{\mathrm{H}}{\widehat{\mathbf{w}}}_{p,k}}{{\displaystyle \sum _{j=1,j\ne k}^K}{\mathbf{h}}_{k,p}^{\mathrm{H}}{\widehat{\mathbf{w}}}_{p,j}{\left({\mathbf{h}}_{k,p}^{\mathrm{H}}{\widehat{\mathbf{w}}}_{p,j}\right)}^{\mathrm{H}}+{\Xi }_{k,p}}}.$$

(10)

Accordingly, the WSR considering all K users can be expressed as

$$R_{\mathsf{sum}}=\sum _{k=1}^K\sum _{p=1}^P{\eta }_{k}log\left(1+{\gamma }_{k,p}\right).$$

(11)

2.3. Problem Formula

This section formulates the optimization problem, with the detailed mathematical representation provided below:

$$\begin{array}{cc}\hfill & P_0:\underset{\mathbf{\Psi },\mathbf{W},\mathbf{Z}}{max}{R}_{\mathrm{sum}}\left(\mathbf{\Psi },\mathbf{W},\mathbf{Z}\right)=\sum _{k=1}^K\sum _{p=1}^P{\eta }_k{log}_2\left(1+{\gamma }_{k,p}\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.C_1:\sum _{k=1}^K\sum _{p=1}^P{∥{\widehat{\mathbf{w}}}_{b,p,k}∥}^2\le P_{b,\max },\forall b\in \mathcal{B},\hfill \\ \hfill & C_2:\sum _{k=1}^K\sum _{p=1}^P{∥{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{G}}_{b,r,p}{\mathbf{w}}_{b,p,k}∥}^2\hfill \\ \hfill & +{∥{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r∥}_{\mathrm{F}}^2{\sigma }_{k,p}^2\le P_{r,\max },\forall r\in \mathcal{R},\hfill \\ \hfill & C_3:{\theta }_{r,n}\in (0,2\pi ),\forall r\in \mathcal{R},\forall n\in {\mathcal{N}}_S,\hfill \\ \hfill & C_4:z_{r,n}\left(z_{r,n}-1\right)=0,\forall r\in \mathcal{R},\forall n\in {\mathcal{N}}_S,\hfill \\ \hfill & C_5:{\mathbf{1}}^{\mathrm{T}}\mathbf{z}=RN,\hfill \end{array}$$

(12)

where $\mathbf{W}\triangleq {\left[{\widehat{\mathbf{w}}}_{1,1}^{\mathrm{T}},\dots ,{\widehat{\mathbf{w}}}_{1,K}^{\mathrm{T}},{\widehat{\mathbf{w}}}_{2,1}^{\mathrm{T}},\dots ,{\widehat{\mathbf{w}}}_{P,K}^{\mathrm{T}}\right]}^{\mathrm{T}}$ denotes the aggregate transmit precoding vector stacking all per-$(p,k)$ precoders, and ${\eta }_k$ denotes the weight of user k. The transmit power constraints for BS b and active RIS r are denoted by $C_1$ and $C_2$, respectively. $C_3$ represents the phase shift constraint for the optimized deployment of active RIS r, while $C_4$ and $C_5$ denote the topology constraints for the optimized deployment of active RISs. Here, ${\mathbf{Z}}_r$ denotes the activation matrix of RIS r, which has exactly N unit diagonal entries—activated elements—and $(N_s-N)$ zero diagonal entries—deactivated elements.

Equation (12) highlights the non-convex nature of the problem $P_0$, making direct solution impractical. To address this challenge, the approach proposed in this paper decouples the problem into three subproblems: topological deployment, active RIS beamforming matrix, and BS precoding vector.

3. Joint Optimization Scheme

This section elaborates the proposed joint optimization framework that systematically addresses and separates the coupled subproblems.

3.1. Overview of Joint Precoding Schemes

This paper employs the ATS algorithm [25,26] to address the subproblem of RIS topology deployment. The algorithm is initialized with a random topology and proceeds through an iterative process of neighborhood search. In each iteration, it generates a number of neighbor solutions by swapping a certain number of active and inactive elements (0 s and 1 s) within the current topology matrix and evaluates their performance using the WSR. A key feature of the algorithm is the dynamic adjustment of the search neighborhood size, which promotes broad exploration initially, transitioning to fine-tuning later. Concurrently, a tabu list mechanism prevents revisiting previously explored topologies. The iterative process continues until the termination criteria are met, ultimately yielding a suboptimal topology configuration. With a given topological matrix ${\mathbf{Z}}^{★}$, problem $P_0$ is reduced to $P_1$:

$$\begin{array}{cc}\hfill & P_1:\underset{\mathbf{\Psi },\mathbf{W}}{max}{R}_{\mathrm{sum}}\left(\mathbf{\Psi },\mathbf{W}\right)=\sum _{k=1}^K\sum _{p=1}^P{\eta }_k{log}_2\left(1+{\gamma }_{k,p}\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.C_1:\sum _{k=1}^K\sum _{p=1}^P{∥{\widehat{\mathbf{w}}}_{b,p,k}∥}^2\le P_{b,\max },\forall b\in \mathcal{B},\hfill \\ \hfill & C_2:\sum _{k=1}^K\sum _{p=1}^P{∥{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{G}}_{b,r,p}{\mathbf{w}}_{b,p,k}∥}^2\hfill \\ \hfill & +{∥{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r∥}_{\mathrm{F}}^2{\sigma }_{k,p}^2\le P_{r,\max },\forall r\in \mathcal{R},\hfill \\ \hfill & C_3:{\theta }_{r,n}\in (0,2\pi ),\forall r\in \mathcal{R},\forall n\in {\mathcal{N}}_S,\hfill \\ \hfill & C_4:\mathbf{Z}={\mathbf{Z}}^{★},\hfill \end{array}$$

(13)

After generating the neighborhood of $\mathbf{Z}$, the optimal candidate for the subsequent iteration is selected by exhaustively comparing the WSR of all neighboring solutions. The algorithm terminates when the iteration count exceeds the threshold, resulting in suboptimal solutions ${\mathbf{Z}}^{\mathrm{opt}}$, ${\mathbf{W}}^{\mathrm{opt}}$, and ${\mathbf{\Psi }}^{\mathrm{opt}}$ for the original problem (12).

3.2. Optimized Deployment of RIS Based on ATS

For the topological matrix of RIS r, N 1s and $N_S-N$ 0s are randomly selected. The WSR is calculated based on the BS precoding and RIS beamforming. In the i-th iteration, the neighborhood set $\mathcal{N}\left({\mathbf{Z}}^i\right)$ is generated through uniform random transpositions of q zero-valued and q one-valued elements in ${\mathbf{Z}}^i$, with parameter q controlling the exploration radius. An initial solution is generated, and the tabu list is initially empty. The value of q is set to a higher number at the beginning of the iterative optimization and gradually reduced as the iteration progresses. The ATS algorithm only keeps qualified candidate solutions in the tabu list according to its design principles. By exhaustively evaluating the WSR of all neighboring solutions, the optimal topology maximizing WSR is chosen for subsequent iterations. The algorithm terminates upon reaching the prescribed iteration limit $I_T$, yielding a suboptimal RIS topology configuration. The complete algorithmic procedure is formally presented in Algorithm 1.

Algorithm 1 Joint Optimization Algorithm.

Input:  Channel $\mathbf{F}$, $\mathbf{H}$, $\mathbf{\Psi }$, $\mathbf{G}$. Output:  Optimal $\mathbf{W}$, $\mathbf{\Psi }$, $\mathbf{Z}$ and WSR.   1: Initialize the tabu set $\mathcal{H}$ as empty, and configure the maximum capacity $H_{\mathsf{size}}$, neighborhood radius p, candidate pool size Q, together with the maximum iteration count $I_{\mathsf{T}}$.   2: Initialize the iteration index i at zero and assign a feasible starting RIS topology ${\mathbf{Z}}^{\left(0\right)}$   3: repeat   4:       Update p based on the value of i to generate alternate neighbors of ${\mathbf{Z}}^{\left(i\right)}$;   5:       Remove neighbors marked in the tabu list $\mathcal{H}$ and retain Q feasible candidates;   6:       Select the candidate topology with the largest WSR as the initial topology ${\mathbf{Z}}^{\left(i\right)}$ for the next iteration;   7:       if $\left|\mathcal{H}\right|<H_{\mathsf{size}}$ then   8:             Insert ${\mathbf{Z}}^{\left(i\right)}$ into $\mathcal{H}$;   9:       else 10:             Update $\mathcal{H}$ by appending ${\mathbf{Z}}^{\left(i\right)}$ and discarding its oldest element; 11:       end if 12:       $i=i+1$ 13: until $i>I_{\mathsf{T}}$ 14: Initialize ${\mathbf{W}}^{\left(0\right)}$ and ${\mathbf{\Psi }}^{\left(0\right)}$ as feasible values for optimizing the neighbor ${\mathbf{Z}}^{\mathsf{opt}}$; 15: repeat 16:       $j=j+1$ 17:       Update $\mathit{\rho }$ via Equation (17); 18:       Update $\mathit{\varsigma }$ via Equation (A2); 19:       Update $\mathbf{W}$ by solving (A7); 20:       Update $\mathit{\epsilon }$ via Equation (A14); 21:       Update $\mathbf{\Psi }$ by solving (A20); 22: until (12) converges

3.3. Optimal Conversion

The LDR method simplifies constrained optimization problems by constructing the Lagrangian function and solving its dual problem. The core idea is to introduce the constraints through Lagrange multipliers, thereby leveraging duality to indirectly solve the original problem. Based on this principle, this paper employs the LDR method proposed in ref. [27] to handle the non-convex summation problem in Equation (13). By decoupling the variables, it achieves separable optimization for multiple variables, and based on this, the following lemma is derived.

To improve readability, we summarize in

Table 2. Summary of new symbols introduced in Lemmas 1, A1, and A2.

Symbol	Description
${\rho }_{p,k}$	Auxiliary variable introduced in Lemma 1 for reformulation
$\rho ={\left[{\rho }_{p,k}\right]}_{p\in P,k\in K}$	Vector form of auxiliary variables in Lemma 1
${\varsigma }_{p,k}\in {\mathbb{C}}^U$	Auxiliary variable introduced in Lemma A1
$\varsigma =[{\varsigma }_{1,1},{\varsigma }_{1,2},\dots ,{\varsigma }_{P,K}]$	Combined vector of all ${\varsigma }_{p,k}$ in Lemma A1
${\alpha }_p$	Matrix term defined from ${\varsigma }_{p,k}$ in Lemma A1
$A_p=I_K\otimes {\alpha }_p$	Kronecker-structured matrix in Lemma A1
$v_{k,p}=h_{k,p}{\varsigma }_{k,p}$	Intermediate vector in Lemma A1
${\epsilon }_{p,k}\in {\mathbb{C}}^U$	Auxiliary variable introduced in Lemma A2
$\epsilon =[{\epsilon }_{1,1},{\epsilon }_{1,2},\dots ,{\epsilon }_{P,K}]$	Combined vector of all ${\epsilon }_{p,k}$ in Lemma A2
$Q_{k,p,j}(\Psi )$	Auxiliary function for simplifying $g_5(\Psi ,\epsilon )$ in Lemma A2

the additional symbols introduced in Lemmas 1, A1 and A2 for reformulating the weighted sum-rate maximization problem into tractable subproblems. Although the full statements and proofs of Lemmas A1 and A2 are relegated to the Appendix A and Appendix B for brevity, the newly defined symbols therein are consolidated here together with those from Lemma 1.

Lemma 1. 

Equivalence problem for maximizing WSR: The original formulation $P_1$ in Equation (13) can be cast into an equivalent form through the introduction of auxiliary variables $\rho p,k$, organized in vector form as $\mathbf{\ae }={\left[{\rho }_{p,k}\right]}_{p\in \mathcal{P},k\in \mathcal{K}}\in {\mathbb{R}}^{PK}$, yielding the following:

$$\begin{array}{cc}\hfill & {\overline{P}}_1:\underset{\mathbf{\Psi },\mathbf{W},\mathit{\rho }}{max}f(\mathbf{\Psi },\mathbf{W},\mathit{\rho })\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.C_1:\sum _{k=1}^K\sum _{p=1}^P{∥{\widehat{\mathbf{w}}}_{b,p,k}∥}^2\le P_{b,\max },\forall b\in \mathcal{B},\hfill \\ \hfill & C_2:\sum _{k=1}^K\sum _{p=1}^P{∥{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{G}}_{b,r,p}{\mathbf{w}}_{b,p,k}∥}^2\hfill \\ \hfill & +{∥{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r∥}_{\mathrm{F}}^2{\sigma }_{k,p}^2\le P_{r,\max },\forall r\in \mathcal{R},\hfill \\ \hfill & C_3:{\theta }_{r,n}\in (0,2\pi ),\forall r\in \mathcal{R},\forall n\in {\mathcal{N}}_S,\hfill \\ \hfill & C_4:\mathbf{Z}={\mathbf{Z}}^{★},\hfill \end{array}$$

(14)

where

$$\begin{array}{cc}\hfill & f(\mathbf{\Psi },\mathbf{W},\mathit{\rho })=\sum _{k=1}^K\sum _{p=1}^P{\eta }_k{log}_2(1+{\rho }_{k,p})-\sum _{k=1}^K\sum _{p=1}^P{\eta }_k{\rho }_{k,p}\hfill \\ \hfill & +\sum _{k=1}^K\sum _{p=1}^P{\eta }_k(1+{\rho }_{k,p})f_{k,p}(\mathbf{\Psi },\mathbf{W}),\hfill \end{array}$$

(15)

where

$$f_{k,p}(\mathbf{\Psi },\mathbf{W})={\displaystyle \frac{{\widehat{\mathbf{w}}}_{p,k}^{\mathrm{H}}{\mathbf{h}}_{k,p}{\mathbf{h}}_{k,p}^{\mathrm{H}}{\widehat{\mathbf{w}}}_{p,k}}{{\sum }_{j=1}^K{\mathbf{h}}_{k,p}^{\mathrm{H}}{\widehat{\mathbf{w}}}_{p,j}{\left({\mathbf{h}}_{k,p}^{\mathrm{H}}{\widehat{\mathbf{w}}}_{p,j}\right)}^{\mathrm{H}}+{\Xi }_{k,p}}}$$

(16)

Given the optimal values of $\mathbf{W}$, $\mathbf{\Psi }$, and $\mathit{\rho }$, a locally optimal solution to Equation (14) can be achieved through alternating optimization, converging to $R_{\mathsf{sum}}$. Algorithm 1 formalizes the precoding scheme with auxiliary variables $\mathit{\varsigma }$ and $\mathit{\epsilon }$, and the implementation details are as follows:

(1) Fix $\left(\mathbf{\Psi },\mathbf{W}\right)$ and find ${\mathit{\rho }}^{\mathrm{opt}}$

With $({\mathbf{\Psi }}^{★},{\mathbf{W}}^{★})$ fixed, the optimal $\mathit{\rho }$ satisfies the zero-gradient condition ${\nabla }_{\mathit{\rho }}f=\mathbf{0}$, leading to

$${\rho }_{k,p}^{\mathrm{opt}}={\gamma }_{k,p}^{★},\forall k\in \mathcal{K},\forall p\in \mathcal{P}.$$

(17)

(2) Fix $\left(\mathbf{\Psi },\mathit{\rho }\right)$ and find ${\mathbf{W}}^{\mathrm{opt}}$

Given fixed $\left({\mathbf{\Psi }}^{★},{\mathit{\rho }}^{★}\right)$, problem ${\overline{P}}_1$ in (14) can be transformed into

$$\begin{array}{cc}\hfill & P_2:\underset{\mathbf{W}}{max}g\left(\mathbf{W}\right)=\sum _{k=1}^K\sum _{p=1}^P{\mu }_{k,p}{f}_{k,p}\left({\mathbf{\Psi }}^{★},\mathbf{W}\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.C_1:\sum _{k=1}^K\sum _{p=1}^P{∥{\widehat{\mathbf{w}}}_{b,p,k}∥}^2\le P_{b,\max },\forall b\in \mathcal{B},\hfill \\ \hfill & C_2:\sum _{k=1}^K\sum _{p=1}^P{∥{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{G}}_{b,r,p}{\mathbf{w}}_{b,p,k}∥}^2\hfill \\ \hfill & +{∥{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r∥}_{\mathrm{F}}^2{\sigma }_{k,p}^2\le P_{r,\max },\forall r\in \mathcal{R},\hfill \\ \hfill & C_3:\mathbf{Z}={\mathbf{Z}}^{★}.\hfill \end{array}$$

(18)

where ${\mu }_{k,p}={\eta }_k\left(1+\rho {k,p}^{★}\right)$, the reformulated subproblem $P_2$ remains computationally intractable due to the high-dimensional non-convexity of $f_{k,p}$ in Equation (18). Building upon the Multidimensional Complex Quadratic Transform (MCQT) framework [27], we introduce Lemma A1 to optimize $\mathbf{W}$, with the detailed formulation and solution procedure provided in Appendix A.

(3) Fix $\left(\mathbf{W},\mathit{\rho }\right)$ and find ${\mathbf{\Psi }}^{\mathrm{opt}}$

Given fixed $\left({\mathbf{W}}^{★},{\mathbf{\rho }}^{★}\right)$, problem ${\overline{P}}_1$ in Equation (14) can be rewritten as

$$\begin{array}{cc}\hfill & P_3:\underset{\mathbf{\Psi }}{max}{g}_4(\mathbf{\Psi })=\sum _{k=1}^K\sum _{p=1}^P{\mu }_{k,p}{f}_{k,p}\left(\mathbf{\Psi },{\mathbf{W}}^{★}\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.C_1:\sum _{k=1}^K\sum _{p=1}^P{∥{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{G}}_{b,r,p}{\mathbf{w}}_{b,p,k}∥}^2\hfill \\ \hfill & +{∥{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r∥}_{\mathrm{F}}^2{\sigma }_{k,p}^2\le P_{r,max},\forall r\in \mathcal{R},\hfill \\ \hfill & C_2:{\theta }_{r,n}\in (0,2\pi ),\forall r\in \mathcal{R},\forall n\in {\mathcal{N}}_S,\hfill \\ \hfill & C_3:\mathbf{Z}={\mathbf{Z}}^{★},\hfill \end{array}$$

(19)

where ${\mu }_{k,p}={\eta }_k\left(1+{\rho }_{k,p}^{★}\right)$. To reduce complexity and simplify the expression for $g_4$, first, define a new auxiliary function about $\mathbf{\Psi }$:

$${\mathbf{Q}}_{k,p,j}\left(\mathbf{\Psi }\right)=\sum _{b=1}^B\left({\mathbf{H}}_{b,k,p}^{\mathrm{H}}+{\widehat{\mathbf{F}}}_{k,p}^{\mathrm{H}}{\mathbf{\Psi }}^{\mathrm{H}}\mathbf{Z}{\mathbf{G}}_{b,p}\right){\widehat{\mathbf{w}}}_{b,p,j}.$$

(20)

$$g_4\left(\mathbf{\Psi }\right)=\sum _{k=1}^K\sum _{p=1}^P\sqrt{{\mu }_{k,p}}{\mathbf{Q}}_{k,p,k}^{\mathrm{H}}\left(\mathbf{\Psi }\right){\left(\sum _{j=1}^K{\mathbf{Q}}_{k,p,j}\left(\mathbf{\Psi }\right){\mathbf{Q}}_{k,p,k}^{\mathrm{H}}\left(\mathbf{\Psi }\right)\right)}^{-1}{\mathbf{Q}}_{k,p,k}\left(\mathbf{\Psi }\right)$$

(21)

Therefore, $g_4$ can be rewritten as Equation (21), subproblem (19) satisfies the concave–convex condition [27], so the MCQT method is used to solve subproblem $P_3$ with Lemma A2, and the detailed formulation and solution procedure are provided in Appendix B.

The optimized deployment of RIS based on ATS, as detailed in Algorithm 1, proceeds as follows. Steps 1–2 initialize the tabu list $\mathcal{H}$, neighborhood distance p, neighborhood size Q, maximum iteration count $I_T$, and the initial RIS topology ${\mathbf{Z}}^{\left(0\right)}$. In Step 4, p is dynamically adjusted based on iteration i—using a larger value initially for global exploration and a smaller one later for local refinement. Candidate solutions are generated by randomly swapping p ones and zeros in the diagonal of ${\mathbf{Z}}^{\left(i\right)}$. Step 5 checks candidates against the tabu list to avoid duplication, yielding Q valid solutions. Step 6 selects the solution with the highest WSR as ${\mathbf{Z}}^{(i+1)}$. Steps 8–11 update the tabu list by adding the current solution and removing the oldest one. Upon reaching $I_T$ iterations, the suboptimal topology ${\mathbf{Z}}^{\mathrm{opt}}$ is obtained.

The algorithm then enters Stage 2. Step 13 initializes ${\mathbf{W}}^{\left(0\right)}$ and ${\mathbf{\Psi }}^{\left(0\right)}$ using ${\mathbf{Z}}^{\mathrm{opt}}$. Steps 15–20 perform alternating optimization: iteratively updating auxiliary variables $\mathit{\rho }$, $\mathit{\varsigma }$, $\mathit{\epsilon }$ and solving convex problems for $\mathbf{W}$ and $\mathbf{\Psi }$ until Equation (9) converges. The final outputs are the optimized $\mathbf{W}$, $\mathbf{\Psi }$, $\mathbf{Z}$, and the maximum WSR.

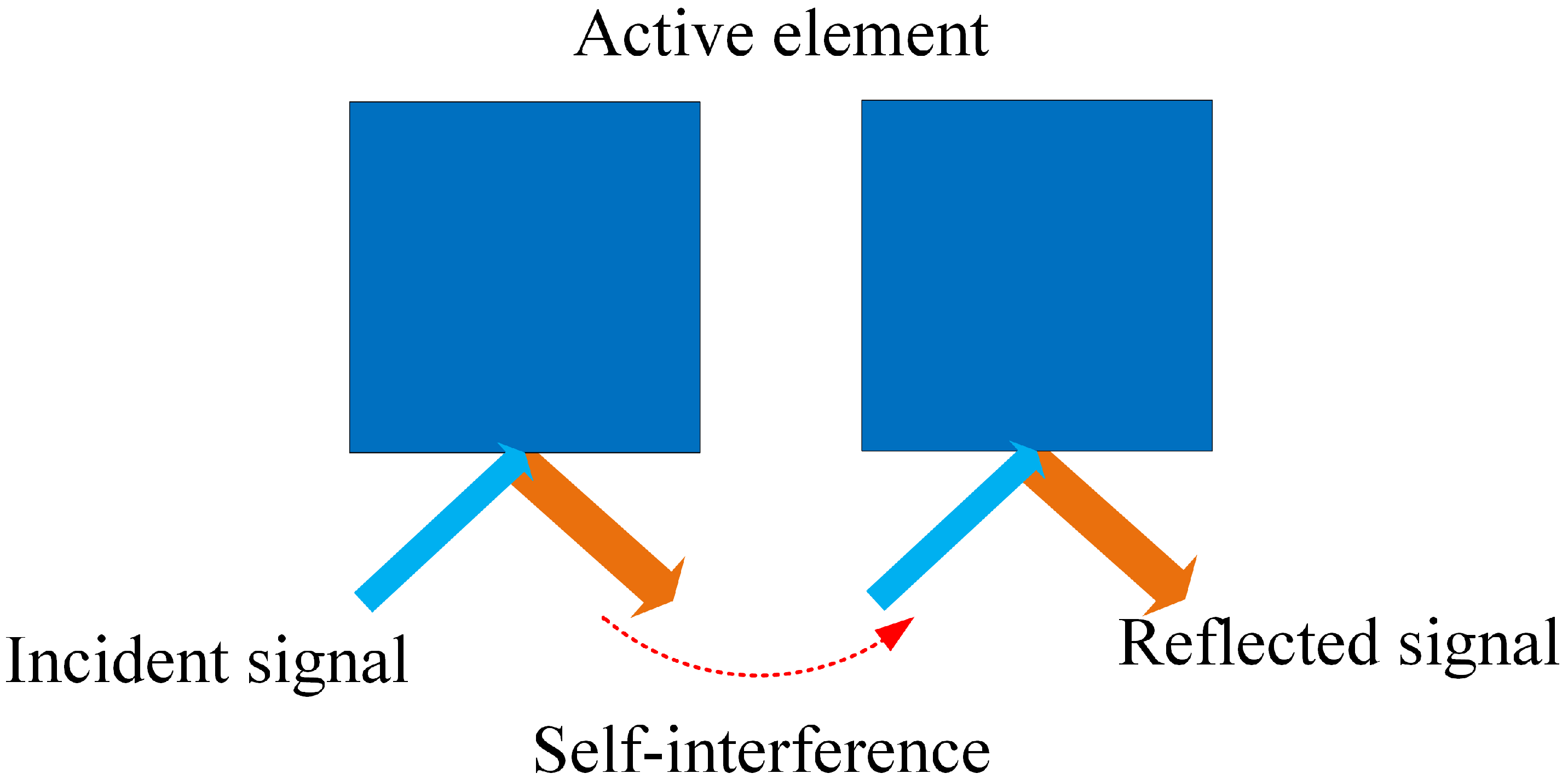
3.4. Self-Interference Suppression of Active RIS

The active RIS operates in full-duplex mode. However, suboptimal array element spacing can lead to multipath reception effects, where reflected signals are recaptured by the active RIS, leading to feedback self-interference in the actual system [18], as illustrated in Figure 2.

To account for the impact of self-interference on the system’s performance, the self-interference matrix $\mathbf{S}$ [28] is defined. The distribution of each element in $\mathbf{S}$ obeys $\mathbf{S}\sim \mathcal{C}\mathcal{N}\left(0,{\delta }^2\right)$,where the self-interference coefficient $\delta$ exhibits an inverse proportionality to the inter-element spacing in the physical array configuration, that is, $\delta \propto \lambda /2$, with $\lambda$ representing the wavelength of the carrier frequency. In the presence of non-negligible self-interference, the reflected signal at an active RIS follows the modified model:

$$\begin{array}{cc}\hfill & {\mathbf{r}}^{\prime }=\underset{\mathrm{Desires}\mathrm{signal}}{\underbrace{\sum _{r=1}^R{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{x}}_{b,p}}}+\underset{\mathrm{Self}-\mathrm{interference}}{\underbrace{\sum _{r=1}^R{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r\mathbf{S}\mathbf{y}}}\hfill \\ \hfill & +\underset{\mathrm{Amplified}\mathrm{noise}}{\underbrace{\sum _{r=1}^R{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{v}_{r,p}}}+{\mathbf{e}}_{k,p}.\hfill \end{array}$$

(22)

$${\mathbf{r}}^{\prime }={\left({\mathbf{I}}_{N_S}-\sum _{r=1}^R{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r\mathbf{S}\right)}^{-1}\sum _{r=1}^R{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r\left({\mathbf{x}}_{b,p}+v_{r,p}\right)+{\mathit{e}}_{k,p}.$$

(23)

Through algebraic transformation we obtain Equation (23). A comparative analysis with Equation (3) reveals the key enhancement lies in replacing the RIS beamforming matrix $\mathbf{\Psi }{r}^{\mathrm{H}}$ in Equation (2) with the augmented expression ${\left({\mathbf{I}}_{N_S}-{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r\mathbf{S}\right)}^{-1}{\mathbf{\Psi }}_r^{\mathrm{H}}$. Notably, when $\mathbf{S}=\mathbf{0}$, the equivalent beamforming matrix reduces to the diagonal form $\mathbf{\Psi }{r}^{\mathrm{H}}$, representing the ideal scenario. By defining ${\mathbf{\Phi }}_r^{\mathrm{H}}={\left({\mathbf{I}}_{N_S}-{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r\mathbf{S}\right)}^{-1}{\mathbf{\Psi }}_r^{\mathrm{H}}$ as the self-interference-aware phase shift matrix for optimized active RIS deployment, the transmitted signal from the b-th BS to the k-th user on the p-th subcarrier under non-ideal conditions (with self-interference) can be expressed as follows:

$${\mathbf{y}}_{b,k,p}^{\prime }=\left({\mathbf{H}}_{b,k,p}^{\mathrm{H}}+\sum _{r=1}^R{\mathbf{F}}_{r,k,p}^{\mathrm{H}}{\mathbf{\Phi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{G}}_{b,r,p}\right)\sum _{j=1}^K{\mathbf{w}}_{b,p,j}{s}_{p,j}+\sum _{r=1}^R{\mathbf{F}}_{r,k,p}^{\mathrm{H}}{\mathbf{\Phi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{v}_{r,p}+{\mathit{e}}_{k,p}$$

(24)

$${\mathbf{y}}_{b,k,p}^{\prime }=\left({\mathbf{H}}_{b,k,p}^{\mathrm{H}}+\sum _{r=1}^R\left({\mathbf{F}}_{r,k,p}^{\mathrm{H}}+v_{r,p}\right){\mathbf{\Phi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{G}}_{b,r,p}\right)\sum _{j=1}^K\sqrt{{\mathbf{w}}_{b,p,j}}{\widehat{s}}_{p,j}+{\mathit{e}}_{k,p}.$$

(25)

Similarly, referring to ref. [15], Equation (24) is simplified as shown in Equation (25). When the self-interference matrix $\mathbf{S}$ is a zero matrix, the ideal system model can be obtained. The equivalent channel with self-interference is

$${\overline{\mathbf{h}}}_{b,k,p}^{\mathrm{H}}={\mathbf{H}}_{b,k,p}^{\mathrm{H}}+\sum _{r=1}^R{\widehat{\mathbf{F}}}_{r,k,p}^{\mathrm{H}}{\mathbf{\Phi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{G}}_{b,r,p}.$$

(26)

According to Equations (25) and (26), in the presence of self-interference, the achievable SINR at user k over subcarrier p is

$${\gamma }_{k,p}^{\prime }={\displaystyle \frac{{\widehat{\mathbf{w}}}_{p,k}^{\mathrm{H}}{\overline{\mathbf{h}}}_{k,p}{\widehat{\mathbf{h}}}_{p,k}^{\mathrm{H}}{\widehat{\mathbf{w}}}_{p,k}}{{\displaystyle \sum _{j=1,j\ne k}^K}{\overline{\mathbf{h}}}_{p,k}^{\mathrm{H}}{\widehat{\mathbf{w}}}_{p,j}{\left({\overline{\mathbf{h}}}_{p,k}^{\mathrm{H}}{\widehat{\mathbf{w}}}_{p,j}\right)}^{\mathrm{H}}+{\Xi }_{k,p}}}.$$

(27)

The WSR across all K users is given by

$$R_{\mathrm{sum}}^{\prime }=\sum _{k=1}^K\sum _{p=1}^P{\eta }_k\log \left(1+{\gamma }_{k,p}^{\prime }\right).$$

(28)

Consequently, the optimization problem under self-interference conditions is formulated as follows:

$$\begin{array}{cc}\hfill & P_0^{\prime }:\underset{\mathbf{\Phi },\mathbf{W},\mathbf{Z}}{max}{R}_{\mathrm{sum}}^{\prime }\left(\mathbf{\Phi },\mathbf{W},\mathbf{Z}\right)=\sum _{k=1}^K\sum _{p=1}^P{\eta }_k{log}_2\left(1+{\gamma }_{k,p}\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.C_1:\sum _{k=1}^K\sum _{p=1}^P{∥{\widehat{\mathbf{w}}}_{b,p,k}∥}^2\le P_{b,max},\forall b\in \mathcal{B},\hfill \\ \hfill & C_2:\sum _{k=1}^K\sum _{p=1}^P{∥{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r{\mathbf{G}}_{b,r,p}{\mathbf{w}}_{b,p,k}∥}^2\hfill \\ \hfill & +{∥{\mathbf{\Psi }}_r^{\mathrm{H}}{\mathbf{Z}}_r∥}_{\mathrm{F}}^2{\sigma }_{k,p}^2\le P_{r,max},\forall r\in \mathcal{R},\hfill \\ \hfill & C_3:{\theta }_{r,n}\in (0,2\pi ),\forall r\in \mathcal{R},\forall n\in {\mathcal{N}}_S,\hfill \\ \hfill & C_4:z_{r,n}\left(z_{r,n}-1\right)=0,\forall r\in \mathcal{R},\forall n\in {\mathcal{N}}_S,\hfill \\ \hfill & C_5:{\mathbf{1}}^{\mathrm{T}}\mathbf{z}=RN.\hfill \end{array}$$

(29)

Since the optimization process for problem $P_0^{\prime }$ closely mirrors that of problem $P_0$, we first employ the ATS algorithm to derive the suboptimal topology ${\mathbf{Z}}^{\mathrm{opt}}$. Following this, the LDR method is applied to decouple the variables in the optimization problem. Subsequently, an alternating iterative optimization algorithm is used to optimize each variable individually. As the algorithmic steps follow the same structure as outlined in Algorithm 1, they are omitted for brevity.

3.5. Complexity Analysis

For the proposed Algorithm 1, the optimization variables include the precoding matrix $\mathbf{W}$, RIS phase shift vector $\mathit{\psi }$, auxiliary variables $\mathit{\rho }$, $\mathit{\epsilon }$, and $\mathit{\varsigma }$, as well as RIS topology matrix $\mathbf{Z}$. These variables play a critical role in the joint optimization framework, where the algorithm alternately updates them to maximize the system weighted sum-rate. The dominant computational cost is introduced by the iterative updating of these variables, particularly the $I_T$ iterations required for the ATS procedure and the neighborhood size parameter Q, in addition to the $I_a$ and $I_b$ iterations for subproblems (46) and (50), respectively.

It is worth noting that the complexity of a conventional active RIS scheme is essentially captured by the latter part of this analysis, namely the iterative updates for precoding and phase-shift optimization (i.e., without the ATS-related terms $I_T$ and Q). Therefore, the additional complexity of the proposed scheme stems primarily from the topology optimization stage. This added cost remains manageable since Q is limited to a moderate neighborhood size, and $I_T$ typically converges within a small number of iterations in practice. Consequently, the proposed method achieves significant performance gains with only a modest increase in computational complexity compared to conventional active RIS schemes.

Table 3. Computational complexity for updating each variable.

Variable	Computational Complexity $\mathcal{O}\left(·\right)$
$\mathbf{Z}$	$I_{\mathrm{T}}Q$
$\mathit{\rho }$	$PK\left(KUBM+U^3+\left(K+1\right)U^2+U\right)$
$\mathit{\varsigma }$	$PK\left(KUBM+U^3+\left(K+1\right)U^2\right)$
$\mathbf{W}$	$I_{\mathrm{a}}\left(B^2{M}^2{P}^2{K}^2+BMPK\right)$
$\mathit{\epsilon }$	$PK\left(U^3+\left(K+1\right)U^2\right)$
$\mathbf{\Psi }$	$I_{\mathrm{b}}\left(R^2{N}_S^2+R{N}_S\right)$

demonstrates that while $\mathit{\rho }$, $\mathit{\varsigma }$, and $\mathit{\epsilon }$ have closed-form update expressions, both ${\mathbf{W}}^{\mathrm{opt}}$ and ${\mathbf{\Psi }}^{\mathrm{opt}}$ require iterative solutions to the QCQP problem. Consequently, the computational burden of $\mathit{\rho }$, $\mathit{\varsigma }$, and $\mathit{\epsilon }$ is significantly lighter than that of ${\mathbf{W}}^{\mathrm{opt}}$ and ${\mathbf{\Psi }}^{\mathrm{opt}}$. Furthermore, considering the dense deployment of BSs and users in CF networks [6], as well as the typically large RIS element counts [10], the conditions $BMPK\gg U$ and $R{N}_S\gg U$ hold in practice. These scaling relationships yield an overall algorithmic complexity of the method given by $\mathcal{O}\left(I_o(I_a{B}^2{M}^2{P}^2{K}^2+I_b{R}^2{N}_S^2+I_{T}Q)\right)$, where $I_o$ denotes the outer-loop iteration count.

4. Simulation Results

This section provides numerical validation of the performance gains achieved through optimized active RIS deployment in CF networks. The simulation setup includes five BSs and two optimized deployment active RISs, collaboratively serving four users, as illustrated in Figure 3. In our simulation scenario, the i-th BS is placed at $\left(40(i-1),-50,3\right)$ meters (x, y, and z coordinates respectively), while the two optimized deployment active RISs are positioned at $\left(60\mathrm{m},10\mathrm{m},6\mathrm{m}\right)$ and $\left(100\mathrm{m},10\mathrm{m},6\mathrm{m}\right)$, respectively. For each BS and user, the number of antennas is configured to $M=2$ and $U=2$, respectively. The optimized active RIS deployment configuration comprises $N=100$ active elements distributed over $N_S=200$ candidate grid points. The system configuration employs $P=4$ subcarriers, with user-terminal noise power ${\sigma }^2=-100\mathrm{dBm}$ and active RIS-induced noise power ${\sigma }_v^2=-100\mathrm{dBm}$. For fair performance benchmarking, the total transmit power in the active RIS-assisted system is constrained to $P_{\mathrm{A}}^{\max }=0\mathrm{dBm}$, allocated as $P_{b,\max }=0.9P_{\mathrm{A}}^{\max }$ per base station and $P_{R,\max }=0.1P_{\mathrm{A}}^{\max }$ aggregate power across all RIS elements. Meanwhile, the total power allocated to the active RIS-assisted system is also set at $P_{\mathrm{B}}^{\max }=0\mathrm{dBm}$. To broaden the scope of the search, the tabu list size is established at 1, and the weight assigned to each user is ${\eta }_k=1$. To demonstrate the performance advantages of our proposed approach, detailed parameters are provided in

Table 4. Simulation parameters.

Number of BSs (B)	5	Number of UEs (K)	4
Number of RISs (R)	2	Antennas per BS (M)	2
Antennas per UE (U)	2	Reflecting elements per RIS (N)	100
Candidate grid points ($N_S$)	200	Number of subcarriers (P)	4
Carrier frequency ($f_c$)	$2.93\mathrm{GHz}$	System bandwidth (B)	$10\mathrm{MHz}$
Path loss model (${\mathrm{PL}}_s$)	$37.3+22{log}_{10}d$	UE noise power (${\sigma }^2$)	$-100\mathrm{dBm}$
RIS noise power (${\sigma }_v^2$)	$-100\mathrm{dBm}$	Amplifier noise figure (NF)	$4\mathrm{dB}$
Coupling coefficient for self-interference ($\delta$)	$-40\mathrm{dB}$	Channel state information(CSI) error parameters ($\iota$)	$0.1$
Total transmit power (active RIS) ($P_A^{max}$)	$0\mathrm{dBm}$	Total transmit power (passive RIS) ($P_B^{max}$)	$0\mathrm{dBm}$
Per-BS transmit power ($P_{b,max}$)	$0.9P_A^{max}$	RIS aggregate power ($P_{R,max}$)	$0.1P_A^{max}$
User weight (${\eta }_k$)	1	Tabu list size	1
BS positions	$\left(40\right(i-1),-50,3)$ m	RIS positions	$(60,10,6)$ m; $(100,10,6)$ m

. We evaluate four comparative schemes:

• Optimized deployment active RIS: The proposed scheme employs Algorithm 1 to jointly optimize BS precoding, active RIS beamforming, and topology configuration in a cell-free MIMO system with optimally deployed active RIS elements.
• Conventional active RIS: This baseline adopts the joint BS-RIS optimization framework from [29] for conventional active RIS-assisted cell-free MIMO systems, optimizing both BS beamforming and RIS precoding.
• Passive RIS: Following [9], this benchmark implements joint BS precoding and passive RIS beamforming optimization in a passive RIS-enabled, cell-free MIMO system.
• Without RIS: As a fundamental reference, this configuration allocates all transmit power to direct BS-user links in a traditional RIS-free cell-free MIMO system.
• Active RIS with Power Allocation and Precoding (ARIS-JOP) [30]: This scheme maximizes the system sum-rate in active RIS-aided CF massive MIMO by jointly optimizing user power allocation, BS beamforming, and RIS precoding under active RIS power constraints, solved via an alternating optimization framework.
• Passive RIS with Joint UE Association and Beamforming (PRIS-JAB) [31]: This scheme addresses RIS-assisted CF MIMO with RIS-UE association and WSR maximization, using a two-stage design: many-to-many matching for RIS-UE association and MM-based optimization for RIS phase shifts with BS beamforming.

Our analysis concentrates on strong direct-link scenarios, employing the 3GPP-standardized path loss model [32] for large-scale fading characterization:

$$\mathrm{P}{\mathrm{L}}_s=37.3+22.0\log d,$$

(30)

where d is the distance between two devices. The path loss model $\mathrm{P}{\mathrm{L}}_s$ is used to generate strong BS-user links.

All considered channels in this work are modeled by Rayleigh fading distributions. The channel matrix $\mathit{G}$ is given by

$$\mathit{G}=\sqrt{\mathrm{PL}}\left(\sqrt{{\displaystyle \frac{\chi }{\chi +1}}}{\mathit{G}}_{\mathrm{LoS}}+\sqrt{{\displaystyle \frac{1}{\chi +1}}}{\mathit{G}}_{\mathrm{NLoS}}\right),$$

(31)

where PL denotes the path loss of channel matrix $\mathit{G}$, $\chi$ represents the Ricean factor, and ${\mathit{G}}_{\mathrm{LoS}}$ and ${\mathit{G}}_{\mathrm{NLoS}}$ correspond to the line-of-sight (LoS) and non-line-of-sight (NLoS) components, respectively.

In Figure 4, we examine the relationship between the WSR and user distance D, where users move along a straight line from (0 m, 0 m) to (160 m, 0 m), following the simulation setup in ref. [9]. In comparison to configurations without RIS, two significant peaks are observed at (60 m, 0 m) and (100 m, 0 m) in scenarios employing RISs. This indicates that users in proximity to RISs benefit from enhanced SINR owing to the signals reflected by the RISs, thereby improving the users’ WSR. Furthermore, active RIS schemes significantly elevate the achievable sum-rate for users when compared to passive RIS configurations. It is also noted that the performance of optimized deployment active RIS surpasses that of conventional active RIS approaches. This demonstrates that the proposed scheme provides additional spatial degrees of freedom.

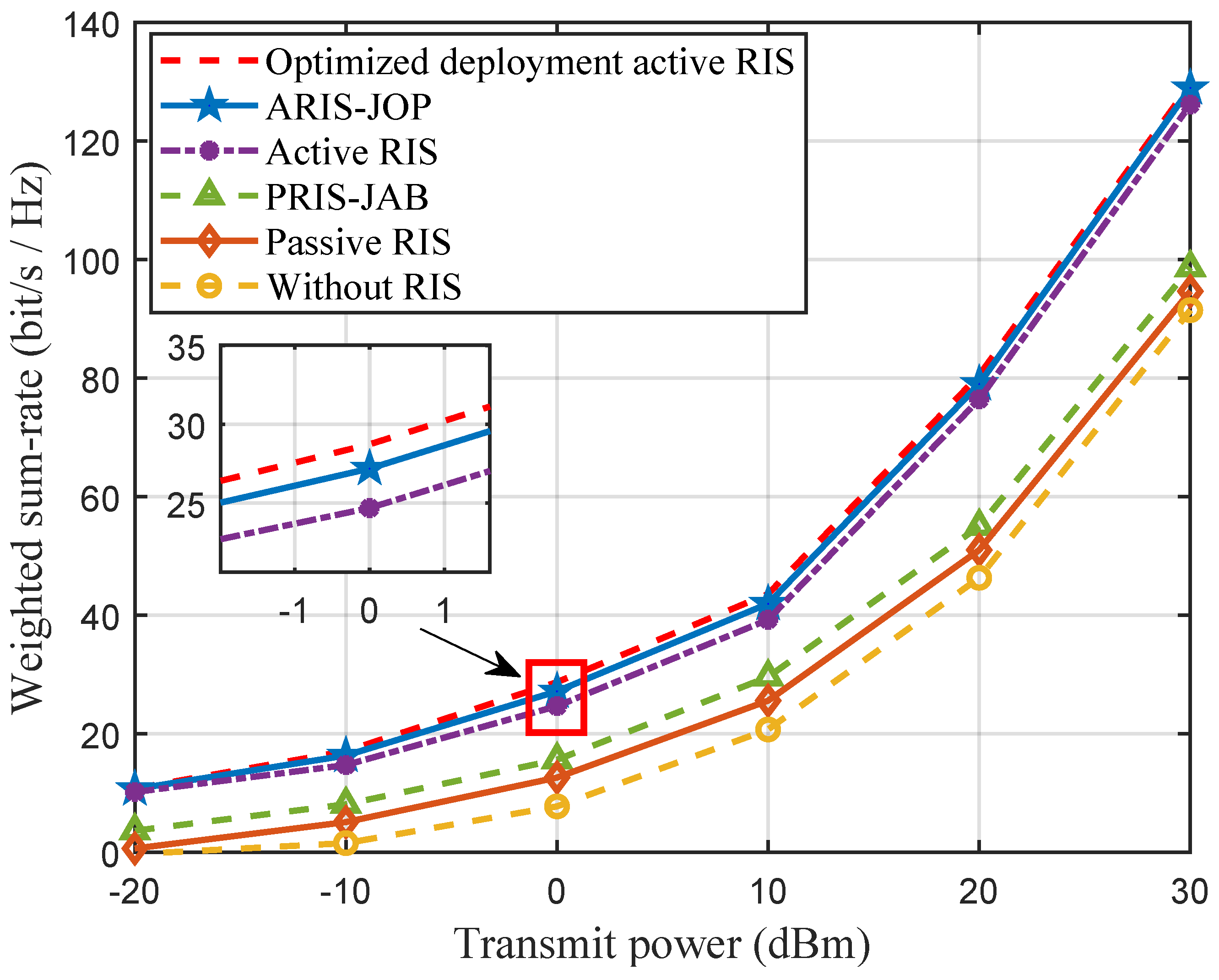
When the user distance is set to $D=80\mathrm{m}$, Figure 5 depicts the WSR performance as a function of the transmit power under six representative schemes: optimized deployment active RIS (proposed), conventional active RIS [29], passive RIS [9], active RIS with power allocation and precoding [30], passive RIS with joint UE association and beamforming [31], and a baseline without RIS. Taking the passive RIS as a benchmark, at 0 dBm transmit power, the proposed optimized deployment active RIS achieves a $127.34\%$ gain in WSR, while the conventional active RIS achieves $107.23\%$. Compared with the passive RIS with joint UE association and beamforming in [31], our scheme still demonstrates superior performance due to its element-level topology optimization and self-interference suppression, which effectively exploit spatial degrees of freedom and maintain robustness against amplifier noise. As the transmit power increases, active RIS architectures exhibit more pronounced advantages over both passive RIS and passive RIS with joint UE association and beamforming baselines. Importantly, the proposed optimized deployment active RIS consistently provides the highest WSR across the full transmit power range, validating that the integration of topology design, SI suppression, and joint precoding yields substantial additional capacity gains in CF MIMO networks.

In Figure 6, we consider the relationship between WSR and RIS element number N, where the grid number of the proposed scheme is set to $N_S=200$. The figure demonstrates a monotonic improvement in WSR with increasing RIS element count for both schemes. Notably, the performance advantage of the proposed method over conventional active RIS ($N=120$) diminishes as the quantity of active components grows. This reveals that under constrained active-element budgets, our scheme achieves significant capacity enhancement, confirming its architectural superiority.

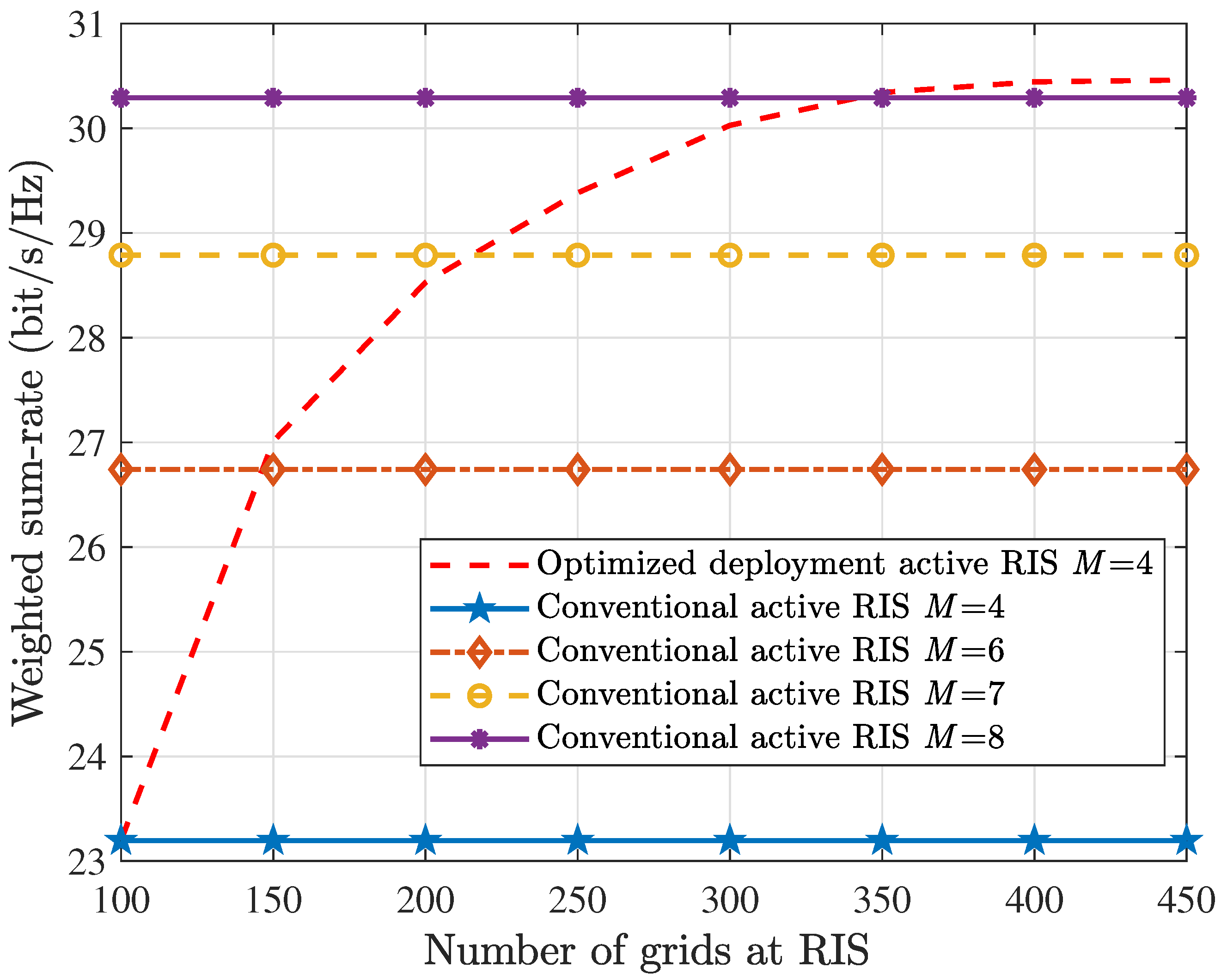
In Figure 7, WSR performance is a function of grid point density, comparing the proposed optimized active RIS deployment with conventional active RIS implementations under different transmit antenna configurations. Using the scheme of conventional active RIS with $(M=2,N=100)$ as a benchmark, the WSR exhibits measurable enhancement through physical aperture expansion of the optimized active RIS while maintaining fixed $N=100$ elements. Furthermore, multiple benchmark scenarios employing conventional active RIS architectures are evaluated, which deployed multi-antennas at the BS. The quantities of RIS elements and users remain invariant throughout the analysis. Note that when the number of grids is increased to $N_S=150$, $N_S=210$, and $N_S=350$, the optimized deployment active RIS with achieves identical WSR performances comparable to the conventional active RIS with $M=4$, $M=6$, and $M=8$, respectively. Consequently, the optimized active RIS deployment offers a cost-efficient approach for enhancing system capacity while maintaining hardware affordability.

In order to validate the performance advantages of the proposed framework in suppressing self-interference between active elements, we present the variation of users’ WSR against the self-interference factor $\delta$ in Figure 8. As observed from the figure, the weighted sum-rate (WSR) becomes insensitive to self-interference variations when $\delta <-55$ dB. However, as the self-interference enhances, the performance of conventional active RISs-assisted systems decreases rapidly. In particular, when $\delta >-37$ dB, the WSR of conventional active RIS with self-interference is inferior to the passive RIS. This degradation stems from the self-interference matrix $\mathbf{S}$, which both defocuses the RIS-reflected signals and destructively interferes with the direct-link signals. Nevertheless, the proposed scheme demonstrates robust performance under such interference conditions. For example, at $\delta <-40$ dB, the performance of optimized deployment active RIS-assisted CF system with self-interference slowly degrades compared to the ideal case. Especially when $\delta$ increases from $-35$ dB to $-20$ dB, the proposed scheme can compensate the sum-rate loss of 17.05 bps/Hz compared with conventional active RIS. Thanks to the sparse distribution of active elements, our scheme consistently outperforms both conventional active RIS and passive RIS systems, demonstrating superior self-interference suppression capabilities. Consequently, subsequent simulations will consider only the ideal scenario devoid of self-interference.

In the proposed optimized deployment active RIS-assisted CF massive MIMO networks, channel estimation presents significant challenges due to the high-dimensionality of the channel. This paper analyzes the robustness of the proposed scheme to CSI errors. CSI uncertainty is modeled through an additive zero-mean Gaussian random variable, yielding the estimated channel response $\widehat{h}=h+\iota$, where h and $\iota$ represent the actual channel and the estimation error, respectively, where $\iota \sim \mathcal{C}\mathcal{N}\left(0,{\sigma }_{\iota }^2\right)$ and ${\sigma }_{\iota }^2\triangleq \rho {\left|h\right|}^2$ represent the error power. 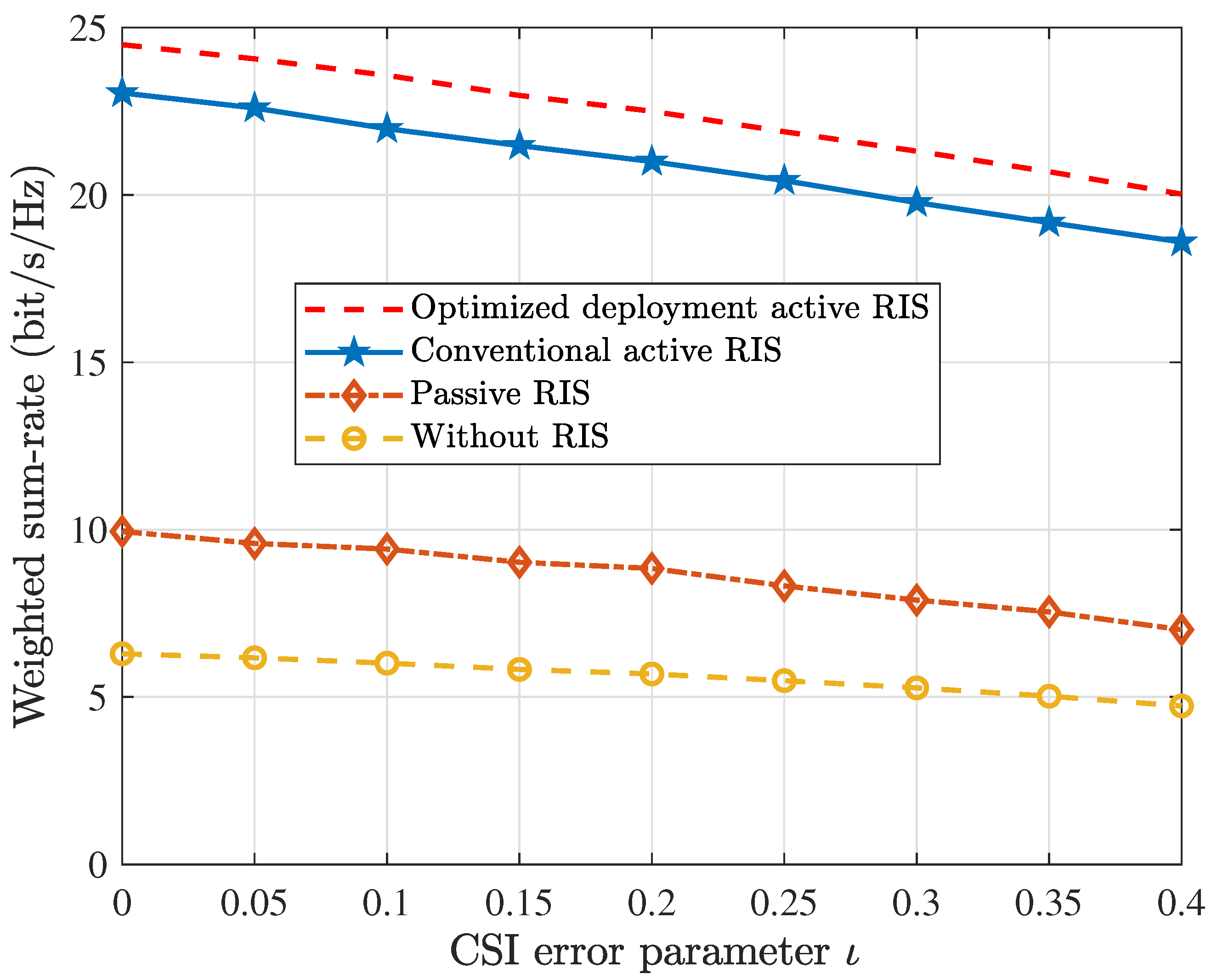Figure 9 illustrates the relationship between WSR and the CSI error factor $\iota$. As the CSI error factor increases, the performance degradation of all schemes gradually intensifies. Specifically, when $\iota =0.4$, the WSR of without RIS, passive RIS, conventional active RIS, and optimized deployment active RIS decrease by 24.8%, 29.5%, 19.3%, and 18.3%, respectively. Therefore, the proposed scheme demonstrates the highest level of robustness.

To provide a more intuitive illustration of the performance gain achieved by the proposed scheme,

Table 5. Comparison of WSR performance at $0\mathrm{dBm}$ under different schemes, sorted in ascending order of performance.

Scheme	WSR Gain
Without RIS	Baseline
Passive RIS [9]	$+62.49\%$
Passive RIS with Joint UE Association and Beamforming [31]	$+101.06\%$
Conventional Active RIS [29]	$+217.46\%$
Active RIS with Power Allocation and Precoding [30]	$+249.67\%$
Proposed Optimized Active RIS	$+269.43\%$

presents the WSR improvement percentages under a transmit power of $0\mathrm{dBm}$, along with a technical analysis of the performance differences. Compared to the without RIS baseline, the passive RIS [9] scheme achieves a WSR improvement of approximately $62.49\%$ by leveraging phase-programmable passive reflection to emulate beamforming, which partially reconfigures the multipath environment and coverage while generating weaker responses in undesired directions. Building on this, the passive RIS with joint UE association and beamforming [31] further prioritizes the allocation of limited coherent gain to users or clusters with better channel conditions, while steering weak-link or strongly coupled users to avoid interference, thereby reducing ineffective reflection and mutual interference and increasing the performance gain to $101.06\%$.

The conventional active RIS [29] scheme introduces active amplification before reflection, significantly mitigating the multiplicative fading effect inherent in passive links. By jointly adjusting both amplitude and phase, it concentrates beam gain more effectively in the desired directions and suppresses radiation in the undesired directions, thereby reducing multi-user interference and achieving a significantly higher improvement of $217.46\%$. On this basis, the active RIS with power allocation and precoding [30] incorporates a joint power allocation and precoding strategy into the active RIS framework. The reason for its superior performance lies in the additional degrees of freedom it provides under amplifier and noise constraints, enabling dynamic resource allocation based on the marginal benefits of different users or directions to better balance signal enhancement and multi-user interference suppression, which leads to a further gain of $249.67\%$.

In contrast, the proposed optimized active RIS introduces an element/topology-level selection mechanism and explicitly accounts for self-interference and amplified noise. Its ability to outperform both aforementioned schemes and achieve the highest WSR improvement of $269.43\%$ stems from the coupling of element/topology selection with precoding that explicitly handles self-interference and amplified noise. This design concentrates the active amplification capability on elements with good spatial matching and low coupling/interference, while effectively suppressing harmful coupling and amplified noise. As a result, it achieves the highest performance in the system with comparable complexity, further verifying its effectiveness and superiority.

5. Conclusions

This paper investigates optimized deployment active RIS-assisted CF massive MIMO networks to overcome the capacity limitations observed in conventional active RIS-assisted systems. In the proposed framework, multiple optimized deployment active RISs and multiple BSs collaboratively serve multiple users, where a joint topology optimization and precoding scheme is introduced to maximize the WSR. Simulation results demonstrate that, compared with conventional active RIS architectures, the proposed scheme achieves more significant performance gains, and under scenarios with a limited number of active elements, the system capacity can still be further enhanced.

The key contribution of this work lies in exploiting element-level spatial freedom and integrating interference suppression with joint precoding, thereby improving the capacity of CF MIMO systems. Future work may focus on developing new optimization algorithms tailored for large-scale RIS-assisted CF networks (e.g., hybrid strategies that combine metaheuristics and convex optimization) to further accelerate convergence and enhance scalability. In addition, extending the framework to more practical system conditions, such as imperfect CSI and user mobility, would provide valuable insights for the deployment of the proposed scheme in real-world communication systems.