Abstract
As artificial intelligence continues to evolve, reinforcement learning (RL) has shown remarkable potential for solving complex sequential decision problems and is now applied in diverse areas, including robotics, autonomous vehicles, and financial analytics. Among the various RL paradigms, multi-agent reinforcement learning (MARL) stands out for its ability to manage cooperative and competitive interactions within multi-entity systems. However, mainstream MARL algorithms still face critical challenges in training stability and policy generalization due to factors such as environmental non-stationarity, policy coupling, and inefficient sample utilization. To mitigate these limitations, this study introduces an enhanced algorithm named MATD3_AHD, developed by extending the MATD3 framework, which integrates TD3 and MADDPG principles. The goal is to improve the learning efficiency and overall policy effectiveness of agents operating in complex environments. The proposed method incorporates three key mechanisms: (1) an Adaptive Exploration Policy (AEP), which dynamically adjusts the perturbation magnitude based on TD error to improve both exploration capability and training stability; (2) a Hierarchical Sampling Policy (HSP), which enhances experience utilization through sample clustering and prioritized replay; and (3) a Dynamic Delayed Update (DDU), which adaptively modulates the actor update frequency based on critic network errors, thereby accelerating convergence and improving policy stability. Experiments conducted on multiple benchmark tasks within the Multi-Agent Particle Environment (MPE) demonstrate the superior performance of MATD3_AHD compared to baseline methods such as MADDPG and MATD3. The proposed MATD3_AHD algorithm outperforms baseline methods—by an average of 5% over MATD3 and 20% over MADDPG—achieving faster convergence, higher rewards, and more stable policy learning, thereby confirming its robustness and generalization capability.
1. Introduction
The continuous progress of artificial intelligence (AI) has brought reinforcement learning (RL) to the forefront as a key branch of intelligent decision-making. RL provides a mechanism for agents to learn behaviors through repeated interaction with their surroundings, adjusting actions according to the feedback received as rewards or penalties [1]. By maximizing cumulative rewards over time, agents iteratively optimize their behavior to learn an optimal policy [2,3]. In recent years, the incorporation of deep learning (DL) techniques has greatly strengthened RL by endowing it with strong feature extraction and perception capabilities. This integration, commonly referred to as deep reinforcement learning (DRL), enables agents to infer effective strategies directly from raw sensory inputs. DRL is not only effective in solving decision-making problems in discrete action spaces [4,5,6,7,8]; more importantly, it addresses optimization in continuous action spaces [9], a breakthrough that has empowered autonomous agents to perform remarkably well in complex, dynamic environments such for as autonomous driving [10,11,12] and robotic motion control [13,14,15]. As a result, most state-of-the-art reinforcement learning algorithms are now based on deep learning frameworks [16,17]. Building on this foundation, multi-agent deep reinforcement learning (MARL) has become a natural extension, enabling intelligent coordination among multiple agents. It has found widespread applications in areas such as multi-robot collaboration, autonomous systems control, and intelligent transportation systems.
MARL faces unique difficulties arising from the complexity of interactive dynamics between agents, particularly environmental non-stationarity and credit assignment. Environmental non-stationarity arises from the simultaneous policy evolution of multiple agents, which makes state transitions difficult to predict. Credit assignment refers to the difficulty in quantifying an individual agent’s contribution to the global reward, especially in cooperative MARL settings, where agents must coordinate to achieve shared goals through co-evolution. To address this, Foerster et al. introduced the Counterfactual Multi-Agent (COMA) algorithm [18], which uses a counterfactual baseline to compute the marginal contribution of each agent’s action. This enables the quantification of an agent’s impact on the global reward. However, its computational complexity increases rapidly with the dimension of the action space due to the need to evaluate all alternative actions. Yu et al. extended the Proximal Policy Optimization (PPO) algorithm to multi-agent scenarios and introduced the Multi-Agent PPO (MAPPO) algorithm [19]. By leveraging a centralized critic to estimate the advantage function and employing a clipped objective to stabilize policy updates, MAPPO demonstrates strong robustness in heterogeneous agent tasks. Nevertheless, its reliance on global information limits its applicability in partially observable environments.
Due to the stable performance and strong effectiveness of the Multi-Agent Deep Deterministic Policy Gradient (MADDPG) algorithm in multi-agent systems, numerous improved variants have been developed based on it. Gao et al. proposed the LSTM-MADDPG algorithm with an asynchronous cooperative update mechanism, which significantly enhances the convergence stability of the algorithm [20]. Wen et al. introduced a decoupled MADDPG-based architecture for autonomous UAV swarm tracking and obstacle avoidance, demonstrating better accuracy and real-time performance compared to the original MADDPG [21]. Zhu et al. applied MADDPG to flocking control tasks in dynamic obstacle environments, validating its adaptability in non-static conditions [22]. Building upon this, Li et al. proposed the M3DDPG algorithm with policy generalization capabilities to address uncertainty caused by opponent policy shifts [23]. Mao et al. developed the ATT-MADDPG algorithm, which leverages attention mechanisms to adaptively model the dynamic joint policies of teammates, thereby improving multi-agent coordination [24]. In addition, Ding et al. applied MADDPG to unsignalized intersection control by introducing reference vehicles to construct partially static environments, effectively addressing real-time control issues in dynamic traffic scenarios [25]. Ma et al. proposed the OM-TCN model, which utilizes a Temporal Convolutional Network (TCN) to model and predict opponent behaviors, aiming to mitigate the challenges of environmental non-stationarity [26]. For further integration of diverse strategic concepts, Iqbal et al. introduced the Multi-Agent Actor–Attention–Critic (MAAC) algorithm in 2019, combining the advantages of MADDPG, COMA, and VDN [27]. Subsequently, Xia et al. introduced the HER-MAAC framework, which integrates hindsight experience replay to improve data utilization and boost learning stability [28].
In 2019, Ackermann formulated the MATD3 method, which extends the MADDPG architecture by embedding the key concepts of TD3 [29]. Given the promising performance of multi-agent cooperative tasks across diverse application scenarios, numerous researchers have introduced enhancements to MATD3 tailored to specific domains. Zhou, C.H. et al. [30] improved learning efficiency by integrating Prioritized Experience Replay (PER) into the MATD3 framework. Additionally, they designed a hybrid reward design that applies distinct formation-keeping rules for regions with and without obstacles. By adaptively adjusting formations, their method successfully achieves obstacle avoidance and resolves the formation control challenges encountered by conventional methods in complex environments. Wang Kun et al. [31] proposed the PSARD-MATD3 algorithm, which addresses the low training efficiency of homogeneous agents and inconsistencies in reward mechanisms by introducing a parameter-sharing mechanism and an auxiliary reward decay factor. Zhou Yatong et al. [32] introduced a novel Task-Decomposed Multi-Agent Twin Delayed Deep Deterministic Policy Gradient (TD-MATD3) algorithm for UAV path-planning tasks. Their approach enables UAVs to efficiently navigate complex environments with multiple obstacles. Focusing on multi-UAV cooperative trajectory planning, Xing X.J. et al. [33] innovatively incorporated a Long Short-Term Memory (LSTM) recurrent neural network into the environment perception module of MATD3. This modification enhances policy learning efficiency and accelerates convergence.
Despite its advantages, MATD3 still suffers from several limitations, including fixed exploration strategies, low sample utilization efficiency, and lagging policy update rhythms, all of which adversely affect its convergence performance and stability in complex environments. First, the fixed policy noise mechanism cannot adapt to task complexity or the dynamics of policy evolution, which may lead to insufficient exploration in the early stages or excessive perturbation in later stages. Second, the experience samples are not effectively stratified or prioritized, making it difficult to highlight valuable data, thereby hindering policy learning efficiency. Finally, the fixed frequency of policy updates tends to cause gradient instability in the early training phase and slow convergence in the later stages.
Despite the progress of MATD3-style MARL, three practical challenges persist in dynamic multi-agent environments: (C1) exploration–exploitation imbalance caused by a fixed policy-noise schedule, which either under-explores early or over-perturbs late; (C2) inefficient experience utilization, where uniform replay (or PER alone) overlooks cluster-level diversity and leads to homogenized updates; and (C3) s sub-optimal update rhythm, in which a fixed actor update frequency can amplify critic errors and slow convergence. To address these issues, we propose MATD3_AHD, which integrates three mechanisms that directly align with the above challenges: an Adaptive Exploration Policy (AEP) dynamically adjusts noise intensity according to the TD error to resolve C1; a Hierarchical Sampling Policy (HSP) combines sample clustering with prioritized sampling to improve replay efficiency and diversity, addressing C2; and a Dynamic Delayed Update (DDU) modulates the actor update interval based on the stability of the critic network, mitigating C3. Together, these components form an adaptive exploration-oriented, co-evolutionary framework that improves exploration efficiency, sample usage, and training stability. Ots effectiveness is validated through simulations in multiple task environments.
The key contributions of this study can be outlined as follows:
- AEP: To address the exploration–exploitation trade-off in multi-agent reinforcement learning, we propose an adaptive exploration strategy based on TD error. By introducing a training stability evaluation criterion and a dynamic noise modulation factor, this mechanism enhances agents’ adaptive exploration ability in dynamic environments.
- HSP: A hierarchical sampling strategy that integrates clustering and prioritization mechanisms is proposed to optimize the sample selection process during experience replay, thereby improving sample utilization and the quality of policy updates.
- DDU: A dynamic delay mechanism is designed to adjust the actor update frequency based on the critic network’s estimation error. This mechanism improves the stability of policy learning and mitigates convergence challenges in non-stationary environments.
- Experimental validation: Extensive comparisons were conducted in typical multi-agent simulation environments against mainstream baselines such as MADDPG and MATD3. The results demonstrate that the proposed algorithm significantly outperforms baselines in terms of convergence speed, stability, and generalization performance.
2. Related Work
In a system composed of n agents, the joint state space (S) is represented as , where denotes the local observation or state of agent i. Similarly, the joint action space (A) is given as , where corresponds to the action executed by agent i. The reward function (R) can be expressed as , with indicating the reward obtained by agent i. The state transition process is described by the probability function , which specifies the likelihood of moving to the next state () given the current state (s) and the joint action profile (). The discount factor () is applied to balance immediate and future returns. Hence, this multi-agent Markov Decision Process (MDP) can be formalized as a high-dimensional tuple .
The Multi-Agent Twin Delayed Deep Deterministic Policy Gradient (MATD3) algorithm extends the essential ideas of TD3 in a multi-agent structure. By adopting the Centralized Training with Decentralized Execution (CTDE) framework, MATD3 utilizes centralized critic networks, along with a twin Q-network configuration, to effectively reduce the overestimation bias that often arises during training. Each agent maintains two independent critic networks to estimate its Q-values, denoted as and , respectively. The target Q-values are computed as follows:
During training, MATD3 selects the minimum value between the two critic estimates to construct the target Q-value, thereby effectively suppressing Q-value overestimation:
The critic network is updated by minimizing the following loss function:
where denotes the target Q-value, is the critic network of agent i, and represents the experience replay buffer.
MATD3 adopts a delayed policy update mechanism, where the critic network is updated more frequently than the actor network. Specifically, for every two updates of the critic network, the actor network undergoes one parameter update, which is defined as follows:
To enhance exploration, MATD3 also introduces target policy smoothing regularization. During action selection, exploration noise () is added to the deterministic output of the current policy, injecting Gaussian noise into the actions to encourage broader exploration:
where represents a clipped Gaussian distribution and and denote the lower and upper bounds for the noise, respectively.
However, MATD3 still faces three critical challenges when applied to complex dynamic environments: (1) the use of fixed policy noise leads to either insufficient exploration or excessive perturbation; (2) experience replay lacks prioritization or hierarchical processing, resulting in inefficient sample utilization; and (3) the fixed frequency of policy updates fails to adapt based on network error, which adversely affects convergence stability.
Therefore, this paper introduces mechanism-level improvements to the MATD3 framework to address these issues, laying the theoretical foundation for the design of the proposed algorithm and subsequent experimental validation.
3. Methodology
To achieve coordinated optimization of policy exploration, sample utilization, and policy updating, this study introduces a multi-agent co-evolution algorithm named MATD3_AHD, which integrates three enhanced strategies—AEP, HSP, and DDU—into the MATD3 framework. The overall schematic is illustrated in Figure 1. The algorithmic workflow includes the initialization of each agent’s actor and critic network parameters, target network parameters, replay buffer, and the hyperparameters required by the AEP, HSP, and DDU. During each training episode, the process includes adaptive modulation of exploration noise according to the AEP mechanism. Furthermore, diverse and high-quality experiences are sampled from the replay buffer using HSP, and the policy update frequency is regulated according to the TD error through the DDU. This iterative process continuously optimizes the agents’ policies and enhances their collaborative decision-making capability. Our three modules co-evolve through a shared TD error-driven feedback loop. HSP reshapes the replay distribution using cluster TD errors; this changes critic loss and, thus, the TD error, which, in turn, drives the AEP to adapt exploration noise (Equation (7)) and the DDU to adjust the actor update frequency via a TD error threshold. The updated policy then generates new trajectories that refresh the buffer and priorities, closing the loop and making the modules adapt jointly rather than independently.
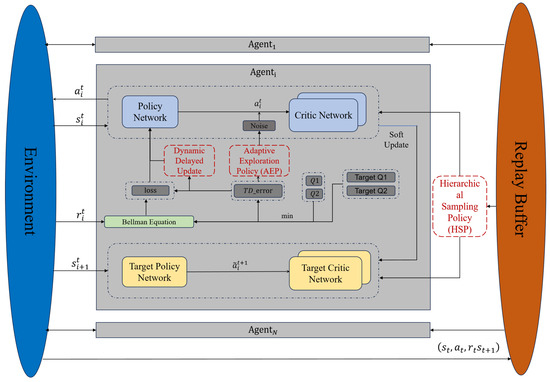
Figure 1.
Schematic of the proposed MATD3_AHD framework.
3.1. Adaptive Exploration Policy
In multi-agent reinforcement learning, fixed-level exploration noise may lead to inefficient policy learning and make it difficult to adapt to the dynamic changes in policy stability during training. To address this issue, this paper proposes a two-phase AEP, which adjusts the noise intensity based on the dynamic variation of the TD error, thereby enabling more efficient policy exploration and exploitation. The overall structure of the proposed strategy is illustrated in Figure 2, which is divided into two phases:
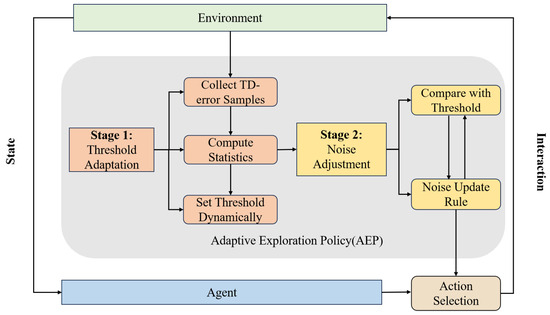
Figure 2.
Schematic of the Adaptive Exploration Policy (AEP).
3.1.1. Phase 1: Threshold Adaptation
In the early stages of training, when the policy has not yet converged, it is crucial to assess its stability. To this end, the algorithm samples the TD error values from the previous K steps, denoted as .
These samples are used to estimate the current fluctuation in training by computing the mean and standard deviation of the TD error. Based on this, a dynamic exploration threshold () is defined to distinguish between “normal” variations and abnormal fluctuations that may warrant intensified exploration. The threshold is computed as follows:
where m is a sensitivity coefficient that determines the response of the exploration strategy to variations in TD error.
The current TD error exceeding the threshold () indicates that the policy may be in an unstable state and that the agent should increase exploration to facilitate more effective learning.
3.1.2. Phase 2: Noise Adjustment
In the second phase, the intensity of exploration is controlled by dynamically adjusting the standard deviation of noise based on the current TD error and the adaptively set threshold. The relationship between the TD error and the standard deviation of noise determines the degree of exploration. When the policy is unstable (i.e., the TD error exceeds the threshold), the noise increases to encourage more exploration. Conversely, when the policy is stable (i.e., the TD error is below the threshold), the noise decreases to reduce unnecessary perturbations.
At each time step (t), the algorithm determines whether to increase or decrease the exploration noise based on the comparison between the current TD error and the threshold (). The standard deviation of noise () is updated using exponential smoothing as follows:
where and denote the growth and decay factors of the noise standard deviation, respectively, and and define the upper and lower bounds to prevent the noise scale from becoming excessively large or too small. The parameter values are set as , , , and .
If , the standard deviation of noise gradually increases during unstable training phases, thereby enhancing exploration.
indicates that during stable policy training, the standard deviation of noise gradually decreases to reduce unnecessary perturbations. The pseudocode for MATD3_AEP is presented in Table 1.

Table 1.
MATD3_AEP algorithmic process.
3.2. Hierarchical Sampling Policy
Traditional experience replay (ER) mechanisms typically rely on uniform random sampling, which makes it difficult to fully exploit critical experience samples. On the other hand, Prioritized Experience Replay (PER) may lead to sample homogenization, thereby limiting policy diversity. To address these issues, this paper proposes an HSP, which integrates K-means clustering with a priority-based replay mechanism to improve both sample efficiency and diversity.
The HSP process consists of two stages: first, samples in the replay buffer are clustered using K-means based on features such as state, action, and reward, forming several experience clusters; then, the priority of each cluster is calculated according to the average TD error of samples within the cluster as follows:
Clusters are sampled in proportion to their priority, meaning that clusters with higher priority have a greater probability of being selected. The sampling probability of cluster is computed as follows:
where K is the total number of clusters and the denominator normalizes the priority scores across all clusters.
After selecting a cluster, experiences are further sampled within the cluster. To ensure diversity in sampling, uniform sampling is adopted within each cluster, meaning that each experience in a given cluster has an equal probability of being selected. Specifically, let cluster contain experiences; then, the sampling probability of experience within cluster is expressed as follows:
To correct for sampling bias in experience replay [34], importance sampling (IS) weights are introduced. Since the overall sampling process is non-uniform (i.e., certain experiences have higher sampling probabilities), IS weights are used to offset the bias introduced by non-uniform sampling. These weights adjust the contribution of each experience during model updates, preventing overfitting to highly prioritized samples.
The IS weight () of each experience () is calculated as follows:
In this paper, N represents the total number of samples stored in the replay memory, while indicates the likelihood of selecting the experience during sampling. The coefficient is introduced to balance the correction intensity of the importance-sampling process.
To avoid excessive magnitude of the IS coefficients, they are normalized as follows:
The normalized importance weights ensure that each experience contributes proportionally to policy updates, preventing imbalance caused by non-uniform sampling probabilities.
Consequently, the proposed sampling mechanism increases the participation of diverse experience types, reduces the omission of informative samples, and further strengthens both the robustness and generalization performance of the learned policy. The schematic of this mechanism is illustrated in Figure 3.
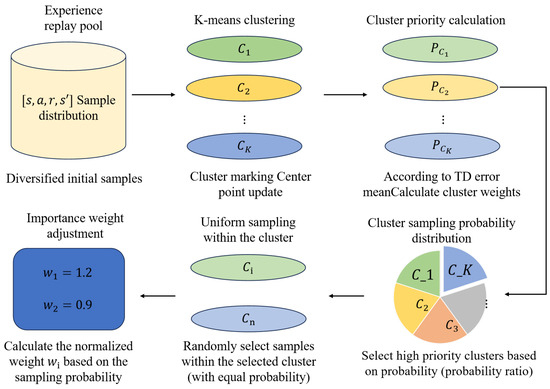
Figure 3.
Schematic of the Hierarchical Sampling Policy (HSP).
The pseudocode for MATD3_HSP is presented in Table 2.

Table 2.
MATD3_HSP algorithmic process.
3.3. Dynamic Delayed Update Mechanism
In the standard MATD3 algorithm, the update frequency of the actor network is fixed and does not adapt to the dynamic changes in Q-value estimation errors. This may lead to unstable policy updates or convergence to suboptimal solutions. To address this issue, we propose a DDU mechanism based on TD error, which adjusts the actor update interval dynamically using an exponentially weighted moving average approach. The core idea is outlined as follows:
By evaluating the TD error to reflect the estimation error of the critic network, we adjust the update interval of the actor network accordingly. When the TD-error is large, indicating that the Q-value estimates are unreliable, more critic updates are needed before updating the actor. Hence, the actor update should be delayed to avoid optimizing the policy based on unstable Q-values. Conversely, when the TD-error is small, indicating accurate Q-value estimates, the actor can be updated more frequently, thereby accelerating policy optimization and improving training efficiency. The schematic diagram is shown in Figure 4.
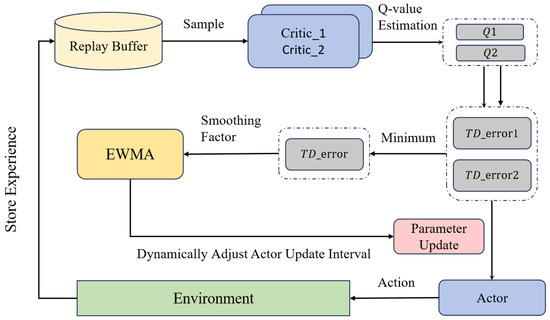
Figure 4.
Schematic of the Dynamic Delayed Update (DDU) mechanism.
To enhance the stability and adaptability of policy updates, the proposed Dynamic Delayed Update (DDU) mechanism employs the TD error as the core indicator. It estimates the trend of critic-network error using an Exponentially Weighted Moving Average (EWMA) and dynamically adjusts the actor update frequency accordingly. The design logic of this mechanism is reflected in the following aspects:
- Error-driven update: A large TD error indicates inaccurate estimation by the critic. In such cases, the critic should be updated first while delaying the actor update to avoid optimizing the policy based on erroneous Q-values.
- Avoidance of local optima: Frequent updates to the actor in the presence of unstable Q-values can trap the policy in a suboptimal solution. Regulating the update pace ensures that policy improvements are based on reliable evaluations.
- Improved convergence stability: When the TD error is small, the critic is considered stable. Accelerating the actor updates under these circumstances helps speed up the overall convergence.
- Coordinated exploration and exploitation: The TD error also reflects the agent’s current exploration status. When combined with the Adaptive Exploration Policy (AEP), reducing the actor update frequency during highly dynamic environmental changes can enhance policy robustness.
In addition, the EWMA is used to smooth the TD error, thereby avoiding the storage of large amounts of historical data and effectively preserving the error trend. This enables efficient update scheduling, even under noise interference. The EWMA is computed as follows:
where denotes the exponentially weighted moving average of the TD error at time step t, is the current TD error, and is the smoothing factor.
The actor update interval denotes the number of environment/critic steps between two actor updates in the DDU schedule. Formally, the actor is updated when . Thus, means updating every 4 steps, indicates updating every other step, and corresponds to updating every step. We adopt a discrete set (): larger intervals are used when the TD error is high to stabilize the critic; as the TD error decreases, the interval is reduced to 1 to accelerate policy fine-tuning.
This method enables the actor network to reduce its update frequency when the critic exhibits high estimation error, thereby ensuring policy stability. Conversely, when critic estimation is more accurate, the actor updates more frequently to improve training efficiency. It is evident that the actor update interval is inversely proportional to the TD error. Table 3 summarizes how the algorithm dynamically adjusts the actor update interval according to the trend of TD error across different training phases, thereby achieving appropriate optimization effects.

Table 3.
Practical scenarios of the dynamic delay policy update.
Therefore, the dynamic delayed update mechanism not only enhances the algorithm’s ability to handle complex scenarios by prioritizing reliable information but also increases the update frequency of high-quality policies, ultimately accelerating the overall decision-making efficiency of the algorithm. The pseudocode for MATD3_DDU is presented in Table 4.

Table 4.
MATD3_DDU algorithmic process.
4. Experiments
This section presents systematic experiments to validate the effectiveness and robustness of the three proposed key improvement strategies—the AEP, HSP, and DDU—as well as their integrated algorithm, MATD3_AHD. We evaluate the canonical MADDPG and MATD3 as baselines; for recent empirical evaluations and strong variants of these families used for performance comparison, please refer to Section 2 and refs. [25,26,27,28].
This work aims to isolate and quantify the contributions of our three plug-in mechanisms (AEP, HSP, and DDU) on an off-policy TD3/MATD3 backbone. Therefore, we adopt the canonical MADDPG and MATD3 as baselines under a matched training pipeline (same budgets, networks, and hyper-parameters). Recent strong MARL baselines from other paradigms—including on-policy actor–critic methods such as MAPPO and IPPO, as well as value decomposition methods such as QMIX and COMA (with variants such as MAAC and R-MAPPO)—are summarized in the Related Work section; a comprehensive cross-paradigm benchmark is left for future work.
The experiments are analyzed from four perspectives: environmental settings, ablation studies, comparative evaluations, and real-world simulations. All experiments were run on a workstation with an Intel Core i7-8700K CPU and an NVIDIA GTX 1060 GPU (PyTorch 1.13.1). For each task, a training budget of steps required approximately 3–4 h of wall-clock time under this configuration, and the three MPE tasks were completed within 24 h in total. The proposed modules introduce only minor overhead: the HSP adds some cost due to clustering and prioritized replay maintenance, while the DDU incurs negligible scheduling overhead; in practice, end-to-end runtime per task remained within the 3–4 h range mentioned above.
4.1. Experimental Environment
The experiments were primarily conducted in the Multi-Agent Particle Environment (MPE), an environment proposed by OpenAI that features high controllability and flexibility, making it well-suited for evaluating MARL algorithms in terms of cooperative control performance. Three MPE scenarios are selected for evaluation in this work: Simple_Speaker_Listener, Simple_Spread, and Simple_Spread_Multigoal. We evaluate on three canonical MPE tasks (Simple_Speaker_Listener, Simple_Spread, and Simple_Spread_Multigoal) to keep training pipelines identical and isolate the effects of the AEP/HSP/DDU. This trio jointly covers communication, cooperative coverage with collision avoidance, and higher non-stationarity, providing a compact yet diverse testbed. We do not claim universality; extending the evaluation to broader suites (e.g., additional PettingZoo/MPE variants, multi-robot navigation, and other cooperative control benchmarks) is left for future work.
The MPE environment is illustrated in Figure 5.
Figure 5.
Illustrations of selected scenarios in the MPE.
The experimental platform is implemented based on Python 3.10 and the PyTorch 1.13.1 framework. The main hyperparameter settings are summarized in Table 5. For the improved variants proposed later, most parameters remain the same and will not be repeated.

Table 5.
MATD3 main parameter settings.
For all evaluated algorithms, each task is trained for a total of time steps. During training, the learned policy is evaluated once every 1000 time steps. Each evaluation runs the current policy for five episodes, and the average cumulative return of these five runs is reported as the evaluation result.
Additionally, all reward curves presented in this paper are smoothed to facilitate performance comparison.
4.2. Ablation Study and Analysis
To verify the contribution of the three key mechanisms in the proposed co-evolution algorithm—AEP, HSP, and DDU—we design a series of ablation experiments by removing each component individually and conducting comparative analysis.
4.2.1. Effectiveness Analysis of AEP
To demonstrate the ability of the AEP to balance exploration and exploitation and accelerate learning efficiency, we evaluate the performance of the MATD3_AEP algorithm in two MPE environments. In addition, to verify the generality of this mechanism across different algorithms, we also integrate AEP into MADDPG, resulting in a variant named MADDPG_AEP, which is used as a reference. All other hyperparameters are kept the same for fair comparison.
By analyzing Figure 6, it can be observed that the MATD3_AEP algorithm significantly improves exploration efficiency compared to other deep reinforcement learning algorithms. In most cases, AEP enables agents to learn effective policies more quickly. Specifically, for the MPE tasks evaluated in this section, MATD3_AEP achieves faster exploration efficiency than the original MATD3. Within the -step budget, MATD3_AEP is about more sample-efficient than vanilla MATD3.
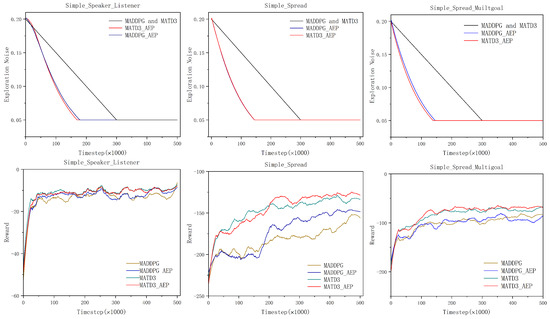
Figure 6.
Noise decay and reward comparison of the AEP strategy in three MPE environments.
Table 6 reports the average maximum cumulative rewards after convergence across the three environments. The data are collected by averaging the maximum returns over the last 10,000 episodes. Compared with MATD3, MATD3_AEP improves the average reward by 3%, 2%, and 5% in the Simple_Speaker_Listener, Simple_Spread, and Simple_Spread_Multigoal environments, respectively. Similarly, MADDPG_AEP achieves average reward improvements of 5% and 7% compared to MADDPG. Overall, the results show that MATD3_AEP consistently outperforms MATD3, while MADDPG_AEP also achieves higher performance than MADDPG, demonstrating the effectiveness of the AEP in enhancing exploration efficiency.

Table 6.
Average rewards of MATD3_AEP and baseline algorithms across MPE environments.
In conclusion, the MATD3_AEP algorithm exhibits improved convergence compared to MATD3 and MADDPG, indicating that AEP effectively balances exploration and exploitation and enhances the efficiency of exploration. By dynamically adjusting the scale of exploration noise, the AEP improves the agent’s learning efficiency and accelerates policy acquisition. Furthermore, the results show that the AEP is also applicable to other multi-agent reinforcement learning algorithms, providing efficient exploration and utilization support.
4.2.2. Effectiveness Analysis of HSP
To evaluate whether the HSP enhances sample utilization and ensures a comprehensive experience replay across different sample types, the MATD3_HSP algorithm was trained and tested in three MPE environments. MADDPG was also included as a reference baseline with identical hyperparameters.
By analyzing the reward curves in Figure 7, it can be observed that the MATD3_HSP algorithm maintains a comparable convergence speed while exhibiting lower variance in the reward trajectories, indicating enhanced stability. In the Simple_Speaker_Listener environment, the improvement is moderate, while in the Simple_Spread environment, the HSP demonstrates more significant benefits, validating its effectiveness in stabilizing training.
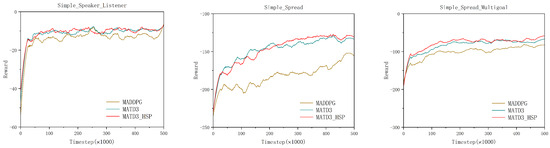
Figure 7.
Reward comparison of the MATD3_HSP algorithm in different MPE environments.
Table 7 presents the standard deviation of evaluation rewards post 10,000 episodes. MATD3_HSP consistently achieved the lowest reward variance in all environments. Compared with MATD3, the improvements in reward stability were approximately 4.7%, 3.4%, and 6.9%. Compared with MADDPG, the improvements were more pronounced at 16.0%, 21.7%, and 6.6%.

Table 7.
Reward stability analysis of the MATD3_HSP algorithm in different MPE environments.
In summary, MATD3_HSP significantly improves training stability across multiple MPE scenarios. Its hierarchical sampling mechanism—combining experience clustering with prioritized scheduling—enhances sample efficiency and suppresses training variance, providing a viable solution for improving the robustness of multi-agent reinforcement learning.
4.2.3. Effectiveness Analysis of DDU
To verify that the DDU can enhance the agent’s capacity for processing environmental information and adaptively adjusting the update frequency of the actor network, we trained the MATD3_DDU algorithm and evaluated it in three MPE environments.
As shown in Figure 8, the reward curves of the MATD3_DDU algorithm are more stable with smaller fluctuations, indicating its improved ability to process environmental information and stabilize Q-value estimation through adaptive critic updates. This leads to more accurate and reliable value functions, which accelerates convergence.
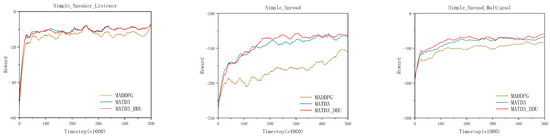
Figure 8.
Reward comparison of the MATD3_DDU algorithm in different MPE environments.
Table 8 reports the average cumulative reward after 10,000 episodes in each environment. Compared to MATD3, the MATD3_DDU algorithm achieves an average reward improvement of 2.5%, 2%, and 2.6% in the Simple_Speaker_Listener, Simple_Spread, and Simple_Spread_Multigoal environments, respectively. Compared to MADDPG, the improvements are even more pronounced, reaching 17%, 22%, and 20%, respectively.

Table 8.
Average reward analysis of the MATD3_DDU algorithm in different MPE environments.
These results confirm that the dynamic delayed policy update mechanism enhances policy learning efficiency and robustness. It improves agents’ responsiveness to complex environments by regulating update frequencies based on TD error trends, thereby increasing the number of high-quality policy updates.
4.3. Comparative Experimental Analysis
This section verifies whether the multi-agent co-evolution algorithm, MATD3_AHD, can simultaneously optimize exploration, sample utilization, and policy update efficiency. Experiments are conducted in three MPE environments, using MADDPG and MATD3 as baselines. To ensure the validity of the comparison, all hyperparameters are kept consistent across algorithms.
Reporting protocol. Unless otherwise stated, learning curves show the mean over 10 random seeds. For readability, we apply light exponential moving average (EMA) smoothing; confidence-interval shading is omitted. Final scalar results are reported in tables, and per seed logs are available upon request.
The reward curves of the MATD3_AHD algorithm and the baseline algorithms are illustrated in Figure 9. As observed from the analysis, MATD3_AHD achieves significantly improved reward performance compared to the other algorithms. Its reward curves show smaller fluctuations and more stable convergence. Although the algorithm experiences partial local optima in the Simple_Speaker_Listener environment, it does not affect the overall experimental conclusions. Moreover, MATD3_AHD reaches training stability using fewer time steps, demonstrating improvements in convergence speed, stability, and efficiency.
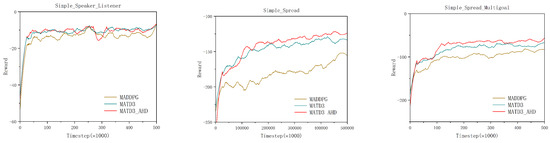
Figure 9.
Comparison of MATD3_AHD algorithm rewards in different MPE environments.
Table 9 and Table 10 summarize the quantitative results across the three MPE environments. Table 9 reports the average maximum cumulative rewards after convergence, whereas Table 10 further presents the final performance as mean ± std over the last training steps. Consistent trends are observed in both tables: MATD3_AHD achieves the best (less negative) returns in Simple_Spread and Simple_Spread_Multigoal and shows comparable performance to MATD3 in Simple_Speaker_Listener. For readability, the MATD3_AHD column is highlighted. The results show that MATD3_AHD outperforms both baseline algorithms in all environments. Specifically, in the Simple_Speaker_Listener environment, MATD3_AHD improves the average reward by 2% over MATD3 and by 18% over MADDPG. In the Simple_Spread environment, the improvements reach 5% and 25%, respectively. In the Simple_Spread_Multigoal environment, MATD3_AHD achieves 7% and 24% higher rewards compared to MATD3 and MADDPG, respectively. These quantitative results strongly validate the superiority of the proposed MATD3_AHD algorithm.

Table 9.
Average reward analysis of the MATD3_AHD algorithm in different MPE environments.

Table 10.
Final performance reported as mean ± std over the last training steps.
In conclusion, the multi-agent co-evolutionary approach, MATD3_AHD, exhibits significant performance gains over the baseline algorithms. It demonstrates improvements in exploration, sample efficiency, and decision-making quality, effectively addressing the key challenges proposed in this study and achieving enhanced collaborative evolution capabilities.
4.4. Simulation Experiments
To validate the practical applicability of the proposed algorithm, a simulated environment was constructed based on ROS and Gazebo, utilizing the Turtlebot3 (Waffle) mobile robot platform. This setup was designed to evaluate the feasibility and efficiency of applying the multi-agent co-evolutionary algorithm in real-world-like multi-robot exploration tasks. The simulation involves three robots and three goals. The robots collaborate in real time through LiDAR and visual perception modules to perform coordinated path planning. The MATD3_AHD algorithm is employed for path regulation and coordination. As shown in Figure 10, the system successfully enables multi-robot coordination for both obstacle avoidance and goal reaching.
Figure 10.
Multiple mobile robot scenarios.
As illustrated in Figure 11, in an obstacle-free environment, all robots are capable of perceiving their surroundings and navigating freely within the space. The co-evolutionary algorithm effectively guides each robot toward its assigned goal without relying on predefined maps, while enabling real-time coordination and collision-free path planning among the robots to ensure timely and accurate arrival at their respective destinations.
Figure 11.
Simulation of barrier-free environments.
To further evaluate the algorithm’s adaptability in more complex environments, an obstacle-rich simulation scenario was designed. In this environment, all three robots must cooperate simultaneously to complete the task while avoiding collisions with obstacles and one another. The co-evolutionary algorithm enables the robots to dynamically adjust their paths in real time, achieving efficient obstacle avoidance and smooth coordination, as demonstrated in Figure 12.
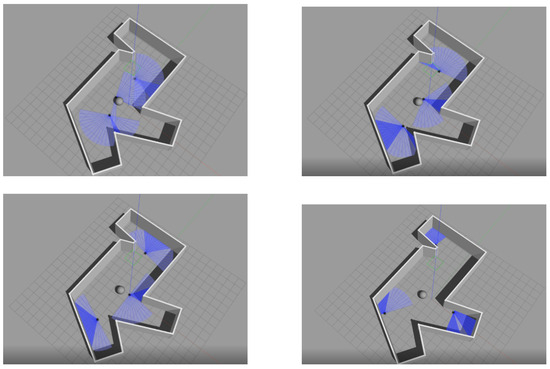
Figure 12.
Simulation of obstacle environments.
The experimental results demonstrate that robots can successfully reach their goals in obstacle-free environments. In obstacle-rich scenarios, the robots are capable of autonomously planning paths, avoiding obstacles, and completing tasks through the co-evolutionary mechanism, thereby validating the practicality and robustness of the proposed algorithm.
5. Conclusions
This paper proposes three enhancement strategies based on the MATD3 algorithm to address the challenges of low exploration efficiency, insufficient sample utilization, and delayed policy updates in multi-agent MARL. These strategies are integrated into a unified co-evolutionary algorithm named MATD3_AHD. Specifically, the AEP dynamically adjusts the scale of exploration noise according to training stability, improving the algorithm’s ability to balance exploration and exploitation across different learning phases. The HSP clusters experience samples and adjusts replay priorities to enhance sample efficiency. The DDU mechanism adaptively regulates the update frequency based on the critic’s error (state-change sensitivity), improving decision-making efficiency and adaptability.
Experimental results show that AEP improves exploration efficiency by approximately 4% and achieves a 17% gain over MADDPG, accelerating policy convergence. HSP enhances algorithmic stability by around 5% and achieves a 21% gain over MADDPG, yielding more stable reward convergence. With DDU, the convergence performance improves by 2.6%. By integrating all three strategies, the proposed MATD3_AHD algorithm achieves an average performance improvement of 5% over baseline MATD3 and 20% over MADDPG across three MARL tasks.
Furthermore, on the ROS + Gazebo simulation platform using Turtlebot3, the proposed algorithm successfully completes multi-robot cooperative navigation tasks, demonstrating its practicality and robustness in real-world-like scenarios. Overall, MATD3_AHD shows excellent performance in terms of training stability, convergence speed, and policy generalization, indicating strong potential for real-world engineering applications.
Future research may focus on the following directions: investigating the influence of AEP parameter dynamics on learning performance, studying the impact of dynamically changing agent populations on co-evolution mechanisms to adapt to more complex environments, and extending the proposed MARL framework to real-world scenarios such as UAVs and unmanned vehicles to promote its application in intelligent systems and the Internet of Things.
Author Contributions
Conceptualization, S.W. and F.G.; methodology, S.W., Z.L. and F.G.; software, Q.Y. and Y.K.; validation, Z.L., Q.S., Y.K. and Q.Y.; formal analysis, Z.L. and Q.Y.; investigation, Z.L., Q.S., Y.K. and Q.Y.; resources, S.W. and F.G.; data curation, Z.L. and Q.S.; writing—original draft preparation, S.W. and Z.L.; writing—review and editing, S.W., Z.L., Q.Y., Q.S., Y.K. and F.G.; visualization, Z.L. and Q.Y.; supervision, F.G.; project administration, S.W. and F.G.; Funding acquisition, S.W. and F.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Key Research and Development Program of China (grant number 2024YFB4711004) and Fundamental Research Fund of China Academy of Railway Sciences corporation limited (grant number 2024YJ097).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Feng Gao was employed by Beijing Huatie Information Technology Co., Ltd., and the Signal & Communication Research Institute, China Academy of Railway Sciences Corporation Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Jia, C.; He, H.; Zhou, J.; Li, J.; Wei, Z.; Li, K. Learning-based Model Predictive Energy Management for Fuel Cell Hybrid Electric Bus with Health-aware Control. Appl. Energy 2024, 355, 122228. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, N.D.; Nahavandi, S. Deep Reinforcement Learning for Multiagent Systems: A Review of Challenges, Solutions, and Applications. IEEE Trans. Cybern. 2020, 50, 3826–3839. [Google Scholar] [CrossRef]
- Jia, C.; Liu, W.; He, H.; Chau, K.T. Deep Reinforcement Learning-based Energy Management Strategy for Fuel Cell Buses Integrating Future Road Information and Cabin Comfort Control. Energy Convers. Manag. 2024, 321, 119032. [Google Scholar] [CrossRef]
- Fan, Z.; Su, R.; Zhang, W.; Yu, Y. Hybrid Actor-Critic Reinforcement Learning in Parameterized Action Space. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Ming, F.; Gao, F.; Liu, K.; Zhao, C. Cooperative Modular Reinforcement Learning for Large Discrete Action Space Problem. Neural Netw. 2023, 161, 281–296. [Google Scholar] [CrossRef]
- Chen, H.; Dai, X.; Cai, H.; Zhang, W.; Wang, X.; Tang, R.; Zhang, Y.; Yu, Y. Large-scale Interactive Recommendation with Tree-structured Policy Gradient. In Proceedings of the National Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Li, K.; Zhou, J.; Jia, C.; Yi, F.; Zhang, C. Energy Sources Durability Energy Management for Fuel Cell Hybrid Electric Bus Based on Deep Reinforcement Learning Considering Future Terrain Information. Int. J. Hydrogen Energy 2024, 52, 821–833. [Google Scholar] [CrossRef]
- Jia, C.; Zhou, J.; He, H.; Li, J.; Wei, Z.; Li, K. Health-conscious Deep Reinforcement Learning Energy Management for Fuel Cell Buses Integrating Environmental and Look-ahead Road Information. Energy 2023, 290, 130146. [Google Scholar] [CrossRef]
- Seyde, T.; Werner, P.; Schwarting, W.; Wulfmeier, M.; Rus, D. Growing Q-Networks: Solving Continuous Control Tasks with Adaptive Control Resolution. In Proceedings of the 6th Annual Learning for Dynamics and Control Conference, Oxford, UK, 15–17 July 2024. [Google Scholar]
- Nie, J.; Du, D.; Zhao, J. Spatio-temporal Value Semantics-based Abstraction for Dense Deep Reinforcement Learning. arXiv 2024, arXiv:2405.15829. [Google Scholar]
- Yang, S. Trajectory Planning and Control Method for Autonomous Vehicles Based on Reinforcement Learning. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2023. (In Chinese). [Google Scholar]
- Xu, H.; Wu, Z.; Liang, Y. A Review on Reinforcement Learning-Based Path Planning for Autonomous Vehicles. Comput. Appl. Res. 2023, 40, 3211–3217. (In Chinese) [Google Scholar]
- Gu, X.; Wang, Y.J.; Chen, J. Humanoid-Gym: Reinforcement Learning for Humanoid Robot with Zero-Shot Sim2Real Transfer. arXiv 2024, arXiv:2404.05695. [Google Scholar]
- Haarnoja, T.; Moran, B.; Lever, G.; Huang, S.H.; Tirumala, D.; Humplik, J.; Wulfmeier, M.; Tunyasuvunakool, S.; Siegel, N.Y.; Hafner, R.; et al. Learning Agile Soccer Skills for a Bipedal Robot with Deep Reinforcement Learning. Sci. Robot. 2024, 9, eadi8022. [Google Scholar] [CrossRef]
- Kuo, P.H.; Yang, W.C.; Hsu, P.W.; Chen, K.L. Intelligent Proximal-Policy-Optimization-Based Decision-Making System for Humanoid Robots. Adv. Eng. Inform. 2023, 56, 102009. [Google Scholar] [CrossRef]
- Hernandez-Leal, P.; Kartal, B.; Taylor, M.E. A Survey and Critique of Multiagent Deep Reinforcement Learning. Auton. Agents Multi-Agent Syst. 2019, 33, 750–797. [Google Scholar] [CrossRef]
- Jia, C.; Liu, W.; He, H.; Chau, K.T. Health-conscious Energy Management for Fuel Cell Vehicles: An Integrated Thermal Management Strategy for Cabin and Energy Source Systems. Energy 2025, 333, 137330. [Google Scholar] [CrossRef]
- Foerster, J.; Farquhar, G.; Afouras, T.; Nardelli, N.; Whiteson, S. Counterfactual Multi-Agent Policy Gradients. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The Surprising Effectiveness of MAPPO in Cooperative, Multi-Agent Games. arXiv 2021, arXiv:2103.01955. [Google Scholar]
- Gao, J.; Wang, G.; Gao, L. LSTM-MADDPG: A Multi-Agent Cooperative Decision-Making Algorithm Based on Asynchronous Cooperative Updates. J. Jilin Univ. (Eng. Technol. Ed.) 2024, 54, 797–806. (In Chinese) [Google Scholar]
- Wen, C.; Dong, W.; Xie, W.; Cai, M.; Hu, D. Autonomous Tracking and Obstacle Avoidance for UAV Swarms Based on Decoupled MADDPG. Flight Dyn. 2022, 40, 24–31. (In Chinese) [Google Scholar]
- Zhu, P.; Dai, W.; Yao, W.; Ma, J.; Zeng, Z.; Lu, H. Multi-Robot Flocking Control Based on Deep Reinforcement Learning. IEEE Access 2020, 8, 150397–150406. [Google Scholar] [CrossRef]
- Li, S.; Wu, Y.; Cui, X.; Dong, H.; Fang, F.; Russell, S. Robust Multi-Agent Reinforcement Learning via Minimax Deep Deterministic Policy Gradient. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4213–4220. [Google Scholar]
- Mao, H.; Zhang, Z.; Xiao, Z.; Gong, Z. Modelling the Dynamic Joint Policy of Teammates with Attention Multi-agent DDPG. In Proceedings of the Adaptive Agents and Multi-Agents Systems, Montreal, QC, Canada, 13–14 May 2019. [Google Scholar]
- Ding, S.; Du, W.; Guo, L.; Zhang, J.; Xiao, X. Multi-Agent Deep Deterministic Policy Gradient Method Based on Dual Critics. J. Comput. Res. Dev. 2023, 60, 2394–2404. (In Chinese) [Google Scholar]
- Ma, Y.; Shen, M.; Zhang, N.; Tong, X.; Li, Y. OM-TCN: A Dynamic and Agile Opponent Modeling Approach for Competitive Games. Inf. Sci. Int. J. 2022, 615, 405–414. [Google Scholar] [CrossRef]
- Iqbal, S.; Sha, F. Actor-Attention-Critic for Multi-Agent Reinforcement Learning. In Proceedings of the 36th International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Xia, L.; Luo, W.; Wang, J.; Huang, Y. MAAC Multi-Agent Reinforcement Learning Algorithm Based on Posterior Experience Replay. Software 2023, 44, 17–22, 41. (In Chinese) [Google Scholar]
- Ackermann, J.; Gabler, V.; Osa, T.; Sugiyama, M. Reducing Overestimation Bias in Multi-Agent Domains Using Double Centralized Critics. arXiv 2019, arXiv:1910.01465. [Google Scholar] [CrossRef]
- Zhou, C.; Li, J.; Shi, Y.; Lin, Z. Research on Multi-Robot Formation Control Based on MATD3 Algorithm. Appl. Sci. 2023, 13, 1874. [Google Scholar] [CrossRef]
- Wang, K.; Zhao, Y.; Wang, G.; Li, J. Improved MATD3 Algorithm and Its Application in Adversarial Scenarios. Command. Control Simul. 2024, 46, 77–84. (In Chinese) [Google Scholar]
- Zhou, Y.; Kong, X.; Lin, K.P.; Liu, L. Novel Task Decomposed Multi-Agent Twin Delayed Deep Deterministic Policy Gradient Algorithm for Multi-UAV Autonomous Path Planning. Knowl.-Based Syst. 2024, 287, 111462. [Google Scholar] [CrossRef]
- Xing, X.; Zhou, Z.; Li, Y.; Xiao, B.; Xun, Y. Multi-UAV Adaptive Cooperative Formation Trajectory Planning Based on an Improved MATD3 Algorithm of Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2024, 73, 12484–12499. [Google Scholar] [CrossRef]
- Neal, R.M. Annealed Importance Sampling. Stat. Comput. 2001, 11, 125–139. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).