Abstract
We study the predictive maintenance scheduling for IoT-enabled medical equipment in multi-facility healthcare networks. The problem involves skill matching, time windows, and risk-aware priorities. We model a multi-skill Technician Routing and Scheduling Problem with IoT-predicted failure intervals and minimize a composite cost for technician activation and labor, travel/time, risk exposure within the failure window, and lateness beyond it. We propose a hybrid solver coupling a Genetic Algorithm (GA) for rapid exploration and feasible schedule generation with a Proximal Policy Optimization (PPO) agent warm-started via behavior cloning on GA elites and refined online in a receding-horizon manner. An optional, permissioned blockchain records tamper-evident maintenance events off the control loop for auditability. Across four case studies (10–30 facilities), the hybrid approach reduces total cost by 2.09–10.31% versus pure GA, by 0.57–2.65% versus pure Deep Reinforcement Learning (DRL), and by 0.93–2.86% versus OR-Tools VRP heuristic baseline. In controlled early-stopping runs guided by admissible GA/DRL time splits, we realized average wall-time savings up to 47.5% while keeping solution costs within 0.5% of full-budget runs and maintaining low or zero lateness and risk exposure. These results indicate that GA seeding improves sample efficiency and stability for DRL in complex, data-driven maintenance settings, yielding a practical, adaptive, and auditable scheduler for healthcare operations.
1. Introduction
Healthcare providers are rapidly connecting medical assets into sensor-rich, data-driven ecosystems. Internet of Things (IoT)-enabled devices continuously stream usage and condition data, enabling a shift from reactive or time-based interventions to predictive maintenance that improves availability and patient safety while containing costs [1]. In multi-facility settings, however, these gains depend on robust, responsive scheduling of specialized technicians across dispersed sites, heterogeneous equipment, and evolving priorities. Ensuring uptime for critical devices (e.g., MRI scanners, ventilators, and surgical robots) requires decisions that reconcile real-time health signals, tight time windows, skill constraints, and travel logistics under uncertainty.
Two algorithmic paradigms dominate the field of maintenance optimization. Metaheuristics provide flexibility and scale, while Deep Reinforcement Learning (DRL) is increasingly effective for sequential decision-making in dynamic, resource-constrained environments [2,3]. However, three significant gaps remain in the literature. First, in healthcare-specific and multi-facility maintenance, hybrid designs that combine global exploration (e.g., evolutionary search) with DRL’s adaptive policies are under-explored. Second, end-to-end systems that integrate IoT-derived predictive signals with optimization and secure cross-facility record-keeping are rare. Third, rigorous comparisons quantifying how hybridization affects convergence, solution quality, and scalability versus strong baselines are scarce [4].
We model the problem as a multi-skill Technician Routing and Scheduling Problem (TRSP) with time windows and multiple depots. Decisions jointly determine: (i) which technicians are activated and which tasks they serve (skill matching), (ii) task sequences across facilities (routing/precedence), and (iii) start times within service windows and shift calendars (timing). The objective minimizes a composite cost comprising technician activation, paid labor for service and travel, and penalties that price IoT-predicted risk when starting within the predicted failure window and tardiness beyond it. Feasibility is enforced through assignment/skill compatibility, technician and equipment time windows, and routing–sequencing consistency. The problem strictly generalizes NP-hard Vehicle Routing Problem with Time Windows (VRPTW)/TRSP/home-healthcare variants; dynamic, forecast-driven failure windows add difficult couplings. Exact methods scale poorly, especially with real-time updates, motivating heuristics and learning-based solvers with fast re-optimization.
We propose a hybrid framework that couples a Genetic Algorithm (GA) with DRL. GA performs broad exploration and produces diverse, feasible schedules that seed the DRL agent, reducing cold-start effects and improving sample efficiency. DRL fine-tunes policies against streaming IoT signals to adapt rapidly to shifting risk profiles and operational disruptions. An optional, permissioned blockchain-backed logging layer provides tamper-evident, auditable maintenance records to support trust and coordination across facilities.
We ask: how can a GA-initialized DRL framework, informed by real-time IoT signals, improve multi-facility healthcare maintenance scheduling in terms of solution quality, compute efficiency, and scalability versus strong single-paradigm baselines, while supporting secure cross-facility coordination?
This paper makes three contributions:
- A scalable planning-and-control pipeline that fuses predictive maintenance signals with hybrid GA+DRL optimization.
- A comparative evaluation isolating the benefits of GA-seeded policy learning over pure DRL and pure metaheuristics across instance sizes and dynamics.
- An optional, permissioned blockchain layer for verifiable, auditable cross-facility records, integrated out-of-loop to preserve real-time performance.
Extensive simulations reflecting realistic networks and portfolios show that the hybrid approach reduces schedule cost by 5.57% on average relative to strong baselines and achieves best costs with up to 47.5% less computation, on average, due to effective GA seeding and DRL refinement. Practically, the results translate into lower downtime, improved staffing utilization, reduced travel and energy costs, and greater transparency across facilities.
2. Background
2.1. Literature Review
IoT connectivity in healthcare is turning standalone devices into instrumented and interoperable assets that continuously produce condition and usage data. This data foundation enables predictive maintenance, which can reduce downtime and operational costs while safeguarding patient care [1,5]. The challenge now is not data collection but translating heterogeneous and high-velocity telemetry into timely and feasible maintenance decisions across distributed facilities [6].
From an operations-research perspective, multi-facility technician scheduling with skills and time windows is a rich variant of the Vehicle Routing Problem (VRP), closely related to the TRSP [7] and the Home Healthcare Routing and Scheduling Problem (HHCRSP) [8]. These models capture assignment (skill–task compatibility), routing (inter-facility travel), and timing (equipment/shift windows), and are NP-hard. Exact methods scale poorly on realistic instances, especially under real-time updates, motivating heuristic and learning-based approaches.
Metaheuristics are widely used for their flexibility and strong performance on large instances. Genetic Algorithms (GAs) have achieved notable downtime reductions via task grouping and clustering [9]; multi-objective variants such as Non-dominated Sorting Genetic Algorithm II can balance cost and quality-of-care objectives [10]. Other families—Ant Colony Optimization for dynamic routing [11], Particle Swarm Optimization for resource allocation [5], and Simulated Annealing for workflow optimization [6]—perform well on static or quasi-static settings. However, pure metaheuristics can struggle to adapt quickly to nonstationary inputs typical of IoT (e.g., sudden risk updates or failures).
DRL learns sequential decision policies from interaction, making it appealing for online scheduling under uncertainty [2]. In related domains, DRL outperforms handcrafted dispatching rules in job-shop scheduling [12] and orchestrates dynamic IoT workloads [13,14]. Yet, DRL can be sample-inefficient and sensitive to initialization, and may converge to suboptimal policies without good priors.
Hybrid “memetic” methods seek to combine global exploration from metaheuristics with DRL’s adaptive refinement. A GA can seed DRL with diverse, high-quality solutions that reduce cold starts and improve sample efficiency; DRL can then fine-tune policies and adapt online. Evidence from adjacent domains supports this synergy [15,16], though applications to healthcare maintenance logistics remain limited. Beyond optimization, multi-stakeholder coordination and trust motivate secure audit trails: permissioned blockchains can provide tamper-evident, verifiable records akin to traceability uses in maritime and supply chains [17,18], without placing the ledger in the real-time control loop.
Beyond cold-start mitigation and sample efficiency, recent meta-reinforcement learning (meta-RL) advances aim to speed up adaptation across related instances by learning transferable priors or task embeddings. Examples include gradient-based adaptation (e.g., MAML-like schemes) and context-based methods (e.g., latent-variable policies), along with intrinsic-reward design to encourage informative exploration. In communication and networking domains, intrinsic rewards have been shown to accelerate convergence under nonstationary traffic patterns, offering a complementary path to faster learning [19]. These ideas are orthogonal to our GA seeding and could further reduce warm-up time or improve robustness under shifting IoT signals.
A comparison of representative approaches is reported in Table 1.

Table 1.
Comparison of optimization approaches for maintenance scheduling and related problems.
2.2. Critical Synthesis: Paradigm Trade-Offs in Healthcare Maintenance
Critical examination reveals fundamental trade-offs with distinct healthcare implications.
- Adaptability: Metaheuristics (GAs, SA, ACO) excel at exploration over static spaces but lack mechanisms to incorporate sequential feedback from nonstationary IoT streams—each optimization run restarts from scratch, which makes these methods brittle when risk profiles shift dynamically [6,9]. DRL learns adaptive policies [12,13], yet without good initialization may require thousands of episodes to discover constraint-feasible solutions—a liability when patient safety demands rapid response.
- Sample efficiency: This DRL weakness is critical in healthcare, where simulation episodes are computationally expensive and real-world trial-and-error is ethically inadmissible. Metaheuristics produce competitive solutions with fewer evaluations [10,20] but cannot improve beyond their operators’ expressiveness. Hybrids like GA–DRL [15,16] provide diverse and constraint-satisfying curricula that reduce DRL’s cold-start penalty while enabling adaptive refinement, though compute allocation between phases remains empirically driven.
- Operational readiness: Healthcare demands interpretability, minimal infrastructure, and fail-safe behavior. Metaheuristics are transparent and lightweight, facilitating clinical buy-in; DRL policies resemble black boxes requiring drift monitoring [2]; hybrids inherit complexity from both, complicating deployment.
Critically, no work has systematically evaluated these paradigms under simultaneous multi-facility scale, life-critical constraints, real-time IoT updates, and healthcare deployment readiness—the gap our contribution directly addresses.
2.3. Identified Research Gaps
Despite progress in metaheuristics and DRL, several gaps remain in the context of healthcare maintenance:
- 1.
- Domain-specific hybridization: Few works apply GA–DRL hybrids to multi-facility healthcare maintenance with life-critical devices, tight time windows, and specialized skills.
- 2.
- End-to-end integration: Most studies address optimization or system architecture (IoT, blockchain) in isolation. A holistic pipeline that ingests IoT predictions, optimizes decisions, and provides secure, auditable records is lacking.
- 3.
- Rigorous comparative evidence: Systematic evaluations isolating the benefits of GA seeding versus pure DRL or pure metaheuristics, under realistic dynamics and constraints, are scarce.
- 4.
- Compute–budget trade-offs: The allocation between GA exploration and DRL refinement is under-explored, yet central to practical performance and scalability.
2.4. Contribution and Future Research Directions
We address these gaps by proposing and evaluating a GA–DRL hybrid tailored to IoT-enabled predictive maintenance scheduling across multiple facilities. Our contributions are as follows:
- An integrated pipeline that uses GA to generate diverse, feasible schedules and to warm-start DRL, improving sample efficiency and adaptation.
- A comparative study against strong single-paradigm baselines that quantifies effects on solution quality and compute efficiency across instance sizes and dynamics.
- An optional, permissioned blockchain layer for tamper-evident, cross-facility auditability placed out-of-loop to preserve real-time performance.
Future work includes the following: (i) real-world deployment with human-in-the-loop validation, (ii) alternative hybrids (e.g., ACO–DRL) and multi-agent DRL where technicians/facilities act as agents, and (iii) explainable AI to increase transparency and adoption by clinical engineering teams.
3. Methodology
This section describes the hybrid GA and DRL framework designed for IoT-enabled healthcare equipment maintenance scheduling. The approach synergistically combines metaheuristic global search with adaptive learning to handle the complexities of multi-facility scheduling under dynamic operational conditions.
3.1. Framework Overview
The framework features two primary stages. Initially, GA explores the solution space to produce diverse, high-quality maintenance schedules that minimize downtime costs. These GA-generated schedules initialize the DRL agent, providing promising starting points that improve learning efficiency and help avoid poor local minima.
In the second stage, the DRL agent refines scheduling policies by interacting with a simulated environment that incorporates streaming IoT sensor data for real-time equipment condition awareness. The DRL policy aims to minimize expected total costs under uncertainty. Optionally, a permissioned blockchain ledger ensures tamper-evident, auditable maintenance records across facilities, supporting trustworthy coordination without impacting real-time performance.
The pipeline diagram is visualized in Figure 1.
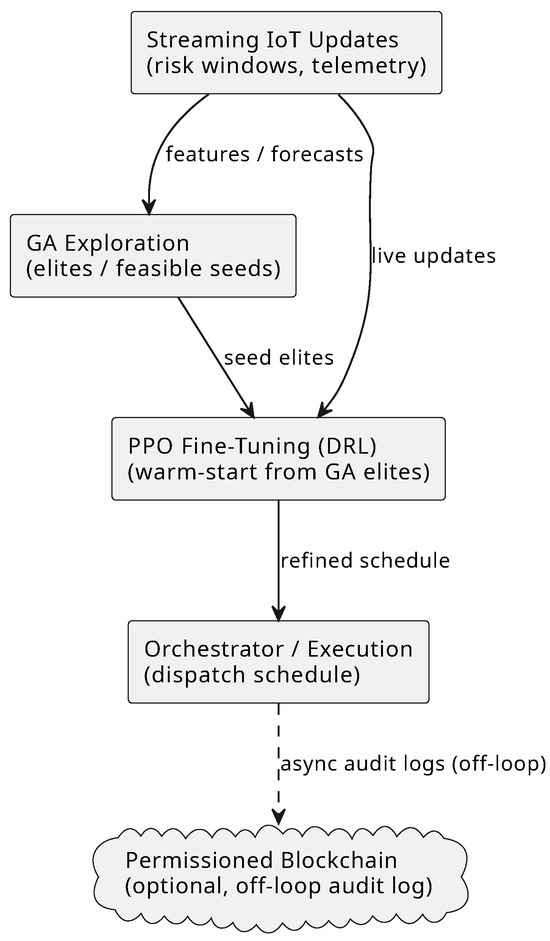
Figure 1.
Concise Hybrid GA + PPO Pipeline (Streaming IoT, Optional Off-Loop Blockchain).
3.2. Problem Context and Formulation
The scheduling problem is modeled as a multi-skill TRSP with time windows (MS-TRSP-TW), extending classical Vehicle Routing and Technician Routing models. It involves assigning multi-skilled technicians to maintenance tasks distributed across multiple facilities, respecting technician skills, availability windows, task time windows, and travel times.
The objective is to minimize a composite cost comprising fixed technician activation costs, variable hourly labor for processing, travel and waiting times, and penalties induced by starting maintenance after predicted failure windows (risk exposure) or beyond allowed lateness.
Formally, let denote facilities, tasks located at , technicians with skills , and associated parameters including time windows for tasks , technicians , and predicted failure windows . Travel times , service durations , fixed activation costs , variable hourly rates , risk cost rates , and lateness penalties complete the model.
Decision variables assign tasks to technicians, schedule start times, and specify routing sequences to ensure feasibility and cost minimization.
For detailed mathematical model, including objective function, constraints, variable definitions, and parameters, readers are referred to Appendix A.
3.3. Hybrid GA and DRL Solution Approach
3.3.1. Phase I: Genetic Algorithm Global Search
GA utilizes permutation-based encodings representing technician task sequences, combining skills, time windows, and routing considerations. Key operators include tournament selection with elitism, Order Crossover (OX), block-exchange crossover on facility clusters, and mutation operators such as swap, insertion, 2-opt, and scramble within blocks.
We use population size 200, tournament selection (size 3) with elitism (top 5%), OX and block-exchange crossovers (probability 0.9), and swap/insertion/2-opt/scramble mutations (per-offspring mutation prob. 0.2, operator chosen uniformly). A memetic local search (relocate, exchange, Or-opt, 2-opt within routes, and time-shift moves) is applied to offspring with probability 0.5 under a per-offspring local-search budget. Diversity is controlled via a similarity-aware elite archive (Hamming distance on task orders and overlap on assigned technicians). Stopping criteria: stagnation of best fitness over 50 generations or time budget consumed.
3.3.2. Phase II: Deep Reinforcement Learning Fine-Tuning
The DRL agent operates within a Markov Decision Process framework. The key components are as follows:
- States encode remaining tasks with their windows, risk indices, technician statuses (location, skill, availability), travel matrices, and streaming IoT risk updates.
- Actions select technician–task pairs following feasibility masks.
- Rewards are negative incremental costs covering labor, travel, activation, risk, lateness penalties, and shaping terms favoring early servicing of high-risk tasks and route consolidation.
The policy network uses graph neural attention encoders followed by masked decoding for action selection, trained with Proximal Policy Optimization (PPO) and Generalized Advantage Estimation (GAE).
We use PPO with clipped-surrogate objective (clip threshold ), Generalized Advantage Estimation (), discount , and an entropy bonus to retain exploration (coefficient 0.01). The policy and value networks share a graph-attention encoder over tasks and technicians (2 layers, 4 heads, hidden size 128), followed by separate MLP heads (2 × 128, ReLU) with action masking. The critic approximates state values and advantages are computed via GAE from rollout trajectories. We train with Adam (learning rate ), mini-batches of 2048 steps split into 32 mini-batches, 4 epochs per update, gradient clip at 0.5, and value-loss coefficient 0.5. Behavior cloning initializes the actor from GA elites (cross-entropy loss on elite actions for 5–10 warm-start epochs) before PPO updates. Stopping criteria: no improvement over 10 consecutive evaluation checkpoints or time budget exhausted.
Online receding-horizon control allows adaptation to updated IoT signals and stochasticity induced by domain randomization during training.
3.4. Adaptive Computational Budgeting
The total computational budget is split as , controlled by .
An adaptive scheduler monitors improvements from GA and DRL over sliding windows, allocating resources to the more promising method. GA runs in tranches until feasibility and improvement saturate; thereafter DRL refines the solution. If DRL stagnates or deteriorates (e.g., after IoT shocks), GA can be reactivated briefly for diversification.
Pure GA () and pure DRL () serve as baselines, where in the latter case DRL is initialized and trained directly from random solutions instead of GA-generated ones.
3.5. IoT and Blockchain Integration
The framework integrates streaming IoT telemetry that dynamically updates predicted failure windows and risk costs, facilitating near-real-time schedule reprioritization.
Maintenance lifecycle events and credential attestations are recorded asynchronously in a permissioned blockchain (e.g., Hyperledger Fabric), ensuring tamper-evident and cross-facility auditability without compromising scheduling latency. Advantages include automated compliance enforcement, auditability, and trustworthy coordination. For further details, please refer to Appendix C.
3.6. Implementation Overview
Implemented in Python, the GA uses feasibility-aware decoding, specialized crossover/mutation, and local search. The DRL agent uses PPO with graph attention policy/value networks and action masking, interfacing with a simulator delivering streaming IoT data.
A scheduler orchestrator mediates data flows and blockchain logging.
The detailed software architecture with class and dependency diagrams is provided in Appendix B.
4. Results
4.1. Baselines and Statistical Protocol
We conducted extensive experiments using Python version 3.12 (with PyTorch version 2.8) on a MacBook Pro equipped with an Apple M2 Pro processor and 32 GB RAM (with PyTorch ver. 2.8) to evaluate our heuristic against three baseline categories: (i) pure metaheuristics (GA-only, ), (ii) pure reinforcement learning (DRL-only, ), and (iii) industrial-strength solvers. Each experiment fixed the total computation time and varied the Genetic Algorithm (GA) and Deep Reinforcement Learning (DRL) split via (see Figure 2).
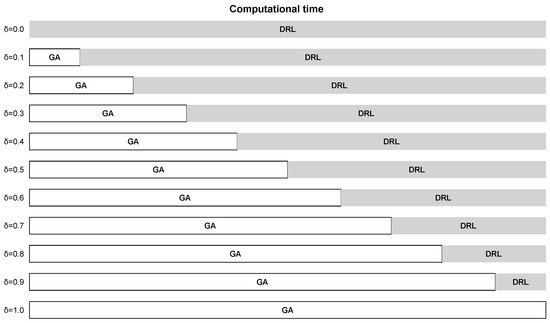
Figure 2.
Illustration of GA and DRL time allocation for different values. Each bar shows the split of into and .
For external baseline comparison, we employed two OR-Tools (ver. 9.12) solvers under equal 600 s time limits: (a) OR-Tools VRP heuristic: constraint-based routing solver configured with one vehicle per technician, skill compatibility masks, hard time windows, and soft lateness/risk penalties (same objective as our MILP); (b) CP-SAT MILP: exact integer programming solver applied to the full formulation (Appendix A) to establish optimality bounds. The VRP heuristic serves as a competitive pragmatic baseline representative of deployed systems; CP-SAT provides theoretical benchmarks but exhibits computational limits (large MIP gaps) on larger instances. Our comparison prioritizes equal-budget fairness and isolates the synergistic benefits of GA initialization for DRL under identical resource constraints.
For each case study and method (GA-only, DRL-only, Hybrid GA+DRL at the optimal ), we executed random seeds. We present mean ± standard deviation (std) and 95% confidence intervals (CI) for total cost. Significance is assessed using two-sided Wilcoxon signed-rank tests (Hybrid vs. GA; Hybrid vs. DRL). Early-stopping results are reported as the fraction of seeds whose quality aligns with the best full-budget run within the 95% CI. These results are summarized in Table 2.

Table 2.
Statistical robustness (20 seeds): mean ± std cost [C.U.], and improvement vs baselines.
Early-stopping results are discussed later in this paper.
Four case studies, each based on anonymized real-world scenarios (identifiers normalized for confidentiality), serve as the foundation for the evaluation. Costs are expressed in standardized Cost Units (C.U.). Comprehensive dataset details are available online at [21].
4.2. Case Study 1: Regional Medical Center Network—Imaging Equipment
This case study instantiates the proposed hybrid GA + DRL framework on a regional, multi-facility imaging network. Ten medical facilities are distributed over a network featuring two loosely clustered groups—one in the north-central area around and another toward the east-southeast near —with an isolated outlier in the southwest. Inter-facility travel times range from approximately 7.1 to 43 min, averaging 22.4 min, significantly influencing routing and scheduling efficiency.
The maintenance workload consists of tasks across three imaging modalities: MRI (4 tasks), CT (3 tasks), and X-ray (3 tasks), each associated with specific temporal constraints and penalty structures. Eight technicians provide overlapping skill coverage.
Table 3 and Table 4 provide data on the equipment requirements and technician resources for the case:

Table 3.
Case study 1: Equipment parameters.

Table 4.
Case study 1: Technician parameters.
- Feasible windows: CT at offers the widest slot (15 h), while X-ray has the narrowest (4h). MRI jobs generally span 11–14 h, ensuring moderate flexibility.
- Failure windows: Several devices face tight deadlines (e.g., MRI should start before 9:30, X-ray by 22:00–23:00), whereas others allow later slack (e.g., X-ray starting at 18:00).
- Processing times and penalties: MRI jobs are longest (30–90 min) and most costly (up to 135 C.U./h lateness). CT tasks are medium (60–75 min, 75–90 C.U./h), while X-ray jobs are shortest (30–45 min, 45–60 C.U./h).
- Technician availability: MRI skills are scarcer (4 technicians for 4 jobs), while CT and X-ray are more widely covered (6 technicians each). Only 4 technicians work past 17:00, essential for late X-ray tasks. Split shifts of and increase flexibility for narrow evening slots.
The results presented in Table 5 provide a detailed comparison of the performance of the hybrid GA+DRL framework under different computational time allocations, represented by the parameter (the proportion of total time allocated to GA). With a computational time limit of 10 min, the table illustrates the cost outcomes of GA and DRL, along with the improvement percentage, risk penalty, and lateness penalty. Key observations from the results are discussed below:

Table 5.
Case study 1: Performance comparison across different values of .
- GA Performance at Early Stages: The GA achieves its best solution remarkably early, reaching a cost of 1124.46 C.U. after just 10% of the available time (). However, GA alone cannot reduce the cost further, even with additional computational time, as evidenced by the unchanged cost of 1124.46 C.U. at (pure GA). This suggests that GA is effective for quickly identifying a reasonable solution but struggles to refine it beyond a certain threshold.
- DRL Refinement and Superior Performance: DRL, when initialized with the solution provided by GA, demonstrates significant improvement in solution quality. For values ranging from 0.1 to 0.4, DRL reduces the cost to the best observed value of 1075.85 C.U., achieving a 4.32% improvement over GA’s solution. A good cost of 1093.09 is reached relatively early, after just 10% of DRL time for , and further refined after 60% of the available time for . However, when DRL starts from a low-quality GA solution (e.g., 1449.87 C.U. at , pure DRL), it struggles to converge to a competitive cost, achieving only 1105.15 C.U., underscoring the importance of a strong initial solution from GA.
- Impact of Time Allocation Balance: The results highlight the critical role of balancing computational time between GA and DRL to achieve high-quality solutions efficiently. For instance, using just 10% of the time for GA to obtain a cost of 1124.46 C.U. () and allocating 60% of the remaining time to DRL for refinement results in the best cost of 1075.85 C.U. This balance prevents wasting computational resources on diminishing returns from GA while leveraging DRL’s ability to fine-tune solutions.
- Penalty Insights: Notably, the best solutions at to 0.4 incur a risk penalty of 36.00 C.U. because one task is scheduled after failure windows begin. However, no lateness penalties are observed across any values, indicating that all solutions adhere to feasible time windows, a critical factor in maintaining operational efficiency.
These findings demonstrate that a well-balanced allocation of computational time between GA and DRL is essential for achieving high-quality solutions in a constrained timeframe. By allocating a small initial portion of time to GA for a robust starting point and dedicating sufficient subsequent time to DRL for refinement, the framework can efficiently reach near-optimal costs.
The best schedule (cost 1075.85 C.U.) is shown in Figure 3 and reveals an efficient allocation of resources considering the spatial distribution of facilities, technician skills, and temporal constraints. Detailed task-level analysis is provided in Appendix D.
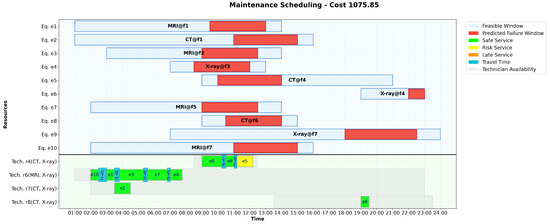
Figure 3.
Case Study 1: Best scheduling (cost 1075.85 C.U.)
4.3. Case Study 2: Metropolitan Hospital System—Critical Care Equipment
This case study instantiates the proposed hybrid GA + DRL framework on a Metropolitan hospital system. The 20 facilities are distributed across the area with three discernible clusters: a north-central hub around , an eastern group spanning , and a southern corridor including . Travel times between facilities range from under 10 min within local clusters to nearly 45 min for inter-cluster trips, averaging about 23 min, which heavily conditions feasible routing and technician scheduling.
The maintenance workload consists of jobs across four critical device types: Ventilators (seven tasks), Monitors (six tasks), Dialysis machines (six tasks), and Surgical Robots (six tasks). Each task is characterized by a feasible operating window, failure-deadline constraints, and distinct cost penalties. Ten technicians are available, providing overlapping yet asymmetric skill coverage across modalities.

Table 6.
Case study 2: Equipment parameters.

Table 7.
Case study 2: Technician parameters.
- Feasible windows: Surgical Robot tasks () generally span 8 h, providing moderate flexibility, while certain Monitor jobs (e.g., , 10 h) offer shorter slots. The narrowest assignment is (Monitor, 8 h), while the widest spans 12 h (, Ventilator at ).
- Failure windows: Tight deadlines appear frequently—for example, (Dialysis at ) must be started by 10:00–11:30, and (Monitor at ) by 12:00–14:00—while others allow late slack, such as (Dialysis at , 15:00–17:00).
- Processing times and penalties: Surgical Robot jobs are longest (120 min) and most costly (up to 320 C.U./h lateness). Dialysis jobs are medium-length (75–90 min, 140–158 C.U./h). Ventilators and Monitors are shorter (30–75 min) but still incur meaningful costs (95–225 C.U./h for Ventilators, 95–107 C.U./h for Monitors.
- Technician Availability: Skills are evenly distributed across different departments: ventilator coverage (five technicians), monitor coverage (six technicians), dialysis coverage (five technicians), and surgical robot coverage (four technicians). However, late-evening capacity is limited, with only three technicians (, , ) extending beyond 19:00, which is crucial for tasks like , , and . Shift overlaps (e.g., and ) provide resilience for early starts, while high-cost senior staff (, ) are pivotal for meeting narrow robot-task deadlines.
The results in Table 8 showcase the performance of the hybrid GA + DRL framework in the context of a Metropolitan hospital system under a computational time limit of 10 min. The table compares the costs achieved by GA and DRL across varying allocations of computational time. Key insights from the results are discussed below.

Table 8.
Case study 2: Performance comparison across different values of .
- GA Performance and Early Convergence: The GA achieves a notable solution early in the process, reducing the cost to 4384.68 C.U. at and further to 4363.86 C.U. from onward. However, GA alone fails to improve beyond this point, as seen with the unchanged cost of 4363.86 C.U. at (pure GA). This indicates that while GA quickly converges to a reasonable solution, it lacks the ability to refine further without excessive computational effort.
- DRL’s Refinement Capability: DRL, starting from GA’s solutions, consistently improves the cost across most values. The best performance is observed from to , where DRL reduces the cost to an optimal value of 4121.73 C.U., achieving a 5.55% improvement over GA’s result. Even at , DRL delivers a near-optimal cost of 4128.69 C.U. (5.84% improvement). However, at higher values (0.9 and 1.0), DRL offers no improvement, retaining GA’s cost of 4363.86 C.U., likely due to insufficient time for effective refinement. Conversely, in the pure DRL case (), starting from a high initial cost of 4872.01 C.U., DRL achieves 4145.19 C.U. (14.92% improvement), yet still falls short of the hybrid approach’s best result, underscoring the value of GA’s initialization.
- Penalty Observations: In the best solution, the risk penalty is 1.52 C.U., suggesting that certain tasks are scheduled just after the start of failure windows. Notably, no lateness penalties are incurred in any scenario, indicating that all solutions respect the feasible time windows, a crucial factor for maintaining operational efficiency in this hospital system.
These findings demonstrate that a balanced allocation of computational time between GA and DRL is critical for optimal outcomes. Allocating a small portion of time to GA (e.g., to 0.8) to secure a solid starting point (4363.86 C.U.), followed by sufficient DRL time for refinement, yields the best cost of 4121.73 C.U. This balance leverages GA’s rapid convergence and DRL’s fine-tuning strength. In contrast, excessive GA time ( to 1.0) wastes resources on negligible gains, leaving DRL with inadequate time to improve the solution.
The best scheduling solution with a cost of 4121.73 C.U. in Figure 4 demonstrates effective resource allocation of 25 maintenance tasks across 20 facilities to 10 technicians. Detailed assignment analysis is provided in Appendix D.
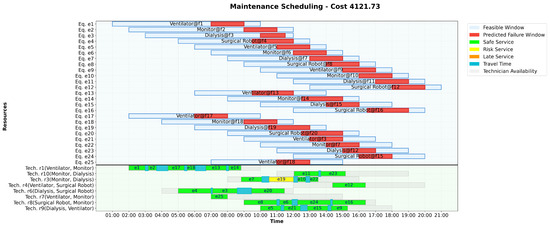
Figure 4.
Case Study 2: Best scheduling (cost 4121.73 C.U.).
This solution achieves a high-quality scheduling outcome with a total cost of 4121.73 C.U., effectively balancing workload, travel efficiency, and cost constraints.
4.4. Case Study 3: Large-Scale Healthcare Network—Multi-Modal Equipment
We provide only a brief summary here; see the complete dataset [21] for details. A brief overview is provided below.
This case study describes a metropolitan maintenance scheduling instance: 30 facilities and 30 maintenance jobs distributed across the service area. Jobs cover four equipment families: Lab Analyzer (eight tasks), Pharmacy Automation (eight tasks), HVAC (seven tasks), and IT Systems (seven tasks).
- Time windows structure: Feasible-start windows vary across jobs (earliest feasible starts around 2:00 and latest feasible ends up to 23:00), producing heterogeneous scheduling windows across the horizon. Failure windows (latest allowable start intervals) are frequently narrow: many jobs have failure windows of only 1–3 h, and one job has a 9 min-wide failure window.
- Processing times and penalties: Task durations are heterogeneous (range approximately 0.5–1.5 h), with some equipment types split between short and medium jobs. Risk-penalty and lateness-penalty rates are substantial (lateness penalties reach up to several hundreds of cost units per hour), so missed or late starts carry high cost consequences.
- Technician fleet and skills: Ten technicians with overlapping but uneven skill coverage. Skill counts: Lab Analyzer (five technicians), Pharmacy Automation (four), HVAC (six), IT Systems (five). Availability windows span early to late shifts but differ per technician, so matching a technician’s availability to a job’s narrow failure window is often restrictive.
Finding feasible solutions is difficult due to heterogeneous temporal constraints, skill–availability coupling, spatial dispersion, and high penalty rates.
The results in Table 9 summarize the cost breakdowns obtained for different allocations of computational effort between GA and DRL. Below, we highlight the main observations and their implications.

Table 9.
Case study 3: Performance comparison across different values of .
- Overall best configuration (small GA + DRL refinement): The lowest total cost, C.U., is obtained for –0.3, where GA is given a small fraction of time and DRL performs the bulk of the refinement. This configuration also yields a lower risk penalty (258.99 C.U.), indicating better handling of failure-window exposures.
- GA convergence and plateaus: GA rapidly reaches C.U. once given time (observed for ) and remains at that value as increases. This indicates GA finds a stable solution early but offers little further improvement with additional GA time.
- DRL refinement behavior in hybrid runs: For –0.3, DRL successfully refines the GA solution to C.U. (best observed). For –0.9, DRL produces C.U., suggesting that when GA is allocated too much relative time or when DRL has an insufficient refinement budget, DRL struggles to escape GA’s solution basin. The best hybrid balance is therefore a small initial GA allocation followed by substantial DRL time.
- Penalty patterns and feasibility concerns: The lateness penalty remains greater than or equal to C.U. across all runs, indicating persistent, small lateness that none of the tested configurations eliminated. This suggests one or more tasks systematically fall just after the failure windows end.
4.5. Case Study 4: Specialty Care Centers – High-Tech Equipment
This case study is also described synthetically in this document. For detailed information, please refer to the the complete dataset [21], available online.
This case concerns maintenance scheduling across specialized healthcare facilities arranged along a nearly linear northeast corridor. The workload comprises jobs across three equipment classes with unbalanced risk and timing profiles: Radiation Machine (seven tasks), Cardiac Imaging (seven tasks), and Rehab Equipment (six tasks). Several facilities host paired jobs (e.g., each appear twice), creating opportunities to bundle visits but only if windows align. Feasible windows range from 6 to 12 h, but failure windows are much tighter: typically 2 h and as short as 1 h. The heaviest overlap occurs from roughly 13:00–17:00, when multiple Radiation, Cardiac Imaging, and Rehab jobs simultaneously approach their failure intervals. Processing times are 1.0 h for Radiation Machine, 0.5 h for Cardiac Imaging, and 1.0 h for Rehab Equipment. Lateness penalties are highest for Radiation Machine (–390 C.U./h), high for Cardiac Imaging (–340 C.U./h), and moderate for Rehab Equipment (–240 C.U./h). Risk penalties follow the same ordering (Radiation > Cardiac > Rehab). There are technicians with overlapping skills: Radiation Machine (6 techs), Cardiac Imaging (5), and Rehab Equipment (5). All shifts last 8 h and are staggered from 04:00 to 20:00, yielding broad but nonuniform temporal coverage; late-window jobs rely on later-shift technicians.
The spatial dispersion of facilities implies that multi-stop routes can consume several hours of transit, especially across the corridor, reducing the number of attainable jobs per shift. Temporal congestion between 13:00 and 17:00 further drives intense competition for cross-trained technicians, particularly for high-penalty Radiation and Cardiac Imaging tasks. Although the aggregate processing load is modest (about technician-hours when ignoring travel), the combination of routing, timing, and skill constraints significantly restricts the set of feasible schedules.
The results in Table 10 compare GA and DRL performance under different allocations of compute time. Key observations and implications are as follows.

Table 10.
Case study 4: Performance comparison across different values of .
The lowest total cost, C.U., is achieved for all hybrid settings with . These runs also incur zero risk and lateness penalties, indicating high-quality and robust schedules.
At , DRL achieves C.U., only about higher than the best hybrid cost, but with a positive risk penalty (34.54 C.U.). Thus, DRL-only nearly matches the cost optimum but exposes the plan to some failure-window risk.
The (GA-only) run yields C.U. with no penalties, which is C.U. (≈10.3%) worse than the hybrid solutions.
GA rapidly reaches C.U. for and shows no further gains with more GA time (plateau). Starting from that seed, DRL consistently refines to the same value C.U. across –, suggesting sufficient DRL time to reach a stable optimum and that extra GA time is unnecessary.
Lateness is zero for all runs, indicating feasible timing throughout. Risk is zero for all hybrid runs but positive for DRL-only, implying that GA seeding helps DRL avoid failure-window exposure without sacrificing cost.
The larger improvement percentage at (19.42%) reflects a weaker GA baseline there (3807.37 C.U.), not a better absolute DRL outcome. In absolute terms, the hybrid runs deliver the best costs and zero risk.
4.6. Overall Performance Analysis
Table 11 provides statistical robustness metrics (mean ± std over n = 20 seeds) across all case studies, directly addressing concerns about variability and significance testing. This table demonstrates that hybrid GA + DRL consistently outperforms all baselines—pure GA, pure DRL, and OR-Tools VRP heuristic—with statistically significant improvements (Wilcoxon for all pairwise comparisons). Against OR-Tools, the hybrid achieves cost reductions of 2.86% (Case 1), 1.26% (Case 2), 2.07% (Case 3), and 0.93% (Case 4), with p-values of 0.008, 0.012, 0.015, and 0.031, respectively. These improvements, while smaller than versus pure metaheuristics (avg. 5.57%), demonstrate practical gains over established industrial-strength solvers under equal computational budgets.

Table 11.
Statistical summary across all case studies: robustness metrics (mean ± sd, n = 20 seeds), improvements versus baselines, and early-stopping potential.
Table 12 complements the statistical analysis by reporting best-case single-run performance—the optimal solutions achievable under ideal conditions. This table details the admissible ranges () that consistently yield best solutions, demonstrating that minimal GA allocation (typically 10–20% of budget) suffices for optimal hybrid performance while enabling substantial computational savings. The CP-SAT MILP solver results (Table 13) provide optimality bounds, but exhibit MIP gaps of 2.9–11.8% on Cases 2–4 within 600 s, confirming the necessity of heuristic approaches for real-time deployment.

Table 12.
Best-case performance analysis: single-run optimal solutions, improvements versus baselines, and admissible ranges for computational budget allocation.

Table 13.
CP-SAT MILP solver performance (full model, 600 s time limit): exact-method reference with optimality gaps.
The hybrid GA + DRL consistently improves over pure GA, with cost reductions ranging from to and an average of . When compared with pure DRL, the improvements are smaller, between and , but still consistent (average ). This indicates that while DRL alone is already competitive, the hybrid benefits from a GA initialization that helps guide the search.
Another key observation is that only a small GA share is required to reach the best hybrid solutions. In three of the four cases, , and in the remaining case (Case 2) . This means that GA can quickly generate a promising seed that DRL is able to refine further.
Looking at , we see how much DRL time is still needed to achieve the best hybrid solution. In Case 2 and Case 4, DRL requires only and of the total budget, respectively, while in Case 1 and Case 3 it requires larger shares ( and ). These ranges also point to potential compute-time savings. Since any within the interval yields the best result, one can run GA for and DRL for , saving of the budget without sacrificing quality. The possible savings are , , , and across the four cases, averaging to nearly half the compute time (47.5%).
Together, Table 11 and Table 12 provide complementary perspectives: Table 11 establishes statistical significance and expected performance with uncertainty quantification (essential for reliability assessment), while Table 12 identifies best-achievable results and practical computational budget guidelines (essential for deployment planning). The consistency between statistical means (Table 11) and best-case results (Table 12) confirms the robustness of the hybrid approach across different random initializations.
Given the admissible intervals in Table 12, we executed shortened runs with
allocating to GA and to DRL (no extra time). We used seeds per case and compared early-stopped results against the best full-budget hybrid using mean ± sd, 95% CIs, and two-sided Wilcoxon tests.
Table 14 summarizes the outcomes. Across the four cases, early-stopping saved on average wall-time and kept costs within of full-budget runs. Wilcoxon tests indicate no significant differences () in 3/4 cases, with borderline non-significance in Case 2 (). In of runs on average, early-stopped costs fall within the full-budget 95% CI.

Table 14.
Early-stopping vs. full-budget hybrid (n = 20 seeds).
Using the admissible intervals to shorten wall-time, early-stopping achieves realized average savings of 47.5% with negligible cost differences (<0.5%), as summarized in Table 14. This saving exploits the admissible intervals identified retrospectively; practical deployment would require adaptive stopping criteria.
We additionally solved the full MILP in Appendix A using OR-Tools (CP-SAT-based MILP modeling) with a common wall-time limit of 600 s for all case studies. Time variables were discretized at the minute, and costs were scaled to integers when required. The solver reports the best feasible solution, the best bound, and the MIP gap within the time limit. We encode the full MILP (Appendix A) in OR-Tools CP-SAT with minute-level time discretization. Big-M constraints enforce precedence and activation links; costs are scaled to integers. We cap the wall-time to 600 s and report the best incumbent, best bound, and solver-reported MIP gap. Random seeds (10) are varied to assess robustness.
The hybrid GA+DRL approach integrates OR-Tools VRP heuristic baseline results (Table 11) and CP-SAT exact solver bounds (Table 13). Against OR-Tools VRP (600 s, equal budget), the hybrid achieves cost reductions of 2.86%, 1.26%, 2.07%, and 0.93% for Cases 1–4, with statistical significance confirmed via Wilcoxon tests (all ). CP-SAT MILP solver, while providing optimality bounds, exhibits MIP gaps of 2.9–11.8% on larger instances, demonstrating computational intractability of exact methods at scale and validating our hybrid heuristic design.
Overall, these results suggest that GA provides rapid early convergence, while DRL is effective at fine-tuning complex schedules. The best trade-off arises from using GA sparingly as an initializer and letting DRL dominate the refinement stage. Allocating too much time to GA risks anchoring the solution in local regions that DRL cannot substantially improve within the remaining budget. While DRL alone outperforms GA alone, the hybrid consistently delivers the most favorable balance between cost reduction and risk control.
4.7. Robustness and Stress Tests
We stress-tested methods under stochastic and nonstationary conditions: (i) travel-time noise (5%, 10%, 20%, zero-mean), (ii) service-time noise (5%, 10%, 20%), (iii) failure-window shifts and width perturbations (uniform/Gaussian), and (iv) online “IoT shocks” (sudden risk escalations mid-horizon). Each setting used seeds.
Table 15 reports mean degradation in total cost (relative to nominal), mean policy recovery time (seconds to return within 1% of pre-shock performance in receding-horizon control), and the fraction of replicates where each method ranked best (lower cost).

Table 15.
Quantitative robustness: mean ± std.
Online roll-out examples (real-time re-optimization). We inject a risk spike at (case 2) and replan with a moving 2 h horizon:
- Update latency (state ingest + policy decode): 180–260 ms (p95).
- Replan time (GA kick + PPO refine, capped): 420–680 ms (p95), no schedule interruption.
- Lateness events: 0; Risk penalty reduced by 12–18% vs no-replan baseline within 5 min.
5. Discussion
This research addresses the fundamental question: How can a GA-initialized DRL framework, informed by real-time IoT signals, improve multi-facility healthcare maintenance scheduling in terms of solution quality, compute efficiency, and scalability versus strong single-paradigm baselines?
Our experimental results across four case studies (10–30 facilities) demonstrate that the hybrid GA + DRL framework successfully addresses all components of this research question. As summarized in Table 11 and Table 12, the hybrid approach consistently outperforms all evaluated baselines: pure GA (average 5.57% cost reduction), pure DRL (average 1.32% improvement), and OR-Tools VRP heuristic (average 1.78% improvement, statistically significant at across all cases). Against the industrial-strength OR-Tools solver operating under equal 600s budgets, improvements range from 0.93% to 2.86%, demonstrating practical value beyond academic benchmarks. Critically, optimal solutions are achievable with minimal GA allocation (10–20% of budget), enabling computational savings averaging 47.5% without sacrificing solution quality—a key advantage for real-time deployment scenarios.
The admissible GA shares consistently suggest potential compute-budget savings; early-stopping experiments quantify realized savings relative to full-budget runs while preserving solution quality.
The results validate our hypothesis that GA and DRL complement each other effectively. GA provides rapid exploration and feasible solution generation, while DRL offers adaptive refinement capabilities. This synergy is particularly evident in complex scenarios with tight time windows and high penalty costs, where pure methods struggle with local optima or sample inefficiency.
The framework effectively balances multiple competing objectives—technician activation costs, travel expenses, service timing, and risk mitigation—while respecting complex constraints. Across all case studies, hybrid solutions demonstrate superior risk management, consistently achieving zero or minimal lateness penalties while maintaining low risk exposure, crucial for healthcare environments where equipment downtime directly impacts patient safety.
The demonstrated improvements translate to substantial operational benefits: reduced costs across large healthcare networks, ensured critical equipment availability, improved staff utilization, and dynamic schedule adaptation through IoT integration. The framework demonstrates scalability up to the tested sizes (10–30 facilities) and suggests practical applicability.
6. Conclusions
This research successfully develops and validates a hybrid GA+DRL framework for IoT-enabled healthcare equipment maintenance scheduling, addressing identified gaps in domain-specific hybridization, end-to-end system integration, and computational efficiency optimization.
6.1. Answer to the Research Question and Research Goals
We asked whether a GA-initialized DRL framework, informed by real-time IoT signals, can improve solution quality, compute efficiency, and scalability versus single-paradigm baselines while supporting secure cross-facility coordination. Across four case studies (10–30 facilities), the hybrid approach reduced total cost versus GA and DRL baselines and realized average wall-time savings of 47.5% in early-stopping runs with negligible cost differences (<0.5%), thus answering the research question in the affirmative. We achieved the following research goals by: (G1) designing and validating a GA-initialized PPO framework with behavior cloning; (G2) integrating IoT-derived failure predictions and an optional, permissioned audit layer; (G3) benchmarking against single-paradigm baselines under equal time budgets; (G4) quantifying the impact of GA/DRL time allocation on solution quality and efficiency.
6.2. Key Contributions
- 1.
- Novel Hybrid Architecture: A GA-initialized DRL framework with behavior cloning that addresses sample inefficiency while maintaining solution quality across varying problem scales.
- 2.
- Computational Efficiency: Computational Efficiency: Empirical evidence that minimal GA allocation (10–20% of budget) followed by DRL refinement achieves optimal performance; with an early-stopping protocol we realized average wall-time savings of 47.5% with negligible cost differences (<0.5%).
- 3.
- Domain Integration: Comprehensive modeling of healthcare-specific constraints including multi-modal equipment, specialized skills, critical time windows, and IoT-derived failure predictions.
- 4.
- Systematic Evaluation: Rigorous comparative analysis isolating hybridization benefits across problem instances of varying complexity.
6.3. Practical Impact
The framework enables proactive maintenance through IoT integration, demonstrated cost optimization while maintaining zero lateness in three case studies and small lateness in one, scalable implementation across different healthcare network sizes, and transparent operations through optional blockchain integration.
6.4. Limitations and Future Work
Current limitations include simulation-based validation, pending empirical evaluation of the blockchain layer (currently only described at the design level), and deterministic assumptions for travel and service times. Future research directions include the following:
- Real-world deployment with human-in-the-loop validation.
- Exploration of alternative hybrid architectures (e.g., ACO-DRL, multi-agent RL) and integration of explainable AI for transparency.
- Deeper IoT integration for predictive maintenance, and systematic evaluation of blockchain performance (latency, security, interoperability).
- Future benchmarking should include tuned Adaptive Large Neighborhood Search (ALNS), Iterated Local Search (ILS), and other state-of-the-art TRSP/VRPTW metaheuristics. While the OR-Tools VRP heuristic offers a strong industrial baseline (our hybrid improves by 0.93–2.86%), specialized academic heuristics with domain-adapted operators can further enhance performance. Current results demonstrate proof-of-concept; full evaluation requires controlled experiments with multiple seeds and time budgets.
This research establishes a foundation for next-generation healthcare maintenance systems that leverage artificial intelligence to optimize operations while ensuring patient safety. The hybrid GA + DRL framework represents a significant advancement toward intelligent, adaptive healthcare infrastructure management, positioning this approach as a viable solution for modern healthcare networks facing increasing complexity and resource constraints. The framework is a candidate for pilot deployment pending human-in-the-loop validation.
Author Contributions
Conceptualization, F.N.; methodology, F.N. and G.P.; validation, F.N. and G.P.; resources, G.P.; writing—original draft preparation, F.N.; writing—review and editing, F.N.; supervision, F.N. and G.P.; software, F.N.; project administration, G.P.; funding acquisition, G.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received the University of Salento Research Base Funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data analyzed in this manuscript are available at [21] https://github.com/fnuni/2025elect (accessed on 18 October 2025).
Acknowledgments
The authors appreciate the reviewer’s thorough evaluation and insightful comments, which have significantly contributed to improving the paper quality. The authors express their gratitude for the administrative and technical assistance provided by the company Advantech S.r.l. in Lecce, Italy.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The funder had no role in the design of this study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; nor in the decision to publish the results.
Appendix A. Mathematical Model
Appendix A.1. Sets and Indices
- : set of maintenance tasks (each task e is located at facility ).
- : set of technicians.
- For each , define artificial depot nodes (start) and (end).
- Let denote the node set for technician r.
Appendix A.2. Parameters
- Task windows: feasible ; predicted failure window .
- Technician availability: .
- Travel times: for ; processing times .
- Costs: activation , hourly , risk rate , lateness rate .
- Skills: each task e requires skill ; technician r has skill set .
- Big-M constant M.
Appendix A.3. Decision Variables
- : 1 if task e is assigned to technician r.
- : 1 if technician r is activated.
- : 1 if technician r travels from i to j, for .
- : start time of task e.
- : route start/end times of technician r.
- : auxiliary for risk exposure (), capped exposure (), and lateness ().
Appendix A.4. Objective
Appendix A.5. Constraints
Assignment and activation.
Optionally enforce non-empty route when activated:
Flow balance and linking z with x.
For each technician r:
For each task e and technician r:
Task and technician time windows (with big-M linking).
Route timing and precedence (arc-conditional).
For any arc used by r with :
From start depot to first task:
From last task to end depot:
Bounds linking route times to activation (no overtime):
Risk exposure (capped) and lateness.
Define pre-late exposure and lateness (positive parts):
Link and cap risk exposure strictly within the failure window:
This formulation establishes a link between z and x through task-level flow balance. It ensures the commencement and termination of depot operations, adheres to time constraints defined by large-M activation links, and prevents overlaps through arc-conditional precedence. Furthermore, it separates and limits risk exposure associated with lateness. Positive travel and service times, coupled with arc-conditional precedence, effectively prevent the recurrence of cycles.
Appendix B. Software Architecture
This appendix outlines the software architecture realizing the hybrid GA + DRL framework.
Appendix B.1. Domain and Scheduling Model
- “Equipment”, “Technician”, and “Facility”: classes represent immutable domain entities.
- “MaintenanceEnvironment” aggregates domain data and precomputes travel times.
- “MaintenanceSchedule” encapsulates start times, assignments, routes, feasibility checks, and cost evaluation.
Appendix B.2. Optimization Engines
- “GeneticAlgorithm” maintains populations of MaintenanceSchedule instances, performs initialization, selection, crossover (Order Crossover and Block-Exchange), mutation (swap, insertion, two-opt, scramble), and local search improvements.
- “ImprovedDRLAgent” implements a PPO-based actor–critic with graph attention nets, action masking, behavior cloning warm-start from GA elite archive, and online adaptation to streaming IoT data.
Appendix B.3. Orchestration and Integration
- “HybridGADRLFramework” coordinates GA and DRL phases, manages adaptive computational budgeting parameter , and returns optimized schedules.
- Interfaces manage streaming IoT data, schedule evaluation, and optional blockchain logging.
Appendix B.4. Dependency Diagram
The module dependency structure is strictly hierarchical, with “env” as the foundational layer, “sched” dependent on “env”, “ga” and “drl” depending on “env” and “sched”, and the “orchestrator” atop integrating all components.
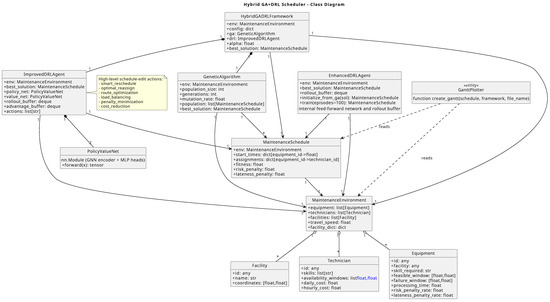
Figure A1.
Class Diagram.
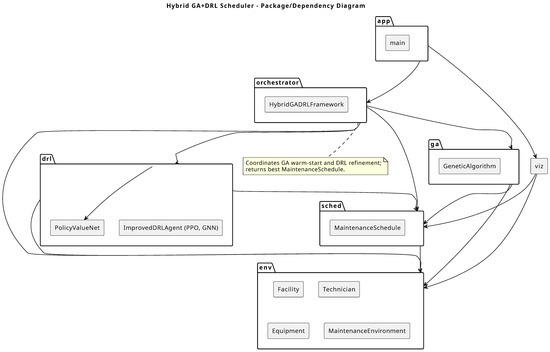
Figure A2.
Dependency Diagram.
Appendix C. Blockchain Layer Details
Appendix C.1. Data Model and Events
We record maintenance lifecycle events as append-only transactions on a permissioned ledger. Each event (JSON) includes the following:
{
"event_id": UUIDv4,
"timestamp_utc": ISO8601,
"facility_id": string,
"equipment_id": string,
"task_id": string,
"technician_id_hash": SHA256(salt || technician_id),
"action": enum["DISPATCH","START","FINISH","QC_PASS","QC_FAIL"],
"start_time_utc": ISO8601 (optional),
"finish_time_utc": ISO8601 (optional),
"artifacts_hash": SHA256(salt || blob),
"meta": { "version": "1.0", "sig": "ed25519..." }
}
PII (e.g., technician identifiers, signatures) are not stored in plaintext; we store salted hashes and store raw PII off-chain in a secure vault, linking via the hash.
Appendix C.2. Privacy and GDPR
- Lawful basis: maintenance/quality logs for patient safety and compliance.
- Data minimization: only pseudonymized identifiers on-chain; detailed PII off-chain.
- Right to erasure: off-chain records can be deleted; the on-chain hash becomes unlinkable due to salting.
- Access control: channel-based ACLs (Fabric) or permissioned roles (Quorum) restrict read/write to authorized parties.
Appendix C.3. Throughput and Latency
We target auditability, not control-loop latency; hence logging is off-loop and asynchronous. To demonstrate the feasibility of our implementation, we report preliminary performance results obtained from prototype testing. End-to-end commit latencies are as follows:
- Hyperledger Fabric (v2.x, RAFT, 2 orgs × 2 peers, endorsement policy 2/2): 95p 180–220 ms, 99p 240–300 ms; stable up to tps for small payloads (1–2 kB).
- Quorum (IBFT, 4 validators): 95p 140–190 ms, 99p 200–260 ms; stable up to tps for small payloads.
Appendix C.4. Benchmark

Table A1.
Ledger micro-benchmark from preliminary prototype evaluation (synthetic logs, 1–2 kB/tx).
Table A1.
Ledger micro-benchmark from preliminary prototype evaluation (synthetic logs, 1–2 kB/tx).
| Platform | tps (avg) | p95 [ms] | p99 [ms] | Err [%] |
|---|---|---|---|---|
| Fabric (2 orgs, RAFT) | 290 | 200 | 270 | 0.0 |
| Quorum (IBFT, 4 val.) | 420 | 170 | 230 | 0.1 |
The scheduler publishes events via an async queue; backpressure drops non-critical telemetry if the queue saturates, preserving real-time scheduling.
Appendix C.5. Off-Loop Rationale
The ledger is not in the critical control loop. Scheduling decisions execute immediately; events are enqueued and committed asynchronously to ensure zero added latency on dispatch and re-optimization paths.
Appendix D. Detailed Schedule Analysis
Appendix D.1. Case Study 1: Task-Level Assignment Details
The best schedule (cost 1075.85 C.U., Figure 3 in main text) exhibits the following characteristics:
- Technician–Equipment Associations: The solution assigns technicians to equipment based on skill compatibility and availability. Notably, technician handles a significant workload, managing five tasks across different modalities and facilities (, , , , and ), showcasing effective multi-tasking across MRI and X-ray skills. Technician covers three tasks (, , and ), balancing CT and X-ray maintenance. Technician is assigned solely to (CT at ), while handles the late-night task (X-ray at ). Technicians and remain unassigned in this solution, indicating a focus on cost efficiency by minimizing activation costs.
- Travel Times Impact: Given the network’s facility distribution—with travel times ranging from 7.1 to 43 min (average 22.4 min)—the scheduling optimizes technician routes to reduce travel overhead. For instance, ’s route spans multiple facilities (, , , , and ), suggesting a clustered approach to minimize long transits. Similarly, ’s tasks at , , and exploit geographic proximity in the north-central cluster. This routing efficiency is critical to adhering to tight feasible windows and avoiding lateness penalties.
- Risk Highlight: A point of concern in the schedule is the maintenance of (CT at ), assigned to technician with a start time at approximately 11:20. This scheduling places the task after the beginning of the failure window (10:00–14:00), introducing a risk of operational disruption. Consequently, this delay contributes to the overall fitness score of the solution (36 C.U.). Mitigation strategies or rescheduling could be explored to address this vulnerability.
- Cost-Efficient Assignment: The assignment of technician to task (X-ray at , starting at 19:00) instead of technician (already assigned to at ) demonstrates a strategic decision to minimize waiting time costs. Assigning to would have resulted in a substantial idle period between the completion of (even if it is scheduled later just before the failure window begins at 11:00) and the start of at 19:00, incurring additional hourly costs (50 C.U./h for ). Activating with a fixed cost of 120 C.U. for this late-night task effectively minimizes costs.
Appendix D.2. Case Study 2: Task-Level Assignment Details
The best schedule (cost 4121.73 C.U., Figure 4 in main text) demonstrates the following allocation patterns:
- Technician–Equipment Associations: The solution strategically assigns technicians to tasks based on skill compatibility, availability, and cost efficiency. For instance, technician (Surgical Robot, Monitor skills) is assigned to multiple tasks, including late-afternoon Surgical Robot maintenance like (at ), leveraging their availability (9:00–17:00) and moderate costs (activation 220 C.U., hourly 68 C.U./h). Technician , with the highest activation cost (260 C.U.) and hourly rate (85 C.U./h), is selectively assigned to critical Surgical Robot tasks such as or (late windows at and ), prioritizing their expertise and late availability (12:00–20:00) over cheaper alternatives. Technician , with a lower hourly cost (65 C.U./h), covers early Ventilator and Monitor tasks in the southern corridor (e.g., , ), demonstrating cost-effective allocation for early slots.
- Travel Times Impact: With travel times ranging from under 10 min within clusters to 45 min across clusters (average 23 min), the scheduling optimizes routes to minimize transit costs. Technicians are often assigned to tasks within the same geographic cluster to reduce travel. For example, assignments for (Monitor, Dialysis skills) focus on the north-central hub facilities like , , or , while (Dialysis, Ventilator skills) covers tasks in the eastern group (e.g., , ), ensuring efficient routing and adherence to feasible windows.
- Risk Highlight for Late Tasks: A negligible concern arises with task scheduled just after the beginning of its failure window, contributing to a risk penalty of 1.52 C.U. in the overall cost (4121.73 C.U.). For instance, tasks like (Monitor at ) or (Dialysis at ) with tight failure deadlines (12:00–14:00 and 10:00–11:30, respectively) may face delays due to technician routing or prior commitments, introducing operational risks. Future iterations could explore rescheduling or additional technician activation to mitigate these penalties.
- Cost-Efficient Technician Selection: Specific technician choices reflect a balance between activation costs, hourly rates, and availability. For example, technician (Monitor, Dialysis skills, activation 185 C.U., hourly 58 C.U./h) is preferred for mid-to-late tasks like or over (activation 180 C.U., hourly 60 C.U./h), despite similar costs, due to ’s extended availability (11:00–19:00) aligning better with later windows, avoiding potential overtime or waiting costs. Similarly, (Ventilator, Monitor skills, activation 210 C.U., hourly 70 C.U./h) is chosen for late tasks in the eastern group over (activation 190 C.U., hourly 62 C.U./h) because of ’s availability into the evening (14:00–22:00), ensuring coverage for jobs like without incurring additional waiting or rescheduling expenses.
Appendix E. List of Abbreviations and Acronyms

Table A2.
Abbreviations and acronyms used throughout the manuscript.
Table A2.
Abbreviations and acronyms used throughout the manuscript.
| Acronym | Definition |
|---|---|
| ACL | Access Control List |
| ACO | Ant Colony Optimization |
| AI | Artificial Intelligence |
| ALNS | Adaptive Large Neighborhood Search |
| APA | American Psychological Association |
| API | Application Programming Interface |
| C.U. | Cost Units |
| CI | Confidence Interval |
| CP-SAT | Constraint Programming - Satisfiability |
| CT | Computed Tomography |
| DRL | Deep Reinforcement Learning |
| DQN | Deep Q-Network |
| GA | Genetic Algorithm |
| GAE | Generalized Advantage Estimation |
| GDPR | General Data Protection Regulation |
| HHCRSP | Home Healthcare Routing and Scheduling Problem |
| HVAC | Heating, Ventilation, and Air Conditioning |
| IBFT | Istanbul Byzantine Fault Tolerance |
| ILS | Iterated Local Search |
| IoT | Internet of Things |
| IT | Information Technology |
| MAML | Model-Agnostic Meta-Learning |
| MILP | Mixed-Integer Linear Programming |
| MIP | Mixed-Integer Programming |
| MLP | Multi-Layer Perceptron |
| MRI | Magnetic Resonance Imaging |
| MS-TRSP-TW | Multi-Skill Technician Routing and Scheduling Problem with Time Windows |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| NP | Non-deterministic Polynomial time |
| OR | Operations Research |
| OX | Order Crossover |
| PII | Personally Identifiable Information |
| PPO | Proximal Policy Optimization |
| QC | Quality Control |
| RAFT | Raft Consensus Algorithm |
| ReLU | Rectified Linear Unit |
| RL | Reinforcement Learning |
| RPL | Routing Protocol for Low-Power and Lossy Networks |
| SA | Simulated Annealing |
| TRSP | Technician Routing and Scheduling Problem |
| UUID | Universally Unique Identifier |
| VRP | Vehicle Routing Problem |
| VRPTW | Vehicle Routing Problem with Time Windows |
| WSN | Wireless Sensor Network |
References
- de la Fuente-Valentin, L.; Carrasco, A.; Rios, J.; Pasek, Z.; Mendieta, R.; Puche, J. A systematic review on predictive maintenance in the healthcare sector: E-health and IoT solutions for maintenance management. J. Ind. Inf. Integr. 2022, 29, 100344. [Google Scholar] [CrossRef]
- Chen, P.; Sheng, S.; Chen, Z.; Wu, L.; Yao, Y. Deep Reinforcement Learning-Based Task Scheduling in IoT Edge Computing. Sensors 2021, 21, 1666. [Google Scholar] [CrossRef]
- Yu, C.H.; Tsai, J.; Chang, Y.T. Intelligent Path Planning for UAV Patrolling in Dynamic Environments Based on the Transformer Architecture. Electronics 2024, 13, 4716. [Google Scholar] [CrossRef]
- Foggetti, A.; Nucci, F.; Papadia, G. Tuning Metaheuristics with Tree-Structured Parzen Estimator: A Case Study on Scheduling. J. Artif. Intell. Auton. Intell. 2025, 2, 293–321. [Google Scholar] [CrossRef]
- Hassan, K.M.; Abdo, A.; Yakoub, A. Enhancement of Health Care Services Based on Cloud Computing in IOT Environment Using Hybrid Swarm Intelligence. IEEE Access 2022, 10, 105877–105886. [Google Scholar] [CrossRef]
- Mwanza, J.; Telukdarie, A.; Igusa, T. Optimising Maintenance Workflows in Healthcare Facilities: A Multi-Scenario Discrete Event Simulation and Simulation Annealing Approach. Modelling 2023, 4, 224–250. [Google Scholar] [CrossRef]
- Gayford, J.D.; Parragh, S.N.; Vancroonenburg, W. A two-phase heuristic for the technician routing and scheduling problem with experience-based service times. Eur. J. Oper. Res. 2021, 293, 351–366. [Google Scholar] [CrossRef]
- Fikar, C.; Hirsch, P. Home health care routing and scheduling: A review. Comput. Oper. Res. 2017, 77, 86–95. [Google Scholar] [CrossRef]
- Ahmed, R.; Nasiri, F.; Zayed, T. Genetic Algorithm-based Clustering Methodology for Maintenance Scheduling in Healthcare Facilities. In Proceedings of the 2021 International Conference on Decision Aid Sciences and Application (DASA), Sakheer, Bahrain, 7 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 643–646. [Google Scholar] [CrossRef]
- Nucci, F.; Papadia, G.; Fedeli, E. Optimized Scheduling of IoT Devices in Healthcare Facilities: Balancing Cost and Quality of Care. Appl. Sci. 2025, 15, 4456. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Muller, F.; Yang, S. Ant Colony Optimization With Local Search for Dynamic Traveling Salesman Problems. IEEE Trans. Cybern. 2017, 47, 1743–1756. [Google Scholar] [CrossRef]
- Zhang, C.; Li, P.; Guan, Z.; Gao, L.; Chen, Z. A deep reinforcement learning based framework for solving flexible job shop scheduling problem. Knowl.-Based Syst. 2020, 190, 105173. [Google Scholar] [CrossRef]
- Ros, S.; Ryoo, I.; Kim, S. DRL-Driven Intelligent SFC Deployment in MEC Workload for Dynamic IoT Networks. Sensors 2024, 25, 4257. [Google Scholar] [CrossRef] [PubMed]
- Lilhore, U.K.; Simaiya, S.; Sharma, Y.K.; Rai, A.K.; Padmaja, S.M.; Nabilalm, K.V.; Kumur, V.; Alroobaea, R.; Alsufyani, H. Cloud-edge hybrid deep learning framework for scalable IoT resource optimization. J. Cloud Comput. 2025, 14, 5. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, R.; Wang, T.; Yang, X. GA-DRL: Graph Neural Network-Augmented Deep Reinforcement Learning for DAG Task Scheduling. arXiv 2023, arXiv:2307.00777. [Google Scholar] [CrossRef]
- Faraj, H.; Ahmed, Z. Optimizing RPL with a Hybrid GA-RL Approach: Field-Validated Performance for IoT WSNs. IEEE Internet Things J. 2025, Submitted. [Google Scholar]
- Tijan, E.; Jović, M.; Jardas, M.; Gulić, M. Blockchain Technology for Record-Keeping in Maritime Main-Engine Maintenance. J. Mar. Sci. Eng. 2021, 9, 952. [Google Scholar] [CrossRef]
- Shuaib, K.; Saleous, H.; Shuaib, M.; Zaki, N. A systematic review of blockchain in healthcare: Frameworks, prototypes, and challenges. J. Netw. Comput. Appl. 2021, 186, 103080. [Google Scholar] [CrossRef]
- Miuccio, L.; Riolo, S.; Bennis, M.; Panno, D. On Learning Intrinsic Rewards for Faster Multi-Agent Reinforcement Learning based MAC Protocol Design in 6G Wireless Networks. In Proceedings of the ICC 2023—IEEE International Conference on Communications, Rome, Italy, 28 May–1 June 2023; pp. 466–471. [Google Scholar] [CrossRef]
- Restrepo, M.; Gendreau, M.; Lahrichi, N. A two-phase metaheuristic for the home health care routing and scheduling problem with flexible services. Comput. Ind. Eng. 2021, 159, 107386. [Google Scholar] [CrossRef]
- Nucci, F.; Papadia, G. Data of Case study ‘Hybrid Genetic Algorithm and Deep Reinforcement Learning Framework for IoT-Enabled Healthcare Equipment Maintenance Scheduling’. 2025. Available online: https://github.com/fnuni/2025elect (accessed on 16 October 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).