MSRDSN: A Novel Deep Learning Model for Fault Diagnosis of High-Voltage Disconnectors
Abstract
1. Introduction
- (1)
- A novel network architecture integrating residual learning and depthwise separable convolution has been proposed, effectively addressing the issues of accuracy degradation and feature redundancy in deep networks.
- (2)
- A combined loss function has been designed to simultaneously maximize inter-class distance and minimize intra-class distance, significantly enhancing feature discriminability.
- (3)
- Extensive experiments demonstrate that the proposed method maintains superior diagnostic accuracy even with imbalanced and limited data, while exhibiting strong generalization capability under different operating conditions.
2. Preliminaries
2.1. Residual Learning
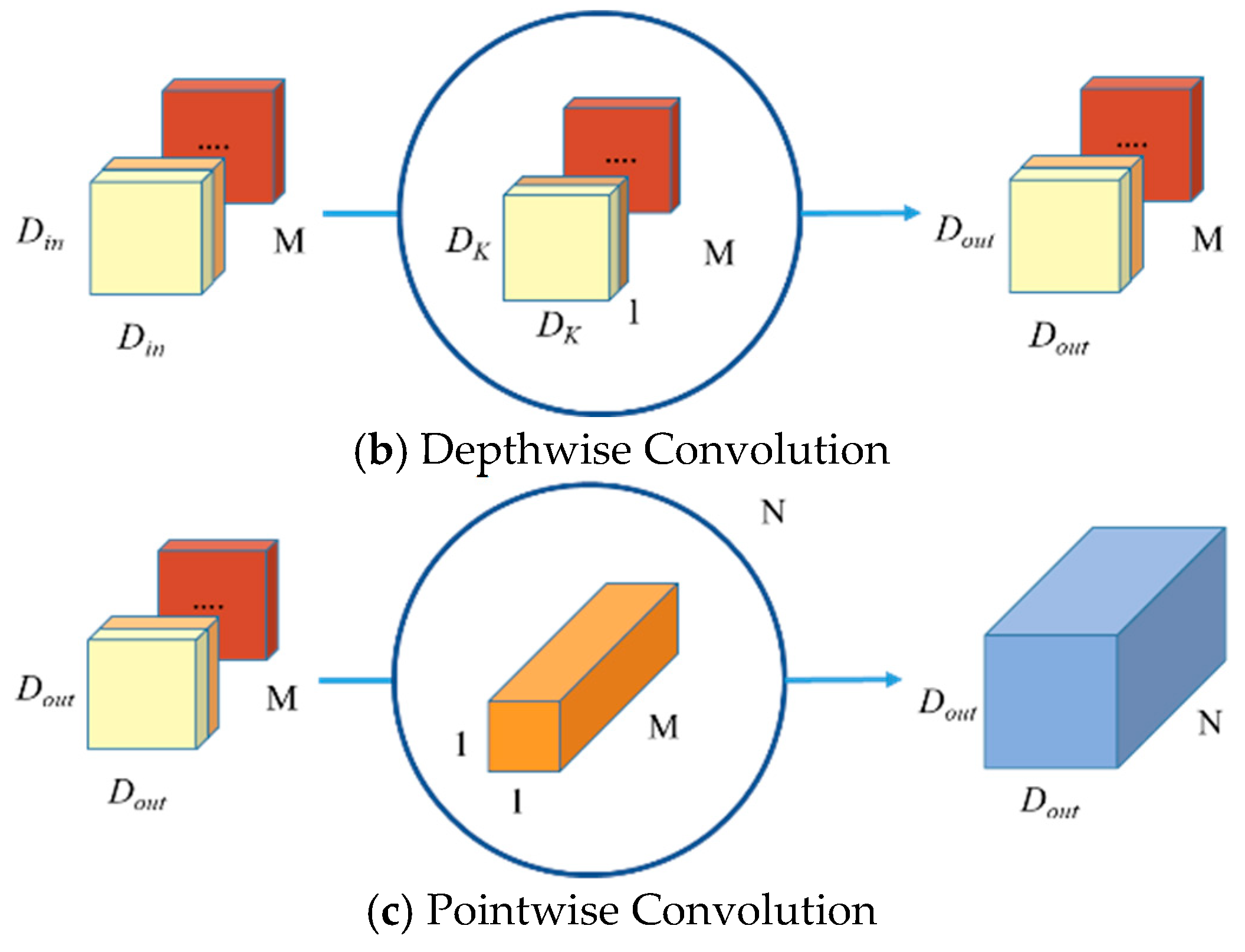
2.2. Depthwise Separable Convolution
2.3. Working Principle of High-Voltage Disconnectors
3. Methodology
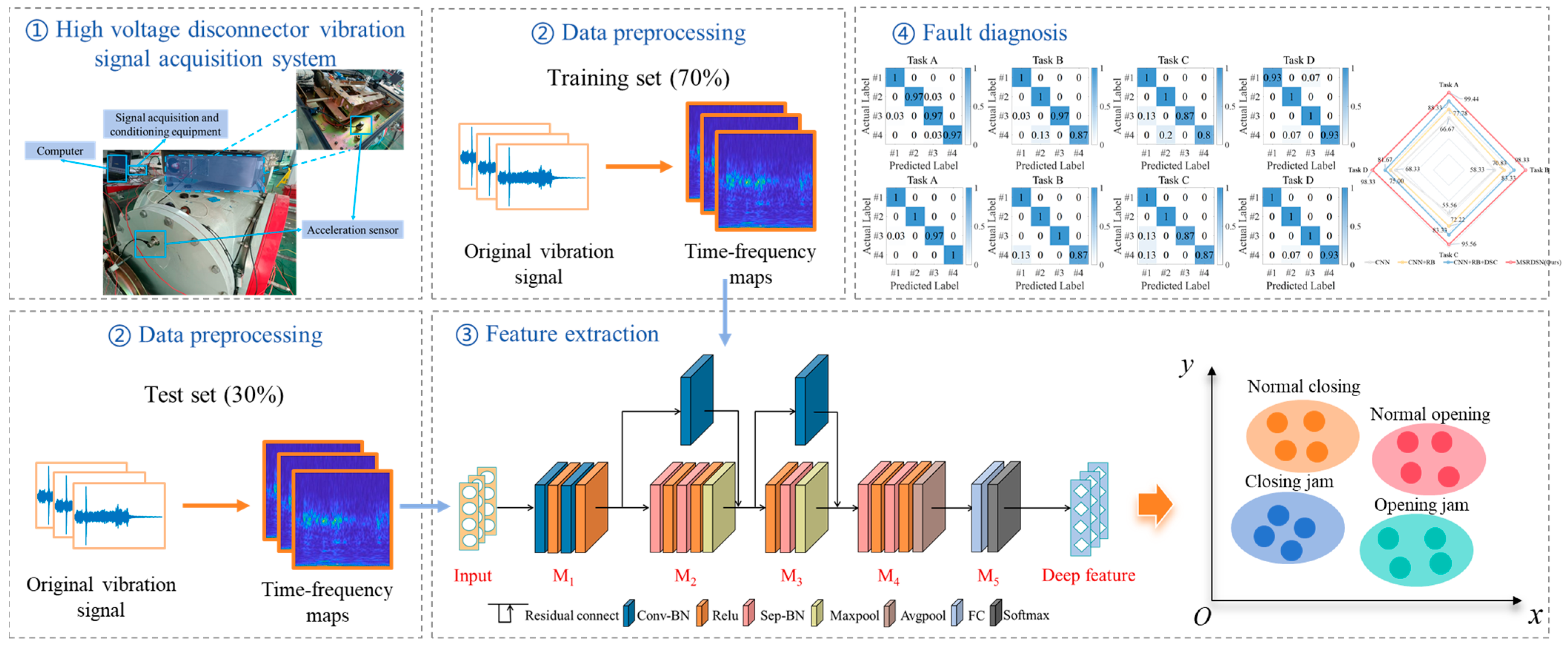
3.1. MSRDSN Fault Diagnosis Procedure
- (1)
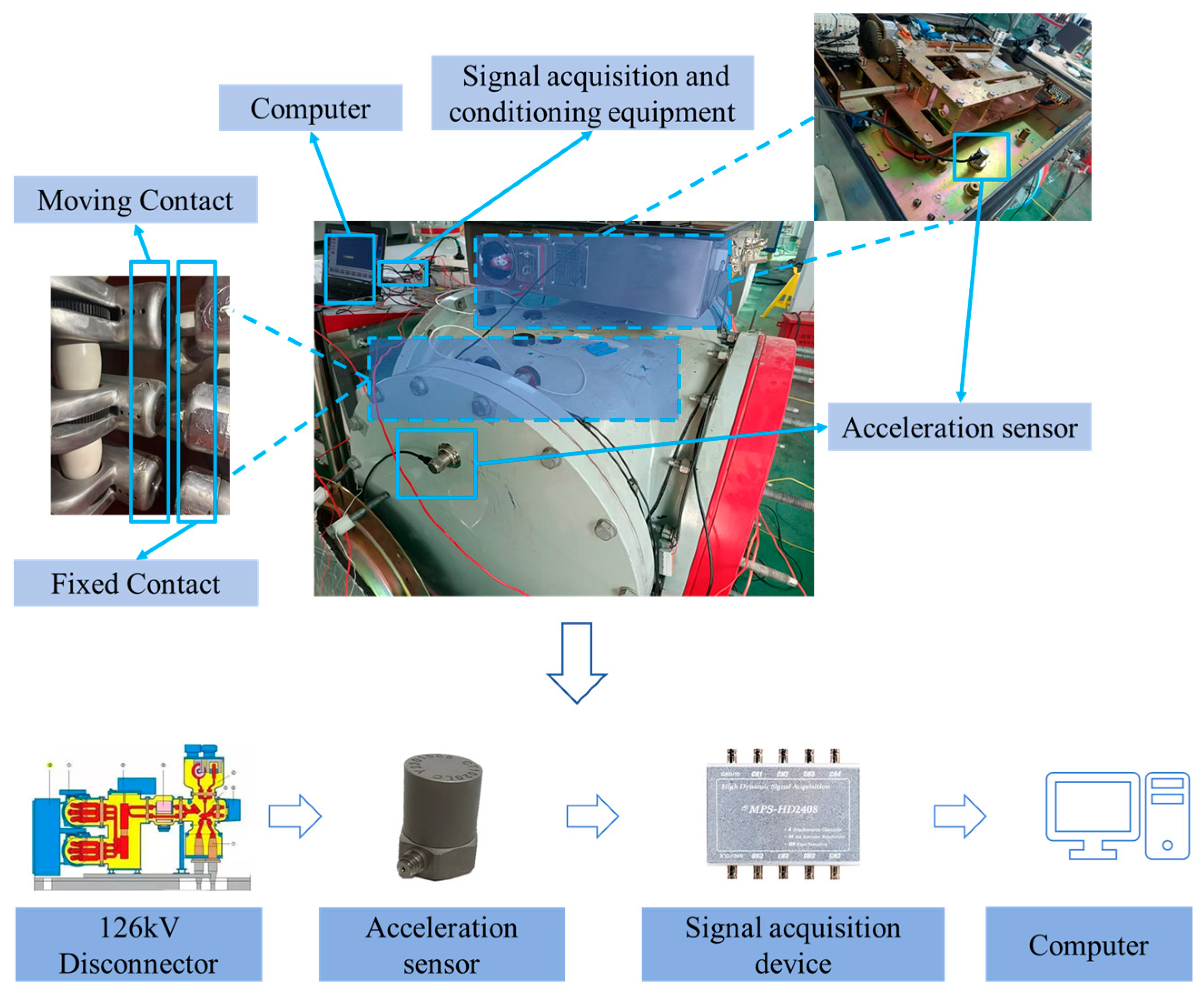
- Fault Signal Preprocessing Stage: First, a vibration signal acquisition system for high-voltage disconnectors is established to collect vibration signals under different fault types. Next, all signal samples undergo wavelet transform to generate a dataset of two-dimensional time-frequency diagrams. Finally, the dataset is divided into training and testing sets in a 7:3 ratio.
- (2)
- Feature Extraction Stage: The two-dimensional time-frequency diagrams of the training set are input into the RDSN, and the parameters of each network layer are adjusted. The trained RDSN is then saved. Subsequently, the test set’s time-frequency diagrams are fed into the network, and downsampling is applied for dimensionality reduction to extract fault features from both the training and test sets. The effectiveness of feature extraction is validated using t-SNE for visualization.
- (3)
- Fault Diagnosis Stage: First, the test set data is input into the model for fault diagnosis. The predicted results are compared with the true labels to compute the confusion matrix and diagnostic accuracy. Finally, the diagnostic results are compared with those from other diagnostic algorithms.
3.2. Wavelet Transform
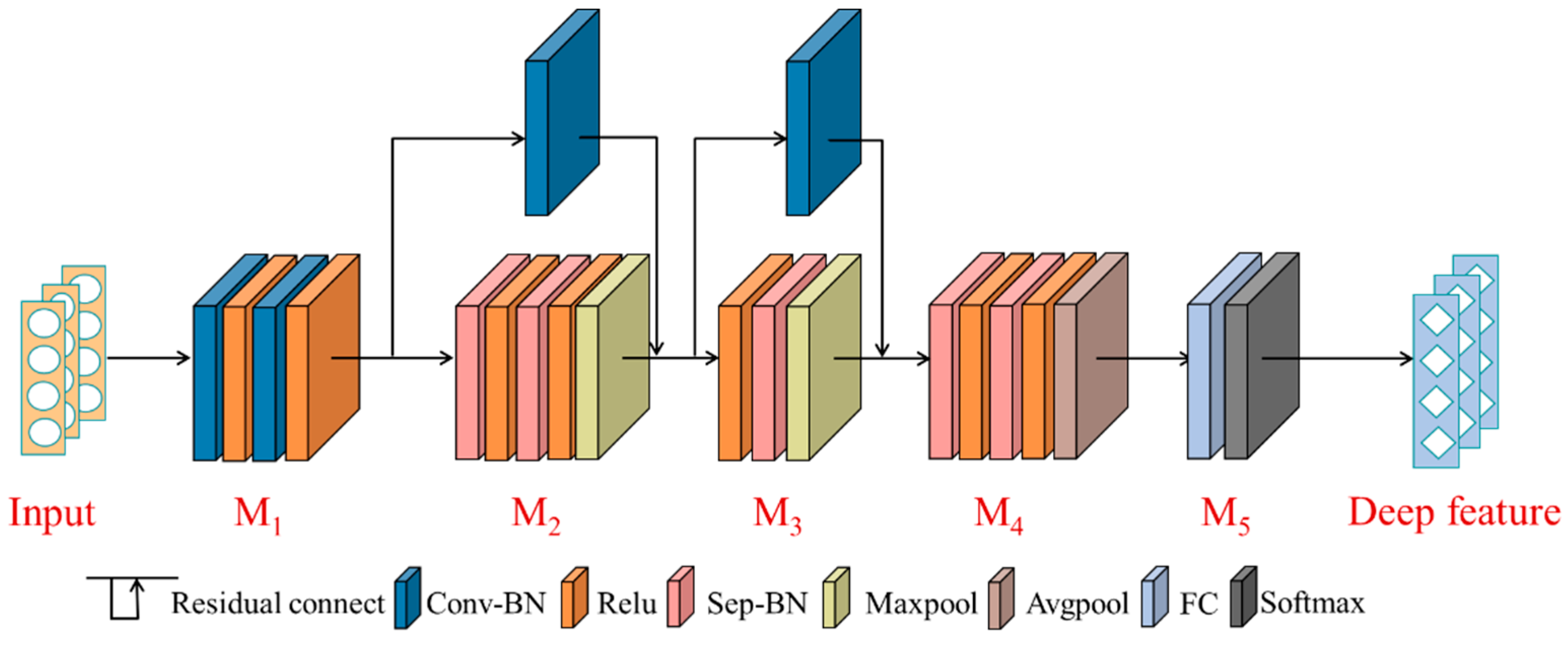
3.3. Feature Extraction
3.4. Fault Diagnosis
4. Experiments and Result Analysis
4.1. Experimental Data
4.2. Analysis of Results
4.2.1. Validity Analysis of RDSN
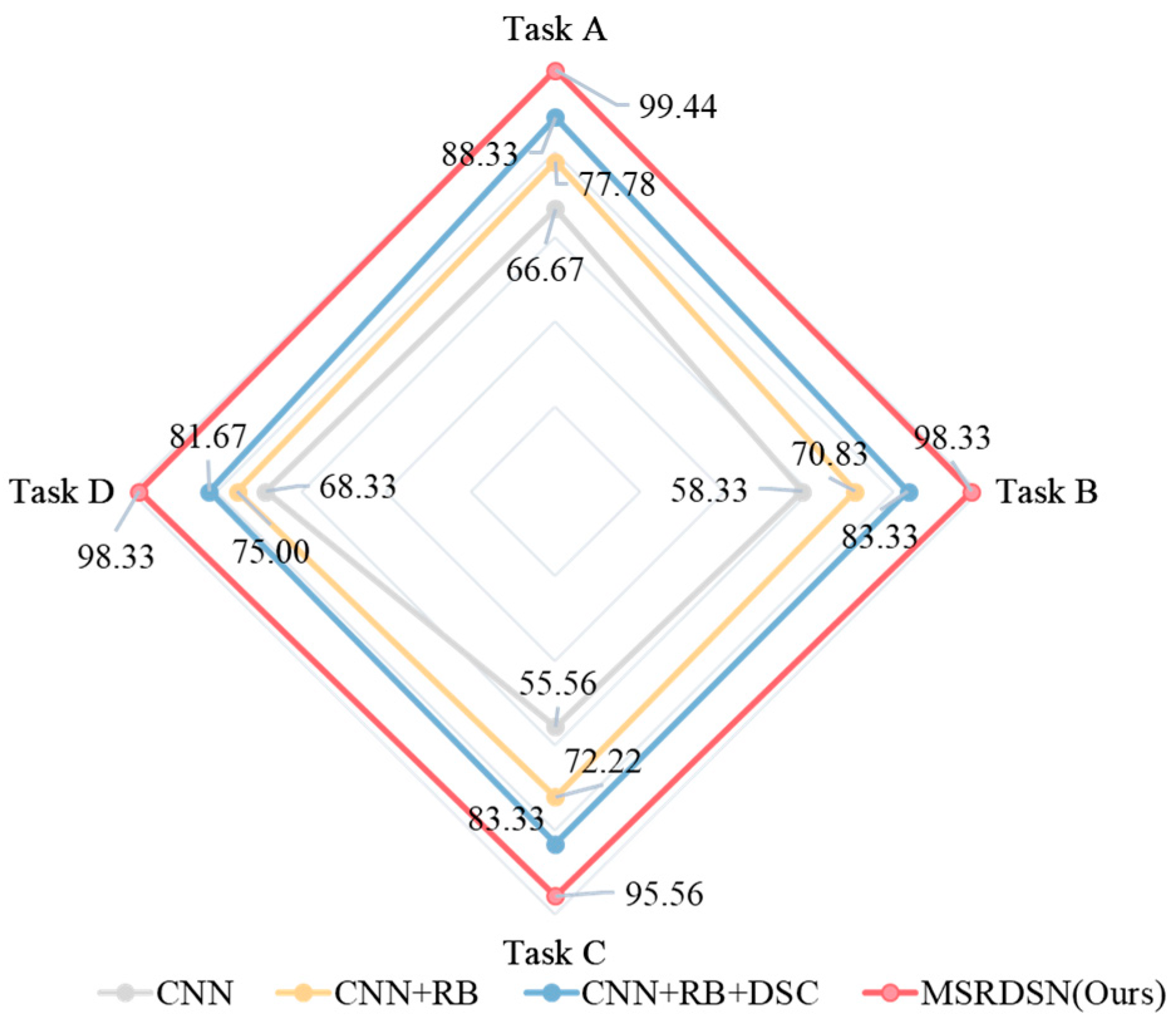
4.2.2. Results and Comparative Analysis
4.2.3. Cross Validation
4.2.4. Multi-Indicator Performance Evaluation
4.2.5. Ablation Experiments
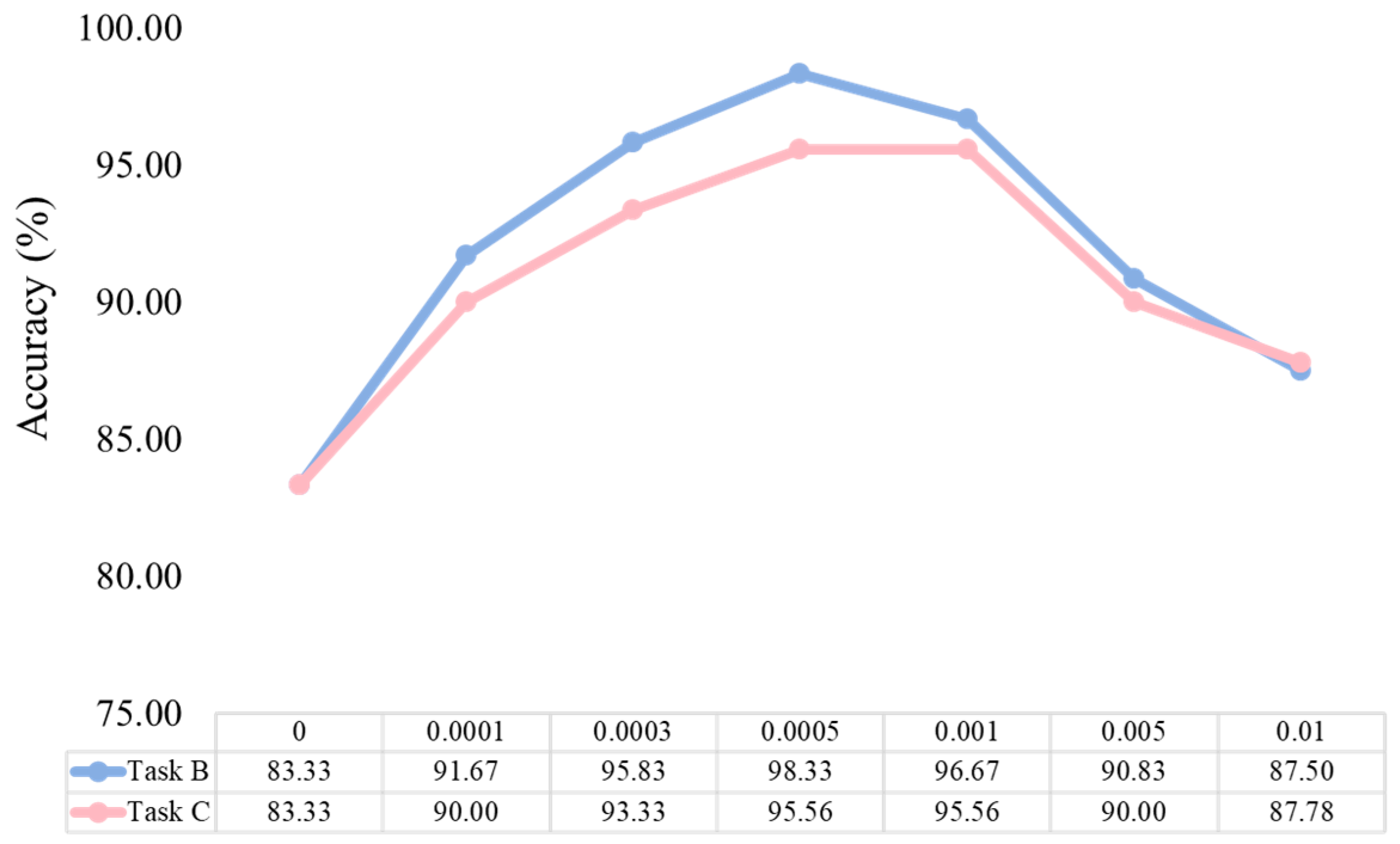
4.2.6. Parameter Analysis
4.2.7. Universal Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Hao, Y.; Peng, J.; Yang, L.; Gao, C.; Wang, G.; Zhou, F.; Yang, Y.; Cao, H.; Li, L. A three-factor accelerated aging test platform of thermal, mechanical compression, pressured sf 6, and a leakage test system for GIS O-RING seals. IEEE Trans. Instrum. Meas. 2021, 70, 7501511. [Google Scholar][Green Version]
- Han, X.; Li, J.; Zhang, L.; Pang, P.; Shen, S. A novel pd detection technique for use in GIS based on a combination of uhf and optical sensors. IEEE Trans. Instrum. Meas. 2018, 68, 2890–2897. [Google Scholar] [CrossRef]
- Xu, H.; Meng, C.; Huang, Q.; Luo, C.; Zhang, J.; Liu, Z. Time-frequency vibration characteristics analysis of disconnectors of GIS equipment with poor contact mechanical defect. In Proceedings of the 2021 IEEE 5th International Conference on Condition Assessment Techniques in Electrical Systems (CATCON), Kozhikode, India, 3–5 December 2021; IEEE: New York, NY, USA, 2021; pp. 215–219. [Google Scholar]
- Schichler, U.; Koltunowicz, W.; Endo, F.; Feser, K.; Giboulet, A.; Girodet, A.; Hama, H.; Hampton, B.; Kranz, H.G.; Lopez-Roldan, J. Risk assessment on defects in GIS based on pd diagnostics. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 2165–2172. [Google Scholar] [CrossRef]
- Carvalho, A.; Cormenzana, M.L.; Furuta, H.; Grieshaber, W.; Hyrczak, A.; Kopejtkova, D.; Krone, J.G.; Kudoke, M.; Makareinis, D.; Martins, J.F. Final Report of the 2004–2007 International Enquiry on Reliability of High Voltage Equipment, Part 1-Summary and General Matters; CigrÉ technical brochure no. 509; CIGRÉ: Paris, France, 2012. [Google Scholar]
- Carvalho, A.; Cormenzana, M.L.; Furuta, H.; Grieshaber, W.; Hyrczak, A.; Kopejtkova, D.; Krone, J.G.; Kudoke, M.; Makareinis, D.; Martins, J.F. Final Report of the 2004–2007 International Enquiry on Reliability of High Voltage Equipment, Part 3-Disconnectors and Earthing Switches; CIGRÉ Technical Brochure No. 511; CIGRÉ: Paris, France, 2012. [Google Scholar]
- Carvalho, A.; Cormenzana, M.L.; Furuta, H.; Grieshaber, W.; Hyrczak, A.; Kopejtkova, D.; Krone, J.G.; Kudoke, M.; Makareinis, D.; Martins, J.F. Final Report of the 2004–2007 International Enquiry on Reliability of High Voltage Equipment, Part 4-Instrument Transformers; CIGRÉ Technical Brochure No. 512; CIGRÉ: Paris, France, 2012. [Google Scholar]
- Zhong, Y.; Hao, J.; Liao, R.; Wang, X.; Jiang, X.; Wang, F. Mechanical defect identification for gas-insulated switchgear equipment based on time-frequency vibration signal analysis. High Volt. 2021, 6, 531–542. [Google Scholar] [CrossRef]
- Zhong, Y.; Hao, J.; Ding, Y.; Liao, R.; Xu, H.; Li, X. Novel GIS mechanical defect simulation and detection method based on large current excitation with variable frequency. IEEE Trans. Instrum. Meas. 2022, 71, 3519815. [Google Scholar] [CrossRef]
- Feng, J.; Sun, L.; Chen, W.; Su, Y.; Shu, Y.; Zhao, L. Vibration characteristics of GIS isolating switch under different operating conditions. High Volt. Eng. 2021, 47, 4314–4322. [Google Scholar]
- Li, K.; Chen, F.; Yang, H.; Yuan, H.; Yang, A.; Wang, X.; Rong, M. Intelligent diagnosis for mechanical faults of high voltage disconnector based on attitude sensor. Power Syst. Technol. 2023, 47, 3781–3790. [Google Scholar]
- Xu, S.; Yu, H.; Wang, H.; Chai, H.; Ma, M.; Chen, H.; Zheng, W. Simultaneous diagnosis of open-switch and current sensor faults of inverters in IM drives through reduced-order interval observer. IEEE Trans. Ind. Electron. 2025, 72, 6485–6496. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Li, K.; Fu, S. Research on feature extraction and condition identification method for transformer vibration signals based on GWO-VMD and SOM neural network. Power Syst. Big Data 2025, 28, 30–40. [Google Scholar]
- Zhang, F.; Wan, A. Fault diagnosis of planetary gearbox of wind turbine based on double attention mechanism and transfer learning. Power Syst. Big Data 2024, 27, 1–9. [Google Scholar]
- Qiu, Z.; Ruan, J.; Huang, D. Mechanical fault diagnosis of outdoor high-voltage disconnector. IEEJ Trans. Electr. Electron. Eng. 2016, 11, 556–563. [Google Scholar] [CrossRef]
- Liu, K. Mechanical fault diagnosis of high voltage disconnector based on intelligent live test technology. In Proceedings of the IEEE 3rd International Conference Electron Device Mechanical Engineering, Suzhou, China, 3 May 2020; IEEE: New York, NY, USA, 2020; pp. 138–140. [Google Scholar]
- Shi, K.; Lin, X.; Xu, J. Design of permanent magnet motor actuator used in 550 kV gas-insulated switchgear disconnector. Adv. Mech. Eng. 2015, 7, 1687814015575428. [Google Scholar] [CrossRef]
- Zhao, L.; Hong, G.; Wang, Z.; Chen, W.; Long, W.; Ren, J.; Wang, Z.; Huang, X. Research on fault vibration signal features of GIS disconnector based on EEMD and kurtosis criterion. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 677–686. [Google Scholar] [CrossRef]
- Zhou, T.; Ruan, J.; Yang, Z.; Liu, Y. Mechanical defect detection of porcelain column high-voltage disconnector based on operating torque. Int. J. Adv. Robot. Syst. 2020, 17, 1729881419900845. [Google Scholar] [CrossRef]
- Zhou, T.; Ruan, J.; Liu, Y.; Peng, S.; Wang, B. Defect diagnosis of disconnector based on wireless communication and support vector machine. IEEE Access 2020, 8, 30198–30209. [Google Scholar] [CrossRef]
- Yang, C.; Wu, X.; Gong, W.; Wang, Q.; Li, L. An intelligent identification algorithm for obtaining the state of power equipment in SIFT-based environments. Int. J. Perform. Eng. 2019, 15, 2382–2391. [Google Scholar] [CrossRef]
- Zhao, W.; Wen, F.; Wu, S.; Chu, Z.; Sheng, Z.; Ji, K. Fault diagnosis of GIS disconnector based on BP neural network. In Proceedings of the 2021 13th International Symposium on Linear Drives for Industry Applications, Wuhan, China, 1–3 July 2021; IEEE: New York, NY, USA, 2021; pp. 1–5. [Google Scholar]
- Teng, Y.; Tan, T.; Lei, C.; Yang, J.; Ma, Y.; Zhao, K.; Jia, Y.; Liu, Y. A novel method to recognize the state of high-voltage isolating switch. IEEE Trans. Power Deliv. 2019, 34, 1350–1356. [Google Scholar] [CrossRef]
- Gong, Z.; Cao, Z.; Zhou, S.; Yang, F.; Shuai, C.; Ouyang, X.; Luo, Z. Thermal fault detection of high-voltage isolating switches based on hybrid data and BERT. Arab. J. Sci. Eng. 2024, 49, 6429–6443. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, K.; Lin, S. Fault diagnosis method of disconnector based on CNN and D-S evidence theory. IEEE Trans. Ind. Appl. 2023, 59, 5691–5704. [Google Scholar] [CrossRef]
- Chi, Y.; Jiao, Z.; Ji, H.; Wang, Q.; Ge, H.; Chi, F. Comparative study on substation isolating switch state recognition algorithms based on image similarity and deep learning. Power Syst. Big Data 2023, 26, 1–10. [Google Scholar]
- Zhang, K.; Zhang, Y.; Wu, J.; Li, Z. Quick identification of open/closed state of GIS switch based on vibration detection and deep learning. Electronics 2023, 12, 3204. [Google Scholar] [CrossRef]
- Huang, S.; Shang, B.; Song, Y.; Zhang, N.; Wang, S.; Ning, S. Research on Real-Time Disconnector State Evaluation Method Based on Multi-Source Images. IEEE Trans. Instrum. Meas. 2021, 71, 3505415. [Google Scholar] [CrossRef]
- Xie, Q.; Tang, H.; Liu, B.; Li, H.; Wang, Z.; Dang, J. Disconnector fault diagnosis based on multi-granularity contrast learning. Processes 2023, 11, 2981. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, C.; Wang, R.; Li, J.; Xiahou, D.; Liu, Q.; Cao, S.; Zhou, S. Mechanical fault diagnosis of a disconnector operating mechanism based on vibration and the motor current. Energies 2022, 15, 5194. [Google Scholar] [CrossRef]
- Sui, G.; Yan, J.; Wu, Y.; Xu, Z.; Qi, M.; Zhang, Z. Mechanical fault diagnosis of high-voltage circuit breakers with dynamic multi-attention graph convolutional networks based on adaptive graph construction. Appl. Sci. 2024, 14, 4036. [Google Scholar] [CrossRef]



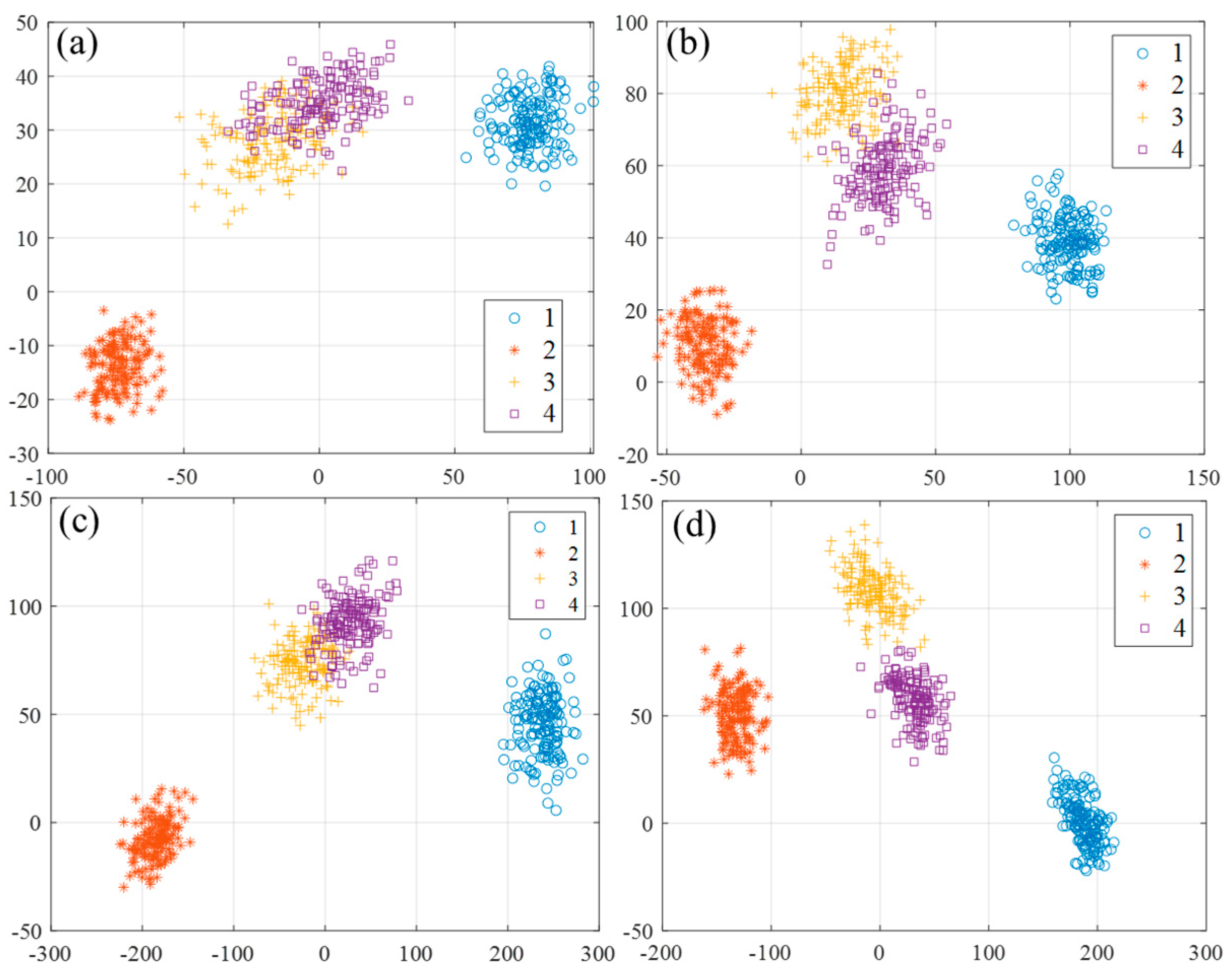
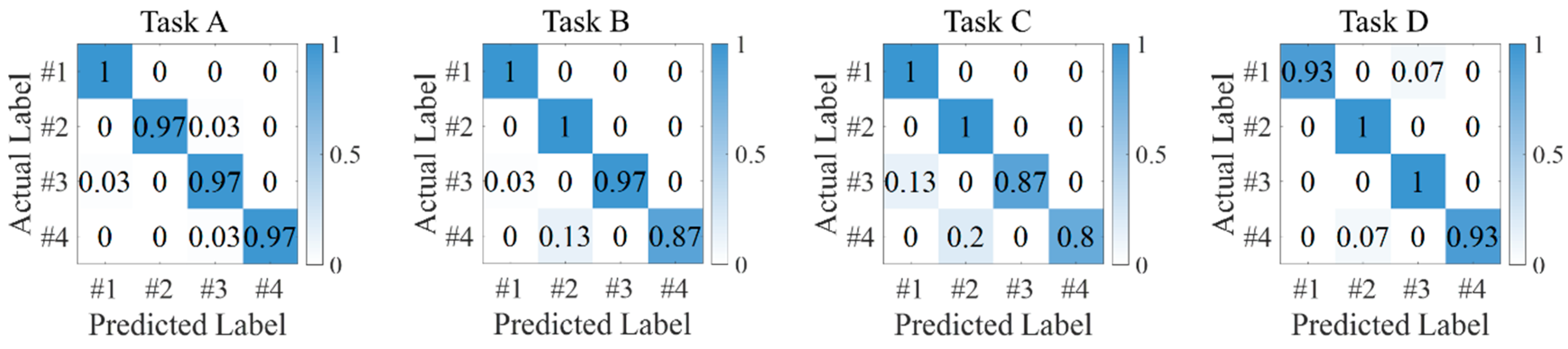
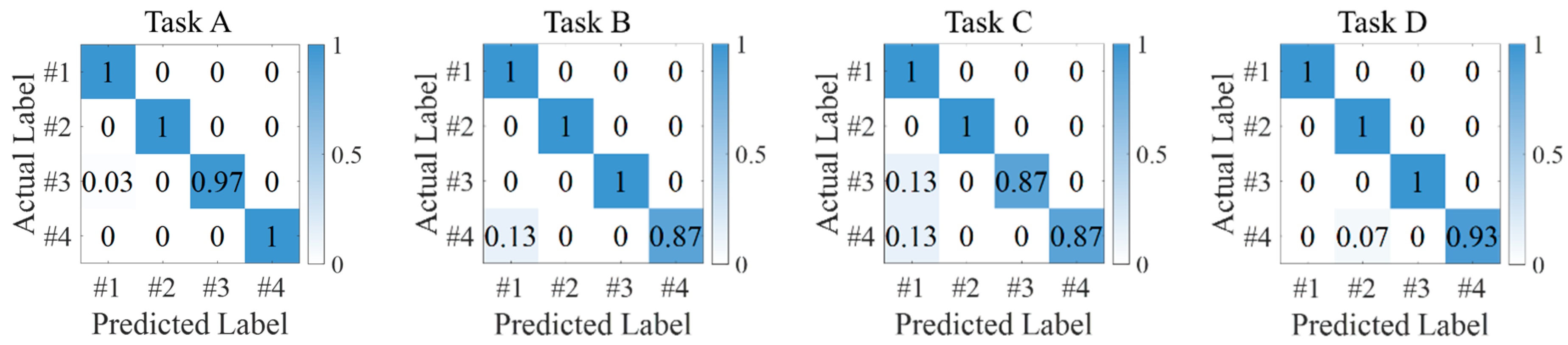
| Label (No.) | Data Type |
|---|---|
| 1 | Normal closing |
| 2 | Normal opening |
| 3 | Closing jam |
| 4 | Opening jam |
| Task (No.) | Samples | |||
|---|---|---|---|---|
| Normal Closing | Normal Opening | Closing Jam | Opening Jam | |
| A | 150 | 150 | 150 | 150 |
| B | 150 | 100 | 100 | 50 |
| C | 100 | 100 | 50 | 50 |
| D | 50 | 50 | 50 | 50 |
| Module | Layer | Parameter |
|---|---|---|
| Module 1 | (Conv-BN + Relu)-1 (Conv-BN + Relu)-2 | Kernel size = 3 × 3 stride = 2 Kernel size = 3 × 3 stride = 1 |
| Residual connection | Conv-BN | Kernel size = 1 × 1 stride = 2 |
| Module 2 | (Sep-BN + Relu) × 2 Maxpool | Kernel size = 3 × 3 stride = 1 Kernel size = 3 × 3 stride = 2 |
| Residual connection | Conv-BN | Kernel size = 1 × 1 stride = 2 |
| Module 3 | Relu + Sep-BN Maxpool | Kernel size = 3 × 3 stride = 1 Pool size = 3 × 3 stride = 2 |
| Module 4 | (Sep-BN + Relu) × 2 Avgpool | Kernel size = 3 × 3 stride = 1 Pool size = 8 × 8 stride = 1 |
| Module 5 | FC + Softmax | Keep_prob = 0.5 |
| Different Methods | Implementation Process |
|---|---|
| MG-CL [29] | First, the data augmentation module enhances the characteristics of the current signals. Then, the coarse-grained contrastive module performs preliminary fault diagnosis. Finally, the fine-grained contrastive module carries out detailed fault diagnosis. |
| Adaboost-SVM [30] | The process first conducts feature extraction on stator motor current signals and vibration signals using the envelope method and VMD. Then, it performs fault diagnosis through an Adaboost-optimized SVM. |
| CNN (D-S) [25] | The process first obtains two-dimensional features through wavelet packet transform and time-domain analysis. Then employs a CNN for fault diagnosis and finally enhances performance further with the support of D-S evidence theory. |
| AKNN-DMGCN [31] | First, a novel adaptive KNN graph construction method is proposed to build informative graphs. Subsequently, a Dynamic Multi-attention Graph Convolutional Network is applied for mechanical fault diagnosis. |
| Methods | Task A | Task B | Task C | Task D |
|---|---|---|---|---|
| MG-CL | 96.67 | 90.83 | 87.78 | 86.67 |
| Adaboost-SVM | 96.11 | 92.50 | 88.89 | 85.00 |
| AKNN-DMGCN | 95.56 | 94.17 | 91.11 | 88.33 |
| CNN (D-S) | 98.33 | 97.50 | 94.44 | 96.67 |
| MSRDSN(Ours) | 99.44 (↑1.11) | 98.33 (↑0.83) | 95.56 (↑1.12) | 98.33 (↑1.66) |
| K-Fold | Accuracy (%) |
|---|---|
| 1 | 96.67 |
| 2 | 93.33 |
| 3 | 100.00 |
| 4 | 96.67 |
| 5 | 96.67 |
| Average | 96.67 |
| Task | Recall (%) | F1 (%) |
|---|---|---|
| A | 96.67 | 98.34 |
| B | 91.67 | 94.88 |
| C | 94.44 | 95.00 |
| D | 96.67 | 97.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Chen, P.; Li, X.; Deng, Q.; Liao, Y.; Ruan, J. MSRDSN: A Novel Deep Learning Model for Fault Diagnosis of High-Voltage Disconnectors. Electronics 2025, 14, 4151. https://doi.org/10.3390/electronics14214151
Zhu S, Chen P, Li X, Deng Q, Liao Y, Ruan J. MSRDSN: A Novel Deep Learning Model for Fault Diagnosis of High-Voltage Disconnectors. Electronics. 2025; 14(21):4151. https://doi.org/10.3390/electronics14214151
Chicago/Turabian StyleZhu, Shijian, Peilong Chen, Xin Li, Qichen Deng, Yuxiang Liao, and Jiangjun Ruan. 2025. "MSRDSN: A Novel Deep Learning Model for Fault Diagnosis of High-Voltage Disconnectors" Electronics 14, no. 21: 4151. https://doi.org/10.3390/electronics14214151
APA StyleZhu, S., Chen, P., Li, X., Deng, Q., Liao, Y., & Ruan, J. (2025). MSRDSN: A Novel Deep Learning Model for Fault Diagnosis of High-Voltage Disconnectors. Electronics, 14(21), 4151. https://doi.org/10.3390/electronics14214151






