Physics-Informed Co-Optimization of Fuel-CellFlying Vehicle Propulsion and Control Systems with Onboard Catalysis
Abstract
1. Introduction
2. Flying Vehicle System Modeling
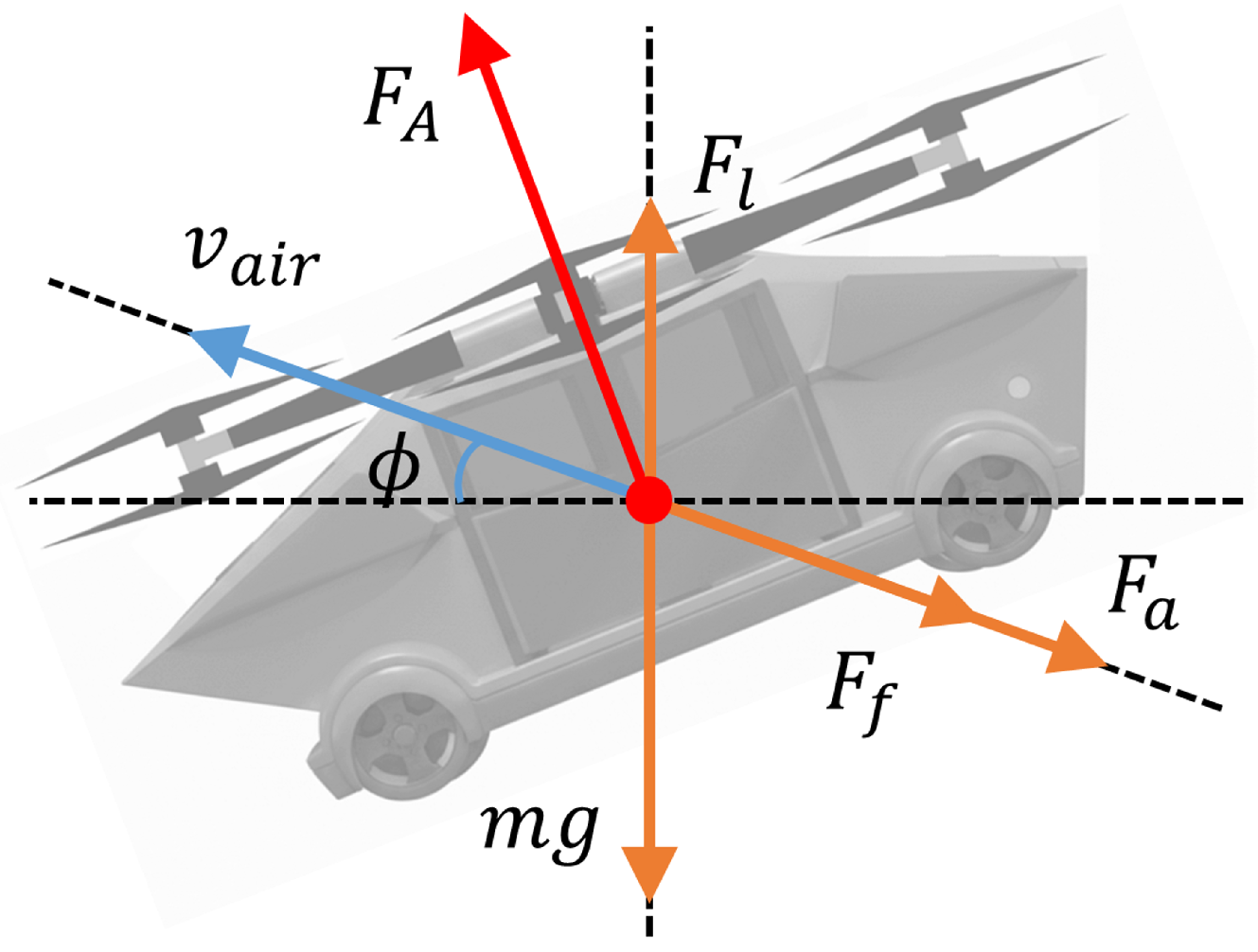
2.1. Vehicle Power Demand Model
2.2. Ammonia–Hydrogen Propulsion System
2.2.1. Ammonia Decomposition Unit
Catalyst Selection and Performance Characterization
| No. | Catalyst | Temp | GHSV | x | |
|---|---|---|---|---|---|
| (A-E/F/G-X/Y) | (°C) | (mL/g/h) | (%) | ( w/w %) | |
| A | 400–500 | 15,000 | 84–100 | 5 | |
| B | 400–500 | 36,000 | 40–84 | 7.8 | |
| C | 400–500 | 30,000 | 10–65 | 100 | |
| D | 400–500 | 7200 | 17–100 | 100 | |
| E | 400–500 | 30,000 | 18–72.4 | 60 | |
| F | 400–500 | 13,800 (Ar:NH3 = 1.3:1) | 14–95 | 10 | |
| G | 400–500 | 13,800 (Ar:NH3 = 1.3:1) | 77–100 | 2 | |
| H | 400–500 | 6000 | 9–73.8 | 34.7 | |
| I | 400–500 | 18,000 | 32–65 | 4.8 | |
| J | 400–500 | 15,000 | 49.7–99.2 | 2.74 |
Catalyst Cost Model
| No. | Catalysts | Cost | Cost | |||
|---|---|---|---|---|---|---|
| (A-E/F/G-X/Y) | ( w/w %) | (CNY/g) | ( w/w %) | (CNY/g) | (CNY/g) | |
| A | 1.38 ( = 3.62) | 9.07 | 95 | 1134.83 | 66.63 | |
| B | 7.8 | 55.54 | 92.2 | 33.92 | 53.85 | |
| C | 100 | - | 0 | 13.36 | 13.36 | |
| D | 100 | - | 0 | 5.44 | 5.44 | |
| E | 60 | 45.13 | 40 | 2.39 | 19.49 | |
| F | 10 | 2.39 | 90 | 45.13 | 6.66 | |
| G | 2 | 2.39 | 98 | 1134.83 | 25.04 | |
| H | 34.7 | 10.55 | 65.3 | 0.57 | 7.09 | |
| I | 4.8 | 5.78 | 95.2 | 1134.83 | 59.97 | |
| J | 2.8 | 2.39 | 97.2 | 180.6 | 7.38 |
Quasi-Steady-State Thermal Model
2.2.2. Proton-Exchange Membrane Fuel-Cell System
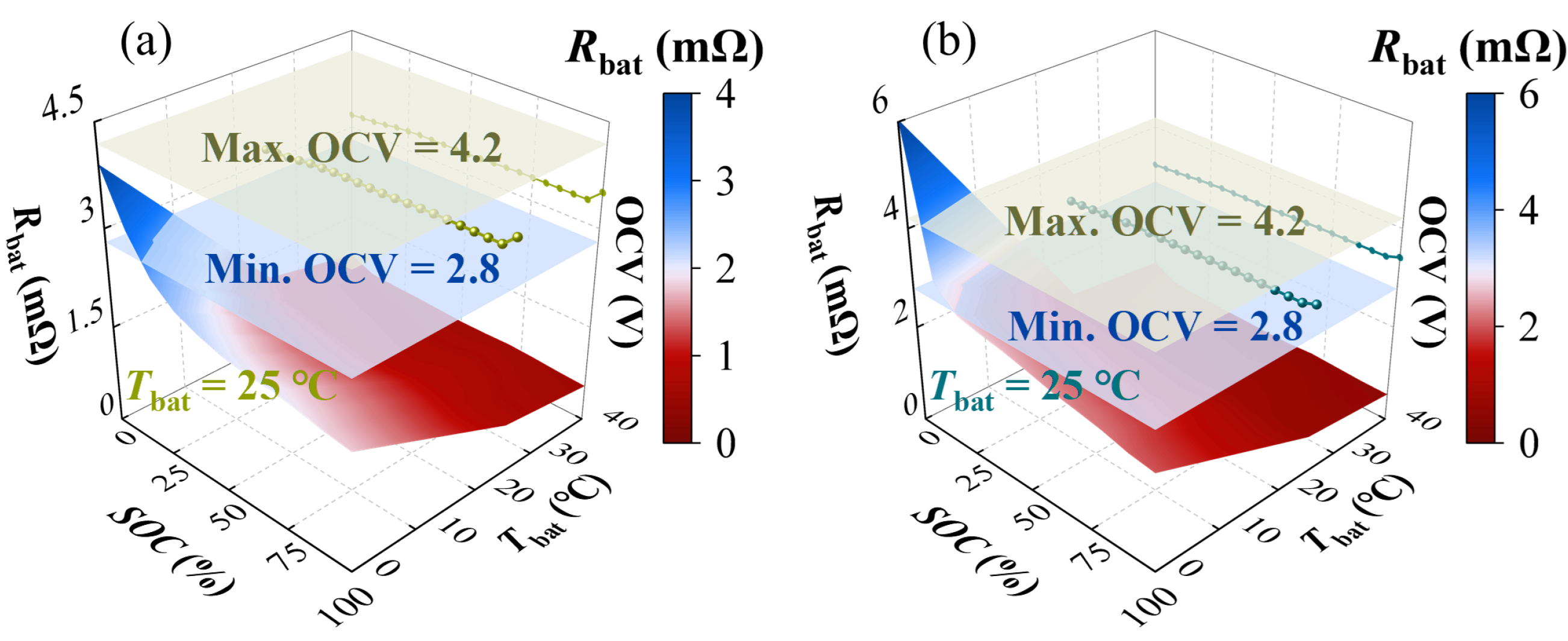
2.2.3. Battery Model and Energy Management System
2.3. Power-Source State-of-Health Model
2.3.1. Fuel-Cell SOH Model
2.3.2. Battery SOH Model
3. The PI-GEMO Optimization Framework
3.1. Problem Formulation
- Physical inconsistency: Black-box surrogates have no intrinsic knowledge of the system’s governing laws. In data-sparse regions, their predictions can violate fundamental principles like energy conservation, leading the optimizer towards physically unrealizable local optimality.
- Inefficient search: Gradient-free evolutionary algorithms operate via stochastic operators (crossover and mutation). While robust for global exploration, this “blind” search is inefficient for the fine-tuning of promising solutions. They lack a sense of direction and do not exploit the local topology of the fitness landscape to accelerate convergence.
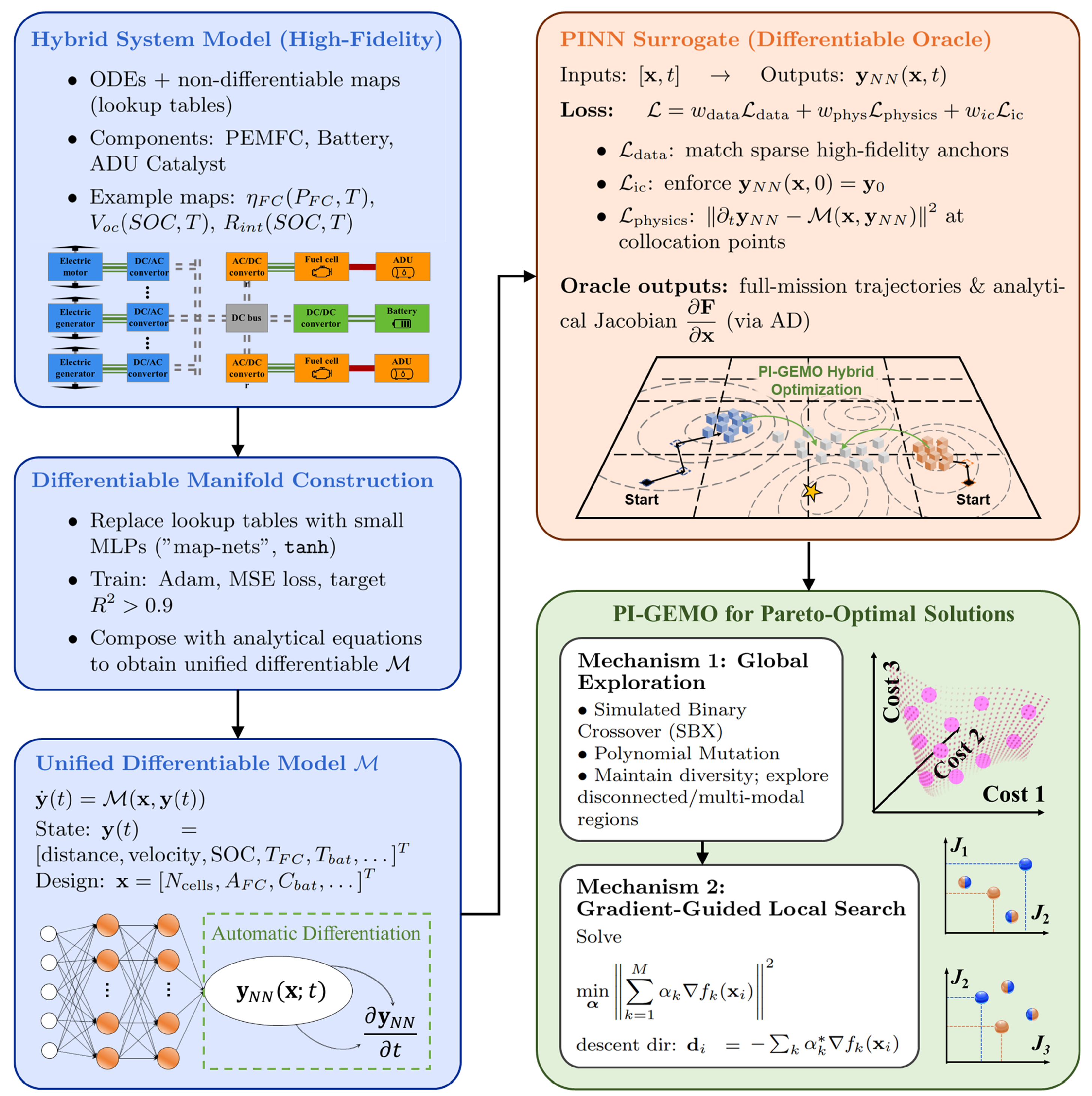
3.2. The Physics-Informed Differentiable Surrogate Model
3.2.1. Construction of the Differentiable System Manifold
3.2.2. Physics-Informed Surrogate Learning
3.3. The PI-GEMO Hybrid Optimization Algorithm
3.3.1. Mechanism 1: Gradient-Free Global Exploration
- Simulated binary crossover (SBX): This operator takes two parent solutions ( and ) and creates two offspring ( and ) by simulating the behavior of a single-point crossover on binary strings. The process for each variable (j) is governed by a spread factor derived from a random number () and a distribution index (). SBX is adept at combining features from good solutions to generate potentially superior new ones within the hyper-rectangle defined by the parents. The offspring are generated as follows:
- Polynomial mutation: This operator introduces small, localized perturbations to a solution vector (), mimicking the effect of random mutation in nature. For each variable (), a perturbation () is calculated based on a random number and a distribution index (). The mutated variable () is given as follows, where and are the upper and lower bounds for the variable. This operator is crucial for the fine-tuning of solutions and the exploration of the immediate neighborhood of existing points on the Pareto front.
3.3.2. Mechanism 2: Gradient-Guided Local Search
| Algorithm 1 The PI-GEMO Algorithm. |
|
4. Results and Discussions
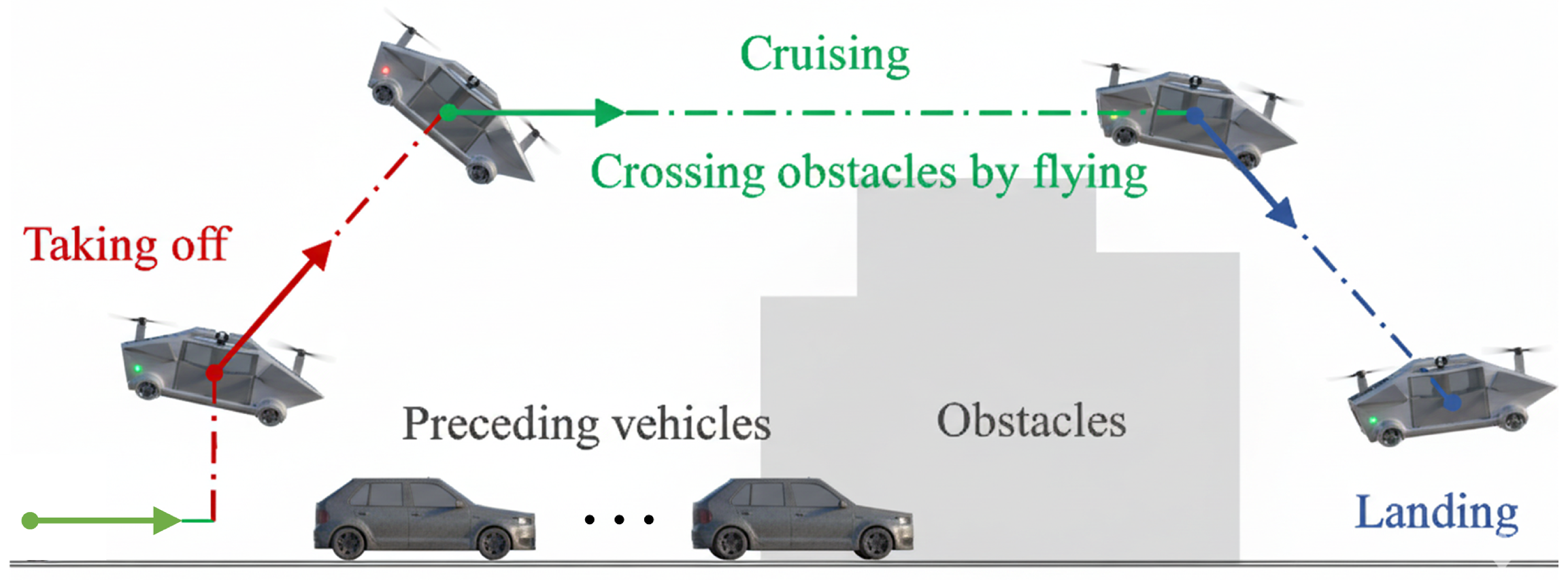
4.1. Case Study and Experimental Setup
| Components | Cost Price (USD) |
|---|---|
| Body and chassis | 85,000 |
| Fuel cell and control system | |
| Motor and control unit | |
| Battery and control unit |
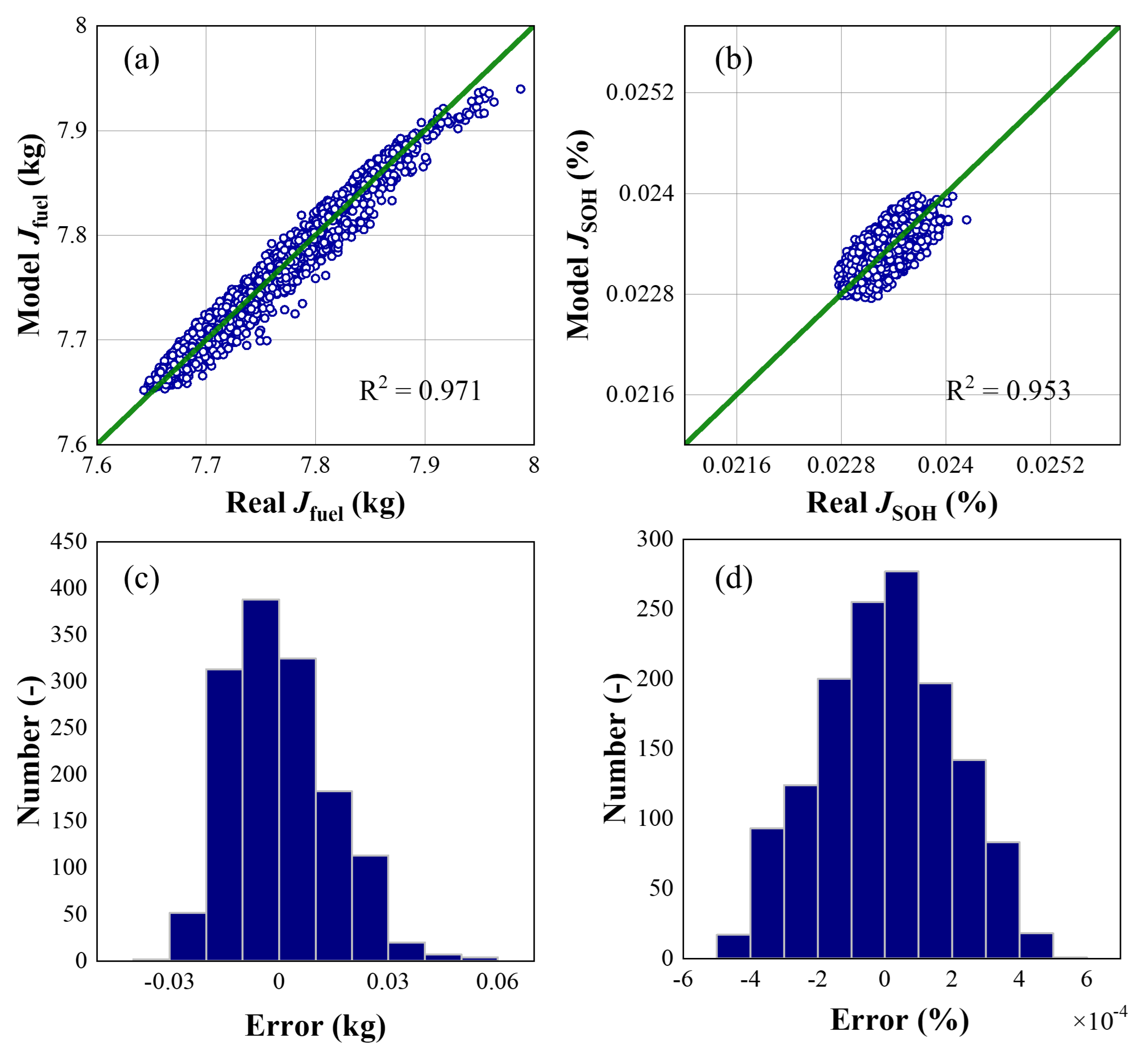
4.2. Validation of the Physics-Informed Surrogate Model and Gradient-Enhanced Pareto Optimization
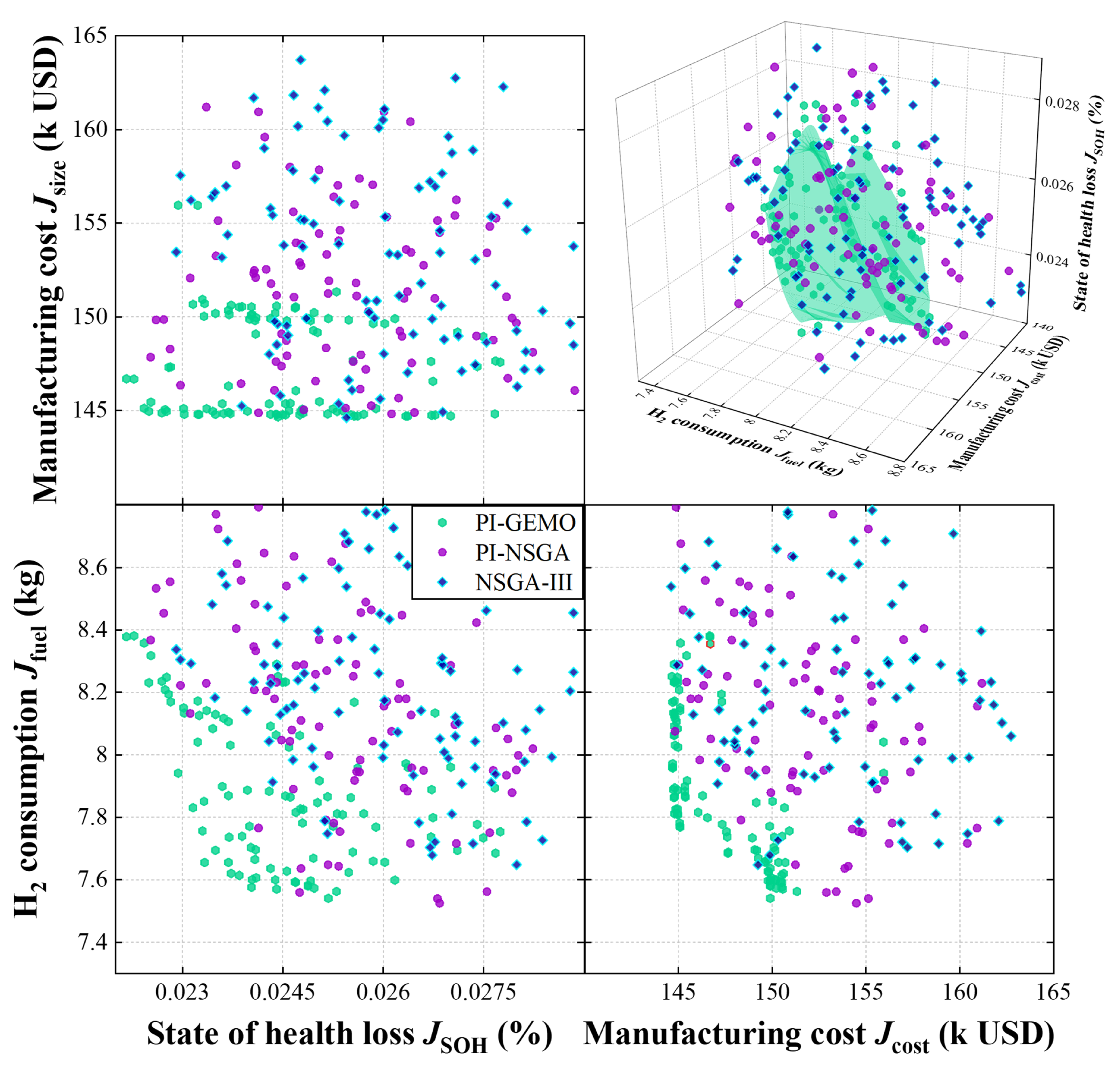
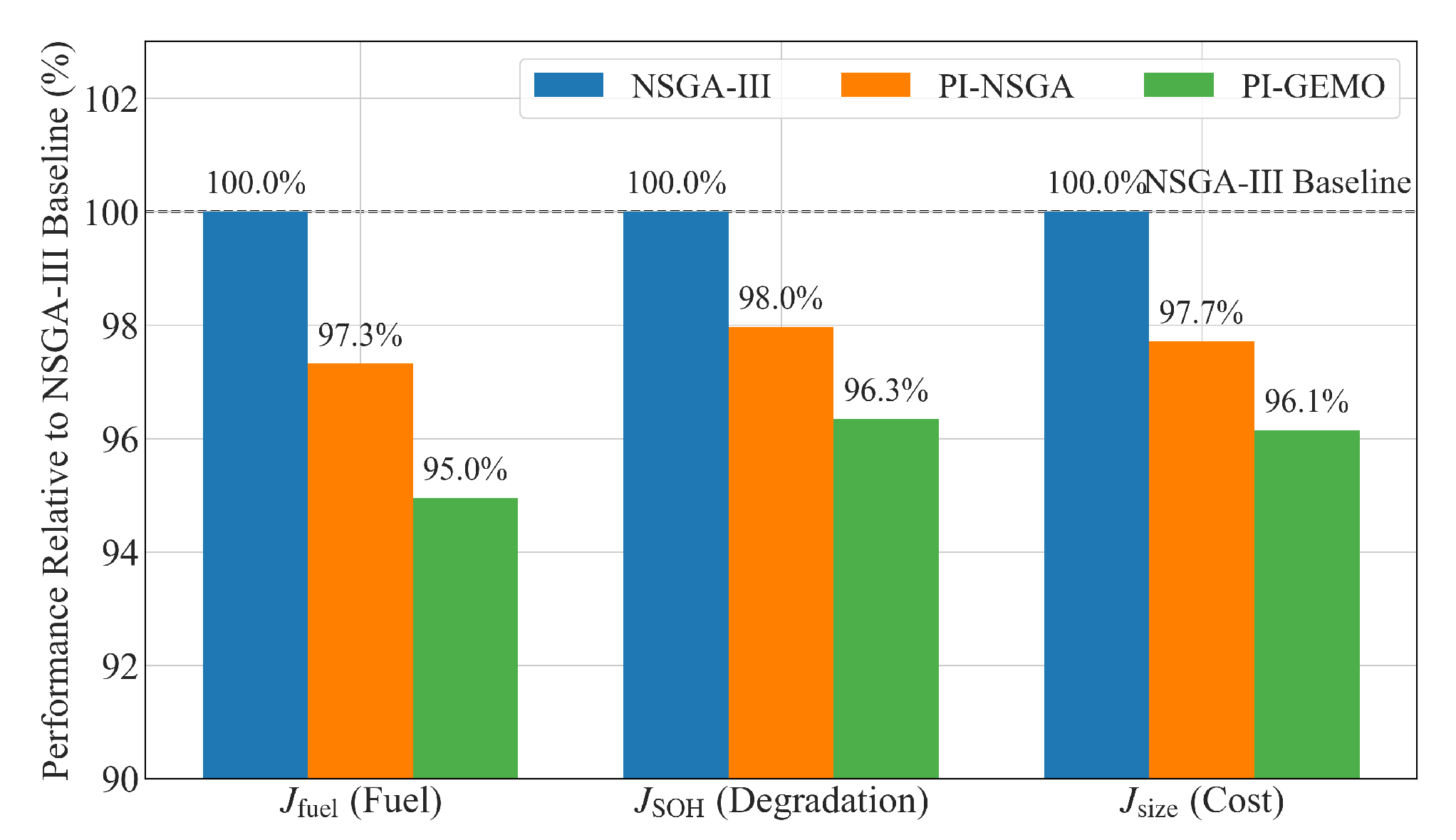
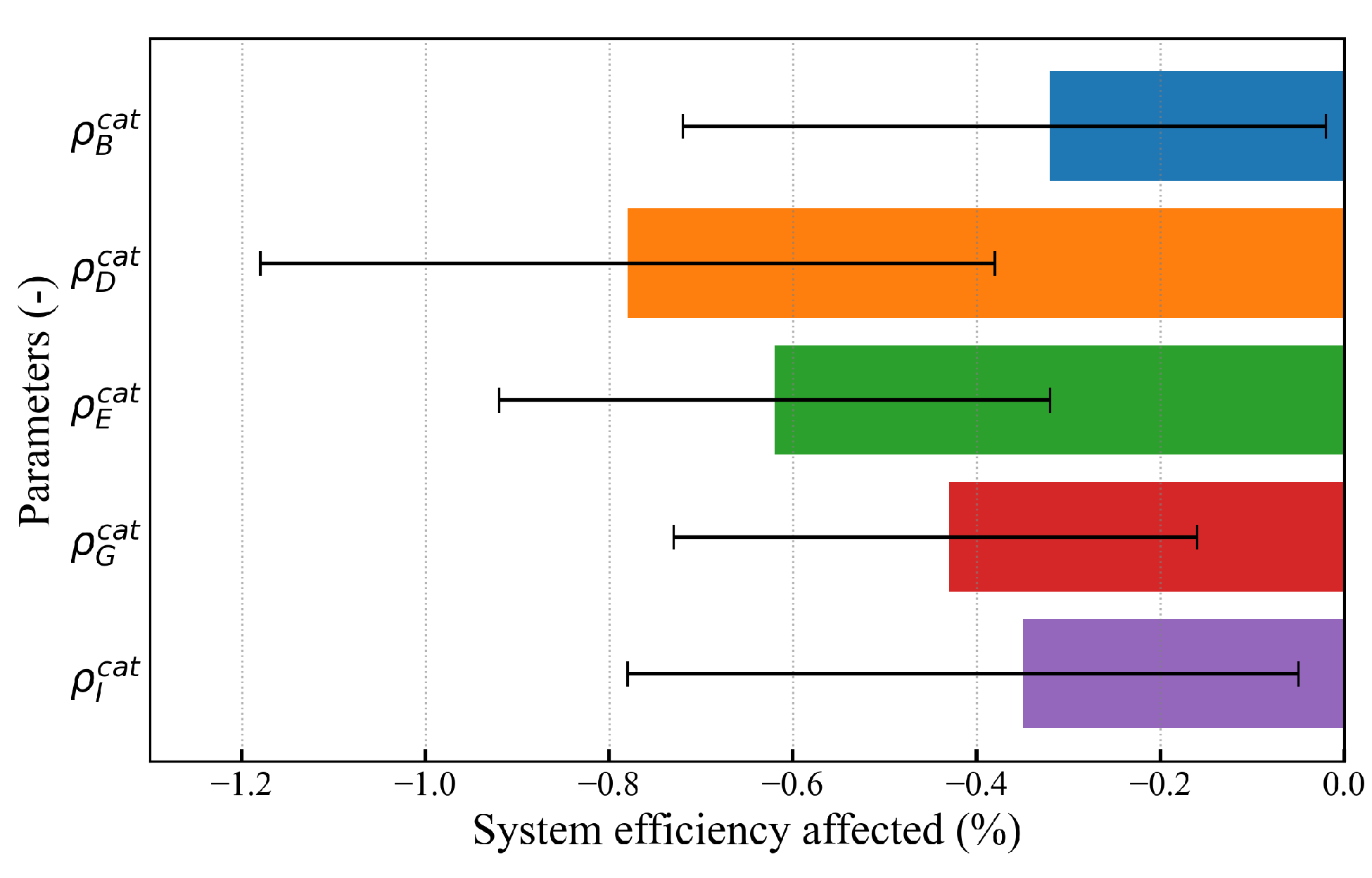
4.3. Comparisons of Optimization Results and Sensitivity Analysis
5. Conclusions
- A high-fidelity, multi-physics dynamic model of an ammonia-powered fuel-cell flying vehicle was developed, holistically capturing the critical couplings between the physical, thermal, electrical, and aerodynamic domains. This model formed the basis for the training of a differentiable PINN surrogate, which not only accelerates fitness evaluations but, by incorporating the system’s governing equations into its loss function, critically ensures the physical plausibility and accuracy of the optimization results.
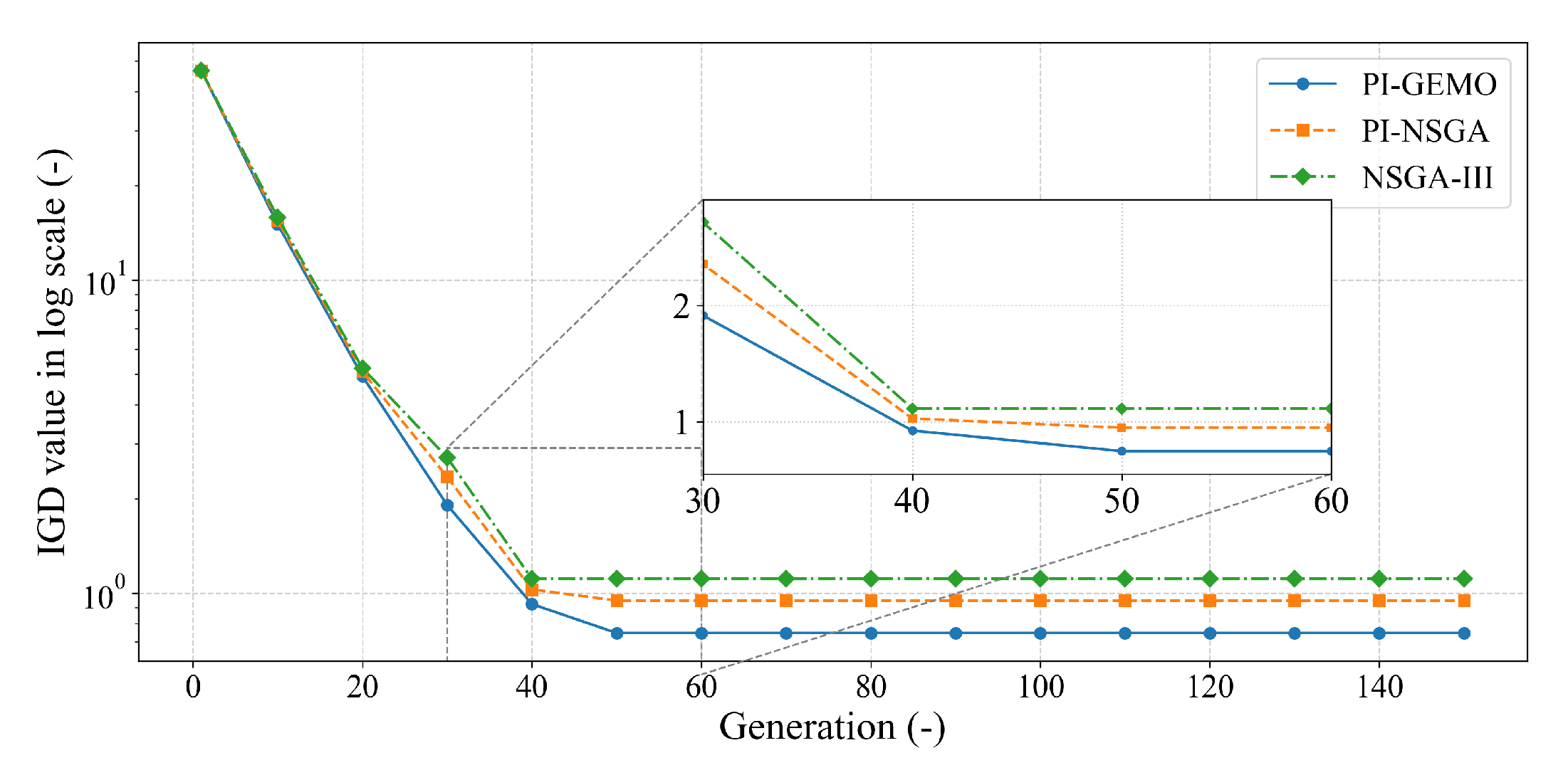
- The proposed PI-GEMO framework introduces a new class of hybrid intelligent optimization. It combines traditional, gradient-free genetic operators for robust global exploration with a novel gradient-guided local search mechanism. This mechanism leverages analytical gradients extracted from the trained PINN via automatic differentiation to efficiently propel promising solutions towards the true Pareto-optimal front. The superiority of this hybrid approach was demonstrated through a significantly faster convergence rate and a lower final IGD value compared to the benchmark NSGA-III algorithm.
- A comprehensive case study demonstrated the practical efficacy of the PI-GEMO framework. The co-optimization of ADU catalyst composition, powertrain component sizing, and energy management control parameters yielded a set of Pareto-optimal solutions that substantially dominated those found by conventional methods. Specifically, the PI-GEMO-derived ‘Trade-off’ design achieved a simultaneous reductions in hydrogen consumption of 5.1%, power source degradation SOH of 3.7%, and total system cost of 3.9% when compared to the solution from a standard NSGA-III optimization, providing critical insights into the synergistic design of next-generation aerial propulsion systems.
- While this study focused on a hexacopter architecture, the proposed PI-GEMO methodology is highly generalizable. The framework’s core—the synergistic integration of a physics-informed differentiable surrogate with a hybrid gradient-enhanced algorithm—is fundamentally model-agnostic. It can be readily adapted to other complex engineering systems, such as eVTOLs with different rotor counts, fixed-wing hybrid aircraft, or even terrestrial vehicles, by simply replacing the underlying set of governing equations within the PINN’s physics loss function. This scalability makes PI-GEMO a powerful and versatile tool for a wide range of multi-domain co-design problems. Future work will also focus on incorporating higher-fidelity transient models for both the ADU thermal dynamics and battery electrochemistry to further refine the design of the control strategy.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lan, R.; Irvine, J.T.S.; Tao, S. Ammonia and related chemicals as potential indirect hydrogen storage materials. Int. J. Hydrogen Energy 2012, 37, 1482–1494. [Google Scholar] [CrossRef]
- Milićević, S.; Blagojević, I.; Milojević, S.; Bukvić, M.; Stojanović, B. Numerical Analysis of Optimal Hybridization in Parallel Hybrid Electric Powertrains for Tracked Vehicles. Energies 2024, 17, 3531. [Google Scholar] [CrossRef]
- Hepperle, M. Electric Flight—Potential and Limitations. In Proceedings of the 30th International Congress of the Aeronautical Sciences (ICAS 2012), Brisbane, Australia, 23–28 September 2012. [Google Scholar]
- Zhang, H.; Lei, N.; Chen, B.; Li, B.; Li, R.; Wang, Z. Modeling and control system optimization for electrified vehicles: A data-driven approach. Energy 2024, 310, 133196. [Google Scholar] [CrossRef]
- Koffler, J.; Fansler, T.D. Hydrogen Fuel for Transportation: A Review. SAE Int. J. Fuels Lubr. 2021, 14, 1–22. [Google Scholar]
- Meng, X.; Sun, C.; Mei, J.; Tang, X.; Hasanien, H.M.; Jiang, J.; Fan, F.; Song, K. Fuel cell life prediction considering the recovery phenomenon of reversible voltage loss. J. Power Sources 2025, 625, 235634. [Google Scholar] [CrossRef]
- Meng, X.; Mei, J.; Tang, X.; Jiang, J.; Sun, C.; Song, K. The Degradation Prediction of Proton Exchange Membrane Fuel Cell Performance Based on a Transformer Model. Energies 2024, 17, 3050. [Google Scholar] [CrossRef]
- Ahluwalia, R.K.; Hua, T.Q.; Peng, J.K.; Lasher, S.; McKenney, K.; Sinha, J.; Weisberg, A. On-board and off-board performance of hydrogen storage systems for light-duty vehicles. Int. J. Hydrogen Energy 2010, 35, 12339–12353. [Google Scholar] [CrossRef]
- Valera-Medina, A.; Xiao, H.; Owen-Jones, M.; David, W.I.F.; Bowen, P.J. Ammonia for power. Prog. Energy Combust. Sci. 2018, 69, 63–102. [Google Scholar] [CrossRef]
- Zhang, H.; Lei, N.; Peng, W.; Li, B.; Lv, S.; Chen, B.; Wang, Z. Bi-Level Transfer Learning for Lifelong-Intelligent Energy Management of Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2025, 1–14. [Google Scholar] [CrossRef]
- International Energy Agency. The Role of Low-Carbon Fuels in the Clean Energy Transitions of the Power Sector; Technical Report; IEA: Paris, France, 2021. [Google Scholar]
- Zhou, J.; Shu, X.; Zhang, J.; Yi, F.; Jia, C.; Zhang, C.; Kong, X.; Zhang, J.; Wu, G. A deep learning method based on CNN-BiGRU and attention mechanism for proton exchange membrane fuel cell performance degradation prediction. Int. J. Hydrogen Energy 2024, 94, 394–405. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, F.; Wang, Y.; Wang, K.; Jiang, J.; Sun, C.; Xue, R.; Song, K. Convective Heat Loss Prediction Using the Concept of Effective Wind Speed for Dynamic Line Rating Studies. Energies 2025, 18, 4452. [Google Scholar] [CrossRef]
- Lucentini, I.; Colli, G.G.; Luzi, C.D.; Serrano, I.; Martínez, O.M.; Llorca, J. Catalytic ammonia decomposition over Ni-Ru supported on CeO2 for hydrogen production: Effect of metal loading and kinetic analysis. Appl. Catal. B Environ. 2021, 286, 119896. [Google Scholar] [CrossRef]
- Meng, X.; Liu, M.; Mei, J.; Li, X.; Grigoriev, S.; Hasanien, H.M.; Tang, X.; Li, R.; Sun, C. Polarization loss decomposition-based online health state estimation for proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2025, 157, 150162. [Google Scholar] [CrossRef]
- Wu, X.; Cao, B.; Li, X.; Xu, J.; Ren, X. Component sizing optimization of plug-in hybrid electric vehicles. Appl. Energy 2011, 88, 799–804. [Google Scholar] [CrossRef]
- Ezzat, M.F.; Dincer, I. Development and assessment of a new hybrid vehicle with ammonia and hydrogen. Appl. Energy 2018, 219, 226–239. [Google Scholar] [CrossRef]
- Isikveren, A.T.; Kaiser, S.; Pornet, C.; Vratny, P.C. A Conceptual Design and Sizing Methodology for Hybrid-Electric Aircraft. J. Aircr. 2014, 51, 1793–1808. [Google Scholar]
- Zhou, J.; Jiang, J.; Fan, F.; Sun, C.; Dong, Z.; Song, K. Real-Time Impedance Detection for PEM Fuel Cell Based on TAB Converter Voltage Perturbation. Energies 2024, 17, 4320. [Google Scholar] [CrossRef]
- Martins, J.R.R.A.; Lambe, A.B. Multidisciplinary Design Optimization: A Survey of Architectures. AIAA J. 2013, 51, 2049–2075. [Google Scholar] [CrossRef]
- Lu, D.; Yi, F.; Hu, D.; Li, J.; Yang, Q.; Wang, J. Online optimization of energy management strategy for FCV control parameters considering dual power source lifespan decay synergy. Appl. Energy 2023, 348, 121516. [Google Scholar] [CrossRef]
- Simpson, T.W.; Peplinski, J.; Koch, P.N.; Allen, J.K. Kriging Models for Global Approximation in Simulation-Based Design. AIAA J. 2001, 39, 2233–2241. [Google Scholar] [CrossRef]
- Li, Y.; Lu, X.; Kar, N.C. Rule-Based Control Strategy With Novel Parameters Optimization Using NSGA-II for Power-Split PHEV Operation Cost Minimization. IEEE Trans. Veh. Technol. 2014, 63, 3051–3061. [Google Scholar] [CrossRef]
- Li, K.; Zhou, J.; Jia, C.; Yi, F.; Zhang, C. Energy sources durability energy management for fuel cell hybrid electric bus based on deep reinforcement learning considering future terrain information. Int. J. Hydrogen Energy 2024, 52, 821–833. [Google Scholar] [CrossRef]
- Wen, Y.; Chu, Z.; Srivastava, A.; Teng, F.; Chen, B. Resilient Microgrid Scheduling With Synthetic Inertia From Electric Vehicles Within a Network of Charging Stations. IEEE Trans. Control Syst. Technol. 2024, 33, 775–787. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Pardhi, S.; El Baghdadi, M.; Hulsebos, O.; Hegazy, O. Optimal Powertrain Sizing of Series Hybrid Coach Running on Diesel and HVO for Lifetime Carbon Footprint and Total Cost Minimisation. Energies 2022, 15, 6974. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, W.; Cash, S.; Olatunbosun, O.; Xu, H.; Lu, G. Intelligent sizing of a series hybrid electric power-train system based on Chaos-enhanced accelerated particle swarm optimization. Appl. Energy 2017, 189, 588–601. [Google Scholar] [CrossRef]
- Chen, B.; Li, X.; Evangelou, S.; Lot, R. Joint Propulsion and Cooling Energy Management of Hybrid Electric Vehicles by Optimal Control. IEEE Trans. Veh. Technol. 2020, 69, 4894–4906. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic Differentiation in Machine Learning: A Survey. J. Mach. Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Tang, X.; Shi, L.; Li, M.; Xu, S.; Sun, C. Health State Estimation and Long-Term Durability Prediction for Vehicular PEM Fuel Cell Stacks Under Dynamic Operational Conditions. IEEE Trans. Power Electron. 2025, 40, 4498–4509. [Google Scholar] [CrossRef]
- Ruan, S.; Ma, Y.; Wei, Z.; Zhang, C.; Xiang, C. Data-Driven Cooperative Differential Game Based Energy Management Strategy for Hybrid Electric Propulsion System of a Flying Car. IEEE Trans. Intell. Transp. Syst. 2024, 25, 14770–14784. [Google Scholar] [CrossRef]
- Li, J.; Wang, W.; Chen, W.; Gong, Q.; Luo, J.; Lin, R.; Xin, H.; Zhang, H.; Wang, D.; Peng, Q.; et al. Sub-nm ruthenium cluster as an efficient and robust catalyst for decomposition and synthesis of ammonia: Break the “size shackles”. Nano Res. 2018, 11, 4774–4785. [Google Scholar] [CrossRef]
- Xie, P.; Yao, Y.; Huang, Z.; Liu, Z.; Zhang, J.; Li, T.; Wang, G.; Shahbazian-Yassar, R.; Hu, L.; Wang, C. Highly efficient decomposition of ammonia using high-entropy alloy catalysts. Nat. Commun. 2019, 10, 4011. [Google Scholar] [CrossRef]
- Xu, K.; Jiang, N.; Wang, P.; Wang, W.W.; Jia, C.J. Highly efficient cobalt catalysts promoted by CeO2-Al2O3 for ammonia decomposition. Catal. Sci. Technol. 2024, 14, 5678–5686. [Google Scholar] [CrossRef]
- Makepeace, J.W.; Wood, T.J.; Hunter, H.M.A.; Jones, M.O.; David, W.I.F. Ammonia decomposition catalysis using non-stoichiometric lithium imide. Chem. Sci. 2015, 6, 3805–3815. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Lei, N.; Liu, S.; Fan, Q.; Wang, Z. Data-driven predictive energy consumption minimization strategy for connected plug-in hybrid electric vehicles. Energy 2023, 283, 128514. [Google Scholar] [CrossRef]
- Lei, N.; Zhang, H.; Hu, J.; Hu, Z.; Wang, Z. Sim-to-real design and development of reinforcement learning-based energy management strategies for fuel cell electric vehicles. Appl. Energy 2025, 393, 126030. [Google Scholar] [CrossRef]
- Song, K.; Hou, T.; Jiang, J.; Grigoriev, S.A.; Fan, F.; Qin, J.; Wang, Z.; Sun, C. Thermal management of liquid-cooled proton exchange membrane fuel cell: A review. J. Power Sources 2025, 648, 237227. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Lei, N.; Zhang, H.; Wang, H.; Wang, Z. An Improved Co-Optimization of Component Sizing and Energy Management for Hybrid Powertrains Interacting With High-fidelity Model. IEEE Trans. Veh. Technol. 2023, 72, 15585–15596. [Google Scholar] [CrossRef]



| Parameter and Symbol | Value and Unit |
|---|---|
| Correction coefficient () | 1.47 |
| Start–stop decay rate () | 0.00196%/cycle |
| Load-change decay rate () | 0.0000593%/cycle |
| Low-load decay rate () | 0.00126%/h |
| High-load decay rate () | 0.00147%/h |
| Parameters | Definition |
|---|---|
| Objective functions | |
| Decision variables | |
| Constraints |
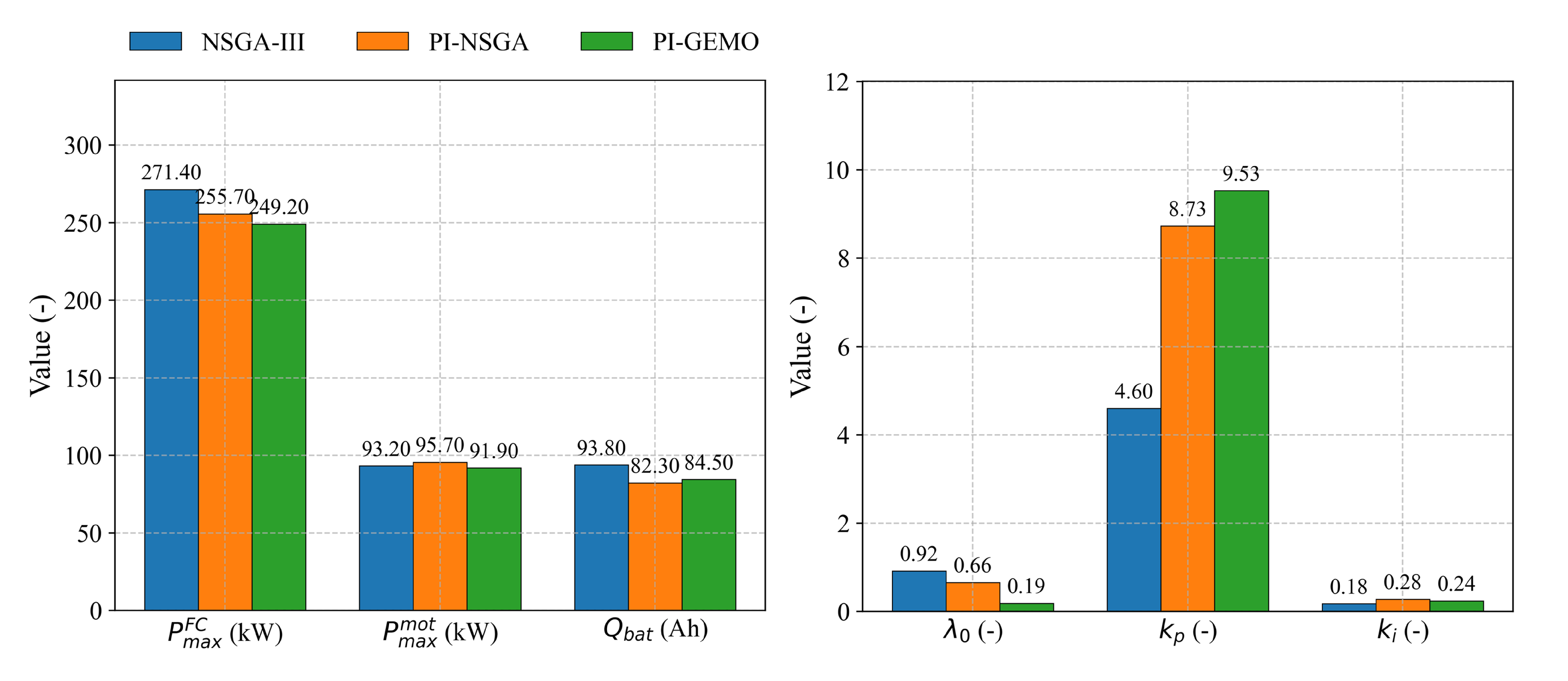
| Parameter | NSGA-III | PI-NSGA | PI-GEMO |
|---|---|---|---|
| (kW) | 271.4 | 255.7 | 249.2 |
| (kW) | 93.2 | 95.7 | 91.9 |
| (Ah) | 93.8 | 82.3 | 84.5 |
| (-) | 0.92 | 0.66 | 0.19 |
| (-) | 4.60 | 8.73 | 9.53 |
| (-) | 0.18 | 0.28 | 0.24 |
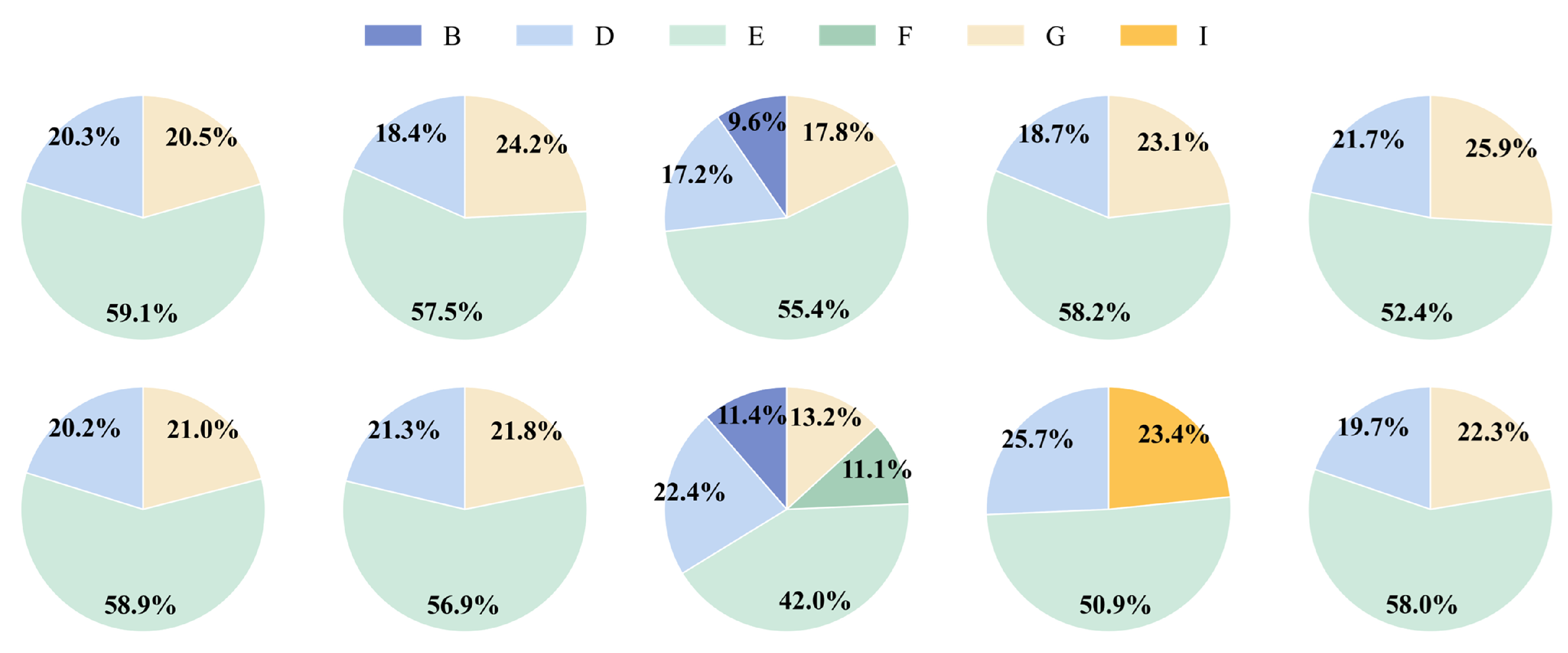
| Catalysts Type Vector (-) | [B, D, E, E, G] | [D, E, E, G, I] | [D, E, E, E, G] |
| Catalysts Proportion Vector (%) | [18.81, 20.69, 19.19, 21.76, 19.55] | [19.34, 20.30, 19.43, 20.71, 20.22] | [20.16, 19.60, 19.94, 19.89, 20.41] |
| (kg) | 7.903 | 7.691 | 7.504 |
| (%) | 0.0246 | 0.0241 | 0.0237 |
| (k USD) | 150.917 | 147.464 | 145.105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, Y.; Chen, C.; Zhang, H.; Lei, N. Physics-Informed Co-Optimization of Fuel-CellFlying Vehicle Propulsion and Control Systems with Onboard Catalysis. Electronics 2025, 14, 4150. https://doi.org/10.3390/electronics14214150
Bao Y, Chen C, Zhang H, Lei N. Physics-Informed Co-Optimization of Fuel-CellFlying Vehicle Propulsion and Control Systems with Onboard Catalysis. Electronics. 2025; 14(21):4150. https://doi.org/10.3390/electronics14214150
Chicago/Turabian StyleBao, Yifei, Chaoyi Chen, Hao Zhang, and Nuo Lei. 2025. "Physics-Informed Co-Optimization of Fuel-CellFlying Vehicle Propulsion and Control Systems with Onboard Catalysis" Electronics 14, no. 21: 4150. https://doi.org/10.3390/electronics14214150
APA StyleBao, Y., Chen, C., Zhang, H., & Lei, N. (2025). Physics-Informed Co-Optimization of Fuel-CellFlying Vehicle Propulsion and Control Systems with Onboard Catalysis. Electronics, 14(21), 4150. https://doi.org/10.3390/electronics14214150






