A High-Impedance Line Self-Packaged Low-Pass Filter Based on SISL Technique
Abstract
1. Introduction
2. SISL LPF Design
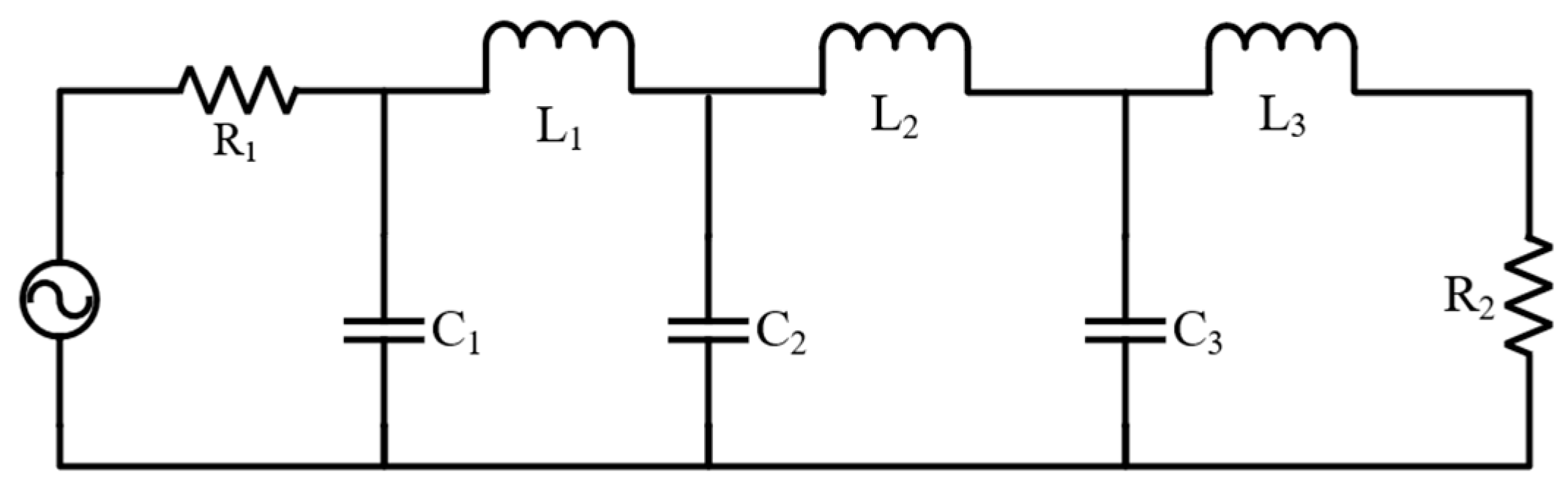
2.1. The Core Circuit of LPF Design
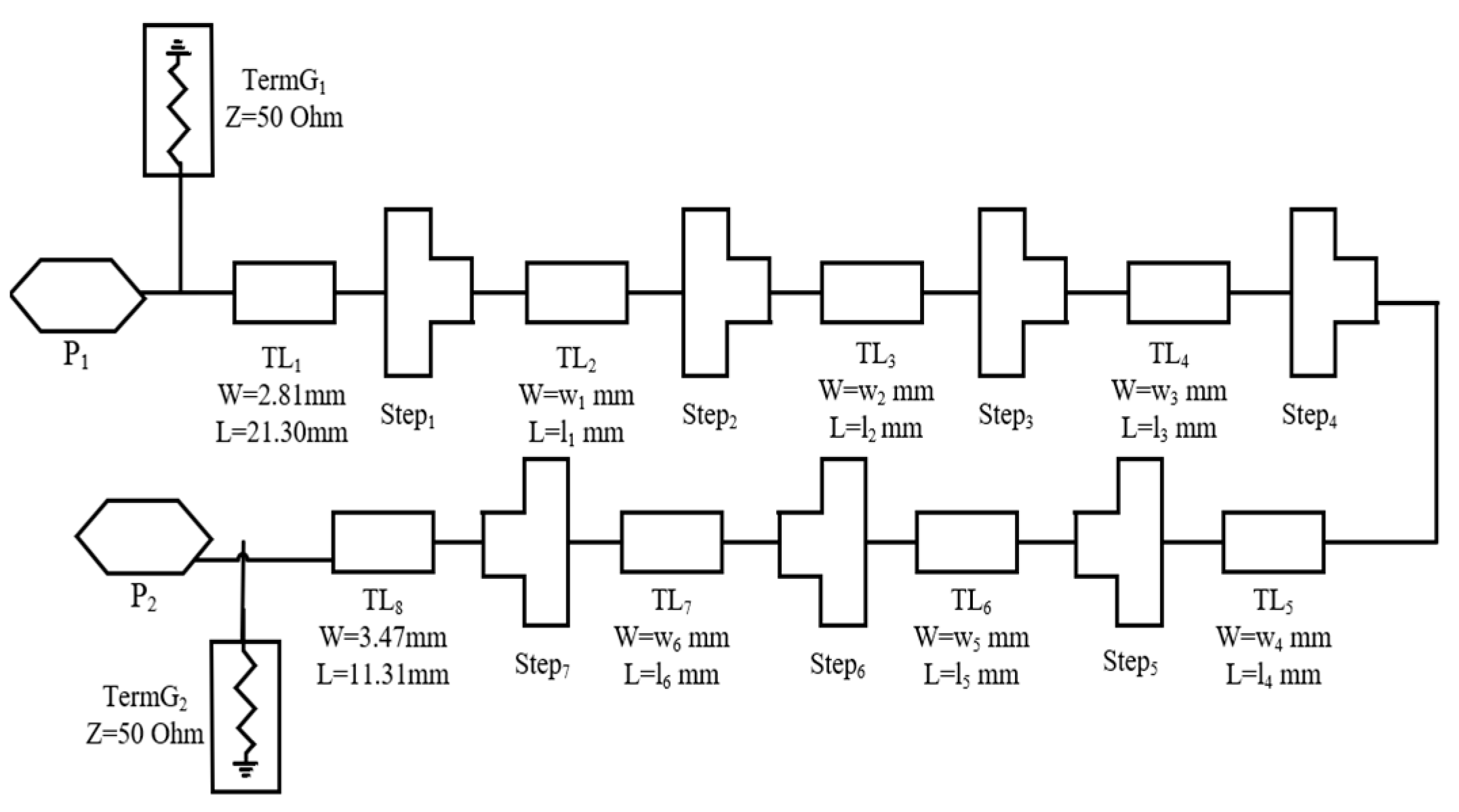
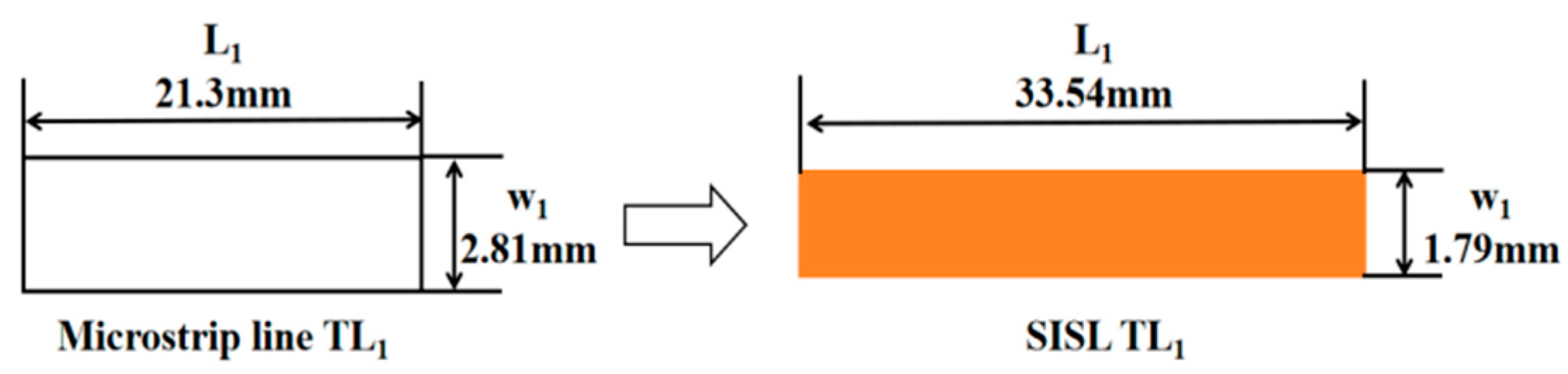
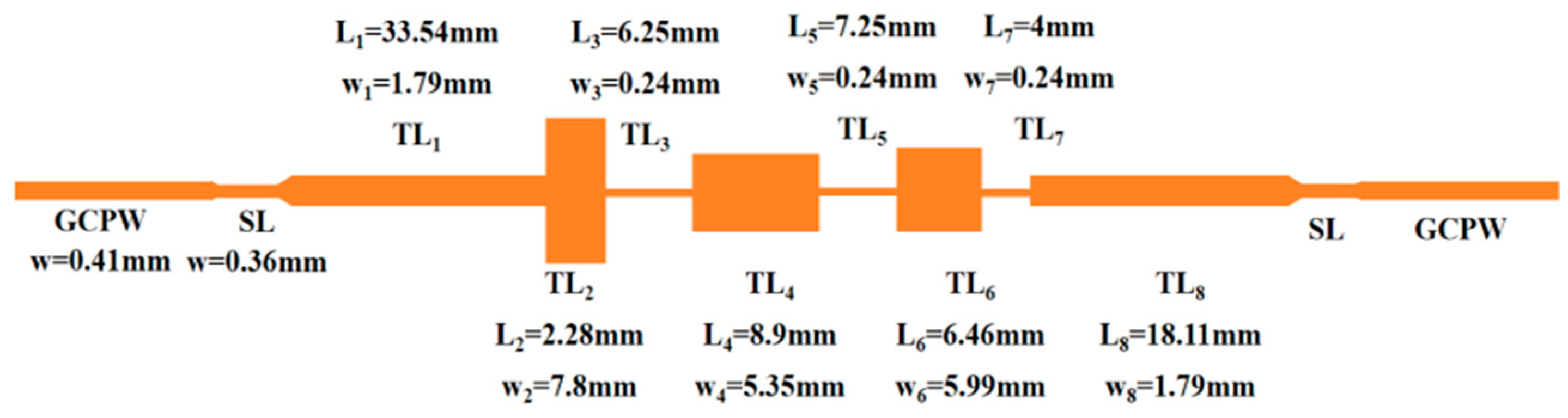
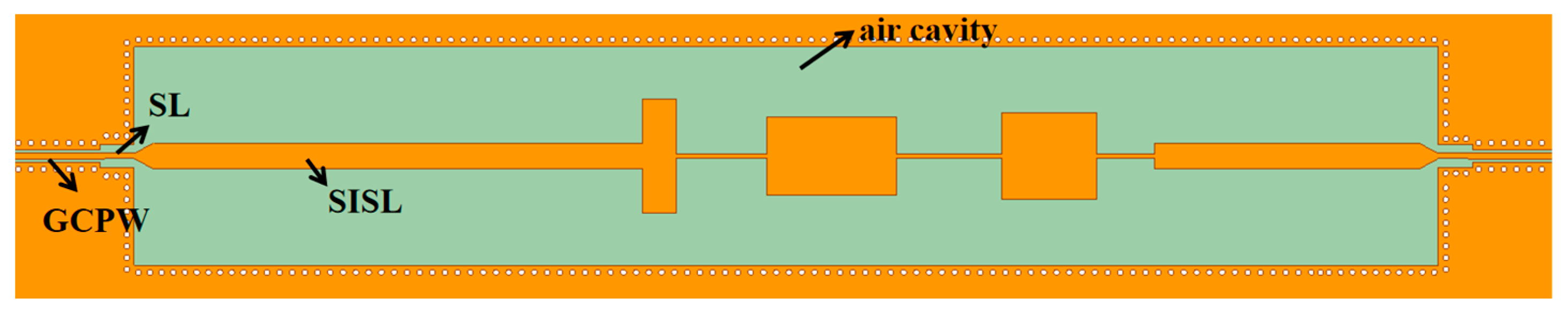
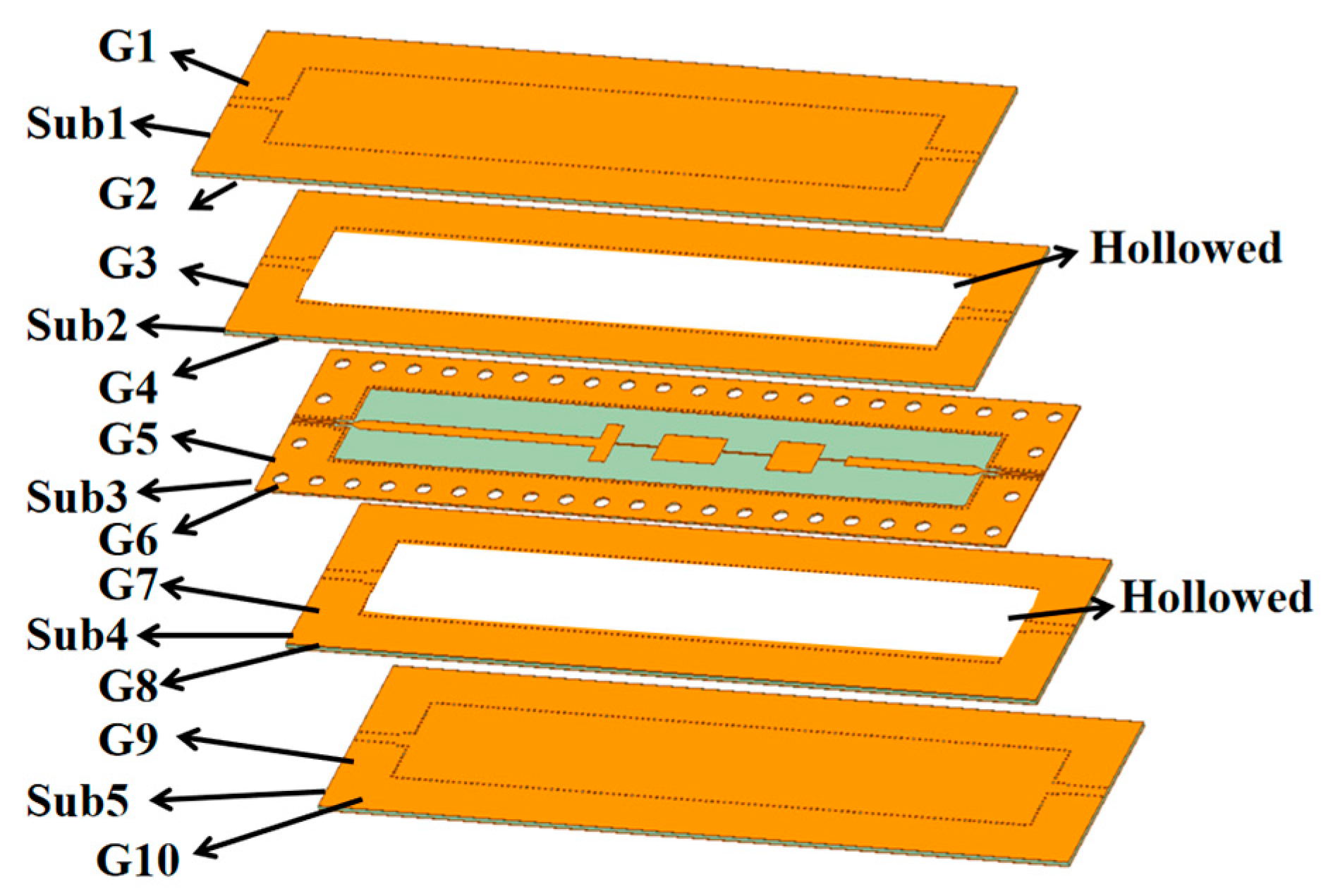
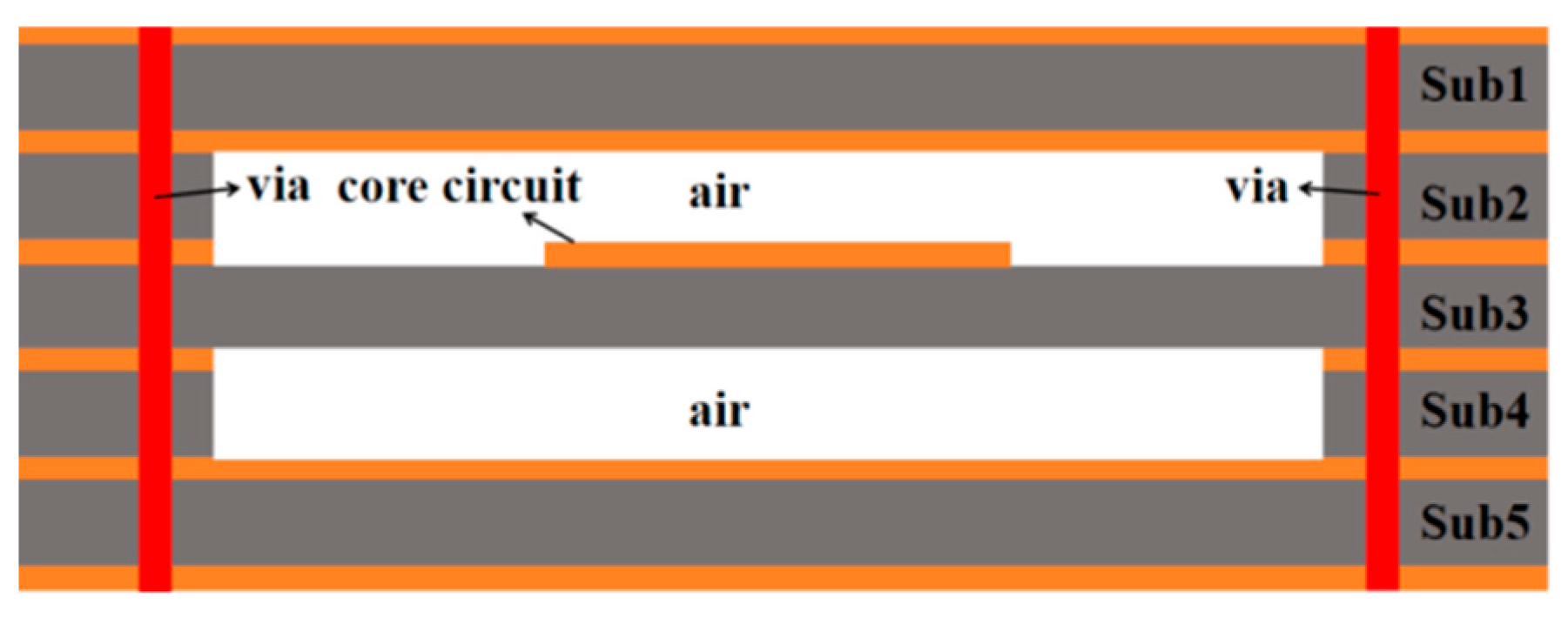
2.2. The Proposed SISL LPF Design
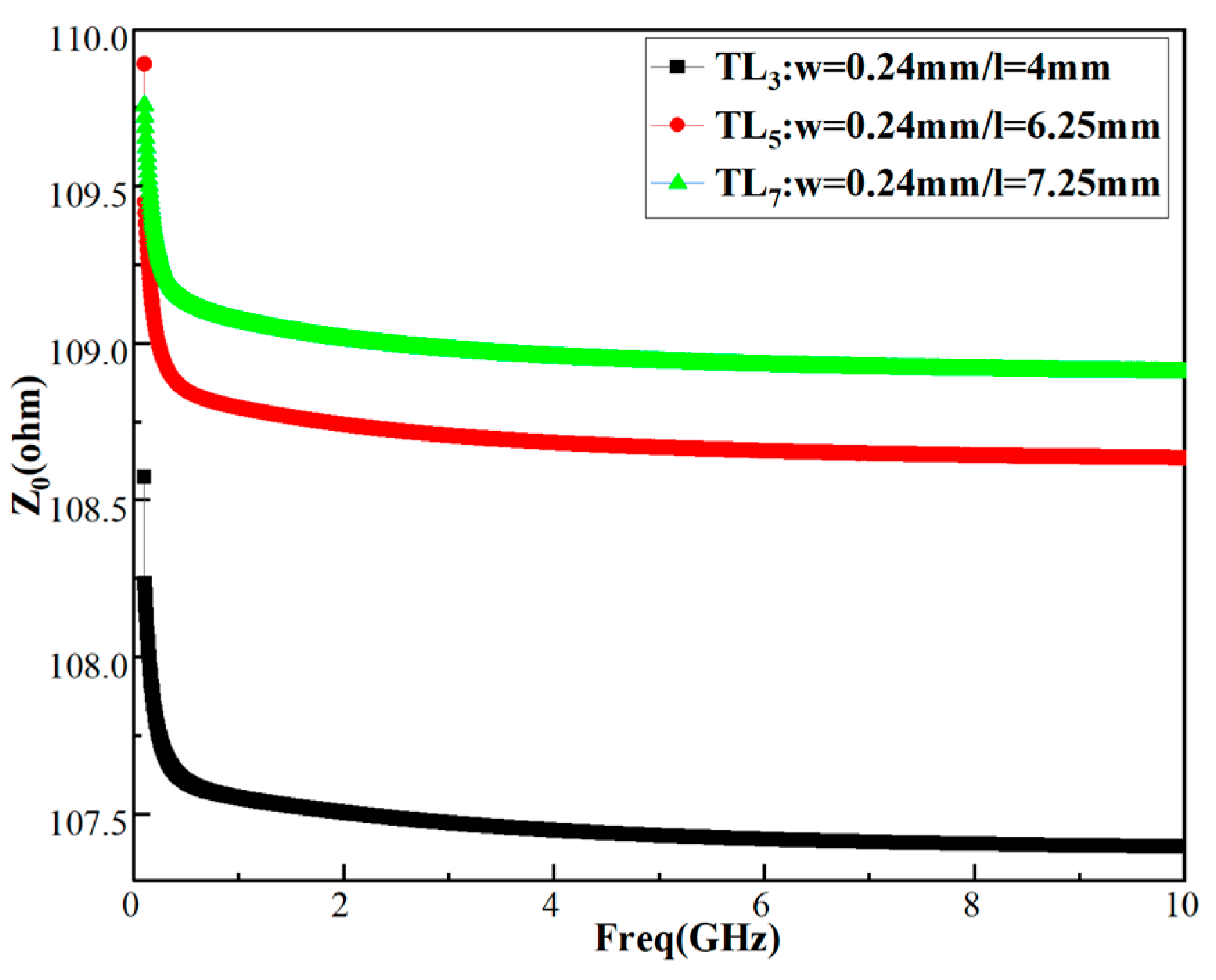
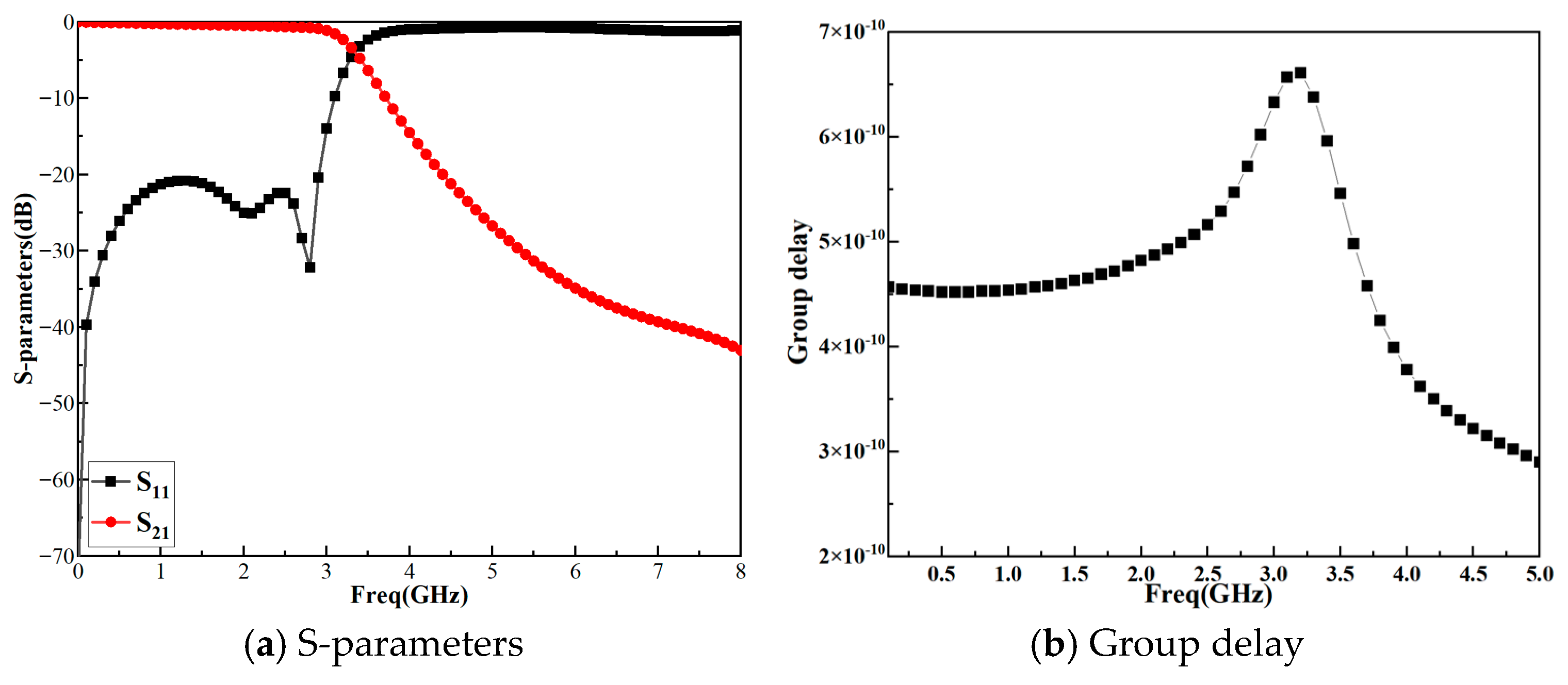
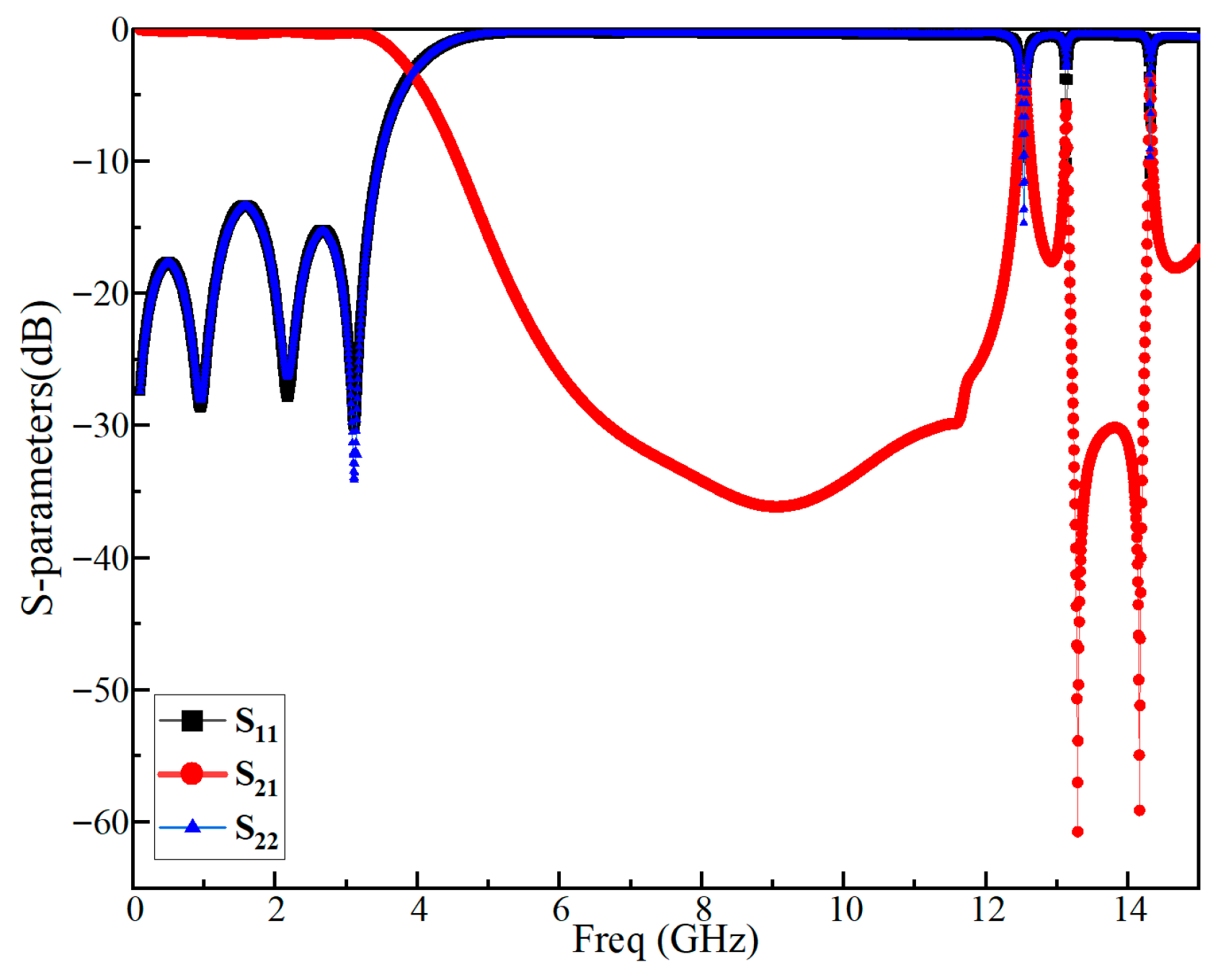
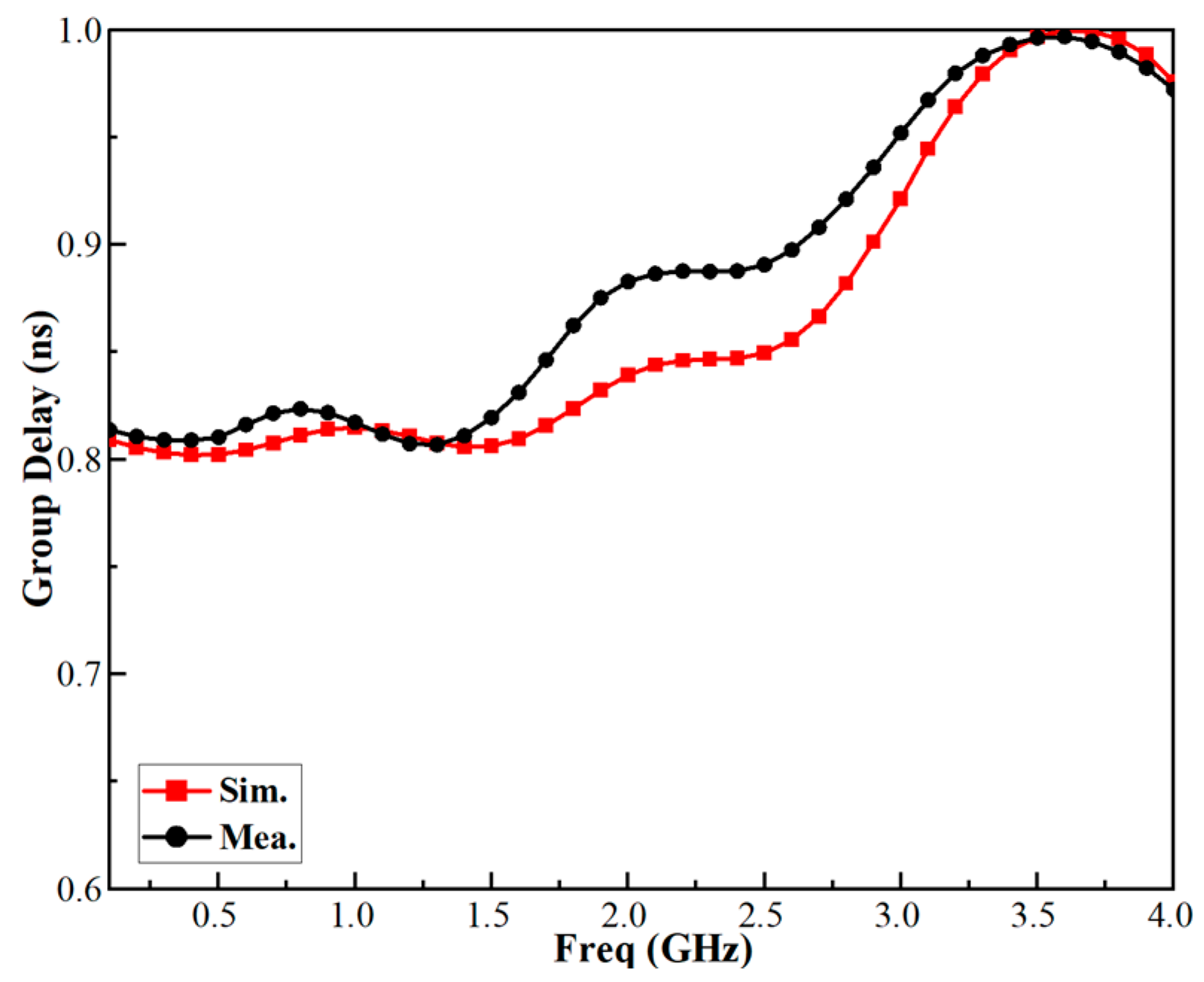
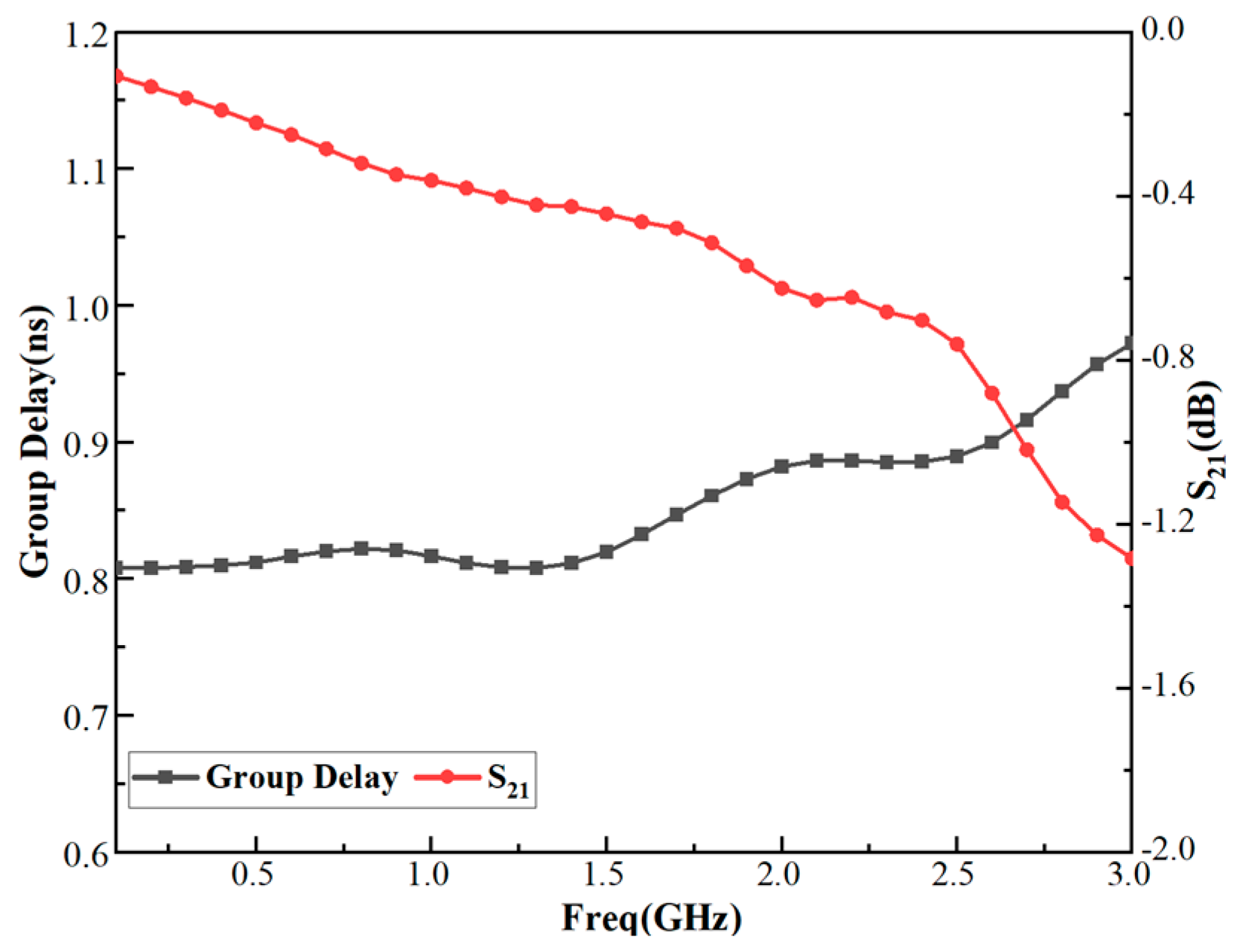
3. Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, L.; Liu, X. All-optical tunable microwave filter with ultra-high peak rejection and low-power consumption. Opt. Express 2020, 28, 13455–13465. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.P.; Zhu, L.; Zhang, S. Differential-mode low-pass filter using hybrid CPS and G-CPS with intrinsic common-mode rejection. IEEE Trans. Microw. Theory Tech. 2019, 67, 1836–1843. [Google Scholar] [CrossRef]
- Han, Y. A flexible microstrip low-pass filter design using asymmetric pi-shaped DGS. IEEE Access 2019, 7, 49999–50006. [Google Scholar] [CrossRef]
- Feng, J.; Wang, X.; Poterjoy, J. A Comparison of Two Local Moment-Matching Nonlinear Filters: Local Particle Filter (LPF) and Local Nonlinear Ensemble Transform Filter (LNETF). Mon. Weather Rev. 2020, 148, 4377–4395. [Google Scholar] [CrossRef]
- ElIssawi, M.L.; Konditi, D.; Usman, A.D. Design of Enhanced Wide Band Microstrip Patch Antenna Based on Defected Ground Structures (DGS) for Sub-6 GHz Applications. Int. J. Electr. Electron. Res. 2024, 12, 315–321. [Google Scholar] [CrossRef]
- Shi, L.F.; Fan, Z.Y. Miniaturized low-pass filter based on defected ground structure and compensated microstrip line. Microw. Opt. Technol. Lett. 2020, 62, 1093–1097. [Google Scholar] [CrossRef]
- Al-hussein, A.; Luhaib, S. Design and miniaturized a high suppression stop band microstrip low pass filter by using slot defected ground structure for 5G applications. AREJ Al-Rafidain Eng. J. 2024, 29, 126–131. [Google Scholar]
- Khairi, K.A.; Jamlos, M.F.; Padmanathan, S.; Jamlos, M.A.; Isa, M.M. Low insertion loss of surface mount device low pass filter at 700 MHz. Bull. Electr. Eng. Inform. 2019, 8, 382–388. [Google Scholar] [CrossRef]
- Lee, T.H.; Lee, B.; Kim, Y.S.; Wu, K.; Lee, J. Higher order lumped element absorptive low-pass and band-pass filter structures. IET Microw. Antennas Propag. 2019, 13, 1166–1173. [Google Scholar] [CrossRef]
- Yuan, B.; Mou, J.; Tong, L.; Lv, X. A miniaturized LTCC lowpass filter with two transmission zeros. In Proceedings of the 2011 4th IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Beijing, China, 1–3 November 2011; pp. 221–223. [Google Scholar]
- Zheng, Y.; Sheng, W. Compact lumped-element LTCC band-pass filter for low-loss VHF-band applications. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 1074–1076. [Google Scholar] [CrossRef]
- Lotfi, S.; Roshani, S.; Roshani, S.; Janda, M.; Blecha, T. Design of a compact low-pass filter with an ultra-wide stop-band using triangular Resonators. In Proceedings of the 2024 47th International Spring Seminar on Electronics Technology, Prague, Czech Republic, 15–19 May 2024; pp. 1–4. [Google Scholar]
- Chemseddine, F.M.; Rahmouna, E.; Didier, V. A Design of Microstrip Low-pass Filter using ground-plane coplanar waveguide. Telecommun. Radio Eng. 2024, 83, 1–8. [Google Scholar] [CrossRef]
- Shome, P.P.; Khan, T.; Koul, S.K.; Antar, Y.M. Two Decades of UWB Filter Technology: Advances and Emerging Challenges in the Design of UWB Band-pass Filters. IEEE Microw. Mag. 2021, 22, 32–51. [Google Scholar] [CrossRef]
- Snyder, R.V.; Macchiarella, G.; Bastioli, S.; Tomassoni, C. Emerging trends in techniques and technology as applied to filter design. IEEE J. Microw. 2021, 1, 317–344. [Google Scholar] [CrossRef]
- Ma, K.; Chan, K.T. Quasi-Planar Circuits with Air Cavities. PCT Patent WO 149046, 27 December 2007. [Google Scholar]
- Ma, Z.; Ma, K.; Mou, S. An ultra-wide stopband self-packaged quasi-lumped-element low pass filter based on substrate integrated suspended line technology. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium, Honololu, HI, USA, 4–9 June 2017; pp. 1084–1087. [Google Scholar]
- Ma, Z.; Ma, K.; Mou, S.; Meng, F. Quasi-lumped-element filter based on substrate-integrated suspended line technology. IEEE Trans. Microw. Theory Tech. 2017, 65, 5154–5161. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, M.; Ma, K. A compact low-pass filter using dielectric-filled capacitor on SISL platform. IEEE Microw. Wirel. Compon. Lett. 2021, 31, 21–24. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Ma, K. A compact low-pass filter using a miniaturized capacitor and honeycomb cavity on substrate integrated suspended line platform. IEEE Microw. Option Technol. Lett. 2023, 65, 1843–1849. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Xie, M.Z.; Wang, L.F.; Zhou, B.B.; Huang, Q.A. An impedance matching method for LC passive wireless sensors. IEEE Sens. J. 2020, 20, 13833–13841. [Google Scholar] [CrossRef]
- Shao, T.; Wang, Z.; Fang, S.; Liu, H.; Chen, Z.N. A full-pass-band linear-phase band-pass filter equalized with negative group delay circuits. IEEE Access 2020, 8, 3336–43343. [Google Scholar] [CrossRef]



| Performance | Index |
|---|---|
| f0 | 3 GHz |
| S21 (f = 5 GHz) | <−15 dB |
| Max solid-line impedance | 120 Ω |
| Min solid-line impedance | 20 Ω |
| n | g1 | g2 | g3 | g4 | g5 | g6 | g7 | g8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 2.00 | 1.00 | ||||||
| 2 | 1.41 | 1.41 | 1.00 | |||||
| 3 | 1.00 | 2.00 | 1.00 | 2.00 | ||||
| 4 | 0.77 | 1.85 | 1.85 | 0.77 | 1.00 | |||
| 5 | 0.62 | 1.62 | 2.00 | 1.62 | 0.62 | 1.00 | ||
| 6 | 0.52 | 1.41 | 1.93 | 1.93 | 1.41 | 0.52 | 1.00 | |
| 7 | 0.45 | 1.25 | 1.80 | 2.00 | 1.80 | 1.25 | 0.45 | 1.00 |
| Variable | Length/mm | Variable | Length/mm |
|---|---|---|---|
| w1 | 1.79 | L1 | 33.54 |
| w2 | 7.8 | L2 | 2.28 |
| w3 | 0.24 | L3 | 6.25 |
| w4 | 5.35 | L4 | 8.9 |
| w5 | 0.24 | L5 | 7.25 |
| w6 | 5.99 | L6 | 6.46 |
| w7 | 0.24 | L7 | 4 |
| w8 | 1.79 | L8 | 18.11 |
| References | f0/GHz | IL/dB | RL/dB | Technique | Self-Packaging |
|---|---|---|---|---|---|
| [6] | 2.2 | >−0.8 | <−10 | DGS | No |
| [8] | 0.7 | >−1 | NA* | SMD | No |
| [10] | 1 | >−0.7 | <−18 | LTCC | No |
| [12] | 2.2 | >−0.7 | <−22 | Microstrip | No |
| [18] | 1 | >−1.2 | <−25 | SISL | Yes |
| [20] | 0.6 | >−2.2 | <−15 | SISL | Yes |
| This work | 3 | >−0.7 | <−15 | SISL | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Q.; Wang, X.; Wu, Y.; Wu, H.; Li, S. A High-Impedance Line Self-Packaged Low-Pass Filter Based on SISL Technique. Electronics 2025, 14, 4139. https://doi.org/10.3390/electronics14214139
Lin Q, Wang X, Wu Y, Wu H, Li S. A High-Impedance Line Self-Packaged Low-Pass Filter Based on SISL Technique. Electronics. 2025; 14(21):4139. https://doi.org/10.3390/electronics14214139
Chicago/Turabian StyleLin, Qian, Xuqin Wang, Yi Wu, Haifeng Wu, and Shuangxu Li. 2025. "A High-Impedance Line Self-Packaged Low-Pass Filter Based on SISL Technique" Electronics 14, no. 21: 4139. https://doi.org/10.3390/electronics14214139
APA StyleLin, Q., Wang, X., Wu, Y., Wu, H., & Li, S. (2025). A High-Impedance Line Self-Packaged Low-Pass Filter Based on SISL Technique. Electronics, 14(21), 4139. https://doi.org/10.3390/electronics14214139







