A Novel DST-IV Efficient Parallel Implementation with Low Arithmetic Complexity

Abstract

Discrete sine transform (DST) has numerous applications across various fields, including signal processing, image compression and coding, adaptive digital filtering, mathematics (such as partial differential equations or numerical solutions of differential equations), image reconstruction, and classification, among others. The primary disadvantage of DST class algorithms (DST-I, DST-II, DST-III, and DST-IV) is their substantial computational complexity (O (N log N)) during implementation. This paper proposes an innovative decomposition and real-time implementation for the DST-IV. This decomposition facilitates the execution of the algorithm in four or eight sections operating concurrently. These algorithms, which encompass 4 and 8 sections, are primarily developed using a matrix factorization technique to decompose the DST-IV matrices. Consequently, the computational complexity and execution time of the developed algorithms are markedly reduced compared to the traditional implementation of DST-IV, resulting in significant time efficiency. The performance analysis conducted on three distinct Graphics Processing Unit (GPU) architectures indicates that a substantial speedup can be achieved. An average speedup ranging from 22.42 to 65.25 was observed, depending on the GPU architecture employed and the DST-IV implementation (with 4 or 8 sections).

1. Introduction

The discrete sine transform (DST) was first introduced in 1979 within the paper [1]. Since the publication of the original paper [1], the DST has undergone numerous implementations, extensions, improvements, and analyses of its original algorithm. The DST primarily finds applications in spectral analysis [2], time-frequency analysis [3], audio coding [4], image compression and coding [5], adaptive digital filtering [6,7], interpolation [8,9], image reconstruction [10], and classification [11,12,13,14].

The main problem of this transformation and its twin brother, the discrete cosine transform (DCT), is the computational costs. These algorithms are computationally intensive and expensive to implement. To be used in real-time applications, they need to be restructured and reimplemented.

As previously mentioned in references [2,3,4,5,6,7,8,9,10,11,12,13,14], the DST-IV transform has a broad range of applications across various fields of science and technology, but its computational costs pose a significant challenge. In this paper, we introduce a new implementation method that can perform faster and requires fewer memory access cycles. As a result, all these applications [2,3,4,5,6,7,8,9,10,11,12,13,14] will operate with much lower latency, leaving more computing power available for other tasks and reducing power consumption when executing the same functions.

This paper introduces an innovative DST-IV algorithm characterized by a unique computational structure comprising either 4 or 8 short segments designed for parallel processing. Each segment exhibits remarkably low arithmetic complexity, owing to the specific implementation method employed and the utilization of precomputed coefficients. Ultimately, the algorithm is proficiently implemented on a system supported by a Graphics Processing Unit (GPU), achieving a reduced overall computational cost. The novel DST-IV algorithm was developed and experimentally validated on a GPU system; however, it is also adaptable for deployment across various parallel architectures, including those based on VLSI technology or other multi-core systems, such as Deep Learning Processing Units (DPU), Neural Processing Units (NPU), Tensor Processing Units (TPU), or processors equipped with multiple Central Processing Units (CPUs).

Various approaches exist to accelerate the execution of algorithms. Many of these methods rely on exploiting specific characteristics of the hardware they operate on, thereby enabling and facilitating certain implementations (e.g., systolic architecture [15], recursive implementations [16], pipeline architecture, utilization of shared memory, shared arithmetic units [17]). The new algorithm introduced in this paper aligns with this previously discussed category, as it leverages the parallelism inherent in different architectures. However, its fundamental concept involves the mathematical factorization of the classical DST-IV algorithm, aimed at reducing both the number of mathematical operations and memory accesses.

The research presented in this paper makes the following contributions to the field:

• We have developed a novel algorithm for DST-IV that can be executed with high efficiency in parallel computing environments.
• We are employing specific computational architectures that can be efficiently reorganized through sub-expression sharing to achieve a reduced arithmetic complexity, particularly minimizing the number of multiplications.
• In the DST-IV algorithm, we have further minimized the number of multiplications by replacing even the multiplications involving ½ and ¼, which are employed in the novel DCT-IV algorithm proposed previously in another research paper [18], with additions and subtractions. This optimization is based on the fact that internal matrices comprise only 1, −1, and 0.
• Provides experimental validation through extensive empirical results and profiling (via NVIDIA Nsight Compute), confirming improvements in execution time, memory usage, and throughput.
• Combines mathematical efficiency and hardware-level optimization for real-time signal and image processing.

The remainder of the paper is structured as follows: Section 2 surveys related research conducted by other scholars on various DST implementations that aim to enhance multiple objectives, including increasing speed, reducing silicon area, decreasing latency, lowering working memory consumption, and improving throughput. Section 3 presents the novel mathematical decomposition of the DST-IV algorithm, which will be implemented, tested, and analyzed in Section 6. The subsequent section, Section 4, provides a comprehensive description and comparative analysis of the Graphics Processing Units (GPUs) used in the algorithm testing. The materials and methodologies used in examining the novel algorithm are detailed in Section 5. In Section 7, the findings are discussed within the context of prior research. The concluding section provides the overall summary of the paper.

2. Related Works

The efficient implementation of DST-IV in VLSI (Very-Large-Scale Integration) architectures garners considerable research interest, and recent studies have proposed significant solutions based on factorizations or recursive forms to reduce complexity and accelerate the execution [15,17,19,20].

In [17], the authors present an innovative approach to implementing the DST in VLSI hardware, with a focus on prime-length sequences. By restructuring the DST computation into eight parallel short pseudo-cycle convolutions of identical length, a high-throughput implementation with reduced hardware complexity was obtained. In this mode, the classical DST-IV algorithm is efficiently mapped onto two linear systolic arrays, which feature modular and regular structures with localized interconnections. This design minimizes I/O costs and simplifies the VLSI implementation.

The authors, L. Poola and P. Aparna [20], propose a highly optimized, novel parallel-pipelined architecture for intra prediction within the High Efficiency Video Coding (HEVC) standard, specifically engineered to improve the efficiency of the DCT/DST engine. The primary innovation of this study involves removing an intermediate buffer between the intra prediction and DCT/DST modules through row-wise sample processing, thereby conserving significant clock cycles and reducing memory consumption. Furthermore, the design incorporates a shared arithmetic unit to reduce hardware redundancy, utilizing only 40 DSP slices while supporting all prediction unit sizes (ranging from 4 × 4 to 32 × 32) and 35 directional modes. This architecture, implemented on a 28 nm Artix-7 FPGA, operates at a frequency of 150 MHz, achieving a throughput of 64 samples per cycle with a hardware utilization of 16.2 K LUTs and 5.7 K registers [20].

The design presented in [15] implements a novel unified VLSI architecture for Type IV Discrete Cosine Transform (DCT-IV) and Discrete Sine Transform (DST-IV). The authors address two critical challenges in VLSI design: the computational efficiency of DCT/DST-IV transforms and the protection of intellectual property (IP) against reverse engineering. The proposed solution leverages quasi-circular correlation structures and systolic array architectures to achieve high throughput while integrating a dynamic obfuscation mechanism with minimal hardware overhead. The authors demonstrate that the two transforms share similar computational patterns, differing only in preprocessing/postprocessing stages and coefficient selection (cosine vs. sine). This similarity allows the architecture to switch between DCT-IV and DST-IV modes with negligible overhead (<0.01% chip area). The systolic array implementation features modular processing elements with configurable control bits, enabling high-speed processing (four outputs per cycle) and localized interconnections for efficient VLSI integration.

In another paper [19], a new method is presented for building a unified VLSI architecture that efficiently performs both the type IV Discrete Cosine Transform (DCT-IV) and the type IV Discrete Sine Transform (DST-IV). The authors develop an innovative algorithm for DST-IV that reduces the number of necessary computational structures from eight, as shown in previous work, to six quasi-cycle convolution structures, thus lowering hardware complexity. Additional efficiency gains are made by using multipliers with fixed operands instead of general-purpose multipliers and by implementing an interleaved systolic array design that reuses processing elements across different computation stages without sacrificing speed. The architecture is synthesized and tested using a 15 nm process, resulting in a highly compact core area of about 1250 μm² and very low power consumption of 0.04 mW at 20 MHz. Despite its small size and low power use, the design shows a high potential operating speed, reaching approximately 7 GHz during pre-place-and-route analysis and about 6.9 GHz after layout is completed.

In the second major class of DST-IV algorithm implementations, the validity and efficiency tests are no longer conducted in hardware (VLSI, FPGA, or ASIC). Instead, this testing is performed in software using the CPU or GPU with the aid of compilers or development environments, such as MATLAB R2023b [21].

The primary objective of numerous research endeavors aiming for the rapid implementation of the DST-IV transform is to diminish the number of complex multiplication operations, which are more resource-intensive and time-consuming in terms of hardware and processing than additions. This makes these algorithms suitable for real-time signal processing applications. Based on this methodology outlined in [21], the complex DST-IV coefficient matrix was decomposed into a product of simpler, structured matrices, such as sparse matrices, permutation matrices, and diagonal matrices containing sine constants. This factorization substitutes a large, complex multiplication with fewer multiplications and a series of simpler additions. The results are highly satisfactory; on average, the new algorithm achieves a 63% reduction in multiplications. The trade-off involves an approximate 8% increase in additions, which is considered reasonable given that additions are considerably less costly to implement.

In [22], an efficient computation of DCT-IV and DST-IV was achieved through a modified discrete cosine transform (MDCT) of double size. The analysis of the fast MDCT algorithm facilitates the derivation of an innovative DCT-IV/DST-IV computational architecture, grounded in a novel sparse matrix factorization of the DCT-IV matrix. This approach provides an effective means of implementing the forward and inverse MDCT within layer III of MPEG audio coding.

In a different study [16], a recursive framework for calculating the type IV Discrete Cosine Transform (DCT-IV) and Discrete Sine Transform (DST-IV) is introduced utilizing Clenshaw’s Recurrence Formula (CRF). This methodology also accommodates the inverse transforms (IDCT-IV/IDST-IV). The recursive nature of the implementation inherently limits throughput compared to parallel architectures, which may restrict its suitability for high-speed applications.

Based on the Duality Theorem, which facilitates efficient conversion between time-domain and frequency-domain representations, an effective implementation of the Discrete Sine Transform (DST) is presented in [23]. This research offers the advantage of opening new avenues for exploring duality in other discrete transforms (e.g., Discrete Cosine Transform) or hybrid transforms.

The authors examine five existing algorithms in [24], categorizing them into DFT-based, matrix factorization-based, and DCT-based approaches, and emphasize their limitations concerning high-speed VLSI implementation. The primary critique of existing methods centers on their inefficiency in managing data movement and the complexities of preprocessing and postprocessing, which hinder real-time performance. The paper proposes a novel architecture for the simultaneous computation of DCT-IV and DST-IV, based on the decomposition of the odd-time, odd-frequency discrete Fourier transform (O² DFT). The proposed architecture decreases the computational burden and demonstrates greater efficiency for systolic array implementations. Nonetheless, the paper lacks experimental validation, such as simulation results or hardware benchmarks, to quantify latency, power consumption, or area savings.

M. Polyakova et al. [25], developed an innovative regressive filter architecture for the efficient computation of arbitrary-length Type-IV Discrete Cosine and Sine Transforms (DCT-IV/DST-IV) and their inverses (IDCT-IV/IDST-IV). This novel approach is based on recursive sinusoidal formulas derived from the transform kernels, facilitating the mapping of these transforms into an IIR filter framework. This configuration enables parallel computation without the necessity for input/output sequence permutations. Although this methodology shows considerable promise, it currently lacks supporting simulation results or hardware benchmarks (such as FPGA or ASIC implementations), thereby leaving the asserted advantages largely unsubstantiated.

In the paper [26], innovative algorithms for calculating the Type-IV Discrete Cosine Transform (DCT-IV), Discrete Sine Transform (DST-IV), and Modified Discrete Cosine Transform (MDCT) are introduced, demonstrating a substantial reduction in arithmetic complexity relative to existing techniques. The authors accomplish this by considering the DCT-IV as a particular instance of a Discrete Fourier Transform (DFT) applied to symmetric inputs of length 8N and subsequently eliminating redundant operations by a recursively rescaled conjugate-pair split-radix FFT algorithm. The primary contribution is the reduction in the flop count. For DCT-IV, the flop count decreases from 56 to 54 when N = 8, and from 21,504 to 20,520 for N = 1024 [26]. Regrettably, the work does not consider contemporary hardware implementation factors such as SIMD optimization or cache efficiency, which predominantly influence real-world performance.

The paper [27] by V. Kober introduces two novel algorithms for the efficient computation of the Discrete Sine Transform (DST) within a sliding window (hopping) framework. The proposed methods, ALG-1 and ALG-2, employ recursive relationships derived from the z-transform and input-pruned DST techniques to reduce computational complexity. These algorithms achieve a lower complexity relative to existing methods. ALG-1 demonstrates flexibility by supporting arbitrary window sizes, whereas ALG-2 is optimized for window lengths that are powers of two, thereby ensuring high efficiency for specific applications.

The publication by Murty et al. [28] introduces two innovative systolic architectures for computing the Type-IV Discrete Sine Transform (DST-IV) through a recursive algorithm, providing a hardware-efficient solution suitable for real-time signal processing applications. The authors develop a recursive formulation of DST-IV based on Horner’s rule, which streamlines the computation into a series of modular operations conducive to VLSI implementation. The proposed systolic architectures—Linear Array-1 and Linear Array-2—utilize parallel processing and localized communication to attain high throughput, thus offering significant advantages for embedded systems and high-performance DSP applications. However, the publication does not include empirical validation, such as FPGA or ASIC implementation results, to substantiate assertions regarding latency, power consumption, or area efficiency.

Another approach used to speed up the execution of DST-IV is to create and compute integer versions of sine and cosine transforms of type IV. In the paper [29], the author presents matrix-based techniques for generating integer sine and cosine transform matrices of sizes 8 and 16. Using factorization methods and specific permutation strategies such as binary-inverse and Gray-code permutations, the paper develops fast algorithms that perform all operations with integers, avoiding floating-point arithmetic. The proposed algorithms for 16-point transforms [29] result in significant computational improvements. Compared to the standard discrete sine and cosine transforms of type IV, the integer versions require 14.29% and 12.5% fewer multiplications, respectively. When compared with the more recent integer transforms used in the Versatile Video Coding (VVC) standard, the new methods demonstrate 3.02 times lower multiplicative complexity and 47.41% fewer addition operations. Previously, the same author proposed another method to construct order-16 integer sine and cosine transforms of type IV, which has a multiplicative complexity 12.7 times lower and requires 26.32% more addition operations compared to the well-known fast DST/DCT algorithms [30].

Based on a novel sparse matrix factorization for the DST types I–IV, a low-complexity, recursive, and radix-2 algorithm was proposed in [31]. The authors decompose each DST matrix into products of simple components—sparse, diagonal, bidiagonal, and scaled orthogonal matrices—allowing for efficient computation. New relationships are established between DST-II and DST-IV, and between DST-I and DST-III, through diagonal and bidiagonal matrices. The resulting algorithms achieve low multiplication complexity for DST-II, DST-III, and DST-IV.

The most common strategy to boost the speed of DCT/DSYT algorithms relies on the GPU’s inherent processing capabilities. Cobrnic et al. [32] achieved a 2.46 speedup for video encoding by leveraging techniques such as thread vectorization, shared memory optimization, and overlapping computation with data transfer. Their implementation used the NVIDIA cuBLAS library and targeted a Kepler-architecture GPU. Other studies, such as [33], integrated the MPEG video coding steps (including DCT, quantization, coefficient reordering, and Huffman encoding) across both GPU and CPU resources. This hybrid method, where the GPU handled parallel DCT and quantization operations while the CPU completed post-processing, resulted in a 3.6-fold speedup with a fourfold increase in parallel cores. In a related investigation [34], researchers exploited NVIDIA’s concurrent kernel execution capability—allowing multiple kernels to run or swap execution when one is stalled—to design a code transformation technique aimed at improving resource utilization. By merging several kernels, the approach efficiently balanced GPU resources across AMD and NVIDIA devices. Consequently, it achieved an average acceleration of 1.28 on an AMD Radeon 5870 and 1.17 on an NVIDIA GTX280, which is based on the Fermi architecture. Similarly, Alqudami et al. [35] employed a range of optimization strategies—such as fine-tuning thread granularity, mapping work-items, balancing workloads, and vectorized memory access—to accelerate DCT computation, achieving a 7.97 performance gain. Their parallel implementation was executed on an AMD Radeon HD 6850 GPU.

3. Proposed DST IV Algorithm for a Parallel Implementation

Due to the wide range of applicability of the DCT-IV and DST-IV transforms and the interest shown by the academic community, this paper presents a novel implementation of the DST-IV algorithm. The basic form of the DST-IV transformation is appropriately reformulated to obtain, besides a parallel decomposition, an efficient implementation due to a reduced complexity form that has been obtained using an appropriate subexpression sharing technique.

For a real input sequence $x\left(i\right): i=\mathrm{0,1},\dots ,N-1$, type IV DST (DST-IV) is defined using the following equation [1]:

$$Y(k)=\sqrt{{\displaystyle \frac{2}{N}}}\cdot \sum _{i=0}^{N-1}x\left(i\right)\cdot \mathit{sin}[(2i+1)(2k+1)\alpha ]$$

(1)

where $k=0, 1,\dots ,N-1$ and where:

$$\alpha ={\displaystyle \frac{\pi }{4N}}$$

(2)

To simplify the presentation, we remove the constant coefficient $\sqrt{{\displaystyle \frac{2}{N}}}$ from the DST-IV equation, and we add this multiplication at the end of the algorithm.

Equations (1) and (2) represent the classical definition of DST-IV, and they can be implemented in parallel but not very efficiently, mainly because the arithmetic complexity can be significantly reduced as in our proposed algorithm.

In the following, we propose a new parallel algorithm that, besides being an efficient parallel implementation by breaking the computation into 4 or 8 computational structures that can be computed in parallel, has a low arithmetic complexity due to the use of the sub-expression sharing technique, as has been put in evidence below.

To obtain an efficient parallel algorithm, we need to reformulate Equation (1) using some auxiliary input and output restructuring sequences, and we have properly reordered them.

In the following, we consider the transform length a prime number N = 17.

We have used an auxiliary output sequence $\left\{T\left(k\right):k=\mathrm{1,2},\dots ,N-1\right\}$ and the following auxiliary input sequence:

$$x_p(N-1)=x(N-1)$$

(3)

$$x_p\left(i\right)={(-1)}^{i}x\left(i\right)-x_p(i+1)$$

(4)

for $i=N-2,\dots ,1, 0$.

$$x_a\left(i\right)=x_p\left(i\right)\cdot \mathit{cos} [\left(2i\right)\alpha ] \mathrm{f}\mathrm{o}\mathrm{r} i=\mathrm{0,1},\dots ,N-1$$

(5)

For a compact expression of the following relations, we note:

$$A= \left[\begin{array}{cc}\begin{array}{c}\begin{array}{ccc}1& 1& 0\end{array}\\ \begin{array}{ccc}0& 1& 1\end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}1& 1& 0\end{array}\\ \begin{array}{ccc}0& 1& 1\end{array}\end{array}\\ \begin{array}{c}\begin{array}{ccc}1& 1& 0\end{array}\\ \begin{array}{ccc}0& 1& 1\end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}-1& -1& 0\end{array}\\ \begin{array}{ccc}0& -1& -1\end{array}\end{array}\end{array}\right]$$

(6)

$$C=\left[\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{ccc}1& -1& 0\end{array}\\ \begin{array}{ccc}0& 1& 0\end{array}\\ \begin{array}{ccc}0& -1& 1\end{array}\end{array}\\ \begin{array}{c}\begin{array}{ccc}0& 0& 0\end{array}\\ \begin{array}{ccc}0& 0& 0\end{array}\\ \begin{array}{ccc}0& 0& 0\end{array}\end{array}\end{array}& \begin{array}{c}\begin{array}{c}\begin{array}{ccc}0& 0& 0\end{array}\\ \begin{array}{ccc}0& 0& 0\end{array}\\ \begin{array}{ccc}0& 0& 0\end{array}\end{array}\\ \begin{array}{c}\begin{array}{ccc}1& -1& 0\end{array}\\ \begin{array}{ccc}0& 1& 0\end{array}\\ \begin{array}{ccc}0& -1& 1\end{array}\end{array}\end{array}\end{array}\right]$$

(7)

Using the above auxiliary input and output sequences and sub-expression sharing technique, we have obtained the following equations that can be efficiently computed in parallel and have a reduced arithmetic complexity that allows an efficient implementation on a GPU significantly faster than other existing algorithms, including the classical algorithm.

Thus, we have the following equations:

$$\begin{gathered} \left[\begin{array}{c}T\left(6\right)\\ T\left(14\right)\\ T\left(10\right)\\ T\left(12\right)\end{array}\right]=A \times diag\left(C\times \underset{\mathrm{X}\mathrm{A}1}{\underbrace{\left[\begin{array}{c}\begin{array}{c}{x}_a\left(8\right)-x_a\left(9\right)+x_a\left(2\right)-x_a\left(15\right)\\ {-x}_a\left(1\right)+x_a\left(16\right)+x_a\left(4\right)-x_a\left(13\right)\\ x_a\left(8\right)-x_a\left(9\right)+x_a\left(2\right)-x_a\left(15\right)\end{array}\\ \begin{array}{c}{x}_a\left(8\right)-x_a\left(9\right)-x_a\left(2\right)+x_a\left(15\right)\\ {-x}_a\left(1\right)+x_a\left(16\right)-x_a\left(4\right)+x_a\left(13\right)\\ {-x}_a\left(8\right)+x_a\left(9\right)+x_a\left(2\right)-x_a\left(15\right)\end{array}\end{array}\right]}}\right) \\ \times \underset{\mathrm{c}\mathrm{o}\mathrm{s}2}{\underbrace{\left[\begin{array}{c}2\mathit{cos}(28\alpha )+2\mathit{cos}(24\alpha )\\ 2\mathit{cos}(12\alpha )+2\mathit{cos}(28\alpha )+2\mathit{cos}(20\alpha )+2\mathit{cos}(24\alpha )\\ \begin{array}{c}2\mathit{cos}(12\alpha )+2\mathit{cos}(20\alpha )\\ \begin{array}{c}2\mathit{cos}(28\alpha )-2\mathit{cos}(24\alpha )\\ \begin{array}{c}2\mathit{cos}(12\alpha )+2\mathit{cos}(28\alpha )-2\mathit{cos}(20\alpha )-\mathit{cos}(24\alpha )\\ 2\mathit{cos}(12\alpha )-2\mathit{cos}(20\alpha )\end{array}\end{array}\end{array}\end{array}\right]}} \\ -A\times diag\left(C\times \underset{\mathrm{X}\mathrm{A}2}{\underbrace{\left[\begin{array}{c}\begin{array}{c}{x}_a\left(7\right)-x_a\left(10\right)-x_a\left(6\right)+x_a\left(11\right)\\ x_a\left(3\right)-x_a\left(14\right)+x_a\left(5\right)-x_a\left(12\right)\\ x_a\left(7\right)-x_a\left(10\right)-x_a\left(6\right)+x_a\left(11\right)\end{array}\\ \begin{array}{c}{x}_a\left(7\right)-x_a\left(10\right)+x_a\left(6\right)-x_a\left(11\right)\\ x_a\left(3\right)-x_a\left(14\right)-x_a\left(5\right)+x_a\left(12\right)\\ {-x}_a\left(7\right)+x_a\left(10\right)-x_a\left(6\right)+x_a\left(11\right)\end{array}\end{array}\right]}}\right) \\ \times \underset{\mathrm{c}\mathrm{o}\mathrm{s}1}{\underbrace{\left[\begin{array}{c}2\mathit{cos}(16\alpha )+2\mathit{cos}(4\alpha )\\ 2\mathit{cos}(32\alpha )+2\mathit{cos}(16\alpha )+2\mathit{cos}(8\alpha )+2\mathit{cos}(4\alpha )\\ \begin{array}{c}2\mathit{cos}(32\alpha )+2\mathit{cos}(8\alpha )\\ 2\mathit{cos}(16\alpha )-2\mathit{cos}(4\alpha )\\ \begin{array}{c}2\mathit{cos}(32\alpha )+2\mathit{cos}(16\alpha )-2\mathit{cos}(8\alpha )-2\mathit{cos}(4\alpha )\\ 2\mathit{cos}(32\alpha )-2\mathit{cos}(8\alpha )\end{array}\end{array}\end{array}\right]}} \end{gathered}$$

(8)

Furthermore, the decomposition can be continued with:

$$\begin{gathered} \left[\begin{array}{c}T\left(16\right)\\ T\left(8\right)\\ T\left(4\right)\\ T\left(2\right)\end{array}\right]=A\times diag\left(C\times \left[\begin{array}{c}\begin{array}{c}{x}_a\left(8\right)-x_a\left(9\right)+x_a\left(2\right)-x_a\left(15\right)\\ {-x}_a\left(1\right)+x_a\left(16\right)+x_a\left(4\right)-x_a\left(13\right)\\ x_a\left(8\right)-x_a\left(9\right)+x_a\left(2\right)-x_a\left(15\right)\end{array}\\ \begin{array}{c}{x}_a\left(8\right)-x_a\left(10\right)-x_a\left(2\right)+x_a\left(15\right)\\ {-x}_a\left(1\right)+x_a\left(16\right)-x_a\left(4\right)+x_a\left(13\right)\\ {-x}_a\left(8\right)+x_a\left(9\right)+x_a\left(2\right)-x_a\left(15\right)\end{array}\end{array}\right]\right)\times B \\ \times \left[\begin{array}{c}2\mathit{cos}(16\alpha )+2\mathit{cos}(4\alpha )\\ 2\mathit{cos}(32\alpha )+2\mathit{cos}(16\alpha )+2\mathit{cos}(8\alpha )+2\mathit{cos}(4\alpha )\\ \begin{array}{c}2\mathit{cos}(32\alpha )+2\mathit{cos}(8\alpha )\\ 2\mathit{cos}(16\alpha )-2\mathit{cos}(4\alpha )\\ \begin{array}{c}2\mathit{cos}(32\alpha )+2\mathit{cos}(16\alpha )-2\mathit{cos}(8\alpha )-2\mathit{cos}(4\alpha )\\ 2\mathit{cos}(32\alpha )-2\mathit{cos}(8\alpha )\end{array}\end{array}\end{array}\right] \\ -A\times diag\left(C\times \underset{\mathrm{X}\mathrm{A}3}{\underbrace{\left[\begin{array}{c}\begin{array}{c}{x}_a\left(3\right)-x_a\left(14\right)+x_a\left(5\right)-x_a\left(12\right)\\ {-x}_a\left(6\right)+x_a\left(11\right)+x_a\left(7\right)-x_a\left(10\right)\\ x_a\left(3\right)-x_a\left(14\right)+x_a\left(5\right)-x_a\left(12\right)\end{array}\\ \begin{array}{c}{x}_a\left(3\right)-x_a\left(14\right)-x_a\left(5\right)+x_a\left(12\right)\\ -x_a\left(6\right)+x_a\left(11\right)-x_a\left(7\right)+x_a\left(10\right)\\ {-x}_a\left(3\right)+x_a\left(14\right)+x_a\left(5\right)-x_a\left(12\right)\end{array}\end{array}\right]}}\right)\times B \\ \times \left[\begin{array}{c}2\mathit{cos}(28\alpha )+2\mathit{cos}(24\alpha )\\ 2\mathit{cos}(12\alpha )+2\mathit{cos}(28\alpha )+2\mathit{cos}(20\alpha )+2\mathit{cos}(24\alpha )\\ \begin{array}{c}2\mathit{cos}(12\alpha )+2\mathit{cos}(20\alpha )\\ \begin{array}{c}2\mathit{cos}(28\alpha )-2\mathit{cos}(24\alpha )\\ \begin{array}{c}2\mathit{cos}(12\alpha )+2\mathit{cos}(28\alpha )-2\mathit{cos}(20\alpha )-\mathit{cos}(24\alpha )\\ 2\mathit{cos}(12\alpha )-2\mathit{cos}(20\alpha )\end{array}\end{array}\end{array}\end{array}\right] \end{gathered}$$

(9)

and:

$$\begin{gathered} \left[\begin{array}{c}T\left(11\right)\\ T\left(3\right)\\ T\left(7\right)\\ T\left(5\right)\end{array}\right]=A\times diag\left(C\times \underset{\mathrm{X}\mathrm{A}4}{\underbrace{\left[\begin{array}{c}\begin{array}{c}{x}_a\left(8\right)+x_a\left(9\right)+x_a\left(2\right)+x_a\left(15\right)\\ x_a\left(1\right)+x_a\left(16\right)+x_a\left(4\right)+x_a\left(13\right)\\ x_a\left(8\right)+\left(9\right)+x_a\left(2\right)+x_a\left(15\right)\end{array}\\ \begin{array}{c}{x}_a\left(8\right)+x_a\left(9\right)-\left(2\right)-x_a\left(15\right)\\ x_a\left(1\right)+x_a\left(16\right)-x_a\left(4\right)-x_a\left(13\right)\\ {-x}_a\left(8\right)-x_a\left(9\right)+x_a\left(2\right)+x_a\left(15\right)\end{array}\end{array}\right]}}\right)\times B \\ \times \left[\begin{array}{c}2\mathit{cos}(28\alpha )+2\mathit{cos}(24\alpha )\\ 2\mathit{cos}(12\alpha )+2\mathit{cos}(28\alpha )+2\mathit{cos}(20\alpha )+2\mathit{cos}(24\alpha )\\ \begin{array}{c}2\mathit{cos}(12\alpha )+2\mathit{cos}(20\alpha )\\ \begin{array}{c}2\mathit{cos}(28\alpha )-2\mathit{cos}(24\alpha )\\ \begin{array}{c}2\mathit{cos}(12\alpha )+2\mathit{cos}(28\alpha )-2\mathit{cos}(20\alpha )-\mathit{cos}(24\alpha )\\ 2\mathit{cos}(12\alpha )-2\mathit{cos}(20\alpha )\end{array}\end{array}\end{array}\end{array}\right] \\ +A\times diag\left(C\times \underset{\mathrm{X}\mathrm{A}5}{\underbrace{\left[\begin{array}{c}\begin{array}{c}{x}_a\left(6\right)+x_a\left(11\right)+x_a\left(7\right)+x_a\left(10\right)\\ x_a\left(3\right)+x_a\left(14\right)+x_a\left(5\right)+x_a\left(12\right)\\ x_a\left(6\right)+x_a\left(11\right)+x_a\left(7\right)+x_a\left(10\right)\end{array}\\ \begin{array}{c}-x_a\left(6\right)-x_a\left(11\right)+x_a\left(7\right)+x_a\left(10\right)\\ x_a\left(3\right)+x_a\left(14\right)-x_a\left(5\right)-x_a\left(12\right)\\ x_a\left(6\right)+x_a\left(11\right)-x_a\left(7\right)-x_a\left(10\right)\end{array}\end{array}\right]}}\right)\times B \\ \times \left[\begin{array}{c}2\mathit{cos}(16\alpha )+2\mathit{cos}(4\alpha )\\ 2\mathit{cos}(32\alpha )+2\mathit{cos}(16\alpha )+2\mathit{cos}(8\alpha )+2\mathit{cos}(4\alpha )\\ \begin{array}{c}2\mathit{cos}(32\alpha )+2\mathit{cos}(8\alpha )\\ 2\mathit{cos}(16\alpha )-2\mathit{cos}(4\alpha )\\ \begin{array}{c}2\mathit{cos}(32\alpha )+2\mathit{cos}(16\alpha )-2\mathit{cos}(8\alpha )-2\mathit{cos}(4\alpha )\\ 2\mathit{cos}(32\alpha )-2\mathit{cos}(8\alpha )\end{array}\end{array}\end{array}\right] \end{gathered}$$

(10)

$$\begin{gathered} \left[\begin{array}{c}T\left(1\right)\\ T\left(9\right)\\ T\left(13\right)\\ T\left(15\right)\end{array}\right]=A\times diag\left(C\times \left[\begin{array}{c}\begin{array}{c}{x}_a\left(8\right)+x_a\left(9\right)+x_a\left(2\right)+x_a\left(15\right)\\ x_a\left(1\right)+x_a\left(16\right)+x_a\left(4\right)+x_a\left(13\right)\\ x_a\left(8\right)+\left(9\right)+x_a\left(2\right)+x_a\left(15\right)\end{array}\\ \begin{array}{c}{x}_a\left(8\right)+x_a\left(9\right)-x_a\left(2\right)-x_a\left(15\right)\\ x_a\left(1\right)+x_a\left(16\right)-x_a\left(4\right)-x_a\left(13\right)\\ {-x}_a\left(8\right)-x_a\left(9\right)+x_a\left(2\right)+x_a\left(15\right)\end{array}\end{array}\right]\right)\times B \\ \times \left[\begin{array}{c}2\mathit{cos}(16\alpha )+2\mathit{cos}(4\alpha )\\ 2\mathit{cos}(32\alpha )+2\mathit{cos}(16\alpha )+2\mathit{cos}(8\alpha )+2\mathit{cos}(4\alpha )\\ \begin{array}{c}2\mathit{cos}(32\alpha )+2\mathit{cos}(8\alpha )\\ 2\mathit{cos}(16\alpha )-2\mathit{cos}(4\alpha )\\ \begin{array}{c}2\mathit{cos}(32\alpha )+2\mathit{cos}(16\alpha )-2\mathit{cos}(8\alpha )-2\mathit{cos}(4\alpha )\\ 2\mathit{cos}(32\alpha )-2\mathit{cos}(8\alpha )\end{array}\end{array}\end{array}\right] \\ +A\times diag\left(C\times \underset{\mathrm{X}\mathrm{A}6}{\underbrace{\left[\begin{array}{c}\begin{array}{c}{x}_a\left(3\right)+x_a\left(14\right)+x_a\left(5\right)+x_a\left(12\right)\\ x_a\left(6\right)+x_a\left(11\right)+x_a\left(7\right)+x_a\left(10\right)\\ x_a\left(3\right)+x_a\left(14\right)+x_a\left(5\right)+x_a\left(12\right)\end{array}\\ \begin{array}{c}{x}_a\left(3\right)+x_a\left(14\right)-x_a\left(5\right)-x_a\left(12\right)\\ x_a\left(6\right)+x_a\left(11\right)-x_a\left(7\right)-x_a\left(10\right)\\ {-x}_a\left(3\right)-x_a\left(14\right)+x_a\left(5\right)+x_a\left(12\right)\end{array}\end{array}\right]}}\right)\times B \\ \times \left[\begin{array}{c}2\mathit{cos}(28\alpha )+2\mathit{cos}(24\alpha )\\ 2\mathit{cos}(12\alpha )+2\mathit{cos}(28\alpha )+2\mathit{cos}(20\alpha )+2\mathit{cos}(24\alpha )\\ \begin{array}{c}2\mathit{cos}(12\alpha )+2\mathit{cos}(20\alpha )\\ \begin{array}{c}2\mathit{cos}(28\alpha )-2\mathit{cos}(24\alpha )\\ \begin{array}{c}2\mathit{cos}(12\alpha )+2\mathit{cos}(28\alpha )-2\mathit{cos}(20\alpha )-\mathit{cos}(24\alpha )\\ 2\mathit{cos}(12\alpha )-2\mathit{cos}(20\alpha )\end{array}\end{array}\end{array}\end{array}\right] \end{gathered}$$

(11)

In Equations (8)–(11), it was noted: $diag\left[a_0,a_1\right]=\left[\begin{array}{cc}{a}_0& 0\\ 0& a_1\end{array}\right]$.

To obtain the output values, the following coefficients must first be computed.

$$T_a(0)=2\times \sum _{i=1}^{(N-1)}{(-1)}^i{x}_a\left(i\right)$$

(12)

$$T_a\left(i\right)=T\left(i\right)-T_a(i-1)$$

(13)

for $i=1,\dots ,N-1$.

In the end, the DST-IV values are computed based on:

$$\left[\begin{array}{c}Y\left(6\right)\\ Y\left(14\right)\\ Y\left(10\right)\\ Y\left(12\right)\end{array}\right]=\left[\begin{array}{c}\left(x_a\right(0)+T_a(6\left)\right)\cdot sin\left(13\alpha \right)\\ \left(x_a\right(0)+T_a(14\left)\right)\cdot sin\left(29\alpha \right)\\ \left(x_a\right(0)+T_a(10\left)\right)\cdot sin\left(21\alpha \right)\\ \left(x_a\right(0)+T_a(12\left)\right)\cdot \mathit{sin}(25\alpha )\end{array}\right]$$

(14)

$$\left[\begin{array}{c}Y\left(16\right)\\ Y\left(8\right)\\ Y\left(4\right)\\ Y\left(2\right)\end{array}\right]=\left[\begin{array}{c}\left(x_a\right(0)+T_a(16\left)\right)\cdot sin\left(33\alpha \right)\\ \left(x_a\right(0)+T_a(8\left)\right)\cdot sin\left(17\alpha \right)\\ \left(x_a\right(0)+T_a(4\left)\right)\cdot sin\left(9\alpha \right)\\ \left(x_a\right(0)+T_a(2\left)\right)\cdot sin\left(5\alpha \right)\end{array}\right]$$

(15)

$$\left[\begin{array}{c}Y\left(11\right)\\ Y\left(3\right)\\ Y\left(7\right)\\ Y\left(5\right)\end{array}\right]=\left[\begin{array}{c}\left(x_a\right(0)+T_a(11\left)\right)\cdot sin\left(23\alpha \right)\\ \left(x_a\right(0)+T_a(3\left)\right)\cdot sin\left(7\alpha \right)\\ \left(x_a\right(0)+T_a(7\left)\right)\cdot sin\left(15\alpha \right)\\ \left(x_a\right(0)+T_a(5\left)\right)\cdot sin\left(11\alpha \right)\end{array}\right]$$

(16)

$$\left[\begin{array}{c}Y\left(1\right)\\ Y\left(9\right)\\ Y\left(13\right)\\ Y\left(15\right)\end{array}\right]=\left[\begin{array}{c}\left(x_a\left(0\right)+T_a\left(1\right)\right)\cdot sin\left(3\alpha \right)\\ \left(x_a\left(0\right)+T_a\left(9\right)\right)\cdot sin\left(19\alpha \right)\\ \left(x_a\left(0\right)+T_a\left(13\right)\right)\cdot sin\left(27\alpha \right)\\ \left(x_a\left(0\right)+T_a\left(15\right)\right)\cdot sin\left(31\alpha \right)\end{array}\right]$$

(17)

In the following sections, we will discuss the efficient parallel implementation of the proposed algorithm using a GPU architecture.

4. Overview of Used NVIDIA Development Boards

In this paper, three distinct NVIDIA CUDA architectures, representing two separate classes of GPU devices, were selected to demonstrate the algorithm’s performance. The first class belongs to the consumer class, which focuses on high throughput, compatibility with gaming engines like Unreal and Unity, and support for machine learning frameworks such as TensorFlow 2 and PyTorch 2.9. The second category of GPU devices is dedicated to Edge AI applications, such as intelligent robotics systems. In this mode, the reader can obtain a clear and comprehensive overview of its performance compared to the traditional implementation of the DST-IV algorithm.

Modern GPUs are designed with varying characteristics, targeting different markets and workloads. As summarized in

Table 1. The main classes of NVIDIA GPU devices.

NVIDIA Type	Series	Application Field
Embedded	Jetson Xavier, Orin, Thor	Edge AI (Aerospace, Automotive, Robotics, IoT, etc.)
Consumer	GeForce RTX 30/40/50 series	Research, Content creation, Gaming
Workstation/ professional	RTX A-series, Quadro	Research, 3D rendering, CAD
Datacenter	A100, H100, H200, H800, L40	Large-scale LLM, Cloud computing

, GPUs can be categorized into four levels: embedded (e.g., Jetson Xavier, Orin), consumer-grade GPUs (e.g., GeForce RTX 30/40/50-series), workstation/professional-grade GPUs (e.g., RTX A4000, A5000, A6000), and data center accelerators (e.g., H100, A100, GH200). Each level offers a unique combination of computing power, memory bandwidth, reliability (including ECC memory features), and power efficiency, thereby affecting their appropriateness for different types of workloads.

In this research, the developed algorithm was tested using three different types of GPUs produced by NVIDIA. The main differences among these GPUs are primarily due to their architectures: Volta, Ampere, and Ada Lovelace. Although NVIDIA developed all the architectures, each represents a different generation of GPUs. The Volta architecture was designed in 2017, the Ampere Architecture in 2020, and the Ada Lovelace architecture in 2022. Each brings technological improvements in performance, power efficiency, and feature set, targeting different market segments.

The NVIDIA Jetson family includes a wide range of embedded computing platforms that vary significantly in computational power, energy efficiency, and physical size. Generally, Jetson Nano boards are intended for beginner AI and robotics projects, where low power consumption and cost savings are more important than high performance. The Jetson lineup features models like Jetson Nano, Jetson NX, and Jetson AGX, which are available in different versions, such as Orin or Xavier. In this hierarchy, the Jetson AGX series—consisting of Jetson AGX Xavier and Jetson AGX Orin—offers the highest performance and most advanced features. These modules provide workstation-level processing in an embedded package, making them perfect for autonomous systems, industrial robots, and edge AI inference. The Jetson NX development boards offer a mid-range option, combining the energy efficiency of the Nano series with the processing power of the AGX line. This makes them a flexible choice for embedded AI applications that need both mobility and high performance.

Each development system has unique features that influence its overall performance, which can sometimes be confusing when comparing the results of the same algorithm run on different development boards. When considering solely memory capabilities, it is evident that the Jetson AGX Orin system provides transfer rates of 204.8 GB/s, surpassing the Jetson AGX Xavier system’s 136.5 GB/s (

Table 2. The main features of the development systems used in this research.

Development System		Jetson AGX Xavier	Jetson AGX Orin	PC with a GeForce RTX 4090 GPU
GPU (NVIDIA type)	Architecture	Volta	Ampere	Ada Lovelace
	Process Node	12 nm TSMC	7/8 nm TSMC/Samsung	TSMC’s 5 nm
	CUDA cores	512	2048	16,384
	Supported CUDA core precisions	INT8, FP16, FP32, FP64	INT8, FP16, Bfloat16, FP32, FP64	INT8, FP8, FP16, Bfloat16, FP32, FP64
	AI performance (INT8)	32 TOPS	275 TOPS	1300 TOPS
	Floating point (FP32)	1.41 TFLOPS	10.6 TFLOPS	82.58 TFLOPS
	Tensor cores	64	64	512
	Supported Tensor Core precisions	FP16	INT1, INT4, INT8, FP16, Bfloat16, TF32, FP64	INT1, INT4, INT8, FP8, FP16, Bfloat16, TF32, FP64
	Memory	-	-	24 GB, 384-bit bus, GDDR6X, 1.01 TB/s
CPU	Processor	8-core NVIDIA Carmel ARM v8.2	12-core Cortex-A78AE ARM v8.2	External 24-core Intel Core i9-14900K
	Memory	32 GB 256-bit bus LPDDR4X 136.5 GB/s	64 GB, 256-bit bus LPDDR5 204.8 GB/s	64 GB, 64-bit bus DDR5 120 GB/s
	CPU max. frequency	2.3 GHz	2.2 GHz	3.2 GHz

)—an expected advantage of a newer generation that embeds a more powerful GPU. In contrast, the personal computer with the most powerful GPU offers a memory transfer rate of only 120 GB/s (the lowest of all 3 systems analyzed). Still, it includes internal memory, allowing a transfer rate of 1.01 TB/s.

The Jetson AGX Xavier offers moderate computational capabilities, equipped with 512 CUDA cores and 64 Tensor Cores, as well as an 8-core ARMv8.2 Cortex-A72 processor, rendering it appropriate for fundamental applications such as object detection, simultaneous localization and mapping (SLAM), and image classification. It achieves up to 32 TOPS of artificial intelligence performance within a configurable power range of 10–30 W. The Jetson AGX Orin represents a significant enhancement in computational power, offering approximately eight times the performance of the Jetson AGX Xavier, and attaining up to 275 TOPS at a power range of 15–60 W. It can execute multiple large-scale models, including transformer-based architectures, in real-time for three-dimensional perception. The RTX 4090 offers an exceptional bandwidth capacity of 1.01 TB/s, suitable for demanding tasks such as large-scale inference, generative processes (including large language models (LLM) or diffusion models), 8K gaming, and scientific simulations. The RTX 4090 is equipped with 16,384 CUDA cores, 512 Tensor Cores, and 24 GB of GDDR6X memory, requiring an input power exceeding 450 W.

The Jetson AGX Orin attains an exceptional equilibrium between energy efficiency and inference capability, establishing itself as the preferred platform for power-sensitive and latency-critical applications at the edge. While the Jetson AGX Xavier remains suitable for less complex AI tasks, it is increasingly constrained by its computational and memory limitations. Conversely, the RTX 4090 delivers unparalleled performance for training and inference of large models; however, it is unsuitable for embedded environments due to its substantial thermal and power demands.

As it is expected, the Jetson Xavier and Orin modules primarily comprise several central processing units (CPUs—8 and 12, respectively) and a graphics processing unit (GPU). To utilize standard interfaces such as Ethernet, USB, and General-Purpose Input/Output (GPIO) pin headers—which facilitate access to UART, SPI, CAN, I2C, I2S, and other communication lines—a carrier board is indispensable for development activities.

In NVIDIA’s architecture, the CUDA cores are grouped into SMs (Streaming Multiprocessors). Depending on the architecture, each SM contains a fixed number of CUDA cores. For example, in NVIDIA’s Ampere architecture, each SM (Streaming Multiprocessor) has 128 CUDA cores. In this situation, the GPU on the Jetson AGX Orin development board has 16 SMs.

5. Materials and Methods

Given that this paper advances the implementation of the DST-IV algorithm, the newly developed algorithm will be compared with the classical algorithm described by relation (1). In Section 7, the newly developed algorithm is also compared with two other recent algorithms that represent alternative state-of-the-art implementations of the DST-IV algorithm [15,19].

The C implementation of the classical DST-IV algorithm [1], as described by relation (1), was executed on each GPU used and served as a reference for all the implemented algorithms. We also conducted an additional analysis, considered as a reference, in which relation (1) was implemented across 17 threads of execution, each operating on a different CUDA core, with each value of k ranging from 0 to 16. This decision is motivated by the intention to emphasize solely the performance enhancement attributable to the new implementation, without considering the performance gains resulting from more advanced architecture or an increased operating frequency of a particular processor type.

In this context, using Equation (1), the sequence of N real numbers, x(i), is transformed into another output sequence, Y(k), of real numbers with the same length as the input sequence, using the DST-IV transform. This traditional implementation was executed on a CUDA core during performance analysis. In the classical DST-IV implementation, the “sin” function was the default library implementation on double precision, unlike “__nv_fast_sinf”, which offers a faster but less accurate way to calculate sine.

In this research, the measurement cycle consists of three sequential stages: first, transferring data from the Central Processing Unit (CPU) to the Graphics Processing Unit (GPU); the second, performing a DST-IV transform, as defined by relation (1) or one of the novel Discrete Sinus Transform (DST) IV implementations introduced in this study—either with four-section or eight-section configurations; and the third, transferring data from the GPU back to the CPU. As a direct conclusion, in all the determinations performed, the measured durations include: (1) the data transfer times between the CPU and GPU in both directions, and (2) the data processing time needed to obtain the result using the new DCT-IV algorithm. The latter covers the calculation time within the CUDA cores, as well as the time required to access internal variables and data structures within the GPU needed by the DCT-IV algorithm.

The data set used as input for calculating the DST-IV transforms was randomly generated and scaled at the beginning of each measurement cycle using the “rand()” function from the C programming language. Ultimately, all generated values fall within the range of [−1, +1]. On a GPU, arithmetic operations are performed on SIMD (Single Instruction, Multiple Data) hardware. Specifically, several fma.rn.f32 assembly instructions were utilized to implement the program as primary components. These instructions execute a fused multiply–add (fma) operation on 32-bit floating-point numbers. Consequently, a PTX (Parallel Thread Execution) instruction such as fma.rn.f32 d, a, b, c, is equivalent to a fused multiply–add (computing a ∗ b + c), followed by rounding the result to the nearest (.rn—round to nearest) representable 32-bit floating-point number (adhering to the IEEE 754 standard) before storing the value in the operand d. All these operations are executed within a single clock cycle per pipeline. As a result, the multiplication and addition operations occur within a constant time interval irrespective of the operand values. Therefore, the data on which the algorithm was tested did not influence its final performance outcomes.

Based on the measurement cycle outlined above, one determination is the average value of 10,000 sequential measurement cycles. For the statistical analysis of the performance values obtained on each architecture supported by each development system, 100 such determinations were conducted. Then, statistical parameters such as average values, standard deviations, minimum, and maximum values were calculated. All measurements were made at the minimum frequency of the GPUs. This approach offers valuable insights into an algorithm’s efficiency, robustness under constrained conditions, and understanding of the worst-case scenario analysis. It also provides high-speed performance with low power consumption.

The computation time for each measurement cycle was determined using events from the CUDA event API. Functions such as “cudaEventCreate()”, “cudaEventRecord()”, and “cudaEventElapsedTime()” were used to measure the elapsed time. This measurement method offers a resolution of about half a microsecond [36]. This approach to measuring time is well-known and accepted for performance evaluations related to GPUs [18,36,37,38,39].

The DST-IV algorithms (both classical and parallel implementations) ran on GPUs as kernel functions mapped as one thread on each block, such as: DST4_clasic <<<1, 1>>> (in_gpu, out_gpu), DST4_4sections <<<4, 1>>> (in_gpu, out_gpu), and DST4_8sections <<<8, 1>>> (in_gpu, out_gpu). In all measurements, the internal data, constants, input, and output data buffers were stored in global memory unless otherwise specified.

Figure 1 demonstrates the operation of the algorithm on both the Central Processing Unit (CPU) and the four CUDA cores within the Graphics Processing Unit (GPU). It depicts the parallel implementation of the novel DST-IV algorithm, segmented into four sections. Furthermore, it is evident from Figure 1 that the four execution threads, each allocated to a CUDA core on the GPU, neither exchange data among themselves nor synchronize their processes in any way. Each thread computes four distinct coefficients from the result buffer provided by the new algorithm, which is executed on the GPU and subsequently transmitted to the CPU.

Additionally, the NVIDIA Nsight Compute package was used to profile the CUDA applications for GPU utilization, data transfer, and memory workload.

The programs were compiled using the NVIDIA CUDA official compiler (“nvcc”), which is part of the NVIDIA JetPack SDK. The SDK provides a comprehensive environment for developing C and C++ GPU-accelerated programs and AI applications optimized for each specific CUDA architecture. To enhance performance, the programs were compiled specifically for each GPU’s architecture and version, see Table 2. This approach ensures that the resulting binary code is compatible with the target architecture and delivers optimal performance.

The following line outlines the NVIDIA compiler arguments:

$ nvcc source_code_name.cu -o binary_name -v -arch = xxx

The xxx flag is specific to the destination architecture to which the program was compiled—the arguments used are listed in

Table 3. The specific architecture flag used to compile the developed applications.

Architecture/ System	Volta	Ampere	Ada Lovelace
	Jetson AGX Xavier	Jetson AGX Orin	GeForce RTX 4090
nvcc architecture flag	sm_72	sm_87	sm_89
CUDA toolkit version	11.4.315	12.6.68	12.6.77

. The same table also presents the version of the CUDA Toolkit utilized in the development and testing of the applications developed.

6. Experimental Results

To accurately measure the performance of the parallel implementation of the proposed novel DST-IV algorithm, each section was executed on a different CUDA core, and no other applications were running on any GPU core during these tests. The results obtained by each algorithm are presented in the following tables, based on the following parameters: mean execution time, standard deviation of the execution time (Mean ± SD), minimum, and maximum execution times for each specific measurement condition (GPU architecture)—listed in red in the tables. All algorithms were implemented using a double-precision numeric format for the data.

The results obtained are presented in

Table 4. Performances achieved by running the two DST-IV computing algorithms (the classical algorithm and the parallel implementation with four sections) on different GPU architectures.

Processing Parameters	Jetson AGX Xavier		Jetson AGX Orin		GeForce RTX 4090
	Classical Implementation	Parallel Implementation	Classical Implementation	Parallel Implementation	Classical Implementation	Parallel Implementation
Mean [ms]	2.726981	0.121616	1.060448	0.045407	1.533704	0.030397
SD:	0.047445	0.013500	0.015143	0.000110	0.030806	0.000474
Min. [ms]	2.715814	0.115398	1.048011	0.045262	1.518988	0.030280
Max. [ms]	3.098767	0.195114	1.168211	0.046345	1.736231	0.035085
Overall speedup (Soall real)	22.422868		23.354518		50.455702

and

Table 5. Performances achieved by running the two DST-IV computing algorithms (classical algorithm and the parallel implementation with eight sections) on different GPU architectures.

Processing Parameters	Jetson AGX Xavier		Jetson AGX Orin		GeForce RTX 4090
	Classical Implementation	Parallel Implementation	Classical Implementation	Parallel Implementation	Classical Implementation	Parallel Implementation
Mean [ms]	2.725423	0.112020	1.093350	0.038822	1.526814	0.023400
SD:	0.037169	0.000779	0.079551	0.005259	0.022835	0.000171
Min. [ms]	2.700831	0.110377	1.048580	0.036764	1.514336	0.022893
Max. [ms]	3.000983	0.115165	1.425861	0.072291	1.638012	0.023708
Overall speedup (Soall real)	24.329686		28.163104		65.249109

. The reference was always a measurement of the classical implementation of DST-IV (relation (1)), executed on a single core of one of the GPU architectures used.

The acceleration attained by the proposed innovative algorithm compared to the traditional one (which relies on the direct implementation of relation (1)) is presented in the final row of Table 4 and Table 5. This acceleration factor is determined as the ratio of the mean execution time of the traditional algorithm to that of the targeted algorithm, employing either 4 or 8 sections.

Table 4 shows the results for the algorithm configured with four sections running in parallel, while Table 5 presents the results for the innovative algorithm with eight sections operating in parallel.

According to Table 4, the DST-IV algorithm, when implemented across four sections, exhibits performance enhancement ranging from 22.42 to 50.46. The performance of the DST-IV algorithm, implemented across eight sections, demonstrates improvements in the speedup factor ranging from 24.33 to 65.25. This can be partially explained by the nature of the proposed parallel algorithm, which, in addition to parallel decomposition, incorporates an algorithm characterized by low arithmetic complexity. This is achieved by utilizing the subexpression sharing technique, minimizing memory accesses, and using constant values that are calculated, stored, and used later.

The Ada Lovelace architecture in the GeForce RTX 4090 system shows greater speedup in executing the new algorithm compared to the classical one, surpassing the performance increases seen on older architectures like the Ampere GPU in the Jetson AGX Orin board—23.35 versus 50.46 (for the DST-IV algorithm in 4 parallel sections, Table 4) or 28.16 versus 65.25 (for the DST-IV algorithm in 8 parallel sections, Table 5). This is a notable observation. It demonstrates that a more powerful or newer architecture achieves higher speed gains with the innovative algorithm compared to the classical one, surpassing the improvements seen in older architectures. This underscores NVIDIA’s ongoing efforts to enhance architectures and eliminate limitations of older designs.

Analyzing relation (1), it is evident that the computation of the classical DST-IV transform for 17 elements necessitates the calculation of 17 sums of products that are mutually independent. Accordingly, this classical algorithm can be efficiently implemented in parallel across 17 distinct segments. Consequently, a pertinent question emerges: what would be the performance of the novel developed algorithm if the reference point is the implementation of the classical algorithm with 17 segments executed concurrently?

Table 6. Performances achieved by running the two DST-IV computing algorithms (the classical algorithm implemented with 17 sections and the parallel implementation with four sections) on different GPU architectures.

Processing Parameters	Jetson AGX Xavier		Jetson AGX Orin		GeForce RTX 4090
	Classical Implementation	Parallel Implementation	Classical Implementation	Parallel Implementation	Classical Implementation	Parallel Implementation
Mean [ms]	0.304001	0.121616	0.132488	0.045407	0.104788	0.030397
SD:	0.001298	0.013500	0.005942	0.000110	0.000167	0.000474
Min. [ms]	0.302748	0.115398	0.107304	0.045262	0.104151	0.030280
Max. [ms]	0.310680	0.195114	0.150337	0.046345	0.105134	0.035085
Overall speedup (Soall real)	2.499679		2.917788		3.447313

and

Table 7. Performances achieved by running the two DST-IV computing algorithms (the classical algorithm implemented with 17 sections and the parallel implementation with eight sections) on different GPU architectures.

Processing Parameters	Jetson AGX Xavier		Jetson AGX Orin		GeForce RTX 4090
	Classical Implementation	Parallel Implementation	Classical Implementation	Parallel Implementation	Classical Implementation	Parallel Implementation
Mean [ms]	0.304557	0.112020	0.116269	0.038822	0.106276	0.023400
SD	0.001312	0.000779	0.008623	0.005259	0.000300	0.000171
Min. [ms]	0.300802	0.110377	0.106742	0.036764	0.105749	0.022893
Max. [ms]	0.310526	0.115165	0.154314	0.072291	0.106942	0.023708
Overall speedup (Soall real)	2.718773		2.994925		4.541709

answer this question.

The performance gains are between 2.49 and 3.45 for the new algorithm implemented with 4 sections, and between 2.72 and 4.54 for the new algorithm with 8 sections. Analyzing these results, presented in Table 6 and Table 7, reveals that the new algorithm remains faster than the classic DST-IV algorithm, which is implemented with 17 sections running in parallel. The methodology employed to acquire these results is similar to that used for obtaining the data presented in Table 4 and Table 5. Furthermore, these results also include the duration necessary for data transfer between the CPU and GPU, and vice versa.

The execution time for each algorithm mainly depends on three factors: (1) the number and type (integer, float, double, bfloat, etc.) of computations performed on specific hardware (CPU, GPU, NPU, etc.), (2) the number of memory accesses and the type of memory accessed, and (3) how the algorithm is implemented (e.g., parallel or sequential).

By counting the operations performed by an algorithm—such as addition, subtraction, division, multiplication, or any other operation involving floating-point values—one can determine the FLOPs (Floating Point Operations). The FLOPs serve as an estimate of the model’s complexity. In

Table 8. The number of Floating-Point Operations (FLOPs) required by an algorithm to complete its execution.

	Classical Implementation	4 Sections in Parallel	8 Sections in Parallel
FLOPS	8670	872	864

, the number of FLOPs required by each kernel (only for the component(s) that are executed on the GPU) to complete its execution is shown.

The information in Table 8 was derived using NVIDIA Nsight Compute, a profiling tool that provides detailed performance metrics for software components (kernels) running on CUDA cores. To obtain the values presented in the previous table, the recorded count of DFMA (Double-precision Fused Multiply–Add) instructions, captured by NVIDIA Nsight Compute, was multiplied by two. The classical algorithm consumes so many FLOPs to complete, mainly due to the use of “sin” library functions. Additionally, it should be noted that the eight-section algorithm requires slightly fewer instructions to finish (compared to the four-section implementation); however, some of these instructions are executed in parallel across eight sections.

Another important observation from Table 4 and Table 5 is that an NVIDIA GPU utilizes various types of memory, each with distinct characteristics and purposes: registers, shared memory, surface memory, texture memory, local memory, and global memory. In Figure 2, a schematic shows all types of memory present in a GPU; in this case, the GPU is part of the Jetson AGX Xavier development board.

Global memory is the largest type of memory on a GPU, but it also has the slowest access speed. It can be accessed by all threads running on the GPU and the host CPU. Shared memory, located on the GPU chip, provides faster access but is limited to threads within the GPU. Local memory is an abstraction of global memory used for thread-local variables. Texture and surface memory are specialized types optimized for specific data access patterns; however, they are not helpful for the algorithm described in this paper.

The developed algorithms (with 4 and 8 sections) do not use shared memory, surface memory, or texture memory. In

Table 9. Number of requests from global and local memory generated by the classical algorithm and by the developed algorithms (with 4 and 8 sections).

Memory Type and Access Type		Memory Access [Number of Requests]
		Classical Implementation	4 Sections in Parallel	8 Sections in Parallel
Global	Read	2310	64	64
	Write	306	16	32
Local	Read	0	0	0
	Write	289	0	0

, the number of memory accesses to local and global memories is shown. The data were obtained using the NVIDIA Nsight Compute tool. For the classical implementation of DST-IV, the same information from Table 9 is also displayed in Figure 2.

Memory poses a significant limitation for nearly all applications because it operates more slowly than CUDA core units. As shown in Table 9, the new algorithm introduced in this study is more efficient based on the write/read operations performed by the algorithms. The classical algorithm needs a total of 2310 read requests and 306 write requests to global memory, along with 289 write requests from local memory to complete its execution. The new algorithms (with 4 and 8 sections) do not utilize local memory and require 64 reads from global memory, along with 16 writes for the 4-section algorithm and 32 writes for the 8-section algorithm, to accomplish their goals.

Considering the substantial influence of memory access on overall performance, all kernel variables and constants were stored in shared memory (placed on the L1 cache of the Streaming Multiprocessor) in the following analysis. The performance of the new DST-IV algorithm within this configuration was evaluated in accordance with the methodology detailed in Section 5. The results are presented in

Table 10. The analysis of the new algorithm (with 4 and 8 sections) considers the case when the variables and constants of each kernel function are placed in shared memory.

Measured Parameters	Parallel Implementation with 4 Sections		Parallel Implementation with 8 Sections
	Global Memory	Shared Memory	Global Memory	Shared Memory
Mean [ms]	0.045407	0.045006	0.038822	0.038509
SD	0.000110	0.000325	0.005259	0.000356
Min. [ms]	0.045262	0.044321	0.036764	0.037835
Max. [ms]	0.046345	0.045679	0.072291	0.039264

.

An analysis of the data presented in Table 10 indicates that the inclusion of internal constants and variables of each kernel within shared memory results in marginal enhancements in the execution durations of the revised kernel—0.045407 ms compared to 0.045006 ms in the case of the four-section algorithm, and 0.038822 ms relative to 0.038509 ms for the eight-section algorithm. These slight improvements are primarily attributable to the limited number of memory accesses (as listed in the preceding table, Table 9) performed by the new algorithm. This characteristic constitutes one of the fundamental advancements and distinctive features introduced by the new algorithm.

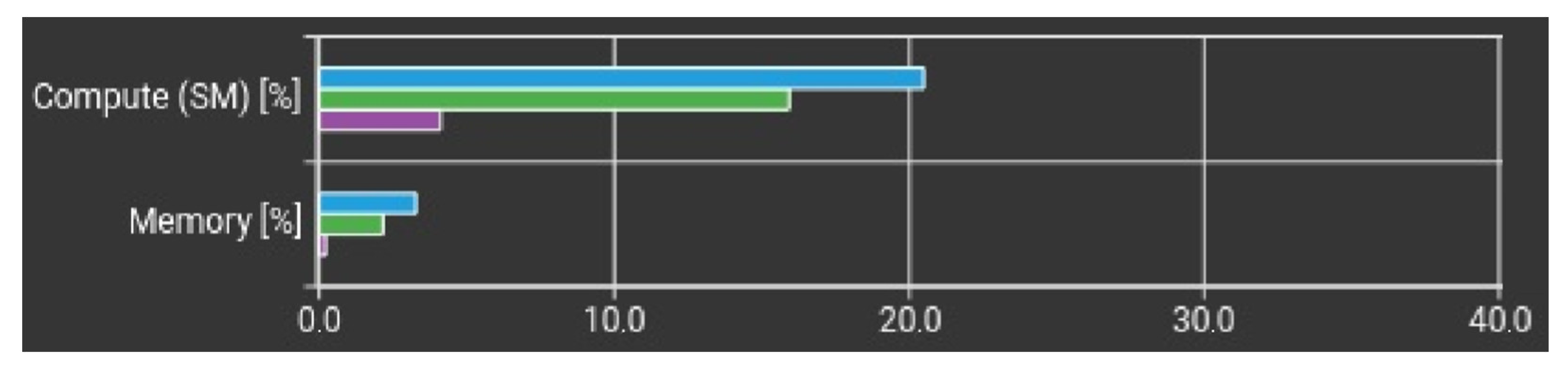
To evaluate the performance of all three methods for implementing the DST-IV algorithm—namely, the classical approach based on relation (1), the new algorithm with four sections, and the version with eight sections—Figure 3 shows the throughput concerning the GPU’s computing and memory resources during a specific working period outlined in

Table 11. The execution time of each kernel unit implementation.

	The Time Intervals of Kernel Execution
Jetson AGX Xavier	Classical implementation	4 sections in parallel	8 sections in parallel
	2.65 ms	66.24 us	53.98 us

. All data was collected using the NVIDIA Nsight Compute tool on the Jetson AGX Xavier development board.

The results in Figure 3 are presented per SM unit, indicating the utilization percentage relative to the theoretical maximum limit.

The traditional implementation of the DST-IV algorithm achieved 4.13% of the total computing throughput of an SM unit and 0.23% memory throughput during a 2.65 ms kernel execution time, as shown in Table 11. Under the same conditions, the new four-section parallel implementation of the DST IV algorithm reached a computational throughput of 15.93% and 2.17% memory throughput in just 66.24 microseconds. The highest computational throughput was obtained with the eight-section algorithm, which achieved 20.51%.

To attain a thorough understanding and a comprehensive overview of the novel DST-IV developed algorithm, this algorithm (implemented with four and eight sections) was compared with the traditional implementation of DST-IV executed on a single-threaded CPU core, as well as with the sequential implementation of the new algorithm on a CPU, as detailed in

Table 12. Algorithm’s performance analysis: CPU versus GPU.

Execution Place	CPU		GPU
Algorithm	Classical Implementation	Novel Algorithm Sequential Implementation	Parallel Implementation 4 Sections	Parallel Implementation 8 Sections
Mean [ms]	0.039204	0.070162	0.045407	0.038822
SD	0.000371	0.000013	0.000110	0.005259
Min. [ms]	0.038603	0.070116	0.045262	0.036764
Max. [ms]	0.040764	0.070195	0.046345	0.072291

. The tests were conducted on a Jetson AGX Orin GPU (2048 CUDA cores, operating at 306 MHz) and a Cortex-A78AE CPU (12 cores, operating at 345.6 MHz). The Cortex-A78AE CPU is integrated into the Jetson AGX Orin development board. The closest values to the GPU’s operating frequency (306 MHz) are 268 MHz and 345.6 MHz.

To establish a fair and transparent baseline for comparing the running results of algorithms on CPU and GPU (devices with different (1) architectures and (2) main concepts supporting these architectures), the CPU’s operating frequency was chosen to be as close as possible to the GPU’s operating frequency. The operating frequency of the CPU can only be set through software to specific fixed operation points. The CPU’s closest values to the GPU’s operating frequency (306 MHz) are 268 MHz and 345.6 MHz. From this perspective, the CPU works at a higher frequency than the GPU in this analysis. The execution time exhibits an inverse proportionality to the CPU frequency. Assuming an inverse linear relationship between execution time and CPU frequency, the execution time for the classical implementation of the DST-IV algorithm on a CPU operating at 306 MHz is estimated at 44.28 ms. Under identical conditions, the execution time for the newly developed algorithm, implemented sequentially on the CPU, is 79.24 ms. In the results shown in Table 12, the time taken for data transfer between the CPU and GPU, in both directions, was also included in the algorithms’ execution times on the GPU.

The time required to execute the classic algorithm on the CPU (44.28 ms) is similar to that of the 4-section algorithm on the GPU (45.41 ms) and longer than that required to execute the new 8-section algorithm (38.82 ms). In this instance, the overall benefit of the new algorithm (with 4 sections) is derived from an additional factor. Even a high-performance processor like the Intel Core i9-14900K, with 24 cores, can execute only 24 conventional DST-IV algorithms concurrently. Within the same timeframe, the GeForce RTX 4090 graphics card, equipped with 16384 CUDA cores, can perform 4096 DST-IV transformations (with four sections). This analysis presumes that both the CPU and GPU are operating at identical frequencies.

7. Discussion

Comparing different algorithms that implement the DST-IV is a difficult task. The different implementations of DST are made on different development systems (FPGA, ASIC, GPU, or CPU), running at different working frequencies, having different architectures, based on different frameworks (like Matlab [21], which is known as a slow development environment), many of these algorithms are based on certain technical specificities of the support system on which they run and which are not found on other development systems.

For these reasons, we selected to implement two distinct DST-IV algorithms, namely [15,19], as documented in the literature, and subsequently evaluate them under identical conditions to those utilized for testing the algorithm described in this paper. The analytical methodology used to test these algorithms is identical to the one employed in Subchapter 5 of this paper. Furthermore, both algorithms exhibit conceptual similarities to the algorithm presented herein and are founded on the decomposition of the traditional DST-IV algorithm into four sections [15] and six sections [19], which operate concurrently.

The results are presented in

Table 13. Performance analysis of several DST-IV implementations (done on Jetson AGX Orin development board) when the GPU frequency was set to the minimum value.

DST-IV Algorithm Implementation Type	Classical Implementation Execution Mean Time [ms]	Parallel Implementation Execution Mean Time [ms]	Speedup Factor
4 sections	1.060448	0.045407	23.35
8 sections	1.093350	0.038822	28.16
1st algorithm, with 4 sections [15]	0.612998	0.058482	10.48
2nd algorithm, with 6 sections [19]	0.619165	0.055502	11.16

and were acquired using the Jetson AGX Orin development board. On the second and third lines, the performances of the novel proposed algorithm for the cases of implementation on 4 and 8 sections are presented. These results are from Table 4 and Table 5. In the last two lines, the performances of the algorithms [15,19] are presented.

One of the primary differences between the proposed algorithm and the two algorithms referenced in the literature [15,19], which were implemented, pertains to the number of working samples; specifically, References [15,19] utilize 13 samples, whereas the proposed algorithm employs 17 samples. This is why the execution times of the classical algorithm in Table 13 differ, with one being around 1 ms and the other 0.61 ms.

In conclusion, the direct comparison of execution times remains irrelevant, even if the proposed algorithm demonstrates faster performance than the algorithms [15] and [19]—specifically, 0.045407 and 0.038822 versus 0.058482 and 0.055502. Consequently, the speed improvement of each of the four DST-IV algorithms was compared to a reference algorithm. The classical implementation of DST-IV, based on relation (1), served as the benchmark algorithm, using the same number of samples as the algorithm it was compared to.

Based on the data provided in Table 13, it is evident that the newly proposed algorithm outperforms the algorithms described in [15,19]. This increase in performance of the new algorithm is impressive, being more than twice that of the algorithms presented in [15,19]—23.35 and 28.16 versus 10.48 and 11.16.

Previously, we implemented a faster parallel execution method for the DCT-IV algorithm [18]. When comparing the performance of this new algorithm with the previous one, we see that the new DST-IV implementation clearly and significantly exceeds the old performance. For example, in the case of the Jetson AGX Xavier development system, the execution speed multiplication factor for the 4-section algorithm was 12.1 [18], while for the current algorithm, it is 22.42.

However, because the novel DST-IV has a different form and was derived using other methods and equations compared to DCT-IV [18], the two algorithms differ. In both cases, we aim to highlight 4 or 8 computational structures that can be computed in parallel. Moreover, in the DST-IV algorithm, we have further reduced the number of multiplications to a minimum, replacing also the multiplications with ½ and ¼ that are used in the DCT-IV algorithm [18] with additions and subtractions only, because matrices A and C contain only 1, −1, and 0—see relations (6) and (7) presented above.

A potential drawback of the novel proposed algorithm is its limitation to parallelization on only four or eight distinct sections. This restriction primarily arises from the mathematical factorization method underlying its implementation. However, due to data communication overhead, the performance enhancements are not substantial when increasing the number of parallel sections, as evidenced by our analysis when transitioning from 4 to 8 sections.

8. Conclusions

All the results shown earlier, especially the comparison with other cutting-edge DST-IV algorithms, clearly demonstrate that the newly developed DST-IV algorithm greatly surpasses all expectations.

The enhancement in execution speed ranges from 22.42 to 50.46 times for the implementation divided into four sections (see Table 4), and from 24.33 to 65.25 times when applying the DST-IV algorithm based on eight independent sections (see Table 5). These performances arise from a combination of several factors: the enhanced factorization technique of the DST-IV algorithm, the reduced number of mathematical operations involved, the a priori calculation of the coefficients, a low number of memory accesses, and their implementation in parallel.

Another significant aspect to consider is that the Ada Lovelace architecture offers considerable enhancements in execution speed compared to the Volta and Ampere architectures, resulting in more than double the performance.

As future work, we are considering investigating how speed performance can be enhanced by increasing the degree of parallelism, with particular attention to the impact of data transfers that may constrain speed improvements as parallelism increases. Additionally, we plan to explore alternative parallel architectures suitable for implementing our algorithms. Furthermore, we are considering implementing other discrete transforms on GPU architectures and examining their specific features to adapt our algorithms accordingly for such parallel systems.

In conclusion, based on the results obtained, it is evident that the novel DST-IV algorithm presented in this paper demonstrates exceptional performance, establishing it as a leading example among the contemporary state-of-the-art DST-IV algorithms.