Simplification of Indirect Resonant Switched-Capacitor Converter Based on State-Space Average Model Method
Abstract
1. Introduction
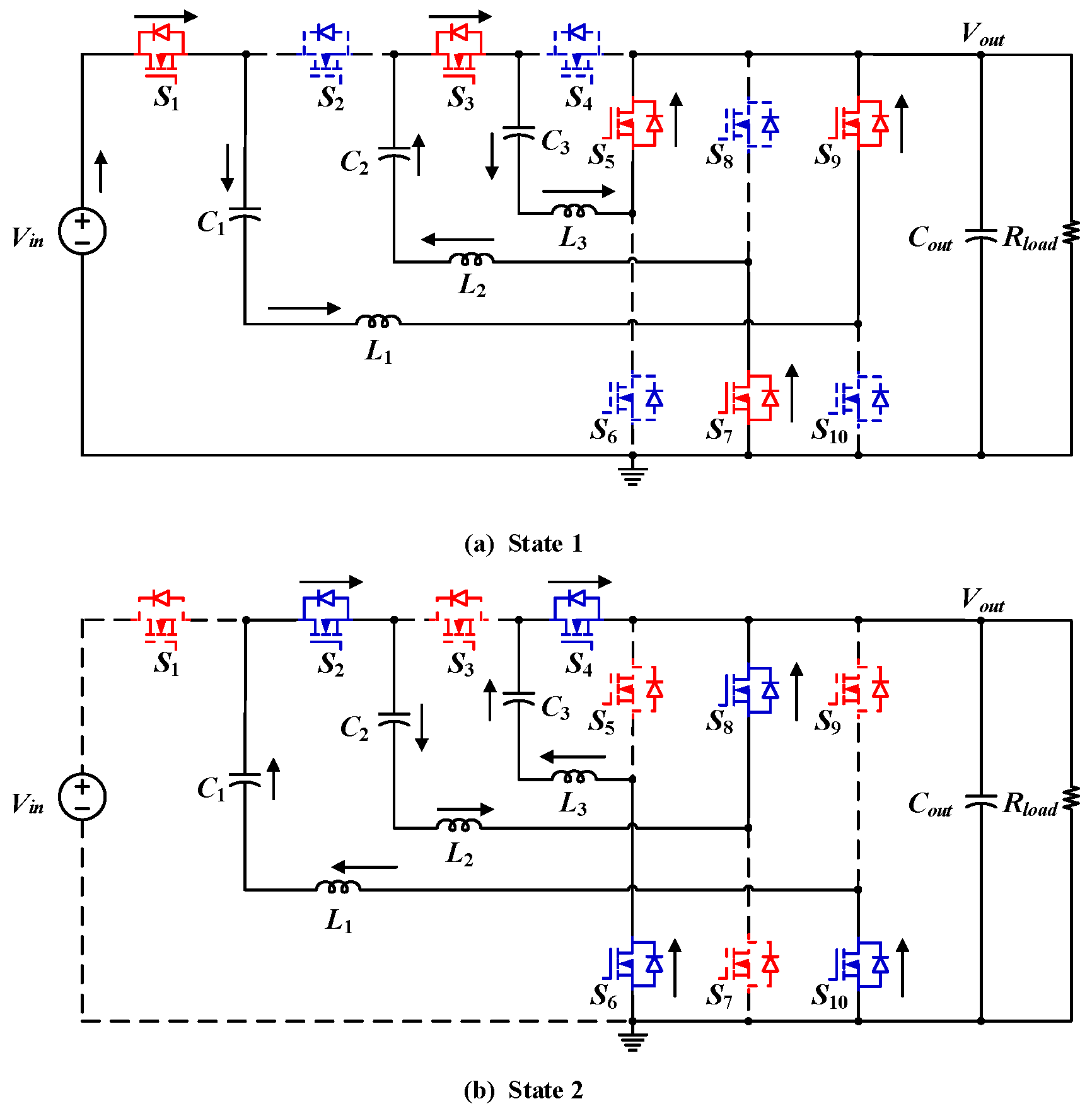
2. Operation Principle of Indirect ReSC Converter
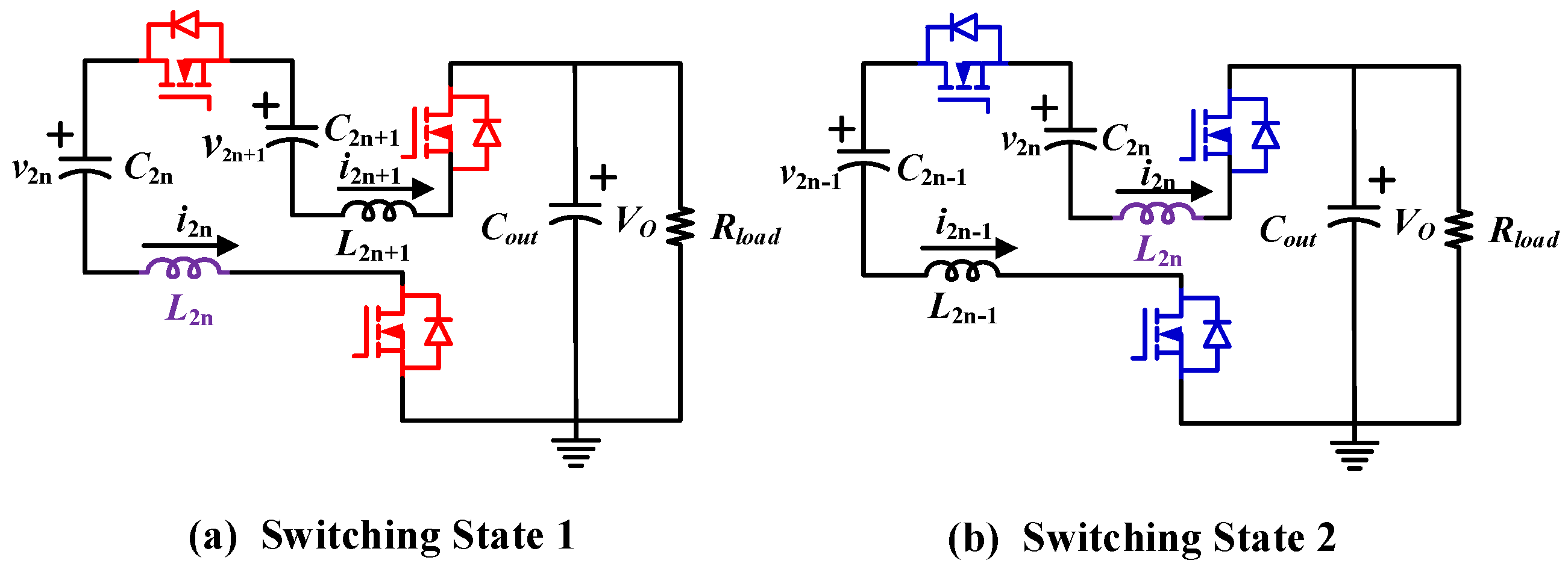
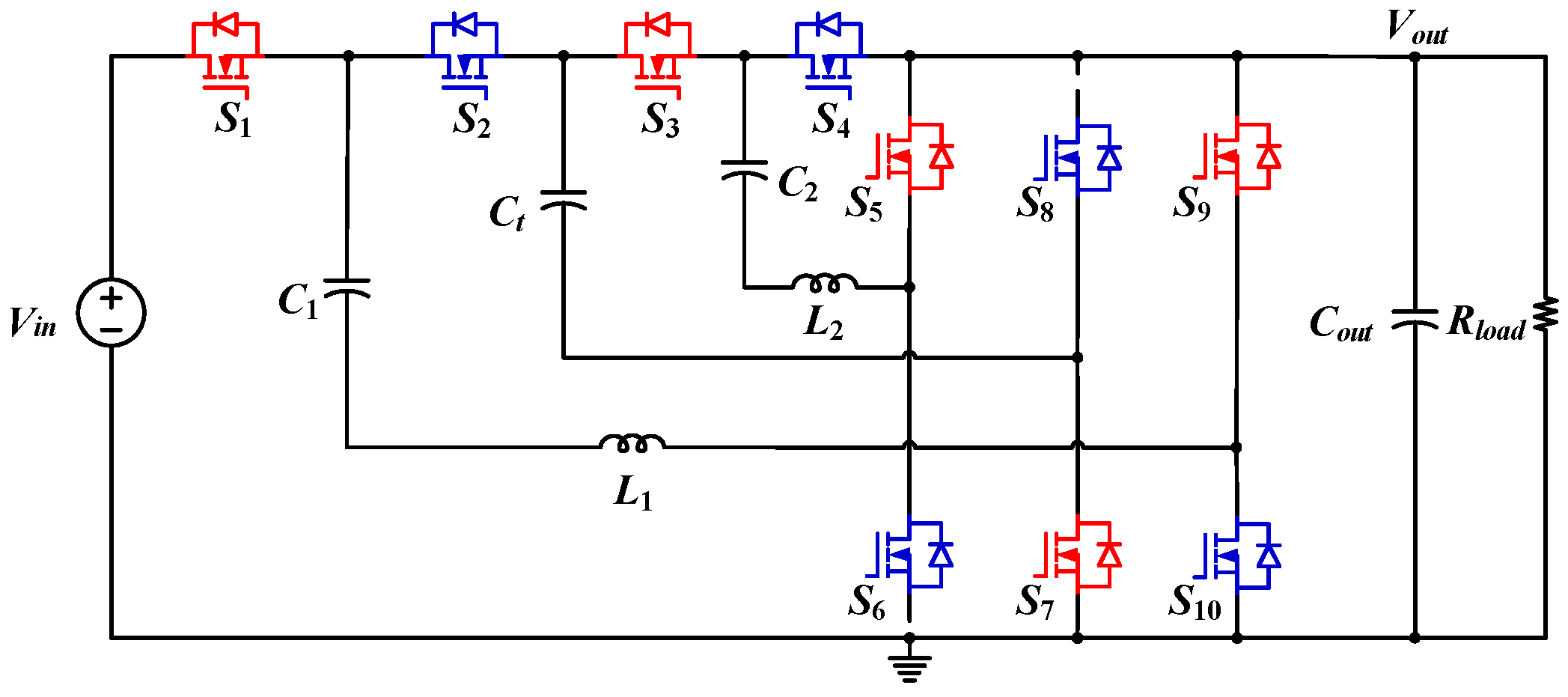
3. State-Space Average Model of Indirect ReSC Converter
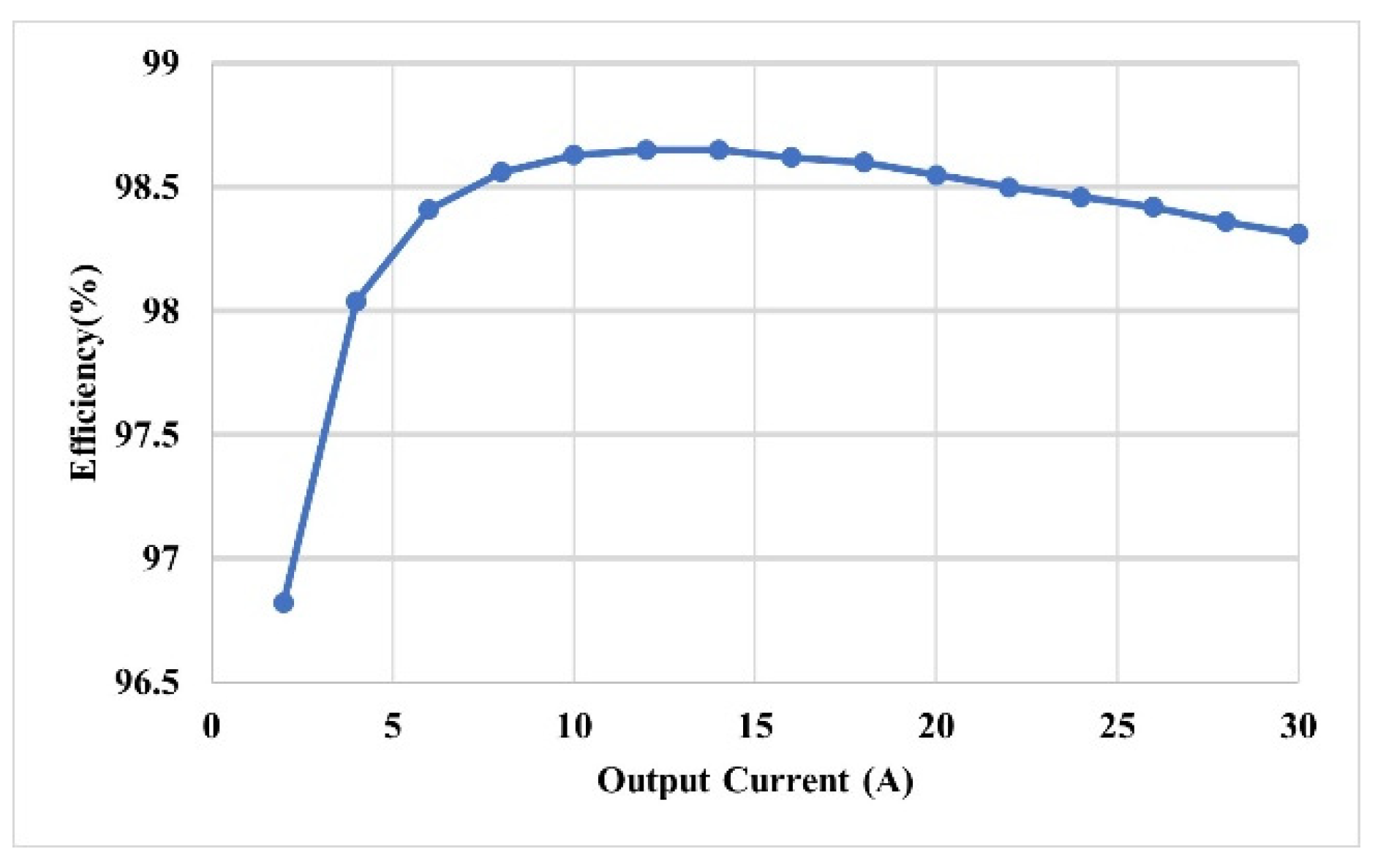
4. Simulation and Experiment Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ReSC | Resonant switched-capacitor |
| VCR | Voltage conversion ratio |
Appendix A
References
- Shehabi, A.; Smith, S.J.; Sartor, D.A.; Brown, R.E.; Herrlin, M.; Koomey, J.G.; Masanet, E.R.; Horner, N.; Azevedo, I.L.; Lintner, W. United States Data Center Energy Usage Report. 2016. Available online: https://datacenters.lbl.gov/sites/default/files/EnergyUsageWebinar12062016.pdf (accessed on 2 April 2023).
- Li, Y.; Lyu, X.; Cao, D.; Jiang, S.; Nan, C. A 98.55% Efficiency Switched-Tank Converter for Data Center Application. IEEE Trans. Ind. Appl. 2018, 54, 6205–6222. [Google Scholar] [CrossRef]
- Lyu, X.; Li, Y.; Ren, N.; Nan, C.; Cao, D.; Jiang, S. Optimization of High-Density and High-Efficiency Switched-Tank Converter for Data Center Applications. IEEE Trans. Ind. Electron. 2020, 67, 1626–1637. [Google Scholar] [CrossRef]
- Whitney, J.; Delforge, P. Data Center Efficiency Assessment; Technical Report 14-08-A; Natural Resources Defense Council: New York, NY, USA, 2014. [Google Scholar]
- Dago, A.; Leoncini, M.; Saggini, S.; Levantino, S.; Ghioni, M. Hybrid Resonant Switched-Capacitor Converter for 48–3.4 V Direct Conversion. IEEE Trans. Power Electron. 2022, 37, 12998–13002. [Google Scholar] [CrossRef]
- Baek, J.; Nomiyama, T.; Park, S.; Jung, Y.-H.; Kim, D.; Han, J.; Bang, J.-S.; Lee, Y.; Kim, I.-H.; Paek, J.-S.; et al. 11.7 A voltage-tolerant three-level buck-boost DC-DC converter with continuous transfer current and flying capacitor soft charger achieving 96.8% power efficiency and 0.87 μs/V DVS rate. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 16–20 February 2020; pp. 202–204. [Google Scholar]
- Ko, M.-W.; Kim, K.-D.; Woo, Y.-J.; Shin, S.-U.; Han, H.-K.; Huh, Y.; Kang, G.-G.; Cho, J.-H.; Lim, S.-J.; Park, S.-H.; et al. A 97% high-efficiency 6μsfast-recovery-time buck-based step-up/down converter with embedded 1/2 and 3/2 charge-pumps for li-lon battery management. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 11–15 February 2018; pp. 428–430. [Google Scholar]
- Nishijima, K.; Harada, K.; Nakano, T.; Nabeshima, T.; Sato, T. Analysis of double step-down two-phase buck converter for VRM. In Proceedings of the Twenty-Seventh International Telecommunications Conference (INTELEC 05), Berlin, Germany, 18–22 September 2005; pp. 497–502. [Google Scholar]
- Hu, T.; Huang, M.; Martins, R.P.; Lu, Y. A 12-to-1 Flying Capacitor Cross-Connected Buck Converter with Inserted D > 0.5 Control for Fast Transient Response. IEEE J. Solid-state Circuits 2023, 58, 3207–3218. [Google Scholar] [CrossRef]
- Huang, J.; Lam, C.-S.; Lu, Y.; Martins, R.P. A Symmetrical Double Step-Down Converter with Extended Voltage Conversion Ratio. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 4761–4773. [Google Scholar] [CrossRef]
- Yuan, J.; Liu, Z.; Wu, F.; Cheng, L. A 12 V/24 V-to-1V DSD power converter with 56 mV droop and 0.9 μs 1% settling time for a 3 A/20 ns load transient. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 20–26 February 2018; pp. 1–3. [Google Scholar]
- Wei, K.; Ramadass, Y.; Ma, D.B. 11.1 A direct 12 V/24 V-to-1 V 3 W 91.2%-efficiency tri-state DSD power converter with online VCF rebalancing and in-situ precharge rate regulation. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 16–20 February 2020; pp. 190–192. [Google Scholar]
- Seo, G.-S.; Le, H.-P. An inductor-less hybrid step-down DC-DC converter architecture for future smart power cable. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 247–253. [Google Scholar]
- Hardy, C.; Le, H.-P. 8.3 A 10.9 W 93.4%-efficient (27 W 97%-efficient) flying-inductor hybrid DC-DC converter suitable for 1-cell (2-cell) battery charging applications. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 17–21 February 2019; pp. 150–152. [Google Scholar]
- Sanders, S.R.; Alon, E.; Le, H.-P.; Seeman, M.D.; John, M.; Ng, V.W. The Road to Fully Integrated DC–DC Conversion via the Switched-Capacitor Approach. IEEE Trans. Power Electron. 2013, 28, 4146–4155. [Google Scholar] [CrossRef]
- Le, H.-P.; Sanders, S.R.; Alon, E. Design Techniques for Fully Integrated Switched-Capacitor DC-DC Converters. IEEE J. Solid-state Circuits 2011, 46, 2120–2131. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, K.; Chen, M.; Xu, D. Data Center Power Supply Systems: From Grid Edge to Point-of-Load. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 2441–2456. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, F.; Peng, F.Z. Power losses and efficiency analysis of multilevel dc–dc converters. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Austin, TX, USA, 6–10 March 2005; pp. 1393–1398. [Google Scholar]
- Wai, V.; Ng, S.; Sanders, S.R. Switched Capacitor DC-DC Converter: Superior Where the Buck Converter Has Dominated. Ph.D. Thesis, Electrical Engineering and Computer Sciences Department of the University of California, Berkeley, CA, USA, 2011. [Google Scholar]
- Lei, Y.; May, R.; Pilawa-Podgurski, R. Split-Phase Control: Achieving Complete Soft-Charging Operation of a Dickson Switched-Capacitor Converter. IEEE Trans. Power Electron. 2016, 31, 770–782. [Google Scholar] [CrossRef]
- Liang, J.; Wang, L.; Liang, J.; Fu, M.; Long, T.; Wang, H. A Switched-Capacitor and Series-Resonant Hybrid MHz DCX in Data Center Applications. IEEE Trans. Power Electron. 2024, 39, 13389–13400. [Google Scholar] [CrossRef]
- Dago, A.; Balutto, M.; Saggini, S.; Leoncini, M.; Levantino, S.; Ghioni, M. Hybrid Resonant Switched Tank Converters for High Step-Down Voltage Conversion. IEEE Trans. Power Electron. 2024, 39, 14838–14851. [Google Scholar] [CrossRef]
- Yu, L.; Wang, L.; Mu, W.; Yang, C. An Ultrahigh Step-Down DC–DC Converter Based on Switched-Capacitor and Coupled Inductor Techniques. IEEE Trans. Ind. Electron. 2022, 69, 11221–11230. [Google Scholar] [CrossRef]
- Lei, Y.; Pilawa-Podgurski, R.C.N. A General Method for Analyzing Resonant and Soft-Charging Operation of Switched-Capacitor Converters. IEEE Trans. Power Electron. 2014, 30, 5650–5664. [Google Scholar] [CrossRef]
- Tse, C.; Wong, S.; Chow, M. On lossless switched-capacitor power converters. IEEE Trans. Power Electron. 1995, 10, 286–291. [Google Scholar] [CrossRef]
- Kesarwani, K.; Sangwan, R.; Stauth, J.T. Resonant-Switched Capacitor Converters for Chip-Scale Power Delivery: Design and Implementation. IEEE Trans. Power Electron. 2014, 30, 6966–6977. [Google Scholar] [CrossRef]
- Ye, Z.; Sanders, S.R.; Pilawa-Podgurski, R.C.N. Modeling and Comparison of Passive Component Volume of Hybrid Resonant Switched-Capacitor Converters. IEEE Trans. Power Electron. 2022, 37, 10903–10919. [Google Scholar] [CrossRef]
- Qi, Q.; Ghaderi, D.; Guerrero, J.M. Sliding mode controller-based switched-capacitor-based high DC gain and low voltage stress DC-DC boost converter for photovoltaic applications. Int. J. Electr. Power Energy Syst. 2021, 125, 106496. [Google Scholar] [CrossRef]
- Ayachit, A.; Kazimierczuk, M.K. Averaged Small-Signal Model of PWM DC-DC Converters in CCM Including Switching Power Loss. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 262–266. [Google Scholar] [CrossRef]
- Sarif, M.S.M.; Pei, T.X.; Annuar, A.Z. Modeling, design and control of bidirectional DC-DC converter using state-space average model. In Proceedings of the 2018 IEEE Symposium on Computer Applications & Industrial Electronics (ISCAIE), Penang, Malaysia, 28–29 April 2018; pp. 416–421. [Google Scholar] [CrossRef]
- Davoudi, A.; Jatskevich, J. Realization of parasitics in state-space average-value modeling of PWM DC-DC converters. IEEE Trans. Power Electron. 2006, 21, 1142–1147. [Google Scholar] [CrossRef]








| Model Name | Model Accuracy | Model Complexity | Main Application Areas |
|---|---|---|---|
| State-space average model | Low- frequency accuracy | Low | Circuit topology and simulation analysis |
| Generalized average model | Medium accuracy | Medium | Simulation and large-signal analysis |
| Average small-signal model | Low- frequency accuracy | Low | Controller design and stability analysis |
| Describing function method | Both low- frequency and high- frequency accuracy | High | Loop gain phase delay and subharmonic oscillation |
| Description | Item | Value |
|---|---|---|
| Input voltage | Vin | 48 V/60 V |
| Output voltage | Vout | 12 V |
| Output current | Iout | 30 A |
| Resistor load | Rload | 0.167 Ω |
| Resonant capacitor | Cr | 2.82 μF |
| Tank capacitor | Ct | 100 μF |
| Resonant inductor | Lr | 100 nH |
| Resonant frequency | fr | 300 kHz |
| Switching frequency | fs | 300 kHz |
| Deadtime | td | 40 ns |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Ba, D.; Niu, Y.; Chen, X.; Cao, Q.; Lyu, X. Simplification of Indirect Resonant Switched-Capacitor Converter Based on State-Space Average Model Method. Electronics 2025, 14, 4131. https://doi.org/10.3390/electronics14204131
Wang Y, Ba D, Niu Y, Chen X, Cao Q, Lyu X. Simplification of Indirect Resonant Switched-Capacitor Converter Based on State-Space Average Model Method. Electronics. 2025; 14(20):4131. https://doi.org/10.3390/electronics14204131
Chicago/Turabian StyleWang, Yihe, Dejun Ba, Yuxin Niu, Xinran Chen, Qi Cao, and Xiaofeng Lyu. 2025. "Simplification of Indirect Resonant Switched-Capacitor Converter Based on State-Space Average Model Method" Electronics 14, no. 20: 4131. https://doi.org/10.3390/electronics14204131
APA StyleWang, Y., Ba, D., Niu, Y., Chen, X., Cao, Q., & Lyu, X. (2025). Simplification of Indirect Resonant Switched-Capacitor Converter Based on State-Space Average Model Method. Electronics, 14(20), 4131. https://doi.org/10.3390/electronics14204131





