Abstract
Human Activity Recognition (HAR) is a key technology with applications in healthcare, security, smart environments, and sports analytics. Despite advances in deep learning, challenges remain in building models that are both efficient and generalizable due to the large scale and variability of video data. To address these issues, we propose a novel Dual-Teacher Knowledge Distillation (DTKD) framework tailored for HAR. The framework introduces three main contributions. First, we define static and dynamic activity classes in an objective and reproducible manner using optical-flow-based indicators, establishing a quantitative classification scheme based on motion characteristics. Second, we develop subset-specialized teacher models and design a hybrid scoring mechanism that combines teacher confidence with cross-entropy loss. This enables dynamic weighting of teacher contributions, allowing the student to adaptively balance knowledge transfer across heterogeneous activities. Third, we provide a comprehensive evaluation on the UCF101 and HMDB51 benchmarks. Experimental results show that DTKD consistently outperforms baseline models and achieves balanced improvements across both static and dynamic subsets. These findings validate the effectiveness of combining subset-aware teacher specialization with hybrid scoring. The proposed approach improves recognition accuracy and robustness, offering practical value for real-world HAR applications such as driver monitoring, healthcare, and surveillance.
1. Introduction
Action recognition refers to the automatic identification and classification of human activities in video sequences and has emerged as a core challenge in artificial intelligence with applications in autonomous driving, smart security, and related domains. With the emergence of deep learning-based approaches, models capable of effectively learning spatiotemporal patterns have been developed, thereby significantly broadening the practical applicability of action recognition [1,2].
However, ensuring reliability and robustness in real-world environments remains a critical challenge. Numerous previous studies have repeatedly reported that action recognition models tend to rely excessively on background information instead of the actions themselves, leading to significant performance degradation when background scenes change or recording conditions vary [3,4,5,6]. A contributing factor is the tendency of existing datasets to depend on subjective or intuitive judgments by researchers, instead of on objective criteria when distinguishing motion characteristics across classes. Consequently, consistency and reproducibility are compromised, and model robustness to environmental changes is insufficiently guaranteed. Consequently, the present study quantitatively evaluates the motion characteristics for each class in two large-scale action recognition benchmarks and explicitly separates all classes into static (St-subset) and dynamic (Dy-subset) subsets based on statistical indicators.
However, simple subset partitioning alone is insufficient to substantially improve the model performance and generalization. Consequently, we independently trained expert teacher models specialized for each subset and employed an architecture that integrated information at different temporal resolutions through a dual-pathway structure [7]. Furthermore, we propose a dual-teacher knowledge distillation (DTKD) framework in which the knowledge of both teachers is selectively transferred and integrated into a single student model covering all classes via knowledge distillation (KD) [8]. The proposed framework enhances both robustness and generalization by combining the strengths of subset-specific experts—each reflecting distinct motion distributions and background dependencies. Moreover, this study experimentally demonstrated the ability to overcome the limitations of subjective partitioning and single-model approaches by organically integrating quantitatively defined subsets with the KD paradigm.
The main contributions of this study can be summarized as follows:
- Objective subset definition: We defined static and dynamic activity groups in an objective and reproducible manner using optical-flow-based statistical indicators [9], thereby establishing a quantitative classification scheme grounded in motion characteristics.
- Dual-teacher selective distillation: Unlike existing multi-teacher KD approaches that mainly rely on structural diversity or ensemble averaging, we independently trained subset-specialized teachers and integrated their knowledge into the student through a selective KD strategy. To support this process, we proposed a hybrid weighting mechanism that combines teacher confidence with loss, enabling selective transfer that simultaneously reflects teacher reliability and complementary signals.
- Comprehensive evaluation: We conducted a subset-based performance analysis together with a teacher–student distribution similarity assessment. Results show that the proposed DTKD not only improves overall accuracy but also enables students to selectively mimic teacher distributions and effectively acquire subset-specific knowledge.
The remainder of this paper is organized as follows: Section 2 reviews the related work and highlights the distinct contributions of our study. Section 3 describes the proposed methodology and experimental setup. Section 4 presents the quantitative results of the various experiments. Section 5 discusses key implications and limitations, and Section 6 concludes the paper with directions for future research.
2. Related Works
2.1. Quantitative Analysis of Motion in Action Recognition
Numerous studies have leveraged optical flow to extract discriminative features and enhance performance. Ref. [10] introduced the two-stream ConvNet architecture, which independently learns from RGB and optical flow, thereby utilizing flow as a core representation of motion. This approach achieved strong results for large-scale benchmarks, such as UCF101 [11] and HMDB51 [12]. Notably, HMDB51 is considered more challenging owing to visually similar classes (e.g., smile, eat, and chew) and lower video quality; indeed, Ref. [13] reported accuracies exceeding 95% on UCF101 but only approximately 70% on HMDB51.
Subsequent studies proposed fusion architectures such as I3D [1], whereas Ref. [14] demonstrated that optical flow is crucial in capturing fine-grained motion and human boundaries, and that its quality directly impacts recognition accuracy. Nevertheless, few attempts have been made to quantitatively measure the motion intensity, partition classes into subsets, and extend these analyses to distillation strategies.
Traditional flow-based recognition typically relies on a precomputed flow fed into convolutional neural network (CNN) classifiers in a two-stage pipeline, which entails a high computational cost, large storage requirements, and difficulties with end-to-end training. Consequently, methods such as MotionNet-based hidden two-stream CNN [15] and cross-modal self-supervised representation learning [16], which enable end-to-end training and improved generalization, have been proposed.
Additionally, attempts have been made to quantify motion intensity using a trajectory motion [17]. However, previous studies have largely remained at the level of analyzing mean distributions or motion intensity, without systematically leveraging optical-flow statistics to characterize class-specific properties or extending such analyses to subset partitioning and performance evaluation.
2.2. Action Recognition Architectures
If the key factor in action recognition performance is in the motion characteristics, practical realization depends on the choice of an appropriate architecture. The existing models can be largely categorized into ConvNet- and Transformer-based approaches. ConvNet models extract spatiotemporal features through two-dimensional (2D) or three-dimensional (3D) convolutions; I3D, C3D [18], and SlowFast [7] are representative examples. These models achieve a robust performance with relatively few parameters, making them widely adopted across benchmarks.
In contrast, Transformer-based models exploit self-attention to capture long-range dependencies, as in video Swin Transformer [19], TimeSformer [20], and ViViT [21], which, when combined with large-scale pretraining, have achieved state-of-the-art performance. However, their structural complexity and high computational demands impose significant limitations.
This study adopted SlowFast as the backbone architecture, owing to its proven efficiency and reliability. The reported accuracies were approximately 95–96% for UCF101 and 75–77% for HMDB51 [22,23,24], making SlowFast a reasonable backbone for evaluating KD-based performance.
The superiority of spatiotemporal convolutional structures has been demonstrated consistently. For instance, 3D CNNs have been shown to outperform 2D CNNs in action recognition, and the R(2 + 1)D block was proposed to further improve the performance [25]. Extensions combining SlowFast with BERT have achieved enhanced results [26], and a wide range of ConvNet-based studies have been conducted on UCF101 and HMDB51 [27,28,29,30,31,32,33]. Nevertheless, issues of efficiency and scalability remain unresolved, which motivated the integration of KD techniques in this study.
2.3. Knowledge Distillation
KD is a representative framework for transferring knowledge from large teacher models to lightweight student models; numerous strategies and variants have been proposed. A comprehensive review [34] summarized the theoretical foundations of KD and emphasized the need for multiteacher, cross-modal, and ensemble distillation to overcome the limitations of single-teacher approaches. Accordingly, methods such as knowledge amalgamation [35], heterogeneous KD [36,37], and attention-based teacher aggregation [38] have been introduced to enhance student generalization by integrating knowledge from multiple teachers.
Dual-teacher approaches have also been explored under certain conditions. For instance, one study employed both enhancement and raw video teachers to handle dark video scenarios [39], whereas another applied dual-teacher KD to natural language processing by separating teachers based on high- and low-frequency word distributions [40]. In addition, a recent study [41] proposed dynamically adjusting the temperature based on the sharpness of teacher–student distributions, thereby enabling more effective knowledge transfer.
Despite these advances, most previous studies have focused primarily on structural diversity or prediction aggregation among teachers, with minimal emphasis placed on class-specific characteristics. By contrast, the proposed DTKD explicitly partitions classes into St- and Dy-subsets using optical-flow statistics, assigns specialized teachers to each subset, and selectively transfers their knowledge to the student. This design enables students to acquire both specialized expertise and overall generalization. The following section details the structure and training procedures of the DTKD framework.
3. Methods
This paper proposed a method that integrates three key components: (1) motion characteristic quantification based on optical flow, (2) efficient action recognition backbone architecture, and (3) DTKD strategy. By combining these elements, the framework enables training tailored to class-specific characteristics and ultimately aims to construct a more robust and efficient action recognition model.
3.1. Optical Flow-Based Quantification of Motion Characteristic
Building on this research background, this study quantifies class-specific motion characteristics in action recognition datasets using optical flow-based statistical indicators. Optical flow computes pixel variations between consecutive frames, thereby capturing not only human motion but also camera movement and background changes, which allows for the numerical expression of video-level motion intensity.
In particular, UCF101 and HMDB51 contain diverse actions, complex backgrounds, and camera motions, making the average optical flow a valid metric for distinguishing motion levels across classes. However, the resulting statistics may vary depending on the flow algorithm employed or the aggregation strategy—for instance, whether the average is computed over the entire video, spatial regions, or temporal segments.
In this study, optical flow was calculated for each video sequence, and the class-wise mean value was obtained. The first quartile (Q1) of the overall distribution was used as the threshold. According to Equation (1), classes with were assigned to the St-subset, whereas the remainder were assigned to the dynamic subset (Dy-subset). Q1 was selected to ensure that the St-subset contained classes with clear low-motion characteristics while allowing the Dy-subset to encompass a broader range of motion intensities.
Table 1 summarizes the optical flow distributions of the overall dataset and each subset of UCF101 and HMDB51 to validate the classification criteria. The Dy-subset consistently exhibited higher values across key metrics than the St-subset, indicating that the difference in motion intensity between the classes was statistically significant. These results support the necessity and effectiveness of subset-specific learning strategies.

Table 1.
Statistical summary of optical flow mean distributions for each class group, including the first quartile (Q1), mean, STD, and interquartile range (IQR).
Figure 1 shows the distribution of class-wise optical flow as a histogram, with the first quartile (Q1) indicated by a red vertical line, providing an intuitive basis for defining the St-subset. Figure 2 shows the mean and standard deviation (STD) of the optical flow for each subset in a scatter plot. The St-subset was concentrated in the region of low mean and variance, whereas the Dy-subset exhibited higher means with broader variance, confirming a clear separation of motion characteristics.
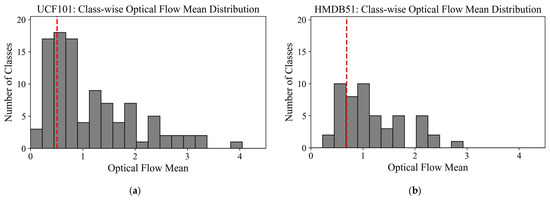
Figure 1.
Histogram of class-wise optical flow means used for subset separation. The red vertical line indicates the first quartile (Q1), which serves as the threshold for distinguishing static and dynamic classes. (a) UCF101; (b) HMDB51.
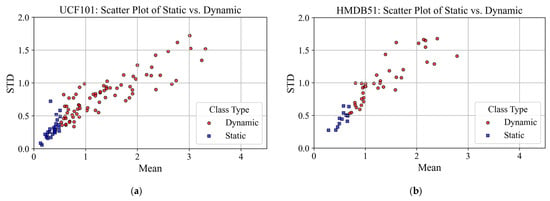
Figure 2.
Scatter plots with regression lines of class-wise optical flow statistics. Each point represents a class, plotted using the mean and STD of optical flow, demonstrating the separation between St- and Dy-subsets. (a) UCF101; (b) HMDB51.
Specifically, the St-subset of UCF101 includes the following classes: ApplyLipstick, Archery, BaseballPitch, Billiards, BodyWeightSquats, CleanAndJerk, CricketShot, GolfSwing, Handstand-Pushups, JumpRope, PlayingCello, PlayingDhol, PlayingFlute, PlayingGuitar, PlayingPiano, PlayingSitar, PlayingTabla, PullUps, ShavingBeard, SoccerPenalty, TableTennisShot, TaiChi, TennisSwing, Typing, WallPushups, and WritingOnBoard.
For HMDB51, the classes belonging to the St-subset were chew, draw_sword, eat, golf, kiss, pour, pullup, shoot_bow, situp, smile, smoke, sword_exercise, and talk, whereas all the remaining classes were categorized as part of the Dy-subset.
The final numbers of training and testing videos for the overall dataset and each subset are listed in Table 2. Notably, UCF101 was larger than HMDB51, and in both datasets, the Dy-subset contained substantially more videos than the St-subset.

Table 2.
Composition of the UCF101 and HMDB51 datasets after subset division, showing the number of training and test videos for the overall set, and St- and Dy-subsets.
The proposed optical-flow-based class-partitioning strategy reconstructs a dataset by quantifying the motion characteristics of each class according to the statistical criteria established in this study. This enables future action recognition models to be designed in a class-aware manner, and can be extended as a generalized, data-driven partitioning approach applicable to other datasets.
3.2. Proposed Dual Teacher Knowledge Distillation Framework
3.2.1. Backbone Architecture Based on Dual Pathways
The static and dynamic class partitioning introduced in the previous section demonstrate that each subset exhibits distinct motion characteristics.
To capture these differences effectively, this study adopts SlowFast as the backbone architecture. SlowFast employs a dual-pathway design with different temporal resolutions, allowing the slow pathway to capture static contextual information and the fast pathway to model fine-grained dynamic motions. This aligns well with the static and dynamic class characteristics defined in this study.
In particular, the network structure of SlowFast itself was not modified; instead, pretrained models from the PyTorch Hub [42] were directly utilized. The core contribution of this research is in the design of the KD framework and its performance analysis instead of architectural modifications.
In the SlowFast notation , represents the number of frames sampled by the slow pathway, and denotes the relative frame rate of the fast pathway with respect to the slow one. For instance, SlowFast_16 × 8 indicates that the slow pathway processes 16 frames, whereas the fast pathway processes 128 frames over the same temporal window. This parameterization provides a key trade-off between temporal coverage and computational efficiency. In this study, the 16 × 8 configuration was primarily employed, and 8 × 8 configurations were included in the comparative analysis.
We constructed the proposed DTKD framework by leveraging the structural advantage of SlowFast’s dual-pathway design in capturing both static and dynamic motions.
3.2.2. DTKD Framework Structure
The UCF101 and HMDB51 datasets used in this study exhibit clear differences in motion intensity across classes. For instance, ApplyLipstick primarily involves static features, whereas running involves strong dynamic movements. Such differences affect not only the classification accuracy but also the degree to which models rely on background information.
Consequently, the overall dataset was quantitatively analyzed using optical flow statistics and divided into an St-subset and a Dy-subset. Independent teacher models were then trained on each subset, and their output logits served as inputs for the DTKD procedure.
Figure 3 provides an overview of the entire framework, from dataset partitioning to teacher–student knowledge transfer. The detailed training procedure that operationalized this design into step-by-step learning is described in the following section.
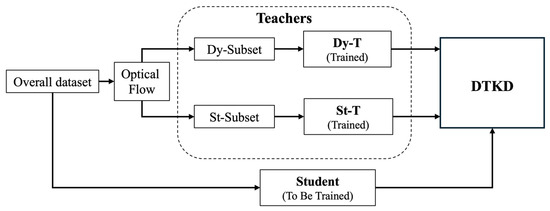
Figure 3.
Overview of the proposed DTKD framework comprising two stages: (1) subset-based training of St-T and Dy-T; and (2) student training on the full dataset with dual-teacher distillation.
3.2.3. DTKD Training Procedure
We define a seven-step training procedure to implement the DTKD framework described in the previous section. The core idea was to combine teacher confidence and prediction loss through hybrid weighting, thereby incorporating both reliability and error information. The weighted soft targets were then aggregated to provide students with optimized supervision signals. In addition, batch-wise loss normalization and logit masking for out-of-subset classes were applied to prevent value distortions and irrelevant interference.
Figure 4 summarizes the overall DTKD pipeline, where steps 1–7 correspond to Section Temperature-Adjusted Softmax for Distillation–Section Final Loss. Among them, steps 2–5 represent the novel processes proposed in this study. The following sections describe each step in detail.
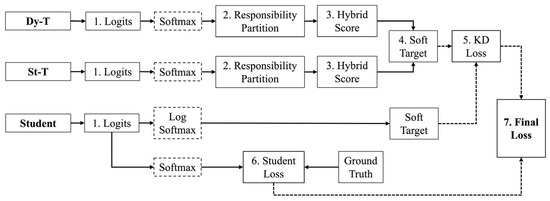
Figure 4.
Training procedure of the proposed DTKD, organized into eight sequential steps.
Temperature-Adjusted Softmax for Distillation
In KD, temperature scaling was applied to compare the output distributions of the teacher and student under the same criterion. Temperature T () was applied to the logits to generate soft labels. As increased, the softmax distribution became smoother, thereby emphasizing inter-class similarities.
The teacher produced probability distributions using softmax, whereas the student generated log-probability distributions using log-softmax. The student then minimized the difference between these two distributions using the Kullback–Leibler divergence (KL-Div) loss [43].
Because the PyTorch implementation of KL-Div requires the first input as log-probabilities and the second as probabilities, student logits are passed through log-softmax. This ensures that the gradients are propagated only to the students [44]. Accordingly, the student distribution is defined in Equation (2), whereas the teacher outputs and are used as probability distributions obtained via softmax, as expressed in Equation (3).
The teacher–student distribution pairs defined in this manner are subsequently compared selectively, depending on the subset to which each class belongs. To enable this, the proposed method first establishes a responsibility partition for each teacher.
Responsibility Partition
In this step, each sample y is checked to determine whether its class belongs to or , and a binary mask is generated accordingly, as defined in Equation (4). This mask serves as a mechanism for partitioning the responsibilities of teachers: static teacher (St-T) provides learning signals only for static classes, whereas dynamic teacher (Dy-T) does so only for dynamic classes. In this manner, each teacher supplies soft targets exclusively within its specialized subset, ensuring that the student receives optimized knowledge without unnecessary interference.
Each teacher defines the maximum value of its softmax probability for a given subset sample as the confidence score, as shown in Equation (5). This score quantifies the prediction confidence and is incorporated into the distillation process to reduce teacher uncertainty and promote a more stable knowledge transfer.
Each teacher computes the cross-entropy (CE) loss for its assigned subset samples, as defined in Equation (6). This loss serves as a quantitative measure of prediction accuracy at the sample level, where larger values indicate lower accuracy and thus provide a numerical evaluation of the teacher’s performance.
For each teacher, the CE loss was normalized at the batch level using min–max normalization, as defined in Equation (7). This procedure scales the loss values into the range [0, 1], thereby mitigating the effects of scale differences and outliers and ensuring that the predictive performance of each teacher is reflected under a consistent criterion across batches.
Hybrid Score
The hybrid score and serves as the core metric of DTKD, dynamically assigning weights to each teacher’s soft target. Conventional confidence- or loss-based strategies rely on a single indicator, which limits their ability to fully capture teacher reliability. Consequently, we combined the confidence score (certainty of prediction) with the normalized CE loss (prediction accuracy), thereby integrating the two complementary measures in a balanced manner.
As defined in Equation (8), the hybrid score assigns greater weight to teachers with higher confidence and lower error while reducing the influence of uncertain or inaccurate knowledge transfer. This design maximized the effectiveness of distillation.
The adjustment of the hybrid score is defined in this study by the hyperparameter . This parameter controls the relative weight between the confidence score and inverse of the normalized CE loss; larger values emphasize the confidence signal, whereas smaller values highlight the CE loss-based signal. In this way, the teacher contributions can be flexibly optimized to reflect the characteristics of the dataset and training environment while avoiding bias toward a single indicator.
Teacher Soft Target
The hybrid scores computed in the previous step were converted into soft weights that reflected the relative contributions of the teachers. For each sample, the hybrid scores of the St-T and Dy-T were normalized according to Equation (9), ensuring that their weights always summed up to one. Here, and denote the soft weights of the St-T and Dy-T, respectively.
For samples outside a teacher-assigned subset, the corresponding soft weight is set to zero such that St-T contributes only to the St-subset, whereas Dy-T contributes only to the Dy-subset. This design combines responsibility partitioning with continuous weighting, enabling the student to be optimized according to teacher confidence and predictive accuracy.
The soft weights determine the contribution of each teacher and are multiplied by their softmax distributions. Finally, the weighted distributions of St-T () and Dy-T () are combined as shown in Equation (10) to yield the final teacher soft target .
The resulting serves as the ultimate target distribution for KD. Rather than imitating a single teacher, the students learned from a dynamically weighted ensemble distribution tailored to each sample. Thus, and function as balancing factors that regulate the relative contributions of the two teachers.
KD Loss
The final teacher soft target serves as the reference distribution for KD. For each sample, soft labels from St-T and Dy-T were combined with their respective soft weights to construct .
The student then learns by minimizing the divergence between the predicted distribution and this reference, as defined by the KL-Div loss in Equation (11). This design allowed students to incorporate sample-specific teacher knowledge rather than relying on a single teacher, thereby maximizing the distillation effect.
Student Loss
Whereas guides the student to mimic the teacher’s soft-target distribution, the student loss directly evaluates how accurately the model predicts the ground-truth labels. Specifically, the discrepancy between the student predictions and true labels is measured by the CE loss , as defined in Equation (12). A lower indicates better alignment with the ground-truth and, thus, higher predictive accuracy.
Final Loss
As previously defined, encourages the students to mimic the teacher’s soft target distribution, whereas directly evaluates the prediction accuracy against the ground-truth labels. The final loss L_{total} was obtained by combining these two objectives, as expressed in Equation (13).
Here, the weighting coefficient controls the trade-off between teacher imitation and ground-truth supervision. In addition, the temperature parameter smoothens the soft-label distribution, enabling the student to capture richer interclass similarity information. However, as increases, the gradient magnitudes tend to vanish; therefore, the correction factor is multiplied by the distillation term to ensure training stability [8].
Consequently, the proposed final loss achieves a balanced integration of teacher-guided distillation and ground-truth learning, thereby maximizing the generalization performance of the student model.
The proposed method comprises optical-flow-based class partitioning followed by the DTKD procedure in which each stage is designed to act complementarily to enhance both the performance and generalization ability of the student model. In the next section, we apply this framework to benchmark datasets, verify its effectiveness through experiments, and quantitatively analyze the impact of the proposed DTKD strategy.
4. Experiments
This section describes the validation of the proposed method using two representative benchmark datasets for action recognition. Section 4.1 describes the experimental settings and datasets, whereas Section 4.2 presents the results of the baseline models. Section 4.3 reports the training outcomes of the class-specific teacher models, and finally, Section 4.4 analyzes the performance and effectiveness of the proposed DTKD framework.
4.1. Experimental Setup
All training in this study employed the SlowFast architecture as the backbone, with the frame rate ratio between the two pathways set to four. The pretrained weights were initialized using the Kinetics-400 [45] model provided by PyTorchVideo in the PyTorch framework [46].
The training configuration was standardized with the SGD optimizer, an initial learning rate of 10−3, and a dropout rate of 0.5. Data augmentation included RandomShortSideScale, RandomCrop, and RandomHorizontal Flip, whereas normalization was performed using dataset-specific statistics. The proposed DTKD framework was implemented based on the code in [47].
For evaluation, cross-validation was performed using three official splits (List-{1,2,3}) provided by UCF101 and HMDB51. For HMDB51, however, because of class imbalance, only splits id = 1 (train) and id = 2 (test) were used, excluding id = 0.
In DTKD experiments, sensitivity analyses were performed on the major hyperparameters , , and . Additional experiments were conducted to investigate the effects of freezing teacher parameters during training and tuning strategies when integrating teachers into student learning. Subset-based comparisons were used to verify the performance gains of DTKD, and the KL-Div analysis quantitatively assessed how effectively the student mimicked teacher distributions.
All the experiments were conducted in an environment with Ubuntu 20.04, Python 3.7, PyTorch 1.8.0, and CUDA 11.1. The hardware setup included an RTX 3090 Ti GPU (NVIDIA, Santa Clara, CA, USA) for the UCF101 experiments and an RTX TITAN GPU (NVIDIA, Santa Clara, CA, USA) for the HMDB51 experiments.
4.2. Baseline Model
Baseline experiments were designed to train each dataset independently and to evaluate the classification performance on the overall dataset. This provided a quantitative reference for comparing the performance improvements achieved using the proposed DTKD framework.
During training, the model checkpoints were saved at every epoch and subsequently evaluated on the test set to ensure the reliability of the results. In addition, comparative experiments were conducted with frozen teacher settings and the training of the SlowFast 8 × 8 model.
Table 3 summarizes the results of models U1–U3 and H1–H3, which were trained using three official split lists provided by UCF101 and HMDB51, respectively. The models trained with List-3 (U3, H3) achieved the best performance for both datasets. However, because previous studies have predominantly adopted List-1 as the standard for experiments and comparisons, this study selected U1 and H1 as the baselines to ensure consistency and comparability with the existing literature. All subsequent experiments were conducted using List-1.

Table 3.
Training loss, Top-1 accuracy, and Top-5 accuracy of baseline models trained on the overall datasets (UCF101 and HMDB51), evaluated on the test set. The results include models trained with three official lists (U1–U3, H1–H3), Frozen models trained on List-1 (R4, H4), and SlowFast 8 × 8 architectures with ResNet-101 (R5, H5) and ResNet-50 backbones (U6, H6).
Figure 5 shows the cross-validation results obtained from the three official split lists, demonstrating that models U1–U3 and H1–H3 stably converged. Each graph presents the training loss recorded during training on the training set, along with the Top-1 accuracy evaluated on the test set using the checkpoints saved at each epoch.
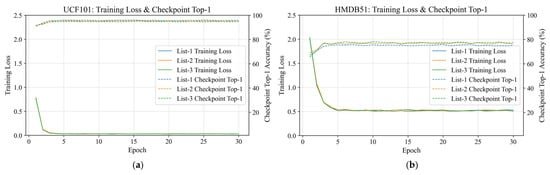
Figure 5.
Cross-validation results of models trained with three official lists, presenting training loss and Top-1 accuracy across all checkpoint models using the test set. (a) UCF101; (b) HMDB51.
Models U4 and H4, which were trained with the feature extractor frozen from the baseline, exhibited degraded performance, highlighting the importance of fine-tuning for adaptation to the target dataset. Models U5, H5 and U6, H6, trained with the SlowFast 8 × 8 architecture based on ResNet-101 and ResNet-50, respectively, exhibited a lower accuracy than the baseline. This indicates that extended temporal resolution and network depth play critical roles in performance improvement.
Furthermore, HMDB51 exhibited a large discrepancy between the Top-1 and Top-5 accuracies, confirming that the Top-5 accuracy serves as an important evaluation metric in action recognition tasks in which classes are highly similar and class boundaries are ambiguous.
The parameter counts for UCF101 and HMDB51 were calculated as follows: the Baseline models (U1–U3 and H1–H3) contained 53.78 M (millions) parameters, while the SlowFast 8 × 8 models with R101 (U5, H5) and R50 (U6, H6) backbones contained 62.83 M and 34.57 M, respectively. In the Frozen configuration (U4, H4), the parameter counts were 0.23 M for UCF101 and 0.12 M for HMDB51. In the Frozen setting, the backbone of the Kinetics-400 pretrained SlowFast model was frozen, and only the classifier head was retrained. Although the Baseline models share identical architectures and thus the same total number of parameters, the Frozen setting trains only the classifier head, resulting in different numbers of trainable parameters due to the class-size difference.
4.3. Class Specific Teacher Models
In the previous section, we evaluated the baseline performance of the entire dataset. Next, we trained class-specific models specialized for the St-subset and Dy-subset to validate the feasibility of using them as teachers. Each teacher was independently trained on its corresponding subset, and the results are summarized in Table 4.

Table 4.
Top-1 accuracy and Top-5 accuracy of class-specific teacher models trained on the Dy-subset and St-subset.
The St-subset models (TU2, TH2) exhibited clear performance improvements compared with the baseline, as static characteristics—often overshadowed by the strong motion cues of dynamic classes in the overall training—were more effectively captured through subset-specific learning. In contrast, the Dy-subset models (TU1, TH1) exhibited only marginal gains, because the baseline models had already internalized sufficient motion features during the overall training.
Two conditions were defined to further examine the effect of teacher adaptability and freezing strategies on student performance.
Locked teacher (LT) specifies whether teacher parameters are frozen during subset training: LT = True corresponds to frozen teachers (TU3, TU4, TH3, TH4), whereas LT = False corresponds to regular teachers (TU1, TU2, TH1, TH2).
Frozen teacher at the student stage (FT) determines whether they are frozen during student training. Thus, LT controls freezing during the teacher-training stage, whereas FT governs freezing during student training.
Frozen teachers provide stable output distributions, but may lack dataset adaptability, whereas non-frozen teachers can capture more refined representations, but may produce unstable supervision signals. Therefore, comparing LT and FT offers empirical evidence of the influence of teacher-freezing strategies on the generalization ability of students, with the corresponding results presented in the next section.
4.4. Evaluation of the Dual Teacher Knowledge Distillation Framework
In the previous section, the performances of class-specific teacher models were validated. Building on this foundation, this section presents the experimental results of applying the DTKD framework, where both teachers are combined to perform KD on the overall dataset.
In DTKD, a student is trained to learn from the soft targets provided by each subset-specific teacher. To evaluate the effectiveness of the framework, we systematically examined the impact of the key distillation hyperparameters: , , and the proposed α.
The comparative performances across different dataset splits for UCF101 and HMDB51 are summarized in Table 5. For UCF101, the DTKD model SU12 showed a 1.00% improvement over the baseline model U1, while for HMDB51, the model SH3 achieved a 2.30% increase compared with H1.

Table 5.
Experimental results of the proposed DTKD framework on UCF101 and HMDB51 under LT and FT conditions with varying hyperparameters.
4.4.1. Hyperparameter Sensitivity
Initial experiments were conducted with both LT and FT enabled while fixing = 2 and = 0.2 and varying ∈ {0.3, 0.5, 0.7}. The results demonstrated that the best performance was achieved at = 0.3 for UCF101 and = 0.7 for HMDB51, indicating that the optimal balance between hard labels and soft targets is dataset-dependent and that S_α has a direct impact on DTKD performance.
Further experiments with different and combinations (SU4–SU9, SH4–SH9) revealed that excessively large (e.g., SU5, SH5 at = 0.8) degraded performance below the baseline, as the reliance on soft targets suppressed the contribution of ground-truth supervision. In contrast, moderate settings consistently improved performance over the baseline, highlighting the importance of carefully tuning distillation strength to enhance model generalization.
4.4.2. Effect of Teacher Tuning
We compared the models with different LT/FT configurations (SU10–SU12, SH10–SH12) to examine the effect of teacher tuning. The results demonstrated that SU12 (without LT or FT) achieved the highest performance on UCF101, whereas SH3 (with both LT and FT) yielded the best results on HMDB51. These findings suggest that teacher adaptation was not beneficial. On UCF101, with its relatively simple class structure, flexible adaptation improved transfer, whereas on HMDB51, characterized by higher class similarity and complex backgrounds, retaining pretrained stability was more effective.
Therefore, teacher-tuning strategies cannot be applied uniformly, and the optimal configuration depends on dataset complexity and motion characteristics. This highlights the need to carefully consider teacher freezing in DTKD and experimentally validate its impact when extending it to other tasks.
4.4.3. Contribution of Selective Transfer in DTKD
We compared the proposed DTKD with a baseline selective KD (BSKD) to assess the impact of teacher selection and weighting. BSKD applies a simple rule: each sample is assigned to either a St-T or Dy-T based on its label, and the KD loss is computed only from that teacher using KL-Div.
Although effective in single-teacher settings, this approach ignores teacher reliability and error signals in dual-teacher environments, leading to unstable supervision and the risk of imitating inappropriate distributions near class boundaries or noisy samples.
By contrast, DTKD introduces confidence–loss based soft weighting, which dynamically combines the outputs of both teachers. This strategy suppresses uncertain signals, leverages complementary knowledge, and overcomes the limitations of a single-teacher imitation.
As shown in Figure 6, DTKD (SU12, SH3) converges faster and more stably than BSKD (SU13, SH13), consistently achieving a higher test accuracy throughout training. These results demonstrate that selective transfer plays a central role in enhancing both training stability and generalization in DTKD.
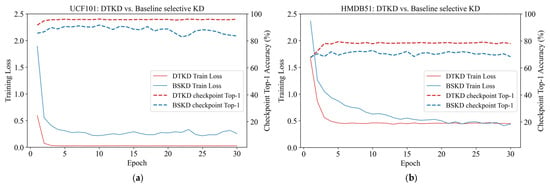
Figure 6.
Comparison between DTKD (SU12, SH3) and BSKD (SU13, SH13). Training loss and Top-1 accuracy across checkpoints demonstrate that DTKD achieves faster and more stable convergence, as along with consistently higher accuracy. (a) UCF101; (b) HMDB51.
4.4.4. Subset-Based Aggregate Performance Analysis
The purpose of this experiment was to verify whether DTKD provides consistent performance improvements across both static and dynamic classes instead of being limited to specific classes. Hence, in UCF101 and HMDB51, the baseline models (U1, H1) and DTKD models (SU12, SH3) were evaluated on the same test set.
First, per-class accuracy, defined as the ratio of correct classifications among the samples belonging to each class, was calculated. Accordingly, the per-class mean accuracy, St-subset mean, and Dy-subset mean were defined as the average accuracies of the overall, static, and dynamic classes, respectively. This approach reflects all classes with equal weights regardless of the sample size, thereby removing the bias caused by class imbalance and enabling a fairer comparison.
According to the results in Figure 7, for UCF101, the DTKD student (SU12) exhibited an improvement of 0.96% in the overall per-class mean accuracy compared with the baseline (U1). In the St-subset, a slight decrease of −0.18% was observed, which appears to be due to the baseline performance of St-T already being high, leaving little room for improvement, and statistical variation in the distillation process. In contrast, the Dy-subset exhibited a clear improvement of 1.36%, which can be interpreted as an effective transfer of knowledge from the Dy-T specialized in motion cues.
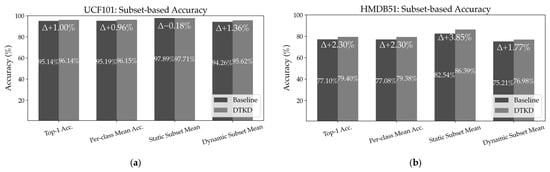
Figure 7.
Subset-based aggregate performance of Baseline and DTKD on UCF101 and HMDB51. Bars indicate Top-1 accuracy, per-class mean, St-subset mean, and Dy-subset mean, with annotations presenting absolute accuracy and gain (Δ). (a) UCF101; (b) HMDB51.
In HMDB51, the DTKD student (SH1) exhibited an improvement of 2.30% in per-class mean accuracy compared with the baseline (H3). Improvements of 3.85% and 1.77% in the St- and Dy-subsets, respectively, were confirmed. The St-subset of HMDB51 includes classes such as chew, smile, and smoke, which involve small changes in the face or hands instead of large movements, along with low-frequency classes with few data samples, making motion pattern learning difficult. In such cases, since the soft target weight of the St-T increases for static classes, the St-T, which is strong in static features, effectively plays a compensatory role, leading to performance improvement.
These results demonstrate that DTKD not only improves the overall accuracy but also practically enhances the subset-specific performance through teacher designs tailored to class motion characteristics. In particular, the significant improvement in the St-subset of HMDB51 validates the effectiveness of the subset-specific teacher structure.
We demonstrated that DTKD consistently improves performance across both static and dynamic subsets through aggregate accuracy analysis. However, verifying whether these performance gains truly stem from the student’s ability to imitate the correct teacher distribution requires a separate quantitative evaluation. Therefore, in Section 4.4.5, we conducted a teacher–student distribution similarity analysis using KL-Div, which confirmed that the DTKD student selectively reproduced the appropriate teacher distribution for each class. This provides direct evidence that the improvements of DTKD are not merely due to ensemble effects but rather result from selective knowledge transfer.
4.4.5. Teacher–Student Distribution Similarity Analysis
This experiment quantitatively evaluated how faithfully the DTKD student reproduced the teacher’s soft-target distribution using the KL-Div. In UCF101, student SU12 and teachers TU1, TU2 were compared, whereas in HMDB51, student SH3 and teachers TH3, TH4 were used as comparison targets.
Table 6 summarizes the results of the difference between the student and teacher softmax distributions for the same test set input. The KL-Div score was high in the overall test set, because it included classes outside the responsibility of each teacher. In contrast, in the subset-level analysis, the KL-Div between matched teacher–student pairs was significantly reduced, whereas the KL-Div between cross-teacher–student pairs increased significantly. This quantitatively demonstrates that DTKD selectively imitates the correct teacher distribution while suppressing unnecessary knowledge.

Table 6.
Average KL-Div between student and teacher models on UCF101 and HMDB51. Results are reported for the overall test set and for the St- and Dy-subsets.
This experiment verifies whether the DTKD student selectively imitates the teacher distribution using KL-Div. By calculating the difference between the student and teacher softmax distributions for the same test set input, we found that in the overall test set, which contained numerous dynamic classes, the KL-Div between the student and Dy-T was lower than that between the student and St-T.
As shown in Figure 8, the Dy-T distribution (orange) was more concentrated in the lower ranges than the St-T distribution (blue).
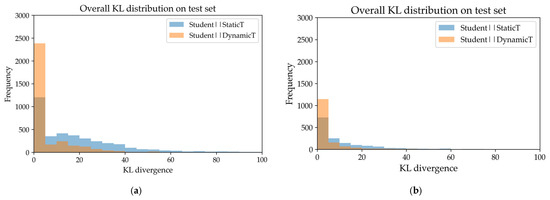
Figure 8.
Overall KL-Div distribution between student and teacher models on the test set. The x-axis represents KL values, whereas the y-axis indicates the number of test samples within each KL interval. (a) UCF101; (b) HMDB51.
However, the key finding lies in the subset-level analysis. The KL-Div with matched teachers consistently remained low, whereas the KL-Div with cross-teachers increased significantly. This quantitatively confirms that the student did not merely learn a mixture but selectively reproduced the teacher distribution appropriate to each class. To further quantify this selectivity, we define the Selectivity Margin (SM) and the Selective Imitation Ratio (SIR). SM represents the difference between the KL-Div of matched and cross teacher–student pairs, with larger values indicating clearer preference for the correct teacher distribution. SIR is defined as the ratio of cross-teacher KL to matched-teacher KL, reflecting the degree to which the student suppresses irrelevant teachers while faithfully imitating the appropriate one. Together, SM and SIR provide objective evidence that the DTKD student performs selective knowledge transfer, rather than merely relying on mixed teacher signals.
In UCF101, the matched KL was low, and the cross KL was high, resulting in large SM and SIR values, which demonstrated that the student clearly imitated the correct teacher distribution. In HMDB51, however, SIR values were observed at a relatively low level of 7–10. This indicated that the difference between the matched and cross-teacher distributions was not as distinct as that in UCF101. In other words, owing to inter-class visual similarity and lower video quality, teacher predictions formed less distinct boundaries, and, consequently, the student exhibited relatively weaker teacher differentiation during selective transfer.
5. Discussion
The DTKD proposed in this study is distinct from previous KD studies in that it selectively delivers soft targets optimized for class characteristics. The St-T specializes in background and low-frequency static features, whereas the Dy-T captures motion and temporal variations. The student learns all classes while using the teacher distribution corresponding to each sample subset as the supervision signal, and achieves a balance between hard and soft supervision by combining distillation loss and CE loss.
This selective transfer is grounded in optical-flow-based subset partitioning. Although classes were divided into St and Dy subsets using the Q1 threshold of the mean optical flow values, Q1 cannot always be regarded as the optimal criterion. Alternatives, such as the median (Q2), third quartile (Q3), trajectory motion intensity, or adaptive thresholding, may serve as viable options. Furthermore, the optical flow computation algorithm and aggregation method (e.g., overall mean vs. region-based or temporal mean) can also influence the dataset composition and distillation outcomes. Although the proposed approach provides a rational and reproducible criterion, further comparative and validation studies using diverse methodologies are warranted.
Experimental results demonstrated that DTKD achieved stable and consistent improvements over the baseline, with the key hyperparameters (, , and the proposed α) directly impacting the performance. In particular, excessive led to degraded accuracy, highlighting the importance of balancing hard and soft supervision. Both LT and FT conditions yielded improvements over the baseline, suggesting that DTKD can be designed to balance knowledge transfer stability (LT) and dataset adaptability (FT). The KL-Div analysis confirmed that when subsets were matched, the distribution gap between students and teachers was significantly reduced, demonstrating that selective transfer was effective. Conversely, for the non-responsible subsets, the KL values were high, confirming that unnecessary knowledge imitation was suppressed.
Additionally, BSKD, which distills knowledge by simply matching teacher distributions to subsets, recorded lower performance than the baseline, despite using the same data. This likely stems from a structural difference: BSKD masks classes as static or dynamic and references only a single teacher distribution for the KL-Div calculation, whereas DTKD combines both teacher distributions with hybrid score–based soft weighting before comparing with students. Consequently, DTKD was able to reflect both teacher reliability and complementary signals, whereas BSKD suffered from instability in the boundary and noisy samples, leading to degraded performance.
Furthermore, whereas self-distillation, a widely used KD method, retransfers augmented data representations within the same network, DTKD divides the same dataset into subsets, specializes in teachers, and combines them using a selective KD strategy. This process minimizes the distribution mismatch and validates the performance gain over the baseline. However, because the information gap between teachers and students may not be large, the transfer effect could be limited and dataset bias could potentially be reinforced. Therefore, additional validation of external datasets is necessary.
6. Conclusions
Action recognition research still faces limitations owing to excessive reliance on background cues and insufficient consideration of class-specific characteristics. Most previous studies have not objectively distinguished between static and dynamic classes, and single-teacher KD approaches have been constrained in terms of performance and generalization because of a lack of domain-specific expertise.
Consequently, this study proposed a DTKD framework in which action classes are divided into St- and Dy-subsets based on an optical flow-based statistical criterion. Expert teachers were independently trained for each subset and their knowledge was distilled into a student model.
Experimental results demonstrated that DTKD not only achieved higher accuracy than the baseline across the entire dataset but also reached performance levels close to those of the expert teachers within each subset. Furthermore, the KL-Div analysis between teachers and students revealed a lower divergence when the student was paired with the corresponding subset teacher, confirming that the proposed framework successfully implemented selective knowledge transfer. These findings indicate that DTKD overcomes the limitations of the single-teacher KD by complementarily combining domain-specific soft targets, thereby enhancing both the representational capacity and generalization ability of the student.
This study established the validity of a subset-specific selective KD strategy by providing consistent performance improvements and stabilized decision boundaries over the baseline. Simultaneously, it acknowledged the limitations related to teacher dependency, subset definition, and dataset scope, leaving directions for future research. In future work, we plan to further evaluate the proposed DTKD framework on larger and more diverse datasets to better assess its scalability and generalization capability. In addition, since the DTKD structure is designed to be architecture-agnostic, it can be extended to transformer-based video models such as TimeSformer or Video Swin Transformer to explore its applicability to attention-driven architectures. By addressing these directions, DTKD has the potential to evolve into a robust and scalable distillation paradigm applicable to diverse video-understanding tasks.
Moreover, the current subset-division criterion—based on the Q1 quartile of the optical flow averages—can be further extended by exploring Q2, Q3, or adaptive thresholding strategies. Such extensions could strengthen the generality of DTKD and lead to more refined subset-aware KD strategies. Finally, validating this approach in complex real-world scenarios such as pedestrian and driver action recognition in autonomous driving is expected to further consolidate the practicality and scalability of DTKD.
Author Contributions
Y.-J.P.: Conceptualization, Methodology, Investigation, data curation, Supervision, Project administration, Software, Validation, Visualization, and Writing—original draft preparation; H.-S.C.: Writing—review. Y.-J.P. conceived and supervised the overall research design, conducted dataset construction and experiments, developed the DTKD methodology, and implemented and trained the deep learning models. He was primarily responsible for data processing, model development, and manuscript drafting. H.-S.C. contributed to reviewing the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the DGIST R&D Program of the Ministry of Science and ICT of Korea (25-IT-03).
Data Availability Statement
The datasets analyzed in this study are publicly available benchmarks: UCF101 [11] (https://www.crcv.ucf.edu/data/UCF101.php) (accessed on 19 October 2025) and HMDB51 [12] (https://serre.lab.brown.edu/hmdb51.html) (accessed on 19 October 2025). No new raw data were collected. However, derived subsets (static and dynamic groups based on optical-flow thresholds) were generated for this work. These derived data are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| St-T | Static Teacher |
| Dy-T | Dynamic Teacher |
| St-subset | Static subset |
| Dy-subset | Dynamic subset |
| KL-Div | Kullback–Leibler divergence |
| KD | Knowledge Distillation |
| DTKD | Dual Teacher Knowledge Distillation |
| BSKD | Baseline Selective Knowledge Distillation |
| LT | Locked Teacher |
| FT | Frozen Teacher at student stage |
| TU | Teacher UCF101 |
| TH | Teacher HMDB51 |
| SU | Student UCF101 |
| SH | Student HMDB51 |
| SM | Selectivity Margin |
| SIR | Selective Imitation Ratio |
References
- Carreira, J.; Zisserman, A. Quo vadis, action recognition? A new model and the kinetics dataset. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 9 November 2017; pp. 6299–6308. [Google Scholar] [CrossRef]
- Feichtenhofer, C. X3D: Expanding architectures for efficient video recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 5 August 2020; IEEE: New York, NY, USA, 2020; pp. 200–210. [Google Scholar] [CrossRef]
- Choi, J.; Gao, C.; Messou, J.C.; Huang, J.B. Why can’t I dance in a mall? learning to mitigate scene bias in action recognition. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates Inc.: Red Hook, NY, USA; pp. 853–865. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Vasconcelos, N. RESOUND: Towards action recognition without representation bias. In Proceedings of the Computer Vision—ECCV 2018. ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 11210, pp. 520–535. [Google Scholar] [CrossRef]
- Rezazadegan, F.; Shirazi, S.; Upcroft, B.; Milford, M. Action Recognition: From Static Datasets to Moving Robots. arXiv 2017. [Google Scholar] [CrossRef]
- Kaseris, M.; Kostavelis, I.; Malassiotis, S. A comprehensive survey on deep learning methods in human activity recognition. Mach. Learn. Knowl. Extr. 2024, 6, 842–876. [Google Scholar] [CrossRef]
- Feichtenhofer, C.; Fan, H.; Malik, J.; He, K. SlowFast networks for video recognition. arXiv 2018, arXiv:1812.03982. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. In Proceedings of the NeurIPS Deep Learning and Representation Learning Workshop, Montreal, QC, Canada, 9 March 2015; Available online: https://arxiv.org/abs/1503.02531 (accessed on 9 September 2025).
- Horn, B.K.P.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef]
- Simonyan, K. Zisserman, Two-stream convolutional networks for action recognition in videos. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA (NIPS’14). ; Volume 1, pp. 568–576. [Google Scholar] [CrossRef]
- Soomro, K.; Zamir, A.R.; Shah, M. UCF101: A Dataset of 101 Human Action Classes from Videos in the Wild. CRCV-TR, 2012. Available online: https://www.crcv.ucf.edu/data/UCF101.php (accessed on 2 September 2025).
- Kuehne, H.; Jhuang, H.; Stiefelhagen, R.; Serre, T. HMDB51: A large video database for human motion recognition. In High Performance Computing in Science and Engineering ’12; Nagel, W.E., Kröner, D.H., Resch, M.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 571–582. [Google Scholar] [CrossRef]
- Yosry, S.; Elrefaei, L.; ElKamaar, R.; Ziedan, R.R. Various frameworks for integrating image and video streams for spatiotemporal information learning employing 2D–3D residual networks for human action recognition. Discov. Appl. Sci. 2024, 6, 141. [Google Scholar] [CrossRef]
- Sevilla-Lara, L.; Liao, Y.; Güney, F.; Jampani, V.; Geiger, A.; Black, M.J. On the Integration of Optical Flow and Action Recognition. arXiv 2017. [Google Scholar] [CrossRef]
- Zhu, Y.; Lan, Z.; Newsam, S.; Hauptmann, A.G. Hidden two-stream convolutional networks for action recognition. In Computer Vision—ACCV 2018; Lecture Notes in Computer Science; Jawahar, C.V., Li, H., Mori, G., Schindler, K., Eds.; Springer: Cham, Switzerland, 2019; Volume 11363, pp. 363–378. [Google Scholar] [CrossRef]
- Sayed, N.; Brattoli, B.; Ommer, B. Cross and learn: Cross-modal self-supervision. In Pattern Recognition. GCPR 2018; Lecture Notes in Computer Science; Brox, T., Bruhn, A., Fritz, M., Eds.; Springer: Cham, Switzerland, 2019; Volume 11269, pp. 228–243. [Google Scholar] [CrossRef]
- Wang, H.; Schmid, C. Action recognition with improved trajectories. In Proceedings of the IEEE International Conference on Computer Vision (ICCV 2013), Sydney, NSW, Australia, 1–8 December 2013; IEEE: New York, NY, USA, 2013; pp. 3551–3558. [Google Scholar] [CrossRef]
- Tran, D.; Bourdev, L.; Fergus, R.; Torresani, L.; Paluri, M. Learning spatiotemporal features with 3D convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV 2015), Santiago, Chile, 7–13 December 2015; IEEE: New York, NY, USA, 2015; pp. 4489–4497. [Google Scholar] [CrossRef]
- Liu, Z.; Ning, J.; Cao, Y.; Wei, Y.; Zhang, Z.; Lin, S.; Hu, H. Video Swin transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2022), New Orleans, LA, USA, 18–24 June 2022; pp. 3202–3211. [Google Scholar] [CrossRef]
- Bertasius, G.; Wang, H.; Torresani, L. Is space-time attention all you need for video understanding? In Proceedings of the 38th International Conference on Machine Learning (ICML 2021), Online, 18–24 July 2021; PMLR: Cambridge, MA, USA, 2021; pp. 813–824. [Google Scholar] [CrossRef]
- Arnab, A.; Dehghani, M.; Heigold, G.; Sun, C.; Lučić, M.; Schmid, C. ViViT: A video vision transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV 2021), Montreal, QC, Canada, 10–17 October 2021; pp. 6836–6846. [Google Scholar] [CrossRef]
- Xu, Y.; Lu, Y. An Action Recognition Method based on 3D Feature Fusion. In Intelligent Human Systems Integration (IHSI 2025): Integrating People and Intelligent Systems. AHFE (2025) International Conference; Ahram, T., Karwowski, W., Martino, C., Giuseppe Di Bucchianico, C., Maselli, V., Eds.; AHFE International-AHFE Open Access: Honolulu, HI, USA, 2025; Volume 160. [Google Scholar] [CrossRef]
- Ye, Q.; Tan, Z.; Zhang, Y. Human action recognition method based on motion excitation and temporal aggregation module. Heliyon 2022, 8, e11401. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.; Wang, Y.; Zhang, Y. Object action recognition algorithm based on asymmetric fast and slow channel feature extraction. In Proceedings of the 2024 2nd International Conference on Signal Processing and Intelligent Computing (SPIC), Guangzhou, China, 20–22 September 2024; IEEE: New York, NY, USA, 2024; pp. 549–553. [Google Scholar] [CrossRef]
- Tran, D.; Wang, H.; Torresani, L.; Ray, J.; LeCun, Y.; Paluri, M. A closer look at spatiotemporal convolutions for action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2018), Salt Lake City, UT, USA, 18–23 June 2018; pp. 6450–6459. [Google Scholar] [CrossRef]
- Kalfaoglu, M.E.; Kalkan, S.; Alatan, A.A. Late temporal modeling in 3D CNN architectures with BERT for action recognition. In Proceedings of the Computer Vision—ECCV 2020 Workshops. ECCV 2020, Glasgow, UK, 23–28 August 2020; Lecture Notes in Computer Science. Bartoli, A., Fusiello, A., Eds.; Springer: Cham, Switzerland, 2020; Volume 12539, pp. 731–747. [Google Scholar] [CrossRef]
- Meng, L.; Zhao, B.; Chang, B.; Huang, G.; Sun, W.; Tung, F.; Sigal, L. Spatio-temporal attention for action recognition in videos. arXiv 2018. [Google Scholar] [CrossRef]
- Wang, J.; Wen, X. A spatio-temporal attention convolution block for action recognition. J. Phys. Conf. S. 2020, 1651, 012193. [Google Scholar] [CrossRef]
- Han, X.; Lu, Y.; Guo, Q.; Liu, J.; Fei, C. Human action recognition research based on channel-temporal self-attention block network. In Proceedings of the 2024 6th International Conference on Robotics and Computer Vision (ICRCV), Wuxi, China, 20–22 September 2024; pp. 79–87. [Google Scholar] [CrossRef]
- Huang, L.; Liu, Y.; Wang, B.; Pan, P.; Xu, Y.; Jin, R. Self-supervised video representation learning by context and motion decoupling. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 13881–13890. [Google Scholar] [CrossRef]
- Haoze, W.; Jiawei, L.; Xierong, Z.; Meng, W.; Zheng-Jun, Z. Multi-scale spatial-temporal integration convolutional tube for human action recognition. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence (IJCAI’20), Yokohama, Japan, 7–15 January 2021; pp. 753–759. [Google Scholar] [CrossRef]
- Zhang, Y. MEST: An action recognition network with motion encoder and spatio-temporal module. Sensors 2022, 22, 6595. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Meng, F.; Tang, H.; Tong, G. Two-level attention module based on Spurious-3D residual networks for human action recognition. Sensors 2023, 23, 1707. [Google Scholar] [CrossRef] [PubMed]
- Gou, J.; Yu, B.; Maybank, S.J.; Tao, D.; Distillation, K. Knowledge distillation: A survey. Int. J. Comput. Vis. 2021, 129, 1789–1819. [Google Scholar] [CrossRef]
- Shen, C.; Wang, X.; Song, J.; Sun, L.; Song, M. Amalgamating knowledge towards comprehensive classification. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3068–3075. [Google Scholar] [CrossRef]
- Wu, M.-C.; Chiu, C.-T.; Wu, K.-H. Multi-teacher knowledge distillation for compressed video action recognition on deep neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2019), Brighton, UK, 12–17 May 2019; IEEE: New York, NY, USA, 2019; pp. 2202–2206. [Google Scholar] [CrossRef]
- Jiang, Y.; Feng, C.; Zhang, F.; Bull, D. MTKD Multi-teacher knowledge distillation for image super-resolution. In Proceedings of the Computer Vision—ECCV 2024, Milan, Italy, 4 October 2024; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany; Milan, Italy, 2024; Volume 14233, pp. 364–382. [Google Scholar] [CrossRef]
- Cheng, X.; Zhou, J. LGFA-MTKD: Enhancing multi-teacher knowledge distillation with local and global frequency attention. Information 2024, 15, 735. [Google Scholar] [CrossRef]
- Chang, C.-J.; Chen, O.; Tseng, V. DL-KDD: Dual-Light Knowledge Distillation for Action Recognition in the Dark. arXiv 2024. [Google Scholar] [CrossRef]
- Guo, Y.; Zan, H.; Xu, H. Dual-teacher Knowledge Distillation for Low-frequency Word Translation. In Findings of the Association for Computational Linguistics: EMNLP 2024; Association for Computational Linguistics: Miami, FL, USA, 2024; pp. 5543–5552. [Google Scholar]
- Wei, Y.; Bai, Y. Dynamic Temperature Knowledge Distillation. arXiv 2024. [Google Scholar] [CrossRef]
- Fan, H.; Murrell, T.; Wang, H.; Alwala, K.V.; Li, Y.; Li, Y.; Xiong, B.; Ravi, N.; Li, M.; Yang, H.; et al. PyTorchVideo: A deep learning library for video understanding. In Proceedings of the 29th ACM International Conference on Multimedia (MM ’21), Chengdu, China, 20–24 October 2021; ACM: New York, NY, USA, 2021; pp. 3800–3803. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Statist. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- PyTorch Documentation. KLDivLoss. Available online: https://pytorch.org/docs/stable/generated/torch.nn.KLDivLoss.html (accessed on 2 September 2025).
- Kay, W.; Carreira, J.; Simonyan, K.; Zhang, B.; Hillier, C.; Vijayanarasimhan, S.; Viola, F.; Green, T.; Back, T.; Natsev, P.; et al. The kinetics human action video dataset. arXiv 2017, arXiv:1705.06950. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An imperative style, high-performance deep learning library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- SlowFast Baseline Code, GitHub Repository. Available online: https://github.com/leftthomas/SlowFast (accessed on 12 June 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).