Enhancing JPEG XL’s Weighted Average Predictor: Genetic Algorithm Optimization of Expanded Sub-Predictor Ensemble

Abstract

Lossless image compression relies heavily on prediction algorithms to reduce spatial redundancy before entropy coding. The JPEG XL standard employs a weighted average predictor that combines four sub-predictors with adaptive weighting; however, it uses fixed initial scaling factors regardless of the image content. This study introduces WOP8 (weighted optimization predictor for 8 sub-predictors), which extends the predictor diversity and optimizes initial weights using a genetic algorithm. Four additional predictors were incorporated—adaptive MED (JPEG-LS), enhanced adaptive median, Paeth (PNG), and GAP-based (CALIC)—forming an eight-predictor ensemble. A genetic algorithm with a population of 30 and 24 generations optimized the weight configurations by minimizing the compressed file size of the training data. Experiments were conducted on the Kodak and Tecnick datasets to evaluate performance and generalizability. The Kodak color dataset showed notable gains: with the weighted average predictor in isolation, WOP8 achieved a 0.24 BPP reduction (2.7% improvement) at high effort levels. Under standard JPEG XL operation mode, improvements were minor but consistent. These results confirm the value of targeted predictor optimization and demonstrate that genetic algorithms can effectively discover dataset-specific weighting patterns, offering a foundation for future component-level enhancements in JPEG XL.

1. Introduction

In lossless image compression, all image data are preserved, bit by bit, ensuring perfect reconstruction of the original file [1]. The lossless compression process consists of two primary stages: prediction and encoding, without any quantization. Our work focused specifically on extending the prediction stage, particularly the JPEG XL’s weighted average predictor.

Predictors play a crucial role in lossless image compression by estimating a pixel’s value based on its surrounding context and encoding only the prediction residual (error). This approach exploits the spatial correlation between neighboring pixels, effectively reducing data redundancy and making subsequent entropy encoding more efficient [1,2]. Traditional lossless codecs employ fixed predictors, such as the median edge detector (MED) used in JPEG-LS [3] and the Paeth predictor implemented in PNG [4]. More sophisticated prediction approaches have emerged including the gradient-adjusted predictor (GAP) used in CALIC, which adapts predictions based on local gradient characteristics [5].

JPEG XL, standardized in 2023, represents the current state-of-the-art in image compression technology, offering substantial improvements over legacy formats [6]. While JPEG XL supports both lossless and lossy compression, the focus in this work was on lossless compression. The codec’s lossless mode, known as modular mode, employs a sophisticated prediction system that utilizes multiple predictors in conjunction with a meta-adaptive (MA) tree to dynamically select the most appropriate predictor based on local image context [6]. Within this framework, JPEG XL provides flexibility in balancing the compression speed versus compression ratio through its effort level parameter. In lossless mode, higher effort levels result in greater compression, albeit at the expense of increased computational time [7].

Central to our research is JPEG XL’s weighted average predictor, also known as the error-correcting predictor. This predictor consists of four sub-predictors whose individual contributions are dynamically weighted based on recent prediction errors, creating a self-correcting prediction mechanism [8].

The initial predictor weights serve as scaling factors in the error weight calculation process. The weights are continuously updated using a fixed heuristic function that analyzes local prediction errors. During this adaptive process, the initial predictor weights are passed into the max weight parameter, where they function as scaling factors that influence how aggressively the weights adapt over time [9].

The significance of these initial weights as scaling factors cannot be overstated—they fundamentally control how the predictor adapts and learns from prediction errors throughout the compression process. However, these weight adjustment formulas and the four initial weight settings are fixed and built into the standard implementation [9].

Genetic algorithms (GAs) were initially introduced by Holland [10] and later popularized in engineering applications by Goldberg [11]. GAs have found successful application in numerous optimization contexts including image compression. Mitra et al. [12] demonstrated the effectiveness of GA in fractal image compression by optimizing parameters to achieve better convergence and image quality. Similarly, Kumar et al. [13] stated that GAs were already established tools for optimizing JPEG quantization tables, and that modifications made to the traditional GA model could further enhance compression performance.

Recent studies have explored adaptive and optimization-driven approaches in information processing. Ke et al. [14] applied a multilayer content-adaptive recurrent framework to dynamically refine feature extraction through hierarchical parameter tuning, demonstrating the effectiveness of adaptive optimization principles similar to those used in this work. Likewise, Xing et al. [15] introduced a multi-modal quantum watermarking method emphasizing efficient and distortion-resilient data embedding, a concept similar to the goals of predictive compression, where optimization techniques such as genetic algorithms aim to balance compactness and fidelity.

Given that JPEG XL’s weighted average predictor relies on multiple sub-predictors with fixed initial weights that serve as crucial scaling factors in the adaptive weight calculation, this presents an ideal optimization target for genetic algorithms. The interdependent nature of these scaling factors and their fundamental role in controlling predictor adaptation suggest that a GA could discover alternative weight configurations that yield improved compression performance.

It is worth mentioning that the novelty of this work lies not in inventing new predictors or GA mechanisms, but instead in the systematic integration of additional predictors and the adaptive GA-based weight optimization within JPEG XL’s predictive framework. This integration demonstrates performance gains while maintaining full codec compatibility.

The remainder of this paper is organized as follows. The core algorithm is presented in Section 2, the results are shown in Section 3, the results are discussed in Section 4, and the paper is concluded in Section 5.

2. Materials and Methods

2.1. System Overview

WOP8 (weighted optimization predictor for 8 sub-predictors) is a system that enhances the JPEG XL weighted average predictor [8]. The system builds upon the existing four-predictor framework by extending it to an eight-predictor configuration. The enhancement is achieved through the integration of four additional sub-predictor rules combined with a genetic algorithm-based initial weight optimization for all sub-predictors. Since this optimization only modifies the initial weights and adds four sub-predictors to the weighted average predictor definition, WOP8 maintains complete bitstream compatibility with the JPEG XL standard.

2.2. Original Predictors

The JPEG XL weighted average predictor framework consists of four foundational sub-predictors. The sub-predictors implement a multi-strategy approach to image prediction [8]. Sub-predictors 0–3 represent four distinct prediction strategies that dynamically adapt their specific formulas based on the prediction mode.

Sub-predictor 0 (simple gradient) maintains consistency across all modes by implementing the classic gradient, W + NE − N (see Figure 1), which provides reliable edge-aware prediction regardless of the chosen prediction mode. This consistency makes it a stable reference point within the adaptive framework. Sub-predictor 1 (adaptive north) employs simple directional prediction with basic error correction, providing a foundational northward-biased approach. Sub-predictor 2 (adaptive west) provides an alternative directional strategy with refined error handling, typically emphasizing westward prediction and averaging error compensation. Sub-predictor 3 (adaptive multicontext) employs the most sophisticated approach, utilizing advanced spatial modeling with trend analysis, which incorporates second-order spatial differences and complex error weighting schemes to capture local image structure and prediction trends.

The system demonstrates significant mode dependency, where each prediction mode optimizes the predictors for different image characteristics and directional biases. This adaptability allows the framework to specialize in various image content types while maintaining the core predictive philosophies of each sub-predictor.

2.3. Predictor Enhancement

Building on the foundation of the existing JPEG XL weighted average predictor framework, we implemented four strategically selected additional predictors to enhance the compression performance:

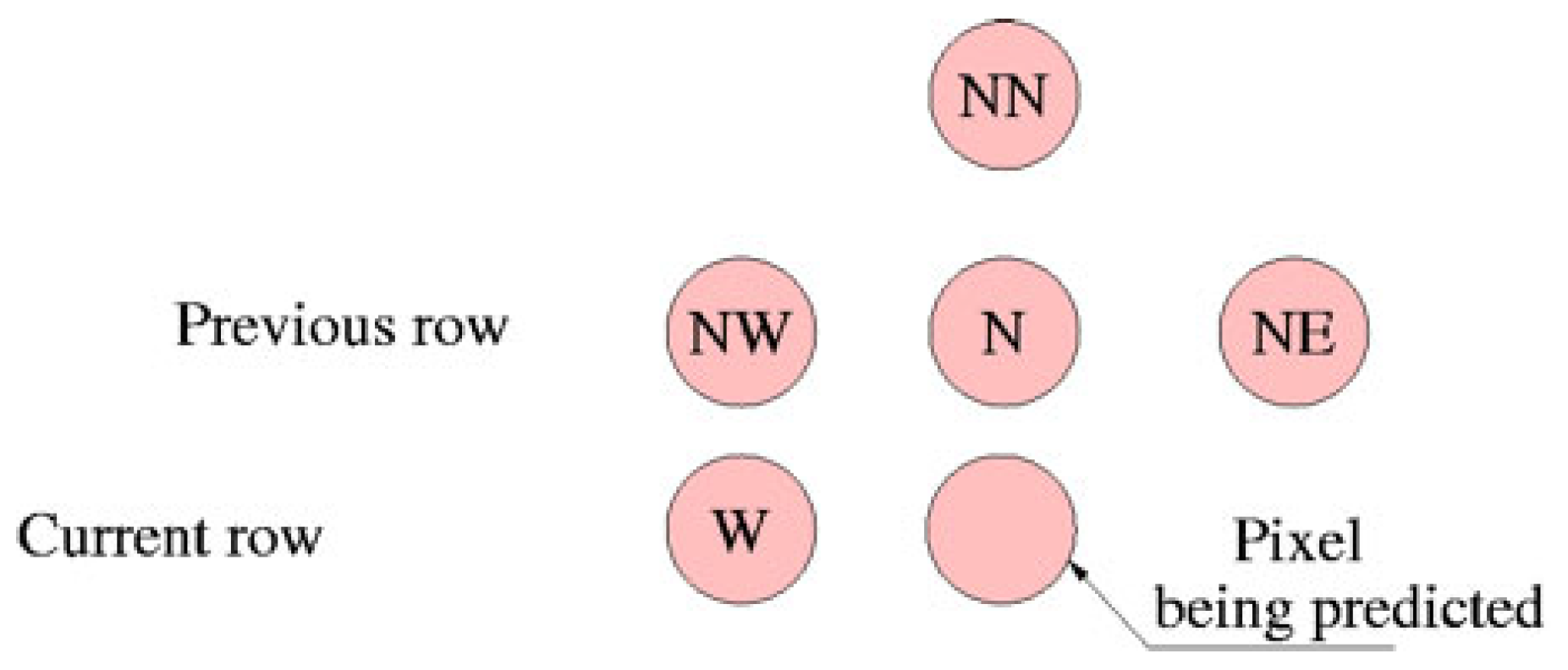
• Adaptive MED predictor: This predictor was selected for its established role as the core predictor in the JPEG-LS standard [3]. Weinberger et al. [3] demonstrated that MED provides competitive compression performance while maintaining low computational complexity through its simple edge detection mechanism. MED tends to pick N in cases where a vertical edge exists left of the current location, W in cases of a horizontal edge above the current location, or W + N − NW if no edge is detected. The traditional MED predictor was augmented with error correction capabilities.
• Adaptive Median predictor: This predictor implements a computationally efficient approach that incorporates error feedback mechanisms. Building upon the median filter’s inherent robustness, it adds adaptive error correction capabilities to improve the prediction accuracy. This predictor calculates the median of W, N, and NW pixels, whereas the adaptive MED predictor also considers edges. The adaptive nature of these first two additional predictors is based on a dynamic error-correcting mechanism that is utilized by the original sub-predictors of the weighted average predictor [9].
• Paeth predictor: We selected this predictor for its proven prediction reliability in the PNG standard [16]. The Paeth predictor uses the formula (W + N − NW) to estimate pixel values by selecting from the neighboring pixel (W, N, or NW) closest to this computed value [16]. The Paeth predictor offers a unique computational approach that complements the strengths of our prediction ensemble.
• Simplified GAP-based predictor: This predictor was incorporated due to its documented success in the CALIC algorithm, where it demonstrated superior prediction accuracy compared with simpler predictors [5]. The GAP (gradient-adjusted prediction) predictor utilizes W, NW, N, NE, and NN. It first estimates the local horizontal (|W − NW| + |N − NN|) and vertical (|N − NW| + |N − NE|) gradients. This estimation simplifies the original GAP estimation, which also relies on WW and NNE pixels. Next, three heuristic-defined thresholds that utilize the estimated local horizontal and vertical gradients are used to obtain the value of the predicted pixel. This context-aware approach allows it to switch between different prediction strategies based on local image characteristics, making it particularly effective at preserving sharp edges while maintaining accuracy in smooth regions [5].

Together, these four additional predictors work in conjunction with the original four predictors to provide comprehensive coverage across diverse image content types and compression. It is worth mentioning that the four predictors used in this study (adaptive MED, adaptive median, Paeth, and GAP) serve as representative examples. Still, the framework is not limited to these specific choices. Other predictors can also be seamlessly integrated.

2.4. WOP8 Core Algorithm

Our WOP8 algorithm enhances (Algorithm 1) JPEG XL’s weighted average predictor through two fundamental modifications. First, we expanded the original four sub-predictors to eight by incorporating four additional predictors (adaptive MED, adaptive median, Paeth, and GAP) that provide complementary prediction capabilities for different image characteristics. Second, instead of using JPEG XL’s fixed initial weights, WOP8 employs a genetic algorithm to discover the optimal initial weight configurations for each predictor. The GA trains on dataset samples to find weights (ranging from 0 to 15) that maximize the compression efficiency for the image dataset. These optimized weights serve as the initial weights and then the scaling factors in JPEG XL’s adaptive weight adjustment mechanism, allowing the system to start with better predictor emphasis before making runtime corrections. The algorithm maintains JPEG XL’s existing adaptive weight adjustment during compression while initializing with our GA-optimized weights, creating a hybrid approach that combines intelligent initialization and more accurate scaling with dynamic adaptation.

Algorithm 1. WOP8 (weighted optimization predictor for 8 sub-predictors)

Algorithm: WOP8 Predict

INPUT: pixel_position(x,y),           neighboring_pixels(W, NW, N, NE, and NN),           ga_optimized_weights [8] OUTPUT: predicted_pixel_value BEGIN     // Initialize adaptive weights using GA-optimized initial values     FOR each predictor i in [0 to 7]:         weights[i] ← CalculateAdaptiveWeight(ga_optimized_weights[i])     END FOR     // Original JPEG XL predictors (0–3)     predictions[0] ← GradientPredictor(W, NE, N)     predictions[1] ← AdaptiveNorthPredictor(N)     predictions[2] ← AdaptiveWestPredictor(W)     predictions[3] ← AdaptiveMulticontextPredictor(N)     // New WOP8 predictors (4–7)     // MED with error feedback     predictions[4] ← AdaptiveMEDPredictor(N, W, NW)     // Robust median prediction     predictions[5] ← EnhancedMedianPredictor(N, W, NW)     // PNG-style predictor     predictions[6] ← PaethPredictor(N, W, NW)     // Gradient-adjusted prediction     predictions[7] ← GAPPredictor(W, NW, N, NE, NN)     // Compute weighted average using GA-optimized weights     final_prediction ← WeightedAverage(predictions[0…7], weights[0…7])     RETURN final_prediction END

2.5. Modified Weighted Average Predictor Implementation

The key modification here is extending the prediction array from four to eight elements, incorporating our four new predictors (adaptive MED, enhanced adaptive median, Paeth, and simplified GAP) alongside the original four JPEG XL weighed average sub-predictors.

2.6. Initial Weight Optimization

In our algorithm, the initial weights were optimized using a genetic algorithm [9]. These weights serve as crucial scaling factors that control how aggressively each predictor’s weight adapts based on prediction errors [9].

2.7. Genetic Algorithm Implementation

Our genetic algorithm (Algorithm 2) discovers the optimal weight configurations for the eight predictors by treating each weight set as a candidate solution and evolving them toward better compression performance [17]. Each candidate represents a vector of eight integer weights ranging from 0 to 15, corresponding to the initial weights for our expanded predictor set [10,11]. The algorithm begins with a randomly initialized population and iteratively improves solutions through evolutionary operators: tournament selection identifies high-performing weight configurations as parents, uniform crossover combines successful weight patterns from different candidates, and mutation introduces random variations to prevent premature convergence. An elitism strategy preserves the best-performing solutions across generations, ensuring that superior weight configurations are not lost due to the stochastic nature of crossover and mutation operations while working with slightly lower population and generation numbers. The fitness of each candidate is determined by measuring the actual compression improvement achieved when those weights are applied to a training subset of the target dataset. Through this evolutionary process, the algorithm automatically discovers which predictors should receive higher emphasis for specific image types, eliminating the need for manual weight tuning and enabling dataset-specific optimization that adapts to the unique characteristics of different image categories.

Algorithm 2. Genetic Algorithm Weight Optimizer

Algorithm: GA OptimizeWeights

INPUT: training_dataset,           population_size,           generations,           mutation_rate,           crossover_rate OUTPUT: optimal_weight_configuration [8] BEGIN     population ← InitializeRandomPopulation(population_size)     best_solution ← null     best_fitness ← negative_infinity     FOR each generation in [0 to generations-1]:         fitness_scores ← empty_list         // Evaluate compression performance for each weight configuration         FOR each candidate in the population:             compression_improvement ← TestCompressionRatio(candidate,                                                                   training_dataset)             fitness ← CalculateFitness(compression_improvement)             ADD fitness to fitness_scores             IF fitness > best_fitness:                 best_fitness ← fitness                 best_solution ← candidate             END IF         END FOR         // Preserve elite solutions         elite_candidates ← SelectTopPerformers(population, fitness_scores)         next_generation ← elite_candidates         // Generate offspring through selection and reproduction         WHILE population not full:             parent_a ← TournamentSelection(population, fitness_scores)             parent_b ← TournamentSelection(population, fitness_scores)             IF random_probability < crossover_rate:                 offspring ← UniformCrossover(parent_a, parent_b)             ELSE                 offspring ← parent_a             END IF             offspring ← ApplyMutation(offspring, mutation_rate)             ADD offspring to next_generation         END WHILE         population ← next_generation     END FOR     RETURN best_solution END

The GA operates with the following configuration: population size of 30, tournament selection (size = 3), uniform crossover (rate = 0.9), mutation (rate = 0.05), and elitism (n = 2) across 24 generations [10,11,18,19]. After all generations are completed, the candidate achieving the highest fitness score from the final generation represents the optimal weight configuration. These parameter values fall within ranges commonly reported in literature [20] and were refined through preliminary testing to optimize performance for the specific problem domain.

2.8. Weight Integration

The optimal weights obtained from the genetic algorithm process were integrated into the JPEG XL framework by modifying the predictor mode weight initialization. These optimized initial weights replace the default weights, serving as the scaling factors that control the adaptive behavior of each predictor throughout the compression process [19].

3. Implementation Setup and Results

3.1. Experimental Design

3.1.1. Dataset Selection and Validation

To ensure robust evaluation, we assessed predictor performance using the Kodak Lossless True Color Suite and Tecnick Color Dataset [21,22,23]. The Kodak Lossless True Color Suite contains twenty-four 768 × 512 colored images. We used the subset of the Tecnick Color Dataset, which includes forty 600 × 600 colored images. Our analysis and discussion focused on the Kodak dataset, while the Tecnick Color Dataset was used as evidence for generalizability.

3.1.2. Data Partitioning

The dataset was randomly partitioned into training and testing sets. We employed a default allocation of 10% for training and 90% for testing, with the training set size capped at a maximum of 10 images to prevent overfitting with large datasets. To ensure reproducibility across experiments, images were randomly shuffled using a seed value of 42 prior to partitioning [24].

3.1.3. Baseline Measurements

With the data splits established, we generated baseline compression statistics for both uncompressed images and standard JPEG XL compression. During WOP8 development, we utilized the -Predictor_Mode 6 flag, which constrains the system to employ only the weighted average predictor [9]. This isolation approach ensures that any observed performance improvements derive from our predictor enhancements rather than complex predictor interactions. Additionally, Distance = 0 settings guarantee mathematically lossless compression throughout the evaluation process [9].

3.1.4. Training and Evaluation Process

Once the GA determines optimal weights through training, these weights are applied to the modified weighted average predictor and evaluated on the reserved test set. During evaluation, the system records comprehensive metrics for each processed image including the file size in bytes, bits per pixel (BPP), and performance differentials between the baseline JPEG XL and WOP8 configurations.

To ensure compression integrity, we verified the lossless compression through mean absolute error (MAE) calculations, with zero values confirming perfect reconstruction.

3.1.5. Implementation

The complete WOP8 system operates through four sequential stages [25]: (1) data partitioning, (2) baseline statistic collection, (3) GA optimization execution, and (4) results compilation [19]. To facilitate ease of use, we developed a terminal user interface that enables system operation and parameter configuration [26]. The system generates comprehensive output including spreadsheet-formatted results, JavaScript object notation (JSON) files containing complete GA optimization records, and the compressed dataset [19].

3.1.6. Computing Environment

All experiments were conducted on a MacBook Pro equipped with a 2.3 GHz 8-Core Intel Core i9 CPU, 16 GB of RAM, and 1.0 TB of storage (Apple Inc., Cupertino, CA, USA; Intel Corporation, Santa Clara, CA, USA). The system operated on macOS 15.3.1 using Python version 3.13.1 (Python Software Foundation, Wilmington, DE, USA) and the JPEG XL v0.11.1 implementation [9].

3.2. Compression Performance Analysis

To properly evaluate the contribution of WOP8, we conducted experiments under two distinct operational configurations. The isolated mode configuration utilizes the -Predictor_Mode 6 flag to force JPEG XL to operate exclusively with the weighted average predictor, thereby bypassing the meta-adaptive tree (MA tree) that typically selects between multiple predictors based on local image context [9]. In contrast, the default mode represents the standard JPEG XL operation where the MA tree dynamically selects the best predictor for each image region including our enhanced weighted average predictor.

In modular mode, the amount of compression achieved varies with the effort level, which controls the resources and strategies used [9]. Effort levels 1 and 2 utilize a simpler, fixed predictor that does not employ the weighted average predictor enhanced by WOP8. Starting with effort level 3, JPEG XL begins using the weighted average predictor with a fixed configuration, while effort levels 4 and above utilize a learned MA tree that can select between the clamped gradient and weighted average predictors [7]. Higher effort levels allocate increasing computational resources to the predictor optimization and parameter tuning, with effort level 8 specifically enabling more weighted predictor parameters [9]. This relationship directly explains the performance patterns observed in our experimental results. For more details on effort levels, please refer to

Table 1. JPEG XL effort level configurations for the modular (lossless) mode, highlighting predictor usage relevant to the WOP8 evaluation. Adapted from JPEG XL encode effort documentation [7].

Effort Level	Predictor Configuration	Other Key Features
1	Fixed ClampedGradient predictor	Fast-lossless, fixed YCoCg RCT, simple palette detection
2	Fixed ClampedGradient predictor	Global channel palette, fixed MA tree
3	Fixed weighted predictor	Fixed the MA tree with WP-error context
4	ClampedGradient + weighted predictor, learned MA tree	Global palette
5	Same as effort level 4	Patches, local palette/channel palette
6	Same as effort level 5	More RCTs and MA tree properties
7	Same as effort level 6	Additional RCTs and MA tree properties
8	Same as effort level 7	Enhanced RCTs, MA tree properties, and more weighted predictor parameters

.

The compression performance evaluation demonstrates the effectiveness of WOP8 across the two operational configurations and effort levels.

Table 2. Compression performance comparison between the baseline JPEG XL and WOP8 in isolated predictor mode across different effort levels on the Kodak dataset. BPP values represent bits per pixel, with lower values indicating better compression efficiency.

Effort Level	Baseline BPP	WOP8 BPP	Difference BPP
8	8.85	8.61	0.24
7	8.91	8.67	0.24
6	9.05	8.85	0.20
5	9.23	9.14	0.09
4	9.40	9.31	0.09
3	9.46	9.36	0.10
2	10.33	10.33	0.00

presents the results for isolated predictor mode testing, while

Table 3. Compression performance comparison between the baseline JPEG XL and WOP8 in default mode using the standard JPEG XL configuration with all predictors available on the Kodak dataset.

Effort Level	Baseline BPP	WOP8 BPP	Difference BPP
8	8.61	8.55	0.06
7	8.65	8.58	0.07
6	8.81	8.74	0.07
5	9.20	9.16	0.04
4	9.39	9.36	0.03
3	9.46	9.36	0.10
2	10.33	10.33	0.00

shows the default performance using standard JPEG XL configurations. All results presented in Table 2 and Table 3 represent performance on the test set of the Kodak dataset, using the data described in Section 3.1.1.

The isolated mode results revealed consistent compression improvements across effort levels 3–8, with the most significant gains occurring at higher effort levels. Specifically, effort levels 7 and 8 achieved improvements of 0.24 BPP over the JPEG XL baseline performance. Effort level 6 demonstrated a 0.20 BPP improvement, while effort levels 3–5 showed a small gain, ranging from 0.09 to 0.10 BPP. Effort level 2 showed no improvements as the weighted predictor was not utilized.

3.3. Generalizability Validation

To validate WOP8’s generalizability, we evaluated its performance on the Tecnick Color Dataset using the methodology described in Section 3.1, with GA optimization performed separately on the Tecnick training images.

Table 4. Compression performance comparison between the baseline JPEG XL and WOP8 on the Tecnick Color Dataset in isolated predictor mode on the test set.

Effort Level	Baseline BPP	WOP8 BPP	Difference BPP
8	8.52	8.46	0.06
7	8.66	8.57	0.09
6	8.79	8.70	0.09
5	8.88	8.80	0.08
4	9.22	9.14	0.08
3	9.25	9.17	0.08
2	10.33	10.33	0.00

presents the compression performance results in isolated predictor mode.

The Tecnick dataset demonstrates consistent improvements across effort levels 3–7 (0.08–0.09 BPP), with effort level 8 showing reduced gains (0.06 BPP). While the performance pattern differed from Kodak (where effort level 8 achieved maximum improvement), WOP8 maintained improvements across both datasets without performance degradation, confirming the approach’s general applicability.

3.4. Computational Performance Analysis

To assess the computational overhead of WOP8, we measured the compression and decompression times for both the baseline JPEG XL and WOP8 configurations on the Kodak and the Tecnick datasets. The WOP8 execution time showed an average overhead over all effort levels on both datasets of an extra 103 ms per image, increasing from 726 ms (baseline) to 829 ms (WOP8) for compression, and an additional 45 ms per image, increasing from 122 ms (baseline) to 167 ms (WOP8), for decompression. Meanwhile, the GA optimization requires an average of 105 min. However, this represents a one-time training cost per dataset that is amortized across all subsequent compressions using the optimized weights.

3.5. Genetic Algorithm Parameter Optimization

To validate the sufficiency of our GA configuration, we evaluated the impact of increased population size and generation count on optimization effectiveness. Testing was conducted in isolated mode on the Kodak test set using three configurations: a population of 30 with 24 generations, a population of 50 with 50 generations, and a population of 100 with 100 generations.

The results demonstrated diminishing returns with increased computational investment. The baseline configuration (at a population of 30 with 24 generations) achieved a 0.244 BPP improvement. In comparison, the larger configurations yielded only marginal gains of 0.248 BPP (at a population of 50 with 50 generations) and 0.249 BPP (at a population of 100 with 100 generations). These minimal improvements do not justify the substantial computational overhead, validating our choice configuration (a population of 30 with 24 generations) as providing an optimal balance between optimization effectiveness and computational efficiency.

4. Discussion

4.1. Interpretation of Compression Performance Results

4.1.1. Mechanisms of WOP8 Compression Improvement

The consistent improvements achieved by WOP8 in isolated mode demonstrate the effectiveness of enhancing JPEG XL’s weighted average predictor through expanded sub-predictor diversity and GA-optimized initial weights. The enhanced predictor ensemble offers broader coverage of image characteristics compared with the original four-predictor framework. At the same time, the GA-optimized weights ensure that the most effective sub-predictors receive appropriate emphasis during the adaptive weight calculation process.

The superior performance validates our hypothesis that incorporating established predictors (MED from JPEG-LS, adaptive median, Paeth from PNG, GAP from CALIC) with adaptive enhancements would provide superior prediction capabilities within the weighted average framework. This approach demonstrates that predictor-specific optimization can yield significant improvements, even within sophisticated compression frameworks.

4.1.2. Significance of Weighted Average Predictor Improvements

The 0.24 BPP improvement in the Kodak dataset achieved at effort levels 7 and 8 in isolated mode represents a substantial enhancement to the weighted average predictor’s compression efficiency. In the context of lossless image compression, where individual predictor improvements are typically measured in fractions of bits per pixel, this 2.71% reduction demonstrates the significant potential of targeted predictor optimization.

The consistency of improvements across effort levels 3–8 (ranging from 0.09 to 0.24 BPP) demonstrates that WOP8’s enhancements provide value across different computational configurations when the weighted average predictor is utilized.

4.1.3. Scope and Validation of the Enhancement Approach

The distinction between the isolated and default mode results validates the targeted nature of WOP8’s contribution. In isolated mode, where only the weighted average predictor is operational, the enhancements consistently produce improvements. In default mode, the improvements are more modest but notably do not degrade performance, demonstrating that WOP8 enhances the weighted average predictor without interfering with JPEG XL’s sophisticated meta-adaptive tree selection mechanisms.

This outcome confirms that WOP8 successfully improves a specific component of JPEG XL’s prediction system rather than attempting broad-scale optimization. The approach proves that targeted predictor enhancement can be effective within modern compression frameworks, providing a foundation for component-specific optimization strategies in sophisticated codecs.

4.2. Genetic Algorithm Effectiveness and Predictor Optimization

The GA optimization results revealed a critical distinction between the effectiveness of isolated and default modes. In isolated mode, the GA demonstrated clear optimization capability, producing varied weight configurations across effort levels and consistently outperforming the baseline performance. However, in default mode, the weight configuration remained unchanged across effort levels (used the first weight configuration produced by the GA), indicating that the MA tree’s dynamic predictor selection overrides the influence of initial weights or scaling factors. This suggests that the modest improvements observed in default mode are not a result of GA optimization, but rather the addition of sub-predictors made available to the MA tree for selection.

The weight configurations discovered by the GA in the Kodak dataset in isolated mode demonstrate systematic optimization rather than random parameter assignment. The optimal configuration at effort level 8 (0, 2, 3, 0, 15, 0, 13, 6) showed clear discrimination, assigning the maximum weight to the adaptive MED predictor (15) and substantial weight to the Paeth predictor (13), while effectively disabling the original predictors (weights of 0–3). This systematic differentiation validates the GA’s capability of identifying superior prediction strategies through empirical evaluation.

These findings demonstrate that static parameter optimizations prove highly effective within controlled environments where the optimization target operates without competition from other strategies. The GA’s limited effectiveness in default mode does not diminish its capability. Instead, it defines its appropriate scope, providing valuable insight into the interaction between static optimization and dynamic selection in modern compression systems.

4.3. Limitations and Future Works

The current implementation extends the predictor ensemble to eight sub-predictors, representing only one possible extension of the original four-predictor framework. While the GA optimization introduces computational overhead during training, it is a one-time, offline cost per dataset that does not impact the time complexity of the compression/decompression processes.

Future research directions include evaluating WOP8’s effectiveness across diverse image datasets to assess the generalizability of predictor enhancement and weight optimization strategies. Investigating additional predictors could further improve the weighted average predictor. The methodology developed for isolated testing or predictor enhancements provides a framework for systematically evaluating other individual predictors within the JPEG XL modular architecture.

5. Conclusions

This study demonstrated that the WOP8 system provides a targeted enhancement to JPEG XL’s weighted average predictor. The system’s core contributions—an expanded sub-predictor ensemble and genetic algorithm (GA) optimization—were validated by consistent performance improvements in isolated mode, achieving a reduction of up to 0.24 BPP.

The GA successfully optimizes predictor weights in isolated mode, producing varied and intelligent configurations. The modest improvements seen in default mode (0.03–0.10 BPP) were attributed to the added sub-predictors in the weighted average predictor. This outcome demonstrates that WOP8’s enhancements translate to practical scenarios without interfering with JPEG XL’s dynamic predictor selection mechanisms. The approach’s effectiveness was validated across two datasets, confirming the generalizability of the enhancement methodology. The research establishes a framework for enhancing targeted predictors, proving its effectiveness within sophisticated compression architectures.