A Novel Gating Adversarial Imputation Method for High-Fidelity Restoration of Missing Electrical Disturbance Data
Abstract
1. Introduction
- 1.
- First of all, an innovative GAI framework is proposed for the high-fidelity restoration of missing electrical disturbance data.
- 2.
- The critical introduction of a gating architecture significantly enhances imputation robustness and feature representation, preserving critical original characteristics.
- 3.
- A refined experimental environment is carefully designed using a high-quality disturbance dataset with standard missingness.
- 4.
- Imputation training’s stability is maintained by applying a strict clipping on the adversarial imputation loss.
2. Problem Formulation
2.1. Electrical Disturbance Modeling
2.2. Missingness in Disturbance Data
- MCAR: This holds when the missing probability is entirely independent of both observed and unobserved variables [33]. This indicates that missingness occurs as a purely stochastic process, with every data point having an equal and constant probability of being absent.
- MNAR: This occurs when the missing probability of a value is dependent on the unobserved data itself [34]. In this case, a non-ignorable selection bias is introduced, which cannot be corrected without explicitly modeling the missingness process.
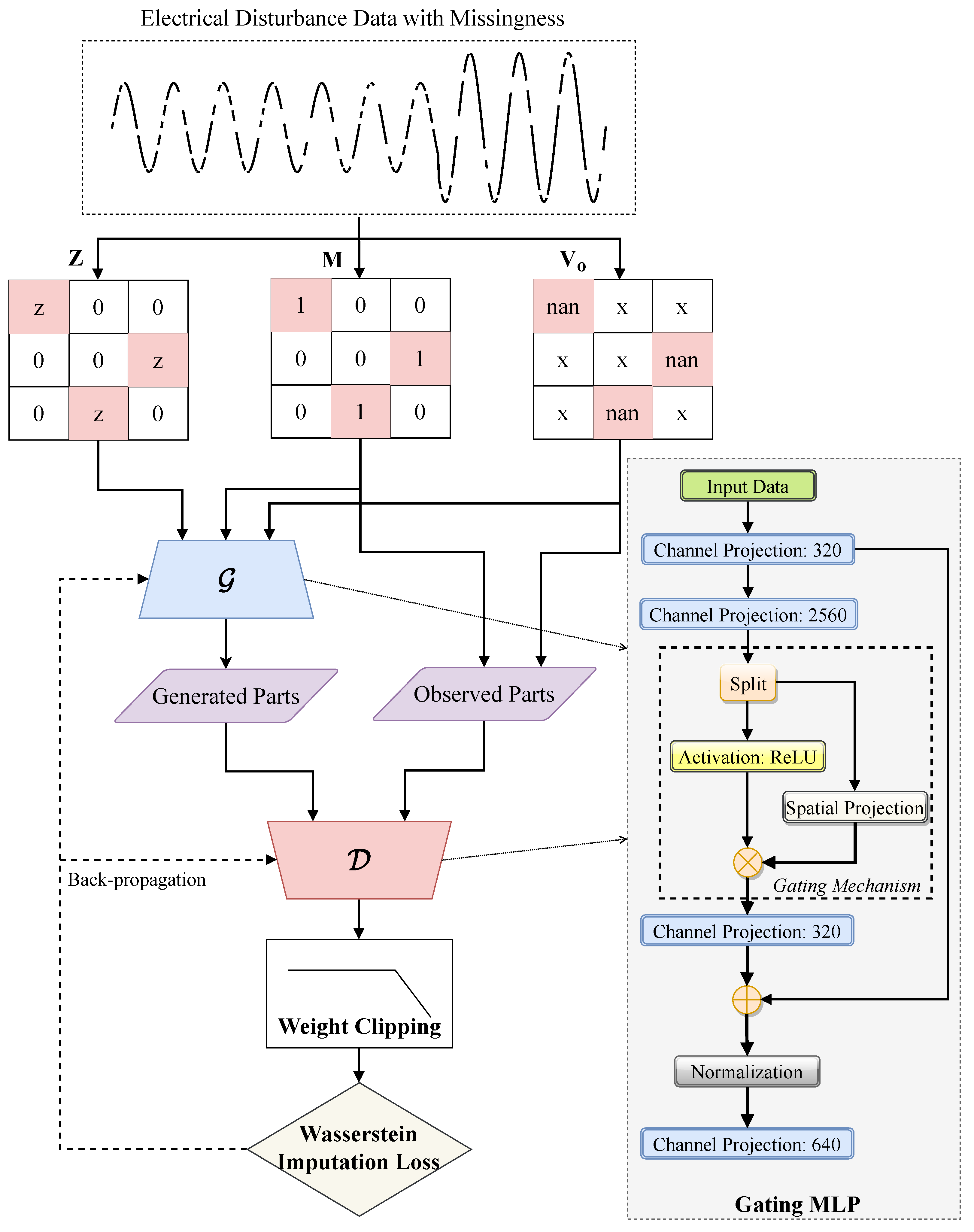
3. Proposed Gating Adversarial Imputation
3.1. Gating Mechanism
3.2. Improved Adversarial Imputation
| Algorithm 1 Proposed Gating Adversarial Imputation Algorithm |
|
4. Experiments and Results
4.1. Experimental Settings
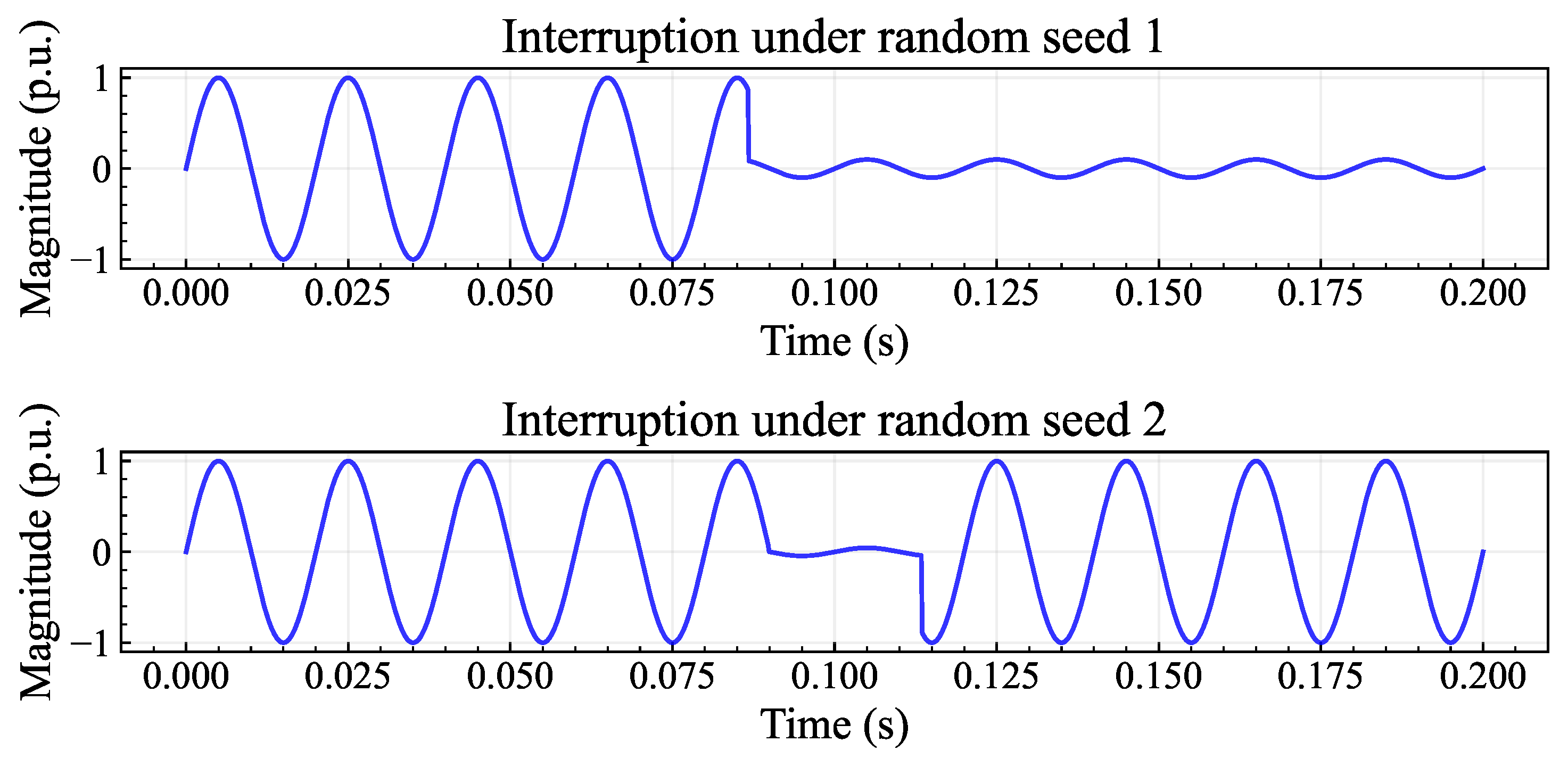
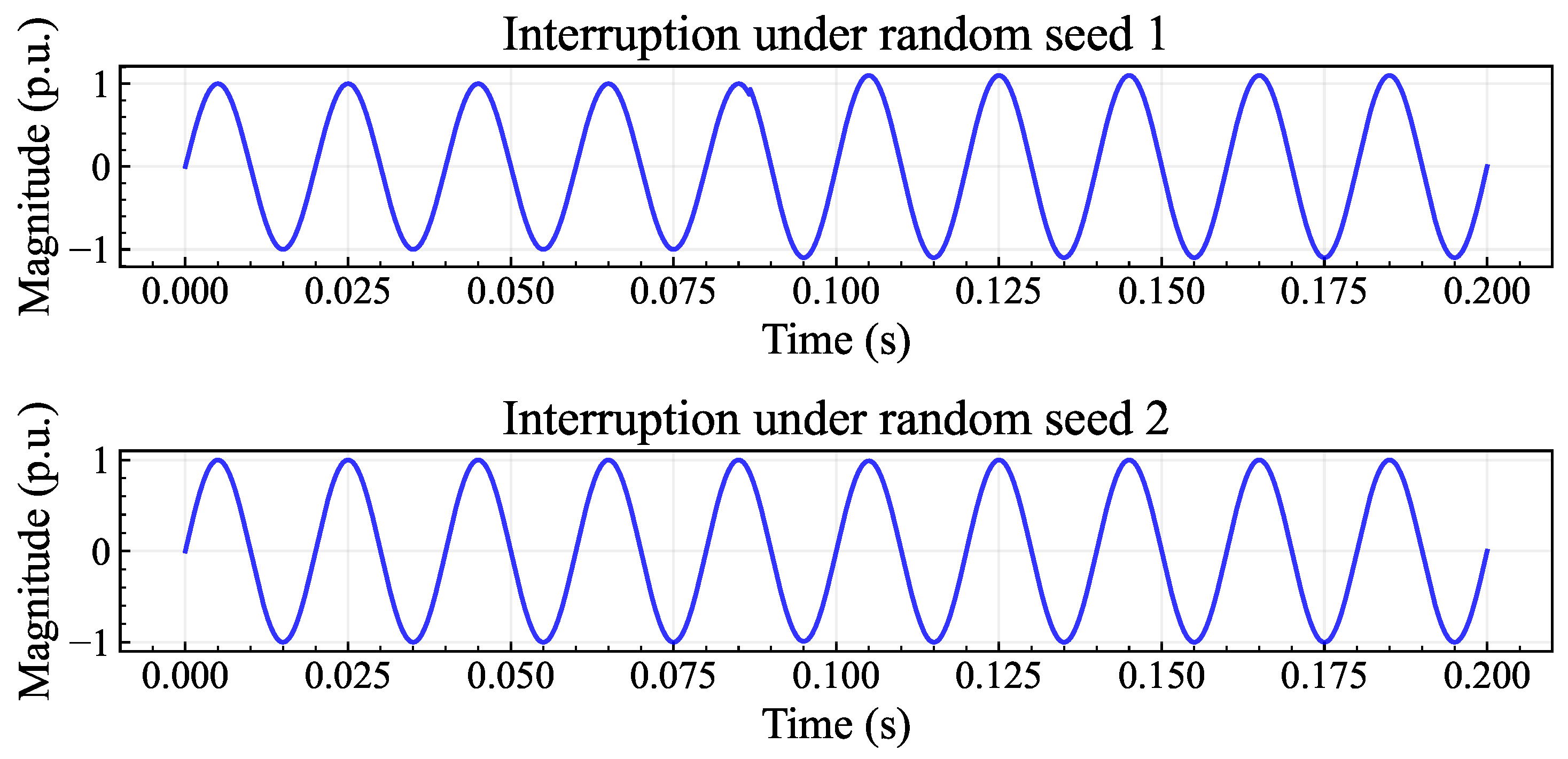
4.1.1. Disturbance Data Generation
- Step 1:
- Assign basic constant parameters like the normalized amplitude , fundamental frequency Hz, and fundamental angular frequency ; then, define the array of parametric equations with random parameters.
- Step 2:
- Initialize the disturbance output array with a -shaped zero array. Here, 16 is the number of disturbance types, and 641 is the sum of signal length 640 and its corresponding label length 1.
- Step 3:
- For each iteration k, a different random seed is set for array .
- Step 4:
- For each disturbance type , run the parametric equation . Then, assign it with into the corresponding array .
- Step 5:
- For each iteration k, output an array and stack all together into the dataset .
- Step 6:
- Shuffle the generated dataset in random order. The total shape of is .
4.1.2. Experimental Configuration
- 1.
- RF refers to random forest imputation. RF iteratively fits a forest of decision trees to the observed data; then, the model is utilized to predict missing data [19].
- 2.
- 3.
- EGAIN [20] stands for the enhanced GAIN algorithm. It is enhanced by a structured five-layer MLP with 2560, 640, 640, 640, and 640 units.
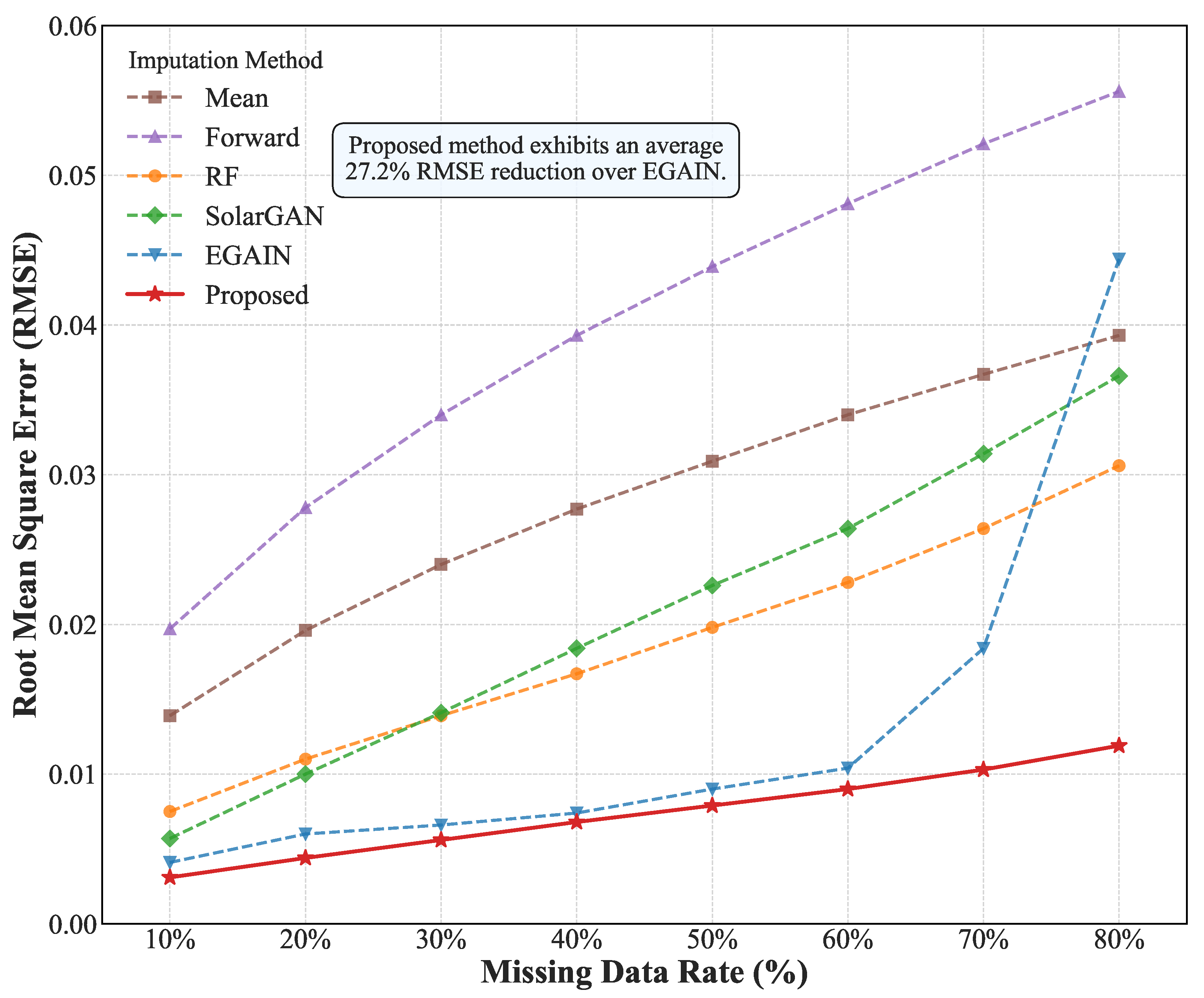
4.2. Imputation Performance Evaluation
4.2.1. Analysis of Imputation Scores
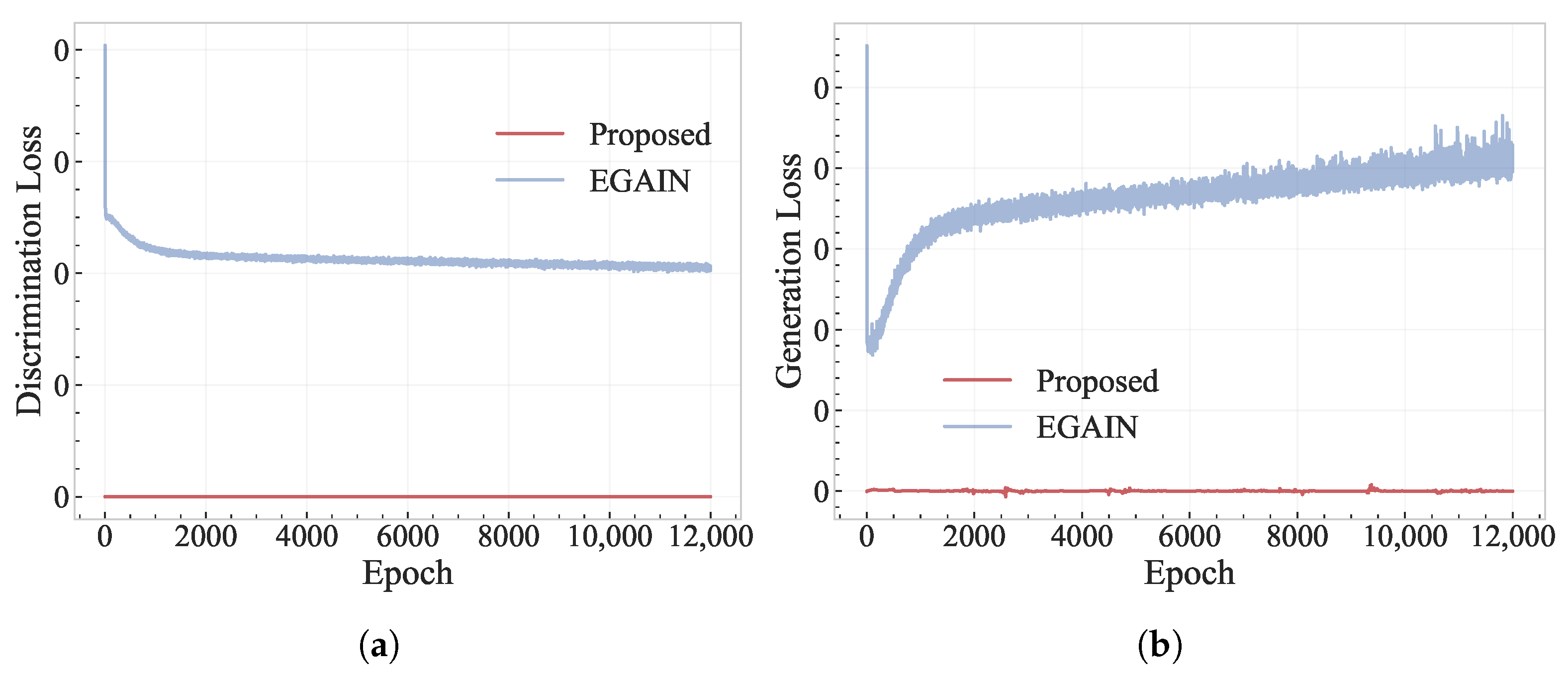
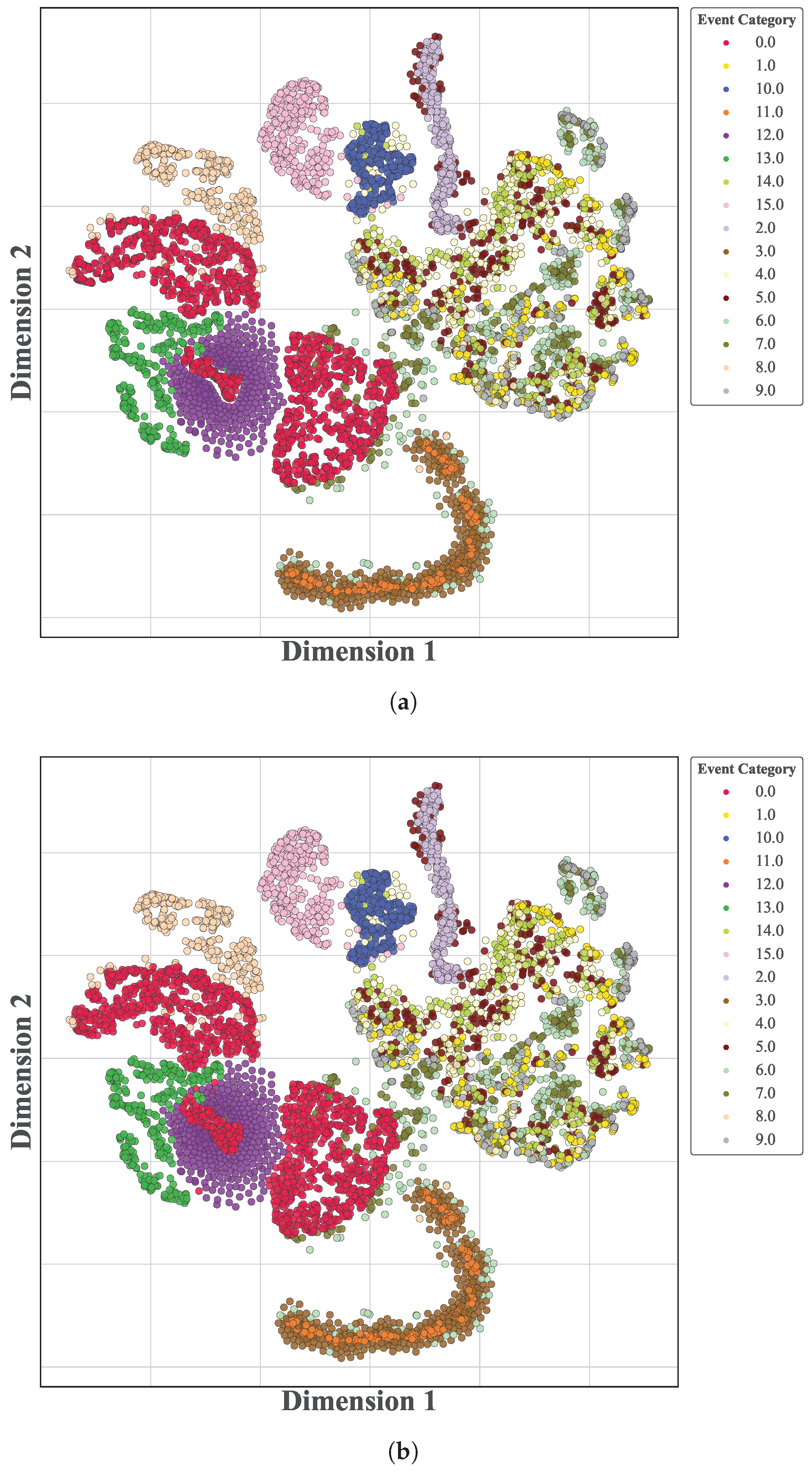
4.2.2. Analysis of Imputation Characteristics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GAI | Gating adversarial imputation; |
| CPPS | Cyber-physical power system; |
| MLP | Multi-layer perceptron; |
| PMU | Phasor measurement unit; |
| PQD | Power quality disturbance; |
| MAR | Missing at random; |
| MCAR | Missing completely at random; |
| MNAR | Missing not at random; |
| SOTA | State of the art; |
| EGAIN | Enhanced generative adversarial imputation net; |
| RMSE | Root mean squared error; |
| MAE | Mean absolute error; |
| MAPE | Mean absolute percentage error. |
References
- Feng, G.; Lao, K.W.; Chen, G. Out-of-Distribution Detection of Unknown False Data Injection Attack with Logit-Normalized Bayesian ResNet. IEEE Trans. Smart Grid 2024, 15, 6005–6017. [Google Scholar] [CrossRef]
- Sugunaraj, N.; Balaji, S.R.A.; Chandar, B.S.; Rajagopalan, P.; Kose, U.; Loper, D.C.; Mahfuz, T.; Chakraborty, P.; Ahmad, S.; Kim, T.; et al. Distributed Energy Resource Management System (DERMS) Cybersecurity Scenarios, Trends, and Potential Technologies: A Review. IEEE Commun. Surv. Tutor. 2025. [Google Scholar] [CrossRef]
- Alvarez-Alvarado, M.S.; Apolo-Tinoco, C.; Ramirez-Prado, M.J.; Alban-Chacón, F.E.; Pico, N.; Aviles-Cedeno, J.; Recalde, A.A.; Moncayo-Rea, F.; Velasquez, W.; Rengifo, J. Cyber-physical power systems: A comprehensive review about technologies drivers, standards, and future perspectives. Comput. Electr. Eng. 2024, 116, 109149. [Google Scholar] [CrossRef]
- Vahidi, S.; Ghafouri, M.; Au, M.; Kassouf, M.; Mohammadi, A.; Debbabi, M. Security of wide-area monitoring, protection, and control (WAMPAC) systems of the smart grid: A survey on challenges and opportunities. IEEE Commun. Surv. Tutor. 2023, 25, 1294–1335. [Google Scholar] [CrossRef]
- Theodorakatos, N.P.; Babu, R. Hybrid Optimization Strategies for Global Optimality in Non-Convex Programming Using SQP and IPMs: Avoiding the Maratos Effect in PMU Placement–A Case Study. J. Phys. Conf. Ser. 2025, 3027, 012041. [Google Scholar] [CrossRef]
- Phadke, A.G.; Bi, T. Phasor measurement units, WAMS, and their applications in protection and control of power systems. J. Mod. Power Syst. Clean Energy 2018, 6, 619–629. [Google Scholar] [CrossRef]
- Theodorakatos, N.P.; Babu, R.; Theodoridis, C.A.; Moschoudis, A.P. Mathematical models for the single-channel and multi-channel PMU allocation problem and their solution algorithms. Algorithms 2024, 17, 191. [Google Scholar] [CrossRef]
- Tang, H.; Wu, J.; Chen, L.; Liu, Z.; Wu, F.; Li, K.; Wu, Z.; Yu, F.; Bi, Q. A control optimization model for CVaR risk of distribution systems with PVs/DSs/EVs using Q-learning powered adaptive differential evolution algorithm. Int. J. Electr. Power Energy Syst. 2021, 132, 107209. [Google Scholar]
- Xygkis, T.C.; Löfberg, J.; Korres, G.N. Investigation of Optimal Phasor Measurement Selection for Distribution System State Estimation Under Various Uncertainties. IEEE Trans. Instrum. Meas. 2025, 74, 1–16. [Google Scholar] [CrossRef]
- Ravi, T.; Sathish Kumar, K. Analysis, monitoring, and mitigation of power quality disturbances in a distributed generation system. Front. Energy Res. 2022, 10, 989474. [Google Scholar] [CrossRef]
- Feng, G.; Lao, K.W. Wasserstein Adversarial Learning for Identification of Power Quality Disturbances with Incomplete Data. IEEE Trans. Ind. Inform. 2023, 19, 10401–10411. [Google Scholar] [CrossRef]
- Du, J.; Hu, M.; Zhang, W. Missing data problem in the monitoring system: A review. IEEE Sensors J. 2020, 20, 13984–13998. [Google Scholar] [CrossRef]
- Elimam, M.; Isbeih, Y.J.; Azman, S.K.; El Moursi, M.S.; Al Hosani, K. Deep learning-based PMU cyber security scheme against data manipulation attacks with WADC application. IEEE Trans. Power Syst. 2022, 38, 2148–2161. [Google Scholar] [CrossRef]
- Li, Z.; Liu, H.; Zhao, J.; Bi, T.; Yang, Q. A power system disturbance classification method robust to PMU data quality issues. IEEE Trans. Ind. Inform. 2021, 18, 130–142. [Google Scholar] [CrossRef]
- Zhu, L.; Lin, J. Learning spatiotemporal correlations for missing noisy PMU data correction in smart grid. IEEE Internet Things J. 2020, 8, 7589–7599. [Google Scholar] [CrossRef]
- Wang, Y.; Hespanha, J.P. Distributed estimation of power system oscillation modes under attacks on GPS clocks. IEEE Trans. Instrum. Meas. 2018, 67, 1626–1637. [Google Scholar] [CrossRef]
- Foggo, B.; Yu, N. Online PMU Missing Value Replacement Via Event-Participation Decomposition. IEEE Trans. Power Syst. 2021, 37, 488–496. [Google Scholar] [CrossRef]
- Ribeiro, S.M.; Castro, C. Missing data in time series: A review of imputation methods and case study. Learn. Nonlinear Model. 2022, 20, 31–46. [Google Scholar] [CrossRef]
- Hong, S.; Lynn, H.S. Accuracy of random-forest-based imputation of missing data in the presence of non-normality, non-linearity, and interaction. BMC Med Res. Methodol. 2020, 20, 199. [Google Scholar] [CrossRef]
- Yoon, J.; Jordon, J.; Schaar, M. Gain: Missing data imputation using generative adversarial nets. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 5689–5698. [Google Scholar]
- Li, Q.; Yang, X.; Xie, X.; Liu, G. The data recovery strategy on machine learning against false data injection attacks in power cyber physical systems. Meas. Control 2025, 58, 632–642. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Zhang, W.; Luo, Y.; Zhang, Y.; Srinivasan, D. SolarGAN: Multivariate Solar Data Imputation Using Generative Adversarial Network. IEEE Trans. Sustain. Energy 2021, 12, 743–746. [Google Scholar] [CrossRef]
- Liu, H.; Dai, Z.; So, D.; Le, Q.V. Pay attention to mlps. Adv. Neural Inf. Process. Syst. 2021, 34, 9204–9215. [Google Scholar]
- Caicedo, J.E.; Agudelo-Martínez, D.; Rivas-Trujillo, E.; Meyer, J. A systematic review of real-time detection and classification of power quality disturbances. Prot. Control Mod. Power Syst. 2023, 8, 1–37. [Google Scholar] [CrossRef]
- Martinez, R.; Castro, P.; Arroyo, A.; Manana, M.; Galan, N.; Moreno, F.S.; Bustamante, S.; Laso, A. Techniques to locate the origin of power quality disturbances in a power system: A review. Sustainability 2022, 14, 7428. [Google Scholar] [CrossRef]
- Razo-Hernandez, J.R.; Valtierra-Rodriguez, M.; Amezquita-Sanchez, J.P.; Granados-Lieberman, D.; Gomez-Aguilar, J.F.; Rangel-Magdaleno, J.d.J. Homogeneity-PMU-based method for detection and classification of power quality disturbances. Electronics 2018, 7, 433. [Google Scholar] [CrossRef]
- Chen, S.; Li, Z.; Pan, G.; Xu, F. Power quality disturbance recognition using empirical wavelet transform and feature selection. Electronics 2022, 11, 174. [Google Scholar] [CrossRef]
- IEEE Std 1159-2019; IEEE Recommended Practice for Monitoring Electric Power Quality. IEEE: Piscataway, NJ, USA, 2019. [CrossRef]
- Little, R.J. Missing data assumptions. Annu. Rev. Stat. Its Appl. 2021, 8, 89–107. [Google Scholar] [CrossRef]
- Heitjan, D.F.; Basu, S. Distinguishing “missing at random” and “missing completely at random”. Am. Stat. 1996, 50, 207–213. [Google Scholar] [PubMed]
- Moreno-Betancur, M.; Chavance, M. Sensitivity analysis of incomplete longitudinal data departing from the missing at random assumption: Methodology and application in a clinical trial with drop-outs. Stat. Methods Med. Res. 2016, 25, 1471–1489. [Google Scholar] [CrossRef] [PubMed]
- Jamshidian, M.; Jalal, S. Tests of homoscedasticity, normality, and missing completely at random for incomplete multivariate data. Psychometrika 2010, 75, 649–674. [Google Scholar] [CrossRef] [PubMed]
- Steck, H. Training and testing of recommender systems on data missing not at random. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 June 2010; pp. 713–722. [Google Scholar]
- Li, Q.; Xu, Y.; Chew, B.S.H.; Ding, H.; Zhao, G. An integrated missing-data tolerant model for probabilistic PV power generation forecasting. IEEE Trans. Power Syst. 2022, 37, 4447–4459. [Google Scholar] [CrossRef]
- Petzka, H.; Fischer, A.; Lukovnikov, D. On the regularization of Wasserstein GANs. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Van Rossum, G.; Drake, F.L., Jr. Python Tutorial; Centrum voor Wiskunde en Informatica: Amsterdam, The Netherlands, 1995; Volume 620. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]

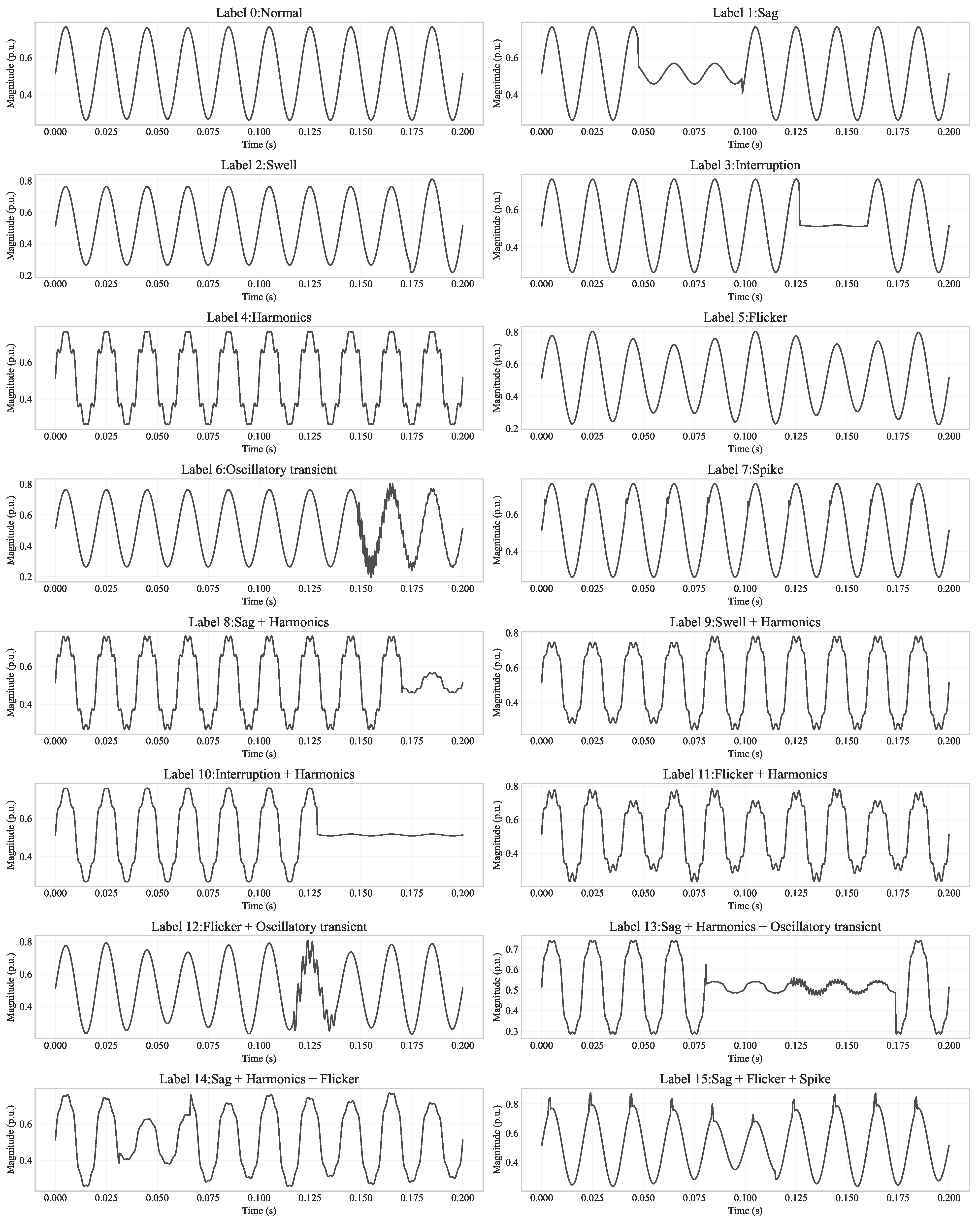


| Label | Disturbance Type | Label | Disturbance Type |
|---|---|---|---|
| 0 | Normal | 8 | Sag + harmonics |
| 1 | Sag | 9 | Swell + harmonics |
| 2 | Swell | 10 | Interruption + harmonics |
| 3 | Interruption | 11 | Flicker + harmonics |
| 4 | Harmonics | 12 | Flicker + oscillatory transient |
| 5 | Flicker | 13 | Sag + harmonics + oscillatory transient |
| 6 | Oscillatory transient | 14 | Sag + harmonics + flicker |
| 7 | Spike | 15 | Sag + flicker + spike |
| Missing Percentage | Mean | Forward | RF | SolarGAN | EGAIN | Proposed |
|---|---|---|---|---|---|---|
| MAE (Mean Absolute Error) | ||||||
| 10% | 0.0029 | 0.0041 | 0.0011 | 0.0010 | 0.0007 | 0.0005 |
| 20% | 0.0058 | 0.0081 | 0.0023 | 0.0027 | 0.0014 | 0.0009 |
| 30% | 0.0087 | 0.0122 | 0.0037 | 0.0048 | 0.0019 | 0.0014 |
| 40% | 0.0116 | 0.0163 | 0.0054 | 0.0071 | 0.0024 | 0.0021 |
| 50% | 0.0145 | 0.0203 | 0.0075 | 0.0099 | 0.0034 | 0.0027 |
| 60% | 0.0174 | 0.0244 | 0.0097 | 0.0128 | 0.0043 | 0.0034 |
| 70% | 0.0203 | 0.0285 | 0.0128 | 0.0162 | 0.0060 | 0.0042 |
| 80% | 0.0232 | 0.0325 | 0.0163 | 0.0200 | 0.0149 | 0.0055 |
| MAPE (Mean Absolute Percentage Error) | ||||||
| 10% | 0.0067 | 0.0093 | 0.0024 | 0.0023 | 0.0016 | 0.0010 |
| 20% | 0.0133 | 0.0185 | 0.0053 | 0.0060 | 0.0033 | 0.0021 |
| 30% | 0.0199 | 0.0278 | 0.0086 | 0.0108 | 0.0042 | 0.0032 |
| 40% | 0.0266 | 0.0372 | 0.0124 | 0.0162 | 0.0055 | 0.0046 |
| 50% | 0.0332 | 0.0463 | 0.0172 | 0.0224 | 0.0077 | 0.0060 |
| 60% | 0.0399 | 0.0557 | 0.0224 | 0.0294 | 0.0099 | 0.0076 |
| 70% | 0.0466 | 0.0651 | 0.0293 | 0.0371 | 0.0129 | 0.0095 |
| 80% | 0.0531 | 0.0743 | 0.0375 | 0.0457 | 0.0317 | 0.0122 |
| RMSE (Root Mean Square Error) | ||||||
| 10% | 0.0139 | 0.0197 | 0.0075 | 0.0057 | 0.0041 | 0.0031 |
| 20% | 0.0196 | 0.0278 | 0.0110 | 0.0100 | 0.0060 | 0.0044 |
| 30% | 0.0240 | 0.0340 | 0.0139 | 0.0141 | 0.0066 | 0.0056 |
| 40% | 0.0277 | 0.0393 | 0.0167 | 0.0184 | 0.0074 | 0.0068 |
| 50% | 0.0309 | 0.0439 | 0.0198 | 0.0226 | 0.0090 | 0.0079 |
| 60% | 0.0340 | 0.0481 | 0.0228 | 0.0264 | 0.0104 | 0.0090 |
| 70% | 0.0367 | 0.0521 | 0.0264 | 0.0314 | 0.0184 | 0.0103 |
| 80% | 0.0393 | 0.0556 | 0.0306 | 0.0366 | 0.0444 | 0.0119 |
| R2 (Coefficient of Determination) | ||||||
| 10% | 0.8994 | 0.7980 | 0.9649 | 0.9697 | 0.9932 | 0.9949 |
| 20% | 0.7994 | 0.5982 | 0.9269 | 0.8830 | 0.9879 | 0.9907 |
| 30% | 0.7001 | 0.3977 | 0.8826 | 0.8416 | 0.9797 | 0.9855 |
| 40% | 0.5990 | 0.1965 | 0.8340 | 0.7628 | 0.9745 | 0.9784 |
| 50% | 0.5000 | −0.0039 | 0.7706 | 0.6474 | 0.9632 | 0.9706 |
| 60% | 0.3997 | −0.1993 | 0.7011 | 0.4797 | 0.9505 | 0.9618 |
| 70% | 0.3009 | −0.4016 | 0.6060 | 0.3238 | 0.8456 | 0.9495 |
| 80% | 0.2002 | −0.5992 | 0.4731 | 0.1356 | 0.1077 | 0.9336 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Feng, G.; Wang, L. A Novel Gating Adversarial Imputation Method for High-Fidelity Restoration of Missing Electrical Disturbance Data. Electronics 2025, 14, 4108. https://doi.org/10.3390/electronics14204108
Chen L, Feng G, Wang L. A Novel Gating Adversarial Imputation Method for High-Fidelity Restoration of Missing Electrical Disturbance Data. Electronics. 2025; 14(20):4108. https://doi.org/10.3390/electronics14204108
Chicago/Turabian StyleChen, Lidan, Guangxu Feng, and Lei Wang. 2025. "A Novel Gating Adversarial Imputation Method for High-Fidelity Restoration of Missing Electrical Disturbance Data" Electronics 14, no. 20: 4108. https://doi.org/10.3390/electronics14204108
APA StyleChen, L., Feng, G., & Wang, L. (2025). A Novel Gating Adversarial Imputation Method for High-Fidelity Restoration of Missing Electrical Disturbance Data. Electronics, 14(20), 4108. https://doi.org/10.3390/electronics14204108






