Power Grid Fault Location Method Based on Variational Mode Decomposition and Symmetric Pulse Injection with Teager Operator
Abstract
1. Introduction
2. Analysis of Traveling Wave at Fault Point
2.1. Fault Characteristic Signal Extraction
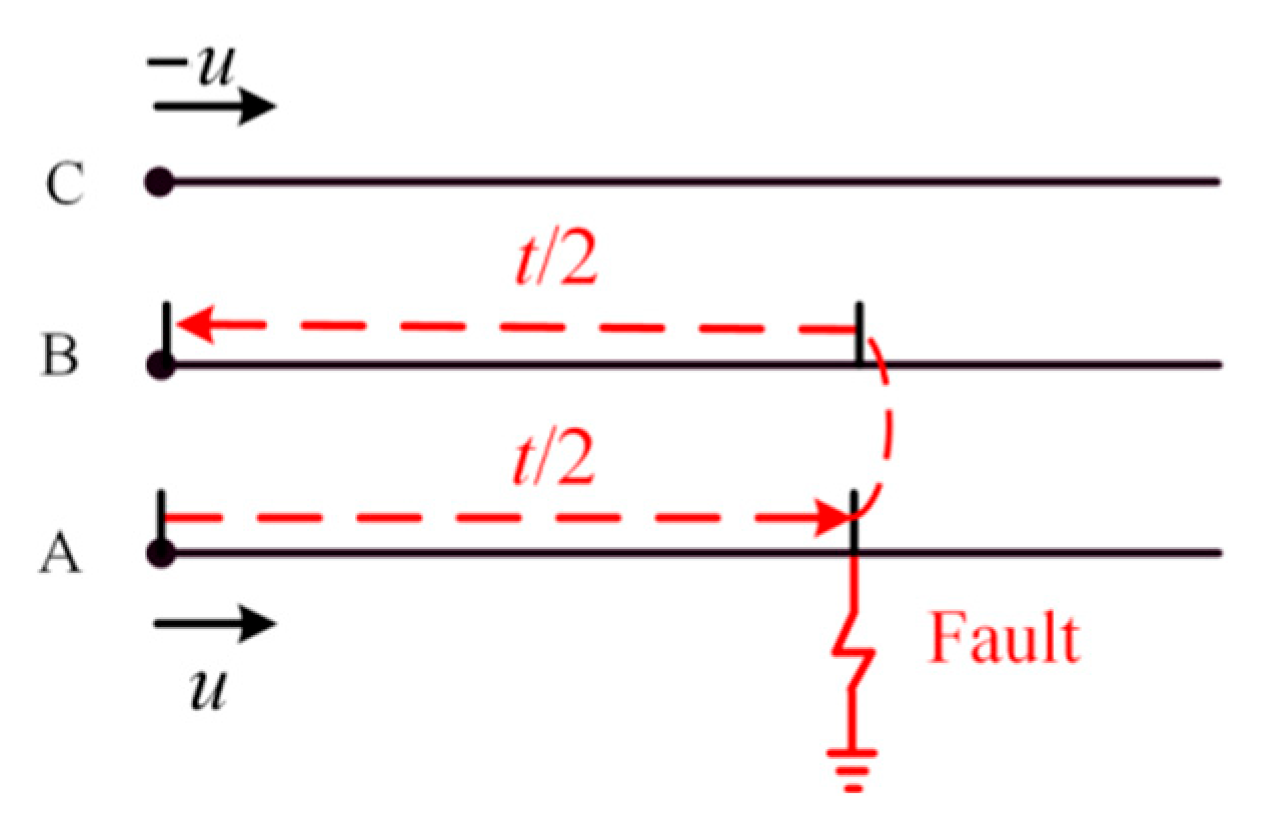
2.2. Calculation Method for Fault Localization
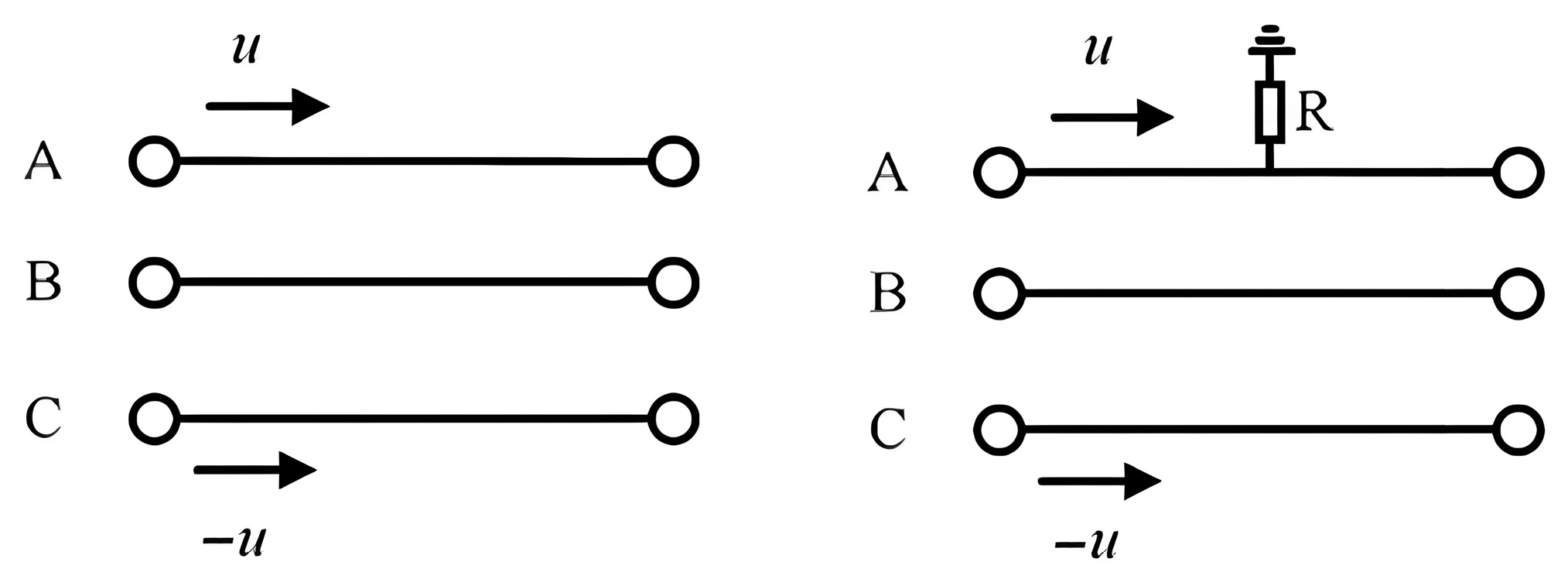
2.3. Effect of Asymmetrical Loading of Distribution Transformers
3. Traveling Wave Detection Method
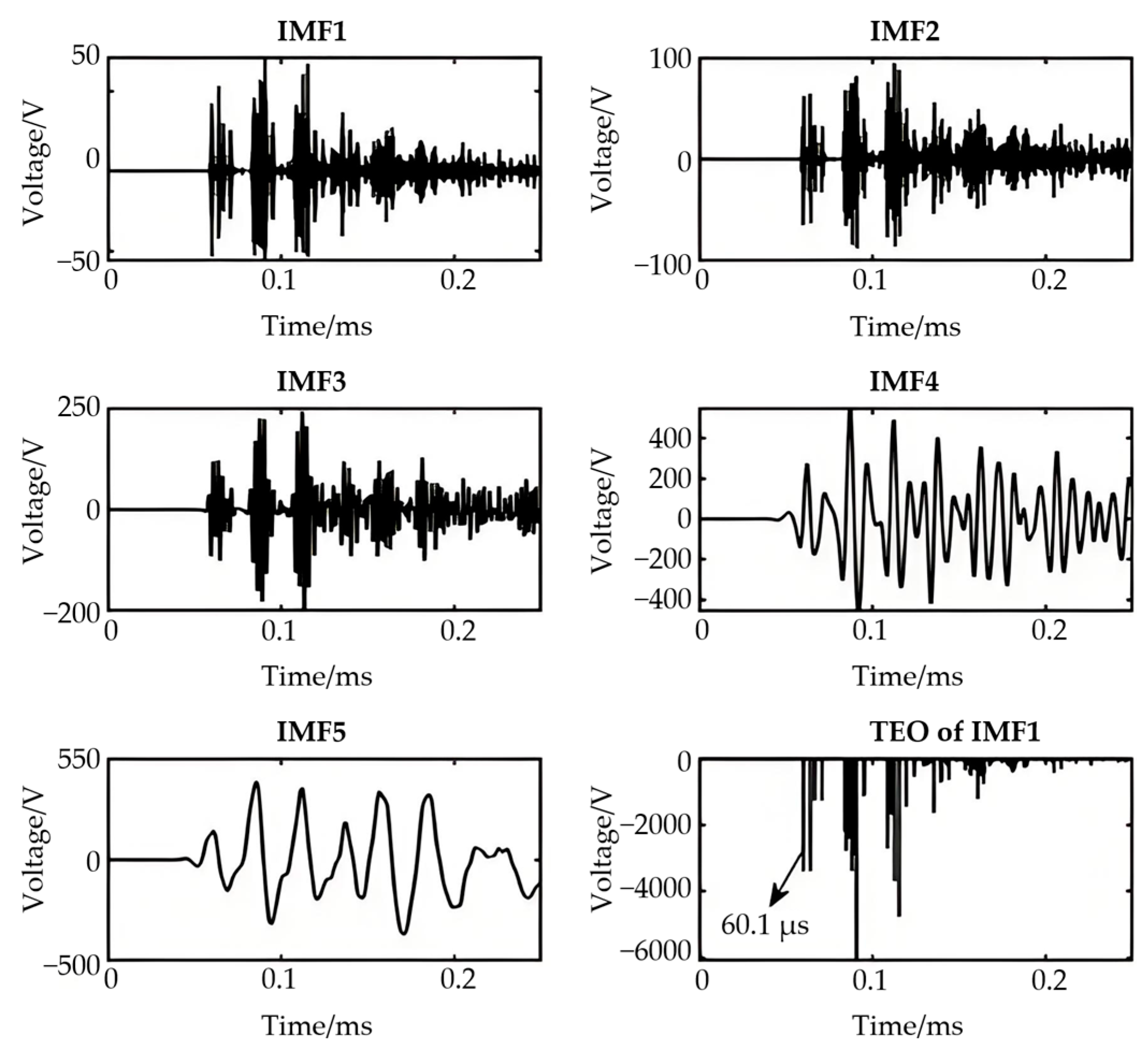
3.1. Variational Mode Decomposition (VMD)
- (1)
- Initialize the parameters: set , , , and n to 0, and assign k to the positive integer indicating the number of modes to be decomposed. Then update n = n + 1;
- (2)
- Iteratively update uk and ωk by applying Equations (17) and (18) respectively, repeating the process until k iterations are completed;
- (3)
- Update using ;
- (4)
- If , terminate the process and output the result; otherwise, return to steps (2) and (3).
3.2. Teager Energy Operator
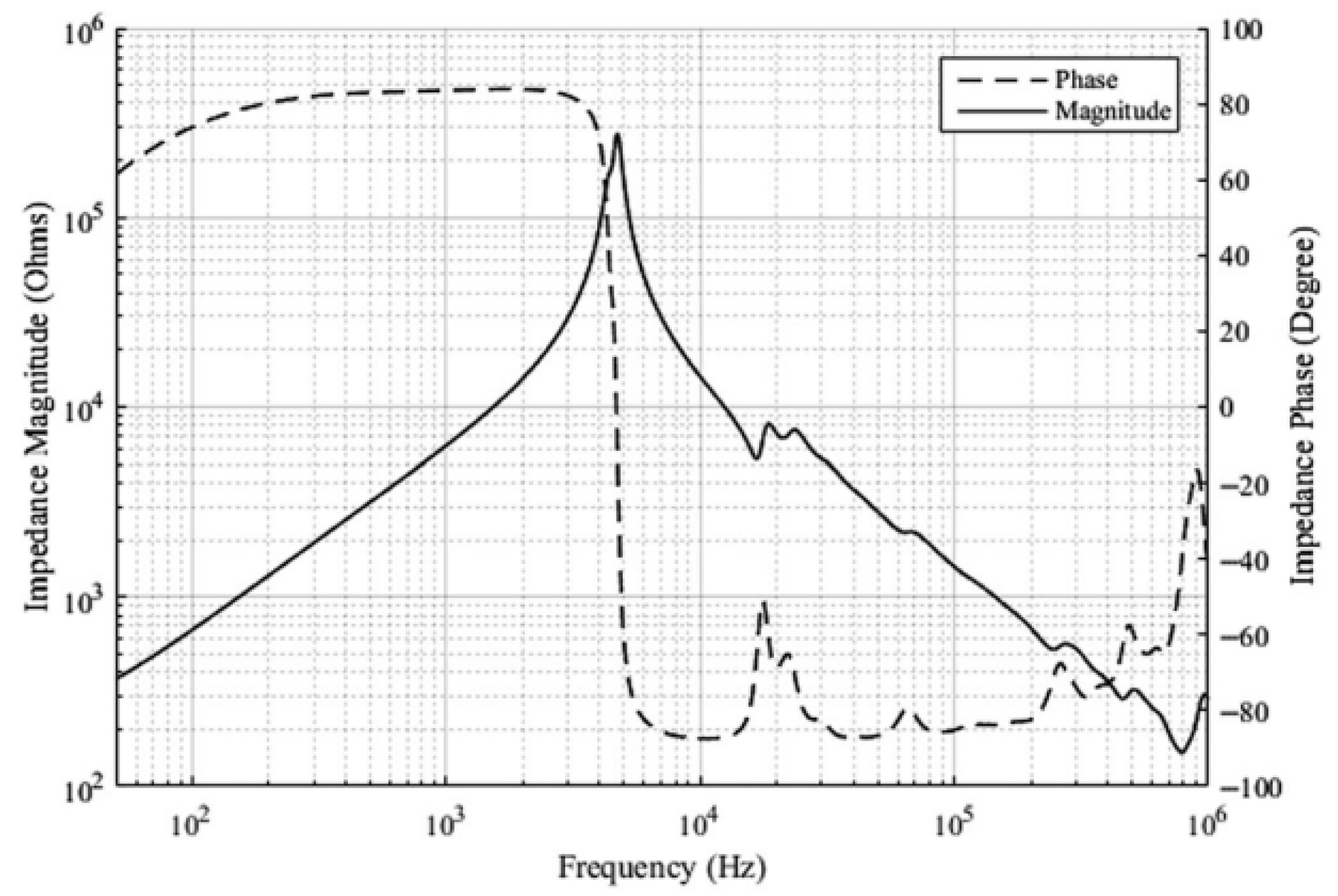
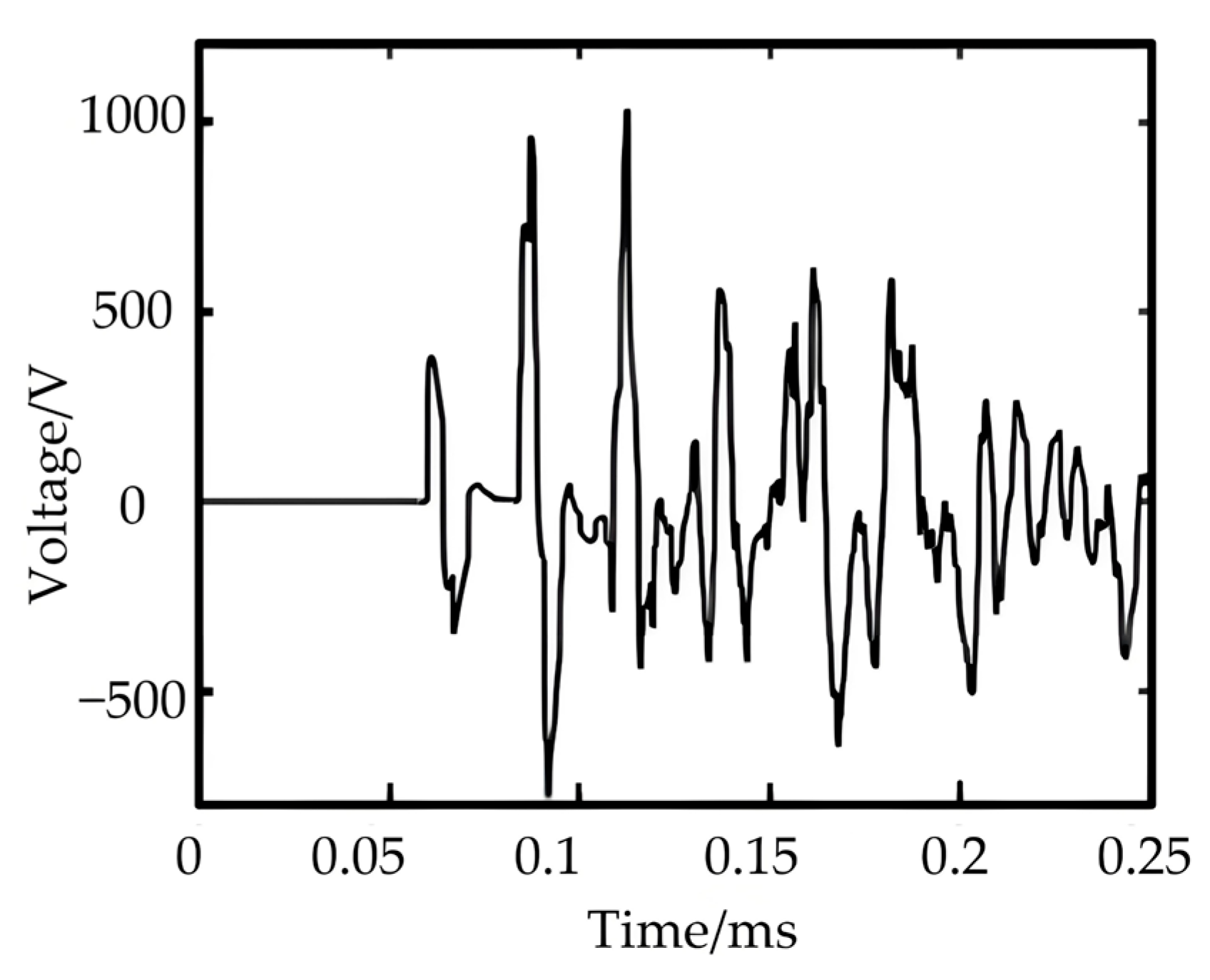
3.3. Traveling Wave Detection
4. PSCAD and Matlab Simulation Results
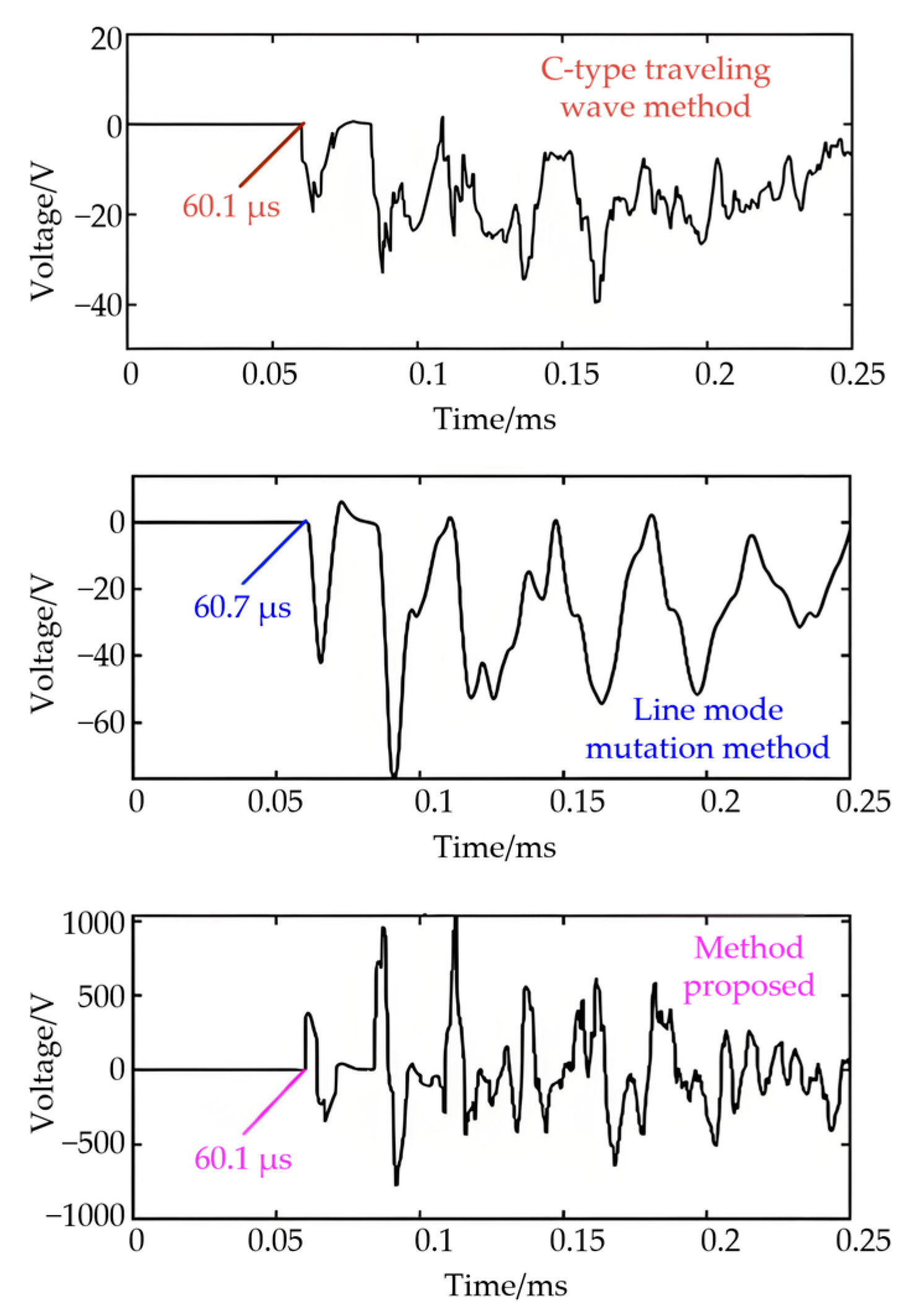
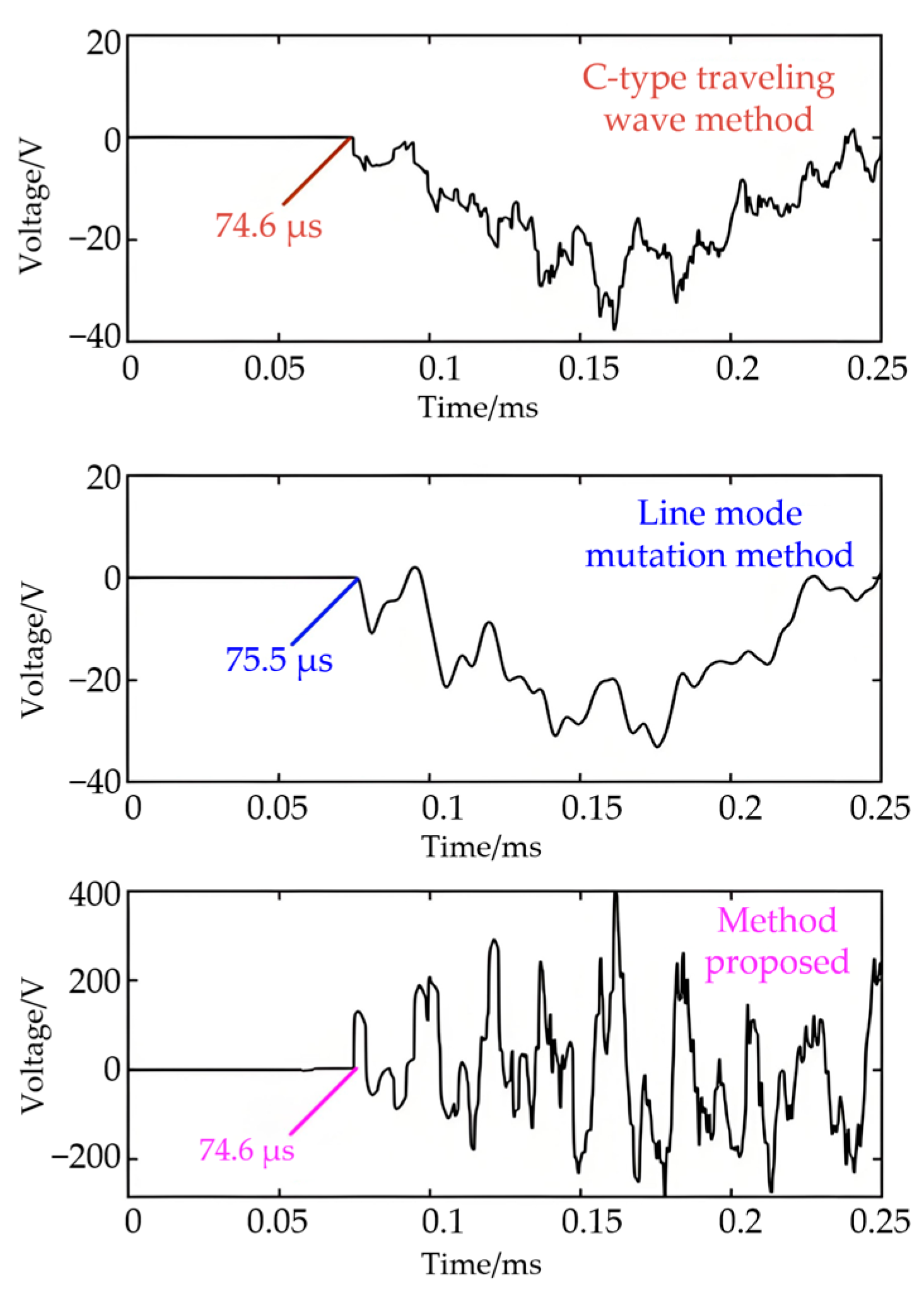
4.1. Comparison of the Localization Effect of This Double-Ended Pulse Injection Method with Existing Methods
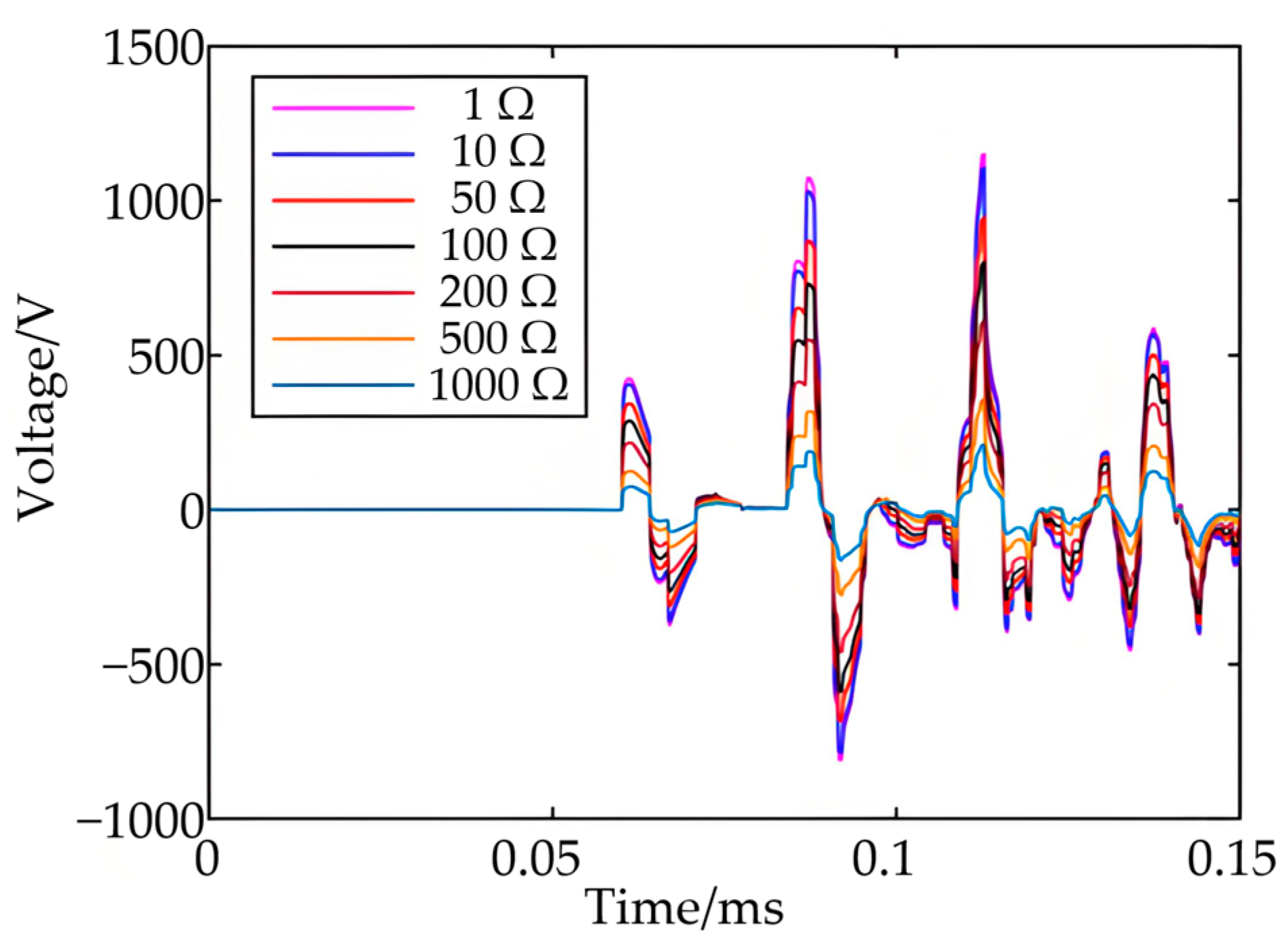
4.2. Effect of Fault Distance, Fault Resistance, and Noise on Positioning Accuracy
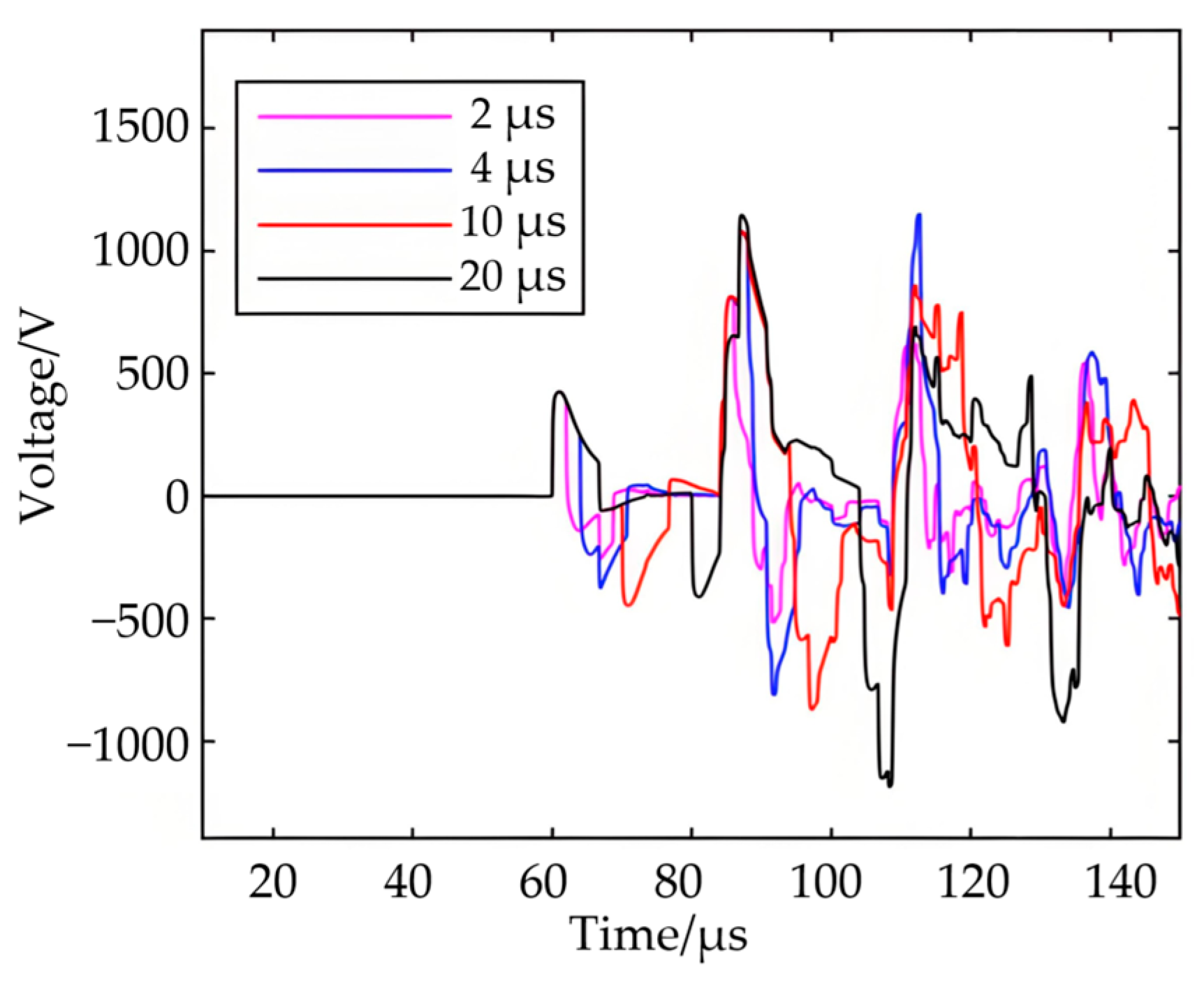
4.3. Effect of Pulse Width on Positioning Accuracy
4.4. Effect of Asymmetrical Load of Distribution Transformer on Localization
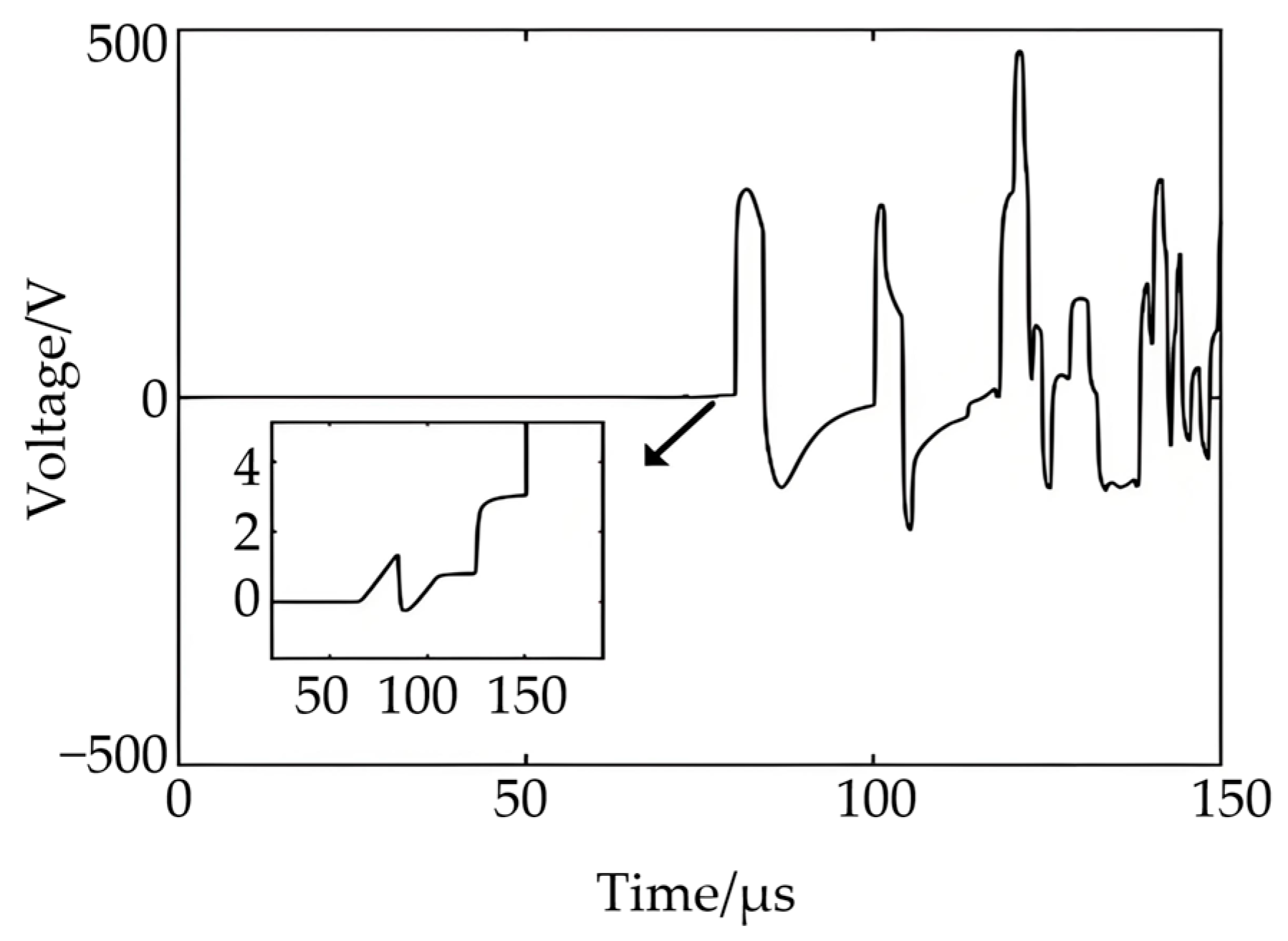
4.5. Pulse Signal Generation and Acquisition
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tao, W.; Li, X.; Hua, Y.; Xiao, S.; Wu, Y.; Zhang, Y. Fault location of single-phase grounding fault based on Manhattan average distance and cosine similarity in distribution network. Electr. Power Eng. Technol. 2023, 42, 130–138. [Google Scholar] [CrossRef]
- Qi, Z.; Zhao, X.; Chen, Y. Single-phase grounding fault sensing technology in distribution network based on transient and steady state phase asymmetrical signals. High Volt. Eng. 2022, 48, 1264–1276. [Google Scholar] [CrossRef]
- Mei, F.; Chen, Z.; Pei, X.; Zheng, J. Fault-tolerant method for fault location of active distribution network based on matrix algorithm. Electr. Power Eng. Technol. 2022, 41, 109–115. [Google Scholar] [CrossRef]
- Dong, X.; Chen, B.; Dong, Q.; Dai, Y. Traveling wave fault location of distribution lines using distributed voltage sensing technology. Power Grid Technol. 2023, 47, 4837–4847. [Google Scholar] [CrossRef]
- Cai, X.; Yang, Y.; Tian, H.; Che, Y.; Guo, C. Research on fault location method of distribution network based on pulse emission principle. Power Syst. Prot. Control 2007, 35, 1–5. [Google Scholar] [CrossRef]
- Yang, Q.; Ke, K.; Hu, J.; Yao, Z.; Wu, S.; He, J. Lightning transient sensing, monitoring and applications in power systems. High Volt. Eng. 2024, 50, 3303–3323. [Google Scholar] [CrossRef]
- Yu, S.; Bao, H.; Yang, Y. A practical method for distribution line fault location. Proc. CSEE 2008, 28, 86–90. [Google Scholar] [CrossRef]
- Zhou, C.; Shu, Q.; Han, X. Distribution network single-phase ground fault location method based on line mode traveling wave mutation. Power Netw. Technol. 2014, 38, 1973–1978. [Google Scholar] [CrossRef]
- Ren, Q.; Shu, Q.; Liu, Y. Distribution network fault location algorithm based on symmetric injection reflection wave signature extraction. Power Syst. Prot. Control 2015, 43, 19–25. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Q.; Wang, Y.; Zou, Q.; Wang, Y. Optimization of voltage differential protection for UHVDC transmission line. Electr. Power Eng. Technol. 2022, 41, 102–109. [Google Scholar] [CrossRef]
- Sima, W.; Wang, J.; Yang, Q.; Xie, B. Application of Hilbert-Huang transform to power system over-voltage recognition. High Volt. Eng. 2010, 36, 1480–1486. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, X.; Ma, H.; Li, Z. Grid fault traveling wave location method based on Hilbert-Huang transform. Electr. Power Syst. Autom. 2008, 08, 64–68. [Google Scholar] [CrossRef]
- Fan, X.; Zhu, Y.; Lu, W. Transmission line traveling wave fault location based on EMD-TEO. Power Syst. Prot. Control 2012, 40, 8–12+17. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Y. Traveling-wave fault location of double-pole HVDC transmission system. High Volt. Eng. 2007, 07, 124–128. [Google Scholar] [CrossRef]
- Abad, M.; García-Gracia, M.; El Halabi, N.; López Andía, D. Network impulse response based-on fault location method for fault location in power distribution systems. IET Gener. Transm. Distrib. 2016, 10, 3962–3970. [Google Scholar] [CrossRef]
- Lefort, R.; Vauzelle, R.; Courtecuisse, V.; Idir, N.; Poussard, A.-M. Influence of the MV/LV transformer impedance on the propagation of the PLC signal in the power grid. IEEE Trans. Power Deliv. 2017, 32, 339–1349. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Chen, H.; Fang, C.; Pu, Z.; Wu, T. Double-ended positioning of partial discharge for long cable based on VMD-WVD phase method. Electr. Power Eng. Technol. 2022, 41, 171–177. [Google Scholar] [CrossRef]
- Zhang, R.; Jin, S.; Du, G. Method of partial discharge localization for cable under oscillatory wave voltage conditions based on EMD and DTW algorithm. High Volt. Eng. 2020, 46, 273–281. [Google Scholar] [CrossRef]
- Qi, Z. Research on Fault Location System of Power Cable Integrated Branch Network Based on Transient Traveling Wave. Master Thesis, Xidian University, Xi’an, China, 2022. [Google Scholar]
- Wang, Z.; He, S.; Li, Q.; Liu, B.; Razzaghi, R.; Paolone, M. A full-scale experimental validation of electromagnetic time reversal applied to locate disturbances in overhead power distribution lines. IEEE Trans. Electromagn. Compat. 2018, 60, 1562–1570. [Google Scholar] [CrossRef]
- Yang, Q.; Yin, L.; Liu, H.; Wang, K.; Huang, J. Measurement of lightning-induced overvoltage in power distribution lines using ceramic-capacitor insulators. IEEE Trans. Electromagn. Compat. 2019, 61, 788–795. [Google Scholar] [CrossRef]

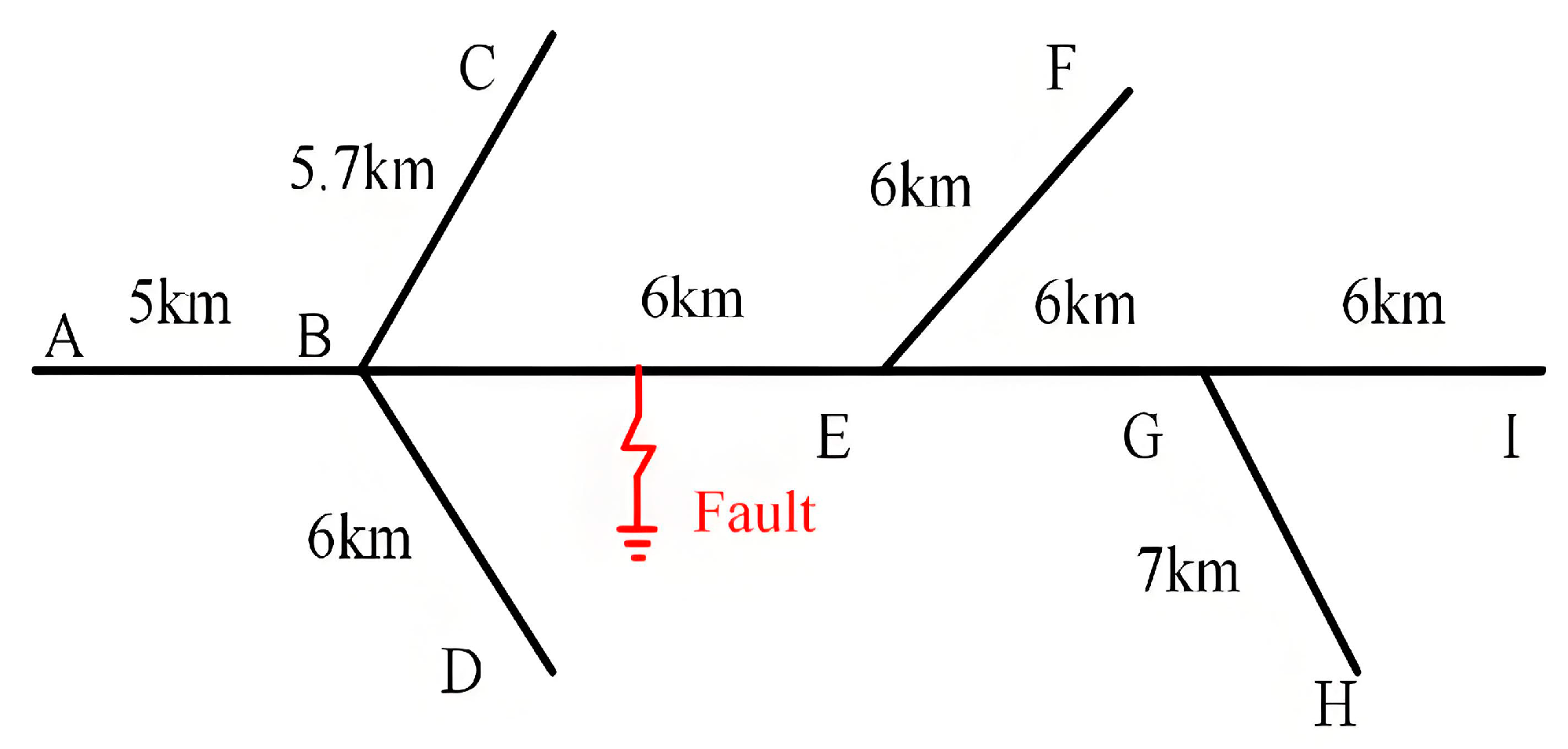
| Fault Section | Fault Distance (km) | Calculated Distance (km) | Positioning Error (km) |
|---|---|---|---|
| AB | 4 | 3.98 | 0.02 |
| BC | 7.7 | 7.68 | 0.02 |
| BD | 8 | 7.995 | 0.005 |
| BE | 9 | 9.015 | 0.015 |
| EF | 14 | 13.99 | 0.01 |
| EG | 15 | 19.97 | 0.03 |
| GH | 18 | 18 | 0 |
| GI | 22 | 21.97 | 0.03 |
| Fault Resistance (Ω) | Calculated Distance (km) | Positioning Error (km) |
|---|---|---|
| 1 | 9.015 | 0.015 |
| 10 | 9.015 | 0.015 |
| 50 | 9.015 | 0.015 |
| 100 | 9.015 | 0.015 |
| 200 | 9.015 | 0.015 |
| 500 | 9.015 | 0.015 |
| 1000 | 9.03 | 0.03 |
| Signal-to-Noise Ratio (dB) | Calculated Distance (km) | Positioning Error (km) |
|---|---|---|
| 30 | 9.015 | 0.015 |
| 20 | 9.015 | 0.015 |
| 10 | 9.015 | 0.015 |
| Pulse Width (μs) | Calculated Distance (km) | Positioning Error (km) |
|---|---|---|
| 2 | 9.015 | 0.015 |
| 10 | 9.015 | 0.015 |
| 20 | 9.015 | 0.015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Xiang, H.; Li, S.; Gan, W.; Chen, W.; Zhou, J.; Yang, Q. Power Grid Fault Location Method Based on Variational Mode Decomposition and Symmetric Pulse Injection with Teager Operator. Electronics 2025, 14, 4084. https://doi.org/10.3390/electronics14204084
Zhao J, Xiang H, Li S, Gan W, Chen W, Zhou J, Yang Q. Power Grid Fault Location Method Based on Variational Mode Decomposition and Symmetric Pulse Injection with Teager Operator. Electronics. 2025; 14(20):4084. https://doi.org/10.3390/electronics14204084
Chicago/Turabian StyleZhao, Jing, Huiying Xiang, Shengfang Li, Wenyan Gan, Wei Chen, Jianglin Zhou, and Qing Yang. 2025. "Power Grid Fault Location Method Based on Variational Mode Decomposition and Symmetric Pulse Injection with Teager Operator" Electronics 14, no. 20: 4084. https://doi.org/10.3390/electronics14204084
APA StyleZhao, J., Xiang, H., Li, S., Gan, W., Chen, W., Zhou, J., & Yang, Q. (2025). Power Grid Fault Location Method Based on Variational Mode Decomposition and Symmetric Pulse Injection with Teager Operator. Electronics, 14(20), 4084. https://doi.org/10.3390/electronics14204084






