Finite-Time Fuzzy Tracking Control for Two-Stage Continuous Stirred Tank Reactor: A Gradient Descent Approach via Armijo Line Search
Abstract
1. Introduction
- References [34,38] adopt NN-type adaptive controllers that use a constant learning rate for parameter updates. This paper optimizes the FLS parameters by GD algorithm with Armijo line search on a cost tied to the FLS approximation error. The Armijo rule adaptively selects the step size, reducing manual retuning and improving convergence reliability. To the best of our knowledge, this is the first application of GD-based FLSs tuning with Armijo line search to a two-stage CSTR system.
- Reference [26] establishes an asymptotic stability controller rather than finite-time stability. Such a guarantee lacks a deterministic settling-time bound, which is often mandatory for two-stage CSTR systems. In contrast, this paper integrates FLSs with finite-time stability criteria, ensuring that the states reach the desired trajectories within a finite time. Consequently, the proposed method meets fast-response requirements for two-stage CSTR systems.
2. Preliminaries and Problem Description
2.1. Preliminaries
2.2. Two-Stage Continuous Stirred Tank Reactor Systems
2.3. Fuzzy Logic Systems
3. Finite-Time Adaptive Fuzzy Learning Control Design
| Algorithm 1 Adaptive Learning Rate Update via Armijo Line Search |
|
4. Computational Complexity Analysis
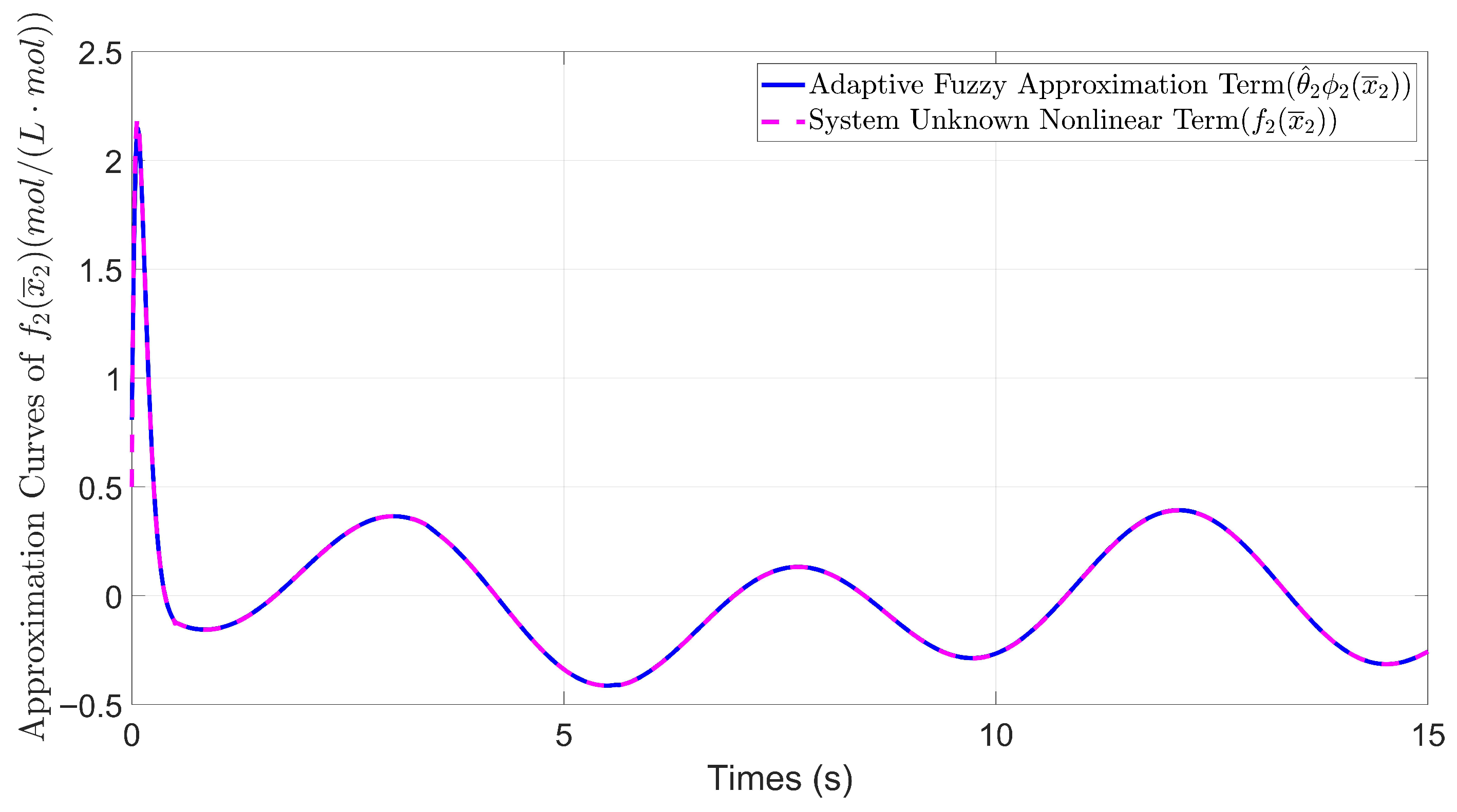
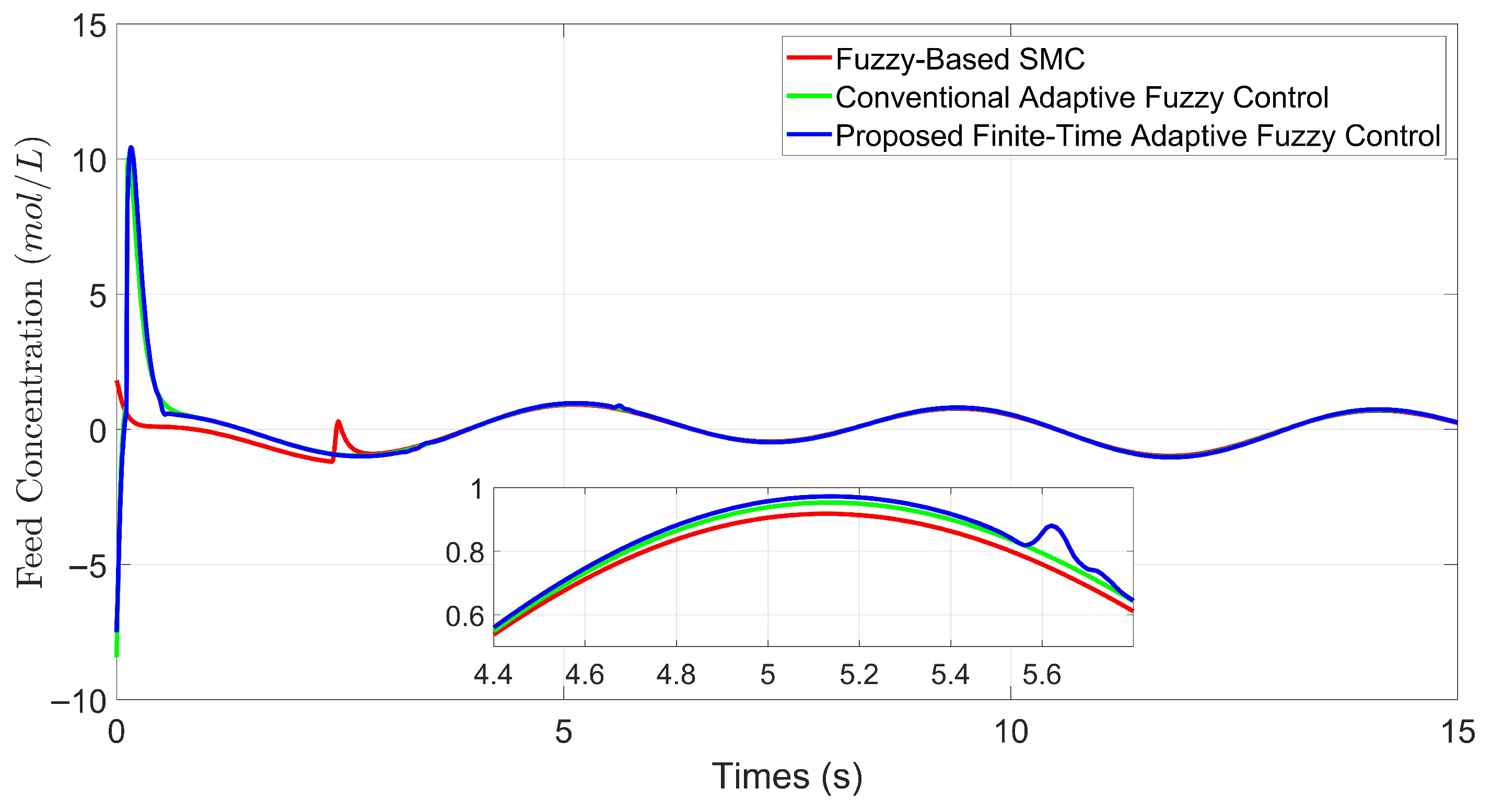
5. Simulation Examples
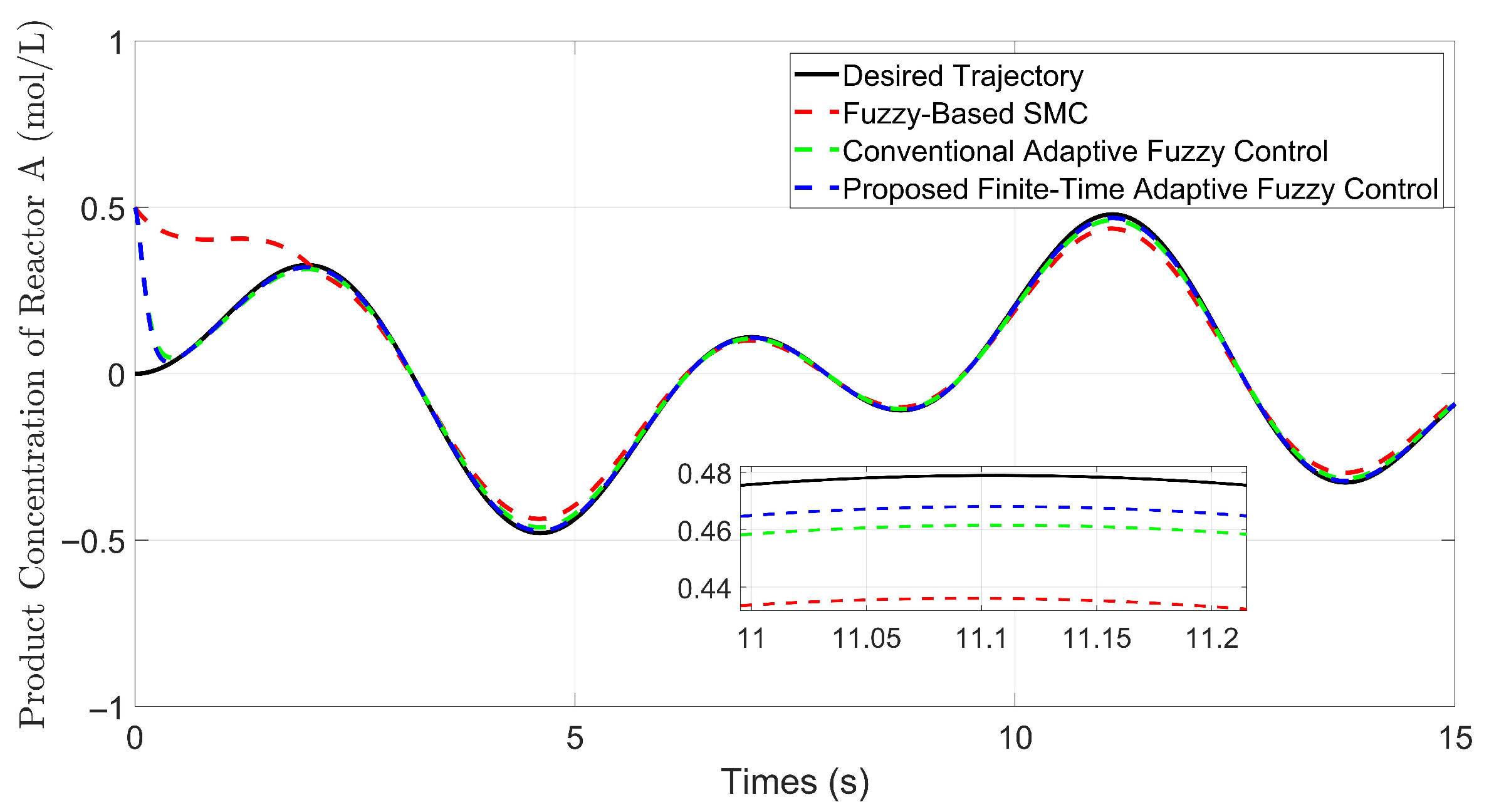
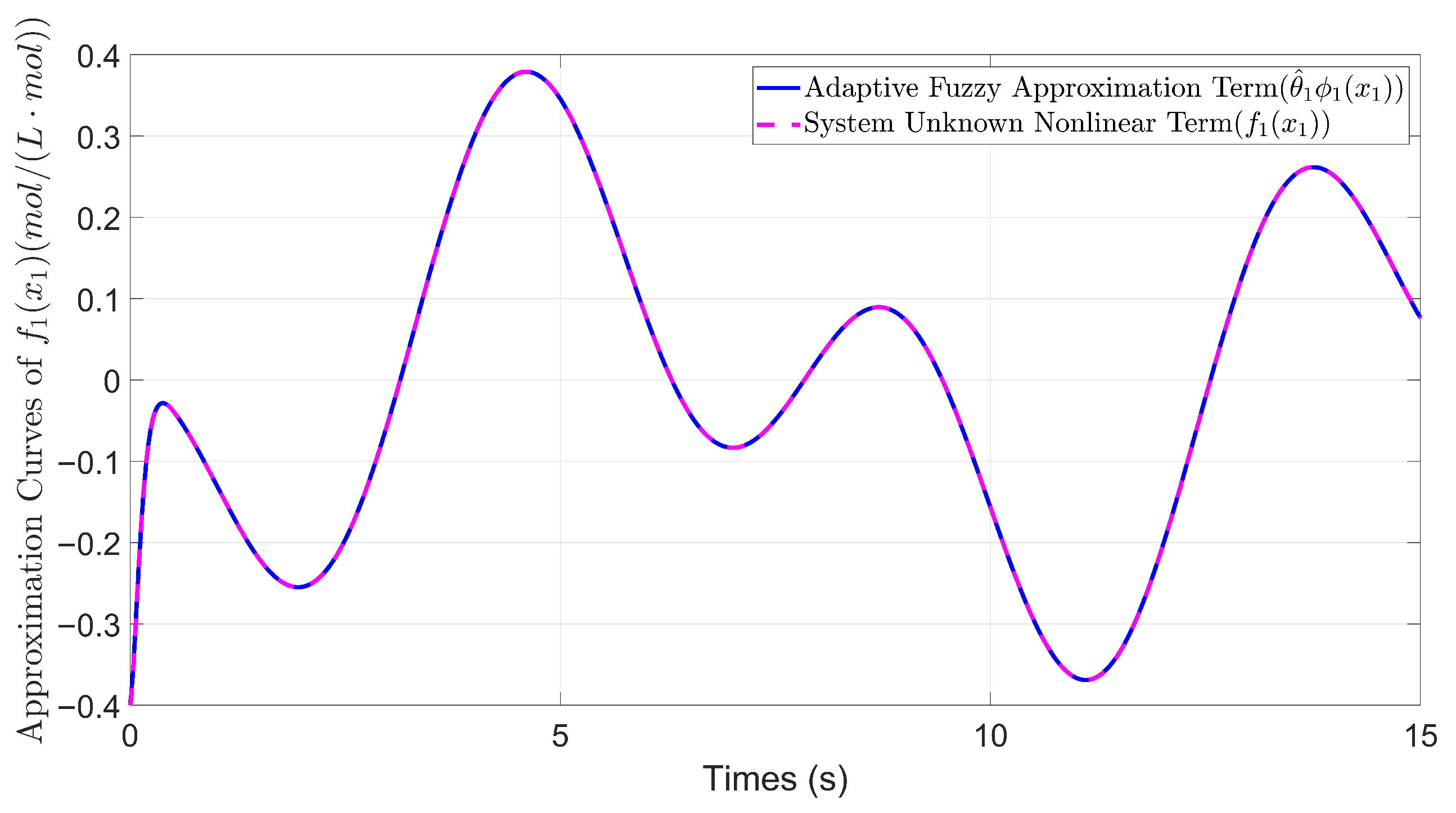
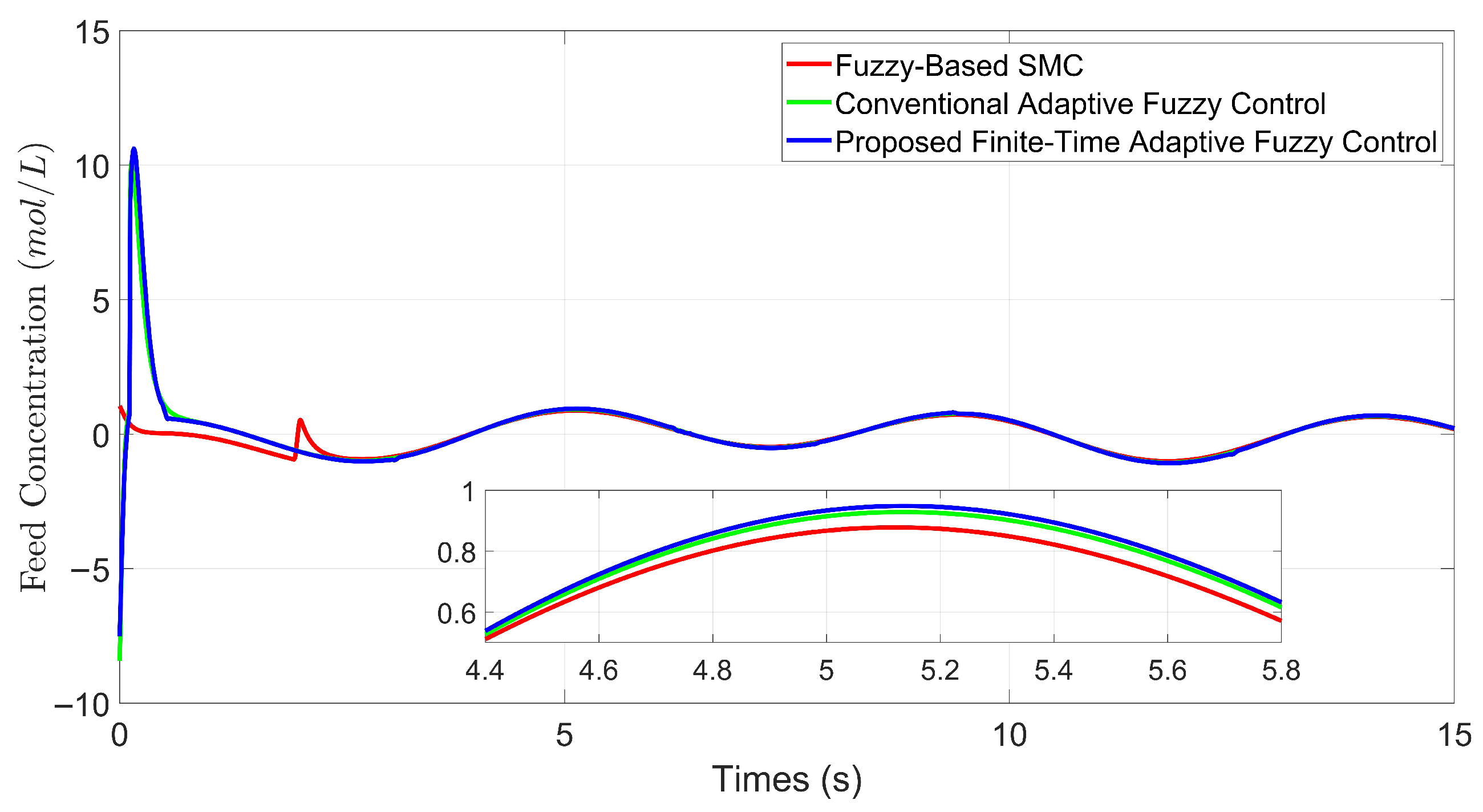
5.1. Example 1: Comparative Analysis Under Nominal Conditions
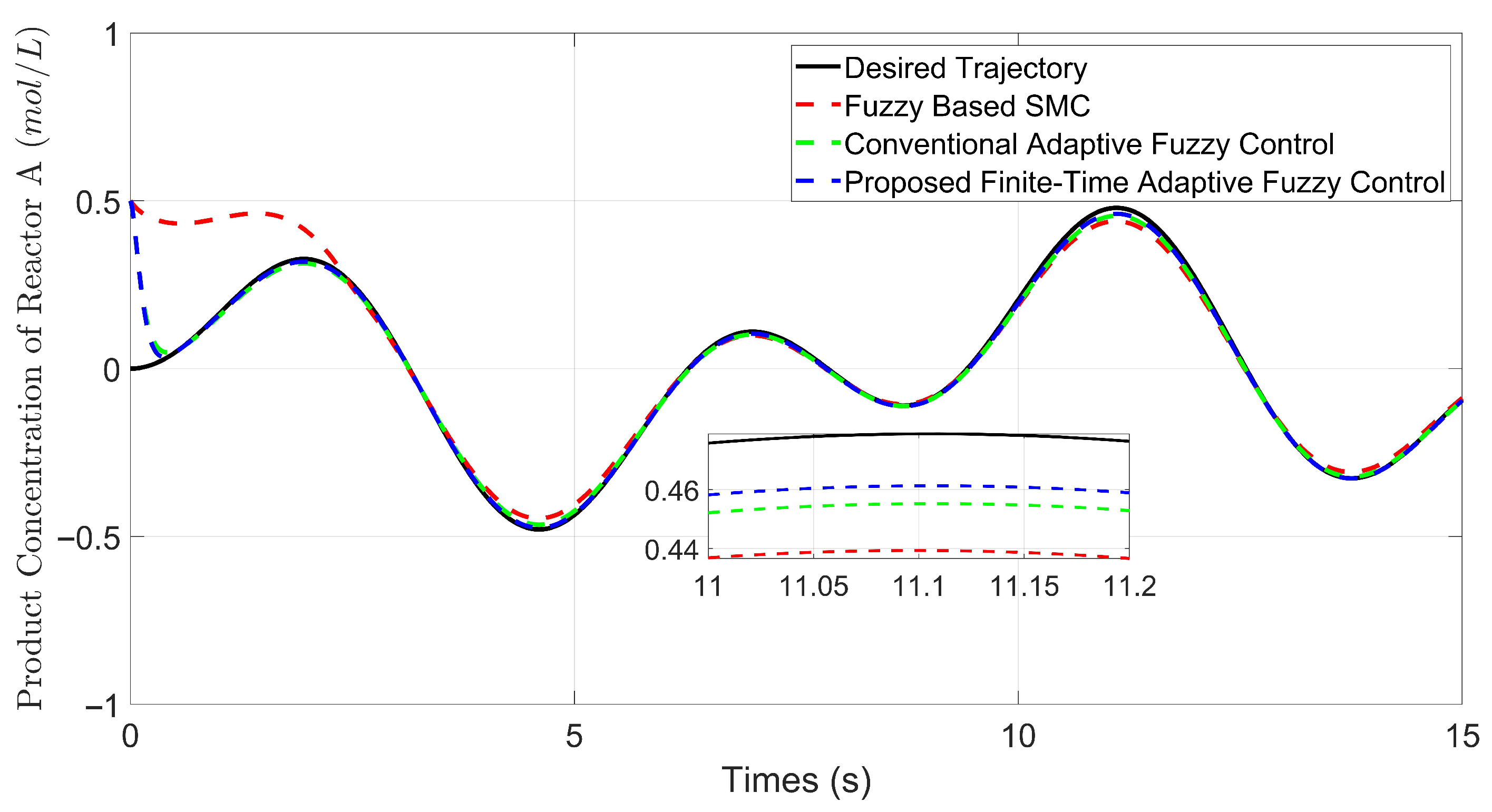
5.2. Example 2: Comparative Analysis Under Disturbance Conditions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brison, A.; Rossi, P.; Derlon, N. Single CSTR can be as effective as an SBR in selecting PHA-storing biomass from municipal wastewater-derived feedstock. Water Res. X 2023, 18, 100165. [Google Scholar] [CrossRef]
- Czyżniewski, M.; Łangowski, R. An observability and detectability analysis for non-linear uncertain CSTR model of biochemical processes. Sci. Rep. 2022, 12, 22327. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Y.; Li, D. Temperature Optimization Control of CSTR. In Proceedings of the 2020 IEEE International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA), Chongqing, China, 6–8 November 2020. [Google Scholar]
- So, G.B.; Jin, G.G. Fuzzy-based nonlinear PID controller and its application to CSTR. Korean J. Chem. Eng. 2018, 35, 819–825. [Google Scholar] [CrossRef]
- Abadi, A.S.S.; Dehkordi, P.H.; Hajiyan, R.; Kowalik, R. Design and real-time evaluation of a novel observer-based predefined-time controller for the industrial processes. ISA Trans. 2024, 156, 551–564. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, F.; Gao, S.; Zhao, D.; Yan, X.; Spurgeon, S. Output consensus for interconnected heterogeneous systems via a combined model predictive control and integral sliding mode control with application to CSTRs. Control Eng. Pract. 2024, 153, 106100. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.; Lin, W.; Yu, X.; Buccella, C.; Cecati, C. Disturbance Rejection-Based Motion Control of Linear Motors Via Integral Sliding Mode Observer. IEEE Trans. Ind. Electron. 2025, 72, 3061–3071. [Google Scholar] [CrossRef]
- Xie, S.; Xie, Y.; Gui, W.; Yang, C. Weighted-coupling CSTR modeling and model predictive control with parameter adaptive correction for the goethite process. J. Process Control 2018, 68, 254–267. [Google Scholar] [CrossRef]
- Wang, G.; Jia, Q.-S.; Qiao, J.; Bi, J.; Zhou, M. Deep learning-based model predictive control for continuous stirred-tank reactor system. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3643–3652. [Google Scholar] [CrossRef] [PubMed]
- Tofighi, S.R.; Bayat, F.; Merrikh-Bayat, F. Robust feedback linearization of an isothermal continuous stirred tank reactor: H∞ mixed-sensitivity synthesis and DK-iteration approaches. Trans. Inst. Meas. Control 2017, 39, 344–351. [Google Scholar] [CrossRef]
- Yazdi, M.B.; Jahed-Motlagh, M. Stabilization of a CSTR with two arbitrarily switching modes using modal state feedback linearization. Chem. Eng. J. 2009, 155, 838–843. [Google Scholar] [CrossRef]
- Mathew, E.; Pawar, T.; Jaganatha Pandian, B. Control of a Coupled CSTR Process using MRAC-MIT Rule. In Proceedings of the 2019 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 22–23 March 2019; pp. 1–5. [Google Scholar]
- Cao, L.; Yao, D.; Li, H.; Meng, W.; Lu, R. Fuzzy-based dynamic event triggering formation control for nonstrict-feedback nonlinear MASs. Fuzzy Sets Syst. 2023, 452, 1–22. [Google Scholar] [CrossRef]
- Meda-Campaña, J.A.; Rodríguez-Manzanarez, R.A.; Ontiveros-Paredes, S.D.; de Jesús Rubio, J.; Tapia-Herrera, R.; Hernández-Cortés, T.; Obregón-Pulido, G.; Aguilar-Ibáñez, C. An algebraic fuzzy pole placement approach to stabilize nonlinear mechanical systems. IEEE Trans. Fuzzy Syst. 2021, 30, 3322–3332. [Google Scholar] [CrossRef]
- Ma, M.; Wang, T.; Qiu, J.; Karimi, H.R. Adaptive Fuzzy Decentralized Tracking Control for Large-Scale Interconnected Nonlinear Networked Control Systems. IEEE Trans. Fuzzy Syst. 2021, 29, 3186–3191. [Google Scholar] [CrossRef]
- Qiu, J.; Ma, M.; Wang, T. Event-Triggered Adaptive Fuzzy Fault-Tolerant Control for Stochastic Nonlinear Systems via Command Filtering. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1145–1155. [Google Scholar] [CrossRef]
- Li, D.; Li, D. Adaptive tracking control for nonlinear time-varying delay systems with full state constraints and unknown control coefficients. Automatica 2018, 93, 444–453. [Google Scholar] [CrossRef]
- Li, S.; Ahn, C.K.; Guo, J.; Xiang, Z. Neural-network approximation-based adaptive periodic event-triggered output-feedback control of switched nonlinear systems. IEEE Trans. Cybern. 2020, 51, 4011–4020. [Google Scholar] [CrossRef]
- Liang, H.; Chen, L.; Pan, Y.; Lam, H.K. Fuzzy-based robust precision consensus tracking for uncertain networked systems with cooperative–antagonistic interactions. IEEE Trans. Fuzzy Syst. 2022, 31, 1362–1376. [Google Scholar] [CrossRef]
- López-Estrada, F.R.; Astorga-Zaragoza, C.M.; Theilliol, D.; Ponsart, J.C.; Valencia-Palomo, G.; Torres, L. Observer synthesis for a class of Takagi–Sugeno descriptor system with unmeasurable premise variable. Application to fault diagnosis. Int. J. Syst. Sci. 2017, 48, 3419–3430. [Google Scholar] [CrossRef]
- Arifi, A.; Bouallègue, S. Takagi–Sugeno fuzzy-based approach for modeling and control of an activated sludge process. Int. J. Dyn. Control 2024, 12, 3123–3138. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.-J.; Tong, S. Fuzzy-Based Multierror Constraint Control for Switched Nonlinear Systems and Its Applications. IEEE Trans. Fuzzy Syst. 2019, 27, 1519–1531. [Google Scholar] [CrossRef]
- Chen, Y.F.; Tang, B.; Liu, Q.H. Adaptive fixed-time fuzzy control for delayed recycling continuous stirred tank reactor with asymmetric time-varying full-state constraints. J. Frankl. Inst. 2025, 362, 107410. [Google Scholar] [CrossRef]
- Kang, S.; Liu, P.X.; Wang, H. Adaptive Fuzzy Finite-Time Command Filtering Control for Flexible-Joint Robot Systems Against Multiple Actuator Constraints. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 4554–4558. [Google Scholar] [CrossRef]
- Qiu, J.; Ma, M.; Wang, T.; Gao, H. Gradient descent-based adaptive learning control for autonomous underwater vehicles with unknown uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5266–5273. [Google Scholar] [CrossRef]
- Yang, X.; Zheng, X. Gradient descent algorithm-based adaptive NN control design for an induction motor. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1027–1034. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X.; Yu, X.; Wang, H. Finite-time cooperative control for bearing-defined leader-following formation of multiple double-integrators. IEEE Trans. Cybern. 2022, 52, 13363–13372. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, K.; Tong, S. Reinforcement learning-based adaptive finite-time performance constraint control for nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 1335–1344. [Google Scholar] [CrossRef]
- Zhao, G.-H.; Liu, S.J. Decentralized adaptive finite-time stabilization for a class of non-local Lipschitzian large-scale stochastic nonlinear systems. Automatica 2025, 171, 111900. [Google Scholar] [CrossRef]
- Li, R.; Jin, F.F. Finite-time stabilization output-feedback control of Schrödinger’s equation. J. Process Control 2024, 140, 103258. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Continuous finite-time stabilization of the translational and rotational double integrators. IEEE Trans. Autom. Control 2002, 43, 678–682. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Wang, H.; Yu, W.; Ren, W.; Lü, J. Distributed adaptive finite-time consensus for second-order multiagent systems with mismatched disturbances under directed networks. IEEE Trans. Cybern. 2021, 51, 1347–1358. [Google Scholar] [CrossRef]
- Li, D.; Wang, D.; Liu, L.; Gao, Y. Adaptive finite-time tracking control for continuous stirred tank reactor with time-varying output constraint. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 5929–5934. [Google Scholar] [CrossRef]
- Sang, H.; Wang, P.; Zhao, Y.; Nie, H.; Fu, J. Input–Output Finite-Time Stability for Switched T–S Fuzzy Delayed Systems with a Time-Dependent Lyapunov–Krasovskii Functional Approach. IEEE Trans. Fuzzy Syst. 2023, 31, 3823–3837. [Google Scholar] [CrossRef]
- Huang, J.; Wen, C.; Wang, W.; Song, Y.D. Design of adaptive finite-time controllers for nonlinear uncertain systems based on given transient specifications. Automatica 2016, 69, 395–404. [Google Scholar] [CrossRef]
- Yang, Y.; Hua, C.; Guan, X. Adaptive fuzzy finite-time coordination control for networked nonlinear bilateral teleoperation system. IEEE Trans. Fuzzy Syst. 2013, 22, 631–641. [Google Scholar] [CrossRef]
- Wang, F.; Chen, B.; Liu, X.; Lin, C. Finite-time adaptive fuzzy tracking control design for nonlinear systems. IEEE Trans. Fuzzy Syst. 2017, 26, 1207–1216. [Google Scholar] [CrossRef]
- Li, D.; Wang, Y.; Liu, Y.-J.; Liu, L. IBLFs-based adaptive fuzzy control for Continuous Stirred Tank Reactors with full state constraints and actuator faults. J. Process Control 2023, 124, 14–24. [Google Scholar] [CrossRef]
- Zhu, Z.; Xia, Y.; Fu, M. Attitude stabilization of rigid spacecraft with finite-time convergence. Int. J. Robust Nonlinear Control 2011, 21, 686–702. [Google Scholar] [CrossRef]
- Bruckner, A.M.; Bruckner, J.B.; Thomson, B.S. Problems in Real Analysis: Advanced Calculus on the Real Axis; Springer: New York, NY, USA, 2008; pp. 294–300. [Google Scholar]
- Qian, C.; Lin, W. Non-Lipschitz continuous stabilizers for nonlinear systems with uncontrollable unstable linearization. Syst. Control Lett. 2001, 42, 185–200. [Google Scholar] [CrossRef]
- Yan, X.; Chen, M.; Feng, G.; Wu, Q.; Shao, S. Fuzzy Robust Constrained Control for Nonlinear Systems with Input Saturation and External Disturbances. IEEE Trans. Fuzzy Syst. 2021, 29, 345–356. [Google Scholar] [CrossRef]
- Liu, L.; Yin, S.; Zhang, L.; Yin, X.; Yan, H. Improved results on asymptotic stabilization for stochastic nonlinear time-delay systems with application to a chemical reactor system. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 195–204. [Google Scholar] [CrossRef]
- Wang, L.X. Fuzzy systems are universal approximators. In Proceedings of the IEEE International Conference on Fuzzy Systems, San Diego, CA, USA, 8–12 March 1992; pp. 1163–1170. [Google Scholar]
- Wei, Z.X.; Li, G.Y.; Qi, L.Q. New nonlinear conjugate gradient formulas for large-scale unconstrained optimization problems. Appl. Math. Comput. 2006, 179, 407–430. [Google Scholar] [CrossRef]
- Karimi, H.; Nutini, J.; Schmidt, M. Linear Convergence of Gradient and Proximal-Gradient Methods Under the Polyak-Łojasiewicz Condition. In Proceedings of the European Conference on Machine Learning and Knowledge Discovery in Databases, Riva del Garda, Italy, 19–23 September 2016; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9851, pp. 795–811. [Google Scholar]





| Symbol | Model Variable | Unit |
|---|---|---|
| Feed Concentration | ||
| , | Outlet Concentration | |
| , | Recirculation Flow Rate | |
| , | Reaction Constant | |
| F | Feed Flow Rate | |
| , | Outlet Flow Rate | |
| , | Reactor Volume | L |
| , | Reaction Time | min |
| Control Method | Time for Error (s) | RMSE () | IAE | ITAE |
|---|---|---|---|---|
| Conventional Adaptive Fuzzy Control | 0.46 | 3.926 | 0.195851 | 0.966123 |
| Fuzzy-Based SMC | 11.377 | 0.780447 | 2.212518 | |
| Proposed Finite-Time Adaptive Fuzzy Control | 0.37 | 3.806 | 0.142353 | 0.641499 |
| Control Method | Time for Error (s) | RMSE () | IAE | ITAE |
|---|---|---|---|---|
| Conventional Adaptive Fuzzy Control | 0.75 | 3.586 | 0.291084 | 1.377014 |
| Fuzzy-Based SMC | 1.90 | 8.046 | 0.780444 | 2.212526 |
| Proposed Finite-Time Adaptive Fuzzy Control | 0.58 | 3.312 | 0.218131 | 1.022666 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Ma, M. Finite-Time Fuzzy Tracking Control for Two-Stage Continuous Stirred Tank Reactor: A Gradient Descent Approach via Armijo Line Search. Electronics 2025, 14, 4069. https://doi.org/10.3390/electronics14204069
Liu Y, Ma M. Finite-Time Fuzzy Tracking Control for Two-Stage Continuous Stirred Tank Reactor: A Gradient Descent Approach via Armijo Line Search. Electronics. 2025; 14(20):4069. https://doi.org/10.3390/electronics14204069
Chicago/Turabian StyleLiu, Yifan, and Min Ma. 2025. "Finite-Time Fuzzy Tracking Control for Two-Stage Continuous Stirred Tank Reactor: A Gradient Descent Approach via Armijo Line Search" Electronics 14, no. 20: 4069. https://doi.org/10.3390/electronics14204069
APA StyleLiu, Y., & Ma, M. (2025). Finite-Time Fuzzy Tracking Control for Two-Stage Continuous Stirred Tank Reactor: A Gradient Descent Approach via Armijo Line Search. Electronics, 14(20), 4069. https://doi.org/10.3390/electronics14204069





