Abstract
Integrated sensing and communication (ISAC) is a transformative technology for sixth-generation (6G) wireless networks. In this paper, we investigate end-to-end constellation mapping and demapping in ISAC systems, leveraging OFDM-based waveforms and an adaptive DNN architecture for pulse-based transmission. Specifically, we propose an end-to-end autoencoder framework that optimizes the constellation through adaptive symbol distribution shaping via deep learning, enhancing communication reliability with symbol mapping and boosting sensing capabilities with an improved peak-to-sidelobe ratio (PSLR). The autoencoder consists of an autoencoder mapper (AE-Mapper) and an autoencoder demapper (AE-Demapper), jointly trained using a composite loss function to optimize constellation points and achieve flexible performance balance in communication and sensing. Simulation results demonstrate that the proposed DNN-based end-to-end design achieves dynamic balance between PSLR of the autocorrelation function (ACF) and bit error rate (BER).
1. Introduction
As research and standardization efforts toward sixth-generation (6G) intensify, integrated sensing and communications (ISAC) has emerged as a key enabler for intelligent, interconnected, and perceptive wireless systems [1,2,3,4,5]. This joint design can effectively reduce hardware cost and enhances energy efficiency compared with operating separate sensing and communication systems [6,7].
Facing this issue, one solution is to leverage pulse-based signaling, which can eliminate the stringent isolation requirements between transmitter and receiver in CW implementations [8]. This advantage directly translates to improved peak transmit power levels and consequently extends the achievable sensing range.
Operating in synergy with this pulsed transmission framework, Orthogonal Frequency Division Multiplexing (OFDM) modulation delivers distinct benefits through its inherent multi-carrier architecture. This structure ensures efficient spectrum utilization and provides robustness against frequency-selective fading via cyclic prefix (CP), essential for reliable communication [8]. Moreover, OFDM-based signaling achieves significantly higher communication rates than radar-centric waveforms, which, although optimized for sensing, are less efficient for data transmission [4,6,9]. For sensing functionality, OFDM offers exceptional flexibility via frequency-domain waveform shaping. This allows precise optimization of autocorrelation properties, which is critical for accurate pulse-Doppler radar processing [10,11,12]. Overall, the synergistic combination of pulsed transmission and OFDM modulation thus provides a solution that overcomes CW power limitations while harnessing multi-carrier efficiency to enhance both communication and sensing capabilities.
In ISAC waveform design, the modulation design plays a crucial role, as it directly affects both sensing and communication capabilities [13,14]. The key challenge lies in balancing the contradictory requirements between sensing and communication through constellation shaping. In general, for communication, Gaussian-distributed constellations are theoretically optimal in additive white Gaussian noise (AWGN) channels. Traditional communication-focused modulation schemes, such as quadrature amplitude modulation (QAM) and phase shift keying (PSK), primarily aim to optimize spectral efficiency and minimize BER under typical communication channel conditions [15]. From the sensing perspective, radar waveform design typically favors constant-modulus constellations due to their beneficial autocorrelation properties, which result in enhanced target detection and radar resolution [16].
Recent research efforts have been devoted to constellation mapping and demapping in ISAC systems. For instance, Du et al. [17] proposed probabilistic constellation shaping to optimize the ISAC trade-off by adjusting symbol probabilities. Similarly, Yang et al. investigated probabilistic constellation shaping for ISAC systems using random waveforms, aiming to simultaneously reduce ambiguity sidelobes and improve detection capabilities by constraining the signal’s energy variance and communication entropy [18]. Additionally, Geiger et al. studied various constellation shaping methods specifically tailored for ISAC systems, comparing geometric, probabilistic, and joint approaches [19]. However, previous research has concentrated on static probability distributions, resulting in significant performance drops in dynamic environments. To address this limitation, an adaptive joint geometric and probabilistic constellation shaping approach has been proposed in [20], which adjusts both symbol positions and transmission probabilities. Nevertheless, this method introduces significant computational complexity due to its intricate optimization, posing challenges for real-time implementation. Furthermore, the advancement of ISAC is pivotal for the next-generation Internet of Things (IoT), which demands ultra-reliable communication and high-accuracy sensing simultaneously. Recent studies on innovative modulation schemes [21,22] have shown great potential in enhancing the efficiency and reliability of IoT networks, aligning with the objectives of ISAC systems discussed in this work. These works highlight the distinctions between probabilistic shaping, which adjusts symbol probabilities to optimize entropy and energy variance, and geometric shaping, which modifies symbol positions in the constellation plane. While probabilistic methods excel in entropy maximization for communication under random waveforms, geometric approaches focus on adaptive point distribution for autocorrelation optimization in sensing [19,20].
To reduce computational complexity, a DNN-based end-to-end constellation mapping and demapping mechanism has emerged as an effective solution [23]. In [24], Aref et al. proposed an end-to-end system that integrates error correction mechanisms directly into the constellation design, aiming at enhance BER performance. Additionally, in [25], Chimmalgi et al. developed an autoencoder-based learning method for probabilistic constellation shaping, leveraging importance sampling to improve mutual information and BER over standard benchmarks. In [26], Hu et al. proposed a deep learning-based constellation design for optimizing constellation geometry to enhance target sensing accuracy. Despite these advances, applying such frameworks to ISAC systems remains challenging, as most prior studies prioritize either sensing or communication, rarely achieving joint optimization [27,28].
The main contributions of this paper are summarized as follows:
- We propose a novel end-to-end autoencoder (AE) framework for ISAC systems that jointly optimizes constellation mapping and demapping using a deep neural network (DNN).
- The proposed framework, comprising an AE-Mapper and an AE-Demapper, is trained with a composite loss function to adaptively shape the symbol distribution, enhancing both communication reliability (BER) and sensing capability (PSLR).
- Unlike prior studies that often prioritize one function, our method achieves a flexible and tunable trade-off between sensing and communication performance.
- Simulation results demonstrate that our DNN-optimized constellation significantly improves PSLR over conventional schemes like 16QAM and 16PSK while maintaining competitive BER performance.
The rest of this paper is organized as follows: Section 2 presents the signal model and optimization criteria formulation. Section 3 details the proposed DNN-based constellation mapping and demapping methodology. Section 4 provides comprehensive simulation results and analysis. Finally, Section 5 concludes the paper and outlines future research directions.
2. System Model
We consider a communication-centric ISAC system where a base station transmits OFDM signals. An illustration of the considered ISAC system is shown in Figure 1.
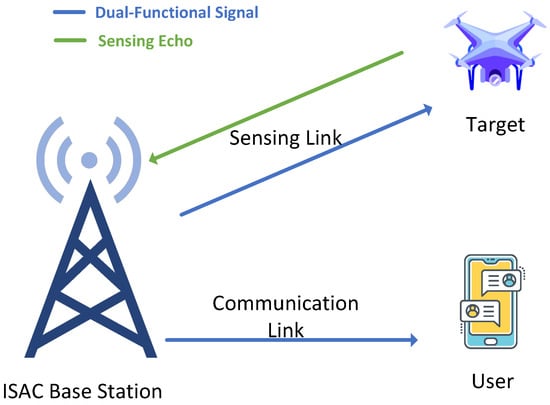
Figure 1.
An illustration of the considered ISAC system.
The transmitter process begins with generating an information bit sequence , where K is the number of information bits, and encoding it into a codeword , with denoting the code length. Next, p is mapped to frequency-domain symbols , where and M is the modulation order; each group of bits yields , with denoting the mapping function. Finally, s is assigned to subcarriers, and an -point IFFT generates the time-domain signal , as follows:
Optimization Criteria in ISAC Systems
At the receiver, the received echoed signals matched filtering to enhance SNR [28,29]. Specifically, pulse compression is achieved through matched filtering, producing the compressed signal, as follows:
where is the matched filter impulse response for the transmitted waveform . This process improves SNR, with the matched filter gain being
where is the signal-to-noise ratio at the output of the matched filter, and is the signal-to-noise ratio at the input of the matched filter [29]. The matched filter gain directly quantifies the SNR enhancement achieved by pulse compression, which is fundamental for detecting weak targets.
In complex electromagnetic environments, radar systems need to detect low-intensity targets amidst clutter, requiring waveforms with low sidelobe levels and a sharp main lobe [30]. To evaluate signal characteristics, the autocorrelation function (ACF) serves as a primary tool by quantifying self-similarity, which directly impacts sensing performance. The ACF is computed as
where is the pulse duration. The ACF quantifies self-similarity over time delays, revealing sidelobe levels that impact ambiguity in range and Doppler dimensions [10].
The ACF of a radar waveform reflects key characteristics, such as sidelobe levels and main lobe width. Low sidelobes indicate reduced interference from clutter or multipath echoes, signifying improved target detection accuracy. Low sidelobes in the ACF are essential to prevent weak targets from being masked by the sidelobes of stronger nearby targets or clutter. Consequently, it indicates the reduced interference from clutter or multipath echoes, signifying improved target detection accuracy. Conversely, high sidelobes signify potential performance degradation. To quantify the sidelobe suppression effect in the ACF, PSLR is a widely used metric, defined in dB as the ratio of the main peak to the highest sidelobe level [10], as follows:
Higher PSLR values indicate better waveform quality, corresponding to stronger main lobe dominance over sidelobes, facilitating superior radar performance.
The impact of constellation shaping on the ACF and the peak-to-sidelobe ratio (PSLR) is predicated on several key assumptions within an OFDM radar framework. First, a sufficiently large number of subcarriers are assumed to approximate a continuous spectrum, which is fundamental for the validity of the ACF structure. Second, the absence of pulse shaping is typically assumed to isolate the effect of the constellation from other spectral shaping factors. The use of a cyclic prefix (CP) is considered sufficient to mitigate inter-symbol interference, ensuring that the analyzed ACF is that of a single OFDM symbol. Crucially, the subcarriers are assumed to be modulated by independent and identically distributed (i.i.d.) symbols. Under these conditions, the composition of the constellation—specifically the distribution of complex symbol values—directly influences the expected ACF and PSLR. A constant modulus constellation such as PSK minimizes inherent sidelobes, while non-constant modulus or probabilistically shaped constellations can intentionally alter the ACF properties at the cost of increased variance or controlled correlation noise. Higher PSLR values indicate better waveform quality by signifying stronger main lobe dominance over sidelobes, which corresponds to superior resolution and improved interference suppression. The optimization of PSLR is consequently a well-established objective in radar waveform design for enhancing target detection performance [16]. A higher PSLR directly translates to an improved capability in distinguishing weak targets from strong sidelobes originating from clutter or other targets, which is critical for the detection probability () and false alarm rate ().
Typically, the sidelobe level has to be lower than a predetermined threshold, as follows:
where is the maximum permissible sidelobe magnitude, minimizing artifacts that mask weak targets in cluttered environments.
Therefore, optimizing PSLR is crucial for sensing performance in ISAC systems. Since PSLR can be effectively influenced by waveform design, our proposed framework leverages constellation mapping and demapping to enhance sensing capabilities.
For communication, to minimize BER, the optimization criterion focuses on minimizing the binary cross-entropy loss between the input bits and the estimated probabilities at the receiver. The binary cross-entropy loss is defined as
where is the true value (0 or 1), and is the probability of each bit estimated from the demapper.
3. End-to-End Network Design
The proposed transceiver design leverages an end-to-end DNN-based framework, with its architecture illustrated in Figure 2. It comprises two core components: (1) the autoencoder mapper (AE-Mapper) for generating optimized constellation points; (2) the autoencoder demapper (AE-Demapper) for robust signal decoding. These components are jointly trained using a loss function that simultaneously accounts for communication reliability and sensing accuracy, achieving balanced optimization of ISAC performance. Detailed designs of the transmitter and receiver are provided in the following subsections.
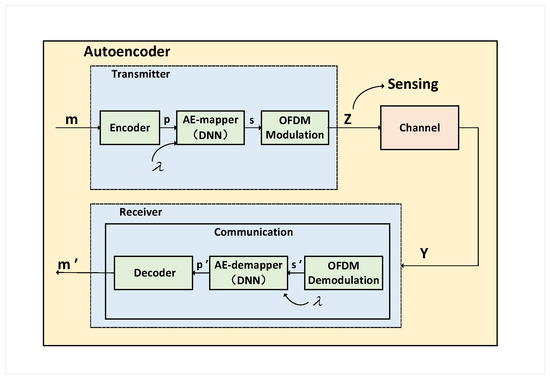
Figure 2.
DNN-based end-to-end ISAC constellation mapping and demapping.
3.1. AE-Mapper
As illustrated in Figure 2, the main component of the transmitter is the AE-Mapper. The transmitted signal z is generated using the following steps: Implemented as a DNN-based waveform generator, the AE-Mapper processes the polar-coded sequence p to generate a frequency-domain waveform . The AE-Mapper employs a fully connected neural network (FCNN) with two hidden layers, chosen for its simplicity, ability to approximate complex mappings, and low computational overhead, making it suitable for real-time ISAC applications. The generator, denoted as with parameters , is inspired by the autoencoder structure and consists of two hidden layers optimized to balance communication and sensing performance for ISAC. The inputs to the network include the polar-coded sequence p and a channel state parameter (SNR), enabling adaptive waveform optimization.
Initially, p is transformed into a one-hot encoded matrix , where each column corresponds to a group of bits and is a unit vector indicating the activated symbol index among the M possibilities. Subsequently, the DNN generates a constellation matrix , whose rows represent the optimized (real, imaginary) coordinate pairs for each of the M constellation points, adapted according to the channel condition . The final optimized waveform is given by
where denotes the weights in the l-th layer, and is the rectified linear unit (ReLU) activation function, chosen for computational simplicity and its ability to mitigate the vanishing gradient problem.
The physical essence of the operation can be interpreted as a trainable, adaptive modulation lookup table. Matrix V acts as a selection matrix, where each one-hot column picks a specific row from the codebook . This is analogous to traditional modulation mapping such as QAM, where a group of bits indexes a pre-defined constellation point. The constellation codebook is not fixed but is dynamically generated and optimized by the DNN based on the channel state , allowing for adaptive geometric constellation shaping beyond conventional designs.
The channel state parameter (SNR) is fed into the DNN to enable adaptive constellation shaping, which acts as a conditioning variable that guides the DNN’s optimization trajectory. The network learns to interpret and accordingly adjusts the weights that generate the constellation matrix . Mechanistically, this allows the AE-Mapper to produce fundamentally different constellation geometries depending on the channel condition. For instance, in low-SNR scenarios, the network might learn to generate constellations with larger minimum Euclidean distances between points to combat noise, prioritizing reliability. In high-SNR conditions, it might shift towards more densely packed constellations that maximize spectral efficiency and data rate, while still adhering to the sensing constraint imposed by the PSLR term in the loss function.
3.2. AE-Demapper
The receiver, illustrated in Figure 2, simultaneously performs data extraction and environmental sensing tasks using the received signal y. The main design of the receiver lies in the AE-Demapper. The received signal impinging at the single-antenna receiver can be expressed as
where represents the channel coefficients, and ⊙ denotes element-wise multiplication. Here, modeling independent Rayleigh fading per sample, while the additive white Gaussian noise follows . Since the normalization layer of the AE-Mapper ensures that and is the complex noise variance, , with denoting the average SNR. Unlike conventional ISAC architectures that separately process sensing and communication tasks, our system employs an AE-Demapper, implemented as a DNN, to jointly process the demodulated symbols for efficient communication decoding. The AE-Demapper utilizes a fully connected neural network (FCNN) with two hidden layers, selected for its effectiveness in learning non-linear mappings from received signals to bit estimates, computational efficiency, and compatibility with end-to-end training in ISAC systems. The AE-Demapper directly maps to the estimated polar-coded sequence ,as follows:
where the estimated polar-coded sequence is .
The mapping function , parameterized by , is formulated as follows:
for , where L represents the dimensionality of the demodulated symbol vector. Here,
- denotes the task-specific network weights in the communication branch;
- is the ReLU activation function; and
- The hyperbolic tangent activation (tanh) ensures bounded outputs suitable for generating near-binary estimates, compatible with polar decoding.
Weights and biases are initialized using He initialization [31], as follows:
The AE-Demapper network, as depicted in Figure 3b, comprises two hidden layers.
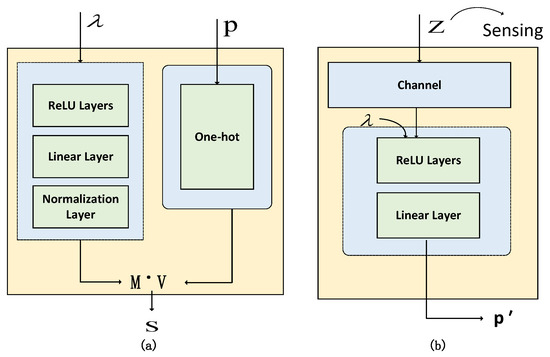
Figure 3.
An illustration of network architecture of AE-Mapper (a) and AE-Demapper (b).
After obtaining , we feed it into the neural SCL-based polar decoder. Although we do not explicitly compute log-likelihood ratios, the DNN can learn a robust mapping that preserves reliability implicitly, enabling effective decoding.
We formulate an optimization problem that minimizes the binary cross-entropy loss under the PSLR sensing constraint, optimizing the waveform represented by frequency-domain symbols s and time-domain signals z, as described in Section 2. We first formulate communication and sensing constraints, which define the feasible region for waveform optimization. Then, we construct a joint objective function that incorporates these requirements into an end-to-end trainable architecture.
3.3. Joint Objective Function Design
To effectively achieve the dual goals of ISAC—reliable data transmission and accurate environmental sensing—we define explicit constraints governing bit estimation reliability and autocorrelation sidelobe suppression, as outlined in Section 2. These constraints serve as the foundation for the optimization problem.
The communication objective minimizes the binary cross-entropy loss to enhance bit estimation accuracy and reduce BER, subject to power constraints. The sensing objective maximizes the main-to-sidelobe ratio in the ACF, subject to sidelobe constraints.
With these constraints defined, we formulate the unified optimization objective that balances communication and sensing. The joint loss function is defined as
where is the binary cross-entropy loss for communication, PSLR is the peak-to-sidelobe ratio for sensing, and is a tunable trade-off parameter that balances the two objectives. A larger prioritizes sensing by emphasizing the maximization of PSLR, while a smaller focuses more on minimizing the communication loss.
This formulation ensures that the training process strikes a compromise between minimizing BER (via cross-entropy) and maximizing sensing performance (via PSLR), while adhering to power constraints.
3.4. Network Design and Parameter Optimization
The proposed ISAC system is trained end to end by minimizing the joint loss function in Equation (14), subject to the communication and sensing constraints. The optimization uses the Adam optimizer, with the following parameter updates:
where is the learning rate, t is the iteration, and ensures stability.
For efficient training, we use He initialization for DNN parameters, as follows:
where is the number of input features.
3.5. Complexity Analysis
To evaluate the computational complexity of the proposed system, we analyze the number of parameters and floating-point operations (FLOPs) required for the AE-Mapper and AE-Demapper. Both networks are fully connected with two hidden layers of 128 neurons each. For the AE-Mapper, assuming an input dimension of 64 (corresponding to the coded bit sequence) and an output dimension of 32 (real and imaginary parts of 16 symbols), the network has approximately 28,960 trainable parameters and requires about 57,344 FLOPs per forward pass. Similarly, for the AE-Demapper, with an input dimension of 32 and an output dimension of 64, it has 28,992 parameters and 57,344 FLOPs.
Our DNN-based approach introduces moderate complexity due to the neural network inference. However, this is offset by the performance gains in balancing BER and PSLR. In contrast with optimization-based probabilistic constellation shaping methods as in [17,18], which often require iterative algorithms with high runtime complexity (potentially thousands of operations per iteration), our end-to-end DNN framework offers lower inference-time complexity after training, making it more suitable for real-time applications. The inference speed per sample is about 0.1 ms on the GPU and 0.5 ms on the CPU, enabling real-time operation in ISAC systems.
4. Simulation Results
In this section, we evaluate the performance of the proposed DNN-enabled ISAC system. For reproducibility, all simulations were conducted using Python 3.8 with TensorFlow 2.10.0 and NumPy 1.21.0 on a machine with an Intel Core i5 CPU (manufactured by Intel Corporation, Santa Clara, CA, USA) and an NVIDIA RTX 4060ti GPU (manufactured by NVIDIA Corporation, Santa Clara, CA, USA). The random seed was set to 42 for all experiments to ensure consistent results. The system employs a (64, 32) polar coding scheme with information bits and coded bits and OFDM with subcarriers. The neural network uses a two-layer fully connected structure with 128 neurons per layer, implemented in Python using TensorFlow.
To investigate the impact of hyperparameters on system performance, we analyze the effects of learning rate and batch size on the convergence of the joint loss function. Figure 4 illustrates the joint loss versus epoch for different learning rates (). The results show that a learning rate of achieves the lowest joint loss after 300 epochs, balancing convergence speed and stability, while lower rates (e.g., ) exhibit oscillations and higher rates (e.g., ) converge slowly.
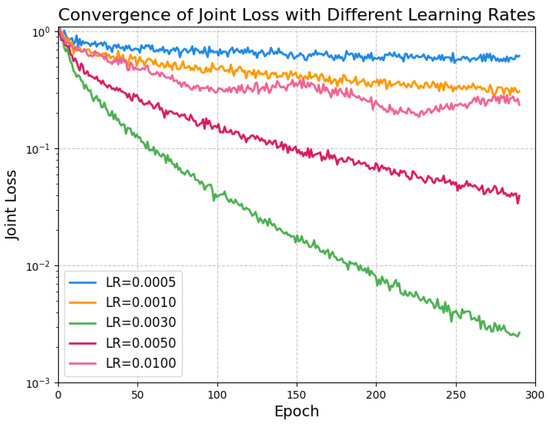
Figure 4.
Convergence behavior of joint loss with different learning rates ().
Similarly, Figure 5 depicts the joint loss versus epoch for different batch sizes (). The results indicate that a batch size of 400 provides the optimal trade-off between gradient accuracy and computational efficiency, converging close to zero within 300 epochs. Smaller batch sizes (e.g., 50, 100) introduce significant gradient noise, leading to erratic convergence, while larger batch sizes (e.g., 1000, 2000) converge slowly.
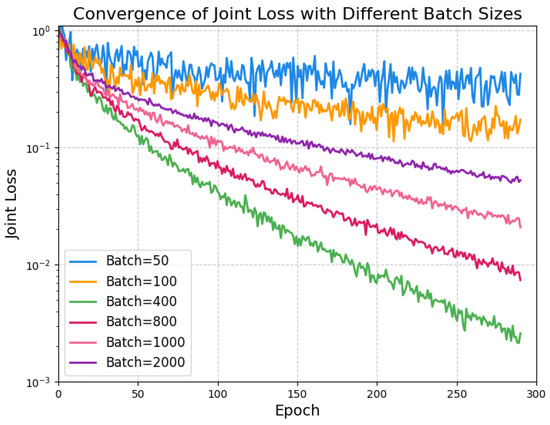
Figure 5.
Convergence of joint loss with different batch sizes (50, 100, 400, 800, 1000, 2000).
To facilitate a simpler comparison, Table 1 summarizes quantitative convergence metrics, including the ultimate loss value and the convergence epoch.

Table 1.
Quantitative convergence metrics for different learning rates and batch sizes.
The table summarizes convergence metrics for various learning rates and batch sizes, highlighting optimal hyperparameters. For learning rates, achieves the lowest ultimate loss (0.0025) and the fastest convergence (86 epochs), balancing speed and stability, while lower rates (e.g., 0.0005) result in higher losses (>0.3) and slower convergence (>290 epochs) due to gradual updates, and higher rates (e.g., 0.01) lead to instability. Similarly, a batch size of 400 yields the minimal loss (0.0026) and quick convergence (89 epochs), offering an efficient trade-off between gradient noise in small batches (e.g., 50 with loss 0.3924) and computational overhead in large ones (e.g., 2000 with loss 0.0512).
Based on hyperparameter results before, in subsequent simulations, the Adam optimizer is applied with a learning rate of , and the batch size is set as 400. Each training process consists of 300 epochs.
In Figure 6, we evaluate the joint loss function, defined as Equation (14), under different trade-off parameters . The results show that, with , the loss decreases most rapidly, stabilizing close to zero within approximately 200 epochs, since , ensuring a balanced optimization that effectively minimizes both S&C losses simultaneously. Conversely, for , the loss exhibits the slowest convergence, stabilizing at a higher value after 300 epochs. On the other hand, for , the loss converges at a moderate rate. These findings validate that the selected hyperparameters and effectively ensure stable convergence.
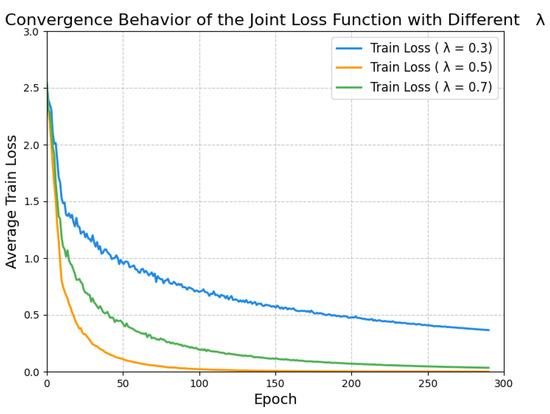
Figure 6.
Convergence in terms of the average joint loss with different values.
In Figure 7, we show the optimized constellation set with different coefficients , where two modulation orders are considered, i.e., M = 16 and M = 32. Specifically, a smaller , prioritizing communication, results in larger minimum Euclidean distance (MED), thereby enhancing symbol detection performance. Conversely, a larger , favoring sensing, boosts average symbol power, improving target detection performance. This demonstrates the trade-off between communication reliability and sensing precision in ISAC constellation design.
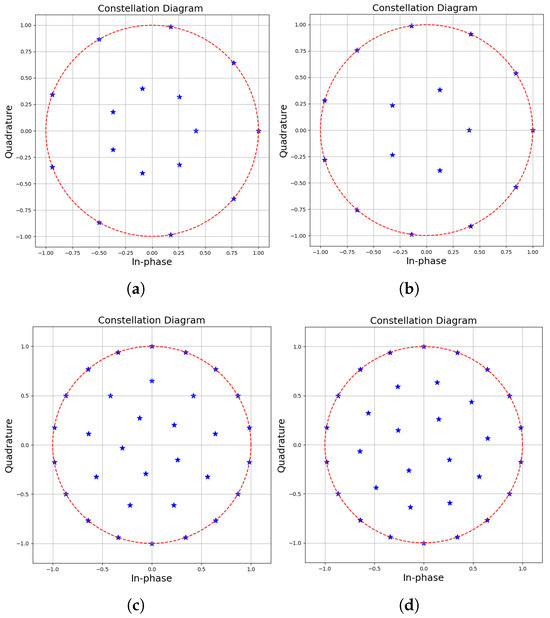
Figure 7.
Constellation with varying sizes and values. (a) Constellation with (, MED = 0.3832, average power = 0.652). (b) Constellation with (, MED = 0.3366, average power = 0.720). (c) Constellation with (, MED = 0.1512, average power = 0.673). (d) Constellation with (, MED = 0.1833, average power = 0.734) (The blue stars are constellation points, and the red circle are unit circles).
Furthermore, to provide empirical validation of the trade-off dynamics, we present visualizations of BER and PSLR as functions of the trade-off parameter . These results, derived from Monte Carlo simulations, illustrate the non-linear interplay between communication reliability and sensing resolution, as shown in Figure 8a for normalized PSLR and Figure 8b for BER.
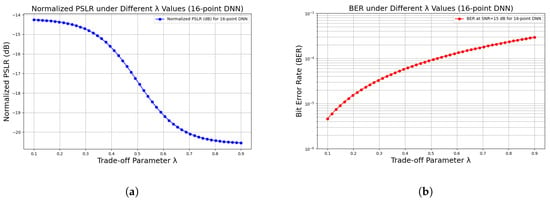
Figure 8.
BER and PSLR under different values for 16-point DNN in ISAC system. (a) Normalized PSLR under different . (b) BER under different at SNR = 15 dB.
We analyze the tendencies through both theoretical insights and empirical data. Theoretically, the joint loss function in Equation (14) weights the communication loss in Equation (7) against the sensing term involving the inverse of PSLR in Equation (5). For small (e.g., 0.3), the optimizer prioritizes the communication loss, leading to lower BER but potentially reduced PSLR, as the focus is on communication reliability. Conversely, for larger (e.g., 0.7), the sensing term dominates, resulting in higher PSLR for improved target detection, but possibly elevated BER. Empirically, from our simulations, as increases from 0.3 to 0.7, PSLR improves (e.g., higher sidelobe suppression), while BER may rise, confirming the causal trade-off driven by loss weighting. This balance is optimal at , achieving competitive BER and PSLR, as it equidistantly optimizes both objectives without extreme bias.
In Figure 9, we present a comparison of the autocorrelation function (ACF) for time-domain waveforms, which is generated by the proposed constellation and conventional modulations (16QAM, 16PSK, and 16APSK). As can be seen in Figure 9, the proposed DNN-optimized constellation achieves PSLR improvements of approximately 5.8 dB, 4.6 dB, and 0.4 dB over 16QAM, 16PSK, and 16APSK. Specifically, 16QAM exhibits higher sidelobes due to its significant and unstructured amplitude variations. In contrast, 16PSK, with its fixed-amplitude constellation, offers a constant envelope but relies solely on phase shifts. For 16APSK, the structured multi-ring design incorporates controlled amplitude variations alongside phase modulation, enabling better statistical decorrelation in the time domain and thus lower sidelobes compared with 16QAM and 16PSK, though remaining inferior when compared with the DNN-optimized approach.
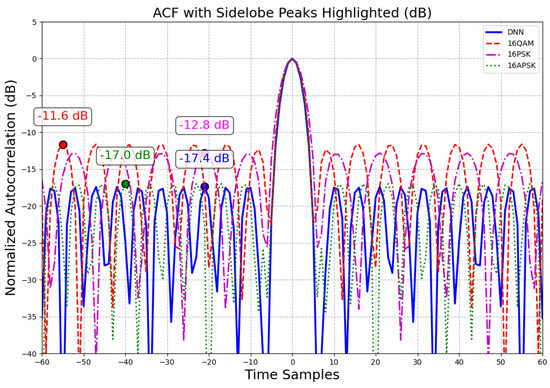
Figure 9.
Autocorrelation function comparison for DNN, 16QAM, and 16PSK waveforms ().
To further evaluate the communication performance trade-off, Figure 10 compares the BER for the proposed DNN-based constellation scheme against conventional modulations (16QAM, 16PSK, and 16APSK). Specifically, the proposed constellation outperforms 16PSK and 16APSK, achieving SNR gains of approximately 1.5 dB and 0.5 dB at the BER of , respectively. Nevertheless, compared with 16QAM, it requires a slightly higher SNR (0.3 dB) to achieve the same BER. Additionally, the performance gap holds for the polar coded system.
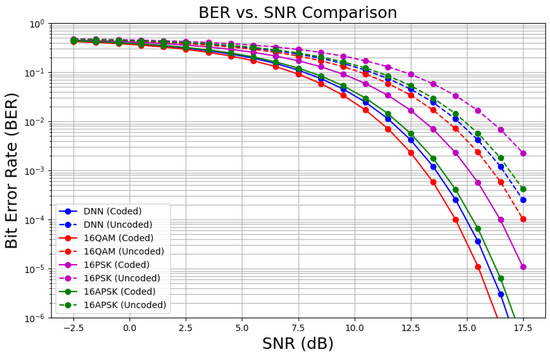
Figure 10.
Comparison of BER performances for the DNN-based approach, 16QAM, and 16PSK ().
These results indicate that the proposed DNN-optimized constellation achieves an improvement in PSLR compared with conventional modulation schemes, thereby enhancing the sensing capability while maintaining competitive communication performance. This trade-off highlights the effectiveness of the proposed end-to-end optimization framework for joint sensing and communication.
5. Conclusions
In this paper, we propose an end-to-end DNN-based ISAC framework to optimize constellation mapping and demapping for both sensing and communication performance. We integrated OFDM modulation within the proposed architecture, employing a joint loss function that simultaneously optimizes BER for communication reliability and PSLR for sensing accuracy. Numerical results confirmed the efficiency of the proposed constellation, explicitly highlighting the performance trade-offs in ISAC systems. The proposed architecture, particularly the AE-Mapper, which adapts to channel state information, is designed with such challenges in mind. Its ability to generate waveforms with optimized statistics is a promising pathway towards addressing real-world distortions like multi-path fading, phase noise, and hardware non-linearities.
In our future work, we will conduct a comprehensive investigation of the framework’s performance under realistic scenarios—such as standardized multi-path models, carrier frequency offset and phase noise, power amplifier non-linearity and quantization effects, and dynamic multi-target sensing cases—to further validate and generalize our DNN-driven ISAC approach.
Author Contributions
Formal analysis, F.X.; Data curation, J.F.; Writing—original draft, J.Y.; Writing—review & editing, J.B. and X.W.; Supervision, J.H. and Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Beijing Natural Science Foundation, project number QY24169 and the National Natural Science Foundation of China under Grant No. 62201044.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| AE | autoencoder |
| APSK | amplitude and phase shift keying |
| AWGN | additive white Gaussian noise |
| BER | bit error rate |
| DNN | deep neural network |
| IFFT | inverse fast Fourier transform |
| ISAC | integrated sensing and communication |
| OFDM | Orthogonal Frequency Division Multiplexing |
| PSLR | peak-to-sidelobe ratio |
| QAM | quadrature amplitude modulation |
| PSK | phase shift keying |
| ReLU | rectified linear unit |
| SCL | successive cancellation list |
| SGD | stochastic gradient descent |
| SNR | signal-to-noise ratio |
References
- Wild, T.; Grudnitsky, S.; Mandelli, M.; Hemminger, J.; Guan, F.; Schaich, F. 6G integrated sensing and communication: From vision to realization. In Proceedings of the European Radar Conference (EuRAD), Berlin, Germany, 20–22 September 2023; pp. 355–358. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, J.; Zhu, H.; Huo, M.; Cheng, X.; Chao, K.; Li, J.; Guan, J.; Liu, X.; Gao, J. 5G/5G-A private network: Construction, operation and applications. In Proceedings of the IEEE 22nd International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Exeter, UK, 1–4 November 2023; pp. 2234–2239. [Google Scholar] [CrossRef]
- Liu, F.; Cui, C.; Masouros, J.; Xu, T.; Han, Y.; Eldar, Y.; Buzzi, S. Integrated sensing and communications: Toward dual-functional wireless networks for 6G and beyond. IEEE J. Sel. Areas Commun. 2022, 40, 1728–1767. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Petropulu, A.P.; Clerckx, B.; Li, J. Joint radar and communication design: Applications, state-of-the-art, and the road ahead. IEEE Trans. Commun. 2020, 68, 3834–3862. [Google Scholar] [CrossRef]
- Liu, F.; Yuan, W.; Masouros, C.; Yuan, J. Intelligent integrated sensing and communication: A survey. Sci. China Inf. Sci. 2024, 67, 1–30. [Google Scholar] [CrossRef]
- Lu, S.; Liu, F.; Li, Y.; Zhang, K.; Huang, H.; Zou, J.; Li, X.; Dong, Y.; Dong, F.; Zhu, J.; et al. Integrated sensing and communications: Recent advances and ten open challenges. IEEE Internet Things J. 2024, 11, 19094–19120. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Poor, H.V. 6G Internet of Things: A comprehensive survey. IEEE Internet Things J. 2022, 9, 359–383. [Google Scholar] [CrossRef]
- Saberinia, E.; Tang, J.; Tewfik, A.; Parhi, K. Pulsed-OFDM Modulation for Ultrawideband Communications. IEEE Trans. Veh. Technol. 2009, 58, 720–726. [Google Scholar] [CrossRef]
- Hassanien, A.; Amin, M.G.; Zhang, Y.D.; Ahmad, F. Signaling Strategies for Dual-Function Radar Communications: An Overview. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 36–45. [Google Scholar] [CrossRef]
- Hu, Z.; Ye, Q.; Huang, Y.; Hu, S.; Yang, G. Joint Range-Velocity-Azimuth Estimation for OFDM-Based Integrated Sensing and Communication. IEEE Trans. Wirel. Commun. 2024, 23, 12933–12948. [Google Scholar] [CrossRef]
- Bouziane, A.; Eddine Zegrar, S.; Arslan, H. A Novel OFDM-FMCW Waveform for Low-Complexity Joint Sensing and Communication. IEEE Wirel. Commun. Lett. 2025, 14, 425–429. [Google Scholar] [CrossRef]
- Fazli, A.; Tohidi, E.; Utkovski, Z.; Agostini, P.; Stanczak, S. On the Impact of OFDM Waveform in ISAC Systems. In Proceedings of the 2025 IEEE Wireless Communications and Networking Conference (WCNC), Milan, Italy, 24–27 March 2025; pp. 1–6. [Google Scholar] [CrossRef]
- Feskin, M.; Mojahdian, C.; Marcus, O.; Eriksson, A.; Giorgietti, J.; Widmer, H.; Wynmeersch, H. Fundamental Trade-Offs in Monostatic ISAC: A Holistic Investigation Towards 6G. 2024. Available online: https://arxiv.org/abs/2401.18011v2 (accessed on 15 July 2025).
- Xiong, F.; Liu, K.; Wan, W.; Yuan, Y.; Cui, G.; Caire, G. From torch to projector: Fundamental tradeoff of integrated sensing and communications. IEEE BITS Inf. Theory Mag. 2024, 4, 73–90. [Google Scholar] [CrossRef]
- Proakis, J.G.; Salehi, M. Digital Communications, 5th ed.; McGraw-Hill Education: New York, NY, USA, 2008. [Google Scholar]
- Levanon, N.; Mozeson, E. Radar Signals; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Du, Z.; Liu, F.; Masouros, C.; Yuan, X. Reshaping the ISAC tradeoff under OFDM signaling: A probabilistic constellation shaping approach. IEEE Trans. Signal Process. 2024, 72, 4782–4797. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, R.; Zhai, D.; Liu, F. Constellation design for integrated sensing and communication with random waveforms. IEEE Trans. Wirel. Commun. 2024, 23, 17415–17428. [Google Scholar] [CrossRef]
- Geiger, B.; Liu, F.; Lu, S.; Rode, A.; Schmalen, L. Joint optimization of geometric and probabilistic constellation shaping for OFDM-ISAC systems. arXiv 2025, arXiv:2501.11583. [Google Scholar] [CrossRef]
- Stark, M.; Aït Aoudia, F.; Hoydis, J. Joint Learning of Geometric and Probabilistic Constellation Shaping. In Proceedings of the IEEE Globecom Workshops (GC Wkshps), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, Z.; Zhang, Z. Differential fault attack of lightweight cipher GIFT based on byte model. IEEE Internet Things J. 2025, 12, 435–444. [Google Scholar] [CrossRef]
- Ma, H.; Tao, Y.; Fang, Y.; Chen, P.; Li, Y. Multi-carrier initial-condition-index-aided DCSK scheme: An efficient solution for multipath fading channel. IEEE Trans. Veh. Technol. 2025, 1–14. [Google Scholar] [CrossRef]
- O’Shea, T.J.; Hoydis, J. An Introduction to Deep Learning for the Physical Layer. IEEE Trans. Cogn. Commun. Netw. 2017, 3, 563–575. [Google Scholar] [CrossRef]
- Aref, V.; Chagnon, M. End-to-End Learning of Joint Geometric and Probabilistic Constellation Shaping. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 6–10 March 2022. [Google Scholar] [CrossRef]
- Chimmalgi, S.; Schmalen, L.; Aref, V.A. End-to-end learning of probabilistic constellation shaping through importance sampling. arXiv 2025, arXiv:2506.16098. [Google Scholar] [CrossRef]
- Hu, J.; Han, K.; Lai, J.; Meng, K.; Liu, F.; Masouros, C. Learning-based constellation design for uplink bi-static integrated sensing and communication. IEEE Trans. Veh. Technol. 2024, 74, 13219–13224. [Google Scholar] [CrossRef]
- Mateos-Ramos, J.M.; Song, J.; Wu, Y.; Häger, C.; Keskin, M.F.; Yajnanarayana, V.; Wymeersch, H. End-to-End Learning for Integrated Sensing and Communication. In Proceedings of the IEEE International Conference on Communications (ICC), Seoul, Republic of Korea, 16–20 May 2022; pp. 1942–1947. [Google Scholar] [CrossRef]
- Zhang, J.A.; Liu, F.; Masouros, C.; Heath, R.W.; Feng, Z.; Zheng, L.; Petropulu, A. An Overview of Signal Processing Techniques for Joint Communication and Radar Sensing. IEEE J. Sel. Top. Signal Process. 2021, 15, 1295–1315. [Google Scholar] [CrossRef]
- Richards, M.A. Fundamentals of Radar Signal Processing, 2nd ed.; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Tang, B.; Tang, J. Joint Design of Transmit Waveforms and Receive Filters for MIMO Radar Space-Time Adaptive Processing. IEEE Trans. Signal Process. 2016, 64, 4707–4722. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. arXiv 2015, arXiv:1502.01852. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).