Low-Frequency Measurements in Electrochemical Impedance Spectroscopy: A Brief Review
Abstract
1. Introduction
2. A Brief Summary of EIS Applications
2.1. Energy Storage Systems
2.2. Biomedical Applications
2.3. Other Applications
2.4. Challenges in Experimental Environments
3. Electronic Circuits and Solutions for EIS
- −
- Accuracy: the impedance measurement has to be reliable, even if the performance parameters to be evaluated are highly dependent on the specific application. Along with the applied method, the measurement accuracy is critically affected by the stimulus signal, which needs to be stable and highly controllable. For this reason, special care is usually dedicated to the waveform generator design.
- −
- Portability: most of the applications of EIS can involve in-situ measurement, requiring the system to be embedded or having a certain degree of integration. This is specific, for instance, to a bio-impedance sensor with wearability requirements, but can be preferable for material or system characterization as well.
- −
- Measurement time: as said, the impedance spectrum requires multiple acquisitions over the entire frequency range of operation; moreover, the investigation at extremely low frequencies usually implies time-consuming measurements even for the single harmonic. When possible, dedicated strategies have to be put in place to reduce, manage, or control the measurement time.
- −
- Versatility: as already mentioned, different frequency ranges evaluate different properties; hence, broadband solutions ensure a robust system, albeit at the expense of architectural complexity. At the same time, a wide measurable impedance range could allow the system to adapt to more than one application.
3.1. Solutions Based on Howland’s Circuit
- −
- Resistors matching: the VCCS behavior is possible only if the bridge condition is exactly fulfilled. Indeed, only in this case the output impedance of the circuit is infinite, while a small deviation from the perfect matching condition leads to a finite output impedance, or in other words, a current dependent on the load value. The acceptable tolerance for the resistors depends on the accuracy needed for the measurements, although it affects mostly the high-frequency measurements [63]. Remarkably, resistor matching certainly represents a constraint for all read-out circuits employed in low-frequency impedance spectroscopy as well.
- −
- Output voltage swing: the input-voltage-dependent current is provided as long as the op-amp output voltage is below the saturation region, directly affecting the maximum range of measurable impedance. In this case both the maximum current and the transconductance coefficient can be optimized to adapt the device to different impedance values.
3.2. Solutions Based on System Integration
4. Discussion
- −
- Drift. In applications requiring a mHz frequency range, the system’s state may evolve due to factors such as temperature fluctuations, changes in electrode surface properties, or shifting concentration gradients. Such drift can introduce artifacts into the impedance spectrum, potentially causing data unreliability. Averaging the measurement over successive acquisitions results in further time consumption to assess systematic temporal deviations. Time-saving alternatives include applying algorithms to compensate for drift in real time. For instance, first-order effects can be corrected via linear interpolation between consecutive DC values, while in cases of more pronounced variations, more advanced trend-removal techniques are recommended [94]. Alternative methods employ the Fourier Transform of input and output signals to correct for drift, providing a robust approach for systems with very long relaxation times [95]. Remarkably, Operando EIS [96] has been proposed as a promising technique for EIS under time-varying conditions, not only mitigating the limitations associated to drift but also enabling the study of dynamic processes occurring under realistic operating conditions.
- −
- Noise. Extremely low-frequency measurements are particularly susceptible to both random and deterministic noise. The signal-to-noise ratio is inherently lower at frequencies 1 mHz–1 Hz due to the small amplitude of the applied perturbation and the extended acquisition time, which increases the likelihood of interference from environmental sources. To reduce the impact of noise, the experimental setup should be properly shielded and grounded, typically by employing a Faraday cage [65]. A good practice for the identification and elimination of noise sources is to use a test cell with known impedance values to evaluate the system’s susceptibility to noise and to calibrate the measurement setup.
- −
- Calibration Errors. The accuracy of EIS measurements strongly depends on the proper calibration of the impedance analyzer. Calibration inaccuracies—particularly in the current and voltage ranges—can introduce systematic errors in the measured impedance, more pronounced at very low frequencies. Phase measurements are especially sensitive to such errors, as even small phase shifts can significantly impact data in the low-frequency regime. To reduce these errors, proper calibration using traceable standards (open, short, and known loads) is crucial, with special focus on current and voltage ranges. Compensation for cables and fixtures through open/short/load corrections near the device under test is also recommended. Also, in this case, drift correction methods—such as baseline adjustments over multiple sinusoidal periods—help mitigate phase errors caused by thermal or environmental instabilities [97]. Finally, repeated measurements with dummy cells enable verification of system stability and accuracy across frequencies [98].
- −
- Non-linearity. EIS relies on the assumption that the system’s response is linear. However, at low frequencies, the applied voltage or current may induce larger-than-expected changes in the system’s state, driving it into a non-linear regime. For instance, a low-frequency signal can significantly alter the concentration of reactants at the electrode surface. Once the system exhibits non-linearity, the EIS data can no longer be accurately interpreted using standard equivalent circuit models.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bonanos, N.; Steele, B.C.H.; Butler, E.P. Applications of Impedance Spectroscopy. In Impedance Spectroscopy: Theory, Experiment, and Applications, 2nd ed.; Barsoukov, E., Macdonald, J.R., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 205–520. [Google Scholar]
- Sunil, V.; Pal, B.; Misnon, I.I.; Jose, R. Characterization of supercapacitive charge storage device using electrochemical impedance spectroscopy. Mater. Today Proc. 2021, 46, 1588–1594. [Google Scholar] [CrossRef]
- Hernández, H.H.; Reynoso, A.M.R.; Juan, C.; González, T.; Morán, C.O.G. Electrochemical impedance spectroscopy (EIS): A review study of basic aspects of the corrosion mechanism applied to steels. In Electrochemical Impedance Spectroscopy; IntechOpen: London, UK, 2020; Volume 1, pp. 1–16. [Google Scholar]
- Anantharaj, S.; Noda, S. Appropriate use of electrochemical impedance spectroscopy in water splitting electrocatalysis. ChemElectroChem 2020, 7, 2297–2308. [Google Scholar] [CrossRef]
- Santoni, F.; De Angelis, A.; Moschitta, A.; Carbone, P.; Galeotti, M.; Cinà, L.; Giammanco, C.; Di Carlo, A. A guide to equivalent circuit fitting for impedance analysis and battery state estimation. J. Energy Storage 2024, 82, 110389. [Google Scholar] [CrossRef]
- Dong, T.K.; Kirchev, A.; Mattera, F.; Kowal, J.; Bultel, Y. Dynamic modeling of Li-ion batteries using an equivalent electrical circuit. J. Electrochem. Soc. 2011, 158, A326. [Google Scholar] [CrossRef]
- Moss, P.L.; Au, G.; Plichta, E.J.; Zheng, J.P. An electrical circuit for modeling the dynamic response of Li-ion polymer batteries. J. Electrochem. Soc. 2008, 155, A986–A994. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, S.; Ono, K. Electrochemical Impedance Spectroscopy. In Microscopy and Microanalysis for Lithium-Ion Batteries; CRC Press: Boca Raton, FL, USA, 2023; pp. 301–350. [Google Scholar]
- Huang, J. Diffusion impedance of electroactive materials, electrolytic solutions and porous electrodes: Warburg impedance and beyond. Electrochim. Acta 2018, 281, 170–188. [Google Scholar] [CrossRef]
- Gateman, S.M.; Gharbi, O.; De Melo, H.G.; Ngo, K.; Turmine, M.; Vivier, V. On the use of a constant phase element (CPE) in electrochemistry. Curr. Opin. Electrochem. 2022, 36, 101133. [Google Scholar] [CrossRef]
- Moya, A.A. Low-frequency development approximations to the transmissive Warburg diffusion impedance. J. Energy Storage 2022, 55, 105632. [Google Scholar] [CrossRef]
- Locorotondo, E.; Pugi, L.; Berzi, L.; Pierini, M.; Scavuzzo, S.; Ferraris, A. Modeling and simulation of constant phase element for battery electrochemical impedance spectroscopy. In Proceedings of the IEEE 5th International forum on Research and Technology for Society and Industry (RTSI), Florence, Italy, 9–12 September 2019. [Google Scholar] [CrossRef]
- Karden, E. Using Low Frequency Impedance Spectroscopy for Characterization, Monitoring, and Modeling of Industrial Batteries; Shaker: Aachen, Germany, 2002. [Google Scholar]
- Peter, L.M.; Vanmaekelbergh, D. Time and frequency resolved studies of photoelectrochemical kinetics. Adv. Electrochem. Sci. Eng. 1999, 6, 77–163. [Google Scholar]
- Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying degradation patterns of lithium ion batteries from impedance spectroscopy using machine learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [CrossRef]
- Andre, D.; Meiler, M.; Steiner, K.; Wimmer, C.; Soczka-Guth, T.; Sauer, D.U. Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. I. Experimental investigation. J. Power Sources 2011, 196, 5334–5341. [Google Scholar] [CrossRef]
- Spielbauer, M.; Berg, P.; Ringat, M.; Bohlen, O.; Jossen, A. Experimental study of the impedance behavior of 18650 lithium-ion battery cells under deforming mechanical abuse. J. Energy Storage 2019, 26, 101039. [Google Scholar] [CrossRef]
- Dai, H.; Jiang, B.; Wei, X. Impedance characterization and modeling of lithium-ion batteries considering the internal temperature gradient. Energies 2018, 11, 220. [Google Scholar] [CrossRef]
- Fang, J.; Shen, W.; Cheng, S.H.S.; Ghashghaie, S.; Shahzad, H.K.; Chung, C.Y. Four-electrode symmetric setup for electrochemical impedance spectroscopy study of lithium–sulfur batteries. J. Power Sources 2019, 441, 227202. [Google Scholar] [CrossRef]
- Li, J.; Sun, D.; Jin, X.; Shi, W.; Sun, C. Lithium-ion battery overcharging thermal characteristics analysis and an impedance-based electro-thermal coupled model simulation. Appl. Energy 2019, 254, 113574. [Google Scholar] [CrossRef]
- Oldenburger, M.; Beduerftig, B.; Gruhle, A.; Grimsmann, F.; Richter, E.; Findeisen, R.; Hintennach, A. Investigation of the low frequency Warburg impedance of Li-ion cells by frequency domain measurements. J. Energy Storage 2019, 21, 272–280. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Dai, H.; Wu, Q. State estimation of lithium ion battery based on electrochemical impedance spectroscopy with on-board impedance measurement system. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–5. [Google Scholar]
- Srinivasan, R.; Carkhuff, B.G.; Butler, M.H.; Baisden, A.C. Instantaneous measurement of the internal temperature in lithium-ion rechargeable cells. Electrochim. Acta 2011, 56, 6198–6204. [Google Scholar] [CrossRef]
- McCarthy, K.; Gullapalli, H.; Kennedy, T. Real-time internal temperature estimation of commercial Li-ion batteries using online impedance measurements. J. Power Sources 2022, 519, 230786. [Google Scholar] [CrossRef]
- Al-Zubaidi R-Smith, N.; Kasper, M.; Kumar, P.; Nilsson, D.; Mårlid, B.; Kienberger, F. Advanced electrochemical impedance spectroscopy of industrial Ni-Cd batteries. Batteries 2022, 8, 50. [Google Scholar] [CrossRef]
- Du, X.; Meng, J.; Amirat, Y.; Gao, F.; Benbouzid, M. Dynamic impedance spectrum: A novel metric for lithium-ion batteries overcharging diagnosis. IEEE Trans. Ind. Electron. 2025, 72, 4238–4247. [Google Scholar] [CrossRef]
- Clemente, F.; Romano, M.; Bifulco, P.; Cesarelli, M. EIS measurements for characterization of muscular tissue by means of equivalent electrical parameters. Measurement 2014, 58, 476–482. [Google Scholar] [CrossRef]
- Jung, M.H.; Namkoong, K.; Lee, Y.; Koh, Y.J.; Eom, K.; Jang, H.; Park, J. Wrist-wearable bioelectrical impedance analyzer with miniature electrodes for daily obesity management. Sci. Rep. 2021, 11, 1238. [Google Scholar] [CrossRef]
- Hong, S.; Lee, J.; Bae, J.; Yoo, H.J. A 10.4 mW electrical impedance tomography SoC for portable real-time lung ventilation monitoring system. IEEE J. Solid-State Circuits 2015, 50, 2501–2512. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, D.; Bardill, A.; De Gelidi, S.; Bayford, R.; Demosthenous, A. A high frame rate wearable EIT system using active electrode ASICs for lung respiration and heart rate monitoring. IEEE Trans. Circuits Syst. I 2018, 65, 3810–3820. [Google Scholar] [CrossRef]
- Liu, B.; Wang, G.; Li, Y.; Zeng, L.; Li, H.; Gao, Y.; Heng, C.H. A 13-channel 1.53 mW 11.28 mm2 electrical impedance tomography SoC based on frequency division multiplexing for lung physiological imaging. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 938–949. [Google Scholar] [CrossRef]
- Xu, J.; Hong, Z. Low power bio-impedance sensor interfaces: Review and electronics design methodology. IEEE Rev. Biomed. Eng. 2020, 15, 23–35. [Google Scholar] [CrossRef] [PubMed]
- Vizvari, Z.; Gyorfi, N.; Odry, A.; Sari, Z.; Klincsik, M.; Gergics, M.; Toth, A. Physical validation of a residual impedance rejection method during ultra-low frequency bio-impedance spectral measurements. Sensors 2020, 20, 4686. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Lu, M.; Yin, W. Cellular structure analysis based on magnetic induction finite element method simulations and measurements. bioRxiv 2018. bioRxiv:275271. [Google Scholar] [CrossRef]
- Sarode, G.S.; Sarode, S.C.; Kulkarni, M.; Karmarkar, S.; Patil, S. Role of bioimpedance in cancer detection: A brief review. Int. J. Dent. Sci. Res. 2016, 3, 15–21. [Google Scholar] [CrossRef]
- Kaushik, V.; Yakisich, J.S.; Way, L.F.; Azad, N.; Iyer, A.K. Chemoresistance of cancer floating cells is independent of their ability to form 3D structures: Implications for anticancer drug screening. J. Cell. Physiol. 2019, 234, 4445–4453. [Google Scholar] [CrossRef]
- Crowell, L.L.; Yakisich, J.S.; Aufderheide, B.; Adams, T.N. Electrical impedance spectroscopy for monitoring chemoresistance of cancer cells. Micromachines 2020, 11, 832. [Google Scholar] [CrossRef]
- Abasi, S.; Aggas, J.R.; Garayar-Leyva, G.G.; Walther, B.K.; Guiseppi-Elie, A. Bioelectrical impedance spectroscopy for monitoring mammalian cells and tissues under different frequency domains: A review. ACS Meas. Sci. Au 2022, 2, 495–516. [Google Scholar] [CrossRef]
- Mansouri, S.; Alhadidi, T.; Ben Azouz, M. Breast cancer detection using low-frequency bioimpedance device. Breast Cancer Targets Ther. 2020, 12, 109–116. [Google Scholar] [CrossRef]
- Cherepenin, V.; Karpov, A.; Korjenevsky, A.; Kornienko, V.; Mazaletskaya, A.; Mazourov, D.; Meister, D. A 3D electrical impedance tomography (EIT) system for breast cancer detection. Physiol. Meas. 2001, 22, 9–18. [Google Scholar] [CrossRef] [PubMed]
- Huerta-Nuñez, L.F.E.; Gutierrez-Iglesias, G.; Martinez-Cuazitl, A.; Mata-Miranda, M.M.; Alvarez-Jiménez, V.D.; Sánchez-Monroy, V.; González-Díaz, C.A. A biosensor capable of identifying low quantities of breast cancer cells by electrical impedance spectroscopy. Sci. Rep. 2019, 9, 6419. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.J.; Kim, K.; Kim, H.W.; Park, Y. Classification between normal and cancerous human urothelial cells by using micro-dimensional electrochemical impedance spectroscopy combined with machine learning. Sensors 2022, 22, 7969. [Google Scholar] [CrossRef]
- Bannwarth, S.; Trieu, T.; Oberschelp, C.; Wessling, M. On-line monitoring of cake layer structure during fouling on porous membranes by in situ electrical impedance analysis. J. Membr. Sci. 2016, 503, 188–198. [Google Scholar] [CrossRef]
- Sengur-Tasdemir, R.; Guler-Gokce, Z.; Sarac, A.S.; Koyuncu, I. Determination of membrane protein fouling by UV spectroscopy and electrochemical impedance spectroscopy. Polym.-Plast. Technol. Eng. 2018, 57, 59–69. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Y.; You, Z.; Bao, H.; Zhang, L.; Wang, J. Electrochemical impedance spectroscopy (EIS) reveals the role of microbial fuel cell-ceramic membrane bioreactor (MFC-CMBR): Electricity utilization and membrane fouling. Water Res. 2022, 222, 118854. [Google Scholar] [CrossRef]
- Achtenberg, K.; Gawron, W.; Bielecki, Z. Low-frequency noise and impedance measurements in Auger suppressed LWIR N+ p (π) P+ n+ HgCdTe detector. Infrared Phys. Technol. 2024, 137, 105110. [Google Scholar] [CrossRef]
- Tailor, N.K.; Senanayak, S.P.; Abdi-Jalebi, M.; Satapathi, S. Low-frequency carrier kinetics in triple cation perovskite solar cells probed by impedance and modulus spectroscopy. Electrochim. Acta 2021, 386, 138430. [Google Scholar] [CrossRef]
- Zhang, D.; Allagui, A.; Elwakil, A.S.; Yan, Z.; Lu, H. Active circuit model of low-frequency behavior in perovskite solar cells. Org. Electron. 2020, 85, 105804. [Google Scholar] [CrossRef]
- Gomes, M.P.; Costa, I.; Pébère, N.; Rossi, J.L.; Tribollet, B.; Vivier, V. On the corrosion mechanism of Mg investigated by electrochemical impedance spectroscopy. Electrochim. Acta 2019, 306, 61–70. [Google Scholar] [CrossRef]
- Pippione, G.; Olivero, P.; Fischer, M.; Schreck, M.; Pasquarelli, A. Characterization of CVD heavily B-doped diamond thin films for multi electrode array biosensors. Phys. Status Solidi A 2017, 214, 1700223. [Google Scholar] [CrossRef]
- Martins, J.C.; Neto, J.C.D.M.; Passos, R.R.; Pocrifka, L.A. Electrochemical behavior of polyaniline: A study by electrochemical impedance spectroscopy (EIS) in low-frequency. Solid State Ionics 2020, 346, 115198. [Google Scholar] [CrossRef]
- Placidi, P.; Delle Vergini, C.V.; Papini, N.; Cecconi, M.; Mezzanotte, P.; Scorzoni, A. Low-cost and low-frequency impedance meter for soil water content measurement in the precision agriculture scenario. IEEE Trans. Instrum. Meas. 2023, 72, 1–13. [Google Scholar] [CrossRef]
- Ernst, S.; Heins, T.P.; Schlüter, N.; Schröder, U. Capturing the current-overpotential nonlinearity of lithium-ion batteries by nonlinear electrochemical impedance spectroscopy (NLEIS) in charge and discharge direction. Front. Energy Res. 2019, 7, 151. [Google Scholar] [CrossRef]
- Jacobs, D.A.; Shen, H.; Pfeffer, F.; Peng, J.; White, T.P.; Beck, F.J.; Catchpole, K.R. The two faces of capacitance: New interpretations for electrical impedance measurements of perovskite solar cells and their relation to hysteresis. J. Appl. Phys. 2018, 124, 225702. [Google Scholar] [CrossRef]
- Daniels, J.S.; Pourmand, N. Label-free impedance biosensors: Opportunities and challenges. Electroanalysis 2007, 19, 1239–1257. [Google Scholar] [CrossRef]
- Meddings, N.; Heinrich, M.; Overney, F.; Lee, J.-S.; Ruiz, V.; Napolitano, E.; Seitz, S.; Hinds, G.; Raccichini, R.; Gaberšček, M.; et al. Application of electrochemical impedance spectroscopy to commercial Li-ion cells: A review. J. Power Sources 2020, 480, 228742. [Google Scholar] [CrossRef]
- Wang, L.; Snihirova, D.; Havigh, M.D.; Deng, M.; Lamaka, S.V.; Terryn, H.; Zheludkevich, M.L. Non-stationarity in electrochemical impedance measurement of Mg-based materials in aqueous media. Electrochim. Acta 2023, 468, 143140. [Google Scholar] [CrossRef]
- Plank, C.; Rüther, T.; Jahn, L.; Schamel, M.; Schmidt, J.P.; Ciucci, F.; Danzer, M.A. A review on the distribution of relaxation times analysis: A powerful tool for process identification of electrochemical systems. J. Power Sources 2024, 594, 233845. [Google Scholar] [CrossRef]
- Bragós, R.; Sarro, E.; Fontova, A.; Soley, A.; Cairó, J.; Bayés-Genís, A.; Rosell, J. Four versus two-electrode measurement strategies for cell growing and differentiation monitoring using electrical impedance spectroscopy. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2006, 2006, 2106–2109. [Google Scholar] [CrossRef] [PubMed]
- BS EN 60601-1:2006; Medical Electrical Equipment—General Requirements for Safety. British Standards Institution: London, UK, 2006. Available online: https://www.boutique.afnor.org/en-gb/standard/bs-en-6060112006-a132024/medical-electrical-equipment-general-requirements-for-safety/eu186785/421996 (accessed on 12 September 2025).
- Sheingold, D.H. Impedance and admittance transformation using operational amplifiers. Light. Empiricist 1964, 12, 1–8. Available online: http://www.philbrickarchive.org/1964-1_v12_no1_the_lightning_empiricist.htm (accessed on 11 October 2025).
- Ghorbani, R.; Nahvi, M. Analysis of performance of Howland AC current source for electrical impedance spectro-tomography. Sens. Imaging 2019, 20, 28. [Google Scholar] [CrossRef]
- Mahnam, A.; Yazdanian, H.; Mosayebi Samani, M. Comprehensive study of Howland circuit with non-ideal components to design high performance current pumps. Measurement 2016, 82, 94–104. [Google Scholar] [CrossRef]
- Schalenbach, M.; Durmus, Y.E.; Tempel, H.; Kungl, H.; Eichel, R.-A. Double layer capacitances analysed with impedance spectroscopy and cyclic voltammetry: Validity and limits of the constant phase element parameterization. Phys. Chem. Chem. Phys. 2021, 23, 21097–21105. [Google Scholar] [CrossRef] [PubMed]
- Roy, J.; Poulichet, P.; Rousseau, L.; Rezgui, A.; Français, O. Bioimpedance measurement device based on an active terminated current source and a four-point measurement technique. Measurement 2024, 236, 115108. [Google Scholar] [CrossRef]
- Analog Devices. AD8132. Available online: https://www.analog.com/en/products/ad8132.html (accessed on 24 September 2025).
- Pettinato, S.; Piccardi, A.; Rossi, M.C.; Salvatori, S. Design, implementation, and characterization of a compact lock-in add-on for low-frequency impedance measurements. Electronics 2023, 12, 3406. [Google Scholar] [CrossRef]
- Salvatori, S. Gain-selectable IC yields voltage-to-current converter. EDN Eur. 2015, 7, 30–32. Available online: https://www.edn.com/gain-selectable-ic-yields-voltage-to-current-converter (accessed on 11 October 2025).
- Pettinato, S.; Orsini, A.; Salvatori, S. Compact current reference circuits with low temperature drift and high compliance voltage. Sensors 2020, 20, 4180. [Google Scholar] [CrossRef]
- Salvatori, S.; Rossi, M.C.; Girolami, M. High-precision voltage-to-current converters based on single-chip gain-selectable amplifiers. Analog. Integr. Circuits Signal Process. 2019, 99, 491–495. [Google Scholar] [CrossRef]
- Analog Devices. LT1995. Available online: https://www.analog.com/en/products/lt1995.html (accessed on 24 September 2025).
- Nusev, G.; Gaberšček, M.; Boškoski, P. Fast impedance measurement of Li-ion battery using discrete random binary excitation and wavelet transform. IEEE Access 2021, 9, 46152–46165. [Google Scholar] [CrossRef]
- de Beer, C.; Barendse, P.S.; Pillay, P. Fuel cell condition monitoring using optimized broadband impedance spectroscopy. IEEE Trans. Ind. Electron. 2015, 62, 5306–5316. [Google Scholar] [CrossRef]
- Sanchez, B.; Rojas, C.R.; Vandersteen, G.; Bragos, R.; Schoukens, J. Basics of broadband impedance spectroscopy measurements using periodic excitations. Meas. Sci. Technol. 2012, 23, 105501. [Google Scholar] [CrossRef]
- Al-Ali, A.; Elwakil, A.; Maundy, B.; Majzoub, S. Fast sub-Hz potentiostatic/galvanostatic bio-impedance measurements using chaotic oscillators. Biomed. Microdevices 2022, 24, 39. [Google Scholar] [CrossRef]
- Li, H.; Li, Z.; Zhang, B.; Wang, F.; Tan, N.; Halang, W.A. Design of analogue chaotic PWM for EMI suppression. IEEE Trans. Electromagn. Compat. 2010, 52, 1001–1007. [Google Scholar] [CrossRef]
- Maundy, B.J.; Elwakil, A.S.; Gift, S.J.G. Enhancing the improved Howland circuit. Int. J. Circuit Theory Appl. 2019, 47, 532–541. [Google Scholar] [CrossRef]
- Scandurra, G.; Arena, A.; Cardillo, E.; Giusi, G.; Ciofi, C. Portable and highly versatile impedance meter for very low frequency measurements. Appl. Sci. 2021, 11, 8234. [Google Scholar] [CrossRef]
- Ciofi, C.; Scandurra, G.; Giusi, G. QLSA: A software library for spectral estimation in low-frequency noise measurement applications. Fluct. Noise Lett. 2019, 18, 1940004. [Google Scholar] [CrossRef]
- Wu, J.; Bai, W.; Zhang, L.; Zhang, X.; Lin, H.; Dai, H.; Liu, J.; Zhang, F.; Yang, Y. Design of a portable electrochemical impedance spectroscopy measurement system based on AD5941 for lithium-ion batteries. J. Energy Storage 2024, 84, 110856. [Google Scholar] [CrossRef]
- Analog Devices. AD5941. Available online: https://www.analog.com/en/products/ad5941.html (accessed on 24 September 2025).
- Analog Devices. AD830. Available online: https://www.analog.com/en/products/ad830.html (accessed on 24 September 2025).
- Analog Devices. AD8066. Available online: https://www.analog.com/en/products/ad8066.html (accessed on 24 September 2025).
- Cordesses, L. Direct digital synthesis: A tool for periodic wave generation (part 1). IEEE Signal Process. Mag. 2004, 21, 50–54. [Google Scholar] [CrossRef]
- Cordesses, L. Direct digital synthesis: A tool for periodic wave generation (part 2). IEEE Signal Process. Mag. 2004, 21, 110–112. [Google Scholar] [CrossRef]
- Faktorová, D.; Kuba, M.; Pavlíková, S.; Fabo, P. Implementation of the impedance spectroscopy using a modern microcontroller. Procedia Struct. Integr. 2023, 43, 288–293. [Google Scholar] [CrossRef]
- Piasecki, T.; Chabowski, K.; Nitsch, K. Design, calibration and tests of versatile low frequency impedance analyser based on ARM microcontroller. Measurement 2016, 91, 155–161. [Google Scholar] [CrossRef]
- Hedayatipour, A.; Aslanzadeh, S.; Hesari, S.H.; Haque, M.A.; McFarlane, N. A wearable CMOS impedance to frequency sensing system for non-invasive impedance measurements. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 1108–1121. [Google Scholar] [CrossRef] [PubMed]
- Allegri, D.; Donida, A.; Malcovati, P.; Barrettino, D. CMOS-based multifrequency impedance analyzer for biomedical applications. Proc. IEEE Int. Symp. Circuits Syst. 2018, 2018, 1–5. [Google Scholar] [CrossRef]
- Venz, A.; Duckert, B.; Lagae, L.; Takalloo, S.E.; Braeken, D. Impedance mapping with high-density microelectrode array chips reveals dynamic heterogeneity of in vitro epithelial barriers. Sci. Rep. 2025, 15, 1592. [Google Scholar] [CrossRef]
- da Silva, P.D.; Bertemes Filho, P. Switched CMOS current source compared to enhanced Howland circuit for bio-impedance applications. J. Electr. Bioimpedance 2024, 15, 145–153. [Google Scholar] [CrossRef]
- Viswam, V.; Bounik, R.; Shadmani, A.; Dragas, J.; Urwyler, C.; Boos, J.A.; Obien, M.E.J.; Muller, J.; Chen, Y.; Hierlemann, A. Impedance spectroscopy and electrophysiological imaging of cells with a high-density CMOS microelectrode array system. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 1356–1368. [Google Scholar] [CrossRef]
- Dragas, J.; Viswam, V.; Shadmani, A.; Chen, Y.; Bounik, R.; Stettler, A.; Radivojevic, M.; Geissler, S.; Obien, M.E.J.; Muller, J.; et al. In vitro multi-functional microelectrode array featuring 59,760 electrodes, 2048 electrophysiology channels, stimulation, impedance measurement, and neurotransmitter detection channels. IEEE J. Solid-State Circuits 2017, 52, 1576–1590. [Google Scholar] [CrossRef] [PubMed]
- McCormack, A.S.; Flower, J.O.; Godfrey, K.R. The suppression of drift and transient effects for frequency-domain identification. IEEE Trans. Instrum. Meas. 2022, 43, 232–237. [Google Scholar] [CrossRef]
- Messing, M.; Shoa, T.; Habibi, S. Electrochemical impedance spectroscopy with practical rest-times for battery management applications. IEEE Access 2021, 9, 66989–66998. [Google Scholar] [CrossRef]
- Drvarič Talian, S.; Kapun, G.; Moškon, J.; Dominko, R.; Gaberšček, M. Operando impedance spectroscopy with combined dynamic measurements and overvoltage analysis in lithium metal batteries. Nat. Commun. 2025, 16, 2030. [Google Scholar] [CrossRef] [PubMed]
- Diard, J.P.; Petrescu, B. Méthode de compensation de dérive lors d’une mesure d’impédance électrochimique. Matér. Tech. 2007, 95, 427–433. Available online: https://www.biologic.net/documents/eis-non-stationarity-electrochemistry-battery-corrosion-application-note-17/ (accessed on 26 September 2025). [CrossRef]
- Kasper, M.; Leike, A.; Thielmann, J.; Winkler, C.; R-Smith, N.A.Z.; Kienberger, F. Electrochemical impedance spectroscopy error analysis and round robin on dummy cells and lithium-ion-batteries. J. Power Sources 2022, 536, 231407. [Google Scholar] [CrossRef]
- Hallemans, N.; Widanage, W.D.; Zhu, X.; Moharana, S.; Rashid, M.; Hubin, A.; Lataire, J. Operando electrochemical impedance spectroscopy and its application to commercial Li-ion batteries. J. Power Sources 2022, 547, 232005. [Google Scholar] [CrossRef]





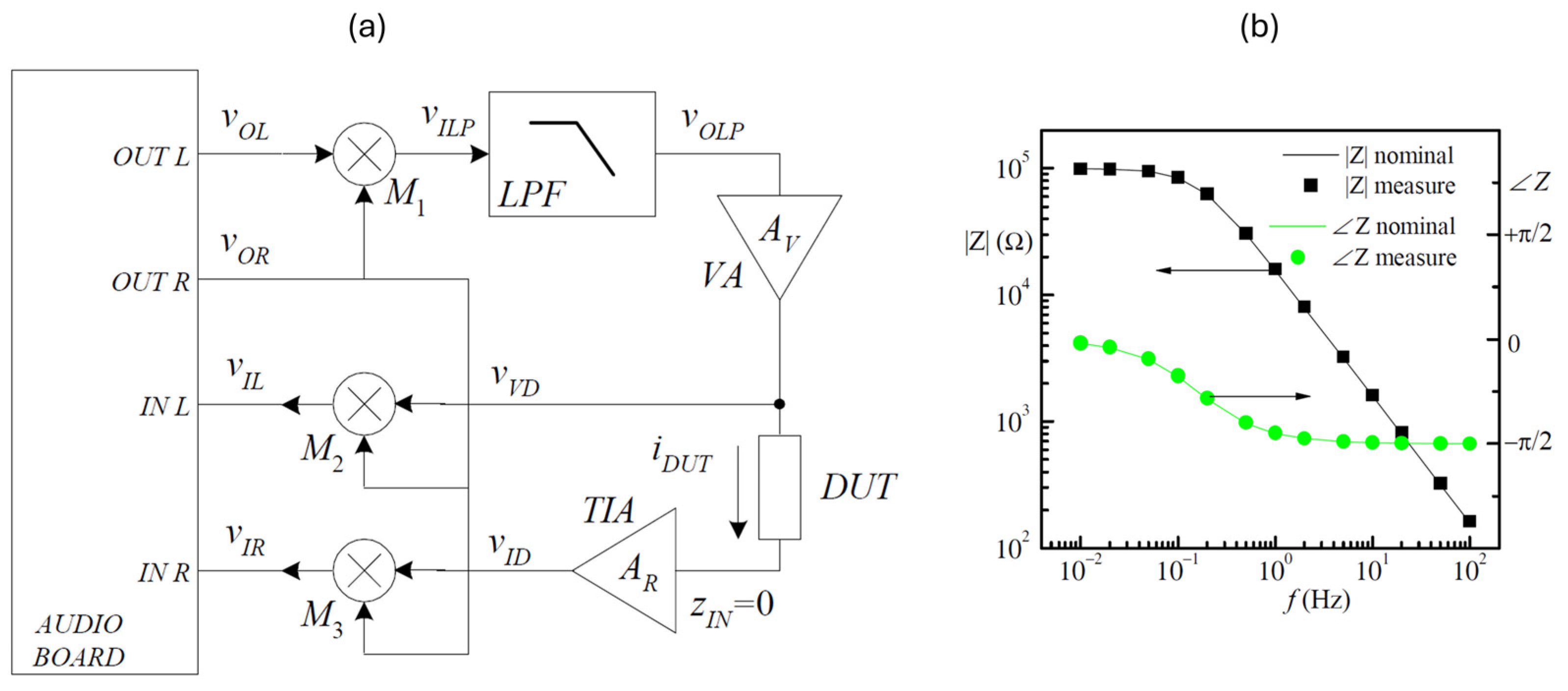


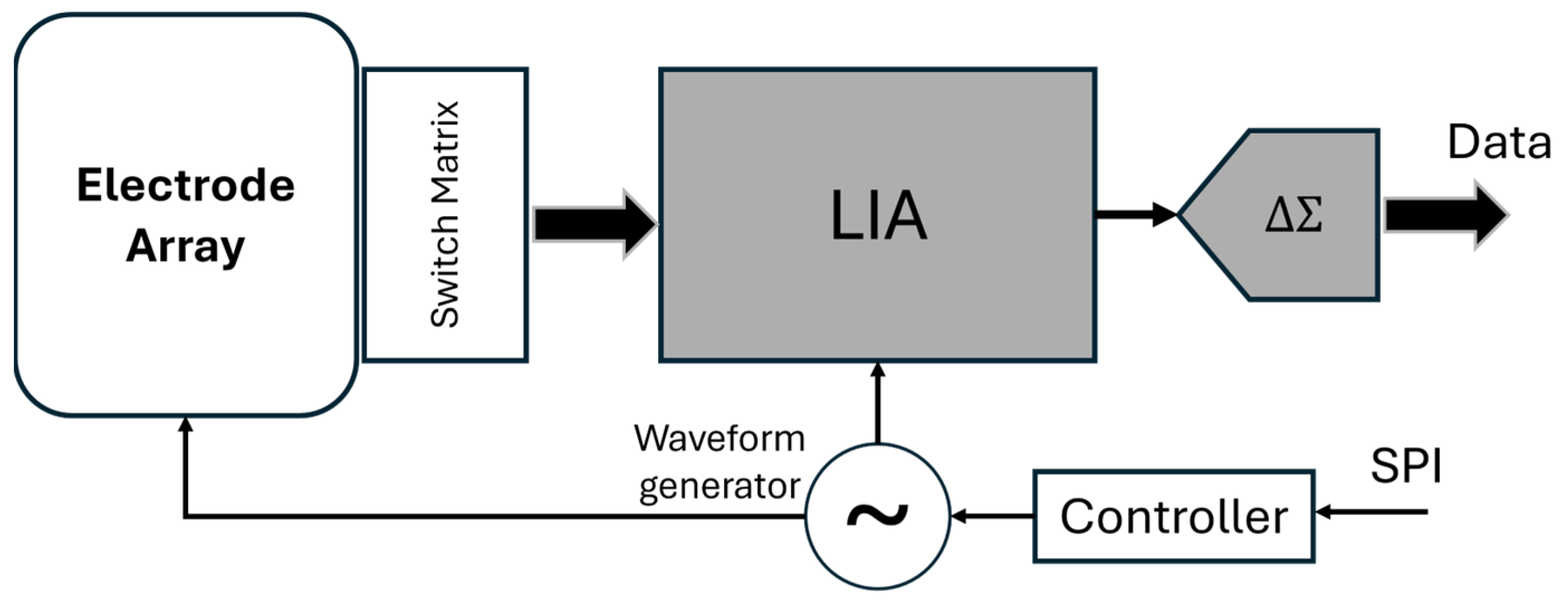
| Reference | Frequency Range [Hz] | Measured Range [Ω] | Accuracy [%] | Portability |
|---|---|---|---|---|
| [65] | 10−3 ÷ 107 | 100 ÷ 106 | 1 | High |
| [67] | 10−3 ÷ 106 | 102 ÷ 108 | n.r. | Medium |
| [75] | 10−2 ÷ 100 | 103 ÷ 104 | 1.6 | High |
| [78] | 10−2 ÷ 102 | 102 ÷ 105 | n.r. | Low |
| [80] | 10−1 ÷ 103 | 103 ÷ 104 | 2.8 | High |
| [87] | 10−1 ÷ 105 | 10−1 ÷ 109 | 0.1–3 | High |
| [92] | 10−3 ÷ 108 | 10−1 ÷ 109 | 0.1–10 | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piccardi, A.; Pettinato, S.; Rossi, M.C.; Girolami, M.; Salvatori, S. Low-Frequency Measurements in Electrochemical Impedance Spectroscopy: A Brief Review. Electronics 2025, 14, 4048. https://doi.org/10.3390/electronics14204048
Piccardi A, Pettinato S, Rossi MC, Girolami M, Salvatori S. Low-Frequency Measurements in Electrochemical Impedance Spectroscopy: A Brief Review. Electronics. 2025; 14(20):4048. https://doi.org/10.3390/electronics14204048
Chicago/Turabian StylePiccardi, Armando, Sara Pettinato, Maria Cristina Rossi, Marco Girolami, and Stefano Salvatori. 2025. "Low-Frequency Measurements in Electrochemical Impedance Spectroscopy: A Brief Review" Electronics 14, no. 20: 4048. https://doi.org/10.3390/electronics14204048
APA StylePiccardi, A., Pettinato, S., Rossi, M. C., Girolami, M., & Salvatori, S. (2025). Low-Frequency Measurements in Electrochemical Impedance Spectroscopy: A Brief Review. Electronics, 14(20), 4048. https://doi.org/10.3390/electronics14204048








