A Novel Analog-Computing-in-Memory Architecture with Scalable Multi-Bit MAC Operations and Flexible Weight Organization for DNN Acceleration

Abstract

Deep neural networks (DNNs) require efficient hardware accelerators due to the high cost of vector–matrix multiplication operations. Computing-in-memory (CIM) architectures address this challenge by performing computations directly within memory arrays, reducing data movement and improving energy efficiency. This paper introduces a novel analog-domain CIM architecture that enables flexible organization of weights across both rows and columns of the CIM array. A pipelining scheme is also proposed to decouple the multiply-and-accumulate and analog-to-digital conversion operations, thereby enhancing throughput. The proposed architecture is compared with existing approaches in terms of latency, area, energy consumption, and utilization. The comparison emphasizes architectural principles while deliberately avoiding implementation-specific details.

1. Introduction

Rapid growth of artificial intelligence has led to the widespread use of DNNs in applications such as natural language processing and autonomous driving. These applications require complex DNN models and intensive computational operations. As models grow, communication between memory and processing units becomes a significant bottleneck, known as the memory wall. This results in high latency and excessive energy consumption, especially in edge computing, where power efficiency is critical.

Traditional solutions, such as hierarchical cache designs and advanced memory technologies, have struggled to meet the growing demands for memory bandwidth. To address this challenge, CIM technology, also known as in-memory computing (IMC), has emerged as a promising alternative. CIM integrates computation directly within memory units, reducing the need for frequent data transfers between memory and processing elements. These units consist of an array of memory elements, such as SRAM cells. This integration not only boosts computational speed but also enhances energy efficiency and increases compute density. A comprehensive survey on CIM processors is presented in [1], while an overview of in-memory computing circuits for artificial intelligence and machine learning applications is provided in [2].

Several types of CIM architectures exist, including SRAM-based, DRAM-based, and non-volatile memory-based (NVM-based). SRAM-based CIMs are widely adopted due to their reliability and well-established technology. A recent survey on SRAM-based CIM designs is available in [3]. DRAM-based CIMs provide large memory capacities, making them suitable for large-scale models, though they face challenges related to high-density integration [2]. NVM-based CIMs, known for their low power consumption, are particularly well-suited for energy-efficient edge computing [4]. A review on resistive NVM-based CIMs is presented in [5]. An overview of analog architectures for CIMs and their mapping to actual DNNs is presented in [6].

A frequently used operation in DNNs is the MAC. The MAC operation is defined as multiplying each of the R inputs $X_i$ by the corresponding weight $W_i$, and then summing these products to obtain ${\sum }_{i=0}^{R-1}{W}_i·X_i$. The input $X_i$ and weight $W_i$ are represented by M-bit and N-bit precision, respectively. The MAC operation in CIM can be performed in analog, digital, or time domains [1]. Although analog-CIM architectures efficiently perform MAC operations, they require ADCs to convert the analog signals into the digital domain [7,8]. This conversion constitutes a significant portion of the overall energy consumption of the CIM [4]. Several techniques have been proposed to reduce the number of ADC conversions [9,10,11,12,13,14]. All of these studies store the bits of a weight $W_i$ in successive columns of the memory array. Thus, a weight $W_i$ occupies N columns of the memory array. For instance, a 4-bit weight occupies four columns of the memory array.

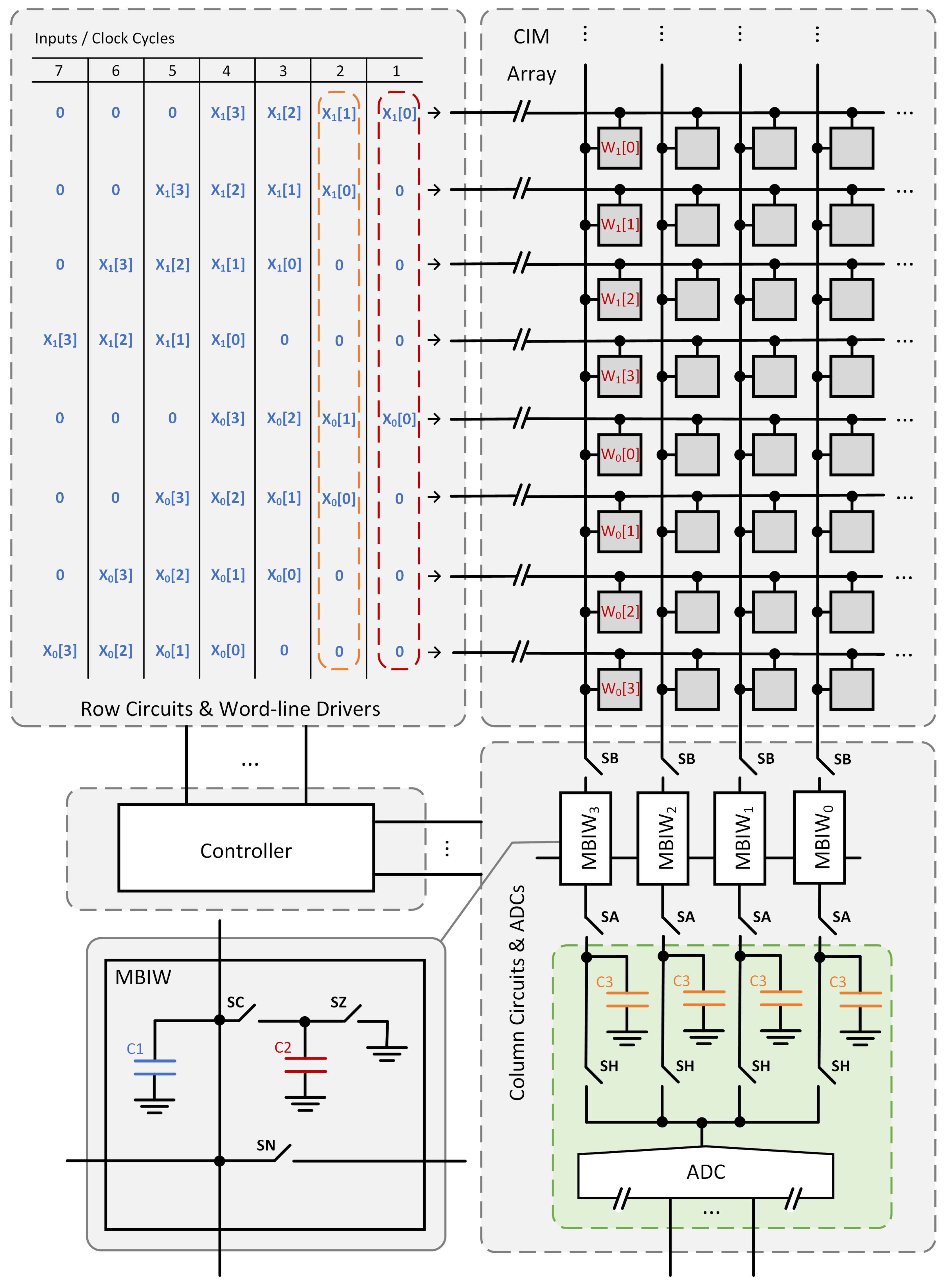
This paper introduces a novel analog-CIM architecture that allows weights $W_i$ to be flexibly organized across both the rows and columns of the CIM array. Although the architecture is general and compatible with all memory-based CIMs, the primary focus of this work is on SRAM-based implementations. Despite the flexibility of the proposed approach, a single ADC operation remains sufficient to digitize the MAC result. In addition, a pipelining scheme is introduced to decouple the analog-domain MAC and ADC operations, thereby reducing the cycle time. Finally, the proposed architecture is evaluated against existing approaches in terms of latency, area, energy consumption, and utilization, with the analysis centered on architectural principles rather than implementation-specific details.

The paper is organized as follows. Section 2 provides a detailed review of available architectures. The proposed architecture is presented in Section 3. Section 4 compares it with previous work. The contributions of the work are discussed in Section 5.

2. Related Work

The MAC operation is defined as multiplying each of the R inputs $X_i$ by the corresponding weight $W_i$, and then summing these products to obtain ${\sum }_{i=0}^{R-1}{W}_i·X_i$. An input $X_i$ is an M-bit vector: $X_i={\sum }_{m=0}^{M-1}{2}^m·X_i\left[m\right]$, where $X_i\left[m\right]\in \{0,1\}$ is the m-th bit of $X_i$. The weight $W_i$ is an N-bit vector: $W_i={\sum }_{n=0}^{N-1}{2}^n·W_i\left[n\right]$, where $W_i\left[n\right]\in \{0,1\}$ is the n-th bit of $W_i$. Analog-CIM architectures are efficient in performing MAC operations. However, they require ADCs to convert the analog signals into the digital domain [7,8].

Analog-to-digital conversion constitutes a significant portion of the overall energy consumption in CIM systems [4]. Researchers have addressed this challenge either by developing more energy-efficient ADCs or by reducing the number of ADC operations. The use of hybrid ADC structures has been shown to improve both area and energy efficiency, as reported in [15]. Although the primary focus of this paper is not on ADC design, the hybrid ADC proposed in [15] is noteworthy. This design integrates a resistor-DAC with a SAR ADC, achieving significant hardware savings compared to conventional SAR and flash ADCs. Specifically, the number of capacitors and comparators is reduced by 87.5% and 93.3%, respectively. The CIM architecture proposed in this work does not mandate a specific type of ADC, and the hybrid ADC described in [15] can be readily adopted to improve overall efficiency.

Several studies have aimed to reduce the energy consumption of ADCs by decreasing the number of conversions required. In [9,10], multi-bit weights are mapped to adjacent columns of the CIM, and the corresponding results are combined in the analog domain using binary-weighted capacitors. The architectures presented in [11,12,13] also employ binary-weighted capacitors but process 2 or 4 bits of the input $X_i$ per cycle. More recently, ref. [14] reported a CIM architecture in which sequential charge sharing between adjacent columns replaces the use of binary-weighted capacitors. Furthermore, a phase-change memory-based analog CIM was proposed in [16], which requires sequential activation of the word-lines, while an RRAM-based CIM was introduced in [17], where the weights $W_i$ are repeated and shifted.

In the remainder of this section, prior architectures are reviewed under three categories: bit-serial scheme, binary-weighted capacitor scheme, and sequential-halving scheme.

2.1. Bit-Serial Scheme

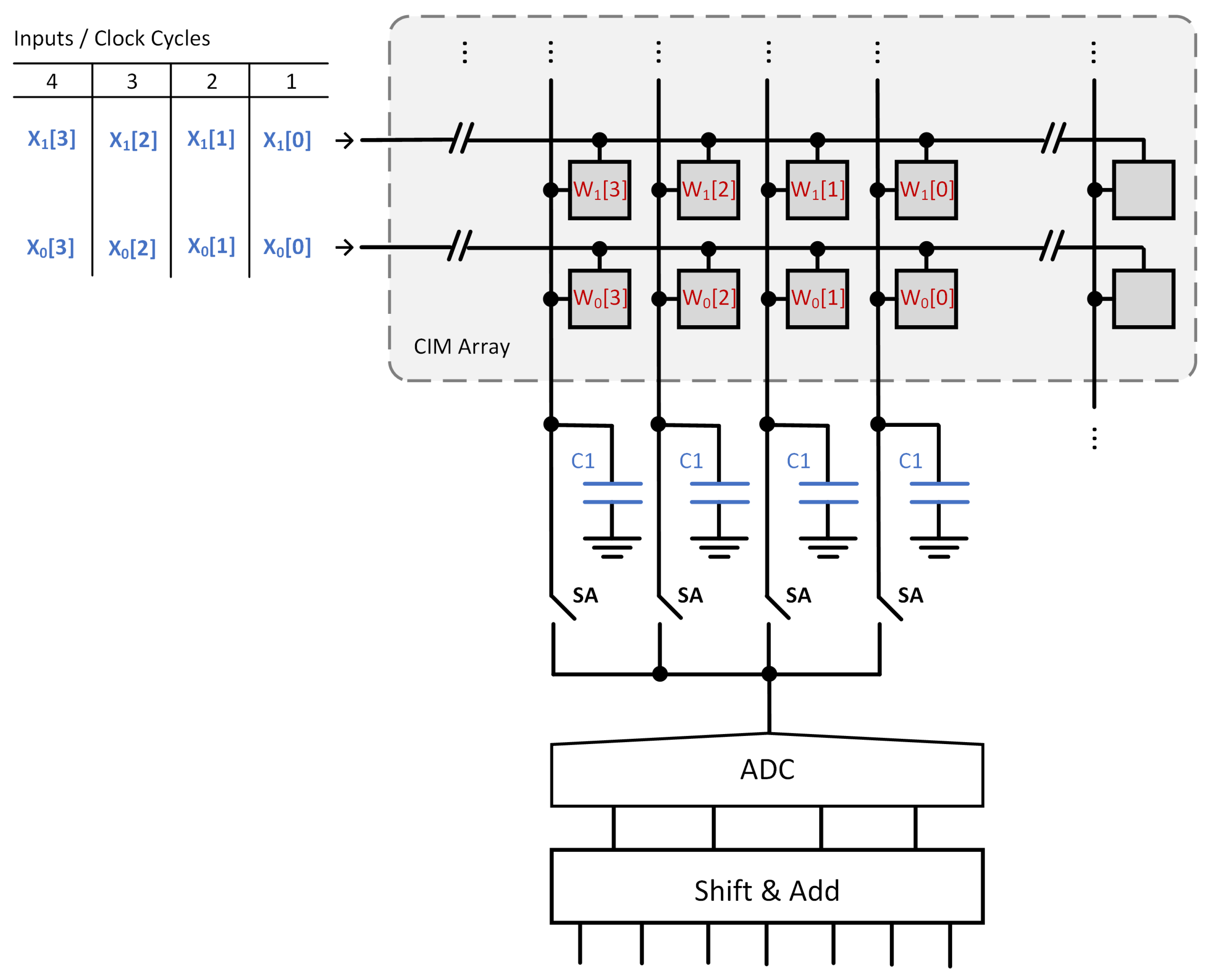
The simplest analog-CIM architecture is based on bit-serial architecture [7]. The input $X_i$s are applied to the rows of the CIM array, one bit at a time, starting from the LSB. Figure 1 shows a schematic of a simplified bit-serial architecture for $M=4$. In this figure, the CIM array has 4-bit weights ($N=4$). The entire structure is referred to as the CIM macro, while the section inside the dashed rectangle is the CIM array.

The operating principle of the architecture is explained using the schematic in Figure 1. The capacitors are first discharged to ground. In the actual implementation, the bit lines are initially pre-charged and then discharged. However, to facilitate a clearer and more straightforward explanation, it is assumed that the bit lines are first discharged to ground and subsequently charged. This simplification is consistently applied to the descriptions of other architectures discussed in this section. When the LSB $X_i\left[0\right]$s are applied, a potential proportional to ${\sum }_{i=0}^{R-1}{W}_i\left[n\right]·X_i\left[0\right]$ appears on the bit-line capacitors. The ADC then digitizes the potentials stored on the capacitors. The capacitors are then discharged, and the next bits, $X_i\left[1\right]$s, are applied. The new potentials on the capacitors are proportional to ${\sum }_{i=0}^{R-1}{W}_i\left[n\right]·X_i\left[1\right]$. After ADC conversion, the new results are shifted and accumulated with the previous ones. This yields ${\sum }_{i=0}^{R-1}{W}_i\left[n\right]·(2^1·X_i\left[1\right]+X_i\left[0\right])$. Repeating this procedure for all input bits results in ${\sum }_{i=0}^{R-1}{W}_i\left[n\right]·X_i$. The partial results, one for each bit of the weight $W_i\left[n\right]$, are then shifted and accumulated to obtain the MAC result ${\sum }_{i=0}^{R-1}{W}_i·X_i$. There are several studies utilizing the bit-serial architecture. The survey in [1] provides a detailed discussion about these. A recent study [8] presents a highly efficient implementation that exploits temporal and spatial input correlations to reduce power consumption.

2.2. Binary-Weighted Capacitors Scheme

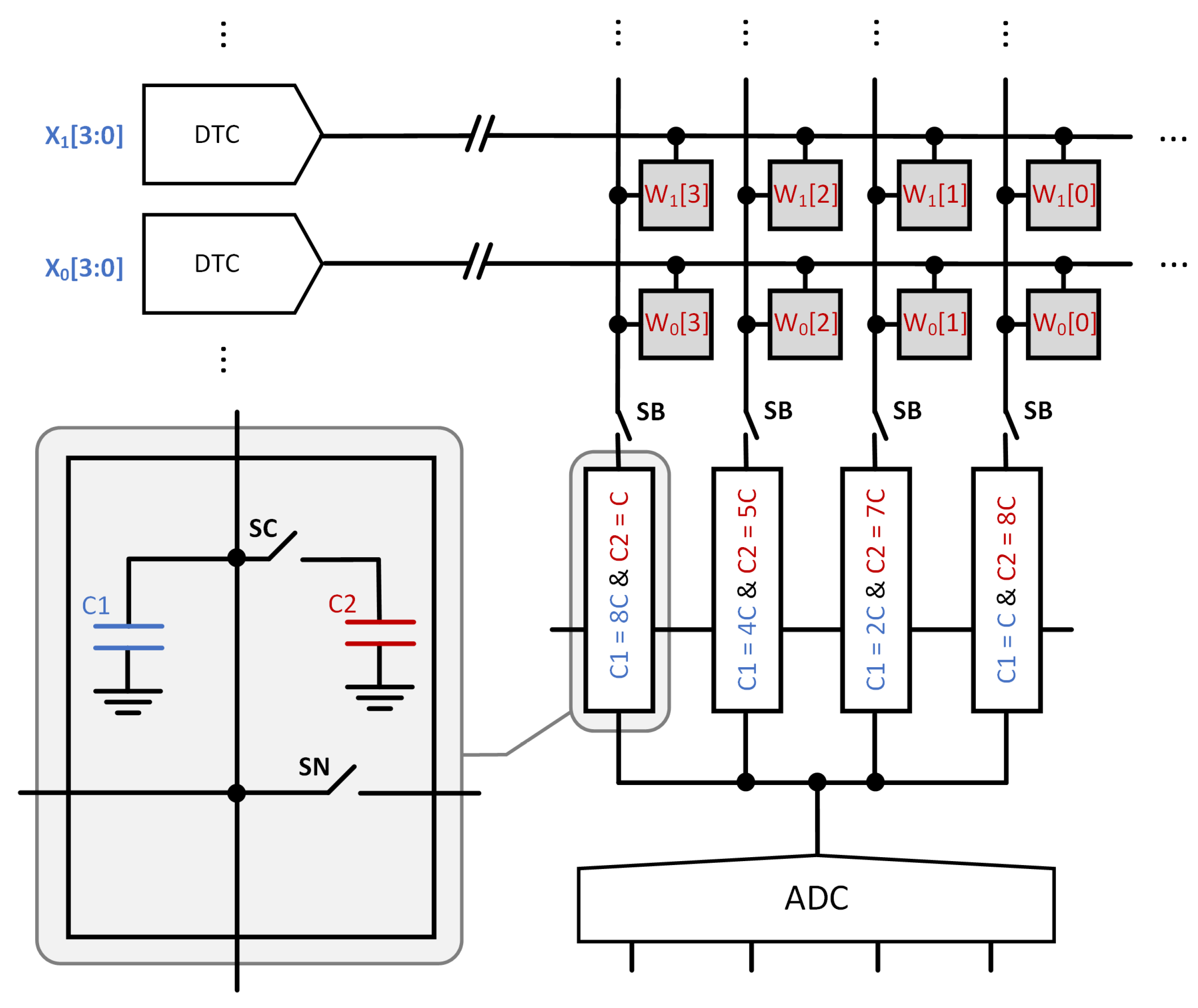
A novel analog-CIM architecture is presented in [10]. The architecture supports $M=4$-bit inputs and $N=4$-bit weights. A simplified schematic of the architecture is shown in Figure 2. The rows of the CIM array are driven by a digital-to-time converter (DTC). An input $X_i$ is encoded as a sequence of ${\sum }_{m=0}^3{2}^m\times X_i\left[m\right]$ pulses. For example, if $X_i=1010$, the DTC generates 10 pulses. These charge the bit lines proportional to the value of $X_i$, enabling MAC computation through charge accumulation.

In Figure 2, each weight $W_i$ is stored across four successive columns in a row, with each bit $W_i\left[n\right]$ occupying a single column. The pulses generated by the DTC enable the multiplication of the input $X_i$ with each bit $W_i\left[n\right]$, resulting in partial products of the form $W_i\left[n\right]·X_i$. The resulting charges are initially accumulated on a capacitor network with a total capacitance of $9C$. Since all rows are activated simultaneously, the total potential change on the capacitors becomes proportional to the sum of partial products across all inputs as ${\sum }_{i=0}^{R-1}{W}_i\left[n\right]·X_i$, where R denotes the number of rows. Next, the $C_2$ capacitors and the bit-lines are disconnected from the $C_1$ capacitors. Thus, the product corresponding to $W_i\left[3\right]$ is stored in the $C_1$ capacitor with capacitance $8C$, while those corresponding to $W_i\left[2\right]$, $W_i\left[1\right]$, and $W_i\left[0\right]$ are stored in the $C_1$ capacitors with capacitances of $4C$, $2C$, and C, respectively. Then, all $C_1$ capacitors are shorted together. This way, the circuit performs the full analog computation ${\sum }_{i=0}^{R-1}{W}_i·X_i$. Finally, 4-bit flash ADC converts the resulting voltage into a digital value.

A similar CIM architecture was presented in [9]. This circuit also supports $M=4$-bit inputs and $N=4$-bit weights and uses binary-weighted capacitors. The authors introduced enhancements to the word-line drivers, which deliver the pulses generated by the DTC to the rows of the CIM array. Both circuits in [9,10] are designed for 4-bit weights and are not suitable for scaling in the analog domain, as they rely on binary-weighted capacitors. The architectures in [11,12] support MAC operations for $M=2$-bit inputs and $N=4$-bit weights in the analog domain. Similar to [10], they utilize a binary-weighted capacitor network. For inputs with more than 2 bits, the designs perform successive computations and combine the results using a digital shift-and-accumulate circuit. Likewise, for 8-bit weights, the circuits in [11] execute two 4-bit computations and reconstruct the final result in the digital domain. These designs also leverage input sparsity to reduce power consumption.

In [13], the design processes $M=4$-bit inputs simultaneously and supports $N=2$-bit and $N=4$-bit weights. It uses binary-weighted capacitors to perform analog accumulation. The prototype chip, fabricated in 28 nm technology, is reported to achieve a peak 1-bit energy efficiency of 8161 TOPS/W and compute density of 112 TOPS/mm². It demonstrates high accuracy on complex DNN benchmarks, achieving 92.34% on CIFAR-10 and 69.88% on ImageNet classification.

2.3. Sequential Halving Scheme

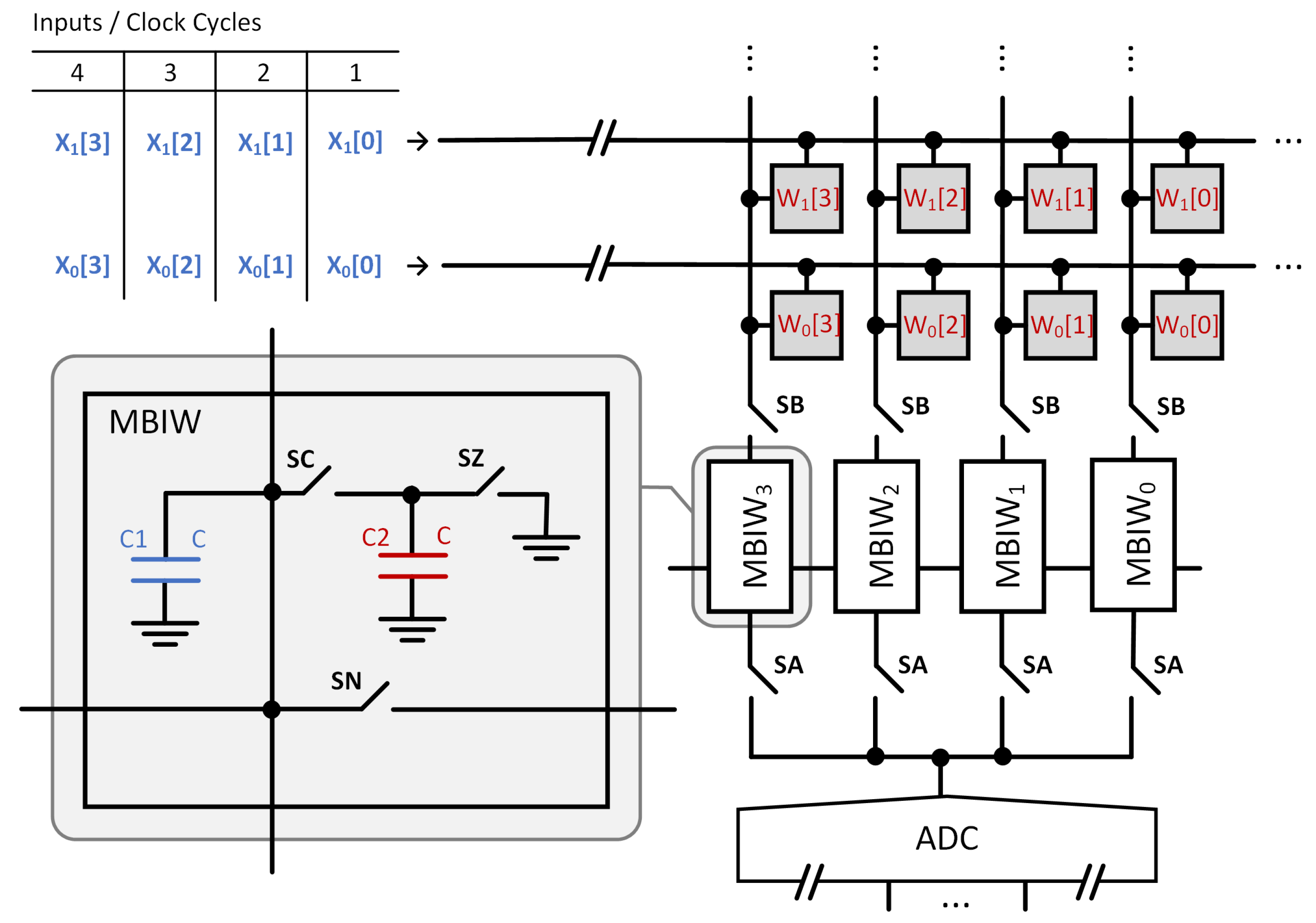
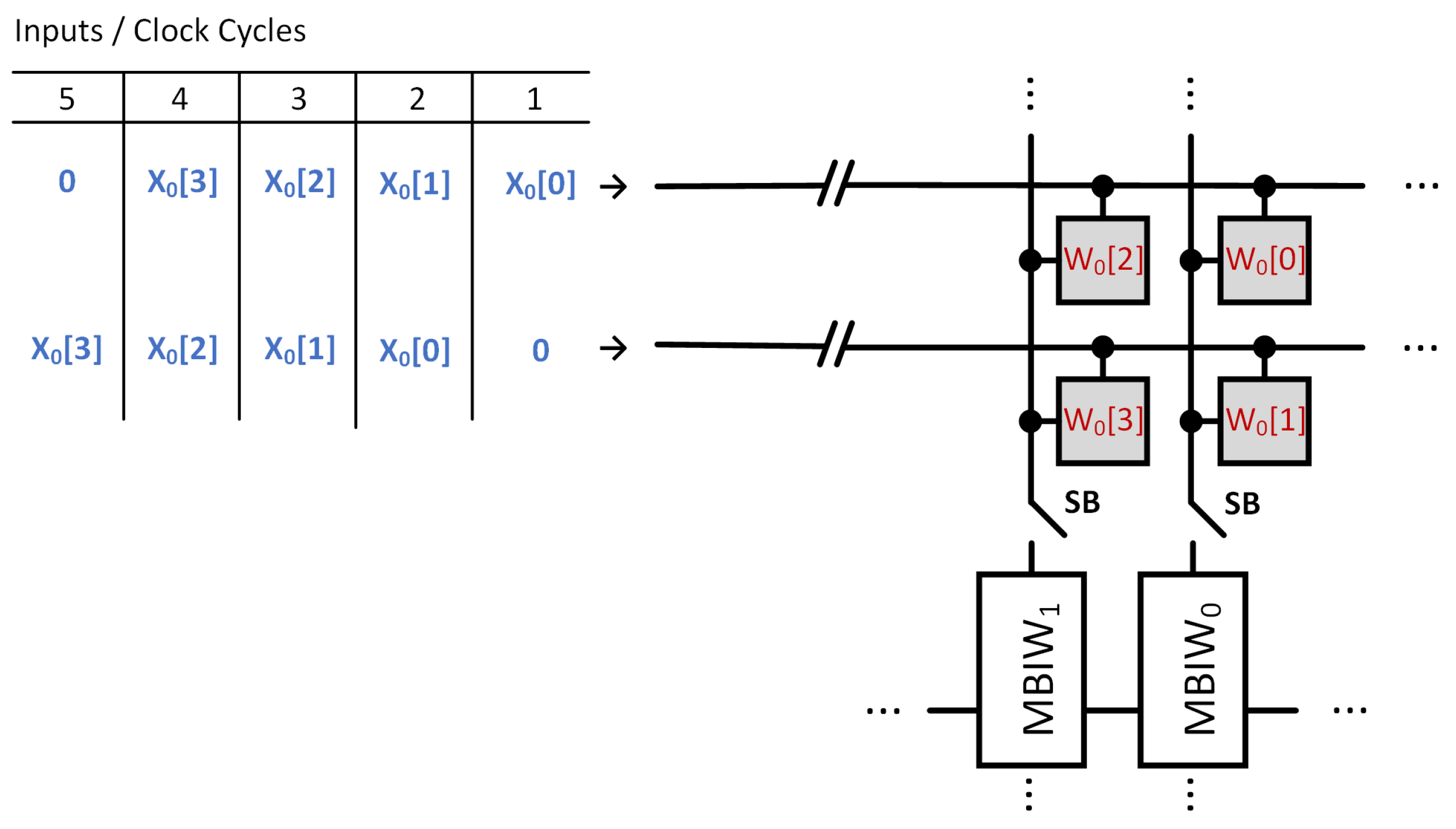
Recently, a new analog-CIM architecture was presented in [14]. This circuit supports $M=8$-bit inputs and $N=4$-bit weights. A simplified schematic of the circuit for the $M=4$-bit input version is shown in Figure 3. The columns of the CIM array are connected to multi-bit input-and-weight (MBIW) circuits, which include two equally sized capacitors, $C_1$ and $C_2$, as illustrated in Figure 3.

The circuit in Figure 3 operates as follows. First, the LSBs of the inputs $X_i\left[0\right]$ are fed into the CIM array. The resulting charges are stored on the $C_1$ capacitors in the MBIWs, while the $C_2$ capacitors are grounded. This sets the potential on each $C_1$ proportional to ${\sum }_{i=0}^{R-1}{W}_i\left[n\right]·X_i\left[0\right]$, where $W_i$ is the weight in the $i\mathrm{th}$ row and n is the bit index. Next, the $C_1$ capacitors are disconnected via SB switches. The $C_1$ capacitors are then connected to the $C_2$ capacitors in the same MBIWs. This causes charge redistribution. As a result, the initial potentials on the $C_1$ capacitors are halved. Now, the potentials on the $C_1$ and $C_2$ capacitors in the same MBIW are equal. After this charge sharing, the $C_2$ capacitors are disconnected. And its potential is proportional to ${\sum }_{i=0}^{R-1}\frac{1}{2}·(W_i\left[n\right]·X_i\left[0\right])$. Then, the SB is closed and the bit-lines are discharged. Next, the second input bits $X_i\left[1\right]$ are applied. After that, the $C_1$ and $C_2$ capacitors are connected. The resulting potential on $C_2$ is now proportional to ${\sum }_{i=0}^{R-1}{W}_i\left[n\right]·\left(\frac{1}{2}·X_i\left[1\right]+\frac{1}{4}·X_i\left[0\right]\right)$. This process is repeated for the remaining bits of $X_i$. After all bits are processed, the final potential on each $C_1$ capacitor becomes proportional to the binary-weighted sum ${\sum }_{i=0}^{R-1}{W}_i\left[n\right]·X_i$. Note that the result is normalized such that the smallest coefficient equals 1. This normalization preserves proportionality and will be consistently applied in the subsequent descriptions.

The operation above results in four separate sums, one for each bit index n of the weights. These sums need to be weighted and added. First, the potential on the $C_1$ capacitor in ${\mathrm{MBIW}}_0$ is halved. This is performed by grounding $C_2$, then reconnecting it to $C_1$. After this step, the potential on $C_1$ in ${\mathrm{MBIW}}_0$ becomes proportional to $\frac{1}{2}{\sum }_{i=0}^{R-1}{W}_i\left[0\right]·X_i$. Then, ${\mathrm{MBIW}}_0$ and ${\mathrm{MBIW}}_1$ are shorted via the switch connecting them. After charge redistribution, the switch is opened. The resulting potential on $C_1$ in ${\mathrm{MBIW}}_1$ will be proportional to ${\sum }_{i=0}^{R-1}(\frac{1}{2}·W_i\left[1\right]+\frac{1}{4}·W_i\left[0\right])·X_i$. This procedure continues for the remaining MBIWs. After completing all steps, the final potential on the $C_1$ capacitor in ${\mathrm{MBIW}}_3$ becomes proportional to ${\sum }_{i=0}^{R-1}{W}_i·X_i$. Finally, an ADC converts the resulting voltage to a digital value.

3. The Proposed CIM Architecture

The bit-serial, binary-weighted capacitor, and sequential-halving schemes discussed in Section 2 store the weights in successive columns of the CIM array. However, these architectures lack flexibility in weight organization. In contrast, the proposed architecture allows flexible placement of weights $W_i$ across both rows and columns of the CIM array. Despite its flexibility, only a single ADC operation is required to digitize each MAC result. A pipelining scheme is further introduced to decouple the analog MAC from ADC operations, thereby reducing the overall cycle time. An overall view of the CIM macro is shown in Figure 4. In this section, the operating principles and implementation details for different weight organizations are discussed. The circuit used to generate the word-line pulses and the pipelining scheme are also presented.

3.1. Operating Principals

To explain the operational principles of the proposed architecture, the partial products in $W_i·X_i=\left({\sum }_{n=0}^{N-1}{2}^n{W}_i\left[n\right]\right)\left({\sum }_{m=0}^{M-1}{2}^m{X}_i\left[m\right]\right)$ are first analyzed. The bit-wise expansion of $W_i·X_i$ for $M=4$-bit inputs and $N=4$-bit weights is given in Equation (1). The partial products with identical coefficients are then grouped together.

$$\begin{array}{ccccccccc}\hfill W_i·X_i& =\hfill & \hfill 2^6·(W_i\left[3\right]·X_i\left[3\right]& \hfill & & \hfill & & & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em})\\ \hfill & +\hfill & \hfill 2^5·(W_i\left[3\right]·X_i\left[2\right]& \hfill +& W_i\left[2\right]·X_i\left[3\right]\hfill & \hfill & & & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em})\\ \hfill & +\hfill & \hfill 2^4·(W_i\left[3\right]·X_i\left[1\right]& \hfill +& W_i\left[2\right]·X_i\left[2\right]\hfill & \hfill +& W_i\left[1\right]·X_i\left[3\right]\hfill & & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em})\hfill \\ \hfill & +\hfill & \hfill 2^3·(W_i\left[3\right]·X_i\left[0\right]& \hfill +& W_i\left[2\right]·X_i\left[1\right]\hfill & \hfill +& W_i\left[1\right]·X_i\left[2\right]\hfill & +& W_i\left[0\right]·X_i\left[3\right])\\ \hfill & +\hfill & 2^2·(\hfill & & W_i\left[2\right]·X_i\left[0\right]\hfill & \hfill +& W_i\left[1\right]·X_i\left[1\right]\hfill & +& W_i\left[0\right]·X_i\left[2\right])\\ \hfill & +\hfill & 2^1·(\hfill & & & & W_i\left[1\right]·X_i\left[0\right]\hfill & +& W_i\left[0\right]·X_i\left[1\right])\\ \hfill & +\hfill & 2^0·(\hfill & & & & \hfill & & W_i\left[0\right]·X_i\left[0\right])\end{array}$$

(1)

The proposed analog-CIM architecture performs this multiplication in sequential steps. It first computes the term in the parentheses with the coefficient $2^0$ and stores it on a capacitor. In the next step, the term with coefficient $2^1$ is computed, scaled by two, and added to the stored value. This process continues for all remaining terms until the full result is accumulated.

3.2. The Proposed Architecture

The proposed CIM architecture is explained with reference to Figure 4. In this figure, the weights for the $N=4$ case are stored vertically in a $4\times 1$ configuration within a single column. It should be noted that the proposed analog-CIM architecture enables flexible placement of weights $W_i$ across both rows and columns of the CIM array. The operation of the circuit for the single-column case is explained below. Other scenarios will be discussed afterward.

Initially, the SB and SZ switches in the MBIW network are closed, discharging the red $C_2$ capacitor. First, the LSBs of the inputs $X_i\left[0\right]$, highlighted in the red dashed rectangle in the figure, are fed into the rows containing the $W_i\left[0\right]$. The corresponding partial products $W_i\left[0\right]·X_i\left[0\right]$ are summed on the $C_1$ capacitor. Then, the result is divided by two. The division is performed by opening the SB switches and closing the SC switches. After charge redistribution between the $C_1$ and $C_2$ capacitors is complete, the switches are returned to their initial positions. The bit-lines and the $C_1$ are discharged. Next, the inputs $X_i\left[0\right]$ and $X_i\left[1\right]$, shown in the orange dashed rectangle in the figure, are fed into the rows containing $W_i\left[1\right]$ and $W_i\left[0\right]$, respectively. This adds the partial products $W_i\left[1\right]·X_i\left[0\right]+W_i\left[0\right]·X_i\left[1\right]$ onto the $C_1$ capacitor. Opening the SB switches and closing the SC switches starts charge sharing between the $C_1$ and $C_2$ capacitors. After charge sharing, the potential on the $C_1$ capacitor becomes proportional to

$$\sum _{i=0}^{R-1}\left(2^1·(W_i\left[1\right]·X_i\left[0\right]+W_i\left[0\right]·X_i\left[1\right])+2^0·(W_i\left[0\right]·X_i\left[0\right])\right)$$

(2)

Here, R represents the number of weights stored in the rows. Repeating this procedure for the remaining bits leads to the sum of the expression in Equation (1) for $i\in \{0,\dots ,R-1\}$. The sum can be written as ${\sum }_{i=0}^{R-1}{W}_i·X_i$, which matches the expected MAC result.

3.3. Flexible Weight Distribution

The proposed architecture also supports weights that occupy a single row. In this case, the circuit operates in the same manner as that in [14]. In addition to mapping weights to a single row or column, weights can also be distributed across both rows and columns. For example, $N=4$-bit weights can be arranged in the MAC array in a $2\times 2$ configuration, as shown in Figure 5. For this case, the procedure for the MAC operation on the columns is similar to that of the $4\times 1$ configuration but applied to the $2\times 1$ arrangement. The results for each column are stored in the $C_1$ capacitors. After column processing, the potential stored on the $C_1$ capacitor of ${\mathrm{MBIW}}_0$ is proportional to the expression given in Equation (3).

$$\begin{array}{cc}\hfill \sum _{i=0}^{R-1}& (2^4·(W_i\left[1\right]·X_i\left[3\right])\hfill \\ \hfill & +2^3·(W_i\left[1\right]·X_i\left[2\right]+W_i\left[0\right]·X_i\left[3\right])\hfill \\ \hfill & +2^2·(W_i\left[1\right]·X_i\left[1\right]+W_i\left[0\right]·X_i\left[2\right])\hfill \\ \hfill & +2^1·(W_i\left[1\right]·X_i\left[0\right]+W_i\left[0\right]·X_i\left[1\right])\hfill \\ \hfill & +2^0·(W_i\left[0\right]·X_i\left[0\right]))\hfill \end{array}$$

(3)

Similarly, the potential on the $C_1$ capacitor of ${\mathrm{MBIW}}_1$ is proportional to Equation (3), with $W_i\left[0\right]$ replaced by $W_i\left[2\right]$ and $W_i\left[1\right]$ replaced by $W_i\left[3\right]$. The potentials on the $C_1$ capacitors must be combined to obtain the desired MAC result in Equation (1). To do so, the $C_1$ potential in ${\mathrm{MBIW}}_0$ is scaled by $1/4$. This potential is halved twice via charge sharing with the $C_2$ capacitor in the same MBIW. Prior to each charge-sharing step, the $C_2$ capacitor is discharged to ground via the SZ switch. Finally, the potential on the $C_1$ of ${\mathrm{MBIW}}_1$ is combined with the scaled potential on the $C_1$ of ${\mathrm{MBIW}}_0$. This combination is achieved by charge sharing through the SN switch, which connects the two capacitors. Although the charge sharing halves the resulting potential, the proportionality is preserved.

The concept can be generalized so that a weight is organized in an array of size $r\times c$. If the weight precision N is not a multiple of r, the weights can be zero-padded on the right to make N a multiple of r. Before adding results from successive columns, the potential of the less significant column must be scaled by $1/2^r$. This process allows weights $W_i$ to be flexibly distributed across both the rows and columns of the CIM array. The advantages of this approach are discussed in Section 4.

Although the proposed approach supports weights organized in an array of size $r\times c$, it does not support assigning different precisions to different inputs. The macro can be programmed for a specific weight precision, but this configuration applies uniformly to all inputs. Input-wise precision is therefore not supported. Moreover, the macro lacks a mechanism to exploit sparsity in the weights.

3.4. Generation of Word-Line Pulses

If the weights are organized in r rows, then the inputs need to be delayed and repeated across each set of r rows. For example, in the case of $r=2$ shown in Figure 5, the input to the second row is identical to that of the first row but delayed by one cycle. Thus, in the proposed circuit, the driver inputs cannot be directly connected to the input buffer. Instead, the required delay is introduced by a programmable delay circuit. A block diagram of the corresponding circuit and a detailed view of the programmable delay circuit are shown in Figure 6. The drivers in the figure are connected to the word-lines. Compared to a standard RAM, the proposed approach requires, in addition to the input buffer, one extra multiplexer, latch, and D flip-flop per row.

The latches are pre-configured depending on the weight organization $r\times c$. For instance, in the case shown in Figure 5, Latch 1 in Figure 6 stores a one, while Latch 2 stores a zero. Thus, the first row receives the direct input from the buffer, while the second row receives its delayed version. Because the latches are pre-configured, the select bits of the multiplexer are also predetermined. Thus, the only additional delay introduced by this architecture is the input-to-output propagation delay of the multiplexer. The DFF’s clock-to-Q delay introduces no additional latency, as it is already accounted for in that of the input buffer. To prevent glitches on the word-lines, a common practice in memory design is to use a word-line trigger signal to gate the outputs of the row decoder before they reach the drivers. This ensures that the inputs from the input buffer arrive at the row decoder while the word-lines remain deactivated. The approach in [10] utilizes a DTC circuit rather than the delay circuit illustrated in Figure 6. In contrast, the approaches in [7,14] do not require any delay circuit. Figure 7 illustrates a sample word-line trigger signal (Trg) alongside the corresponding driver output (WL).

In Figure 7, $T_{on}$ denotes the time required to turn on the word-lines, during which the cells inject sufficient charge into the bit-lines. $T_{off}$ denotes the time required to completely turn off the word-lines and, accordingly, to activate/deactivate the switches discussed in Section 3.1. During this interval, the input bits from the input buffer are read and fed to the AND gates in Figure 6. Since this operation takes place concurrently within $T_{off}$, it does not introduce any additional delay.

3.5. Pipelining

When the circuit operates, potentials proportional to the desired MAC results are built on the $C_1$ capacitors in the MBIW networks. These potentials must subsequently be digitized by the ADCs. Previous approaches [7,10,14] do not utilize the memory array during ADC conversions. In this study, a pipelining scheme is introduced to decouple the MAC and ADC operations, thereby enhancing throughput. The proposed idea is not limited to the presented architecture but can also be applied to prior works [7,10,14].

Here, the operating principles of the pipelining architecture are discussed based on Figure 4. In this figure, the proposed pipelining scheme is shown in the dashed green rectangle. After charge accumulation on the $C_1$ capacitors, the SA switches are closed while the SH switches remain open. Through charge redistribution between the $C_1$ and $C_3$ capacitors, the results on $C_1$ are transferred to $C_3$. Depending on the capacitance of $C_3$ relative to $C_1$, the resulting potential is scaled. In this way, while the ADC converts the potentials on the $C_3$ capacitors, the CIM array can perform a new MAC operation.

4. Results

The proposed design is compared against the bit-serial architecture [7] and the architectures in [10,14]. The corresponding implementations for $M=4$-bit inputs and $N=4$-bit weights are shown in Figure 1, Figure 2, Figure 3 and Figure 4. The comparison focuses on architectural principles while deliberately avoiding implementation-specific details. To this end, an event-based simulator was developed. The simulator, available at https://github.com/ahmetunu/flexible-CIM (accessed on 1 October 2025), reports statistics for latency, area, energy consumption, and hardware utilization. For example, it records the number of bit-line charging operations and ADC activations. These outputs are technology-independent, ensuring fair comparison. This methodology avoids cross-technology bias. The proposed architecture and the previous ones are modeled in this simulator. To verify the correctness of these models, the ADC outputs produced by the macros are validated with the results obtained by directly multiplying the input vector with the weight matrix.

The objective of this study is twofold: (i) to introduce an architecture that enables flexible placement of weights across the rows and columns of the CIM array, and (ii) to propose a pipelining scheme. The design of a specific ADC at a specific technology node is not in the scope of this work. To ensure a fair comparison, the same ADC model is employed across all architectures, with identical reference potentials applied. Thus, any noise introduced by ADC operation affects all designs equally, provided that the same input and reference potentials are used. Since ADC noise depends on its type, resolution, and implementation, using a common ADC ensures that it does not introduce bias into the comparison.

For all designs, the word-line drivers and memory arrays are identical. Likewise, the duration of the word-line pulses and the amount of charge injected by the cells are identical. The capacitor sizes are chosen such that they yield the same potential for $M=8$-bit inputs and $N=8$-bit weights. To determine the required total capacitance for the proposed architecture and the previous ones [7,10,14], the maximum potential built on the $C_1$ capacitor is adjusted to be the same. For this purpose, the CIM arrays are filled with ones, and the inputs are also set to ones, yielding the maximum potential on the capacitors.

Table 1. Comparison of the total required capacitance.

	Bit-Serial [7]	Binary Weights [10]	Binary Weights [10]	Seq. Halving [14]	This Work
Maximum Input Precision (M)	8	4	8	8	8
Normalized Total Capacitance	0.5	7.5	135	1	1

lists the normalized total required capacitance for the proposed architecture and the previous designs [7,10,14]. Bit-line capacitors, which are identical across all designs, are excluded. To give the reader an idea of the order of magnitude, the proposed macro is implemented in 22 nm technology. The required capacitance for each column of the CIM array is 500 fF.

The proposed architecture requires twice the capacitance of the bit-serial design and the same amount as [14]. The concept presented in [10] can be extended to $M=4$-bit and $M=8$-bit inputs. In this case, increasing M exponentially raises the number of word-line pulses, and the capacitors must be scaled accordingly to maintain the same ADC reference. Even the $M=4$-bit implementation requires significantly more capacitance than the other designs. This demonstrates that [10] does not scale well with input precision.

The analyses are performed for a CIM array of size $256\times 64$ with $N=8$-bit weights and $M=8$-bit inputs. Based on the architectures in [7,10,14], macros are simulated for the same input and weight precision. These designs can perform eight independent ${\sum }_{i=0}^{255}{W}_i·X_i$ operations at a time. If 16 independent ${\sum }_{i=0}^{127}{W}_i·X_i$ operations are required on the same macro, they must be operated twice. However, the proposed architecture can execute both 8 independent ${\sum }_{i=0}^{255}{W}_i·X_i$ and 16 independent ${\sum }_{i=0}^{127}{W}_i·X_i$ operations within a single macro operation, owing to its flexible weight organization capability. The required number of macro operations for different scenarios is listed in

Table 2. Number of macro operations required.

	Bit-Serial [7]	Binary Weights [10]	Seq. Halving [14]	This Work $(\mathit{r}\times \mathit{c})$
8 Independent ${\sum }_{i=0}^{255}{W}_i·X_i$	1	1	1	1 $(1\times 8)$
16 Independent ${\sum }_{i=0}^{127}{W}_i·X_i$	2	2	2	1 $(2\times 4)$
32 Independent ${\sum }_{i=0}^{63}{W}_i·X_i$	4	4	4	1 $(4\times 2)$
64 Independent ${\sum }_{i=0}^{31}{W}_i·X_i$	8	8	8	1 $(8\times 1)$

for the proposed architecture and the designs in [7,10,14]. For the proposed architecture, the weight organization $(r\times c)$ is also provided in the table.

As shown in Table 1, the proposed architecture requires the same total capacitance as that reported in [14]. The primary architectural distinction between the two is the inclusion of a programmable delay circuit, described in Section 3.4. When the weights are organized in the $1\times 8$ configuration, this delay circuit acts as a buffer, resulting in operation equivalent to that of [14], as summarized in Table 2. The operation of the proposed architecture diverges when the weights are not arranged horizontally across columns. In such cases, the delay circuit adjusts the input timing accordingly, and a different control sequence is applied to the switches, as detailed in Section 3.2 and Section 3.3. Consequently, all results obtained for the $1\times 8$ configuration are also applicable to the architecture in [14].

For the $1\times 8$ configuration, the latency of the proposed architecture is identical to that of [14]. A detailed latency comparison between the proposed design and those in [7,10] is presented in Section 4.1. The total area of the proposed architecture and that of [14] are also very similar, as discussed in Section 4.2, which further includes comparisons with [7,10]. When the weights are organized in the $1\times 8$ configuration, the energy consumption of the proposed design closely matches that of [14], differing by only 0.4 pJ for a 22 nm implementation. Section 4.3 provides a detailed energy comparison with [7,10,14]. The pipelining scheme described in Section 3.5 is general and can be applied not only to the proposed approach but also to the architectures in [7,10,14]. In Section 4.4, the memory utilization of the proposed and prior architectures is compared, while Section 4.5 reports the performance of the proposed design on the VGG16 network trained on the CIFAR-10 dataset. Finally, the practical limitations of the proposed architecture are discussed in Section 4.6.

4.1. Latency

The macro begins operation with a bit-line pre-charge phase. Next, pulses are applied to the word-line drivers. The number of pulses varies depending on the architecture and is reported in

Table 3. Critical path comparison among designs to perform eight independent ${\sum }_{i=0}^{255}{W}_i·X_i$ operations.

	Bit-Serial [7]	Binary Weights [10]	Sequential Halving [14]	This Work (1 × 8)
#Word-line Pulses	8	255	8	8
#SB Switch Activations	N/A	0	8	8
#SC Switch Activations	N/A	1	9	9
#SZ Switch Activations	N/A	N/A	1	1
#SN Switch Activations	N/A	1	7	7
#SA Switch Activations	64	N/A	1	1
#Bit-line Pre-charges	8	1	8	8
#ADC Operations	64	1	1	1
#Intra-column Shift and Add	7	N/A	N/A	N/A
#Inter-column Shift and Add	1	N/A	N/A	N/A

. These pulses activate the word-line drivers, which in turn activate the memory cells. The activated cells charge the bit-lines and the capacitors connected to them. The design in [10] charges both the $C_1$ and $C_2$ capacitors, whereas the proposed design and those in [7,14] charge only the $C_1$ capacitors, as discussed in Section 2. Next, the word-lines are turned off. Then, depending on the architecture, the switches SC, SZ, SN, SB, and SA are activated, and, finally, the bit-lines are pre-charged again. When SC is closed to redistribute the charge between the $C_1$ and $C_2$ capacitors, sufficient time must elapse for the capacitors to reach steady state. 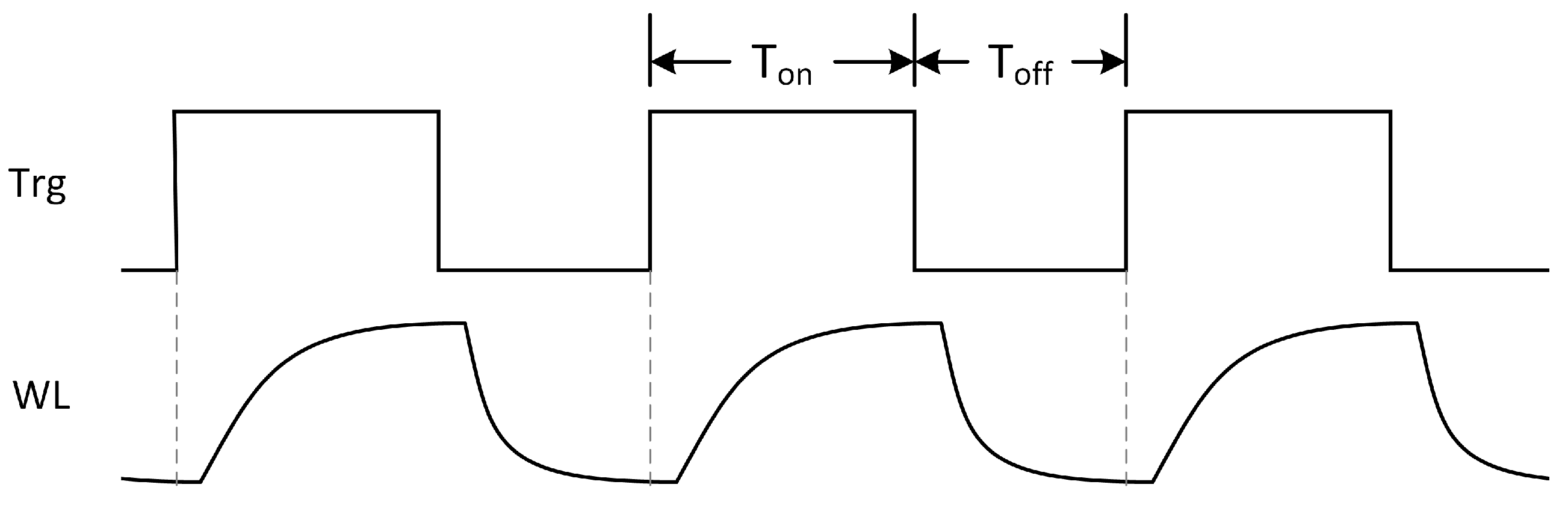Similarly, when SZ is closed, a discharge interval is required for the $C_2$ capacitor. When SN is closed, a time interval is required for charge sharing between neighboring capacitors. To illustrate the duration of the control signals, the proposed macro is simulated in SPICE with 22 nm transistor models. The resulting control signals are shown in Figure 8. The ADC is not simulated, and its selection is left to the system designer.

Switching activities along the critical path are reported for two cases: (i) 8 independent ${\sum }_{i=0}^{255}{W}_i·X_i$ operations (Table 3) and (ii) 64 independent ${\sum }_{i=0}^{31}{W}_i·X_i$ operations (

Table 4. Critical path comparison among designs to perform 64 independent ${\sum }_{i=0}^{31}{W}_i·X_i$ operations.

	Bit-Serial [7]	Binary Weights [10]	Sequential Halving [14]	This Work (8 × 1)
#Word-line Pulses	64	2040	64	15
#SB Switch Activations	N/A	0	64	15
#SC Switch Activations	N/A	8	72	16
#SZ Switch Activations	N/A	N/A	8	1
#SN Switch Activations	N/A	8	56	0
#SA Switch Activations	512	N/A	8	8
#Bit-line Pre-charges	64	8	64	15
#ADC Operations	512	8	8	8
#Intra-column Shift and Add	56	N/A	N/A	N/A
#Inter-column Shift and Add	8	N/A	N/A	N/A

). If an architecture cannot perform all the sums at once, it is executed the necessary number of times to complete the operations.

Some switches are not present in all architectures. The reader is referred to Figure 1, Figure 2, Figure 3 and Figure 4 for architectural details. The inputs and weights are sampled from a uniform distribution. Assuming there are eight ADCs in the design (one ADC per eight columns), the number of ADC activations in the critical path is also reported in these tables. The bit-serial design requires intra-column and inter-column digital shift-and-add operations.

Table 3 reports the critical paths for the case of eight independent ${\sum }_{i=0}^{255}{W}_i·X_i$ operations. The latency of the bit-serial architecture is dominated by the required number of ADC operations, whereas the performance of the architecture proposed in [10] is limited by the number of required word-line pulses. The proposed architecture and the one in [14] exhibit same performance.

Table 4 reports the critical paths for the case of 64 independent ${\sum }_{i=0}^{31}{W}_i·X_i$ operations. Previous approaches [7,10,14] can perform only eight independent MAC operations in a single run. As a result, they utilize only 32 of the 256 available rows in the memory array. In contrast, the proposed architecture can flexibly distribute the weights across both columns and rows, allowing it to perform 64 independent MAC operations in a single run. The latency of the bit-serial architecture is dominated by ADC operations, while that of the architecture in [10] is dominated by word-line pulses. The proposed architecture requires fewer switching activities and achieves lower latency than the design in [14]. The exact performance improvement depends on the implementation details and the technology node used.

The critical paths discussed in this section exclude the pipelining scheme presented in Section 3.5. Pipelining is most effective when the delays of the memory array and the ADC are comparable. In the bit-serial architecture, latency is dominated by ADC operations, whereas in [10], it is dominated by word-line pulses. Therefore, pipelining has little impact on the overall latency of these architectures. In contrast, pipelining is beneficial for both the proposed architecture and the design presented in [14]. For the latter, the effect of pipelining is identical to that in the proposed work when the weights are organized in a $1\times 8$ configuration. The impact of pipelining on the proposed architecture is summarized in

Table 5. Latency reduction compared to design w/o pipelining (%).

	ADC Latency/Memory Latency
$r\times c$	$1/8$	$1/4$	$1/2$	$1$	$2$	$4$	$8$
$1\times 8$	50	50	50	50	33	20	11
$2\times 4$	50	50	50	33	20	11	6
$4\times 2$	50	50	33	20	11	6	3
$8\times 1$	50	33	20	11	6	3	2

.

In Table 5, the latency reduction achieved by applying pipelining is reported relative to that without pipelining. Since the latencies of the ADC and memory depend on their respective implementations, the results are provided for different ratios of ADC latency to memory latency. As shown in Table 5, the proposed approach shows a smaller benefit from pipelining as the value of r increases.

4.2. Area

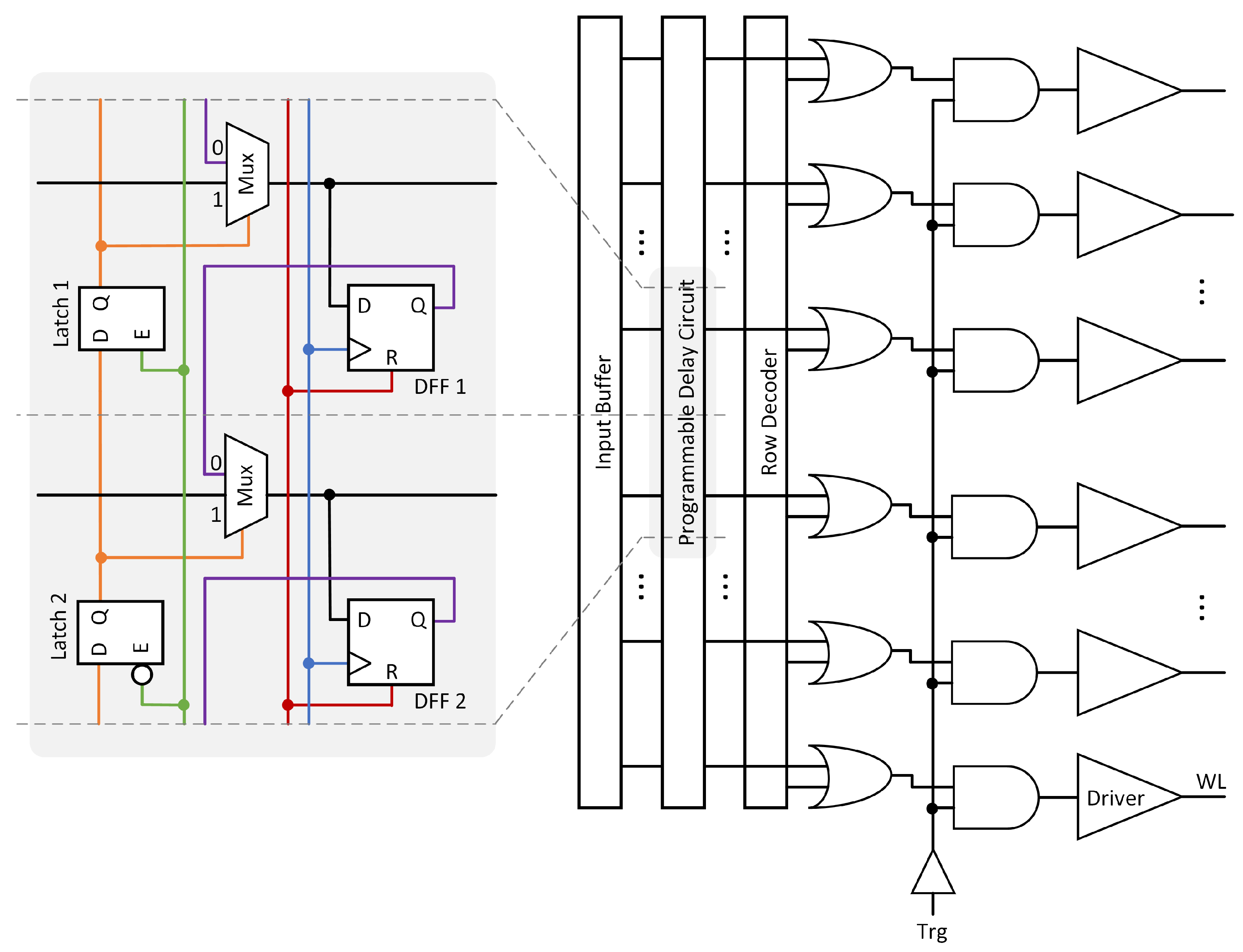
A CIM macro consists of the row circuit, cell array, column circuit, and control logic. A schematic of the row circuitry is shown in Figure 6, which includes the input buffer, row decoder, basic gates, and word-line drivers. Identical input buffers are used in both the proposed architecture and the previous designs [7,10,14], resulting in equivalent buffer areas. Likewise, the sizes of the word-line drivers and the cell arrays are the same across all architectures. The timing signals and control for the switches are generated by the control logic. Unlike the row or column circuitry, the control logic does not have a periodic structure and occupies only a small portion of the CIM macro. The area difference of the control logic circuits represents a negligible fraction of the total CIM macro and is therefore not analyzed in this study. The designs in [7,14] do not require the delay circuit shown in Figure 6. In contrast, the proposed architecture requires a programmable delay circuit comprising a latch, a D flip-flop, and a multiplexer for each row. The architecture in [10] utilizes a down counter per row rather than the delay circuit.

The column circuit contains the necessary capacitors, switches, and ADCs, as shown in Figure 1, Figure 2, Figure 3 and Figure 4.

Table 6. Number of components in the column circuit.

	Bit-Serial [7]	Binary Weights [10]	Sequential Halving [14]	This Work
Normalized Capacitor Area	0.5	135	1	1
#SB Switches	N/A	64	64	64
#SC Switches	N/A	64	64	64
#SZ Switches	N/A	N/A	64	64
#SN Switches	N/A	56	64	64
#Intra-column Shift and Add	64	N/A	N/A	N/A
#Inter-column Shift and Add	8	N/A	N/A	N/A

lists the components of the column circuits for both the proposed and previous approaches. Each design uses eight ADCs. However, since this number is identical across all architectures, it is not included in the table. Similarly, the write circuits are identical across all architectures and are therefore not reported in the table. The bit-serial architecture additionally requires shift-and-add circuits, as reported in the table.

The bit-serial architecture requires several shift-and-add circuits. In the approach of [10], larger capacitors are required in the columns compared to the other designs. The bit-serial architecture does not include any switches, whereas switches are required in the columns of the proposed approach and those in [10,14]. The exact areas of the column circuits strictly depend on the utilized technology node. Providing exact figures is beyond the scope of this work.

To provide an estimate of the area, a schematic implementation of a $256\times 64$ macro is carried out in 22 nm technology. The required capacitance area is 3200 $\mathsf{\mu }{\mathrm{m}}^2$, assuming MIM capacitors with a capacitance density of 10 $\mathrm{fF}/\mathsf{\mu }{\mathrm{m}}^2$. The total gate area of the switches is 33 $\mathsf{\mu }{\mathrm{m}}^2$. In addition, the programmable delay circuit in Figure 6 requires an extra 8 $\mathsf{\mu }{\mathrm{m}}^2$ of gate area.

4.3. Energy Consumption

The proposed approach and the designs in [7,10,14] are compared in terms of energy consumption for two cases: (i) 8 independent ${\sum }_{i=0}^{255}{W}_i·X_i$ operations (

Table 7. Energy consumption comparison among designs to perform eight independent ${\sum }_{i=0}^{255}{W}_i·X_i$ operations.

	Bit-Serial [7]	Binary Weights [10]	Sequential Halving [14]	This Work (1 × 8)
#Word-line Driver Activities	1026	31081	1026	1026
Pre-charge Energy (Norm.)	1	30	1	1
#SB Switch Activities	N/A	128	1024	1024
#SC Switch Activities	N/A	128	1040	1040
#SZ Switch Activities	N/A	N/A	128	128
#SN Switch Activities	N/A	112	112	112
#ADC Operations	512	8	8	8
#Intra-column Shift and Add	512	N/A	N/A	N/A
#Inter-column Shift and Add	8	N/A	N/A	N/A

) and (ii) 64 independent ${\sum }_{i=0}^{31}{W}_i·X_i$ operations (

Table 8. Energy consumption comp. among designs to perform 64 independent ${\sum }_{i=0}^{31}{W}_i·X_i$ operations.

	Bit-Serial [7]	Binary Weights [10]	Sequential Halving [14]	This Work (8 × 1)
#Word-line Driver Activities	8208	248648	8208	1040
Pre-charge Energy (Norm.)	8	240	8	1
#SB Switch Activities	N/A	1024	8192	1920
#SC Switch Activities	N/A	1024	8320	2048
#SZ Switch Activities	N/A	N/A	1024	128
#SN Switch Activities	N/A	896	896	0
#ADC Operations	4096	64	64	64
#Intra-column Shift and Add	4096	N/A	N/A	N/A
#Inter-column Shift and Add	64	N/A	N/A	N/A

). Instead of reporting energy consumption for a specific implementation, the events contributing to energy consumption are listed in the tables. Normalized energy consumption for charging the $C_1$ and $C_2$ capacitors is also provided. Since the same ADC model is used for all designs, the number of ADC operations is directly proportional to their energy consumption. The number of SA switch activations is identical to the number of ADC operations and is therefore not reported in the tables. If the pipelining scheme in Section 3.5 is applied to all designs, the number of SH switch activations will likewise equal the number of ADC operations.

The bit-serial architecture requires significantly more ADC operations compared to the other approaches. In contrast, the approach in [10] turns the word-lines on and off far more frequently than the others. For the case of eight independent ${\sum }_{i=0}^{255}{W}_i·X_i$ operations, the proposed architecture and the design in [14] consume comparable amounts of energy.

The designs based on [7,10,14] can execute only eight independent MAC operations in a single run. Consequently, they utilize only 32 rows, even though the memory arrays contain 256 rows. In contrast, the proposed architecture can flexibly distribute the weights across both columns and rows, enabling it to perform 64 independent MAC operations in a single run. Owing to this flexibility, the proposed approach achieves lower energy consumption compared to the others when executing 64 independent ${\sum }_{i=0}^{31}{W}_i·X_i$ operations.

To provide an estimate of energy consumption, the proposed macro with a CIM array size of $256\times 64$ is simulated in SPICE using 22 nm transistor models. The weights are organized in a $1\times 8$ format. The energy consumed per MAC operation is 3.2 pJ for the word-line drivers and 14.3 pJ for the pre-charge circuits. The SB and SC switches consume 7.9 pJ and 8.5 pJ, respectively, while the SZ and SN switches consume 0.6 pJ and 1.3 pJ, respectively. The programmable delay circuit in Figure 6 consumes 0.4 pJ. The total energy consumption per MAC operation of the macro, excluding the ADC and the input buffer, is 46.5 pJ.

4.4. Memory Cell Utilization

Based on the operation performed in the CIM, the percentage of utilized cells in the array varies. Each CIM array contains 256 rows. If an operation requires fewer than 256 inputs, the remaining rows are unused. The proposed approach provides the flexibility to organize weights across both rows and columns, allowing higher memory utilization. For different use cases, the percentage of utilized memory cells is listed in

Table 9. Percentage of memory cells utilized.

	Bit-Serial [7]	Binary Weights [10]	Seq. Halving [14]	This Work $(\mathit{r}\times \mathit{c})$
8 Independent ${\sum }_{i=0}^{255}{W}_i·X_i$	100	100	100	100 $(1\times 8)$
16 Independent ${\sum }_{i=0}^{128}{W}_i·X_i$	50	50	50	50 $(1\times 8)$
16 Independent ${\sum }_{i=0}^{127}{W}_i·X_i$	50	50	50	100 $(2\times 4)$
20 Independent ${\sum }_{i=0}^{79}{W}_i·X_i$	26	26	26	88 $(3\times 3)$
32 Independent ${\sum }_{i=0}^{63}{W}_i·X_i$	25	25	25	100 $(4\times 2)$
33 Independent ${\sum }_{i=0}^{127}{W}_i·X_i$	41	41	41	69 $(2\times 4)$
33 Independent ${\sum }_{i=0}^{63}{W}_i·X_i$	21	21	21	52 $(4\times 2)$
64 Independent ${\sum }_{i=0}^{31}{W}_i·X_i$	12.5	12.5	12.5	100 $(8\times 1)$

.

The proposed architecture supports flexible weight orientations, whereas the other designs in Table 9 are limited to a $(1\times 8)$ orientation. As a result, the utilization achieved with the proposed architecture is always equal to or greater than that of the other architectures. As reported in the table, it is also possible to arrange $N=8$-bit weights in a $(3\times 3)$ orientation by padding with a zero on the right.

4.5. Benchmark Performance

The performance of the proposed architecture is evaluated on the VGG16 network trained on the CIFAR-10 dataset. The kernel size is $3\times 3$ for all convolution layers. Number of input channels, number of output channels, and output size are reported in

Table 10. Number of CIM macro operations.

#Input Channels	#Output Channels	Output Size	#Terms in a MAC	#MAC Ops.	#CIM (1 × 8)	#CIM (Flexible)
3	64	$32\times 32$	27	65k	8k	1k $(8\times 1)$
64	64	$32\times 32$	576	65k	24k	18k $(4\times 2)$
64	128	$16\times 16$	576	33k	12k	9k $(4\times 2)$
128	128	$16\times 16$	1152	33k	20k	18k $(2\times 4)$
128	256	$8\times 8$	1152	16k	10k	9k $(2\times 4)$
256	256	$8\times 8$	2304	16k	18k	18k $(1\times 8)$
256	256	$8\times 8$	2304	16k	18k	18k $(1\times 8)$
256	512	$4\times 4$	2304	8k	9k	9k $(1\times 8)$
512	512	$4\times 4$	4608	8k	18k	18k $(1\times 8)$
512	512	$4\times 4$	4608	8k	18k	18k $(1\times 8)$
512	512	$2\times 2$	4608	2k	5k	5k $(1\times 8)$
512	512	$2\times 2$	4608	2k	5k	5k $(1\times 8)$
512	512	$2\times 2$	4608	2k	5k	5k $(1\times 8)$
				Total:	172k	153k

for the convolution layers. The number of terms in each MAC operation, as well as the total number of MAC operations, is also provided. The table also reports CIM macro usage under fixed $(1\times 8)$ and flexible organizations.

As shown in Table 10, the flexibility of the proposed architecture improves the overall system performance. If the weights are restricted to the $1\times 8$ form, 172k CIM macro operations are required per image. In contrast, when the proposed architecture is utilized, the number of CIM macro operations decreases to 153k.

The proposed architecture with a CIM array size of $256\times 64$ is simulated in SPICE using 22 nm transistor models. An ADC is not implemented; however, to provide a fair comparison between fixed ($1\times 8$) and flexible weight organizations, identical 6-bit ADCs are assumed in both cases. The ADC is assumed to occupy eight columns, with a latency of 5 ns. For the fixed organization, the macro requires 2.1 ms per inference, corresponding to a throughput of 141 GOPS. The product of an $N=8$-bit weight and an $M=8$-bit input is considered as one operation when calculating the throughput. With flexible weight organization, the latency decreases to 1.9 ms per inference, resulting in a throughput of 156 GOPS. Assuming an energy dissipation of 10 pJ per ADC conversion in both cases, the fixed and flexible organizations achieve energy efficiencies of 13.6 TOPS/W and 14.7 TOPS/W, respectively. The pipelining scheme described in Section 3.5 is also applied to evaluate its impact. The clock frequency is dynamically adjusted to maximize performance in different weight organizations. With pipelining, the latency for both the fixed ($1\times 8$) and flexible organizations is reduced to 1.2 ms per inference, resulting in a throughput of 247 GOPS. Thus, pipelining yields a decrease of 43% and 37% in latency for the fixed and flexible organizations, respectively. The corresponding energy efficiencies are 13.8 TOPS/W and 14.4 TOPS/W for the fixed and flexible organizations, respectively.

4.6. Practical Concerns

Although the proposed architecture is general enough to support any precision, in practice, the achievable precision is limited by implementation quality, noise, and mismatches. To assess these limitations, the architecture is implemented in 22 nm technology with a CIM array size of $256\times 64$. The $N=8$-bit weights and $M=8$-bit inputs are sampled from a uniform distribution. The ADC is not implemented; instead, the resulting potentials are discretized assuming an ideal 8-bit ADC. The macro successfully performs the MAC operation, but with 2-bit precision loss. Therefore, for this specific implementation, even an ADC with 6-bit precision is sufficient. Moreover, mismatches of 1%, 2%, 5%, and 10% between the $C_1$ and $C_2$ capacitors in Figure 4 and Figure 5 result in precision losses of 2, 3, 4, and 5 bits, respectively. An improved implementation may achieve full 8-bit output precision. However, from a practical standpoint, achieving precision beyond 8 bits remains challenging.

The macro is tested with the VGG16 network, trained on the CIFAR-10 dataset. The baseline accuracy of the network is 93.5%. When the MAC results include 2-bit errors, the accuracy decreases only slightly to 93.4%. However, the effect of a 2-bit precision loss is more pronounced on the larger ImageNet dataset. In [18], a 2-bit precision loss at the output of CIM macros during ImageNet classification is reported to reduce accuracy by approximately 7–15%, depending on the network. In cases where there is a precision loss of 3, 4, or 5 bits due to mismatches between the $C_1$ and $C_2$ capacitors, the corresponding accuracies of the VGG16 network on the CIFAR-10 dataset become 92.6%, 85.1%, and 33.3%, respectively.

5. Discussion

This paper introduced a novel analog-CIM architecture and compared it with prior approaches in terms of latency, area, energy consumption, and utilization, with the focus placed on architectural principles rather than implementation-specific details. A key advantage of the proposed architecture is its flexibility in distributing weights across both rows and columns of the CIM array. In certain cases, this flexibility enables higher memory utilization, improved energy efficiency, and reduced latency compared to previous architectures. In addition, a pipelining mechanism was introduced, which can reduce macro latency by up to half and can also be applied to existing CIM architectures. Overall, the proposed design provides a flexible and efficient framework that addresses the limitations of prior CIM approaches while opening new opportunities for customizable, scalable, and energy-efficient computing. By utilizing the proposed approach, the number of CIM macro operations required for the VGG16 network on the CIFAR-10 dataset is reduced by more than 10%. Future work will focus on evaluating the proposed CIM macro on large-scale DNN layers. In this way, the impact of different weight organizations on system performance can be explored. These evaluations will provide deeper insights into the practical benefits of the proposed architecture in real-world deep learning workloads.