Abstract
We present a quantum-assisted data authentication protocol that integrates classical information-theoretic security with quantum communication techniques. We assume only that the participants have access to open classical and quantum channels, and share a random static key material. Building on the Wegman–Carter paradigm, our scheme employs universal hashing for message authentication and leverages quantum channels to securely transmit random nonces, eliminating the need for key recycling. The protocol utilizes polar codes within Wyner’s wiretap channel model to ensure confidentiality and reliability, even in the presence of an all-powerful adversary. Security analysis demonstrates that the protocol inherits strong guarantees from both classical and quantum frameworks, provided the quantum channel maintains low loss and noise.
1. Introduction
Data authentication—guaranteeing the integrity and origin of messages—is an indispensable primitive in modern cryptography, supporting secure communication, distributed control, and cryptographic key management. In practice, most deployed authentication mechanisms, such as block-cipher-based or hash-based MACs and digital signatures, provide only computational security: their guarantees rely on hardness assumptions and on large software stacks. By contrast, the Wegman–Carter construction [1] achieves unconditional authenticity. Its security follows from information-theoretic arguments, but at the cost of requiring new shared key material for each authenticated message [2]. This “fresh-key bottleneck” becomes a serious limitation in long-lived or high-throughput deployments.
Quantum information offers the possibility of detecting eavesdropping: any attempt to observe quantum states unavoidably disturbs them. This feature motivates quantum authentication schemes that can reuse keys as long as no disturbance is detected. Barnum et al. [3] introduced the encrypt-then-encode approach, combining a quantum one-time pad with purity-testing codes. Subsequent work developed trap-code authenticators embedding hidden qubits [4], design-based schemes with strong post-accept security [5], and efficient unitary two-design authenticators [6]. Portmann [7] and Dulek–Speelman [8] extended this line to composable settings, proving that strong purity-testing codes enable key recycling. These results demonstrate that unconditional authentication with key reuse is theoretically possible, but their reliance on quantum tags, entanglement, or unitary designs makes near-term implementation difficult.
A more practical direction keeps the authentication tag classical and employs quantum communication only to enable key reuse. The core insight, first noted by Bennett et al. [9], is that if quantum transmission reveals tampering, then keys may be safely reused when verification succeeds. Damgård et al. [10] provided the first rigorous realization using mutually unbiased bases in high dimensions, achieving near-optimal key recycling but requiring legitimate parties being equipped with quantum computers because of the nature of quantum states manipulation. Fehr and Salvail [11] reduced the quantum requirements to BB84 prepare-and-measure qubits. Their scheme transmits the plaintext and Wegman–Carter tag over the classical channel, while a hidden nonce is delivered via BB84 states. If verification succeeds, the full key may be reused; otherwise, part of the secret must be refreshed. Follow-up work improved noise tolerance by employing extended encoding [12,13] and further reduced interaction, showing that only an authenticated one-bit acknowledgement is necessary [14]. Despite these advances, authenticated feedback and occasional key renewal remain unavoidable, and dependence on robust classical authenticated channels introduces tension between quantum and classical resources [15,16].
We present a new approach to the construction of data authentication protocols that leverages both classical and quantum resources. The protocol is designed upon three fundamental pillars:
- Shannon’s security model: the authentication tag is computed using a classical Wegman–Carter construction, ensuring information-theoretic protection against forgery.
- Wyner’s wiretap model: confidentiality arises from the intrinsic errors occurring in the adversary’s channel, which limit the amount of information that can be extracted.
- Quantum communication: the use of quantum states guarantees that the assumptions underlying Wyner’s model are satisfied, since any eavesdropping attempt unavoidably introduces disturbances that can be detected.
This line of research is closely related to the work of Fehr and Salvail [11], who showed that classical authentication combined with quantum communication enables secure key recycling. Our protocol can be seen as a continuation of this direction, with the main innovation being a different technique for confidentiality provision. Instead of embedding random nonces directly into BB84 states, we construct and transmit a structured sequence of polar-coded codewords, which improves confidentiality guarantees. Recent results demonstrate wiretap-style secure transmission implemented with polar codes, both at the conceptual level and in practical optical systems [17,18], which directly motivates our use of polar-coded structures.
By combining these elements, the protocol achieves data authenticity, even in the presence of an all-powerful adversary. The net effect is the elimination of the key recycling requirement. The remainder of this paper is organized as follows. First, we review the required background on Wegman–Carter authentication, quantum communication, wiretap channels, and polar codes (Section 2). Next, the proposed authentication protocol is introduced together with the underlying security model (Section 3). Afterwards, a security analysis is presented, establishing unconditional integrity and confidentiality of the nonce (Section 4.1). The discussion then turns to practical aspects, including resource requirements and implementation feasibility (Section 4.2). Finally, this paper concludes with a summary of the main contributions and an outlook on future work (Section 5).
2. Preliminaries
2.1. Notation
We follow standard information- and coding-theoretic conventions. Random variables and random vectors are denoted by capital letters (e.g., X, Y, ), and their realizations by lowercase letters (x, y, ). For , we write and . All logarithms are base 2 unless stated otherwise. Concatenation of bit strings is written and bitwise XOR as ⊕.
A discrete memoryless channel (DMC) is with transition law and N-fold product . We use the mutual information in the usual sense. Binary symmetric and erasure channels are denoted and with flip and erasure probabilities p and q, respectively.
The protocol assumes a pre-shared secret key , known to Alice and Bob and unknown to Eve. Its components are used at different stages of the transmit chain: selects the preparation/measurement basis in the quantum physical layer; are used exclusively for the Wegman–Carter message authentication tag; and parametrizes the coding layer. Where relevant, we state explicitly which component of K is in use and whether additional fresh randomness independent of K is employed.
2.2. Wiretap Channel Model
Physical Layer Security (PLS) is a core concept in contemporary data security, focusing on confidentiality provision at the physical layer of a communication system [19]. In contrast to conventional cryptographic methods predominantly operating at higher protocol layers, PLS aims to exploit the properties of the physical communication channel to protect transmitted data. A Wiretap Channel Model (WCM), depicted in Figure 1, forms a mathematical framework to develop and analyze PLS systems.
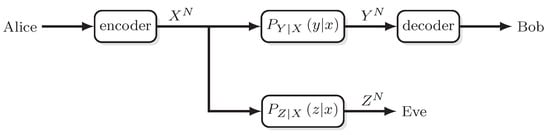
Figure 1.
Wyner model. The represents input to N independent uses of Discrete Memoryless Channel (DMC) described by the conditional probability . The adversary’s eavesdrops transmitted information via another DMC described by conditional probability .
This model assumes that the communication channel between legitimate parties (sender and receiver) introduces fewer errors than the channel available to an adversary. Exploiting this distinction facilitates the achievement of confidential communication. Key contributions from Wyner [20] and Csiszar and Körner [21] emphasize that Alice can employ a Forward Error Code (FEC) to achieve reliable transmission of confidential messages at rate
where optimization is taken over random variables forming a Markov chain in that order. Here, denotes mutual information, is referred to as the secrecy capacity, , , are random variables describing the channel input and output of legitimate parties and the channel output of the adversary, respectively. In the above, we used the notation to denote vector random variables. The auxiliary random variables U and V are referred to as rate splitting and channel prefixing parameters. Unfortunately, in these milestone works the proofs are unconstructive and do tell how to construct a secrecy capacity achieving code. The solution to that problem is presented in the next section.
However, the main challenge in practical application of PLS techniques is ensuring that the adversary’s channel is sufficiently degraded. In classical systems, various sophisticated methods are employed to achieve this [22]. The use of quantum channels, due to their unique properties, opens entirely new possibilities in this regard. An adversary must possess knowledge of the quantum symbol preparation method to deterministically decode the encoded information; otherwise, her measurements are probabilistic and subject to errors. Moreover, an incorrect measurement setup destroys the information contained in quantum symbols and contributes to the error rate observed by legitimate parties. As a result, they can estimate potential information leakage based on the observed error rate and terminate the protocol execution if the leakage is excessive. The adversary’s situation is further complicated by the no-cloning theorem, which prevents faithful copying of quantum symbols for later measurement or for producing multiple copies for statistical analysis. In the following section, we describe the method of encoding classical information into quantum states that ensures these properties. The description is presented in a manner accessible to engineers who do not routinely work with quantum information processing.
2.3. Quantum Physical Layer
The proposed further encoding of classical information in quantum states can be considered as special case of channel modulation that uses symbols of unusual properties. We rely solely on elementary properties of quantum measurement (no entanglement is used in this work). For readers new to these concepts, the measurement model we adopt and the Dirac notation used throughout are briefly reviewed in Appendix C. For clarity, we summarize the quantum features that our protocol exploits. First, measurement outcomes are inherently probabilistic when the way of symbol preparation is unknown to the observer, so Eve cannot deterministically infer the transmitted symbol. Second, by the no-cloning principle, Eve cannot create additional perfect copies of the state and thus has only a single copy available for measurement. Third, measurement is digital in the sense that outcomes come from a finite set; for qubits there are exactly two possible results. By contrast, in the classical setting copying is unrestricted, observation can be effectively analog, and the state can often be determined without knowing how it was prepared.
Let us consider the operation of a channel modulator used in the famous BB84 QKD protocol [9]. The classical bit m is encoded as the m-th element of the basis selected by bit . In our protocol, the bit is a part of a key secretly shared by legitimate parties. The encoding process is described by the following expression
where H represents the Hadamard gate, defined as
The resulting quantum states are summarized in Table 1. The decoding is simple for the legitimate recipient. Bob just has to employ the same transformation to the received state using the same value of the secret bit k,
and measure the resulting state on a computational basis to recover the transmitted bit. The above correctness is guaranteed by the property of Hadamard gate , where I is the identity operator. However, the eavesdropper lacks knowledge of whether to apply the Hadamard transformation. Consequently, with probability , Eve selects an incorrect measurement basis when attempting to decode the symbol . When the correct basis is chosen, her measurement outcome is deterministic. For incorrect basis selection, the measurement outcome is probabilistic, yielding either “0” or “1” with equal likelihood. Therefore, the average BER observed by the eavesdropper is 25%. Moreover, for instances in which Eve employs the incorrect basis, the post-measurement qubit collapses into a state incompatible with the legitimate basis, rendering subsequent measurements by the legitimate receiver non-deterministic. This process irreversibly disturbs the transmitted information, leading to an increased BER for the legitimate parties. Thus, there exists a direct correspondence between the BER observed by legitimate parties and the extent of information leakage to the adversary; this property is not exploited in our design. The described method of encoding classical information into quantum states ensures that an adversary, lacking knowledge of the secret bit , cannot deterministically decode the transmitted information.

Table 1.
Rules used to encode classical bits into quantum states. The symbol in Table 1 denotes the secret basis–selection key, shared by Alice and Bob and never transmitted. It selects the preparation/measurement basis in the quantum layer.
2.4. Polar Coding for Wiretap Channel
Recently, considerable research has focused on the construction of practical encoding schemes that achieve secrecy capacity. The WCM results can be applied almost directly to the physical layer implementation proposed in Section 2.3. Further, we advocate for the adoption of polar codes [23] for sensitive information encoding, as proposed in [24,25]. This choice is motivated by the availability of effective decoders and theoretical proofs demonstrating the achieved security measures. The key problem of the polar code design for the WCM is the proper mapping of sensitive information to codewords.
Let , where . Consider a transformation of the form
where ⊗ denotes the Kronecker product. Assume that the variable is transmitted through the channel is transmitted as N independent uses of channel , the received values of must be decoded sequentially. Arikan proved [23] that in the limit of long codewords, () virtual channels responsible for transmission of the variable fall into two distinct categories (hence the name polarization):
- almost perfect channels with ;
- almost useless channels with .
Following this observation, the set of indices can be divided into reliable and useless ones:
In the above, we have used the Bhattacharyya distance [26] as an alternative way of quantitative characterization of the mentioned feature. It follows that the so-called frozen bits cannot be reliably delivered and must be known in advance at the decoder. At the same time, it is proved that whole information can be transmitted on
Unfortunately, for the finite codeword length N, the polarization is not complete and there exists some small subset of indices that cannot be accounted for nor .
This fact has to be accounted for in the design of polar coding for WCM.
When designing polar code for WCM, two channels must be considered simultaneously: and . This introduces two classes of polarization we are interested in: —bits that can be delivered reliably to Bob and —bits that are random for Eve. The intersections of these classes as shown in Figure 2 are used to design the secure mapping of information to codewords.

Figure 2.
Partitioning of codeword indices into four polarization classes. Indices are divided in the following subsets: , , , .
For degraded WCM, i.e., when Eve eavesdrops Bob’s device, the situation is relatively simple because and , where the mentioned classes are defined as in (6) and (7) with respect to channels and . However, when Eve eavesdrops Alice, the mentioned inclusion of classes does not take place. Another obstacle arises from the fact that, for finite-length codewords, there exists a small subset of indices that cannot be assigned to the reliable or random bit classes. The solution presented further exploits the following bit classes:
- —bits known to Bob;
- —bits unreliable for Bob;
- —bits random for Eve;
- —bits partially decodable by Eve.
The employed mapping is proven to be secure in [27] and is shown in Figure 2. To achieve secrecy goals, the sensitive information is transmitted through channels that are both good for Alice and bad for Eve . Bits in subset cannot be reliably decoded by Bob, but also, they are not accessible for Eve. In general, some random secret value, the same for each codeword and shared between Alice and Bob, can be assigned to this field. It is the part of the shared secret. Bits in subset can be reliably decoded by Bob, but they are also partially accessible for Eve, so they cannot carry any useful information. Bits from this set are assigned randomly and differently for each codeword. The main problem is related to bits from the set . Bits from this set cannot be reliably delivered to Bob, but they are partially accessible to Eve. In consequence, they cannot be statically shared and must be random for each codeword.
This delivery problem is resolved by the chaining mechanism shown in Figure 3 [27]. The bit values for indices for the k-th codeword are transmitted in the confidential part of codeword . The lent positions are denoted in Figure 3 as set . They carry random values regenerated for each codeword. For the last codeword, the confidential part can be used in its fullest extent. Special attention is required for the selection of the for the first codeword. This value can be publicly known. As long as the carry random bits for the first codeword, the eavesdropper obtains no useful information.

Figure 3.
Mechanism of codewords chaining. Random bits from for the k-th codeword are transmitted in the confidential part of the preceding codeword. Indices are divided on the following subsets: , , , .
The security of the proposed chain is founded on proper estimation of sets and for both channels. This task poses a serious problem in classical communication systems as there is no guarantee concerning quality of Eve’s channel. However, the proposed physical layer uses encoding in mutually unbiased bases, and, in consequence, Eve experiences a high bit error rate (BER) as long as she does not know the key controlling the encoding process. The rules of quantum mechanics allow the estimation of Eve’s BER lower bound and this parameter can be used for the design of polar code with the desired properties [28]. Throughout this work, Eve is assumed to access an ideal quantum channel; consequently, her BER lower bound stems solely from basis ignorance (unknown ), not from additional channel noise.
2.5. Wegman-Carter MAC
We recall a basic form of information-theoretic message authentication based on the Wegman–Carter method. Assume the parties share long-term secrets and , where selects a function from a universal hash family, and is a uniformly random mask of tag length.
For a message , the sender chooses a fresh nonce and computes the tag
The pair is sent over the public channel, while must be delivered confidentially to the verifier. The verifier recomputes the tag from and using the shared key, and accepts only if the result matches the received t.
This scheme inherits the one-time security guarantee of Wegman–Carter authentication: any change in is detected except with probability , where is the tag length. The fresh nonce prevents correlation across tags when the same long-term key is reused, which protects both and . In practice, we recommend setting the nonce length equal to the tag length . For uniformly random nonces, the collision probability among q authentications is approximately ; choosing keeps this risk negligible at the same level as the MAC security while minimizing confidential-transmission overhead.
A central requirement is that remains confidential. If an adversary learns , correlations across multiple transcripts may reveal information about the long-term key. The protocol specification therefore assumes that is transmitted securely. If this can be achieved, then the long-term secrets and can be reused for multiple sessions. However, purely classical means cannot guarantee information-theoretic secrecy of without additional fresh key material delivered per communication session. This motivates alternative approaches to achieve confidential delivery of and thus enable safe key reuse beyond what is possible in classical message authentication.
3. Quantum-Assisted Data Authentication Protocol
In this section, we present the protocol that combines quantum communication methods with classical information-theoretic security to achieve robust data authentication. Participants are assumed to have access to both classical and quantum channels, along with a shared static random key. Following the Wegman–Carter approach, the protocol uses universal hashing for authenticating messages and employs quantum channels to securely deliver random nonces, thereby removing the need for shared key updates. Polar codes are applied within Wyner’s wiretap channel framework to guarantee both confidentiality and reliability, even against adversaries with unlimited computational power.
The parties share a secret key K, which consists of four components:
- and —used to compute the Wegman–Carter authentication tag as described in Section 2.5;
- —used to select the measurement bases between two mutually unbiased bases (e.g., the computational and the dual basis) as described in Section 2.3;
- —used to initialize the polar encoder and decoder for information hiding in the WCM model as described in Section 2.4.
The shared key is static and is not updated during protocol execution.
The size of each component depends on the length of the authentication tag and the chosen Wegman–Carter construction. The key must be long enough to specify the measurement basis for every transmitted bit, which means that its length is a multiple of the codeword size. The key has the size of the set , and thus depends on the parameters of the polar code.
With these assumptions in place, we now specify the step-by-step execution of the protocol. The procedure outlined below is depicted in Figure 4.

Figure 4.
Diagram illustrating the operation of the protocol. Blocks and data labels are prefixed by a circled numeral (➀, ➁, …) indicating the protocol step, matching the numbered description in the text.
- Alice generates a random nonce of length equal to the authentication tag size.
- She transmits the message m and the resulting tag t to Bob over the classical channel. Bob treats them as unreliable data and .
- The random value is divided into blocks of size . The sequence is extended with an additional block consisting of random bits.
- Alice constructs a chain of codewords as illustrated in Figure 3. The codewords are concatenated into a sequence c of classical bits.
- Each bit of the sequence is mapped into a quantum state aswhere H is the Hadamard operator and the states are prepared on a computational basis.
- Immediately after preparation, the quantum states are sent sequentially to Bob.
- Bob applies the inverse transformationto the received states, and then measures on a computational basis. To account for quantum channel losses, Bob encodes outcomes asobtaining a sequence of symbols. After grouping them into codewords, the sequence is passed to the polar code Successive Cancellation decoder.
- Successful decoding requires that the decoder knows in advance the values of the bits in sets and . Decoding proceeds as in Figure 3. The set always contains the private key , unknown to Eve. In the zeroth codeword, the set is filled with zeros. Once Bob decodes the zeroth codeword, he learns the values necessary for decoding the first codeword. The process continues until the entire chain of codewords is decoded.
- From the information sets of all codewords except the zeroth one, Bob reconstructs the value .
- Using , the received message , and tag , Bob verifies correctness by checking
- The message is accepted if the equality holds; otherwise, it is rejected.
4. Analysis
4.1. Security
In the proposed scheme, message authentication is performed by computing a checksum:
where denotes a universal hash function [1], and are the shared secrets, m is the message to be authenticated, and is a one-time random value known only to Alice and Bob. We assume that the keys , can be reused without the need for refreshing.
In the considered attack model, Eve observes the pair and attempts to guess the secrets and or to substitute m and forge t. Such an attack was analyzed by Fehr and Salvail [11] in the Shannon security model, where they proved the security of the scheme. The probability of a successful forgery equals , where is the length of the checksum in bits. However, if the confidentiality of is compromised, information leakage about shared secrets occurs, forcing the keys to be refreshed.
Confidentiality of is therefore critical to the overall security of the protocol and can be ensured in two ways: by selecting a fresh value of from a shared random bit pool for each authentication instance (as in a one-time pad (OTP)) or by transmitting securely within the protocol. In the classical information model, secure transmission of is possible only with the OTP, which still requires a shared pool of random bits. This limitation can be overcome by leveraging quantum information processing techniques. In [11], secure delivery of was proposed using BB84 encoding, under the assumption of an ideal quantum channel. However, the protocol requires an authenticated classical feedback channel, which also consumes a shared random bit resource, though of smaller size.
To achieve reliable and confidential delivery of , we rely on Wyner’s wiretap model [20], in which noise is an inherent component of data protection. Within this model, can be transmitted confidentially if the Alice–Eve channel is of lower quality than the Alice–Bob channel. This requires encoding with a properly constructed redundancy code. The existence of such codes has been proven, while their practical construction remains challenging.
In the classical setting, constructions based on polar codes have been developed and analyzed in the literature [25,27]. These results show that, in the wiretap channel model, polar codes enable confidential and reliable transmission with probabilities and , respectively, where and are design parameters of the code. The requirement is that the error rate in the Alice–Bob channel must remain below the design threshold, while the error rate in the Alice–Eve channel must not be lower than the assumed bound. Exceeding the error threshold in the Alice–Bob channel does not compromise confidentiality but prevents Bob from decoding correctly. Conversely, Eve may gain partial access to the protected information only if her channel quality improves beyond the design threshold.
The proposed protocol directly employs these constructions and thus inherits the corresponding security proofs. Therefore, the security analysis reduces to evaluating the error rate of the Alice–Eve channel under the adopted quantum-layer encoding method and estimating the probability that this rate falls below the design threshold.
For Eve, the only feasible attack on the protocol is to compromise the confidentiality of the transmitted value . To achieve this, she must decode the codeword transmitted in the quantum layer. The most straightforward approach is to guess the bits of the key and measure on the basis specified by this guess. Since the key is random and secret, her only option is trial and error. In the limit of infinitely long sequences, her error rate converges to 25%. This follows from the fact that in 50% of the cases, she selects the wrong measurement basis, leading to random outcomes. Eve has no oracle to reveal which guessed bits are correct. To validate her guesses for , she would need to decode a hypothetical value and verify it by computing
Correctly determining requires satisfying three conditions: (a) reducing the error rate in the eavesdropping channel to the design threshold assumed for the Alice–Bob channel, (b) obtaining the key required for polar decoding, and (c) knowing the key and required for the MAC computation. Consequently, Eve must test the entire key . There is no tolerance for errors—every bit of must be correct, otherwise the MAC verification fails. Thus, she must guess at least bits of the key correctly. Eve therefore faces an all-or-nothing problem: either she compromises the protocol by correctly guessing almost the entire key, which is highly improbable, or she learns nothing about the key or the transmitted value .
Instead of guessing the random key and measuring in the corresponding basis, Eve may apply more advanced quantum state discrimination techniques to infer the bits of the codeword. The encoding adopted in the quantum layer is directly borrowed from the BB84 Quantum Key Distribution (QKD) protocol. This canonical encoding method has been extensively analyzed in the literature. It has been shown that for BB84 encoding, optimal state discrimination can be achieved using the so-called Brandt probe [29]. The Brandt probe enables unambiguous state discrimination, meaning that the measurement outcome is either correct or inconclusive. In the case of an inconclusive outcome, Eve obtains no information about the bit value, which at the logical level corresponds to its erasure (value in Equation (14)). In the case of a conclusive outcome, Eve is certain that the recovered bit value is correct. However, she gains no information about the basis in which the bit was encoded. Thus, this discrimination method does not reveal the key used to select the basis but only the form of x. Moreover, the method provides information about the encoded bit at the cost of introducing errors in the Alice–Bob channel. There is a direct trade-off between Eve’s information gain and the induced error rate .
The expression follows directly from the Brandt probe analysis; see Appendix A for the derivation and operating point. The design of the probe allows controlling the induced error rate . We assume Eve ignores the disturbance she induces and maximizes her information gain. The function (18) reaches its maximum at . Under this operating point, her gain is upper bounded by (i.e., she can learn at most of the codeword bits). Our code is designed so that secrecy would be compromised only if Eve could learn more than of the codeword bits; thus, her optimal gain remains below the breaking threshold.
In summary, the security analysis demonstrates that Eve’s ability to gain information is fundamentally constrained by the properties of the quantum encoding and the applied polar coding scheme. Eve faces an all-or-nothing problem: she must correctly guess almost the entire key, which would completely compromise the protocol but is highly improbable; otherwise, she obtains no information about the key or the transmitted value . Moreover, optimal quantum eavesdropping cannot reduce the error rate below the required threshold, preventing her from acquiring even partial information about the bits of needed to attack the data authentication function.
4.2. Performance
Our goal was to design a protocol suitable for practical implementation. To verify this, we constructed a polar code tailored to the constraints of the eavesdropper’s channel. During the design phase, we assumed that the adversary (Eve) has access to an ideal quantum channel, and the bit error rate experienced during eavesdropping arises solely from the lack of knowledge of the basis key . Thus, the eavesdropper’s channel can be modeled as a binary symmetric channel (BSC) with bit-flip probability . In contrast, the channel between Alice and Bob is affected by both losses and errors. We model this situation as a cascade of a binary erasure channel (BEC) with bit erasure probability q and a BSC with bit-flip probability p. A schematic representation of both channels is shown in Figure 5.
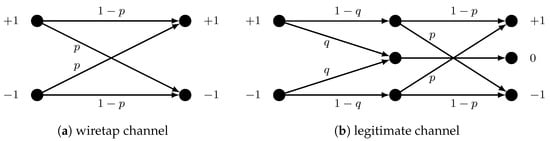
Figure 5.
Schematic representation of the wiretap channel and the legitimate channel used in the authentication protocol design. The Bhattacharyya parameter for these channels is equal to and , respectively.
The polar code construction was performed using the Bhattacharyya parameter method [23], which provides an upper bound on the error probability for each bit channel. Determining the indices belonging to the sets from Figure 2 is crucial for ensuring security. Membership in these sets is strictly determined by the threshold values and from (6) and (7), which guarantee the reliability and confidentiality of the code, respectively. The sizes of these sets also depend on the codeword length and channel characteristics. In the numerical simulations presented below, the thresholds were set to and . During polarization, the eavesdropper’s channel was always modeled as a BSC with bit-flip probability . The legitimate channel was analyzed as a function of bit-flip probability p and erasure probability q. It should be noted that in the presented communication model, errors and losses in the quantum channel constitute a common budget and are counted as errors at the classical bit transmission level; thus, the total error rate and loss sum must not exceed the error rate in the eavesdropper’s channel.
Given a binary-input DMC W with Bhattacharyya parameter (see Appendix B), the polarization step replaces two copies of W by the synthetic channels and [23] (section II). For the Alice→Bob link, we propagate the standard upper bounds (Equations (26) and (27), [23]).
This is a conservative choice for reliability (estimate is higher than real value) and may exclude some reliable bit channels from .
For the Alice → Eve link, using the same upper bound for the “minus” recursion can overestimate the Bhattacharyya parameter and thus misclassify a channel decodable by Eve as a secure one. To avoid this, one should use a lower estimate for . A general inequality is available but is very coarse and does not lead to satisfactory designs in practice.
When Eve’s channel is , there exists an exact closed form expression for Bhattacharyya parameter recursions:
which we propagate along the polarization tree to obtain for all bit channels. After computing for legitimate and wiretap channels, we select and using the thresholds in (6) and (7), and then form sets , , , and , as described in Section 2.4. The obtained set sizes for codewords of length , , and are shown in Table 2.

Table 2.
Sizes of the sets , , , for different codeword lengths N and channel parameters p and q.
A key feasibility condition is that the set , which contains indices unreliable for Bob and simultaneously informative for Eve, must not exceed the size of the secure set . Whenever , the chaining construction from Figure 3 cannot be realized because the number of indices available for secure transmission is insufficient to compensate for the “critical” positions.
As the block length grows, the efficiency of the scheme improves markedly. This follows directly from the polarization effect: with larger N, the fraction of indices that polarize towards being almost perfect () for Bob or almost useless () for Eve increases. Consequently, the relative size of the uncertain region shrinks, and the effective secure set grows. This effect is clearly visible when comparing the ratios for increasing block sizes.
In the special case of high-quality information channels (), the problematic set vanishes almost entirely. In such scenarios, there is no need to employ multi-block chaining, since no indices fall into the “bad-for-Bob and good-for-Eve” category. A single-block construction then suffices.
From a practical standpoint, the central quantity is the size of the effective secure field . Typical requirements are on the order of 256 or 512 bits. The data show that for , even with moderate block sizes (), the secure field exceeds 512 bits across all considered eavesdropper channel qualities. For noisier information channels (), larger block lengths are required: at , secure fields reach 256 bits in most cases, while comfortably provides more than 512 bits of effective secrecy.
5. Conclusions
We have presented a quantum-assisted data authentication protocol that combines classical Wegman–Carter message authentication with quantum physical-layer secrecy, instantiated via polar coding in the wiretap channel model. The protocol achieves integrity and origin guarantees, while enabling safe key reuse by securely transmitting the authentication nonce using quantum resources. Security analysis demonstrates that the adversary’s ability to compromise the protocol is fundamentally limited by quantum measurement constraints and the structure of polar codes, resulting in an all-or-nothing scenario for key recovery. Performance evaluation confirms that practical code parameters yield secure payload sizes suitable for real-world applications, with quantum resource consumption scaling efficiently with block length. The proposed approach eliminates the need for authenticated classical feedback and is robust to channel noise, making it a promising candidate for future quantum-secure communication systems. In its current formulation, the protocol can only be used in high-quality quantum channels with low loss rates, which is its main drawback.
Looking ahead, we identify several directions to enhance the protocol’s applicability and robustness. First, we will pursue efficiency improvements in polar-code design, focusing on practical selection and optimization methods for finite block lengths. Second, we plan to develop an adaptive rate-selection strategy that dynamically adjusts to observed channel conditions, thereby improving both reliability and confidentiality. Third, we will explore alternative quantum transmission techniques compatible with our framework—such as higher-dimensional encodings—to further impede eavesdropping while ensuring reliable reception.
Author Contributions
Conceptualization, P.Z.; methodology, P.Z. and G.D.; software, A.Z., M.K. and W.I.; validation, G.D., W.S., W.F. and J.I.; formal analysis, W.S., M.K. and A.D.; investigation, J.M., K.P., W.F. and P.K.; data curation, A.Z., J.M. and W.I.; visualization, J.I., P.K., K.P. and A.D.; supervision, P.Z.; project administration, G.D.; funding acquisition, none; writing—original draft preparation, P.Z.; writing—review and editing, P.Z., A.Z., G.D., M.K., J.M., W.S., J.I., W.I., P.K., A.D., W.F. and K.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Science and Higher Education funding for statutory activities BK-270/RAu13/2025.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Brandt’s Probe
The following paragraph demonstrates the operation of this probe. The bases utilized by the legitimate parties are designated as computational— and dual—, with dual bases being subjected to a rotation of . The basis employed for probe definition is positioned between these, as illustrated in Figure A1. The relationship between the bases of legitimate parties and the probe basis is expressed by the following transformations:
where and . The encoding of logical bit “0” is represented by based on the chosen basis, while “1” is encoded as .

Figure A1.
Orientation of Brandt’s probe bases.
The basis used by Eve to construct a probe will be further treated as computational and hence the subscript E
will be omitted hereafter. Eve entangles the travel qubit with the probe register using gate controlled by the travel qubit
where I is the identity operator and denotes the bit flip applied to the target register. Eve has flexibility to choose the initial state placed in the probe register. The post-entanglement state can take the following form regardless of the specific value of :
If the legitimate party accurately detects the bit, the post-measurement states are given by the following:
independent of the basis used for encoding. Conversely, if the bit is detected erroneously, the post-measurement state is as follows:
Assuming a parametrization of the initial state as
where , the bit error rate is , as evident from the following:
If logical bit detection is accurate, then the post-measurement states take the following form:
Because states and are correlated with logical bits independent on the basis of their encoding, Eve can eavesdrop on communication by discriminating between these states. However, since the states and are not orthogonal, there is no perfect technique for Eve to perform this discrimination.
The minimum error discrimination technique, while affording maximum average information, comes with the trade-off of limited confidence of the single event detection. To achieve the promised information gain, Eve must repeat the discrimination procedure multiple times for copies of the quantum systems being in the same state. Obviously, this condition does not hold for the considered protocol. In contrast, the unambiguous discrimination technique provides Eve with 100% confident information even when dealing with a single copy of the state to be discriminated. However, this advantage is counterbalanced by the occurrence of inconclusive results with a finite rate. Given the characteristics of the analyzed protocol, the unambiguous discrimination technique appears to be more fitting, offering certainty in the obtained information at the expense of occasional inconclusive outcomes. The rate of inconclusive measurements is equal to the overlap between discriminated states [30]. Consequently, Eve lacks information about the bit value with a probability defined as follows (see Figure A2):
In consequence, her information gain per bit is equal to the following (see Figure A2):
The multiplication by a factor in the above expression arises from the necessity of discrimination failure for bits erroneously detected by legitimate parties, as, in such cases, Eve’s ancilla consistently remains in the same state.
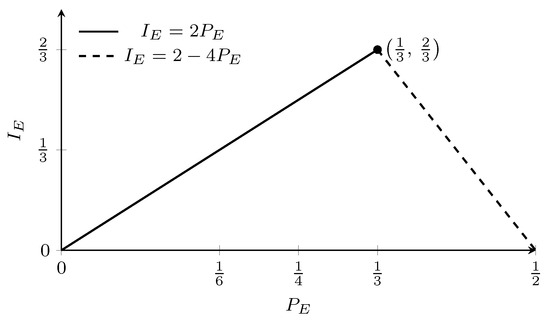
Figure A2.
Information gain for Eve using the Brandt’s probe as a function of the bit error rate in legitimate communication.
Appendix B. Bhattacharyya Parameter
The Bhattacharyya parameter is a measure of the reliability of a communication channel. It is defined for a discrete memoryless channel W with input alphabet and output alphabet as
where is the conditional probability of receiving output y given input x.
For , the output alphabet is , with
Therefore, the Bhattacharyya parameter of the BSC is
For , the output alphabet is , with
The only non-zero contribution comes from the erasure symbol; hence, the Bhattacharyya parameter of the BEC is
Consider the cascade of a binary erasure channel followed by a binary symmetric channel . In the cascade, the output alphabet is with transition probabilities
Therefore,
The Bhattacharyya parameter of the resulting channel can be written as
Appendix C. Elements of Quantum Formalism
The formal description of quantum systems is based on the framework of Hilbert spaces. A Hilbert space is a complex vector space equipped with an inner product. Elements of in matrix representation take the form of column vectors, e.g., . The inner product is a function satisfying linearity and positive definiteness. The norm of an element is defined as
A set of orthonormal vectors , such that every can be expressed as
is called a basis of the Hilbert space. The most common choice is the computational basis
and its dual basis
Linear maps describe transformations of elements of the Hilbert space. For an operator A, its Hermitian conjugate satisfies
In matrix representation, is the conjugate transpose of A.
For notational convenience, Dirac notation is introduced. A column vector is written as a ket . Its Hermitian conjugate is written as a bra , which is a row vector. The inner product is denoted and the outer product represents a linear operator.
In quantum mechanics, only normalized vectors are physically relevant, i.e., , or equivalently . Elements of the Hilbert space with this property represent quantum states A qubit is a quantum state described in a two-dimensional Hilbert space. Examples of qubit states are
In quantum mechanics, unitary and Hermitian operators play a central role. An operator U is unitary if it preserves the norm of vectors, i.e., for every . Unitary operators satisfy , where I denotes the identity matrix. The evolution of quantum states in an isolated system is assumed to be governed by unitary operators. Conceptually, this is analogous to uniform motion of material points in classical mechanics.
Hermitian (self-adjoint) operators satisfy . They have real eigenvalues and orthonormal eigenvectors. Hermitian operators correspond to observables, i.e., physically measurable quantities that can be measured in a quantum system. If a Hermitian operator A representing the observable has spectral decomposition
then the measurement of a state yields outcome with probability
and the post-measurement state collapses to . From the above, it follows that two vectors differing only by a global phase, , yield the same probability distribution under measurement and are physically indistinguishable.
Consider the observables Z and X defined as
The eigenvectors of these observables are the computational basis and the dual basis elements, respectively. Their corresponding eigenvalues are and . Suppose the system is in state . A measurement in the computational basis is deterministic, since and . The post-measurement state remains unchanged, . In contrast, a measurement in the dual basis is probabilistic, since and . After measurement, the system collapses with equal probability to or . A symmetric situation occurs if the system is initially in state . In this case, measurement of X is deterministic, while measurement of Z is probabilistic.
This illustrates a fundamental feature of quantum mechanics: measurement in a basis different from that in which the state was prepared introduces randomness and disturbs the state of the system. This property is a key element distinguishing quantum from classical information processing and forms the foundation of security in many quantum cryptographic protocols.
Another fundamental limitation is given by the no-cloning theorem, which states that there is no physical operation capable of producing an exact copy of an unknown quantum state. This impossibility follows directly from the linearity of quantum mechanics and ensures that information encoded in a quantum state cannot be duplicated without disturbance. The no-cloning theorem, together with the disturbance caused by incompatible measurements, provides the basis for the security of quantum communication.
The concepts introduced above are sufficient to characterize the properties of the proposed protocol. However, quantum mechanics is considerably richer and includes, among others, the description of mixed states, composite systems and entanglement, as well as non-unitary evolutions. These aspects are beyond the scope of this short explanation.
References
- Wegman, M.N.; Carter, J.L. New hash functions and their use in authentication and set equality. J. Comput. Syst. Sci. 1981, 22, 265–279. [Google Scholar] [CrossRef]
- Li, B.H. One-time universal hashing quantum digital signatures without perfect keys. Phys. Rev. Appl. 2023, 20, 044011. [Google Scholar] [CrossRef]
- Barnum, H.; Crepeau, C.; Gottesman, D.; Smith, A.; Tapp, A. Authentication of quantum messages. In Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science, Vancouver, BC, Canada, 19 November 2002; Proceedings. pp. 449–458, ISSN 0272-5428. [Google Scholar] [CrossRef]
- Broadbent, A.; Gutoski, G.; Stebila, D. Quantum One-Time Programs. In Proceedings of the Advances in Cryptology—CRYPTO, Santa Barbara, CA, USA, 18–22 August 2013; Canetti, R., Garay, J.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 344–360. [Google Scholar] [CrossRef]
- Garg, S.; Yuen, H.; Zhandry, M. New Security Notions and Feasibility Results for Authentication of Quantum Data. In Proceedings of the Advances in Cryptology—CRYPTO, Santa Barbara, CA, USA, 20–24 August 2017; Katz, J., Shacham, H., Eds.; Springer: Cham, Switzerland, 2017; pp. 342–371. [Google Scholar] [CrossRef]
- Alagic, G.; Majenz, C. Quantum Non-malleability and Authentication. In Proceedings of the Advances in Cryptology—CRYPTO, Santa Barbara, CA, USA, 20–24 August 2017; Katz, J., Shacham, H., Eds.; Springer: Cham, Switzerland, 2017; pp. 310–341. [Google Scholar] [CrossRef]
- Portmann, C. Quantum Authentication with Key Recycling. In Proceedings of the Advances in Cryptology—EUROCRYPT, Paris, France, 30 April–4 May 2017; Coron, J.S., Nielsen, J.B., Eds.; Springer: Cham, Switzerland, 2017; pp. 339–368. [Google Scholar] [CrossRef]
- Dulek, Y.; Speelman, F. Quantum Ciphertext Authentication and Key Recycling with the Trap Code. In Proceedings of the 13th Conference on the Theory of Quantum Computation, Communication and Cryptography (TQC 2018), Sidney, Australia, 16–18 July 2018; Leibniz International Proceedings in Informatics (LIPIcs). Jeffery, S., Ed.; Dagstuhl Publishing Team: Dagstuhl, Germany, 2018; Volume 111, pp. 1:1–1:17, ISSN 1868-8969. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Breidbart, S. Quantum Cryptography II: How to re-use a one-time pad safely even if P=NP. Nat. Comput. 2014, 13, 453–458. [Google Scholar] [CrossRef] [PubMed]
- Damgård, I.; Pedersen, T.B.; Salvail, L. A Quantum Cipher with Near Optimal Key-Recycling. In Proceedings of the Advances in Cryptology—CRYPTO, Santa Barbara, CA, USA, 14–18 August 2005; Shoup, V., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 494–510. [Google Scholar] [CrossRef]
- Fehr, S.; Salvail, L. Quantum Authentication and Encryption with Key Recycling. In Proceedings of the Advances in Cryptology—EUROCRYPT, Paris, France, 30 April–4 May 2017; Coron, J.S., Nielsen, J.B., Eds.; Springer: Cham, Switzerland, 2017; pp. 311–338. [Google Scholar] [CrossRef]
- Škorić, B.; de Vries, M. Quantum Key Recycling with 8-state encoding (The Quantum One-Time Pad is more interesting than we thought). Int. J. Quantum Inf. 2017, 15, 1750016. [Google Scholar] [CrossRef]
- Leermakers, D.; Škorić, B. Security proof for quantum key recycling with noise. Quantum Inf. Comput. 2019, 19, 913–934. [Google Scholar] [CrossRef]
- Leermakers, D.; Škorić, B. Quantum Alice and silent Bob: Qubit-based quantum key recycling with almost no classical communication. Quantum Inf. Comput. 2021, 21, 1–18. [Google Scholar] [CrossRef]
- Lim, N.H.; Choi, J.W.; Kang, M.S.; Yang, H.J.; Han, S.W. Quantum authentication method based on key-controlled maximally mixed quantum state encryption. EPJ Quantum Technol. 2023, 10, 35. [Google Scholar] [CrossRef]
- Qin, J.Q. Efficient quantum digital signatures over long distances with likely bit strings. Phys. Rev. Appl. 2024, 21, 024012. [Google Scholar] [CrossRef]
- Fang, J.; Pan, J.; Huang, X.; Lin, J.; Jiang, C. Integrated physical-layer secure visible light communication and positioning system based on polar codes. Opt. Express 2023, 31, 41756–41772. [Google Scholar] [CrossRef] [PubMed]
- An, C.; Huang, M.; Lu, X.; Bi, L.; Li, W. Polar code-based secure transmission with higher message rate combining channel entropy and computational entropy. Cybersecurity 2024, 7, 36. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J. Physical-Layer Security: From Information Theory to Security Engineering; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Csiszar, I.; Korner, J. Broadcast channels with confidential messages. IEEE Trans. Inf. Theory 1978, 24, 339–348. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.H.; Wang, L. Physical Layer Security for Next Generation Wireless Networks: Theories, Technologies, and Challenges. IEEE Commun. Surv. Tutor. 2017, 19, 347–376. [Google Scholar] [CrossRef]
- Arikan, E. Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Mahdavifar, H.; Vardy, A. Achieving the Secrecy Capacity of Wiretap Channels Using Polar Codes. IEEE Trans. Inf. Theory 2011, 57, 6428–6443. [Google Scholar] [CrossRef]
- Gulcu, T.C.; Barg, A. Achieving Secrecy Capacity of the Wiretap Channel and Broadcast Channel with a Confidential Component. IEEE Trans. Inf. Theory 2017, 63, 1311–1324. [Google Scholar] [CrossRef]
- Bhattacharyya, A. On a Measure of Divergence between Two Multinomial Populations. Sankhya Indian J. Stat. 1946, 7, 401–406. [Google Scholar]
- Şaşoğlu, E.; Vardy, A. A new polar coding scheme for strong security on wiretap channels. In Proceedings of the 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; pp. 1117–1121, ISSN 2157-8117. [Google Scholar] [CrossRef]
- Tal, I.; Vardy, A. How to Construct Polar Codes. IEEE Trans. Inf. Theory 2013, 59, 6562–6582. [Google Scholar] [CrossRef]
- Brandt, H.E. Unambiguous State Discrimination in Quantum Key Distribution. Quantum Inf. Process. 2005, 4, 387–398. [Google Scholar] [CrossRef]
- Jaeger, G.; Shimony, A. Optimal distinction between two non-orthogonal quantum states. Phys. Lett. A 1995, 197, 83–87. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).