A Novel Multi-Mode Resonator-Based Ultra-Wideband Bandpass Filter Topology
Abstract
1. Introduction
- i
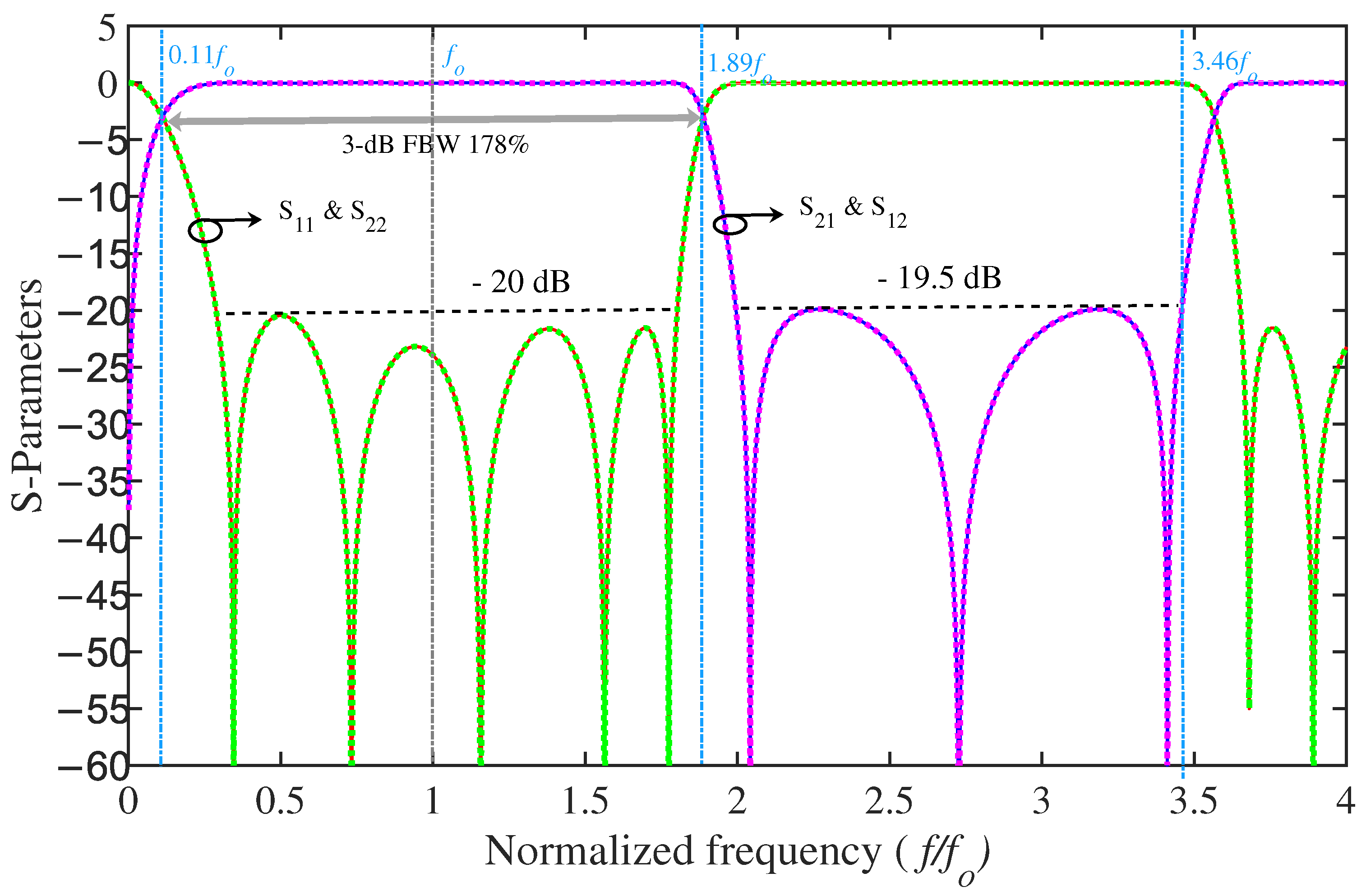
- A 3 dB FBW of 176% is achieved, which is substantially wider than that of the ultra-wideband microstrip filters reported in the state-of-the-art works. In addition, it can be adjusted by varying the impedance ratio of the short-shunt-stepped impedance resonator.
- ii
- The filter outperforms most existing designs in the literature in terms of IL, RL, and flat group delay response.
- iii
- The filter is fabricated using microstrip technology, offering a simpler and cost-effective alternative compared to HTS thin-film and LTCC-based multilayer design approaches reported in the literature.
- iv
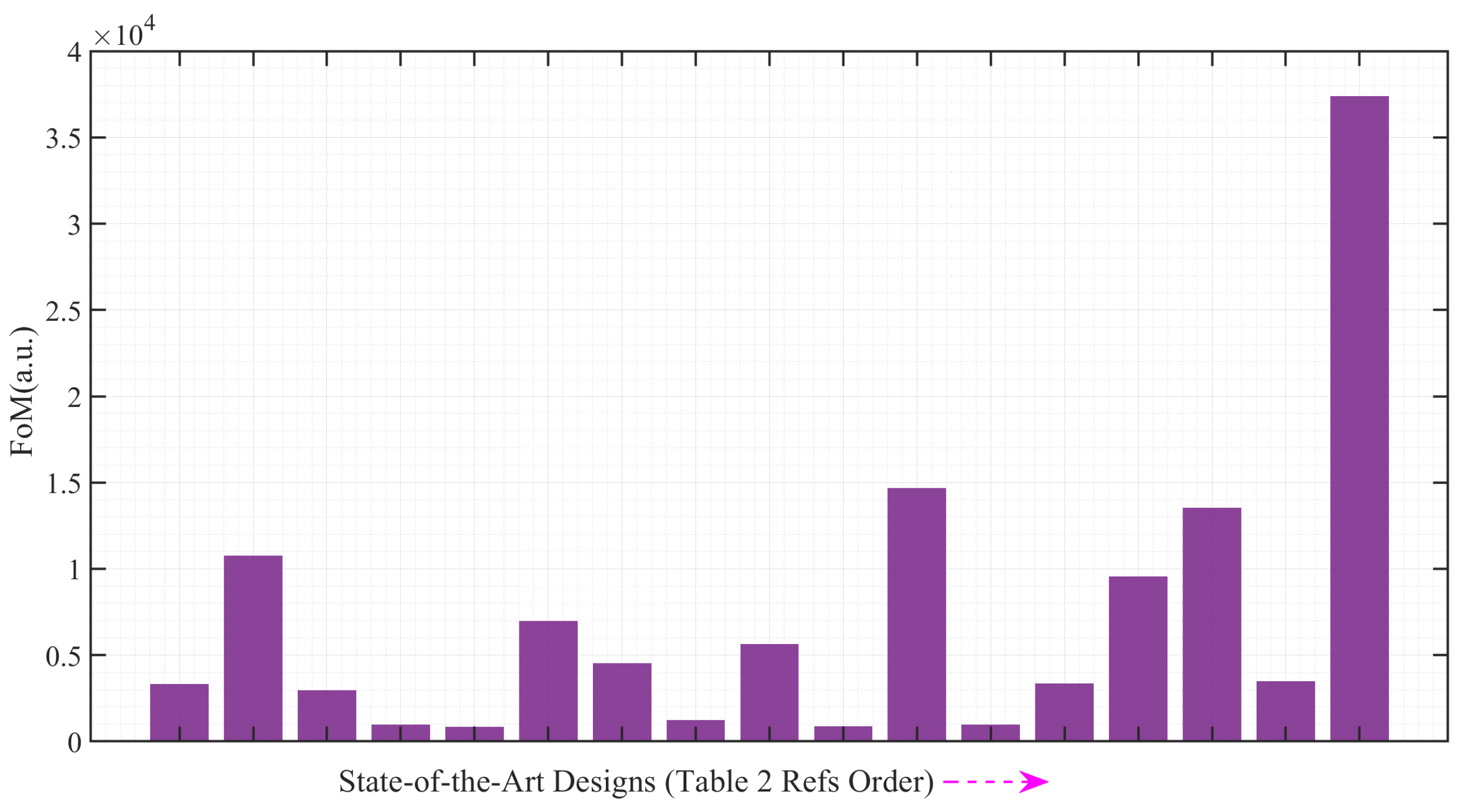
- A figure of merit (FoM) has been proposed to measure the optimal trade-off among key filter performance parameters, such as IL, RL, FBW, SF, group delay flatness, and center frequency and confirms that the proposed bandpass filter exhibits the best FoM compared to existing designs.
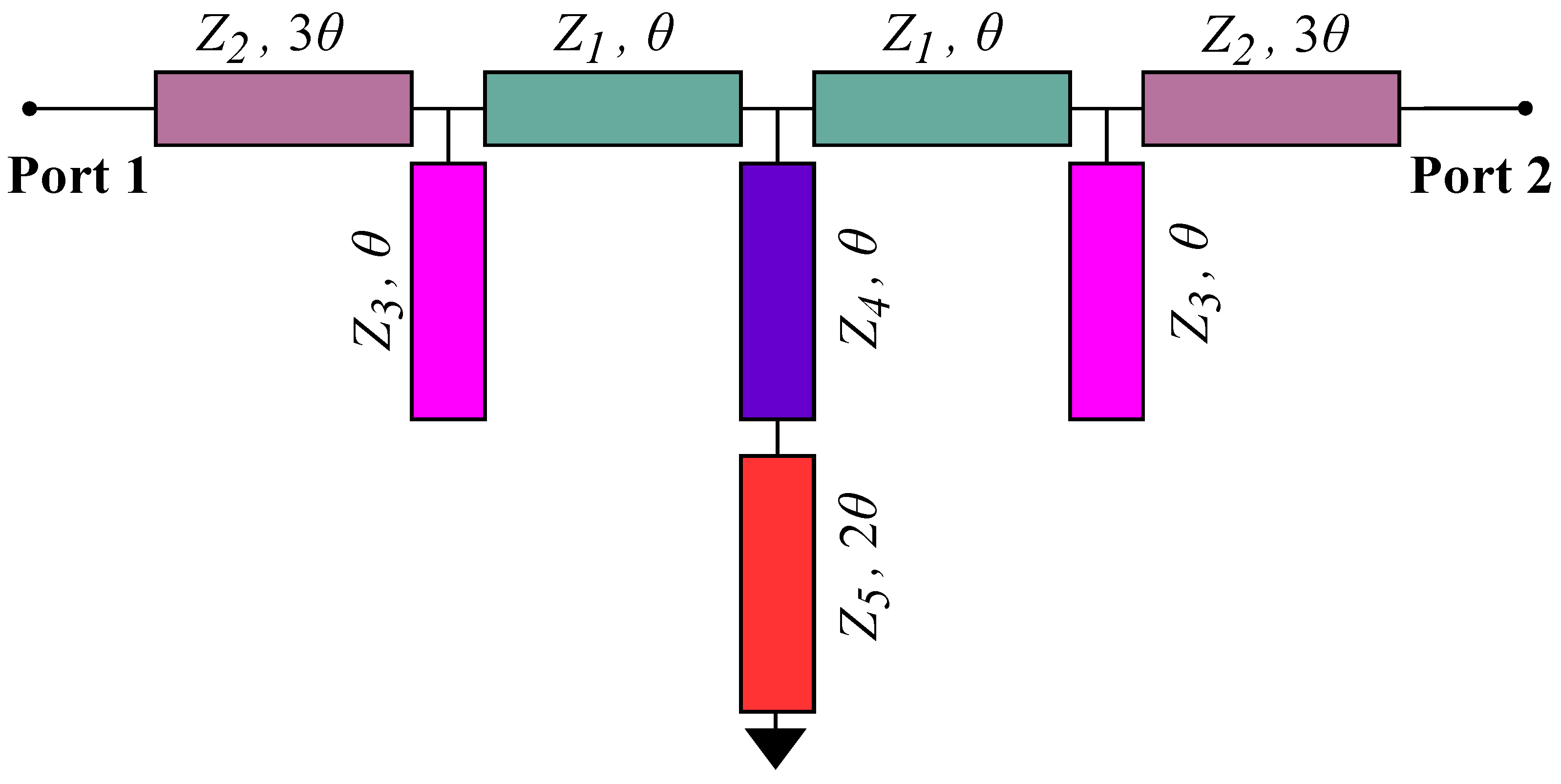
2. Proposed Ultra-Wideband Bandpass Filter Topology and Analysis
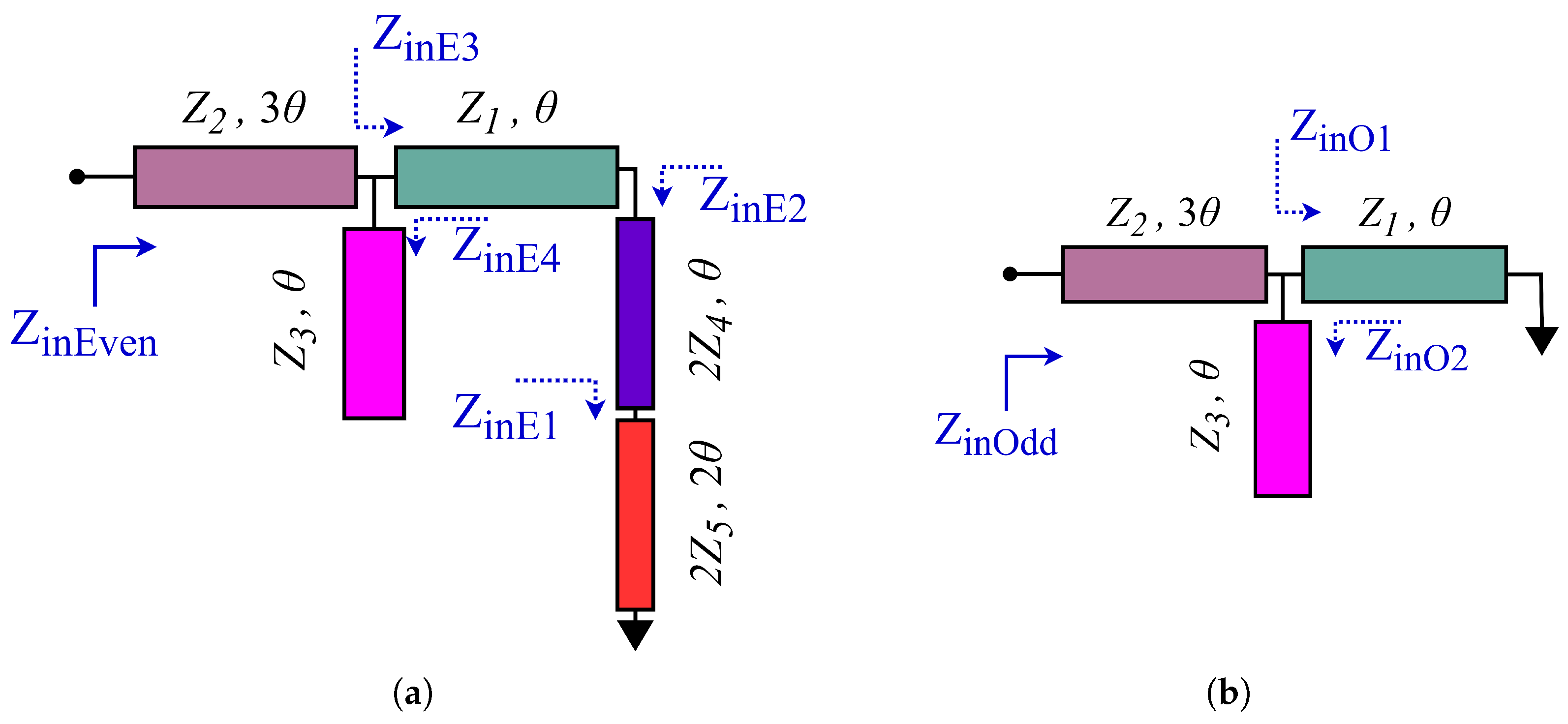
2.1. The Analysis of Even- and Odd-Mode Resonances
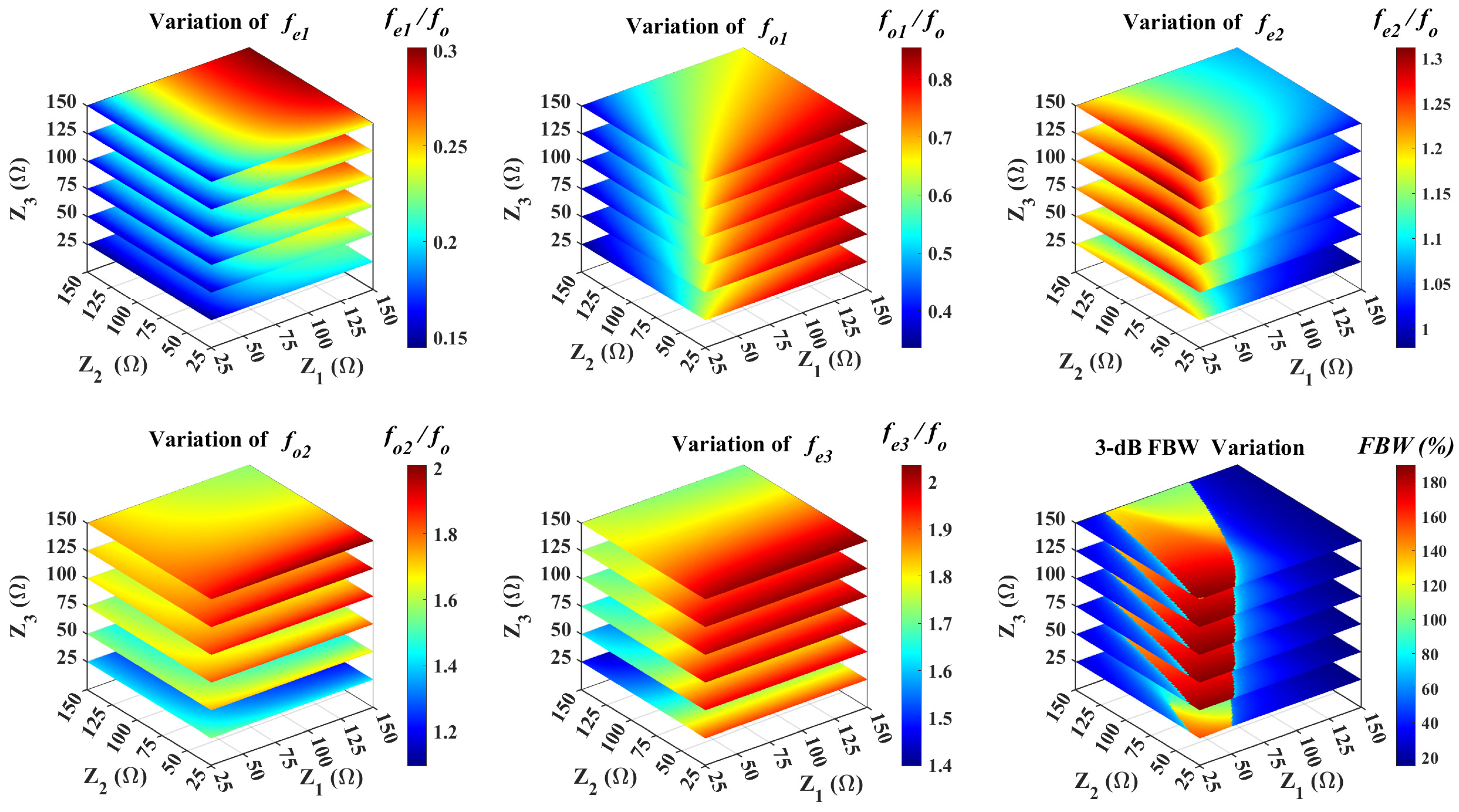
- The filter overall bandwidth is mainly characterized by two even-mode resonances and , while the mid-passband behavior can be modified by , , and .
- The largest bandwidth for a given (i.e., the location of is known) is obtained when the even-mode resonances and simultaneously diverge from the center frequency (), i.e., and .
- When and (i.e., when and are increased proportionally), the magnitude of at the lower and upper passband edges becomes steeper and higher selectivity is achieved.
- The even mode and the odd mode present in the upper stopband can be suppressed by a transmission zero , and a wide stopband can be achieved.
2.2. Impedance Fine-Tuning and Filter Ideal Performance
- Decide the center frequency of the filter.
- Define the location of the transmission zero based on the bandwidth requirements (see Figure 3) and compute the impedance ratio using (7). To achieve better selectivity, and must be maximized while maintaining the same ratio, considering the range of impedance values allowed by the fabrication process.
- Finally, fine-tune the remaining impedances , , and to obtain accurate filter characteristics.
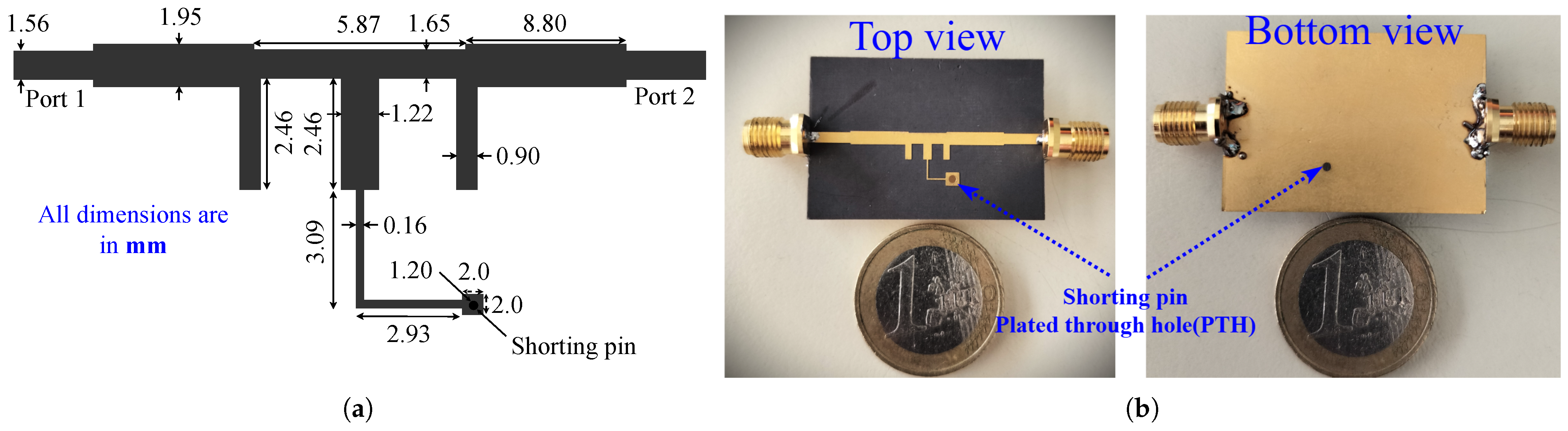
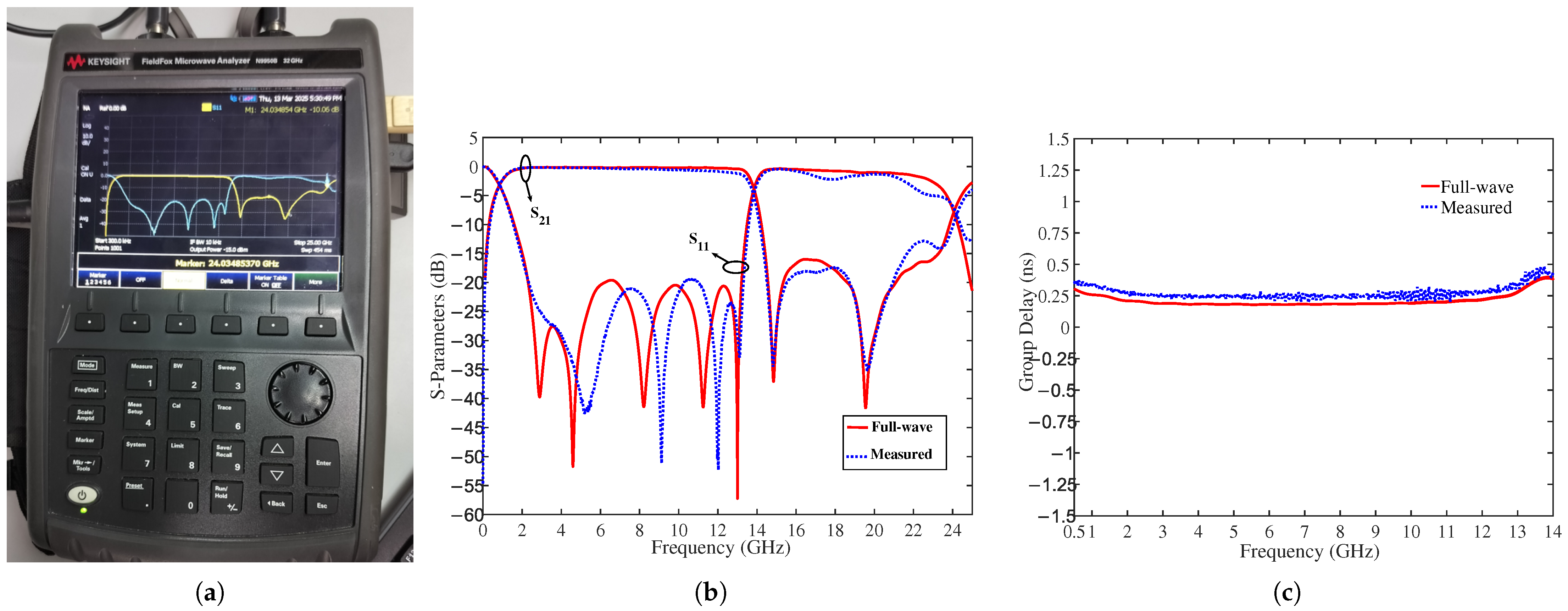
3. Experimental Results and Discussion
Figure of Merit
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Aiello, G.; Rogerson, G. Ultra-wideband wireless systems. IEEE Microw. Mag. 2003, 4, 36–47. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering: Theory and Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Hsu, C.L.; Hsu, F.C.; Kuo, J.K. Microstrip bandpass filters for Ultra-Wideband (UWB) wireless communications. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Long Beach, CA, USA, 17 June 2005; pp. 679–682. [Google Scholar] [CrossRef]
- Tang, C.W.; Chen, M.G. A Microstrip Ultra-Wideband Bandpass Filter with Cascaded Broadband Bandpass and Bandstop Filters. IEEE Trans. Microw. Theory Tech. 2007, 55, 2412–2418. [Google Scholar] [CrossRef]
- Ramkumar, S.; Anitha, M.; Boopathi Rani, R.; Muthuramya, C. Compact Ultra-Wide-Stopband Microwave Bandpass Filter with Multiple Transmission Zeros by Integrating an L-Shaped Bandpass Filter and a Stepped Impedance Lowpass Filter. IEEE Lat. Am. Trans. 2025, 23, 437–443. [Google Scholar] [CrossRef]
- Lee, J.K.; Kim, Y.S. Ultra-Wideband Bandpass Filter with Improved Upper Stopband Performance Using Defected Ground Structure. IEEE Microw. Wirel. Compon. Lett. 2010, 20, 316–318. [Google Scholar] [CrossRef]
- Xie, J.; Tang, D.; Shu, Y.; Luo, X. Compact UWB BPF with Broad Stopband Based on Loaded-Stub and C-Shape SIDGS Resonators. IEEE Microw. Wirel. Compon. Lett. 2022, 32, 383–386. [Google Scholar] [CrossRef]
- Song, Y.; Yang, G.M.; Geyi, W. Compact UWB Bandpass Filter with Dual Notched Bands Using Defected Ground Structures. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 230–232. [Google Scholar] [CrossRef]
- Breed, G. An introduction to defected ground structures in microstrip circuits. High Freq. Electron. 2008, 7, 50–54. [Google Scholar]
- Wang, H.; Zhu, L.; Menzel, W. Ultra-wideband bandpass filter with hybrid microstrip/CPW structure. IEEE Microw. Wirel. Compon. Lett. 2005, 15, 844–846. [Google Scholar] [CrossRef]
- Thomson, N.; Hong, J.S. Compact Ultra-Wideband Microstrip/Coplanar Waveguide Bandpass Filter. IEEE Microw. Wirel. Compon. Lett. 2007, 17, 184–186. [Google Scholar] [CrossRef]
- Ghazali, A.N.; Sazid, M.; Virdee, B. A compact UWB-BPF based on microstrip-to-CPW transition with multiple transmission zeros. Microw. Opt. Technol. Lett. 2018, 60, 1925–1928. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, W.; Wu, Y. Synthesis of High-Selectivity Ultra-Wideband Reflective/Absorptive Bandpass Filters with Unequal-Width Three-Coupled Line Sections. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 1961–1965. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, G.; Tam, K.W.; Zhou, X.; Chen, S. Millimeter-Wave On-Chip Ultrawideband Bandpass Filter on Coupled Line Based Bi-Path Topology Using GaAs Technology. IEEE Trans. Compon. Packag. Manuf. Technol. 2025, 15, 553–559. [Google Scholar] [CrossRef]
- Makimoto, M.; Yamashita, S. Bandpass Filters Using Parallel Coupled Stripline Stepped Impedance Resonators. IEEE Trans. Microw. Theory Tech. 1980, 28, 1413–1417. [Google Scholar] [CrossRef]
- Shome, P.P.; Khan, T.; Koul, S.K.; Antar, Y.M. Two Decades of UWB Filter Technology: Advances and Emerging Challenges in the Design of UWB Bandpass Filters. IEEE Microw. Mag. 2021, 22, 32–51. [Google Scholar] [CrossRef]
- Li, M.; Yang, Y.; Iacopi, F.; Yamada, M.; Nulman, J. Compact Multilayer Bandpass Filter Using Low-Temperature Additively Manufacturing Solution. IEEE Trans. Electron Devices 2021, 68, 3163–3169. [Google Scholar] [CrossRef]
- Wang, M.; Sun, S.; Ma, H.F.; Cui, T.J. Supercompact and Ultrawideband Surface Plasmonic Bandpass Filter. IEEE Trans. Microw. Theory Tech. 2020, 68, 732–740. [Google Scholar] [CrossRef]
- Yang, L.; Zhu, L.; Zhang, R.; Wang, J.; Choi, W.W.; Tam, K.W.; Gómez-García, R. Novel Multilayered Ultra-Broadband Bandpass Filters on High-Impedance Slotline Resonators. IEEE Trans. Microw. Theory Tech. 2019, 67, 129–139. [Google Scholar] [CrossRef]
- Wu, C.H.; Lin, Y.S.; Wang, C.H.; Chen, C.H. A compact LTCC ultra-wideband bandpass filter using semi-lumped parallel-resonance circuits for spurious suppression. In Proceedings of the 2007 European Microwave Conference, Munich, Germany, 9–12 October 2007; pp. 532–535. [Google Scholar] [CrossRef]
- Tian, H.; Liu, H. Miniaturized Ultra-Wideband HTS Bandpass Filter Using High-Q CRLH Transmission Line. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 2599–2603. [Google Scholar] [CrossRef]
- Long, Z.; Tian, M.; Zhang, T.; Qiao, M.; Wu, T.; Lan, Y. High-Temperature Superconducting Multimode Dual-Ring UWB Bandpass Filter. IEEE Trans. Appl. Supercond. 2020, 30, 1500204. [Google Scholar] [CrossRef]
- Dai, J.; Wu, Y.; Yuan, Y.; Wang, X.; Zhang, C.; Wang, J.; Li, G.; Li, C.; Sun, L.; Luo, S.; et al. HTS Wideband Bandpass Filter Based on Ladder Topology Circuit and Microstrip Transformation. IEEE Trans. Appl. Supercond. 2021, 31, 1501007. [Google Scholar] [CrossRef]
- Zhu, L.; Sun, S.; Menzel, W. Ultra-wideband (UWB) bandpass filters using multiple-mode resonator. IEEE Microw. Wirel. Compon. Lett. 2005, 15, 796–798. [Google Scholar] [CrossRef]
- Wang, H.; Chu, Q.X.; Gong, J.Q. A Compact Wideband Microstrip Filter Using Folded Multiple-Mode Resonator. IEEE Microw. Wirel. Compon. Lett. 2009, 19, 287–289. [Google Scholar] [CrossRef]
- Nosrati, M.; Mirzaee, M. Compact Wideband Microstrip Bandpass Filter Using Quasi-Spiral Loaded Multiple-Mode Resonator. IEEE Microw. Wirel. Compon. Lett. 2010, 20, 607–609. [Google Scholar] [CrossRef]
- Weng, M.H.; Liauh, C.T.; Wu, H.W.; Vargas, S.R. An Ultra-Wideband Bandpass Filter with an Embedded Open-Circuited Stub Structure to Improve In-Band Performance. IEEE Microw. Wirel. Compon. Lett. 2009, 19, 146–148. [Google Scholar] [CrossRef]
- Song, K.; Xue, Q. Inductance-Loaded Y-Shaped Resonators and Their Applications to Filters. IEEE Trans. Microw. Theory Tech. 2010, 58, 978–984. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, F. An UWB Bandpass Filter Based on a Novel Type of Multi-Mode Resonator. IEEE Microw. Wirel. Compon. Lett. 2012, 22, 506–508. [Google Scholar] [CrossRef]
- Ahmed, K.U.; Virdee, B.S. Ultra-Wideband Bandpass Filter Based on Composite Right/Left Handed Transmission-Line Unit-Cell. IEEE Trans. Microw. Theory Tech. 2013, 61, 782–788. [Google Scholar] [CrossRef]
- Zhang, T.; Tian, M.; Long, Z.; Qiao, M.; Fu, Z. High-Temperature Superconducting Multimode Ring Resonator Ultrawideband Bandpass Filter. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 663–665. [Google Scholar] [CrossRef]
- Sheikhi, A.; Alipour, A.; Mir, A. Design and Fabrication of an Ultra-Wide Stopband Compact Bandpass Filter. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 265–269. [Google Scholar] [CrossRef]
- Kanaparthi, V.P.K.; Velidi, V.K.; Rajkumar, R.; Rama Rao, T. A Compact Ultra-Wideband Multimode Bandpass Filter with Sharp-Rejection Using Stepped Impedance Open Stub and Series Transformers. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4824–4828. [Google Scholar] [CrossRef]
- Tang, C.W.; Chen, C.A. Analysis and Design of Planar Extremely-Wideband Bandpass Filter with Broad Stopband Performance. IEEE Access 2024, 12, 131785–131793. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Sarkar, P.; Ghatak, R. A Bandwidth Reconfigurable Bandpass Filter for Ultrawideband and Wideband Applications. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 2747–2751. [Google Scholar] [CrossRef]
- Rajender, R.; Ciarpi, G.; Genovesi, S.; Rossi, D. Design of an Ultra-wideband Multiple-Mode Resonator (MMR)-Based High Selectivity Bandpass Filter. In Applications in Electronics Pervading Industry, Environment and Society, Proceedings of the ApplePies 2024, Turin, Italy, 19–20 September 2024; Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2024; Volume 1369, pp. 304–312. [Google Scholar]
- Zeng, J.; Li, X.; Qi, Z. UWB bandpass filter with compact size and wide upper stopband. Microw. Opt. Technol. Lett. 2020, 62, 1521–1525. [Google Scholar] [CrossRef]
- Zhou, C.X.; Guo, P.P.; Zhou, K.; Wu, W. Design of a Compact UWB Filter with High Selectivity and Superwide Stopband. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 636–638. [Google Scholar] [CrossRef]
- Nadeem, A.; Shoaib, N.; Papadakis, A.; Nikolaou, S.; Psychogiou, D.; Vryonides, P. Advanced Techniques for Designing Wideband and Highly Selective Bandpass Filters Through Cascaded Modules. IEEE Access 2025, 13, 34936–34945. [Google Scholar] [CrossRef]
- Xie, Y.; Chen, F.C.; Li, Z. Design of Dual-Band Bandpass Filter with High Isolation and Wide Stopband. IEEE Access 2017, 5, 25602–25608. [Google Scholar] [CrossRef]
- Krishna, I.S.; Barik, R.K.; Karthikeyan, S.S. A miniaturized wideband bandpass filter based on 3λ/4 resonator loaded with stepped impedance. In Proceedings of the 2017 Twenty-Third National Conference on Communications (NCC), Chennai, India, 2–4 March 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Psychogiou, D.; Gómez-García, R.; Peroulis, D. Constant In-Band Group-Delay Acoustic-Wave-Lumped-Element-Resonator-Based Bandpass Filters and Diplexers. IEEE Trans. Microw. Theory Tech. 2018, 66, 2199–2209. [Google Scholar] [CrossRef]
- Abbosh, A.M. Planar Bandpass Filters for Ultra-Wideband Applications. IEEE Trans. Microw. Theory Tech. 2007, 55, 2262–2269. [Google Scholar] [CrossRef]
- Qian, S.; Hong, J. Miniature Quasi-Lumped-Element Wideband Bandpass Filter at 0.5–2-GHz Band Using Multilayer Liquid Crystal Polymer Technology. IEEE Trans. Microw. Theory Tech. 2012, 60, 2799–2807. [Google Scholar] [CrossRef]


| Parameter | ||||||
| Value | 47.09 | 42.20 | 71.88 | 57.60 | 137.28 | 33° |
| Ref. | (GHz) | FBW (%) | IL (dB) | RL (dB) | SF | Group Delay (ns) | HS | Size () | ML | Filt. Conf./Fabr. Pro. |
|---|---|---|---|---|---|---|---|---|---|---|
| [5] | 2.10 | 140.4 | 0.8 | >15.0 | N/A | 0.4 e–0.8 | 14.3 (22.5 dB) | 0.23 × 0.37 | No | BPF + LPF/Conv. PCB |
| [7] | 6.85 | 114.0 | 0.60 | >14.0 | N/A | 0.30–0.60 | 9.70 (26 dB) | 0.354 × 0.302 | Yes | SIDGS Res./ML-PCB |
| [13] | 3.04 | 110.3 | 0.79 | >12.9 | N/A | 0.60–2.00 | 2.53 (18.7 dB) | 0.70 × 0.30 | No | UWTCL/Conv. PCB |
| [18] | 2.40 | 174.0 | 1.10 | >11.0 | N/A | 0.90–2.06 | 2.91 (20 dB) | 1.30 × 0.19 | Yes | SSPP/ML-PCB |
| [19] | 2.001 | 133.7 | 0.65 | >13.6 | N/A | 1.23 | 2.09 (10 dB) | 0.8 × 0.51 | Yes | HISL Res./ML-PCB |
| [21] | 6.00 | 73.0 | 0.18 | >17.8 | 0.84 | 0.5 e–0.90 | 2.0 (22 dB) | 0.07 × 0.23 | No † | High-Q CRLH-TL/HTS-PCB |
| [22] | 6.85 | 125.3 | 0.42 | >15.2 | 0.87 | 0.16–1.06 | 2.33 (20 dB) | 1.57 × 1.18 | No † | Dual-Ring Res./HTS-PCB |
| [23] | 1.75 | 108.0 | 0.29 | >14.0 | N/A | N/A | 2.28 (40 dB) | 0.73 × 0.47 | No † | LPF-Derived BPF/HTS-PCB |
| [30] | 6.82 | 115.0 | 0.50 | >11.0 | 0.86 | 0.10–0.50 | 2.34 (18 dB) | 0.56 × 0.16 | No | CRLH-TL/Conv. PCB |
| [31] | 4.04 | 122.3 | 0.75 | >10.7 | 0.91 | 0.19–1.78 | 2.22 (20 dB) | 1.53 × 0.45 | No † | Ring-MMR/HTS-PCB |
| [32] | 6.95 | 97.0 | 0.42 | >19.0 | N/A | 0.025–0.37 + | 4.31 * (24 dB) | 0.128 × 0.378 | No | Two 5-Stage SIRs/Conv. PCB |
| [33] | 2.49 | 103.2 | 0.87 | >15.0 | 0.93 | 0.99–2.20 | 2.20 (25 dB) | 0.165 | No | SIOS & ST/Con. PCB |
| [34] | 4.50 | 155.6 | 0.72 | >13.5 | N/A | 0.60 e–1.40 | 8.9 (30 dB) | 0.60 × 0.44 | No | MSCLP/Conv. PCB |
| [35] | 6.80 | 132.8 | 1.60 | >10.0 | N/A | 0.68–0.90 | 2.72 (12 dB) | 0.80 × 0.42 | No | OSSLR-SSSLR/Conv. PCB |
| [37] | 6.85 | 110.9 | 0.9 | >13.0 | N/A | 0.2–0.40 | 4.38 (18 dB) | 0.22 × 0.20 | No | CRLH-TL/Conv. PCB |
| [38] | 6.85 | 110.1 | 1.6 | >12.0 | 0.92 | N/A | 3.50 * (15 dB) | 0.60 × 0.54 | No | HM-SIW + EBG/SIW-PCB |
| T.W. | 6.85 | 176.6 | 0.33 | >19.3 | 0.87 | 0.20–0.45 | 3.44 (14 dB) | 0.79 × 0.28 | No | SSSIS & SOS/Conv. PCB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajender, R.; Barik, R.K.; Ciarpi, G.; Koziel, S.; Genovesi, S.; Rossi, D. A Novel Multi-Mode Resonator-Based Ultra-Wideband Bandpass Filter Topology. Electronics 2025, 14, 3992. https://doi.org/10.3390/electronics14203992
Rajender R, Barik RK, Ciarpi G, Koziel S, Genovesi S, Rossi D. A Novel Multi-Mode Resonator-Based Ultra-Wideband Bandpass Filter Topology. Electronics. 2025; 14(20):3992. https://doi.org/10.3390/electronics14203992
Chicago/Turabian StyleRajender, Rathod, Rusan Kumar Barik, Gabriele Ciarpi, Slawomir Koziel, Simone Genovesi, and Daniele Rossi. 2025. "A Novel Multi-Mode Resonator-Based Ultra-Wideband Bandpass Filter Topology" Electronics 14, no. 20: 3992. https://doi.org/10.3390/electronics14203992
APA StyleRajender, R., Barik, R. K., Ciarpi, G., Koziel, S., Genovesi, S., & Rossi, D. (2025). A Novel Multi-Mode Resonator-Based Ultra-Wideband Bandpass Filter Topology. Electronics, 14(20), 3992. https://doi.org/10.3390/electronics14203992










