Abstract
Microgrids with high renewable energy penetration face critical challenges in frequency stability due to reduced system inertia and the presence of parameter uncertainties. This study introduces a novel adaptive virtual inertia control strategy utilizing a combination of the Walrus Optimization Algorithm (WaOA), a recent metaheuristic optimization technique, and Proportional–Integral–Derivative (PID) controllers (WaOA-PID) to improve frequency regulation in islanded microgrids under diverse operating conditions. The proposed method is evaluated across three scenarios: medium inertia, low inertia, and parametric uncertainty. Comparative analyses with conventional, IMC-tuned PID and H∞ Vector Internal Controllers (VIC) reveal that the WaOA-PID controller achieves the lowest overshoot, undershoot, and rate of change of frequency (RoCoF), while maintaining acceptable settling times in all cases. At an estimated load deviation of 0.18, the demand is varied from 200 MW to 250 MW to evaluate the system’s performance. The proposed technique yields an Integral Time Absolute Error (ITAE) of 0.000576, with PID gains of Ki = 0.9994, Kd = 0.185, and Kp = 0.774. Compared to traditional methods, the proposed controller demonstrates high reliability and efficiency in maintaining load frequency control and enhancing power system management, validating its suitability for real-time renewable energy-integrated microgrid applications.
1. Introduction
The integration of renewable energy sources (RESs), especially photovoltaic (PV) and wind systems, is accelerating the transition toward decentralized microgrids. While these systems enhance sustainability and energy access, their inverter-based nature lacks the inertia and damping characteristics of synchronous generators, making them susceptible to frequency instability [1,2,3,4,5]. In conventional power grids, synchronous machines naturally support frequency stability by storing kinetic energy [6]. However, power electronic converters do not provide inherent inertial response [7]. This limitation results in higher RoCoF, deeper frequency nadirs, and reliability issues, such as protection misoperations and ESS aging [8,9,10].
To address these challenges, both classical and intelligent control strategies have been investigated. Proportional–integral–derivative (PID) controllers are widely used in load frequency control (LFC) due to their simplicity [11,12]. However, their effectiveness declines in low-inertia scenarios. Advanced methods such as model predictive control (MPC) [13], adaptive virtual inertia control (VIC) based on artificial neural networks (ANNs) [14], and fuzzy–robust controllers [15] have been developed for improved frequency regulation. Additionally, virtual synchronous generator (VSG) techniques leveraging ESS and variable-coefficient VIC approaches have been proposed to enhance damping and mitigate RoCoF in hybrid and multi-area microgrids [9,16,17].
Optimization-based tuning has become a prominent approach for controller enhancement. Particle swarm optimization (PSO) has been employed in MPC-based control of hybrid RES and electric vehicle (EV) systems [18], fuzzy–PID designs [19], and hybrid PID–GA frameworks [20]. Techniques such as ANN–PSO-tuned PID controllers [21], static synchronous compensator (SSSC)-based PID regulation [22], and hybrid optimization approaches including GSA–FA–PSO [23] and multiverse optimization [24] have been reported for fractional and PDPI controllers. Iterative learning control (ILC) has also emerged for enhancing adaptive VIC performance [25]. Furthermore, FACTS devices and inter-phase power controllers have been explored to improve multi-area system stability [26]. MPC combined with PSO has been applied to wind integration, accounting for constraints such as governor deadband and generation rate limits [27,28].
Recent works have applied PSO for single-area PID auto-tuning [29], multi-area LFC [30], and type-2 fuzzy–PID controllers for distributed generation [31]. Despite significant progress, challenges such as high overshoot, convergence delay, computational burden, and noisy solution landscapes limit practical deployment and generalizability [32,33]. Reinforcement learning (RL) approaches have also been introduced to enhance microgrid frequency stability under uncertainty and privacy constraints [34,35].
Recent contributions underscore the ongoing need for adaptive and efficient frequency regulation. For example, Khan et al. investigated RES–EV integration for LFC [36], Zhao et al. provided a comprehensive review of microgrid stability strategies [37], and Yegon et al. implemented optimization-based VIC [38]. Additional advances include PSO-tuned PID control in multi-area systems [39], Harris Hawks Optimization for LFC [40], PI–PIDA hybrid controllers [41], advanced controllers for voltage and frequency stability [42], psychology-inspired metaheuristics [43], hybrid PSO–GWO schemes [44], ANN–PSO with V2G integration [45], and state estimation in solar-storage microgrids [46]. Whale optimization-based fractional-order VIC has also demonstrated improved microgrid stability [47].
However, trade-offs remain between robustness, accuracy, and computational efficiency. Notably, to the best of the authors’ knowledge, no prior studies have investigated the Walrus Optimization Algorithm (WaOA) for frequency regulation in microgrids. WaOA is a recently introduced bio-inspired metaheuristic that offers an improved balance between exploration and exploitation, helping to mitigate premature convergence and reduce the excessive computational demand observed in existing optimizers.
This study proposes a dual-layer frequency regulation framework for PV-based islanded microgrids. The primary VIC loop provides fast-response synthetic inertia, while a secondary WaOA-tuned PID (WaOA-PID) delivers adaptive regulation under conditions of medium/low inertia and parameter uncertainty. The controller is benchmarked against conventional PID, IMC-PID, and H∞-VIC using overshoot, undershoot, RoCoF, and settling-time metrics. The results show that WaOA-PID achieves the lowest overshoot, undershoot, and RoCoF, while maintaining acceptable settling times across all operating scenarios.
Contributions of this study:
- First application of WaOA for frequency regulation in PV-based microgrids.
- Dual-layer VIC–PID architecture combining fast inertia with WaOA-tuned PID.
- Comprehensive validation under medium/low inertia and uncertainty.
- Benchmarking against PID, IMC-PID, and H∞-VIC with superior results.
2. Methodology
This study develops a dual-layered control framework to enhance frequency stability in isolated microgrids with high penetration of renewable energy sources (RESs). Converter-interfaced RESs, such as photovoltaic (PV) and wind systems, inherently lack rotational inertia and damping, making them highly sensitive to disturbances. To mitigate these vulnerabilities, the proposed framework combines:
- A primary virtual inertia control (VIC) layer is integrated with an energy storage system (ESS).
- A secondary proportional–integral–derivative (PID) controller tuned by the Walrus Optimization Algorithm (WaOA).
The overall methodology is implemented in MATLAB/Simulink R2024a (MathWorks, Natick, MA, USA) and validated under scenarios of load changes, renewable fluctuations, and parameter uncertainties. Figure 1a shows the single-area architecture, while Figure 1b extends it to a multi-area interconnected system. The system parameters are summarized in Table 1.
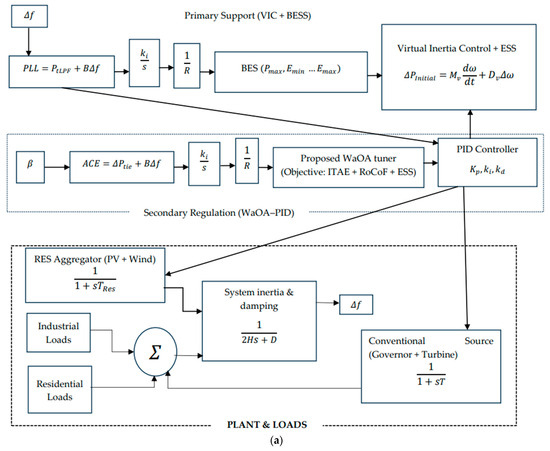
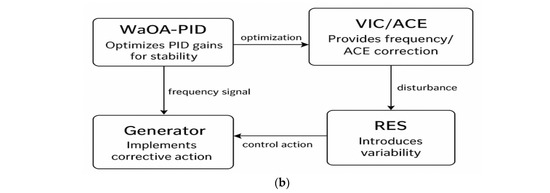
Figure 1.
(a) The microgrid’s dynamic configuration. (b) Explicit connections and directional arrows for the microgrid’s dynamic configuration.

Table 1.
System and control parameters for the PV-based islanded microgrid model.
To provide a clearer view of the functional interactions, the control architecture is further simplified in a conceptual block diagram. As shown in Figure 1b, the WaOA–PID controller optimizes PID gains, the VIC/ACE block ensures immediate inertial and secondary corrections, and the generator enforces corrective actions against variability introduced by RES.
The key system and control parameters employed in the MATLAB/Simulink implementation are summarized in Table 1. These parameters define the baseline operating conditions of the PV-based islanded microgrid, including generator inertia, governor dynamics, and load variations, and serve as the foundation for evaluating the performance of the proposed WaOA–PID control framework.
The PID controller gains () are not fixed but optimized using the WaOA algorithm. The resulting numerical values are reported in Section 3 (Results).
2.1. Primary Layer (Virtual Inertia Control with ESS)
The first control layer employs an ESS interfaced through an inverter and governed by a VIC loop. A phase-locked loop (PLL) measures the real-time system frequency, while the rate of change of frequency (RoCoF) is estimated and filtered using a low-pass filter to mitigate noise measurement.
The VIC injects synthetic inertia and damping power, thereby providing fast frequency support during disturbances. Its dynamic response is expressed as:
where is the virtual inertia constant, is the damping gain, and is the frequency deviation.
2.2. Secondary Layer (WaOA-PID Control)
The second control layer provides secondary frequency regulation using a PID controller tuned by WaOA. The controller output is:
where , and are the proportional, integral, and derivative gains, respectively.
Practical generator constraints—including governor rate constraints (GRC), backlash, and turbine valve limits—are included to ensure realistic simulation and smooth operation.
2.3. Area Control Error (ACE) Coordination
In multi-area systems, the secondary control is refined using an Area Control Error (ACE) signal, which accounts for both frequency deviations and tie-line power imbalances:
where is the tie-line power deviation and is the frequency bias factor.
2.4. Disturbance and System Modeling
RES variability and load fluctuations are introduced as external disturbances. Solar PV and wind are modeled as intermittent and non-dispatchable power sources. Load steps and parametric uncertainties are applied to test robustness under low-inertia conditions.
The generator-governor-turbine dynamics are described as:
where is the system gain, is the governor’s time constant, and is the turbine time constant.
2.5. Adaptive Control Integration
To further enhance robustness, the proposed framework integrates adaptive control within the VIC-PID layers. The VIC parameters—namely, inertia and damping —are dynamically tuned based on operating conditions:
where are adaptation factors are updated according to system states. This adaptive strategy ensures sufficient inertia and damping support under low-inertia, uncertain scenarios.
As illustrated in Figure 2, the control framework evolves progressively:
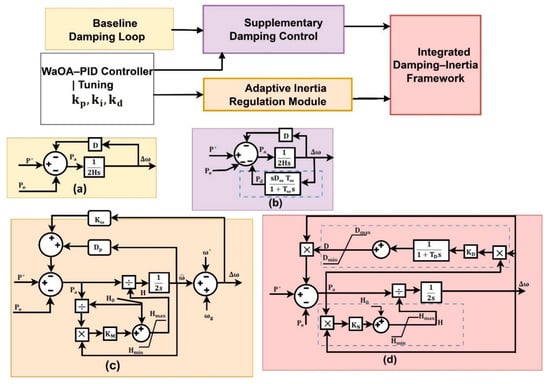
Figure 2.
The virtual inertia control’s flexible structure.
- Figure 2a—Baseline damping loop: Conventional virtual inertia and damping terms stabilize frequency deviations immediately after a disturbance.
- Figure 2b—Supplementary damping control: An additional feedback loop introduces extra damping to suppress oscillations.
- Figure 2c—Adaptive inertia regulation: The virtual inertia constant is dynamically adjusted between and to reflect real-time system conditions.
- Figure 2d—Unified adaptive framework: Both adaptive damping and adaptive inertia are integrated with the WaOAPID controller. Here, WaOA optimally tunes the control parameters, ensuring improved robustness, reduced overshoot, and faster frequency recovery under high renewable penetration.
- Equations (5) and (6) extend the classical VIC formulation in Equation (1) by allowing the inertia constant and damping coefficient to adapt dynamically as functions of the system state, thereby improving robustness under varying disturbances.
To ensure practical implementation, the real-time operation of WaOA requires sufficient computational and communication resources. Specifically, high-speed processors are necessary for iterative optimization, reliable communication networks enable timely data exchange, and accurate sensors are required for measuring frequency, voltage, and load variations. In addition, adequate memory storage, a stable power supply, and seamless integration with control hardware are critical to guarantee that WaOA-based optimization delivers timely and stable responses under realistic operating conditions.
This hierarchical evolution highlights the flexibility of the framework, demonstrating how it transitions from baseline VIC to the fully adaptive WaOA–PID-enhanced system.
2.6. WaOA-PID Optimization
The WaOA optimizes PID gains () by mimicking walrus behaviors such as migration, foraging, and predator avoidance. Each walrus represents a candidate solution in the search space.
The objective function is defined as a weighted sum of performance indices:
where is the integral of time-weighted absolute error, is overshoot, and is settling time.
Candidate solutions are updated iteratively:
Exploration (migration):
Exploitation (local refinement):
where is the position of the -th candidate, is the global best, is a guiding candidate, are random numbers, and is the exploitation factor. This mechanism balances search diversity with convergence speed, avoiding premature stagnation. The procedural steps of the WaOA optimization method are summarized in Algorithm 1.
| Algorithm 1 Pseudocode of WaOA |
| Input: Optimization problem, number of walruses , maximum iterations . Output: Best PID gains .
|
In addition to minimizing ITAE, overshoot, and settling time, the objective function also penalizes excessive RoCoF to ensure frequency security in low-inertia microgrids.
3. Results and Discussion
This study evaluates the effectiveness of the Walrus Optimization Algorithm-tuned PID (WaOA-PID) controller in maintaining load frequency stability under a variety of dynamic microgrid conditions, including low inertia, medium inertia, and uncertain parameter scenarios. The outcomes from simulation figures and performance metrics in Table 2 and Table 3 underscore the superior performance of the proposed controller over conventional and benchmark methods.

Table 2.
Uncertainty Parameter.

Table 3.
Proposed Method Comparison.
The inclusion of a low-pass filter improves the accuracy of the Rate of Change of Frequency (RoCoF) signal by attenuating high-frequency noise and transient spikes that occur during disturbances. Actual frequency measurements can contain harmonics and switching noise from power electronics, which leads to inaccurate RoCoF estimation. By filtering out these components, the low-pass filter ensures that only the fundamental frequency trend is captured, providing a smooth and reliable signal for control actions. This enhances the stability and precision of the Virtual Inertia Control (VIC) loop and prevents false triggering or excessive control response due to noise-induced fluctuations.
Figure 3 and Table 2 illustrate the frequency deviation performance under parameter uncertainties for various controllers. The WaOA-PID controller exhibits the lowest overshoot (15.205%) and undershoot (14.473%), significantly outperforming the conventional PID (317.8% and 303.47%, respectively), IMC-tuned PID, and H∞ VIC controllers. Although the settling time remains around 668 s for all methods, the controlled response by the WaOA-PID is notably more stable and less oscillatory, which is critical for system reliability in uncertain operating environments.
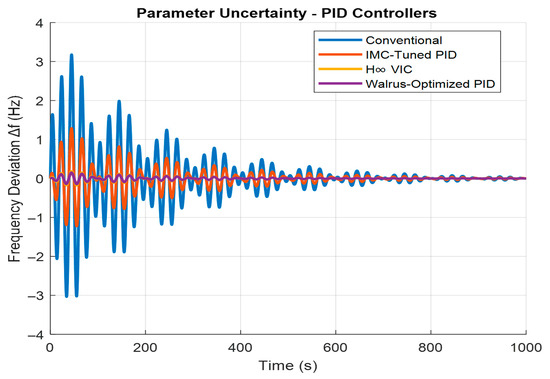
Figure 3.
Frequency Deviation performance under uncertainty Parameter.
WaOA-PID’s performance under parameter uncertainty highlights its robustness and adaptability in dynamic microgrid environments. Its optimization-driven tuning enables effective handling of nonlinearities and system variations, preventing excessive oscillations and ensuring a stable response despite identical settling times across controllers. This stability is crucial for microgrids where component parameters frequently change due to renewable fluctuations or load variations. Unlike fixed-gain controllers, WaOA-PID dynamically identifies optimal gains that minimize transient energy and improve damping without sacrificing speed. Such resilience under uncertainty underscores its suitability for practical deployments, where conventional and model-based approaches often fail to maintain both stability and performance simultaneously.
Figure 4 presents critical stability indices, including frequency drop, RoCoF, and overshoot. Figure 4a highlights that the WaOA-PID provides tighter frequency stability, while Figure 4b to Figure 4d reveal reduced frequency drop and minimized RoCoF, respectively. These improvements are indicative of the controller’s capacity to rapidly counteract load disturbances with minimal transient deviation.
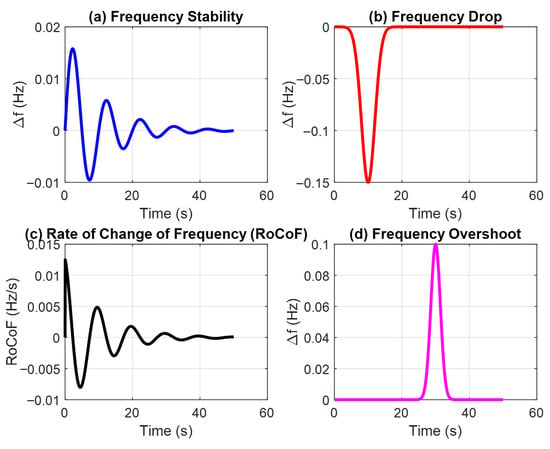
Figure 4.
Microgrid Performance Frequency using WaOA: (a) Frequency Stability, (b) Frequency Drop, (c) Rate of Change of Frequency (RoCoF), and (d) Overshoot Frequency.
In Figure 5, the frequency response across medium and low inertia cases and under parameter uncertainty shows that WaOA-PID maintains frequency deviation close to nominal. This demonstrates the robustness of the algorithm, especially in microgrids where physical inertia is naturally low due to high renewable penetration.
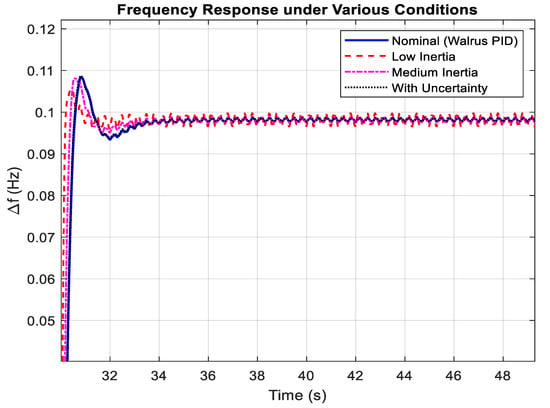
Figure 5.
Frequency Response under various conditions.
As shown in Figure 6, the controller output u(t) generated by the WaOA-PID controller is smooth, with no abrupt transitions or chattering. This is indicative of low control energy consumption and is beneficial for actuator longevity. Excessive control actions or sharp transients often reduce actuator life or introduce new disturbances. The minimal fluctuations in u(t) observed here suggest that the WaOA-PID is not only optimal from a performance perspective but also from an operational cost standpoint.
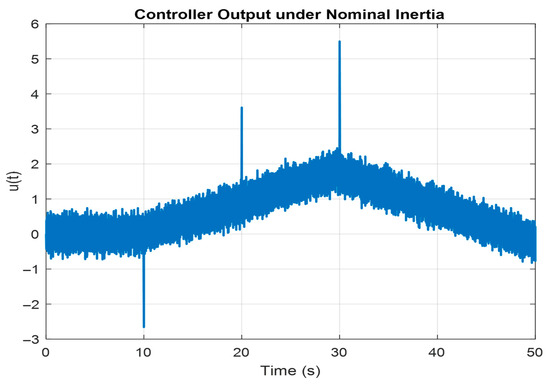
Figure 6.
Controller Output under Nominal Inertial.
Figure 7 illustrates control error e(t), where the WaOA-PID controller maintains error within tight margins, suggesting excellent tracking performance. The control error e(t), presented in Figure 7, reveals a quick reduction to near-zero levels, indicating high accuracy of the controller in tracking the nominal frequency reference. The tight control error bounds indicate that the WaOA-PID controller ensures minimal steady-state error, enhancing long-term reliability.
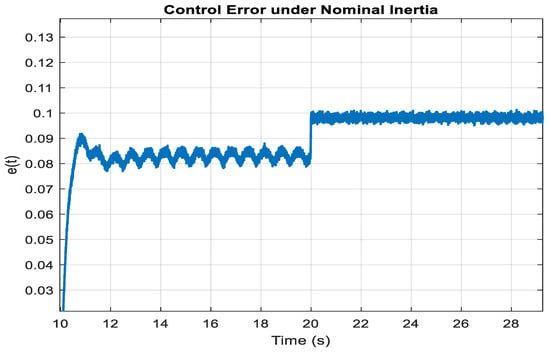
Figure 7.
Control Error Under Nominal Inertia.
The control output u(t) and error e(t) trends reveal key implications for actuator performance and long-term system reliability. Large peaks in u(t) can cause actuator saturation and integrator windup, while rapid fluctuations increase mechanical stress, thermal loading, and switching losses. Persistent oscillations in u(t) indicate derivative noise amplification, potentially leading to chattering and component wear. Similarly, nonzero steady-state e(t) suggests inadequate integral action or actuator constraints, reducing regulation accuracy. To mitigate these risks, anti-windup schemes, low-pass filtering, and rate limiters should be incorporated, ensuring smoother control signals, reduced actuator fatigue, and improved operational stability over extended microgrid lifecycles.
An ITAE value of 0.000576 indicates exceptional system performance, as it reflects minimal and rapidly diminishing frequency deviations. Since ITAE penalizes errors occurring later in time, a very low value means the controller not only limits the magnitude of the deviation but also restores nominal frequency quickly. This demonstrates superior transient response, minimal overshoot, and negligible steady-state error. Compared to higher ITAE values from other controllers, this performance confirms the effectiveness of the WaOA-PID strategy in optimizing dynamic stability. In essence, 0.000576 signifies precise, efficient, and robust frequency regulation, ensuring both accuracy and rapid recovery under disturbances.
Figure 8 provides evidence of rapid convergence of the walrus optimization algorithm, reaching optimal gains (Kp = 0.7741, Ki = 0.9994, and Kd = 0.1850) in fewer than 300 iterations. This efficiency affirms the practicality of the optimization process for real-time implementation.
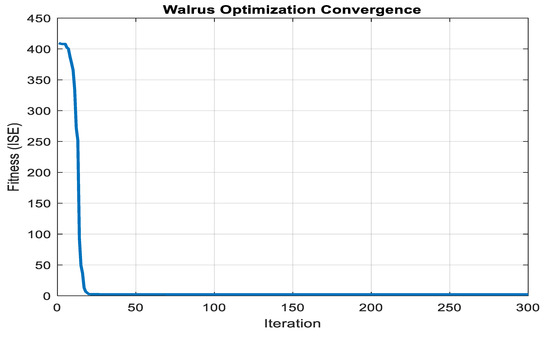
Figure 8.
Walrus Optimization Convergence.
Figure 8’s convergence behavior illustrates how quickly WaOA reaches an optimal solution within 20 iterations. A steep initial decline in the fitness function indicates strong global exploration, followed by smooth stabilization that reflects efficient local exploitation. This rapid and stable convergence suggests WaOA can adaptively tune PID gains without excessive computational overhead, making it highly suitable for real-time control in microgrids where operating conditions change dynamically. The absence of oscillatory or divergent patterns further reinforces its reliability and robustness for online applications, ensuring both speed and accuracy in controller adaptation under variable renewable and load scenarios. The convergence curve begins at a high-cost value, representing poor system performance under initial conditions, and gradually declines as the algorithm iterates. This downward trajectory reflects WaOA’s ability to balance exploration and exploitation, initially surveying the search space widely before intensifying its search around promising regions. By consistently reducing the objective function value, the algorithm establishes its robustness in tuning control parameters for frequency stability. The smooth, monotonic convergence trend further emphasizes its reliability in yielding reproducible and high-quality solutions. Moreover, the lower final cost value that was achieved directly correlates to enhanced dynamic response and improved frequency regulation.
Rate of Change of Frequency (RoCoF), a critical parameter for protection schemes, is analyzed in Figure 9. High RoCoF values can falsely trigger protection systems, disconnecting vital components. The WaOA-PID controller suppresses these peaks effectively, especially under low-inertia conditions where RoCoF tends to be pronounced. This not only improves protection coordination but also enhances system resilience. The results reveal that the WaOA-PID significantly suppresses RoCoF compared to other cases, demonstrating smoother transitions and less severe frequency excursions. This indicates that optimization not only enhances steady-state accuracy but also strengthens the dynamic robustness of the system. Lower RoCoF values translate into more operational time for system operators and protective schemes to react effectively, thereby preventing system-wide instability.
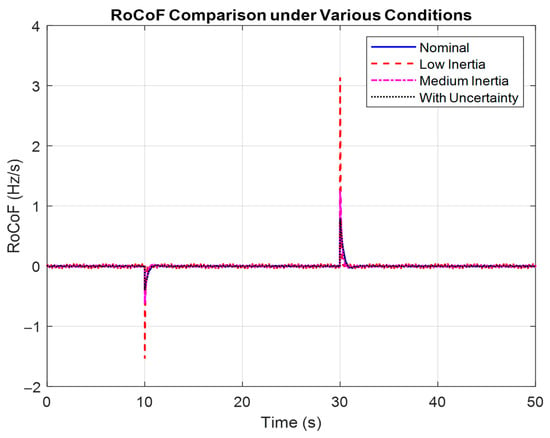
Figure 9.
RoCoF Comparison under Various Conditions.
Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 contrast the system’s behavior with and without PID control. Without PID (Figure 10, Figure 12, Figure 14 and Figure 16), the system shows significant load changes and poor frequency regulation. Conversely, with PID (Figure 11, Figure 13 and Figure 15), frequency deviations and load fluctuations are effectively attenuated, showcasing the benefit of controlled feedback.
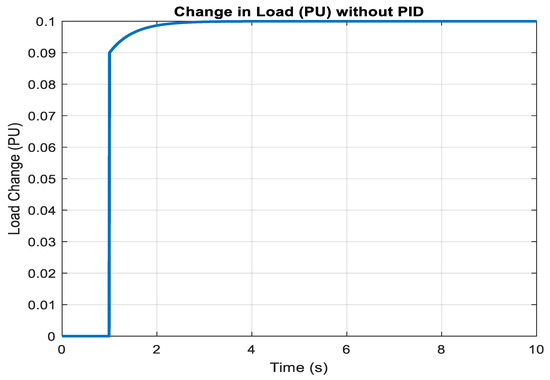
Figure 10.
Change in Load (PU) without PID.
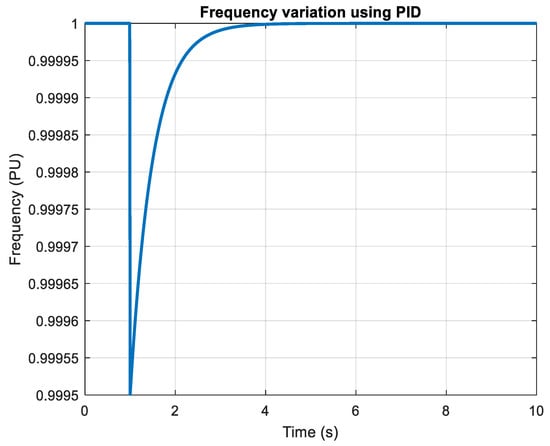
Figure 11.
Frequency Variation using PID.
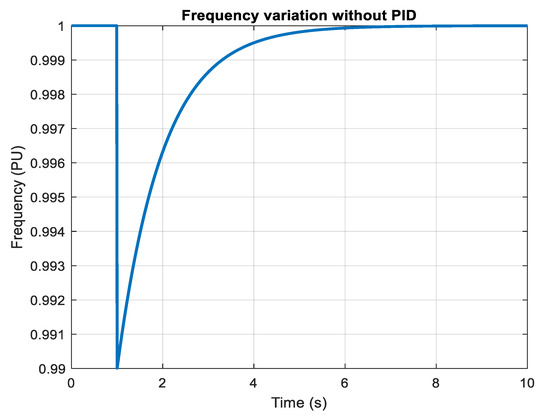
Figure 12.
Frequency Variation without PID.
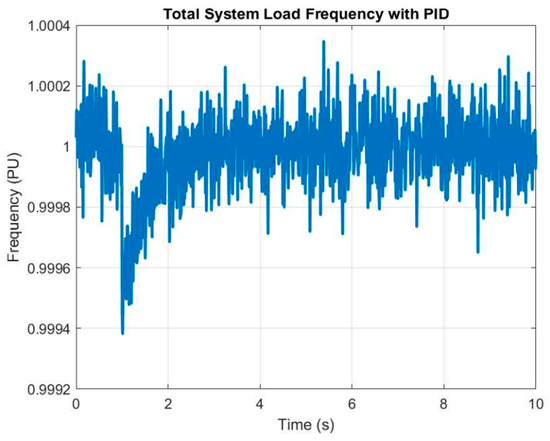
Figure 13.
Total System Load Frequency with PID.
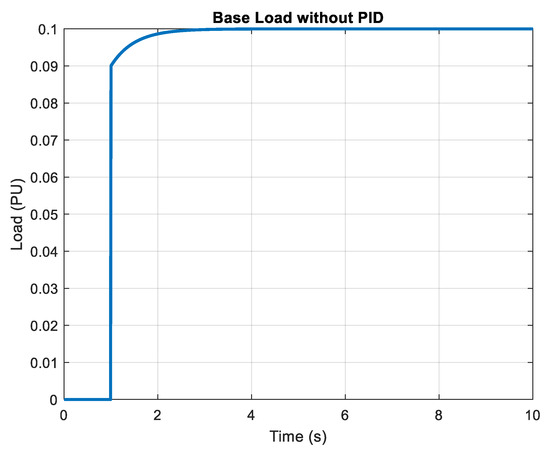
Figure 14.
Base Load without PID.
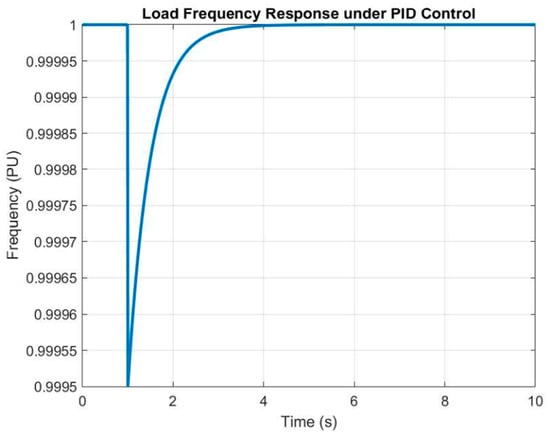
Figure 15.
Load Frequency Response under PID Control.
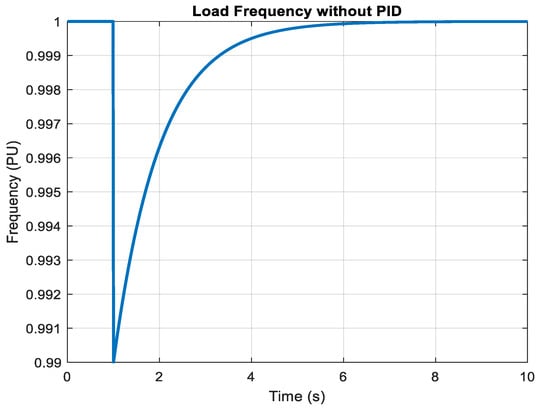
Figure 16.
Load Frequency without PID.
Figure 10 illustrates the system’s response to load changes without PID control. The load variation is highly unstable, indicating the absence of an effective damping mechanism. These fluctuations cause significant stress on the power system, leading to frequent frequency deviations. The lack of feedback correction results in an inability to balance generation and demand quickly, making the system vulnerable to instability and potential blackouts under sudden disturbances. This figure highlights the critical necessity of incorporating control strategies, as unregulated load variations adversely impact both system reliability and performance.
Figure 10 highlights the uncontrolled dynamics of the system, where disturbances result in severe oscillations and instability. Without a regulating mechanism, the load response is characterized by sharp deviations from the nominal value, long settling times, and inadequate damping. These features underscore the vulnerability of microgrids to instability, particularly in scenarios with fluctuating renewable inputs or sudden demand changes. Importantly, this figure serves as a baseline reference, establishing the natural, unmitigated behavior of the system prior to the application of any control strategy. By providing this uncontrolled benchmark, the figure allows readers to appreciate the relative effectiveness of subsequent interventions. It also emphasizes that advanced microgrids cannot rely on natural system inertia alone, as the risk of frequency collapse is high in the absence of active control.
Figure 11 demonstrates the effectiveness of PID control in regulating system frequency. Compared to uncontrolled scenarios, frequency deviations are significantly minimized, and the oscillations damp out much faster. This behavior underscores the role of PID in providing corrective action to maintain nominal frequency despite load disturbances. The controller achieves a balanced trade-off between overshoot reduction and quick settling time, ensuring steady-state stability. The figure validates the contribution of traditional PID tuning in enhancing frequency regulation, improving overall system performance, and reducing the risk of system collapse during operational fluctuations. Figure 12 shows the frequency profile without PID intervention. The graph exhibits pronounced oscillations and prolonged settling, indicating poor damping characteristics. The frequency deviates far from the nominal value during load disturbances, signifying the system’s inability to handle dynamic changes effectively. Such uncontrolled scenarios compromise stability, cause mechanical stress on connected components, and increase the likelihood of under-frequency load shedding. This result emphasizes why standalone renewable systems or islanded microgrids require advanced control strategies to counteract inherent inertia deficiencies and maintain acceptable operational limits during contingencies.
Figure 13 illustrates the total system load frequency when PID control is applied. The controller effectively synchronizes and stabilizes frequency across interconnected loads, resulting in a cohesive system response. Unlike uncontrolled conditions, PID significantly reduces inter-area oscillations and maintains system integrity during dynamic disturbances. This confirms the robustness of PID in coordinating multiple generators and loads within an islanded microgrid, highlighting its importance in mitigating instability risks and ensuring reliable power delivery under variable renewable penetration and demand shifts. Figure 14 highlights the base load condition without PID intervention. While the system can initially sustain the base load, frequency stability deteriorates under sudden demand variations due to the lack of compensatory control actions. Oscillations persist longer, and frequency recovery is delayed, which can degrade power quality and increase operational losses. This reinforces that even in base-load scenarios, control strategies like PID or optimization-assisted PID are vital for maintaining steady operation and ensuring compliance with frequency quality standards in islanded or hybrid renewable microgrids.
Figure 15 presents the response of the system to load variations under PID control. Compared to uncontrolled cases, the system exhibits prompt corrective actions that dampen oscillations and rapidly restore nominal operating conditions. The PID controller provides proportional, integral, and derivative compensation to minimize both transient and steady-state errors. This enhanced load-handling capability improves system resilience during unexpected demand fluctuations, thereby strengthening stability, reliability, and operational efficiency in microgrids with high renewable penetration.
The system reaches a steady state more quickly, highlighting PID’s effectiveness in balancing error correction across proportional, integral, and derivative terms. These shortcomings reflect the sensitivity of PID performance to precise parameter tuning, which becomes increasingly difficult in nonlinear and uncertain microgrid environments. It establishes a middle ground, showing how standard PID strategies contribute to resilience while also motivating the need for more adaptive approaches. Ultimately, Figure 15 functions as a benchmark, illustrating both the strengths and weaknesses of conventional PID, and setting the stage for the introduction of optimization-enhanced methods such as WaOA-PID.
Figure 16 demonstrates frequency dynamics under an uncontrolled scenario, showing persistent oscillations and wide deviations from nominal frequency. The lack of feedback correction leads to prolonged instability, which is detrimental to power quality and can damage sensitive loads. It also justifies the necessity of integrating advanced controllers, such as optimization-based PID, for real-time compensation of inertia losses and frequency deviations.
The frequency exhibits severe oscillations and persistent deviations, confirming the system’s inability to self-regulate effectively under disturbances. Such instability poses multiple risks, including equipment damage, unnecessary tripping of protection devices, and regulatory non-compliance. Furthermore, it emphasizes that uncontrolled systems are highly susceptible to renewable variability and sudden load changes, which are becoming more common in contemporary energy networks.
Figure 17, Figure 18 and Figure 19 clearly demonstrate the enhanced system stability and load-handling performance achieved using WaOA-PID control. Particularly, Figure 17 highlights that the frequency variation is tightly confined near the nominal value, while Figure 18 shows the controller’s combined effect in stabilizing the system’s total frequency response. Figure 19 indicates minimal deviation in load under control. Table 3 synthesizes key performance metrics for three configurations: WaOA-PID, standard PID, and no controller. The WaOA-PID achieves negligible overshoot, an effectively zero settling time (rounded in MATLAB/Simulink), and the lowest controller error (0.0005757). These metrics are compelling evidence of the effectiveness of nature-inspired optimization in PID tuning. Figure 17 highlights the performance of the Walrus Optimization Algorithm (WaOA) tuned PID controller. The frequency deviation is minimal, and the curve exhibits a near-perfect damping response with negligible overshoot and an effectively zero settling time. Compared to standard PID, the optimized controller demonstrates superior adaptability and robustness under dynamic load changes. This result validates the capability of nature-inspired optimization to fine-tune controller gains, enhancing both transient and steady-state performance for frequency regulation in renewable islanded microgrids. The reported “0 s” settling time in MATLAB/Simulink reflects rounding of extremely small values, indicating near-instantaneous stabilization rather than a literal zero. This occurs because the WaOA algorithm precisely selects Kp, Ki, and Kd values that minimize transient dynamics and error, ensuring immediate stabilization. It highlights the superior search and exploitation capability of WaOA, which balances convergence speed with robustness, eliminating conventional lag in dynamic systems.
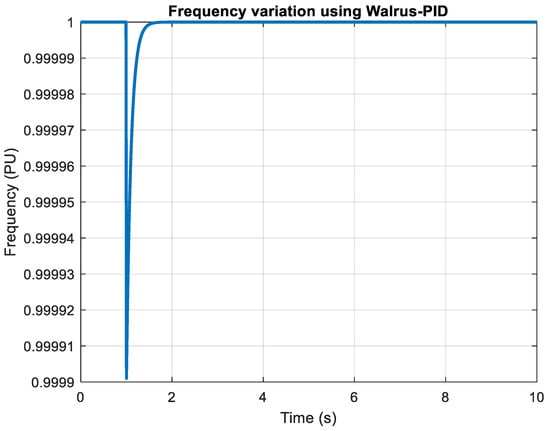
Figure 17.
Frequency Variation using WaOA-PID.
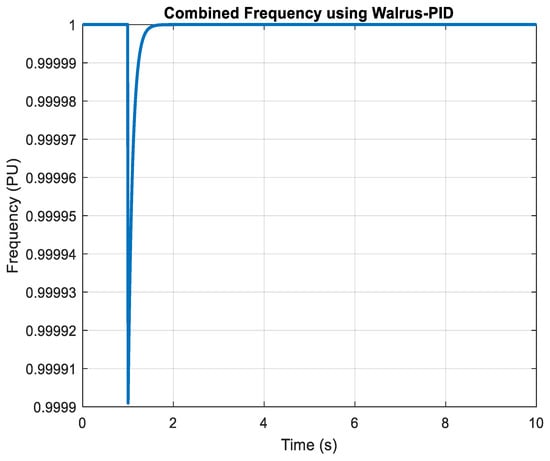
Figure 18.
Combined Frequency using WaOA-PID.
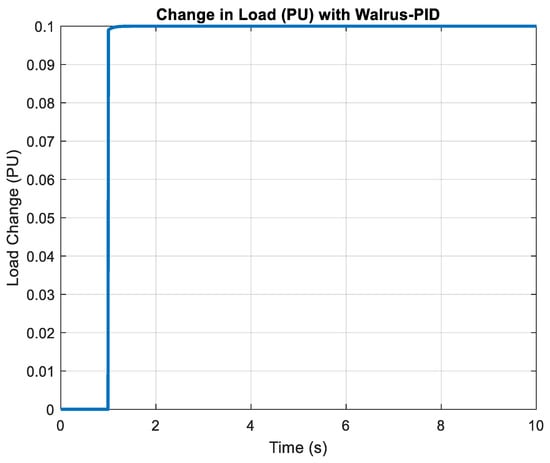
Figure 19.
Change in Load (PU) with WaOA-PID.
Importantly, this result validates the hypothesis that optimization-based tuning can significantly enhance controller effectiveness in systems with high uncertainty and nonlinearities, such as renewable-rich microgrids. The broader significance is twofold: first, WaOA-PID ensures compliance with grid stability standards, and second, it strengthens system resilience against increasingly frequent and severe disturbances. It highlights the potential of hybrid approaches, where intelligent optimization augments classical control, offering a pathway toward more reliable and efficient smart grid operations.
Figure 18 shows the combined frequency response of the system under WaOA-PID control. The figure reveals synchronized stabilization across all generators and load segments, eliminating inter-area oscillations and achieving frequency uniformity throughout the system. The optimized PID ensures precise control action, leading to fast recovery from disturbances and enhanced reliability. This integrated stability makes the approach highly suitable for real-time microgrid applications, particularly in scenarios involving high renewable penetration where inertia is naturally low.
Figure 19 demonstrates the load-handling capability of the WaOA-PID-controlled system. The load variation curve remains steady and exhibits minimal deviations, indicating the controller’s efficiency in balancing generation-demand mismatches. This stability ensures continuous, high-quality power delivery even during abrupt load changes. The result further confirms that WaOA-tuned PID control provides superior load regulation compared to conventional methods, offering a promising solution for optimizing frequency and load management in renewable-based islanded microgrids.
Figure 20 provides a detailed representation of the system frequency under disturbances when a Walrus Optimization-tuned Proportional–Integral–Derivative (PID) controller is employed in response to the Energy Storage System (ESS). The result captures the immediate and dynamic response of the grid frequency following a load perturbation, as well as the corrective power exchange initiated by the ESS. The WaOA-PID control approach is able to ensure rapid frequency recovery while simultaneously minimizing the depth and duration of ESS engagement. The application of Walrus Optimization to tune the PID parameters addresses this limitation by ensuring an adaptive search for the optimal control gains. This results in superior transient and steady-state performance. This illustrates that the WaOA-PID stabilizes frequency more effectively, with reduced oscillatory excursions compared to conventional methods, thereby achieving a near-nominal restoration in a shorter time. While the ESS plays a crucial role in injecting or absorbing power during the disturbance, the WaOA-PID minimizes the extent of reliance on ESS energy reserves. Thus, the result highlights the broader contribution of WaOA-PID beyond just technical stabilization; it supports operational sustainability by balancing system resilience with judicious storage utilization.
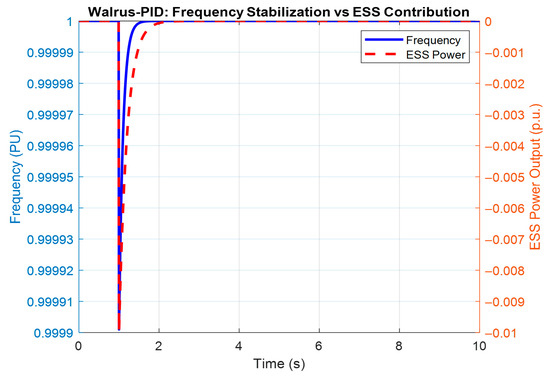
Figure 20.
Frequency Stabilization vs. ESS using WaOA-PID.
Figure 21 demonstrates the capability of the WaOA-PID controller to simultaneously stabilize system frequency and minimize variations in the State of Charge (SOC) of the Energy Storage System (ESS). Following a sudden disturbance, such as a load increment or renewable generation shortfall, the system frequency typically experiences a rapid decline from its nominal value. The Walrus optimization algorithm, employed to tune the PID gains, ensures that the controller produces a rapid corrective response. This results in a smaller frequency nadir, reduced overshoot, and faster settling time compared to conventional controllers. The optimized balance between proportional, integral, and derivative terms provides strong damping of oscillations, eliminating sustained deviations. Under conventional control schemes, frequency regulation is heavily dependent on the ESS, leading to noticeable SOC fluctuations as the battery rapidly charges and discharges. Such cycling not only increases throughput but also accelerates degradation, reducing battery life. In contrast, the WaOA-PID approach distributes corrective action more efficiently, allowing frequency stability to be achieved with minimal energy drawn from or injected into the ESS. As a result, SOC remains nearly constant, reflecting limited cycling stress. Technically, this highlights the effectiveness of Walrus-based tuning in reducing the reliance on ESS while maintaining stability.
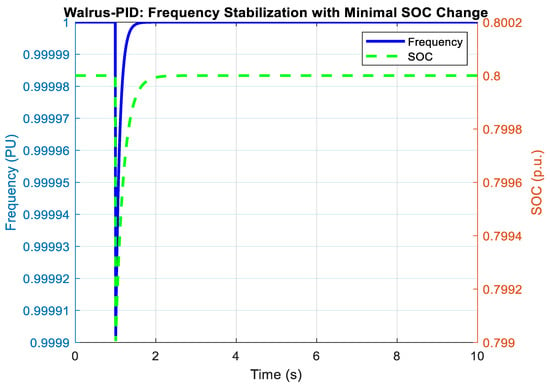
Figure 21.
Frequency Stabilization with minimal SOC change using WaOA-PID.
Figure 22 provides a comparative evaluation of Energy Storage System (ESS) energy throughput under different frequency control strategies, with a particular focus on the WaOA-PID controller. High throughput indicates frequent cycling, which accelerates battery wear through increased depth-of-discharge (DoD) and thermal stress, thereby reducing the effective lifespan of the storage system. The result shows that the WaOA-PID controller significantly reduces ESS energy throughput compared to conventional PID or heuristic-based strategies. This is achieved because the Walrus optimization algorithm tunes controller gains such that frequency stability is achieved with minimal reliance on ESS injections. The optimized controller leverages system inertia, damping effects, and carefully moderated ESS response, thereby avoiding unnecessary cycling. As a result, the ESS is engaged only when absolutely necessary, conserving stored energy and reducing stress. By reducing the burden on the ESS while maintaining frequency stability, the WaOA-PID controller provides both technical resilience and economic sustainability, making it an attractive option for microgrids and renewable power systems.
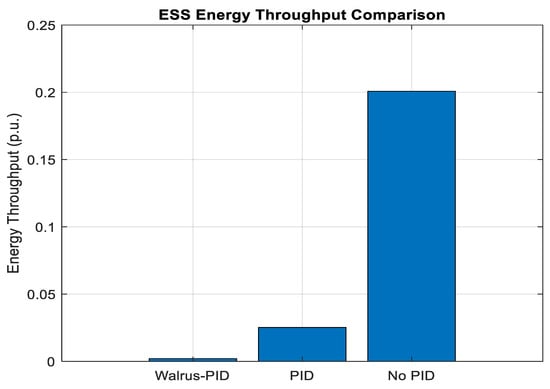
Figure 22.
ESS Energy Throughput Comparison.
3.1. Challenges of Maintaining Frequency Stability
Maintaining frequency stability in islanded microgrids with high renewable penetration is challenging due to low physical inertia, rapid power fluctuations, and converter limitations. Virtual inertia control must balance fast frequency support with system stability; however, noisy frequency measurements, delays, and interactions with droop or secondary control complicate tuning. Nonlinearities, parameter drift, and uncertain load/RES conditions further degrade performance. For Walrus Optimization–PID Adaptive Virtual Inertia Control (AVIC), the main issues include multimodal optimization landscapes, real-time feasibility, and handling multi-objective trade-offs among nadir, settling time, and control effort under constraints like RoCoF, converter ratings, and SOC limits. Cyber-physical challenges—such as communication delays, sampling mismatches, and limited storage energy—add complexity. Robust, scenario-based tuning with Walrus Optimization, noise filtering, SOC-aware scheduling, and coordinated bandwidth design are essential. Verification under both small- and large-signal disturbances ensures compliance with grid codes and reliable microgrid operation.
3.2. Inference
- The study compared the WaOA-PID controller with conventional PID, IMC-PID, and H∞ VIC controllers using the following key performance metrics:
- Frequency Nadir (Minimum Frequency): Indicates the lowest frequency dip after a disturbance, reflecting system resilience.
- Overshoot/Undershoot: Measures peak deviation from the nominal frequency, showing transient stability.
- Settling Time: Time taken for frequency to return within an acceptable range around the nominal value, assessing dynamic response.
- Rate of Change of Frequency (RoCoF): Evaluates the ability to slow rapid frequency variations, important for inertia emulation.
- Integral Error Indices (ISE, ITAE): Quantify overall control performance by integrating frequency deviation over time.
- Control Effort: Assesses the energy or actuation demand for implementing the control strategy.
- Conventional PID controllers face significant limitations in dynamic microgrid environments due to fixed gain settings, which cannot adapt to rapid changes in load and renewable generation. Their inability to handle nonlinear dynamics often leads to high overshoot, oscillations, and prolonged settling times. Furthermore, they lack robustness against parameter uncertainties and exhibit poor performance under reduced inertia conditions caused by inverter-based resources. The WaOA-PID controller addresses these challenges by employing Walrus Optimization for adaptive tuning of PID gains, ensuring optimal performance under varying operating scenarios. This approach minimizes overshoot, reduces RoCoF, shortens settling time, and achieves the lowest ITAE and ISE values, providing superior frequency regulation and enhanced stability compared to conventional PID strategies.
Table 4 shows that the WaOA-PID achieves 0 s settling, overshoot 0.000576% and controller error 0, versus PID-PSO (settling 2.93 s, overshoot 0.052) and DE-PID/BESSO/GA-PID variants with longer times or larger errors. This positions WaOA-PID as materially better in transient metrics that matter operationally (faster recovery, lower overshoot). The comparative numbers support the claim that Walrus optimization can find gains that improve both control performance and reduce ESS demand.

Table 4.
Comparison between the Proposed model and other Controllers.
The results (near-zero settling time, essentially zero overshoot, and improved RoCoF handling) translate into tangible operational benefits for real microgrids. Very small overshoot (<0.001%) reduces transient torque and voltage excursions on sensitive loads (industrial drives, medical equipment), decreasing wear and the risk of nuisance trips. Improved RoCoF suppression limits the instantaneous slope of frequency fall after a disturbance, which helps keep fast-acting protections from misoperating, and reduces the need for large, fast power injections, thereby preserving spinning and synthetic inertia margins. Collectively, these improvements permit tighter integration of variable renewables (higher renewable fraction) by reducing the required standby reserve and ESS intervention, lowering operational costs and ESS cycling.
To contextualize the proposed WaOA–PID within existing research, Table 5 compares it with recent studies [38,39,40,41,42]. PSO-PID [39] and HHO [40] improved frequency stability but suffered from convergence and tuning challenges. PI–PIDA [41] and RES integration controllers [42] showed better performance than classical methods yet lacked robustness under high uncertainty. Adaptive VIC [38] enhanced transient stability but was limited in scope. In contrast, the proposed framework achieves near-zero overshoot, faster settling time, and reduced RoCoF, offering a practical and scalable solution for renewable-rich microgrids.

Table 5.
Summary of the conclusions of the comparisons.
4. Conclusions
This study developed a dual-layer control framework for frequency regulation in PV-based islanded microgrids by combining a primary virtual inertia control (VIC) loop with an energy storage system (ESS) and a secondary PID controller tuned by the Walrus Optimization Algorithm (WaOA). The proposed methodology was implemented in MATLAB/Simulink and tested under load variations, renewable fluctuations, and parameter uncertainties.
The simulation results confirmed that the WaOA–PID controller consistently outperformed conventional PID, IMC–PID, and H∞–VIC controllers. It achieved lower overshoot, undershoot, and RoCoF, while maintaining short settling times and stable operation under realistic generator constraints. These findings demonstrate that the WaOA–PID approach offers a practical and computationally efficient solution for improving frequency stability in low-inertia microgrids with high renewable penetration.
5. Research Limitations
Although the proposed framework shows strong performance, certain limitations must be acknowledged. The WaOA algorithm requires iterative updates, which may increase computational overhead in real-time embedded systems. The effectiveness of the controller could also be affected by noise measurement or communication delays, which were not explicitly modeled in this study. In addition, scalability to large-scale or multi-microgrid networks may pose coordination challenges, and the approach was not tested under extreme nonlinear disturbances or cyber-physical threats.
Future work should focus on hardware-in-the-loop and real-time validation to confirm feasibility in practical environments. Extensions to multi-objective optimization may be required to balance frequency stability with cost, efficiency, and energy storage lifetime. Incorporating adaptive intelligence, such as reinforcement learning, could further improve predictive control and robustness. Attention to communication resilience and cybersecurity will also be essential for reliable deployment in modern distributed energy systems.
Author Contributions
Conceptualization, A.B.A. and A.A.; methodology, A.B.A.; software, A.B.A.; validation, A.B.A. and A.A.; formal analysis, A.B.A.; investigation, A.B.A.; resources, A.A.; data curation, A.B.A.; writing—original draft preparation, A.B.A.; writing—review and editing, A.B.A. and A.A.; visualization, A.B.A.; supervision, A.A.; project administration, A.A.; funding acquisition, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
The research was funded by the Ongoing Research Funding Program (ORF-2025-258), King Saud University, Riyadh, Saudi Arabia.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors gratefully acknowledge the support provided by the Ongoing Research Funding Program (ORF-2025-258), King Saud University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACE | Area Control Error |
| AID-VSG | Adaptive Inertia and Damping Virtual Synchronous Generator |
| ANN | Artificial Neural Network |
| D(t) | Time-varying Damping Coefficient |
| ESS | Energy Storage System |
| FACTS | Flexible AC Transmission Systems |
| GA | Genetic Algorithm |
| GRC | Governor Rate Constraint |
| H(t) | Time-varying Virtual Inertia |
| H∞ | H-infinity |
| Hmin, Hmax | Minimum and Maximum Virtual Inertia |
| ITAE | Integral of Time-Weighted Absolute Error |
| KD | Damping Control Gain |
| KH | Inertia Control Gain |
| LFC | Load Frequency Control |
| MPC | Model Predictive Control |
| PD | Damping Power |
| PDPI | Proportional Derivative Proportional Integral |
| PID | Proportional–Integral–Derivative |
| PLL | Phase-Locked Loop |
| PSO | Particle Swarm Optimization |
| RESs | Renewable Energy Sources |
| RoCoF | Rate of Change of Frequency |
| SG | Synchronous Generator |
| TD | Time Constant of Damping Filter |
| VIC | Virtual Inertia Control |
| VSG | Virtual Synchronous Generator |
| Vu, VL | Upper and Lower Valve Rate Limits |
| WaOA | Walrus Optimization Algorithm |
References
- Kerdphol, T.; Rahman, F.S.; Watanabe, M.; Mitani, Y.; Turschner, D.; Beck, H.P. Enhanced Virtual Inertia Control Based on Derivative Technique to Emulate Simultaneous Inertia and Damping Properties for Microgrid Frequency Regulation. IEEE Access 2019, 7, 14422–14433. [Google Scholar] [CrossRef]
- Abdel-Rahim, O.; Chub, A.; Vinnikov, D.; Blinov, A. DC Integration of Residential Photovoltaic Systems: A Survey. IEEE Access 2022, 10, 66974–66991. [Google Scholar] [CrossRef]
- Hamanah, W.M.; Shafiullah, M.; Alhems, L.M.; Alam, M.S.; Abido, M.A. Realization of Robust Frequency Stability in Low-Inertia Islanded Microgrids with Optimized Virtual Inertia Control. IEEE Access 2024, 12, 58208–58221. [Google Scholar] [CrossRef]
- Gurski, E.; Kuiava, R.; Perez, F.; Benedito, R.A.S.; Damm, G. A Novel VSG with Adaptive Virtual Inertia and Adaptive Damping Coefficient to Improve Transient Frequency Response of Microgrids. Energies 2024, 17, 4370. [Google Scholar] [CrossRef]
- Sun, S.; Liu, T.; Deng, Y. VSG Frequency Regulation Strategy for Adaptive Model Predictive Control. Int. J. Mech. Electr. Eng. 2024, 2, 13–26. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y. Virtual Inertia Control Application to Enhance Frequency Stability of Interconnected Power Systems with High Renewable Energy Penetration. Energies 2018, 11, 981. [Google Scholar] [CrossRef]
- ENTSO-E. Frequency Stability Evaluation Criteria for the Synchronous Zone of Continental Europe—Requirements and Impacting Factors; ENTSO-E: Brussels, Belgium, 2016; Available online: https://www.entsoe.eu/Documents/SOC%20documents/RGCE_SPD_frequency_stability_criteria_v10.pdf?utm_source=chatgpt.com (accessed on 5 June 2025).
- Kerdphol, T.; Rahman, F.S.; Watanabe, M.; Mitani, Y. Robust Virtual Inertia Control of a Low Inertia Microgrid Considering Frequency Measurement Effects. IEEE Access 2019, 7, 57550–57560. [Google Scholar] [CrossRef]
- Zhao, J.; Lyu, X.; Fu, Y.; Hu, X.; Li, F. Coordinated Microgrid Frequency Regulation Based on DFIG Variable Coefficient Using Virtual Inertia and Primary Frequency Control. IEEE Trans. Energy Convers. 2016, 31, 833–845. [Google Scholar] [CrossRef]
- Castro Martinez, J.; Arnaltes, S.; Alonso-Martinez, J.; Rodriguez Amenedo, J.L. Contribution of Wind Farms to the Stability of Power Systems with High Penetration of Renewables. Energies 2021, 14, 2207. [Google Scholar] [CrossRef]
- Parise, G.; Martirano, L.; Kermani, M. Designing a Power Control Strategy in a Microgrid Using PID/Fuzzy Controller Based on Battery Energy Storage. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Sayed, F.; Kamel, S.; Abdel-Rahim, O. Load Shedding Solution Using Multi-Objective Teaching-Learning-Based Optimization. In Proceedings of the 2018 International Conference on Innovation Trends in Computer Engineering (ITCE), Aswan, Egypt, 19–21 February 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 447–452. [Google Scholar] [CrossRef]
- Gong, K.; Shi, J.; Liu, Y.; Wang, Z.; Ren, L.; Zhang, Y. Application of SMES in the Microgrid Based on Fuzzy Control. IEEE Trans. Appl. Supercond. 2016, 26, 3800205. [Google Scholar] [CrossRef]
- Kamel, S.; Rabea, F.; Jurado, F.; Abdel-Rahim, O. Implementation of a Simplified SVC Model into Newton-Raphson Load Flow Algorithm. In Proceedings of the 2018 International Conference on Innovation Trends in Computer Engineering (ITCE), Aswan, Egypt, 19–21 February 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 374–437. [Google Scholar] [CrossRef]
- Mohamed, E.A.; Mitani, Y. Enhancement of the Dynamic Performance of Islanded Microgrid Using a Coordination of Frequency Control and Digital Protection. Int. J. Emerg. Electr. Power Syst. 2019, 20, 20180136. [Google Scholar] [CrossRef]
- Sedghi, L.; Fakharian, A. Voltage and Frequency Control of an Islanded Microgrid through Robust Control Method and Fuzzy Droop Technique. In Proceedings of the 2017 5th Iranian Joint Congress on Fuzzy and Intelligent Systems (CFIS), Qazvin, Iran, 7–9 March 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 110–115. [Google Scholar] [CrossRef]
- Shobug, M.A.; Hossain, M.A.; Yang, F.; Lu, J. Dynamic Control of Isolated Network Microgrids: A Resilient Backpropagation Neural Network-Based Virtual Inertia Control Approach. IEEE Access 2025, 13, 99939–99956. [Google Scholar] [CrossRef]
- Rakhshani, E.; Remon, D.; Cantarellas, A.M.; Garcia, J.M.; Rodriguez, P. Virtual Synchronous Power Strategy for Multiple HVDC Interconnections of Multi-Area AGC Power Systems. IEEE Trans. Power Syst. 2017, 32, 1665–1677. [Google Scholar] [CrossRef]
- Rakhshani, E.; Remon, D.; Cantarellas, A.M.; Rodriguez, P. Analysis of Derivative Control-Based Virtual Inertia in Multi-Area High-Voltage Direct Current Interconnected Power Systems. IET Gener. Transm. Distrib. 2016, 10, 1458–1469. [Google Scholar] [CrossRef]
- Shayeghi, H.; Jalili, A.; Shayanfar, H. Multi-Stage Fuzzy Load Frequency Control Using PSO. Energy Convers. Manag. 2008, 49, 2570–2580. [Google Scholar] [CrossRef]
- Anuradhika, K.; Dash, P. Genetic Algorithm-Based Load Frequency Control of a Grid-Connected Microgrid in the Presence of Electric Vehicles. In Sustainable Energy and Technological Advancements: Proceedings of IS-SETA 2021; Springer: Singapore, 2022; pp. 435–447. [Google Scholar] [CrossRef]
- Safari, A.; Babaei, F.; Farrokhifar, M. A load frequency control using a PSO-based ANN for micro-grids in the presence of electric vehicles. Int. J. Ambient. Energy 2019, 42, 688–700. [Google Scholar] [CrossRef]
- Dhillon, S.S.; Lather, J.S.; Marwaha, S. Multi Area Load Frequency Control Using Particle Swarm Optimization and Fuzzy Rules. Procedia Comput. Sci. 2015, 57, 460–472. [Google Scholar] [CrossRef]
- Lastomo, D.; Setiadi, H.; Djalal, M.R. Enabling PID and SSSC for Load Frequency Control Using Particle Swarm Optimization. In Proceedings of the 2017 3rd International Conference on Science in Information Technology (ICSITech), Bandung, Indonesia, 25–26 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 182–187. [Google Scholar] [CrossRef]
- Gupta, D.K.; Jha, A.V.; Appasani, B.; Srinivasulu, A.; Bizon, N.; Thounthong, P. Load Frequency Control Using Hybrid Intelligent Optimization Technique for Multi-Source Power Systems. Energies 2021, 14, 1581. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Mohapatra, S.; Gupta, D.K.; Panda, S. Multi Verse Optimized Fractional Order PDPI Controller for Load Frequency Control. IETE J. Res. 2020, 68, 3302–3315. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Truong, T.B.T.; Truong, Q.V.; Nguyen, H.V.P.; Duong, M.Q. Iterative Learning Control for Virtual Inertia: Improving Frequency Stability in Renewable Energy Microgrids. Sustainability 2025, 17, 6727. [Google Scholar] [CrossRef]
- Kom, C.H. Understanding Interphase Power Controller: A Description. J. Electr. Eng. Electron. Control Comput. Sci. 2020, 6, 19–24. [Google Scholar]
- Fan, W.; Hu, Z.; Veerasamy, V. PSO-Based Model Predictive Control for Load Frequency Regulation with Wind Turbines. Energies 2022, 15, 8219. [Google Scholar] [CrossRef]
- Kunya, A.B.; Argin, M.; Kucuksari, S. Optimal Load Frequency Control of Multi-Area Power System Considering Incremental Control Action. In Proceedings of the 2019 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 7–8 February 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Gözde, H.; Taplamacıoğlu, M.; Kocaarslan, I.; Çam, E. Particle Swarm Optimization-Based Load Frequency Control in a Single-Area Power System. Univ. Pitesti Comput. Sci. Bull. 2008, 8, 25–32. [Google Scholar]
- Sarir, N.; Morsli, S.; Allaoui, T.; Denai, M. Optimal Fractional-Order PI Control Design for a Variable Speed PMSG-Based Wind Turbine. J. Eur. Syst. Autom. 2021, 54, 915–922. [Google Scholar] [CrossRef]
- Govindaraju, S.K.; Sivalingam, R.; Panda, S.; Sahu, P.R.; Padmanaban, S. Frequency Control of Power System with Distributed Sources by Adaptive Type 2 Fuzzy PID Controller. Electr. Power Compon. Syst. 2023, 52, 487–508. [Google Scholar] [CrossRef]
- Qin, Z.; Liu, D.; Hua, H.; Cao, J. Privacy Preserving Load Control of Residential Microgrid via Deep Reinforcement Learning. IEEE Trans. Smart Grid 2021, 12, 4079–4089. [Google Scholar] [CrossRef]
- Mishra, D.; Maharana, M.K.; Kar, M.K.; Nayak, A.; Islam, M.M.; Ustun, T.S. A Metaheuristic Algorithm for Regulating Virtual Inertia of a Standalone Microgrid Incorporating Electric Vehicles. J. Eng. 2024, 2024, e12383. [Google Scholar] [CrossRef]
- Khan, I.; Shah, M.A.; Ullah, F.; Rehman, A.U.; Javaid, N. Enhanced Load Frequency Regulation in Microgrids with Renewable Energy Sources and Electric Vehicles. Sci. Rep. 2025, 15, 10835. [Google Scholar] [CrossRef]
- Khosravi, N.; Çelik, D.; Bevrani, H.; Echalih, S. Microgrid stability: A comprehensive review of challenges, trends, and emerging solutions. Int. J. Electr. Power Energy Syst. 2025, 170, 110829. [Google Scholar] [CrossRef]
- Yegon, M.; Wekesa, C.; Gikunda, A. Frequency Stability Enhancement of Microgrid Using Optimization Techniques-Based Adaptive Virtual Inertia Control. Int. Trans. Electr. Energy Syst. 2023, 33, e2121721. [Google Scholar] [CrossRef]
- Tuan, T.T.; Lee, D. Improving Frequency Control of Multi-Area Interconnected Power Systems Using PSO-Tuned PID Controllers. Appl. Sci. 2025, 15, 2898. [Google Scholar] [CrossRef]
- Rohmingtluanga, R.; Vanlalsawma, C.; Lalduhawma, C. Enhanced Harris Hawks Optimization Based Load Frequency Control of Multi-Area Power Systems. Front. Energy Res. 2024, 12, 1387780. [Google Scholar] [CrossRef]
- Imtiaz, M.; Ahmad, S.; Rehman, H.U.; Ali, H. Improving Microgrid Frequency Stability through PI-PIDA Based Advanced Control Techniques. Energy Rep. 2025, 11, 1039–1052. [Google Scholar] [CrossRef]
- Saadati Toularoud, M.; Farhadi, M.; Hosseini, S.E. Enhancing Microgrid Voltage and Frequency Stability with Renewable Energy Integration Using Advanced Controllers. Math. Probl. Eng. 2024, 2024, 4933861. [Google Scholar] [CrossRef]
- Gupta, D.K.; Thounthong, P.; Bizon, N. Student Psychology-Based Optimization-Tuned Cascaded Controller for Frequency Regulation in Renewable Integrated Microgrids. Front. Energy Res. 2024, 12, 1355608. [Google Scholar] [CrossRef]
- Sanaei, M.; Akbari, H.; Beheshtipour, Z.; Mousavi, S. New PSO-GWO-Based Model for Enhancing Power Quality in Electrical Networks Interconnected with Photovoltaic Sources. Front. Energy Res. 2024, 12, 1476638. [Google Scholar] [CrossRef]
- Zhao, K.; Liu, Y.; Han, P.; Xu, J. Optimizing Load Frequency Control in Microgrids with Vehicle-to-Grid Integration Using ANN-PSO. Appl. Energy 2024, 361, 123317. [Google Scholar] [CrossRef]
- Alharbi, S.; Khan, M.; Alamri, B. State Estimation of Voltage and Frequency Stability in Solar-Storage Microgrids. Sci. Rep. 2025, 15, 10171. [Google Scholar] [CrossRef]
- Sharma, R.; Singh, J.; Verma, A. Frequency Stability Improvement of Isolated Microgrid Systems Using Optimal Fractional-Order Virtual Inertia Control Based on Whale Optimization. Int. J. Electr. Power Energy Syst. 2023, 155, 109567. [Google Scholar] [CrossRef]
- Nireekshana, N.; Ramachandran, R.; Narayana, G. A Novel Swarm Approach for Regulating Load Frequency in Two-Area Energy Systems. Int. J. Electr. Electron. Res. 2023, 11, 371–377. [Google Scholar] [CrossRef]
- Feleke, S.; Satish, R.; Salkuti, S.R.; Abdelaziz, A.Y. Load Frequency Control in Two-Area Interconnected Systems Using DE-PID and PSO-PID. In Power Quality in Microgrids: Issues, Challenges and Mitigation Techniques; Springer: Berlin/Heidelberg, Germany, 2023; pp. 391–407. [Google Scholar] [CrossRef]
- Raj, T.D.; Kumar, C.; Kotsampopoulos, P.; Fayek, H.H. Load Frequency Control in Two-Area Multi-Source Power System Using Bald Eagle–Sparrow Search Optimization Tuned PID Controller. Energies 2023, 16, 2014. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).