Communication Base Station Site Selection Method Based on an Improved Genetic Algorithm
Abstract
1. Introduction
2. Analysis of Issues Related to Communication Base Station Site Selection Decisions
2.1. Principles of Radio Communication
2.1.1. Path Loss Model
- Free Space Propagation Model
- 2.
- Okumura-Hata Model
2.1.2. Decay Characteristics
- 1.
- Shadow Fading
- 2.
- Multipath Fading
2.2. Link Budget Theory
2.3. Interference Theory
2.3.1. Co-Channel Interference
2.3.2. Adjacent Channel and Spurious Interference Control
3. Construction of a Site Selection Optimization Model for Communication Base Stations
3.1. Core Elements and Decision Variables
3.2. Multi-Objective Function Design
3.2.1. Cost Minimization
3.2.2. Coverage Contribution Maximization
3.2.3. Interference Minimization
3.2.4. Multi-Objective Fusion and Normalization
3.3. Constraint Conditions
3.3.1. Base Station Quantity Constraint
3.3.2. Coverage Constraints for Critical Areas
3.3.3. Minimum Distance Constraint Between Base Stations
4. Improved Genetic Algorithms
4.1. Genetic Algorithms
4.2. Improvement Strategies for Genetic Algorithms
4.2.1. Introduction of Adaptive Strategies
4.2.2. Hybrid Particle Swarm Optimization
4.2.3. Introduction of Migration Strategy
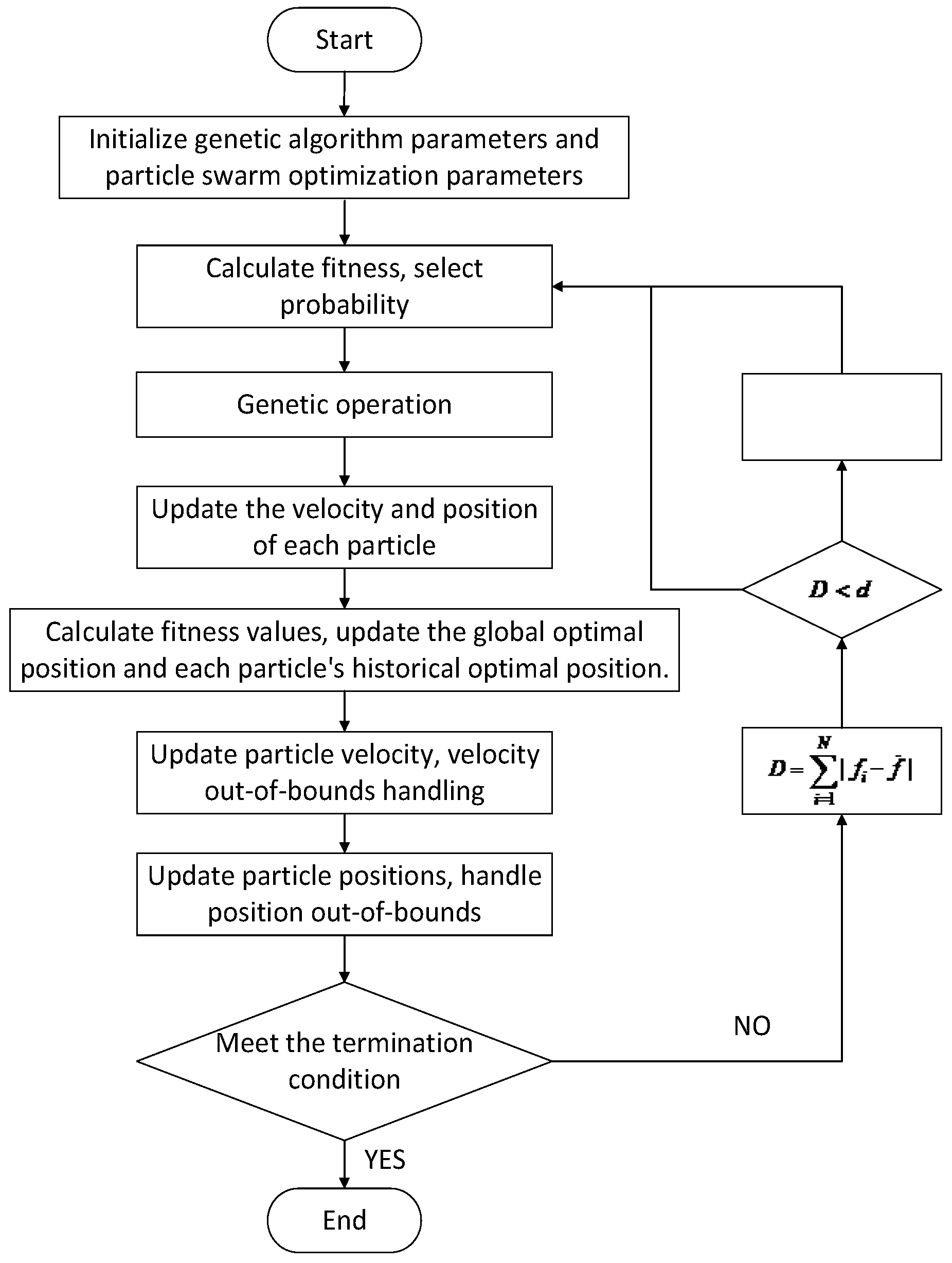
4.3. Algorithm Flow
4.3.1. Initialization
- 1.
- Parameter Initialization
- 2.
- Population Initialization
- 3.
- Optimizing Variable Initialization
4.3.2. Iterative Optimization
- 1.
- Selection Operation
- 2.
- Cross-Operations
- 3.
- Mutation Operation
- 4.
- Population Renewal and Migration Strategy
- 5.
- Optimal Solution Update
4.3.3. Result Output
4.4. Algorithm Performance Testing
5. Experimental Results and Analysis
5.1. Experimental Setup
5.1.1. Experimental Environment and Tools
5.1.2. Experimental Parameters
5.2. Experimental Simulation
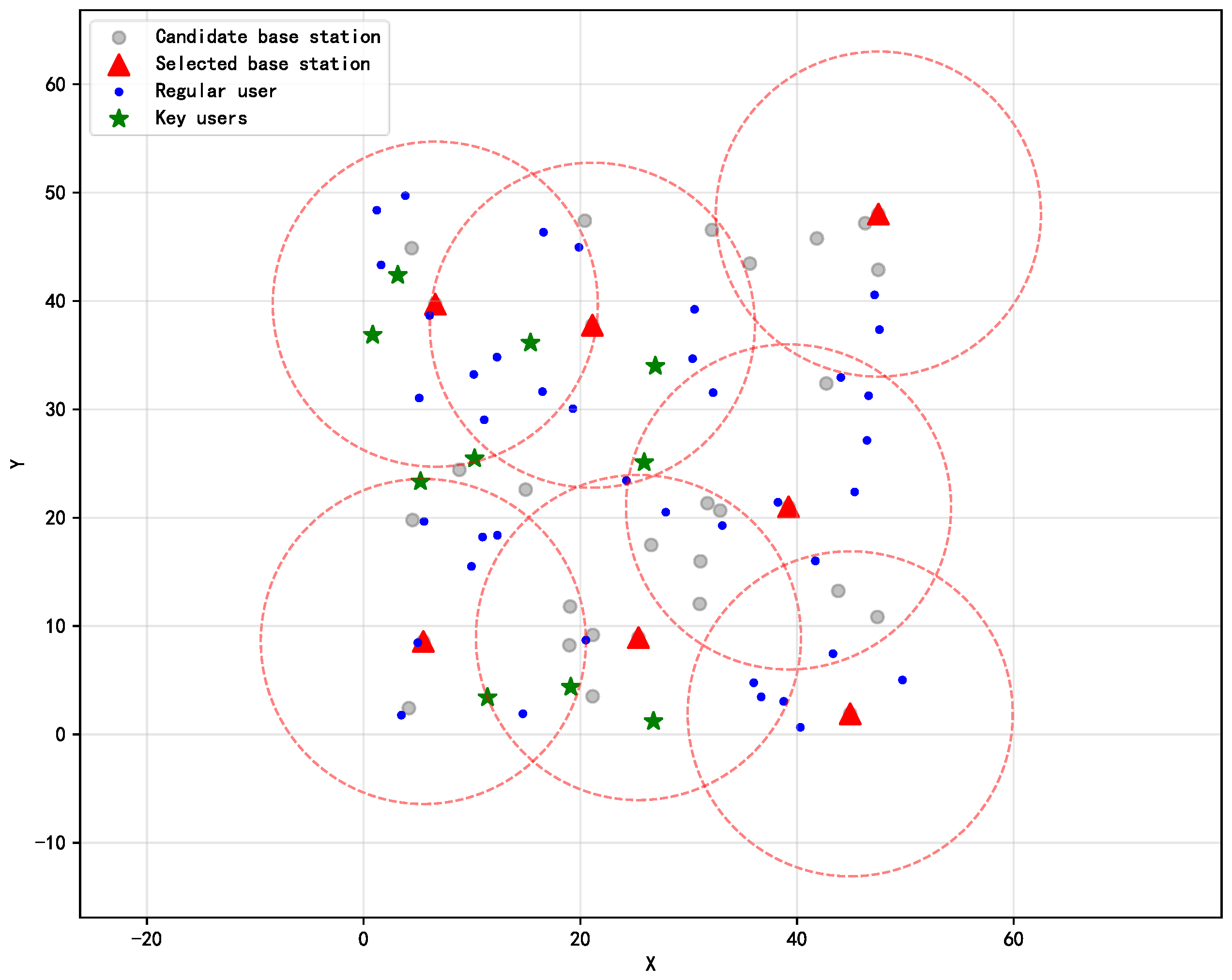
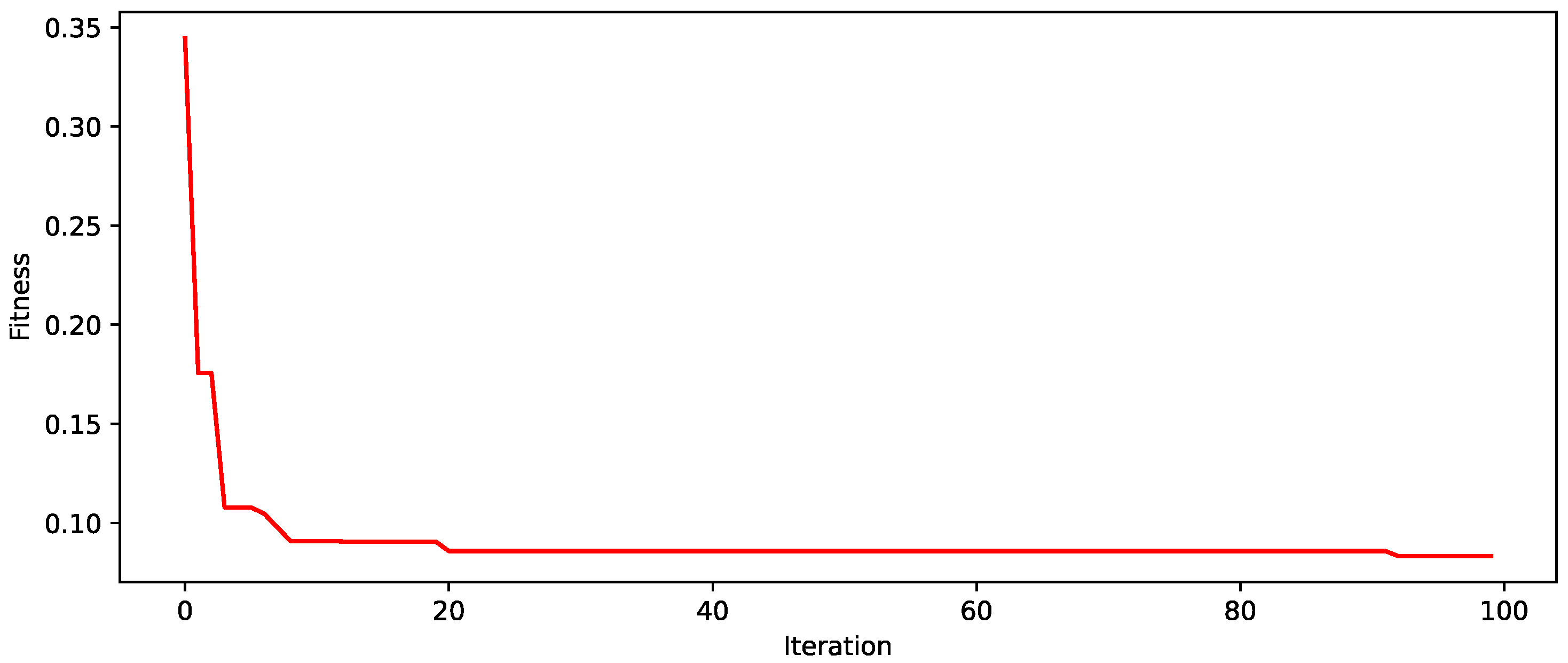
5.2.1. Feasibility Verification
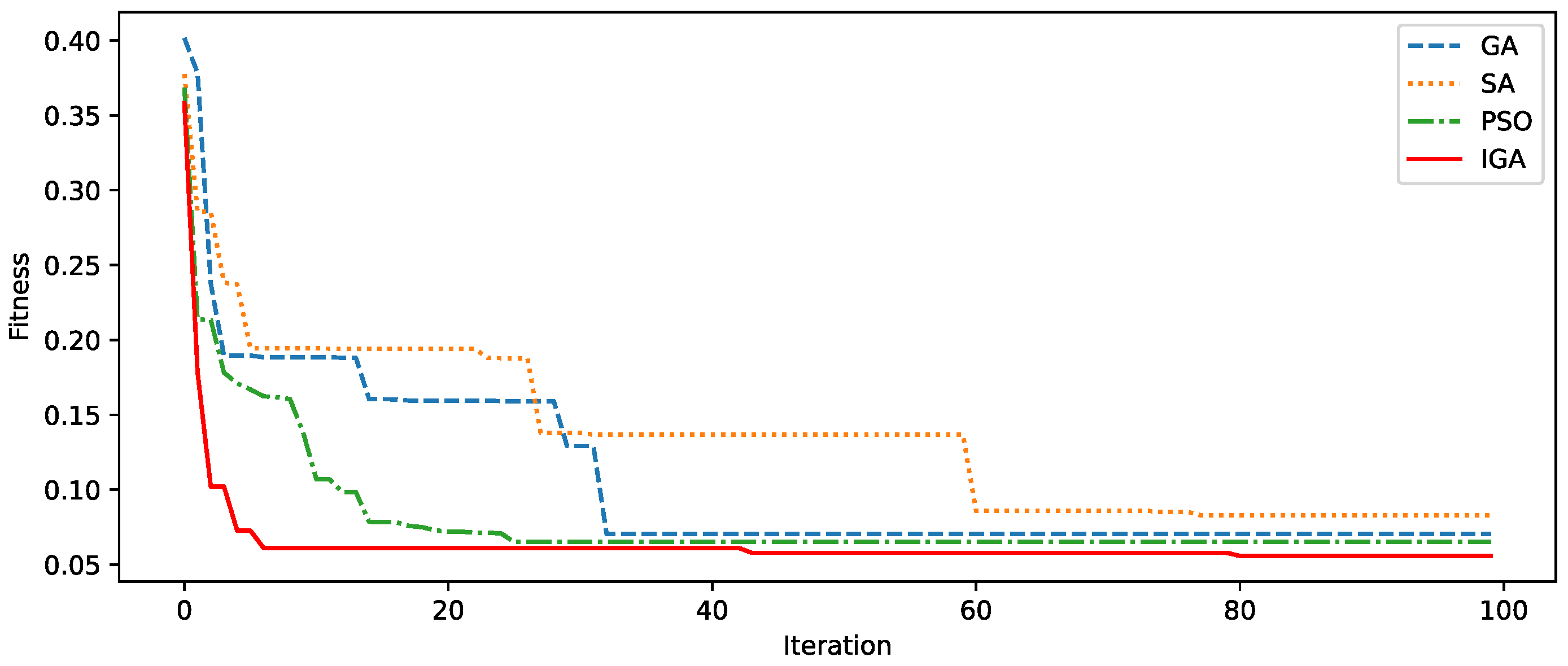
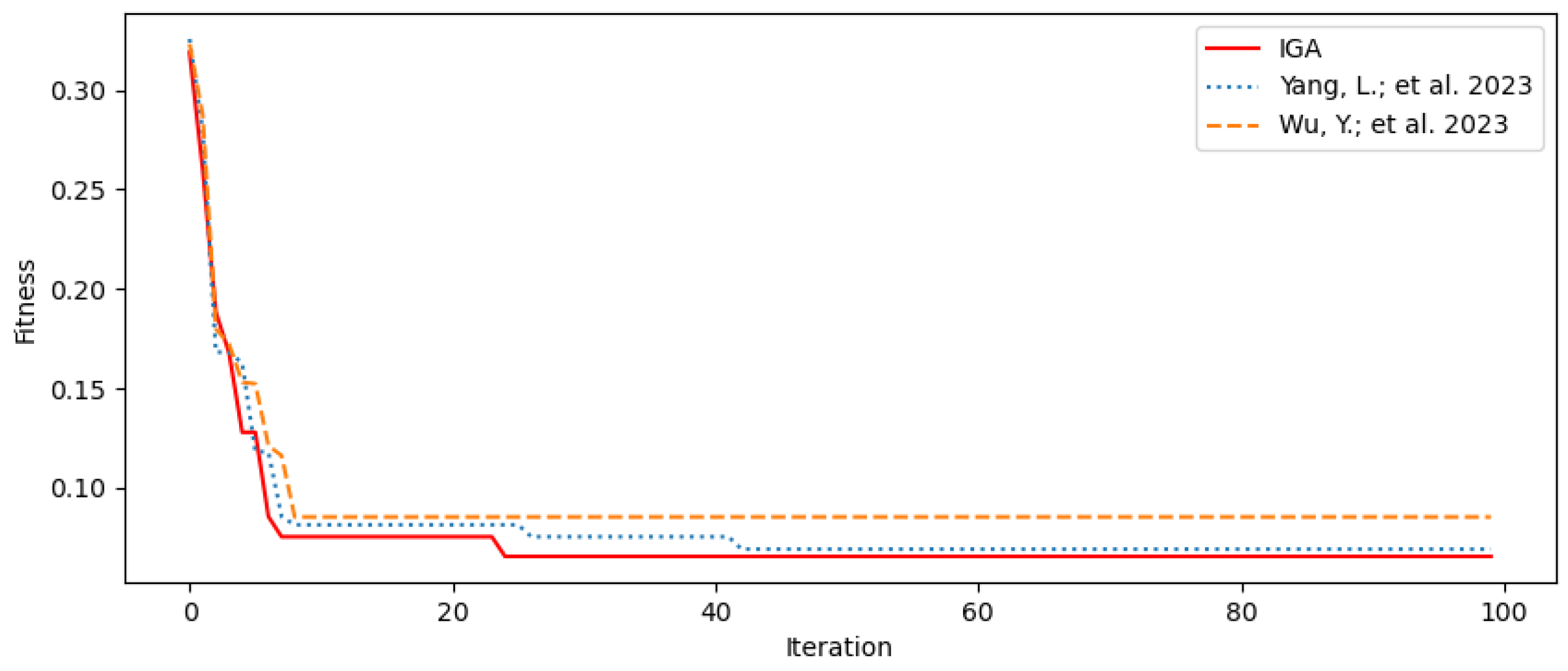
5.2.2. Effectiveness Validation
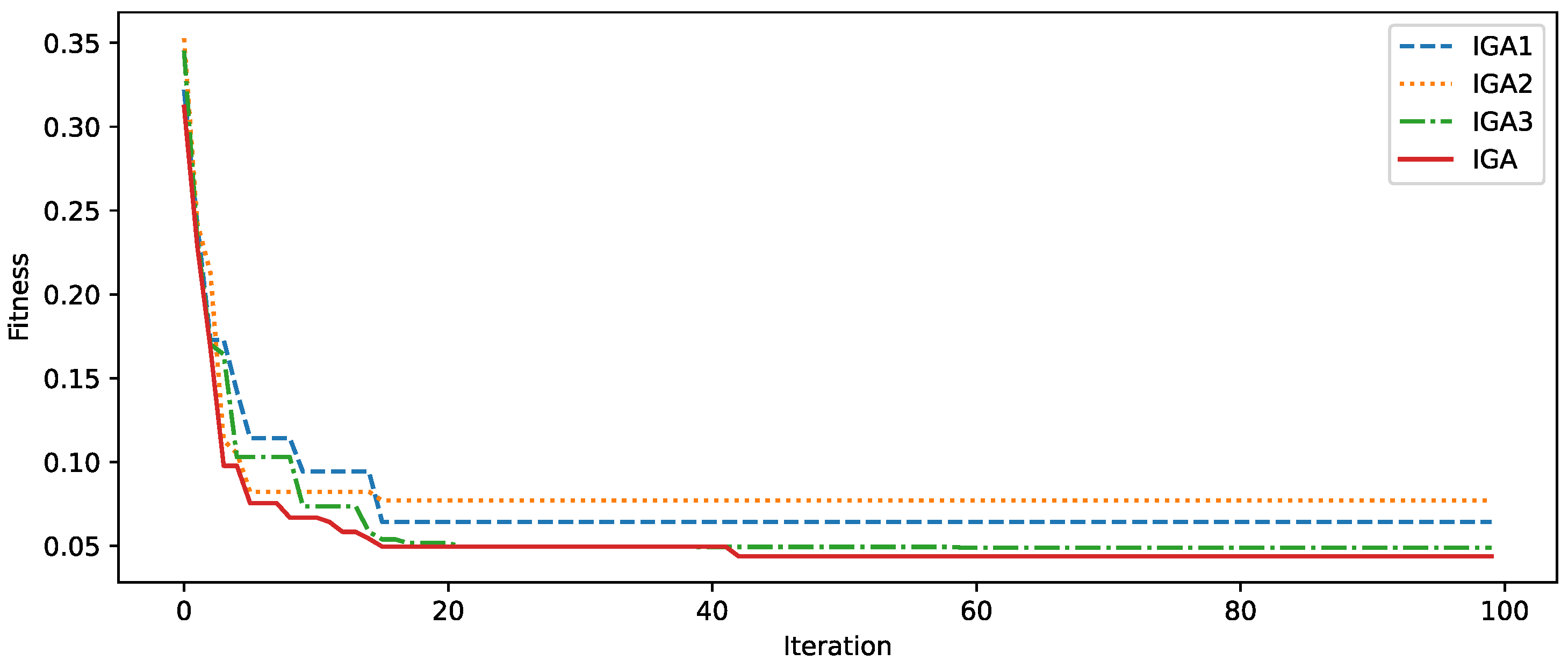
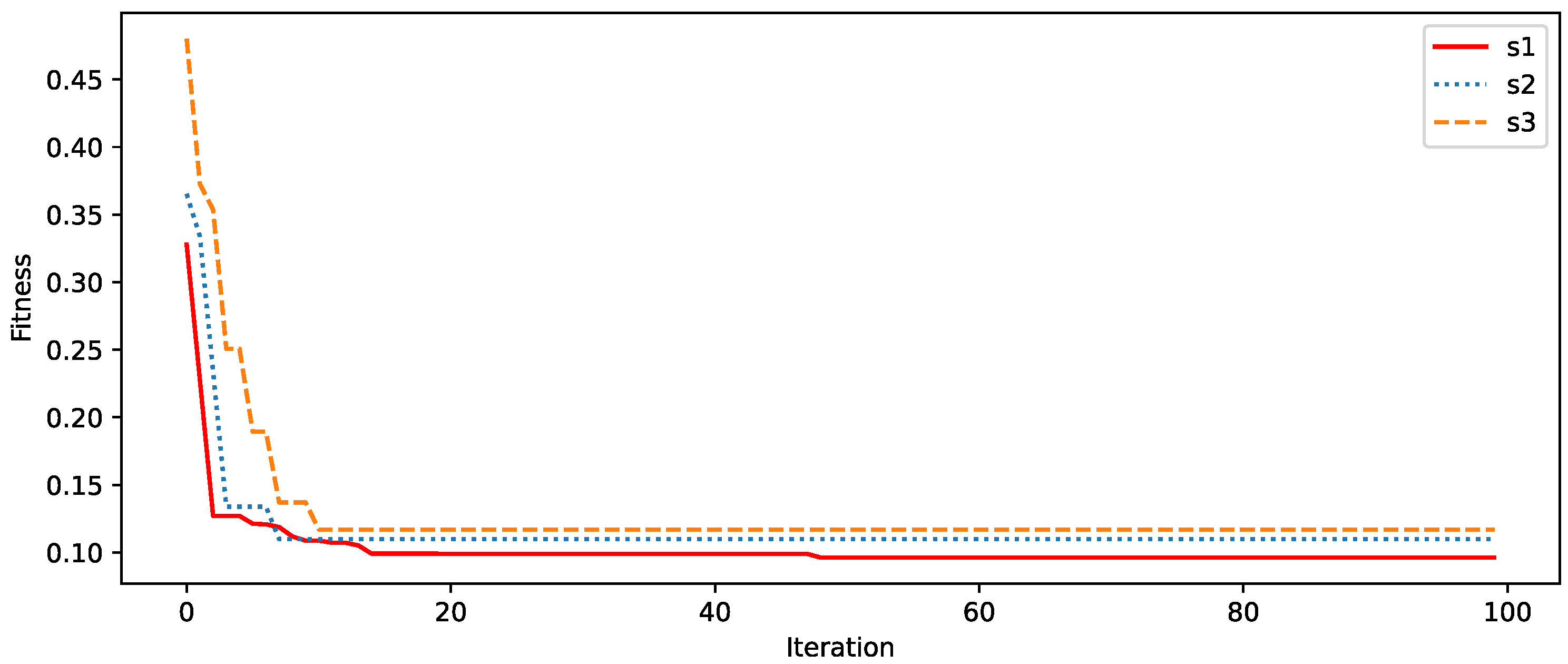
5.2.3. Ablation Studies
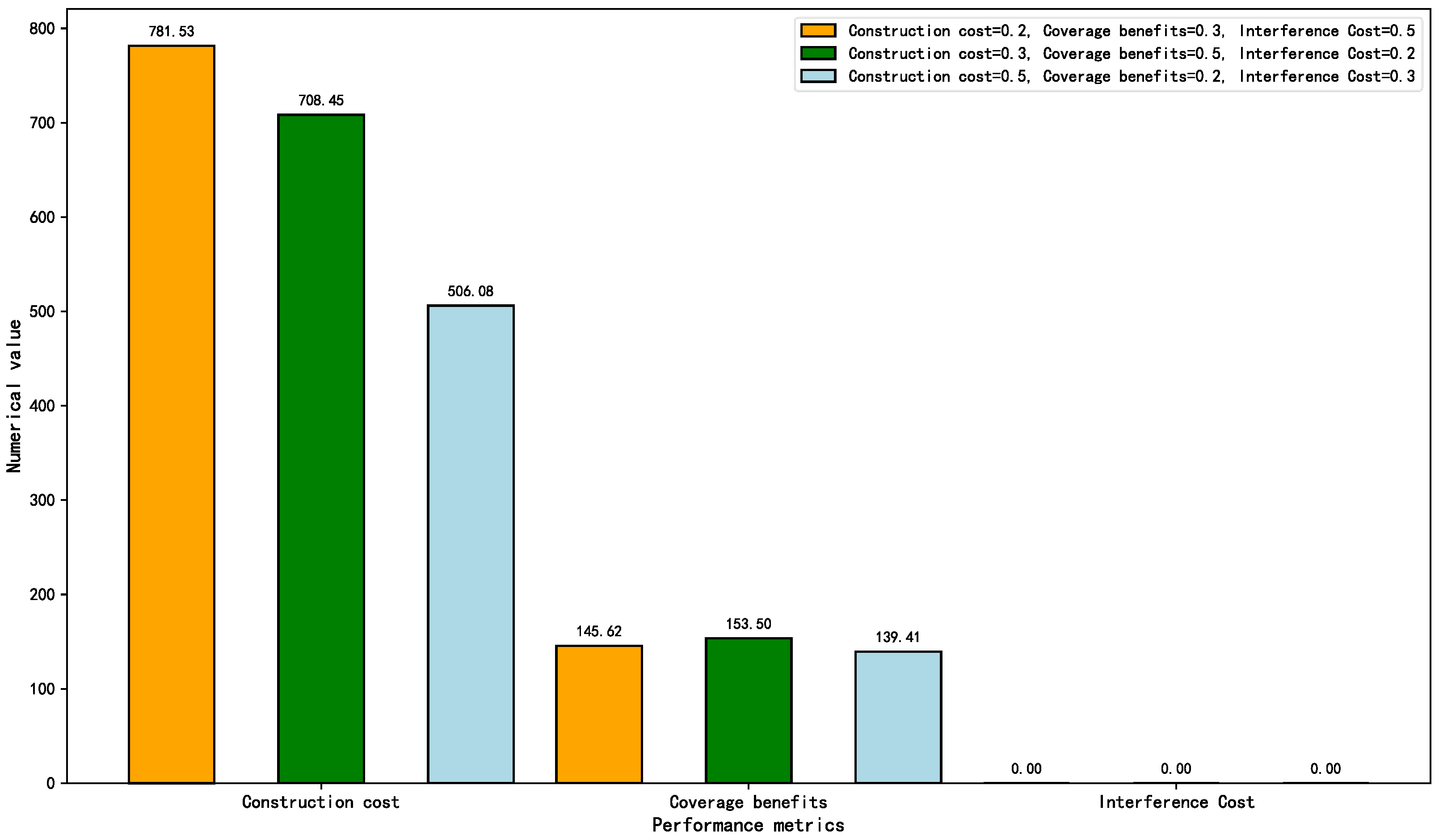
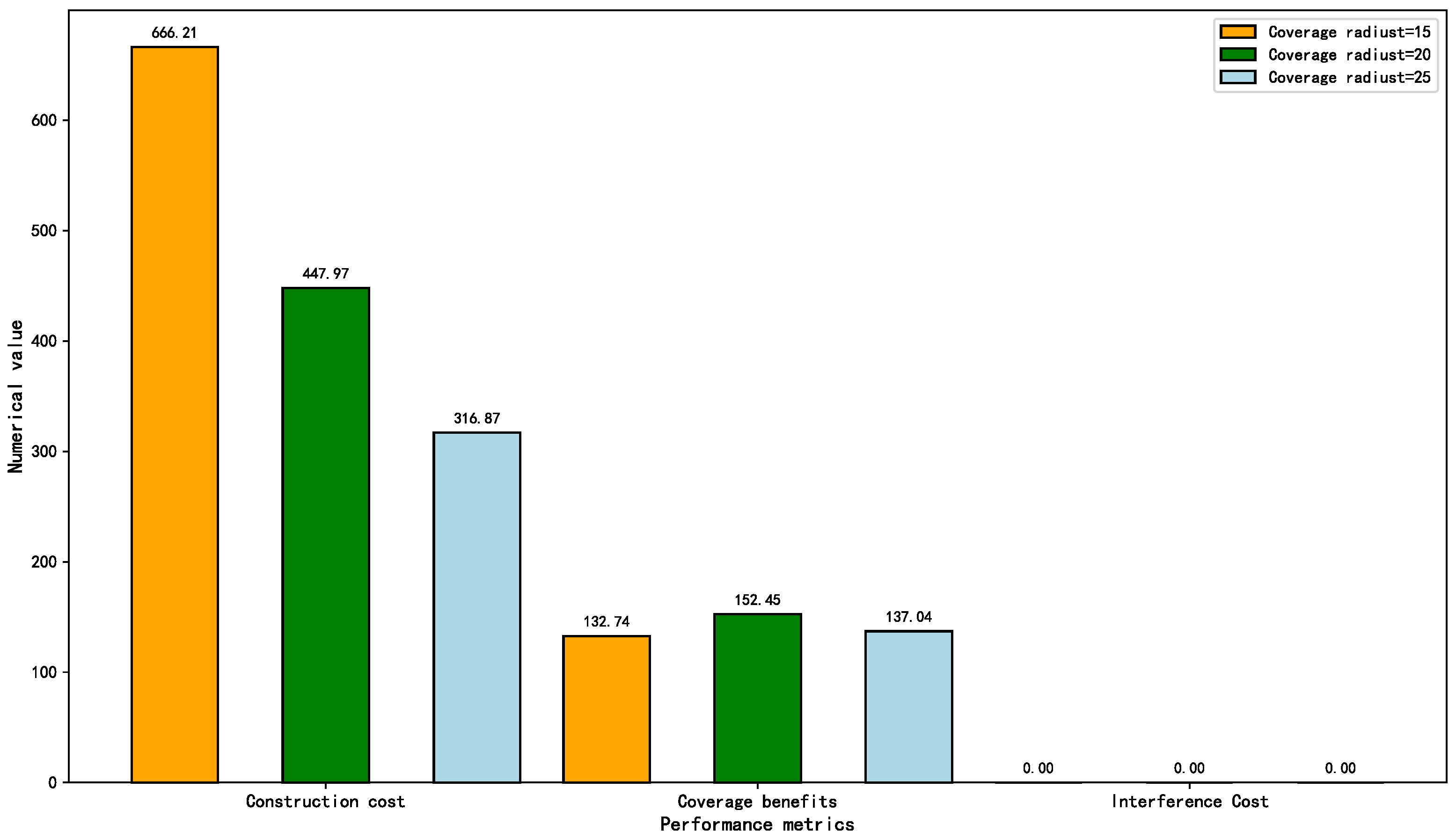
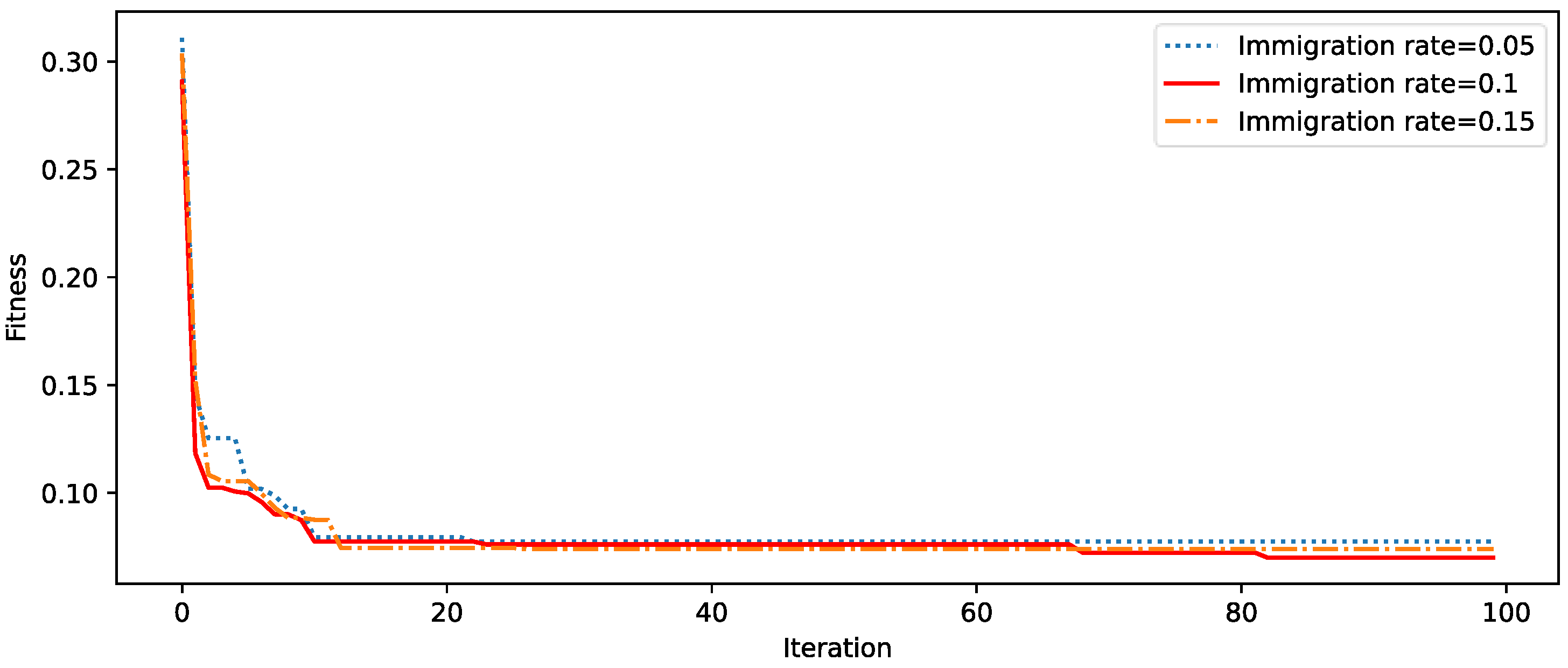
5.2.4. Parameter Sensitivity Analysis
- 1.
- Objective Weight
- 2.
- Base Station Coverage Radius
- 3.
- Immigration rate
- 4.
- Base Station Scale
5.3. Experimental Analysis Summary
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, X. 3GPP evolution from 5G to 6G: A 10-year retrospective. Telecom 2025, 6, 32. [Google Scholar] [CrossRef]
- Singh, R.; Jadaan, D.; Ghimire, D.; Berger, M.; Skavhaug, A.; Dittmann, L. Comparative Analysis of Power Consumption in LTE, 5G-NSA, 5G-SA, and Private 5G Networks. In Proceedings of the 2025 IEEE 22nd Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 10–13 January 2025; pp. 1–2. [Google Scholar]
- Zhou, Y.; Liu, L.; Wang, L.; Hui, N.; Cui, X.; Wu, J.; Peng, Y.; Qi, Y.; Xing, C. Service-Aware 6G: An Intelligent and Open Network Based on the Convergence of Communication, Computing and Caching. Digit. Commun. Netw. 2020, 6, 253–260. [Google Scholar] [CrossRef]
- Auwul, M.R. Robust Statistical Machine Learning Method for Transcriptome Data Analysis. Ph.D. Thesis, Guangzhou University, Guangzhou, China, 2022. [Google Scholar]
- Arora, S. Approximation Schemes for NP-Hard Geometric Optimization Problems: A Survey. Math. Program. 2003, 97, 43–69. [Google Scholar] [CrossRef]
- Liu, Y.; Huangfu, W.; Zhang, H.; Wang, H.; An, W.; Long, K. An Efficient Geometry-Induced Genetic Algorithm for Base Station Placement in Cellular Networks. IEEE Access 2019, 7, 108604–108616. [Google Scholar] [CrossRef]
- Lakshminarasimman, N.; Baskar, S.; Alphones, A.; Iruthayarajan, M.W. Base Station Placement for Dynamic Traffic Load Using Evolutionary Algorithms. Wirel. Pers. Commun. 2013, 72, 671–691. [Google Scholar] [CrossRef]
- Ali, H.M.; Liu, J.; Ejaz, W. Planning Capacity for 5G and Beyond Wireless Networks by Discrete Fireworks Algorithm with Ensemble of Local Search Methods. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 185. [Google Scholar] [CrossRef]
- Mathar, R.; Niessen, T. Optimum Positioning of Base Stations for Cellular Radio Networks. Wirel. Netw. 2000, 6, 421–428. [Google Scholar] [CrossRef]
- Elkamchouchi, H.M.; Elragal, H.M.; Makar, M.A. Cellular Radio Network Planning Using Particle Swarm Optimization. In Proceedings of the National Radio Science Conference, Cairo, Egypt, 13–15 March 2007; pp. 1–8. [Google Scholar]
- Berman, O.; Kalcsics, J.; Krass, D. On Covering Location Problems on Networks with Edge Demand. Comput. Oper. Res. 2016, 74, 214–227. [Google Scholar] [CrossRef]
- Amine, O.M.; Cilia, Z.; Khireddine, A. Optimal Base Station Planning Using Genetic Algorithm for LTE Network. In Advances on Broad-Band Wireless Computing, Communication and Applications; Barolli, L., Xhafa, F., Conesa, J., Eds.; Springer: Cham, Switzerland, 2018; pp. 731–740. [Google Scholar]
- Yang, L.-S.; Wen, B.; Yan, J.-J. Network Site Optimization and Clustering Study Based on Simulated Annealing Algorithm. IEEE Access 2023, 11, 108167–108177. [Google Scholar] [CrossRef]
- Wu, Y.; Shen, Y.; Fan, H. Location Planning of 5G Base Station Based on Immune Algorithm and Clustering Algorithm. In Proceedings of the 2023 IEEE Smart World Congress (SWC), Portsmouth, UK, 28–31 August 2023; pp. 1–7. [Google Scholar]
- Lv, Z.; Xu, C.; Wei, J. Data Sinks Deployment for Backbone-Assisted Real-Time PD-NOMA Networks Based on Reinforcement Learning. In Proceedings of the 2024 IEEE Smart World Congress (SWC), Nadi, Fiji, 12–15 November 2024; pp. 1091–1097. [Google Scholar]
- Guo, Q.; Liu, R.Z.; Liu, J.G. Research on Emergency Logistics Facility Location Based on Graph Neural Networks. J. Shanghai Univ. Sci. Technol. 2025. [Google Scholar]
- Li, P.; Cao, J.; Pang, W.; Luo, Y. UAV Base Station Scheduling Optimization Using Genetic Algorithm Based on Population Dynamic Clustering Strategy. J. Inf. Eng. Univ. 2022, 23, 245–252. [Google Scholar]
- Wang, C. Site Selection for Communication Base Stations Based on an Improved Particle Swarm Optimization Algorithm. Master’s Thesis, Nanjing University of Posts and Telecommunications, Nanjing, China, 2017. [Google Scholar]
- Guo, Y. Research on Base Station Site Selection Methods Based on Communication Visibility. Master’s Thesis, Nanjing Normal University, Nanjing, China, 2021. [Google Scholar]
- Yang, C. Research on Coverage Issues in 3G Base Station Site Selection. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2011. [Google Scholar]
- Han, C. Adaptive Mitigation Method for Overlapping Interference in Ship Communication Processes. Nav. Sci. Technol. 2021, 43, 130–132. [Google Scholar]
- Wang, Y.; Chen, C.; Yu, Z. Research on 5G Base Station Site Selection Decision-Making and Optimization Based on Particle Swarm Optimization Algorithm. J. Eng. Math. 2024, 41, 1170–1178. [Google Scholar]
- Alsan, Y.; Puskely, J.; Janssen, J.H.J.; Geurts, M.; Roederer, A.; Yarovoy, A. Thermal-Aware Synthesis of 5G Base Station Antenna Arrays: An Overview and a Sparsity-Based Approach. IEEE Access 2018, 6, 58868–58882. [Google Scholar]
- Li, Y.; Xia, M.; Wu, Y.-C. Activity Detection for Massive Connectivity Under Frequency Offsets via First-Order Algorithms. IEEE Trans. Wirel. Commun. 2019, 18, 1988–2002. [Google Scholar] [CrossRef]
- Yang, Y.; Gong, Y.; Wu, Y.-C. Intelligent-Reflecting-Surface-Aided Mobile Edge Computing with Binary Offloading: Energy Minimization for IoT Devices. IEEE Internet Things J. 2022, 9, 12973–12983. [Google Scholar] [CrossRef]
- Ma, Y.; Yun, W. Research Progress on Genetic Algorithms. Comput. Appl. Res. 2012, 29, 1201–1206+1210. [Google Scholar]
- Yang, C. Application of an Improved Adaptive Genetic Algorithm in Function Optimization. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2018. [Google Scholar]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science (MHS ‘95), Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Qian, Q.; Zhang, J. Feasibility Study on Anti-Missile Defense Strategy for a Single Ship Based on Adaptive Genetic Algorithm. Nav. Electron. Eng. 2020, 40, 23–26. [Google Scholar]
- Lü, L. Research and Application of an Improved Adaptive Multi-Objective Genetic Algorithm. Master’s Thesis, Tianjin University of Technology and Education, Tianjin, China, 2020. [Google Scholar]
- Rong, Y. Research on Evolutionary Algorithm-Based Site Planning Optimization for Boundary-Free Positioning. Master’s Thesis, Xidian University, Xi’an, China, 2023. [Google Scholar]
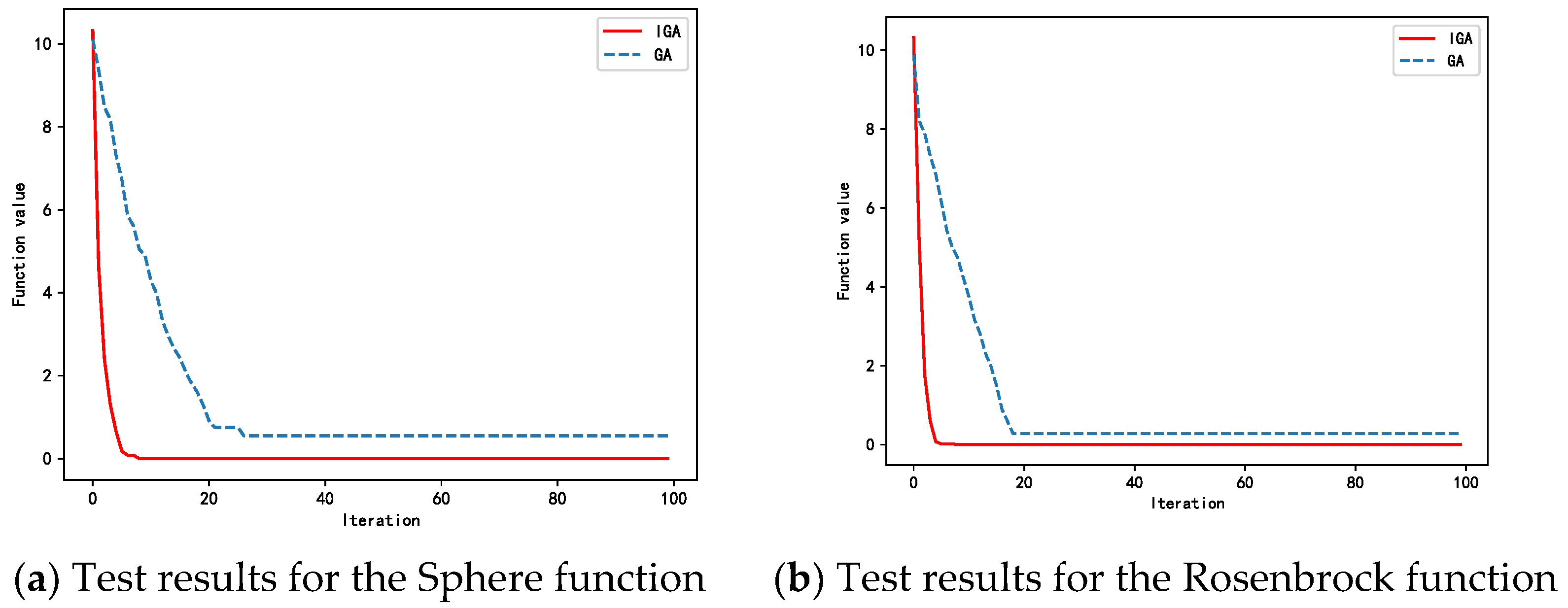
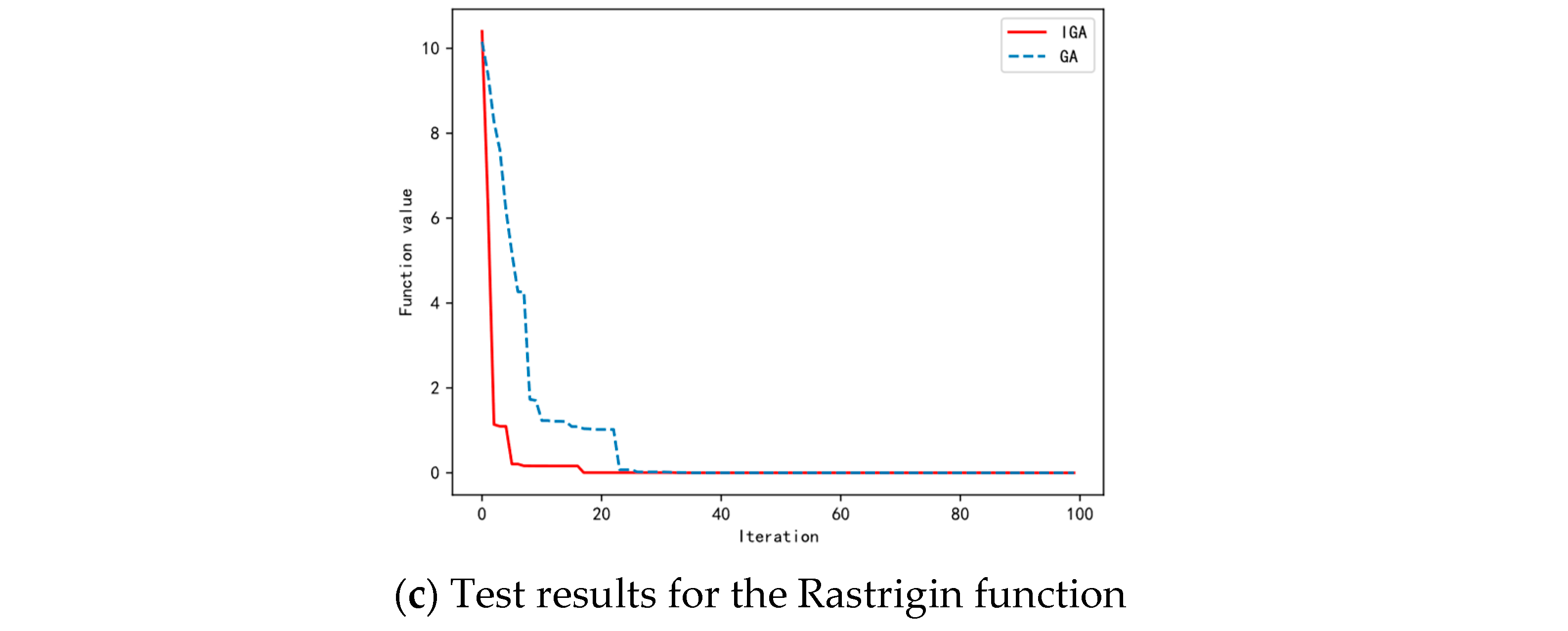
| Testing Function | Function Expression | Dimensionality | Value Range | Optimum Value | Error Target |
|---|---|---|---|---|---|
| Sphere | 30 | [−100, 100]n | 0 | 10−2 | |
| Rosenbrock | 30 | [−30, 30]n | 0 | 10−2 | |
| Rastrigin | 30 | [−5.12, 5.12]n | 0 | 10−2 |
| Algorithm Basic Parameters | Population size | 100 |
| Number of iterations | 100 | |
| Base Station Parameters | Number of Candidate Base Stations | 30 |
| Number of User Demand Points | 50 | |
| Coverage Radius | 15 | |
| Minimum Distance | 10 | |
| Maximum Number of Base Stations | 10 | |
| Base Station Parameters | Adaptive Crossover Probability Base Value | 0.8 |
| Adaptive Mutation Probability Base Value | 0.05 | |
| Particle Swarm Inertia Weight | 0.8 | |
| Migration Ratio | 0.1 | |
| Maximum particle velocity | 0.5 | |
| Model Target Parameters | Cost Weight α | 0.3 |
| Coverage Weight β | 0.5 | |
| Disturbance Weight γ | 0.2 |
| Algorithm | Parameters | Value |
|---|---|---|
| GA | Population size | 100 |
| Crossover probability | 0.8 | |
| Mutation probability | 0.05 | |
| PSO | Population size | 100 |
| Inertial weight | 0.8 | |
| Cognitive factor (c1) | 2.0 | |
| Social factor (c2) | 2.0 | |
| SA | Initial temperature | 1000 |
| Cooling rate | 0.95 | |
| Long Markov chain | 100 | |
| Termination temperature | 10−5 |
| Algorithm | Coverage Contribution | Construction Cost (104 CNY) | Interference Cost (Dimensionless) | Number of Selected Base Stations |
|---|---|---|---|---|
| IGA | 147.264 | 674.03 | 0 | 6 |
| GA | 147.176 | 703.965 | 0 | 6 |
| SA | 146.635 | 742.69 | 0 | 7 |
| PSO | 143.942 | 996.778 | 0 | 8 |
| Algorithm | Coverage Contribution | Construction Cost (104 CNY) | Interference Cost (Dimensionless) | Number of Selected Base Stations |
|---|---|---|---|---|
| IGA | 147.201 | 647.271 | 0 | 6 |
| Reference [13] | 147.153 | 647.165 | 0 | 6 |
| Reference [14] | 146.012 | 691.842 | 0 | 7 |
| Objective Weight | Parameter Variation |
|---|---|
| Cost Weight | 0.3 → 0.2 → 0.5 |
| Coverage Weight | 0.5 → 0.3 → 0.2 |
| Interference Weight | 0.2 → 0.5 → 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wang, H.; Fang, S.; Fan, Y.; Zhang, S. Communication Base Station Site Selection Method Based on an Improved Genetic Algorithm. Electronics 2025, 14, 3977. https://doi.org/10.3390/electronics14203977
Li J, Wang H, Fang S, Fan Y, Zhang S. Communication Base Station Site Selection Method Based on an Improved Genetic Algorithm. Electronics. 2025; 14(20):3977. https://doi.org/10.3390/electronics14203977
Chicago/Turabian StyleLi, Jinxuan, Hongyan Wang, Shengliang Fang, Youchen Fan, and Shuya Zhang. 2025. "Communication Base Station Site Selection Method Based on an Improved Genetic Algorithm" Electronics 14, no. 20: 3977. https://doi.org/10.3390/electronics14203977
APA StyleLi, J., Wang, H., Fang, S., Fan, Y., & Zhang, S. (2025). Communication Base Station Site Selection Method Based on an Improved Genetic Algorithm. Electronics, 14(20), 3977. https://doi.org/10.3390/electronics14203977





