Ensemble Learning Model for Industrial Policy Classification Using Automated Hyperparameter Optimization

Abstract

The Global Trade Alert (GTA) website, managed by the United Nations, releases a large number of industrial policy (IP) announcements daily. Recently, leading nations including the United States and China have increasingly turned to IPs to protect and promote their domestic corporate interests. They use both offensive and defensive tools such as tariffs, trade barriers, investment restrictions, and financial support measures. To evaluate how these policy announcements may affect national interests, many countries have implemented logistic regression models to automatically classify them as either IP or non-IP. This study proposes ensemble models—widely recognized for their superior performance in binary classification—as a more effective alternative. The random forest model (a bagging technique) and boosting methods (gradient boosting, XGBoost, and LightGBM) are proposed, and their performance is compared with that of logistic regression. For evaluation, a dataset of 2000 randomly selected policy documents was compiled and labeled by domain experts. Following data preprocessing, hyperparameter optimization was performed using the Optuna library in Python 3.10. To enhance model robustness, cross-validation was applied, and performance was evaluated using key metrics such as accuracy, precision, and recall. The analytical results demonstrate that ensemble models consistently outperform logistic regression in both baseline (default hyperparameters) and optimized configurations. Compared to logistic regression, LightGBM and random forest showed baseline accuracy improvements of 3.5% and 3.8%, respectively, with hyperparameter optimization yielding additional performance gains of 2.4–3.3% across ensemble methods. In particular, the analysis based on alternative performance indicators confirmed that the LightGBM and random forest models yielded the most reliable predictions.

1. Introduction

In recent years, both developed and developing nations have actively pursued aggressive or defensive industrial policies to strengthen domestic economies and benefit citizens [1,2,3,4,5,6,7,8,9]. Notably, the United States and China have been strategically leveraging industrial policies as a means to secure technological dominance in global trade competition, particularly in critical sectors such as semiconductors, automobiles, chemicals, and energy [3,4,5,6,7,8,9]. Industrial policy (IP) refers to the measures and guidelines implemented by national governments to direct and coordinate various industrial sectors for the purpose of fostering economic development and stability [1,3,4,5,6,7,8,9]. It is generally designed to achieve national economic objectives and enhance the growth and competitiveness of targeted industries. Typical interventions under IP include the imposition of tariffs, capital controls, exchange rate policies, export and import regulations, restrictions on foreign investment, subsidies, and financial aid [1,6,7]. On the other hand, non-industrial policy (non-IP) encompasses measures aimed at stabilizing the prices of domestic products and services, as well as policies with a social welfare orientation [5,8]. Unlike IPs, non-industrial policies are not motivated by the goal of shaping or transforming the structure of a nation’s economy.

The Global Trade Alert (GTA) database [1], maintained by the UN, publishes a large volume of IPs and non-IPs each day. These policies provide detailed descriptions, along with affected products, jurisdictions, and implementation timelines. From these descriptions, one can determine whether a given policy is classified as an IP or non-IP. Therefore, it has become increasingly important to develop strategies and policies that enable countries to quickly respond by automatically interpreting the numerous policy announcements issued daily and determining whether these policies impact their own economies [2,3,4,5,6,7]. To address this, Juhasz [3,4,5,6] proposed an automated classification system that utilizes text mining [10,11,12,13,14,15,16,17,18,19,20,21] to process policy documents and applies logistic regression [22,23,24,25,26,27,28] to distinguish between IPs and non-IPs. However, as shown in prior research [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63], ensemble models often achieve superior performance in binary classification tasks compared to logistic regression.

This study analyzes policy descriptions using text mining techniques and applies an ensemble learning-based classification model. The results are then compared with those from a logistic regression model. For this study, a total of 2000 policy descriptions published between 2018 and 2023 were randomly collected, and experts from the Korea Information Society Development Institute (KISDI) labeled each policy as either IP or non-IP [2]. During the labeling process, the dependent variable was set to 1 for IP and 0 for non-IP. After removing stopwords from the policy descriptions, independent variables were generated through feature extraction using the term frequency and inverse document frequency (TF-IDF) method [13,14,15,16,17,18,19,20,21]. In this study, TF-IDF weighting was used to evaluate term importance, which is consistent with previous research [3,4,5,6]. Data preprocessing involved sparse matrix transformation, standardization, and minority-class oversampling [17,18,19,20,21]. For model training and evaluation, five different random samples were created, splitting the data into 70% for training purposes and 30% for testing to assess model performance. Finally, the Python Optuna library [64,65,66,67] was utilized for hyperparameter optimization, and cross-validation was applied to build the optimal model. Note that Optuna automates hyperparameter search to optimize the objective function and maximize model prediction accuracy. It uses a technique called ‘define-by-run’, which dynamically defines the search space within the code, allowing for more flexible and intuitive parameter tuning [64,65].

The ensemble methods proposed in this study are categorized into bagging and boosting techniques based on their respective learning strategies. Specifically, this work constructs and evaluates representative ensemble models, including the random forest algorithm [30,31,32,33,34,35,36,37,38] for bagging and gradient boosting [39,40,41,42,43,44,45,46], XGBoost [47,48,49,50,51,52], and LightGBM [53,54,55,56,57,58] for boosting. The model’s performance was evaluated using standard classification metrics: precision, recall, F1-score, ROC-AUC and accuracy [59,60,61,62,63,64,65,66,67].

This paper is organized as follows. Section 2 presents an overview of industrial policy, while Section 3 describes the research approach and procedures. Section 4 briefly introduces logistic regression and ensemble models. Section 5 investigates the model’s performance under two scenarios: one using default hyperparameters (baseline) and the other employing tuned parameters (optimized). Finally, Section 6 concludes with a summary of the key findings and suggestions for future research directions.

2. Definition of Industrial Policy

The GTA website [1] provides daily updates on policies announced by various countries. Each policy announcement includes a detailed description, allowing for the identification of whether it qualifies as an IP. A policy is classified as an IP if it seeks to enhance the growth of domestic industries and competitiveness by modifying industrial and economic structures. Conversely, a policy is classified as a non-IP if it aims to stabilize domestic product and service prices, enhance public welfare, or improve social welfare without altering the fundamental economic structure. According to Juhasz [3,4,5,6], IPs differ from non-IPs by exhibiting two distinct characteristics (Parts A and B), as shown in

Table 1. Definition of industrial policy [5].

(Part A) Stated goal

Industrial policy encompasses deliberate governmental interventions aimed at restructuring economic activity. It strives to influence sectoral resource allocation and relative pricing mechanisms, thereby guiding long-term transformations of the economic structure—particularly through focused initiatives such as export promotion and investment in research and development (R&D).

(Part B) National state implementation

The objective of industrial policy is to achieve predefined targets related to the national economy. These policies are implemented by governmental or supranational organizations. Authorization and funding for these initiatives come from national governments, supranational institutions, or collaborative arrangements between these entities.

.

IP encompasses government-formulated strategies and guidelines designed to foster the development and stability of industrial sectors within a national economy. These policies are typically crafted to achieve national economic objectives while boosting the growth and competitiveness of targeted industries. According to Parts A and B in Table 1, the key objectives of IPs include the following.

(1)

Promotion of economic growth: Providing strategic direction to support the expansion of gross domestic product and overall economic growth. This includes fostering the development of emerging industrial sectors and encouraging innovation and advancement in existing industries.

(2)

Export promotion: Strengthening the nation’s export capabilities to compete in the global market. This involves enhancing the competitiveness of domestic products and services abroad while promoting international trade opportunities.

(3)

Technological innovation and R&D: Developing strategic initiatives to enhance national technological capabilities and drive innovation. This includes supporting R&D efforts, stimulating collaboration between industry and academia, and integrating novel technologies to boost the competitiveness of key industrial sectors.

(4)

Balanced regional and industrial development: Implementing strategies to ensure equitable growth across domestic regions and industrial sectors. This incorporates reducing regional disparities, supporting sustainable industrial expansion, and promoting infrastructure development to support long-term economic balance.

(5)

Job creation: Stimulating employment growth by promoting the expansion of emerging and developing industrial sectors. This requires supporting workforce development programs, advancing investment in high-potential industries, and implementing policies that reduce unemployment and enhance job stability.

To further clarify the distinction between industrial and non-industrial policies,

Table 2. Examples of industrial and non-industrial policies [1].

Example of IP (China)

On 1 August 2023, China’s General Administration of Customs under the Ministry of Commerce released Announcement No. 27 (2023) introducing export control measures for products associated with unmanned aerial vehicles and unmanned airships. The new requirement comes into force on 1 September 2023. Thirty items specified in a 10-digit HS code level were identified for requiring export licenses. Another announcement was issued for different products.

Example of non-IP (Thailand)

On 31 March 2022, the Ministry of Finance of Thailand issued Notification on the Exemption of Customs Duty for Goods imported for the Production of Face Masks granting a tax concession to producers of face masks under the subheading 630,790 in the form of import duty exemption on raw materials. This action only applies to a subset of the potential buyers of this good. According to the regulation, the objective was to meet the demand for face masks in the country following the COVID-19 outbreak. The raw materials include nonwovens and plaited bands. As the import duties exemption was provided to certain companies, it was considered selective. The regulation entered into force temporarily from 3 April to 30 September 2022.

presents representative examples.

Note that China’s IP fulfills both criteria outlined in Parts A and B of Table 1. As for Part A’s criterion, the policy introduces export control measures to strengthen domestic production of unmanned aerial vehicles and airships [68,69,70]. This corresponds to Part A’s definition, since it explicitly aims to promote specific industrial sectors. With respect to Part B, the policy is overseen by China’s General Administration of Customs, underscoring national-level governance. In contrast, the policy introduced by Thailand is considered a non-IP. This is because the Thai government’s measure—a tariff exemption on imported goods for mask production—is intended to meet domestic demand and support a social welfare initiative to curb the spread of COVID-19. Regarding its objective, it fails Part A’s IP criterion as it does not intend to drive structural economic transformation.

Since the onset of the COVID-19 pandemic, the competition for technological and trade dominance—especially in advanced fields like artificial intelligence and semiconductors—has escalated, primarily driven by the United States and China. As a result, the GTA website now publishes a growing volume of IP and non-IP policies each day, along with policy briefs that could profoundly affect domestic industries and global economies. Given this trend, countries must take proactive steps to anticipate and respond to potential risks posed by foreign IPs. To address this challenge, developing a machine learning algorithm capable of automatically classifying newly announced policies as either IP or non-IP has become increasingly imperative. These tools would empower policymakers to react quickly and strategically to policy shifts.

3. Research Methodology

As shown in Figure 1, the research workflow consists of six sequential stages: from data collection and labeling to model assessment. Each stage can be outlined as follows.

(1)

Data collection and labeling

The data used for analysis were collected from the GTA database [1]. Each policy document was categorized as either IP or non-IP. The dataset comprises 2000 policy documents randomly selected over a 68-month period, spanning from January 2018 to August 2023. Policy classification (IP versus non-IP) was determined through majority vote among five domain experts after deliberation [2]. The industrial policy entries from the GTA database include, in addition to the policy description, information such as the inception date, implementing jurisdiction, affected jurisdiction, intervention type, affected products, etc. The policy documents collected via the GTA website were extracted, and then domain experts analyzed these documents. Based on the definition of industrial policy presented in Section 2, the descriptions were labeled to distinguish industrial policies from non-industrial policies.

(2)

Data preprocessing

A total of 4563 stopwords were compiled, including 179 defaults from Python’s NLTK (Natural Language Toolkit 3.9.1) library [10,11,12] and 4384 custom additions. The designated stopwords comprise English alphabets, proper nouns, numbers, temporal terms (e.g., October, November), currency units, prepositions, and frequent function words (e.g., also, well). In Python, the stopwords consist of English articles, prepositions, pronouns, and auxiliary verbs, and additional stopwords were defined by domain experts for the classification of IPs [16,17,18,19,20,21]. After removing stopwords, the policy documents constitute a corpus. In this study, stopwords were defined to include numbers and punctuation. To ensure comparability with previous research [3,4,5,6], stemming and lemmatization were not applied. Each policy document in the corpus was tokenized and then weighted using term frequency-inverse document frequency (TF-IDF) to determine the significance of words in both individual documents and the corpus as a whole. TF calculates the number of times a word occurs within a document, whereas IDF reflects its inverse document frequency. Specifically, TF quantifies a word’s occurrence in a document and is calculated as follows [13,14,15,19,20,21]:

TF(t) = (number of appearances of a specific word t)/(the document’s total word count)

(1)

On the other hand, IDF measures a term’s significance by calculating how frequently it appears across the entire document collection. The IDF formula is defined as follows [15,16,17,18,19,20,21]:

IDF(t) = log((the corpus’s total number of documents)/(count of documents that include the specific term t + 1))

(2)

In the IDF calculation, a value of 1 is typically added to the denominator to prevent division by zero when a term does not appear in any document. The TF-IDF score for each term is then computed by multiplying its TF and IDF values to measure the importance of the term. The formula is given below.

TF-IDF(t) = TF(t) × IDF(t)

(3)

TF-IDF(t) quantifies the significance of each word within a document. A higher TF-IDF score signifies that the word holds greater importance in the document. TF evaluates a word’s importance based on its occurrence within a document, whereas IDF assigns higher significance to words that appear in a few documents but are rare overall. This contrasts with common words (e.g., articles) that appear ubiquitously. Thus, a word appearing frequently in one document but rarely in others will yield a high TF-IDF score. TF-IDF is extensively applied in text mining tasks such as information retrieval, document classification, clustering, search engine development, and text summarization [15,16,17,18,19,20,21].

As part of data preprocessing, tokenization was applied to policy descriptions following the removal of stopwords. Next, a TF-IDF matrix was constructed from the preprocessed words to serve as the independent variable, while the dependent (target) variable was coded as 1 (IP) or 0 (non-IP). Note that TF-IDF weighting was applied to both the training and testing datasets to evaluate term importance. Corpus analysis of policy descriptions identified 7312 words as independent variables across 2000 policy documents.

(3)

Data loading

A dataset consisting of 2000 entries was randomly split into a training set (70%, 1400 entries) and a test set (30%, 600 entries). The training and test datasets were separated using a random sampling method rather than stratified sampling, and oversampling was applied to the minority class to balance the number of samples in the majority class [17,18,19,20,21]. To fairly evaluate the model’s performance, five distinct pairs of training and test datasets were generated by varying the random seed in Python. In this study, training and test datasets were generated using five different random seed numbers, and each model’s performance was evaluated five times, with the average value used. The reasons for this approach are as follows.

(i)

A single random split may, by chance, result in a ‘favorable’ or ‘unfavorable’ division. Therefore, using multiple random seed numbers allows such randomness to be averaged out.

(ii)

This allows us to verify whether the model consistently performs well across different data splits and to ensure that it generalizes rather than overfits to a specific split.

(iii)

By measuring performance on five different test datasets, more reliable estimates of model performance can be obtained, and the corresponding mean and standard deviation of the performance metrics can be assessed.

(iv)

This allows us to examine the extent to which the randomness in data splitting affects model performance.

Ultimately, this approach has the advantage of providing a more accurate assessment of the model’s true performance compared to relying on a single test set.

The independent variables, stored as TF-IDF values, are represented as a sparse matrix with mostly zero entries. For efficient representation of this sparse matrix, the coordinate list method (CLM) [13,14,15,16], which was also applied in previous studies [3,5], was utilized. In the CLM, each entry is stored as a triplet, (document index, word index, TF-IDF value), rather than storing all 7312 term frequencies for each document. This approach improves memory management and processing efficiency when handling large datasets [15,16,19,20,21].

Additionally, Z-score normalization was conducted on the TF-IDF values to ensure consistent data scaling, yielding a mean of zero and a standard deviation of one [10,11,12,13,14].

Normalized TF-IDF = (original TF-IDF value − mean)/standard deviation

(4)

This standardization guarantees that all features are on a consistent scale, allowing the model to treat each feature with equal importance during analysis.

(4)

Machine learning model development

A data analysis model was developed using four ensemble methods and the logistic regression approach as proposed in existing literature. Ensemble techniques such as random forest [36,37,38], gradient boosting [46], XGBoost [50,51,52], and LightGBM [55,56,57,58] have recently demonstrated robust classification performance and are thus employed in this study. The baseline models with default hyperparameter values were evaluated across five samples. Here, hyperparameters refer to configuration settings that control the performance and behavior of machine learning models during training [66,67]. These values are not learned from the data but must be manually set by the user before model training begins. The choice of hyperparameters affects the design of the model, the degree of regularization, and the learning rate, all of which critically influence the model’s performance.

(5)

Hyperparameter tuning

Hyperparameter optimization was performed using the following process. First, 5-fold cross-validation was performed on the dataset, identifying the hyperparameter configuration that delivers optimal performance. The Optuna Python library [64,65,66,67] was also used to optimize the hyperparameters of the machine learning models. Optuna is a Python-based tool specifically developed for automating the process of hyperparameter tuning, making it easier to discover the best-performing setups. In particular, it formulates an objective function—focused on maximizing classification accuracy—that accepts hyperparameters as inputs and returns the model performance metric. After constructing independent training and testing datasets with different Python random seeds, the above process was repeated. Subsequently, after performing this procedure five times for each model, the average value of accuracy was used to evaluate as the performance of the model.

(6)

Model evaluation

Model performance was first evaluated using accuracy, ROC (receiver operating characteristic) curves, and AUC (area under the curve) values. In addition, precision, recall, and F1-scores were employed to assess classification performance for both IP and non-IP classes.

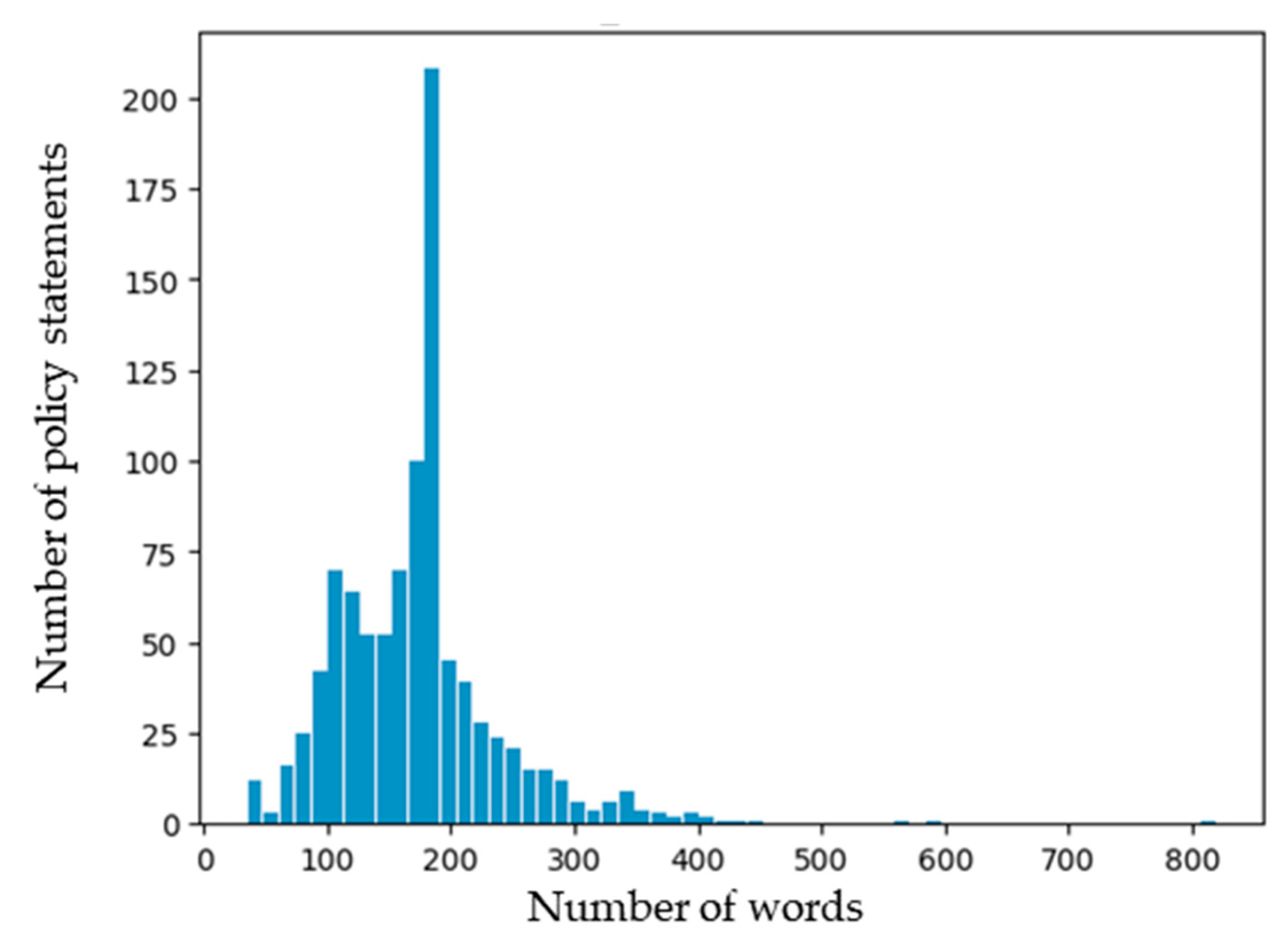
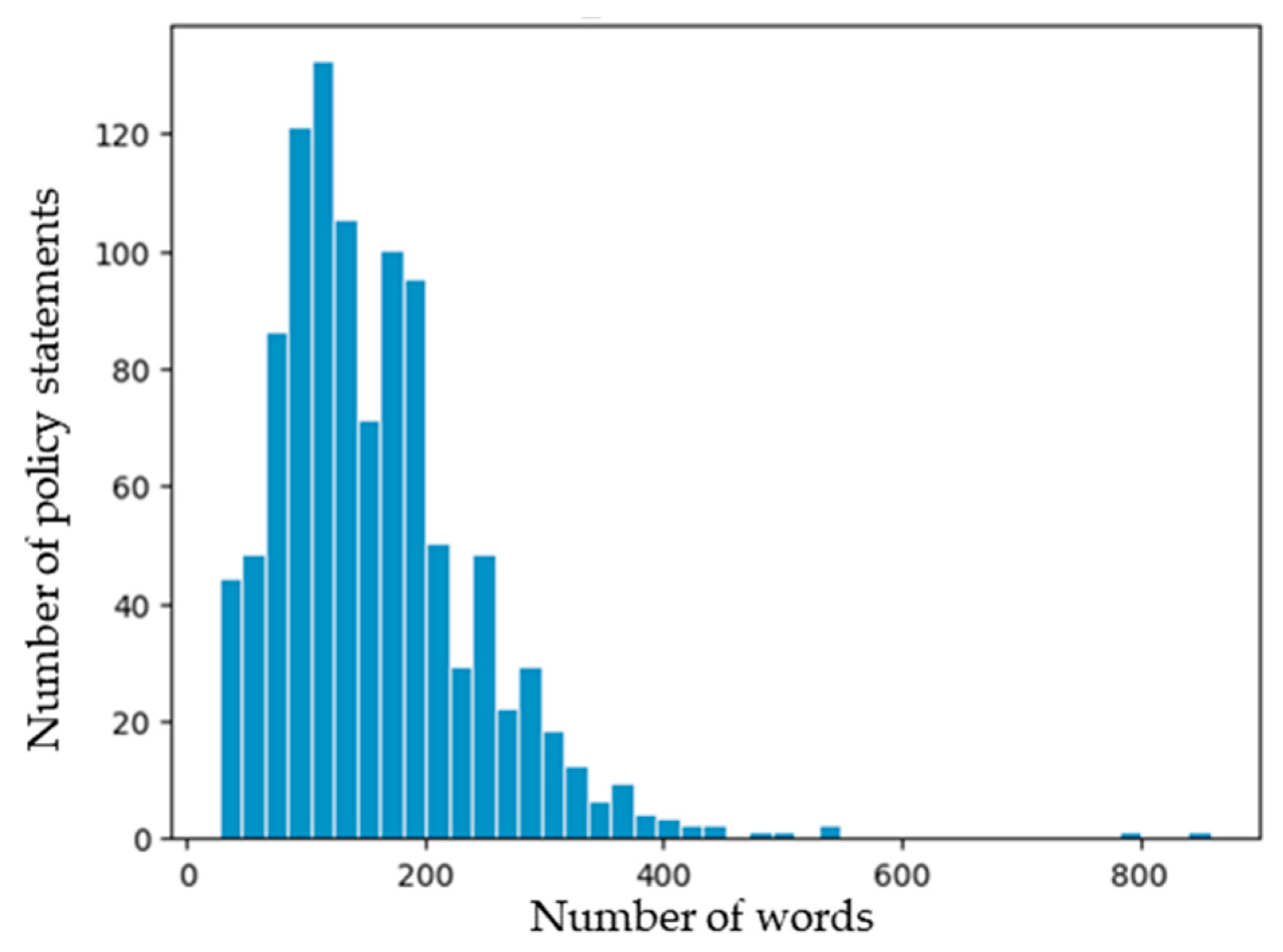
3.1. Data for Analysis

Of the 2000 policy statements categorized by five specialists, 958 (47.9%) were labeled as IPs, while the remaining 1042 (52.1%) were identified as non-IPs. Figure 2 shows the word count distribution for the 958 IP statements, and Figure 3 displays corresponding word cloud visualizations. From the results, the number of words used to describe industrial policies appears to approximately follow a normal distribution. After excluding stopwords, terms such as million, state, support, and firm were found to be frequently used in defining industrial policies.

After stopword removal,

Table 3. Top 10 items by TF in IP statements.

Word	TF	Word	TF
million	108.77	foreign	56.26
state	95.53	financial	49.32
support	75.38	export	48.92
firm	63.48	products	48.49
government	59.95	subsidy	48.38

lists the highest-frequency terms in the policy statements. Note that each TF value in Table 3 was obtained by summing its TF values across all 2000 documents. The terms ‘million’, ‘state’, and ‘support’ appear significantly more frequently than others.

Figure 4 and Figure 5 present the analysis results for non-IP statements. The word count of non-IP explanations follows a right-skewed distribution (skewness > 0) when compared to IPs, implying that they generally contain fewer words. In the case of non-IPs, fewer words are used to describe the policies compared to IP descriptions. Similarly to IPs, the terms million and state are frequently used; however, unlike IPs, words such as tariff, related, and duty are also commonly observed.

Table 4. Top 10 items by TF in non-IP statements.

Word	TF	Word	TF
million	89.59	duty	52.56
state	75.47	government	52.47
tariff	69.97	support	49.83
import	54.09	see	48.14
related	53.40	loan	47.41

shows the most common explanatory terms identified in non-IP descriptions.

An examination of Table 3 and Table 4 reveals that ‘million’, ‘state’, ‘support’, and ‘government’ appear frequently across both IP and non-IP documents. However, statements related to IPs predominantly feature terms such as ‘firm’, ‘foreign’, ‘financial’, ‘export’, ‘products’, and ‘subsidy’. In contrast, non-IPs are more commonly associated with words like ‘tariff’, ‘import’, ‘related’, ‘duty’, ‘see’, and ‘loan’. Following the elimination of stopwords, 2000 policy statements were analyzed, resulting in the extraction of 7312 unique terms as independent features. The ten terms with the highest TF-IDF values included ‘million’, ‘state’, ‘firm’, ‘export’, ‘support’, ‘government’, ‘loan’, ‘tariff’, ‘aid’, and ‘subsidy’.

3.2. Main Contributions of Research

In this study, the results of applying the well-known ensemble learning model and hyperparameter optimization technology to a given binary classification problem are presented, and there is a limitation in not being able to present new algorithms or innovative methodologies for performance improvement. Nevertheless, the primary contributions of this study are outlined below.

(1)

A new approach is introduced to categorize a large volume of policy documents, released daily by GTA, into IP or non-IP classifications. Thus, the findings of this study can be utilized to automatically classify these policy documents, facilitating more timely and strategic responses to IPs that may impact the domestic markets.

(2)

This study recommends employing ensemble-based analytical frameworks that outperform the conventional logistic regression approach. First, the adoption of random forest, a widely recognized bagging technique, is proposed, followed by an assessment of its predictive performance. Next, the outcomes of boosting algorithms commonly applied in classification tasks—such as gradient boosting, LightGBM, and XGBoost—are examined and discussed.

(3)

Finally, an innovative approach integrated with the cross-validation technique is proposed to optimize the parameters of logistic regression and ensemble-based models. The Optuna technique, designed for automated hyperparameter optimization, is applied to further enhance model accuracy.

In summary, this study employs text mining techniques to analyze policy announcements and proposes an ensemble learning framework for automated classification. The proposed method’s performance is compared with that of the traditional logistic regression model. This methodology is expected to facilitate timely and strategic responses to domestic industrial policies by enabling automated classification of new policy documents.

4. Machine Learning Model

In this study, logistic regression and ensemble learning models are employed to address a binary classification problem for categorizing IPs. The advantages and disadvantages of each model can be summarized as follows. First, in the case of logistic regression, the classification results are easy to interpret, and the coefficient values of each feature allow us to readily identify both the effect and the relative magnitude of each variable on the target variable. Therefore, the basis of the model’s prediction can be clearly explained, and its computational efficiency enables relatively fast model construction and testing. However, as in the problems presented in this work, when the relationships among features are non-linear and involve complex patterns, the prediction accuracy tends to be lower. In contrast, ensemble learning models combine multiple weak learners (commonly decision trees) to achieve superior prediction accuracy and robustness compared to a single model. In particular, they naturally capture non-linear relationships and interactions and are effective in preventing overfitting. However, due to their complex structure, the prediction process exhibits a strong ‘black-box’ characteristic, making interpretability more difficult. In addition, the hyperparameter tuning process is relatively complicated, and compared with logistic regression, ensemble methods require greater computational resources and longer training time. The descriptions of each model are as follows.

4.1. Logistic Regression

Logistic regression is a statistical approach designed for binary classification problems, where the outcome variable is categorical and typically falls into one of two groups, such as ‘yes or no’, ‘true or false’, or ‘IP vs. non-IP’ [22,23,24,25,26,27,28]. The logistic (sigmoid) function is used to calculate the probability that a given input belongs to a particular group. The model outputs a probability between 0 and 1 using a predefined threshold (commonly set at 0.5) to allocate the input to one of the two groups. Logistic regression assumes that there is a linear association between the independent variables and the log-odds of the outcome (dependent) variable [22,23]. For the baseline model, the fundamental hyperparameter settings are as follows.

(i)

Regularization strength (C) controls the inverse of the penalty applied during model training. Lower C values impose stronger regularization, whereas higher values allow for weaker constraints. By default, C is set to 1.0.

(ii)

The regularization type (penalty) specifies the form of constraints imposed on the model during training. Commonly used options are l1 (Lasso), l2 (Ridge, default setting), elasticnet (a blend of l1 and l2), or none (no regularization constraints applied).

(iii)

The optimization algorithm (solver) specifies the method used to adjust the model parameters during training. Available options include liblinear, lbfgs, newton-cg, sag, and saga, each characterized by distinct computational efficiency profiles [16,17,18]. By default, lbfgs is selected as the solver.

(iv)

The class weight parameter (class_weight) modifies the importance assigned to each class in order to compensate for imbalanced class distributions. Options include ‘none’ (default: uniform weighting) and ‘balanced’ (assigns weights inversely proportional to class occurrence rates).

(v)

The max_iter parameter sets the maximum number of iterations the solver may execute to reach convergence. A higher value for this parameter may enhance stability when handling complex or high-dimensional datasets. The default is 100.

4.2. Ensemble Model

Ensemble learning integrates multiple individual models to improve prediction accuracy and reduce overfitting. By combining the predictions of multiple models, ensemble methods may offer more robust results than relying on a single model alone [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58]. Ensemble strategies are generally categorized into two types: bagging and boosting [30,31,32,33,34,35,36,37,38]. Bootstrap aggregating (bagging) decreases variance by training multiple models on randomly drawn bootstrapped subsets of the data and then combining their predictions via averaging. A well-known example is random forest, which utilizes multiple decision trees to enhance both stability and accuracy [30,31,32,33,34,35,36,37,38]. In contrast, boosting strengthens weak learners iteratively by emphasizing misclassified instances to reduce bias. Notable boosting algorithms include gradient boosting [39,40,41,42,43,44,45,46], XGBoost [47,48,49,50,51,52], and LightGBM [53,54,55,56,57,58]. These methods construct decision trees sequentially, with each model correcting previous errors. Due to their high predictive performance, ensemble techniques are extensively adopted in machine learning competitions and practical applications. The following section presents an overview of the ensemble algorithms and the key hyperparameters selected for this study.

4.2.1. Random Forest

Random forest algorithm enhances predictive performance and mitigates overfitting by constructing and aggregating multiple decision trees [30,31,32,33,34,35,36,37,38]. Each tree is built using a randomly selected bootstrap sample from the dataset, and predictions are made by averaging in regression or by majority vote in classification. Since individual trees are trained independently, random forest is effective in handling noisy data and high-dimensional feature spaces [35,36,37,38]. Additionally, it mitigates variance compared to a single decision tree, which contributes to its widespread use across diverse applications. The following hyperparameters are considered.

(i)

The number of trees, defined by n_estimators, determines how many decision trees are built in the model. Using a larger value generally improves model stability and performance, but increases computational expense. By default, n_estimators is set to 100.

(ii)

The max_features (maximum number of features) specifies how many predictor variables are considered when splitting nodes during the decision tree building process. Smaller values increase model randomness and can help reduce overfitting. In classification tasks, max_features is often defined as the square root of the total feature count (sqrt).

(iii)

The max_depth (maximum depth) controls how deep each tree can grow. Allowing greater depth helps the model learn more complex relationships but can also lead to overfitting. The default setting is ‘none’.

(iv)

The minimum samples required to split (min_samples_split) defines the smallest number of observations that must be present in a node for it to be divided. Higher values result in simpler trees, which can help mitigate overfitting by limiting unnecessary splits. By default, min_samples_split is set to 2.

(v)

The min_samples_leaf (minimum number of samples per leaf) sets the minimum number of data points that must be contained in a leaf node. Increasing this value can help smooth the model’s structure by reducing the occurrence of minor or irregular branches. The default setting is 1.

4.2.2. Gradient Boosting

Gradient boosting is an iterative ensemble approach that adds trees one by one, with each new tree focusing on correcting the prediction errors made by its predecessor [39,40,41,42,43,44,45,46]. Unlike random forest, where trees are constructed independently, gradient boosting sequentially generates decision trees by using gradient descent to optimize the specified loss function [39,40,41]. This technique allows the model to accurately predict outcomes while capturing sophisticated interactions present in the dataset. However, without proper regularization, it is susceptible to overfitting. Key hyperparameters are listed below.

(i)

The n_estimators parameter (number of trees) indicates how many boosting stages are sequentially created. Using a larger value may improve predictive accuracy but may also raise the likelihood of overfitting and computational cost. The default setting is 100.

(ii)

The learning_rate controls how much each individual tree contributes to the final model. A lower value necessitates more iterations to reach a comparable level of accuracy but typically improves generalization. The default setting is 0.1.

(iii)

Maximum tree depth (max_depth) restricts the maximum depth each tree is allowed to reach. Allowing deeper trees helps the model learn more complex patterns in the data, but it also raises the chance of overfitting. The default setting is 3, resulting in relatively shallower trees.

(iv)

The minimum samples for splitting (min_samples_split) specify the minimum number of samples required to split an internal node. Higher values yield simpler trees, preventing overfitting. The default value is 2.

(v)

The minimum samples per leaf (min_samples_leaf) parameter sets the smallest number of observations needed to create a leaf node. Setting this parameter higher discourages the formation of extremely small leaves, helping to reduce model complexity and overfitting. The default setting is 1.

4.2.3. XGBoost

XGBoost (extreme gradient boosting) is an enhanced version of gradient boosting, designed for high efficiency, speed, and scalability [47,48,49,50,51,52]. It is extensively applied in both data science competitions and real-world implementations because of its adaptability, high computing efficiency, and suitability for handling large-scale datasets. Like conventional boosting methods, XGBoost constructs models sequentially, but it incorporates enhanced regularization strategies and advanced functionalities to improve generalization and reduce computational costs [50,51,52]. Key hyperparameters are as follows.

(i)

The n_estimators parameter determines how many boosting iterations are performed (total number of trees). Setting this parameter higher can strengthen predictive results, though it could also increase overfitting tendencies. The default value is 100.

(ii)

The learning_rate governs how much the model’s parameters are adjusted in each step (learning rate) while the loss function is being minimized. A lower value requires more trees to achieve comparable predictive accuracy but generally improves model adaptability. The default setting is 0.3.

(iii)

Maximum tree depth (max_depth) defines the limit on how deep each tree can grow. Higher model depth facilitates the discovery of complex patterns but can heighten the chance of overfitting. By default, max_depth is set to 6.

(iv)

The colsample_bytree parameter specifies the proportion of features (column subsampling) randomly picked to create each tree. This process incorporates variability and aids in reducing overfitting. The default setting is 1.0, meaning all features are used.

(v)

Subsample ratio (subsample) sets how much of the training dataset is randomly selected to construct each tree. Using a smaller value can help mitigate overfitting and improve computational efficiency. The default value is 1.0, indicating that the entire dataset is applied.

4.2.4. LightGBM

As an optimized and scalable gradient boosting framework, LightGBM (light gradient boosting machine) was developed by Microsoft [53,54,55,56,57,58]. Designed for high-speed training and low memory consumption, it efficiently handles large-scale data. Unlike standard gradient boosting, which builds trees in a level-wise fashion, LightGBM adopts a leaf-wise growth method to focus on splits that most effectively reduce loss [56,57,58]. This approach often improves model accuracy while accelerating training. The essential hyperparameters are described below.

(i)

The num_leaves parameter (number of leaves) determines how many leaf nodes are allowed at most in a single tree. Given LightGBM’s leaf-wise growth strategy, this parameter plays a critical role in managing model complexity. Increasing this value enables the model to capture more complex patterns, though it simultaneously raises the chance of overfitting. The default setting is 31.

(ii)

Learning rate (learning_rate) influences the step size at each iteration during loss function optimization. Lower values generally require more trees to sustain predictive accuracy but often result in better generalization. The default setting is 0.1.

(iii)

Maximum tree depth (max_depth) sets an upper bound on how deep each tree can grow. Although LightGBM primarily uses a leaf-wise growth strategy, this parameter allows explicit depth limitation to help mitigate overfitting. By default, it is assigned a value of −1, indicating no restriction.

(iv)

The feature_fraction parameter specifies the proportion of features (columns) randomly selected to generate each individual tree. This technique incorporates variability and aids in minimizing overfitting. The default value of 1.0 indicates that the model includes all available features.

(v)

The min_data_leaf (minimum data in leaf) sets the smallest number of data points that must be present in a leaf node. Setting this value higher discourages the formation of leaves with insufficient data, aiding in mitigating overfitting and promoting better generalization. In the baseline model, the default value is 20.

The operation methods, advantages, and disadvantages of the ensemble learning models described thus far are summarized in

Table 5. Comparison of ensemble learning models.

Model	Operating Methods	Advantages and Disadvantages
random forest	⋅ Bagging (bootstrap samples) ⋅ Multiple decision trees are independently generated, and final prediction is obtained using averaging and voting ⋅ Pre-pruning method is applied to restrict tree growth ⋅ Prevention of overfitting relies mainly on bagging	⋅ Robust against overfitting ⋅ Fast training speed through parallel processing ⋅ Provides variable importance ⋅ Stable performance
		⋅ Performance degradation due to the limitation of bagging ⋅ Slow prediction speed when a large number of trees are required ⋅ Strong black-box tendency
gradient boosting	⋅ Boosting ⋅ Weak learners are generated sequentially to improve errors ⋅ The first tree predicts the target value, and subsequent trees predict the residuals ⋅ The final classification is obtained by a weighted sum of all tree predictions ⋅ Pre-pruning is applied to control tree complexity ⋅ Shallow trees are primarily used	⋅ High prediction accuracy ⋅ Supports various loss function
		⋅ Slow training speed due to sequential learning ⋅ Sensitive to overfitting ⋅ Highly sensitive to hyperparameters
XGBoost	⋅ Boosting (shares the same principles as gradient boosting) ⋅ Overfitting is mitigated by adding a regularization term to the objective function ⋅ More accurate gradient descent is applied using second-order approximation ⋅ Post-pruning is applied through regularization ⋅ Leaf nodes with negative gain after splitting are removed	⋅ Very high accuracy ⋅ Supports parallel processing and distributed computing ⋅ Handles missing values internally
		⋅ Relatively slow training speed ⋅ Hyperparameter tuning is complex
LightGBM	⋅ Boosting (operates based on gradient boosting) ⋅ Uses gradient-based one-side sampling method ⋅ Focuses on optimizing efficiency in speed and memory usage ⋅ Reduces the number of features using the exclusive feature bundling method ⋅ Adopts a leaf-wise tree growth strategy ⋅ Pre-pruning through maximum depth limitation ⋅ Leaf-wise growth inherently provides efficient pruning	⋅ Very fast training speed ⋅ Low memory usage ⋅ Suitable for large-scale data processing ⋅ Relatively good accuracy
		⋅ High risk of overfitting on small datasets ⋅ Leaf-wise growth may produce unbalanced trees

. To address the limitations of random forest—such as issues with training speed, overfitting, and prediction performance—various boosting algorithms have been developed and applied. In particular, the XGBoost and LightGBM techniques employ gradient boosting-based data sampling methods and have been proposed to improve training speed, prediction performance, and the efficient use of computational resources.

5. Analytical Results

To evaluate the performance of the models, a cloud-based Google Colab environment with GPU support was used. The hardware consisted of a processor with a 2.8 GHz clock speed, 4 cores, and 8 threads. The software environment was Windows 11.

5.1. Results of Baseline Model

In this study, the baseline model refers to the configuration in which all hyperparameters are set to their default values. The following assumptions are adopted to evaluate the model’s performance.

(1)

The preset hyperparameter values for each model are applied as outlined in Section 4. To enhance robustness, experiments are conducted on five distinct datasets (including training and test sets) using varied random seed values. The average performance across all iterations is then computed for comparison.

(2)

To construct the training dataset, the Python library RandomOverSampler [2,5,65,66,67] is used to apply an oversampling strategy so that the minority class is increased to match the majority class. This technique improves training accuracy by addressing class imbalance. RandomOverSampler, a function within the imbalanced-learn package, alleviates dataset disparity by randomly replicating samples from the minority class. This straightforward method effectively balances class distributions to achieve either equal or predefined class ratios.

Figure 6 displays the baseline model’s results, with white bars showing training accuracy and black bars indicating test accuracy. The model achieves over 95% predictive accuracy on the training data, whereas test accuracy ranges from 82.7% to 85.8%. Evaluation on the test data shows that ensemble models consistently outperform logistic regression in accuracy. Specifically, LightGBM achieves a 3.5% improvement, and random forest yields a 3.8% gain relative to logistic regression.

5.2. Results of Optimization Model

To find the optimal hyperparameters for each model, the techniques listed below were employed.

(1)

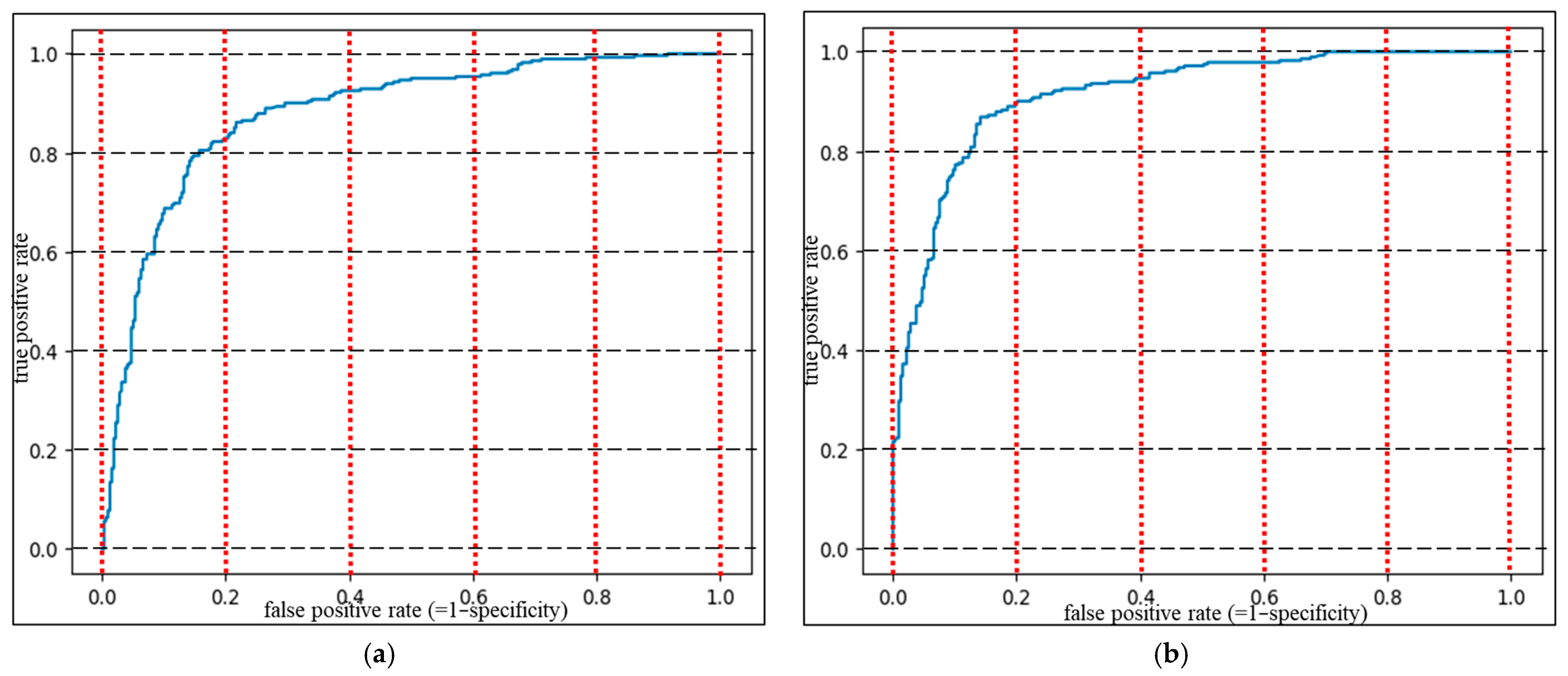
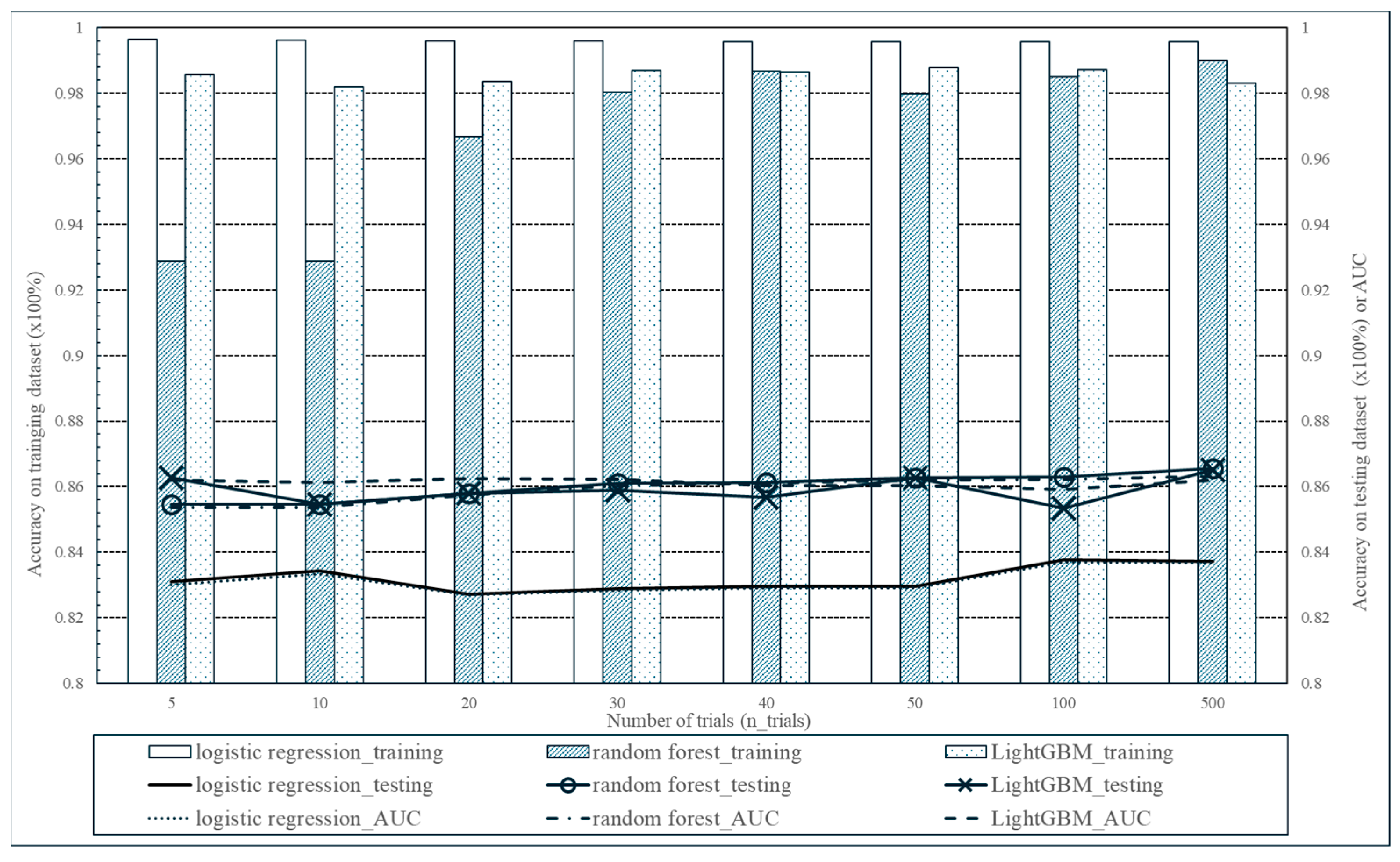
For model tuning, the Optuna library [64,65,66,67] was used. Optuna is an open-source tool created to automate the process of finding the best configurations for machine learning models. It implements advanced techniques such as Bayesian optimization and tree-structured Parzen estimators, as well as pruning mechanisms that terminate less promising trials at an early stage [64,65,66]. In Optuna, the n_trials parameter indicates the number of times the tuning procedure is executed, with each trial evaluating a unique combination of parameters. A higher n_trials value tends to improve the model’s accuracy but requires more processing time. Variations in n_trials were explored for high-performing models to assess their impact on the results.

(2)

For each model, five hyperparameters influencing analytical performance were selected, as shown in

Table 6. Tuned and optimal hyperparameters (n_trials = 10).

Model	Hyperparameters
logistic regression	name	C regularization strength	penalty regularization type	solver optimization algorithm	class_weight class weight	max_iter maximum_iterations
	baseline	1.0	l2 (Ridge)	lbfgs	none	100
	tuned values	[10−5, 100]	[l1, l2]	[l1: liblinear, l2: newton-cg, lbfgs, sag, saga]	[none, balanced]	[100, 1000]
	optimal	3.274	l2	sag	balanced	168
random forest	name	n_estimators number of trees	max_features maximum number of features	max_depth maximum depth of trees	min_samples_split minimum number of samples to split	min_samples_leaf minimum number of samples in a leaf
	baseline	100	sqrt	none	2	1
	tuned values	[50, 1000]	[none, sqrt, log2]	[5, 50]	[2, 20]	[1, 20]
	optimal	105	none	23	3	7
gradient boosting	name	n_estimators number of trees	learning_rate learning rate	max_depth maximum depth of trees	min_samples_split minimum number of samples to split	min_samples_leaf minimum number of samples in a leaf
	baseline	100	0.1	3	2	1
	tuned values	[50, 1000]	[0.01, 0.3]	[3, 32]	[2, 100]	[1, 50]
	optimal	553	0.027	11	69	12
XGBoost	name	n_estimators number of trees	learning_rate learning rate	max_depth maximum depth of trees	colsample_bytree column subsampling	subsample subsample ratio
	baseline	100	0.3	6	1	1
	tuned values	[50, 1000]	[0.01, 0.3]	[3, 32]	[0.5, 1]	[0.5, 1]
	optimal	272	0.027	18	0.839	0.638
LightGBM	name	num_leaves number of leaves	learning_rate learning rate	max_depth maximum depth of trees	feature_fraction feature fraction	min_data_leaf minimum data in leaf
	baseline	31	0.1	−1	1	20
	tuned values	[2, 256]	[0.01, 0.3]	[−1, 32]	[0.5, 1]	[1, 50]
	optimal	174	0.037	13	0.668	26

. These hyperparameters are chosen based on insights from the original studies that proposed each model, together with findings from recent research [28,29,37,38,52,58,67]. Table 6 further provides the tuning ranges for each hyperparameter, as well as the optimal values determined for a sample case when n_trials = 10.

(3)

Additionally, a 5-fold cross-validation technique was used on each training dataset to identify hyperparameter settings that maximize accuracy. Using these selected parameters, the final performance of the model was assessed.

Figure 7 shows a comparison between the baseline model and the optimized model. The optimized model uses hyperparameters adjusted for improved outcomes. The optimized version was obtained using the Optuna library, with n_trials set to 10 and a 5-fold cross-validation approach. In Figure 7, the left y-axis depicts prediction accuracy on the training set (shown as vertical bar graphs), whereas the right y-axis indicates accuracy on the testing set (illustrated as a line graph). The key findings can be summarized as follows.

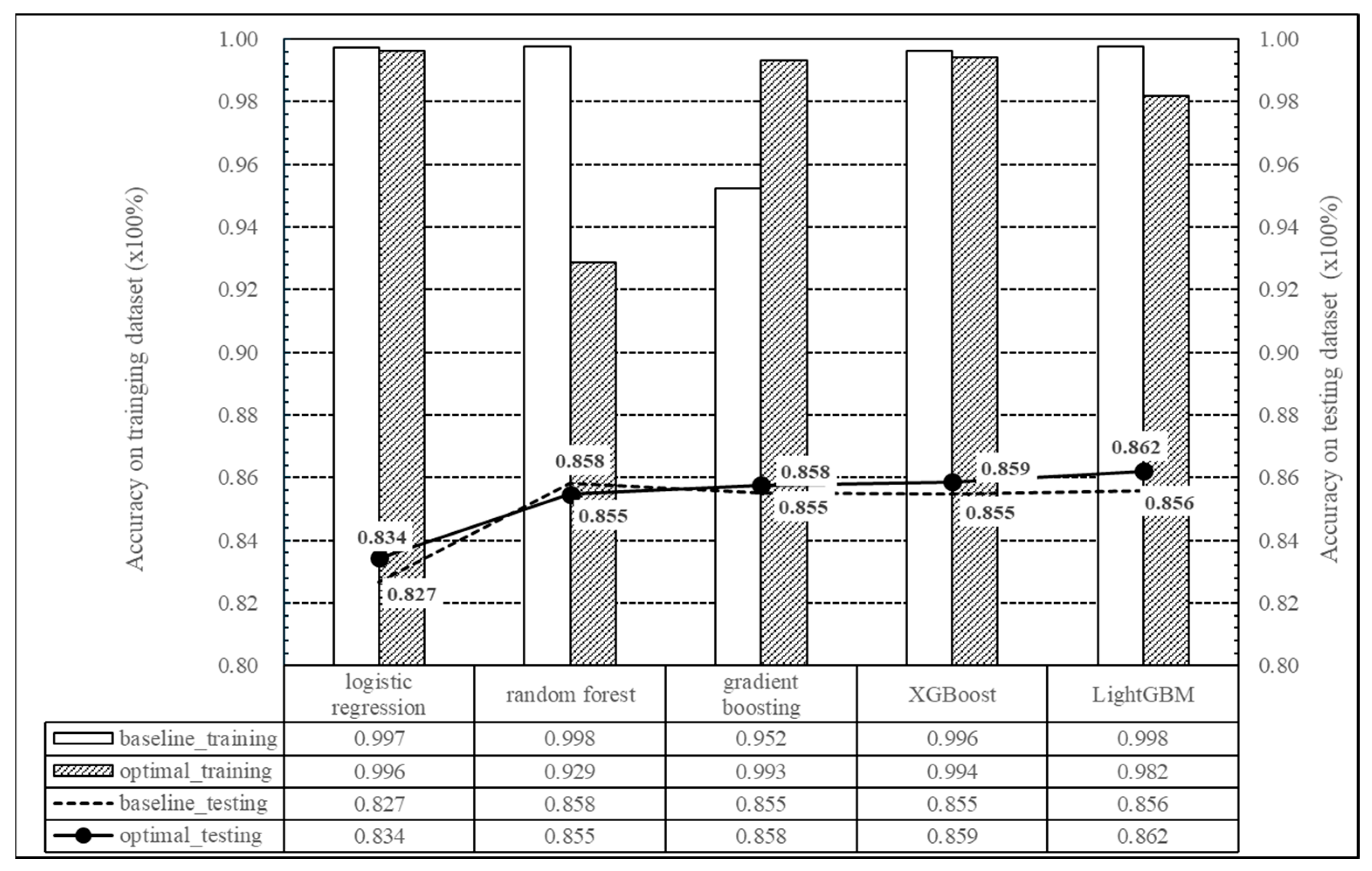
(1)

For the training dataset, the baseline model achieves higher accuracy than the optimized model. However, in gradient boosting techniques, the optimized model outperforms the baseline in predictive accuracy on the training data. For the random forest, the optimized configuration yields approximately 6.9% lower training accuracy compared to the baseline. This occurs because the baseline uses default hyperparameters without explicit regularization, which may overfit the training data and thus results in higher accuracy. In contrast, the optimized model applies regularization and constrained hyperparameters, which may reduce training accuracy but typically improve generalization performance on the testing dataset.

(2)

When evaluating performance on the testing dataset, ensemble-based models consistently achieve higher accuracy than logistic regression. For the testing dataset, the optimal configuration yields prediction accuracy gains of 2.4% (random forest), 2.8% (gradient boosting), 2.9% (XGBoost), and 3.3% (LightGBM) compared with logistic regression

(3)

Analysis of testing dataset accuracy indicates that, except for random forest, all models perform better under the optimized configuration compared with the baseline. Random forest exhibits negligible performance difference between baseline and optimized versions (about 0.4% difference in accuracy).

(4)

The results of the comparison between the performance of the baseline model and the results after hyperparameter tuning on the testing dataset are summarized as follows. In the case of logistic regression, the accuracy after hyperparameter tuning improved by 0.9% compared to the baseline model. On the other hand, for the four ensemble models, the accuracy improved by about 0.3%. In particular, the highest improvement in accuracy (0.7%) was observed in LightGBM after hyperparameter tuning compared to the baseline.

In this study, to enhance the reliability of accuracy performance evaluation for the models, their performance was assessed across five datasets, each of which was generated with a different random seed. Subsequently, it was examined whether statistically significant differences were observed due to variations in random seeds and in the accuracy performance of each model under a 1% significance level (alpha). That is, a one-way analysis of variance (ANOVA) was conducted to test the following null hypothesis. First, the null hypothesis (H₀) regarding the performance differences among models is stated as follows.

H₀: 

There is no statistically significant difference in performance among the models.

In addition, for each model, the following null hypothesis was tested.

H₀: 

There is no statistically significant difference in performance across the training and test datasets classified using different random seed numbers.

The results of the one-way ANOVA, i.e., the significance probabilities (p-values) for each case, are presented in

Table 7. One-way ANOVA results (p-values) for performance differences between models and random seed variations.

Model		Training Dataset	Testing Dataset	AUC
Baseline	Model’s accuracy	0 *	0.0001 *	0.0002 *
	Random seed	0.2033	0 *	0 *
Optimal	Model’s accuracy	0.0001 *	0 *	0.0001 *
	Random seed	0.6913	0 *	0 *

* denotes a statistically significant difference in performance (significance level of 1%).

. Note that if the p-value is smaller than the significance level (1%), the H₀ is rejected, indicating that there is a statistically significant difference in performance.

From the test results, it was confirmed that significant differences exist in model performance and random seed variations with respect to the testing dataset and AUC values. However, in the case of the training data, significant differences were observed in performance across models, whereas no substantial differences were found when random seeds were varied. In summary, for the training dataset, no significant performance differences were caused by random seeds, while significant differences were identified across models, thereby supporting the proposal and validity of the ensemble analysis model.

Meanwhile, the significance of performance with respect to oversampling was tested, and it was confirmed that no significant performance differences existed for the training dataset (p-value = 0.1988) and the testing dataset (p-value = 0.2201) at a 1% significance level. Since the oversampling technique previously applied in the logistic regression model was proposed in this study, the results obtained by applying the same oversampling method to all models were compared with each other.

When assessing model performance, metrics other than accuracy, including the ROC curve and AUC, are taken into account. The ROC curve visually represents classification effectiveness by plotting the false positive rate (fpr) against the true positive rate (tpr), both of which are derived from the confusion matrix [64,65,66]. The AUC, which stands for area under the curve, quantifies the space under the ROC curve and ranges from 0 to 1—a higher AUC means greater ability to distinguish between classes. An AUC value of 0.8 or higher is generally regarded as an indication of strong classification performance. Figure 8 depicts the ROC curves of the optimized logistic regression and random forest models using a sample dataset. The ROC curve was generated using the roc_curve (actual, predicted) function included in the sklearn.metrics library in Python [64,65,66,67]. In this study, due to page limitations, the ROC curve presented was generated based on the results of a single example (i.e., one random sample with n_trials = 10). When comparing the performance of models using ROC curves, it is necessary to construct and compare ROC curves based on the results obtained from all experiments. This should also be considered in future work when developing more advanced or innovative algorithms. Therefore, Figure 8 illustrates the ROC curve for a single sample example, where the AUC represents predictive performance; a larger AUC indicates better performance. It is noteworthy that the ROC curve of the random forest model is positioned nearer to the upper-left corner, reflecting a higher AUC value. When comparing the results in Figure 8 within the range of fpr values (0, 0.8) and tpr values (0, 1), it is observed that the AUC for random forest is larger compared to the logistic regression model. These results suggest that the random forest (AUC = 0.868) achieves superior discriminative ability compared to the logistic regression model (AUC = 0.845).

Figure 9 shows a comparison of AUC values between the baseline and optimized models using test data. All models achieve AUC ≥ 0.8, indicating strong predictive capability. Additionally, ensemble models consistently outperform logistic regression, as evidenced by their superior AUC values. Among the baseline models, the random forest demonstrates the highest AUC, whereas LightGBM achieves the best results in the optimized configuration. Comparing AUC values, the random forest in the baseline setup exceeds that of the logistic regression model by 3.8%, while in the optimized setup, LightGBM improves its AUC by 3.4% relative to logistic regression.

The performance metrics—precision, recall, and F1-score—of both the baseline and optimized models are presented in Figure 10. In Figure 10, the left y-axis displays the baseline model outcomes (depicted as vertical bar graphs), while the right y-axis shows the optimized model performance (illustrated as a line graph). Key findings include:

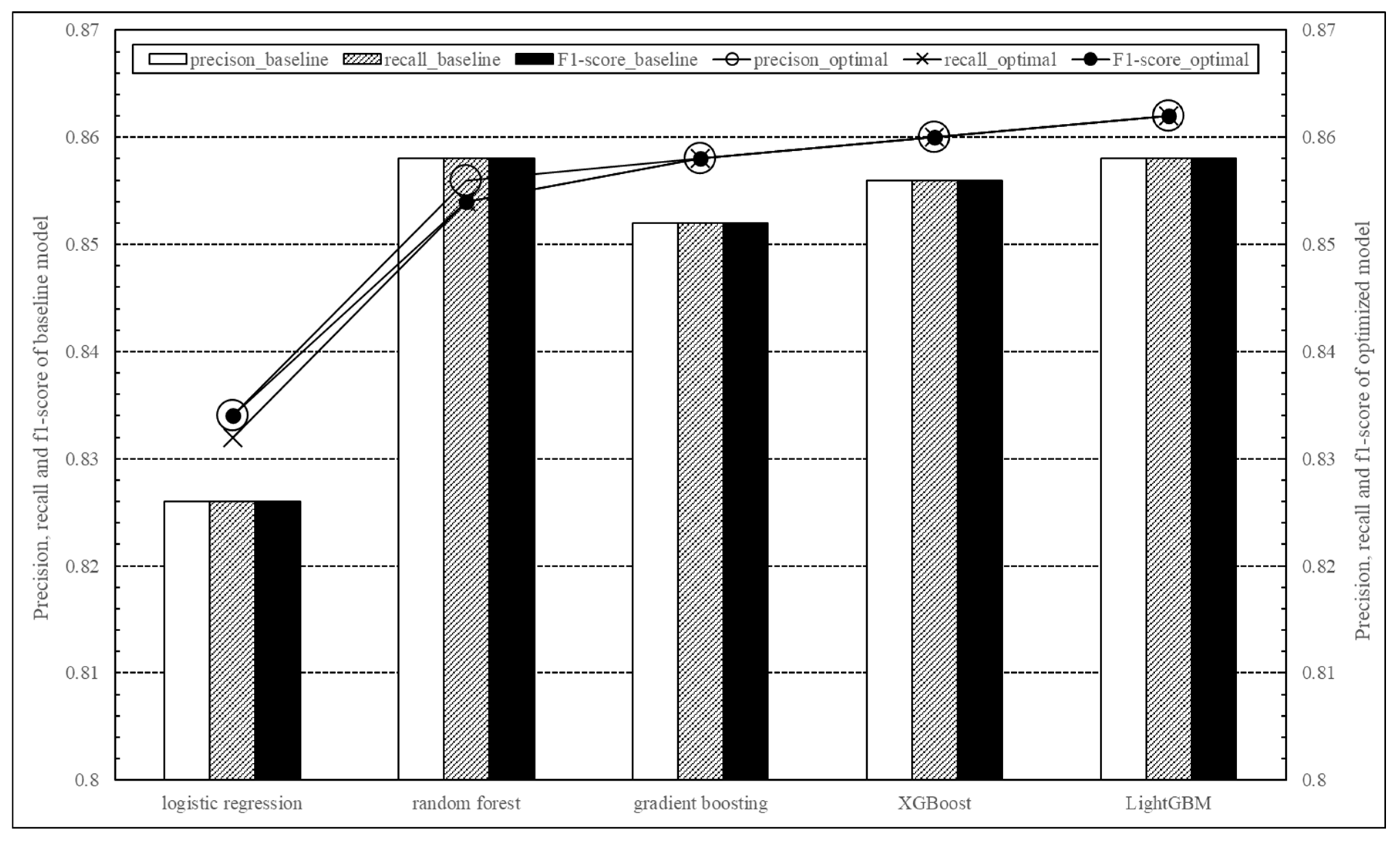
(1)

For each baseline model, there is little difference in the performance of precision, recall, and F1-score. This indicates that, when assuming the default hyperparameter values for each model, the prediction performance for each class does not differ significantly. That is, when precision, recall, and F1-score have similar values, the corresponding model can be considered to predict both classes (IP and non-IP) in a balanced manner [64,65,66,67]. In other words, the model’s predictions are consistent, reliable, and fair, performing without bias between classes. Conversely, for the optimal models of logistic regression and random forest, the prediction performance appears to exhibit a slight bias toward certain dependent variables. The evaluation results of precision, recall, and F1-score for each model are provided in the Appendix A.

(2)

Analysis of the test dataset indicates that the performance of the ensemble models consistently exceeds that of the logistic regression model.

(3)

Random forest and LightGBM achieve the best precision, recall, and F1-score among the baseline models, demonstrating their superior performance. The baseline configurations across various models yield similar results for these criteria.

(4)

Except for random forest, all models exhibit improved performance in their optimized configurations relative to their baseline versions. The three boosting algorithms—gradient boosting, XGBoost, and LightGBM—deliver comparable outcomes across evaluation metrics.

Finally, Figure 11 presents a comparative analysis of how the performance of logistic regression, random forest, and LightGBM models varies with an increasing number of trials (n_trials). In Figure 11, the left y-axis shows training accuracy, while the right y-axis denotes test accuracy or AUC. In general, increasing n_trials enhances model performance by enabling a more thorough and extensive exploration of the hyperparameter space. However, this benefit diminishes when the search space is constrained or when the algorithm converges early. The test results show that, despite increasing n_trials, the ensemble models consistently outperform the logistic regression model. The results further show that, compared to other models, the random forest exhibits greater performance improvements as n_trials increases. Specifically, for the random forest model, expanding n_trials from 5 to 500 leads to a 1.27% increase in test accuracy and a 1.14% improvement in AUC.

6. Conclusions

Globally, both advanced and emerging nations have consistently implemented industrial policy frameworks—whether proactive or defensive—to reinforce national industrial competitiveness and protect public welfare. In particular, the United States and China have increasingly adopted industrial policy as a central mechanism to secure technological dominance within an intensely competitive global market. To properly track and examine the evolution of industrial policies, states are required to develop forward-looking governance frameworks that strengthen economic adaptability and long-term stability. For economies with restricted fiscal means—particularly when compared to dominant actors like the U.S. and China—the adoption of machine learning approaches represents a key strategy for the automated identification and classification of newly enacted industrial policies. This progress holds significant importance in escalating international trade competition.

To achieve this objective, an automated method for identifying industrial policies was proposed. This method leverages text mining techniques to analyze policy statements and uses a logistic regression model for classification. However, it is widely recognized that ensemble-based analytical models typically outperform logistic regression when dealing with non-linear feature interactions, high-dimensional data, numerous predictors, and missing values. In this study, classification accuracy is evaluated by introducing an ensemble model designed to automatically determine whether a given policy statement constitutes an industrial policy. Ensemble methods fall into two categories—bagging and boosting—based on their data sampling methodologies. As a representative bagging technique, the random forest model is employed. Furthermore, boosting approaches (gradient boosting, XGBoost, and LightGBM) are applied, as they have shown superior performance in classification tasks. The dataset consists of 2000 policy statements randomly selected from 2018 to 2023, with 70% allocated for training and 30% for testing. To ensure robustness, different random seed values were used to create distinct training and test sets, enabling a thorough evaluation of model performance. During data preprocessing, stopwords within policy statements were removed, and the TF-IDF (term frequency-inverse document frequency) value for each word was computed to indicate its relative significance. These TF-IDF values were designated as independent variables, while policies were labeled as IP = 1 for industrial policies and IP = 0 for non-industrial policies, with the labels serving as the dependent variable.

Performance analysis showed that, for the baseline model with default hyperparameters, ensemble models consistently outperformed logistic regression in terms of test data accuracy. Specifically, LightGBM and random forest yielded improvements in accuracy of 3.5% and 3.8%, respectively, relative to logistic regression. Even after optimizing hyperparameters via cross-validation, ensemble models maintained superior performance. On the test dataset, the optimized models achieved accuracy gains of 2.4% (random forest), 2.8% (gradient boosting), 2.9% (XGBoost), and 3.3% (LightGBM) compared to logistic regression. To further evaluate predictive performance, additional metrics such as AUC, precision, and recall were examined. In the baseline configuration, random forest achieved an AUC value 3.8% higher than logistic regression, whereas in the optimized model, LightGBM showed a 3.4% increase in AUC over logistic regression. Among the ensemble models, boosting algorithms (LightGBM and XGBoost) showed minimal differences in precision and recall. Nonetheless, in their baseline form, LightGBM and random forest achieved higher performance than the other models. In conclusion, this study confirms that LightGBM and random forest significantly outperform the previously proposed logistic regression model. Finally, this study investigated whether expanding the range of hyperparameter combinations—represented by the number of optimization attempts—would lead to additional performance improvements for the top-performing models (LightGBM and random forest). The analysis indicated that, compared to other models, random forest achieved a 1.3% performance gain as the number of optimization attempts increased.

This study showed the results of applying the ensemble learning model, which is commonly applied in binary classification problems, and it is limited in that it cannot present new algorithms or methodologies to improve performance. That is, this study did not propose an innovative methodology for the classification of industrial policies and, consequently, did not provide new and significant knowledge in the related field. It is expected that the performance of ensemble learning models can be further enhanced in future work by developing more efficient text analysis techniques for industrial policy documents. Along with the study of innovative methodologies, the recommended directions for future work are as follows. In this study, the use of 2000 policy statements was found to result in some degree of overfitting. Therefore, future research is required to prevent overfitting by utilizing a larger set of policies. The application of online or incremental learning methods is expected to improve performance. In addition, all feature variables were considered for the classification of industrial policies; however, future research should compare classification performance by applying dimensionality reduction methods to consider only significant variables. In this case, a comparison and analysis of the training time and computer memory usage for each machine learning model are also required. That is, the trade-off between training time and prediction performance should be analyzed to propose a more efficient (in terms of computational cost) model. This study proposed an ensemble machine learning model designed to autonomously classify whether a given policy document constitutes an industrial policy based on its description. Compared to logistic regression, the proposed ensemble model showed better performance. However, a discussion on the ‘explainability’ of the ensemble model’s classification results has not been presented. This study only evaluates the importance of individual words to present the classification results for comparison with previous research, which represents a limitation. Therefore, further research focusing on the explainability of machine learning models is necessary. Future research also should integrate N-gram analysis to capture the significance of sequential word patterns and refine the ensemble model to improve computational efficiency by developing new and innovative algorithms. In addition, to further improve the model, it is important to conduct comparative evaluation using advanced methods such as clustering, support vector machines, and artificial neural networks incorporating the transformer technique.