Scaling Nuclear Magnetic Resonance with Integrated Planar Coil and Transceiver Front-End: Co-Design Considerations
Abstract
1. Introduction
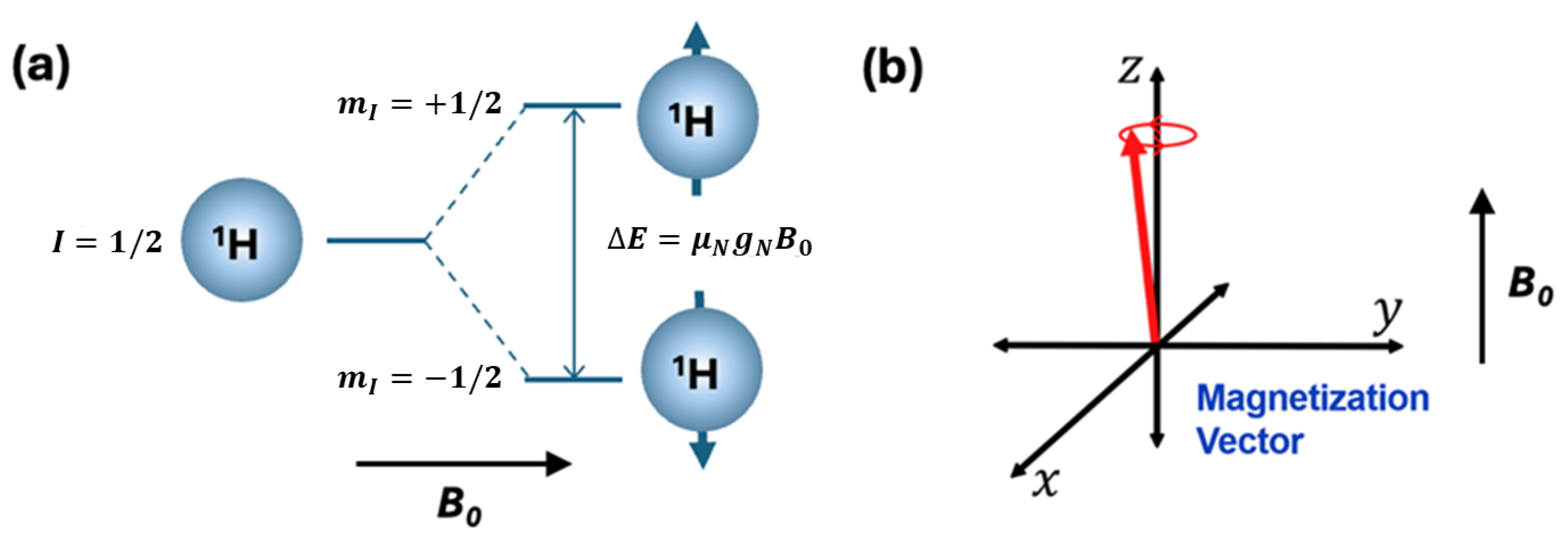
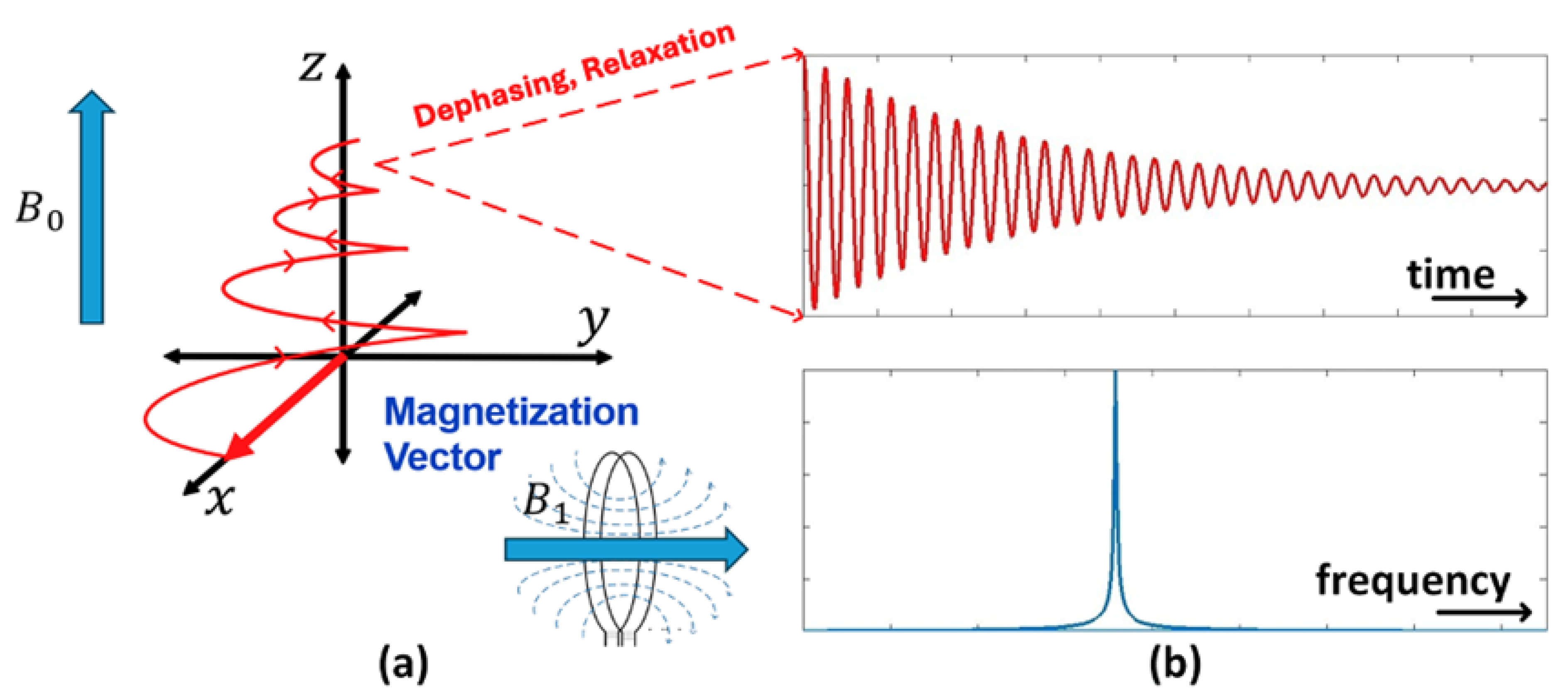
2. Key Concepts in NMR Spectroscopy
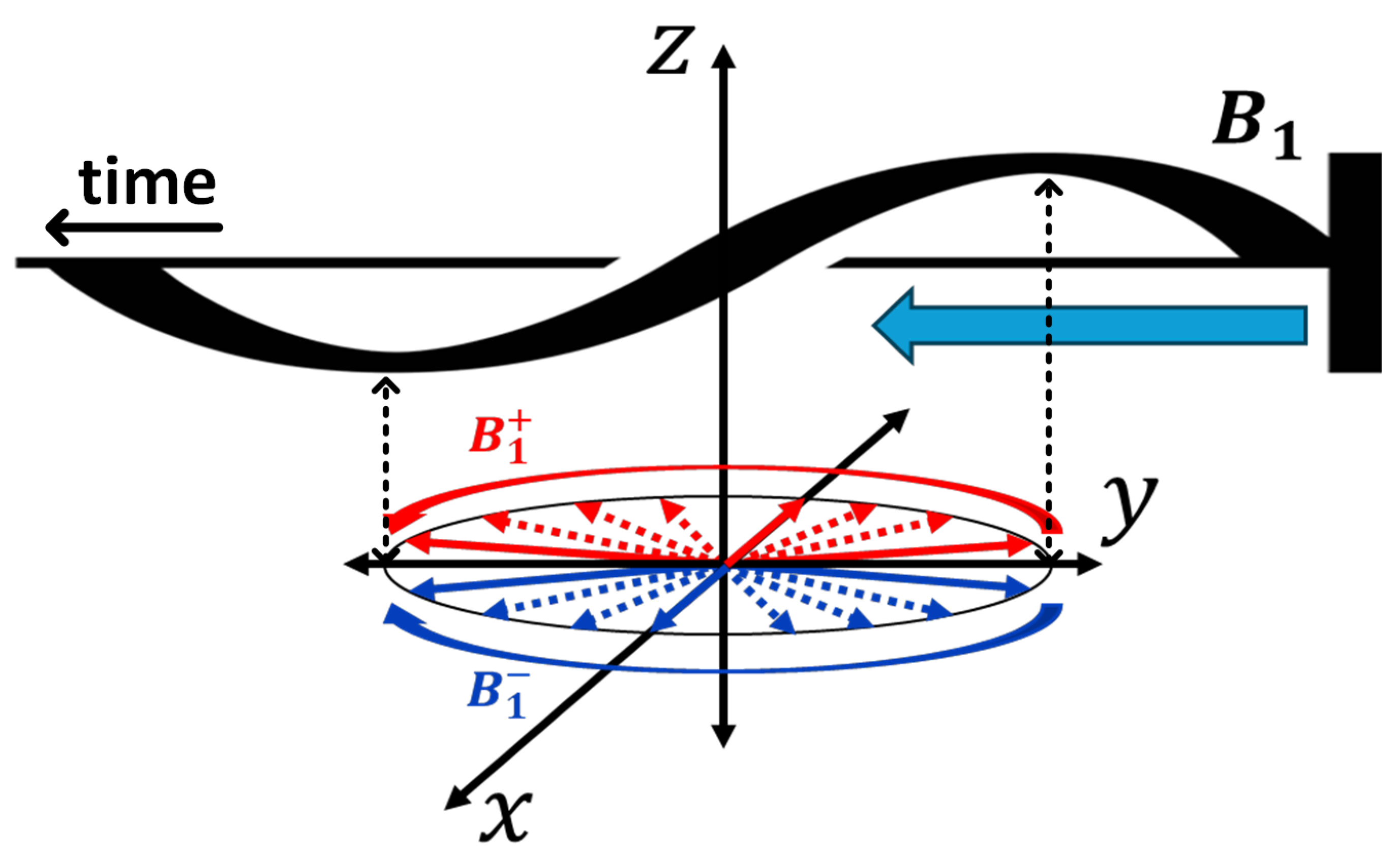
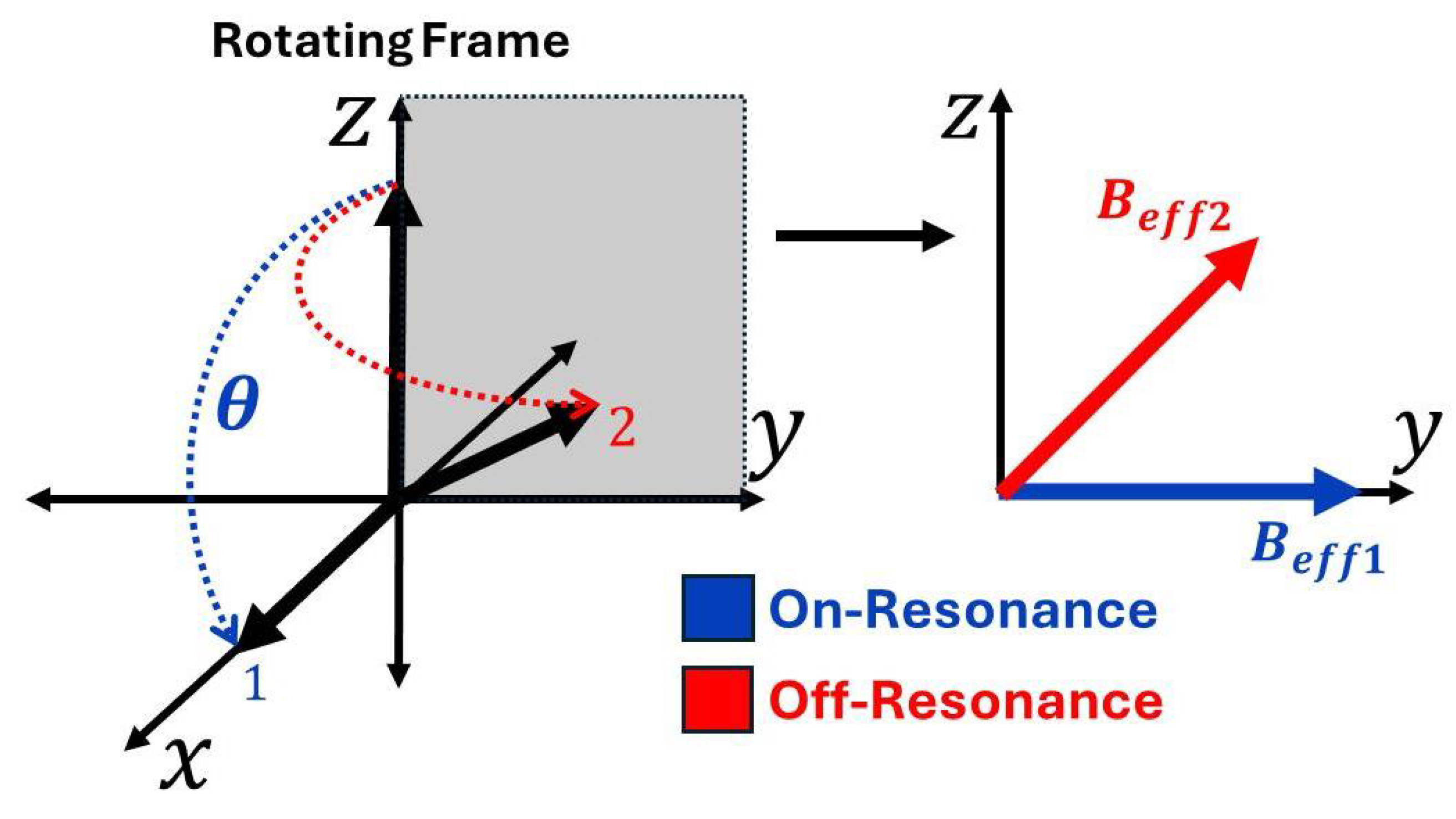
3. Vector-Based Representation of NMR Phenomena and the Mathematical Framework for RF Engineering
4. Design Considerations
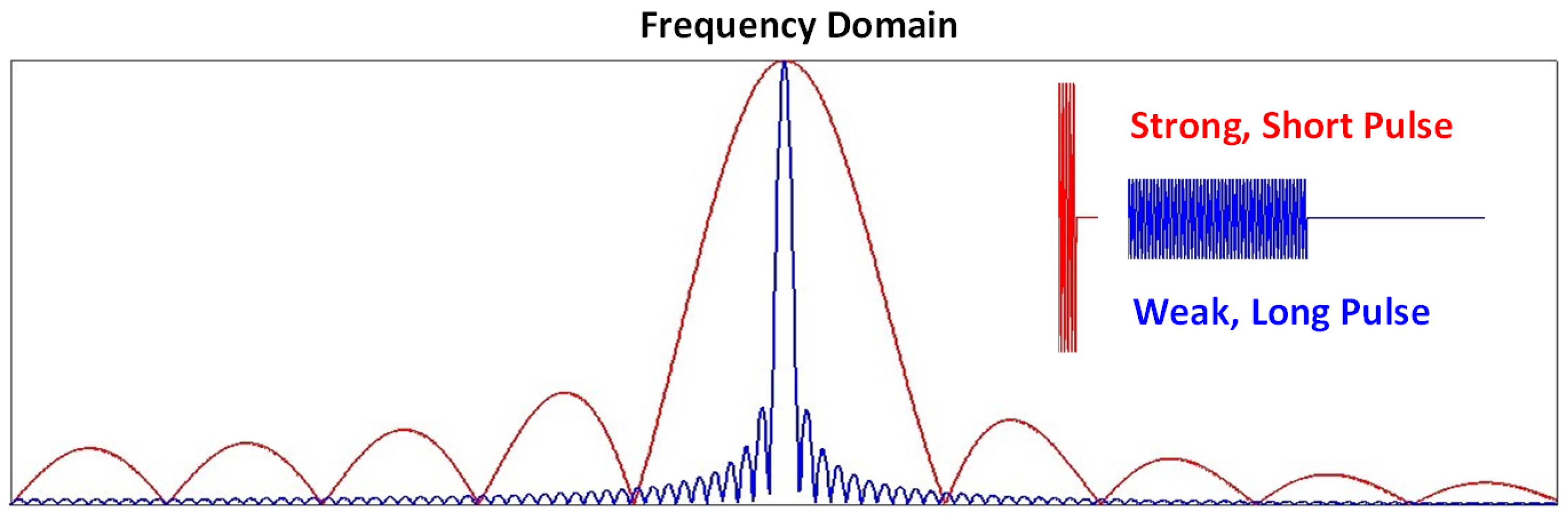
4.1. Signal Maximization
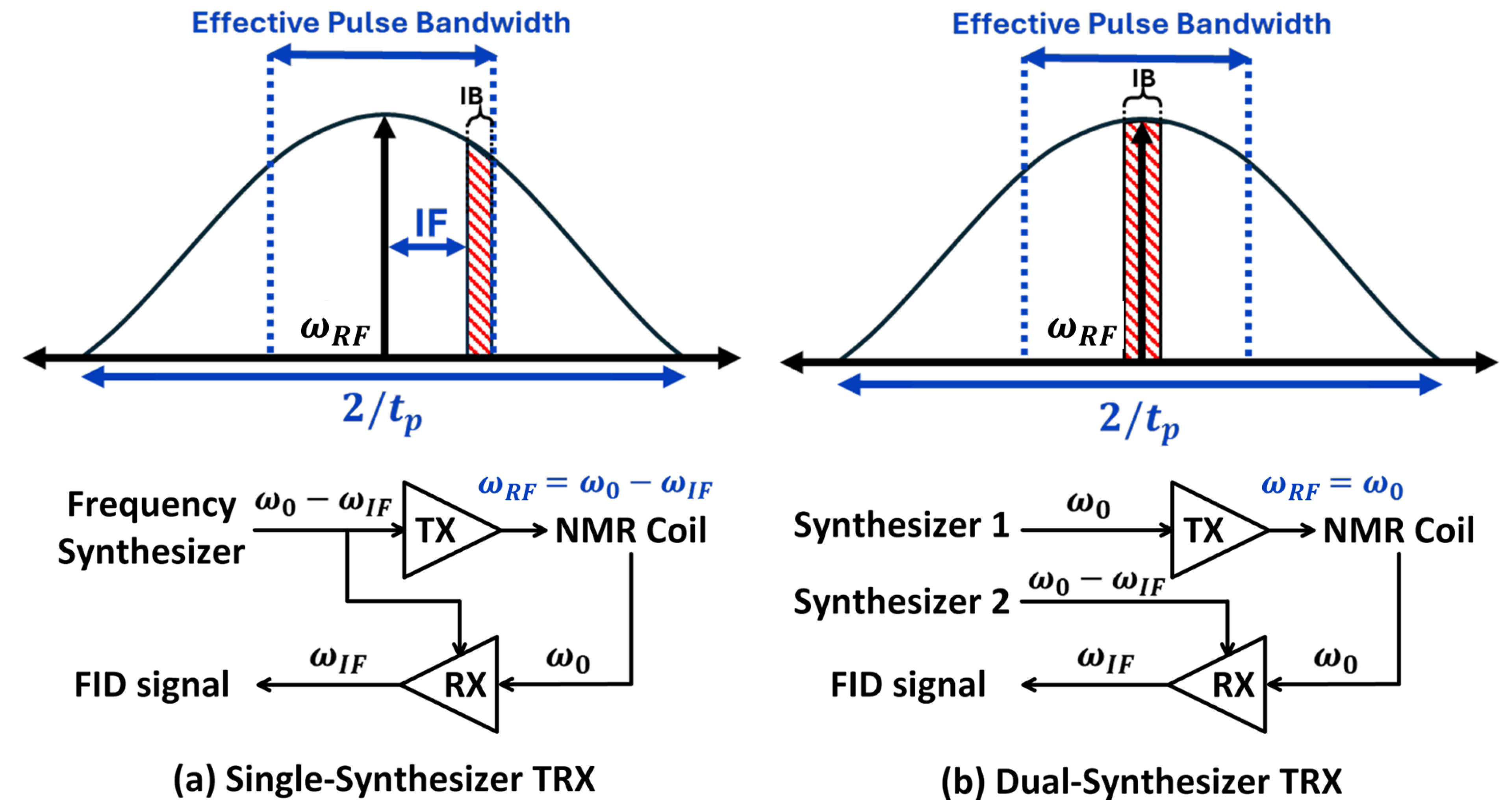
4.1.1. Strength of and
4.1.2. Inhomogeneity
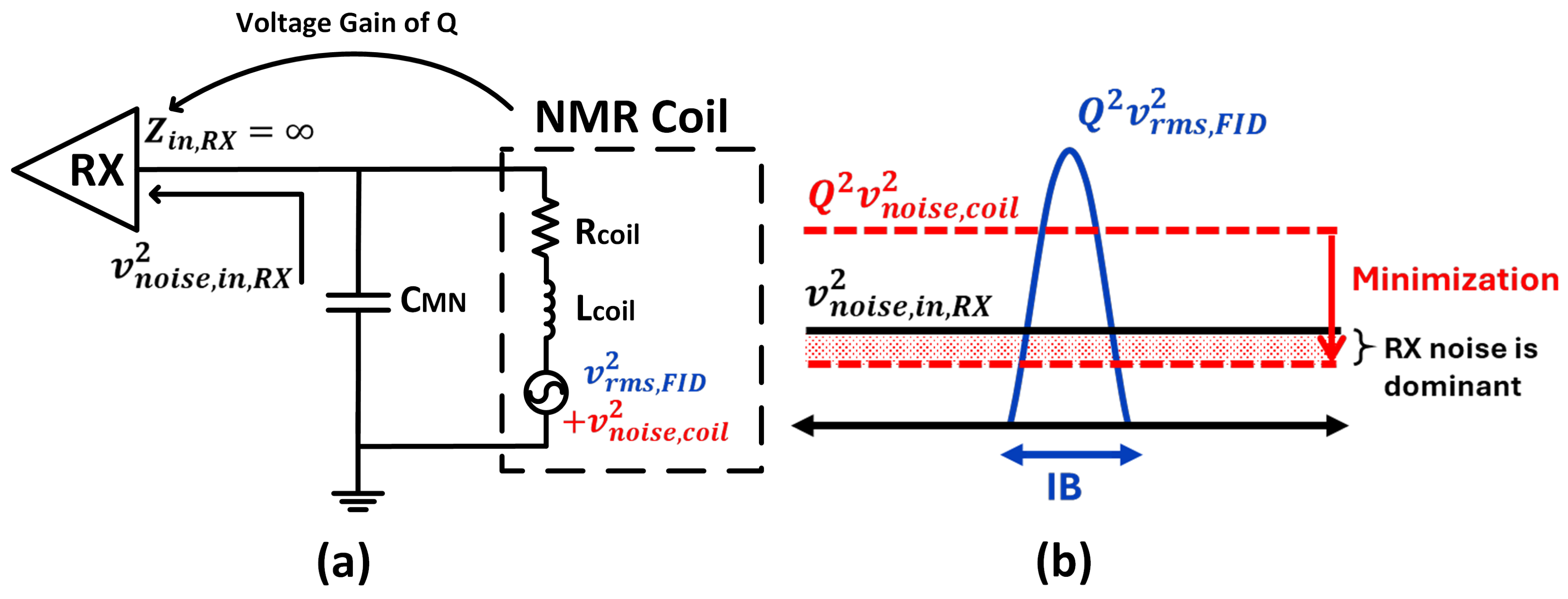
4.2. Noise Minimization
5. Coil Optimization
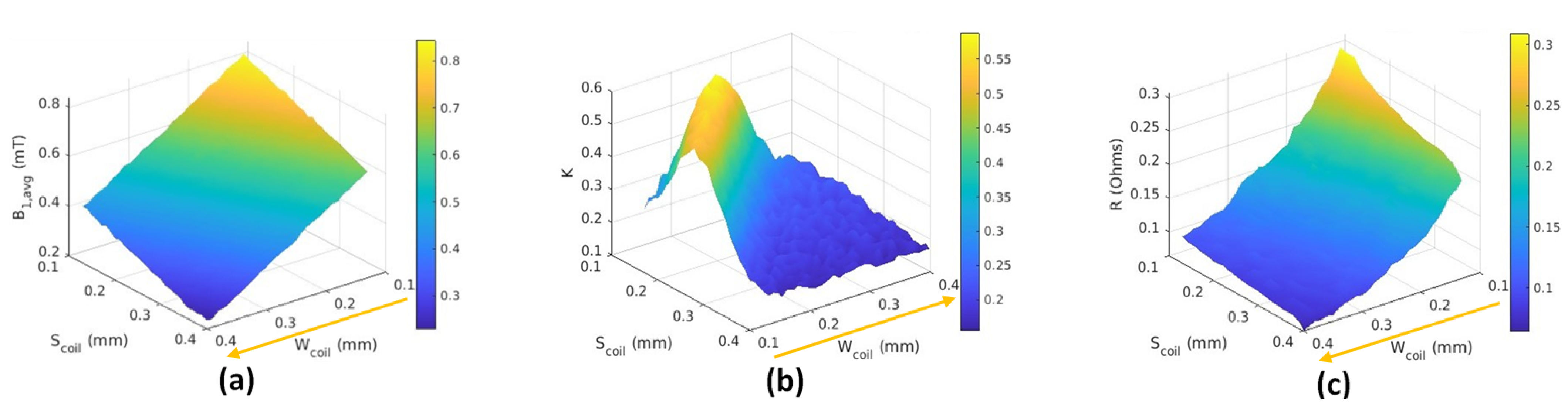
5.1. Coil Performance Factor
5.2. Parameter Extraction
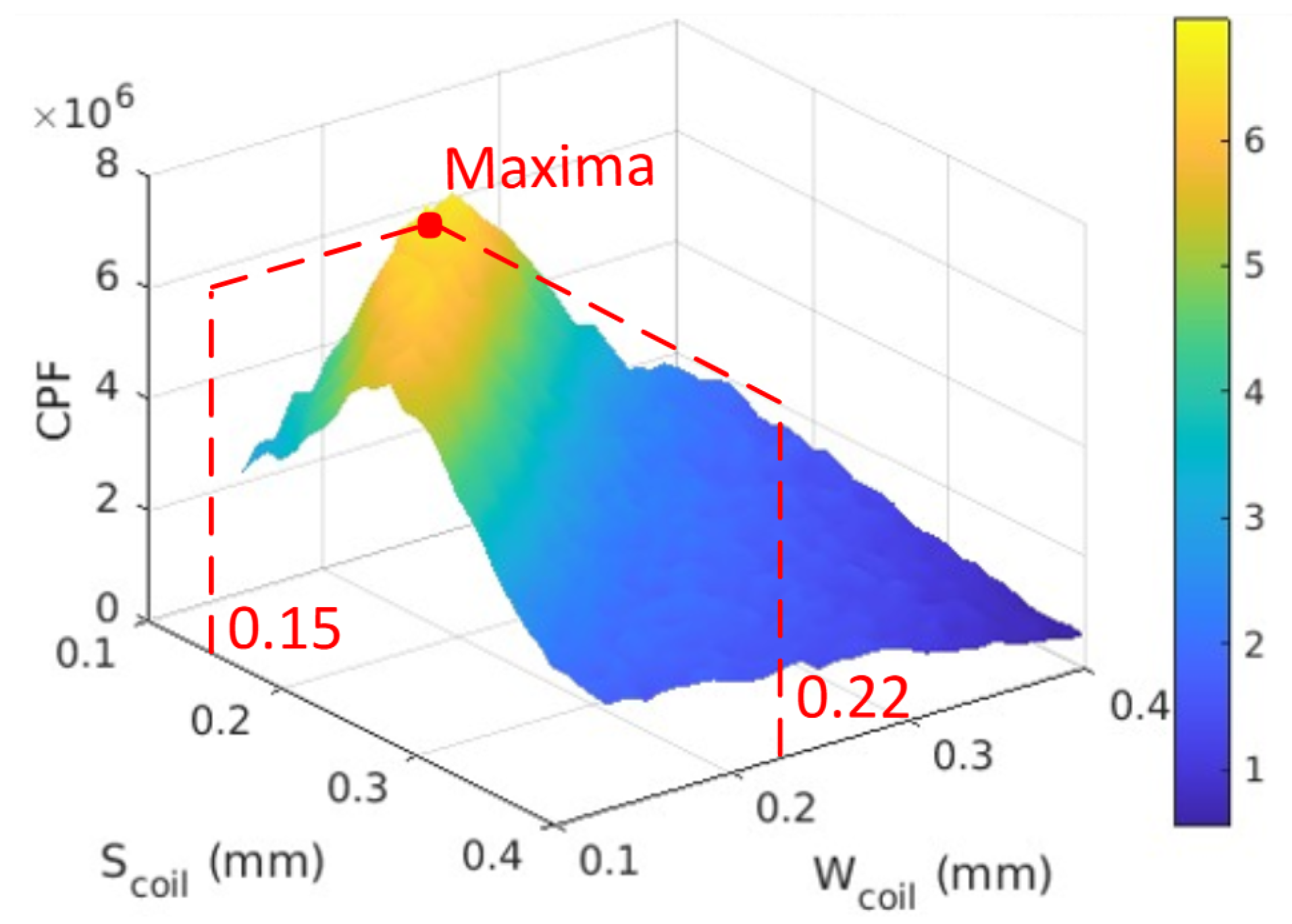
5.3. Optimization Process
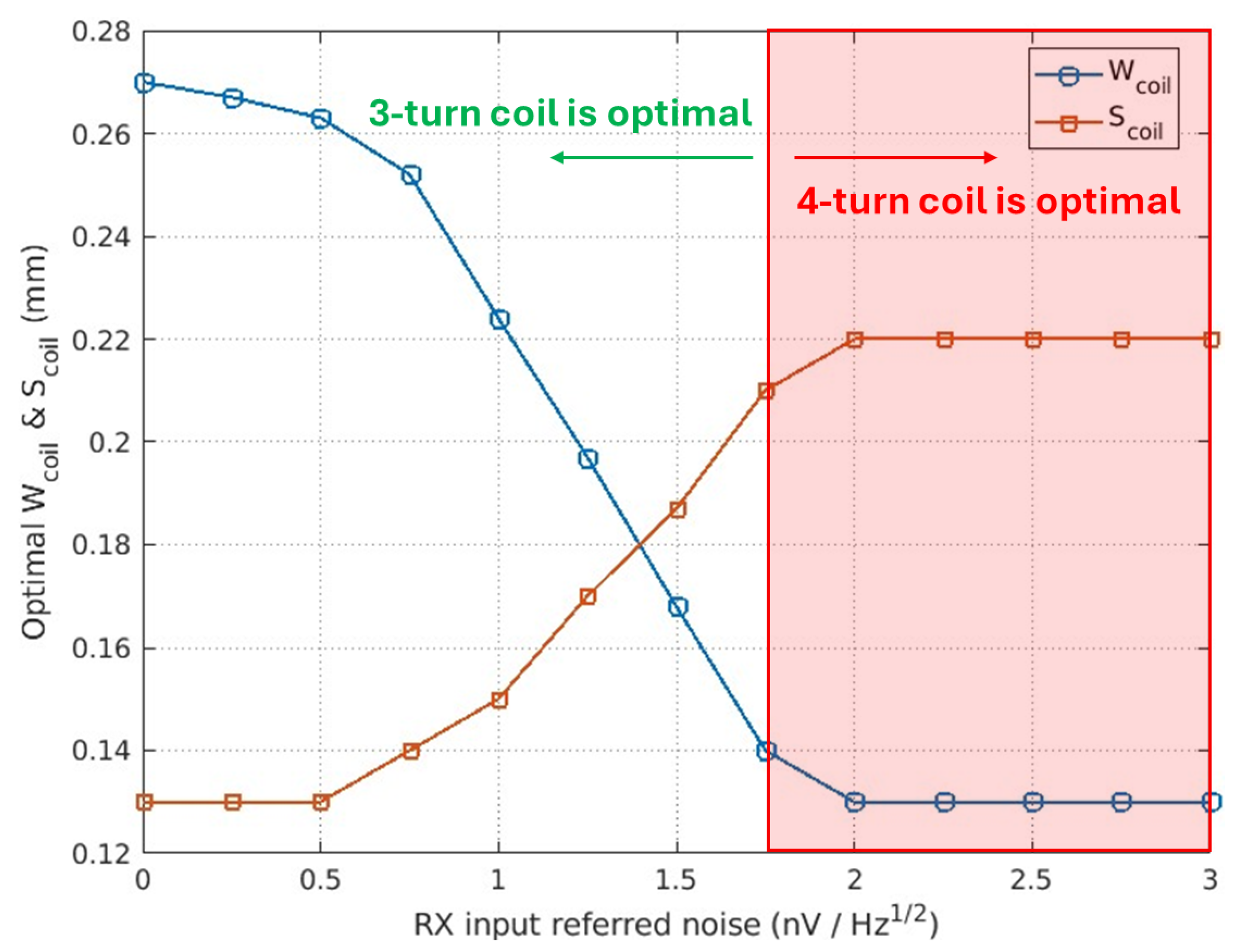
6. Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NMR | Nuclear Magnetic Resonance |
| TRX | Transceiver |
| ICs | Integrated Circuits |
| PCB | Printed Circuit Board |
| FID | Free Induction Decay |
| TX | Transmitter |
| SNR | Signal-to-Noise Ratio |
| IB | Inhomogeneity Bandwidth |
| IF | Intermediate Frequency |
| DSP | Digital Signal Processing |
| RX | Receiver |
| CPF | Coil Performance Factor |
| EM | Electromagnetic |
References
- Elsayed, M.; Isah, A.; Hiba, M.; Hassan, A.; Al-Garadi, K.; Mahmoud, M.; El-Husseiny, A.; Radwan, A.E. A review on the applications of nuclear magnetic resonance (NMR) in the oil and gas industry: Laboratory and field-scale measurements. J. Pet. Explor. Prod. Technol. 2022, 12, 2747–2784. [Google Scholar] [CrossRef]
- Unser, M.; Aldroubi, A. A review of wavelets in biomedical applications. Proc. IEEE 1996, 84, 626–638. [Google Scholar] [CrossRef]
- Bottomley, P.A. NMR in medicine. Comput. Radiol. 1984, 8, 57–77. [Google Scholar] [CrossRef]
- Lei, K.-M.; Mak, P.-I.; Law, M.-K.; Martins, R.P. A μNMR CMOS transceiver using a butterfly-coil input for integration with a digital microfluidic device inside a portable magnet. In Proceedings of the 2015 IEEE Asian Solid-State Circuits Conference (A-SSCC), Xiamen, China, 9–11 November 2015; pp. 1–4. [Google Scholar]
- Anders, J.; Handwerker, J.; Ortmanns, M.; Boero, G. A low-power high-sensitivity single-chip receiver for NMR microscopy. J. Magn. Reson. 2016, 266, 41–50. [Google Scholar] [CrossRef]
- Lei, K.-M.; Heidari, H.; Mak, P.-I.; Law, M.-K.; Maloberti, F.; Martins, R.P. A Handheld High-Sensitivity Micro-NMR CMOS Platform with B-Field Stabilization for Multi-Type Biological/Chemical Assays. IEEE J. Solid-State Circuits 2017, 52, 284–297. [Google Scholar] [CrossRef]
- Fan, S.; Zhou, Q.; Lei, K.-M.; Mak, P.-I.; Martins, R.P. A Miniaturized 3-D-MRI Scanner Featuring an HV-SOI ASIC and Achieving a 10 × 8 × 8 mm3 Field of View. IEEE J. Solid-State Circuits 2023, 58, 2028–2039. [Google Scholar] [CrossRef]
- Anders, J.; SanGiorgio, P.; Boero, G. A fully integrated IQ-receiver for NMR microscopy. J. Magn. Reson. 2010, 209, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Dreyer, F.; Krüger, D.; Baas, S.; Velders, A.; Anders, J. A 5–780-MHz Transceiver ASIC for Multinuclear NMR Spectroscopy in 0.13-µm BiCMOS. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 3484–3496. [Google Scholar] [CrossRef]
- Yamauchi, K.; Janssen, J.W.G.; Kentgens, A.P.M. Implementing solenoid microcoils for wide-line solid-state NMR. J. Magn. Reson. 2003, 167, 87–96. [Google Scholar] [CrossRef]
- Ehrmann, K.; Saillen, N.; Vincent, F.; Stettler, M.; Jordan, M.; Wurm, F.M.; Besse, P.A.; Popovic, R. Microfabricated solenoids and Helmholtz coils for NMR spectroscopy of mammalian cells. Lab A Chip 2007, 7, 373. [Google Scholar] [CrossRef]
- Inamura, T.; Dohi, T. Cone-shaped micro coil for magnetic resonance imaging. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 335–338. [Google Scholar]
- Khelifa, M.; Mounier, D.; Yaakoubi, N. Design of high performance scroll microcoils for nuclear magnetic resonance spectroscopy of nanoliter and subnanoliter samples. Sensors 2020, 21, 170. [Google Scholar] [CrossRef]
- Fantasia, M.; Galante, A.; Maggiorelli, F.; Retico, A.; Fontana, N.; Monorchio, A.; Alecci, M. Numerical and Workbench Design of 2.35 T Double-Tuned (1H/23Na) Nested RF Birdcage Coils Suitable for Animal Size MRI. IEEE Trans. Med. Imaging 2020, 39, 3175–3186. [Google Scholar] [CrossRef]
- Haase, A.; Odoj, F.; Von Kienlin, M.; Warnking, J.; Fidler, F.; Weisser, A.; Nittka, M.; Rommel, E.; Lanz, T.; Kalusche, B.; et al. NMR probeheads for in vivo applications. Concepts Magn. Reson. 2000, 12, 361–388. [Google Scholar] [CrossRef]
- Özen, A.C.; Spreter, F.; Schimpf, W.; Fischer, J.; Ilbey, S.; Reiss, S.; Maier, A.; von Elverfeldt, D.; Heidt, T.; von Zur Mühlen, C.; et al. Scalable and modular 8-channel transmit and 8-channel flexible receive coil array for 19F MRI of large animals. Magn. Reson. Med. 2022, 89, 1237–1250. [Google Scholar] [CrossRef] [PubMed]
- Blank, A.; Alexandrowicz, G.; Muchnik, L.; Tidhar, G.; Schneiderman, J.; Virmani, R.; Golan, E. Miniature self-contained intravascular magnetic resonance (IVMI) probe for clinical applications. Magn. Reson. Med. 2005, 54, 105–112. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Yi, H.; Chen, D.; Lu, R.; Yuan, T.; Chen, J.; Ni, Z. The design and fabrication of a low-field NMR probe based on a multilayer planar microcoil. Microsyst. Technol. 2013, 20, 419–425. [Google Scholar] [CrossRef]
- Peck, T.L.; Magin, R.L.; Kruse, J.; Feng, M. NMR microspectroscopy using 100 µm planar RF coils fabricated on gallium arsenide substrates. IEEE Trans. Biomed. Eng. 1994, 41, 706–709. [Google Scholar] [CrossRef]
- Sun, N.; Yoon, T.-J.; Lee, H.; Andress, W.; Weissleder, R.; Ham, D. Palm NMR and 1-Chip NMR. IEEE J. Solid-State Circuits 2011, 46, 342–352. [Google Scholar] [CrossRef]
- Gupta, M.; Safvan, C.P.; Singh, K.; Lobiyal, D.K.; Yadav, P.; Singh, S. Radio Frequency Planar Coil-Based On-Chip Probe for Portable Nuclear Magnetic Resonance. IEEE Sensors J. 2019, 19, 2500–2508. [Google Scholar] [CrossRef]
- Keeler, J. Understanding NMR Spectroscopy; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Slichter, C.P. Principles of Magnetic Resonance; Springer: New York, NY, USA, 1990. [Google Scholar]
- Hong, S.; Sun, N. Portable CMOS NMR System with 50-kHz IF, 10-μs Dead Time, and Frequency Tracking. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4576–4588. [Google Scholar] [CrossRef]
- Hoult, D.I.; Lauterbur, P.C. The sensitivity of the zeugmatographic experiment involving human samples. J. Magn. Reson. 1979, 34, 425–433. [Google Scholar] [CrossRef]
- Gadian, D.G.; Robinson, F.N.H. Radiofrequency losses in NMR experiments on electrically conducting samples. J. Magn. Reson. 1979, 34, 449–455. [Google Scholar] [CrossRef]
- Terawatsakul, N.; Saberkari, A.; Madec, M. Optimal Design of Planar Micro-NMR Coils for High Signal-to-Noise Ratio. In Proceedings of the 2024 18th European Conference on Antennas and Propagation (EuCAP), Glasgow, UK, 17–22 March 2024; pp. 1–5. [Google Scholar]
- Hoult, D.I.; Richards, R.E. The signal-to-noise ratio of the nuclear magnetic resonance experiment. J. Magn. Reson. 1976, 24, 71–85. [Google Scholar] [CrossRef]



| Component | Parameter | Value (Units) |
|---|---|---|
| TRX | Architecture | Single-synthesizer |
| TRX | 1 kHz | |
| TX | Max. output power () | 10 mW |
| RX | 1.2 nV/ | |
| Magnet | 0.5 T | |
| Magnet | IB | ≈2 kHz |
| Coil | Type | Planar micro-coil |
| Coil | Substrate | 5 × 5 mm2 FR-4 |
| Coil | Substrate thickness | 0.6 mm |
| Coil | Diameter | 4 mm |
| Coil | Conductor thickness | 0.035 mm |
| Coil | Min trace/spacing | 0.15 mm |
| Sample | Type | 5 μL droplet |
| Sample | Diameter | 3 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terawatsakul, N.; Saberkari, A.; Puttisong, Y.; Madec, M. Scaling Nuclear Magnetic Resonance with Integrated Planar Coil and Transceiver Front-End: Co-Design Considerations. Electronics 2025, 14, 398. https://doi.org/10.3390/electronics14020398
Terawatsakul N, Saberkari A, Puttisong Y, Madec M. Scaling Nuclear Magnetic Resonance with Integrated Planar Coil and Transceiver Front-End: Co-Design Considerations. Electronics. 2025; 14(2):398. https://doi.org/10.3390/electronics14020398
Chicago/Turabian StyleTerawatsakul, Natachai, Alireza Saberkari, Yuttapoom Puttisong, and Morgan Madec. 2025. "Scaling Nuclear Magnetic Resonance with Integrated Planar Coil and Transceiver Front-End: Co-Design Considerations" Electronics 14, no. 2: 398. https://doi.org/10.3390/electronics14020398
APA StyleTerawatsakul, N., Saberkari, A., Puttisong, Y., & Madec, M. (2025). Scaling Nuclear Magnetic Resonance with Integrated Planar Coil and Transceiver Front-End: Co-Design Considerations. Electronics, 14(2), 398. https://doi.org/10.3390/electronics14020398







