Estimating Word Lengths for Fixed-Point DSP Implementations Using Polynomial Chaos Expansions
Abstract
1. Introduction
2. Related Work
2.1. Quantization Effects
2.2. Importance of Modeling Quantization Effects
- Errors arising from representing infinite-precision filter coefficients with finite-precision coefficients.
- Round-off errors due to the multiplication of two fixed-point numbers being quantized into fewer bits than required.
- The quantization of the input signal into discrete levels.
2.3. Current Methods in Modeling Quantization Effects
3. Elementary Operations Using PCE
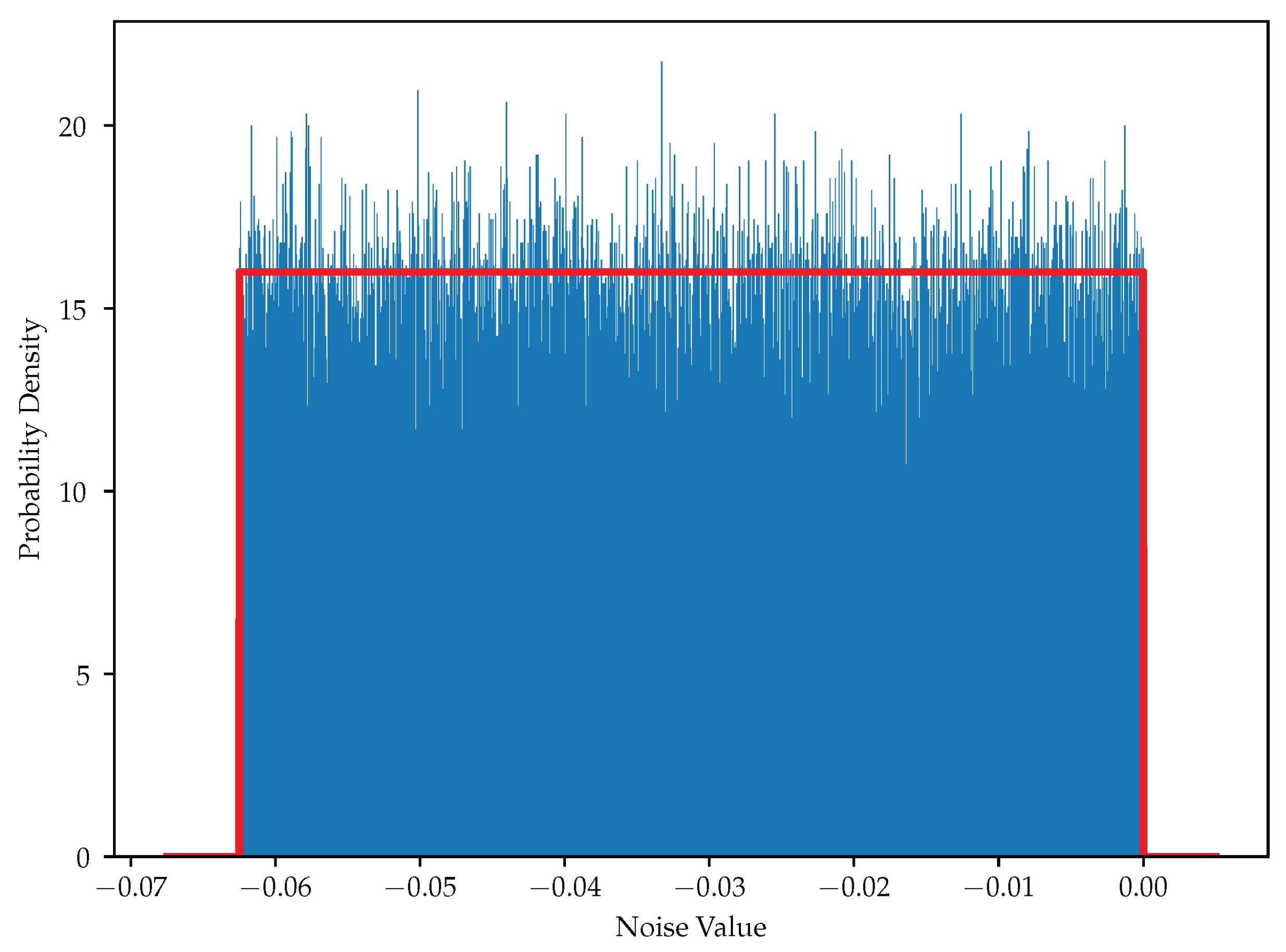
3.1. Probability Distribution of Quantization Noise
3.2. Polynomial Chaos Expansion (PCE)
3.3. Non-Standard Distributions
3.4. Multivariate Basis Polynomials
3.5. Elementary Operations on PCE
- Scaling.
- Addition/subtraction.
- Multiplication.
- Time delay.
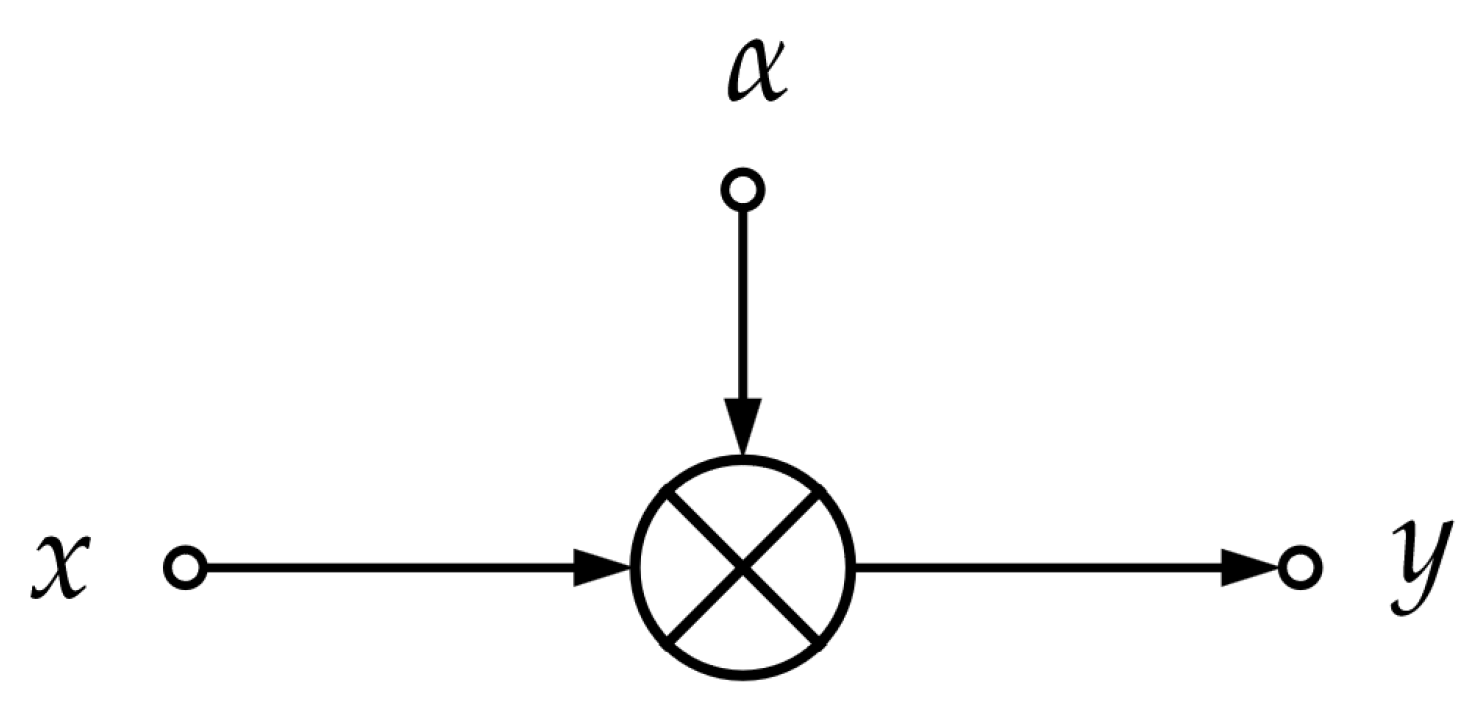
3.5.1. Scaling
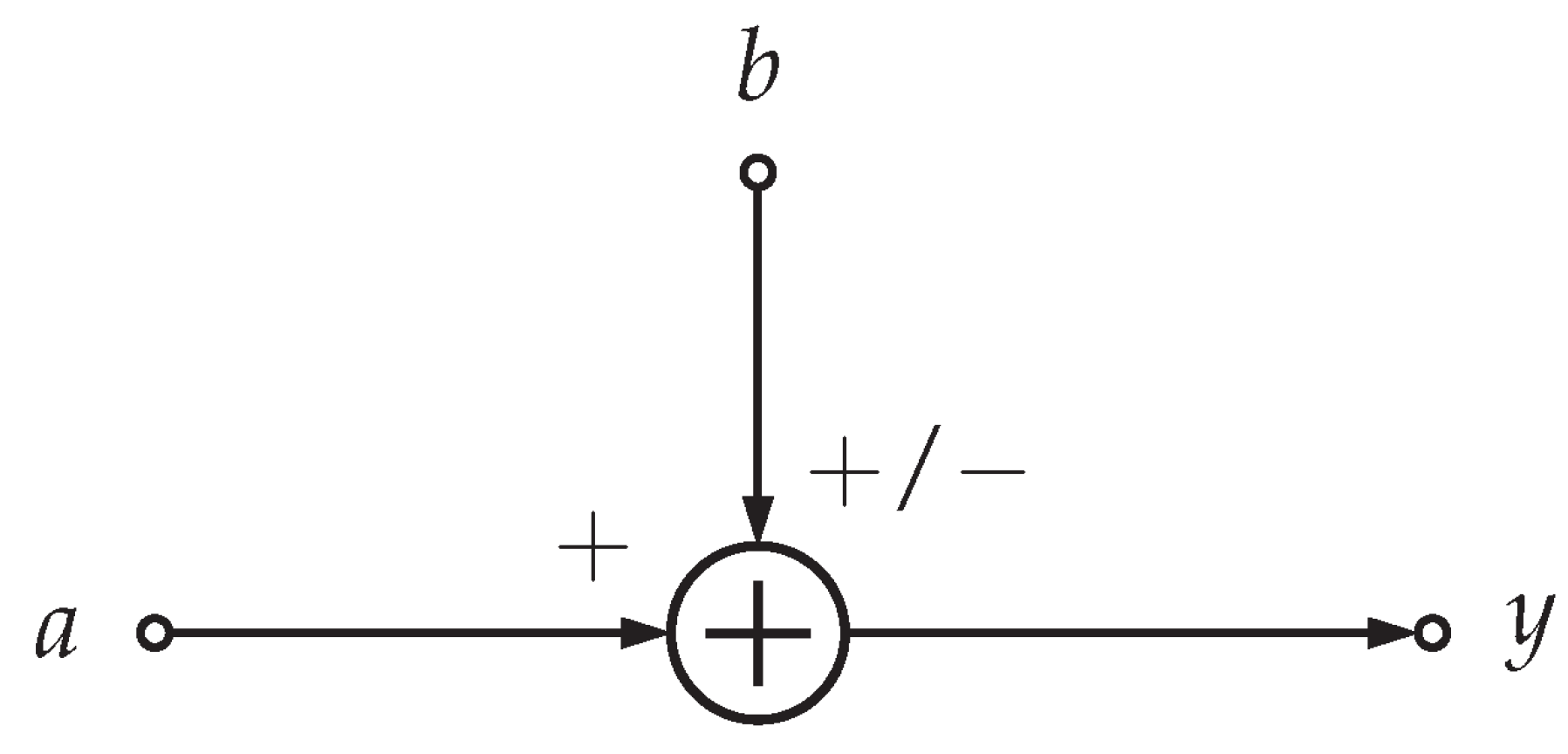
3.5.2. Addition/Subtraction
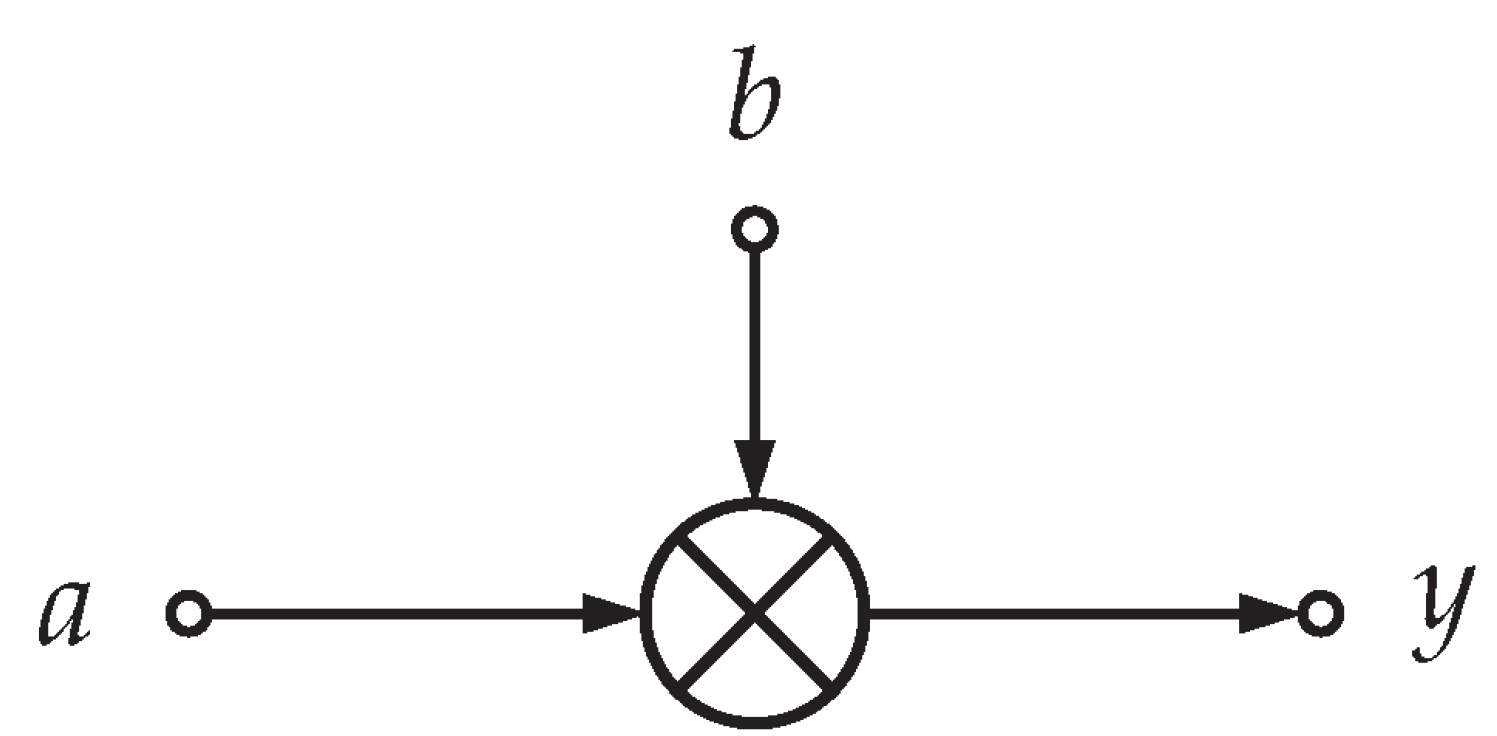
3.5.3. Multiplication
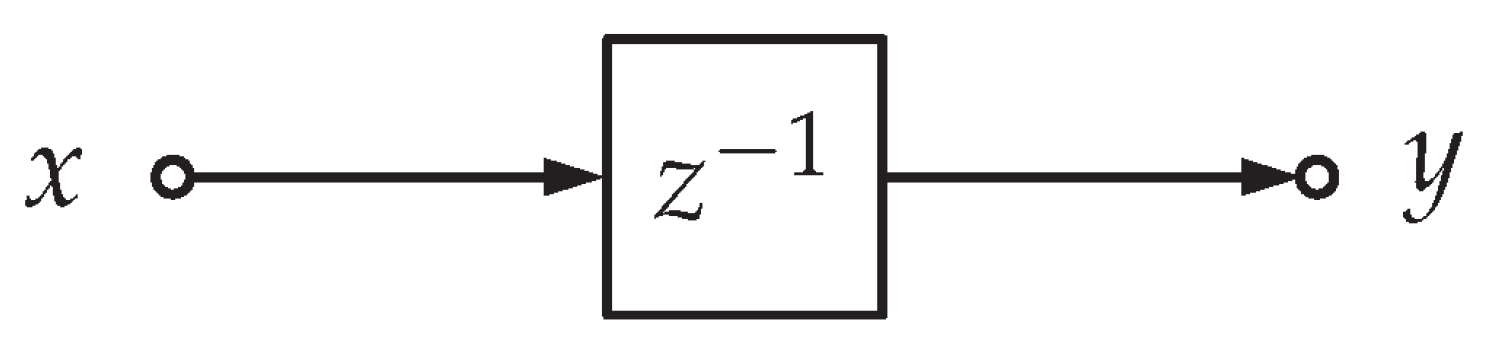
3.5.4. Time Delay
4. PCE for DSP Blocks
- Represent the DSP block as a DFG.
- Model the input signal to the DSP block using an array of PCE coefficients.
- Propagate the PCE coefficient array through DFG.
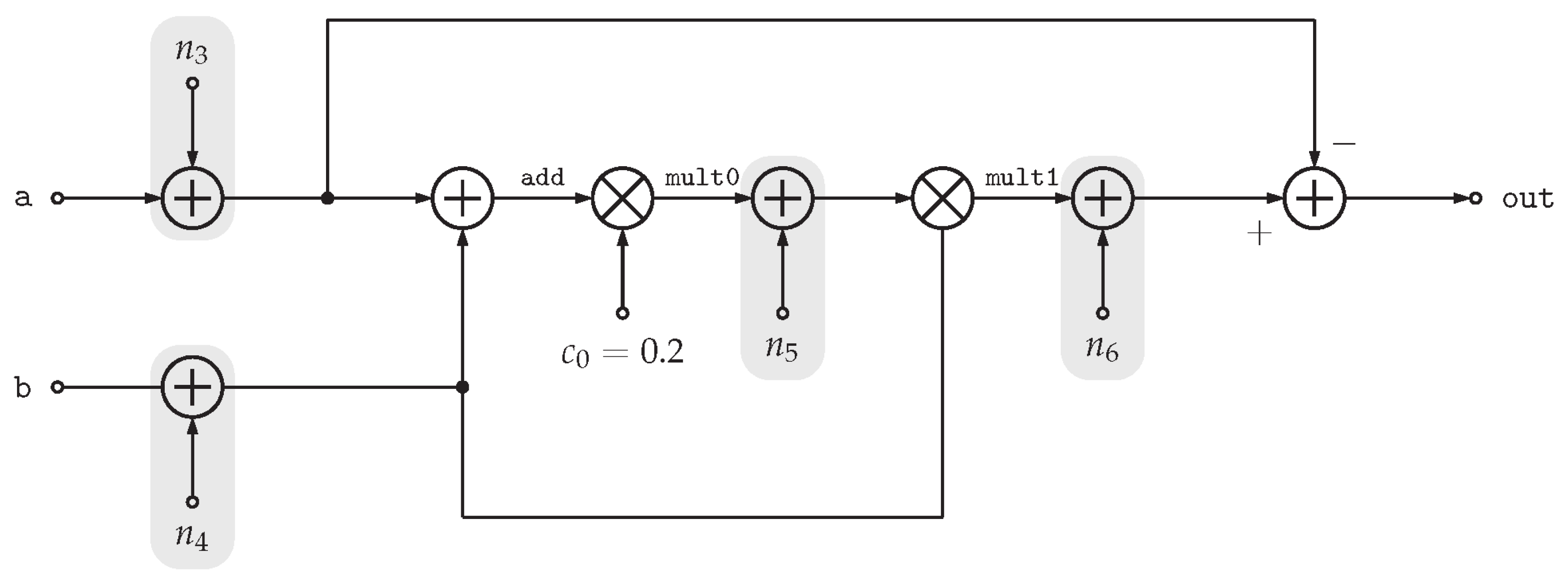
- Add quantization noise sources to DFG corresponding to a particular bit width configuration.
- Propagate the signal-and-noise PCE coefficient arrays through DFG.
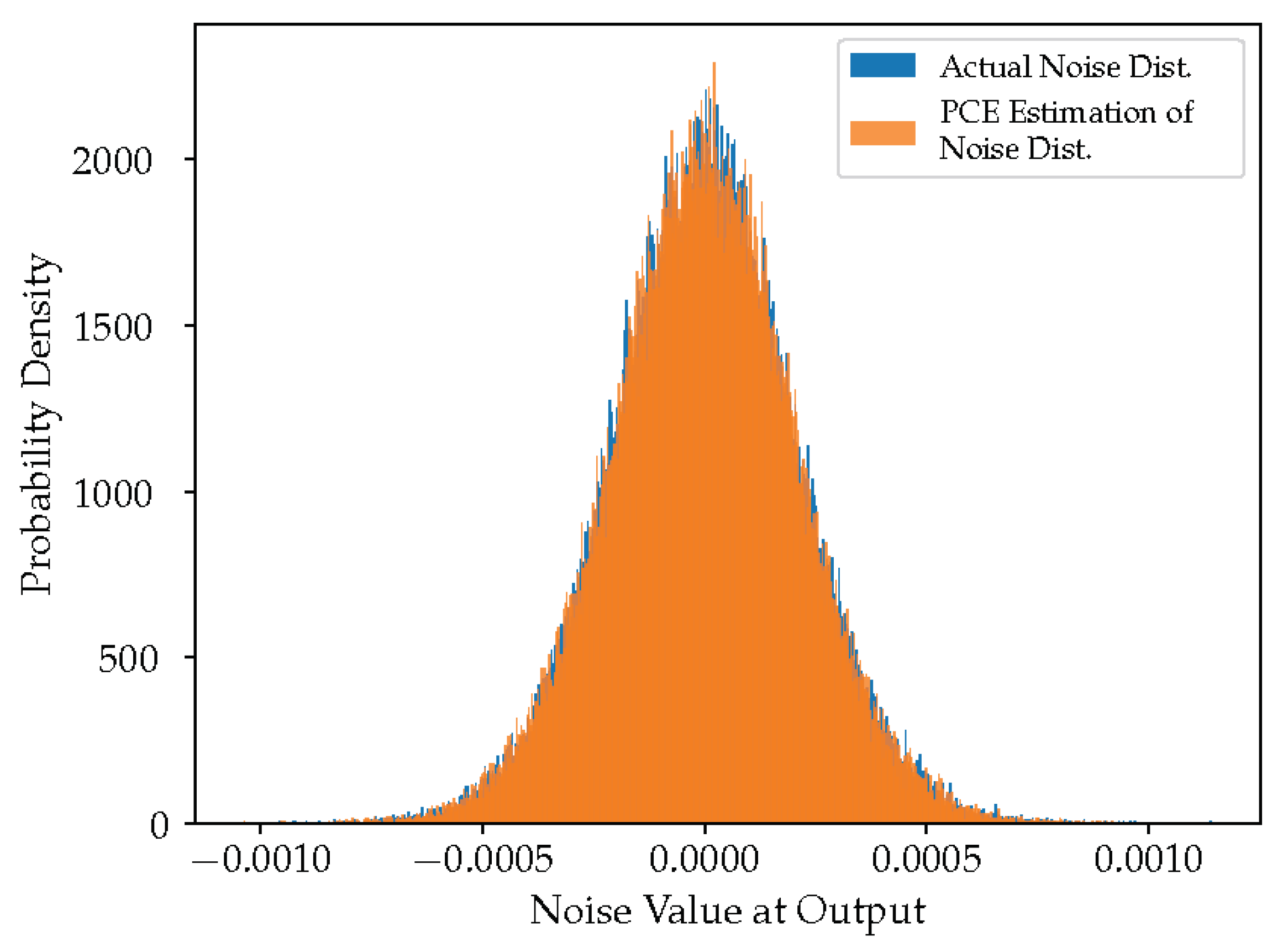
- Remove the signal distribution at the output to obtain statistics on the noise distribution.
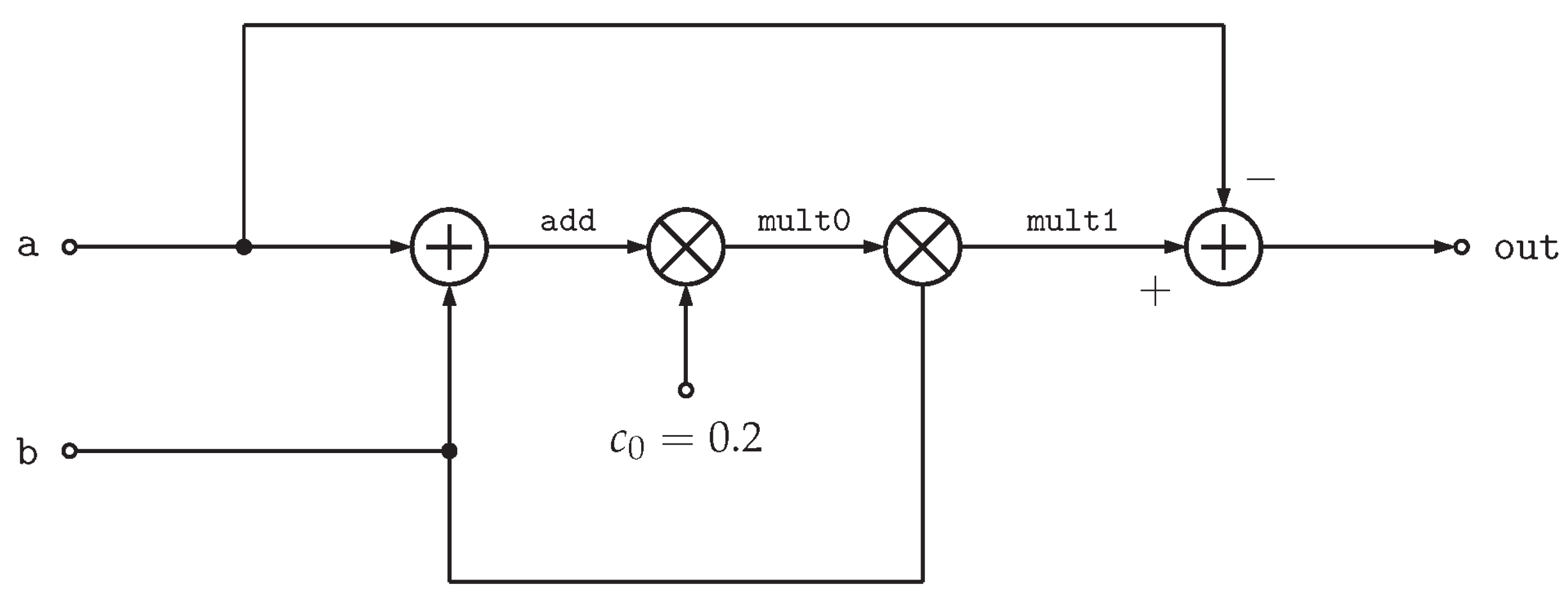
A Simple Example
5. Design Space Exploration
| Algorithm 1 PCE simulation for a given bit width configuration |
 |
5.1. Using Simulated Annealing to Estimate Bit Widths
| Algorithm 2 Simulated annealing |
 |
5.2. Improved Design Space Exploration Algorithm
| Algorithm 3 TrySolution |
 |
5.3. Neighbor Selection
| Algorithm 4 An algorithm for aggressive neighbor selection |
 |
| Algorithm 5 A non-greedy neighbor selection algorithm |
 |
6. Results
6.1. PCE vs. AA
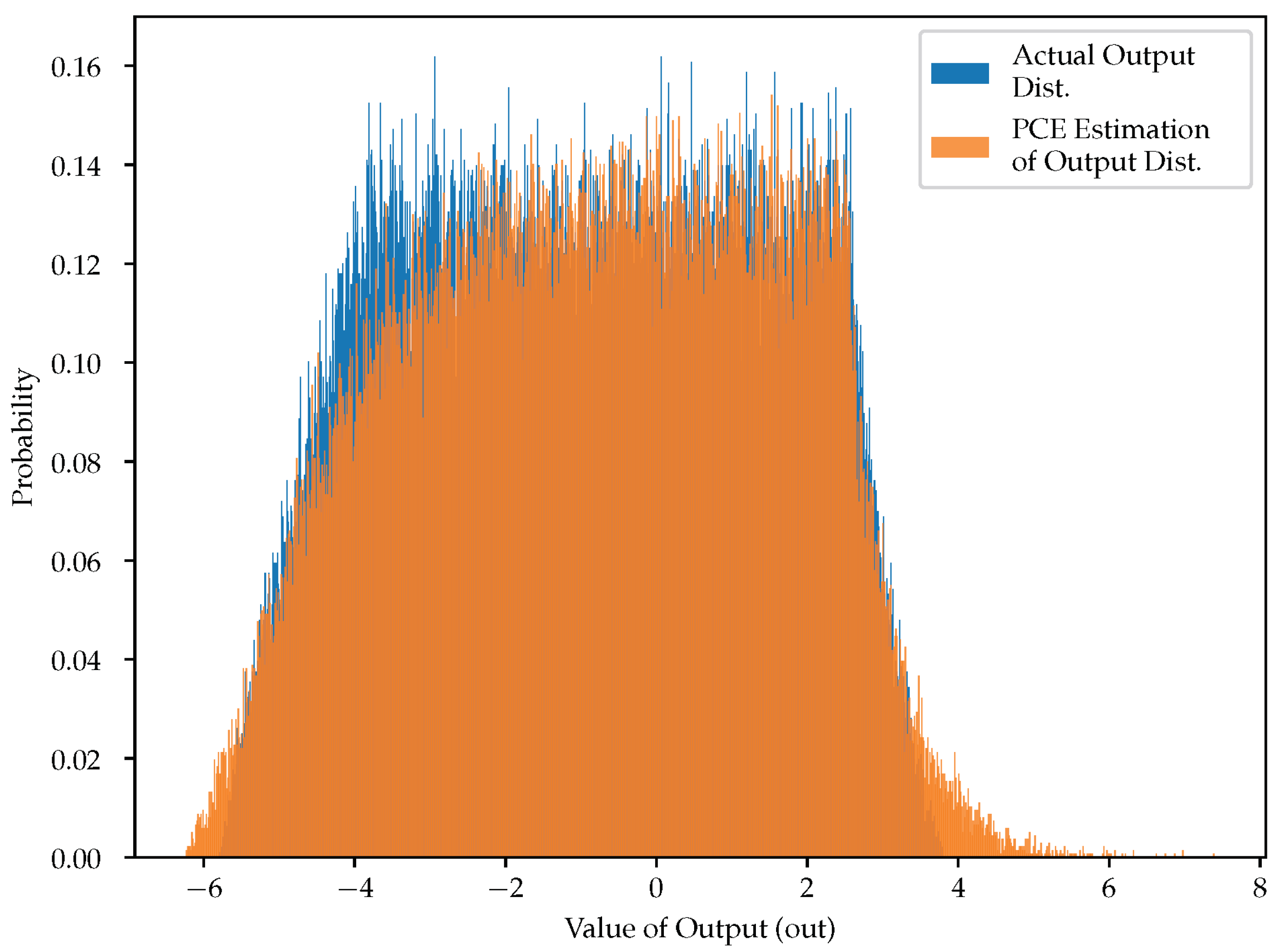
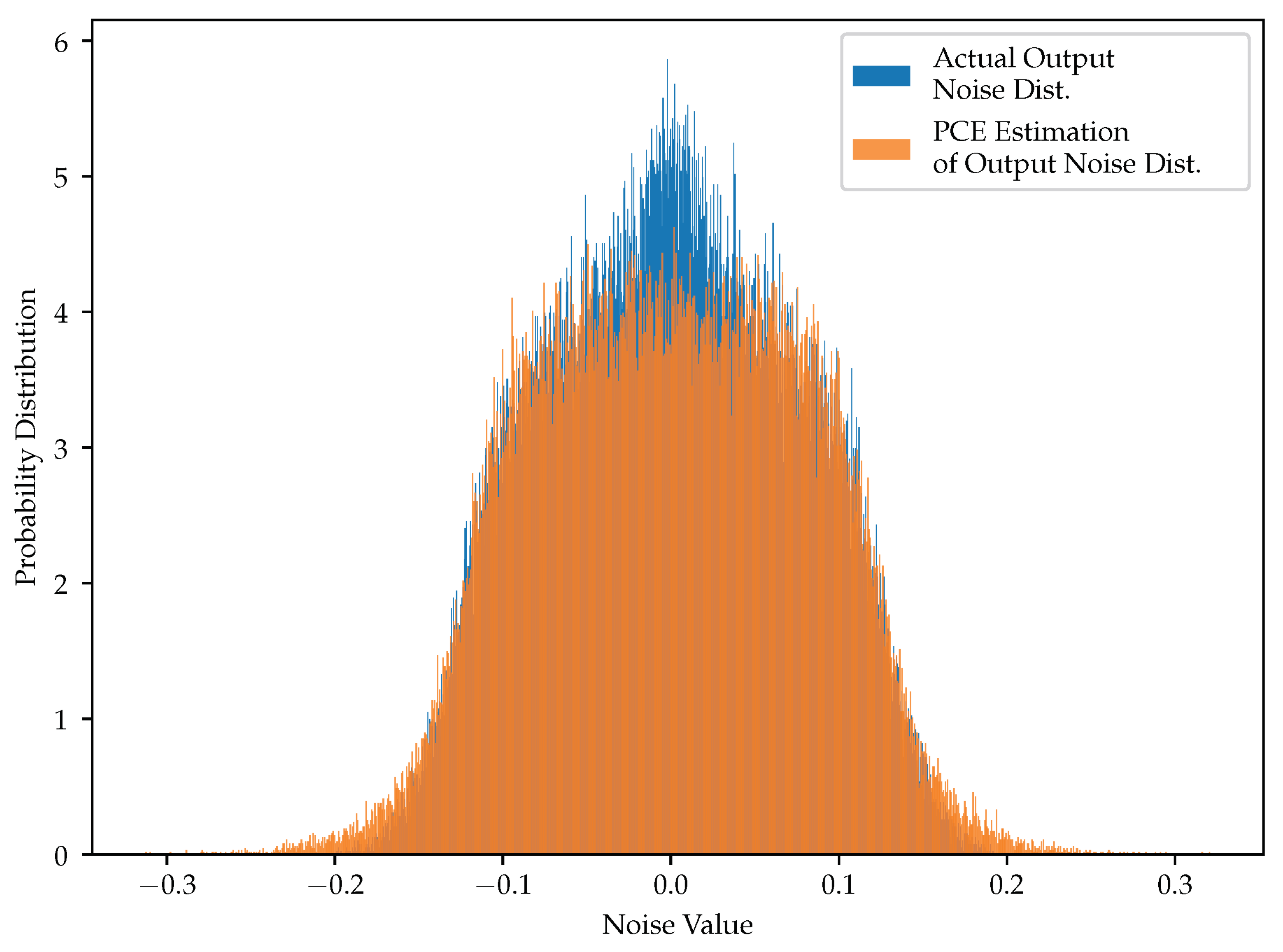
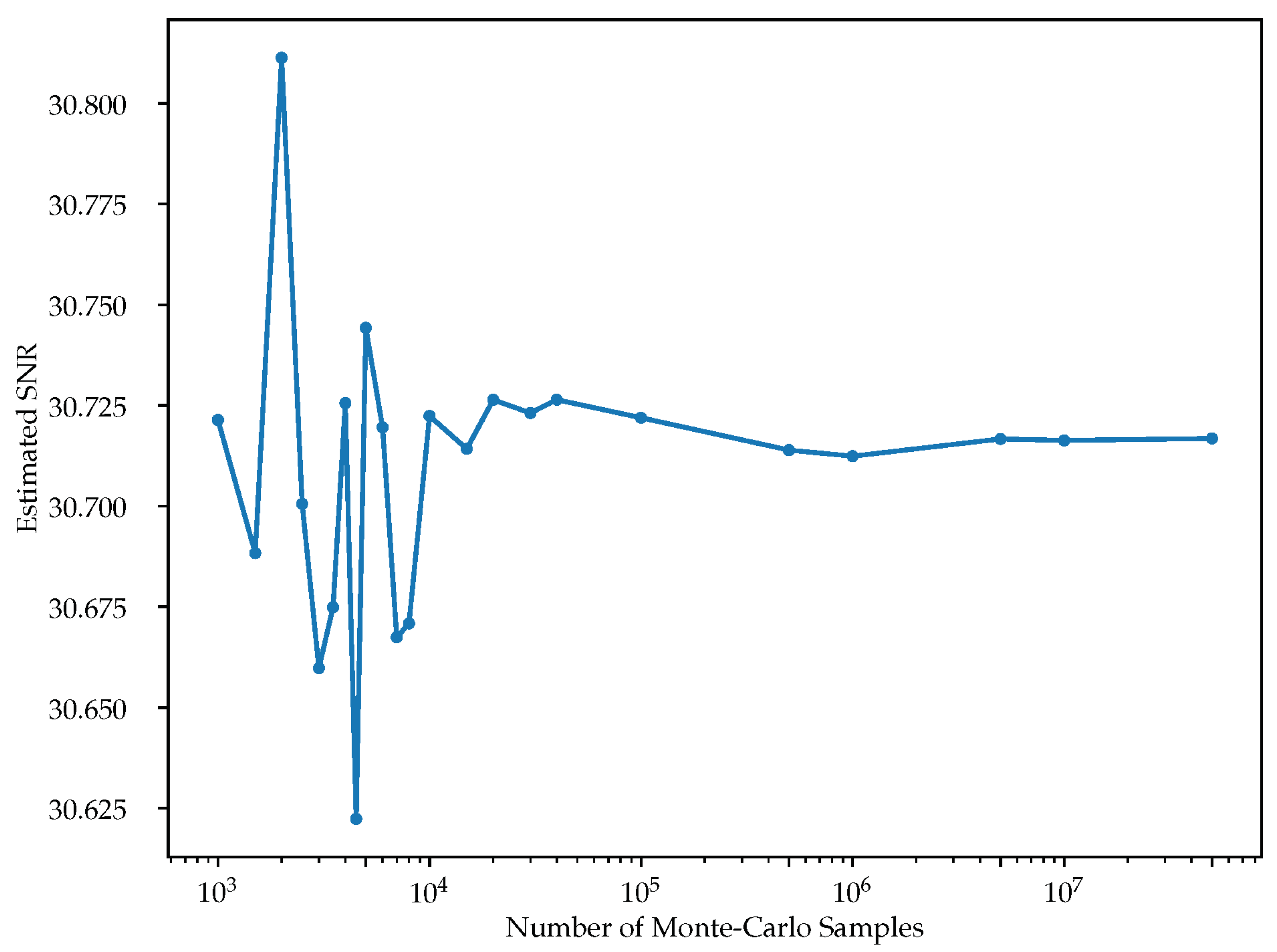
6.2. PCE vs. MC
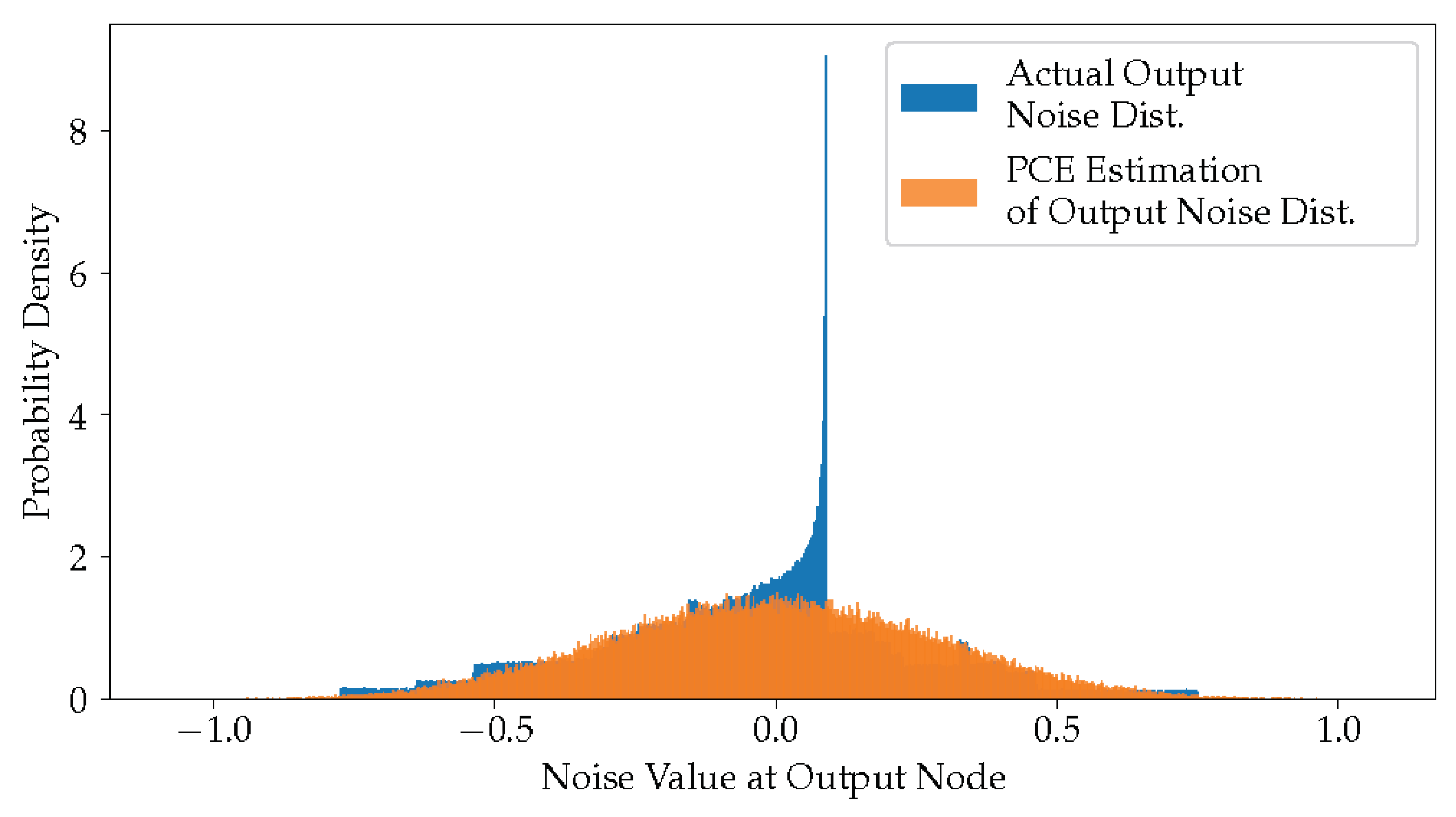
6.3. Third-Order Taylor Series Sine/Cosine Expansion Around
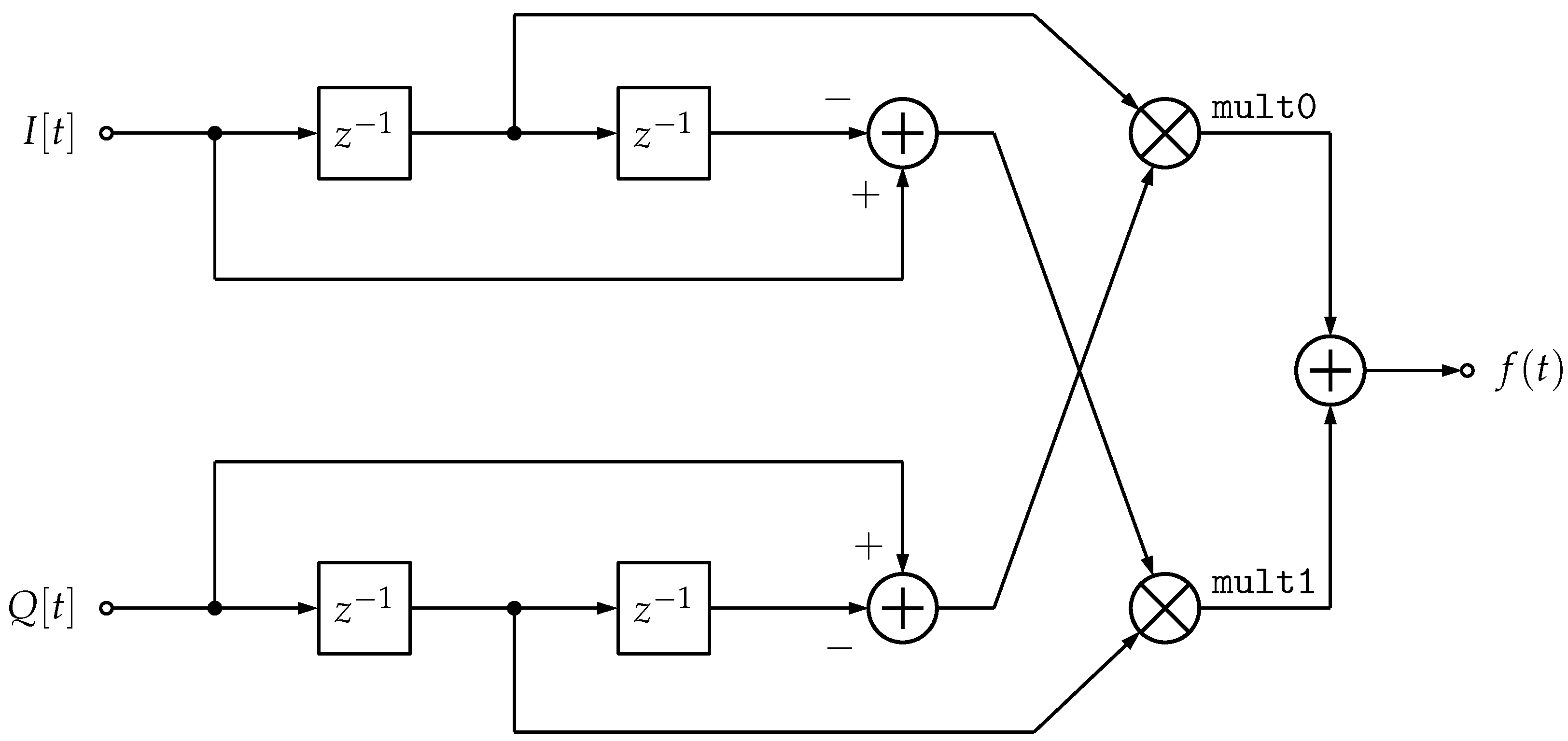
6.4. FM Demodulator
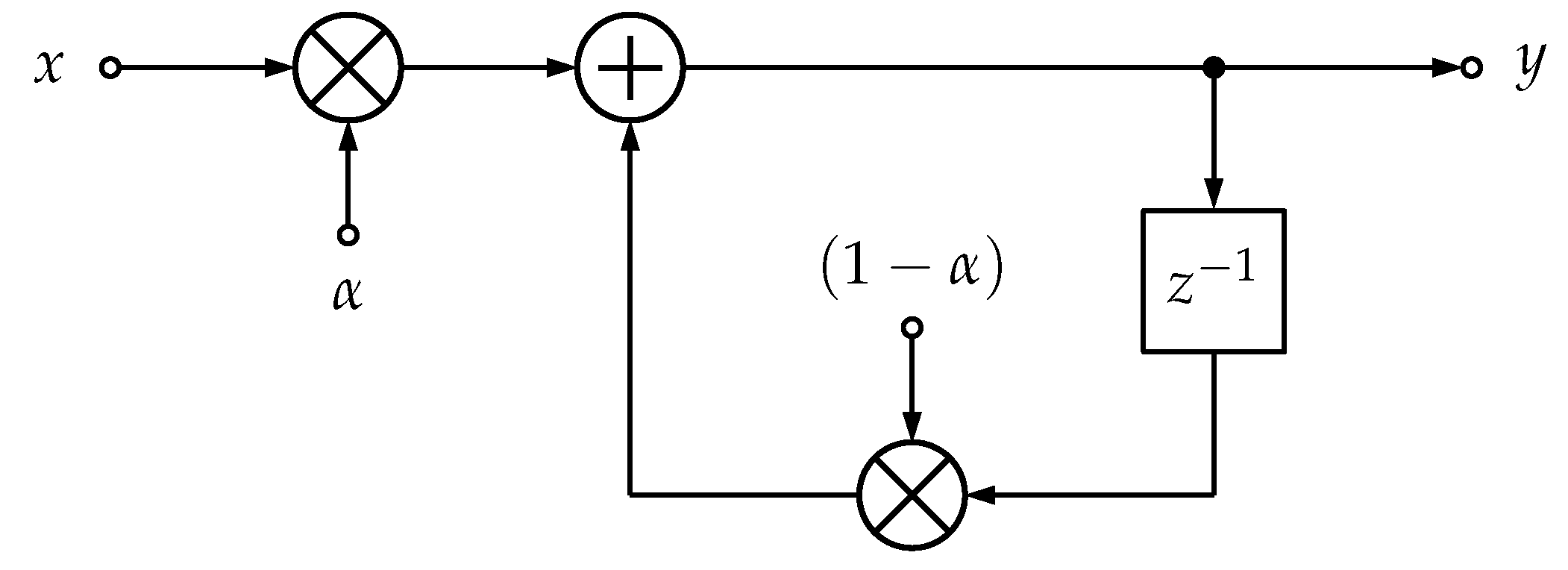
6.5. Single Pole IIR Filter
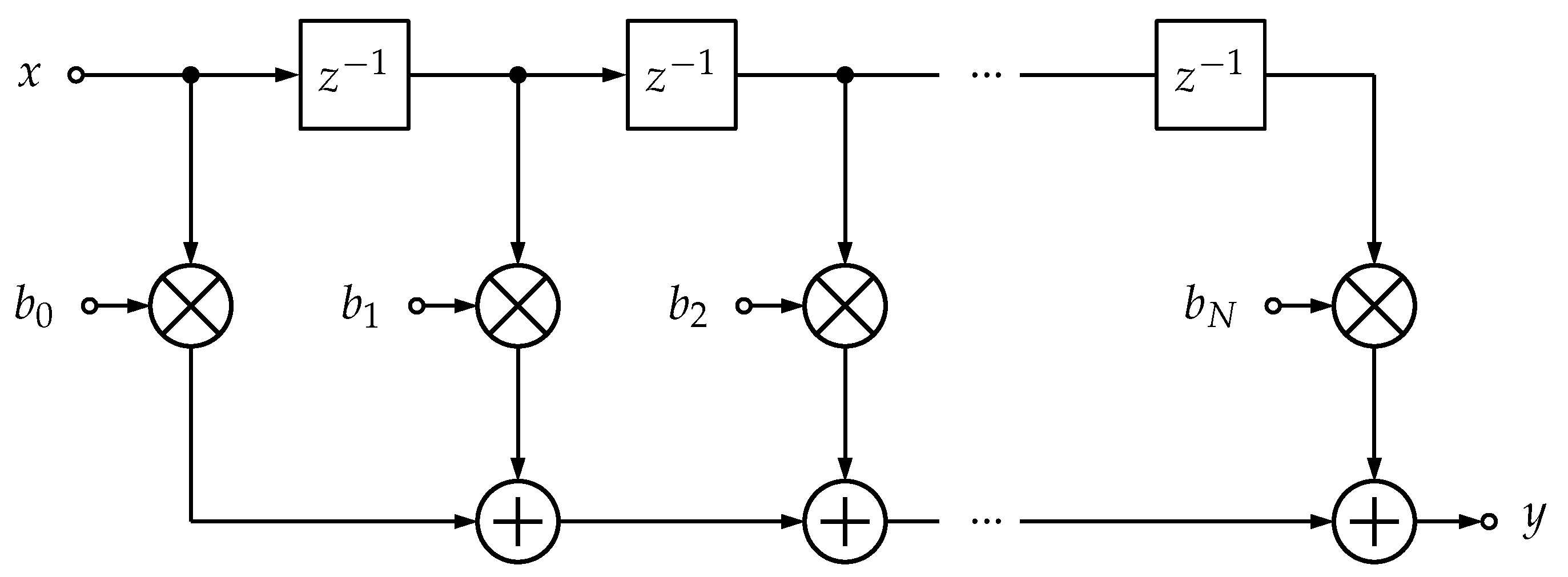
6.6. FIR Filters
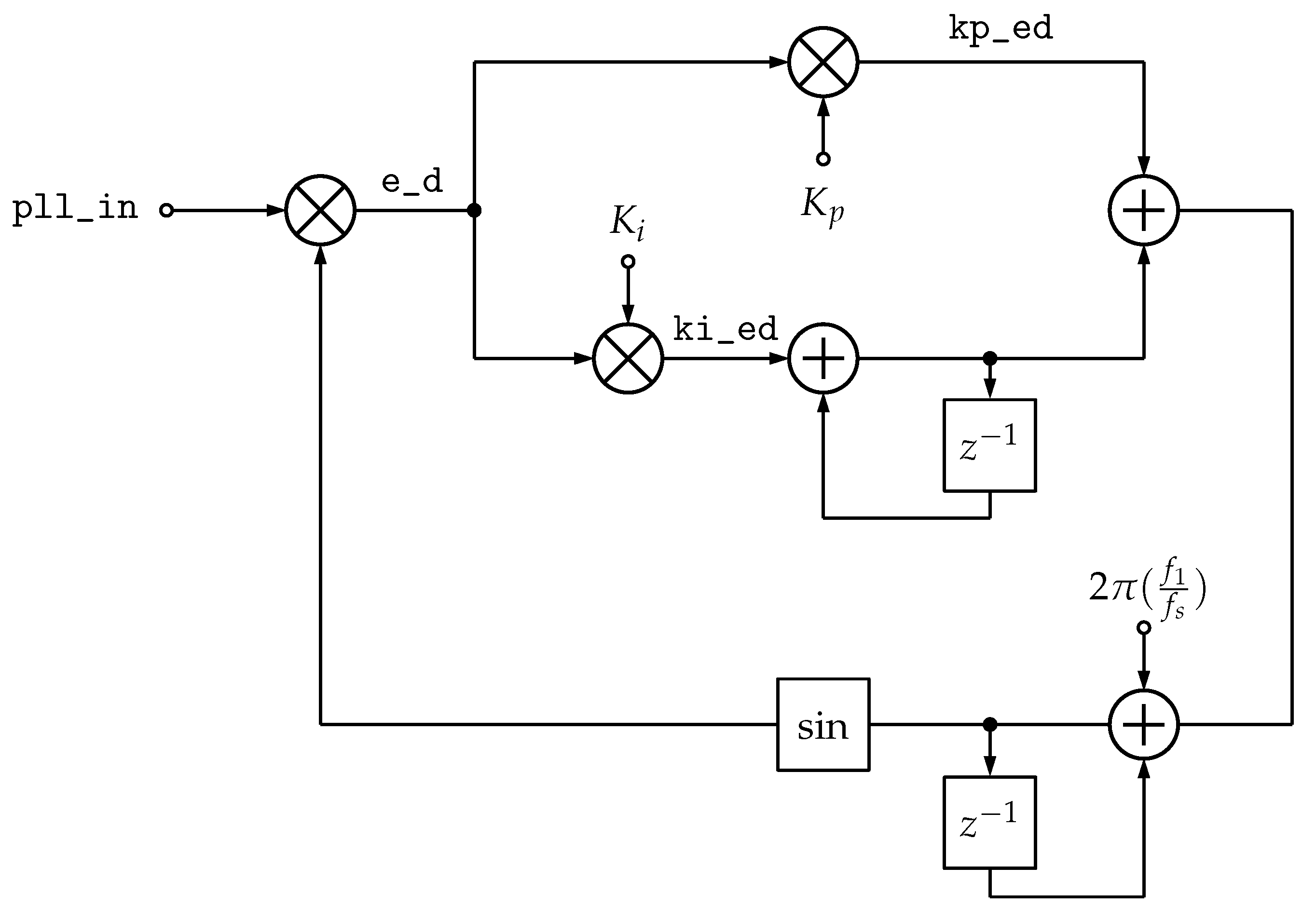
6.7. Phase-Locked Loop (PLL)
7. Discussion
8. Conclusions
Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bishop, P. A Tradeoff Between Microcontroller, DSP, FPGA and ASIC Technologies. EE Times. 2009. Available online: https://www.eetimes.com/a-tradeoff-between-microcontroller-dsp-fpga-and-asic-technologies/ (accessed on 12 January 2025).
- Martin, C.; Mike, M.; Dave, J.; Darel, L.; The MathWorks, Inc. Accelerating Fixed-Point Design for MB-OFDM UWB Systems. 2005. Available online: https://www.design-reuse.com/articles/9559/accelerating-fixed-point-design-for-mb-ofdm-uwb-systems.html (accessed on 12 January 2025).
- Hill, T. Floating- to Fixed-Point MATLAB Algorithm Conversion for FPGAs. 2007. Available online: https://www.eetimes.com/floating-to-fixed-point-matlab-algorithm-conversion-for-fpgas/ (accessed on 12 January 2025).
- Wyglinski, A.; Getz, R.; Collins, T.; Pu, D. Software-Defined Radio for Engineers; Artech House Mobile Communications Series; Artech House: Norwood, MA, USA, 2018; Available online: https://books.google.ca/books?id=cKR5DwAAQBAJ (accessed on 12 January 2025).
- McClarren, R.G. Uncertainty Quantification and Predictive Computational Science, 1st ed.; Springer International Publishing: Basel, Switzerland, 2018. [Google Scholar]
- Zhou, S.; Gao, W.; Mu, W.; Zheng, Y.; Shao, Z.; He, Y. Machine Learning Based Waveform Reconstruction Demodulation Method for Space Borne AIS Signal. In Proceedings of the 2023 IEEE Globecom Workshops (GC Wkshps), Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 2123–2128. [Google Scholar] [CrossRef]
- Lammers, D. Moore’s Law Milestones. 2022. Available online: https://spectrum.ieee.org/moores-law-milestones (accessed on 12 January 2025).
- Theodore, S. Rappaport. Wireless Communications: Principles and Practice, 2nd ed.; Pearson Education: Philadelphia, PA, USA, 1996. [Google Scholar]
- Fernández–Prades, C.; Arribas, J.; Closas, P.; Avilés, C.; Esteve, L. GNSS-SDR: An Open Source Tool For Researchers and Developers. In Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 20–23 September 2011; pp. 780–794. [Google Scholar]
- Ossmann, M. Software Defined Radio with HackRF, Lesson 1. Available online: https://greatscottgadgets.com/sdr/1/ (accessed on 12 January 2025).
- OpenBTS—Ettus Knowledge Base. 2016. Available online: https://kb.ettus.com/OpenBTS (accessed on 12 January 2025).
- Mpala, J.; van Stam, G. Open BTS, a GSM Experiment in Rural Zambia. In e-Infrastructure and e-Services for Developing Countries, Proceedings of the 4th International ICST Conference, AFRICOMM 2012, Yaounde, Cameroon, 12–14 November 2012; Jonas, K., Rai, I.A., Tchuente, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 65–73. [Google Scholar]
- Plazas, J.E.; Rojas, J.S.; Corrales, J.C. Improving Rural Early Warning Systems Through the Integration of OpenBTS and JAIN SLEE. Rev. Ing. Univ. Medellín 2015, 16, 195–207. [Google Scholar] [CrossRef][Green Version]
- Goldberg, D. What every computer scientist should know about floating-point arithmetic. ACM Comput. Surv. 1991, 23, 5–48. [Google Scholar] [CrossRef]
- Parhami, B. Computer Arithmetic Algorithms and Hardware Designs; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Chung, C.; Kintali, K. HDL Coder Self-Guided Tutorial. 2023. Available online: https://github.com/mathworks/HDL-Coder-Self-Guided-Tutorial/releases/tag/1.72.0 (accessed on 12 January 2025).
- Hettiarachchi, D.L.N.; Davuluru, V.S.P.; Balster, E.J. Integer vs. Floating-Point Processing on Modern FPGA Technology. In Proceedings of the 2020 10th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 6–8 January 2020; pp. 0606–0612. [Google Scholar] [CrossRef]
- Oberstar, E.L. Fixed-Point Representation & Fractional Math. Oberstar Consulting. 2007. Available online: http://darcy.rsgc.on.ca/ACES/ICE4M/FixedPoint/FixedPointRepresentationFractionalMath.pdf (accessed on 12 January 2025).
- Esteban, L.; López, J.A.; Sedano, E.; Hernández-Montero, S.; Sánchez, M. Quantization Analysis of the Infrared Interferometer of the TJ-II Stellarator for its Optimized FPGA-Based Implementation. IEEE Trans. Nucl. Sci. 2013, 60, 3592–3596. [Google Scholar] [CrossRef]
- Liu, B. Effect of finite word length on the accuracy of digital filters—A review. IEEE Trans. Circuit Theory 1971, 18, 670–677. [Google Scholar] [CrossRef]
- Chan, D.; Rabiner, L. Analysis of quantization errors in the direct form for finite impulse response digital filters. IEEE Trans. Audio Electroacoust. 1973, 21, 354–366. [Google Scholar] [CrossRef]
- Rabiner, L.; McClellan, J.; Parks, T. FIR digital filter design techniques using weighted Chebyshev approximation. Proc. IEEE 1975, 63, 595–610. [Google Scholar] [CrossRef]
- Kan, E.; Aggarwal, J. Error analysis of digital filter employing floating-point arithmetic. IEEE Trans. Circuit Theory 1971, 18, 678–686. [Google Scholar] [CrossRef]
- Sarbishei, O.; Radecka, K.; Zilic, Z. Analytical Optimization of Bit-Widths in Fixed-Point LTI Systems. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2012, 31, 343–355. [Google Scholar] [CrossRef]
- Rowell, A.S. Digital Filters with Quantized Coefficients: Optimization and Overflow Analysis Using Extreme Value Theory. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2012. [Google Scholar]
- McClellan, J.; Parks, T.; Rabiner, L. A computer program for designing optimum FIR linear phase digital filters. IEEE Trans. Audio Electroacoust. 1973, 21, 506–526. [Google Scholar] [CrossRef]
- López, J.; Caffarena, G.; Carreras, C.; Nieto-Taladriz, O. Fast and accurate computation of the round-off noise of linear time-invariant systems. IET Circuits Devices Syst. 2008, 2, 393. [Google Scholar] [CrossRef]
- Mehrotra, A. Noise analysis of phase-locked loops. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 1309–1316. [Google Scholar] [CrossRef]
- Kinsman, A. A Computational Approach to Custom Data Representation for Hardware Accelerators. Ph.D. Thesis, McMaster University, Hamilton, ON, USA, 2010. [Google Scholar]
- de Figueiredo, L.H.; Stolfi, J. Affine Arithmetic: Concepts and Applications. Numer. Algorithms 2004, 37, 147–158. [Google Scholar] [CrossRef]
- Vakili, S.; Langlois, J.M.P.; Bois, G. Enhanced Precision Analysis for Accuracy-Aware Bit-Width Optimization Using Affine Arithmetic. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2013, 32, 1853–1865. [Google Scholar] [CrossRef]
- Lee, D.U.; Gaffar, A.; Cheung, R.; Mencer, O.; Luk, W.; Constantinides, G. Accuracy-Guaranteed Bit-Width Optimization. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2006, 25, 1990–2000. [Google Scholar] [CrossRef]
- Caffarena, G.; Carreras, C.; López, J.A.; Fernández, Á. SQNR Estimation of Fixed-Point DSP Algorithms. EURASIP J. Adv. Signal Process. 2010, 2010, 171027. [Google Scholar] [CrossRef]
- Wu, B. Dynamic range estimation for systems with control-flow structures. In Proceedings of the Thirteenth International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 19–21 March 2012; pp. 370–377. [Google Scholar] [CrossRef]
- Grupp, A.; Albaraghtheh, T. Polynomial Chaos Expansion. Available online: https://dictionary.helmholtz-uq.de/content/PCE.html (accessed on 12 January 2025).
- Xiu, D.; Karniadakis, G.E. The Wiener–Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Lyons, R.G. Understanding Digital Signal Processing, 3rd ed.; Prentice Hall: Philadelphia, PA, USA, 2010. [Google Scholar]
- Wu, B.; Zhu, J.; Najm, F. An analytical approach for dynamic range estimation. In Proceedings of the 41st Design Automation Conference, San Diego, CA, USA, 7–11 July 2004; pp. 472–477. [Google Scholar]
- Sullivan, T.J. Introduction to Uncertainty Quantification, 1st ed.; Texts in Applied Mathematics; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
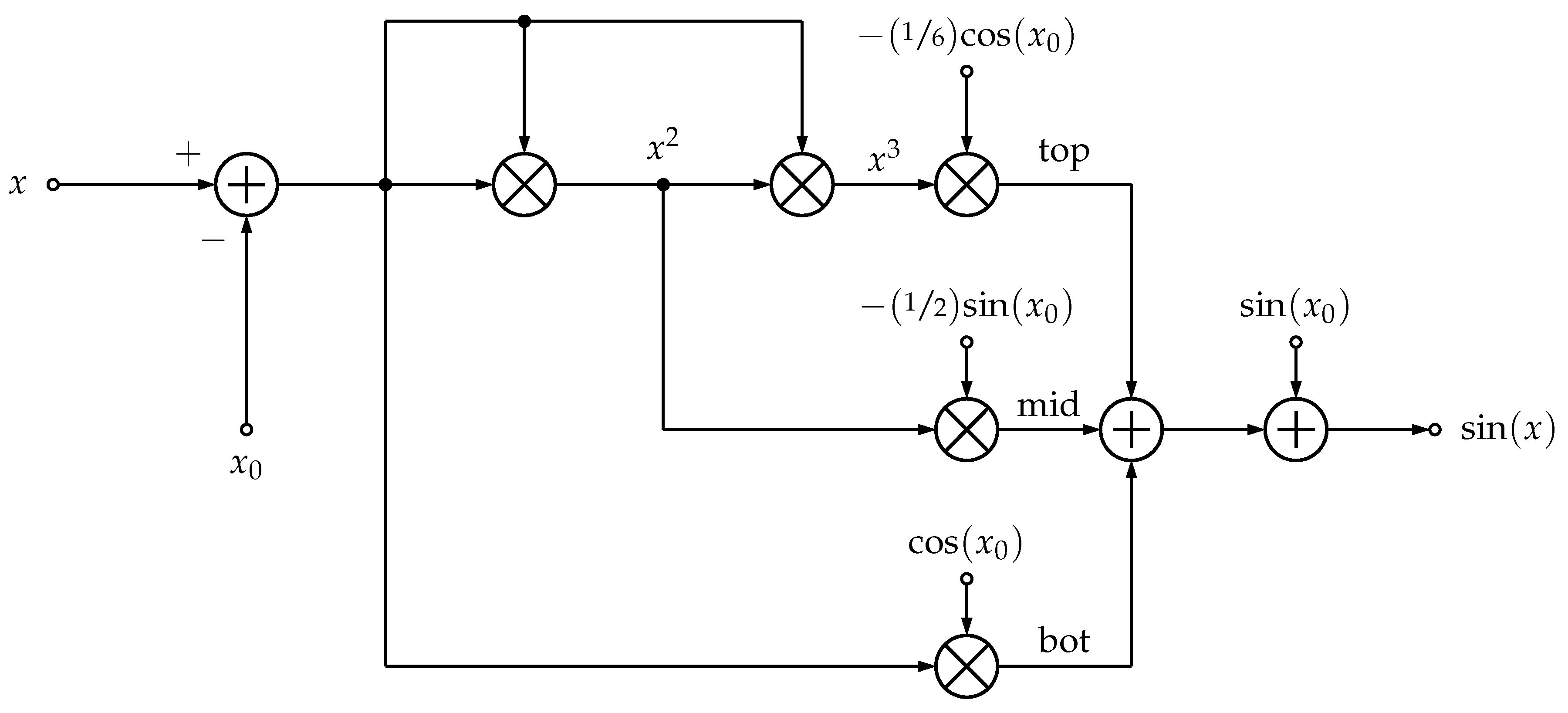
| Distribution | Basis Functions for PCE |
|---|---|
| Uniform | Legendre polynomials |
| Gaussian | Hermite polynomials |
| Beta | Jacobi polynomials |
| Gamma | Laguerre polynomials |
| Poisson | Charlier polynomials |
| Negative binomial | Meixner polynomials |
| Binomial | Krawtchouk polynomials |
| Hypergeometric | Hahn polynomials |
| Node Label | PCE Coefficient |
|---|---|
| a | |
| b | |
| add | |
| mult0 | |
| mult1 | |
| out |
| Signal | Bit Width |
|---|---|
| a | 5 |
| b | 5 |
| mult0 | 3 |
| mult1 | 2 |
| Simulation Method | SNR |
|---|---|
| MC (10,000,000 samples) | 30.71 dB |
| MC (100,000 samples) | 30.78 dB |
| AA | 19.68 dB |
| PCE with maximum polynomial degree = 1 | 30.70 dB |
| (dB) | Signal Bit Width (Bits) | (dB) | |||
|---|---|---|---|---|---|
| a | b | mult0 | mult1 | ||
| 20 | 1 | 1 | 1 | 1 | 20.93 |
| (dB) | Signal Bit Width (Bits) | (dB) | |||||
|---|---|---|---|---|---|---|---|
| top | mid | bot | |||||
| 15 | 1 | 1 | 1 | 1 | 1 | 1 | 15.93 |
| 20 | 2 | 2 | 1 | 3 | 1 | 3 | 20.37 |
| 25 | 5 | 1 | 1 | 4 | 2 | 4 | 26.00 |
| 30 | 5 | 3 | 2 | 3 | 6 | 3 | 30.63 |
| 35 | 4 | 7 | 5 | 4 | 4 | 8 | 35.18 |
| 40 | 5 | 6 | 1 | 5 | 6 | 6 | 40.18 |
| 45 | 6 | 5 | 2 | 6 | 7 | 7 | 45.79 |
| 50 | 8 | 7 | 4 | 9 | 7 | 6 | 50.26 |
| 60 | 11 | 11 | 4 | 10 | 11 | 8 | 60.24 |
| 70 | 12 | 8 | 9 | 12 | 12 | 10 | 70.17 |
| 80 | 11 | 11 | 9 | 12 | 13 | 13 | 82.25 |
| 90 | 14 | 12 | 9 | 16 | 14 | 16 | 90.07 |
| 100 | 16 | 15 | 12 | 15 | 15 | 15 | 100.22 |
| (dB) | Signal Bit Width (Bits) | (dB) | |||
|---|---|---|---|---|---|
| I | Q | mult0 | mult1 | ||
| 15 | 3 | 3 | 2 | 2 | 15.04 |
| 20 | 3 | 6 | 3 | 3 | 20.18 |
| 25 | 4 | 4 | 4 | 5 | 25.46 |
| 30 | 8 | 4 | 7 | 8 | 30.02 |
| 35 | 5 | 8 | 7 | 6 | 35.17 |
| 40 | 6 | 7 | 7 | 7 | 40.03 |
| 45 | 8 | 7 | 7 | 9 | 45.05 |
| 50 | 9 | 8 | 9 | 8 | 50.80 |
| 60 | 10 | 12 | 9 | 12 | 60.08 |
| 70 | 11 | 12 | 12 | 12 | 70.13 |
| 80 | 15 | 13 | 13 | 13 | 80.18 |
| 90 | 17 | 15 | 14 | 16 | 90.08 |
| 100 | 18 | 18 | 16 | 16 | 100.27 |
| (dB) | Signal Bit Width (bits) | (dB) | ||
|---|---|---|---|---|
| x | x_c | y_dc | ||
| 15 | 2 | 3 | 4 | 17.15 |
| 20 | 3 | 4 | 4 | 20.08 |
| 25 | 4 | 5 | 5 | 26.14 |
| 30 | 4 | 7 | 6 | 29.12 |
| 35 | 5 | 7 | 7 | 35.15 |
| 40 | 6 | 7 | 9 | 41.89 |
| 45 | 7 | 8 | 9 | 47.15 |
| 50 | 8 | 9 | 9 | 50.24 |
| 60 | 11 | 11 | 12 | 63.22 |
| 70 | 12 | 13 | 12 | 70.82 |
| 80 | 13 | 14 | 14 | 80.32 |
| 90 | 14 | 16 | 17 | 90.06 |
| 100 | 16 | 18 | 17 | 97.62 |
| (dB) | Signal Bit Width (Bits) | (dB) | ||
|---|---|---|---|---|
| x | x_c | y_dc | ||
| 15 | 2 | 4 | 5 | 17.79 |
| 20 | 3 | 5 | 5 | 23.09 |
| 25 | 4 | 6 | 6 | 29.17 |
| 30 | 6 | 7 | 6 | 34.69 |
| 35 | 6 | 8 | 7 | 38.23 |
| 40 | 7 | 8 | 8 | 44.17 |
| 45 | 7 | 9 | 10 | 47.92 |
| 50 | 8 | 10 | 10 | 53.21 |
| 60 | 10 | 13 | 11 | 62.28 |
| 70 | 12 | 13 | 13 | 74.27 |
| 80 | 13 | 15 | 15 | 83.32 |
| 90 | 16 | 16 | 17 | 93.34 |
| 100 | 17 | 18 | 18 | 104.44 |
| (dB) | Signal Bit Width (Bits) | (dB) | |
|---|---|---|---|
| x | branch_bitwidth | ||
| 15 | 4 | 7 | 18.95 |
| 20 | 5 | 8 | 24.59 |
| 25 | 4 | 10 | 29.08 |
| 30 | 4 | 16 | 30.13 |
| 35 | 6 | 11 | 39.01 |
| 40 | 9 | 11 | 41.69 |
| 45 | 9 | 12 | 47.40 |
| 50 | 10 | 13 | 53.34 |
| 60 | 11 | 15 | 64.85 |
| 70 | 14 | 16 | 71.49 |
| 80 | 15 | 18 | 83.36 |
| 90 | 16 | 20 | 94.82 |
| 100 | 19 | 21 | 101.65 |
| (dB) | Signal Bit Width (Bits) | (dB) | |
|---|---|---|---|
| x | branch_bitwidth | ||
| 15 | 3 | 5 | 20.75 |
| 20 | 3 | 7 | 23.74 |
| 25 | 5 | 7 | 32.26 |
| 30 | 5 | 8 | 34.87 |
| 35 | 6 | 9 | 40.75 |
| 40 | 7 | 10 | 46.69 |
| 45 | 8 | 10 | 49.96 |
| 50 | 8 | 12 | 53.66 |
| 60 | 10 | 13 | 64.67 |
| 70 | 13 | 14 | 75.30 |
| 80 | 14 | 16 | 85.95 |
| 90 | 15 | 18 | 94.71 |
| 100 | 18 | 19 | 105.31 |
| (dB) | Signal Bit Width (Bits) | (dB) | |
|---|---|---|---|
| x | branch_bitwidth | ||
| 15 | 3 | 7 | 22.41 |
| 20 | 5 | 7 | 26.85 |
| 25 | 5 | 8 | 30.84 |
| 30 | 5 | 10 | 35.34 |
| 35 | 6 | 10 | 39.66 |
| 40 | 9 | 10 | 43.15 |
| 45 | 9 | 11 | 48.59 |
| 50 | 10 | 12 | 54.51 |
| 60 | 10 | 15 | 65.32 |
| 70 | 14 | 15 | 72.42 |
| 80 | 15 | 17 | 84.19 |
| 90 | 16 | 19 | 95.43 |
| 100 | 19 | 20 | 102.42 |
| (dB) | Signal Bit Width (Bits) | (dB) | |||
|---|---|---|---|---|---|
| pll_in | e_d | kp_ed | ki_ed | ||
| 15 | 3 | 4 | 4 | 9 | 27.34 |
| 20 | 3 | 4 | 9 | 13 | 32.75 |
| 25 | 6 | 5 | 6 | 10 | 36.30 |
| 30 | 10 | 5 | 10 | 13 | 45.57 |
| 35 | 7 | 7 | 7 | 12 | 44.79 |
| 40 | 8 | 7 | 8 | 14 | 51.67 |
| 45 | 10 | 9 | 11 | 13 | 60.34 |
| 50 | 9 | 11 | 10 | 14 | 59.14 |
| 60 | 10 | 11 | 13 | 16 | 78.24 |
| 70 | 12 | 13 | 13 | 18 | 79.47 |
| 80 | 14 | 16 | 14 | 20 | 87.03 |
| 90 | 17 | 15 | 18 | 23 | 103.23 |
| 100 | 18 | 17 | 19 | 23 | 111.16 |
| (dB) | Signal Bit Width (Bits) | (dB) | |||
|---|---|---|---|---|---|
| pll_in | e_d | kp_ed | ki_ed | ||
| 15 | 3 | 4 | 4 | 9 | 27.34 |
| 20 | 4 | 4 | 5 | 10 | 33.06 |
| 25 | 4 | 5 | 6 | 11 | 37.41 |
| 30 | 6 | 6 | 6 | 12 | 37.82 |
| 35 | 6 | 8 | 7 | 12 | 44.70 |
| 40 | 8 | 7 | 8 | 14 | 51.76 |
| 45 | 9 | 8 | 9 | 14 | 55.77 |
| 50 | 9 | 9 | 10 | 15 | 58.93 |
| 60 | 10 | 11 | 13 | 16 | 70.86 |
| 70 | 12 | 13 | 13 | 16 | 82.17 |
| 80 | 14 | 14 | 15 | 20 | 89.14 |
| 90 | 16 | 17 | 16 | 21 | 98.78 |
| 100 | 15 | 17 | 16 | 22 | 110.84 |
| (dB) | Total Number of Bits | Bit Savings | |
|---|---|---|---|
| Greedy Algorithm | Non-Greedy Algorithm | ||
| 15 | 20 | 20 | 0 |
| 20 | 29 | 23 | 6 |
| 25 | 27 | 26 | 1 |
| 30 | 38 | 30 | 8 |
| 35 | 33 | 33 | 0 |
| 40 | 37 | 37 | 0 |
| 45 | 43 | 40 | 3 |
| 50 | 44 | 43 | 1 |
| 60 | 50 | 50 | 0 |
| 70 | 56 | 54 | 2 |
| 80 | 64 | 63 | 1 |
| 90 | 73 | 70 | 3 |
| 100 | 77 | 70 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.; Nicolici, N. Estimating Word Lengths for Fixed-Point DSP Implementations Using Polynomial Chaos Expansions. Electronics 2025, 14, 365. https://doi.org/10.3390/electronics14020365
Rahman M, Nicolici N. Estimating Word Lengths for Fixed-Point DSP Implementations Using Polynomial Chaos Expansions. Electronics. 2025; 14(2):365. https://doi.org/10.3390/electronics14020365
Chicago/Turabian StyleRahman, Mushfiqur, and Nicola Nicolici. 2025. "Estimating Word Lengths for Fixed-Point DSP Implementations Using Polynomial Chaos Expansions" Electronics 14, no. 2: 365. https://doi.org/10.3390/electronics14020365
APA StyleRahman, M., & Nicolici, N. (2025). Estimating Word Lengths for Fixed-Point DSP Implementations Using Polynomial Chaos Expansions. Electronics, 14(2), 365. https://doi.org/10.3390/electronics14020365






