A GNN-Based Placement Optimization Guidance Framework by Physical and Timing Prediction
Abstract
1. Introduction
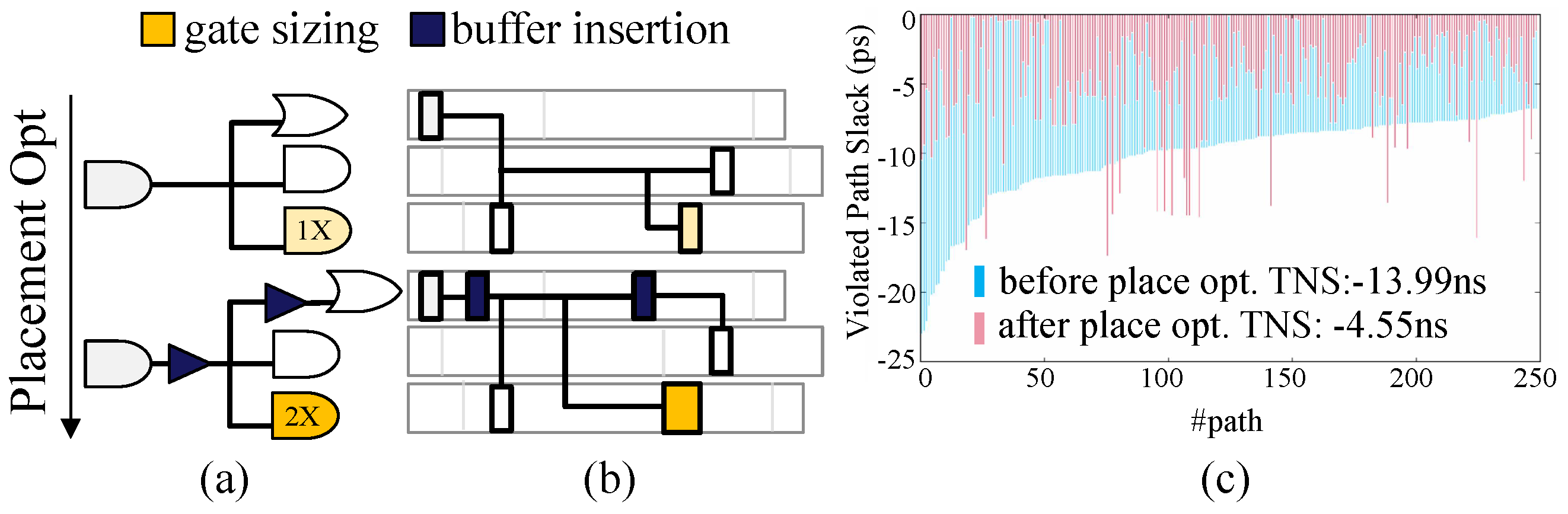
- A physical- and timing-related placement guidance framework is proposed based on a GNN to achieve significant quality improvement over traditional design tool flow with candidate solutions for gate sizing and buffer insertion as well as weighted path groups for potential violated paths.
- The physical-related prediction is proposed with a matricized encoding and decoding mechanism for buffer tree representation for accurate and efficient prediction of candidate buffer insertion solutions.
- The proposed framework was validated by benchmark circuits with commercial design flow, demonstrating significant timing improvement at detail placement and later routing stages without any unacceptable runtime and area cost.
2. Related Work and Motivations
2.1. Learning-Based Physical Prediction
2.2. Learning-Based Timing Prediction
2.3. Graph Neural Network
2.4. Motivations
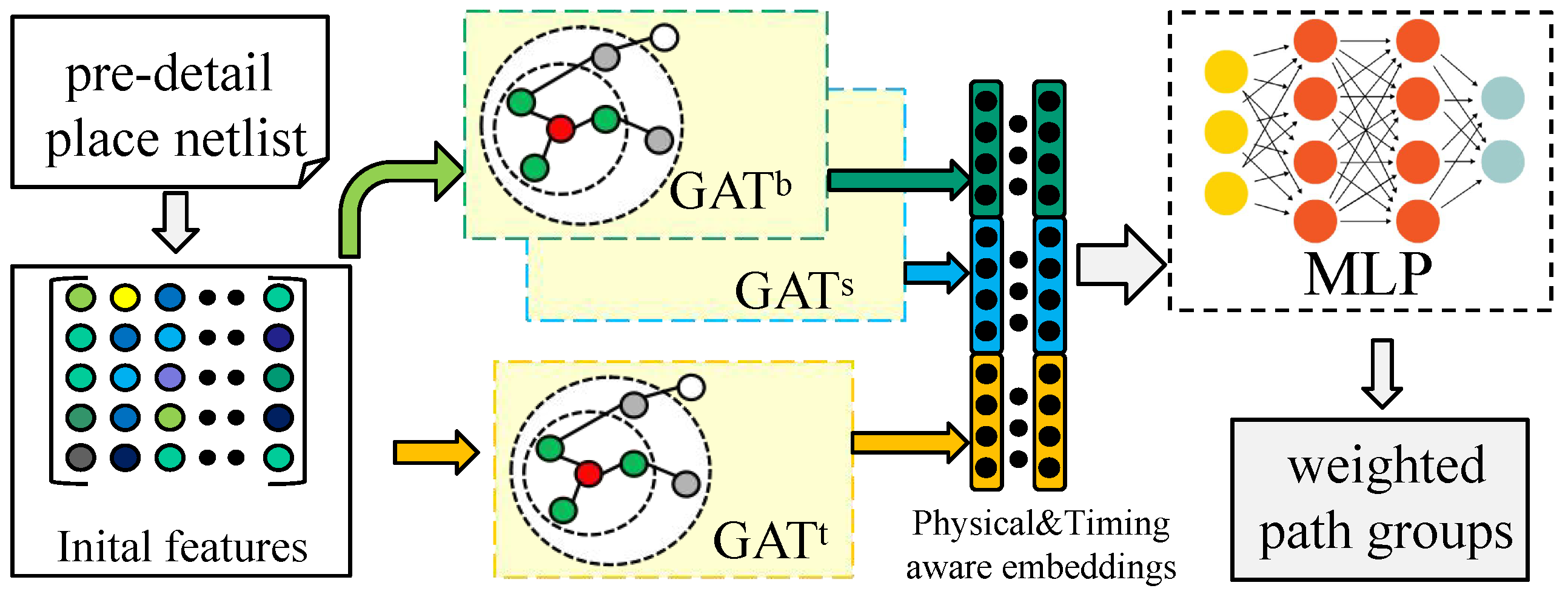
3. Proposed Placement Optimization Framework
3.1. Overview
3.2. Node Representation
3.3. Loss Function
3.3.1. Physical Classification Loss
3.3.2. Timing Prediction Loss
3.4. Physical Prediction
3.4.1. Gate Sizing Prediction Model
3.4.2. Buffer Insertion Prediction Model
3.5. Timing Prediction
3.6. Optimization Guidance with Physical and Timing Prediction
- size_cell According to the predicted gate sizing solution by , the logic cells in the pre-detail placement netlist are upsized or downsized by this command.
- insert_buffer According to the predicted buffer insertion solution by , the candidate buffer trees are inserted between the logic cells with different driving strengths.
- group_path According to the predicted path group solution by , the selected paths are grouped separately using this command and set with the appropriate weights.
4. Experiment Results
4.1. Experiment Setup
4.2. Physical and Timing Prediction Evaluation
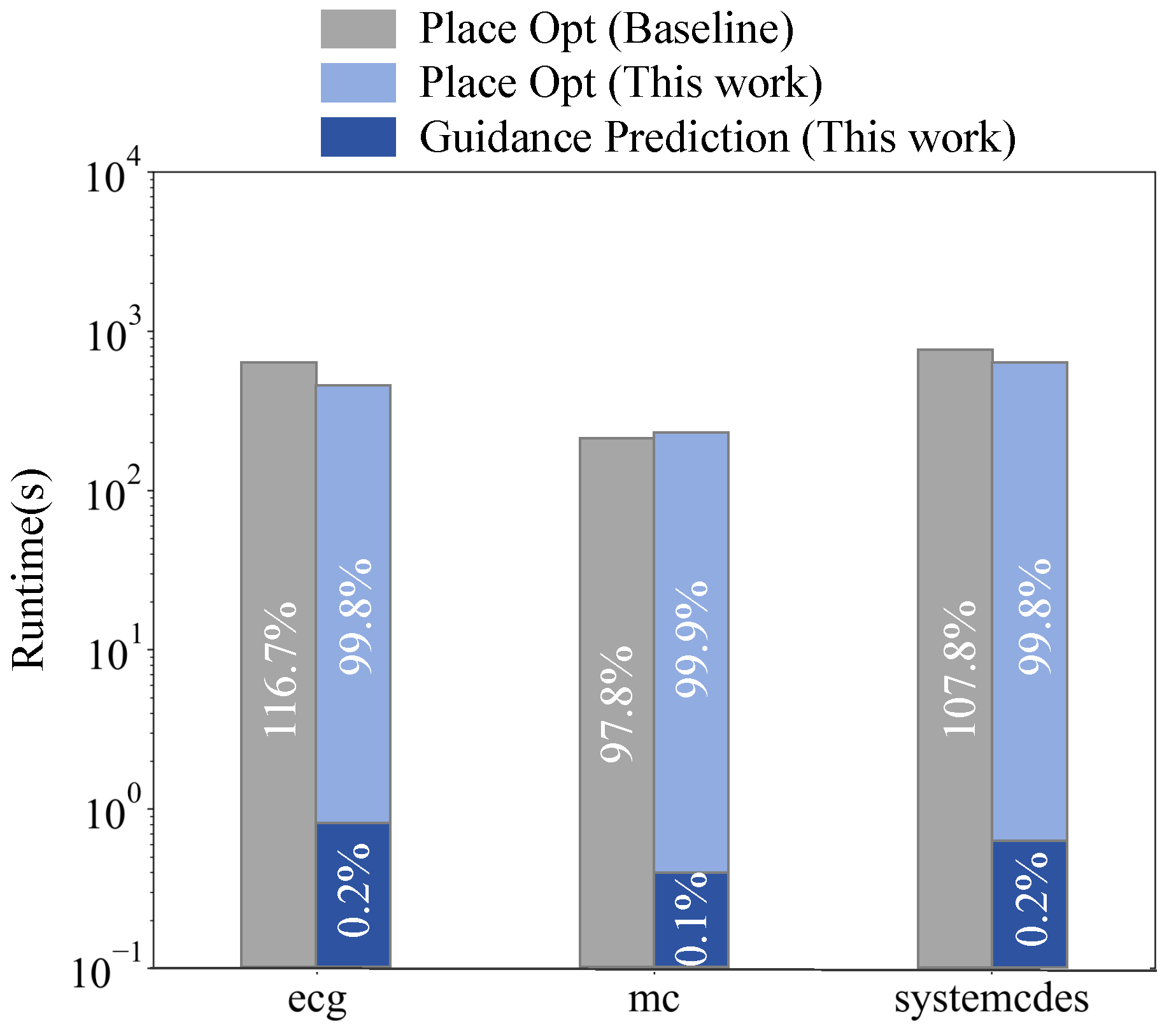
4.3. Physical- and Timing-Related Optimization Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, W.; Li, X.; Song, X.; Hao, Y.; Zhang, R.; Du, Z.; Chen, Y. Chip design with machine learning: A survey from algorithm perspective. Sci. China Inf. Sci. 2023, 66, 211101. [Google Scholar] [CrossRef]
- Kahng, A.B. Advancing Placement. In Proceedings of the 2021 International Symposium on Physical Design, Virtual, 22–24 March 2021. [Google Scholar]
- Li, W. Strongly NP-hard discrete gate sizing problems. In Proceedings of the IEEE International Conference on Computer Design: VLSI in Computers and Processors, (ICCD), Cambridge, MA, USA, 3–6 October 1993. [Google Scholar]
- Shi, W.; Li, Z.; Alpert, C. Complexity analysis and speedup techniques for optimal buffer insertion with minimum cost. In Proceedings of the Asia and South Pacific Design Automation Conference (ASP-DAC), Yokohama, Japan, 27–30 January 2004. [Google Scholar]
- Krishna Kashyap, S.; Ozev, S. IMPRoVED: Integrated Method to Predict PostRouting Setup Violations in Early Design Stages. ACM Trans. Des. Autom. Electron. Syst. 2023, 28, 49. [Google Scholar] [CrossRef]
- Nath, S.; Pradipta, G.; Hu, C.; Yang, T.; Khailany, B.; Ren, H. TransSizer: A Novel Transformer-Based Fast Gate Sizer. In Proceedings of IEEE International Conference on Computer Aided Design (ICCAD), San Diego, CA, USA, 29 October–3 November 2022. [Google Scholar]
- Liao, P.; Guo, D.; Guo, Z.; Liu, S.; Lin, Y.; Yu, B. DREAMPlace 4.0: Timing-Driven Placement With Momentum-Based Net Weighting and Lagrangian-Based Refinement. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2023, 42, 3374–3387. [Google Scholar] [CrossRef]
- Synopsys. IC Compiler Implementation User Guide; Synopsys: Sunnyvale, CA, USA, 2011. [Google Scholar]
- Barboza, E.C.; Shukla, N.; Chen, Y.; Hu, J. Machine Learning-Based Pre-Routing Timing Prediction with Reduced Pessimism. In Proceedings of the Design Automation Conference, (DAC), Las Vegas, NV, USA, 2–6 June 2019. [Google Scholar]
- He, X.; Fu, Z.; Wang, Y.; Liu, C.; Guo, Y. Accurate Timing Prediction at Placement Stage with Look-Ahead RC Network. In Proceedings of the Design Automation Conference, (DAC), San Francisco, CA, USA, 10–14 July 2022. [Google Scholar]
- Liang, R.; Nath, S.; Rajaram, A.; Hu, J.; Ren, H. BufFormer: A Generative ML Framework for Scalable Buffering. In Proceedings of the Asia and South Pacific Design Automation Conference, (ASP-DAC), Tokyo, Japan, 16–19 January 2023. [Google Scholar]
- Lu, Y.C.; Nath, S.; Khandelwal, V.; Lim, S.K. RL-Sizer: VLSI Gate Sizing for Timing Optimization using Deep Reinforcement Learning. In Proceedings of the Design Automation Conference, (DAC), San Francisco, CA, USA, 5–9 December 2021. [Google Scholar]
- Lu, Y.C.; Pentapati, S.; Lim, S.K. The Law of Attraction: Affinity-Aware Placement Optimization Using Graph Neural Networks. In Proceedings of the International Symposium on Physical Design, (ISPD), Virtual, USA, 22–24 March 2021. [Google Scholar]
- Lu, Y.C.; Yang, T.; Lim, S.K.; Ren, H. Placement Optimization via PPA-Directed Graph Clustering. In Proceedings of the ACM/IEEE International Symposium on Machine Learning for CAD, (MLCAD), Virtual, China, 12–13 September 2022. [Google Scholar]
- Cheng, H.H.; Jiang, I.H.R.; Ou, O. Fast and Accurate Wire Timing Estimation on Tree and Non-Tree Net Structures. In Proceedings of the Design Automation Conference, (DAC), San Francisco, CA, USA, 20–24 July 2020. [Google Scholar]
- Xie, Z.; Liang, R.; Xu, X.; Hu, J.; Chang, C.C.; Pan, J.; Chen, Y. Preplacement Net Length and Timing Estimation by Customized Graph Neural Network. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2022, 41, 4667–4680. [Google Scholar] [CrossRef]
- Lu, Y.C.; Nath, S.; Kiran Pentapati, S.S.; Lim, S.K. A Fast Learning-Driven Signoff Power Optimization Framework. In Proceedings of the IEEE International Conference on Computer-Aided Design, (ICCAD), San Diego, CA, USA, 2–5 November 2020. [Google Scholar]
- Wang, Z.; Liu, S.; Pu, Y.; Chen, S.; Ho, T.Y.; Yu, B. Restructure-Tolerant Timing Prediction via Multimodal Fusion. In Proceedings of the Design Automation Conference, (DAC), San Francisco, CA, USA, 9–13 July 2023. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. arXiv 2018. [Google Scholar] [CrossRef]
- Qiu, J.; Reda, S.; Hassoun, S. Fast, Accurate a Priori Routing Delay Estimation. In Proceedings of the 24th ACM/IEEE Workshop on System Level Interconnect Pathfinding, (SLIP), Anaheim, CA, USA, 13 June 2010. [Google Scholar]
- Cheng, C.Y.; Wang, T.C. Routability-aware Placement Guidance Generation for Mixed-size Designs. In Proceedings of the 2023 24th International Symposium on Quality Electronic Design (ISQED), San Francisco, CA, USA, 5–7 April 2023. [Google Scholar]


| Type | Parameters | Description |
|---|---|---|
| timing feature | wst input slack | worst slack of input pin (s) |
| wst output slack | worst slack of output pin | |
| max input slew | max slew of input pin (s) | |
| max output slew | max slew of output pin | |
| wst delay | worst delay of cell | |
| physical feature | cell area | area of the given cell |
| cell x/y coordinate | coordinate of the given cell | |
| driving strength | driving strength of cell | |
| total output cap | total output load capacitance | |
| fanins | fanin number of cell | |
| fanouts | fanout number of cell | |
| max cell distance | max Manhattan distance |
| Benchmark | Circuit Statistics | F1-Score of Target | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| #Cell | #Sized Cell | #Buf | #Add Buf | Buffering | [5] | Sizing | [5] | [6] | Path Group | [10] | |
| training set | |||||||||||
| ac97 | 7896 | 3384 | 616 | 1071 | 98.54% | 90.74% | 84.01% | 86.06% | 81.32% | 92.87% | 88.35% |
| aes | 4124 | 1539 | 980 | 100 | 92.14% | 86.94% | 96.56% | 94.84% | 93.53% | 91.57% | 85.23% |
| des | 1375 | 596 | 133 | 68 | 89.39% | 84.32% | 92.46% | 83.28% | 88.34% | 90.51% | 77.76% |
| vga_enh | 48,728 | 4980 | 1157 | 968 | 92.43% | 93.87% | 97.67% | 94.19% | 96.74% | 88.54% | 83.52% |
| eth | 32,985 | 11,226 | 537 | 936 | 97.67% | 92.21% | 92.23% | 91.07% | 93.58% | 80.21% | 83.32% |
| pci_bridge32 | 11,897 | 2435 | 487 | 851 | 90.56% | 88.53% | 92.79% | 87.98% | 91.54% | 87.08% | 87.21% |
| ave. | 17,834 | 4026 (31.3%) | 651 | 665 (111.3%) | 93.46% | 89.43% | 92.62% | 89.57% | 90.84% | 88.46% | 84.23% |
| testing set | |||||||||||
| ecg | 52,401 | 25,474 | 1607 | 4627 | 71.68% | 69.43% | 72.33% | 68.44% | 76.41% | 72.55% | 64.32% |
| mc | 5064 | 582 | 487 | 657 | 82.34% | 74.43% | 87.61% | 67.71% | 80.63% | 80.11% | 73.32% |
| systemcdes | 1463 | 663 | 321 | 187 | 81.16% | 80.01% | 81.04% | 72.16% | 75.74% | 78.86% | 71.85% |
| ave. | 19,642 | 8906 (35.1%) | 805 | 1823 (160.3%) | 78.93% | 74.62% | 80.32% | 69.44% | 77.59% | 77.17% | 69.83% |
| Benchmark | Baseline | w/Physical Guidance Only | w/Timing Guidance Only | w/Full Guidance (This Work) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WNS | TNS | NVP | area | WNS | TNS | NVP | WNS | TNS | NVP | WNS | TNS | NVP | Area | |
| ecg | −0.076 | −7.056 | 5502 | 33,701.4 | −0.0568 (−25.26%) | −0.0568 (39.46%) | 2353 (−57.23%) | −0.0628 (−17.37%) | −3.81 (−46.00%) | 908 (−83.50%) | −0.0683 (−10.13%) | −5.232 (−25.85%) | 2323 (−57.78%) | 33,763.4 (0.18%) |
| mc | −0.049 | −2.436 | 1626 | 4487.83 | −0.045 (−8.16%) | −0.0399 (−13.38%) | 1986 (22.14%) | −0.0401 (−18.16%) | −3.37 (38.34%) | 1928 (18.57%) | −0.0191 (−61.02%) | −0.417 (−82.88%) | 736 (−54.74%) | 4534.37 (1.04%) |
| systemcdes | −0.012 | −0.078 | 225 | 1161.89 | −0.019 (58.33%) | −0.039 (41.03%) | 502 (123.11%) | −0.012 (0.00%) | −0.09 (15.38%) | 372 (65.33%) | −0.0077 (−35.83%) | −0.061 (−21.79%) | 126 (−44.00%) | 1147.58 (−1.23%) |
| average | 0% | 0% | 0% | 0% | 8.30% | 22.37% | 29.34% | −11.84% | −2.57% | 0.13% | −35.66% | −43.51% | −52.17% | 0.003% |
| Benchmark | Baseline | ISQED’23 [21] | This Work | ||||||
|---|---|---|---|---|---|---|---|---|---|
| TNS | NVP | WL | TNS | NVP | WL | TNS | NVP | WL | |
| ecg | −68.61 | 25,489 | 6.31 | −65.45 (−4.61%) | 21,435 (−15.90%) | 6.35 (0.63%) | −74.94 (9.22%) | 13,791 (−45.89%) | 6.33 (0.32%) |
| mc | −6.64 | 9393 | 0.57 | −5.89 (−11.29%) | 8965 (−4.56%) | 0.56 (−1.75%) | −5.53 (−16.78%) | 8467 (−9.86%) | 0.61 (7.01%) |
| systemcdes | −1.04 | 34,048 | 0.15 | −0.87 (−16.34%) | 30,431 (−10.62%) | 0.15 (0.0%) | −0.36 (−65.09%) | 2438 (−92.83%) | 0.12 (−20%) |
| average | 0% | 0% | 0% | −10.75% | −10.36% | −0.37% | −24.21% | −31.32% | −2.33% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, P.; Li, Z.; Ding, W. A GNN-Based Placement Optimization Guidance Framework by Physical and Timing Prediction. Electronics 2025, 14, 329. https://doi.org/10.3390/electronics14020329
Cao P, Li Z, Ding W. A GNN-Based Placement Optimization Guidance Framework by Physical and Timing Prediction. Electronics. 2025; 14(2):329. https://doi.org/10.3390/electronics14020329
Chicago/Turabian StyleCao, Peng, Zhi Li, and Wenjie Ding. 2025. "A GNN-Based Placement Optimization Guidance Framework by Physical and Timing Prediction" Electronics 14, no. 2: 329. https://doi.org/10.3390/electronics14020329
APA StyleCao, P., Li, Z., & Ding, W. (2025). A GNN-Based Placement Optimization Guidance Framework by Physical and Timing Prediction. Electronics, 14(2), 329. https://doi.org/10.3390/electronics14020329






