Day-Ahead Coordinated Scheduling of Distribution Networks Considering 5G Base Stations and Electric Vehicles

Abstract

The rapid growth of 5G base stations (BSs) and electric vehicles (EVs) introduces significant challenges for distribution network operation due to high energy consumption and variable loads. This paper proposes a coordinated day-ahead scheduling framework that integrates 5G BS task migration, storage utilization, and EV charging or discharging with mobility constraints. A mixed-integer second-order cone programming (MISOCP) model is formulated to optimize network efficiency while ensuring reliable power supply and maintaining service quality. The proposed approach enables dynamic load adjustment via 5G computing task migration and coordinated operation between 5G BSs and EVs. Case studies demonstrate that the proposed method can effectively generate an optimal day-ahead scheduling strategy for the distribution network. By employing the task migration strategy, the computational workloads of heavily loaded 5G BSs are dynamically redistributed to neighboring stations, thereby alleviating computational stress and reducing their associated power consumption. These results highlight the potential of leveraging the joint flexibility of 5G infrastructures and EVs to support more efficient and reliable distribution network operation.

1. Introduction

The rapid deployment of 5G communication networks and the accelerated adoption of EVs are reshaping the demand profiles of modern distribution networks [1,2,3]. On one hand, 5G BSs are characterized by dense deployment, continuous operation, and substantial energy consumption driven by communication, computing, and energy storage functions [4]. On the other hand, large-scale EV charging introduces considerable and often unpredictable loads, while V2G technologies enable bidirectional power exchange, further increasing operational complexity [5].

The simultaneous growth of these two emerging loads places unprecedented stress on distribution networks. Peak load levels may rise significantly, voltage deviations can become more severe, and network losses tend to increase, especially in urban areas with overlapping high densities of 5G BSs and EVs. Without effective coordination, the temporal and spatial concentration of power demand may threaten supply reliability, reduce power quality, and accelerate equipment aging.

In this context, integrating 5G BSs and EVs into a coordinated scheduling framework offers a promising pathway to enhance flexibility in distribution network operation. By leveraging the controllability of EV charging and discharging, as well as the adjustable computing and energy storage capacities of 5G BSs, it is possible to optimize power allocation, reduce network losses, and improve voltage profiles. This study is motivated by the need to develop a mathematical model and scheduling strategy that captures these interactions while ensuring the safe, stable, and economical operation of the distribution network.

Significant research has been conducted on the energy management of 5G BSs, focusing on power consumption modeling, energy-saving strategies, and computing task migration [6,7,8]. Most existing studies emphasize optimizing energy efficiency within the communication network itself, often considering a single base station or homogeneous networks. For instance, the authors of [9] investigated the energy consumption of 5G small-cell BSs and demonstrate that over 50% of the total energy is devoted to computation, underscoring the need for workload-aware power modeling. In a similar vein, the authors of [10] proposed an energy-saving scheme for separated control and data planes in 5G networks, achieving notable energy reductions through sleep-mode strategies tailored to traffic loads. The authors of [11] review energy-efficiency opportunities in Massive MIMO 5G systems, highlighting that antenna scaling and hybrid architectures can yield substantial gains even under homogeneous deployment. Moreover, in [12], a comprehensive overview of energy-efficiency techniques in 5G systems is provided, emphasizing strategies such as enabling/disabling base station components that are effective at the single-cell level. However, these works rarely integrate 5G BS operation with the surrounding distribution network, neglecting the potential for coordinated scheduling that leverages both computing and storage capabilities to support grid operations. This limitation highlights the necessity of modeling task migration in conjunction with distribution network dispatch to exploit the full flexibility of 5G infrastructure.

Similarly, extensive studies have addressed EV charging and V2G scheduling, considering SOC constraints, mobility requirements, and interactions with distributed energy resources [13,14,15]. For example, the authors of [16] developed a large-scale EV charging/discharging scheduling model that incorporates SOC limits, grid load variance, and user availability, demonstrating improved load smoothing via a multi-level grouping competitive swarm optimizer. The authors of [17] proposed a V2G scheduling framework in a coupled power–transportation network that jointly optimizes EV charging, discharging, and user mobility under dynamic pricing, highlighting enhanced coordination across domains. The authors of [18] introduced a distributed coordination mechanism that leverages EV bidirectional capabilities and renewable DER synergies to minimize network load variance and improve voltage profiles. While these approaches provide effective strategies for reducing charging costs and managing local grid loads, they generally focus on EVs in isolation or their impact on the distribution network without accounting for interactions with emerging information infrastructure. Consequently, the spatial-temporal coordination between EVs and 5G BSs remains largely unexplored, limiting opportunities for optimizing power flows and reducing system losses.

Some research has explored integrated multi-energy systems and coordinated scheduling of distributed energy resources [19,20,21], yet none systematically consider the joint effects of 5G BS task migration, energy storage, and EV mobility in the context of distribution network day-ahead scheduling. For instance, a study proposed a coordinated scheduling strategy leveraging the flexible load management capabilities of 5G base stations and their potential for inter-regional power demand response within the smart grid framework [22]. Another research developed a collaborative optimization approach for power distribution and communication networks with 5G base stations, aiming to enhance the synergy between communication and power systems [23]. Additionally, a paper introduced a co-regulation method for distribution network voltage control, enabling base station energy storage systems to participate in grid interactions, thereby improving grid stability [24]. Furthermore, a study proposed a scheduling strategy for demand response in flexible resources under the 5G-V2X framework, highlighting the integration of vehicle-to-everything communication in energy management [25]. Specifically, the combination of 5G computing load transfer, EV charging/discharging flexibility, and network constraints has not been formulated into a unified optimization framework. This gap motivates the current study to develop a coordinated model that captures these interactions, enabling both 5G BSs and EVs to participate in distribution network operation without compromising communication service quality or EV user mobility.

Recent studies have increasingly focused on the cost–energy implications of task migration in edge computing. For instance, the authors of [26] demonstrated that migration decisions can reduce both energy consumption and cost, yet the model is designed primarily for homogeneous service environments and overlooks the interaction with distribution networks. Similarly, the authors of [27] addressed energy and cost trade-offs in hybrid systems, but its scope is confined to generic cloud–edge scenarios without considering the unique characteristics of 5G base stations. A broader synthesis is provided in [28], which highlights task offloading and resource allocation strategies, but does not incorporate the joint effect of EV charging demand and BS workload migration. In contrast, our work explicitly integrates the cost-energy aspects of task migration with the coordinated scheduling of EVs and BSs in distribution networks, thereby capturing a cross-domain coupling that has been largely neglected in prior literature.

On the latency and QoS side, the validity of migration is tightly constrained by service requirements in 5G systems. The authors of [29] emphasized that overlooking end-to-end latency budgets can negate the benefits of migration, but the analysis remains at the service orchestration level without considering power system implications. The authors of [30] incorporated delay and mobility into migration decisions yet focuses only on algorithmic performance and does not account for the energy cost of additional communication loads. The authors of [31] thoroughly reviewed service coexistence in 5G, but it discusses resource allocation at the radio level rather than workload migration across BSs. By jointly modeling latency, QoS, and the induced communication overhead of task migration within the context of EV and distribution network scheduling, our study advances the state of the art by ensuring that migration strategies remain both energy-aware and service-compliant.

The proposed model extends existing research in two key aspects. First, it integrates EV scheduling and 5G BS energy management into a coordinated day-ahead scheduling framework, explicitly capturing their mutual interactions within the distribution network; Then, it incorporates a task migration mechanism for 5G base stations, including the additional communication load incurred by migration, which has not been addressed in existing literature, thereby enabling a more realistic and practical evaluation of system-level energy efficiency and operational flexibility. By bridging these gaps, the proposed model provides a novel and comprehensive approach for optimizing the joint operation of EVs and 5G infrastructure, enhancing distribution network efficiency, reliability, and adaptability under dynamic operational conditions.

In summary, while prior research provides valuable insights into individual energy management and scheduling problems, there remains a lack of systematic approaches that integrate 5G BSs and EVs for coordinated distribution network dispatch. Addressing this gap, the present work constructs a comprehensive optimization model that combines 5G task migration, storage utilization, and EV mobility constraints, forming the foundation for the proposed coordinated scheduling strategy.

Existing studies either focus on 5G BS energy management or EV charging and V2G scheduling but rarely address their joint impact on distribution network operation. Current approaches lack a systematic framework to coordinate 5G task migration, storage utilization, and EV mobility while ensuring grid stability, communication service quality, and user travel requirements. The key research problem addressed in this study is how to develop a coordinated day-ahead scheduling strategy that simultaneously optimizes the operation of 5G BSs and EVs, capturing their interactions and constraints, to enhance distribution network efficiency and reliability.

To summarize, our contributions are listed as follows:

• A dynamic load adjustment mechanism is proposed by modeling 5G BS computing task migration.
• A coordinated framework is developed for 5G BSs and EVs, considering 5G task migration, storage capabilities, and EV charging or discharging and mobility characteristics.
• A MISOCP model is formulated for day-ahead distribution network scheduling, integrating 5G BSs and EVs for improved operational efficiency and reliability.

The remainder of this paper is organized as follows. Section 2 presents the interaction mechanisms of 5G base stations and electric vehicles, including the task migration strategy, EV charging and mobility models, and their coordinated operation rules. Section 3 develops the day-ahead scheduling model for the distribution network, formulating the objective function and operational constraints for both 5G base stations and EVs. Section 4 provides case studies to validate the proposed coordination strategies and demonstrates their effectiveness in improving network efficiency and reliability. Finally, Section 5 summarizes the key findings and outlines potential directions for future research.

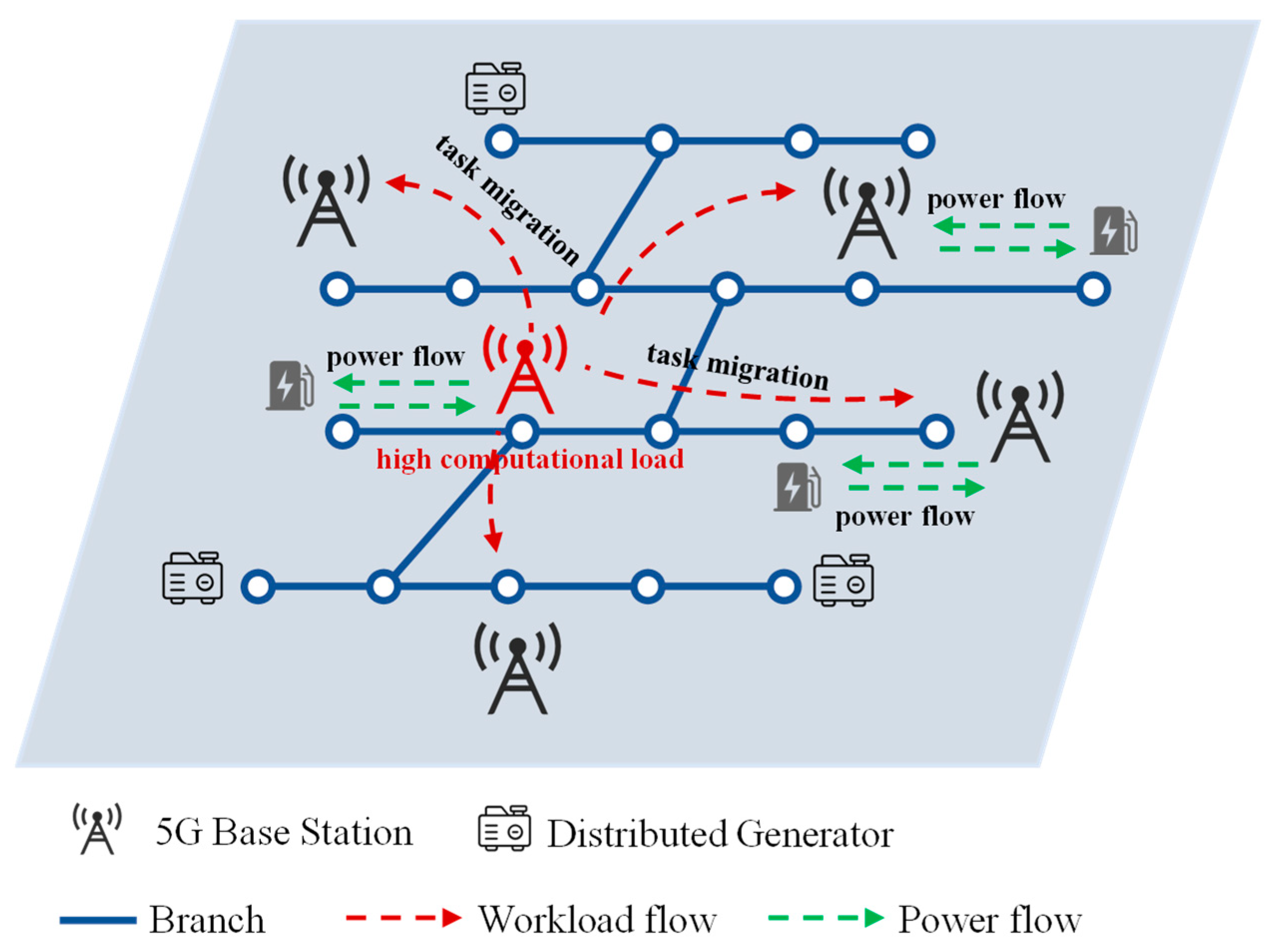
2. Coordinated Interaction of 5G Base Stations and Electric Vehicles Incorporating Task Migration Strategy

2.1. Task Migration Strategy of 5G Base Stations

With the rapid proliferation of 5G communication infrastructure, base stations have become significant energy consumers in distribution networks due to their continuous operation and high computational workloads. Unlike conventional loads with fixed consumption patterns, 5G base stations possess the capability to dynamically adjust part of their computational demand through task migration. This mechanism allows computationally intensive tasks to be offloaded from one base station to another via high-speed communication links, enabling spatial redistribution of power consumption. By strategically shifting workloads from stations in high-load regions to those in low-load regions, task migration not only helps balance the energy demand within the network but also provides a new form of flexible load that can be coordinated with other distributed energy resources.

2.1.1. Power Characteristics of 5G Base Stations

In modern distribution networks, the total power consumption of a 5G base station consists of three main components: communication load, computation load, and energy storage. Each component contributes differently depending on traffic intensity, computation workload, and storage operation. Accurately capturing these components is essential for evaluating the dynamic load characteristics of 5G base stations.

The communication load $P_{i,t}^{\mathrm{com}}$ arises from the operation of radio units, power amplifiers, fronthaul and backhaul transceivers, as well as supporting systems such as cooling and auxiliary power. This load depends on the real-time traffic intensity $r_{i,t}$ in megabits per second, the configured spectrum bandwidth, the number of active antennas, and ambient conditions affecting cooling requirements. A linear approximation suitable for day-ahead scheduling is adopted:

$$P_{i,t}^{\mathrm{com}}={\alpha }_{0,i}+{\alpha }_{1,i}{r}_{i,t}$$

(1)

where ${\alpha }_{0,i}$ denotes the baseline communication power at zero traffic, ${\alpha }_{1,i}$ maps traffic intensity to incremental radio and fronthaul power.

The computation load $P_{i,t}^{\mathrm{cmp}}$ is associated with processing tasks on the baseband or edge-computing platform. To maintain a fully linear form, it is expressed as a linear function of the normalized workload utilization $u_{i,t}\in [0, 1]$

$$P_{i,t}^{\mathrm{cmp}}=P_i^{\mathrm{idle}}+{\beta }_i{u}_{i,t}$$

(2)

$${\beta }_i=P_i^{\mathrm{peak}}-P_i^{\mathrm{idle}}$$

(3)

where $P_i^{\mathrm{idle}}$ is the idle power of the computing platform, and ${\beta }_i$ represents the linear increase in power from idle to peak utilization.

The energy storage power accounts for local batteries that ensure uninterrupted operation. Let $E_{i,t}$ denote the state of charge at the end of interval t, $P_{i,t}^{\mathrm{ch}}$ and $P_{i,t}^{\mathrm{dis}}$ the charging and discharging powers, ${\eta }_i^{\mathrm{ch}}$ and ${\eta }_i^{\mathrm{dis}}$ the efficiencies, and $\Delta t$ the time step. The storage dynamics are:

$$E_{i,t+1}=E_{i,t}+{\eta }_i^{\mathrm{ch}}{P}_{i,t}^{\mathrm{ch}}\Delta t-{\displaystyle \frac{1}{{\eta }_i^{\mathrm{dis}}}}{P}_{i,t}^{\mathrm{dis}}\Delta t$$

(4)

subject to

$$E_i^{\min }\le E_{i,t}\le E_i^{\max }$$

(5)

$$0\le P_{i,t}^{\mathrm{ch}}\le {\overline{P}}_i^{\mathrm{ch}}$$

(6)

$$0\le P_{i,t}^{\mathrm{dis}}\le {\overline{P}}_i^{\mathrm{dis}}$$

(7)

To prevent simultaneous charging and discharging, a binary variable $y_{i,t}\in \left\{0,\left.1\right\}\right.$ can be introduced:

$$P_{i,t}^{\mathrm{ch}}\le y_{i,t}{\overline{P}}_i^{\mathrm{ch}}$$

(8)

$$P_{i,t}^{\mathrm{dis}}\le \left(1-y_{i,t}\right){\overline{P}}_i^{\mathrm{dis}}$$

(9)

Finally, the total power demand of base station i at time t, including communication, computation, and storage effects, is expressed as:

$$P_{i,t}^{\mathrm{BS}}=P_{i,t}^{\mathrm{com}}+P_{i,t}^{\mathrm{cmp}}+\left(P_{i,t}^{\mathrm{ch}}-P_{i,t}^{\mathrm{dis}}\right)$$

(10)

This linearized framework provides a tractable representation of the 5G base station’s electrical load suitable in day-ahead scheduling studies.

2.1.2. Mathematical Modeling and Constraints of Task Migration

Task migration refers to the process of transferring computational tasks from one 5G base station to another in order to balance processing workloads across the network. The underlying principle is that, by reallocating tasks among base stations with spare computational capacity, it is possible to reduce local peak loads, improve resource utilization, and maintain service quality. In essence, task migration allows the system to distribute computational demand dynamically according to available resources and network conditions.

Through task migration, the distribution of computational load can be optimized, effectively achieving a more balanced power consumption profile across multiple base stations. This not only reduces the probability of local overloads but also decreases line losses in the associated distribution network. By shifting tasks to base stations that are electrically closer to high-demand points or are operating under lighter loads, the overall efficiency of the network can be improved, leading to potential energy savings and enhanced operational flexibility.

To model task migration within the 5G base station network, let $w_{i,t}^{\mathrm{loc}}$ denote the portion of computational workload processed locally at base station i at time t, and $w_{i,j,t}^{\mathrm{mig}}$ represent the workload migrated from base station i to base station j at the same time. The total workload processed by base station i then satisfies the linear relationship:

$$w_{i,t}^{\mathrm{tot}}=w_{i,t}^{\mathrm{loc}}+{\displaystyle \sum _{j\in {\mathcal{N}}_i}{w}_{j,i,t}^{\mathrm{mig}}}-{\displaystyle \sum _{j\in {\mathcal{N}}_i}{w}_{i,j,t}^{\mathrm{mig}}}$$

(11)

where ${\mathcal{N}}_i$ denotes the set of neighboring base stations capable of receiving migrated tasks. This expression ensures that the total workload at each base station equals the local processing plus incoming migrated tasks minus outgoing migrated tasks.

The task migration is subject to several linear constraints. First, the migrated workload must be non-negative and cannot exceed the available processing capacity of the destination base station:

$$0\le w_{i,j,t}^{\mathrm{mig}}\le {\overline{w}}_j-w_{j,t}^{\mathrm{loc}},\hspace{1em}\forall i,j\in {\mathcal{N}}_i$$

(12)

where ${\overline{w}}_j$ is the maximum computational capacity of base station j. Second, the local workload must not exceed the base station’s capacity:

$$0\le w_{i,t}^{\mathrm{loc}}\le {\overline{w}}_i,\hspace{1em}\forall i$$

(13)

To ensure that the total computational demand is fully processed, the sum of local processing and outgoing migrations should meet the initial workload at each base station:

$$w_{i,t}^{\mathrm{loc}}+{\displaystyle \sum _{j\in {\mathcal{N}}_i}{w}_{i,j,t}^{\mathrm{mig}}}={\overline{w}}_i^{\mathrm{demand}}$$

(14)

where ${\overline{w}}_i^{\mathrm{demand}}$ denotes the total workload demand at base station i at time t.

Finally, the power consumption of computation is modeled as a linear function of the computation load:

$$P_{i,t}^{\mathrm{cmp}}={\alpha }_i{w}_{i,t}^{\mathrm{tot}}+{\beta }_i$$

(15)

where ${\alpha }_i$ represents the dynamic power coefficient and ${\beta }_i$ corresponds to the static idle power consumption. In order to determine the computation power coefficients ${\alpha }_i$ and ${\beta }_i$, three procedures can generally be considered, namely direct extraction from manufacturer specifications, regression based on empirical measurements, and component-level decomposition. Each of these approaches has its own merits, where the regression method allows fine-grained calibration from field data, and the component-based decomposition provides interpretability at the subsystem level. However, in this study we adopt the direct specification-based approach, as it offers a straightforward, reproducible, and vendor-consistent way to obtain parameters without requiring additional measurement campaigns. Specifically, we set ${\beta }_i$ as the idle power reported in the equipment datasheet, representing the baseline consumption when no workload is processed, and we define ${\alpha }_i$ as the difference between the peak power and the idle power, reflecting the incremental consumption associated with the full utilization of the computation resource [32,33,34,35]. This formulation captures the effect of task migration on total system energy consumption.

To account for the additional communication load induced by task migration, the communication load expression is extended as follows:

$$P_{i,t}^{\mathrm{com}}={\alpha }_{0,i}+{\alpha }_{1,i}{r}_{i,t}+{\displaystyle \sum _{j\in {\mathcal{N}}_i}{\gamma }_{i,j}{w}_{i,j,t}^{\mathrm{mig}}}$$

(16)

where ${\gamma }_{i,j}$ is the communication load coefficient per unit of migrated workload. This formulation reflects the additional energy consumption in communication due to workload migration, enabling more realistic evaluation of task migration costs in coordinated scheduling.

These linear constraints collectively define a feasible task migration scheme, enabling the network to achieve optimal load distribution while ensuring that each base station operates within its computational limits. Integrating this task migration model with the power consumption model of 5G BSs provides a foundation for optimizing energy efficiency and reducing line losses in the distribution network.

2.2. Coordinated Mechanism of 5G Base Stations and Electric Vehicles

The integration of 5G BSs and EVs within the distribution network offers a promising approach to enhance system flexibility and energy efficiency. In addition to task migration strategies at 5G BSs, coordinated operation with EVs enables dynamic adjustment of both supply and demand, as EVs can function as mobile loads or distributed energy resources depending on their location and state of charge. By leveraging the combined capabilities of BS energy storage, computation task migration, and EV charging/discharging flexibility, the network can achieve more efficient load allocation and reduced line losses.

2.2.1. EV Charging and Discharging Model

EVs exhibit a bidirectional interaction with the distribution network, acting as either loads during charging periods or as distributed energy sources when discharging. The charging and discharging process can be modeled as a controllable power exchange between the EV battery and the grid, constrained by the technical limits of the on-board charger and battery system. Let $P_{e,t}^{\mathrm{ch}}$ and $P_{e,t}^{\mathrm{dis}}$ denote the charging and discharging power of EV e at time t, respectively. The operational limits can be expressed as

$$0\le P_{e,t}^{\mathrm{ch}}\le P_e^{\mathrm{ch},\max }$$

(17)

$$0\le P_{e,t}^{\mathrm{dis}}\le P_e^{\mathrm{dis},\max }$$

(18)

where $P_e^{\mathrm{ch},\max }$ and $P_e^{\mathrm{dis},\max }$ are the maximum charging and discharging power ratings of EV e. To avoid simultaneous charging and discharging, a binary variable ${\delta }_{e,t}^{\mathrm{ch}}$ is introduced, leading to

$$P_{e,t}^{\mathrm{ch}}\le {\delta }_{e,t}^{\mathrm{ch}}\cdot P_e^{\mathrm{ch},\max }$$

(19)

$$P_{e,t}^{\mathrm{dis}}\le \left(1-{\delta }_{e,t}^{\mathrm{ch}}\right)\cdot P_e^{\mathrm{dis},\max }$$

(20)

The state-of-charge (SOC) of EV e evolves according to the battery dynamics, which can be expressed as

$${\mathrm{SOC}}_{e,t}={\mathrm{SOC}}_{e,t-1}+{\displaystyle \frac{{\eta }_e^{\mathrm{ch}}{P}_{e,t}^{\mathrm{ch}}\Delta t}{E_e^{\mathrm{cap}}}}-{\displaystyle \frac{P_{e,t}^{\mathrm{dis}}\Delta t}{{\eta }_e^{\mathrm{dis}}{E}_e^{\mathrm{cap}}}}$$

(21)

where ${\eta }_e^{\mathrm{ch}}$ and ${\eta }_e^{\mathrm{dis}}$ are the charging and discharging efficiencies, $E_e^{\mathrm{cap}}$ is the battery energy capacity, and $\Delta t$ is the scheduling interval. The SOC is restricted within its operational limits as

$${\mathrm{SOC}}_e^{\min }\le {\mathrm{SOC}}_{e,t}\le {\mathrm{SOC}}_e^{\max }$$

(22)

The mobility of EVs introduces additional constraints, as they may connect to different nodes of the distribution network over time. Let $a_{e,n,t}$ be a binary variable indicating whether EV e is connected to node n at time t. The following constraint ensures that an EV can only be connected to one node at each time step:

$${\displaystyle \sum _n{a}_{e,n,t}}=1$$

(23)

The charging and discharging power of an EV can only be non-zero when it is connected to a node, represented as

$$P_{e,t}^{\mathrm{ch}}\le {\displaystyle \sum _n{a}_{e,n,t}}\cdot P_e^{\mathrm{ch},\max }$$

(24)

$$P_{e,t}^{\mathrm{dis}}\le {\displaystyle \sum _n{a}_{e,n,t}}\cdot P_e^{\mathrm{dis},\max }$$

(25)

This mobility-aware modeling approach captures the dual role of EVs as flexible loads and mobile distributed energy resources, enabling a more adaptive and efficient coordination with 5G BSs in the distribution network.

2.2.2. Coordination Mechanism Between 5G BSs and EVs

The interaction between 5G BSs and EVs is enabled through bidirectional energy exchange and flexible load management. On one hand, EVs can supply stored energy to BSs during periods of high communication demand or when grid power is constrained, thereby enhancing the resilience of the communication network. On the other hand, BSs can schedule EV charging in periods of low power demand or high renewable generation, which helps to improve network load balancing and reduce operating costs. This interaction occurs via V2G and G2V processes, coordinated through intelligent scheduling algorithms that consider spatial locations, temporal demand patterns, and energy storage priorities.

To ensure that such interactions do not compromise system performance or user experience, three coordination rules are defined:

The spatial coordination rule stipulates that each EV can only exchange power with the BS to which it is physically connected. This avoids unnecessary power losses in long-distance transfers and prevents complex routing that could endanger distribution network stability.

The temporal coordination rule requires that EV-to-BS energy supply occurs primarily during BS peak load periods. This ensures that the exchanged energy is most effectively used to reduce grid stress and improve communication reliability without unnecessary battery cycling.

The storage priority rule ensures that the SOC of each EV remains sufficient to meet its expected travel needs before participating in V2G support. This prevents the energy cooperation from interfering with EV users’ travel schedules and guarantees user satisfaction while enabling flexible grid support.

These rules are not a mere combination of existing methods but are developed based on the specific operational challenges of integrating high computational demand, dynamic workload distribution, and bidirectional energy flow. The spatial rule is designed to address workload balancing across geographically distributed BSs by dynamically allocating computation tasks based on spatial proximity and network load conditions. This approach reduces local congestion and optimizes the utilization of nearby resources, which extends beyond traditional static load balancing by introducing real-time migration decisions. The temporal rule focuses on optimizing scheduling over time, incorporating the dynamic nature of computational demand, EV charging/discharging patterns, and electricity price variations. Unlike conventional fixed-time scheduling methods, this rule integrates predictive workload trends and price signals to improve overall operational efficiency. The energy storage rule governs the coordination between EV batteries and BS energy storage systems, enabling intelligent scheduling of charge/discharge actions. This rule not only supports peak load shaving and energy cost minimization but also integrates a user incentive mechanism that compensates for battery degradation and encourages EV participation in V2G services. Together, these coordination rules form a cohesive framework that considers workload migration costs, communication load adjustments, user incentives, and energy constraints, thereby ensuring robust, adaptive, and practical scheduling decisions. The design of this set of coordination rules represents a novel contribution to the literature, providing a comprehensive methodology for day-ahead coordinated scheduling in distribution networks with integrated 5G BSs and EVs.

The Schematic diagram of 5G BS task migration and power interaction is shown in Figure 1.

3. Day-Ahead Scheduling Model of Distribution Networks Considering 5G BSs and EVs

In this chapter, an optimization model is developed to coordinate the operation of 5G BSs and EVs within the distribution network. The objective function is formulated to minimize the total operational cost and network power losses, while ensuring the secure and reliable operation of the system. The model incorporates various operational constraints, including power balance and capacity limits of 5G BSs, charging/discharging and mobility constraints of EVs, coordination rules between 5G BSs and EVs, and electrical constraints of the distribution network. Based on these objectives and constraints, the coordinated scheduling problem is formulated as a MISOCP model, which enables accurate representation of non-convex power flow relationships while maintaining computational tractability.

3.1. Objective Function

The objective function in this study aims to minimize the total operating cost of the distribution network while maintaining efficient utilization of resources and reducing power losses. From a physical perspective, this objective reflects the need to balance the electricity consumption of 5G BSs, the charging and discharging behaviors of EVs, and the power losses in the network. Minimizing this cost not only ensures economic operation but also contributes to enhancing the stability and reliability of the system by avoiding excessive energy demand peaks and optimizing resource allocation.

The objective function is formulated as:

$$\min \hspace{0.33em}{C}_{\mathrm{total}}={\displaystyle \sum _{t\in T}\left[{\displaystyle \sum _{i\in \mathcal{B}}{\lambda }_t}{P}_{i,t}^{\mathrm{BS}}+{\displaystyle \sum _{j\in \mathcal{E}}{\lambda }_t}\left(P_{j,t}^{\mathrm{EVc}}-P_{j,t}^{\mathrm{EVd}}\right)+{\displaystyle \sum _{j\in \mathcal{E}}{\kappa }_t}{P}_{j,t}^{\mathrm{EVd}}+\mu {\displaystyle \sum _{l\in \mathcal{L}}{P}_{l,t}^{\mathrm{loss}}}\right]}$$

(26)

where $t\in T$ denotes the scheduling time periods, $\mathcal{B}$ is the set of 5G BSs, $\mathcal{E}$ is the set of EVs, and $\mathcal{L}$ is the set of distribution lines. The parameter ${\lambda }_t$ ($/kWh) represents the electricity price at time t, $\mu$ is the cost coefficient for network power losses and ${\kappa }_t$ is the incentive coefficient, captures both the direct user reward and an allowance for battery degradation. In practice, user reward may be tied to the electricity price and degradation compensation is estimated from replacement cost and cycle life. The variable $P_{i,t}^{\mathrm{BS}}$ (kW) denotes the total power consumption of BS I at time t, which includes communication, computation, and storage components. The variables $P_{j,t}^{\mathrm{EVc}}$ and $P_{j,t}^{\mathrm{EVd}}$ represent the charging and discharging power of EV j at time t, respectively, with charging contributing to cost and discharging reducing it. The term $P_{l,t}^{\mathrm{loss}}$ (kW) corresponds to the active power loss on line l at time t, which is penalized to encourage loss minimization.

This formulation ensures that the optimization process takes into account both the direct energy consumption costs and the indirect costs associated with network inefficiencies. By integrating the BS power, EV charging/discharging behavior, and line losses into a unified objective, the model achieves a comprehensive balance between operational economy and network performance.

3.2. Constraints

3.2.1. Distribution System Constraints

The operation of the distribution network during the coordinated scheduling of 5G BSs and electric vehicles must comply with several physical and operational constraints. These constraints are expressed mathematically while preserving their physical interpretations as follows.

$${\displaystyle \sum _{g\in {\mathcal{G}}_i}{P}_{g,t}}-{\displaystyle \sum _{l\in {\mathcal{L}}_i}{P}_{l,t}}-P_{i,t}^{\mathrm{loss}}={\displaystyle \sum _{j:(i,j)\in \mathcal{E}}{P}_{ij,t}}$$

(27)

Here, $P_{g,t}$ denotes the active power output of generator g at time t; $P_{l,t}$ is the active load at node i at time t; $P_{i,t}^{\mathrm{loss}}$ is the active power loss at node i at time t; $P_{ij,t}$ is the active power flow from node i to node j at time t.

This constraint ensures that, at each node, the sum of active power generation minus the active power consumption (including loads and network losses) equals the total active power flowing out through connected branches. This maintains real-time power equilibrium across the network.

$${\displaystyle \sum _{g\in {\mathcal{G}}_i}{Q}_{g,t}}-{\displaystyle \sum _{l\in {\mathcal{L}}_i}{Q}_{l,t}}-Q_{i,t}^{\mathrm{loss}}={\displaystyle \sum _{j:(i,j)\in \mathcal{E}}{Q}_{ij,t}}$$

(28)

Here, $Q_{g,t}$ denotes the reactive power output of generator g at time t; $Q_{l,t}$ is the reactive load at node i at time t; $Q_{i,t}^{\mathrm{loss}}$ is the reactive power loss at node i at time t; $Q_{ij,t}$ is the reactive power flow from node iii to node j at time t.

Similarly to the active power balance, this constraint maintains reactive power equilibrium at each node. It ensures that the reactive power supplied by generators minus reactive load demand and losses equals the total reactive power flow to connected branches.

$$V_i^{\min }\le V_{i,t}\le V_i^{\max }$$

(29)

Here, $V_{i,t}$ denotes the voltage magnitude at node i at time t; $V_i^{\min }$ and $V_i^{\max }$ represent the minimum and maximum allowable voltages at node i, respectively.

To guarantee voltage stability and protect sensitive electrical equipment, the voltage at each node is constrained within a safe operational range.

$$I_{ij,t}\le I_{ij}^{\max },\forall (i,j)\in \mathcal{E}$$

(30)

Here, $I_{ij,t}$ denotes the current magnitude in branch (i,j) at time t; $I_{ij}^{\max }$ is the thermal limit of branch (i,j).

This constraint restricts the current flowing through each branch to within its thermal capacity, preventing overheating and prolonging asset lifespan.

$$\sqrt{P_{ij,t}^2+Q_{ij,t}^2}\le V_{i,t}{I}_{ij,t},\forall (i,j)\in \mathcal{E},\forall t$$

(31)

Here, $P_{ij,t}$ and $Q_{ij,t}$ denote the active and reactive power flow from node i to node j at time t.

The nonlinear relationship between active/reactive power, voltage, and current is convexified into second-order cone form, ensuring computational tractability while maintaining physical accuracy.

$$V_{j,t}^2=V_{i,t}^2-2(R_{ij}{P}_{ij,t}+X_{ij}{Q}_{ij,t})+(R_{ij}^2+X_{ij}^2)I_{ij,t}^2,\hspace{1em}\forall (i,j)\in \mathcal{E}$$

(32)

Here, $R_{ij}$ and $X_{ij}$ are the resistance and reactance of branch (i,j).

This equation captures the voltage drop from one node to another along a branch, considering the effects of branch resistance, reactance, and current magnitude.

3.2.2. EV Constraints

In Section 2.1.1, the fundamental operational constraints of EVs, including the SOC evolution equation, SOC limits, and charging or discharging exclusivity, have been introduced. In this section, two additional constraints are formulated to address the specific requirements of the joint scheduling problem: (i) the mobility demand constraint, which ensures sufficient SOC for travel at the departure time, and (ii) the coordination power allocation constraint with 5G BSs, which guarantees that EVs can effectively participate in supporting 5G BSs operation while respecting grid stability.

To ensure that the mobility of EV users is not compromised, the SOC at the departure time must be no less than the minimum required level for the planned trip.

$$SO{C}_{e,T_e^{\mathrm{dep}}}\ge SO{C}_e^{\mathrm{req}},\hspace{1em}\forall e\in \mathcal{E}$$

(33)

Here, $SO{C}_{e,T_e^{\mathrm{dep}}}$ is the SOC of EV e at its departure time $T_e^{\mathrm{dep}}$; $SO{C}_e^{\mathrm{req}}$ is the minimum SOC required for the planned trip of EV e.

When EVs are scheduled to support 5G BSs, their discharging power is allocated based on a priority mechanism. EVs first meet the 5G BS’s energy demand within their operational limits, and any remaining discharging capability can be used for other grid-support purposes.

$$P_{e,t}^{\mathrm{dis}}\ge {\beta }_{e,t}{P}_{n,t}^{5\mathrm{G},\mathrm{req}},\hspace{1em}\forall e\in {\mathcal{E}}_n$$

(34)

Here, $P_{e,t}^{\mathrm{dis}}$ is the discharging power of EV e at time t; $P_{n,t}^{5\mathrm{G},\mathrm{req}}$ is the power demand of the 5G BS located at node n at time t; ${\mathcal{E}}_n$ is the set of EVs connected to node n; ${\beta }_{e,t}$ is a binary variable indicating whether EV e is actively supporting the 5G BS at time t.

3.2.3. Fifth-Generation BS Constraints

In Section 2.2.2, the basic operational constraints of 5G BSs, including their power demand characteristics and interaction with EVs, have been described. In this section, additional coordination constraints are formulated to reflect the spatial coordination, temporal coordination, and energy storage priority rules between 5G BSs and EVs, which aim to ensure secure and reliable operation of the distribution network while maximizing resource utilization.

To reduce distribution network losses and avoid overloading local feeders, EVs are prioritized to support 5G BSs located at the same or adjacent nodes.

$${\beta }_{e,t}\le {\delta }_{e,n},\hspace{1em}\forall e\in {\mathcal{E}}_n$$

(35)

Here, ${\delta }_{e,n}$ is a binary parameter equal to 1 if EV e is physically located at node n or directly connected nodes, and 0 otherwise. This ensures spatial proximity between the EV and the supported 5G BS.

To ensure stable service, EVs providing power to 5G BSs must maintain continuous support over a predefined minimum time window once the service starts.

$${\beta }_{e,t}-{\beta }_{e,t-1}\le {\gamma }_{e,t}$$

(36)

Here, ${\gamma }_{e,t}$ is a binary parameter that enforces the minimum consecutive service duration requirement. This prevents frequent switching that could disrupt both EV battery operation and 5G service stability.

When both EVs and other storage devices are available for supporting 5G BSs, EV discharging is scheduled only after fixed storage resources are fully utilized, in order to preserve EV SOC for user mobility needs.

$$P_{e,t}^{5\mathrm{G},\sup }\le {\eta }_t\left(P_{n,t}^{5\mathrm{G},\mathrm{req}}-P_{n,t}^{5\mathrm{G},\mathrm{stor}}\right),\hspace{1em}\forall e\in {\mathcal{E}}_n$$

(37)

Here, $P_{e,t}^{5\mathrm{G},\sup }$ is the actual power supplied by EV e to the 5G BS at time ttt; $P_{n,t}^{5\mathrm{G},\mathrm{stor}}$ is the power supplied from fixed storage devices at node n at time t; ${\eta }_t$ is a binary coordination factor that allows EV participation only when the remaining demand is positive.

3.2.4. Coordination Constraints Between 5G BSs and EVs

In this section, additional coordination constraints are formulated to explicitly link the operation of both resources in the optimization model. These constraints aim to guarantee that the joint operation respects the technical limits of each resource, maintains distribution network stability, and ensures service continuity for both 5G communication and EV user mobility.

To ensure that the total power supplied by EVs matches the deficit of 5G BSs after local generation and fixed storage are considered, a balance equation is enforced:

$${\displaystyle \sum _{e\in {\mathcal{E}}_n}{P}_{e,t}^{5\mathrm{G},\sup }}=P_{n,t}^{5\mathrm{G},\mathrm{req}}-P_{n,t}^{5\mathrm{G},\mathrm{gen}}-P_{n,t}^{5\mathrm{G},\mathrm{stor}}$$

(38)

Here, $P_{n,t}^{5\mathrm{G},\mathrm{gen}}$ is the generator output. This ensures supply-demand matching in the coordination process.

To avoid frequent mode switching that may reduce EV battery life and impact 5G stability, EVs are restricted from charging and discharging within the same time step:

$$u_{e,t}^{\mathrm{ch}}+u_{e,t}^{\mathrm{dis}}\le 1$$

(39)

Here, $u_{e,t}^{\mathrm{ch}}$ and $u_{e,t}^{\mathrm{dis}}$ are binary variables indicating whether EV e is charging or discharging at time t, respectively. This guarantees a single operating mode at any time step.

To maintain the safe and stable operation of the distribution network, the total coordinated power exchange between EVs and 5G BSs at any node must not exceed the allowable network margin:

$$-P_n^{\mathrm{margin}}\le {\displaystyle \sum _e{P}_{e,t}^{5\mathrm{G},\sup }}-{\displaystyle \sum _e{P}_{e,t}^{\mathrm{EV},\mathrm{ch}}}\le P_n^{\mathrm{margin}}$$

(40)

Here, $P_n^{\mathrm{margin}}$ is the maximum allowable net power change at node n. This constraint prevents sudden power fluctuations that could threaten network stability.

To capture the operational coupling between BSs and EVs, let $P_{e,b,t}^{\mathrm{EV-BS}}$ denote the power supplied from EV e to BS b at time t, and $P_{b,e,t}^{\mathrm{BS}-\mathrm{EV}}$ denote the charging power delivered from BS b to EV e. The following constraints describe their mutual operation:

$$0\le P_{e,b,t}^{\mathrm{EV-BS}}\le a_{e,b,t}\cdot P_e^{\mathrm{dis},\max }$$

(41)

$$0\le P_{b,e,t}^{\mathrm{BS}-\mathrm{EV}}\le a_{e,b,t}\cdot P_e^{\mathrm{ch},\max }$$

(42)

where $a_{e,b,t}$ s a binary variable indicating whether EV e is physically connected to BS b at time t. These constraints ensure that power transfer is only possible when a physical connection exists.

The spatial coordination rule ensures that an EV can only interact with the BS to which it is currently connected. This is enforced by

$${\displaystyle \sum _b{a}_{e,b,t}}\le 1$$

(43)

which prevents simultaneous interactions with multiple BSs. Temporal coordination is achieved by synchronizing EV discharge periods with BS peak demand periods. Let $P_{b,t}^{\mathrm{BS}}$ represent the total power demand of BS b time t and $P_b^{\mathrm{BS},\mathrm{thr}}$ be a threshold value for peak demand identification. The following constraint enforces that EV to BS power transfer is activated only when the BS demand exceeds the threshold:

$$P_{e,b,t}^{\mathrm{EV}-\mathrm{BS}}\le \mathrm{M}\cdot \mathbb{I}(P_{b,t}^{\mathrm{BS}}>P_b^{\mathrm{BS},\mathrm{thr}})$$

(44)

where M is a sufficiently large constant and $\mathbb{I}(·)$ is an indicator function.

The storage priority rule governs the allocation of available EV battery capacity between mobility needs and BS support. Let ${\mathrm{SOC}}_e^{\mathrm{mob}}$ denote the SOC required to meet the mobility demand of EV e. The priority rule ensures that discharging to a BS is only allowed when the remaining SOC exceeds the mobility requirement:

$${\mathrm{SOC}}_{e,t}-{\mathrm{SOC}}_e^{\mathrm{mob}}\ge {\displaystyle \frac{P_{e,b,t}^{\mathrm{EV}\_\mathrm{to}\_\mathrm{BS}}\Delta t}{E_e^{\mathrm{cap}}}}$$

(45)

Through this set of spatial, temporal, and storage priority coordination constraints, the interaction between 5G BSs and electric vehicles is optimized to achieve both reliable communication service and efficient energy utilization in the distribution network.

To sum up, the complete mathematical model is as follows:

• Objective function: (26)
• Constraints: (3)–(25), (27)–(45)

The framework of proposed method is shown in Figure 2.

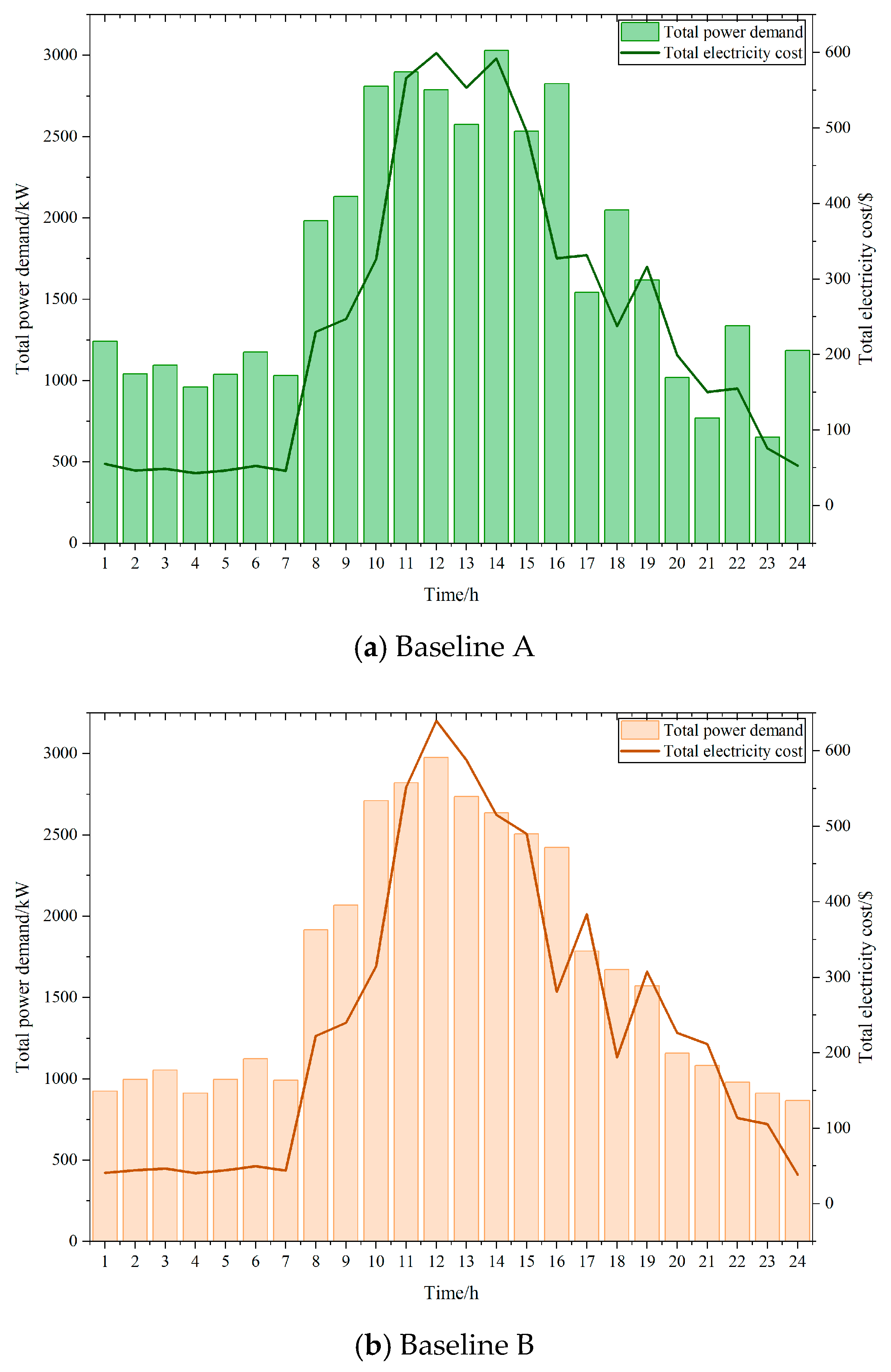
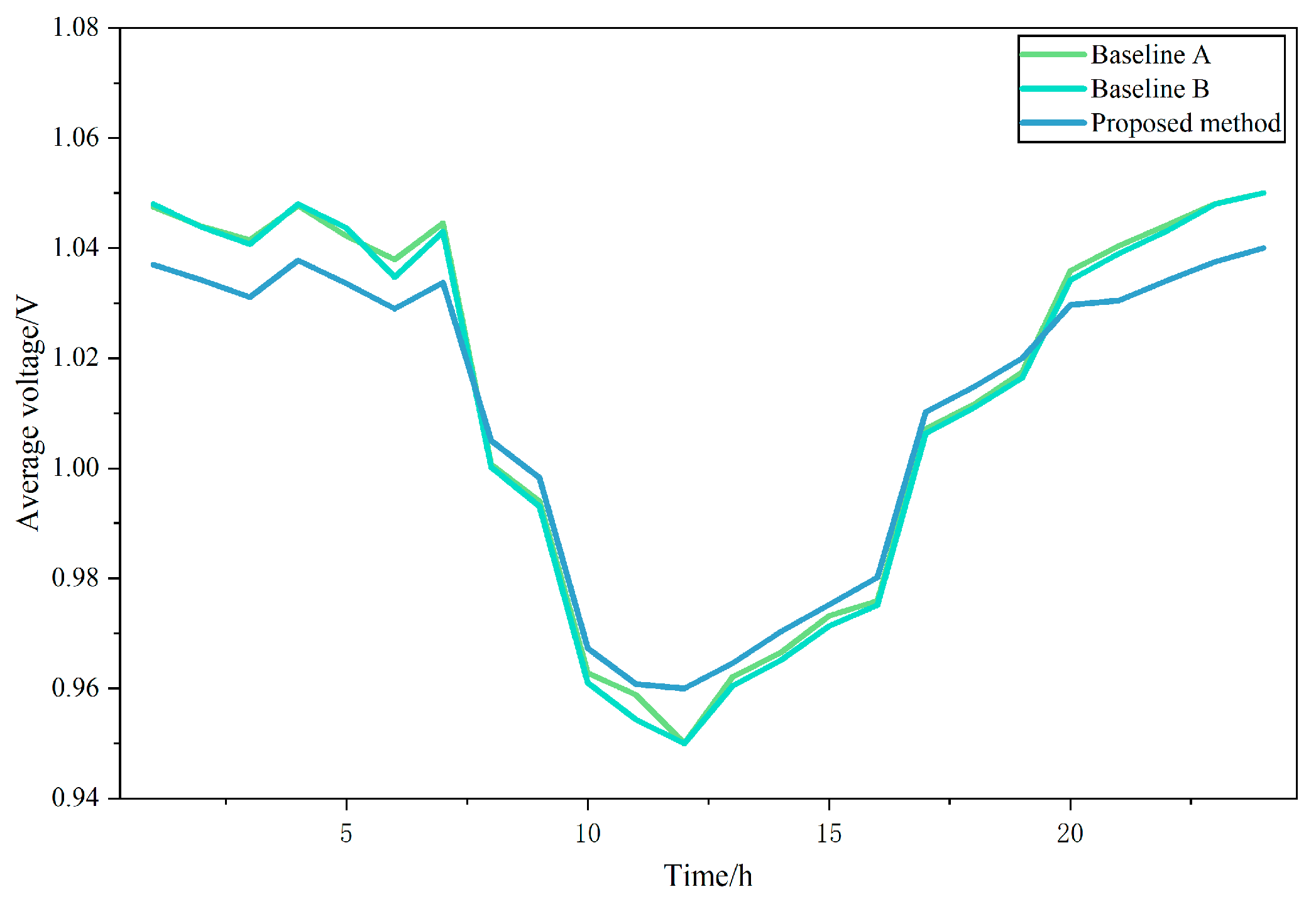
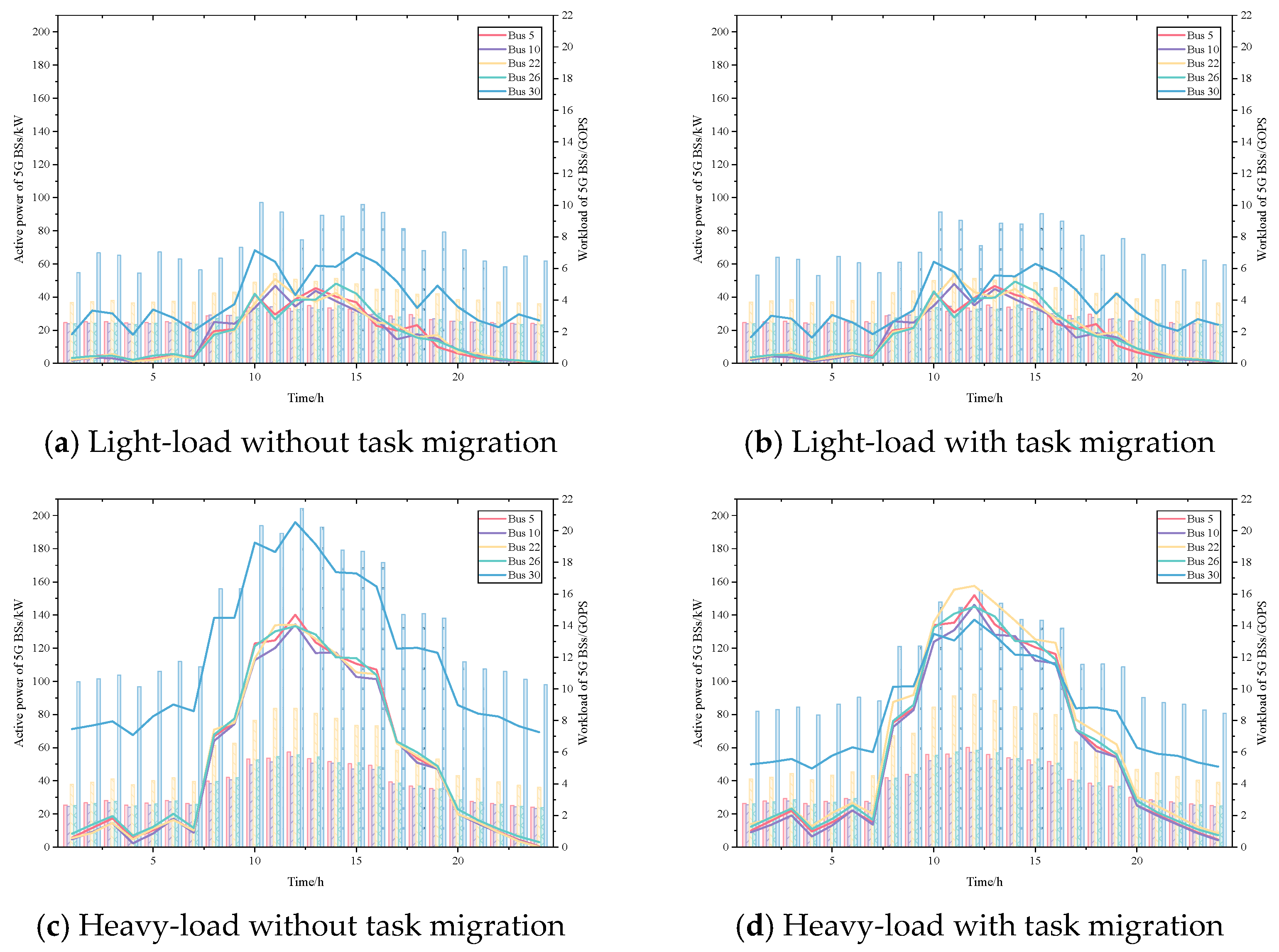
4. Case Study

To validate the effectiveness of the proposed method, numerical simulations are carried out on the improved IEEE 33-bus distribution network. The test system is modified to incorporate the integration of 5G BSs and EVs, thereby enabling the evaluation of the proposed coordinated restoration strategy under earthquake-induced disturbances.

All simulations are implemented in the MATLAB R2023b platform, with YALMIP employed as the modeling framework and GUROBI 12.0.1 as the optimization solver. The computations are executed on a workstation equipped with an Intel Core i7-12700 processor (Intel Corporation, Santa Clara, CA, USA), 32 GB of RAM, and the Windows 11 operating system. This setup ensures both computational efficiency and reproducibility of the numerical experiments.

The test system shown in Figure 3 is equipped with multiple distributed resources in order to reflect a practical scenario that integrates both 5G BSs and EVs. Specifically, two distributed generators (DGs) are installed at buses 4 and 23, while two EV charging stations are located at buses 12 and 25. In addition, the network includes five 5G BSs, which are deployed at buses 5, 10, 22, 26, and 30. The detailed configuration parameters of the distributed generators are listed in

Table A1. The parameters of distributed generators.

DG No.	Location	Pmax (kW)	Qmax (kVar)
1	Bus 4	200	120
2	Bus 23	250	150

, and the parameters of the 5G BSs are presented in

Table A2. The parameters of 5G base stations.

5G BS No.	Location	Pidle (kW)	Ppeak (kW)	Emax (kWh)
1	Bus 5	24	58	20
2	Bus 10	23.4	56.5	20
3	Bus 22	36	87	20
4	Bus 26	23	58	20
5	Bus 30	40	200	20

. The load data of each bus are summarized in

Table A3. The parameters of loads in IEEE-33 system.

Bus No.	P (kW)	Q (kVar)
1	0	0
2	100	60
3	90	40
4	120	80
5	60	30
6	60	20
7	200	100
8	200	100
9	60	20
10	60	20
11	45	30
12	60	35
13	60	35
14	120	80
15	60	10
16	60	20
17	60	20
18	90	40
19	90	40
20	90	40
21	90	40
22	90	40
23	90	50
24	420	200
25	420	200
26	60	25
27	60	25
28	60	20
29	120	70
30	200	600
31	150	70
32	210	100
33	60	40

, and parameters of branches are shown in

Table A4. The parameters of branches in IEEE-33 system.

Branch No.	from	to	R (Ω)	X (Ω)
1	1	2	0.0922	0.0470
2	2	3	0.4930	0.2511
3	3	4	0.3660	0.1864
4	4	5	0.3811	0.1941
5	5	6	0.8190	0.7070
6	6	7	0.1872	0.6188
7	7	8	0.7114	0.2351
8	8	9	1.0300	0.7400
9	9	10	1.0440	0.7400
10	10	11	0.1966	0.0650
11	11	12	0.3744	0.1298
12	12	13	1.4680	1.1550
13	13	14	0.5416	0.7129
14	14	15	0.5910	0.5260
15	15	16	0.7463	0.5450
16	16	17	1.2890	1.7210
17	17	18	0.7320	0.5740
18	2	19	0.1640	0.1565
19	19	20	1.5042	1.3554
20	20	21	0.4095	0.4784
21	21	22	0.7089	0.9373
22	3	23	0.4512	0.3083
23	23	24	0.8980	0.7091
24	24	25	0.8960	0.7011
25	6	26	0.2030	0.1034
26	26	27	0.2842	0.1447
27	27	28	1.0590	0.9337
28	28	29	0.8042	0.7006
29	29	30	0.5075	0.2585
30	30	31	0.9744	0.9630
31	31	32	0.3105	0.3619
32	32	33	0.3410	0.5302
33	8	21	2.0000	2.0000
34	9	15	2.0000	2.0000
35	12	22	2.0000	2.0000
36	18	33	0.5000	0.5000
37	25	29	0.5000	0.5000

. The time-of-use electricity prices are provided in

Table 1. The time-of-use electricity prices.

Time Period (h)		Electricity Price ($/kWh)
Critical Peak	11:00–13:00 16:00–17:00	0.2149
Peak	10:00–11:00 13:00–15:00 18:00–21:00	0.1954
Level	7:00–10:00 15:00–16:00 17:00–18:00 21:00–23:00	0.1159
Valley	23:00–7:00	0.04441

, and the regulation period T = 24h.

To demonstrate the advantages of the proposed method, two baseline strategies are considered for comparison.

• Baseline A: Without task migration strategy but considering 5G-EV interaction
• Baseline B: With task migration strategy but without 5G-EV interaction
• Proposed Method: With task migration and 5G-EV interaction

In Baseline A, the cooperation between 5G BSs and EVs is taken into account, enabling bidirectional energy exchange and temporal-spatial coordination. However, task migration among 5G BSs is not applied. This configuration highlights the impact of interaction between 5G infrastructure and EVs, while disregarding the potential benefits of computational workload flexibility. And in Baseline B, task migration among 5G BSs is enabled, which allows flexible reallocation of computational workloads to minimize line losses and balance power supply. Nevertheless, the interaction between 5G BSs and EVs is not considered, meaning that EV charging/discharging operations are independent of 5G BS energy demand. This setup isolates the effect of task migration from cross-domain coordination. The proposed method integrates both task migration and the interaction between 5G BSs and EVs. Computational workloads can be flexibly migrated among BSs, while EVs provide charging/discharging flexibility under mobility and user demand constraints. By jointly optimizing task migration, EV charging/discharging, and BS energy allocation, the proposed method achieves improved system efficiency, reduced line losses, and enhanced supply-demand balance compared with the baseline strategies. Solving the optimization models under the three strategies, the total power demand and corresponding electricity cost are summarized in

Table 2. Comparison of total power demand and cost under three strategies.

Strategy	Total Power Demand	Total Electricity Cost
Baseline A	41,328.8 kWh	5790.19
Baseline B	39,825.0 kWh	5584.40
Proposed Method	39,129.4 kWh	5489.78

.

Compared with Baseline A, the Proposed Method achieves a reduction of 2199.4 kWh in purchased energy. Relative to Baseline B, the proposed strategy still reduces 695.6 kWh of purchased energy, demonstrating its superior performance. For Baseline A, since computation task migration is not considered, the workloads of several 5G BSs located at nodes 5, 10, and 22 remain highly concentrated. This concentration induces significant local power demands, resulting in greater reliance on grid-supplied power. Although EVs are involved in the system operation, the absence of coordination with 5G computation workloads limits their ability to effectively alleviate demand peaks. As a result, the purchased energy reaches 41,328.8 kWh, leading to a purchasing cost of $5790.19. Furthermore, the unbalanced power distribution causes higher total network losses of 2412.5 kWh, maximum feeder loadings up to 96.3%, reflecting degraded power quality and operational reliability. In Baseline B, task migration is enabled, which effectively balances computational workloads across BSs, thereby reducing local power demand peaks and improving power flow distribution. Consequently, the purchased energy decreases to 39,825.0 kWh, resulting in a lower purchasing cost of $5584.40. Network losses are also reduced by approximately 12.0% compared with Baseline A, while the maximum feeder loading drops to 91.5%. However, since EVs are not actively utilized to support local power balancing, the system still heavily depends on grid-supplied energy during high-demand periods, especially at nodes with large computational workloads. The proposed method integrates both EV flexibility and task migration into a unified optimization framework, achieving superior performance across all evaluated metrics. By coordinating EV charging and discharging schedules with BS power demand, the proposed method effectively mitigates local demand peaks and exploits distributed energy resources to reduce grid dependency. As a result, the purchased energy is minimized to 39,129.4 kWh, corresponding to the lowest purchasing cost of $5489.78, which represents cost reductions of 5.2% and 1.7% compared with Baseline A and Baseline B, respectively. Additionally, the coordinated optimization achieves the lowest total network losses of 1895.2 kWh, a significant improvement of 21.4% compared with Baseline A and 10.8% compared with Baseline B. The maximum feeder loading is reduced to 84.7%, ensuring better power quality and operational stability. The curve of 24 h power demand and cost under three strategies are shown in Figure 4.

As shown in

Table 3. Computational complexity of proposed method.

Strategy	Binary Variables	Continuous Variables	Total Constraints	MIP Gap Settings	Solution Time
Baseline A	3840	6240	8160	1 × 10−4	309s
Baseline B	4010	8160	10,080	1 × 10−4	533s
Proposed Method	4180	9120	11,040	1 × 10−4	652s

, the proposed method scenario results in 4800 binary variables, 9120 continuous variables, and 11,040 constraints for the reported instance. Reported solution times and precise MIP gaps are 652 s and 1 × 10⁻⁴.

The hourly average voltages under Baseline A, Baseline B, and the Proposed Method are presented in Figure 5. Overall, the Proposed Method maintains a more stable and higher average voltage across the 24 h period compared with the two baseline strategies, indicating improved voltage regulation and system reliability.

For Baseline A, the average voltage fluctuates significantly over the day, ranging from 0.95 p.u. during low-voltage periods to 1.05 p.u. during peak voltage periods. The pronounced dips in the early and late hours indicate that some parts of the network experience undervoltage, likely due to concentrated loads from uncoordinated 5G BSs and EV charging patterns. The higher voltages observed during midday reflect localized overvoltage, which can be caused by uneven distribution of generation from distributed energy resources. Baseline B shows moderate improvement in average voltage stability. The inclusion of task migration allows computational workloads to be redistributed across 5G BSs, reducing peak demand in certain areas and slightly raising the lower-voltage periods. The average voltage fluctuates between approximately 0.961–1.05 p.u., indicating a more balanced network operation compared with Baseline A. However, voltage variations are still present, suggesting that task migration alone cannot fully mitigate voltage dips and peaks without considering EV coordination. The Proposed Method provides the most uniform and controlled voltage profile. The average voltage remains above 0.967 p.u. even during the lowest-voltage hours and does not exceed 1.04 p.u. during peak periods. This stability is attributed to the coordinated interaction between 5G BSs and EVs, which not only balances computational load but also leverages EV charging and discharging flexibility to support the network. As a result, voltage fluctuations are minimized, maintaining all hourly averages comfortably within the standard operational range of 0.95~1.05 p.u., and ensuring reliable operation throughout the day.

Based on the parameters of the 5G BSs, the power-performance coefficients ${\alpha }_i$ and ${\beta }_i$ for each station were first calculated, and the specific values are listed in

Table 4. Coefficient of workload and power for 5G BSs.

5G BS No.	αi	βi
Bus 5	2.27 W/GOPS	24 W
Bus 10	2.21 W/GOPS	23.4 W
Bus 22	3.40 W/GOPS	36 W
Bus 26	2.33 W/GOPS	23 W
Bus 30	8.00 W/GOPS	40 W

. Using these coefficients, the power data of each BS can be converted into the corresponding computational workload, providing a basis for task migration analysis. The results of the task migration are shown in Figure 6, where panel (a) depicts the 5G BS power and workload without considering the task migration strategy. It can be observed that the BS located at Bus 30 exhibits a relatively high overall load, with a peak computational workload of 19.45 GOPS and a corresponding power of approximately 195.6 kW. Such a high load may not only strain the computational resources of the BS but also increase local line losses in the distribution network, slow down task processing, and elevate energy consumption. By applying the task migration method proposed in this study, the pressure on high-load BSs can be effectively alleviated. Panel (b) in Figure 6 illustrates the results after implementing the task migration strategy. Under the constraint that each BS does not exceed its maximum allowable workload, the Bus 30 BS distributes part of its workload to neighboring stations, reducing its peak computational workload and power to 16.53 GOPS and 172.27 kW, respectively. This strategy effectively lowers the system peak power, decreases distribution network losses, enhances energy utilization efficiency, and ensures that computational tasks are processed promptly while maintaining communication service quality, thereby significantly improving the stability and reliability of the overall system.

The results demonstrate that the proposed strategy achieves a more balanced distribution of computational workloads and power flows, enabling the system to significantly reduce grid power purchases, minimize network losses, and maintain stable voltage profiles. Through the synergistic coordination of 5G BSs and EVs, the proposed method outperforms both baseline strategies in terms of economic efficiency, system reliability, and operational quality.

To further evaluate the effectiveness of the proposed scheduling model, a sensitivity analysis was carried out by increasing the EV penetration level, which provides more flexible and dispatchable resources. Two test scenarios were considered: A light-load case and a heavy-load case. The simulation results are summarized in

Table 5. Comparison of total power demand and cost under light-load and heavy-load.

Scenarios	Total Power Demand	Total Electricity Cost
Light-load	16,677.6 kWh	2373.84
Heavy-load	49,515.3 kWh	6919.74

, where the total purchased electricity and corresponding costs are presented. In the light-load scenario, the system purchases 16,677.6 kWh with a total cost of $2373.84. In contrast, under the heavy-load scenario, the purchased electricity reaches 49,515.3 kWh with a total cost of $6919.74.

The 24 h workloads and power consumption of 5G BSs are illustrated in Figure 7. These results demonstrate that, under different loading conditions, the proposed method effectively enables task migration and coordinated scheduling between EVs and 5G BSs, thereby reducing the purchased electricity from the grid and lowering the overall operational cost.

5. Discussion

It is worth noting that the proposed mobility model of EVs assumes deterministic travel plans and constant grid connection, which simplifies the modeling process but neglects the off-grid state during driving and the randomness of user behaviors. In reality, EV travel behaviors are uncertain, and their availability to provide flexible resources may vary. In this study, the deterministic MILP method was adopted mainly to balance modeling accuracy and computational efficiency, with the objective of capturing the key characteristics of 5G BS and EV coordinated scheduling in a tractable manner. We fully agree that considering stochastic mobility models and distributed scheduling approaches is very meaningful, as highlighted by prior studies [36,37,38]. Inspired by these works, future research will extend the current deterministic model by incorporating stochastic features of EV travel, such as probabilistic departure/arrival times or uncertainty-aware optimization, to better capture the robustness of the scheduling results. The related discussion has been added to this section, and we sincerely appreciate the reviewer’s insightful comments.

Although the proposed deterministic MILP method demonstrates good performance in the presented case studies, the scalability of the optimization model under large-scale scenarios remains a challenge. As the number of 5G BSs and EVs increases, the problem size grows rapidly, which may lead to high computational burden and limit real-time applicability. In future work, distributed optimization methods and decomposition techniques will be considered to improve computational efficiency. Moreover, the integration with distribution network operators will be further explored, so that the proposed scheduling strategy can be seamlessly embedded into real-world operation frameworks and coordinated with grid-level constraints.

6. Conclusions

In this paper, a comprehensive framework for optimizing the interaction between 5G BSs and EVs in a distribution network under high computational and energy demands is proposed. The presented approach jointly considers the computational workload management of 5G BSs, energy storage dispatch, and EV charging behaviors to achieve a coordinated and efficient operation. First, the relationship between the computational workload and energy consumption of 5G BSs was characterized through the estimation of coefficients α_i and β_i, as shown in Table 4. Based on these parameters, a task migration strategy was proposed to dynamically reallocate workloads among neighboring 5G BSs. Simulation results indicate that the proposed strategy effectively alleviates the pressure on heavily loaded BSs. Furthermore, the interaction between EVs and the energy storage systems embedded in 5G BSs was integrated into the optimization framework. By leveraging the bidirectional energy flow between EV batteries and the BSs’ storage systems, the proposed strategy enables peak-load shaving and enhances the overall resilience of the distribution network. This coordination not only improves the power balance within the grid but also supports the quality of service for 5G communications during periods of high demand. The results demonstrate that the proposed framework achieves significant improvements in energy efficiency, computational resource utilization, and grid stability compared to traditional independent optimization methods.

To highlight the scientific originality of this work, it should be emphasized that the proposed coordinated day-ahead scheduling framework is the first to systematically integrate 5G base station task migration, energy storage capabilities, and electric vehicle charging/discharging with mobility constraints into a unified optimization model. Unlike existing studies that treat EV scheduling or 5G energy management in isolation, this work establishes an integrated MISOCP model that captures the spatiotemporal interactions between EVs and 5G BSs within distribution network operations. This integration not only advances the state of the art in multi-resource coordination but also provides a novel methodological contribution by linking communication load dynamics, computation migration, and flexible demand response. Such a framework represents a meaningful step toward enhancing both the operational efficiency and reliability of future smart distribution networks.

In future research, several important directions will be further explored to enhance the applicability and robustness of the proposed model. First, cybersecurity and privacy issues should be carefully addressed, as secure data exchange between 5G base stations, EVs, and the distribution network is critical for reliable operation. Moreover, the interoperability between telecom infrastructures and power systems needs to be strengthened, ensuring seamless coordination and efficient information sharing across different domains.

In addition, practical implementation issues must be considered for the integration of the proposed model into current distribution network operation. Specifically, data acquisition from both 5G base stations and EVs requires reliable real-time monitoring and secure communication interfaces. The computational overhead associated with solving large-scale optimization problems should be mitigated by employing efficient decomposition algorithms or parallel computing techniques. Furthermore, the real-time feasibility of the scheduling model needs to be validated under actual operational conditions to ensure that scheduling decisions can be executed within acceptable time frames. Addressing these challenges will help bridge the gap between theoretical modeling and practical deployment, making the proposed framework more suitable for real-world applications.