Recent Advances in Sliding Mode Control Techniques for Permanent Magnet Synchronous Motor Drives

Abstract

As global industry enters the digital era, automation is becoming increasingly pervasive. Due to their superior efficiency and reliability, Permanent Magnet Synchronous Motors (PMSMs) are playing an increasingly prominent role in industrial applications. Sliding Mode Control (SMC) has emerged as a modern control strategy that is widely employed not only in PMSM drive systems, but also across broader power and industrial control domains. This technique effectively mitigates key challenges associated with PMSMs, such as nonlinear behavior and susceptibility to external disturbances, thereby enhancing the precision of speed and torque regulation. This paper provides a thorough review and evaluation of recent advancements in SMC as applied to PMSM control. It outlines the fundamentals of SMC, explores various SMC-based strategies, and introduces integrated approaches that combine SMC with optimization algorithms. Furthermore, it compares these methods, identifying their respective strengths and limitations. This paper concludes by discussing current trends and potential future developments in the application of SMC for PMSM systems.

1. Introduction

The Fourth Industrial Revolution (Industry 4.0) [1] is characterized by the integration of advanced automation, digitalization, and intelligent control systems, fundamentally reshaping operational processes across manufacturing, transportation, and renewable energy sectors. Modern industrial systems increasingly deploy automated production lines, CNC machines, and robotic workcells, enabled by real-time data acquisition, Artificial Intelligence (AI)-based sensor networks, and IoT-enabled control platforms. Within this technological paradigm, the Permanent Magnet Synchronous Motor (PMSM) has emerged as a preferred solution due to its high power density, superior energy efficiency, low torque ripple, and precision control capabilities [2,3]. PMSMs are extensively implemented in applications requiring dynamic response and high performance, including Electric Vehicles (EVs) [4], industrial automation [5], and robotics [6]. The deployment of PMSMs supports both energy-efficient system architectures and sustainable development goals, thereby contributing significantly to the ongoing green transition and the digital transformation of the global industrial landscape. However, PMSMs exhibit certain limitations, such as nonlinear characteristics [7], susceptibility to external disturbances [8], and parameter variations [9]. Thus, fast dynamic response and disturbance rejection demand advanced control techniques.

In the speed control system of PMSM, control methods primarily include two categories: traditional control methods featuring a speed control loop integrated with independent current control, and advanced control methods based on AI networks with complex architectures [10]. Among these, traditional control methods remain widely preferred due to their algorithmic simplicity, ease of research, straightforward deployment, and reliable response to control requirements under normal operating conditions. Currently, numerous control strategies are being developed and refined, such as Model Predictive Control (MPC) [9,11,12,13,14], fuzzy control [15,16,17,18,19], adaptive control [20,21,22,23], Active Disturbance Rejection Control (ADRC) [24,25,26,27], fault-tolerant control [28,29,30,31], and Sliding Mode Control (SMC) [32,33,34,35,36,37], etc. These nonlinear control techniques possess the capability to enhance system performance and strengthen the anti-disturbance capability of PMSM drive systems to varying degrees. Notably, SMC stands out as a prominent control technique and has undergone extensive research in the field of PMSM control, owing to its robust anti-disturbance capability and high stability in the presence of parameter variations.

SMC is a widely used technique for managing complex control challenges, particularly in nonlinear systems. Originating in the 1950s as part of Variable Structure Control (VSC) in the Soviet Union [38], SMC has attracted significant attention within the control engineering community. It is applicable to a broad range of systems, including nonlinear, Multi-Input Multi-Output (MIMO) [39], discrete-time [40], large-scale [41], infinite-dimensional [42], and stochastic systems [43]. The primary advantage of SMC is its robustness to parameter uncertainties and external disturbances once the system operates in sliding mode. VSC achieves this by employing a high-frequency switching control law that drives the system state trajectory onto a predefined sliding surface in the state space and maintains it there. This sliding surface defines a reduced-order system with dynamics that are less sensitive to modeling errors and disturbances. The SMC design process involves two key steps [44]: first, designing the sliding surface to ensure the reduced system meets desired dynamic performance; second, synthesizing the switching control law to drive the system state to and keep it on this surface. Both steps rely on generalized Lyapunov theory, ensuring closed-loop system stability during control.

SMC is widely applied in robotic systems [45,46,47], power converters [48,49,50,51], aerospace control [52,53], wind energy [54,55,56], industrial processes [57,58], EVs [59,60,61], and electric motor drives [62,63]. In robotic systems [45], SMC ensures robust performance under parameter uncertainties and external disturbances (for example, friction, collision forces), maintaining stability despite unmodeled dynamics. When combined with techniques such as fractional-order calculus or disturbance estimation, it effectively mitigates chattering and improves trajectory tracking, making it well-suited for rigid manipulators and complex tasks. In active power filters, SMC demonstrates strong robustness against parameter uncertainties (for example, inductance/capacitance variations due to temperature) and external disturbances, ensuring stable compensation current tracking and harmonic suppression [51]. It provides fast dynamic response to load or voltage variations, while advanced variants reduce chattering and steady-state error without complex tuning. Additionally, SMC can integrate with neural networks to approximate lumped disturbances, enhancing anti-interference performance and meeting power quality standards. In wind power generation [55], SMC provides strong robustness against system uncertainties (for example, Permanent Magnet Synchronous Generator (PMSG) parameter variations) and external disturbances (for example, fluctuating wind speeds), ensuring stable operation. It enables precise tracking of the generator’s reference shaft speed for optimal power extraction, though traditional SMC may induce chattering that affects actuator performance. In EVs, SMC ensures robust lateral motion control by handling uncertainties such as tire cornering stiffness variations (from road friction changes) [59,61], input delays (from networked control), and external disturbances (for example, wind resistance). It maintains a stable sideslip angle and yaw rate tracking under challenging conditions like lane changes or low-adhesion roads. Advanced variants—such as Sliding Mode Predictive Control (SMPC) [59] with adaptive reaching laws or barrier function-based neural network [61] adaptive integral SMC—reduce actuator chattering (in-wheel motors, steering systems) and accelerate convergence. Integration with disturbance observers [59], delay estimators, and neural networks [61] enhances anti-interference capability and addresses modeling complexity in multi-axle EVs without extensive parameter tuning.

In electric motor control, SMC has been successfully implemented for various motor types, including Induction Motors (IMs) [64,65,66], Switched Reluctance Motors (SRM) [33,67,68], Brushless DC motors (BLDC) [69,70,71], PMSMs [35,72], and other specialized machines [73,74,75,76,77]. In IMs, including linear types for metro systems [66], SMC ensures robust speed, thrust, and flux tracking under parameter variations and load disturbances. Advanced variants of SMC [64,66], enhance dynamic response, improve efficiency by reducing Total Harmonic Distortion (THD), and support coordinated control via cascaded loops. Integrated with advanced Sliding Mode Observer (SMO), SMC also enables fault-tolerant operation during sensor failures with minimal performance loss [65]. In SRMs, SMC is effective for sensorless control and dynamic performance optimization, addressing nonlinear inductance and torque ripple. Advanced variants of SMC [67] suppress startup peaks, improve speed response, and reduce chattering using saturation functions and power-term-augmented reaching laws. When combined with SMOs based on inductance models [67], SMC enables accurate rotor position estimation and wide-range speed tracking, lowering maximum speed error and improving Torque Sharing Function (TSF) performance [68]—making it suitable for EV traction and industrial applications requiring robustness and precision.

Specifically, in PMSM control, SMC is utilized for both sensored and sensorless configurations, the latter often employing a SMO [78,79,80]. In addition, SMC is also applied in higher-order control systems, including Higher-Order SMC (HOSMC) [81,82,83], and Higher-Order SMO (HOSMO) [68,84]. This control approach effectively compensates for parameter variations and external disturbances, ensuring system stability and precision within complex nonlinear environments. Its robust ability to maintain desired state trajectories and adapt to dynamic changes makes SMC well-suited for high-accuracy and safety-critical applications. Though chattering is inherent in SMC, advanced control techniques can significantly reduce it.

This paper primarily investigates SMC strategies for PMSMs, along with advanced adaptive algorithms integrated with SMC to enhance system performance. It begins by introducing the fundamentals of PMSMs, including their modeling, operating principles, and structural configuration. Next, it outlines the key concepts of SMC, such as the reaching law, sliding surface design, and Lyapunov-based stability analysis. The key focus is on SMC design for PMSMs, covering approaches to reaching law formulation and sliding surface construction—both linear and terminal types. The discussion is further extended to HOSMC (including arbitrary-order and second-order forms), observer-based SMC, and intelligent SMC methods that incorporate Fuzzy Logic (FL), Neural Networks (NNs), and metaheuristic algorithms such as Genetic Algorithms (GA). Overall, this paper provides a comprehensive exploration of SMC applications in PMSM control, progressing from foundational concepts to advanced control techniques.

This review paper aims to examine current research trends in the application of SMC for PMSM systems. The key contributions of this paper are as follows:

(1)

A concise overview of PMSM dynamics and the fundamental principles of SMC;

(2)

A thorough review of SMC design, including Reaching Law methods, Sliding Surface design, Second-Order SMC, Arbitrary-Order SMC, as well as both classical and advanced control strategies;

(3)

An in-depth discussion of Observer-Integrated SMC and Intelligent SMC incorporating advanced control techniques;

(4)

An assessment of open challenges and identification of potential directions for future research.

The remainder of this paper is structured as follows. Section 2 introduces the structural configuration of the PMSM and analyzes its dynamic mathematical model. Section 3 provides a review of the fundamental principles of SMC. Section 4 presents the design methodologies for various SMC strategies. In Section 5, an observer-integrated SMC scheme is proposed to enhance disturbance rejection and system robustness. Section 6 explores intelligent SMC techniques, including approaches that incorporate adaptive and data-driven algorithms. Section 7 discusses simulation results and offers insights into potential directions for future research. Finally, Section 8 concludes this paper.

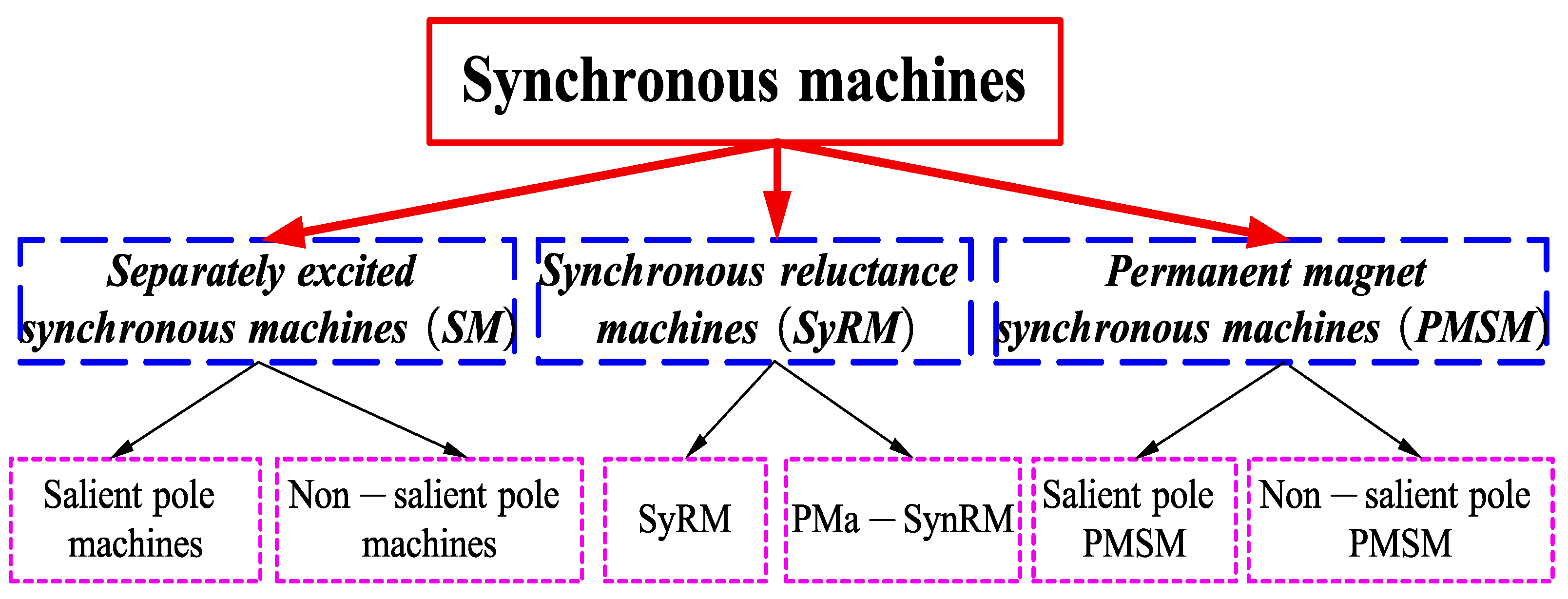
2. Permanent Magnet Synchronous Motor

2.1. Structural Configuration of PMSM

A synchronous motor is a type of Alternating Current (AC) machine in which the stator contains armature windings similar to those found in an induction motor, while the rotor is equipped with either Direct Current (DC)-excited field windings or Permanent Magnets (PMs), (Figure 1) [85]. A balanced three-phase supply applied to the stator generates a varying magnetic flux in the motor’s air gap, rotating at synchronous speed. The motor operates at a constant speed and maintains perfect synchronism, which depends on the supply frequency and the number of poles of the motor. This means that the rotor speed equals the speed of the rotating magnetic field produced by the AC stator (armature) windings. The DC excitation current, supplied either through field windings or PMs mounted on the rotor, produces a constant magnetic flux. The mechanical torque is generated from the interaction between the rotor’s magnetic flux and that of the stator. The rotor rotates at a fixed synchronous speed and is unaffected by changes in mechanical load. In a conventional synchronous machine, the armature system (stator) remains stationary while the excitation system (rotor) rotates. In the reverse configuration, for example in brushless synchronous exciters, the excitation system (stator) is stationary, and the armature windings are mounted on the rotor.

The stator comprises laminated electrical steel sheets with slots housing distributed three-phase windings that generate a rotating magnetic field. The stator windings can be designed as either concentrated or distributed coils; distributed windings, whether overlapping or non-overlapping, consume more copper but help reduce current harmonics. The rotor is manufactured with PMs, which are lighter in weight, more compact, and generate a fixed magnetic flux. A rotor equipped with PMs (Figure 2) is known as a PMSM. PMSMs can use either salient pole rotors (with embedded PMs) or non-salient pole rotors (with surface-mounted PMs) [86]. In the Surface PMSM (SPMSM) structure (Figure 2a), the magnetic flux is uniformly distributed across the air gap, whereas in the Interior PMSM (IPMSM) structure (Figure 2b), the flux is concentrated along the poles.

2.2. Mathematical Model of PMSM Dynamics

The dynamic control system of a PMSM driven by a Voltage Source Inverter (VSI) is analyzed [87]. As shown in Figure 3, the system employs a two-level VSI that utilizes Space Vector Pulse Width Modulation (SVPWM) to convert DC voltage from the battery into three-phase AC voltage by modulating sinusoidal waveforms.

Under ideal operating conditions, the two switching devices in each inverter leg operate in a complementary manner to ensure correct operation and prevent shoot-through faults. To facilitate the analysis of the motor’s electrical and mechanical behavior, the PMSM dynamic model is represented in the rotating d-q reference frame (Figure 4). The stator voltage, torque, and mechanical motion equations are as follows:

$$u_d=R_s{i}_d+L_d{\displaystyle \frac{\mathrm{d}{i}_d}{\mathrm{d}\mathrm{t}}}-{\omega }_e{L}_q{i}_q,$$

(1)

$$u_q=R_s{i}_q-L_q{\displaystyle \frac{\mathrm{d}{i}_q}{\mathrm{d}\mathrm{t}}}+{\omega }_e{L}_d{i}_d+{\omega }_e{\psi }_f,$$

(2)

$${\displaystyle \frac{\mathrm{d}{\omega }_m}{\mathrm{d}\mathrm{t}}}={\displaystyle \frac{1}{\mathrm{J}}}\left(T_e-B{\omega }_m-T_L\right),$$

(3)

$$T_e={\displaystyle \frac{3}{2}}p{i}_q\left[\left(L_q-L_d\right)i_d+{\psi }_f\right],$$

(4)

where u_d, u_q, i_d, and i_q denote the stator voltages and currents in the the d and q axes, respectively. L_d, L_q, and R_s represent the d-axis inductance, q-axis inductance, and stator resistance. ω_e and ω_m are the electrical and mechanical angular speeds, respectively, and ψ_f is the PM flux linkage, respectively; Furthermore, T_L and T_e are the load torque and electromagnetic torque, respectively. The parameters p, J, and B refer to the number of pole-pairs, the moment of inertia, and the viscous coefficient of the load.

3. Fundamentals of Sliding Mode Control

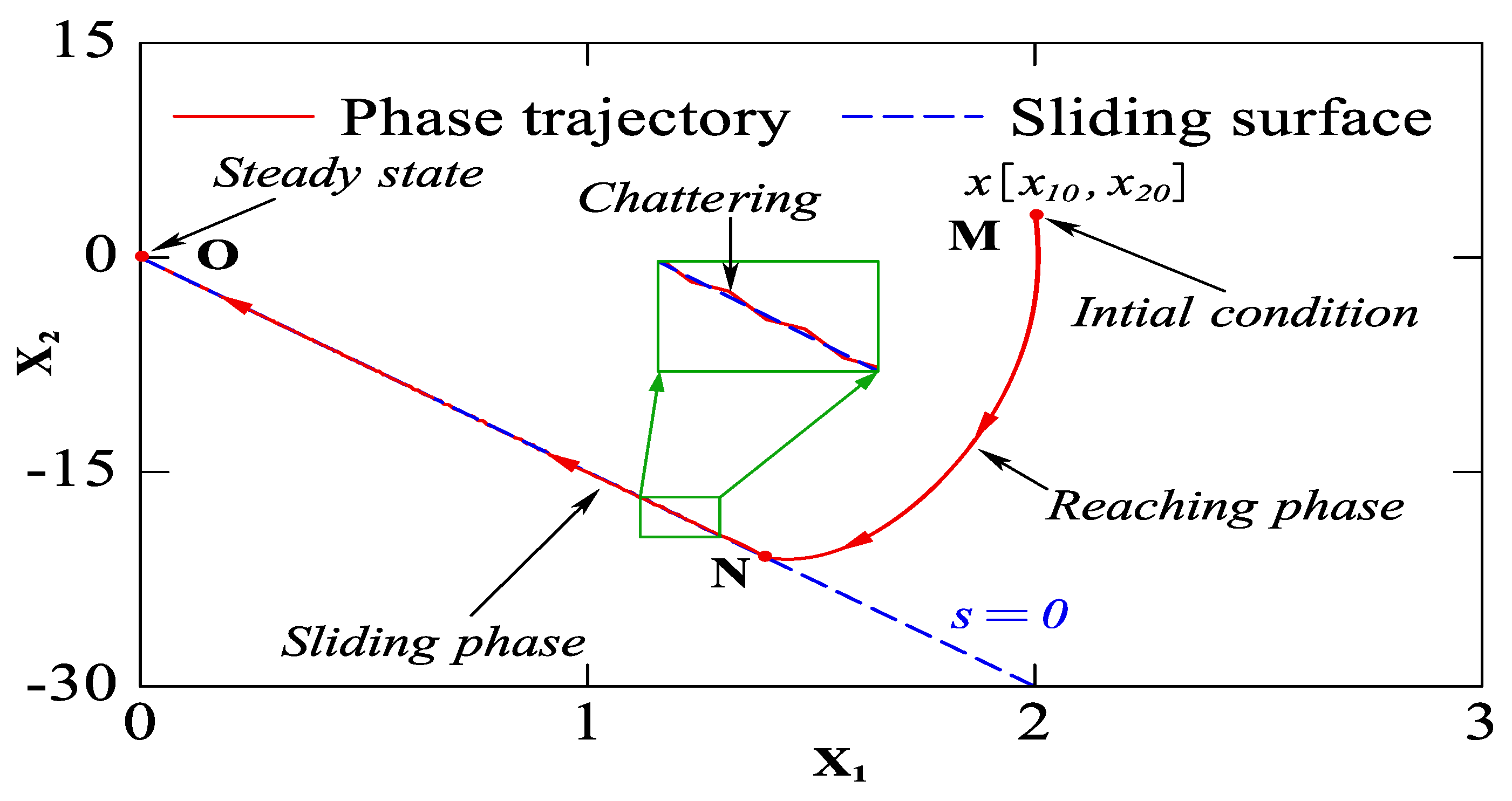
3.1. Operating Principles of SMC

In practical control applications, there are always discrepancies between the actual system and its mathematical model due to unknown disturbances, parameter variations, and unmodeled dynamics. Ensuring the desired system performance under such uncertainties poses a significant challenge in controller design. This prompted the development of robust control strategies, with SMC being a widely recognized and effective method.

Consider a nonlinear system with the motor angular position and angular velocity: $x_1=x, x_2={\dot{x}}_1$ described by the following system of equations [89]:

$$\left\{\begin{array}{cc}{\dot{x}}_1\left(t\right)=x_2\left(t\right)& x_1\left(0\right)=x_{10}\\ {\dot{x}}_2\left(t\right)=u\left(t\right)+f\left({x_1,x}_2,t\right)& x_2\left(0\right)=x_{20}\end{array}\right.,$$

(5)

where $x\left(t\right)\in R^m$ is the system state in an m-dimensional space, $u\left(t\right)\in R^m$ denotes input control in an n-dimensional space.

The variable s(x,t) is defined as the sliding variable, with the sliding surface defined as follows [90]:

$$s\left(x,t\right)=0,$$

(6)

And $u\left(t\right)$ is the discontinuous control action expressed as [91]:

$$u\left(t\right)=\left\{\begin{array}{cc}{u}^{+}\left(x,t\right)& if s\left(x,t\right)>0\\ u^{-}\left(x,t\right)& if s\left(x,t\right)<0\end{array}\right.,$$

(7)

If the control variable $u\left(t\right)$ satisfies the attractiveness condition $s\left(x,t\right)\dot{s}\left(x,t\right)<0$, the system is considered to be in sliding mode.

The behavior of a SMC system can be divided into two distinct phases: the reaching phase and the sliding phase [92], as depicted in Figure 5. The reaching law drives the system state toward the sliding surface, after which it converges to the origin along the surface. Typically, the sliding surface is defined by a linear convergence equation of a lower order than the original system. This design ensures that, after reaching the surface, the system state follows a trajectory governed by the sliding equation and exponentially converges to the origin. The motion during this phase is constrained by the sliding surface and becomes independent of the system’s internal dynamics.

During the reaching phase, the system may cross the sliding surface a limited number of times, but sliding mode behavior and robustness are not yet established. True sliding mode operation begins only after the system reaches the surface. From that point forward, system performance is determined solely by the properties of the sliding surface and becomes immune to external disturbances and model uncertainties—provided they meet certain matching conditions. Continuous switching control maintains the system state on the sliding surface, driving it to the origin—this mechanism underpins SMC’s robustness to parameter variations and external disturbances.

Lyapunov stability analysis is a widely used approach for evaluating the stability of SMC controllers [93,94], especially for proving and assessing stable convergence behavior. The most commonly used function [95,96,97,98] is as follows:

$$V\left(x,t\right)={\displaystyle \frac{1}{2}}{s}^2\left(t\right),$$

(8)

The reaching condition is met when the following criterion is satisfied:

$$\dot{V}\left(x,t\right)=s\left(t\right)\dot{s}\left(t\right)<0,$$

(9)

Equation (9) ensures finite-time reachability of the sliding surface.

In addition to Lyapunov-based stability analysis, nonlinear systems can also be evaluated using the input-to-state stability (ISS) criterion [99,100]. In this case, a function V(x) is used that satisfies the following condition:

$${\alpha }_1\left(‖s‖\right)\le V\left(s,u\right)\le {\alpha }_2\left(‖s‖\right),$$

(10)

If the derivative of the function V(x) satisfies the following condition Equation (11), then the sliding surface is reached in finite time with guaranteed stability.

$$V\left(s,u\right)\le {-\alpha }_3\left(‖s‖\right)+\gamma \left(‖u‖\right),$$

(11)

where u(t) represents a noise, disturbance, or input signal; α₁, α₂, and α₃ are functions that ensure positive definiteness and are monotonically increasing; and $\gamma \left(‖u‖\right)$ denotes the influence of the input on the derivative of the Lyapunov function.

ISS is a powerful tool for analyzing the stability of nonlinear systems subject to inputs or disturbances. Unlike the classical Lyapunov approach, ISS enables the evaluation of how external disturbances affect system states, making it highly suitable for modern control applications [101,102].

3.2. Current Research and Development Trends in SMC

Integrating advanced adaptive algorithms with SMC has significantly improved its performance, addressing limitations in convergence speed and relative order. These advancements have become integral components of SMC theory. Current research in SMC design primarily focuses on mitigating chattering, enabling self-adaptive control for uncertain systems, and improving the dynamic performance of closed-loop systems. To tackle these challenges, various improved methods and research directions in SMC have been proposed, as illustrated in Figure 6.

The methods presented in Figure 6 effectively illustrate their ability to suppress chattering and enhance the practical applicability of SMC in real-world systems.

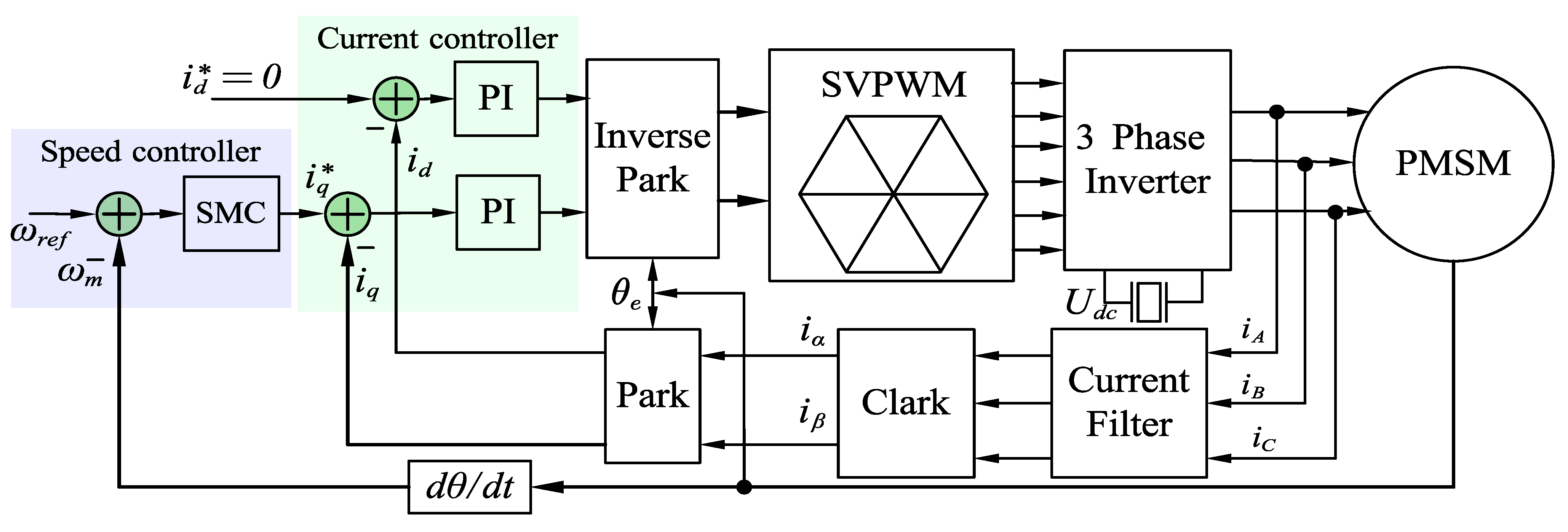
4. Sliding Mode Control Design

SMC is commonly applied in the speed loop of PMSM systems, as illustrated in Figure 7, to achieve high-performance and robust speed regulation. Within the speed loop, SMC utilizes a specially designed sliding surface along with a reaching law to drive the speed error toward the sliding surface, enabling rapid convergence to zero. By leveraging feedback, SMC enforces control over the speed error, thereby ensuring precise tracking and regulation of the PMSM’s rotational speed.

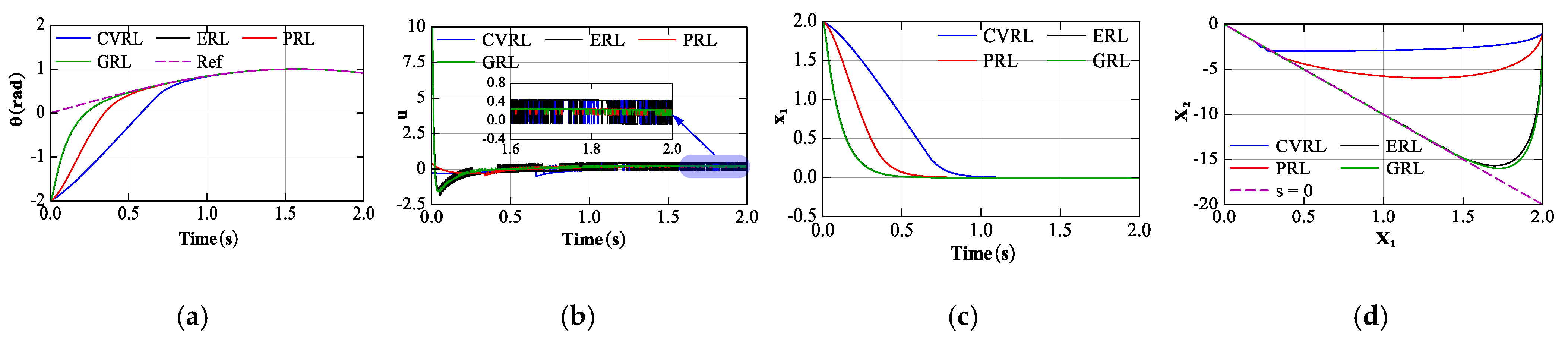
4.1. Reaching Law Approach

Four conventional Sliding Mode Reaching Laws (SMRLs) are described as follows [103]:

✓

Constant Velocity Reaching Law (CVRL):

$$\dot{s}=-k_1\mathrm{s}\mathrm{g}\mathrm{n}\left(s\right), k_1>0,$$

(12)

✓

Exponential Reaching Law (ERL):

$$\dot{s}=-k_1\mathrm{s}\mathrm{g}\mathrm{n}\left(s\right)-k_{2}s, k_1, k_2>0,$$

(13)

✓

Power Reaching Law (PRL):

$$\dot{s}=-k_1{\left|s\right|}^{\lambda }\mathrm{s}\mathrm{g}\mathrm{n}\left(s\right), k_1>0, 1>\lambda >0,$$

(14)

✓

General Reaching Law (GRL):

$$\dot{s}=-k_{1}s\mathrm{s}\mathrm{g}\mathrm{n}\left(s\right)-g\left(s,x\right), k_1>0,$$

(15)

In this system, the state reaches the sliding-mode surface via two types of reaching laws: the variable speed reaching law and the variable index reaching law. Both the ERL and the GRL incorporate components of each type. Specifically, k₁sgn(s) (ERL) and k₁ssgn(s) (GRL) represent the traditional variable speed reaching laws, while qs (ERL) and g(s,x) (GRL) correspond to the variable index reaching laws. In contrast, the CVRL and PRL include only the traditional variable speed reaching law components.

For comparing the four methods, the example model Equation (5) is implemented as follows:

$$\left\{\begin{array}{cc}{\dot{x}}_1\left(t\right)=x_2\left(t\right)& x_1\left(0\right)=x_{10}\\ {\dot{x}}_2\left(t\right)=f\left(x,t\right)+bu\left(t\right)+d\left(t\right)& x_2\left(0\right)=x_{20}\end{array}\right.,$$

(16)

where f(x,t) denotes the function related to position instructions, u(t) is the control input, and d(t) denotes the external disturbance.

The sliding surface is defined as follows:

$$s=he\left(t\right)+\dot{e}\left(t\right),$$

(17)

where h satisfies the Hurwitz condition, meaning h > 0.

Simulation tests are carried out in MATLAB 2019/Simulink to evaluate and compare four existing reaching laws. For the GRL, the basic function is defined as g(s,x) = k₂s. The system parameters are assigned as follows: $f\left(x\right)=-20\dot{x, b=100, d\left(t\right)}=5sin\left(\pi t\right), h=10,k_1=20,$ $k_2=100,$ and $\lambda =0.5$. The initial condition of the controlled system is set to $x\left(0\right)=\left[x_{10}\left(0\right),x_{20}\left(0\right)\right]=\left[-2, 2\right]$, with the reference trajectory defined as $x_d=sin\left(t\right)$.

Based on the results shown in Figure 8,

Table 1. The gains of the SMC controller and the disturbance observers for the simulation.

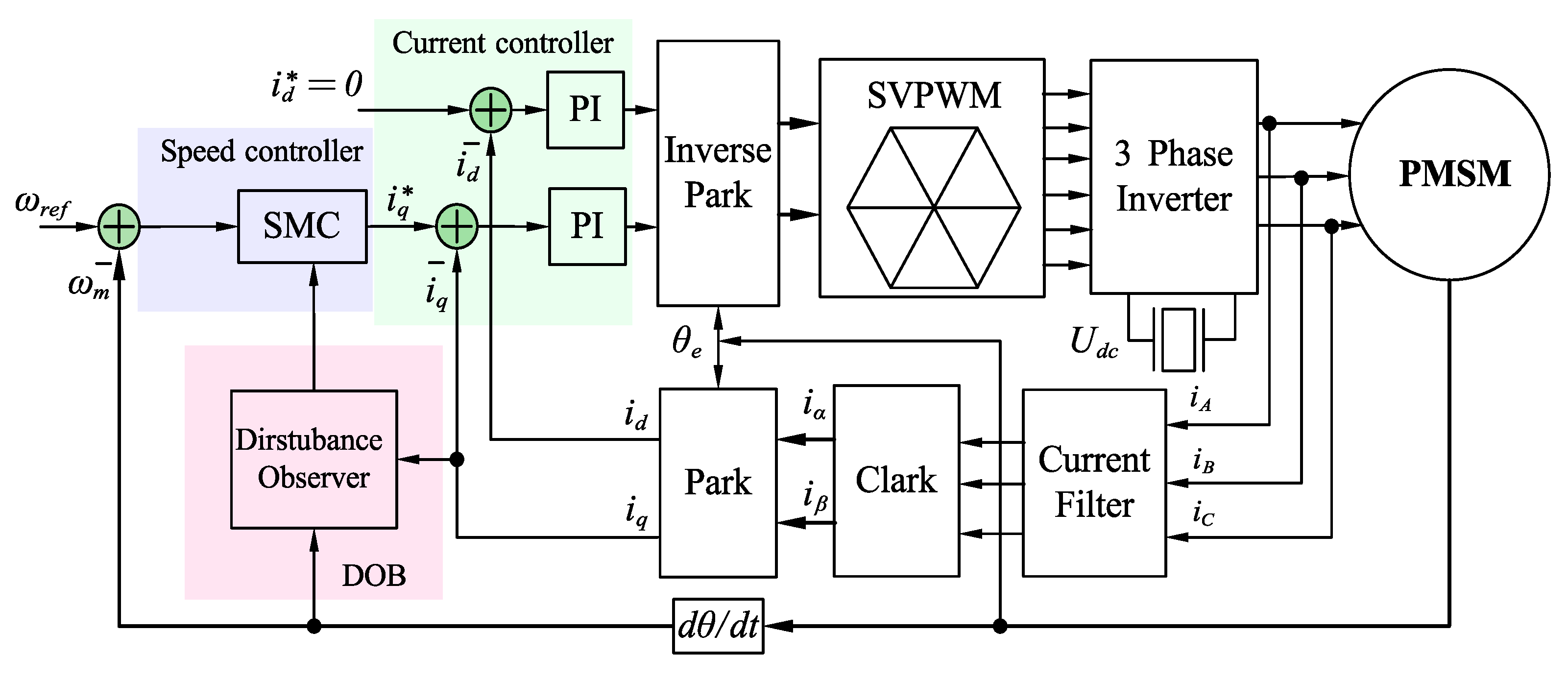
Reaching Law	Advantages	Disadvantages	Accuracy	Anti—Interference Ability	Application
CVRL	✓ Simple and efficient, with low cost; and moderate variability (standard deviation ≈ 0.2824) ensures steady convergence.	✓ Higher trajectory deviation (MAE 0.0848) and higher input variability versus PRL.	✓ High MAE limits tracking, unsuitable for precision-critical applications.	✓ High variability slows recovery and weakens disturbance handling.	✓ Suitable for low-precision systems that prioritize simplicity over chattering suppression and adaptability.
ERL	✓ Achieves fast convergence to the sliding surface and robust disturbance handling despite high variability (σ ≈ 0.5073).	✓ Sensitive tuning (MAE 0.0221); high variability may cause instability and overreaction.	✓ Higher accuracy than CVRL, but sensitive to tuning and variability.	✓ High variability reduces robustness, causing instability and slow recovery.	✓ Common in servo systems—reduces chattering, improves speed and accuracy.
PRL	✓ Fast, precise convergence (MAE ≈ 0.0450) and stable, low-variability control.	✓ Complex tuning and poor settings lead to instability and high complexity.	✓ Outperforms CVRL but lags GRL/ERL, ensuring precise tracking.	✓ Strong anti-interference, low input variability, and stable control.	✓ Suitable for systems requiring smooth reaching and stable disturbance environments.
GRL	✓ Flexible (MAE ≈ 0.0218), robust to disturbances despite high input variability.	✓ Complex, requiring expertise and optimization, with high computational cost.	✓ Lowest MAE (0.0218), high accuracy, and tailored control for minimal tracking error.	✓ High input (0.4884) induces fluctuations, needing disturbance optimization.	✓ Ideal for complex systems like aerospace control, requiring high accuracy, anti-interference, and adaptability.

presents a comparative analysis of the performance of different reaching laws. Accuracy, evaluated using Mean Absolute Error (MAE), indicates that GRL performs best (MAE = 0.0218), followed by ERL (0.0221), PRL (0.0450), and CVRL (0.0848). GRL’s high flexibility allows it to minimize tracking errors, while ERL benefits from exponential decay but is sensitive to parameter variations. PRL achieves moderate accuracy through adaptive convergence, whereas CVRL shows the lowest accuracy due to overshoot from its constant velocity approach. Anti-interference capability, measured by the standard deviation of the control input, ranks PRL highest (0.1495), followed by CVRL (0.2824), GRL (0.4884), and ERL (0.5073). PRL ensures stable control, while ERL exhibits significant variability. Each method has trade-offs: CVRL offers simplicity but low precision, ERL provides fast response with stability issues, PRL excels in disturbance rejection but is complex, and GRL balances adaptability with high computational cost. CVRL suits basic systems, ERL is for servo control, PRL fits stable environments with smooth transitions, and GRL is ideal for complex, high-precision applications like aerospace control.

Design studies can be improved by transitioning from traditional CVRL method to a new law with an equivalent design equation [104,105]:

$$\dot{s}=-k_{1}f\left(x,s\right)\mathrm{s}\mathrm{g}\mathrm{n}\left(s\right), k_1>0,$$

(18)

Or improvements based on PRL [35,106,107]:

$$\dot{s}=-k_{1}f\left(x,s\right){\left|s\right|}^{\alpha }\mathrm{s}\mathrm{g}\mathrm{n}\left(s\right)-k_{2}g\left(x,s\right){\left|s\right|}^{\beta }\mathrm{s}\mathrm{g}\mathrm{n}\left(s\right), k_1, k_2>0, 1>\alpha , \beta >0,$$

(19)

The comparative analysis in

Table 2. Summary Table of Control Strategies Derived from Enhanced CVRL and PRL Approaches.

Techniques	Year	Structures	Advantages	Disadvantages
New variable gain reaching law (NVGRL) [35]	2025	$\left\{\begin{array}{c}\dot{s}=-k_{1}f\left(x,s\right){\left|s\right|}^{\alpha }sgn\left(s\right)-k_{2}g\left(x,s\right){\left|s\right|}^{\beta }sgn\left(s\right) \\ f\left(x,s\right)={\left|s\right|}^{1-2\alpha }\left\{{\displaystyle \frac{2\left|x\right|+\beta }{2\left[\left|x\right|+\beta e^{-\lambda \left|x\right|}\right]}}+{\displaystyle \frac{\beta sgn\left(\left|s\right|-1\right)}{2\left[\left|x\right|+\beta e^{-\lambda \left|x\right|}\right]}}\right\}\\ g\left(x,s\right)=s^{\partial \left(s\right)}; \partial \left(s\right)=1-0.5\alpha +0.5\alpha sgn\left(\left|s\right|-1\right)\end{array}\right.$ where $k_1, k_2>0, 1>\alpha , \beta , \lambda$> 0,	✓ Dual-speed convergence (0.334 s), noise-robust at 150 rpm (RMSE 0.6651), and disturbance-compensated with ESMDO (41 rpm drop).	✓ Complex 7+ parameter tuning (2 times longer), flux linkage mismatch raises ripple 30%, and untested above 1000 rpm.
Modified exponential reaching law (MERL) [104]	2024	$\left\{\begin{array}{c}\dot{s}=-k_{1}f\left(x,s\right)sgn\left(s\right)\\ f\left(x,s\right)={\displaystyle \frac{1}{\mu +\left(\frac{{\left|x\right|}^{\alpha }+\lambda }{{\left|x\right|}^{\alpha }}-\mu \right)e^{-\gamma \left|s\right|}cos\left(\chi \left|s\right|\right)}}\end{array}\right.$ where $k_1, \gamma , \lambda >0, 1>\alpha , \mu$> 0, $\chi <0$	✓ Fastest convergence (0.011 s), minimal chattering (0.03–1.5 A), and resilient to 10 Nm load torque (25 rpm drop).	✓ Complex tuning of 8+ parameters, untested below 500 rpm, and high k1 (8000) may cause current saturation.
Adaptive SMC (ASMC) [105]	2022	$\left\{\begin{array}{c}\dot{s}=-k_{1}f\left(x,s\right)sgn\left(s\right)\\ f\left(x,s\right)=\left|x\right|{\displaystyle \frac{1+\lambda -e^{-\eta \left|s\right|}}{\lambda }}\end{array}\right.$ where $k_1>0, 1>\lambda$> 0, $\eta >0$	✓ Adaptive gain accelerates convergence (0.043 s) and suppresses chattering (0.5 A), compatible with MROPIO for zero overshoot.	✓ No integral term (steady-speed offset ~5.2 rpm), increased low-speed chattering (<500 rpm, 0.5 A), and coupled parameters where high η slows convergence.
New compound reaching law (NCRL) [106]	2023	$\left\{\begin{array}{c}\dot{s}=-k_1{\left|s\right|}^{\alpha }h\left(s\right)-k_{2}f\left(x,s\right)h\left(s\right)\\ h\left(s\right)=\left\{\begin{array}{cc}sgn\left(s\right)& \left|s\right|\ge \sigma \\ sgn\left(s\right){\left({\displaystyle \frac{\left|s\right|}{\sigma }}\right)}^{\sigma }& \left|s\right|<\sigma \end{array}\right.\\ f\left(x,s\right)=e^{\left|s\right|}-1\end{array}\right.$ where $k_1, k_2>0, 1>\sigma , \alpha$ > 0, $1>\sigma +\alpha$	✓ Eliminates overshoot (0%), robust to 2 times inertia mismatch (75.16 rpm drop), and ensures finite-time convergence.	✓ Anti-windup gain k3 couples with integral gain, slowing convergence if high; heavy-load (>6 Nm) raises ISMO error (1.2 Nm), and exponential term increases computation (25.9 μs).
Composite reaching law (CRL) [107]	2025	$\left\{\begin{array}{c}\dot{s}=-k_{1}f\left(x,s\right){\left|s\right|}^{\alpha }h\left(s\right)-k_{2}g\left(x,s\right){\left|s\right|}^{\beta }sgn\left(s\right) \\ h\left(s\right)=\left\{\begin{array}{cc}sgn\left(s\right)& \left|s\right|\ge D\\ tanh\left(\lambda s\right)& \left|s\right|<D\end{array}\right.\\ f\left(x,s\right)={\displaystyle \frac{1}{\left(1-\beta \right)e^{-\mu \left|s\right|}+\beta }};g\left(x,s\right)=s\end{array}\right.$ where $k_1, k_2>0, 1>\alpha , \beta , \lambda ,\mu$> 0,	✓ Hybrid chattering suppression (0.16 A), robust to ±100% inductance mismatch (0.08 A), and fast response (0.31 s settling).	✓ Thick boundary layer reduces chattering but slows response (+30% settling), flux weakening causes >3% fluctuation above 1500 rpm, and 2 × Ls raises prediction error 60%.

highlights significant improvements in advanced control methods over traditional CVRL and PRL. Methods such as NVGRL [35], MERL [104], ASMC [105], NCRL [106], and CRL [107] offer fast dynamic response (for example, MERL reaches 1000 rpm in 0.01 s, NVGRL starts up in 0.334 s), high steady-state accuracy (for example, NVGRL speed RMSE of 0.4845, NCRL RMS error of 0.5097 at 1000 rpm), and strong disturbance rejection (for example, NCRL limits speed drop to 47.15 rpm under half-rated load, NVGRL to 109 rpm under inertia mismatch). Chattering is effectively reduced (for example, MERL’s control input range of −0.081 to 1.595 A, compared to wider ranges in traditional methods), enhancing system stability. CRL maintains stable current ripple between 0.20 and 0.32 A and low total harmonic distortion of 4.13–4.91% even under significant inductance variation. However, these methods often require complex parameter tuning, increasing design effort. Performance may also degrade under extreme conditions, such as slight chattering (for example, NVGRL exhibits 1.8 rpm fluctuation at 150 rpm with noise) or increased speed drop under sudden load (for example, MERL drops 25 rpm under a 10 Nm load).

Control laws based on the improved and upgraded GRL and ERL control laws usually include both components: the variable speed reaching law and the variable index reaching law. Studies improving upon ERL/GRL often feature control laws [34,72,97,108,109] of the following form:

$$\dot{s}=-k_{1}f\left(x,s\right)\mathrm{s}\mathrm{g}\mathrm{n}\left(s\right)-k_{2}g\left(x,s\right)s, k_1, k_2>0,$$

(20)

Table 3. Summary Table of Control Strategies Derived from Enhanced ERL and GRL Approaches.

Techniques	Year	Structures	Advantages	Disadvantages
Modified variable ERL (MVERL) [72]	2025	$\left\{\begin{array}{c}\dot{s}=-k_{1}f\left(x,s\right)sgn\left(s\right)-k_{2}g\left(x,s\right)s \\ f\left(x,s\right)=\left|x\right|\left[1+\alpha \left(1-e^{-\beta \left|s\right|}\right)\right]\\ g\left(x,s\right)={\left|x\right|}^{\lambda }\end{array}\right.$ where $k_1, k_2, \alpha >0, \beta >1, 2>\lambda$> 0	✓ Adaptive gain speeds convergence (0.095 s) and reduces chattering, avoids singularity at x1 = 0, and resilient to disturbances with STESO (4 rpm drop).	✓ Six-parameter tuning required; high $\lambda$ increases chattering (0.8 A), heavy-load harmonics reduce STESO accuracy (+40% error), and low-speed (<500 rpm) chattering rises (0.5 A).
Variable exponential reaching law [VERL] [97]	2022	$\left\{\begin{array}{c}\dot{s}=-f\left(x,s\right)sat\left(s\right)/k_1-k_{1}s\\ f\left(x,s\right)={\left|x\right|}^2\end{array}\right.$ $\mathrm{s}\mathrm{a}\mathrm{t}\left(s\right)=\left\{\begin{array}{cc}1& s>\Delta \\ {\displaystyle \frac{1}{\Delta }}s& -\Delta <s<\Delta \\ -1& s<-\Delta \end{array}\right.$ where $k_1>0, \Delta$> 0	✓ Integrated position-speed control (2nd-order), transient speed limited to 1250 rpm, and high positioning accuracy (±0.5 pulses).	✓ Depends on trapezoidal trajectory (5% overshoot under 3 Nm load), small-angle speed limiting inactive (<20 k pulses), and saturation boundary Δ requires load-specific tuning.
New SMRL (NSMRL) [98]	2025	$\left\{\begin{array}{c}\dot{s}=-k_{1}f\left(x,s\right)tanh\left(s\right)-k_{2}g\left(x,s\right)s \\ f\left(x,s\right)={\displaystyle \frac{1}{\alpha +\left(1-\alpha \right)e^{-\beta \left|s\right|}}}\\ g\left(x,s\right)={\left|x\right|}^2\end{array}\right.$ where $k_1, k_2, \beta >0, 1>\alpha$> 0	✓ Simplified 4-parameter tuning (50% faster), robust to 2J inertia mismatch (38% drop reduction), and low chattering (0.23 A).	✓ Slow steady-state inertia updates (0.2 s), heavy-load (>6 Nm) increases observer error (1.2 Nm), and untested above 1000 rpm.
Novel reaching law (NRL) [108]	2021	$\left\{\begin{array}{c}\dot{s}=-k_{1}f\left(x,s\right)sgn\left(s\right)-k_{2}g\left(x,s\right)s \\ f\left(x,s\right)=arcsinh\left(\alpha \left|x\right|\right)\\ g\left(x,s\right)={\left|s\right|}^{\beta sgn\left(\left|s\right|-1\right)}\end{array}\right.$ where $k_1, k_2, \alpha >0, 1>\beta$> 0	✓ Dual-speed convergence (2 times faster), high steady-state precision (<0.5 rpm), and compatible with ITSMO for disturbance estimation (<0.6 Nm).	✓ Five-parameter tuning; high $k_1$ causes overshoot (3.36%), 300% Ls mismatch raises error 60%, and execution time increases (16.8 μs).
Novel reaching law (NNRL) [109]	2025	$\left\{\begin{array}{c}\dot{s}=-k_{1}f\left(x,s\right)r\left(s\right)-k_{2}g\left(x,s\right)s \\ f\left(x,s\right)={\displaystyle \frac{1}{\lambda +\alpha e^{-\beta \left|s\right|}}}\\ \begin{array}{cc}g\left(x,s\right)={\left|s\right|}^{\sigma }& 1>\sigma >0\end{array}\end{array}\right.$ $r\left(s\right)=\left\{\begin{array}{cc}sgn\left(s\right)& \left|s\right|\ge \Delta \\ tanh\left(\eta s\right)& \left|s\right|<\Delta \end{array}\right.$ where $k_1, k_2, \alpha , \beta , \Delta , \lambda >0, \eta =2\pi /∆$	✓ Hybrid chattering suppression (0.17 A), robust to ±50% parameter mismatch (0.45 A), and real-time feasible (1.36 μs).	✓ Thick boundary layer reduces chattering but slows response (+30% settling), flux linkage mismatch raises ripple 30%, and untested above 2200 rpm.

highlights the clear advantages of advanced control methods over traditional ERL and GRL. These advanced reaching laws for PMSM control introduce nonlinear functions and state-dependent adjustments to balance convergence speed and chattering suppression. For example, MVERL’s [72] variable exponential term enables faster stabilization (0.95 s at 500 rpm), VERL [97] reduces positioning time by 17–20%, NSMRL [98] cuts startup settling time by 42.3% compared to ERL, and NRL [108] achieves a 0.66 s rise time, faster than ERL-TSMC. These methods also enhance dynamic response and robustness, with NSMRL shortening recovery time after speed jumps by 58.3% and reducing speed drops under load by over 50% compared to traditional laws. Overshoot is significantly lowered (1.92–3.36% versus 5.76%), and chattering effects are minimized through smooth nonlinear functions, reducing current ripple by up to 52%. The main trade-off is increased tuning complexity, as these methods require 33–100% more parameters, extending debugging time by approximately 25–30%. However, combining NSMRL with optimization algorithms like grey wolf optimization helps mitigate this issue. Overall, compared to traditional ERL/GRL, these enhanced reaching laws offer faster convergence, stronger disturbance rejection, and improved stability—evidenced by NSMRL’s 42.3% shorter settling time and 26.6% lower speed drop under load—demonstrating significant control performance gains despite increased parameter complexity.

The computational cost on representative DSP platforms (TMS320F28335 [98] and RTU-BOX204 [72]) shows that advanced reaching laws (MVERL/NSMRL) combined with HOSMO/STESO significantly increase per-cycle load due to fractional power, nonlinear terms, and observer updates. ERL introduces minimal overhead (≈5–10 cycles) with fixed parameters and a single nonlinear operation, making it suitable for resource-constrained or high-speed PMSM control. NSMRL incurs medium–high overhead (≈80–120 cycles, ~10 times ERL) from tanh(s), exponentials, and adaptive gain updates; although effective in chattering reduction, latency validation on embedded targets remains absent. MVERL imposes the highest overhead (≈100–150 cycles, ~12 times ERL) due to fractional powers, exponentials, and adaptive gains, with no explicit reporting on memory or real-time feasibility. Overall, ERL is optimal for low-cost, real-time PMSM control, NSMRL offers improved robustness at moderate cost but needs latency validation, while MVERL provides the smoothest control yet requires explicit justification for real-time deployment.

4.2. Sliding Surface Design

The design of the sliding mode surface plays a crucial role in determining the convergence behavior of the system state and forms the foundation of SMC. Its main purpose is to steer the system toward the origin along a predefined trajectory. During this process, the system remains unaffected by uncertainties and exhibits invariance. In the early development of SMC theory, the surface was typically defined as follows [96,110]:

$$\left\{\begin{array}{cc}\begin{array}{c}s=k{x}_n+f\left(x_1,x_2,\dots ,x_{n-1}\right)\\ {\dot{x}}_i=x_{i+1}\end{array}& i=1,2,\dots ,n-1\end{array}\right.,$$

(21)

where f is a linear or nonlinear function.

The primary goal of the sliding mode controller is to ensure that the system’s state trajectories reach a predefined sliding surface within a finite time and remain on it thereafter. Various typical sliding mode surfaces will be presented in the following sections.

4.2.1. Linear Sliding Mode Surface

In the initial development of SMC theory, the Linear Sliding Mode Surface (LSMS) [38,44], was commonly expressed as follows:

$$\left\{\begin{array}{cc}\begin{array}{c}s=c_1{x}_1+c_2{x}_2+\cdots +c_n{x}_n\\ {\dot{x}}_i=x_{i+1}\end{array}& i=1,2,\dots ,n-1\end{array}\right.,$$

(22)

where c₁, c₂, …, cₙ are the adjustment coefficients, and x₁, x₂, …, xₙ are the state variables.

The commonly used form of the LSMS equation for investigating new SMC laws [34,98,105] is expressed as follows:

$$\left\{\begin{array}{cc}\begin{array}{c}s=c_1{x}_1+x_2\\ {\dot{x}}_1=x_2\end{array}& c_1>0\end{array}\right.,$$

(23)

The LSMS, as defined in Equation (23), ensures asymptotic stability of the sliding mode, with the convergence rate determined by the parameter c₁. One notable benefit of this design is its simplicity [111,112]. Nevertheless, conventional LSMSs have shown limitations regarding convergence speed and settling time [34,103]. Enhancing the dynamic response of a closed-loop system is possible with the use of nonlinear sliding surfaces. In the context of PMSM speed control, numerous studies have employed linear SMC; however, its shortcomings were addressed by hybrid approaches that develop composite SMC controllers [113] or by modifying the reaching laws [103].

To overcome conventional sliding surface limitations, modern control designs widely adopt Integral Sliding Mode Surfaces (ISMS), as follows:

$$\left\{\begin{array}{c}s=c_1{x}_1+c_2{\int }_0^t{x}_{1}d\tau \\ c_1,c_2>0\end{array}\right.,$$

(24)

The ISMS in Equation (24) outperforms conventional sliding surfaces in Equation (22) through three key advantages [98]: first, the complete elimination of steady-state error via the integrated error integral term; second, the automatic compensation for constant disturbances (such as load variations) without the need to increase the switching gain; third, the reduced sensitivity to system parameter mismatches (inertia, friction). This structure simultaneously enhances transient performance with a faster convergence speed and lower overshoot, making it ideal for high-precision applications in noisy environments.

In addition to ISMS, the Differential-Integral Sliding Mode Surface (DISMS) has been used to improve convergence speed and controller performance, overcoming the limitations of previous methods [103,114] as follows:

$$\left\{\begin{array}{c}s=c_1{x}_1+c_2{\int }_0^t{x}_{1}d\tau +c_3{x}_2\\ c_1,c_2,c_3>0\end{array}\right.,$$

(25)

In this study, linear sliding surfaces feature simpler structures, yet the PMSM is a nonlinear system. Therefore, the research on SMC for PMSM primarily focuses on nonlinear sliding surfaces. The subsequent section of this paper introduces the complex nonlinear sliding surfaces under investigation to address the limitations of linear sliding surfaces.

4.2.2. Nonlinear Sliding Mode Surface

Terminal Sliding Mode (TSM) control, introduced in 1993 [115] as a new type of SMC, is based on the concept of terminal attractors, which ensures finite-time convergence of system states. In a TSM control system, a nonlinear term is incorporated into the sliding surface design, shaping the manifold as an attractor. Upon reaching the sliding surface, the trajectory converges to the origin via a power-law.

A typical nonlinear TSM Surface (TSMS) is defined as follows:

$$\left\{\begin{array}{c}s=x_2+c_1{x}_1^{n/m}\\ c_1,n,m>0, m>n\end{array}\right.,$$

(26)

where m, n are properly selected positive odd integers. It is worth noting that the TSMS in Equation (26) becomes identical to that of the linear sliding surface in Equation (23) when n/m = 1. For any initial state x₁(0) ≠ 0, the dynamics Equation (26) converges to x₁ = 0 in finite time [116] as follows:

$$t_{TSM}^s={\displaystyle \frac{m}{c_1\left(m-n\right)}}{\left|x_1\left(0\right)\right|}^{{\displaystyle \raisebox{1ex}{$\left(m-n\right)$}\!\left/ \!\raisebox{-1ex}{$m$}\right.}},$$

(27)

Compared to linear SMC, TSM control offers several advantages, including lower control switching gain, faster convergence, and higher stability accuracy. In recent years, TSM control theory has gained significant attention from researchers in the control field and has been widely and thoroughly explored [117,118]. However, the conventional TSMS in Equation (26) suffers from a singularity issue, which may arise if the initial conditions are not properly chosen, due to the recursive nature of the switching manifolds and the convergence rate Equation (27) of the TSM surface is slow when the system state is far from the origin (because $x_1^{n/m}$ reduces the convergence rate at larger distances).

To enhance convergence performance, the Fast Terminal Sliding Mode Surface (FTSMS) was introduced as follows:

$$\left\{\begin{array}{c}s=x_2+c_1{x}_1^{n/m}+c_2{x}_1\\ c_1,c_2,n,m>0, m>n\end{array}\right.,$$

(28)

The FTSMS in Equation (28) is an improved version of the conventional TSMS in Equation (26), achieved by adding a linear term c_2×1. The convergence time of FTSMS is

$$t_{FTSM}^s={\displaystyle \frac{m}{c_1\left(m-n\right)}}\left[ln\left(c_2{x}_1{\left(0\right)}^{n/m}\right)-ln{c}_1\right],$$

(29)

The system exhibits finite-time convergence to the equilibrium point x₁ = 0 for any initial condition x₁(0) ≠ 0. Its convergence behavior can be divided into two phases: when x₁ is large, the linear term $x_2={-c}_2{x}_1$ dominates, leading to rapid exponential decay toward the equilibrium (global convergence phase). As the state nears the origin, the nonlinear term $x_2={-c}_1{x}_1^{n/m}$ dominates, ensuring finite-time convergence [116].

In addition to the FTSMS, the Non-Singular Terminal Sliding Mode Surface (NTSMS)—an improved version of the traditional TSMS—takes the following form:

$$\left\{\begin{array}{c}s=x_1+{\displaystyle \frac{1}{c_1}}{x}_2^{n/m}\\ c_1,n,m>0, 1< m/n<2\end{array}\right.,$$

(30)

The convergence time of NTSMS is [119]

$$t_{NTSM}^s={\displaystyle \frac{m}{c_1^{n/m}\left(m-n\right)}}{\left|x_1\left(0\right)\right|}^{{\displaystyle \raisebox{1ex}{$\left(m-n\right)$}\!\left/ \!\raisebox{-1ex}{$m$}\right.}},$$

(31)

The NTSMS, defined in Equation (30) with the convergence time given in Equation (31), was designed to eliminate the singularity issues present in conventional TSMS. This enhanced approach has been successfully implemented in PMSM control systems [120].

In addition to the traditional TSMS, FTSMS, and NTSMS, numerous recent studies have developed variations based on these surfaces to optimize PMSM motor control systems, as summarized in

Table 4. Summary Table of Control Strategies Derived from Enhanced LSMS, TSMS, FTSMS, and NTSMS surfaces.

Techniques	Year	Structures	Advantages	Disadvantages
Integral sliding mode surface (ISMS) [98]	2025	$s=c_1{x}_1+c_2{\int }_0^t{x}_{1}d\tau$ where $c_1, c_2>0$	✓ Integral term eliminates steady-state error (<1 rpm), HOSMO improves disturbance rejection (21.54 rpm drop), and Landau integration enhances inertia adaptation (38% drop reduction).	✓ Overshoot risk with high $c_2$ (3.36%), fixed boundary layer degrades high-speed response, and slow inertia updates from reduced γ.
Differential-ISMS (DISMS) [103]	2020	$s=c_1{x}_1+c_2{\int }_0^t{x}_{1}d\tau +c_3{x}_2$ where $c_1, c_2, c_3>0$	✓ Low steady-state error via integral action, balanced dynamics with PD terms, and simple tuning using three gains (c1, c2, c3).	✓ Overshoot sensitivity to high c3, no adaptation to parameter mismatch, and steady-state offset (~5.2 rpm from friction).
Integral-type TSMS (ITSMS) [107]	2025	$s=c_1{x}_1+c_2{\int }_0^t{\left|x_1\right|}^{\alpha }sgn\left(x_1\right)d\tau$ where $c_1, c_2>0, 1> \alpha >0$	✓ Dual-loop optimization with integral-terminal + SM-PEC, robust to ±50% parameter mismatch (0.08 A error), and observer-free design avoiding bandwidth trade-offs.	✓ Inductance-sensitive (60% error at 2 times Ls), boundary layer trade-off, and flux weakening causes >3% speed fluctuation above 1500 rpm.
Noval non-singular TSMS (NNTSMS) [121]	2023	$s=c_1{x}_1+x_2+c_2{\int }_0^t{\left|x_1\right|}^{\alpha }sgn\left(x_1\right)d\tau$ where $c_1, c_2>0, 2> \alpha >1$	✓ Single-loop design reduces parameters by 50%, dual disturbance rejection via TVNDO (<31 rpm fluctuation), and no start-up peak.	✓ Complex HRL parameter tuning, slow start-up due to TVNDO gain, and no flux-weakening validation above 1000 rpm.
Improved nonsingular fast TSMS (INFTSMS) [72]	2025	$s=x_2+c_1{x}_1^{n/m}+c_2{x}_2^{p/q}$ where c1, c2 > 0. p, q, m, and n be odd positive integers such that 1 < p/q < 2 and m/n > p/q.	✓ Fast convergence (0.95 s vs. 1.3 s), anti-chattering without singularity, and disturbance resilience with STESO (4 rpm drop).	✓ Complex tuning of six parameters, sensitivity to torque harmonics under heavy load (>3 Nm), and no low-speed (<500 rpm) validation.
Discrete-time fast TSMS (DTFTSMS) [122]	2024	$s=c_1{x}_1+x_2+c_2{\left|x_1\right|}^{\alpha }\mathrm{s}\mathrm{g}\mathrm{n}\left(x_1\right)$ where $c_1, c_2>0, 1>\alpha >0$	✓ Finite-time convergence with nonlinear power term, zero start-up overshoot, and robustness to 2 times inertia mismatch.	✓ Trade-off between fast convergence and chattering ($c_2$ = 600 → 0.5 A ripple), fixed α = 2/3 limits low-speed performance, and heavy-load torque ripples raise observation error.

.

The comparative analysis in Table 4 and Figure 9 shows that six improved SMS design methods are primarily developed to enhance PMSM control by increasing convergence speed, minimizing overshoot, and improving noise immunity and robustness. Among these, the DTFTSMS [122] demonstrates the best overall performance, achieving up to an 80% faster settling time and zero overshoot, while also exhibiting superior disturbance rejection (0.0026 s recovery time and 53 rpm fluctuation). Other methods, such as INFTSMS [72], NNTSMS [121], and ISMS [98], also deliver strong results, particularly in settling time and load disturbance handling. However, methods like INFTSMS [72] and NNTSMS [121] involve higher tuning complexity due to a large number of nonlinear parameters. In contrast, ISMS [98] offers simpler implementation with competitive disturbance rejection performance. Overall, the optimal method depends on application needs: implementation, robustness, tuning, and real-time constraints.

4.3. Second-Order SMC

Traditional sliding surface theory requires a first-order surface, with the control input appearing in the first derivative of the sliding variable. This constraint limits flexibility in surface design, posing a major challenge for SMC development.

HOSMC [123] extends the conventional SMC framework by overcoming the relative order limitation inherent in first-order designs. It reduces chattering while preserving the key advantages of traditional SMC, thereby enhancing control performance. By incorporating higher-order components into the sliding surface, HOSMC improves state tracking accuracy and better mitigates the effects of uncertainties and disturbances.

Currently, within HOSMC, Second-Order SMC (SOSMC) is the most extensively studied and widely adopted approach. It has been applied across various industrial control domains, including mechatronics and industrial robotics [124,125], power electronics and energy systems [126,127], automotive and autonomous vehicles [128,129,130], as well as smart grid [131,132], and IoT-based systems [133,134]. In motor control, SOSMC is employed for a range of motor types such as IMs [135], DC motors [136,137], PM motors [138], PMSM motors [32,139], and switched reluctance generator [140].

For PMSM applications, in particular, SOSMC offers significant advantages: strong chattering reduction, finite-time convergence, and high robustness to model uncertainties and measurement noises. It enhances control accuracy, minimizes energy loss, and eliminates the need for state derivative measurements. Despite requiring more powerful processing hardware, SOSMC is well-suited for high-performance applications such as robotics, electric vehicles, and industrial drive systems.

Consider a system of nonlinear equations as follows:

$$\left\{\begin{array}{c}\dot{x}=f\left(x,t\right)+g\left(x,t\right)u\\ y=s\left(x,t\right)\end{array}\right.,$$

(32)

where x ∈ Rⁿ is the state vector, t denotes time, and u is the control input; the functions f(x,t) and g(x,t) represent uncertainties, and y ∈ R is the output as well as the sliding variable s.

The sliding surface condition for SOSMC is defined by the following relation:

$$s\left(x,t\right)=\dot{s}\left(x,t\right)=0,$$

(33)

As the most basic form of HOSMC, SOSMC has undergone continuous theoretical refinement. Several notable algorithms have been developed within the SOSMC framework, including the super-twisting algorithm [139,141], twisting control algorithm, prescribed convergence law, and sub-optimal algorithm [142] (Figure 10).

4.3.1. Super-Twisting Algorithm

The Super-Twisting Algorithm (STA) is a SOSMC strategy developed for systems with relative degree one. It effectively suppresses chattering while maintaining the robustness characteristics of conventional SMC. Unlike basic sliding mode approaches, STA generates a continuous control signal without requiring the time derivative of the sliding variable. The control input comprises a nonlinear function of the sliding variable and an integral term ensuring finite-time convergence on the sliding surface.

Accordingly, the general formulation of the STA can be expressed as follows [143]:

$$\left\{\begin{array}{c}u=\alpha {\left|s\right|}^{\beta }sgn\left(s\right)+u_1\left(s,t\right)\\ {\dot{u}}_1\left(s,t\right)=-\epsilon sgn\left(s\right)\end{array}\right.,$$

(34)

where α, β, and ε > 0.

Using the Lyapunov function, which is given by the following equation:

$$V\left(x,t\right)={\displaystyle \frac{1}{2}}{s}^2+{\displaystyle \frac{1}{2}}{u}^2={\displaystyle \frac{1}{2}}{s}^2+{\displaystyle \frac{1}{2}}{\left(\alpha {\left|s\right|}^{\beta }sgn\left(s\right)+u_1\right)}^2,$$

(35)

Calculate the time derivative the Equation (35):

$$\dot{V}=s\dot{s}+u\dot{u}=s\dot{s}+\left(\alpha {\left|s\right|}^{\beta }sgn\left(s\right)+u_1\right)\left(\alpha {\left|s\right|}^{\beta -1}sgn\left(s\right)\dot{s}+{\dot{u}}_1\right),$$

(36)

Substitute Equation (34) into Equation (36) as follows:

$$\begin{array}{l}\dot{V}=s\dot{s}+\left(\alpha {\left|s\right|}^{\beta }sgn\left(s\right)+u_1\right)\left(\alpha {\left|s\right|}^{\beta -1}sgn\left(s\right)\dot{s}-\epsilon sgn\left(s\right)\right)\\ \le s\dot{s}+\left(\alpha {\left|s\right|}^{\beta }sgn\left(s\right)+u_1\right)\alpha {\left|s\right|}^{\beta -1}\dot{s}\\ \le \left[s+\left(\alpha {\left|s\right|}^{\beta }sgn\left(s\right)+u_1\right)\alpha {\left|s\right|}^{\beta -1}\right]\dot{s}\le 0\end{array}$$

(37)

With α, β, and ε > 0.

The difference from FOSMC is that in STA, the control input is a combination of a continuous-like term $\alpha {\left|s\right|}^{\beta }\mathrm{s}\mathrm{g}\mathrm{n}\left(s\right)$ (${\left|s\right|}^{\beta }$ term softens the impact of the sign function compared to the pure sign function in FOSMC) and an integral-type term related to u₁. The finite-time convergence guaranteed by Lyapunov stability means that the system can reach the sliding surface quickly without the need for high-frequency, persistent chattering. The continuous-like nature of the control input components in STA reduces the abrupt changes in control action that cause chattering in FOSMC.

4.3.2. Twisting Control Algorithm

The fundamental form of the Twisting Control Algorithm (TCA) is represented by the following control law [143]:

$$\dot{u}\left(t\right)=\left\{\begin{array}{cc}-u& if \left|u\right|>1\\ -k_{1}sgn\left(s\right)& if s·\dot{s}\le 0, \left|u\right|\le 1\\ -k_{2}sgn\left(s\right)& if s·\dot{s}>0, \left|u\right|\le 1\end{array}\right.,$$

(38)

Here, s denotes the sliding surface, while $\dot{s}$ represents its time derivative. The parameters k₁ and k₂ are positive design gains chosen to ensure desired control performance.

The TCA reduces chattering and enhances robustness in systems with bounded uncertainties or disturbances. Unlike basic first-order SMC (FOSMC), TCA introduces a discontinuous control action based on both the sliding variable’s sign and dynamics.

4.3.3. Prescribed Convergence Law

The Prescribed Convergence Law (PCL) is a key strategy in SOSMC for ensuring finite-time convergence of both the sliding variable s and its derivative $\dot{s}$, while allowing the transient response to follow a predefined trajectory. The general form of PCL-based algorithms can be expressed as follows [143]:

$$\dot{u}\left(t\right)=\left\{\begin{array}{cc}-u& if \left|u\right|>1\\ -k_{1}sgn\left(\dot{s}-f\left(s,t\right)\right)& if \left|u\right|\le 1\end{array}\right.,$$

(39)

where k₁ > 0, and f(s,t) is continuous and smooth except at s = 0.

4.3.4. Sub-Optimal Algorithm

The Sub-Optimal Algorithm (SOA) for SOSMC control was developed as a sub-optimal feedback implementation of classical time-optimal control for a double integrator system. The auxiliary system dynamics of the SOA are described by the following:

$$u\left(t\right)=\alpha \left(t\right)k_1\mathrm{s}\mathrm{g}\mathrm{n}\left[s\left(t\right)-{\displaystyle \frac{1}{2}}{s}_M\left(t\right)\right],$$

(40)

$$s_M\left(t\right)=\left\{\begin{array}{cc}s\left(0\right)& 0\le t<t_{M_i}\\ s\left(t_{M_i}\right)& t_{M_i}\le t<t_{M_{i+1}}\end{array}\right.i=1, 2, \dots ,$$

(41)

$$\alpha \left(t\right)=\left\{\begin{array}{cc}{\alpha }^{*}& \left[s\left(t\right)-{\displaystyle \frac{1}{2}}{s}_M\left(t\right)\right]\left[s_M\left(t\right)-s\left(t\right)\right]>0,\\ 1& \left[s\left(t\right)-{\displaystyle \frac{1}{2}}{s}_M\left(t\right)\right]\left[s_M\left(t\right)-s\left(t\right)\right]\le 0\end{array}\right.,$$

(42)

where k₁ > 0, $t_{M_i}$ are the time instants at which $\dot{s}=0$. α* is constant.

In general, each of these four methods in SOSMC has its own characteristics. STA is suitable for applications requiring chattering suppression and simple implementation; TCA has design flexibility but is relatively complex; PCL focuses on finite-time convergence and trajectory following; SOA is a sub-optimal solution for double-integrator systems but is mathematically complex. The choice of method depends on the specific application requirements, such as system type, control performance indicators (convergence speed, chattering level), and computational resources.

Table 5. Summary Table of Control Strategies Derived from Enhanced SOSMC controls.

Techniques	Year	Structures	Advantages	Disadvantages
New super-twisting algorithm (NSTA) [139]	2022	$\left\{\begin{array}{c}u\left(t\right)=u_1\left(t\right)+u_2\left(t\right)\\ u_1=-k_1{\left|s\right|}^{1/2}sgn\left(s\right)\\ {\dot{u}}_2=-k_{2}sgn\left(s\right)\end{array}\right.$, $k_1, k_2>0$	✓ Simplified surface: no speed derivative (50% less noise), 4 parameters (30% faster tuning), and q-axis ripple 1.2 A under 10 Nm load.	✓ Small speed lag (0.01 s), heavy-load error increase (>10 Nm, 0.8 A), and no sensorless validation.
Discrete-time super-twisting control (DTSTC) [141]	2025	$\left\{\begin{array}{c}u\left(kT\right)=-k_1{\left|e\left(kT\right)\right|}^{1+\rho }sgn\left[e\left(kT\right)\right]+\vartheta \left(kT\right)\\ \vartheta \left(\left(k+1\right)T\right)=\vartheta \left(kT\right)-k_2{\left|e\left(kT\right)\right|}^{1+2\rho }T\end{array}\right.$, where $k_1, k_2>0$, $0>\rho >-1/2$	✓ Chattering reduced (1.32 A), tunable precision via $\rho$ (improved tracking), and discrete-time robustness at 0.25 ms (MAE 1.0397).	✓ Fractional parameter sensitive ($\rho$ ∉ (−0.5,0) raises ripple 30%), high computation (25.9 μs), and untested below 50 rpm.
Second-order sliding-mode (SOSM) [144]	2019	$\left\{\begin{array}{c}u\left(t\right)=-k_{1}sgn\left({⌈\dot{s}⌉}^{\alpha /r}+k_2^{\alpha /r}\sigma {⌈s⌉}^{\alpha /\left(2r\right)}\right)\\ {⌈·⌉}^{\lambda }=sgn\left(·\right){\left|·\right|}^{\lambda };\alpha >2r>0;k_1, k_2>0\end{array}\right.$, $\sigma \left(t\right)=\left\{\begin{array}{cc}\epsilon ·sgn\left(s\right)& \left|x\right|>\epsilon \\ x& \left|x\right|\le \epsilon \end{array}\right.$ $\epsilon >0$	✓ Finite-time stability (0.08 s versus 0.12 s); no mode switching reduces software complexity; pendulum swing constraint respected (0% violation versus 20%).	✓ Saturation level ε affects convergence versus constraints (>π/12 violates limits); no PMSM high-speed tests; conservative k2 (20% above needed).
Cascade SOSMC (CSOSMC) [145]	2019	$\left\{\begin{array}{c}u\left(t\right)=u_1\left(t\right)+u_2\left(t\right)\\ u_1=-k_1{\left|s\right|}^{1/2}sat\left(s/\alpha \right)\\ {\dot{u}}_2=-k_{2}sat\left(s/\alpha \right)\end{array}\right.$, $k_1, k_2>0$ $\mathrm{s}\mathrm{a}\mathrm{t}\left(s/\alpha \right)=\left\{\begin{array}{cc}sgn\left(s\right)& \left|s\right|>\alpha \\ s/\alpha & \left|s\right|\le \alpha \end{array}\right.$ $\alpha >0$	✓ Dual-loop SOSMC: <0.5 rpm error under 50% inertia mismatch, 40% less differentiator noise, and 20 rpm drop for 0.12 Nm load.	✓ Hardware-induced current chattering (0.8 A), untested above 2000 rpm, and coupled parameters where high k1 slows convergence.
State constrained SOSMC (SCSOSMC) [146]	2024	$\left\{\begin{array}{c}u\left(t\right)=-{\eta }_{1}sgn\left({⌈\dot{s}⌉}^{\alpha /\beta }+{\eta }_2^{\alpha /\beta }\sigma {⌈s⌉}^{\alpha /\left(2\beta \right)}\right)\\ {⌈·⌉}^{\lambda }=sgn\left(·\right){\left|·\right|}^{\lambda };\alpha >2\beta >0;{\eta }_1, {\eta }_2>0\end{array}\right.$, $\sigma \left(t\right)=\left\{\begin{array}{cc}\epsilon ·sgn\left(s\right)& \left|x\right|>\epsilon \\ x& \left|x\right|\le \epsilon \end{array}\right.$ $\epsilon >0$	✓ Strict state limits (speed ± 600, derivative ± 200), full attraction domain maintained, and startup q-axis current <6 A.	✓ Trade-off: smaller saturation (ε) reduces overshoot but slows settling; complex Lyapunov analysis; 2 times flux linkage raises current ripple 25%.

summarizes recent research on SOSMC control methods and the advancements made in these approaches.

The comparative analysis in Table 5 shows that SOSMC methods significantly improve speed fluctuation and disturbance rejection. For example, DTSTC [141] reduces speed fluctuation to 6.11 rpm (versus 7.21 rpm in conventional methods) and recovers from a 15 rpm drop in 0.52 s. NSTA [139] reduces speed fluctuation to 20 rpm at 10 Nm and halves q-axis current ripple from 2.4 to 1.2 A. Methods like SOSM [144] and SCSOSMC [146] enhance robustness and enforce state constraints under uncertainties. Challenges include residual chattering (for example, CSOSMC [145]), longer settling times (DTSTC: 1.40 s versus 1.37 s conventional), and complex gain tuning with higher energy consumption.

SOSMC deployment in PMSM drives faces hardware and algorithmic constraints. Limited MCU/DSP capacity hinders real-time execution of cascade and discrete-time controllers [141,145], while sensor noise, sampling errors, ADC conversion, PWM dead-time, and interface delays aggravate chattering and degrade control [139,141]. Discretization introduces current ripple [141], and high gains risk overcurrent and torque overload [139,146]. Parameter sensitivity to resistance and inertia variations necessitates adaptive tuning [145]. On the hardware side, frequent switching increases IGBT losses beyond 60% at 10 kHz [139,141], and inverter nonlinearities further reduce effective torque at low speeds [139]. Sensor or IGBT failures threaten stability without redundancy [141,146], while environmental factors such as temperature, EMI, and vibration exacerbate performance degradation [139,141]. Mitigation strategies include DSP–FPGA co-design, saturation-based protection, thermal management, and adaptive gain adjustment, yet cost–performance trade-offs persist, with high-end FPGA platforms improving accuracy at higher expense, whereas PI plus disturbance observers remain attractive for low-cost drives [144,146].

4.4. Arbitrary-Order SMC

This method effectively addresses both the chattering issue and the relative order constraint of traditional SMC, without compromising system stability.

SOSMC applies the derivative of the control law on a second-order sliding surface to ensure finite-time convergence and eliminate chattering seen in FOSMC.

In recent years, Arbitrary-Order SMC (AOSMC) [147]—a subset of HOSMC has attracted growing interest due to its ability to preserve the simplicity and robustness of traditional SMC while eliminating chattering and removing constraints on system relative degrees. These advantages have driven ongoing advances in both theoretical research and practical applications. The core concept of AOSMC lies in applying discrete functions to higher-order sliding surfaces to enhance performance. Consequently, the sliding surface condition for AOSMC is defined as follows [148]:

$$s\left(x,t\right)=\dot{s}\left(x,t\right)=\cdots s^{\left(r-1\right)}\left(x,t\right)=0,$$

(43)

AOSMC is based on applying discontinuous control to the r-th derivative of the sliding variable. Consider the following nonlinear system [126]:

$$\left\{\begin{array}{c}\dot{x}=f_i\left(x,t\right)+g_i\left(x,t\right)u\\ \begin{array}{c}{y}_2=s_2\left(x,t\right)\\ \cdots \\ y_n=s_n\left(x,t\right)\end{array}\end{array}\right.,$$

(44)

Consider a nonlinear system where x ∈ Rⁿ is the state vector, t denotes time, and u_i is the control input; the functions f_i(x,t) and g_i(x,t) represent uncertainties, and y_i ∈ R is the output, where i indicates the subsystem for the multi-variable system. If i = 1, the system becomes a Single-Input Single-Output (SISO) case. The system dynamics involve smooth functions f_i(x,t) and a sliding variable s. The control input is defined by a feedback law u_i = U(x,t), where U is a discontinuous function. For simplicity, the scalar case is considered, where both the sliding variable s and control u are scalars. Nevertheless, the results can be extended to vector-valued systems.

The sliding variable s and its first r − 1 time derivatives are driven to zero by implementing a properly designed discontinuous control function. This is represented through the following system of equations:

$$\left\{\begin{array}{c}{s}_1\left(x,t\right)={\dot{s}}_1\left(x,t\right)=\cdots s_1^{\left(r-1\right)}\left(x,t\right)\\ \cdots \\ s_n\left(x,t\right)={\dot{s}}_n\left(x,t\right)=\cdots s_n^{\left(r-1\right)}\left(x,t\right)\end{array}\right.,$$

(45)

And

$$\begin{array}{cc}{s}^{\left(r\right)}\left(x,t\right)=a\left(x,t\right)+b\left(x,t\right)u& b\left(x,t\right)\ne 0\end{array},$$

(46)

AOSMC [149] demonstrates several advantages over FOSMC, including smoother control action, reduced switching delays during implementation, elimination of the need for derivative information in the control signal, and improved chattering mitigation—all while preserving key benefits such as robustness and ease of deployment. However, due to its reliance on more complex algorithms like differentiators, HOSMC is more susceptible to measurement noise, which can degrade overall control performance as the number of differentiators increases.

4.5. Reduction of Chattering Phenomenon in SMC

The SMC methodology requires an infinitely fast switching mechanism; however, discontinuous switching combined with time and space delays prevents the sliding motion from occurring exactly on the ideal sliding surface and inevitably induces control signal oscillations in its vicinity. This oscillation, commonly referred to as chattering (Figure 11) or the “quasi-sliding mode,” [150] can be further amplified, leading to degraded controller performance, reduced system stability, and potential damage to mechanical equipment. Chattering is regarded as a major inherent drawback of SMC. To mitigate this issue, various methods have been proposed, with the smoothing function approach being one representative solution.

For traditional controllers, SMC commonly employs the following sign-function switches:

$$sgn\left(s\right)=\left\{\begin{array}{cc}1& s>0\\ 0& s=0\\ -1& s<1\end{array}\right.,$$

(47)

The sign function sgn(s) is simple to implement; however, its abrupt state transitions induce chattering in conventional SMC controllers. To mitigate this drawback, various methods have been proposed to reduce or eliminate chattering in SMC systems.

The continuous sigmoid function sigmoid(s) [151] is employed to enhance system dynamics and is defined as follows:

$$sigmoid\left(s\right)={\displaystyle \frac{2}{1+e^{-\alpha s}}}-1,$$

(48)

The saturation function sat(s/σ) [150] is employed to reduce chattering as follows:

$$sat\left(s/\sigma \right)=\left\{\begin{array}{cc}1& s>\sigma \\ s/\sigma & \left|s\right|\le \sigma \\ -1& s<-\sigma \end{array}\right.,$$

(49)

The hyperbolic tangent function tanh(ks) [152] is expressed as follows:

$$tanh\left(ks\right)={\displaystyle \frac{e^{ks}-e^{-ks}}{e^{ks}+e^{-ks}}},$$

(50)

The relay function χ_r(s) [153] is given by

$${\chi }_r\left(s\right)={\displaystyle \frac{s}{\left|s\right|+\beta }}$$

(51)

where α, σ, k, and β > 0, control the slopes of the sigmoid(s), sat(s/σ), tanh(ks), and χ_r(s) functions, respectively.

Based on Figure 12, the alternative functions mitigate the abrupt switching of the sign function. At unit coefficients, the tanh and saturation functions (Figure 12a) provide the most balanced slope and transition, followed by the sigmoid and the relay function, which shows greater delay. When varying coefficients, the sigmoid and tanh functions (Figure 12b,c) exhibit the smoothest transitions, while the saturation function (Figure 12d) closely resembles the sign function, preserving its control characteristics and reducing chattering. The relay function (Figure 12e), despite its smoothness, suffers from excessive transition time, limiting its effectiveness compared with the others.

Recent studies on SMC for PMSM have employed functions such as sigmoid [154], saturation [97,145], and tanh [98,155,156,157] to replace the sign function and reduce chattering. Among these, the tanh and saturation functions are most widely used due to their effective balance between smooth transitions and control performance.

5. Observer-Integrated SMC

The purpose of an observer is to estimate the unmeasured states of a system using only the measured input and output signals. It functions as a mathematical model of the system, driven by the input signal combined with a correction term based on the difference between the actual system output and the observer’s estimated output. SMO employs nonlinear feedback of this output estimation error through a switching element, offering an effective approach to the estimation problem. With a known noise bound, the SMO can drive the output estimation error to zero within finite time, while the observer’s state variables asymptotically converge to the true system states.

5.1. The Disturbance Observer

SMC often employ high control gains to mitigate the adverse effects of noise and system uncertainties. However, excessively large gains can cause undesirable chattering. To address this issue, the Disturbance Observer (DOB) approach has been introduced, enabling accurate estimation and compensation of disturbances (Figure 13). Functioning as an outer loop, DOB estimates the total disturbance based on measurable variables and feeds this information back to the inner-loop SMC, which then adjusts the control input to counteract the disturbance’s influence.

In

Table 6. Overview of main methods integrating DOB and SMC.

Techniques	Year	Structures	Advantages	Disadvantages
Extended sliding mode disturbance observer (ESMDO) [158]	2021		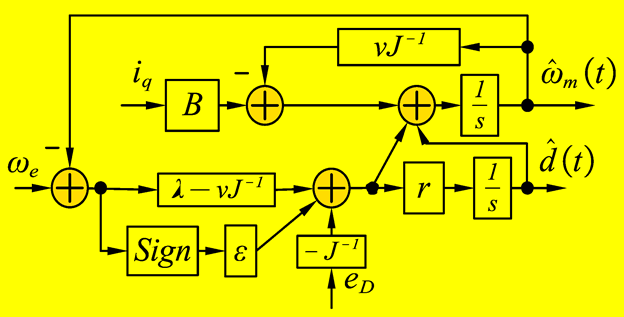✓ HRL ensures fast convergence by combining terminal and exponential reaching, while ESMDO enables precise disturbance estimation. Its variable reaching speed further suppresses chattering compared to constant-rate laws.	✓ HRL’s multiple parameters and combined exponential/terminal terms increase design complexity, while ESMDO’s observer adds computational load.
Extended sliding-mode disturbance observer (ESO) [161]	2023		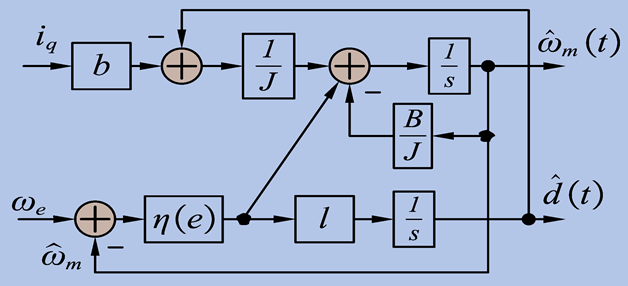✓ Integral terminal surface ensures 0.01 s overshoot-free convergence; ESO compensates disturbances; STA minimizes chattering.	✓ The gain of ESO affects convergence and noise; NSTSMC requires complex tuning of η1, η2, and STA gains (k1–k3).
DOB-Based SOSMC (DOBSOSMC) [159]	2023		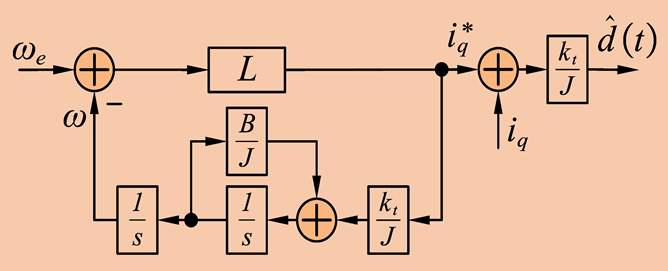✓ The method reduces chattering, applies realistic bounds, needs one DOB parameter, and ensures finite-time convergence.	✓ High α1/α2 and low η speed convergence but increase current surges, while larger DOB L improves disturbance rejection at the cost of higher noise.
Time-varying two-time scale disturbance observer (TV-TTSDO) [160]	2024		✓ TV-TTSDO improves dynamic response by eliminating initial estimation peaks, simplifying control with a single loop, and constraining q-axis current surges.	✓ ISTSMC with TV-TTSDO requires careful parameter coordination to balance convergence and chattering, while its compensation for mismatched disturbances remains limited.
Novel DOB based on iterative learning strategy (ILC-DOB) [162]	2023		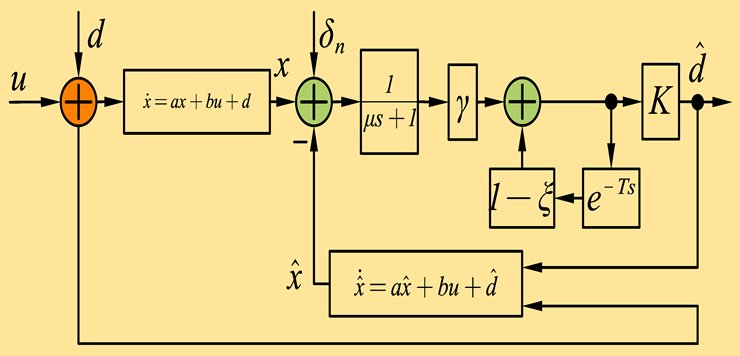✓ ILC-DOB suppresses periodic torque harmonics, FITSMC with integral terms accelerates error convergence, and sigmoid substitution protects q-axis current.	✓ Performance is limited by poor estimation of non-integral harmonics under heavy loads, while ILC dependence on historical data slows initial adaptation.

, DOB integrated with SMC methods show strong disturbance rejection and accurate tracking. ESMDO [158] tracks around −2300 rad/s² disturbances under a 10 Nm load. DOBSOSMC [159] reduces speed drop to 11 rpm and current ripple to 0.52 A, outperforming PI and SOSM. TV-TTSDO [160] removes large initial estimation peaks (around 1000), limits speed drop to 44 rpm, and recovers in 0.1 s. ESO [161] achieves zero overshoot and a 0.01 s settling time, 75–91% faster than others. ILC-DOB [162] cuts the 1st harmonic speed fluctuation at 20 rpm from 0.1272 to 0.0290 rpm and steady-state error at 100 rpm from ±1.237 to ±0.513 rpm. Robustness is demonstrated by DOBSOSMC under inertia mismatch and TV-TTSDO tolerating 30% rotor flux variation with 18 rpm fluctuation. Challenges include high computational load and complex tuning, especially for ESMDO, ESO, TV-TTSDO, and ILC-DOB. Limitations exist with fast or non-periodic disturbances and heavy loads. DOBSOSMC trades off disturbance rejection and steady-state smoothness. TV-TTSDO assumes smooth disturbances and performs worse with rapid changes. Newer methods improve accuracy and harmonic suppression but increase tuning complexity. Choose ESMDO or DOBSOSMC for high-precision systems, TV-TTSDO or DOBSOSMC for robustness under varying conditions, and ILC-DOB for low-speed, harmonic-sensitive applications with some constraints.

5.2. The Sliding Mode Observer

The fundamental principle of a state observer is to estimate system output parameters—such as position, speed, or electromagnetic torque—based on information extracted from the model. For sensorless PMSM motors, SMO is commonly employed due to its robustness and simple control structure [80] (Figure 14).

In

Table 7. Summary of SMO-Based Control Methods for PMSM Drives.

Techniques	Year	Structures	Advantages	Disadvantages
SMO+LPF+ ACPLL [163]	2024		✓ Dual-LPF pre-filter removes DC offset, ACPLL decouples speed/position and suppresses high-frequency noise, with independent cut-offs for chattering and DC rejection.	✓ Sensitive to stator inductance mismatch, requiring parameter identification, and limited low-speed performance due to pre-filter low-frequency gain.
GAHOTSMO+ QPLL [78]	2025		✓ Adaptive-gain GAHOTSMO ensures finite-time convergence, suppresses chattering, improves current/back-EMF estimation, and maintains robustness under speed/load changes.	✓ Adaptive-gain GAHOTSMO increases tuning complexity (SOSM, gain, and QPLL parameters) and computational load, though execution time remains within real-time limits.
Sigmoid SMO-CCSOSF+QPLL [164]	2025		✓ CC-SOSF offers fault tolerance under open-circuit faults (THD reduced from 28.55% to 0.08%), eliminates DC offsets via a mitigation circuit, reduces chattering using a sigmoid function without extra LPFs, and adapts across speeds with OLFE tracking motor resonance.	✓ CC-SOSF requires tuning of four interacting parameters, increasing filter design complexity, and its performance is limited on high-saliency IPMSMs (tested mainly on low-reluctance IPMSMs).
Proposed DSMO+PLL [79]	2024		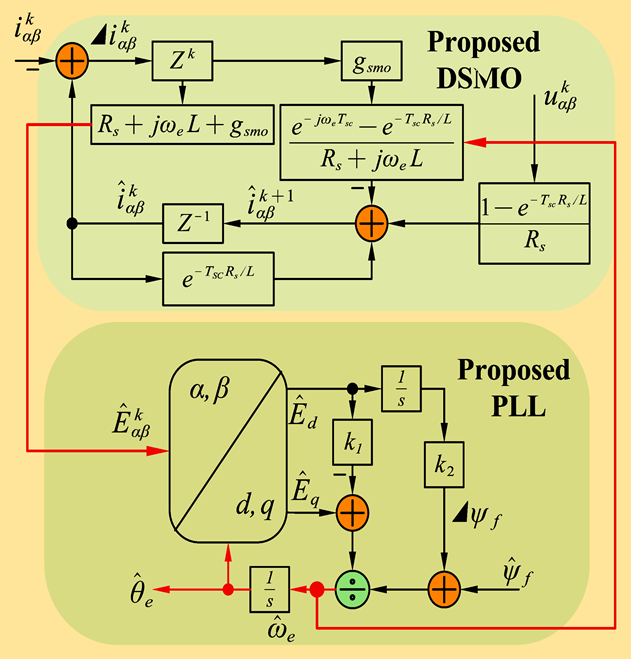✓ The proposed DSMO enhances low sampling ratio adaptability via an accurate discrete-time PMSM model, suppresses transient errors with flux-compensation PLL, and ensures stability through explicit gain conditions. Its design is simple, requiring only two key parameters with clear tuning rules.	✓ At low sampling frequencies, DSMO exhibits current ripple sensitivity, requiring load reduction to prevent overcurrent, and its PLL parameters depend on estimated speed, causing minor coupling during rapid speed changes.

the evaluation of SMO-based PMSM control methods shows significant improvements in estimation accuracy, disturbance rejection, and chattering reduction. The proposed DSMO+PLL [79] achieves near-zero position error at rated speed, outperforming the conventional SMO, which has position errors up to 24.8°. Meanwhile, SMO+LPF+ACPLL [163] reduces speed error from approximately 7–40 rpm at 300 rpm. GAHOTSMO+QPLL [78] enhances speed accuracy during load changes and reduces the sliding mode chattering range from ±410 to ±170 p.u. at 3 Nm and 500 rpm. Sigmoid SMOCCSOSF+QPLL [164] excels in harmonic suppression, lowering THD from 28.55% to 0.08%. Despite these advances, all methods face complex tuning challenges, such as multiple parameter adjustments in GAHOTSMO+QPLL and precise boundary layer design in DSMO+PLL, as well as increased computational demands—GAHOTSMO+QPLL requires 13.72 μs per cycle, 1.35 times longer than HOTSMO. Sensitivity to parameter mismatch remains an issue, causing transient errors (for example, up to ~100° position error in Sigmoid SMO during faults). Newer methods offer enhanced performance but require more complex implementation. Application-driven selection is advised: GAHOTSMO+QPLL or DSMO+PLL for high-precision needs; Sigmoid SMOCCSOSF+QPLL for strong harmonic and DC-offset rejection; and SMO+LPF+ACPLL where a balance of simplicity and moderate performance is preferred.

5.3. Linear Parameter Varying—Observer SMC

Recently, Linear Parameter Varying (LPV) control methods for nonlinear systems have attracted great attention, thanks to the ability to adjust the control coefficient according to real-time measurement parameters. LPV methods have been studied since the 1990s [165], divided into types such as Linear Time-Invariant (LTI) [166,167] and Linear Time-Varying (LTV) systems [121,160,168]. The integration of LPV with SMC has emerged as a promising direction, enabling accurate trajectory tracking under both nominal and uncertain conditions.

By representing nonlinear dynamics in a parameter-varying linear framework, LPV facilitates systematic linear controller design while preserving the fidelity of the original nonlinear system. When combined with state and disturbance observers, LPV-SMC enhances robustness and adaptability. Experimental results confirm that such integration significantly reduces speed fluctuation (from 62 to 52 rpm) and shortens settling time (from 0.25 s to 0.1 s) under abrupt load torque changes [160]. Observer-based estimation further reduces sensor dependency—potentially lowering hardware cost by up to 20% [169]—while advanced reaching laws accelerate convergence by up to 70% compared to PI control [121]. Moreover, incorporating disturbance observers helps suppress chattering and ensures smoother control signals in real-time applications [168]. Nonetheless, LPV-SMC introduces considerable design complexity, requiring careful parameter tuning and accurate modeling of system variations. Estimation errors exceeding 10% can increase tracking error by up to 30% [160], and the added computational burden raises processing time by approximately 40% on embedded platforms [121]. Additionally, its effectiveness diminishes under high-frequency disturbances (>50 Hz) due to observer limitations [168]. LPV-SMC offers a robust and adaptive control solution for nonlinear systems with structured parameter variations, though it necessitates careful co-design and sufficient computational resources for practical deployment.

6. Intelligent SMC

SMC, studied for over 50 years, remains popular for its simplicity and robustness. However, challenges like chattering, unmodeled dynamics, turbulence, uncertainty, and the need for adaptive learning and improved robustness persist. To address these issues, Artificial Intelligence (AI) has been increasingly integrated into SMC [170], offering alternative approaches for adaptive learning and control. In recent years, notable progress has been made in combining SMC with AI techniques. AI has been incorporated into sliding mode controllers for various purposes, such as improving control performance, enhancing AI-based controllers by leveraging SMC’s strengths, tuning SMC parameters both online and offline, estimating uncertainties, and mitigating chattering. Furthermore, some studies have explored the joint application of SMC, AI, and adaptive control to tackle complex control problems, such as Fuzzy Logic (FL) [171,172,173,174], Neural Networks (NNs) [62,81,175,176], Reinforcement Learning (RL) [177,178,179,180], metaheuristic (Genetic Algorithm (GA) [181], Particle Swarm Optimization (PSO) [182,183], Differential Evolution (DE) [184], Salp Swarm Algorithm (SSA) [185]), etc.

6.1. Fuzzy Logic

FL is widely used in intelligent control thanks to its ability to handle uncertain and ambiguous information, closely resembling the way humans make decisions [186]. In recent years, the integration of FL with adaptive control algorithms to develop intelligent control systems has become an important area of research. The application of FL in intelligent control is evident across various fields, including autonomous robots [187,188], UAVs and drones [189], motor control (such as PMSM, BLDC, and IMs) [171,172,173], smart energy management systems (like microgrids, fuel cells, and hybrid systems) [190,191,192], vehicle control [193], etc.

Controlling PMSM using FL combined with SMC is a modern and intelligent approach that addresses the limitations of traditional SMC, such as chattering and lack of adaptability in noisy environments or with imperfect models [174]. The Fuzzy Model-Free Adaptive Control (FMFAC) method significantly improves estimation accuracy, reducing steady-state errors in rotor speed and position compared to traditional super-twisting SMO and model-free adaptive control [174]. FL real-time dynamic adaptation of key parameters based on error magnitude and rate, enhancing performance under rapid stator current fluctuations typical in PMSM control. The model-free nature of FMFAC ensures robustness against parameter uncertainties and external disturbances. Additionally, it mitigates chattering by replacing fixed gains with fuzzy-tuned adaptive parameters, resulting in smoother signal estimation. However, the method introduces increased system complexity due to additional tuning parameters and fuzzy rule design, which requires expert knowledge and extensive validation. Computational demand is higher, needing more operations per control cycle and thus more powerful hardware.

The method integrates SMC+FL [194,195] by using a fuzzy self-tuning algorithm to adapt a key parameter based on the sliding surface and its derivative, guided by fuzzy rules, and by combining FL with segmental self-tuning to adjust another parameter, balancing response speed and chattering reduction. This approach replaces the discontinuous signum function with a smooth nonlinear function, reducing chattering while maintaining rapid convergence to the sliding surface. A load torque observer enhances disturbance rejection, enabling faster recovery and smaller speed drops under load fluctuations. The method also demonstrates superior tracking performance and robustness against parameter variations in the motor. However, it requires complex parameter tuning, relies on heuristic fuzzy rules limiting effectiveness, has low robustness to model mismatches impacting load torque observation, and is sensitive to measurement noises, slightly degrading control precision.

6.2. Neural Networks

AI methods, especially NNs, are popular due to computing advances. Integrating them with pretrained models reduces workload, boosts performance, and improves interpretability [196]. NNs have been widely applied in various control systems due to their strong learning and approximation capabilities, including robotics control [197,198,199], industrial control [200,201], vehicle control [61,202], and renewable energy systems [203]. In motor control, NNs are integrated with adaptive strategies to exploit fault tolerance, parallel processing, and learning capabilities [204,205,206]. Among these, NNs-based SMC has gained significant traction and has been effectively implemented in diverse control scenarios [61,81,202,207,208,209].

In the PMSM control system, combining SMC with NNs creates a hybrid control strategy that reduces chattering and enhances overall performance compared to traditional SMC controllers [62,81,210,211]. SMC provides inherent resilience to disturbances, while NNs—such as radial basis function (RBF) [81] and adaptive NNs [210]—enable online estimation and compensation of unknown nonlinearities, reducing the need for high switching gains. This integration mitigates chattering by using smooth control actions and adaptive gain tuning [62]. Fixed-time and finite-time schemes enhance dynamics by enabling faster response and improved tracking accuracy. NNs also support real-time adaptation to parameter variations and nonlinearity, improving performance under varying loads and operating conditions. The approach is compatible with advanced SMC variants (for example, high-order, integral, and fixed-time SMC), and system stability is rigorously proven via Lyapunov theory. Experimental results demonstrate the practical effectiveness of SMC+NNs composite controllers—for instance, the DFNN-based SMC [211] improves speed control accuracy by 5.9% compared to PID and 26.9% compared to traditional SMC, while the composite controller maintains stable performance even with ±20% variation in the moment of inertia [81].

6.3. Reinforcement Learning

In PMSM motor control systems, the integration of SMC and RL forms a hybrid strategy that combines the robustness of SMC with the adaptive optimization capabilities of RL [177,179,180]. This approach improves dynamic performance, reduces chattering, adapts to diverse disturbances, and ensures system stability, making it well-suited for high-precision and high-reliability applications. First, RL enables adaptive parameter optimization by tuning sliding mode gains, fractional orders, and switching coefficients, thereby improving control precision and eliminating the need for manual tuning. Studies using RL-TD3 [179] and RLNNA [180] demonstrate enhanced convergence and reduced steady-state errors. Second, RL agents provide real-time correction to SMC output signals, increasing disturbance rejection and robustness under parameter uncertainties, as shown in MARL-based frameworks [177]. Third, chattering suppression is achieved through RL-optimized switching actions and fractional-order surfaces, reducing current ripple and mechanical wear. Fourth, enhanced adaptability to multi-scenario disturbances is realized through offline training and online generalization, with stable performance maintained under wide-ranging load and parameter variations. Fifth, theoretical stability is ensured via Lyapunov-based analysis, confirming asymptotic convergence of tracking errors. Finally, offline-trained RL networks improve real-time feasibility by reducing computational load, supporting fast sampling cycles suitable for embedded control platforms.

6.4. Metaheuristic Algorithms

Metaheuristic algorithms are broadly classified based on their underlying principles, such as evolutionary algorithms (for example, GA, DE), swarm intelligence methods (for example, PSO, SSA), and physics-based approaches (for example, Simulated Annealing). These algorithms offer efficient strategies for exploring complex, non-convex search spaces by balancing global exploration and local exploitation.

In PMSM control, the integration of SMC with metaheuristic algorithms—such as GA [181], DE [184], PSO [182,183], and SSA [185]—forms a robust hybrid strategy. This approach addresses key limitations of conventional SMC, including manual parameter tuning, chattering, and limited adaptability under varying operating conditions. GA [181], or its improved variants, optimize nonlinear reaching laws by adaptively adjusting crossover and mutation probabilities based on fitness values, maintaining an effective balance between exploration and exploitation. As a result, improved GA-optimized SMC enhances dynamic performance, achieving faster response, reduced overshoot, and improved robustness. For example, improved GA-based SMC achieves 0.035 s startup without overshoots, and with ESO, effectively mitigates speed drops under disturbances. Additionally, GA helps reduce chattering by shaping the reaching law and minimizing reliance on large switching gains. Experimental results [181] confirm that current and torque ripple are significantly reduced compared to conventional SMC.

PSO is employed to tune critical parameters of SMC—such as reaching law coefficients and equivalent control gains—by minimizing fitness functions that balance tracking accuracy and control effort. In specialized applications like bearingless PMSMs used in blood pumps, hybrid GA-PSO [183] further improves control precision, maintaining rotor suspension with sub-millimeter displacement errors under disturbance. Beyond dynamic response, PSO [182]-optimized SMC enhances robustness and reduces energy consumptions by minimizing control effort RMS values, while maintaining stable performance under load variations. The method also helps reduce overshoot and response time, with rotor speed overshoot reductions of over 60% in some cases. PSO-enhanced SMC significantly improves PMSM control performance by intelligently tuning control parameters and enhancing system adaptability. Despite higher computational cost, it suits precision applications demanding accuracy, robustness, and energy efficiency.

In PMSM control, combining SMC with metaheuristic algorithms like DE and SSA enhances performance through global optimization. SMC+DE [184] focuses on precise tuning of fuzzy SMC parameters. An improved DE dynamically adjusts mutation (F) and crossover (CR) factors, optimizing fuzzy boundaries and switching gains to reduce chattering and overshoot. It achieves faster current response (0.17 s) and lower speed errors (0–2 rpm), making it suitable for high-precision, low-disturbance applications. In contrast, SMC+SSA [185], particularly with Improved SSA (ISSA), targets fractional-order SMC and load torque observers. Using chaotic initialization and adaptive inertia weights, ISSA enhances convergence and robustness. It significantly reduces speed drops under load (2.11% versus 8.7% in SMC) and achieves no overshoot with rapid stabilization (0.025 s at 1000 rpm). SMC with improved DE offers high accuracy and moderate complexity, while SMC with improved SSA enhances the global search and disturbance rejection at the cost of higher computational load from fractional calculus.

The

Table 8. Summary of Intelligent Approaches Integrated with SMC.

Methods	Advantages	Disadvantages	Application Features
SMC+FL	✓ Chattering Suppression: Speed MAE from 1.339 to 0.516, position MAE from 0.044 to 0.035 rad [172]; ✓ Disturbance Rejection: 46% RMS error reduction; efficiency: Control updates reduced from 52.88% to 49.71% [173].	✓ High complexity from fuzzy logic integration; difficult tuning with 8+ variables, sensitive to calibration; limited in ultra-fast systems due to discrete FL updates [172].	✓ PMSM: Ideal for industrial drives, robotics, and EVs requiring precise control; ✓ Disturbance-Rich Systems: Effective for systems with unknown or time-varying disturbances [174]; ✓ Resource-Constrained Networks: Event-triggered SMC +FL reduces data and computation [173].
SMC+NN	✓ Enhanced Dynamics: Fixed-time SMC with RBF-NN converges faster (2.64 s versus 4.54 s PI) [210], near-zero disturbance rejection [81], and ANN-ISMC reduces current error (0.604 A at 500 rpm, 4.75 Nm), outperforming PI/DPCC [62].	✓ High Complexity: NN-SMC increases load and delay (0.05838 ms versus 0.00076 ms for PI); tuning-sensitive, needing precise adjustment [62,81,210].	✓ Precision PMSM: Ideal for robotics, aerospace, and servo drives with high accuracy [81,210]; ✓ Low-Speed Control: Compensates friction and cogging torque for better low-speed accuracy [81]; ✓ Robustness: Stable under load variations and parameter mismatches [62].
SMC+NN +FL	✓ SMC+NN+FL improves speed control (5.9% versus PID, 26.9% versus SMC), reduces estimation error (11.4% PI, 51.9% SMC), and minimizes chattering under load/disturbances [211].	✓ Complex tuning, heavy computation, and model sensitivity hinder real-time use and require intensive maintenance [211].	✓ High-Precision: Ideal for robotics and CNC; ensures accurate control [211]; ✓ Robust in complex conditions: adapting to EVs, wind turbines, and varying loads [211]; ✓ Adaptive: Maintains stability in fast-changing systems, for example, EVs [211].
SMC+RL	✓ Robust with MARL delay 0.4 ms versus 2.1 ms SMC [177,179]; SMC+RL reduces ITAE by 40.2%, RL-TD3 trims step time by 0.9 ms [179,180]; Auto-tuning via RL lowers ISE by 11.3% [180].	✓ High load (MARL-SMC +12% CPU, RL-TD3 10.5 hrs) [177], [179]; training-sensitive (<150 episodes increase ripple 30%, unseen speeds increase ITAE 22%) [179,180].	✓ High-Dynamic: MARL-SMC stable at 10 kHz for EVs/robots [177]; ✓ Sensorless: SMC+RL keeps position error < 0.5 rad [179]; ✓ Handles Variations: SMC+RL cuts error 46% at 50% inertia change [180].
SMC+ Improved GA	✓ IGA achieves 53% fewer iterations, 78% faster startup than PID, with 3.2% speed drop under load, outperforming PID/SMC. Optimized reaching law reduces chattering, and adaptive search cuts steady error by 75% at 1000 rpm [181].	✓ High computational load (requires powerful hardware), parameter sensitivity slows convergence, and less effective above 3000 rpm due to tuning lag [181].	✓ High-Precision Drives: 0% overshoot, 0.035 s adjustment, ideal for CNC/robots [181]; ✓ Robust to Disturbance: Stable under load; only 43 rpm drop—suitable for EVs, wind systems [181]; ✓ Rapid Prototyping: Real-time ready such as dSPACE for fast deployment.
SMC+PSO	✓ Position error reduced by up to 98.8%, velocity error by 95.2% versus PID [182]; chattering reduced (67.2% overshoot, 87.5% offset) [182,183]. RMS effort down 3.9%, ITAE by 95.6% [182]. Recovery time 90% faster than PID/SMC [182,183].	✓ SMC+PSO takes 20.1 s versus 3.6 s (PID), limiting real-time use and Limited for irregular tasks with 15% higher tracking error versus adaptive control [182]; poor PSO tuning increases ITAE by 12% [182].	✓ Precision Servo: 0.002 rad position error, 0.035 mm accuracy—ideal for robotics and wafer stages [182,183]; ✓ Medical: Rotor stable 0.015 mm; 4.89 L/min flow; lowers hemolysis risk [182]; ✓ Energy-Efficient: Saves 8–10% energy in EVs and wind turbines [182].
SMC+ Improved DE	✓ Chattering-free (0 A overshoot versus 0.75 A SMC, 0.3 A FSMC), zero overshoot in sim/exp (SMC: 145.5 rpm, FSMC: 30 rpm), faster recovery (0.2 s versus 0.5 s SMC, 0.4 s FSMC), high robustness (1.2/50 rpm versus 5.5/150 SMC, 3/91 FSMC) [184].	✓ High computation (DE adds load versus SMC/FSMC), tuning sensitivity (depends on parameter choice), limited transferability (fuzzy rules PMSM-specific, re-tuning needed for other motors) [184].	✓ High-Performance PMSM Servo Systems: Designed for precision machines and aerospace systems requiring fast and accurate response [184]; ✓ Robust under load and speed changes: Maintains stable three-phase currents and consistent speed under external disturbances.
SMC+ Improved SSA	✓ IGA achieves fast convergence (53% fewer iterations, 0.035 s startup, 78% faster than PID), robust performance (3.2% speed drop versus 17.5% PID, 11% SMC), chattering-free operation, and IGA-optimized reaching law removes steady oscillations [185].	✓ High computational load (requires powerful hardware), parameter sensitivity may cause slow convergence, and less effective above 3000 rpm due to tuning lag [185].	✓ High-Precision Drives: 0% overshoot, 0.035 s rise (1000→1200 rpm)—ideal for CNC, robots [185]; ✓ Disturbance Resilience: Stable under load; only 43 rpm drop—suitable for EVs, wind turbines [185]; ✓ Rapid Prototyping: Supports real-time platforms for fast deployment.

presents intelligent approaches integrating with SMC, namely combinations with FL, NNs, RL, and Metaheuristic Algorithms. SMC+FL curbs chattering via adaptive gains, boasts disturbance robustness and fixed-time convergence, yet hinges on experiential fuzzy rules and adds complexity, serving position-tracking tasks. SMC+NNs trims chattering through online disturbance approximation, bolsters parameter mismatch robustness, and boosts speed estimation, though its complex network demands careful tuning and Jacobian reliance, fitting high-precision servo and low-speed PMSM control. SMC+NNs+FL enables adaptive sliding mode gain and parameter variation robustness but suffers from complex structure, long training, and high real-time complexity, applied in sensorless PMSM vector control. SMC+RL cuts tracking ripples, delivers superior speed performance, fast convergence, and local optima avoidance, yet incurs high real-time complexity, used for sensorless speed control. Metaheuristic pairings like SMC+Improved GA optimize parameters and energy, though prone to local optima; SMC+PSO trims chattering and resists interference but converges slowly in complex systems; SMC+Improved DE speeds response but is sensitive to factors; SMC+Improved SSA resists interference but converges slowly, each catering to specific tuning or control tasks.

Advanced SMC+FL controllers for PMSM encounter DSP overload, sensor noise [172], and parameter drift with chattering-induced IGBT losses [174], limiting real-time stability in compact drives. SMC with metaheuristic algorithms also face hardware constraints: Improved DE causes MCU overload and current overshoot [184]; improved SSA introduces DSP latency and low-frequency degradation [185]; PSO increases simulation and memory demands on TMS320F28379D [182]; and raises control latency and sensing cost in bearingless drives [183]. SMC+NN approaches impose heavy DSP loads and high sampling requirements for low-speed accuracy [81], increase computation time and THD mitigation costs on TMS320F28075 [62], and demand high-frequency sampling with precision encoders to address parameter variations [210]. SMC+RL controllers further strain hardware: increases real-time load and settling time on low-end DSPs [177]; requires long training and exceeds the capacity of the S32K144 MCU, raising current ripple by 5% under load [179]; and demands 8 GB RAM for tuning, with 12-bit ADC sampling reducing ITAE gains from 42% to 28% [180].

In summary, integrating SMC with metaheuristic algorithms (for example, GA, DE, PSO, SSA) offers an effective hybrid strategy for PMSM parameter optimization. This approach addresses conventional SMC limitations such as manual tuning, chattering, and poor adaptability. By optimizing sliding gains and other key parameters, hybrid methods improve dynamic performance, reduce overshoot and torque ripple, and enhance robustness against disturbances. However, the associated training and optimization processes require substantial computational resources, and complex algorithm design significantly increases controller capacity demands. Despite these challenges, such intelligent strategies provide adaptive and high-precision solutions for PMSM control.

7. Discussions and Future Research Trends

This paper presents an overview of SMC applied to PMSM control, a field of active and ongoing research. For highly nonlinear systems with complex dynamics, SMC has attracted significant attention due to its inherent robustness against external disturbances and parameter uncertainties. Although conventional SMC has demonstrated strong performance in practical applications, limitations such as chattering remain significant—particularly in nonlinear control scenarios. Recent advancements have significantly enhanced SMC performance, enabling new research and application opportunities.

As shown in

Table 9. Comparative Analysis of Reviewed SMC Strategies for PMSM Drives.

Methods	Advantages	Disadvantages	Application Features
Reaching law approach	✓ Simple, fast convergence, disturbance rejection.	✓ Chattering-robustness trade-off, model dependence.	✓ Basic PMSM speed/current control.
Sliding surface design	✓ Speed response, noise immunity, convergence.	✓ Residual chattering, complex tuning.	✓ Servo systems, load-variation environments.
SOSMC	✓ Finite-time stability, derivative-free, fewer params.	✓ Computational load, tuning sensitivity.	✓ Precision control, disturbance-prone systems.
AOSMC	✓ Smoother control, derivative independence.	✓ Noise sensitivity, complex algorithms.	✓ High-precision robotics, theory-driven research.
Observer based SMC	✓ Disturbance compensation, noise suppression.	✓ Model dependence, filter complexity.	✓ Disturbance-rich systems (harmonics, load changes).
Intelligent SMC	✓ Adaptive performance, anti-interference.	✓ Local optima, expert knowledge needed.	✓ Complex conditions (sensorless, torque ripple).

, SMC methods are evaluated across four key dimensions: chattering mitigation, robustness, control performance, and computational complexity. Chattering is addressed using various strategies—structural tuning in reaching law and sliding surface design, higher-order dynamics in SOSMC and AOSMC, smooth functions in observer-based SMC, and adaptive or intelligent algorithms in intelligent SMC. All approaches retain the core robustness of SMC, with observer-based and intelligent SMC demonstrating superior disturbance rejection. SOSMC enhances resilience to uncertainties, while AOSMC maintains robustness with reduced chattering.

Sliding surface design and SOSMC improve speed and accuracy, observer-based SMC enhances transients, and intelligent SMC improves tracking and estimation. Complexity increases from simpler reaching law and sliding surface methods to more advanced AOSMC (differentiator design), observer-based SMC (model and filter dependence), and intelligent SMC (requiring NN/GA/RL-based tuning).

The reviewed literature confirms that SMC has been extensively studied and widely implemented in PMSM applications. As industrial demands for PMSM systems continue to evolve, future progress must focus not only on structural motor optimization [212,213,214] but also on the continued advancement of control algorithms. This section presents future research directions for advancing SMC in PMSM applications.

7.1. Integration and Hybridization of SMC with Advanced Control Methods and Intelligent Algorithms

SMC will increasingly be integrated with other methods and intelligent algorithms to broaden application scope, optimize parameter tuning, and enhance adaptability, stability, and overall performance. Normally, SMC parameters are selected based on experience, analytical methods, or experimental tuning. This approach is simple but does not guarantee optimal performance or stability, particularly in high-order SMCs with many parameters. Parameter selection must balance chattering suppression, fast response, and system stability. In practice, only one condition is often satisfied: with a small gain [97], chattering is reduced but convergence is slow and noise-sensitive; with a large gain, convergence is fast and robust to load changes but chattering is severe. Thus, parameter adjustment requires a trade-off tailored to practical applications, as it is impossible to optimize all conditions simultaneously [141,146]. Applying SMC in combination with intelligent algorithms enhances SMC’s robustness to nonlinearities and uncertainties, while the intelligent algorithms adapt control gains in real time, overcoming the limitations of traditional SMC with fixed parameters. In intelligent transportation, an RBFNN-based data-driven FTSMC coordinates multi-agent subway trains, ensuring speed consensus tracking, safe distance maintenance, and decentralized control under unknown nonlinear dynamics and external disturbances. Moreover, combining SMC with intelligent algorithms such as Memristive NNs (MNN) with LPV [215], and Deep RL (DRL) [216,217] enables adaptive gain scheduling and enhances robustness under dynamic operating conditions.

Integrating SMC with advanced methods overcomes traditional limitations such as fixed gains, chattering, slow convergence, and poor adaptability. Combining SMC with fixed-time stability ensures convergence within a predefined time and suppresses chattering [218,219]. Integration with MPC/EMPC enables online parameter optimization and constraint compliance, reducing tracking errors and computational load [220,221]. Enhanced disturbance rejection is achieved by combining SMC with observers or neural networks, such as RBFNN-based UAV controllers [222], which maintain precise tracking under external disturbances. Overall, these hybrid SMC strategies deliver fast, chattering-free convergence, constraint compliance, and high adaptability for critical applications like grid restoration, autonomous vehicles, and industrial servos.

7.2. Advanced Techniques for Minimizing Chattering in SMC

The chattering phenomenon in SMC control, discussed in Section 4.4, shows that it is difficult to completely eliminate using different functions. Advanced sliding surface design and reaching law strategies—such as HOSMC [81,223]—offer smoother control signals with reduced chattering, without sacrificing convergence speed or robustness. Ongoing advances in saturation functions and adaptive gain tuning are expected to enhance transient response and steady-state accuracy, crucial for high-precision applications like robotics, aerospace, and medical devices.

7.3. Model-Free and Data-Driven SMC

Model-dependent SMC requires accurate system models, limiting performance under unknown nonlinear dynamics, MIMO coupling, or hybrid network attacks. Fully distributed MFASMC uses data-driven dynamic linearization with pseudo-partial derivatives and attack compensation mechanisms, ensuring bounded consensus errors in MASs under DoS/FDI attacks and reducing MSE by ~40% versus traditional MFAC [224]. MFA-SMC for SMA-actuated parallel platforms employs pseudo-Jacobian matrix estimation from I/O data, providing UUB tracking errors with MAE < 0.07° while reducing sensor requirements [225]. These model-free and data-driven approaches eliminate reliance on precise modeling, adapt to unknown disturbances, and handle complex MIMO and security challenges. Overall, they outperform model-dependent SMC in robustness, accuracy, and practical applicability for nonlinear, uncertain, or attack-prone systems.

7.4. Enhancing SMC Reliability Through Fault-Tolerant Design

Fault-tolerant SMC design [226,227,228,229] is a critical area for safety-critical applications. Recent studies combine SMO with control methods such as FL [229] or Backstepping Control (BSC) [228] to achieve active fault tolerance with fault detection and reconfiguration, ensuring minimal speed tracking error and robustness to parameter variations. Future research should integrate fault diagnosis and isolation into the SMC framework, enabling real-time detection, adaptation, and recovery from actuator, sensor, or communication faults—crucial for autonomous systems, medical devices, and mission-critical applications.

8. Conclusions

This paper offers a comprehensive review of recent research and advancements in SMC techniques applied to PMSM. The current classification frameworks, as refined, comprehensively cover fundamental elements such as reaching laws, sliding surfaces, and Lyapunov or ISS stability analysis, alongside advanced designs including HOSMC, observer-based strategies, and intelligent algorithms integrations. Together, these components lay a solid foundation for robust PMSM control, effectively addressing disturbances, parameter variations, and diverse operating conditions.

The development of SMC for PMSM control is expected to advance through deeper interdisciplinary integration. Hybrid frameworks, such as SMC combined with LPV methods, are anticipated to gain prominence for effectively handling complex, time-varying dynamics. Fault-tolerant and extreme-condition SMC will become increasingly essential in safety-critical domains like automotive and aerospace, where reliability under uncertainty is paramount. Intelligent SMC, leveraging FL, DRL, NNs, and metaheuristic algorithms, will enable self-optimizing and transparent control strategies. Current trends also highlight the integration of intelligent algorithms, high-order designs, and fault-tolerant schemes to address challenges such as chattering, parameter uncertainties, and hardware constraints. Real-time implementation will depend on high-performance processors, efficient memory, reliable converters, and hardware-in-the-loop validation, while hardware acceleration and adaptive tuning will further enhance robustness and applicability. Ultimately, SMC for PMSMs is evolving into an adaptive, intelligent, and application-oriented paradigm capable of meeting the growing demands of modern high-performance motor systems.