DAPO: Mobility-Aware Joint Optimization of Model Partitioning and Task Offloading for Edge LLM Inference

Abstract

Deploying Large Language Models (LLMs) in edge environments faces two major challenges: (i) the conflict between limited device resources and high computational demands, and (ii) the dynamic impact of user mobility on model partitioning and task offloading decisions. To address these challenges, this paper proposes the Dynamic Adaptive Partitioning and Offloading (DAPO) framework, an intelligent solution for multi-user, multi-edge Mobile Edge Intelligence (MEI) systems. DAPO employs a Deep Deterministic Policy Gradient (DDPG) algorithm to jointly optimize the model partition point and the task offloading destination. By mapping continuous policy outputs onto valid discrete actions, DAPO efficiently addresses the high-dimensional hybrid action space and dynamically adapts to user mobility. Through extensive simulations, we demonstrate that DAPO outperforms baseline strategies and mainstream RL methods, achieving up to 27% lower latency and 18% lower energy consumption compared to PPO and A2C, while maintaining fast convergence and scalability in dynamic mobile environments.

1. Introduction

With the rapid proliferation of Internet of Things (IoT) devices and the continuous evolution of Artificial Intelligence (AI) technologies, the deep integration of edge computing and AI has become a pivotal trend in contemporary information technology [1]. A particularly promising research frontier is the construction of on-device intelligent agents capable of autonomous perception, decision-making, and action, thereby enabling more personalized and context-aware services. In recent years, foundation models with tens of billions of parameters—exemplified by GPT-4, Claude 3, and Llama 3—have begun to migrate from cloud platforms to edge environments, accelerating the shift from centralized cloud intelligence to distributed edge intelligence.

However, this transition introduces new challenges. Due to their high complexity and computational intensity, Large Language Models demand substantial computational resources to ensure high-precision inference [2], posing a severe challenge for mobile devices with limited computational and energy resources. Although edge servers provide relatively abundant computational capabilities [3], offloading the entire inference task to an edge server can lead to a surge in communication overhead, and the resulting communication latency is unacceptable for delay-sensitive applications such as autonomous driving and augmented reality (AR). Consequently, balancing the trade-off between computational resource constraints and communication overhead has become a critical bottleneck that urgently needs to be addressed in collaborative inference between mobile devices and edge servers.

To effectively mitigate this bottleneck, Edge Intelligence (EI) [4,5] has emerged as a promising solution. EI partitions a large AI model into several segments, executing the less computationally demanding parts locally on the mobile device while offloading the computationally intensive parts to an edge server. This device–edge collaborative inference approach enables efficient resource utilization and latency reduction. In this process, the model’s partition point determines the computational load on both the device and the edge server, which in turn affects the overall inference latency and energy consumption. Excessive on-device computation significantly increases energy consumption, whereas excessive offloading to the edge can incur high communication latency. Therefore, dynamically selecting the optimal partition point is crucial for achieving efficient collaborative inference.

While a substantial body of existing research [6,7,8,9,10,11,12,13] focuses on optimizing the selection of the model partition point, these studies often overlook user mobility in Mobile Edge Computing (MEC) scenarios. In practical applications, users are often in constant motion, frequently traversing the coverage areas of different edge servers. This implies that, in addition to the model partitioning decision, it is also necessary to dynamically determine the target edge server for the inference task to ensure its continuity and efficiency. Particularly in mobile scenarios, the challenge lies in how to effectively readjust the model partition point and task offloading strategy when a user moves into the service range of a new edge server to maintain optimal latency and energy performance. This presents a research problem that is both theoretically challenging and practically relevant.

To address the aforementioned issues, this paper focuses on a multi-user, multi-edge server collaborative inference scenario. We propose the Dynamic Adaptive Partitioning and Offloading (DAPO) framework, which dynamically determines the optimal model partition point and edge server destination. By comprehensively considering a mobile device’s resource constraints, energy limitations, and communication latency, DAPO aims to minimize the overall latency and energy overhead of the collaborative inference process. A key challenge is that the simultaneous optimization of partition points and server selections creates a high-dimensional, mixed-action space, leading to the curse of dimensionality. To tackle this, DAPO employs a Deep Deterministic Policy Gradient (DDPG) algorithm, which utilizes an actor network to navigate this complex space by mapping its continuous outputs to discrete decisions.

The main contributions of this article are as follows:

(1)

We formulate the joint optimization problem of model partitioning and multi-server offloading in mobility-aware LLM inference as a Mixed-Integer Nonlinear Programming (MINLP) problem, explicitly modeling user mobility, multi-user competition, and system constraints.

(2)

We design the DAPO framework based on the DDPG algorithm, which maps continuous policy outputs into valid discrete actions, thereby effectively handling the high-dimensional hybrid action space of partitioning and offloading decisions.

(3)

We implement DAPO in a simulation platform and evaluate it against multiple baselines, providing detailed analyses of convergence, scalability, and robustness under varying user densities and bandwidth conditions. And the experimental results demonstrate that DAPO significantly outperforms static strategies and mainstream RL baselines in terms of reducing latency and energy consumption.

2. Related Work

In recent years, the deep integration of MEC and AI has emerged as a prominent research area. Extensive research has focused on optimizing inference task offloading and model partitioning strategies to balance performance and overhead on resource-constrained mobile devices.

The existing literature has thoroughly explored various architectures and paradigms for collaborative inference. One prominent approach is vertical collaboration across the device–edge–cloud continuum. For instance, DADS [11] enables efficient collaborative inference in dynamic networks by adaptively partitioning DNNs structured as Directed Acyclic Graphs (DAGs). JointDNN [9] develops a hierarchical optimization engine for device–cloud synergy, facilitating the efficient execution of not only inference, but also training tasks. To enhance flexibility in computation distribution, the framework in [8] introduces an adaptive multi-point partitioning method, allowing for computation tasks to be flexibly deployed on the end device and multiple edge nodes. An alternative paradigm is horizontal collaboration among peer devices. CoopAI [7] enables parallel inference across multiple devices by employing model tiling and pre-fetching mechanisms. MeDNN [14] integrates adaptive partitioning with structured pruning to achieve efficient distributed inference among a group of mobile devices. Furthermore, DeepThings [15] presents an adaptive distributed CNN inference framework tailored for highly resource-constrained IoT edge clusters. To better cope with network volatility, a more recent trend involves the deep integration of model partitioning with dynamic early-exit mechanisms. For example, MAMO [6] achieves efficient collaboration in dynamic networks by jointly optimizing exit point selection, model partitioning, and resource allocation. Likewise, DPDS [10] improves the collaborative efficiency of multi-exit DNNs at the edge through dynamic exit design and fine-grained partitioning. The Edgent [13] framework integrates adaptive model partitioning with early-exit mechanisms to dynamically adjust inference strategies in response to network changes. Moreover, the SPINN [16] system employs device–cloud co-design and progressive inference to dynamically and jointly optimize model partitioning and early-exit policies, ensuring both efficient and robust performance under volatile network conditions. In addition, Ref. [17] has summarized edge intelligence techniques for resource-limited environments, highlighting model compression, compiler optimization, and hardware–software co-design for efficient edge deployment.

To enable these collaborative frameworks to achieve optimal decision-making in complex environments, advanced optimization algorithms and learning methods have been widely applied. In vehicular edge computing, Ref. [18] proposes a digital twin-assisted task offloading framework which integrates clustering with the TD3 algorithm to optimize latency and energy efficiency. Among these, Deep Reinforcement Learning (DRL) has emerged as a mainstream technique for addressing dynamic environments. For instance, DPTO [19] leverages DRL to find a jointly optimal partitioning and offloading strategy for mobile devices that minimizes both energy consumption and latency under dynamic communication conditions. EdgeM [20], on the other hand, combines task offloading with dynamic DNN pruning and utilizes reinforcement learning to adaptively adjust the model execution policy, thereby achieving a co-optimization of latency, accuracy, and energy. To address the challenges of Large Language Model inference, the work in [21] innovatively proposes a model-based reinforcement learning framework to optimize partition points, which efficiently evaluates different partitioning strategies via a surrogate reward model. Beyond DRL, other optimization methods have also been employed in specific scenarios. For example, the IAO algorithm [12] employs iterative alternating optimization to address the problem of DNN partitioning and resource allocation in multi-user resource-constrained environments. Concurrently, some studies have begun to incorporate more specific real-world factors. For instance, MCSA [22] accounts for both user mobility and energy costs, designing the Li-GD and MLi-GD optimization algorithms for stationary and mobile scenarios, respectively. Ref. [23] summarize optimization techniques, such as pruning and quantization, and highlight applications across domains, such as healthcare and energy, on intelligent edge computing.

Despite the significant progress achieved by these works, they often overlook the complexity of real-world mobile scenarios or face challenges in handling joint decision-making. In particular, mobility-aware studies such as [19,22] rely on conventional RL algorithms that struggle with inefficient exploration and the curse of dimensionality when jointly optimizing discrete model split points and discrete edge server selections in a high-dimensional hybrid action space. Furthermore, these studies have predominantly focused on conventional models such as CNNs. A unified and efficient end-to-end decision-making framework for optimizing the collaborative inference of Transformer-based LLMs in scenarios with continuous user mobility remains a notable gap. This represents the core challenge that our work aims to address. In addition, we also investigated several non-RL optimization approaches, such as genetic algorithms and heuristic-based search methods, during the early stage of our research. While these approaches can provide feasible solutions in small-scale or static settings, they are essentially offline optimization algorithms that require extensive search and prior knowledge of the environment. As a result, they often incur high computational overhead and fail to adapt to highly dynamic MEC scenarios with user mobility. Our preliminary experiments confirmed that such non-RL approaches yielded inferior performance in terms of latency and scalability compared to RL-based methods. Therefore, we focus on reinforcement learning, which is inherently more suitable for real time, adaptive decision-making in dynamic mobile edge intelligence systems.

3. System Model and Problem Formulation

We consider a MEI system that supports device–edge collaborative inference. In this system, resource-constrained Mobile Devices (MDs), denoted by the set $\mathcal{N}=\{1,2,\dots ,N\}$, move within the coverage area of a set of Edge Servers (ESs), denoted by $\mathcal{M}=\{1,2,\dots ,M\}$. Each MD has an independent and computationally intensive inference task to execute. As illustrated in Figure 1, each mobile device can dynamically select an edge server for collaborative inference based on real time channel conditions and computational resources.

This work focuses on edge inference for large-scale Transformer models (such as Llama or GPT). We assume the model has a total of L layers. For the inference task of MD n, $s_n\in [0,L]$ denotes its model split point, and $a_n\in \mathcal{M}$ denotes its task offloading point. That is, layers 1–$s_n$ of the model are computed locally on MD n, while layers $(s_n+1)$–L are offloaded to ES $a_n$ for inference computation. For convenience, we introduce a task allocation variable:

$$a_{n,m}=\left\{\begin{array}{cc}1,\hfill & a_n=m\hfill \\ 0,\hfill & a_n\ne m\hfill \end{array}\right.$$

where $a_{n,m}=1$ means that the last $L-s_n$ layers of MD n’s inference task are assigned to ES m for execution.

In this section, we introduce the system model of this paper from four aspects, a user mobility model, communication model, and computation offloading model, and then formulate the problem.

Table 1. Notation definition.

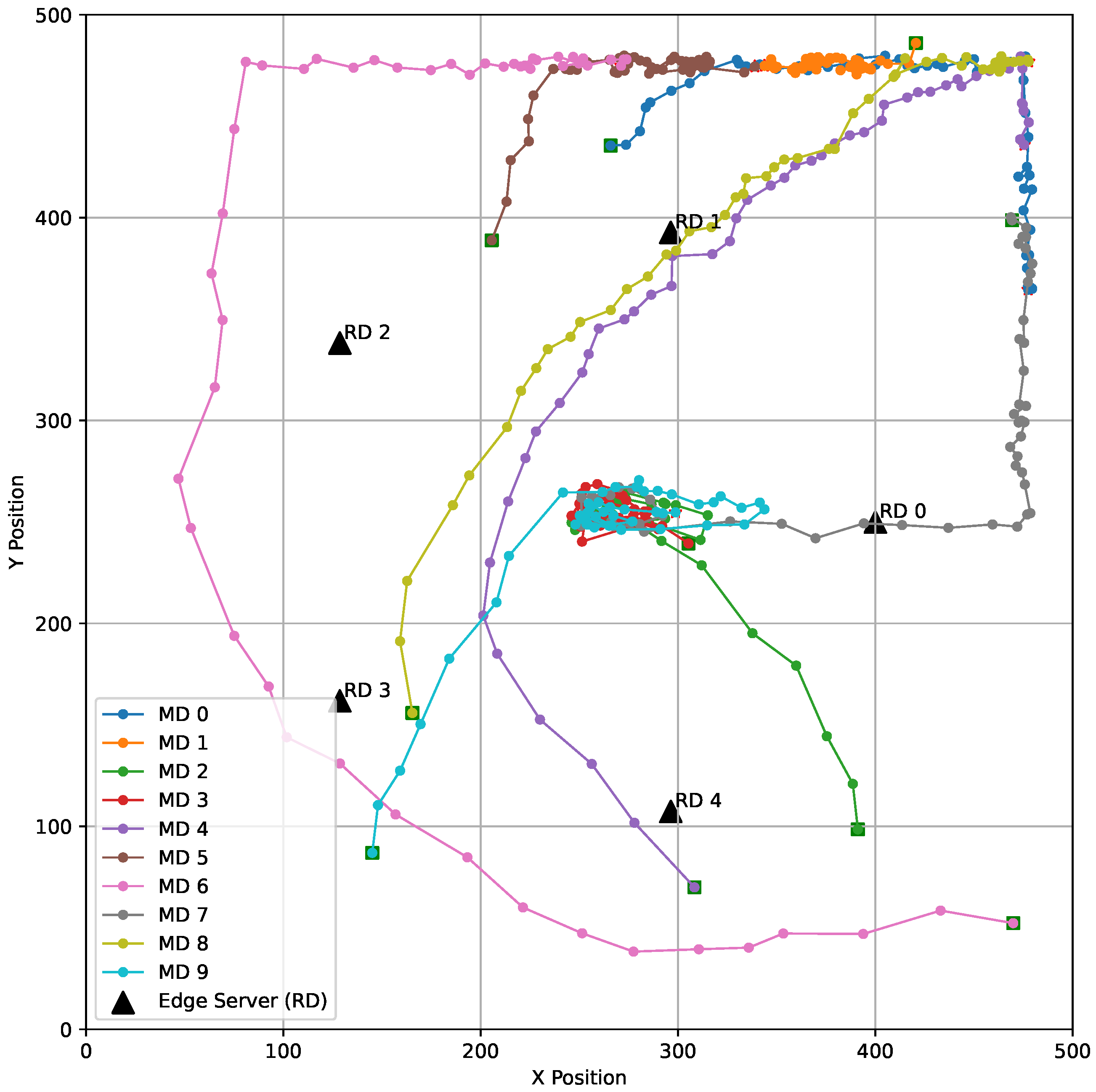
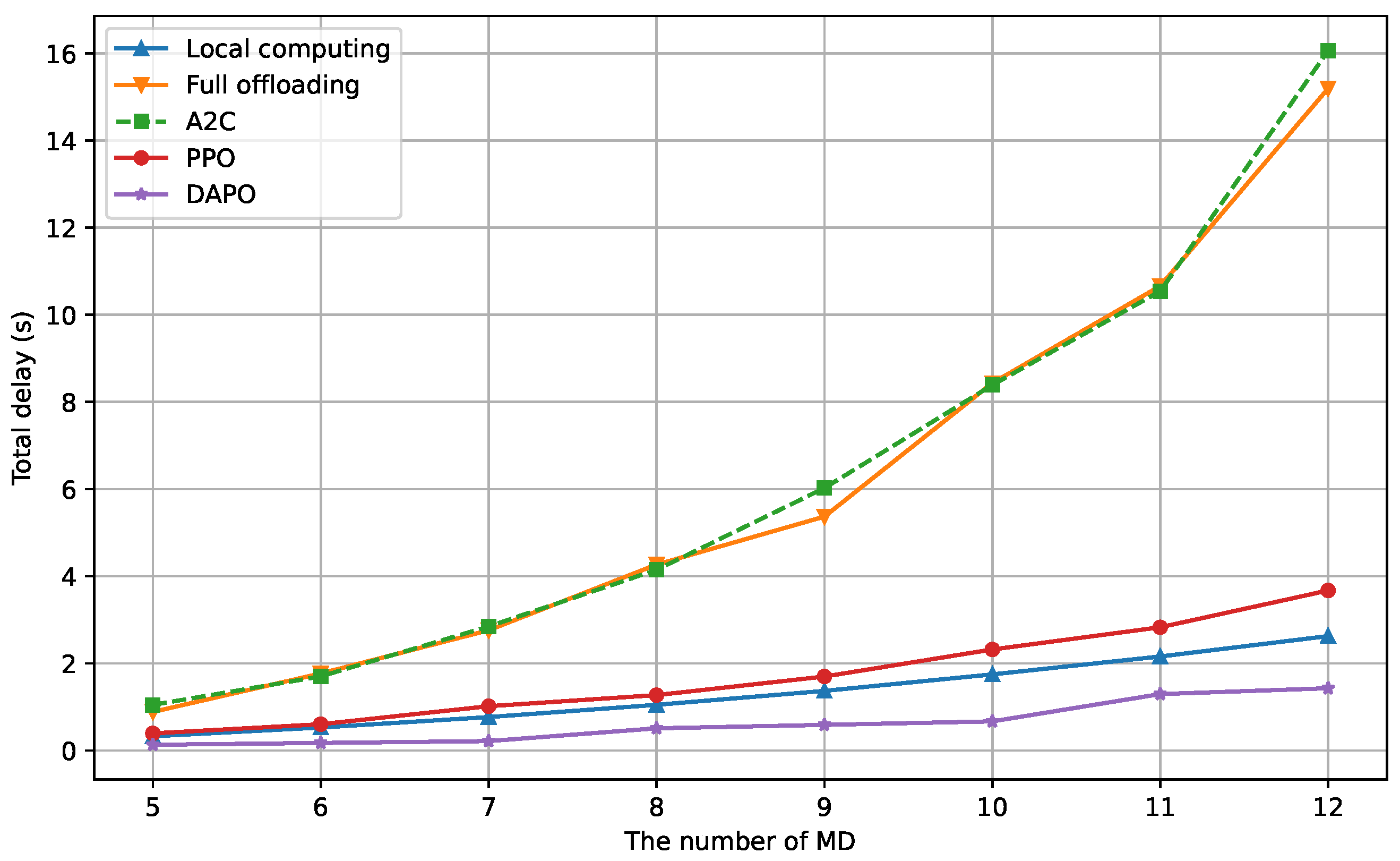
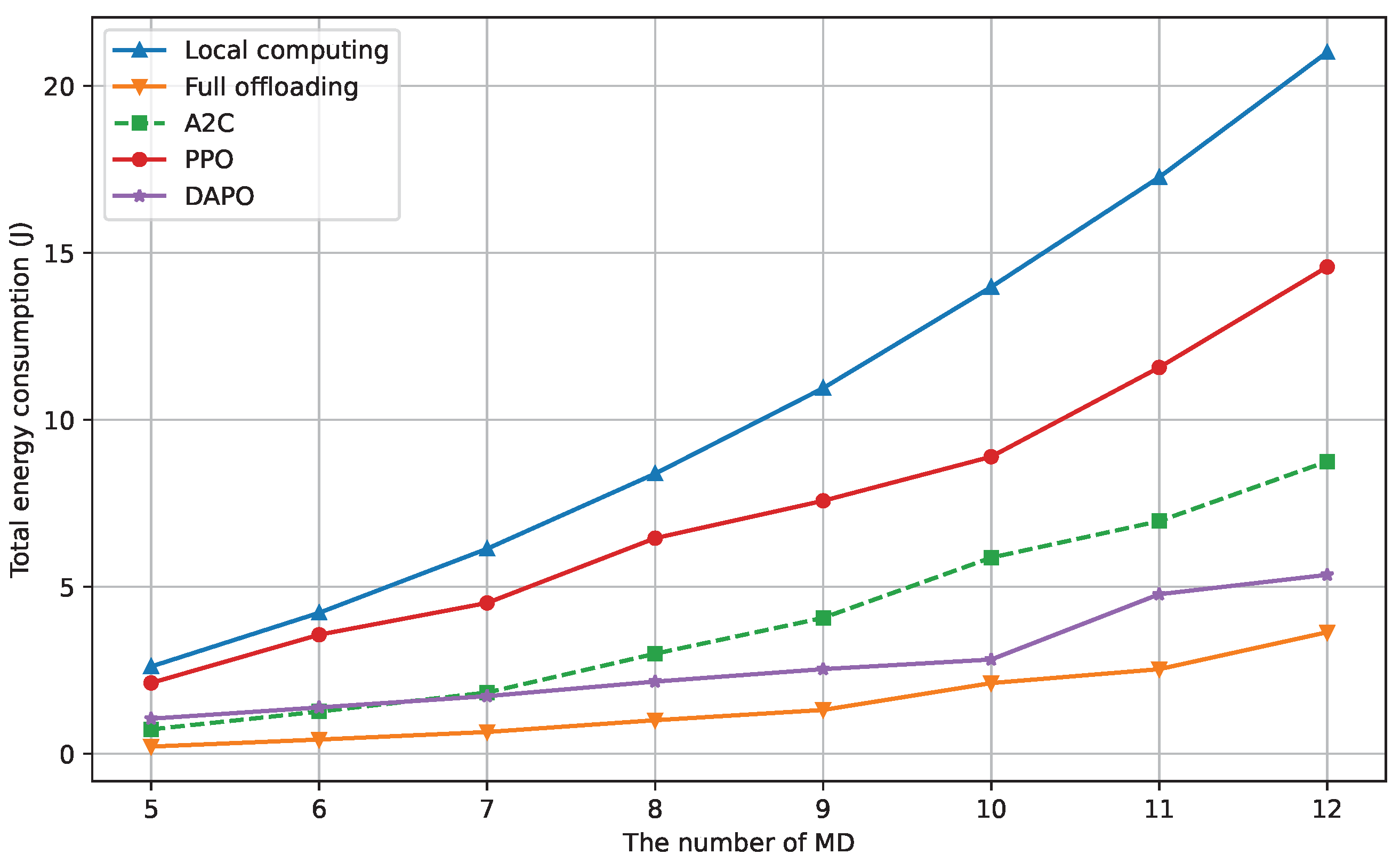
Notation	Description
$\mathcal{N}$	The set of mobile devices (MDs)
$\mathcal{M}$	The set of edge servers (ESs)
B	Bandwidth of the wireless channel
$N_0$	Power spectral density of Gaussian noise
$F^n$	Total computing capability of MD n
$F^m$	Total computing capability of ES m
L	Total number of layers in the LLM
$W_j$	Computational workload of layer j
$s_n$	Model split point for MD n
$a_n$	Offloading decision (target server) for MD n
$D_n$	Size of the intermediate data generated at split point $s_n$
$p_n$	Transmission power of MD n
$P_n$	The operating power consumption of MD n
$P_m$	The operating power consumption of ES m
$F^{m,n}$	Computing resources allocated by ES m to MD n
$R_{m,n}$	The uplink transmission rate between MD n and ES m
$T_n^{all\_local}$	The delay of full local execution of MD n
$E_n^{all\_local}$	The energy of full local execution of MD n
$T_n^{\mathrm{loc}}$	Local computation delay for the task of MD n
$T_n^{\mathrm{remote}}$	Remote computation delay for the task of MD n
$T_{n,m}^{\mathrm{trans}}$	Transmission delay for offloading from MD n to ES m
$T_n^{\mathrm{tot}}$	Total end-to-end inference delay for MD n
$E_n^{\mathrm{tot}}$	Total energy consumption for MD n

lists the notations used in this paper.

3.1. User Mobility Model

To capture the dynamic characteristics of the mobile scenario, we adopt the Gauss–Markov (GM) mobility model [24] to describe the user’s trajectory, as this model effectively captures both the continuity and randomness of a user’s velocity and direction. At a discrete time step t, the velocity $v_n\left(t\right)$ and direction ${\theta }_n\left(t\right)$ of MD n are updated as follows:

$$\begin{array}{cc}\hfill v_n\left(t\right)& ={ϵ}_1{v}_n(t-1)+(1-{ϵ}_1)\overline{v}+\sqrt{1-{ϵ}_1^2}{{\rm Y}}_n\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\theta }_n\left(t\right)& ={ϵ}_2{\theta }_n(t-1)+(1-{ϵ}_2){\overline{\theta }}_n+\sqrt{1-{ϵ}_2^2}{\Psi }_n\hfill \end{array}$$

(2)

where $0\le {ϵ}_1,{ϵ}_2\le 1$ are the memory parameters that adjust the influence of the previous state, $\overline{v}$ is the mean velocity for all MDs, and ${\overline{\theta }}_n$ is the mean direction for MD n. Specifically, we assume that all MDs share the same mean velocity, but each device has a distinct mean direction. Furthermore, ${{\rm Y}}_n$ and ${\Psi }_n$ are two independent Gaussian random variables. For the n-th MD, their means and variances are given by $\left(\overline{{\xi }_{v_n}},{\varsigma }_{v_n}^2\right)$ and $\left(\overline{{\xi }_{{\theta }_n}},{\varsigma }_{{\theta }_n}^2\right)$, respectively, which reflect the randomness of motion for different MDs. Here, $\overline{{\xi }_{v_n}}$ and $\overline{{\xi }_{{\theta }_n}}$ denote the mean velocity and mean direction of MD n, while ${\varsigma }_{v_n}^2$ and ${\varsigma }_{{\theta }_n}^2$ represent their variances.

We denote the location of the MD n at time t as ${\mathrm{Loc}}_n\left(t\right)=[x_n\left(t\right),y_n\left(t\right)]$. The position is then updated according to Equations (1) and (2) as follows:

$$\begin{array}{cc}\hfill x_n\left(t\right)& =x_n(t-1)+v_n(t-1)cos\left({\theta }_n(t-1)\right)\Delta t\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill y_n\left(t\right)& =y_n(t-1)+v_n(t-1)sin\left({\theta }_n(t-1)\right)\Delta t\hfill \end{array}$$

(4)

Based on the updated positions in Equations (3) and (4), the distance between MD n and the stationary ES m at time t is given by

$$d_{n,m}\left(t\right)=\left|\right|{\mathrm{Loc}}_n\left(t\right)-{\mathrm{Loc}}_m\left|\right|$$

(5)

where ${\mathrm{Loc}}_n\left(t\right)$ is the location of the MD n at time t, ${\mathrm{Loc}}_m$ is the location of the ES m.

3.2. Communication Model

When MD n offloads its task to ES m, the intermediate data is transmitted over the wireless channel. This paper employs a block fading channel model that considers path loss, small-scale fading, and large-scale shadowing. According to Equation (5), the channel gain between MD n and ES m is modeled as follows [25]:

$$g_{n,m}={\beta }_0{d}_{n,m}^{-\alpha }{\left|h\right|}^2\zeta$$

(6)

where ${\beta }_0$ is the path loss constant, $\alpha$ is the path loss exponent, $d_{n,m}$ is the distance between MD n and ES m, h is the Rayleigh fading coefficient, and $\zeta$ is a log-normal random variable representing shadowing.

We assume that all MDs have the same task priority. When multiple MDs simultaneously offload tasks to the same ES m, according to Equations (5) and (6), the uplink transmission rate between MD n and ES m is given by

$$R_{n,m}={\displaystyle \frac{B}{K_m}}{log}_2\left(1+{\displaystyle \frac{p_n·g_n}{\frac{B}{K_m}{N}_0}}\right)$$

(7)

where B is the bandwidth of the wireless channel, $K_m={\sum }_{n=1}^N{a}_{n,m}$ denotes the number of inference tasks offloaded to ES m, $p_n$ is the transmit power of MD n, and $N_0$ is the variance of the complex Gaussian white noise.

3.3. Computation Offloading Model

The Transformer layers of a LLM primarily consist of a self-attention layer and a feed-forward network layer. For an input sequence of length $d_{in}$ and hidden dimension $d_{mid}$, using a multi-head attention mechanism with $\kappa$ heads, the computational workload (in FLOPs) of the j-th layer can be expressed as [21]

$$W_j={\displaystyle \frac{3d_{in}{d}_{mid}}{\kappa }}+{\displaystyle \frac{2d_{in}^2{d}_{mid}}{\kappa }}+9d_{in}{d}_{mid}^2$$

(8)

For the inference task on MD n, given a model partition decision at layer $s_n$, the inference latency for executing the first $s_n$ layers locally is given by

$$T_n^{\mathrm{loc}}=\sum _{j=1}^{s_n}{\displaystyle \frac{W_j}{F^n}}$$

(9)

where $F^n$ is the computational capability of MD n.

Similarly, the remote inference latency for executing layers $s_n+1$–L on the selected ES m is

$$T_n^{\mathrm{remote}}=\sum _{m=1}^M{a}_{n,m}\left(\sum _{j=s_n+1}^L{\displaystyle \frac{W_j}{F^{m,n}}}\right)$$

(10)

where $F_{m,n}$ is the computation resource assigned to MD n by ES m. The total computation resource allocated by ES m cannot exceed its capacity: ${\sum }_{n=1}^N{a}_{n,m}{F}_{m,n}\le F_m$.

During collaborative inference between MD n and ES m with split point $s_n$, the intermediate data generated at layer $s_n$ is transmitted to ES m. Let $D_n$ be the amount of intermediate data at layer $s_n$, according to Equation (7), then the transmission delay is

$$T_{n,m}^{\mathrm{trans}}=\sum _{m=1}^M{a}_{n,m}{\displaystyle \frac{D_n}{R_{n,m}}}$$

(11)

Based on Equations (9)–(11), we define the total inference delay for MD n in collaborative inference as

$$T_n^{\mathrm{tot}}=T_n^{\mathrm{local}}+T_n^{\mathrm{remote}}+T_{n,m}^{\mathrm{trans}}$$

(12)

Correspondingly, the energy consumption for MD n during collaborative inference consists of three components: the local inference energy, the transmission energy for intermediate data, and the edge server’s computation energy, given by

$$E_n^{\mathrm{tot}}=E_n^{\mathrm{local}}+E_{n,m}^{\mathrm{trans}}+E_m^{\mathrm{remote}}=P_n·T_n^{\mathrm{local}}+p_n·T_{n,m}^{\mathrm{trans}}+P_m·T_n^{\mathrm{remote}}$$

(13)

where $P_n$ is the operating power consumption of MD n, $p_n$ is the transmission power consumption for MD n, and $P_m$ is the operating power consumption of ES m.

3.4. Problem Formulation

In this work, our objective is to minimize the total inference latency while simultaneously reducing the inference energy consumption of the mobile devices. The objective function and constraints are as follows:

$$\underset{s_n,a_n}{min}\sum _{n=1}^N{T}_n^{\mathrm{tot}}$$

(14)

subject to

$$\begin{array}{cccc}\hfill & E_n^{\mathrm{tot}}\le E_n^{\mathrm{all}\text{\_}\mathrm{local}},\hfill & \hfill & \forall n\in \mathcal{N}\hfill \end{array}$$

(15)

$$\begin{array}{cccc}\hfill & T_n^{\mathrm{tot}}\le T_n^{\mathrm{all}\text{\_}\mathrm{local}},\hfill & \hfill & \forall n\in \mathcal{N}\hfill \end{array}$$

(16)

$$\begin{array}{cccc}\hfill & 0\le s_n\le L,s_n\in \mathbb{Z},\hfill & \hfill & \forall n\in \mathcal{N}\hfill \end{array}$$

(17)

$$\begin{array}{cccc}\hfill & a_n\in \{0,1,\dots ,M\},a_n\in \mathbb{Z},\hfill & \hfill & \forall n\in \mathcal{N}\hfill \end{array}$$

(18)

$$\begin{array}{cccc}\hfill & a_{n,m}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{a}_n=m\hfill \\ 0,\hfill & \mathrm{if}{a}_n\ne m\hfill \end{array}\right.,\hfill & \hfill & \forall n\in \mathcal{N},m\in \mathcal{M}\hfill \end{array}$$

(19)

$$\begin{array}{cccc}\hfill & \sum _{n=1}^N{a}_{n,m}{F}^{m,n}\le F^m,\hfill & \hfill & \forall m\in \mathcal{M}\hfill \end{array}$$

(20)

Here, Equation (14) is our objective function, with the model partitioning decision $s_n$ and the task offloading decision $a_n$ as the optimization variables. The constraints in Equations (15) and (16) ensure that the inference energy and latency resulting from the decision cannot exceed the energy and latency produced by executing the entire inference task locally on MD n. Here, $T_n^{\mathrm{all}\text{\_}\mathrm{local}}$ and $E_n^{\mathrm{all}\text{\_}\mathrm{local}}$ are the latency and energy consumption, respectively, for executing the complete inference task locally on MD n. In Equation (17), $s_n$ is the model partition point and L is the total number of layers in the model. Constraint (18) indicates that the offloading decision $a_n$ is selected from the set of available servers $\mathcal{M}$, where $a_n=0$ signifies local computation. Constraint (19) defines the indicator variable, where $a_{n,m}=1$ signifies that the remaining $L-s_n$ layers of the inference task for MD n are allocated to ES m for execution. Constraint (20) ensures that the computational resources allocated by ES m to all offloaded tasks do not exceed its total computational capacity.

The problem of model partitioning and resource allocation for device–edge collaborative inference proposed in this paper is a Mixed-Integer Nonlinear Programming (MINLP) problem. It consists of two parts: first, the selection of the model partition point (a finite discrete variable); second, the binary decision variables for assigning the inference task to an edge server. In [26], it is shown that if only the task allocation subproblem is considered, the complexity of finding the optimal solution increases exponentially with the number of users, and the problem has been proven to be NP-hard. Therefore, our system, which jointly optimizes partition points and task allocation, can be considered an extension of the NP-hard problem, and thus inherits its NP-hard nature. This makes it difficult to obtain a globally optimal solution in practice using polynomial time algorithms. Hence, this paper proposes the DAPO framework, which utilizes the DDPG algorithm to solve it.

4. Problem Solution

In this section, we will provide a detailed definition of the state space, action space, and reward function within the DDPG algorithm.

4.1. State Space

In this MEI system, the state space needs to reflect the entire system’s state, which includes the number and dynamic locations of mobile devices, inference task attributes, and the computational resources of edge servers. This requires a very large state space dimension. As the number of mobile devices increases, this can easily lead to a state space explosion. To align with our optimization objective of minimizing both energy consumption and inference latency, we define the state space of the MEI system as $S={\sum }_{n=1}^N{T}_n^{\mathrm{tot}}$, where S denotes the system state, represented by the total inference latency.

4.2. Action Space

In this MEI system, for each mobile device’s inference task, we need to optimize its model partition point and task allocation variable, thereby optimizing the overall system’s latency and energy consumption. Therefore, to describe the computation offloading strategies for all mobile devices, we define the action space as the collection of all individual offloading strategies, represented by the action vector $\mathcal{A}=[A_1,A_2,\dots ,A_N]$, where $A_n=(s_n,a_n)$ represents the model partition point $s_n$ and the offloading server destination $a_n$ for the n-th MD’s inference task.

4.3. Reward Function

We use $R(S,\mathcal{A})$ to represent the reward function, which is the reward value the agent obtains for executing the computation offloading strategy $\mathcal{A}$ in state S. Our objective is to minimize the total inference latency while reducing the energy consumption of the mobile devices. Therefore, based on the objective function and its constraints, we define the reward function as

$$R(S,\mathcal{A})=-\sum _{n=1}^N{T}_n^{\mathrm{tot}}-\alpha ·\Delta T-\beta ·\Delta E$$

(21)

where $\Delta T={\sum }_{n=1}^N(T_n^{\mathrm{tot}}-T_n^{\mathrm{all}\text{\_}\mathrm{local}})$ serves as the latency penalty term and $\Delta E={\sum }_{n=1}^N(E_n^{\mathrm{tot}}-E_n^{\mathrm{all}\text{\_}\mathrm{local}})$ serves as the energy penalty term. This ensures that the inference energy and latency resulting from the chosen policy do not exceed those of executing the entire task locally on the mobile device. $\alpha$ and $\beta$ are the penalty weighting factors for latency and energy, respectively. This reward function implies that a better computation offloading strategy leads to lower total system latency and energy consumption and, consequently, a higher reward value.

4.4. Algorithm Design

In traditional reinforcement learning methods, such as PPO and DQN, when the state or action space becomes very large, the so-called “curse of dimensionality” is encountered. In our MEI system, as the number of mobile devices (MDs) increases, the joint action space—which includes each user’s model split point $s_n$ and server selection $a_n$—grows exponentially, making it impractical to maintain and query the Q-table. Furthermore, our optimization objective requires making optimal discrete decisions in continuous system states, which presents challenges for algorithm design.

To address these challenges, we adopt the DDPG algorithm. DDPG is a deep reinforcement learning algorithm based on the actor–critic framework, which is particularly suitable for decision-making problems in continuous state spaces. It leverages neural networks to approximate the policy and value functions, thus effectively mitigating the curse of dimensionality.

However, the standard DDPG algorithm is designed for continuous action spaces, whereas in our problem, both the model partition point $s_n$ and the offloading server selection $a_n$ are discrete integers. To resolve this conflict, we have adaptively modified the DDPG framework. Specifically, the actor network outputs continuous action values during training, which are then converted into discrete, valid actions through a deterministic mapping rule when interacting with the environment.

The DDPG algorithm consists of four neural networks: an actor network $\mu \left(s\right|{\theta }^{\mu })$ and its target network ${\mu }^{\prime }\left(s\right|{\theta }^{{\mu }^{\prime }})$, and a critic network $Q(s,a|{\theta }^Q)$ and its target network $Q^{\prime }(s,a|{\theta }^{Q^{\prime }})$. The actor network, acting as the policy network, is responsible for generating a deterministic action based on the current system state s to perform model partitioning and computation offloading. The critic network, acting as the value network, is responsible for evaluating the long-term cumulative reward (Q-value) that can be obtained by taking action a in state s. DDPG utilizes an experience replay buffer to store records of the agent’s interactions with the environment, i.e., transition tuples $(s_t,a_t,r_t,s_{t+1})$. Here, $(s_t,a_t,r_t,s_{t+1})$ denotes a transition tuple stored in the replay buffer. Specifically, $s_t$ is the system state at time step t, $a_t$ is the action selected by the agent, $r_t$ is the reward received after executing $a_t$ in state $s_t$, and $s_{t+1}$ is the next state observed. During training, the target critic network and target actor network use samples from the experience replay buffer to evaluate the target Q-value and the critic network is responsible for calculating the Q-value. The target Q-value is calculated as follows:

$$Q^{\mathrm{target}}=r_t+\gamma Q^{\prime }(s_{t+1},{\mu }^{\prime }\left(s_{t+1}\right|{\theta }^{{\mu }^{\prime }})|{\theta }^{Q^{\prime }})$$

(22)

where $\gamma$ is the discount factor for future rewards. ${\theta }^{Q^{\prime }}$ and ${\theta }^{{\mu }^{\prime }}$ denote the parameters of the target critic network $Q^{\prime }$ and the target actor network ${\mu }^{\prime }$. ${\mu }^{\prime }\left(s_{t+1}\right|{\theta }^{{\mu }^{\prime }})$ is the action selected by the target actor network in the next state $s_{t+1}$. The critic network updates its parameters ${\theta }^Q$ by minimizing the mean squared error (MSE) loss function $L\left({\theta }^Q\right)$:

$$L\left({\theta }^Q\right)=\mathbb{E}\left[{(Q^{\mathrm{target}}-Q(s_t,a_t|{\theta }^Q))}^2\right]$$

(23)

The update objective for the actor network is to adjust its policy to generate actions that can achieve a higher Q-value. In DDPG, the policy gradient for the actor network is given by

$${\nabla }_{{\theta }^{\mu }}J\approx \mathbb{E}\left[{\nabla }_{a}Q(s,a|{\theta }^Q){|}_{s=s_t,a=\mu \left(s_t\right|{\theta }^{\mu })}{\nabla }_{{\theta }^{\mu }}\mu \left(s\right|{\theta }^{\mu })\right]$$

(24)

To maintain training stability, the DDPG algorithm uses soft updates for the parameters of the target actor and critic networks. The soft update formulas are as follows:

$$\begin{array}{cc}\hfill {\theta }^{Q^{\prime }}& \leftarrow \tau {\theta }^Q+(1-\tau ){\theta }^{Q^{\prime }}\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\theta }^{{\mu }^{\prime }}& \leftarrow \tau {\theta }^{\mu }+(1-\tau ){\theta }^{{\mu }^{\prime }}\hfill \end{array}$$

(26)

where $\tau \ll 1$ is the soft update rate for the target networks, ensuring their stable evolution. Algorithm 1 presents the DAPO based on DDPG algorithm for the MEI system.

Algorithm 1: The DAPO based on the DDPG Algorithm

To address the optimization problem proposed in this paper, we designed a corresponding neural network architecture for the DDPG algorithm. The actor network is responsible for mapping the system state to a specific joint action. Its input layer receives a scalar state $S_t$, which is the total inference latency of the system from the previous step. To realize the mixed action output defined in this paper, the dimension of the actor network’s output layer is designed to be $N\times (M+2)$. For each MD n’s inference task, one neuron uses a Sigmoid activation function followed by a linear transformation to output a continuous value in the interval $[0,L]$, representing the model partition point $s_n$. The remaining $M+1$ neurons utilize a Softmax activation function to generate a probability distribution, which is used to decide whether the task should be executed locally or offloaded to one of the M edge servers. The final discrete offloading location is determined via an argmax operation, yielding the offloading decision $a_n$ for each MD. In this way, the actor network simultaneously determines both the model partition point ($s_n$) and the task offloading destination ($a_n$), thereby explicitly incorporating task offloading into the decision-making process. Figure 2 illustrates the DDPG-based edge intelligence computation offloading framework.

5. Performance Evaluation

In this section, to validate the effectiveness of the proposed DAPO framework, we establish a simulation environment. The algorithm is implemented in Python (3.10) using PyTorch (2.0.1) and runs on an Intel Core i7-12700KF CPU (3.6 GHz), 32 GB RAM, an NVIDIA GeForce RTX 3060 GPU, and Windows 11 64-bit operating system. In this simulation environment, the network area is 500 m × 500 m, and the area contains N = 15 MDs and M = 5 ESs. The mobility of the mobile devices follows the Gauss–Markov model to simulate the continuity and randomness of the user’s velocity and direction during movement. The mobility trajectories of UDs are shown in Figure 3. The mean velocity $\overline{v}$ is set to 2.0 m/s, the memory factors for velocity and direction, ${ϵ}_1$ and ${ϵ}_2$, are both set to 0.8, and the time step $\Delta t$ is 1.0 s. The system’s wireless channel bandwidth is set to B = 10 MHz, the background noise power spectral density $N_0$ is −174 dBm/Hz, and the uplink transmission power of the mobile devices $p_n$ is 500 mW. The computational capacity of the edge servers is randomly selected from the range $[1\times {10}^{15},2\times {10}^{15}]$ FLOPS, and the computational capacity of the mobile devices is from $[2\times {10}^{13},2.5\times {10}^{13}]$ FLOPS. The inference task for the mobile devices is set as the inference of a LLM, with its structural parameters referencing the Llama-2-7B model. The model has a total of L = 32 layers, a hidden dimension $d_{mid}$ = 4096, and $\kappa$ = 32 attention heads. We adopt Llama-2-7B as the inference model because it is openly available and has manageable computational demand, which facilitates reproducible experimentation. Importantly, the underlying principles of partitioning and offloading remain the same for larger LLMs, and thus the conclusions are not limited to this specific model size. The dataset for the tasks is the WikiText-2 dataset [27], which contains 4355 sentences with an average length of 20 words.

The parameters for the DAPO algorithm are shown in

Table 2. Parameter Setting in the DAPO Algorithm.

Parameter	Value	Description
Episode	200	The size of the main loop
T	1000	The size of the secondary loop
Buffer size	100,000	The size of the replay buffer
Batch size	64	The size of the sample in the replay buffer
$\gamma$	0.99	Reward discount factor
Actor learning rate	0.001	The learning rate of Adam optimizer in Actor network
Critic learning rate	0.001	The learning rate of Adam optimizer in Critic network
$\tau$	0.005	The soft update speed of the target network

. These values were selected by combining common practices in DDPG implementations with empirical tuning in our simulation environment. For example, the learning rates of the actor and critic networks were set to 0.001, which is widely adopted in continuous control tasks to ensure stable convergence. The replay buffer size (100,000) and batch size (64) follow standard settings that balance memory cost and sample diversity. The discount factor was fixed at 0.99 to capture long-term optimization goals, while the soft update rate $\tau =0.005$ was chosen to provide stable target network updates. Finally, the number of episodes (200) and steps per episode (1000) were determined through preliminary experiments, where we observed that these values were sufficient for convergence in our scenario. For a fair comparison, the hyperparameters of PPO and A2C were set according to widely used implementations in continuous control tasks. Specifically, the learning rate was set to 0.001, the discount factor to 0.99, and the batch size to 64. The entropy coefficient for PPO was 0.01 to encourage exploration, while A2C used five parallel workers for training stability.

Figure 4 and Figure 5 show the impact of the number of mobile devices on the total system latency and energy consumption. As the number of users increases, the static full offloading strategy suffers from sharply deteriorating latency due to competition for computational resources, while the local computing strategy results in high energy consumption due to its low energy efficiency. In contrast, our proposed DAPO framework demonstrates significant advantages in both latency and energy consumption through intelligent decision-making. Notably, the performance of DAPO is superior to the PPO and A2C baseline. Specifically, when the number of mobile devices reaches 12, DAPO reduces the total latency by about 27% compared to PPO and 34% compared to A2C, while lowering energy consumption by approximately 18% and 22%, respectively. This is because, in our model, the joint optimization of the model partition point and the computation offloading location results in a high-dimensional discrete action space. The PPO and A2C algorithm are prone to getting stuck in inefficient exploration and policy updates for such problems, whereas DAPO solves the problem by transforming it into a continuous action space under a deterministic policy and then mapping the actions to discrete decisions, allowing for more effective optimization. The experimental results confirm that DAPO achieves the lowest system latency in all scenarios and maintains a near-optimal level of energy consumption, demonstrating its superior performance in handling complex decision-making problems and the excellent scalability of the system.

In Figure 6, we investigate the impact of the system’s wireless bandwidth on the total system latency. From the experimental results, it is clear that the latency of the full local computation strategy remains unchanged, as it does not involve network communication. Conversely, the performance of the full offloading strategy is highly sensitive to bandwidth; its latency is extremely high at low bandwidths and decreases rapidly as bandwidth increases, eventually being limited by the computational resources of the edge servers. Our proposed DAPO framework exhibits optimal performance and strong robustness across all bandwidth conditions. For example, under limited bandwidth, DAPO achieves up to 30% lower latency compared to full offloading. Even when bandwidth is limited, DAPO can intelligently adjust the model partition point to reduce the amount of offloaded data, thereby avoiding high communication latency. As bandwidth improves, it dynamically increases the offloading ratio to further reduce the total latency. This experiment fully demonstrates the adaptive capability of our framework to make efficient decisions based on changing network conditions.

In Figure 7, we evaluate the convergence performance of the algorithms. There is a significant difference between the training reward curves of DAPO and PPO. The DAPO algorithm demonstrates extremely fast convergence, rapidly reaching a high and stable reward plateau in the early stages of training. Quantitatively, DAPO converges within about 50 episodes, while PPO requires around 150 episodes, representing a nearly threefold increase in convergence speed. In contrast, the learning process of the PPO algorithm is very slow, taking approximately 150 episodes to gradually converge, and its final policy reward is much lower than that of DAPO. This performance gap primarily stems from the core mechanisms of the two algorithms and their adaptability to our scenario. First, in terms of sample efficiency, DAPO, as an off-policy algorithm, utilizes an experience replay buffer to efficiently reuse historical data, thus enabling rapid learning. PPO, being an on-policy algorithm, needs to discard old data and resample after each update, leading to lower learning efficiency, which is directly reflected in its slow convergence curve. Second, in terms of handling high-dimensional action spaces, this problem involves jointly optimizing model partition points and offloading destinations, forming a vast combinatorial action space. PPO explores through a random policy, which is inefficient in such a high-dimensional space and struggles to find the optimal solution. In contrast, DAPO, through its deterministic policy and guiding critic network, performs a more targeted search in a continuous action space before mapping to a specific decision, which is demonstrably a more effective way to solve such complex decision-making problems. Therefore, DAPO not only finds a better policy, but its superior learning efficiency also makes it more suitable for dynamic scenarios that require rapid adaptation to environmental changes.

As shown in Figure 4, Figure 5, Figure 6 and Figure 7, the proposed DAPO framework consistently outperforms local execution, full offloading, and RL baselines such as PPO and A2C in terms of latency, energy consumption, and convergence speed. These results demonstrate that DAPO effectively addresses the dual challenges of resource constraints and user mobility by jointly optimizing model partitioning and task offloading, leading to significant improvements over baseline methods.

6. Conclusions and Future Work

This paper addresses the challenges of collaborative LLM inference in MEC environments by proposing the DAPO framework based on DDPG. The framework jointly optimizes model partition points and offloading decisions, aiming to minimize system-wide latency and energy consumption in multi-user mobile scenarios. The main contributions of this work are threefold. First, we formulate the joint optimization problem of model partitioning and task offloading under resource constraints and user mobility. Second, we design the DAPO algorithm, which leverages the advantages of DDPG to efficiently handle the high-dimensional mixed action space. Third, extensive experiments demonstrate that DAPO significantly outperforms static strategies and RL baselines such as PPO and A2C, achieving faster convergence and better trade-offs between latency and energy consumption. These findings confirm that DAPO effectively address the identified challenges and provides new insights into dynamic, mobility-aware edge intelligence systems.

Our future research will focus on expanding the decision space by incorporating more fine-grained resource allocation (such as CPU cores, data compression rates) into the optimization scope in order to achieve a deeper level of end-to-end optimization. Concurrently, we will enhance the realism of our environmental model by considering network handover and task migration issues that arise from high-speed user mobility. Furthermore, exploring the Multi-Agent Reinforcement Learning (MARL) paradigm to construct a distributed collaborative decision-making system capable of adapting to future larger-scale and more complex edge intelligence networks will be a key focus of our subsequent work.