Systematic HLS Co-Design: Achieving Scalable and Fully-Pipelined NTT Acceleration on FPGAs

Abstract

Lattice-based cryptography (LBC) is an essential direction in the fields of homomorphic encryption (HE), zero-knowledge proofs (ZK), and post-quantum cryptography (PQC), while number theoretic transformations (NTT) are a performance bottleneck that affects the promotion and deployment of LBC applications. Field-programmable gate arrays (FPGAs) are an ideal platform for accelerating NTT due to their reconfigurability and parallel capabilities. High-level synthesis (HLS) can shorten the FPGA development cycle, but for algorithms such as NTT, the synthesizer struggles to handle the inherent memory dependencies, often resulting in suboptimal synthesis outcomes for direct designs. This paper proposes a systematic HLS co-design to progressively guide the synthesis of NTT accelerators. The approach integrates several key techniques: arithmetic module resource optimization, conflict-free butterfly scheduling, memory partitioning, and template-based automated design fusion. It reveals how to resolve pipeline bottlenecks in HLS-based designs and expand parallel processing, guiding microarchitecture iterations to achieve an efficient design space. Compared to existing HLS-based designs, the area-latency product achieves a performance improvement of 1.93 to 191 times, and compared to existing HDL-based designs, the area-cycle product achieves a performance improvement of 1.7 to 10.6 times.

1. Introduction

Fully homomorphic encryption (FHE) and zero-knowledge proofs (ZK) are driving cryptographic applications into a new era, enabling secure computing and privacy-preserving techniques [1]. How can FHE systems be made to run more efficiently on heterogeneous platforms? The current mainstream choice for practical implementations of these systems is lattice-based cryptography (LBC), which is selected not only for its security against quantum attacks in post-quantum cryptography (PQC), but also due to its underlying algebraic structure. LBC schemes operate over a polynomial ring, which naturally supports the homomorphic addition of ciphertexts and the multiplicative fits to realize the operations required by FHE. However, the core operations of LBC involve polynomial multiplications, which implement this FHE and ZK system [2] with a significant computational overhead [3,4]. The question of how to make FHE and ZK systems run more efficiently on heterogeneous platforms has become a key bottleneck that restricts the large-scale deployment of FHE and ZK. If this challenge is solved, then converting all computer operations to full homomorphism and proxying computations on third-party clouds will become feasible in the future.

The number theoretic transform (NTT) is now commonly employed to overcome the prohibitive computational complexity of direct polynomial multiplication, making it a performance-critical kernel in any practical LBC-based system. However, the NTT algorithm itself poses significant hardware design challenges with its large amount of intrinsic parallelism, intricate memory access patterns, and complex data dependencies across computational stages. These characteristics make achieving high throughput and resource efficiency a major obstacle [3,4]. Ye et al. [5] emphasize a fully unfolded streaming permutation network (SPN) and a compact modulus reduction algorithm to achieve ultra-low latency and high throughput. Similarly, innovating in both algorithmic and handcrafted architectural design, Su et al. [6] propose the fusion of NWC and INTT scaling with unified PE memory cycle sharing. Yang et al. [7] focus on automation, highlighting batch DSE for automated RTL generation from HDL designs. Cheng et al. [8] focused on access conflicts, proposing a rotation table to reorder tuples in-place. These works optimize NTT accelerator performance and adaptability from multiple angles. However, designs based on manual patterns and involving co-design of algorithm and architecture are complex. It presents a difficulty for non-specialists to reuse and integrate into application scenarios. This approach lacks a portable, user-friendly, automated design methodology that incorporates expert knowledge.

High-level synthesis (HLS) has emerged as a possible solution by raising the abstraction level of hardware design. HLS enables designers to quickly explore design trade-offs and optimize performance [9,10]. Despite its capabilities, HLS faces a fundamental synthesis gap when applied to the implementation of demanding algorithms, such as NTT. It is challenging for HLS tools to automatically derive optimal hardware architectures from standard algorithmic descriptions, particularly for deep-pipelined memory systems required to support high-bandwidth data streams. This limitation manifests itself in what is called the HLS memory wall, a structural bottleneck that hinders deep pipelining (e.g., a pipeline II of 1) and impairs performance. Existing work primarily focuses on two approaches: one involves rewriting HLS source code to optimize loop and memory access structures, while the other employs pragma directives to drive HLS tools toward parallel or pipelined explorations, aiming to approximate the efficiency of handwritten RTL. Ozcan et al. [11] modularized the NTT module and added pragma directives after identifying butterfly stages to achieve area and latency improvements without altering the algorithm. However, this approach did not structurally eliminate memory conflicts or cross-data dependencies. El-Kady et al. [12] reconstructed the CT/GS code structure by phasing out inner butterfly stages and combining dual-port RAM to separate read/write operations with odd/even splitting. They also utilized pragma directives to resolve cross-iteration data dependencies, achieving controllable latency reduction at low parallelism (p = 2) in their experiments. However, their approach is limited to p = 2, lacking broad parameter adaptability, which contradicts the flexibility and scalability expected from HLS implementations. Kawamura et al. [13] proposed that constructing independent pipelines in phases outperforms cross-phase pipelines. Their key contribution lies in providing reusable loop optimization guidelines for HLS that restore II = 1 when necessary through array partitioning. However, they did not address memory conflicts in large-scale parallelism. Their limitations similarly rely on manual, experience-based pragma adjustments and source code rewriting. Current research lacks systematic and automated approaches to address fragmented empirical knowledge. As a result, existing HLS-based NTT tends to remain suboptimal, lagging far behind hand-optimized hardware description language (HDL) designs [14,15,16]. It presents inefficiencies in arithmetic operations, memory management, and parallelism [11,17].

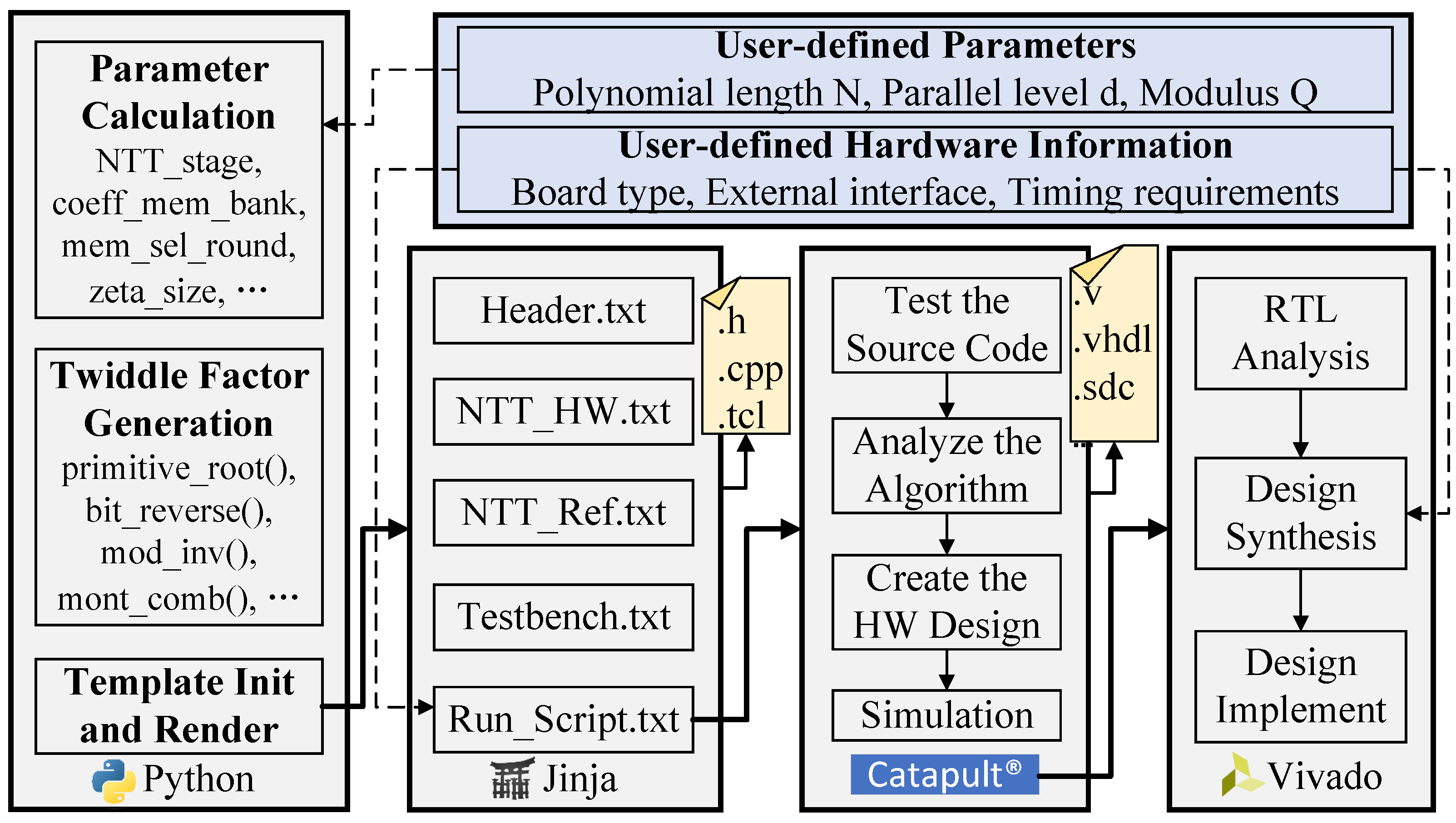
To bridge this gap, we introduce the selection of an arithmetic-level modular multiplication algorithm and algebraically unified butterfly operations. At the microarchitecture level, we avoid memory conflicts and enable system-level template-driven automatic DSE generation for different N/q/d implementations. The goal is to elevate “expert hardware knowledge + pragma parameter tuning” to a portable, reusable, and automatically explorable HLS template framework. This paper describes and validates how a collaborative design approach through HLS can be utilized in a disciplined way to explicitly embed intent into high-level source code, using the NTT algorithm as an example, guiding the synthesis tool towards an optimal hardware implementation. The concept of hardware domain expertise introduced in HLS refers to the practice of analyzing an algorithm’s data structures and computational steps, inspired by software library files, to achieve engineering reuse and innovation in hardware design. By selecting appropriate resources based on the hardware platform, HLS accelerator templates are constructed. Embedding these templates into the workflow enables rapid implementation of high-performance hardware modules. This approach is of importance in an era where algorithms require close collaboration with hardware.

The proposed methodology is based on a hierarchy of co-design principles that systematically address HLS limitations, ranging from the arithmetic level to the system level. The main contributions of this work are summarized as follows:

Contributions:

• We conducted a comparative analysis of modular multiplication to demonstrate its effectiveness for the co-design approach, including a finely tuned general Montgomery modular multiplication and a specific generalized Mersenne number method. Compared to related HDL-based designs, our design achieved similar cycle performance and utilized only 34% of the LUT resources in the best case.
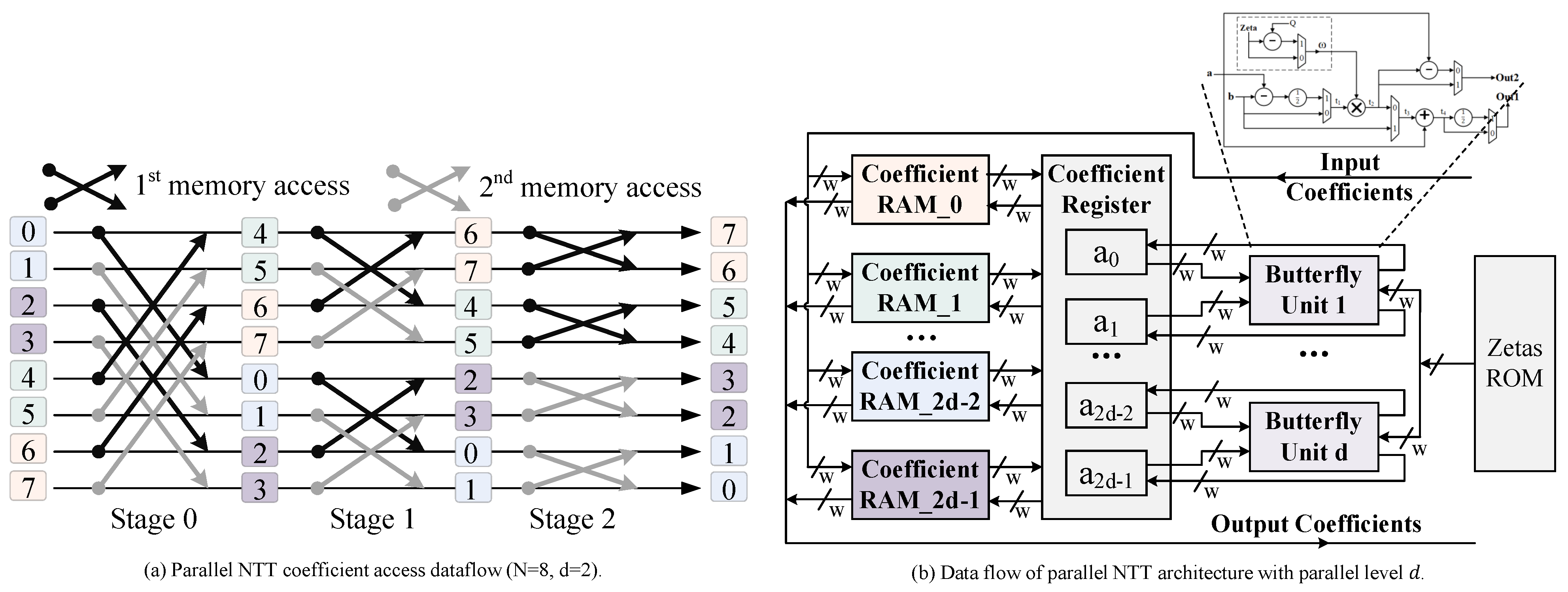
• We introduce a conflict-free memory architecture that structurally resolves the memory access contentions inherent to NTT, enabling a fully pipelined (II = 1) design and achieving a 5.6× latency reduction over naive HLS [11].
• We extend our methodology to the system level, presenting a scalable parallel architecture co-designed with its memory subsystem. A high-parallelism algorithm is developed, along with a compact butterfly structure, enabling the design of unified NTT/INTT architectures. This scalability supports various parameters and parallelism levels, further integrated into an automated framework for design, verification, and implementation [2,4].

Ultimately, this work does more than present a high-performance accelerator, it demonstrates a new paradigm for HLS development. It captures expert hardware knowledge across multiple domains. This includes the selection of modular multiplication algorithms and moduli, the derivation of algebraic butterfly fusion, and the use of parametric HLS pragma insertion. Furthermore, it incorporates twiddle factor precomputation, parallel NTT address generation logic, parameterized data types and memory structures suitable for (N, d), and thorough array partitioning operations. They constrain the design space to a region of optimal performance. This not only facilitates efficient DSE but also lays the groundwork for a future ecosystem of reusable HLS templates, aiming to democratize high-performance FPGA design for non-experts in hardware.

The rest of this article is organized as follows. Section 2 presents the necessary preliminaries and background information. Section 3 focuses on the design and optimization of our method for designing HLS-based NTT. Section 4 demonstrates the application of HLS to improve the performance of the NTT, supported by detailed case studies. Section 5 presents a comparative evaluation of the proposed approach with state-of-the-art implementations and validates the accelerators in an embedded system. Finally, Section 6 concludes the article with a summary of contributions and future directions.

2. Background

2.1. Preliminaries and Notations

In this article, n represents the degree of the polynomial and is a power of 2, while the modulus q is a prime number. The ring of integers modulo q is denoted as ${\mathbb{Z}}_q$. We define $R_q={\mathbb{Z}}_q\left[x\right]/(x^n+1)$ as the polynomial ring, where coefficients are elements of ${\mathbb{Z}}_q$ and polynomials are reduced modulo $x^n+1$. Lowercase letters such as a represent integers, and bold lowercase letters like $\mathbf{a}$ represent polynomials. The i-th coefficient of polynomial $\mathbf{a}$ is expressed as $a_i$, and the polynomial $\mathbf{a}$ is expanded as $\mathbf{a}={\sum }_{i=0}^{n-1}{a}_i{x}^i$, with coefficients stored in natural order unless specified otherwise. The NTT of the polynomial $\mathbf{a}$ is represented as $\widehat{\mathbf{a}}$, where $\widehat{\mathbf{a}}={\sum }_{i=0}^{n-1}{\widehat{a}}_i{x}^i$. The twiddle factor $\omega$ is an n-th primitive root of unity, and $\psi$ is a $2n$-th primitive root of unity. The symbols ·, ×, and ⊙ represent integer multiplication, polynomial multiplication, and pointwise multiplication, respectively.

2.2. Number Theoretic Transform (NTT)

The NTT is a variant of the discrete Fourier transform (DFT) adapted for operations over finite fields. It effectively executes convolutions, a key process in polynomial multiplication, as well as various cryptographic algorithms. In an n-point NTT, n input polynomial coefficients $a_i$ are transformed into ${\widehat{a}}_i={\sum }_{j=0}^{n-1}{a}_j{\omega }^{ij}$ for $i=0,1,\dots ,n-1$. Here, the n-th root of unity, $\omega$, meets the condition ${\omega }^n\equiv 1modq$, and for any $0<k<n$, ${\omega }^k\ne 1modq$. The inverse NTT (INTT) reconstructs the original polynomial $\mathbf{a}$ from its transformed version $\widehat{\mathbf{a}}$ using the formula $a_i=n^{-1}{\sum }_{j=0}^{n-1}{\widehat{a}}_j{\omega }^{-ij}$, thereby guaranteeing the unique recovery of the coefficients.

Traditional polynomial multiplication using direct convolution has a computational complexity of $O\left(n^2\right)$. In contrast, employing the NTT reduces this to $O(nlogn)$ by converting the operation to pointwise multiplication. However, directly applying NTT requires appending n zeros to each input, followed by performing a $2n$-point NTT, $2n$-point pointwise multiplication, and $2n$-point INTT. In the ring $R_q$, the $2n$-point result of the INTT is eventually reduced to n-point. This process can be made more efficient by employing negative wrapped convolution (NWC), which utilizes only n-point NTT/INTT. When computing $\mathbf{c}=\mathbf{a}\times \mathbf{b}$ in $R_q$ using NWC, the first step involves scaling the coefficients $a_i$ and $b_i$ by ${\psi }^i$, resulting in ${\mathbf{a}}^{\prime }$ and ${\mathbf{b}}^{\prime }$. Specifically, ${\mathbf{a}}^{\prime }$ is computed as ${\mathbf{a}}^{\prime }=(a_0,a_1,\dots ,a_{n-1})\odot ({\psi }^0,{\psi }^1,\dots ,{\psi }^{n-1})$. The next step is to compute ${\mathbf{c}}^{\prime }=\mathrm{INTT}(\mathrm{NTT}\left({\mathbf{a}}^{\prime }\right)\odot \mathrm{NTT}\left({\mathbf{b}}^{\prime }\right))$. The final step involves scaling the coefficients $c_i^{\prime }$ by ${\psi }^{-i}$, yielding $\mathbf{c}$.

Applying NWC to polynomial multiplication involves scaling the coefficients by ${\psi }^i$ prior to the NTT and by ${\psi }^{-i}$ after the INTT. Previous studies [18,19] have demonstrated that these scaling operations can be integrated into the NTT and INTT processes. Specifically, they can be incorporated into the decimation-in-time NTT using the Cooley-Tukey (CT) butterfly presented in Algorithm 1 and into the decimation-in-frequency INTT using the Gentle-Sande (GS) butterfly presented in Algorithm 2. With coefficients $a_1,a_2$ and a twiddle factor $\omega$, the CT butterfly performs the calculations $a_1+a_2·\omega$ and $a_1-a_2·\omega$; conversely, the GS butterfly computes $a_1+a_2$ and $(a_1-a_2)·\omega$. Algorithm 1 efficiently computes the NTT of a polynomial $\mathbf{a}\in R_q$ using a three-loop structure, where coefficient updates are performed using the CT butterfly operations (lines 6–7).

Algorithm 1 Cooley-Tukey NTT algorithm [20]

Input:  A polynomial $\mathbf{a}\in R_q$, and a precomputed twiddle factor table W storing powers of $\psi$ in bit reverse order

Output:  $\widehat{\mathbf{a}}\leftarrow$ NTT($\mathbf{a}$), with coefficients in bit reverse order

1: $t\leftarrow n$   2: for $m=1$; $m<n$; $m=2m$ do   3:        $t\leftarrow t/2$   4:        for $i=0$; $i<m$; i++ do   5:              for $j=2i·t$; $j<(2i+1)·t$; j++ do   6:                    $a_j\leftarrow a_j+a_{j+t}·W[m+i]$ mod q   7:                    $a_{j+t}\leftarrow a_j-a_{j+t}·W[m+i]$ mod q   8:              end for   9:        end for 10: end for 11: Return $\mathbf{a}$

Algorithm 2 Gentleman-Sande INTT algorithm [21]

Input: A polynomial $\widehat{\mathbf{a}}\in R_q$, and a precomputed twiddle factor table W storing powers of ${\psi }^{-1}$ in natural order

Output:  $\mathbf{a}\leftarrow$ INTT($\widehat{\mathbf{a}}$), with coefficients in normal order

1: $t\leftarrow 1$   2: for $m=n$; $m>1$; $m=m/2$ do   3:        $t\leftarrow 2t$   4:        for $i=0$; $i<m/2$; i++ do   5:               for $j=2i·t$; $j<(2i+1)·t$; j++ do   6:                     $u\leftarrow a_j$                    ▷ Temporary variable for $a_j$   7:                     $v\leftarrow a_{j+t}·W[m/2+i]$ mod q   8:                     $a_j\leftarrow (u+v)$ mod q   9:                     $a_{j+t}\leftarrow (u-v)$ mod q 10:               end for 11:        end for 12: end for 13: Return $\mathbf{a}$

2.3. Modular Reduction

Modular reduction is a mathematical operation that computes the remainder of a division by a modulus q. In the context of NTT, it ensures that all arithmetic operations remain within a predefined range, preventing overflow and keeping values within the finite field defined by q. The modulus q in NTT can vary from as few as ten bits to several thousand. Smaller bitwidths for q enhance computational speed and reduce resource consumption, while larger moduli increase security but at the cost of higher computational demands. For larger bit numbers, the residue number system (RNS) can be employed to manage complexity, but this often introduces its own overhead.

Modular reduction is computationally intensive, and several optimization methods have been developed. The Montgomery reduction simplifies the process by transforming numbers into Montgomery form, enabling modular multiplications and reductions through arithmetic shifts and additions, rather than traditional divisions. Abd-Elkader et al. [12] advanced this technique by developing a high-frequency, low-area Montgomery modular multiplier specifically for cryptographic applications. Similarly, Barrett reduction uses a pre-computed approximation of the modular inverse to facilitate rapid modular reductions without direct division. Langhammer et al. [22] enhanced this method by introducing a shallow reduction technique that reduces logic costs. Additionally, optimizations targeted at specific moduli have been pursued to boost performance and efficiency. For instance, Zhang et al. [23] utilized a technique that recursively splits features, improving the area-time efficiency for modulus 12,289.

2.4. High-Level Synthesis (HLS)

HLS allows designers to specify hardware functions in high-level programming languages such as C, C++, or SystemC, which are then automatically converted into HDL formats like Verilog or VHDL. This method offers a more abstract and efficient design process, reducing the risk of errors and enabling quicker iterations and better optimizations for complex designs. HLS is particularly valuable in the rapidly evolving field of digital technology and has proven successful in various applications [24]. Among the HLS tools available, Vitis HLS is tailored explicitly for Xilinx FPGA platforms, while Catapult HLS supports a broader range of technologies and is recognized for its vendor-neutral approach. Catapult HLS is chosen for design due to its flexibility in working with both FPGA and ASIC technologies from various manufacturers. Furthermore, it offers advanced optimization techniques that enhance performance and efficiency, which are essential for meeting complex processing needs. Additionally, its user-friendly interface makes it highly adaptable to different design frameworks.

Pragmas and optimization techniques in HLS are vital for efficient hardware design. Pragmas such as ‘unroll’ enhance parallel processing by expanding loops, while the ‘pipeline’ pragma increases throughput by overlapping computation stages. The initiation interval (II) in pipelining, which defines the clock cycle gap between consecutive operations, is crucial for managing throughput. The HLS tool also incorporates optimization strategies such as resource sharing, dataflow optimizations, and advanced memory management, balancing performance, resource efficiency, and power consumption.

3. Methodology

A systematic approach under HLS is introduced that considers arithmetic optimization and then combines the implementation of the memory access strategy to support fully pipelined architectures, further extending to parallel architectures. This can quickly explore the parameter design space using a template-driven automatic framework based on HLS.

3.1. Arithmetic Operations

3.1.1. Improved Montgomery Modular Multiplication

The modular reduction algorithm in NTT is crucial as it transforms modular multiplication into multiplication and shifts to avoid direct division, thereby enabling efficient computation. Montgomery and Barrett reductions are widely employed for modular multiplication across various parameters. Montgomery reduction is particularly effective when multiple modular multiplications are sequentially chained. This circumvents the need for intermediate conversions to standard number forms, thereby enhancing computational efficiency. Conversely, Barrett reduction offers ease of implementation and flexibility, as it does not require precomputed constants tied to the modulus but uses a precomputed approximation of the modular inverse, facilitating dynamic adjustments. In software implementations, Barrett reduction is more efficient for moduli under 32 bits, while Montgomery reduction is advantageous for moduli above 32 bits [25]. In hardware contexts, Montgomery reduction is preferred for its ability to create flexible and efficient structures, with numerous implementations adopting this algorithm [26].

The improved Montgomery modular multiplication algorithm is detailed in Algorithm 3. Inputs x and y, along with the modulus q, are l-bit numbers. The algorithm operates under the premises that $q·q_{inv}=1\left(\mathrm{mod}R\right)$ and $R·R^{-1}=1\left(\mathrm{mod}q\right)$. Differing from traditional modular multiplication, the algorithm yield $x·y·R^{-1}\left(\mathrm{mod}q\right)$ instead of directly computing $x·y\left(\mathrm{mod}q\right)$. This approach is instrumental in NTT calculations, where y often represents the exponent of twiddle factors. Pre-multiplying y by R minimizes additional multiplications when transitioning into and out of the Montgomery domain. Initially, the algorithm computes the product u (step 1), which is then reduced modulo R using a precomputed modular inverse $q_{inv}$ to obtain the intermediate value v (step 2). This value is multiplied by q to produce w (step 3), and the higher bits of u are adjusted by subtracting w (step 4). The final result, r, is ensured to be non-negative by conditionally adding q if r falls below zero (step 5).

Algorithm 3 General modular multiplication using Montgomery reduction

Input:  l-bit integers: x and y as inputs, l-bit modulus: q, $q_{inv}$ with $q·q_{inv}=1$ mod $2^l$, l-bit constant: $R=2^{l}modq$

Output: l-bit $r=x·y·R^{-1}$ mod q in Montgomery domain

1: $u[2l-1:0]=x[l-1:0]·y[l-1:0]$   2: $v[l-1:0]=u[l-1:0]·q_{inv}[l-1:0]$   3: $w[2l-1:0]=v[l-1:0]·q[l-1:0]$   4: $r[l:0]=u[2l-1:l]-w[2l-1:l]$   5: if  $r<0$  then   6:       $r[l-1:0]=r[l:0]+q[l-1:0]$   7: end if   8: Return $r[l-1:0]$

3.1.2. Mersenne for Modular Reduction

Beyond the aforementioned typical approach, employing special modular Mersenne primes enables a lighter-weight modular folding implementation for modular reduction algorithms, offering hardware-friendly characteristics. This paper proposes a generalized Mersenne modular multiplication. It compares its performance with the methods mentioned above, guiding the selection of HLS implementation strategies to establish NTT baseline benchmarks. Specific modular multiplication exploits the unique properties of certain moduli to enhance operational efficiency. Mersenne primes, defined as moduli of the form $q=2^k-1$, simplify modular operations by converting them into straightforward addition operations [27]. This simplification occurs because a number z, which can be expressed as $z=2^k·T+U$, where T and U represent the most and least significant k bits of z, respectively, reduces under a Mersenne prime modulus to $zmodq=T+U$. However, the limited number of Mersenne primes does not meet all the modular requirements. A natural extension is generalized Mersenne numbers, which use moduli of the form $q=2^k-e$ [28]. This configuration allows for the reduction $zmodq=U+T·e$, where $T·e$ can be efficiently computed due to the smaller bit sizes involved. We applied this property in the choice of modulus $q=\mathrm{8,380,417}$, represented as $q=2^{23}-(2^{13}-1)$, conforming to the generalized Mersenne form $2^k-e$, with $k=23$ and $e=2^{13}-1=8191$. The optimized modular multiplication is detailed in Algorithm 4.

In Algorithm 4, the sizes of intermediate results u and v are reduced by 9 bits through the multiplication with a small constant e (Steps 2 and 3). The subsequent multiplication constrains the size of r to be less than $2q$, ensuring that r is maintained within a 24-bit range (Step 4). The final step involves a conditional subtraction to ensure r remains less than q (Step 6). The overall process involves four multiplications: the initial multiplication produces a straightforward product (Step 1), while the following three target reduction (Steps 2–4). Although the algorithm requires multiple multiplications, the intentional limitation of bit width across these operations can enhance computational efficiency. In contrast, Algorithm 3, when implemented with a modulus length of $l=23$, requires a larger multiplication bit width, which may reduce the performance. However, Algorithm 3 simplifies the process by needing only three multiplications, as it computes $x·y·R^{-1}$ instead of $x·y$. A detailed performance comparison of Algorithms 3 and  4 will be presented in subsequent discussions to illustrate their performance characteristics.

Algorithm 4 23-bit modular multiplication using generalized Mersenne numbers

Input:  23-bit integers x and y as inputs, 23-bit modulus $q=2^{23}-2^{13}+1$, and 13-bit constant $e=2^{13}-1$

Output: 23-bit modular reduction result $r=x·ymodq$

1: $u[45:0]=x[22:0]·y[22:0]$   2: $v[36:0]=u[22:0]+u[45:23]·e[12:0]$   3: $w[27:0]=v[22:0]+v[36:23]·e[12:0]$   4: $r[23:0]=w[22:0]+w[27:23]·e[12:0]$   5: if  $r>q$  then   6:       $r[22:0]=r[23:0]-q[22:0]$   7: end if   8: return  $r[22:0]$

3.2. Microarchitectural Co-Design

3.2.1. Initial NTT Design in HLS

The NTT algorithm involves complex control and computation, requiring thorough optimization in HLS to achieve satisfactory performance results. The primary goal is to attain efficient pipeline performance while consuming reasonable hardware resources. Following Algorithm 1, an HLS-based NTT design code template was proposed, as shown in Listing 1. The algorithm has been modified to optimize data read and write operations, adapting it to the HLS implementation style. This code template is tailored for a polynomial length of N = 256 with a general modulus of 23 bits. This template is used as a case study to explore performance enhancements.

In Listing 1, input and output coefficients are transmitted through ac_channel, which includes handshake logic and pipeline registers for synchronization. The Q and QINV values used for Montgomery modular multiplication are input directly via registers. The complete set of coefficients is stored in the array a[N], which is configured as a dual-port RAM to enable simultaneous read and write operations. For the precomputed twiddle factor array zetas[N], configuring it as RAM allows for run-time reconfigurability but requires additional interface and configuration time. Given that the polynomial length is typically fixed in many applications and the twiddle factors rarely need replacement, we opt for a single-port ROM. The modular multiplication function (mod_mul) primarily utilizes Montgomery multiplication as described in Algorithm 3 (line 16). Modular addition (mod_add) and modular subtraction (mod_sub) are performed as standard additions and subtractions, followed by modulus operations (lines 17 and 18). The code template includes three main sections: input data (line 9), NTT computation (lines 12–18), and output data (line 22). In pure hardware applications, input data may be obtained directly from a preceding operation, thereby eliminating the need for additional data transfers. In software-hardware co-design applications, input and output transmissions depend on bus type and width. Therefore, unless specified, the discussion of NTT cycle performance focuses exclusively on the NTT computation.

Listing 1. Template code for basic NTT implementation using HLS.

3.2.2. Pipeline Optimization

A direct HLS implementation of the NTT algorithm, as outlined in Listing 1, immediately encounters a critical performance barrier. The initial simulations revealed an execution time of 7689 cycles, more than seven times the theoretical ideal. Schedule analysis pinpointed the culprit: a debilitating bottleneck termed the HLS Memory Wall.

The basic NTT algorithm requires ${\displaystyle \frac{N}{2}}{log}_{2}N$ butterfly operations (lines 16–18), with ${log}_{2}N$ stages (line 12), and each stage performing ${\displaystyle \frac{N}{2}}$ butterfly operations (lines 13, 15). In a fully pipelined mode, the NTT computation cycle count slightly exceeds ${\displaystyle \frac{N}{2}}{log}_{2}N$ due to the activation of additional control logic and the latency of the butterfly unit. For $N=256$, ${\displaystyle \frac{N}{2}}{log}_{2}N$ equals 1024. However, based on the template in Listing 1, the preliminary implementation, as simulated, revealed that the NTT calculation consumed 7689 cycles, more than seven times the ideal count. The schedule analysis revealed that the NTT_Loop_3 calculation (lines 15–18) consumes seven cycles per iteration, comprising one cycle for address calculation, three cycles for modular multiplication, one cycle for modular subtraction, one cycle for modular addition, and one cycle for writing the result back to memory.

The first challenge in pipelining is addressing memory read and write conflicts. In steps 16–18, sequential read and write operations occur at the exact addresses of a[j] and a[j+u]. The HLS tool cannot determine if the data written later will affect the previously read data. Since each memory location is only read and written once per NTT stage, the tool can be configured to ignore these sequential read and write conflicts. The second challenge is the insufficient number of ports due to multiple accesses of the same data. For instance, steps 17 and 18 both require a[j], necessitating multiple reads, and step 18 requires both reading and writing a[j]. To resolve this, intermediate variables are utilized to separate reading and writing from calculations, thereby consolidating repeated data accesses. This reduces the number of port accesses, allowing for deeper pipelining. After modifying the configuration, the three “for loops” is set in steps 12–18 to an II of 2. Simulations show that with these optimizations, the NTT computation consumes 2567 cycles.

When using a single RAM to store the coefficients, the NTT algorithm cannot achieve optimal pipeline performance. Each butterfly operation requires reading two coefficients and writing back two calculated coefficients, necessitating four interfaces, whereas a dual-port RAM provides only two ports for simultaneous reading and writing. Consequently, the pipeline II can only be set to 2 instead of 1. To address this, a ping-pong memory is constructed, which alternates reading data from one memory block and writing data to another, providing the structural solution that HLS cannot infer on its own. The optimized data flow of NTT, illustrated in Figure 1, utilizes two coefficient RAMs. Initially, coefficients are stored in the first RAM, where the butterfly unit reads data from it and writes the results to the second RAM. In the next NTT stage, data are read from the second RAM and written back to the first, alternating in sequence. This ping-pong memory structure utilizes two BRAMs, offering two read ports and two write ports, and separates memory read and write operations based on address. To validate the effectiveness of the strategy and determine the specific memory access logic, a memory access system was first modeled using Verilog HDL. A cycle-accurate simulation was conducted using a memory module generated by memory generators to evaluate a suitable ping-pong structure.

Based on the constructed ping-pong memory structure, the HLS code is modified for implementation of the butterfly operation, as shown in Listing 2. The HLS tool synthesizes this description into the hardware, and no additional Verilog modules are merged into the final design. In the software, a two-dimensional array is used to represent the ping-pong memory structure, changing the original coefficient array from a[N] to a[2][N]. Here, a[0][N] represents the first block of ping-pong memory, and a[1][N] represents the second block. During the butterfly operation, a 1-bit signal ‘sel’ selects the memory block, and the ‘sel’ signal flips after each NTT stage is completed. In this configuration, setting the pipeline II for NTT_Loop_2 and NTT_Loop_3 to 1, but do not pipeline NTT_Loop_1. This is because in NTT_Loop_1, it is necessary to wait until one NTT stage finishes before starting the next stage. If the next stage begins before the previous stage is completed, the same memory block may be read and written simultaneously, resulting in an insufficient memory port issue. Through simulation, the NTT calculation time is reduced to 1357 cycles, which is close to the ideal pipeline performance.

Listing 2. Two-dimensional array based HLS code style for butterfly unit.

3.3. Architectural Co-Design

3.3.1. Parallel NTT Architecture

Having optimized a single pipeline, scaling performance via parallelism seems straightforward. However, a naive application of the pragma unroll directive immediately resurrects the memory wall, proving that compute parallelism without co-designed memory parallelism is futile in HLS. This reinforces the necessity of the co-design methodology at the system architecture level.

To further enhance the performance of NTT using HLS, higher levels of parallelism need to be explored. The previous results indicate that directly using the unroll pragma is not feasible due to memory port limitations, which hinder pipeline optimization after unrolling. The design of a parallel NTT architecture must address several critical factors. These include managing the parallel data flow for simultaneous operation processing and ensuring robust synchronization and communication between units for data consistency. Additionally, effective resource sharing is necessary to optimize hardware utilization and improve performance. Developing parallelized algorithms and architectures is essential, including generating control logic, obtaining coefficients, accessing twiddle factors in parallel, and performing computations concurrently in multiple butterfly units. The memory banks division and the coefficient index generation pattern proposed in [29] are followed. The read and write order of Algorithm 1 is adapted, and the parallel access order of coefficients is shown in Figure 2.

In Figure 2, the polynomial length N is 8, and the parallel level d is 2, utilizing two butterfly units for computation. The input polynomial coefficients are read sequentially, eliminating the need for bit-reversal operations. During each stage, the two butterfly units collaboratively process four polynomial coefficients. For instance, in the first stage, the first butterfly unit computes the coefficients at indices 0 and 4, while the second butterfly unit computes the coefficients at indices 2 and 6. When the conditions of formula (10) in [29] are satisfied, pipeline computations can be executed between different NTT stages without read-and-write conflicts. Unlike the ping-pong memory access method, the coefficients with the same indices are read from and written back to the same memory block. Consequently, the two butterfly units require a total of four dual-port RAMs for simultaneous reading and writing. The division of the coefficient storage blocks and the address indexing are calculated according to formula (2) in [29]. Generalizing from the parallel access scheme, the parallelized NTT data flow architecture is illustrated in Figure 1.

In Figure 1, the proposed architecture achieves scalable parallelism by parameterizing the number of butterfly units d. Each butterfly unit is paired with two dedicated dual-port RAM blocks, resulting in a total of $2d$ RAMs, while the modulus bit width Q determines data width w. At initialization, the input coefficients are distributed across these RAM blocks to maximize memory bandwidth. During computation, each butterfly unit simultaneously retrieves its required coefficients from the RAMs using dynamically generated addresses, processes them, and writes the results back to the same addresses, ensuring in-place updates. To resolve potential memory port contention and enable efficient data reorganization, a set of $2d$ coefficient registers implemented as the array coeff_reg[d∗2] is introduced. These serve as intermediate buffers for flexible and conflict-free read/write operations without port limitations. A for loop is used to write coefficients into specific locations within the coefficient register, followed by the use of the unroll pragma to fully expand the loop, thereby allowing for full pipelining of the computation. The originally generated twiddle factors $\mathrm{zetas}\left[N\right]$ are extended into zetas_extend$[N+d·{log}_{2}d-d]$, and are organized in parallel and stored in a single-port ROM to coordinate with the parallel NTT computation efficiently. The detailed calculation process is shown in Listing  3. This co-design of memory architecture, register buffering, and parallel-friendly twiddle management forms a highly efficient and scalable solution for high-level-synthesis-based NTT accelerators, addressing typical HLS bottlenecks and substantially improving parallel performance.

3.3.2. Unified NTT/INTT

Based on the established framework, the design can be extended to incorporate the INTT. The primary differences between the INTT and NTT lie in the direction of the transform and the scaling factors used. Traditionally, to adapt the original NTT design for the INTT, the twiddle factors need to be replaced with their inverses, and the final scaling factors need adjustment for proper normalization. To reduce design complexity and achieve a compact design, the unified butterfly design from Zhang et al. [23] is adopted. This unified design integrates NTT pre-processing and post-processing into the butterfly and uses selection logic to reuse arithmetic units.

In the unified NTT/INTT design, coefficient access for NTT follows the pattern shown in Figure 2. For INTT, the GS butterfly is adopted, with coefficient access symmetrical to that in Figure 2. For example, using the same parameters as in Figure 2, the coefficient access order in stage 0 of INTT mirrors that of stage 2 in NTT. This symmetry can be achieved by adjusting a few control parameters within the parallel NTT control logic. To further minimize resource usage, the symmetric relationship between NTT and INTT twiddle factors can be leveraged. When parallelization is not considered, the twiddle factor for NTT is calculated by $\mathrm{zeta}\left[i\right]={\psi }^i$ for $i=0,1,\dots ,n-1$, followed by bit-reversing the coefficient order. In contrast, the twiddle factor for INTT is calculated by $\mathrm{zeta}\left[i\right]={\psi }^i$ for $i=n,n+1,\dots ,2n-1$, and then bit-reversed. Given that ${\psi }^n\equiv -1modq$, the precomputed twiddle factors for INTT can be derived from those of NTT by flipping the sign bit. For parallel NTT computations, multiple twiddle factors are required simultaneously. By comparing the access orders, it can be found the generated parallel NTT twiddle factor in Listing 3 is still applicable to INTT, with only a few external control parameters needing to be reversed.

To extend the NTT design to support both NTT and INTT computations, the primary task is to develop a unified butterfly. The HLS code for the unified NTT/INTT butterfly is shown in the Listing 4. Each butterfly contains two input polynomial coefficients, a_in1 and a_in2, and two output polynomial coefficients, a_out1 and a_out2. The 1-bit sel signal selects between NTT and INTT butterfly computations. For NTT, the butterfly computes $a+b·\omega$ and $a-b·\omega$. For INTT, it computes $(a+b)/2$ and $(a-b)·\omega /2$. The multiplication factor $n^{-1}$ in INTT is integrated into the butterfly computation through multiplication by $1/2$, implemented using the DivideBy2() function. The DivideBy2(x) function computes $(x\gg 1)$ when x is even or $(x\gg 1)+(Q+1)/2$ when x is odd. The twiddle factor zeta for NTT or INTT computations is selected by external control logic. According to the derivation, the twiddle factors for NTT and INTT differ only by a negative sign, thereby optimizing memory requirements by halving the storage required for the twiddle factors. Therefore, expanding the NTT design to a unified NTT/INTT design does not increase the memory requirements.

Listing 3. Parallel twiddle factor generation using Python and Jinja.

Listing 4. Unified butterfly design template of NTT/INTT for HLS.

3.3.3. Automated Generation Framework

To encapsulate the co-design methodology, an automated generation framework was developed and presented in Figure 3. This framework is more than a code generator, but it is an embodiment of the architectural template. It enables rapid design space exploration (DSE), allowing designers to instantiate various parallel configurations (different d) while ensuring that the underlying memory-compute co-design principles are consistently preserved. The framework currently proposed employs grid search within the configurable parameter domain. This search method offers the advantage of requiring fewer points to evaluate, enabling rapid identification of optimal combinations when the range of suspect parameters is narrow or the dimensionality is low. In the case study, NTT has varying parameter requirements in different applications, making parameterizable design essential. Traditional NTT hardware designs often focus on specific or a limited set of parameters due to the complexity and challenges of simultaneously accommodating multiple parameters. HLS design offers convenience and flexibility, allowing parameterized configurations to be set at design time while maintaining a high level of hardware customization to ensure computational efficiency. In addition to manually modifying the HLS code, general templates can be created to fully explore and optimize the performance of NTT hardware, providing a versatile solution for diverse encryption applications. Jinja, a templating engine for Python, facilitates dynamic content generation based on runtime data and is suitable for the parameterized design. The Listing 3 for twiddle factor generation first calculates the complete zetas_extend in Python and then shifts and merges different twiddle factors according to the degree of parallelism d to obtain zetas_combine. Finally, the Jinja template is used to generate code that conforms to the HLS language style for accurate calculation. Based on different design tools and optimization techniques, an automated NTT code generation framework is developed, as shown in Figure 3.

In Figure 3, users initiate the process by defining implementation requirements through minor code definitions, after which the NTT implementation code is generated automatically following the specified workflow. Users can configure parameters for the NTT hardware implementation based on specific application and performance needs, including polynomial length N, parallelism degree d, and modulus Q. Additionally, users can set board and timing requirements for the hardware implementation. To ensure proper integration with external systems, users can select external interfaces such as full handshake wires, FIFO, and AXI channels. During the automated code generation process, Python is employed for pre-computation based on the defined parameters, leveraging a powerful mathematical library. The HLS code is generated using the Jinja template format, with environment settings and parameter configurations managed in Python 3.12.3. The generated script file automates code analysis and testing within Catapult HLS, ultimately producing the Verilog code. The configuration and code files are then automatically imported into Vivado, completing the synthesis and implementation on the board. This automated design process significantly accelerates the iteration of NTT code design and verification.

4. Experiments

4.1. Setup and Development

The experiment utilizes Catapult HLS 2021.1 and Xilinx Vivado 2019.2. In hardware implementation, the C code and optimization commands are provided to generate Verilog code and obtain design results. To ensure accuracy, the Verilog code is tested through the FPGA design flow using Xilinx Vivado 2019.2, targeting the Xilinx Virtex-7 xc7vx690tffg1761-2 board. SCVerify in Catapult is used to simulate the generated Verilog. Input and output interfaces are incorporated to simulate the design and gather implementation results. To ensure consistency with subsequent designs, II is targeted at 1 with a complete pipeline.

To evaluate our proposed work, we compare the results with a series of prior works focused on NTT accelerators. The comparison baseline includes both HLS-based and HDL-based designs. These works were selected for comparison because they were all deployed on FPGA platforms for experimentation, explored multiparameter combinations within NTT, and shared detailed resource conversion methods, enabling fair comparisons of performance and resource overhead. The evaluation matrix includes fundamental performance metrics in the hardware domain such as Latency and Cycle Count. Resource utilization is reported by LUT, FF, DSP, and BRAM overheads. Additional measures of normalized area-time efficiency are conducted by the area-time product and the area-cycle product. The former reveals the absolute time-area efficiency of the hardware design, while the latter observes the relative time-area efficiency independent of frequency. In subsequent testing sections, operations per watt and throughput per watt are used for power efficiency analysis, with detailed elaboration provided at the relevant points. To ensure a fair comparison between experiments and prior work, it is worth noting that this paper first calibrated and validated the resource conversion formula’s validity. This was achieved by performing implementations on Vivado 2019.2 for the resources DSP and BRAM across all compared works involving the Xilinx FPGA Virtex 7, Kintex-7, Zynq UltraScale+, and Spartan 7 series. At a baseline frequency of 100 MHz with no timing violations, the average replacement values were calculated as approximately 478 LUTs and 87 FFs per DSP, and approximately 277 LUTs and 32 FFs per 18 Kb BRAM. The calibration results indicate that the estimation formula used in the previous work [30,31], where one DSP equals 819.2 LUTs and 409.6 FFs, is more conservative in terms of DSP resource conversion. This imposes a penalty on DSP utilization in the final area calculations. This evaluation approach aims to enhance design portability across various mid- to low-end FPGAs. As it aligns with the objectives of this work, subsequent results will be normalized according to their conversion standards.

4.2. Experimental Results

The comparison results of modular multiplication are shown in

Table 1. Comparison of modular multiplication implementation.

Design	Bit	Device	Language	Cycle	LUT	FF	DSP
Comba [32]	32	Virtex-7 XC7VX980T	VHDL	6	199	168	2
SAMS2 [33]	14	Artix-7	N/A	N/A	154	142	0
Special modulus property [5]	16	Virtex-7 XC7VX690	System Verilog	5	246	206	1
	27				485	424	4
	28				458	376	4
	32				534	479	4
Mersenne (ours)	23	Virtex-7 XC7VX690	HLS	4	134	130	4
Montgomery (ours)	23				84	106	5
	32				184	235	11

. Rafferty et al. [32] explored hardware architectures for large integer multiplication and presented results for 32-bit Comba multiplication. Compared to [32], our 32-bit Montgomery multiplication consumes a similar number of LUTs and FFs but utilizes more DSPs. Xing et al. [33] implemented an optimized SAMS2 modular reduction method, a variant of Barrett reduction with low Hamming weight, and optimized 14-bit modular multiplication for the NewHope PQC algorithm. Compared to [33], our 23-bit Mersenne multiplication consumes 87% of the LUTs and 91% of the FFs, and our 23-bit Montgomery multiplication consumes 54% of the LUTs and 74% of the FFs, although our design requires more DSPs. Ye et al. [5] developed a low-latency modular arithmetic implementation utilizing the modulus property $2^j\equiv 2^i-1modq$ for different bit sizes of the modulus q. Compared with [5], our 32-bit Montgomery multiplication achieves similar cycle performance while using 34% of the LUTs, 49% of the FFs, and 2.75 times the DSPs. Overall, our HLS-based design achieves comparable cycle performance to traditional hardware design methods, with relatively fewer LUTs and FFs but a higher DSP resource requirement.

The implementation results of the NTT algorithms are shown in

Table 2. Implementation results of NTT algorithms.

Algorithm a	Bit	Total Area d	LUT/FF/ DSP/BRAM	Cycle/ Freq (MHz)	Latency (μs)
Basic NTT	23	3860	392/257/4/1.5	7689/120	64.0
NTT (II = 2)		3917	482/381/4/1	2567/117	21.9
NTT (II = 1)		5078	419/574/6/2.5	1357/120	11.3
NTT with unrolling b	23	8045	2226/858/6/1	7627/116	65.7
NTT (II = 1)	32	7085	590/710/9/2.5	1357/116	11.6
NTT (II = 1) Mersenne c	23	4561	497/624/4/2.5	1365/121	11.2

^a If not specified, the modular multiplication of the NTT uses Algorithm 3. ^b It sets the unrolling factor of NTT_Loop_2 to 4 and NTT_Loop_3 to 2. ^c The modular multiplication uses the Mersenne algorithm (Algorithm 4). ^d Total area is calculated by Catapult HLS based on algorithm complexity.

. The implementation process and tools are consistent with those described in Section 3. From Table 2, we observe that as we gradually apply pipeline optimizations to the NTT algorithm, the area and the resource consumption for FPGA implementation increase slightly, but the cycle performance improves significantly. Notably, the number of BRAMs used when the pipeline II is set to 2 is less than that of the basic NTT, as some memory resources are implemented using LUTs. When comparing II = 2 with II = 1, fewer LUT resources are consumed with II = 1 because more DSPs, FFs, and BRAMs are utilized to improve performance. The NTT design (II = 1) achieves a latency of 11.3 µs. This represents a 5.6× improvement over the basic implementation of HLS. This validates our hypothesis after systematic HLS co-design analysis, designing an appropriate ping-pong cache structure resolves the primary bottleneck of memory access contention.

The unroll pragma is tested to determine if it can automatically increase algorithm parallelism, using the basic NTT algorithm without pipeline optimization. For NTT_Loop_1, we do not use the unroll pragma due to data dependencies between different NTT stages, which cause invalid calculations if expanded. As shown in Table 2, simple loop unrolling does not significantly improve computing performance. Schedule analysis reveals that although unrolling adds computing units, all units access data from the same memory, which limits speed. Therefore, automatic optimization through tool commands is insufficient for achieving higher parallelism.

From Table 2, as the modulus increases from 23-bit to 32-bit, the area and FPGA resource consumption grow proportionally. This is because the primary resource consumption in NTT lies in the butterfly unit, which operates under the modulus Q. Utilizing a 23-bit Mersenne prime modulus for modular multiplication, Algorithm 4 reduces the total area presented in

Table 3. Implementation results of modular multiplications.

Method	Bit	Total Area a	LUT	FF	DSP	Cycle	Freq (MHz)
Montgomery	23	3719	84	106	5	4	123
	32	6898	184	235	11	4	124
Mersenne	23	3197	134	130	4	4	122

^a Total area is calculated by Catapult HLS based on algorithm complexity.

because of its lower complexity. The reduction in FPGA resources is evident in the decrease in the number of DSPs required, although there is an increase in the number of LUTs and FFs. The experimental results align with expectations from special prime analysis, validating that HLS-based designs enable convenient hardware generation for fast comparisons with reasonable initialization. Subsequently, to accommodate arbitrary prime requirements while maintaining comparable design efficiency, a more robust Montgomery algorithm design template was adopted. Therefore, different modular multiplication algorithms offer trade-offs tailored to specific requirements.

The unified NTT/INTT design integrates into the framework shown in Figure 3. Results for the NTT/INTT design with $N=1024$ and 32-bit modulo are presented in

Table 4. Unified NTT/INTT design results and comparison with power and efficiency metrics.

Design (Device)	N (Bit)	d	LUT	FF	DSP/ BRAM	Cycle/Freq (MHz)	Power (W)	Energy/ trans (μJ)	Throughput/W (k-trans/s/W)
[15] (Artix-7)	1024 (29)	1	1977	991	6/11	11455 (124)	-	-	-
[34] (Virtex-7)	1024 (32)	4	13,455	14,378	0/4	$1331\times 2$ (294)	-	-	-
Ours (Virtex-7)	1024 (32)	1	1528/+13% a	1269/+44% b	13/1	$5133\times 2$ (117)	0.022	0.97	1036.4
		2	2753/+17% a	2445/+36% b	24/2	$2573\times 2$ (115)	0.041	0.92	1090.2
		4	6042/+21% a	4762/+35% b	46/4	1293 × 2 (117)	0.073	0.81	1239.6

^a Percentage increase in LUT: $\frac{\mathrm{LUT} (\mathrm{Unified}\mathrm{NTT}/\mathrm{INTT})}{\mathrm{LUT}\left(\mathrm{NTT}\right)}-1$; ^b Percentage increase in FF: $\frac{\mathrm{FF} (\mathrm{Unified}\mathrm{NTT}/\mathrm{INTT})}{\mathrm{FF}\left(\mathrm{NTT}\right)}-1$. Energy per transform (Energy/trans) and Throughput per Watt are based on a normalized single transform (NTT or INTT). A dash (-) indicates data are not available.

. For reference, the resource increase of the unified module relative to the NTT module under the same parameters is listed. As shown in Table 4, the unified NTT/INTT design results in a 17% increase in LUTs and a 38% increase in FFs on average, while DSPs and BRAMs remain unchanged. The increase in LUTs and FFs is due to additional control and selection logic. The reuse of multiplication within the unified butterfly ensures that the number of DSPs remains constant. Additionally, our optimization reuses the twiddle factors for NTT and INTT, maintaining the same number of BRAMs. The cycle performance for NTT and INTT is identical, resulting in a combined NTT + INTT cycle count that is twice the NTT cycle count. Efficient pipeline divisions ensure that the unified NTT/INTT design does not affect timing performance compared to a standalone NTT design. Our design consumes similar resources and demonstrates comparable cycle performance to Verilog-based designs [15], utilizing more DSPs but fewer BRAMs. Compared to [34], their NTT design was manually fine-tuned on an HDL basis, and the performance and resource overhead obtained are close to our results using an automated design flow to produce an HLS design. Our generated design takes more DSP, while the LUT/FF is half and one-third of their design, respectively. This demonstrates the superior performance and design efficiency of our approach. Furthermore, our design supports different levels of parallelism, enabling a more thorough exploration of trade-offs. Additionally, the module underwent post-placement power analysis on Virtex-7, with its energy efficiency performance shown in the table. When the unified NTT/INTT accelerator $N=1024$, total power consumption increased from 22 mW to 73 mW as the d rose from 1 to 4. However, this increase in power consumption is far outweighed by the substantial reduction in latency achieved by increasing the parallelism level d. Analysis reveals a decreasing trend in energy consumption per operation (NTT or INTT), from 0.97 μJ at $d=1$ to 0.81 μJ at $d=4$. This indicates that despite the parallel architecture theoretically requiring greater total area and power consumption, its substantial computational speedup results in lower overall task energy consumption. The d = 4 design achieves a throughput of 1239.6 k-trans/s/W, representing approximately a 20% efficiency improvement over the d = 1 design. This proves that our system co-design methodology not only constructs scalable, high-performance architectures but also delivers exceptional energy efficiency.

4.3. Design Space Exploration

To evaluate the scalability and adaptability of our proposed architectural template, a design space exploration is performed. The DSE strategy involves conducting a grid search across the most impactful architectural parameters: the degree of parallelism (d) and the transform size (N). Experiments are presented for powers of two, specifically for the parallelism degree d, as it naturally aligns with the inherent radix-2 structure of the NTT algorithm that we employ. This alignment results in highly efficient and straightforward hardware for memory banking, address generation, and twiddle factor distribution, which can be implemented using simple bitwise operations. While supporting non-power-of-two parallelism (e.g., $d=3$) is theoretically possible, it would necessitate the implementation of more complex mixed-radix algorithms and a significantly more intricate memory addressing scheme, leading to substantial control logic overhead. Therefore, the focus on powers-of-two parallelism is a deliberate design trade-off to maximize performance scalability while minimizing hardware complexity. For each configuration point $(d,N)$, we run the complete HLS and physical implementation flow to obtain precise performance and resource cost (LUTs, FFs, BRAMs, DSPs) data. The goal of this exploration is not to find a single optimal point, but to characterize the Pareto-optimal front of the trade-offs between performance and resources, thereby providing a comprehensive guide for designers to select an implementation that best fits their specific constraints.

Different parameters are configured using the automated NTT code generation framework shown in Figure 3, with implementation results summarized in

Table 5. NTT performance under different degrees of parallelism.

N (Bit)	d	LUT	FF	DSP/ BRAM	Cycle	Freq. (MHz)	Cycle×LUT (${10}^6$)
256 (24)	1	810	422	6/1	1033	117	0.83
	2	1678	1023	11/2	522	119	0.87
	4	3761	2008	21/4	266	118	1.00
512 (24)	1	902	688	7/1	2315	117	2.08
	2	1574	1374	13/2	1164	117	1.83
	4	3619	2723	25/4	588	117	2.12
1024 (24)	1	1005	708	8/1	5131	116	5.15
	2	1812	1251	14/2	2571	117	4.65
	4	4304	2132	21/4	1290	117	5.55
16,384 (32)	1	8359	1001	13/16	114,699	116	958
	2	9358	2131	24/16	57,357	115	536
	4	12,444	4219	30/16	28,685	116	356
32,768 (32)	1	15,697	1029	13/32	245,771	116	3857
	2	17,090	1980	24/32	122,892	115	2100
	4	21,002	3925	30/32	61,452	116	1290

. The platform configuration remains consistent with the description in Section 3. Tests are conducted for polynomial lengths N ranging from 256 to 32,768. For $N\le 2048$, the modulus Q is 24 bits, while for $N\ge 4096$, the modulus Q is 32 bits. Various results are tested with parallelism d set to 1, 2, and 4 to investigate the trade-offs between resources and performance. Theoretically, the NTT for a polynomial length N requires ${\displaystyle \frac{N}{2}}·{log}_{2}N$ butterfly operations. With d butterflies, ${\displaystyle \frac{N}{2d}}·{log}_{2}N$ parallel butterfly operations are required, consuming approximately d times the resources. Therefore, the product of Cycle and LUT is relatively fixed, and this metric can roughly reflect the design trade-offs.

As shown in Figure 4, for the same N, increasing d leads to higher resource consumption and shorter calculation cycles. However, tabular data shows that BRAM consumption does not necessarily increase with d. Notably, when N exceeds 2048, the number of BRAMs remains unchanged as d increases for the same N. This is because, for larger N, coefficients are distributed across multiple BRAM blocks even when $d=1$, so increasing d does not require additional BRAM blocks. Conversely, for the same d, resource consumption increases as N grows. This increase is partly due to the added complexity of control logic with larger N, but a more significant factor is the implementation of the memory block. Our designs generate general Verilog code via HLS, which is not optimized for specific FPGA IPs. For memory units, the Vivado tool automatically uses a combination of BRAM and LUT to implement them, causing memory requirements to increase proportionally with N. Consequently, LUT resources rise significantly as N increases. This trend can be clearly observed in Figure 5, where LUTs and BRAMs as a percentage of area overhead increase significantly as N increases. It demonstrates a shift in design resource utilization from logic-intensive to memory-dependent components. For instance, with $d=1$ and NTT length of 256, the DSP area constitutes approximately 79% of the total design footprint. As N increases, when $N=$ 32,768, BRAMs and LUTs used for storage logic account for about 65% of the total area overhead. This observation underscores the importance of our proposed co-design methodology. For long NTTs, optimizing the memory subsystem should be given the highest priority over the algorithm itself. At this scale, the efficiency of the memory subsystem becomes the primary factor constraining the scalability of NTT design.

The frequency of the NTT hardware implementation ranges from 115 to 119 MHz. Analysis indicates that the critical timing path primarily involves the input and output interfaces. Other critical paths include the coefficient RAM interfaces, modular multiplication operations, NTT loop count and control logic, and the data read interface of the twiddle factor ROM. As d increases, the RAM path becomes an increasingly significant timing bottleneck. In practice, connecting the input and output interfaces to high-speed interfaces can prevent them from becoming timing bottlenecks. For modular multiplications, NTT loop count, and control logic, users can increase the target frequency of the HLS tool and use more pipeline stages to split the critical path, thereby avoiding timing bottlenecks. To address the timing constraints of the coefficient RAM, especially when achieving higher parallelism, users can develop improved memory models to better utilize BRAM in FPGA, enabling more efficient parallel memory usage.

5. Discussion and Evaluation

5.1. Comparisons with HLS-Based and HDL-Based NTT Designs

This work focuses on the optimization and generation of the NTT module, whose performance significantly impacts the efficiency of PQC accelerators. For instance, in many PQC accelerators such as CRYSTALS-Dilithium, Kyber, or Falcon, a substantial portion of the area and computational overhead is attributable to NTT/INTT. The unified accelerator generated using the HLS framework can serve as an efficient, plug-and-play IP for these applications. This capability is demonstrated through RISC-V system integration in the following subsection. In this subsection, the experimental results of this work and some prior studies are presented and analyzed in detail.

Note that to conduct a fair comparison between different designs implemented on different devices, we follow [30,31] to assign different ratios to specific hardware resources (LUT, FF, DSP, and BRAM) to calculate the overall area usage. That is AREA = LUT/16 + FF/8 + DSP × 102.4 + BRAM × 56. Taking account of the influence of frequency, the Area-Time Product (ATP) is defined as the product of area and latency. Additionally, in many applications, the frequency is determined by the overall system rather than an individual module, so the product of area and cycle is also compared. The NTT design is compared with related HLS implementations in

Table 6. Comparison results of HLS-based NTT implementation.

Design	N	Bit	Device	LUT	FF	BRAM	DSP	Area (K) a	Freq. (MHz)	Cycle	Cycle× Area (K)	Latency (μs)	ATP b
[35]	1024	26	Spartan 6	182	114	10	3	0.89	N/A	N/A	N/A	69.1	61.6
	32,768	32	Virtex-7 XC7V585T	3392	1920	792	48	49.7				41,120	2043K
				13,568	7680	792	192	65.8				10,280	676K
[13]	1024	N/A	Virtex-7 XC7VX690	38,984	30,498	21.5	19	9.39	100	5291	49.6	52.9	496
	32,768			69,476	87,477	402	53	43.2		197,398	8527	197.3	8523
[36]	1024	19	Ultrascale+ ZCU102	19,185	10,963	54	4	6.0	299	7390	44.3	25	150
	2048	33		21,926	16,444	73	100	17.7	272	15,614	276	58	1026
[11]	1024	N/A	Virtex-7 XC7VX485	4737	3243	2	8	1.63	218	16,569	27.0	76	123
[17]	1024	14	Virtex-7 XC7VX690	1045	N/A	4	3	N/A	100	30,723	N/A	307	N/A
				11,305		16	24			15,363		153
[37]	256	23	Ultrascale+	2590	1885	7	12	2.0	N/A	1685	N/A	N/A	N/A
[38]				2015	1371	5	12	1.80		1424
[39]	256	24	Artix-7 XC7A200T	299	296	1	2	0.31	200	8971	2.78	44.7	13.8
				7849	2827	0	248	26.2	58	574	15.0	9.87	258
Ours	256	24	Virtex-7 XC7VX690	3761	2008	4	21	2.86	118	266	0.76	1.91	5.46
	1024			4304	2132	4	21	2.90	117	1290	3.74	11.0	31.9
	2048			4883	2076	4	22	3.04	119	2826	8.59	23.7	72.0
	32,768	32		21,002	3925	32	30	6.66	116	61,452	409	529	3523

^a The Area is calculated as $\mathrm{LUT}/16+\mathrm{FF}/8+\mathrm{DSP}\times 102.4+\mathrm{BRAM}\times 56$, following [30,31]. ^b The ATP is calculated as Area × Latency.

. Compared with [35] in $N=1024$, our design has lower latency and roughly a 1.93× reduction in ATP. For $N=\mathrm{32,768}$, our design uses fewer BRAMs to achieve lower latency, resulting in $579\times$ and $191\times$ reductions in ATP. Compared with [13], our design achieves a smaller area and latency, achieving $15.5\times$ and $2.4\times$ reductions in ATP. Millar et al. [36] enhanced FFT-based multiplication for HE, using more hardware resources to increase frequency. Our design achieves lower latency through better cycle performance, resulting in $4.7\times$ and $14.25\times$ improvements in ATP.

Compared to [11], our design consumes similar resources but exhibits significantly better cycle performance, with a $3.22\times$ ATP improvement. Our design consumes resources between the two designs in [17], yet provides more than a $10\times$ improvement in cycle performance. When N = 256, due to the deeper pipeline structure, our result exhibits a large area overhead around 45% greater than theirs [37,38], but resulting in $6.33\times$ and $5.35\times$ improvements in cycle performance. Our design consumes resources within the range of [39], but uses fewer computation cycles and achieves $2.52\times$ and $47.2\times$ better ATP results. Compared with other HLS-based NTT designs, our design demonstrates superior cycle performance, maintains comparable frequency, consumes fewer resources, and shows clear advantages in ATP comparisons. In summary, our approach consistently outperforms prior HLS-based works in area-time efficiency, underscoring the effectiveness of our co-design methodology.

The comparison results between our HLS-based design and HDL-based design are shown in

Table 7. Comparison results of HDL-based NTT implementation.

Design	N	Bit	Device	LUT	FF	BRAM	DSP	Area (K) a	Freq. (MHz)	Cycle	Cycle× Area (K)	Latency (μs)	ATP b
[5]	1024	28	Virtex-7 XC7VX690	94,394	104,864	80	640	89.0	215	198	17.6	0.92	81.8
	4096	28		117.3K	135.2K	189	768	113.4	224	446	50.5	1.99	225.6
[7]	1024	28		206K	159K	80	640	102.7	210	231	23.7	1.1	112.9
	4096	30	XCU200	54.1K	56.2K	84	288	44.6	250	6175	275	24.7	1101
[6]	1024	32	Virtex-7 XC7VX485	10,272	6704	79	80	14.0	250	650	9.1	2.6	36.4
	4096	32		14,004	8662	79	80	14.5	250	3075	44.5	12.3	178.3
[8]	1024	32	Virtex-7 XC7V585	4655	4327	9	16	2.97	333	4153	12.3	12.47	37.0
	4096	32		4747	4034	24	16	3.78	297	19,706	74.4	66.35	250.8
Ours	1024	28	Virtex-7 XC7VX690	4679	3577	4	30	4.0	117	1292	5.1	11.0	44.0
		32		4865	3654	4	30	4.0	117	1292	5.1	11.0	44.0
	4096	32		6808	3828	4	30	4.2	115	6156	25.8	53.5	224.7

^a The Area is calculated as $\mathrm{LUT}/16+\mathrm{FF}/8+\mathrm{DSP}\times 102.4+\mathrm{BRAM}\times 56$, following [30,31]. ^b The ATP is calculated as Area × Latency.

. Ye et al. [5] proposed a parameterized NTT architecture supporting various polynomial degrees, moduli, and data parallelism levels, using significant resources to achieve high frequency and low computational cycles, reducing latency by more than $10\times$ compared to ours. However, our design achieves a more balanced use of hardware resources, resulting in $1.85\times$ and $1.03\times$ improvements in ATP results compared to [5]. Yang et al. [7] presented a framework for generating low-latency NTT designs for HE-based applications. Our approach, using simpler logic and more resource-efficient methods, achieves $2.5\times$ and $5\times$ improvements in ATP results despite operating at a lower frequency. Su et al. [6] developed a reconfigurable multicore NTT/INTT architecture with variable PEs, fully optimizing hardware resource usage with high parallelism. Our design achieves similar ATP results at lower frequencies compared to [6]. Cheng et al. [8] presented a radix-4 polynomial multiplication design with an efficient memory access algorithm, enhancing NTT, INTT, and modular multiplication performance. Compared to [8], our design uses similar hardware resources but achieves better cycle performance, resulting in a $1.1\times$ improvement in ATP performance for $N=4096$.

Overall, compared to HDL-based designs, our HLS-based design utilizes resources more efficiently and achieves reasonable cycle performance. While traditional HDL-based designs can fully leverage FPGA IPs to reduce the latency, HLS-based designs provide greater flexibility for rapid design space exploration. Despite operating at lower frequencies, HLS designs can achieve comparable or superior ATP results. In terms of Area-Cycle efficiency, our HLS-based design outperforms the referenced HDL-based designs by $1.7\times$ to $10.6\times$. This validates the significance of our work, demonstrating a pathway to democratize high-performance hardware module design and foster a broader hardware research and developer community.

5.2. System Integration and Future Direction

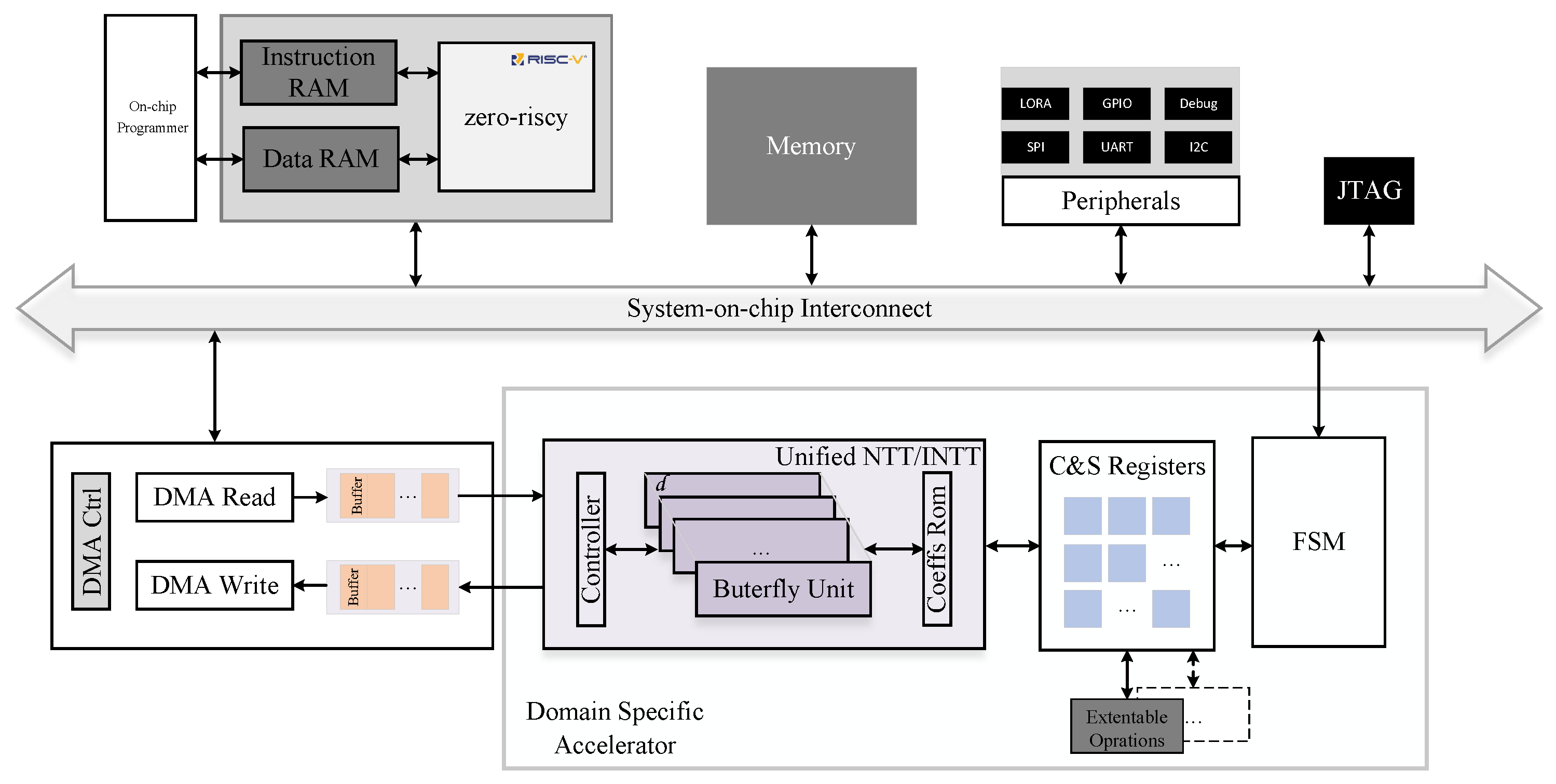
RISC-V is an open-source architecture that offers better reproducibility and flexibility than closed ARM processors, allowing our customized designs to be seamlessly connected at the RTL level. Moreover, our choice of RISC-V is derived from the Pulpino open source project, which has a large community, and therefore, the relevant information is already well established. This allows the design workflow and code in this paper to be open-sourced in the future, making it easy for more researchers and developers to use it freely, explore and implement their designs faster, and provide support for optimizing the lattice code in different ways. To illustrate the usability, we integrate the unified NTT/INTT module into an RISC-V-based processor system and verify its performance on a real FPGA board. The architecture of the integrated system is shown in Figure 6. This platform is built on the open-source PULPino RISC-V system [40,41], which has supported several emerging applications [42,43]. The RISC-V core utilizes the zero-riscy core, a lightweight core with two pipeline stages. The RISC-V core performs software computations by executing instructions stored in the instruction RAM. The data RAM stores the data utilized and manipulated during program execution. The on-chip programmer, configured through online programming, handles loading and updating the memory contents. The system is 32-bit and transmits data and control signals through the AXI bus. The DMA controller reads and writes input and output polynomial coefficients. Additionally, the 1-bit selection signal for NTT and INTT is transferred through the control register.

The overall design utilizes HDL, enabling convenient migration across boards. For our integration board test, we use the Kintex-7 KC705 evaluation board. Compared to the previous Virtex-7 board, this board has only 47% of the LUT resources, which may slightly reduce the performance. The onboard operating frequency adheres to the RISC-V platform setting of 100 MHz, and the test results are presented in

Table 8. System integration and test results.

Design	Ours			[15]
	RISC-V + NTT_1 a	RISC-V + NTT_2 a	RISC-V + NTT_4 a
N	1024			1024
Compute/ IO Transfer	$N{log}_{2}N$/$4N$			$N{log}_{2}N+N$/$3N$
SW Cycle	3,369,800			558,365
HW Cycle	10,266	5146	2586	11,455
SW-HW Cycle	20,600	15,500	12,900	31,473
Overhead (%) b	100.6	201.2	398.8	174.8
DMA Throughput (MB/s)	153.7	153.4	153.9	N/A
Bus Utilization (%) c	38.4	38.4	38.5	N/A
Code Size	SW/SW-HW/Ratio = 11.6 KB/0.58 KB/20			N/A
Freq (MHz)	100	100	100	90
Latency (μs)	206	155	129	349.7

^a 1, 2, and 4 refer to the parallelism degree $d^{\prime }$ in the unified NTT/INTT. ^b The communication overhead is calculated as ${\displaystyle \frac{\mathrm{SW}\text{-}\mathrm{HW}\mathrm{Cycles}-\mathrm{HW}\mathrm{Cycles}}{\mathrm{HW}\mathrm{Cycles}}}$. ^c The bus utilization is calculated as ${\displaystyle \frac{\mathrm{DMA}\mathrm{Throughput}}{\mathrm{Bandwidth}\times \mathrm{Frequency}}}$.

. We independently and continuously perform NTT and INTT computations to obtain the cycle results. The SW cycle is measured using the RISC-V core to compute NTT and INTT. The SW-HW cycle includes the time taken for the RISC-V core to obtain computation results by invoking the hardware accelerator, including the data transmission time. Code sizes for software-only and software-hardware co-design approaches are also provided to demonstrate code size optimization.

The design [15] presented a polynomial multiplier for qTESLA, incorporating NTT, pointwise multiplication, and INTT, and integrated it into a RISC-V processor via an APB bus. Our design performs similar computations but omits pointwise multiplication and requires additional transmission of the NTT output polynomial and the INTT input polynomial. Table 8 compares the two designs from a system integration perspective. Although our RISC-V processor has lower performance and consumes six times more software cycles for similar computations, our design achieves 1.69, 2.25, and 2.71 improvements in latency through software-hardware co-design. Both designs exhibit substantial communication overhead due to the low frequency of the software processor. Higher speeds can be achieved by employing a high-performance processor and a communication bus IP with a higher frequency. The hardware accelerator, which already performs well, can maintain a lower frequency to save power. Additionally, using a wider bus or integrating more hardware modules can reduce transmission overhead, further improving the performance of the system.

As Figure 7 shows, the speed-up ratio of the two strategies, HW and SW/HW co-design, the HW approach has a 328.2 to 1303.1 times improvement, while the SW/HW co-design approach has a 163.6 to 261.2 times improvement. Comparing our SW/HW co-design with the hardware compositions of our work at different levels of parallelism, we can see that the performance improvement in the SW/HW co-design approach with increasing parallelism, while reducing the amount of code by a factor of 20, is not as significant as the average performance improvement of the HW approach, which has a speedup ratio of nearly 99.3%. In our observations of the I/O overhead depicted in the figure, we find that as the number of butterfly units increases, the enhanced parallelism leads to an exponential improvement in the computation speed of the hardware (HW) approach. However, in the software-hardware co-design strategy, the involvement of the processor in scheduling and I/O operations becomes a bottleneck that constrains overall performance. As shown in Table 8, the actual DMA throughput in the system remains nearly constant (approximately 153 MB/s). This implies that regardless of how fast the accelerator computes (from d = 1 to d = 4, computation time is reduced by a factor of 4), the time spent moving data in and out remains virtually unchanged. The bottleneck limiting further performance gains lies in the need for more efficient scheduling and DMA mechanisms to enhance bus data transfer throughput. Future optimization efforts should explore more effective software/hardware scheduling mechanisms to fully utilize the bus, thereby unlocking the potential of highly parallel hardware accelerators.

In summary, our work achieves comparable or superior performance and ATP results compared to existing NTT designs. Through system deployment, we demonstrate that HLS designs can be fully compatible with existing systems, achieving performance levels comparable to Verilog-based designs. Moreover, the proposed approach presents generalization potential when viewed horizontally. For instance, NTT transfer FFT requires only replacing the complex butterfly pattern at the top layer, while the phased control logic and memory subsystem read/write mechanisms can be reused. Although the sorting network architecture differs from NTT, it can also be analyzed systematically, starting with an examination of memory access patterns, identifying parallel bottlenecks, co-designing conflict-free accesses, and constructing new descriptions in HLS. For irregular graph algorithms, such as sparse graph bottlenecks arising from random memory accesses, software-managed caches and prefetching can be designed. This constitutes a reasonable inference for scenarios where the HLS source code has completed migration. Although not yet experimentally validated, it represents a viable extension of this work for thorough exploration. From a vertical perspective, our method studies RNS-NTT and can explore optimizing it by introducing new dimensions from a hardware design standpoint to identify favorable parallelism. In the future, HLS can be used to rapidly and effectively develop cryptographic libraries for performance evaluation and applications.

6. Conclusions

In this paper, we address the challenge of efficiently implementing NTT accelerators using HLS. We demonstrated that overcoming the inherent limitations of HLS requires moving beyond simple pragma-based inserting to a systematic, hierarchical design methodology. Regarding the results of the implementation, our design improves the area latency efficiency by 1.9×–191× compared to the HLS-based design, increases the area cycle efficiency by 1.7×–10.6× compared to the HDL-based design, and improves the speed by 163×–261× and reduces the code size by 20× compared to pure software computation. However, the most significant contribution of this work points to a new direction for the HLS community. We have demonstrated that expert hardware knowledge can be encapsulated in a reusable and parameterizable HLS template. This template acts as a powerful abstraction, shielding non-hardware experts from the complexities of low-level microarchitecture design. It transforms the intractable DSE problem into a manageable exploration within a curated space of high-quality designs.

Our NTT accelerator is the first proof-of-concept. We envision a future where a rich library of expert-designed templates is developed for various domains, from signal processing and linear algebra to bioinformatics. This would create an ecosystem where algorithm designers and software engineers can quickly instantiate and customize high-performance FPGA accelerators, truly fulfilling the original promise of high-level synthesis. This work represents a critical first step towards that future.