1. Introduction
Digital twin and immersive environments are increasingly used to synchronize and mirror physical spaces in real time [
1]. To maintain such synchronization, continuous sensing of the real-world environment is required [
2]. One effective approach is to employ multiple agents that can collectively perform tasks across a wide area [
3,
4,
5,
6]. In order for these agents to efficiently and periodically cover the environment, multi-agent coverage path planning (MCPP) is essential.
MCPP involves generating paths for agents to visit all given points of interest or areas. The path is generated to efficiently traverse the points of interest while avoiding collisions with obstacles and other agents. This problem has broad applications across various domains, such as disaster areas [
7], data collection [
8,
9], monitoring [
10,
11], agriculture [
12], 3D scanning [
13], and autonomous robots [
14].
MCPP is primarily divided into online and offline methods based on the prior knowledge and situation of the target environment. Online MCPP generates paths for either unknown or dynamic areas. For instance, when agents investigate an unexplored area, path modification is necessary to avoid unexpected obstacles or explore unvisited regions [
15]. Meanwhile, during the task, when the number of agents changes, path redesign becomes essential [
16].
Due to these conditions, the algorithm must operate in real time. Therefore, online MCPP has been studied through reinforcement learning [
17], artificial potential fields (APFs) [
18], etc. Moreover, integrating these approaches with immersive VR/AR interfaces can support human-in-the-loop monitoring and the intuitive visualization of agent coverage and coordination.
Conversely, offline MCPP generates a complete coverage path for a known environment. Unlike online methods, it does not require real-time path modification. Moreover, due to prior knowledge of the environment, this method tends to generate a more optimized path than the former approach. It is mainly researched using divide and conquer methods such as graph partitioning [
19], clustering [
20], spanning tree coverage (STC) [
21], and genetic algorithms [
22].
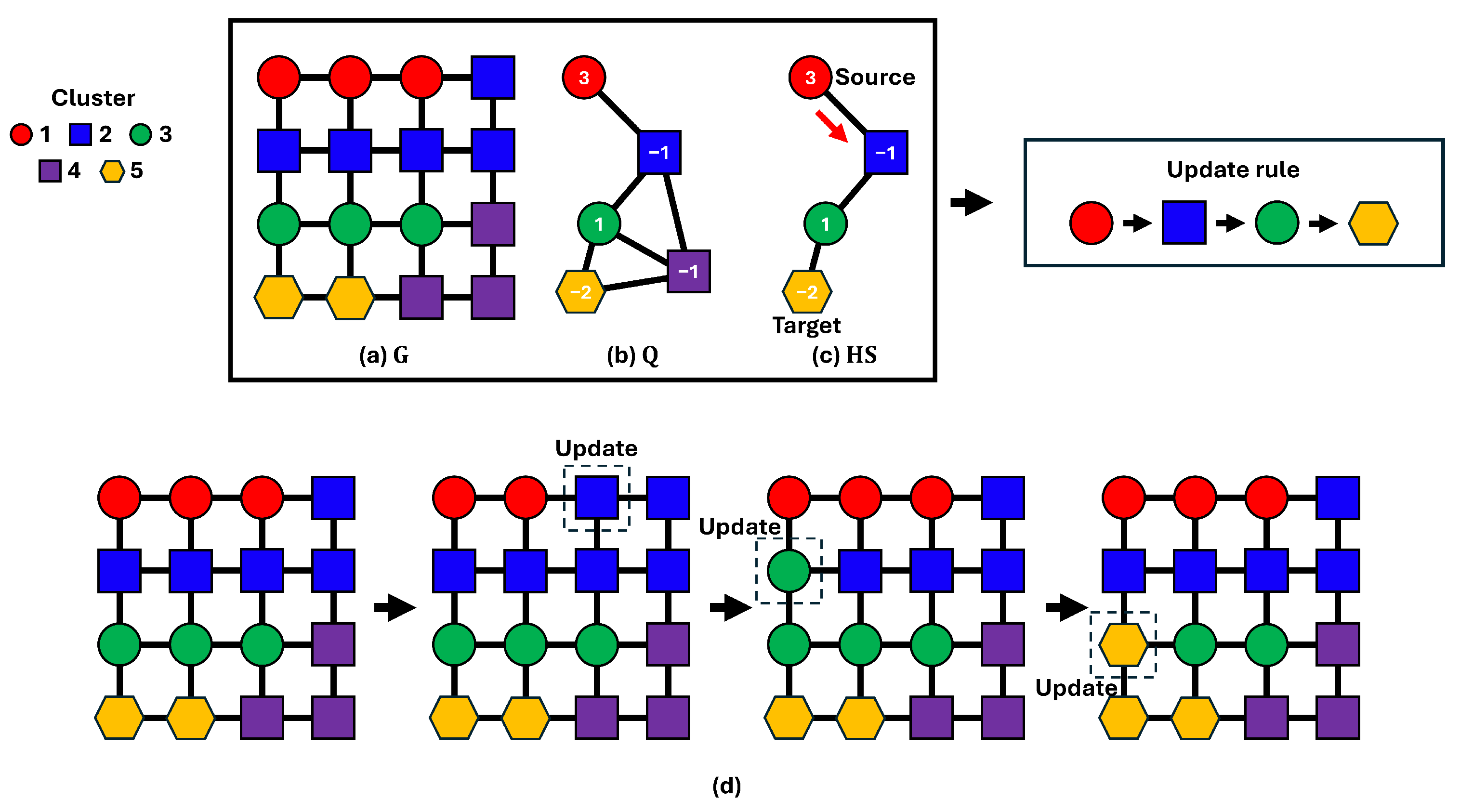
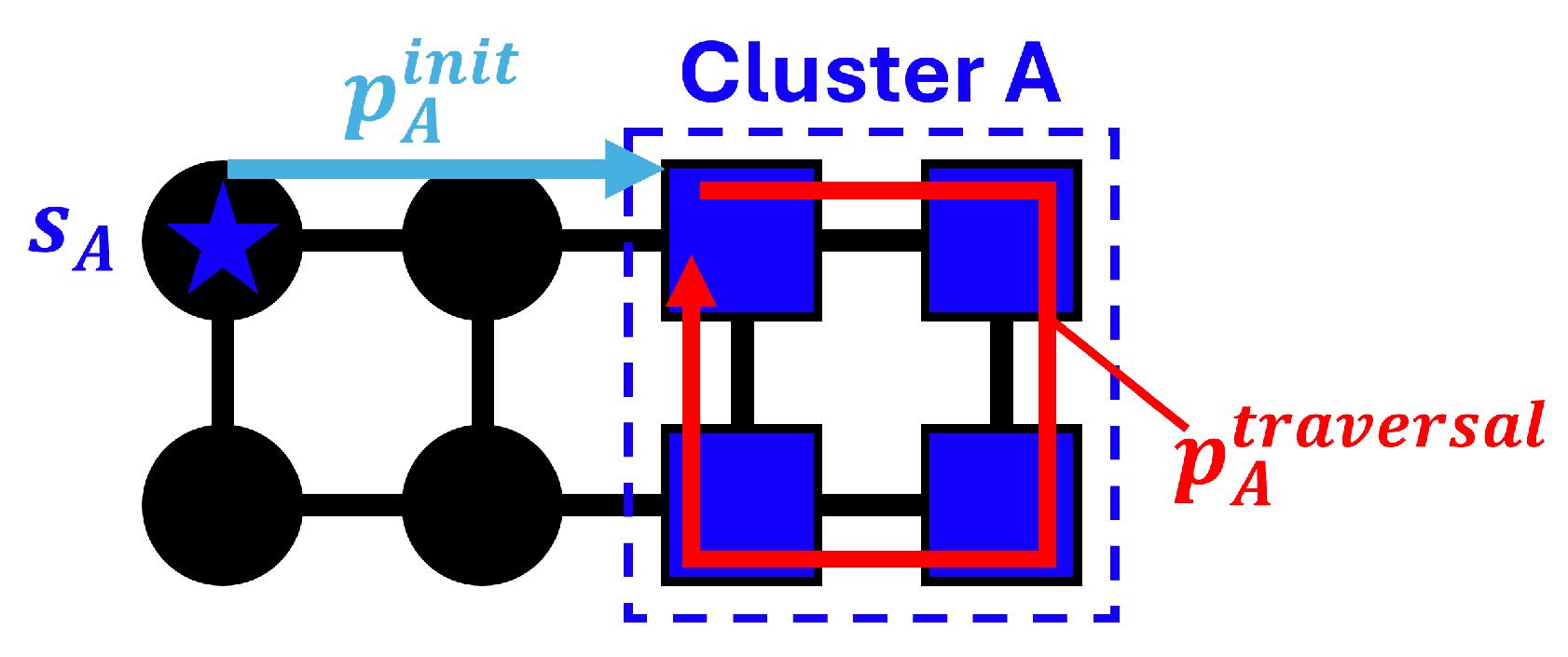
Previous studies on graph-based methods typically employ grid graphs, where the target area is divided into uniform cells. This structure features uniform vertex degrees and a regular arrangement of edges. However, these characteristics are not always guaranteed. Consider a scenario where agents are traversing a non-grid road network digital twin, as in
Figure 1. To address this, the environment should be represented as a non-grid graph with weighted edges. Therefore, we present a clustering-based offline MCPP method applicable to non-grid graphs. The contributions of this paper are as follows.
- 1.
We implement an objective function based on STC by modifying the weights of graph-adapted K-means [
23].
- 2.
We apply an optimized merging method on the update step based on [
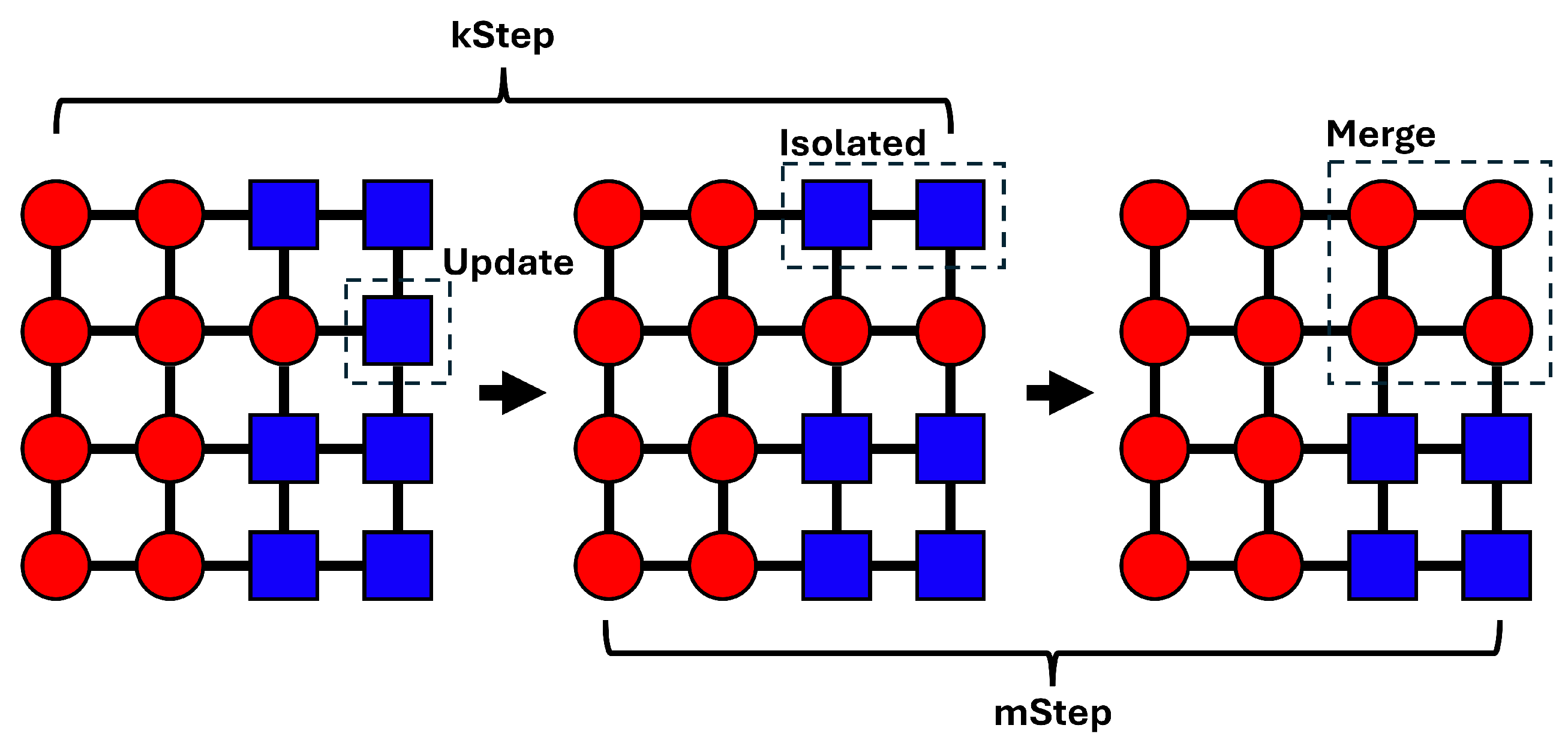
23] to prevent the graph separation problem.
- 3.
We develop a cluster propagation method using a cluster-level graph to alleviate the local minima problem.
2. Related Works
With advances in computational power and communication technologies, multi-agent systems have been drawing significant attention. These systems enable the manipulation of agents in a digital twin to perform collaborative tasks in the real world. For instance, there are cases where multiple virtual agents are employed to efficiently generate paths for each agent in order to conduct large-scale 3D scanning. For example, ref. [
3] extracts a skeleton of the central traversable paths in the map and divides it into multiple agent paths while considering physical constraints. Meanwhile, ref. [
5] generates paths for unmanned aerial vehicles (UAVs) to scan occluded parts of a structure by scheduling exploration plans on a coarse-terrain digital twin via solving the traveling salesman problem. Similarly, there are also studies on swarm robot control within digital twin environments. For example, ref. [
1] demonstrates a control approach where humans issue commands only to a small set of virtual agents in the VR. Each agent controls subordinate robot groups via its hierarchical digital twin, while path coordination ensures collision avoidance. These approaches commonly reinterpret continuous digital twin spaces into alternative forms and generate paths via vertex traversal problems.
MCPP can be classified into centralized and decentralized approaches based on how agents coordinate [
20]. In a centralized approach, a single solver with global information generates paths and controls the agents. Conversely, in decentralized methods, each agent has local information and constructs its own paths through cooperation with other agents. Consequently, the centralized method typically requires substantial computational resources but yields more efficient paths. For these reasons, offline methods are typically employed, coupled with centralized approaches. Previous studies have implemented this method by partitioning the environment into discrete units and then generating paths.
Graph-based approaches rasterize the environment [
10,
24] into a grid map or an adjacency graph through cellular decomposition [
25,
26]. Then, independent subgraphs are formed via clustering, and a path is generated for each cluster. In this process, cellular decomposition employs path patterns such as back and forth or zigzag [
26]. When using a grid map, graph traversal methods such as Euler circuits [
27] and spanning tree coverage (STC) [
21] are commonly adopted for coverage tasks.
Ref. [
10] converts the entire area into a grid of square cells and then applies K-means using the centers of the Voronoi diagram as cluster centroids. Because the boundaries of this diagram are similar to the criteria for cluster partitioning, cells that include a boundary become ‘conflict points’ that are not clearly assigned to any cluster. In this study, these cells are allocated to neighboring clusters with lower weights, creating clusters in which the workload is equally distributed. Nikolaos [
18] employed affinity propagation clustering. After forming initial clusters, the method calculates the similarity based on a four-grid distance to revise the clusters so that travel distances are evenly balanced.
STC [
21] first constructs a minimum spanning tree (MST) of the given graph and then generates a path that circumnavigates it. Expanding on this, multi-robot STC (MSTC) [
24,
28], for multiple agents, creates a traversal path in the same manner and allocates segments of the tree between adjacent agents. However, if agents are positioned too closely, they all move in the same direction, causing the allocation to fail. Although the same study proposed a backtracking approach that revisits previously covered paths to mitigate this issue, optimal allocation was still not achieved.
To address this problem, multi-robot forest coverage (MFC) divides the entire tree into several balanced subgraphs [
29]. Later, MSTC* [
30] was introduced to incorporate physical constraints—such as terrain traversability and material load capacity—into a cost-based framework. Similar to MFC, this method partitions the entire tree equally and propagates coverage among neighboring agents. More recently, researchers have explored minimum-turn MSTC* (TMSTC*) [
31], which uses linear block segments based on tree branches to reduce the number of agent rotations, as well as an online method that adapts to real-time weight changes [
32].
Divide Area based on Robot’s Initial Positions (DARP) [
33] performs area partitioning by optimizing a cost function defined using the distance matrix between robots’ initial positions and all vertices. This cost function is designed based on two criteria, namely cluster connectivity and workload balance, and is computed according to the distances from the initial positions to the vertices. The optimization proceeds by iteratively reassigning vertices adjacent to clusters, which allows DARP to achieve optimal solutions compared to other algorithms. However, it suffers from a high computational cost and may lead to imbalanced partitions in cases where bottlenecks occur around the initial positions.
Reinforcement learning can be deployed to solve this problem. For example, [
34] addresses decentralized multi-robot coverage path planning by framing subarea allocation as a sequential decision-making task with reinforcement learning. Robots expand their territories using local observations enriched with structural and neighbor information. A neural network policy directs these expansions, while robots may pause expansion to prevent unnecessary overlaps. The method yields balanced subareas with minimal overlap and scales to larger maps and more agents, although training is difficult due to delayed rewards and can be unstable, occasionally producing imbalanced partitions.
Ref. [
35] performs cooperative coverage path planning by first partitioning the environment with an improved K-means clustering algorithm that incorporates MST to achieve more balanced divisions. After partitioning, each robot is assigned to a subarea and applies deep reinforcement learning with a dueling network structure. An improved reward function guides robots away from redundant paths and toward unexplored regions, enabling more efficient coverage. This framework achieves higher coverage ratios and reduced path duplication relative to single-robot methods. However, these approaches remain sensitive to the reward design, which can lead to imbalanced paths.
3. Problem Statement
The target environment graph is defined as
, where
is the set of vertices and
is the set of edges.
is the set of edge weights, and
represents the weight assigned to edge
. The number of agents is represented by
k. The initial positions of each agent are defined as
. The path generation algorithm F is a function that outputs a set of paths by taking a graph and an initial position, as shown in Equation (
1).
represents the collision-free paths assigned to each agent. Meanwhile,
is a set of path vertices with length
l,
.
Path group
must visit every vertex of the graph at least once. Furthermore, consider that each path must have the optimal traversal time. Therefore, we set the goal as the ideal path group
in Equation (
2), where
indicates the total traversal time of
.
7. Discussion
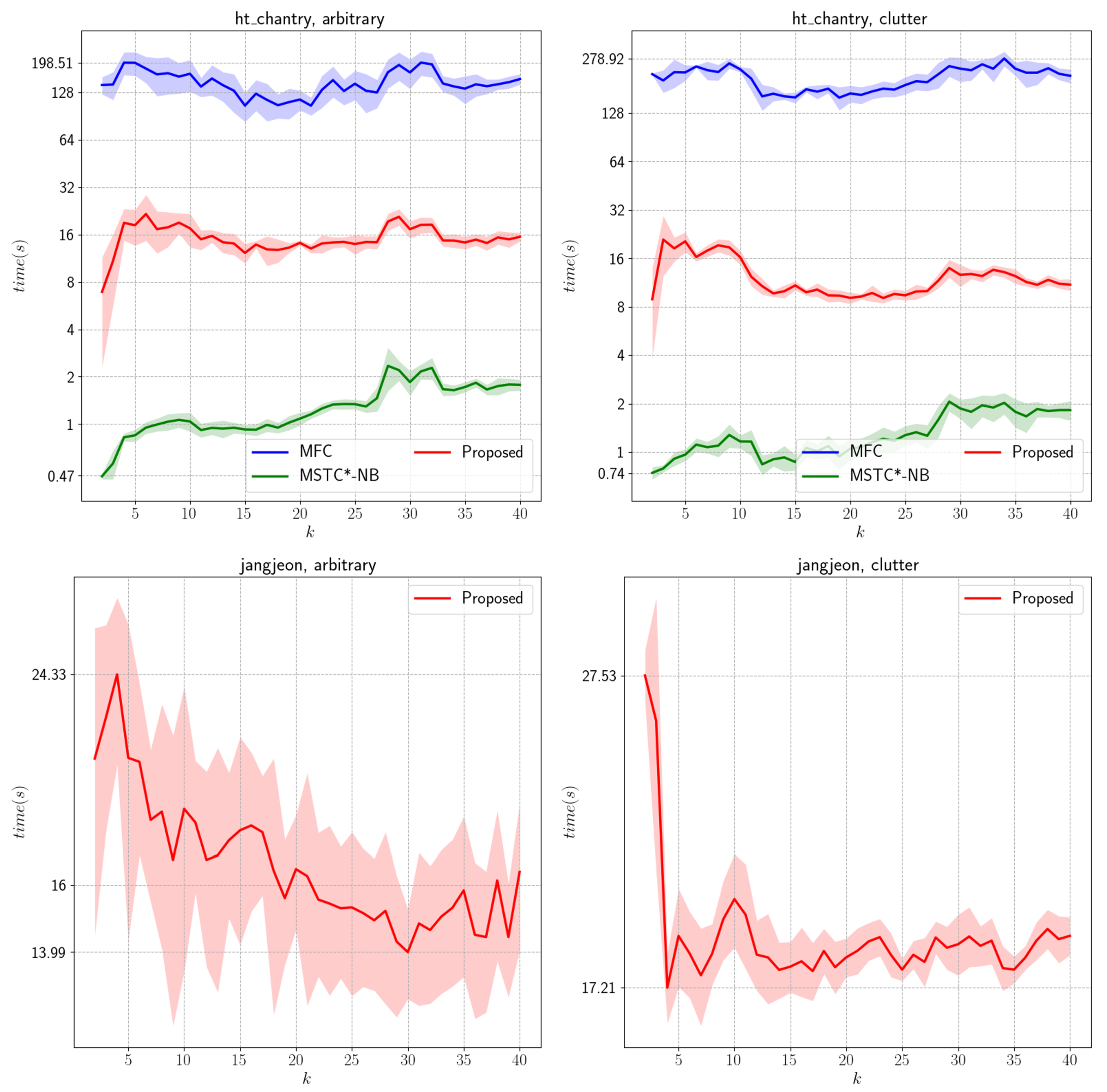
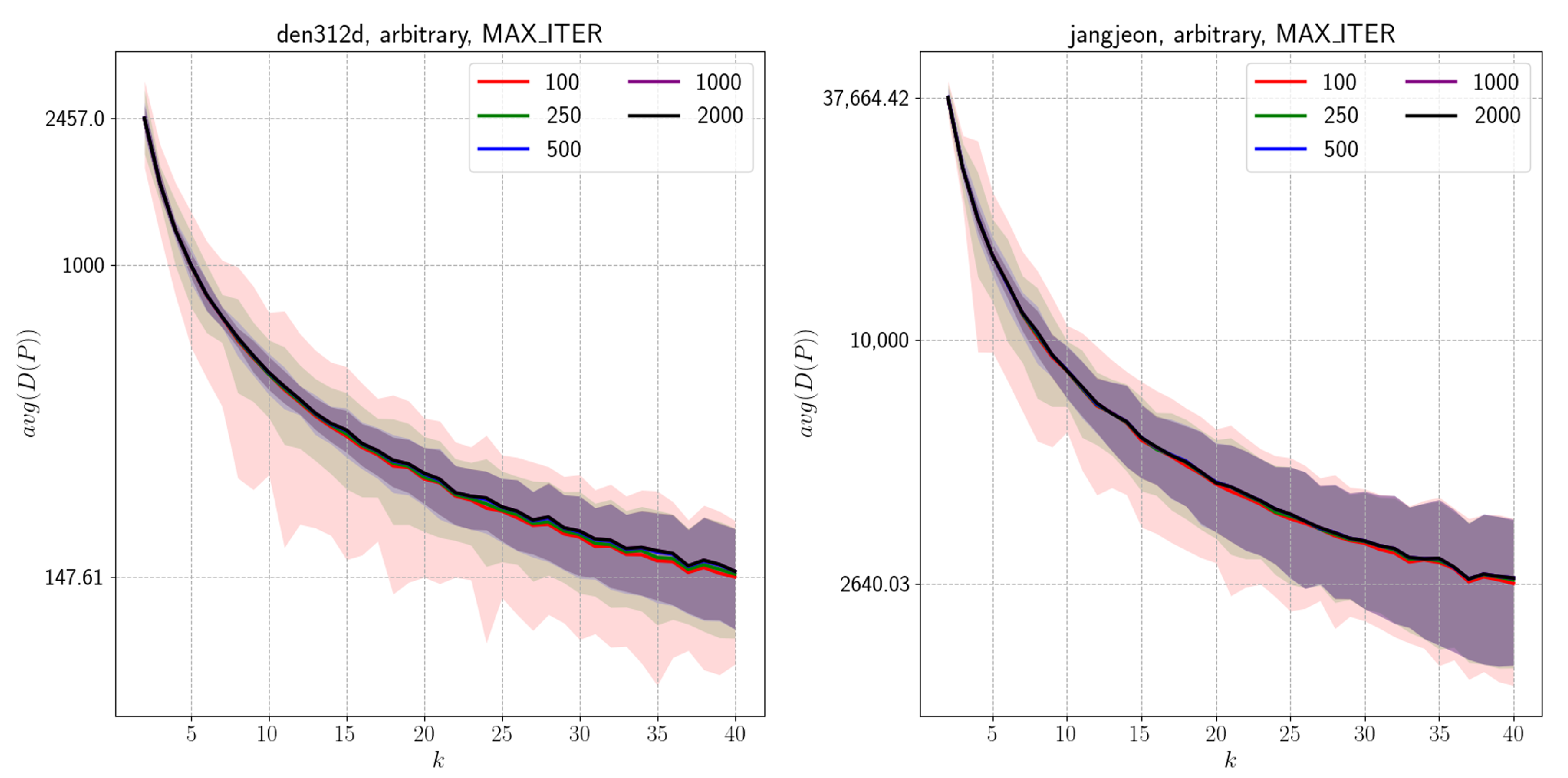
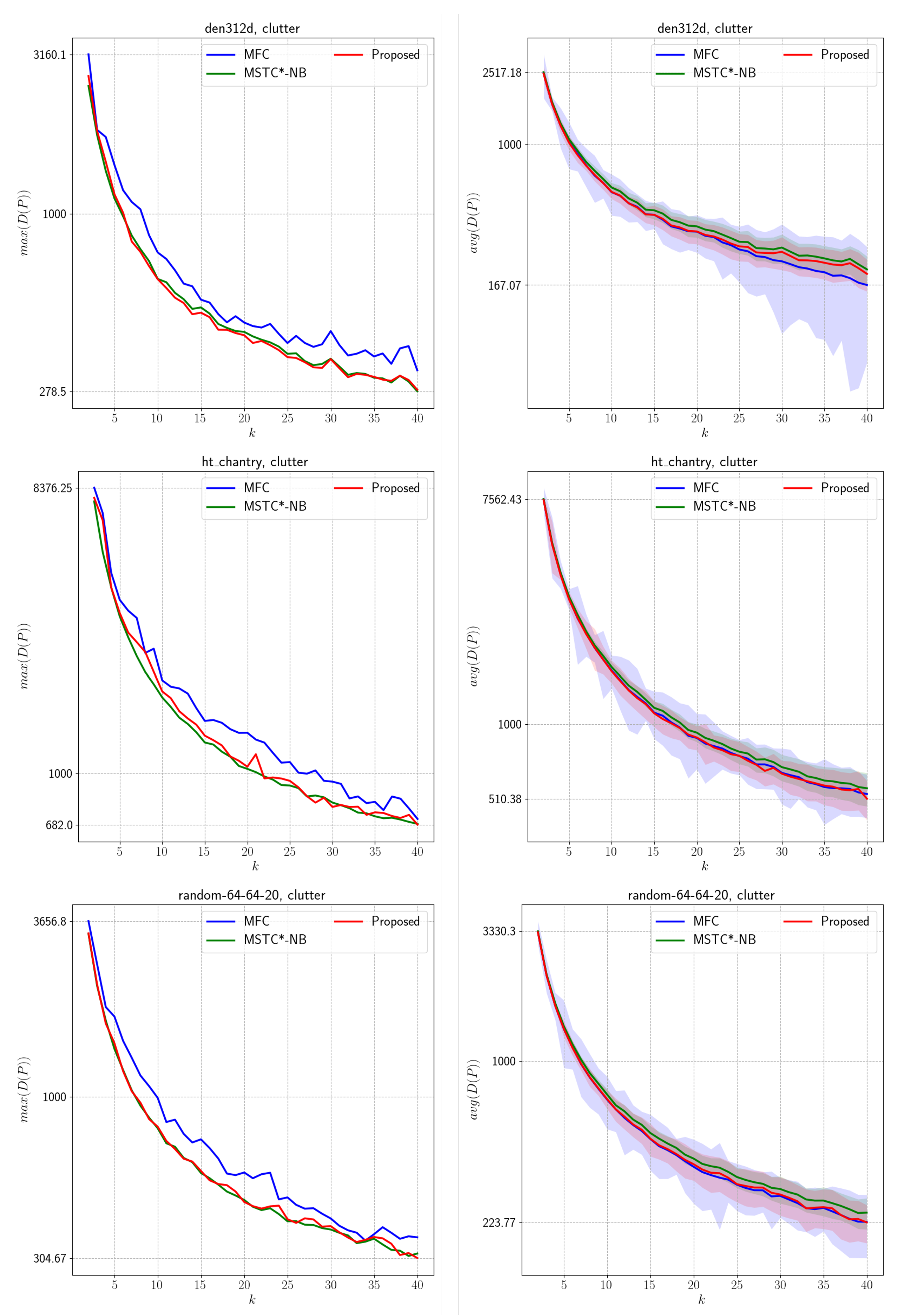
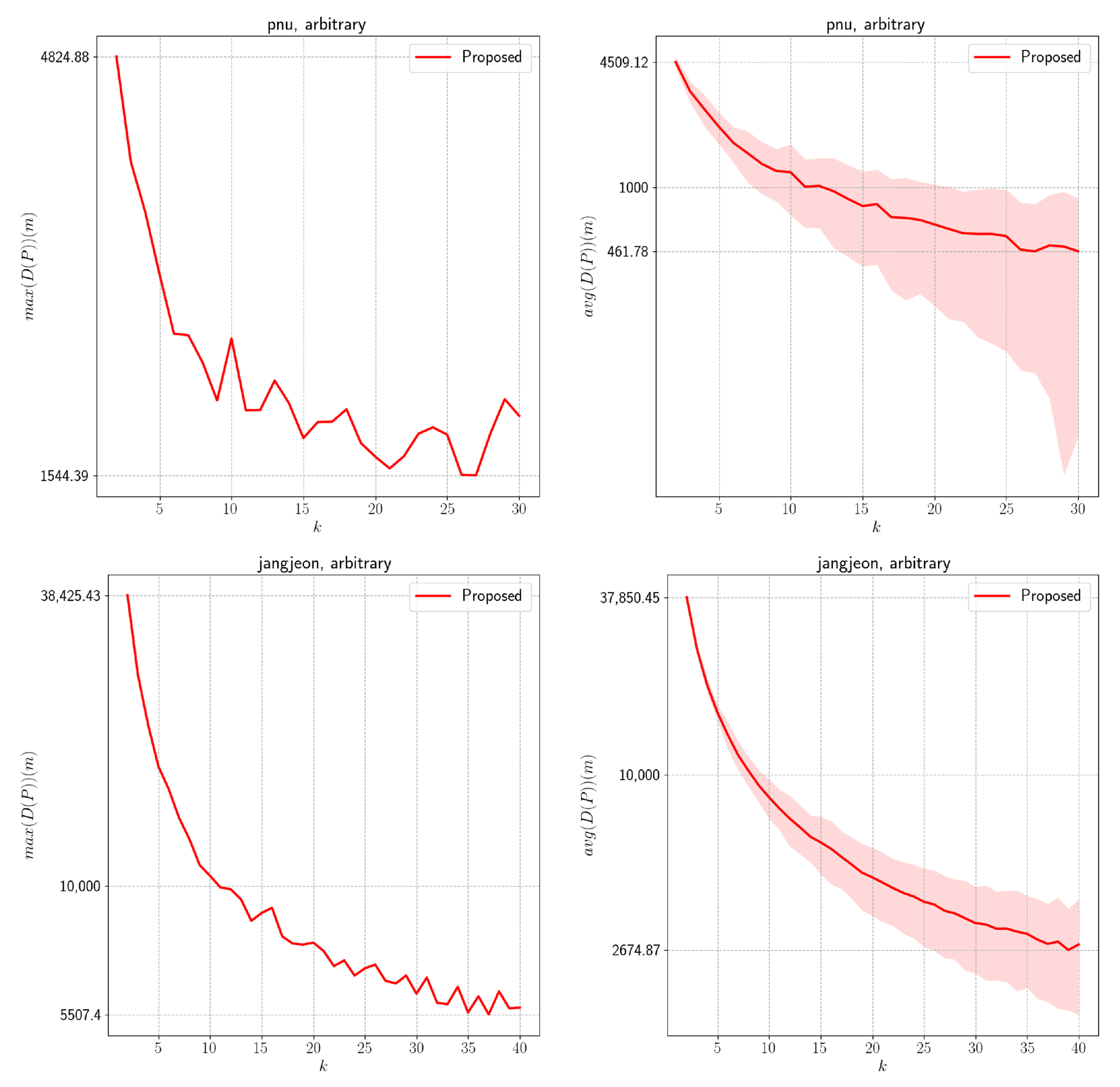
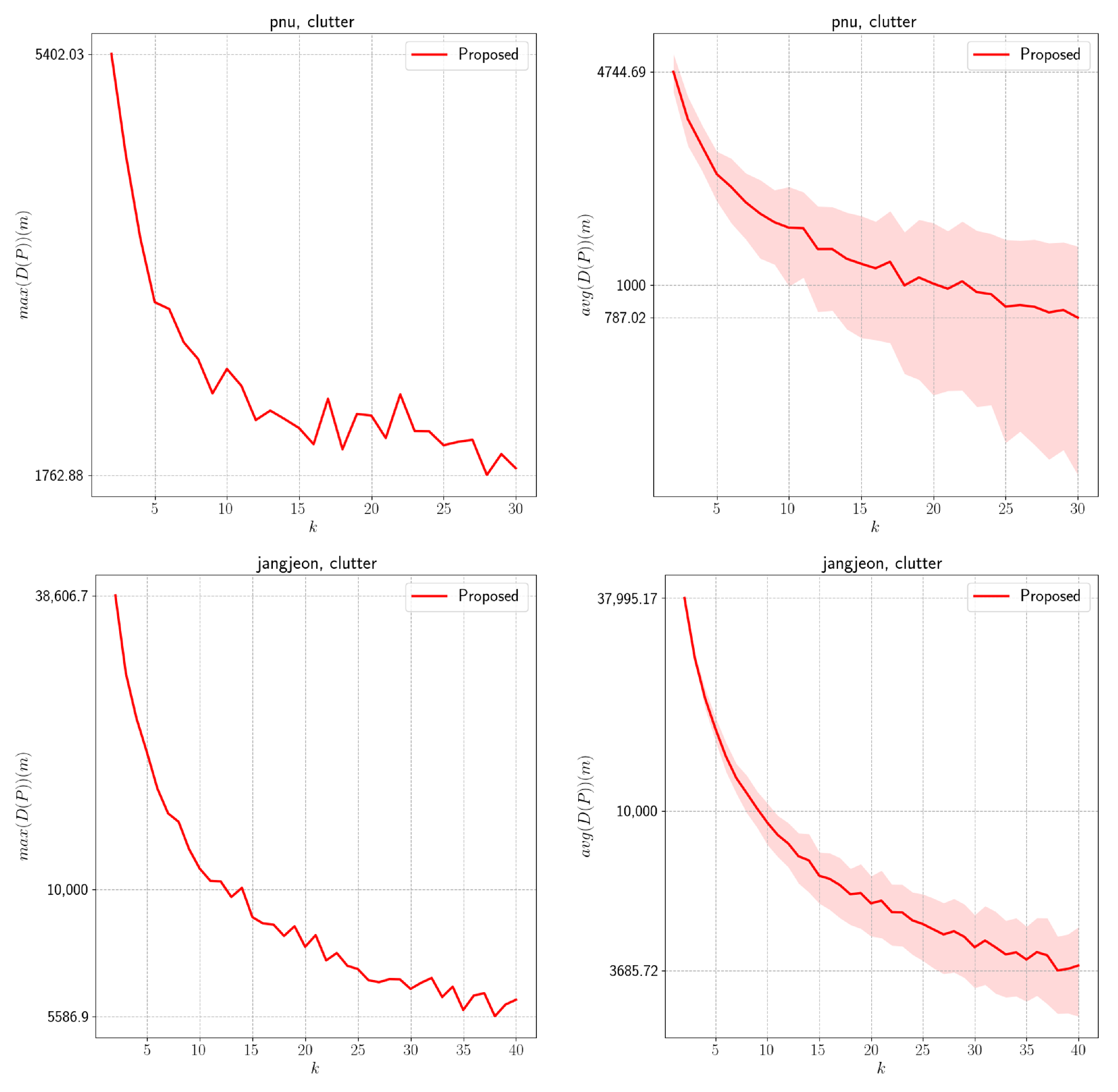
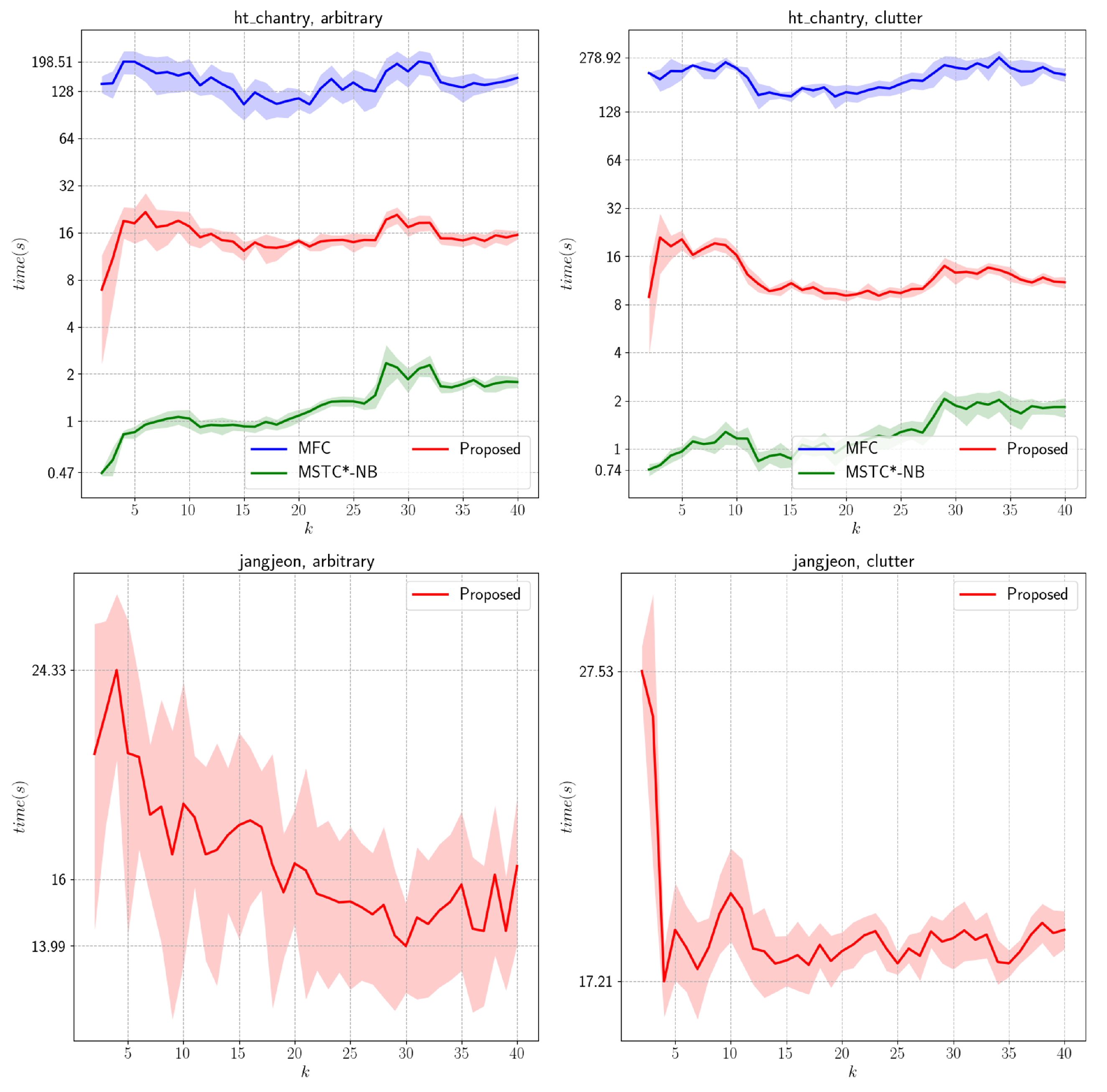
We present an offline MCPP algorithm for non-grid graphs. We employ a graph-adapted K-means method and modify its weights based on decomposing the path into initial and traversal paths. In this process, we explain the isolated component and local minima problems. To mitigate these issues, we introduce a merge step and cluster propagation via a cluster-level graph. Finally, paths are generated using STC and WHCA*. Through comparisons with prior work (MFC, MSTC*), we demonstrate that our algorithm works effectively on both grid and non-grid environments.
However, we observed degraded performance when the number of agents was small or the complexity was high. We attribute these outcomes to two primary limitations of the proposed algorithm. First, the optimally distributed traversal distance
was designed for STC, and it is not directly applicable to weighted graphs. Determining the STC lengths of large clusters in weighted environments is challenging and often yields misleading results. As a result, when
k is small, inaccuracies may arise, potentially yielding incorrect paths. We expect this problem to be mitigated by leveraging techniques for approximating the total weight of a minimum spanning tree [
39]. Another limitation occurs in the merge step, where centroid shifts cause discrepancies between the estimated and actual initial path lengths. This effect is particularly pronounced in cluttered environments and accounts for the instability observed in the evaluation. We anticipate that the periodic recomputation of the initial path with bipartite graph matching will alleviate this issue.
The applicability of non-grid MCPP has significant implications for the design of interactive experiences in VR/AR environments. In particular, establishing a foundation that enables multiple agents to efficiently explore spaces and act cooperatively would enhance both the realism and the utility of immersive content. Furthermore, this study demonstrates the capability to explore paths within digital twins represented through diverse data structures. Non-grid graphs are well suited to represent environments where movement between adjacent cells is constrained. For example, when an agent travels by vehicle on a road, traffic regulations may impose directional restrictions on movement. These limitations are difficult to model with grid-based cells but can be represented easily via edges in non-grid graphs. Therefore, the proposed method can be applied to scenarios involving structured digital twins that can be used for urban, pedestrian-driven citizen science investigations or the vehicle-based monitoring of road networks. These contributions are expected to play a pivotal role in advancing large-scale multi-user virtual simulations, education and training systems, and intelligent collaborative virtual environments.