FFMamba: Feature Fusion State Space Model Based on Sound Event Localization and Detection

Abstract

Previous studies on Sound Event Localization and Detection (SELD) have primarily focused on CNN- and Transformer-based designs. While CNNs possess local receptive fields, making it difficult to capture global dependencies over long sequences, Transformers excel at modeling long-range dependencies but have limited sensitivity to local time–frequency features. Recently, the VMamba architecture, built upon the Visual State Space (VSS) model, has shown great promise in handling long sequences, yet it remains limited in modeling local spatial details. To address this issue, we propose a novel state space model with an attention-enhanced feature fusion mechanism, termed FFMamba, which balances both local spatial modeling and long-range dependency capture. At a fine-grained level, we design two key modules: the Multi-Scale Fusion Visual State Space (MSFVSS) module and the Wavelet Transform-Enhanced Downsampling (WTED) module. Specifically, the MSFVSS module integrates a Multi-Scale Fusion (MSF) component into the VSS framework, enhancing its ability to capture both long-range temporal dependencies and detailed local spatial information. Meanwhile, the WTED module employs a dual-branch design to fuse spatial and frequency domain features, improving the richness of feature representations. Comparative experiments were conducted on the DCASE2021 Task 3 and DCASE2022 Task 3 datasets. The results demonstrate that the proposed FFMamba model outperforms recent approaches in capturing long-range temporal dependencies and effectively integrating multi-scale audio features. In addition, ablation studies confirmed the effectiveness of the MSFVSS and WTED modules.

1. Introduction

As a critical modality in multimodal perception, audio signals carry rich semantic information about the environment, extending perceptual range and enhancing situational awareness [1]. Sound Event Localization and Detection (SELD) is a cutting-edge task in computational auditory perception. It involves jointly identifying the type of sound event and estimating its spatial location—combining Sound Event Detection (SED) with Direction of Arrival (DoA) estimation. This integration is essential for developing human-like auditory systems. SELD has wide applications in speech recognition and localization [2,3,4], intelligent surveillance [5,6], and robotic navigation [7,8], making it both a highly valuable research area and a technology with significant real-world impact.

Due to the complexity of SELD, models must effectively capture and integrate audio features across temporal, spectral, and channel dimensions [9]. To address these challenges, various deep learning-based approaches for SELD have been proposed in recent years. Examples include neural networks with dynamic convolutional kernels to enhance adaptability to local features [10]; bidirectional gated recurrent units (BiGRUs) for capturing temporal dependencies [11,12]; and Transformer architectures for modeling global contextual relationships [13,14]. In addition, multi-scale fusion mechanisms [15] and time–frequency attention techniques [9] have been widely adopted to improve the perception of features at different granularities. These methods have led to significant progress in public benchmarks, such as the Detection and Classification of Acoustic Scenes and Events (DCASE) challenge and the Learning 3D Audio Sources (L3DAS) project.

In recent years, State Space Models (SSMs) [16] have shown strong potential in natural language processing [17] and speech processing [18,19], owing to their linear-time complexity and efficient modeling capabilities. Among these, the selective State Space Model known as Mamba [20] introduces an input-dependent dynamic selection mechanism that significantly enhances the modeling of long-range sequential features, making it a key focus in current sequence modeling research. Mu et al. [21] applied the Mamba architecture to the SELD task, demonstrating its ability to capture broader contextual information while maintaining computational efficiency, thereby providing initial evidence of SSMs’ potential in audio modeling. 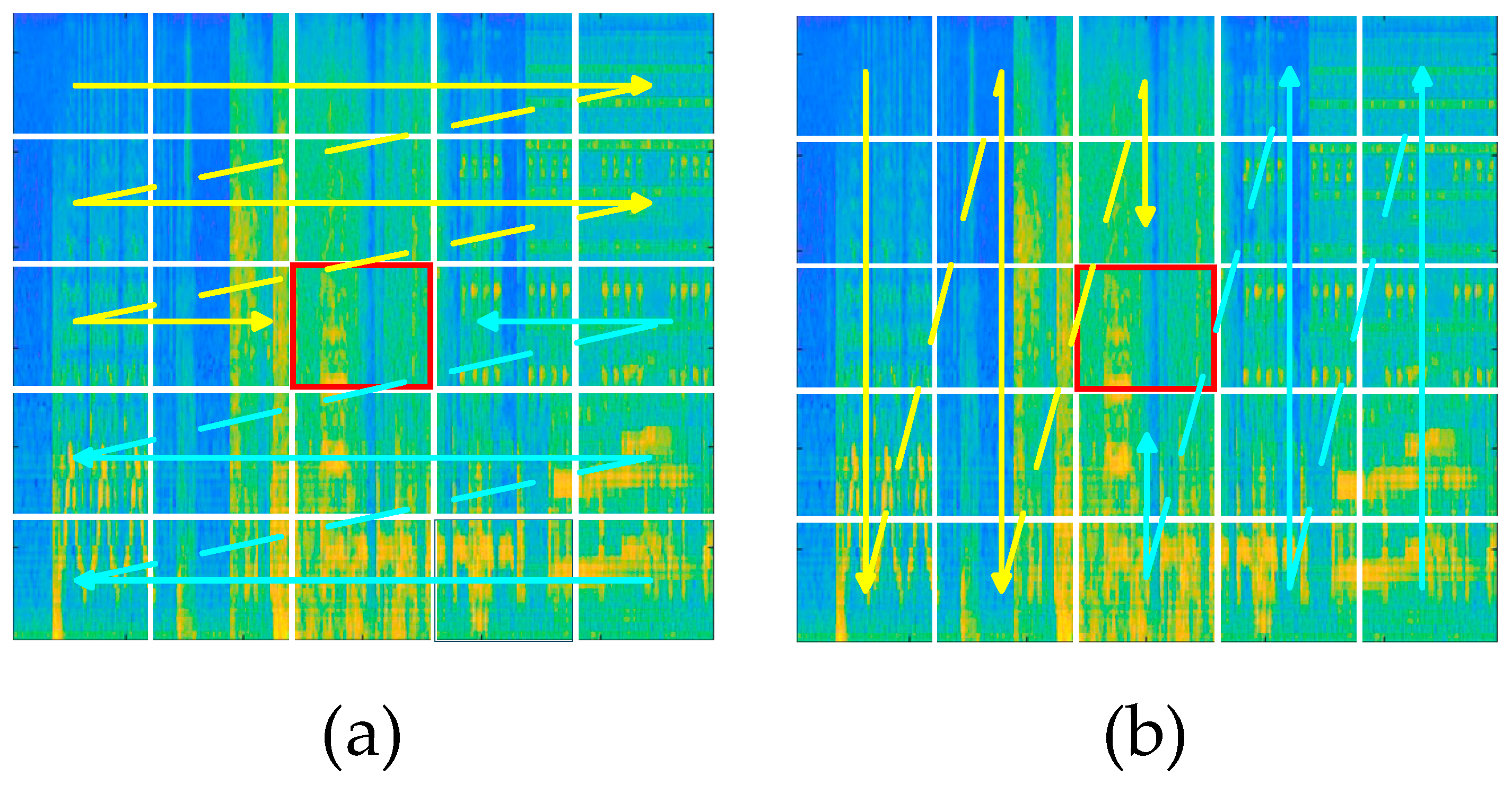Building on this foundation, the Vision Mamba (VMamba) model [22] extends Mamba’s capability to handle two-dimensional spatial data. It features a 2D-Selective-Scan (SS2D) module, which incorporates a cross-scan mechanism to enable directional sensitivity in spatial dimensions (as shown in Figure 1). This design preserves the long-range modeling strength of SSMs while bridging the structural gap between one-dimensional scanning and two-dimensional vision-based architectures, resulting in strong spatial modeling performance and computational efficiency. These architectural innovations introduce a promising new modeling approach for SELD: the SSM framework effectively captures temporal continuity and contextual dependencies in long audio sequences, while the Vision State Space (VSS) structure enables deep spatial feature extraction, potentially addressing the limitations of spatial modeling in complex acoustic environments.

Despite its effectiveness in modeling long-range dependencies, the original Mamba architecture is mainly designed for image tasks and struggles to capture frequency-domain features and multi-scale structures in audio. This limitation, coupled with the inherent time–frequency coupling in SELD, makes single-scale or unidirectional scanning insufficient for modeling local details and multi-scale interactions.

To this end, we propose an attention-based Feature Fusion State Space model (FFMamba), designed to enhance both local spatial detail modeling and long-sequence dependency modeling. First, we develop a Multi-Scale Fusion Visual State Space (MSFVSS) module that integrates feature representations from multiple receptive fields. Unlike conventional state space modules that primarily model sequential dependencies, MSFVSS fuses features across different scales, thereby strengthening local spatial perception while preserving spatial resolution and channel dimensions. This improves the network’s sensitivity to fine-grained local acoustic patterns, such as transient sound events.

Second, we introduce the Wavelet Transform-Enhanced Downsampling (WTED) module, which combines discrete wavelet decomposition with convolutional downsampling. This mechanism preserves frequency-domain features that are often lost in convolution or pooling operations. By integrating spatial and spectral information during downsampling, WTED enhances the model’s ability to capture time–frequency interactions, which are crucial for SELD.

In summary, FFMamba leverages the MSFVSS module to strengthen local feature representation and the WTED module to fuse spatial and spectral features, thereby improving the model’s robustness and accuracy in sound event detection and localization.

The main contributions of this work are as follows:

• In this paper, we propose a Feature Fusion State Space model with an attention mechanism (FFMamba). To the best of our knowledge, this is the first work to apply the VSS architecture to the SELD task, replacing the commonly used Transformer-based structures.
• We introduce a Multi-Scale Fused Visual State Space (MSFVSS) module. In this design, the Multi-Scale Spatial Fusion (MSF) component replaces the deep convolution layer in the original VSS to enhance its capability in modeling local spatial details.
• This paper proposes a Wavelet Transform-Enhanced Downsampling (WTED) module, which combines convolutional downsampling with multi-scale frequency features from wavelet transform and enhances them through channel weighting.

The proposed method is evaluated on two benchmark datasets and compared with existing mainstream approaches, demonstrating its effectiveness and superiority in practical application scenarios.

2. Related Works

2.1. Current Methods for SELD

Early approaches to SELD were primarily based on Convolutional Recurrent Neural Network (CRNN) architectures. Adavanne et al. [23] proposed SELDnet, which combines convolutional layers for extracting local time–frequency features with GRUs for modeling temporal dependencies, serving as a cornerstone for subsequent SELD models. Since then, numerous improvements have been made in both feature modeling and spatial encoding. Grondin et al. [24] were the first to apply a CRNN structure to multi-microphone arrays, enhancing the spatial modeling capabilities for sound source localization. Cao et al. [25] proposed EINV2Net, which introduced a multi-branch design and replaced traditional RNNs with a Multi-Head Self-Attention (MHSA) mechanism [13], achieving higher accuracy in event detection and localization. Zhang et al. [26] introduced the Conformer architecture to the SELD task, combining convolutional networks with Transformers to jointly model local and global information, demonstrating strong robustness in semi-supervised settings. More recently, the CST-former [9] incorporated specialized attention mechanisms across channel, spectral, and temporal dimensions, improving the model’s ability to decouple and model multimodal information, and further extending the applicability of Transformer-based methods in SELD.

2.2. Multi-Scale Feature Fusion

In SELD tasks, multi-scale feature fusion is a key strategy for enhancing the model’s ability to handle complex acoustic environments. By incorporating receptive fields of different scales across temporal, spectral, and spatial dimensions, the model can capture contextual dependencies more effectively, leading to improved robustness in event detection and higher accuracy in spatial localization. Shimada et al. [27] proposed D3Net, a DenseNet-based architecture that combines multi-resolution learning with exponentially expanding receptive fields. Li et al. [28] introduced L2-MS SincNet, an improved version of SincNet based on the Sinc function, which uses multi-scale convolutional layers to extract features across different temporal and frequency ranges. Mu et al. [29] presented a three-stage architecture that generates multi-scale spectral and spatial features through parallel subnetworks. Ouyang et al. [15] developed the Efficient Multi-scale Attention (EMA) module, which leverages parallel branches to learn long- and short-term spatial dependencies, effectively modeling inter-channel relationships while enhancing pixel-level attention to high-level features.

2.3. State Space Models (SSMs)

SSMs are a class of mathematical frameworks designed to describe the dynamic evolution of sequential data, originally derived from the Kalman filter [30]. The core idea is to use latent state variables to capture the temporal dynamics of a sequence. In SSMs, the input signal drives the hidden states to evolve continuously over time within a latent space, and the output sequence is generated through a decoding mapping. The continuous evolution of the system is governed by a set of linear ordinary differential equations (ODEs), as shown below:

$${\mathbf{h}}^{\prime }\left(t\right)=\mathbf{Ah}\left(t\right)+\mathbf{B}u(t)$$

(1)

$$y(t)=\mathbf{Ch}\left(t\right)+\mathrm{D}u(t)$$

(2)

where ${\mathbf{h}}^{\prime }\left(t\right)$ indicate latent state, $u(t)$ and $y(t)$ indicate input signal and output signal. $\mathbf{A}\in {ℝ}^{N\times N},\mathbf{B}\in {ℝ}^{N\times 1},$ $\mathbf{C}\in {ℝ}^{1\times N}$, and are the weighting parameters.

In deep learning implementations, to handle discrete sequences, the continuous-time ODEs are typically discretized using the Zero-Order Hold (ZOH) method, resulting in a discrete-time formulation as follows:

$${\mathbf{h}}^{\prime }\left(t\right)=\overline{\mathbf{A}}\mathbf{h}\left(t\right)+\overline{\mathbf{B}}u(t)$$

(3)

$$y(t)=\mathbf{Ch}\left(t\right)+\mathrm{D}u(t)$$

(4)

$$\overline{\mathbf{A}}=e^{\Delta \mathbf{A}},\overline{\mathbf{B}}={\left(\Delta \mathbf{A}\right)}^{-1}\left(e^{\Delta \mathbf{A}}-1\right)·\Delta \mathbf{B}$$

(5)

where $\overline{\mathbf{A}}=e^{\Delta \mathbf{A}}$, $\overline{\mathbf{B}}={\left(\Delta \mathbf{A}\right)}^{-1}\left(e^{\Delta \mathbf{A}}-1\right)·\Delta \mathbf{B}$, ∆ denotes the time-scale parameter, while $\overline{\mathbf{A}}$ and $\overline{\mathbf{B}}$ represent discrete-time system parameters.

Traditional SSMs model the evolution of inputs and hidden states using linear ODEs, which implies that the projection matrices are fixed and unaffected by variations in the input sequence. This static configuration limits the model’s ability to focus on individual elements within the sequence. To address this, Mamba introduces the Selective State Space model, which incorporates an input-dependent selection mechanism (S6) to enhance modeling capacity [20], computational efficiency, and numerical stability. However, limitations remain when applying this approach to high-dimensional tasks such as computer vision. To better accommodate visual scenarios, the SS2D model has been proposed (as shown in Figure 2). SS2D extends the state space modeling framework to the spatial dimensions of an image—height (H) and width (W)—by independently modeling and fusing state dynamics along both directions, thereby enabling efficient capture of global dependencies in visual data.

3. Proposed Method

3.1. Preprocessing

In this study, first-order Ambisonics (FOA)-format audio is used across all datasets to extract both time–frequency and spatial features for joint SED and DoA estimation. The input audio is sampled at 24 kHz.

In this paper, log-Mel spectrogram features are extracted as the input for the SED branch. To this end, the Short-Time Fourier Transform (STFT), which can simultaneously capture both amplitude and phase information of the audio signal, is applied for multichannel audio time–frequency analysis. The specific parameter settings are as follows: a Hann window is used with a window length of L = 512, a hop size of H = 300, and an FFT size of N = 512. The STFT result $X_m\left(k\right)$ is then computed as follows:

$$X_m\left(k\right)={\displaystyle \sum _{n=0}^{L-1}x\left(mH+n\right)·w\left(n\right)·e^{\frac{-j2\pi kn}{N}}}$$

(6)

where $k$ denotes the frequency index $\left(0\le k<N\right)$, $n$ represents the time index within a frame $\left(0\le n<L\right)$, $w\left(n\right)$ is the window function, and $x\left(mH+n\right)$ indicates the sampled point of the original waveform in the $m$-th frame.

The power spectral density $P_m(k)$ reflects the energy of the audio signal, and is defined as:

$$P_m(k)={\left|X_m\left(k\right)\right|}^2$$

(7)

Finally, a log-Mel filter bank is applied to generate the log-Mel spectrogram, with the number of filters set to b = 128. The computation is given by:

$$L\mathrm{og}Me{l}_m\left(b\right)=\log \left[{\displaystyle \sum _k{P}_m\left(k\right)·H_b\left(k\right)}+\epsilon \right]$$

(8)

where b denotes the filter index, $b=1,\dots ,128$, $H_b\left(k\right)$ represents the triangular filter, and ε is a small positive constant.

Compared with linear filter banks, log-Mel filter banks are more consistent with the characteristics of human auditory perception, providing higher resolution at low frequencies and lower resolution at high frequencies. In addition, the logarithmic transformation compresses the dynamic range and enhances the robustness of the model to energy differences.

For FOA audio, the intensity vector (IV) feature is extracted as the input for the DoA branch. The intensity vector is computed from the phase and magnitude of the four-channel spectrograms, which characterizes the directional flow of energy in the sound field and serves as an important spatial cue for modeling directional features. First, an STFT is applied to each channel signal, and the frequency-domain representation is given by:

$$P_i=S\left(W,X,Y,Z\right)$$

(9)

where $i\in \left\{W,X,Y,Z\right\}$, with W representing the omnidirectional component, and X, Y, and Z representing the components along different directions in the Cartesian coordinate system.

Then, the raw directional components along X, Y, and Z are computed with respect to W within each time–frequency unit as follows:

$$I_i=\mathrm{Re}al\left(P_W,P_i\ast \right)$$

(10)

where ∗ denotes the complex conjugate, and $\mathrm{Re}al\left(\right)$ denotes taking the real part.

To improve numerical stability and obtain directional information, normalization is applied. The energy intensity is defined as:

$$E={\left|P_W\right|}^2+{\left|P_X\right|}^2+{\left|P_Y\right|}^2+{\left|P_Z\right|}^2$$

(11)

The intensity vector is then given by:

$$\widehat{I_i}={\displaystyle \frac{2\times I_i}{{\left|P_W\right|}^2+\epsilon }}$$

(12)

$${\widehat{I}}_E={\displaystyle \frac{E}{E+\epsilon }}$$

(13)

where ${\widehat{I}}_i\in \left[-1,1\right]$, $i\in \left\{X,Y,Z\right\}$, and ε denotes a small positive constant.

The intensity vector is mapped to the Mel frequency scale to ensure alignment with the log-Mel features along the time–frequency axes. The computation is given by:

$$I{V}_i={\displaystyle \frac{{\displaystyle \sum \widehat{I_i}·H_b\left(k\right)}}{{\displaystyle \sum H_b\left(k\right)}+\epsilon }}$$

(14)

where $i\in \left\{X,Y,Z\right\}$, and $b=1,\dots ,128$.

Finally, the input feature F is given by:

$$F=\left[L\mathrm{og}Me{l}_m^{\left(j\right)}\left(b\right),I{V}_i\right],j=1,2,3,4.$$

(15)

The adopted feature F consists of a 4-channel log-Mel spectrogram and a 3-channel IV, enabling joint modeling of time–frequency and spatial characteristics.

3.2. Network Architecture

The overall architecture of the proposed SELD model is illustrated in Figure 3 and follows a hierarchical encoder–decoder structure. The encoder, referred to as FFMamba, consists of one convolutional block, four layers of MSFVSS modules, and three WTED-based downsampling layers. The decoder comprises two BiGRU layers followed by two fully connected layers.

The encoder processes audio features extracted from FOA recordings and encodes them into intermediate representations. The input to the model has a shape of C × T × F, where C denotes the total number of feature channels, consisting of the 4-channel log-Mel spectrogram and the 3-channel IV, T denotes the number of temporal frames, and F is the number of frequency bins. The input features $\mathbf{F}\in {ℝ}^{C\times T\times F}$ are first passed through a convolutional block for preliminary processing, extracting low-level local time–frequency features and expanding the channel dimension. The convolutional block can be expressed using the following formulation:

$$\mathbf{Z}=\mathrm{Avgpool}\left(\mathrm{GELU}\left(\mathrm{BN}\left(\mathrm{Conv}\left(\mathbf{F}\right)\right)\right)\right)$$

(16)

where Z denotes the output of the convolution block, BN denotes batch normalization, GELU is the activation function, Conv denotes a 3 × 3 convolution.

The extracted features are fed into four MSFVSS modules with a 1:2:2:1 configuration, which preserve spatial dimensions and channel size while enriching high-level spatial representations. Each MSFVSS module is followed by a WTED module that halves the spatial resolution and doubles the channel number, thereby compressing the feature maps and enhancing representational capacity. After four stages, a compact high-level semantic representation is obtained.

In the decoder, a two-layer BiGRU is employed as the core structure to capture long-term dependencies in temporal sequences. To reduce temporal dimensionality and mitigate the influence of redundant features, the input is first processed through average pooling before being fed into the two-layer BiGRU. This allows for temporal context modeling and extraction of high-level features with global time dependencies. To support the multi-task learning framework, the decoder adopts a dual-branch structure. Each branch consists of two fully connected layers that perform nonlinear mapping of the shared deep features, enhancing the model’s ability to differentiate task-specific information. At the output stage, the SED branch employs a Sigmoid activation function to ensure that the existence probability of each event class lies within the [0, 1] range, reflecting the likelihood of different sound events occurring in various directions. Meanwhile, the DoA branch uses a Tanh activation function to normalize the three-dimensional coordinate outputs within the [−1, 1] range, satisfying the output constraints of the 3D sound source localization task and representing the unit vector direction of the sound sources.

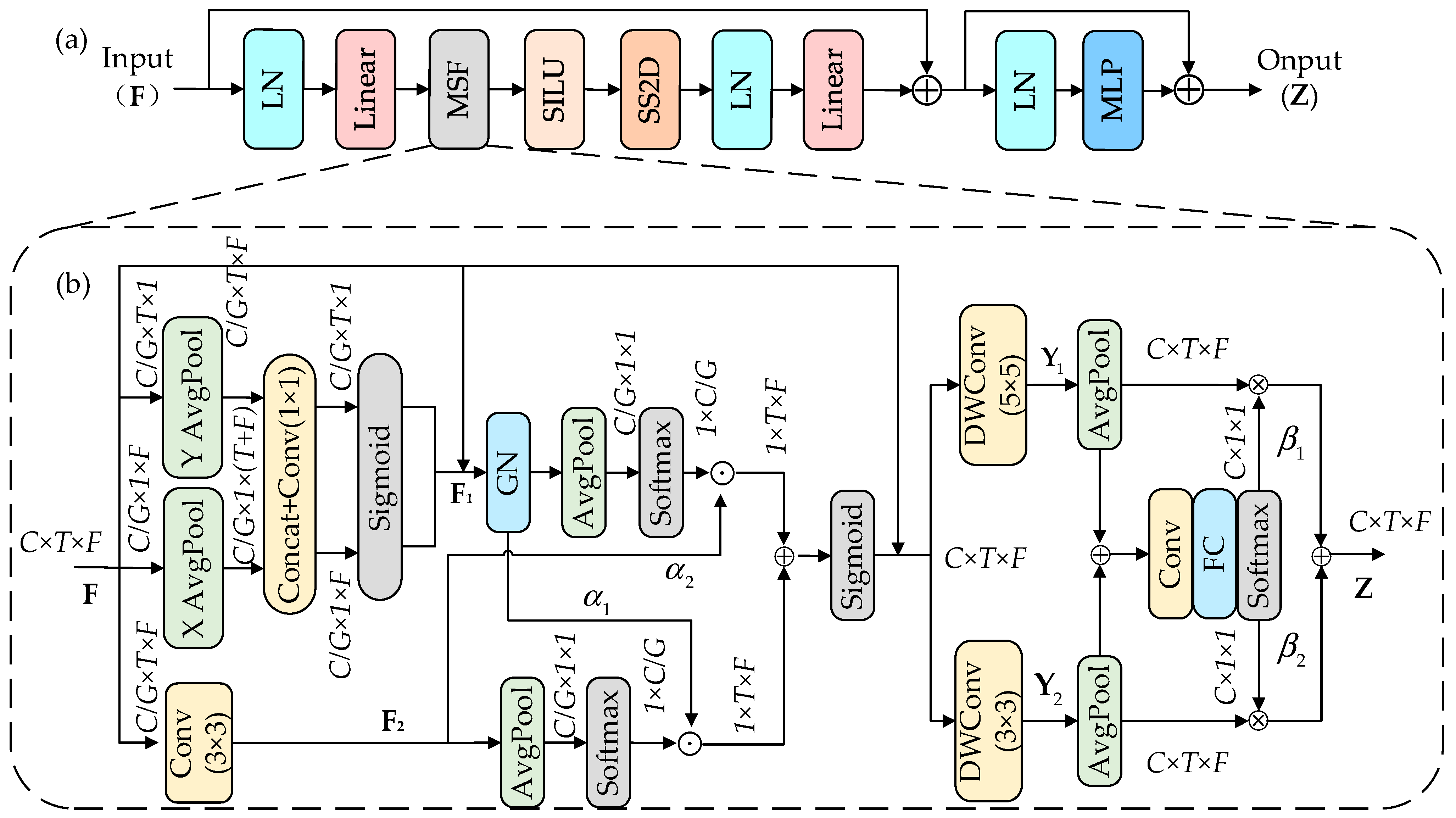
3.3. MSFVSS Module

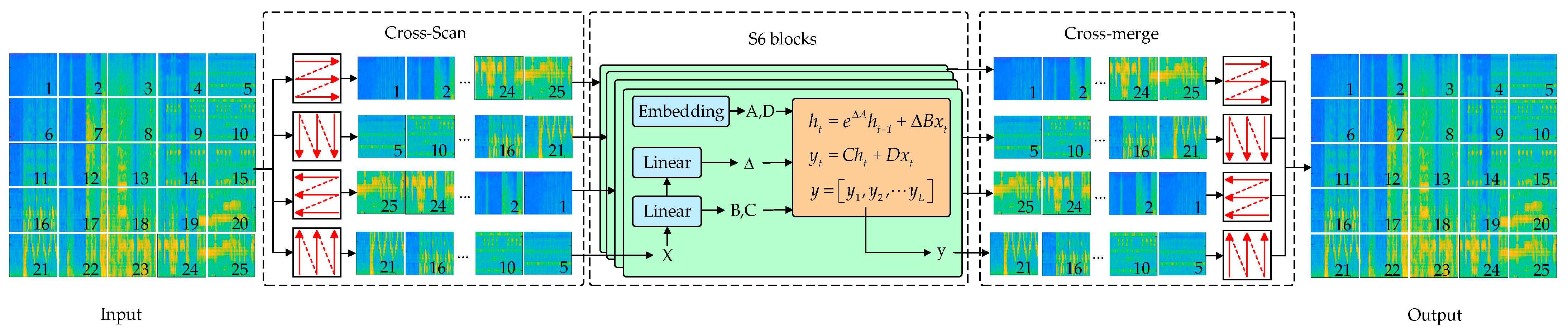
To enhance the local spatial modeling capability of the VSS module while capturing multi-scale audio features, we propose the MSFVSS module, as illustrated in Figure 4a. As shown in Figure 1, SS2D scans the input features along four different directions, encoding positional information and generating four distinct feature sequences $F_S=\left\{\left|f_0^i,f_1^i,f_2^i\dots f_k^i\right|,f_k^i\in {ℝ}^{1\times 2C},i=\left\{1,2,3,4\right\}\right\}$. The S6 module processes each of the four feature sequences independently [22] (as shown in Figure 2), modeling long-range spatial dependencies within each sequence. The outputs are then fused to form a 2D feature map as the final output. Excluding residual connections and Multilayer Perceptron (MLP), the MSFVSS module can be expressed using the following formulation:

$$\mathbf{Z}=\mathrm{Linear}\left(\mathrm{LN}\left(\mathrm{SS}2\mathrm{D}\right(\mathrm{SILU}\left(\mathrm{MSF}\right(\mathrm{Linear}\left(\mathrm{LN}\right(\mathbf{F}\left)\right)\left)\right)\left)\right)\right)$$

(17)

where linear denotes a linear layer, LN refers to layer normalization, SILU is the activation function, and SS2D represents the 2D-selective-scan module.

We propose the MSF module, as illustrated in Figure 4b. By replacing the depthwise convolution in the VSS module, the MSF module effectively mitigates the insufficient utilization of spatial distribution information during local modeling. This enhancement significantly improves the model’s sensitivity to local spatial variations.

First, the input features $\mathbf{F}\in {ℝ}^{C\times T\times F}$ are divided into G groups along the channel dimension, resulting in C/G segments with diverse semantic information. To reduce the number of parameters and improve efficiency, we set G = 32. Each group of features is processed through three parallel branches: two using 1D adaptive average pooling, and one using a 3 × 3 convolution. The 1D adaptive average pooling branches perform channel attention encoding along the temporal and frequency dimensions, respectively, capturing global information in both domains. The outputs of the two pooling branches are concatenated and fused using a 1 × 1 convolution. The result is then split into two 1D vectors, activated by a sigmoid function, and multiplied element-wise with the input feature map to produce the first attention-enhanced feature map ${\mathbf{F}}_1\in {ℝ}^{C^{\prime }\times T\times F}$. The 3 × 3 convolution branch enhances local features, yielding the second attention-aware feature map ${\mathbf{F}}_2\in {ℝ}^{C^{\prime }\times T\times F}$.

Next, the two branches ${\mathbf{F}}_1$ and ${\mathbf{F}}_2$, which encode different types of spatial information, are aggregated across spatial dimensions to enhance the directional representation of the features. Two-dimensional adaptive average pooling is applied separately to ${\mathbf{F}}_1$ and ${\mathbf{F}}_2$ to generate global context vectors along the channel dimension. These vectors are then transformed and activated using a softmax function to produce inter-channel attention weights ${\alpha }_1\in {ℝ}^{C^{\prime }\times TF}$ and ${\alpha }_2\in {ℝ}^{C^{\prime }\times TF}$. The outputs of each branch are multiplied by their corresponding weights through matrix multiplication, resulting in two spatial attention-enhanced feature maps. The two maps are then element-wise summed and passed through a nonlinear activation function to produce the final reweighted feature map $\mathbf{Z}\in {ℝ}^{C\times T\times F}$. The computation process can be formally described as follows:

$${\alpha }_1=\mathrm{Softmax}\left(\mathrm{Avgpool}\left(\mathrm{GN}\left({\mathbf{F}}_1\right)\right)\right)$$

(18)

$${\alpha }_2=\mathrm{Softmax}\left(\mathrm{Avgpool}\left({\mathbf{F}}_2\right)\right)$$

(19)

$$\mathbf{Z}=\mathrm{Sigmoid}\left({\alpha }_1\odot {\mathbf{F}}_2+{\alpha }_2\odot {\mathbf{F}}_1\right)$$

(20)

where GN denotes group normalization, $\odot$ represents matrix multiplication.

Finally, a channel attention mechanism is applied to perform weighted fusion on the feature map Z. The feature map is processed by two convolutional branches with different receptive fields to extract multi-scale feature representations, denoted as ${\mathbf{Y}}_1\in {ℝ}^{C\times T\times F}$ and ${\mathbf{Y}}_2\in {ℝ}^{C\times T\times F}$. The outputs ${\mathbf{Y}}_1$ and ${\mathbf{Y}}_2$ are then summed element-wise to obtain the combined multi-scale feature representation. Adaptive weights ${\beta }_1$ and ${\beta }_2$ for the two branches are subsequently computed. Finally, a weighted fusion of the two branches is performed using ${\beta }_1$ and ${\beta }_2$, enabling adaptive selection of information across different scales. The overall process is outlined as follows:

$${\mathbf{Y}}_1=\mathrm{DWConv}1(\mathbf{Z})$$

(21)

$${\mathbf{Y}}_2=\mathrm{DWConv}2(\mathbf{Z})$$

(22)

$$\left[{\beta }_1,{\beta }_2\right]=\mathrm{Softmax}\left(\mathrm{Conv}(\mathrm{FC}(\mathrm{Avgpool}({\mathbf{Y}}_1+{\mathbf{Y}}_1\left)\right))\right)$$

(23)

$$\mathbf{Z}={\beta }_1\otimes {\mathbf{Y}}_1+{\beta }_2\otimes {\mathbf{Y}}_2$$

(24)

where DWConv1 denotes a 3 × 3 depthwise convolution, DWConv2 represents a 5 × 5 depthwise convolution, Conv refers to a 1 × 1 convolution, and FC indicates a fully connected layer, ⊗ denotes the elemental multiplication.

3.4. WTED Module

To improve feature representation and preserve critical information during the downsampling stage, we propose a Wavelet Transform-Enhanced Downsampling (WTED) module, as illustrated in Figure 5. This module integrates a convolutional downsampling branch and a wavelet transform branch, combined with an adaptive channel-weighted fusion mechanism. It effectively merges features across different spatial scales and frequency bands, providing richer and more robust representations for subsequent layers.

The WTED module consists of two main branches: a convolutional branch and a wavelet transform branch. The convolutional branch utilizes a 2D convolution (k = 2, s = 2), followed by batch normalization, to perform spatial downsampling and extract preliminary features. The wavelet transform branch applies a Discrete Wavelet Transform [31] (DWT) to decompose the input into low-frequency components (LL) and high-frequency components, with the high-frequency details represented as horizontal (HL), vertical (LH), and diagonal (HH). The decomposition is computed as follows:

$$y_{\mathrm{LL}},y_{\mathrm{HL}},y_{\mathrm{LH}},y_{\mathrm{HH}}=\mathrm{DWT}(\mathbf{F})$$

(25)

where $\mathbf{F}\in {ℝ}^{C\times T\times F}$ is the input of the WTED module.

In this study, the db4 wavelet is chosen for its well-balanced trade-off between computational efficiency and the ability to capture local features. Compared to the Haar wavelet, db4 provides greater smoothness and a shorter filter length, allowing for more effective preservation of signal edges and fine-grained details.

To enhance spatial consistency in the wavelet branch, all frequency subbands are rescaled to the target downsampling size via linear interpolation. The low-frequency component and directional high-frequency components are then concatenated along the channel dimension. A 1 × 1 convolution block is applied to compress the features and introduce nonlinearity. The overall computation can be formulated as follows:

$$\mathbf{Y}=\mathrm{ReLU}\left(\mathrm{BN}\left(\mathrm{Conv}\left(\mathrm{Concat}\left(y_{\mathrm{LL}},y_{\mathrm{HL}},y_{\mathrm{LH}},y_{\mathrm{HH}}\right)\right)\right)\right)$$

(26)

To enhance the fusion of features obtained from the two downsampling branches, the WTED module combines channel-weighted summation. The computation is defined as follows:

$$\mathbf{Z}={\lambda }_1\mathbf{X}+{\lambda }_2\mathbf{Y}$$

(27)

where $\mathbf{X}\in {ℝ}^{C\times T\times F}$ denotes the feature map of the convolutional branch, $\mathbf{Y}\in {ℝ}^{C\times T\times F}$ denotes the feature map of the DWT branch, with ${\lambda }_1$ and ${\lambda }_1$ denoting the corresponding channel-wise weighting coefficients and satisfying ${\lambda }_1+{\lambda }_2=1$.

This fusion strategy introduces learnable channel-wise weighting parameters for each branch, enabling the model to adaptively adjust the contribution of convolutional and wavelet features based on the feature distribution of different acoustic scenes or event types. Such dynamic balancing enhances the network’s ability to model both spatial structures and multi-band frequency characteristics.

4. Experiments

4.1. Dataset

In this study, the DCASE 2021 Task 3 and DCASE 2022 Task 3 datasets were selected for model evaluation. Both datasets are officially provided by DCASE and represent the most widely recognized public benchmarks for sound event localization and detection (SELD), making them authoritative and comparable. Compared with other databases, these datasets align more closely with the research objectives in terms of task definition, format, and sound source types, allowing an effective assessment of model performance across different scenarios.

The DCASE 2021 Task 3 dataset is based on the TAU Spatial Room Impulse Response (TAU SRIR) database and the NIGENS sound event library. Multi-channel audio is generated through acoustic simulation and convolution. Specifically, clean event segments are selected from the NIGENS library and assigned class labels. These segments are then spatialized using room impulse responses from TAU SRIR, producing multi-channel audio with precise directional annotations (azimuth and elevation). Each scene contains 1 to 3 simultaneous events, with varying room reverberation and background noise to enhance diversity and realism. The dataset is provided in two formats: first-order Ambisonics (FOA) and microphone array (MIC), sampled at 24 kHz, with signal-to-noise ratios (SNR) ranging from 6 dB to 30 dB, covering 12 common indoor sound event classes (e.g., phone ringing, alarm, door knock, laughter). The dataset contains 600 recordings: 400 for training, 100 for validation, and 100 for testing, ensuring no overlap between training and test sets.

The DCASE 2022 Task 3 dataset (STARSS22) extends the 2021 dataset by including real recording scenarios. Audio was captured in office and meeting environments using high-resolution spherical microphone arrays. Accurate temporal and spatial annotations were obtained through manual labeling combined with optical tracking systems. To increase the number of training samples, the dataset also provides synthetic audio, generated by convolving publicly available event segments with real room impulse responses. The final dataset includes 121 real recordings (67 training, 54 testing; total duration 4 h 52 min) and 1200 one-minute synthetic recordings for training and evaluation. All recordings are available in FOA and MIC formats, sampled at 24 kHz, covering 13 sound event classes.

In addition, ablation experiments were conducted on the DCASE 2021 Task 3 dataset to validate the effectiveness of each model component. By comparing results on both synthetic and real recordings, the experiments comprehensively assess the model’s adaptability and robustness across different acoustic environments and event types.

4.2. Evaluation Indicators

We adopt the same evaluation metrics as those used in DCASE 2021 Task 3, including: event-based error rate (ER_20°) and F-score (F_20°) for Sound Event Detection (SED), and localization error (LE) and localization recall (LR) for Direction-of-Arrival (DoA) estimation. The threshold of 20° indicates that an SED prediction is considered correct only if the corresponding DoA estimation error is less than 20°. The SELD score is computed as follows:

$$SELD={\displaystyle \frac{\left[E{R}_{{20}^{\circ }}+\left(1-F_{{20}^{\circ }}\right)+\frac{LE}{{180}^{\circ }}+\left(1-LR\right)\right]}{4}}$$

(28)

Among these evaluation metrics, ER: Quantifies the proportion of missed detections, false alarms, and insertions in event detection, providing a measure of the system’s reliability in determining whether an acoustic event occurs. F_20°: Combines precision and recall to evaluate the overall performance of event classification, reflecting the model’s accuracy in identifying sound event categories. LE: Represents the average angular deviation between the predicted and reference directions of arrival, given that the event class is correctly detected, indicating the precision of spatial localization. LR: Denotes the percentage of active sources that are correctly localized within a predefined angular threshold (e.g., 20°), highlighting the model’s ability to both detect and approximately localize active sound sources.

In this evaluation scheme, lower ER_20° and higher F_20° values indicate better SED performance, while smaller LE and higher LR values reflect superior DoA estimation accuracy.

4.3. Experimental Configuration

All experiments were conducted on a server equipped with an NVIDIA GeForce RTX 3090 GPU. The software environment included Python 3.8 and the PyTorch deep learning framework (v2.2.1 with CUDA v11.8). The training was performed for 32 epochs using the Adam optimizer [32]. The initial learning rate was set to 3 × 10⁻⁴ and linearly decayed to 1 × 10⁻⁴ over the course of training. The batch size was set to 60. Given the limited size of the dataset, all experiments employed data augmentation techniques, including Channel Swapping (CS) [33], Random Cropping (RC) [34,35], and Frequency Shifting (FS) [36].

4.4. Ablation Experiments

To verify the effectiveness of the proposed modules in long-sequence modeling, multi-scale feature fusion, and spatial feature representation, we conducted a series of ablation studies on the DCASE 2021 Task 3 dataset. The experimental results are summarized in

Table 1. Model ablation experiments on DCASE2021 task3 dataset.

Model	ER20°	F20°/%	LE	LR/%	SELD
FFMamba	0.371	73.7	13.4°	75.7	0.237
Base	0.396	71.7	13.7°	73.4	0.255
MSFVSS	0.380	73.1	13.2°	75.9	0.240
WTED	0.385	72.6	13.4°	75.1	0.245

. The baseline model (Base) was constructed by removing both the MSF and WTED modules, replacing them with conventional deep convolution and standard convolutional downsampling structures, respectively. The results show that the baseline model performed worse across all evaluation metrics. Specifically, the ER_20° and LE increased by 0.025 and 0.3°, respectively, while the overall SELD score dropped by 0.018. In addition, F_20° and LR decreased by 2.0% and 2.3%, respectively. These findings suggest that conventional convolutional structures are limited in their ability to model spatiotemporal features in complex acoustic environments.

After introducing the MSF module to form the MSFVSS module, the model exhibited notable improvements in both SED and DoA estimation tasks. In particular, the F_20° and LR metrics improved significantly by 1.4% and 2.5%, respectively. Meanwhile, the ER_20° and LE metrics decreased by 0.016 and 0.02°, respectively. These results confirm the effectiveness of the MSF module’s multi-scale feature fusion and spatial attention mechanisms in enhancing local spatial awareness.

With the additional integration of the WTED module, the overall model performance was further improved. Although the LE metric slightly increased (from 13.2° to 13.4°), the F_20°, LR, and SELD score still outperformed those of the baseline model. The SELD score decreased from 0.255 to 0.245, indicating an overall performance improvement. This observation suggests that the WTED module enhances the preservation of critical spatial-frequency information by introducing wavelet-based frequency detail modeling.

4.5. Comparative Experiments of Different Models

First, we compared the proposed FFMamba model with several recent methods on the DCASE 2021 Task 3 dataset, as summarized in

Table 2. Comparative experiments of models on DCASE 2021 task3 dataset.

Model	ER20°	F20°/%	LE	LR/%	SELD
DCASE2021baseline	0.69	33.9	24.1°	43.9	0.54
G-SELD [37]	0.50	58.75	13.8°	59.6	0.35
AD-YOLO [38]	0.52	54.4	13.5°	64.7	0.35
FA3-Net [39]	0.51	58.2	14.7°	66.7	0.336
GLFER- Net [40]	0.40	71.1	11.7°	72.1	0.26
STFF-Net [41]	0.42	67.7	11.9°	74.0	0.26
AAC-enhanced EINV2 [42]	0.49	60.0	15.26	70.0	0.321
Base	0.396	71.7	13.7°	73.4	0.255
Ours	0.371	73.7	13.4°	75.7	0.237

. All comparison models are based on Transformer and CNN architectures. The results show that the proposed model achieves superior performance. In addition, the Base model exhibits a higher LE compared to GLFER-Net and AD-YOLO, with differences of 2.0° and 0.2°, respectively. However, the Base model still outperforms the others in overall performance, indicating that incorporating the VSS module into the SELD task can effectively enhance both event classification and localization capabilities. The proposed FFMamba model demonstrates stronger capability in capturing and integrating long-range audio dependencies and complex multi-scale features. It achieves more comprehensive spatial feature extraction, leading to improved localization and classification of diverse sound events.

On the more challenging DCASE 2022 Task 3 dataset (

Table 3. Comparative experiments of the model on the DCASE 2022Task 3 dataset.

Model	ER20°	F20°/%	LE	LR/%	SELD
DCASE2022baseline	0.71	21.0	29.3°	46.0	0.55
Resnet-Confomer [33]	0.65	33.0	23.4	58.0	0.47
LGAF-TIN [43]	0.65	31.1	22.3°	54.8	0.48
GLFER- Net [40]	0.55	46.5	20.7°	64.4	0.46
AAC-enhanced EINV2 [42]	0.54	45.0	17.20°	62.0	0.391
Ours	0.51	54.3	21.0°	68.3	0.35

), our model also demonstrates strong generalization and robustness. The FFMamba model achieved the best overall SELD score (0.35), substantially outperforming the official baseline (0.55) as well as recent models such as GLFER-Net (0.46) and AAC-enhanced EINV2 (0.391). In terms of SED, our model improved the F_20° to 54.3%, far surpassing the baseline’s 21.0%, highlighting its superior event recognition capability in complex real-world environments. In terms of DoA, our model achieved the highest LR of 68.3%. Despite a slightly higher LE compared with AAC-enhanced EINV2, the superior performance on key classification metrics such as ER and F_20° demonstrates that our model maintains a better balance between detection accuracy and reliability, which is critical for practical applications.

4.6. Visual Analysis

A visual analysis was conducted using the “fold6_room1_mix002” audio clip from the DCASE 2021 Task 3 test set, as illustrated in Figure 6. The first and second rows of the figure show the visualizations of azimuth and elevation angles for the DoA estimation task, respectively, while the third row presents the results for the SED task. In the azimuth subplot (Figure 6a,b), the predictions generated by the FFMamba model closely follow the reference trajectories over most time intervals, demonstrating strong horizontal localization accuracy. For sound sources with significant motion trajectories (e.g., the bell sound marked in red), minor tracking deviations are observed near abrupt angular transitions, as highlighted by the orange bounding box in the reference image. In the elevation subplot (Figure 6c,d), the reference trajectories often appear as step functions or constant values, indicating minimal elevation variation among most sound sources. The predicted elevation angles show smooth and continuous trends in some events, suggesting that the FFMamba model possesses temporal modeling capabilities and can effectively capture gradual changes in elevation. Although slight deviations are observed in the initial elevation values for certain events, the overall trend aligns well with the ground truth. In the SED subplot (Figure 6e,f), the model accurately identifies the activity of multiple sound sources at most time points, achieving high consistency with the reference annotations and demonstrating the model’s strong performance in sound event recognition.

5. Conclusions

This paper proposes FFMamba, a multi-scale feature fusion network for SELD. The architecture integrates Visual State Space (VSS) modeling with the strengths of multi-scale convolution, enabling effective capture of long-range temporal dynamics and preservation of local time–frequency features. By introducing two key modules—Multi-Scale Fusion Visual State Space (MSFVSS) and Wavelet Transform-Enhanced Downsampling (WTED)—the model significantly enhances its ability to capture and preserve time–frequency characteristics in audio signals. The MSF module improves local spatial feature representation by fusing multi-scale spatial features with an attention mechanism. The WTED module combines convolutional modeling for local spatial features with wavelet decomposition for multi-band frequency information, thereby improving the retention of critical spatial–spectral features. Extensive experiments on the DCASE 2021 and DCASE 2022 Task 3 datasets—including comparative and ablation studies—demonstrate the robustness and effectiveness of the proposed approach in both SED and DoA subtasks, outperforming mainstream models across multiple key metrics. Visualization results further confirm FFMamba’s accuracy in spatial angle estimation and event detection, highlighting its strong temporal modeling and localization capabilities. Overall, the proposed FFMamba model offers an effective pathway for integrating multi-scale perception with state space modeling in SELD tasks, contributing significantly to sound understanding in complex acoustic environments.

Despite its strong performance, the FFMamba model still has limitations, particularly in terms of computational overhead and the completeness of spatial modeling. Future work may focus on model lightweighting, multi-modal fusion, and enhanced elevation modeling, which are promising directions for further exploration.